A Multi-Granularity Random Mutation Genetic Algorithm for Steel Cold Rolling Scheduling Optimization
Abstract
1. Introduction
2. Problem Formulation
2.1. Basic Model of the FJSP
- (1)
- A machine can process only one job at any given time.
- (2)
- Each operation of a job can be assigned to only one machine at a time.
- (3)
- Once the processing of an operation begins, it cannot be interrupted.
- (4)
- All jobs are available for processing at time zero.
2.2. Model of the Steel Cold Rolling Scheduling Problem
2.2.1. Objective Function
2.2.2. Constraints
- (1)
- Basic ConstraintsThe cold rolling production process of steel coils involves multiple operations, multiple units, and multiple materials, which constitutes an NP-hard problem conforming to the FJSP framework. Accordingly, it is subject to the following basic time-related constraints:where Equations (3)–(7) are derived from the classical modeling framework of the FJSP and represent the fundamental constraints widely adopted in this field. Specifically, Equation (3) restricts each operation to be assigned to only one machine at any given time. Equations (4) and (5) ensure that a single machine can process only one operation at a time. Equations (6) and (7) further require that the processing intervals of any two operations on the same machine do not overlap, thereby preventing temporal conflicts.
- (2)
- Cold Rolling ConstraintsIn the steel cold rolling production line, in addition to the basic temporal constraints defined in the FJSP model, additional production-specific constraints must also be satisfied. Steel coils are required to be produced in batches, and within a production cycle, width and thickness continuity must be maintained to minimize capacity loss. Meanwhile, the total processing time of all operations assigned to a given machine must not exceed the machine’s maximum available capacity. In addition, material inventory must meet safety stock requirements, and advance production beyond demand is prohibited.where Equations (8)–(12) are constructed based on the typical process requirements of steel cold rolling production, aiming to capture the key constraints encountered in practical manufacturing [33]. Specifically, Equation (8) formulates the batching constraint in cold rolling production. Equations (9) and (10) formulate the specification transition constraints. Equation (11) specifies the machine capacity constraint. Equation (12) formulates the safety stock constraint.
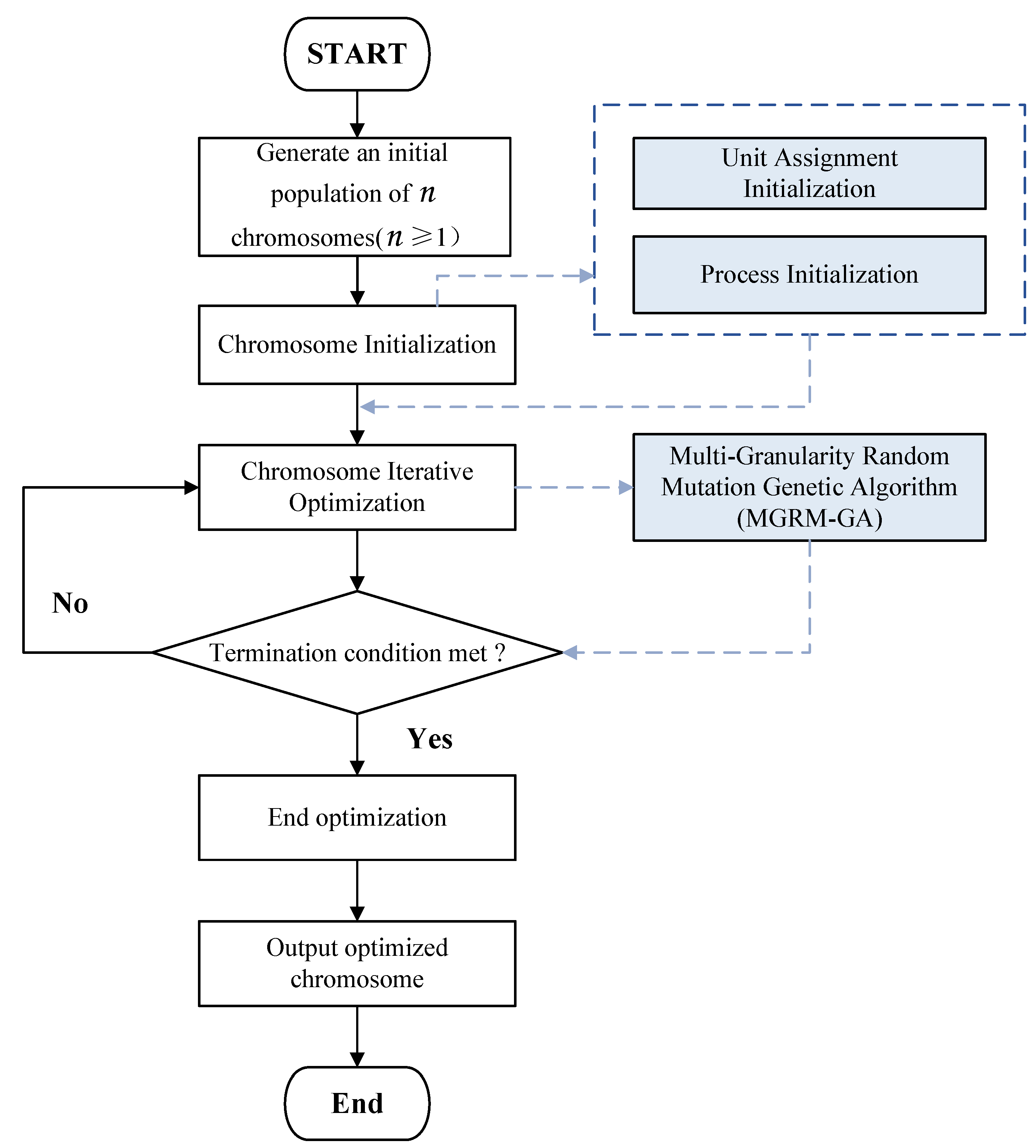
3. Methods
3.1. Heuristic Initialization of Solutions
3.2. Multi-Granularity Random Mutation Genetic Algorithm (MGRM-GA)
3.2.1. Random Single-Task Movement Within the Same Unit
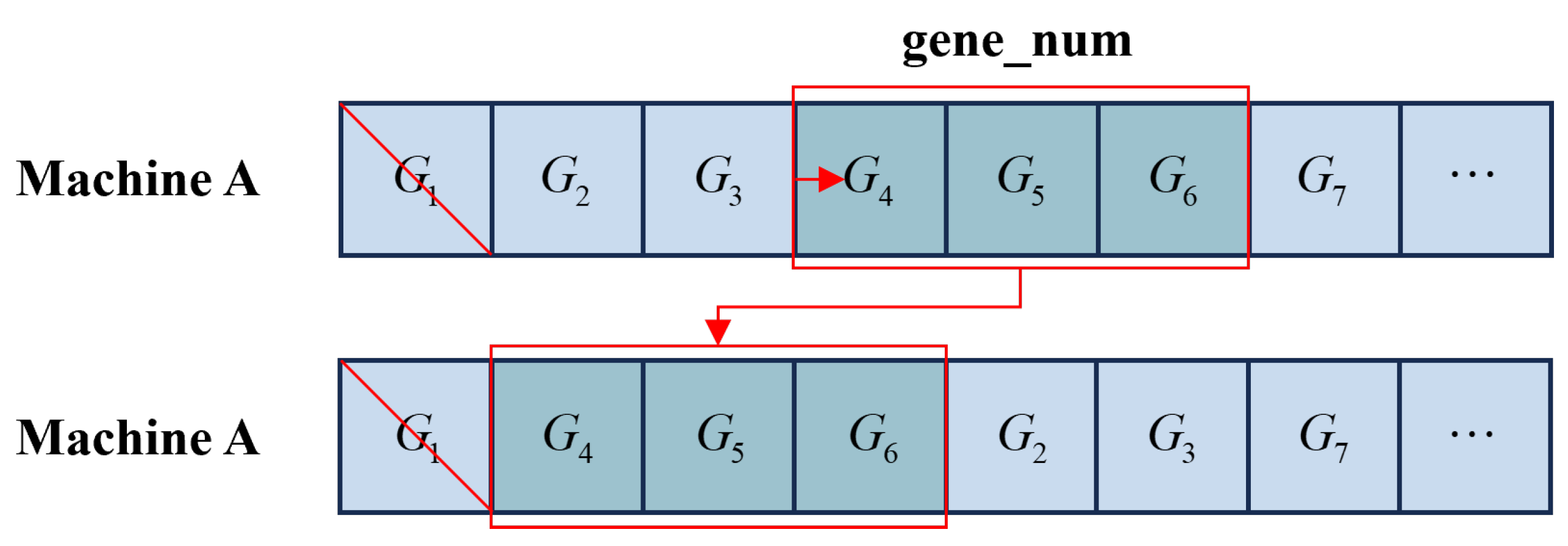
3.2.2. Random Batch-Task Movement Within the Same Unit
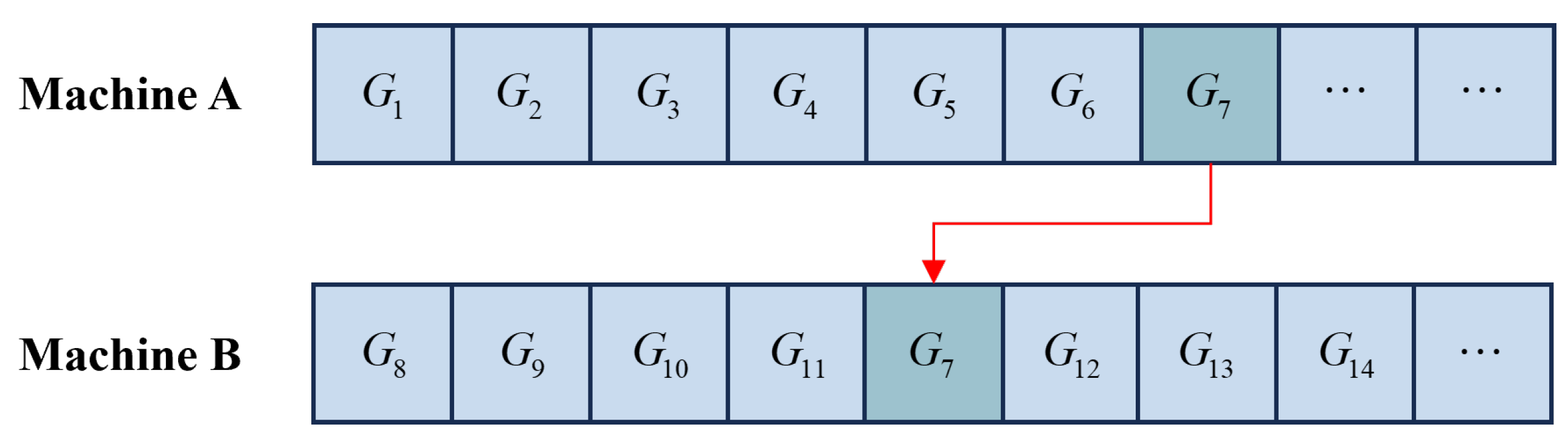
3.2.3. Random Single-Task Movement Across Different Units
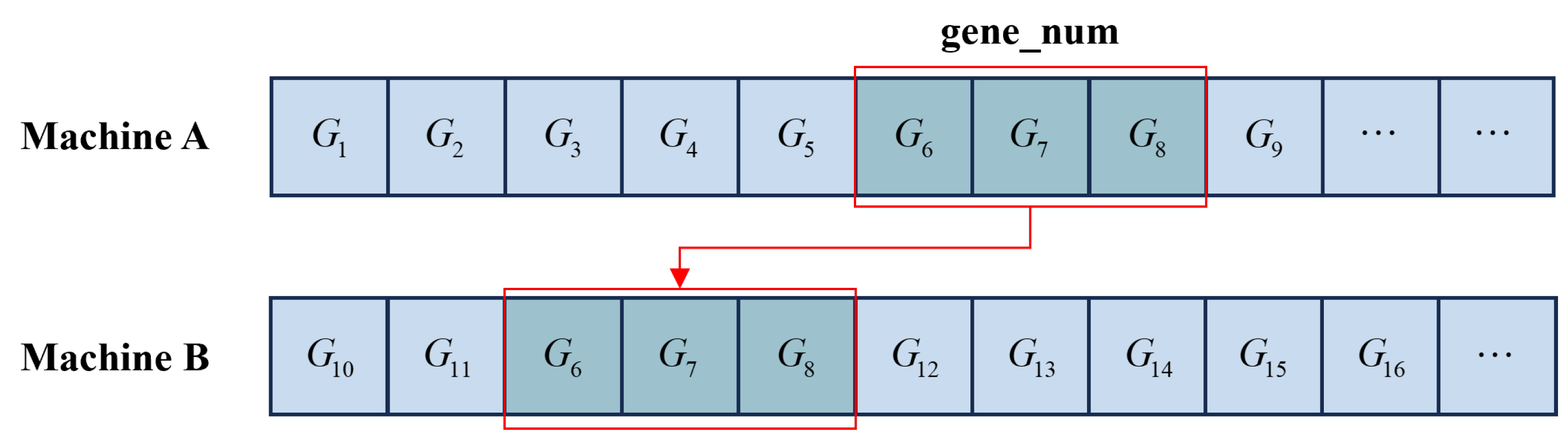
3.2.4. Random Batch-Task Movement Across Different Units
4. Experiments
4.1. Experimental Parameter Settings
4.2. Comparative Experiments
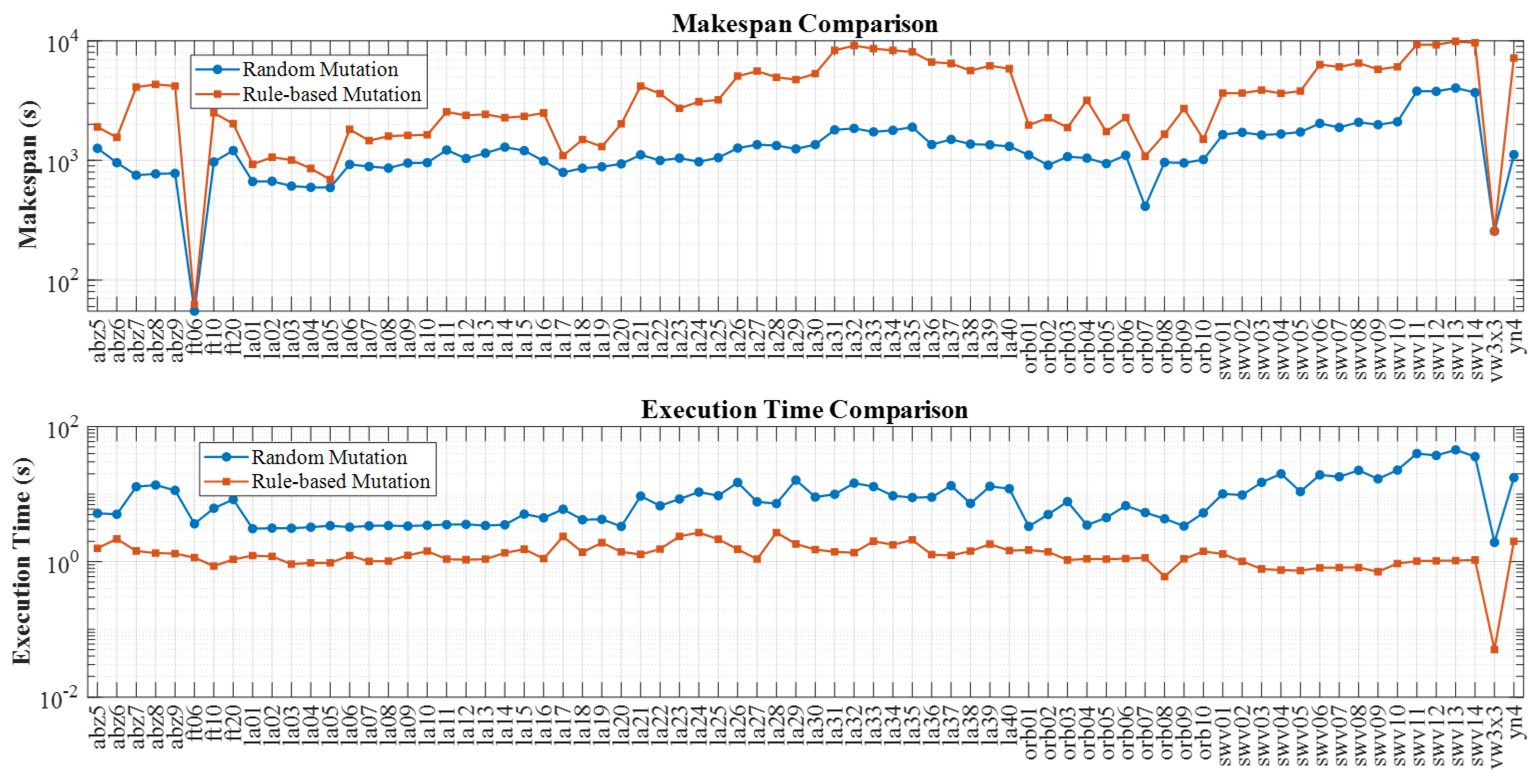
4.2.1. Comparison on Benchmark Datasets
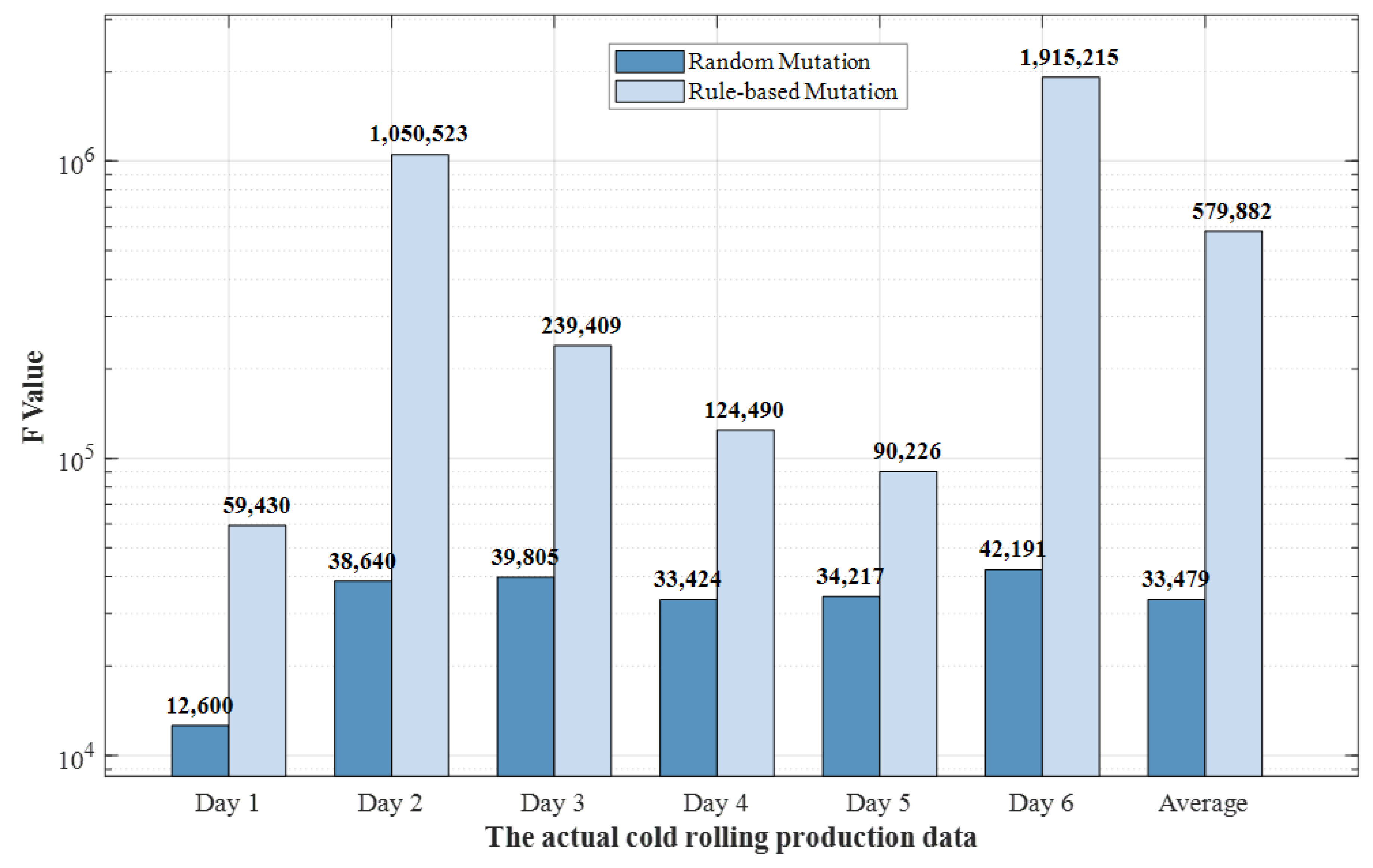
4.2.2. Comparison on Cold Rolling Production Line Data
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Parameter | Description | Parameter | Description |
| J | Set of all production orders (jobs) | Processing time of operation o on machine i (h) | |
| M | Set of all machines | Roll changing time of machine s from type r to (h) | |
| O | Set of all operations | Maximum available time of machine i (h) | |
| R | Set of all roll types | Weighting coefficients | |
| T | Set of scheduling time points | Binary variable, equals 1 if operation o is executed on machine i, and 0 otherwise | |
| Set of machines capable of executing operation o | Binary variable, equals 1 if operation o is executed before operation , and 0 otherwise | ||
| j | Index of order | Binary variable, equals 1 if roll type changes from r to , and 0 otherwise | |
| i,,k | Index of machine | Binary variable, equals 1 if a family switch occurs from operation o to , and 0 otherwise | |
| o, | Index of operation | Binary variable, equals 1 if operation o is transferred from machine i to , and 0 otherwise | |
| r, | Index of roll type | Basic processing cost of executing operation o on machine i (CNY) | |
| t | Index of time point | Roll changing cost from type r to | |
| P | Total number of production lines | h | Index of warehouse (CNY) |
| n | Total number of orders | s | Total number of warehouses |
| Start time of operation o (h) | Operation family switching configuration cost (CNY) | ||
| Completion time of order j (h) | Transfer cost of the same job across different machines (CNY) | ||
| Due date of order j | Thickness and width of coil corresponding to operation o (mm) | ||
| G | Set of specification groups | Maximum allowed thickness/width variation between consecutive operations (mm) | |
| Transition length (mm) | Minimum batch size requirement of machine i (t) | ||
| Priority weight of order j | Minimum/maximum inventory level of buffer in front of machine i (t) | ||
| Work-in-process inventory level at time t (t) | Raw material consumption of operation o on machine i | ||
| Target work-in-process inventory level | Specification switching cost coefficient | ||
| Maximum mutation protection count | Number of tasks on the preceding unit |
References
- Du, H.; Cheng, L.; Qian, Z.; Zhou, Y.; Gao, Z.; Hou, L.; Wei, Y. Study on Smelting Process Parameters of a Blast Furnace with Hydrogen-Rich Gas Injection Using Coalbed Methane. Processes 2025, 13, 1702. [Google Scholar] [CrossRef]
- He, J.; Ji, X.; Chen, Z.; Shen, L.; Gui, W. High-Definition Light and Shadow Reconstruction of Blast Furnace Burden Surface Images Based on a Spatiotemporal Multi-Domain Guided Generative Model. IEEE Trans. Autom. Sci. Eng. 2025, 22, 18243–18254. [Google Scholar] [CrossRef]
- Ma, S.H.; Wen, Z.G.; Chen, J.N.; Wen, Z.C. Mode of circular economy in China’s iron and steel industry: A case study in Wu’an city. J. Clean. Prod. 2014, 64, 505–512. [Google Scholar] [CrossRef]
- Li, K.; Tian, H. A multiobjective variable neighborhood search with learning and swarm for permutation flowshop scheduling with sequence-dependent setup times. Processes 2022, 10, 1786. [Google Scholar] [CrossRef]
- Sun, W.; Wang, Q.; Zhou, Y.; Wu, J. Material and energy flows of the iron and steel industry: Status quo, challenges and perspectives. Appl. Energy 2020, 268, 114946. [Google Scholar] [CrossRef]
- Jiang, S.L.; He, L.; Cao, L.; Sun, L.; Peng, G. A learning-enhanced ant colony optimization algorithm for integrated planning and scheduling in hot rolling production lines under uncertainty. Swarm Evol. Comput. 2025, 93, 101851. [Google Scholar] [CrossRef]
- Jacobs, L.; Rèche, D.; Bán, A.; Colla, V.; Toscanelli, O.; Raulf, M.; Schlupp, M.; Smeulders, B.; Cook, M.; Filemon, W. Development of Oil-Free Lubricants for Cold Rolling of Low-Carbon Steel. Processes 2025, 13, 1234. [Google Scholar] [CrossRef]
- Wang, Y.; Li, C.; Jin, X.; Xiang, Y.; Li, X. Multi-objective optimization of rolling schedule for tandem cold strip rolling based on NSGA-II. J. Manuf. Process. 2020, 60, 257–267. [Google Scholar] [CrossRef]
- Babajamali, Z.; Aghadavoudi, F.; Farhatnia, F.; Eftekhari, S.A.; Toghraie, D. Pareto multi-objective optimization of tandem cold rolling settings for reductions and inter stand tensions using NSGA-II. ISA Trans. 2022, 130, 399–408. [Google Scholar] [CrossRef]
- Peng, G.; Cheng, Y.; Zhang, Y.; Shao, J.; Wang, H.; Shen, W. Industrial big data-driven mechanical performance prediction for hot-rolling steel using lower upper bound estimation method. J. Manuf. Syst. 2022, 65, 104–114. [Google Scholar] [CrossRef]
- Yang, H.; Du, Y.; Li, Y.; Qian, W.; Hu, B. A Heuristic Mutation Based Genetic Algorithm for Fast Parallel Scheduling of Steel Cold Rolling. Chin. J. Mech. Eng. 2025, 38, 100. [Google Scholar] [CrossRef]
- Jiang, M.; Yu, H.; Chen, J. Improved self-learning genetic algorithm for solving flexible job shop scheduling. Mathematics 2023, 11, 4700. [Google Scholar] [CrossRef]
- Li, J.; Li, H.; He, P.; Xu, L.; He, K.; Liu, S. Flexible job shop scheduling optimization for green manufacturing based on improved multi-objective wolf pack algorithm. Appl. Sci. 2023, 13, 8535. [Google Scholar] [CrossRef]
- Gao, K.; Cao, Z.; Zhang, L.; Chen, Z.; Han, Y.; Pan, Q. A review on swarm intelligence and evolutionary algorithms for solving flexible job shop scheduling problems. IEEE/CAA J. Autom. Sin. 2019, 6, 904–916. [Google Scholar]
- Shi, J.; Liu, W.; Yang, J. An enhanced multi-objective evolutionary algorithm with reinforcement learning for energy-efficient scheduling in the flexible job shop. Processes 2024, 12, 1976. [Google Scholar]
- Nouiri, M.; Bekrar, A.; Jemai, A.; Niar, S.; Ammari, A.C. An effective and distributed particle swarm optimization algorithm for flexible job-shop scheduling problem. J. Intell. Manuf. 2018, 29, 603–615. [Google Scholar] [CrossRef]
- Jiang, T.; Zhang, C. Application of grey wolf optimization for solving combinatorial problems: Job shop and flexible job shop scheduling cases. IEEE Access 2018, 6, 26231–26240. [Google Scholar] [CrossRef]
- Pan, Z.; Wang, L.; Zheng, J.; Chen, J.F.; Wang, X. A learning-based multipopulation evolutionary optimization for flexible job shop scheduling problem with finite transportation resources. IEEE Trans. Evol. Comput. 2022, 27, 1590–1603. [Google Scholar] [CrossRef]
- Luan, F.; Cai, Z.; Wu, S.; Liu, S.Q.; He, Y. Optimizing the low-carbon flexible job shop scheduling problem with discrete whale optimization algorithm. Mathematics 2019, 7, 688. [Google Scholar] [CrossRef]
- Li, X.; Gao, L. An effective hybrid genetic algorithm and tabu search for flexible job shop scheduling problem. Int. J. Prod. Econ. 2016, 174, 93–110. [Google Scholar] [CrossRef]
- Ishikawa, S.; Kubota, R.; Horio, K. Effective hierarchical optimization by a hierarchical multi-space competitive genetic algorithm for the flexible job-shop scheduling problem. Expert Syst. Appl. 2015, 42, 9434–9440. [Google Scholar] [CrossRef]
- Gao, K.Z.; Suganthan, P.N.; Pan, Q.K.; Chua, T.J.; Chong, C.S.; Cai, T.X. An improved artificial bee colony algorithm for flexible job-shop scheduling problem with fuzzy processing time. Expert Syst. Appl. 2016, 65, 52–67. [Google Scholar] [CrossRef]
- Li, T.; Meng, Y.; Tang, L. Scheduling of continuous annealing with a multi-objective differential evolution algorithm based on deep reinforcement learning. IEEE Trans. Autom. Sci. Eng. 2023, 21, 1767–1780. [Google Scholar] [CrossRef]
- Zhao, S.; Yang, Y.; Guo, Q.; Tang, L. A differential evolution algorithm with double-mode crossover for supply chain scheduling in cold rolling. In Proceedings of the 2016 IEEE Congress on Evolutionary Computation (CEC), Vancouver, BC, Canada, 24–29 July 2016; pp. 1062–1069. [Google Scholar]
- Zhao, S.; Yang, Y. Differential evolution algorithm for solving coil scheduling problem in parallel continuous annealing lines. In Proceedings of the 2016 Chinese Control and Decision Conference (CCDC), Yinchuan, China, 28–30 May 2016; pp. 3417–3422. [Google Scholar]
- Wang, C.; Chen, J.; Xu, B.; Liu, S. A Discrete Improved Gray Wolf Optimization Algorithm for Dynamic Distributed Flexible Job Shop Scheduling Considering Random Job Arrivals and Machine Breakdowns. Processes 2025, 13, 1987. [Google Scholar] [CrossRef]
- Song, L.; Li, Y.; Xu, J. Dynamic job-shop scheduling based on transformer and deep reinforcement learning. Processes 2023, 11, 3434. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, D.; Zhang, M.; Yang, M.; Liang, C. Quantum particle swarm optimization with chaotic encoding schemes for flexible job-shop scheduling problem. Swarm Evol. Comput. 2025, 93, 101836. [Google Scholar] [CrossRef]
- Sun, L.; Lin, L.; Gen, M.; Li, H. A hybrid cooperative coevolution algorithm for fuzzy flexible job shop scheduling. IEEE Trans. Fuzzy Syst. 2019, 27, 1008–1022. [Google Scholar] [CrossRef]
- Wan, L.; Fu, L.; Li, C.; Li, K. An effective multi-agent-based graph reinforcement learning method for solving flexible job shop scheduling problem. Eng. Appl. Artif. Intell. 2025, 139, 109557. [Google Scholar] [CrossRef]
- Gao, K.Z.; Suganthan, P.N.; Pan, Q.K.; Chua, T.J.; Cai, T.X.; Chong, C.S. Discrete harmony search algorithm for flexible job shop scheduling problem with multiple objectives. J. Intell. Manuf. 2016, 27, 363–374. [Google Scholar] [CrossRef]
- Zhao, L.; Cheng, W.; Meng, L.; Zhang, C.; Ren, Y.; Zhang, B.; Duan, P. MILP modeling and optimization of flexible job shop scheduling problem with preventive maintenance. Comput. Ind. Eng. 2025, 201, 110861. [Google Scholar] [CrossRef]
- Ayuba, E.O.; Bolu, C.A.; John, T.M.; Abioye, A.A. Dataset showing steel cold rolling process parameters for a 6-high cold rolling mill in Nigeria. Data Brief 2018, 18, 891–901. [Google Scholar] [CrossRef] [PubMed]




| Physical Attributes | Value Range | Process Flexibility | Allowable Deviation |
|---|---|---|---|
| Width (mm) | 730, 1100 | Width (mm) | <100 |
| Thickness (mm) | 0.14, 0.30 | Thickness (mm) | <0.15 |
| Temperature (°C) | 730, 1100 | Temperature (°C) | <40 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, H.; Ji, X.; Sun, H.; Li, Y.; Qian, W. A Multi-Granularity Random Mutation Genetic Algorithm for Steel Cold Rolling Scheduling Optimization. Processes 2025, 13, 3311. https://doi.org/10.3390/pr13103311
Yang H, Ji X, Sun H, Li Y, Qian W. A Multi-Granularity Random Mutation Genetic Algorithm for Steel Cold Rolling Scheduling Optimization. Processes. 2025; 13(10):3311. https://doi.org/10.3390/pr13103311
Chicago/Turabian StyleYang, Hairong, Xiao Ji, Haiyan Sun, Yonggang Li, and Weidong Qian. 2025. "A Multi-Granularity Random Mutation Genetic Algorithm for Steel Cold Rolling Scheduling Optimization" Processes 13, no. 10: 3311. https://doi.org/10.3390/pr13103311
APA StyleYang, H., Ji, X., Sun, H., Li, Y., & Qian, W. (2025). A Multi-Granularity Random Mutation Genetic Algorithm for Steel Cold Rolling Scheduling Optimization. Processes, 13(10), 3311. https://doi.org/10.3390/pr13103311







