Abstract
A significant contradiction exists between the demand for standardized processes and the need for precise process parameter design in the rapid design of superplastic forming (SPF). To address this, an SPF process parameter design method integrating a knowledge graph and artificial intelligence is proposed. Firstly, based on process data analysis, the entity labels, relationship categories, and attributes are determined. On this basis, the knowledge graph for the SPF process is constructed, comprising the pattern layer and the data layer, which provides structured knowledge support for process generation. Secondly, the process parameter prediction model based on small samples and an improved back propagation (BP) neural network is constructed, with model convergence ensured through an adaptive maximum iteration strategy. Experimental results show that the improved BP model significantly outperforms support vector regression (SVR), random forest (RF), extreme gradient boosting (XGBoost), and standard BP models in prediction accuracy. Compared to the standard BP model, the improved model reduces the mean squared error (MSE), mean absolute error (MAE), and root mean squared error (RMSE) by 82.1% (to 0.0005), 46% (to 0.0188), and 57.1% (to 0.0229), respectively. Finally, the effectiveness, feasibility, and superiority of the method in the SPF process parameter design are verified by taking typical hemispherical parts as an example.
1. Introduction
Superplastic forming (SPF), as a special process method of thermoforming, is an advanced forming technology that utilizes the superplastic large deformation capability of materials under specific temperature and strain rate conditions to manufacture thin-walled complex components (Li et al. [1]). At present, the superplastic forming process has become a key technology in aerospace, new energy vehicles, and other fields due to its unique advantages in high-precision thin-walled complex components (Williams et al. [2]; Yu et al. [3]). Its research hotspots are mainly focused on the following four aspects: first, the development of new superplastic materials to meet the diversified needs for material properties in different fields (Lakshmanan et al. [4]; Demirel et al. [5]; Akula et al. [6]; Dehkordi et al. [7]). Second, the optimization of the superplastic forming process through numerical simulation and precise control of process parameters to produce high-quality molded parts. Third, the rapid generation of an appropriate superplastic forming process scheme according to the design characteristics, such as part structure, through artificial intelligence, machine learning, and other technological means. Fourth, the study of the integration of superplastic forming, diffusion bonding, additive manufacturing, and other technologies (Chandrappa et al. [8]). With the growing demand for complex lightweight components in fields such as aerospace and new energy vehicles, efficiently and reliably designing optimal superplastic forming process solutions has become the core bottleneck constraining the broader application of this technology. Therefore, this paper aims to overcome the efficiency limitations of traditional process design through artificial intelligence methods, enabling intelligent and rapid design of superplastic forming processes.
In the research field of superplastic forming process design, the traditional approach is to use the step-by-step trial-and-error strategy that combines empirical formulas and finite element simulations. Using the finite element method, (Jun et al. [9] and Alavi et al. [10]) investigated the effects of different process parameters on the final part thickness in a novel hybrid forming process for Ti-6Al-4V. (Giuliano et al. [11]) employed finite element modeling to determine precise pressure–time loading curves. Using AZ31 magnesium alloy as the experimental material, the numerical analysis results for hemispherical shell thickness exhibited a maximum deviation of less than 10% from experimental findings. However, because superplastic forming has the characteristics of high dimensionality and mutual coupling of process parameters, traditional process design methods are not only inefficient, costly for physical experiments and simulations, but also have limited ability to process a large amount of process data. As a result, they cannot fully mine the hidden rules behind the data, and it is difficult to achieve efficient optimization and innovation of the process. In contrast, AI-based design methods for superplastic forming processes demonstrate tremendous potential. With the help of artificial intelligence methods such as machine learning and deep learning, a large amount of process data can be processed quickly, complex patterns hidden within these datasets can be uncovered, and an accurate model of the mapping relationship between product design indicators and process parameters can be established. This approach reduces reliance on individual experience and provides a possibility for the intelligent generation of superplastic forming processes. Therefore, applying artificial intelligence methods to the field of superplastic forming process design—by constructing high-precision process prediction models to replace traditional trial-and-error strategies based on empirical knowledge and finite element simulations—has become an inevitable trend. To address this need, this paper aims to develop an AI-based process generation framework for superplastic forming.
For the process generation method based on artificial intelligence, many domestic and foreign scholars have carried out in-depth research. Research scholars combine knowledge graphs with certain reasoning algorithms to generate new process solutions, such as matching algorithms, machine learning, and deep learning (Xiao et al. [12]). In the literature (Peng et al. [13]; Li [14]; Liu et al. [15]), the researchers constructed the process knowledge graph by combining top–down and bottom–up methods. On this basis, combined with the similarity algorithm, a process route was recommended. Through validation, the feasibility of the model was proved, and the efficiency of the process design was effectively improved. However, the difference lies in the different research objects. (Peng et al. [13]) took the part as the research object, and realized the recommendation of process routes by calculating the similarity between part attributes and feature topological relations. (Li [14]) took the product as the research object, and realized the recommendation of process routes by calculating the similarity between the labels of the target product and those of similar products. (Liu et al. [15]) took the precision transmission part as the research object, and realized the recommendation of process routes by calculating the similarity between the product process units and process route structure. (Su et al. [16]) developed an automatic framework for building the knowledge graph of machining products and proposed an RGAT-PRotatE method for updating the knowledge periodically.
(Wang et al. [17]) proposed a deep-learning-based method for constructing a process knowledge graph and reusing the process. The method realizes the construction of a process knowledge graph by constructing the pattern layer and the data layer. Secondly, the process knowledge inference model based on a graph neural network deep-learning algorithm is constructed. Through experimental verification, the accuracy of process recommendation reaches over 70%, which proves the effectiveness and feasibility of the method in the automatic construction of a knowledge graph and process reuse (Wang et al. [17]). In the literature (Shen et al. [18]; Wu et al. [19]; Huang [20]; Kesri et al. [21]), researchers have studied the recommendation methods based on knowledge graph technology and graph neural network algorithms, which were used to solve the problem of ignoring the overall information in the data mining process in the existing methods. (Li et al. [22]) proposed a method for part machining process design based on a knowledge graph and deep learning. Firstly, the process knowledge graph based on features, parts, feature work-step schemes, and part processes was constructed. Secondly, the part-to-part process mapping model based on BiLSTM + Attention, the part process sequence generation model based on Seq2Seq+Attention, and the part process decision model based on the fusion probability of the feature step scheme and the part process scheme were constructed, respectively. Finally, the effectiveness and feasibility of the method were verified by taking the pin shaft parts as an example (Li et al. [22]). (Devireddy et al. [23]) proposed a neural network-based process recommendation method for providing manufacturing process solutions for new components. (Ming et al. [24]; Hussong et al. [25]) proposed a neural network-based process recommendation method optimized by genetic algorithms. However, their objectives differ: the former addresses the optimal solution for tolerance allocation and process selection, while the latter uses the part’s 3D model as its dataset. Aiming at the problem of insufficient samples, (Ying et al. [26]) proposed a process generation method based on small-sample knowledge learning. The method realizes sample enhancement by studying the geometric model enhancement analysis technology and process knowledge incremental learning technology, and establishes a three-dimensional digital process design method based on artificial intelligence by studying the process analysis technology of three-dimensional CAD models. The research result significantly improves the efficiency of the complex part process design (Ying et al. [26]). (Chengwei et al. [27]; Huang [28]) took the ship plate surface forming as the research object, constructed the prediction model based on the improved gray wolf algorithm to optimize the SVM. The user can automatically determine the processing trajectory and processing parameters of the original steel plate based on the input of the target ship plate information, which initially meet the requirements of automatic processing of the ship plate surface. The ship plate processing has achieved the expected effect. (Zhang et al. [29]; Wang et al. [30]) proposed and optimized a novel four-stage drilling process method. Based on machine-learning algorithms, they developed a predictive model for femtosecond LTD technology, which enabled the rapid and successful design of optimized solutions across a wide range of process parameters.
By analyzing the above research, it is found that for the research of process generation method based on artificial intelligence, researchers mainly carry out research on process route recommendation based on similarity and deep-learning algorithms, such as graph neural network based on constructing knowledge graph, but there are some limitations in the existing research. On the one hand, they primarily focus on process route content without incorporating key process parameter values for each process. On the other hand, relying solely on similarity metrics or deep learning for parameter recommendation may result in substantial deviations from actual requirements, as highly similar products do not always guarantee suitable parameter matches. This challenge is particularly relevant in superplastic forming, where standardized processes demand precise parameter design.
Through the investigation, it is found that, firstly, the core process of superplastic forming for different products follows the standardized process of heating, feeding, mold closing, reverse inflatable forming, forward inflatable forming, cooling, and unloading. Although the process is universal, the key process parameters of each process need to be precisely designed for different part structures and material properties. Secondly, because the SPF involves high temperature and precise air pressure control, the cost of a single experiment is high, the cycle time is long, and the sample size of the public database is seriously insufficient. Thirdly, compared with traditional knowledge storage and representation, the graph structure can structurally organize concepts, entities, and their relationships, and has efficient retrieval capability (Bruendl et al. [31]). Fourthly, compared with the regression algorithms such as SVR, RF, XGBoost, etc., the SVR, RF, and XGBoost are single-output models, while the BP neural network is a multi-output model, which has stronger nonlinear mapping ability and can more accurately fit the complex relationship between the process parameters. At the same time, it has a greater advantage in processing high-dimensional data. Compared with CNN, CNN is more suitable for processing images and time series data (Gu et al. [32]; Wang et al. [33]; Wang et al. [34]; Alzubaidi et al. [35]). Compared with LSTM, LSTM is more suitable for processing time series data (Malashin et al. [36]; Malhotra et al. [37]). BP neural network has the defects of slow convergence speed and being prone to falling into a local extremum. In existing studies, researchers mostly use methods such as adding momentum, global optimization, and adaptive learning rate to improve these defects, while ignoring the fact that the fixed maximum number of iterations affects the training results (Yan [38]; Kaur et al. [39]). Specifically, if the maximum number of iterations is too small, it leads to stopping the training before reaching the best point; if the maximum number of iterations is too large, it leads to prolonging the training time.
Therefore, this paper proposes a SPF process parameter precision design method based on a knowledge graph and artificial intelligence. In this method, the knowledge graph of the SPF process is constructed through the combination of top–down and bottom–up approaches. On this basis, a process parameter prediction model based on small samples and an improved BP neural network is constructed to realize the intelligent design of key process parameters for the target part. Finally, taking the typical hemispherical part as an example, the proposed algorithm is compared with the standard BP neural network, SVR, RF, and XGBoost to verify the effectiveness, feasibility, and superiority of the method in SPF process parameter design.
2. Design and Construction Method of a Knowledge Graph for the Superplastic Forming Process
2.1. Construction Method of a Knowledge Graph
The concept of a knowledge graph was first proposed by Google in 2012. Knowledge graph is used as the core foundation for building the next generation of intelligent search engines (Singhal [40]). In essence, a knowledge graph is a semantic network that describes entities and their relationships in the objective world in the form of triples. Among them, the key elements constituting the triples contain entity 1, relationship, entity 2, attributes, attribute values, etc. (Li [41]; Liu et al. [42]). Compared with traditional data storage tools and knowledge representation methods, the knowledge graph has the advantages of faster data retrieval, wider and deeper data retrieval, stronger reasoning ability, and more convenient human–computer interaction.
The construction of a knowledge graph mainly includes two approaches: top–down and bottom–up. Among them, the top–down refers to first defining the relationships between entities and ontologies, and then adding the corresponding entity data into it. This method requires using some existing structured knowledge bases as its foundation. The bottom–up refers to extracting entities from open data sources, selecting the ones with higher credibility to be added to the knowledge base, and then constructing the ontology layer.
In this paper, a combination of the top–down and bottom–up methods is used to construct the superplastic forming process knowledge graph. Firstly, analyze the superplastic forming historical process data. On this basis, determine the entity categories, relationship categories, and attributes of the entities, etc., and carry out the ontology construction to complete the construction of the pattern layer. Secondly, add the organized superplastic forming process data to the knowledge base to complete the construction of the data layer. Finally, associate the pattern layer with the data layer and import them into the Neo4j graph database to complete the construction of the knowledge graph. The construction process is shown in Figure 1.
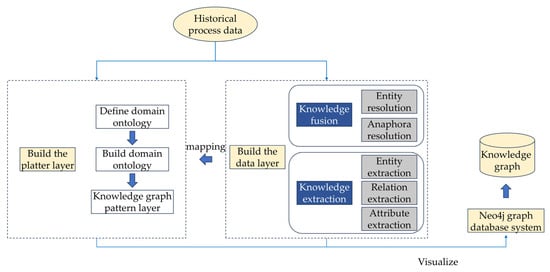
Figure 1.
Flowchart of knowledge graph construction.
2.2. Design and Construction Method of Knowledge Graph for Superplastic Forming Process
Taking the 800T superplastic forming equipment (Beijing, China) as the research object, the 800T superplastic forming equipment mainly consists of a heating system, a forming system, a control system, and auxiliary equipment, among others. Its process mainly includes: heating, feeding, mold closing, reverse inflatable molding, forward inflatable molding, cooling, and unloading, as shown in Figure 2.
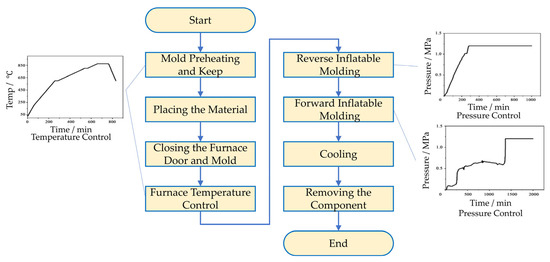
Figure 2.
Superplastic forming process.
By analyzing the superplastic forming process, the key process parameters affecting the quality of parts in each process are identified, and the historical process data are organized into a structured data form to provide data support for the construction of the knowledge graph. Among them, the key parameters for heating process include the chamber temperature and holding time; the key parameters for mold closing process include the lowering speed and blank holder force; the key parameters for reverse inflatable molding process include the gas loading pressure and holding time; the key parameters for forward inflatable molding process include the gas loading pressure and holding time; and the key parameters for cooling process include the chamber temperature. These parameters collectively determine the evolution of the material’s microstructure and directly influence key quality indicators of the final component, such as wall thickness uniformity, geometric characteristics, and mechanical properties. Specifically, the forming temperature directly affects the material’s flow stress and microstructural evolution. Excessively low temperature can lead to increased flow stress and insufficient material ductility, potentially resulting in incomplete filling. Conversely, excessively high temperature may cause surface oxidation, degrading the mechanical properties of the component (Akula et al. [6]). The gas loading pressure is closely related to the material deformation process. Inappropriate pressure level can lead to localized stress concentration, resulting in uneven wall thickness or even fracture.
Based on the analysis of historical process data, entity labels, relationship categories, and attributes are determined to construct the knowledge graph pattern layer. Among them, part name, part number, process, and parameter are identified as entity labels; include_part, include_process, and include_parameter are identified as relationship categories. Among them, the entity under the part number label has the following attributes: part name, part size, plate material, plate size, mold material, and gas type; the entity under the parameter label has the following attribute: parameter value. In addition, entities under all labels and relationships under all relationship categories have the following attributes: id and name.
Using Python 3.9.21 (Python Software Foundation, Wilmington, DE, USA), the structured historical process data and the knowledge graph pattern layer are mapped to complete the construction of the knowledge graph, which is integrated with Neo4j Desktop 1.4.13(Neo4j, Inc., San Mateo, CA, USA). In Neo4j, the knowledge graph of the superplastic forming process for parts is visually displayed, which provides data support for the superplastic forming process parameter generation method.
3. Superplastic Forming Process Parameter Design Method Based on Small Samples and an Improved BP Neural Network
3.1. Basic Principles of an Adaptive Iteration BP Neural Network
The concept of a BP (back propagation) neural network was first proposed by scientists led by Rumelhart and McClelland in 1986. It is a multilayer forward feedback neural network formed by forward propagation of data signals and back propagation of error signals, which has strong adaptive learning ability (Wang et al. [43]; Wen et al. [44]; Wen [45]). The structure of the BP neural network is shown in Figure 3. Among them, , , , represent the input values of the input layer; , , , represent the input values of the hidden layer; and , , , represent the output values of the hidden layer. , , , represent the input values of the output layer; , , , represent the output values of the output layer; represents the weights between the input layer and the hidden layer; and represents the weights between the hidden layer and the output layer.
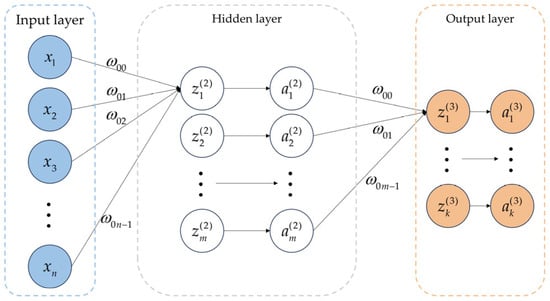
Figure 3.
BP neural network structure.
The basic flow of the adaptive iteration BP neural network algorithm is as follows, and the flowchart of the algorithm is shown in Figure 4.
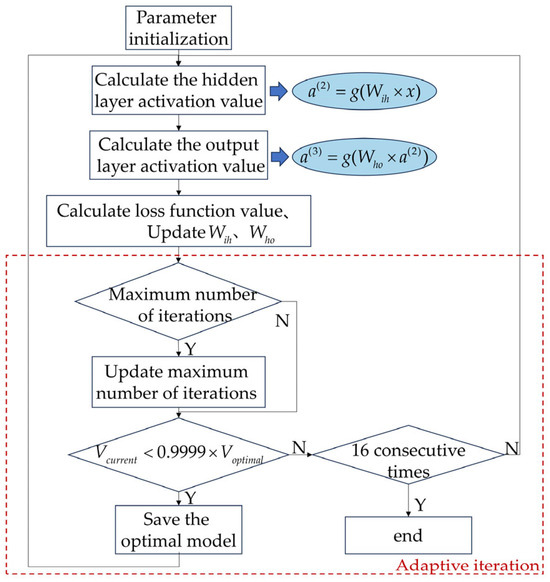
Figure 4.
The flowchart of the adaptive iteration BP neural network algorithm.
- (1)
- Parameter Initialization
We initialize the parameters such as the number of input layer nodes, the number of hidden layer nodes, the number of output layer nodes, the learning rate, and the iteration count. Among them, the number of input layer nodes is determined by the number of influencing factor indicators, the number of output layer nodes is determined by the number of target indicators, and the number of hidden layer nodes is usually determined by the combination of empirical formulas and trial-and-error methods. The empirical formula is as follows:
In Equation (1), represents the number of hidden layer nodes, represents the number of input layer nodes, represents the number of output layer nodes, and represents a constant with values ranging from 1 to 10.
Meanwhile, the activation function, loss function, and optimizer are defined. Among them, the commonly used activation functions include the Sigmoid function and the ReLU function, the commonly used loss functions include the MSELoss and the L1Loss function, and the commonly used optimizer is the Adam optimizer.
- (2)
- Forward Propagation
The input values of the hidden layer are calculated using Equation (2).
The output values of the hidden layer are calculated using Equation (3).
where represents the input values of the hidden layer, is the matrix with the shape of representing the weights between the input layer and hidden layer, represents the input matrix, represents the output values of the hidden layer, and represents the activation function.
The input values of the output layer are calculated using Equation (4).
The output values of the output layer are calculated using Equation (5).
where represents the input values of the output layer, is the matrix with the shape of representing the weights between the hidden layer and output layer, and represents the output values of the output layer.
- (3)
- Back Propagation
The error between the predicted and actual values is calculated using the loss function. , are updated by the Adam optimizer.
- (4)
- Update the Maximum Iteration Count and Save the Optimal Model
For each iteration, we determine whether the maximum iteration count has been reached. If this is attained, we update the maximum iteration count. We use the validation set to calculate the model loss function and compare it with the optimal value to determine whether to stop the iteration. Specifically, if the loss function value is less than 0.9999 times the optimal value, we update and save the current model as the optimal model; conversely, if the condition is not met for 16 consecutive iterations, we stop the iteration and complete the model training.
3.2. Superplastic Forming Process Parameter Design Method Based on Small Samples and an Improved BP Neural Network
When a new product is added to the queue, it includes basic information such as part name, part number, part size, mold material, plate material, plate size, and gas type.
First, according to the part name information in the new product queue, the knowledge graph of the superplastic forming process is searched, and the corresponding data are obtained as the product structure subgraph, which provides data support for the construction of the process parameter generation model.
Second, through analysis, the part name, part size, plate material, plate size, mold material, and gas type are determined as the influencing factor indicators. The chamber temperature and holding time in the heating process, the lowering speed and blank holder force in the mold closing process, the gas loading pressure and holding time in the reverse inflatable molding process, the gas loading pressure and holding time in the forward inflatable molding process, and the chamber temperature in the cooling process are determined as the target indicators.
Third, the model’s performance is affected by the fact that too few samples cannot fully explore the correlation relationship between the data. Therefore, this paper uses the data augmentation approach to expand the training set. Specifically, a sample is randomly selected from the training set, the feature data with string type remains unchanged, the feature data with numerical type generates random noise with a Gaussian distribution, and the noise is added to the initial data to generate new samples.
Fourth, data preprocessing is performed on the training set, validation set, and test set separately. Specifically, we perform One-Hot Encoding on string-type data to convert it into a numeric vector, and Min–Max Normalization on numeric-type data.
Fifth, we initialize the BP neural network structure and parameters, including the number of the input layer nodes, the number of the hidden layer nodes, the number of the output layer nodes, the iteration count, the learning rate, the activation function, and the loss function, among others.
Sixth, the model is trained with the training set and validated with the validation set by calculating MAE, MSE, and RMSE evaluation metrics until the iteration termination condition is met, completing the model training and saving the optimal model.
Finally, the test sample data are input into the prediction model to output the normalized values of the process parameters, and the predicted values of the process parameters are obtained after the inverse normalization of the output values.
The flowchart of the superplastic forming process parameter design method based on small samples and an improved BP neural network is shown in Figure 5.
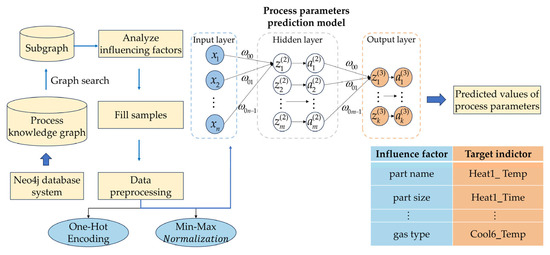
Figure 5.
Superplastic forming process parameter prediction model based on small samples and an improved BP neural network.
4. Case Study
4.1. Data Source
Hemispherical components represent a typical type of deep-cavity thin-walled parts, characterized by geometric features such as deep cavities and a high aspect ratio. The superplastic forming technology is highly suitable for manufacturing such structures, as it fully leverages the material’s extreme deformability under high strain rates. By exploiting the superplastic properties of the material, this process enables precise replication of the mold cavity details, facilitates the one-time production of high-precision, low-residual-stress monolithic parts, and effectively avoids cumulative errors caused by multi-component assembly. These advantages are unattainable with traditional stamping methods, which are prone to issues such as localized thinning and fracture in such components. Therefore, this study takes superplastically formed hemispherical parts as the research object, constructing a knowledge graph of the superplastic forming process through a combination of top–down and bottom–up approaches. On this basis, a BP neural network-based prediction model for superplastic forming process parameters is developed, incorporating small-sample learning and adaptive iteration strategies to achieve intelligent generation of key process parameters for target components. The geometry of the hemispherical part and its corresponding mold are shown in Figure 6.

Figure 6.
Superplastic forming hemispherical part sample and its mold: (a) hemispherical part sample; (b) hemispherical part mold.
Taking the typical hemispherical parts as an example, the dataset required for this study is constructed by combining physical experiments and simulation. On the experimental side, forming tests are conducted on typical hemispherical components using a superplastic forming platform, systematically recording key process parameters such as temperature and pressure, as well as the corresponding forming results. On the simulation side, a numerical model is established based on finite element software, and data samples under different working conditions are obtained through multiple sets of parameter simulations. Historical data on component design indicators are partially shown in Table 1. Historical process parameter data are partially shown in Table 2.

Table 1.
Historical data on component design indicators (partial).

Table 2.
Historical data on process parameters (partial).
4.2. Construction of the Knowledge Graph for Superplastic Forming Process
The superplastic forming process knowledge graph is constructed using the proposed design and construction method. And the entity and relationship information related to the superplastic forming process of the parts are stored in Neo4j. The superplastic forming process knowledge graph is shown in Figure 7. The knowledge graph contains 477 nodes and 476 relationships. Among them, there is 1 entity under the part name label, 28 entities under the part number label, 196 entities under the process label, and 252 entities under the parameter label. There are 28 include_part relationships, 196 include_process relationships, and 252 include_parameter relationships, as shown in Table 3. The process label contains the main processes of superplastic forming: heating, feeding, mold closing, reverse inflatable molding, forward inflatable molding, cooling, and unloading. The key process parameters for each process are included under the parameter label. Specifically, the key parameters for heating process include the chamber temperature and holding time; the key parameters for mold closing process include the lowering speed and blank holder force; the key parameters for reverse inflatable molding process include the gas loading pressure and holding time; the key parameters for forward inflatable molding process include the gas loading pressure and holding time; and the key parameters for cooling process include the chamber temperature.
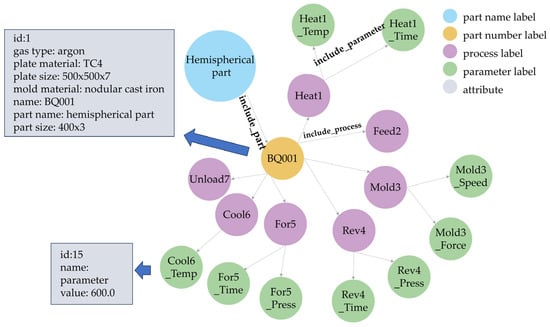
Figure 7.
Knowledge graph of the superplastic forming process (partial).

Table 3.
Overview of entities and relationships of the superplastic forming process knowledge graph.
4.3. Dataset Splitting
We perform a graph search on the knowledge graph based on the input product information to obtain the product structure subgraph. The subgraph data are divided into a training set and a validation set in a 4:1 ratio. For composite input data, it is decomposed into multiple independent metrics. For the training set, partial input data are shown in Table 4, and partial output data are shown in Table 5. For the validation set, input data are shown in Table 6, and output data are shown in Table 7.

Table 4.
Input data of the training set (partial).

Table 5.
Output data of the training set (partial).

Table 6.
Input data of the validation set.

Table 7.
Output data of the validation set.
4.4. Data Preprocessing
Sample padding was performed on the training set. Specifically, a sample is randomly selected from the training set, and the string-type feature data are kept unchanged. For numerical-type feature data with a value range of 10 or less, a noise obeying a normal distribution N (1, 0.1) is added to the original data. And for numerical-type feature data with a value range of more than 10, an integer noise within (0, 10) is added to the original data.
On this basis, preprocessing was performed on the training set and validation set, separately. Specifically, string-type feature data underwent One-Hot Encoding processing, while numerical-type feature data were normalized using Min–Max Scaling.
For the preprocessed training set, partial input data are shown in Table 8, and partial output data are provided in Table 9.

Table 8.
Input data of the preprocessed training set (partial).

Table 9.
Output data of the preprocessed training set (partial).
For the preprocessed validation set, input data are presented in Table 10, and output data are summarized in Table 11.

Table 10.
Input data of the preprocessed validation set.

Table 11.
Output data of the preprocessed validation set.
4.5. Model Training and Evaluation
The parameter settings of the superplastic forming process parameter prediction model based on small samples and an improved BP neural network are shown in Table 12, and the training set after sample filling is used as the training data to complete the model training.

Table 12.
Parameter setting table.
In the epoch-training error/validation error curve, the horizontal axis represents the number of training iterations. The vertical axis indicates the error between predicted and actual values, measured using MSE. The epoch-training error curve can be used to evaluate the model’s convergence during the training process, and the epoch-validation error curve can be used to assess the model’s fitting performance, as shown in Figure 8. From the figure, it can be observed that as the number of iterations increases, both the training error curve and the validation error curve show a decreasing trend and eventually tend to a horizontal state. This indicates that the model has reached a converged state and has good generalization ability without an overfitting problem.
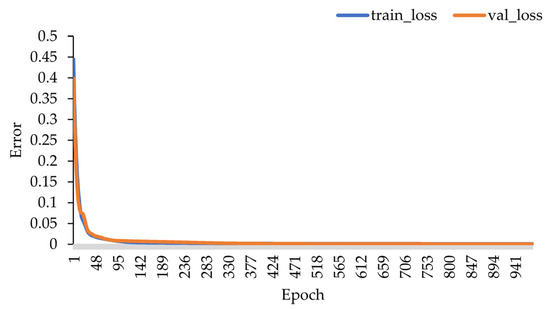
Figure 8.
Epoch-training/validation errors of the improved BP neural network.
In order to verify the superiority of the proposed algorithm, SVR, RF, XGBoost, and standard BP are selected as the comparison algorithms, and comparison experiments are conducted on the same validation set. The prediction performance of each model is quantitatively evaluated using three metrics: MSE, MAE, and RMSE. These evaluation metrics are computed on the same validation set, reflecting the deviation between predicted and actual values after model training. Lower values indicate higher prediction accuracy. The detailed results are presented in Table 13 for clear comparison. The experimental results show that the XGBoost, the standard BP model, and the improved BP model significantly outperform the SVR and RF. The XGBoost and the standard BP model exhibit comparable performance, and the improved BP model is significantly better than the XGBoost and the standard BP model, which demonstrates better prediction accuracy. Specifically, compared to the standard BP model, the improved BP model reduces the MSE, MAE, and RMSE by 82.1% (to 0.0005), 46% (to 0.0188), and 57.1% (to 0.0229), indicating a substantial improvement in prediction performance.

Table 13.
Performance comparison of multiple algorithms.
In order to intuitively compare the gap between the predicted values and the actual values, take the first sample from the validation set as an example, and plot the actual vs. predicted values comparison graph for both the standard BP algorithm and the improved BP algorithm, respectively, as shown in Figure 9. From the figure, it can be found that the gap between the predicted value and the actual value for the improved BP algorithm is smaller compared to the standard BP algorithm.
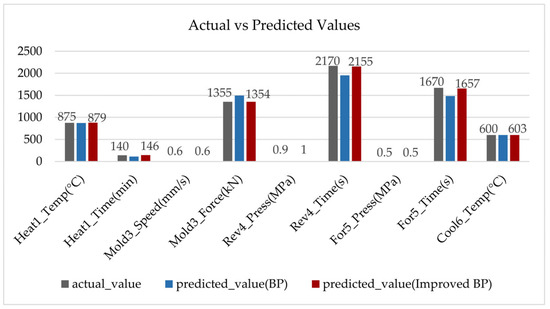
Figure 9.
Actual vs. predicted values.
4.6. Model Testing
After the model training is completed, the preprocessed test sample is input into the trained model to output normalized prediction results of the process parameters. The test sample is shown in Table 14. The preprocessed test sample is shown in Table 15. The normalized prediction results are shown in Table 16. These values are then denormalized to obtain the actual predicted process parameters, as shown in Table 17.

Table 14.
Input product information.

Table 15.
Preprocessed test samples.

Table 16.
Normalized prediction results of process parameters.

Table 17.
Actual predicted results of process parameters.
In practical application, enter “part name”, “part number”, “part size”, “plate material”, “plate size”, “mold material”, “gas type” and other product information in the process intelligence generation interface, as shown in Table 14, the process parameter values of the product can be obtained as shown in Table 17.
5. Conclusions
In order to improve the efficiency of the superplastic forming process design, a precision design method for superplastic forming process parameters based on a knowledge graph and artificial intelligence is proposed for the requirements that the superplastic forming processes of different products are roughly the same, and the values of the process parameters need to be precisely designed. The main contributions include the following:
- (1)
- The knowledge graph for the superplastic forming process is constructed, which adopts the expression of graph structure to store the superplastic forming process information, and more intuitively demonstrates the correlation between the key parts, processes, and process parameters for superplastic forming.
- (2)
- An intelligent superplastic forming process parameter prediction model based on small samples and an improved BP neural network is constructed. The experimental results show that the MSE, MAE, and RMSE of the adaptive iteration BP neural network model are 0.0005, 0.0188, and 0.0229, respectively, which outperform the SVR, RF, XGBoost, and standard BP neural network model. Compared to the BP neural network model, the improved model reduces MSE, MAE, and RMSE by 82.1%, 46% and 57.1%, respectively. The prediction performance of the model has a better enhancement, which verifies the effectiveness, feasibility, and superiority of the proposed method.
However, it is important to acknowledge certain limitations. The current validation relies primarily on model-based analysis. Although the method demonstrates excellent performance in simulation, it cannot fully substitute physical experiments or real industrial data for definitive proof. Its effectiveness in real industrial settings still requires further verification.
To address these limitations, future work will focus on practical validation and application expansion. Physical experiments and trial production will be conducted for typical superplastic forming hemispherical parts. By incorporating key quality metrics such as thinning rate and thickness distribution uniformity as core design requirements, quantitative comparisons will be conducted between the core design specifications of components and the measured results of actual prototype parts produced based on predicted process parameters. This will enable a practical evaluation of the method’s performance and economic benefits under real conditions, facilitating its transition from theoretical validation to engineering application.
Author Contributions
Conceptualization, W.Y.; methodology, X.G. and W.Y.; software, X.G. and J.P.; formal analysis, L.W.; investigation, J.P.; resources, C.X.; data curation, L.W.; writing—original draft preparation, X.G.; writing—review and editing, W.Y.; visualization, C.X.; supervision, Q.Z.; project administration, Q.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Science and Technology Major Project of China, grants number 151. The APC was funded by the National Science and Technology Major Project of China, grants number 151.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
We appreciate our colleagues in the department for their technical assistance. Finally, we thank the anonymous reviewers and editors for their valuable comments, which significantly improved the quality of this work.
Conflicts of Interest
Xiaoke Guo, Wanran Yang, Qian Zhang, Junchen Pan, Chengyue Xiong, and Le Wu were employed by Beijing National Innovation Institute of Lightweight Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| SPF | Superplastic forming |
| SVR | Support vector regression |
| RF | Random forest |
| XGBoost | Extreme gradient boosting |
| BP | Back propagation |
| CNN | Convolutional neural networks |
| LSTM | Long short-term memory |
| MSE | Mean squared error |
| MAE | Mean absolute error |
| RMSE | Root mean square error |
References
- Li, B.; Zhou, Y.; Han, W.; Qin, Z.; Zhang, T.; Chen, H. Status and development of superplastic forming machine technology. Aeronaut. Manuf. Technol. 2023, 66, 55–62. [Google Scholar] [CrossRef]
- Williams, J.C.; Boyer, R.R. Opportunities and Issues in the Application of Titanium Alloys for Aerospace Components. Metals 2020, 10, 705. [Google Scholar] [CrossRef]
- Yu, X.; Xiao, X.; Wu, Z. Analysis of superplastic forming process and equipment. China Met. Equip. Manuf. Technol. 2024, 59, 96–99. [Google Scholar]
- Lakshmanan, P.; Sakthivel, E. Examining the superplastic behavior of (Al-Si-Mg)/SiC metal matrix nanocomposites. In Proceedings of the 2nd International Conference on Engineering Materials, Metallurgy and Manufacturing (ICEMMM), Chennai, India, 15–16 February 2022; pp. 962–966. [Google Scholar] [CrossRef]
- Demirel, M.Y.; Karaagac, I. High-speed superplastic formability and deformation mechanisms of Ti6Al4V sheets. Mater. Sci. Eng. A-Struct. Mater. Prop. Microstruct. Process. 2023, 866, 144652. [Google Scholar] [CrossRef]
- Akula, S.P.; Ojha, M.; Rao, K.L.; Gupta, A.K. A review on superplastic forming of Ti-6Al-4V and other titanium alloys. Mater. Today Commun. 2023, 34, 105343. [Google Scholar] [CrossRef]
- Dehkordi, Z.K.; Malekan, M.; Nili-Ahmadabadi, M. Superplastic formability of the developed Zr40Hf10Ti5Al10Cu25Ni10 high entropy bulk metallic glass with enhanced thermal stability. J. Non-Cryst. Solids 2022, 576, 121265. [Google Scholar] [CrossRef]
- Chandrappa, K.; Sumukha, C.S.; Sankarsh, B.B.; Gowda, R. Superplastic forming with diffusion bonding of titanium alloys. In Proceedings of the International Conference on Materials and Manufacturing Methods (MMM), Tiruchirapalli, India, 5–7 July 2019; pp. 2909–2913. [Google Scholar] [CrossRef]
- Jun, L.; Elangovan, P.; Evgenia, Y.; Nicola, Z.; David, M.M.; Nick, H.; Les, G.; Christopher, G. FEM study of process parameters in a novel superplastic forming of titanium alloy Ti-6Al-4V. In Proceedings of the 20th Metal Forming International Conference, Krakow, Poland, 15–18 September 2024; pp. 209–217. [Google Scholar] [CrossRef]
- Alavi, S.A.; Afshari, M.; Afshari, H.; Samadi, M.R.; Abbaas, H.; Abualigah, L. Investigating the effect of hot preforming combined with superplastic forming on thickness distribution and forming time of Ti-6Al-4V alloy using finite element analysis. J. Strain Anal. Eng. Des. 2025, 60, 286–298. [Google Scholar] [CrossRef]
- Giuliano, G.; Polini, W. FEM Analysis of Superplastic-Forming Process to Manufacture a Hemispherical Shell. Appl. Sci. 2025, 15, 8080. [Google Scholar] [CrossRef]
- Xiao, Y.Z.; Zheng, S.; Shi, J.C.; Du, X.D.; Hong, J. Knowledge graph-based manufacturing process planning: A state-of-the-art review. J. Manuf. Syst. 2023, 70, 417–435. [Google Scholar] [CrossRef]
- Peng, S.; Xiao, B.; Zhao, Z.; Xu, B.; Ding, G.; Wei, Y.; Su, X.; Wang, M. Construction and application of knowledge graph for machining process of complex thin-walled parts. J. Mech. Electr. Eng. 2024, 41, 709–719. [Google Scholar] [CrossRef]
- Li, Z. Research on Process Route Recommendation Method Based on Knowledge Graph. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2021. [Google Scholar]
- Liu, L.; Gao, Y.; Cao, Y.; Liu, K. A Knowledge Graph-Based Model Fbr Process Routes Reconlmending of Precision Transmission Components. Mod. Manuf. Eng. 2025, 26–36. [Google Scholar] [CrossRef]
- Su, C.; Jiang, Q.; Han, Y.; Wang, T.; He, Q.C. Knowledge graph-driven decision support for manufacturing process: A graph neural network-based knowledge reasoning approach. Adv. Eng. Inform. 2025, 64, 103098. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Q.; Ma, Y.; Wang, Z. Construction and Application of Process Knowledge Graph Based on Deep Learning. J. Mech. Electr. Eng. 2024, 41, 2220–2231. [Google Scholar] [CrossRef]
- Shen, H.; Guo, Q.; Xu, H.; Jiang, J.; Chen, L. Recommendation Based on Knowledge Graph and Graph Neural Network. In Proceedings of the 2023 7th Chinese Conference on Swarm Intelligence and Cooperative Control, Singapore, 17–19 November 2024; pp. 593–603. [Google Scholar] [CrossRef]
- Wu, G.; Wang, X.; Liu, Y. Research Advances on Graph Neural Network Recommendation of Knowledge Graph Enhancement. Comput. Eng. Appl. 2023, 59, 18–29. [Google Scholar] [CrossRef]
- Huang, J. Graph Neural Network in Knowledge Graph aided Recommender Systems. In Proceedings of the 2022 4th International Conference on Robotics, Intelligent Control and Artificial Intelligence, Dongguan, China, 16–18 December 2022; pp. 743–746. [Google Scholar] [CrossRef]
- Kesri, V.; Nayak, A.; Ponnalagu, K.; Soc, I.C. AutoKG—An Automotive Domain Knowledge Graph for Software Testing: A position paper. In Proceedings of the 14th IEEE Conference on Software Testing, Verification and Validation (ICST), Online, 12–16 April 2021; pp. 234–238. [Google Scholar]
- Li, J.; Qu, Y.; Qiu, H.; Liu, B.; Li, L.; Zhang, J.; Wei, L. Effective machining process planning method based on knowledge graph and deep learning. Comput. Integr. Manuf. Syst. 2024, 30, 3850–3865. [Google Scholar] [CrossRef]
- Devireddy, C.R.; Ghosh, K. Feature-based modelling and neural networks-based CAPP for integrated manufacturing. Int. J. Comput. Integr. Manuf. 1999, 12, 61–74. [Google Scholar] [CrossRef]
- Ming, X.G.; Mak, K.L. Intelligent approaches to tolerance allocation and manufacturing operations selection in process planning. J. Mater. Process. Technol. 2001, 117, 75–83. [Google Scholar] [CrossRef]
- Hussong, M.; Ruediger-Flore, P.; Klar, M.; Kloft, M.; Aurich, J.C. Selection of manufacturing processes using graph neural networks. J. Manuf. Syst. 2025, 80, 176–193. [Google Scholar] [CrossRef]
- Ying, X.; Jin, Y.; Sun, L.; Guan, J.; Zhang, X.; Liu, F. Method of Process Generation Based on Knowledge Learning of Few Samples. New Technol. New Process 2020, 6–11. [Google Scholar]
- Ge, C.; Qi, L.; Yu, C.; Huang, Y.; Sun, J. Application of a Combined Forecasting Model in the Prediction of Hull Outer Plate Surface Forming; Conference Paper; IEEE: Piscataway, NJ, USA, 2021. [Google Scholar]
- Huang, Y. Research on Intelligent Generation Method of Ship Plate Surface Forming Process Plan Based on Intelligent Decision Support System. Master’s Thesis, Jiangsu University of Science and Technology, Zhenjiang, China, 2022. [Google Scholar]
- Zhang, Z.; Liu, S.; Zhang, Y.; Wang, C.; Zhang, S.; Yang, Z.; Xu, W. Optimization of low-power femtosecond laser trepan drilling by machine learning and a high-throughput multi-objective genetic algorithm. Opt. Laser Technol. 2022, 148, 107688. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, Z.; Jing, X.; Yang, Z.; Xu, W. Optimization of multistage femtosecond laser drilling process using machine learning coupled with molecular dynamics. Opt. Laser Technol. 2022, 156, 108442. [Google Scholar] [CrossRef]
- Bruendl, P.; Stoidner, M.; Huong Giang, N.; Abrass, A.; Franke, J. Optimization of Process, Knowledge, and Manufacturing Management in Customized Production: A Graph-Based Approach for Manufacturing Planning. In Proceedings of the 18th IFAC Symposium on Information Control Problems in Manufacturing (INCOM), Vienna, Austria, 28–30 August 2024; pp. 1174–1179. [Google Scholar]
- Gu, J.; Wang, Z.; Kuen, J.; Ma, L.; Shahroudy, A.; Shuai, B.; Liu, T.; Wang, X.; Wang, G.; Cai, J.; et al. Recent advances in convolutional neural networks. Pattern Recognit. 2018, 77, 354–377. [Google Scholar] [CrossRef]
- Wang, K.; Li, K.; Zhou, L.; Hu, Y.; Cheng, Z.; Liu, J.; Chen, C. Multiple convolutional neural networks for multivariate time series prediction. Neurocomputing 2019, 360, 107–119. [Google Scholar] [CrossRef]
- Wang, J.; Li, Z. Wind speed interval prediction based on multidimensional time series of Convolutional Neural Networks. Eng. Appl. Artif. Intell. 2023, 121, 105987. [Google Scholar] [CrossRef]
- Alzubaidi, L.; Zhang, J.; Humaidi, A.J.; Al-Dujaili, A.; Duan, Y.; Al-Shamma, O.; Santamaria, J.; Fadhel, M.A.; Al-Amidie, M.; Farhan, L. Review of deep learning: Concepts, CNN architectures, challenges, applications, future directions. J. Big Data 2021, 8, 53. [Google Scholar] [CrossRef]
- Malashin, I.; Tynchenko, V.; Gantimurov, A.; Nelyub, V.; Borodulin, A. Applications of Long Short-Term Memory (LSTM) Networks in Polymeric Sciences: A Review. Polymers 2024, 16, 2607. [Google Scholar] [CrossRef]
- Malhotra, R.; Singh, P. Recent advances in deep learning models: A systematic literature review. Multimed. Tools Appl. 2023, 82, 44977–45060. [Google Scholar] [CrossRef]
- Yan, Z. Research and Application on BP Neural Network Algorithm. In Proceedings of the International Industrial Informatics and Computer Engineering Conference (IIICEC), Xi’an, China, 10–11 January 2015; pp. 1444–1447. [Google Scholar]
- Kaur, R.; Roul, R.K.; Batra, S. Multilayer extreme learning machine: A systematic review. Multimed. Tools Appl. 2023, 82, 40269–40307. [Google Scholar] [CrossRef]
- Singhal, A. Official Google Blog: Introducing the Knowledge Graph: Things, Not Strings. 2012. Available online: https://blog.google/products/search/introducing-knowledge-graph-things-not/ (accessed on 12 August 2025).
- Li, J. Research on Generation of Scientific Research Review Based on Knowledge Graph. Ph.D. Thesis, Chinese Academy of Agricultural Sciences, Beijing, China, 2021. [Google Scholar]
- Liu, X.; Mao, T.; Shi, Y.; Ren, Y. Overview of knowledge reasoning for knowledge graph. Neurocomputing 2024, 585, 127571. [Google Scholar] [CrossRef]
- Wang, T.; Li, S.; Yu, W.; Neng, F.; Li, X.; Yang, J.; Xiong, L. Wind power prediction based on BP neural network combined with ERA5 data. Energy Storage Sci. Technol. 2025, 14, 183–189. [Google Scholar] [CrossRef]
- Wen, N.; Yan, B.; Lin, X.; Huang, G.; Lv, Z.; Zhang, B. Prediction model of wire de-icing jump height based on BP neural network BP neural network. J. Vib. Shock 2021, 40, 199–204. [Google Scholar] [CrossRef]
- Wen, N. Prediction Model for Dynamic Responses of Transmission Lines After Ice-shedding Based on Numerical Simulation and Machine Learning. Master’s Thesis, Chongqing University, Chongqing, China, 2020. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).