Impact of Advanced Thyristor Controlled Series Capacitor on Load Frequency Control and Automatic Voltage Regulator Dual Area System with Interval Type-2 Fuzzy Sets-PID Usage

Abstract

A major priority for practicing engineers in an electric power system is preserving the stability of frequency and voltage levels. Any change in these two factors will impact the efficiency and lifespan of the machines connected to the power supply. Therefore, this paper provides a control approach utilizing the Interval Type-2 Fuzzy Sets- Proportional Integral Derivative (IT2FSs-PID) controller and Advanced Thyristor Controlled Series Capacitor (ATCSC) with a combined Load Frequency Control-Automatic Voltage Regulator (LFC-AVR). Several inspections were implemented to demonstrate the controller’s strength, including various disturbances in the power system. The LFC-AVR was studied using two different dynamic models, referred to as open and closed loops on the Generation Rate Constraint (GRC) forms. A comparison was made using different techniques from the literature using the same model. Before using the approach, the frequency deviation of area-1 had a very large settling time value, which was caused by system instability. However, after implementing the approach, this value decreased to 4.9236 s. Finally, an additional ATCSC was added to the proposed model to observe its effect on the power system. The simulation was implemented using MATLAB/SIMULINK tools.

1. Introduction

A major obstacle for electrical power system engineers is the parallel regulation of voltage and frequency levels. Any change in these parameters significantly reduces the productivity and efficiency of devices connected to a power supply. The objective of regulating devices used in large and intricate power systems is to regulate small load disruptions and sustain the system’s frequency and terminal voltage within acceptable thresholds. The generating units contain a loop to control the load frequency and reduce the gap between the load and the generated power. The automatic voltage regulator (AVR) system located in the generating units controls the reactive power, thereby regulating the voltage in the power system [1]. Nearly all industrial processes continue to use traditional PID controllers because of their easy control design, cost-effectiveness, and efficacy when used in linear systems [2]. It is essential to tune the PID controller gains with special care to enhance performance. Therefore, choosing the incorrect gains leads to system instability [3]. Computational intelligence is now being extensively used in the field of optimization issues [4,5,6]. Type-2 Fuzzy Set (T2FS) from computational intelligence is a wider and more comprehensive version of Type-1 Fuzzy Set (T1FS), proposed via Zadeh in [7]. Compared to the mathematics of T1F logic control, the computation of T2F logic control presents a significant challenge. The work in [8] introduced a distinct variant of T2FS known as Interval Type-2 Fuzzy Sets (IT2FSs). IT2FSs outputs are characterized by uncertainty within a time period. The IT2F logic controller has been effectively used for the building of controllers [9,10,11,12,13,14,15]. Moreover, implementing a Flexible Alternating Current Transmission System (FACTS) for coupled power systems is a very efficient method of enhancing the system’s stability [16]. FACTS controllers, such as the Interline Power Flow Controller (IPFC), Thyristor Controlled Phase Shifter (TCPS), Static Synchronous Series (SSSC), and Thyristor Controlled Series Capacitor (TCSC), are operated in the tie line of coupled power systems to minimize frequency and power deviations because of their rapid dynamic responses [17,18,19]. The TCSC is a type of FACTS controller that provides strong, effective performance at a reasonable cost and a robust and practical foundation. A novel approach to dynamic modeling and employing the TCSC for Automatic Generation Control (AGC) has been recently introduced [18]. Previous studies have suggested traditional controllers such as PID cascaded and PID controllers, as well as PI controllers. However, other work has suggested new controllers that utilize computational intelligence methods, such as Fuzzy Logic Systems (FLSs), as well as neural systems that fully substitute for traditional controller methods. Additionally, some studies have suggested hybrid controllers that combine traditional controllers with new controller methods, such as Fuzzy PID (FPID) and Fuzzy PI (FPI) controllers, as well as a Gain Scheduled controller [20]. In [21,22], a Fuzzy-Integral (I) controller is used to improve the stability of LFC for dual-area power systems. The works [2,23] focused on using IT2FL. Reference [23] presents a novel approach called IT2FL-based Dual Mode Gain Scheduling (DMGS) for the PI controller. This proposed method involves scheduling the PI controller using a variable selector. Reference [2] presents the development and implementation of an IT2FPID controller, the IT2FPID comprising FSPI with FSPD controllers. The work in [24] also provided research on a Load Frequency Control (LFC) technique that utilizes the T2FLPID controller on dual isolated power systems. The study in [25] focuses on hybrid power systems, specifically optimizing the gains of PI-PD controller parameters using the Particle Swarm Optimization-Gravitational Search Algorithm (PSO-GSA) approach. An Ant Colony Optimization (ACO)-based classical PID controller is developed in [26], and it uses various objective functions to evaluate the performance of a standalone nuclear station. References [27,28] applied a Fractional Order (FO) PID controller to the power system to achieve high performance. In [27], Gases Brownian motion optimization is used, whereas the work in [28] used Big Bang Big Crunch optimization to tune the controller parameters. The studies in [29,30,31] concentrate on the conventional T1FS self-adapting method for PID control. Numerous flexible AC transmission systems are utilized in conjunction with a tie line to regulate power flow and mitigate inter-area oscillations by implementing a supplementary controller [19]. The study in [32] compares the dynamic performance of TCPS and the Capacitive Energy Storage (CES) of AGC for hydrothermal generating connected with hydro diesel generating. The comparison is done using modern techniques in [32]. The study in [33] examines the coordinated design of TCPS and Superconducting Magnetic Energy Storage (SMES) for an uncontrolled thermal power plant. The study considers the Generation Rate Constraint (GRC) in hydro and non-reheat thermal units [33]. The work in [34] involves installing the TCSC in series with the tie line for a dual-area thermal plant, using a GRC and time delay factors, ideally positioned in both areas, where SMES units collaborate with the TCSC to optimize the areas’ overall dynamic efficiency. The work in [35] employs FACTS devices, including SSSC, TCSC, TCPS, and IPFC, and is compared in the existence of the Two Degree of Freedom Integral plus Double Derivative (2DOF-IDD) controller for the AGC of a multi-area thermal system.

Based on the above literature review and Table 1, this paper presents the importance of using an appropriate control system for a power system; an appropriate control system helps stabilize the power system when undesirable situations occur, such as a sudden increase in the demand for electrical energy. An IT2FSs-PID non-traditional controller and Advanced Thyristor Controlled Series Capacitor (ATCSC) are used, and simulations will show the positive effect of these controllers on the power system. The major contributions of this work are:

Table 1. Literature review.

References	Case Study	Non-Linearities	Controllers	Optimizer
[20]	Two Areas Multi-Sources LFC system	GDB, GRC	IT2FLC	PSO
[21]	Two Areas LFC system	GDB, GRC	T1FLC+I	PSO
[22]	Two Areas LFC system	-	T1FLC+I	GA, SA, PS
[23]	Three Areas Multi-Sources LFC system	GRC	PI	IT2FLC-based DMGS
[2]	The inverted pendulum system	-	PI+PD	IT2FLC
[24]	Hybrid isolated power system	-	PID	T2FLC
[25]	Two Areas Multi-Sources LFC system	-	Cascade PI-PD	PSO-GSA
[26]	LFC system	-	PID	ACO
[27]	Two Areas LFC system	GDB, GRC	FOPID	GBM
[28]	LFC system	-	FOPID	BB-BC
[29]	DC Motor Drive	-	PID	T1FLC
[30]	Multi Sources LFC system	GRC	PID	ACO, T1FLC
[31]	Multi Sources LFC system	GRC	PID	T1FLC
[19]	Two Areas Multi-Sources LFC system	GDB, GRC	TCSC, TCPS, SSSC	IPSO
[32]	Two Areas Multi-Sources LFC system	-	TCPS, CES	CRPSO
[33]	Two Areas LFC system	-	TCPS, SMES	CRPSO
[34]	Two Areas Multi-Units Thermal of LFC system	GRC, Time delay	fuzzy PID controller, TCSC, SMES	GA, DE
[35]	Three-Area Thermal System	GRC	2DOF-IDD, FACTS Devices	CS

• Developing mathematical frameworks that combine AVR and LFC for power systems.
• Analyzing the impact of Interval Type-2 Fuzzy Sets (IT2FSs)-PID, Simulated Annealing (SA)-ATCSC, and SA-PID to improve frequency and power tie line deviations, as well as their effects on the power system’s terminal voltage.
• Performing a comparative analysis of several strategies described in the literature, using the same model to demonstrate the superiority of the strategy used in this study.
• Demonstrating the effect of ATCSC on the connected area via reducing the stilling time of the frequency deviation of the area.

Section 2 describes the methodologies used and the modeling of an LFC coupling AVR which contains the power system’s controllers, Interval Type-2 Fuzzy Sets (IT2FSs), an IT2FSs-PID Controller, an Advanced Thyristor Controlled Series Capacitor (ATCSC) and the Optimization Algorithm and Objective Function. Section 3 provides the results and discussion, including the influence of the controllers on a two-area interconnected thermal power system, simulations of case studies, a sensitivity analysis, and improvements made to the two-area power system by adding a reheat unit. Also discussed are the Generation Rate Constraint (GRC), Governing Dead Band (GDB) nonlinearity, a comparison of IT2FSs-PID+SA (ATCSC+PID) with other strategies, and the comparison effect of adding another ATCSC to the power system. Finally, Section 4 concludes this study and puts forward future research directions.

2. Materials and Methods

2.1. Modeling of LFC Coupling AVR

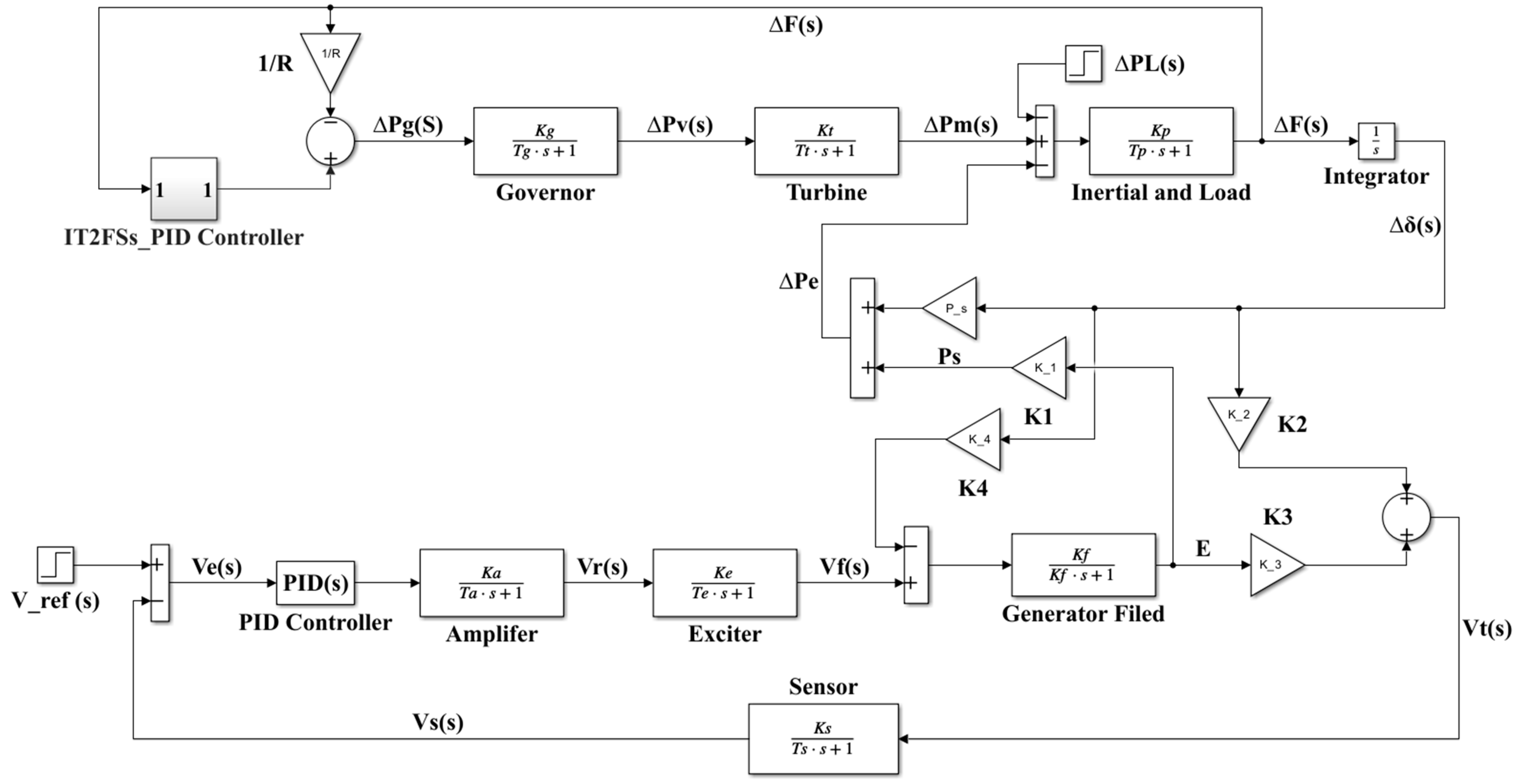
The combined LFC-AVR system allows for simultaneous system frequency and voltage management. The AVR is connected to the LFC using cross-coupling factors K1, K2, K3, and K4 [36]. Any additions or changes in the demand load of area 1, area 2, or both, result in a difference between the power produced by the power system, and the demand load affects the frequency of the entire power system, not just the frequency of the specific area experiencing the change in demand load (∆PL), due to the tie line that connects the power system generating areas [20]. The frequency may be managed by adjusting the actual power production, but the terminal voltage is maintained by adjusting the excitation system of the generator field [1]. The mathematical equations for the link between LFC and AVR are as follows:

$$\Delta \omega \left(\mathrm{s}\right)={\displaystyle \frac{1}{2\mathrm{Hs}+\mathrm{D}}}\left[\Delta P_m\left(s\right)-\Delta P_L\left(s\right)-\Delta P_e\left(s\right)\right]$$

(1)

Equation (1) shows that the inertia constant’s (H) value affects the generator deviation speed value. To reduce the value of the generator deviation speed, Equation (1) states that the appropriate value of the change in mechanical power (∆Pm) must match the appropriate value of the change in the real power (∆Pe) and ∆PL.The percent change in load divided by the percent change in frequency is expressed as (D).

$$\Delta P_e\left(\mathrm{s}\right)=\mathrm{Ps} \Delta \delta \left(\mathrm{s}\right)+K_1 {\mathrm{E}}^{\prime }$$

(2)

It is clear from Equation (2) the effect of changes in the power angle (∆δ), synchronizing power coefficient (Ps), and stator emf (E′) on ∆Pe with the coefficient K₁ is related to the stator emf.

$$\Delta {\mathrm{V}}_t\left(\mathrm{s}\right)=K_2 \Delta \delta \left(\mathrm{s}\right)+K_3 {\mathrm{E}}^{\prime }$$

(3)

$${\mathrm{E}}^{\prime }={\displaystyle \frac{K_f}{1+\mathrm{s}{T}_f}}\left[V_F\left(\mathrm{s}\right)-K_4 \Delta \delta \left(\mathrm{s}\right)\right]$$

(4)

The impact of variations in the power angle (∆δ) and stator emf (E′) on terminal voltage may be deduced from Equation (3), where the coefficients K₂ and K₃ are related to the change in the power angle and stator emf, respectively. Also, Equation (4) states the effect of a change in the power angle (∆δ) on the stator emf (E′), with a coefficient multiplied by the power angle (∆δ), which is K₄. Figure 1 shows the components of an LFC-AVR system.

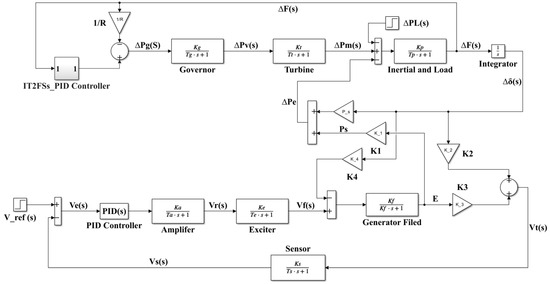
Figure 1. Components of LFC coupling with AVR of a single area.

2.2. Power System’s Controllers

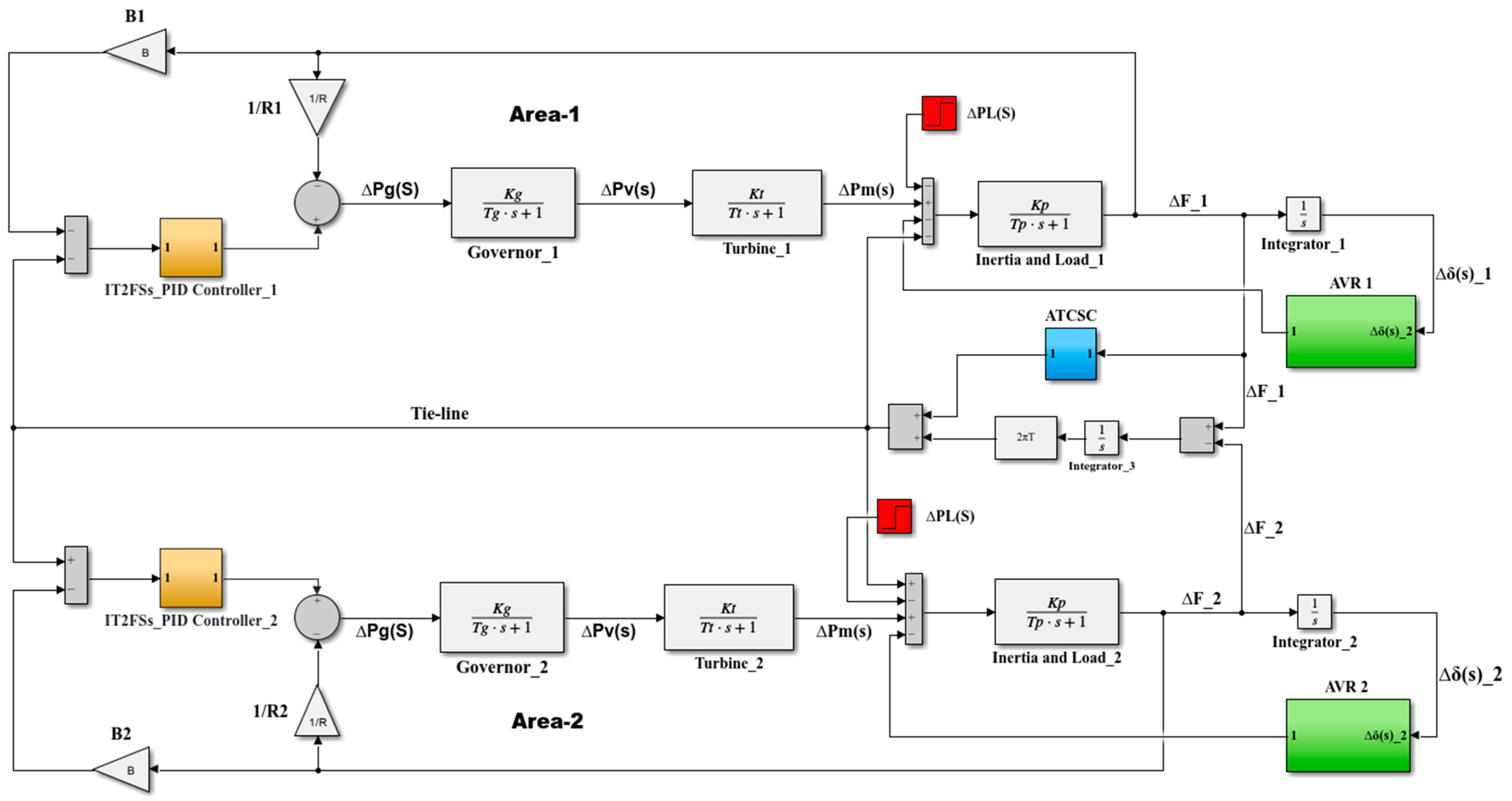
IT2FSs were utilized to adjust the parameters of the PID controller, and this complex controller was installed in the LFC system in the two areas. The PID of the AVR system was also used in the two areas, and the ATCSC was used to improve control of the power system. The parameters of the previous two controllers were tuned using simulated annealing optimization. Appendix A/Table A1 and Figure 2 illustrate the values of dual-area power system equipped with the controllers.

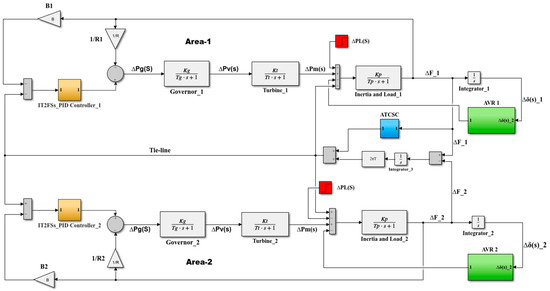
Figure 2. Block diagram of the LFC-AVR scheme of the dual area system.

2.2.1. Interval Type-2 Fuzzy Sets (IT2FSs)

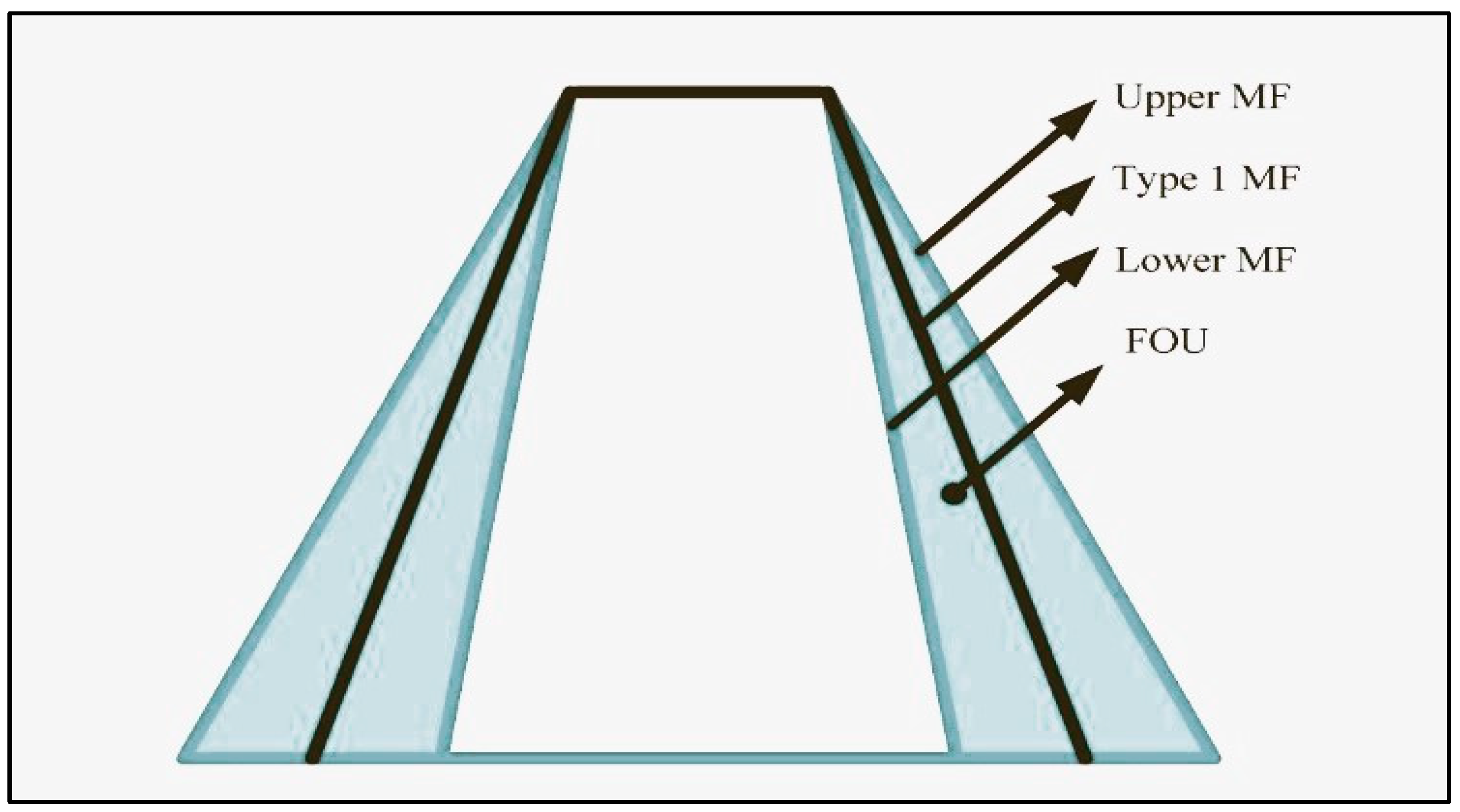
Type-2 Fuzzy Sets (T2FSs) are beneficial when it is hard to calculate an accurate membership function for a fuzzy set, hence facilitating the incorporation of uncertainty [37]. There are two types of Type-2 Fuzzy Set (T2FS): General (G)T2FS and IT2FS. Also, IT2FS calculations are less complex than GT2FS calculations [38], so IT2FSs are used in this paper. In Figure 3, IT2F membership functions are characterized by a pair of Type-1 membership functions, namely the upper membership function and the lower membership function.

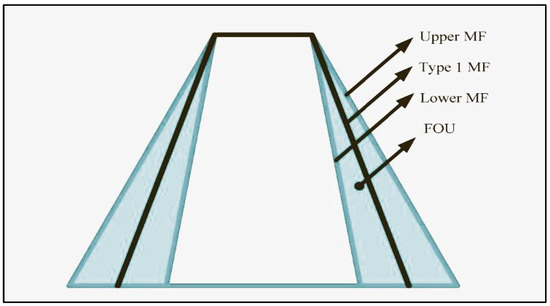
Figure 3. IT2F Membership Function [39].

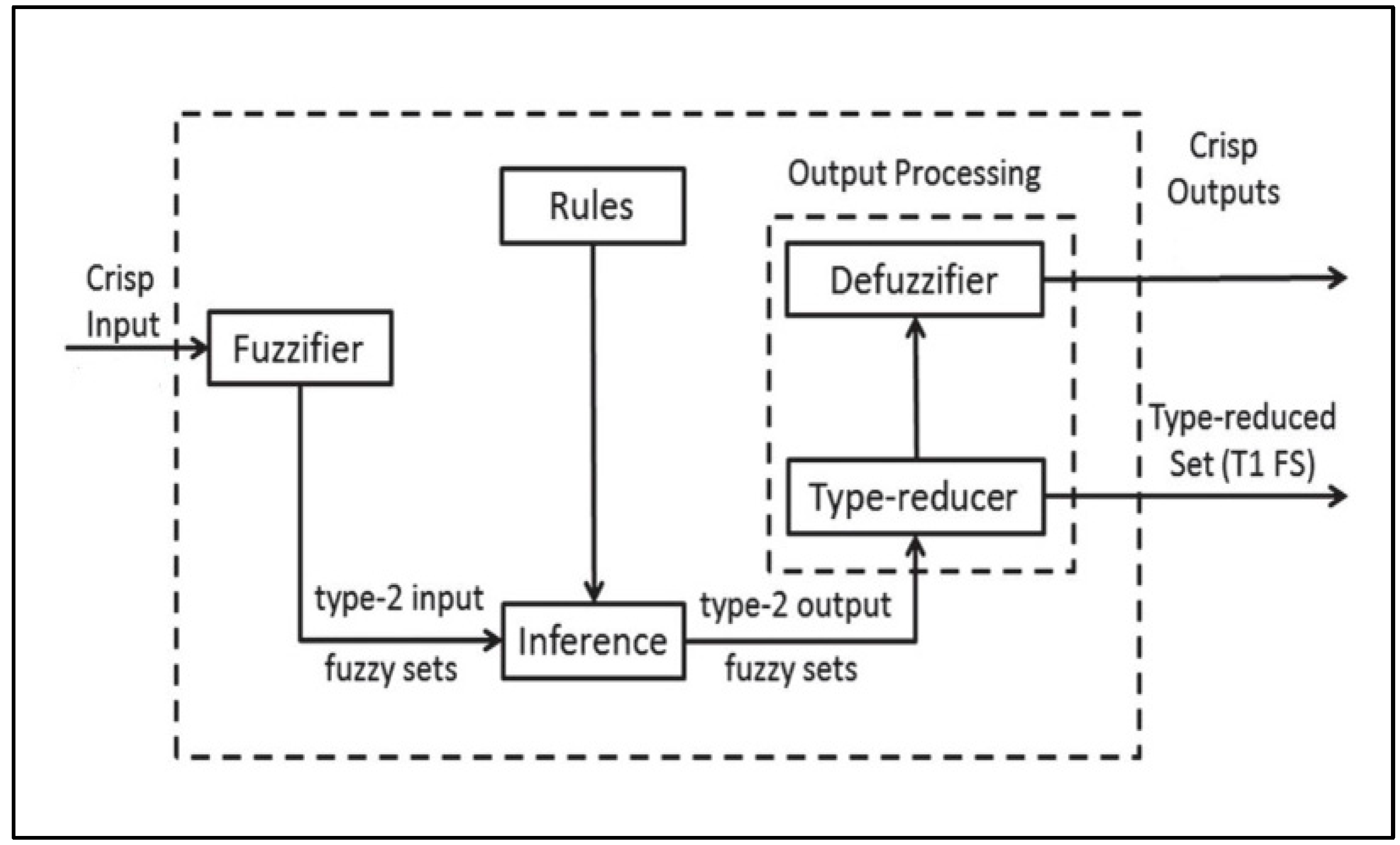
The region enclosed by these membership functions is referred to as the footprint of uncertainty [39]. Also, as shown in Figure 4, an IT2F Logic System comprises five constituents: a fuzzifier, a rule base, a fuzzy inference engine, a type-reducer, and a defuzzifier. The fuzzifier utilizes an attribution mechanism to transform direct external input data into linguistically fuzzy information. The rule base defines the connection between the system’s input and output using If-Then type fuzzy rules, constituting a rule base consisting of control rules. The fuzzy inference engine uses a rule base to perform approximations or fuzzy inferences, resulting in the analysis and acquisition of a fuzzy output [40]. Finally, an output can be obtained by type-reducing the T1FS and defuzzing the crisp value output [39].

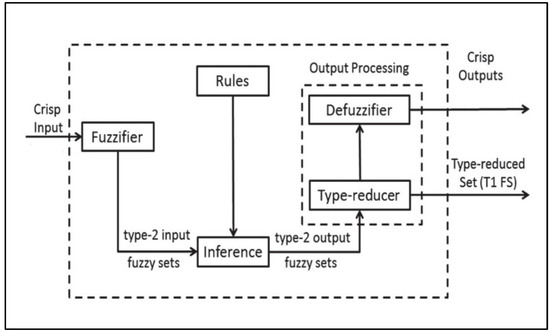
Figure 4. Structure of the IT2F logic system.

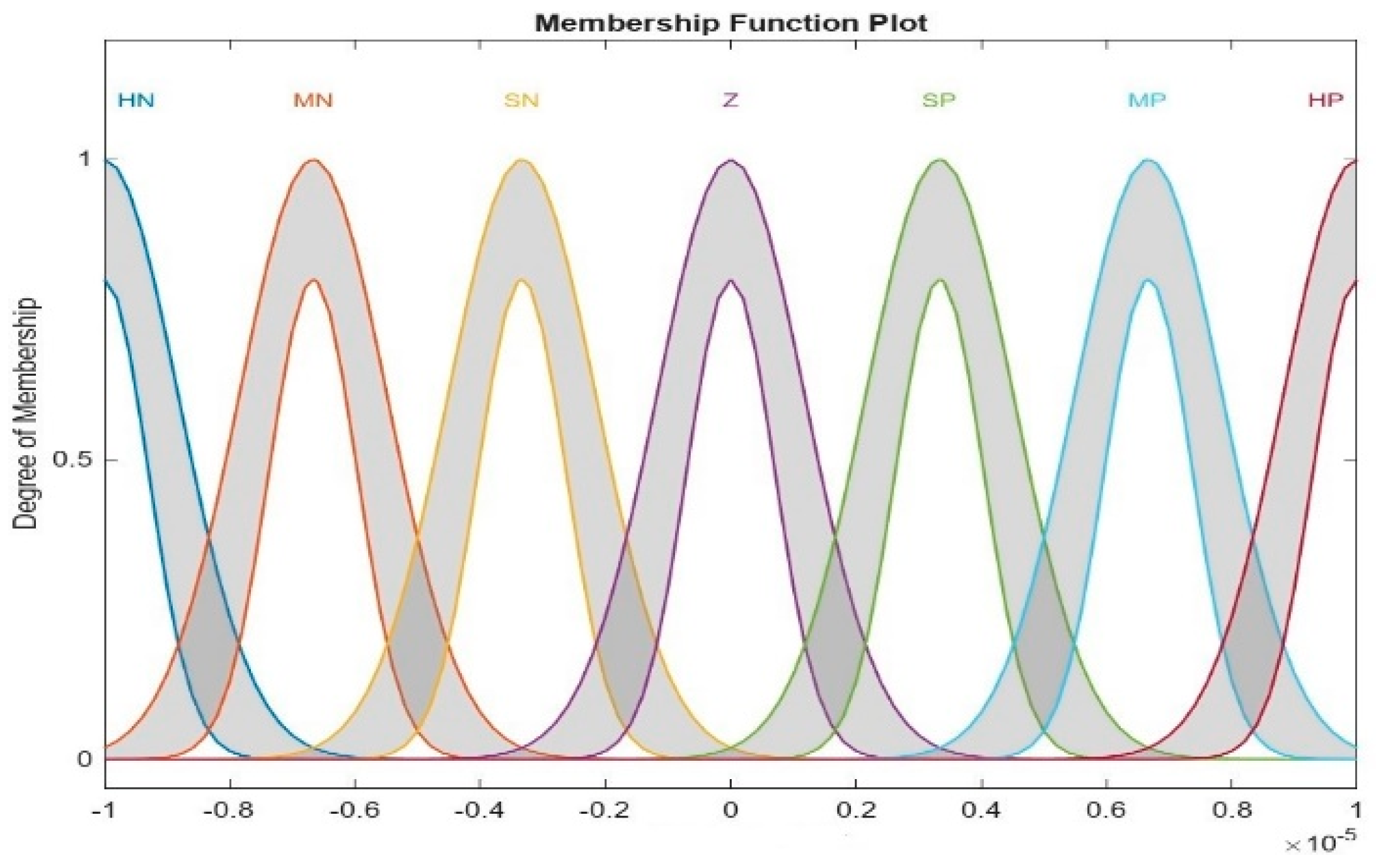
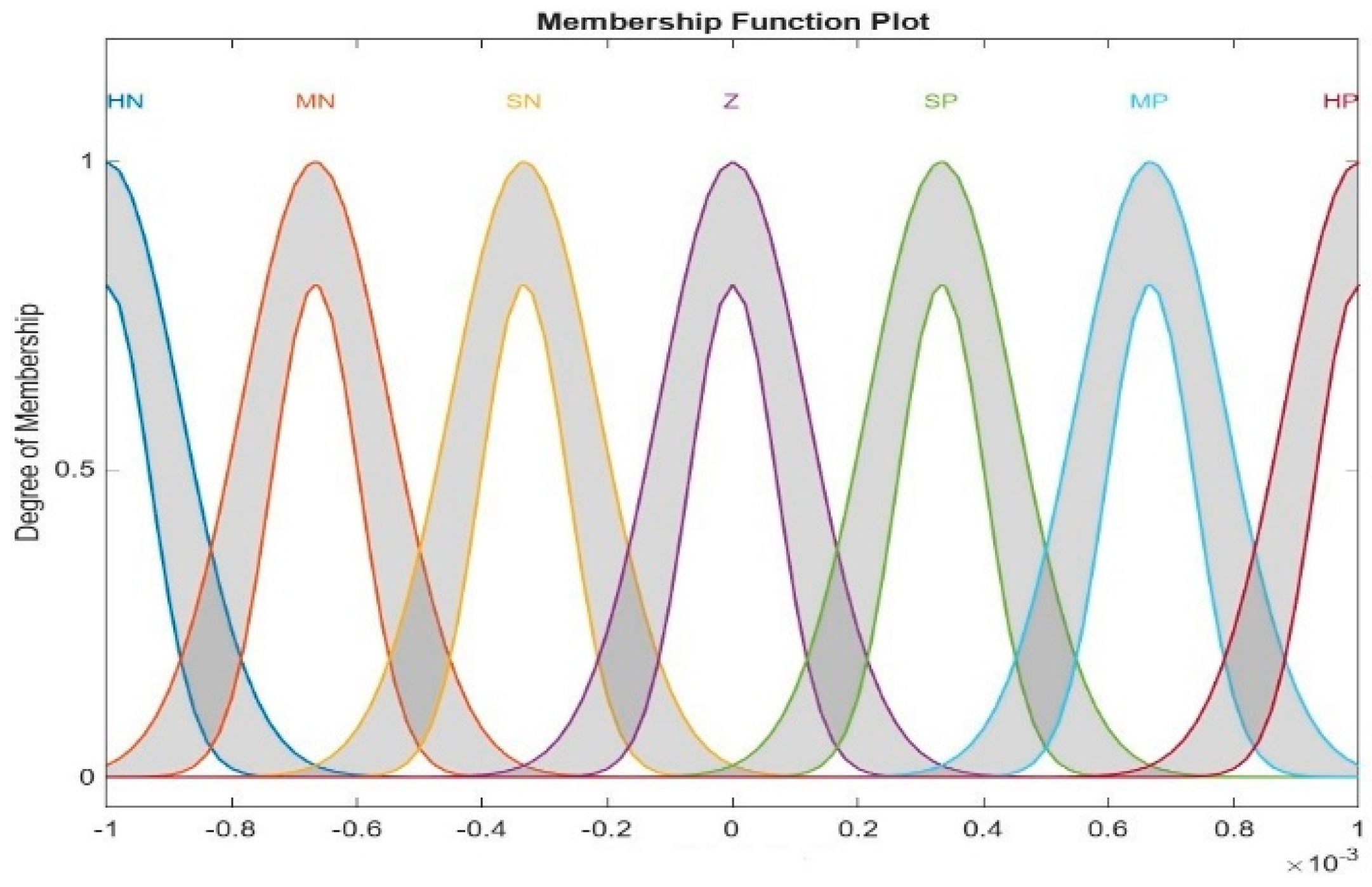
IT2F logic sets in this paper consist of two inputs, namely the Area Control Error (ACE) and ACE derivative (de_ACE), and three outputs, namely Kp, Ki, and Kd. The number of membership functions for each of the inputs and outputs is seven, shown via linguistic variables: High Negative (HN), Medium Negative (MN), Small Negative (SN), Zero (Z), Small Positive (SP), Medium Positive (MP), and High Positive (HP). They are shown in Figure 5 and Figure 6. The type of membership function used is Gaussian for inputs and outputs, and the type reduction method used is the Karnik–Mendel (KM) method because it is an extensive, widely utilized approach for T2F logic uses [41]. The type of fuzzy inference system used is Mamdani type-2, and the centroid method is employed for defuzzification. Table 2 illustrates details about the T2F logic system.

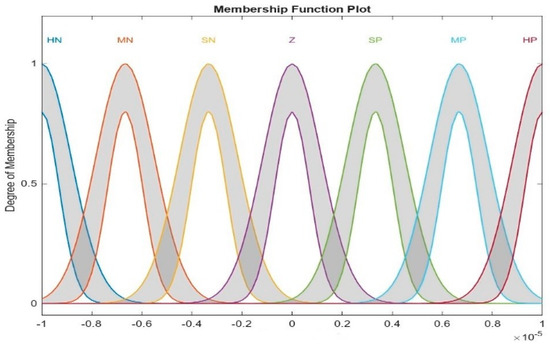
Figure 5. Membership function of ACE and de_ACE.

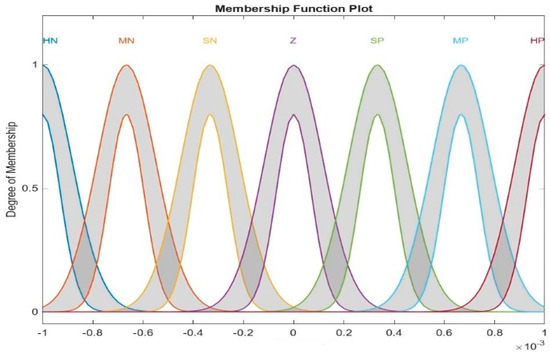
Figure 6. Membership function of Kp, Ki, and Kd.

Table 2. Variables of T2F logic system.

Variables	Selection
And method	min
Or method	max
Implication method	min
Aggregation method	max
Lower scale	0.8
Lower Lag	0.2

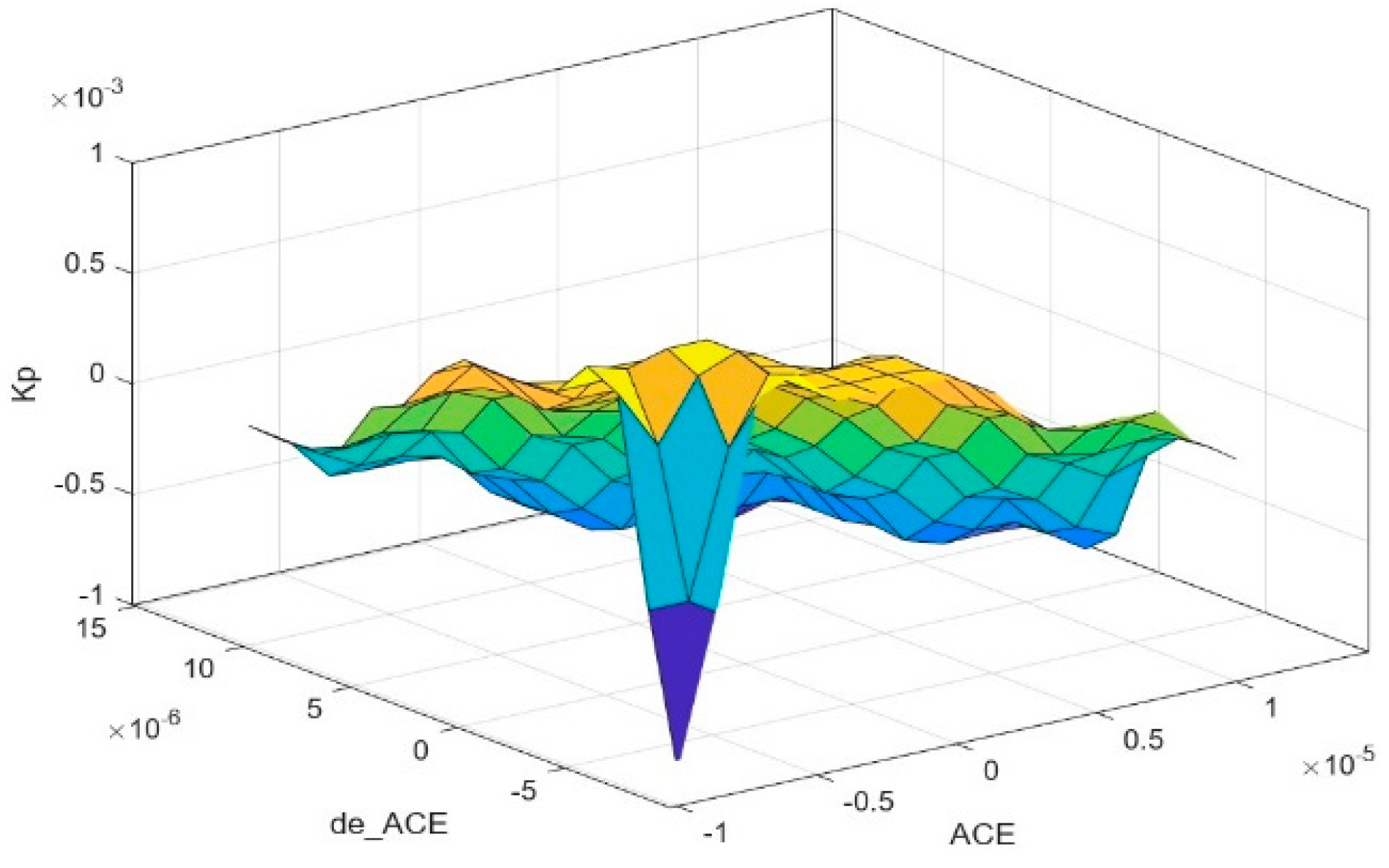
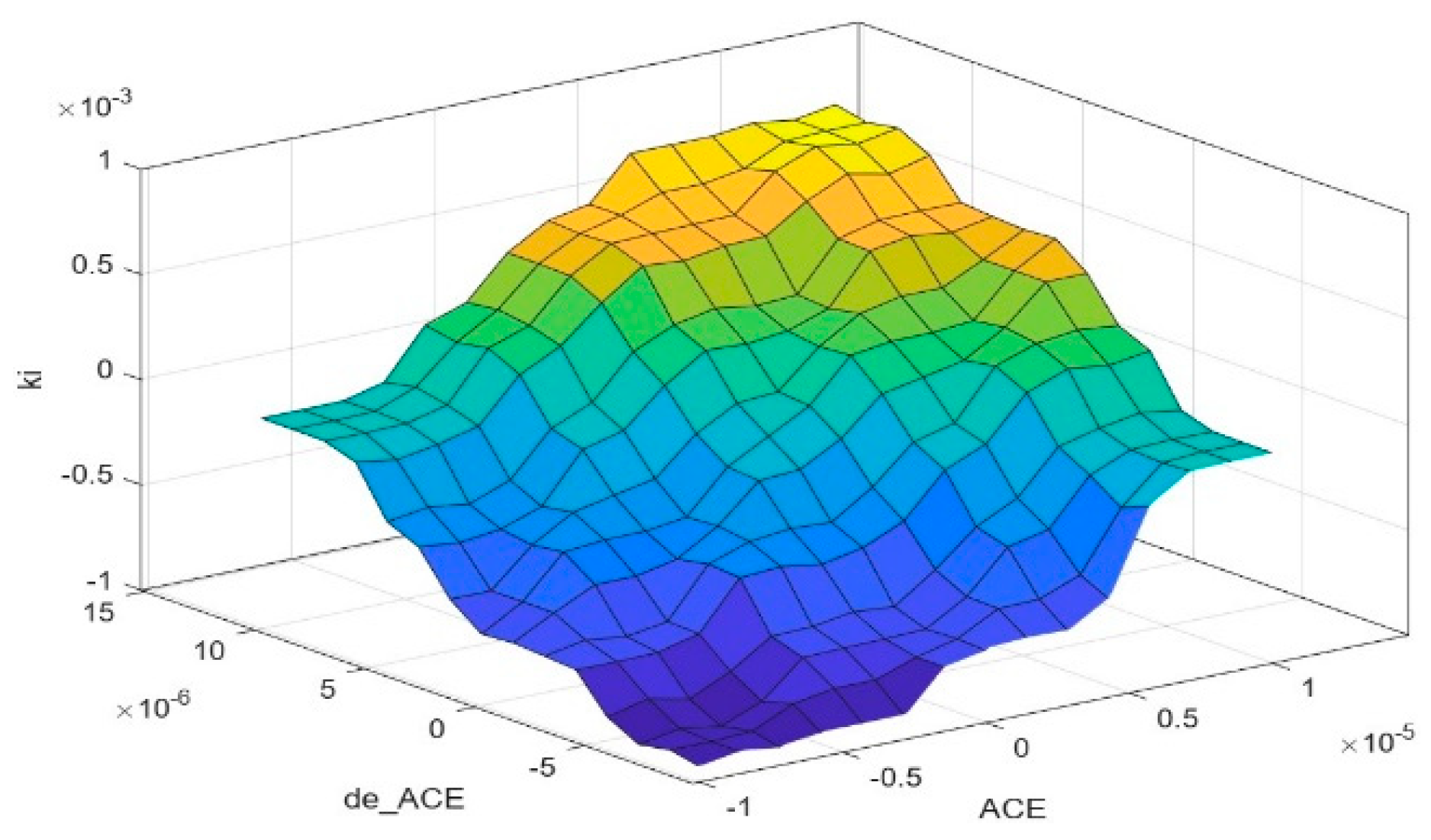
IF-THEN is the rule-based structure utilized by the fuzzy rule base, provided via the IF antecedent, THEN result [42]. This paper’s rule base consists of 49 rules, as illustrated in Table 3, Table 4 and Table 5. Additionally, the Kp, Ki, and Kd control surfaces are shown in Figure 7, Figure 8 and Figure 9.

Table 3. Rule Table for Kp.

	ACE	HN	MN	SN	Z	SP	MP	HP
de_ACE
HN		HN	HP	MP	MP	SP	SP	Z
MN		HP	HP	MP	MP	SP	Z	Z
SN		MP	MP	MP	SP	Z	SN	MN
Z		MP	SP	SP	Z	SN	MN	MN
SP		SP	SP	Z	SN	SN	MN	MN
MP		Z	Z	SN	MN	MN	MN	HN
HP		Z	SN	SN	MN	MN	HN	HN

Table 4. Rule Table for Ki.

	ACE	HN	MN	SN	Z	SP	MP	HP
de_ACE
HN		HN	HN	HN	MN	MN	Z	Z
MN		HN	HN	MN	MN	SN	Z	Z
SN		MN	MN	SN	SN	Z	SP	SP
Z		MN	SN	SN	Z	SP	SP	MP
SP		SN	SN	Z	SP	SP	MP	MP
MP		Z	Z	SP	MP	MP	HP	HP
HP		Z	Z	SP	MP	MP	HP	HP

Table 5. Rule Table for Kd.

	ACE	HN	MN	SN	Z	SP	MP	HP
de_ACE
HN		SP	SP	Z	Z	Z	HP	HP
MN		SN	SN	SN	SN	Z	SP	MP
SN		HN	HN	MN	SN	Z	SP	MP
Z		HN	MN	MN	SN	Z	SP	MP
SP		HN	MN	SN	SN	Z	SP	SP
MP		MN	SN	SN	SN	Z	SP	SP
HP		SP	Z	Z	Z	Z	HP	HP

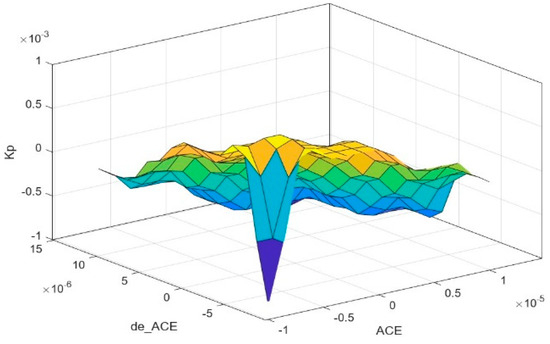
Figure 7. Control surface of Kp.

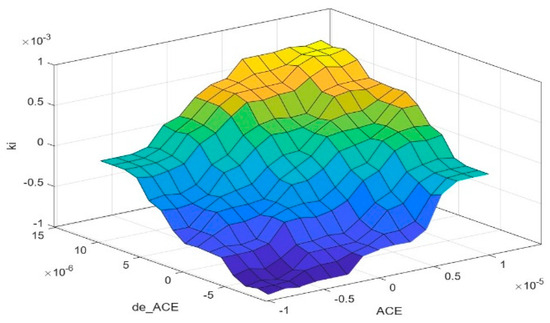
Figure 8. Control surface of Ki.

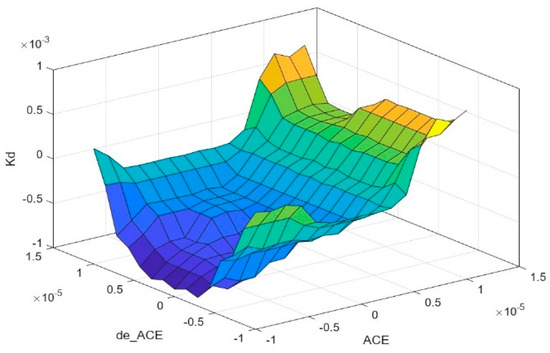
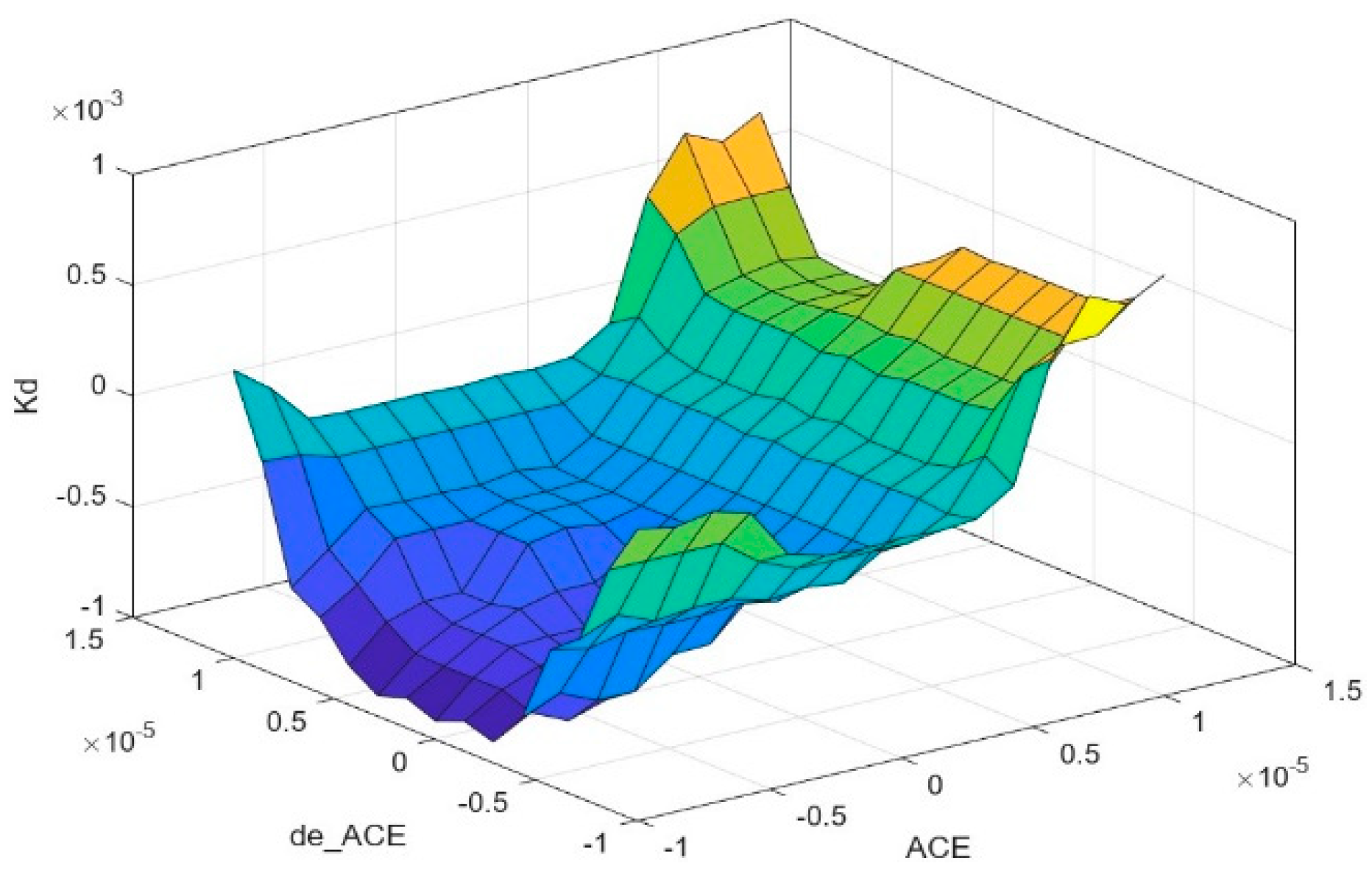
Figure 9. Control surface of Kd.

According to the rules in the tables, 49 laws can be created to determine the linguistic value of the outputs, which are Kp, Ki, and Kd. For example:

Rule: IF ACE is HN and de_ACE is HN, then Kp is HN, ki is HN, and Kd is SP.

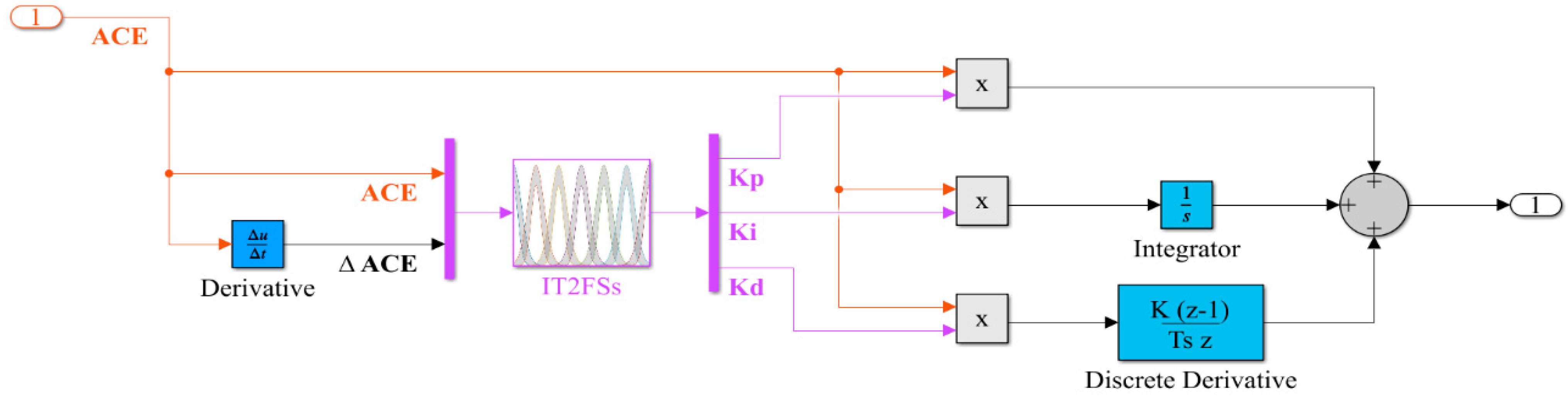
2.2.2. IT2FSs-PID Controller

Through the previous part, a design was made to tune the PID parameters via IT2FSs, as shown in Figure 10.

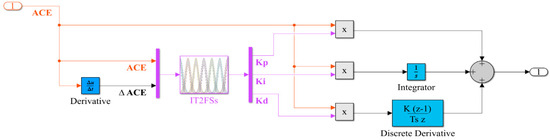
Figure 10. IT2FSs-PID structure.

The following equations represent the signal exiting the controller in the two areas of the LFC system [21]:

$$u{\left(t\right)}_{IT2FSs-PID \left(1\right)}=K_p AC{E}_{\left(1\right)}+K_{i }{\displaystyle \int }AC{E}_{\left(1\right)} dt+K_{d } {\displaystyle \frac{d\left(AC{E}_{\left(1\right)}\right)}{dt}}$$

(5)

$$u{\left(t\right)}_{IT2FSs-PID \left(2\right)}=K_p AC{E}_{\left(2\right)}+K_{i }{\displaystyle \int }AC{E}_{\left(2\right)} dt+K_{d } {\displaystyle \frac{d\left(AC{E}_{\left(2\right)}\right)}{dt}}$$

(6)

where u(t) denotes the signal coming out of the controller and the value of Kp, Ki, and Kd are set via IT2FSs. Also, the following two Equations (7) and (8) provide the ACE value of the two areas power system:

$$AC{E}_{\left(1\right)}=\Delta P_{tie,12}+B_{\left(1\right)}\Delta f_{\left(1\right)}$$

(7)

$$AC{E}_{\left(2\right)}=\Delta P_{tie,21}+B_{\left(2\right)}\Delta f_{\left(2\right)}$$

(8)

Several methods are proposed in the literature to improve power system control by tuning the frequency bias (B) using one of the optimization methods discussed in [21,22]. In this paper, the value of the frequency base is fixed in both areas, and another strategy is used to enhance the stability of the power system. The strategy uses ATCSC to affect power deviations of the tie line $\left(\Delta P_{tie}\right)$ positively to reduce the ACE to zero, as will be discussed in the next section.

2.2.3. Advanced Thyristor Controlled Series Capacitor (ATCSC)

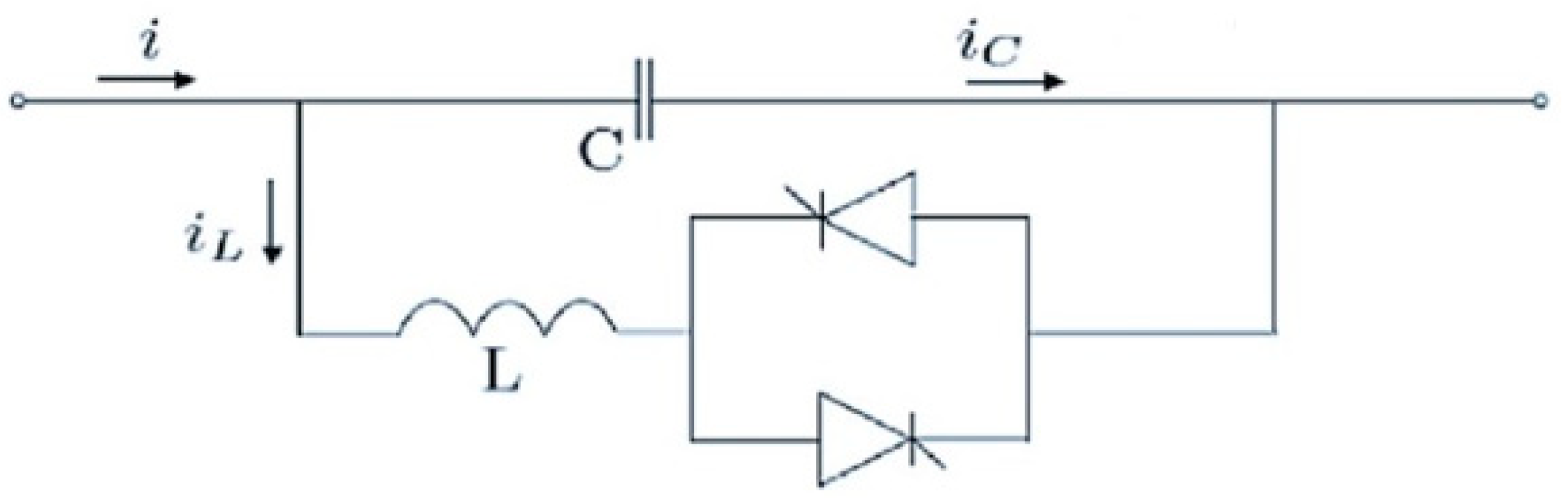
FACTS devices offer enhanced controllability when compared to conventional devices, and they do not contain any dynamic control-providing movable parts, such as mechanical switches [43]. FACTS devices can be configured in two distinct ways: as Series devices or as Shunt devices [43]. TCSC is affiliated with the FACTS group. The TCSC comprises a capacitive reactance in parallel with a Thyristor Controlled Reactor (TCR), as shown in Figure 11, and is mainly used to suppress oscillations, which reflect positively on the stability of the power system and also solve the problem of sub-synchronous oscillation (SSR) [44].

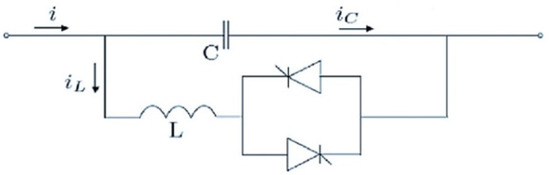
Figure 11. Components of TCSC.

In this work, the ATCSC is installed in series with a tie line connecting the two areas, as shown in Figure 12.

Figure 12. Two-area interconnected thermal power system with ATCSC in series with the tie line.

The following equations illustrate the ATCSC principle [18]:

$$P_{12}={\displaystyle \frac{\left|V_1\right|\left|V_2\right|}{X_{12}-X_{TCSC}}}\mathit{sin}{\delta }_{12}$$

(9)

Equation (9) expresses the value of tie line power flow between two areas, where the variables V1 and V2 illustrate the voltage magnitude of the two areas. Also, X12 represents the tie line reactance, XTCSC represents the TCSC reactance, and ${\delta }_{12}$ denotes the voltage angle. Equation (9) is expressed as Equation (10) if we consider Kc = XTCSC/X12, where Kc denotes the series compensation ratio.

$$P_{12}={\displaystyle \frac{\left|V_1\right|\left|V_2\right|}{X_{12}\left(1-K_C\right)}}\mathit{sin}{\delta }_{12}$$

(10)

One can rewrite Equation (11) as follows [18]:

$$\Delta P_{12}={\displaystyle \frac{\left|V_1\right|\left|V_2\right|}{X_{12}}}\mathit{sin}{\delta }_{12}+{\displaystyle \frac{K_C}{\left(1-K_C\right)}}·{\displaystyle \frac{\left|V_1\right|\left|V_2\right|}{X_{12}}}\mathit{sin}{\delta }_{12}$$

(11)

The second part of Equation (11) shows the effect of TCSC due to the presence of Kc/(1 − Kc). When small disturbances occur in ${\delta }_{12}=\left({\delta }_1-{\delta }_2\right)$ and Kc, the incremental tie line power flow can be expressed by the following equation [18]:

$$\Delta P_{12}={\displaystyle \frac{\left|V_1\right|\left|V_2\right|}{X_{12}\left(1-K_C\right)}}\cos {\delta }_{12}^{°}·\mathit{sin}\Delta {\delta }_{12}+{\displaystyle \frac{\Delta K_C}{\left(1-\Delta K_C\right)}}·{\displaystyle \frac{\left|V_1\right|\left|V_2\right|}{X_{12}}}\mathit{sin}{\delta }_{12}^{°}$$

(12)

When a slight change in power occurs, the change in voltage angle is little. Therefore, it is acceptable to estimate ($\sin \Delta {\delta }_{12}\backsimeq \Delta {\delta }_{12})$, so the equation may be expressed in the following format [44]:

$$\Delta P_{12}={\displaystyle \frac{\left|V_1\right|\left|V_2\right|}{X_{12}\left(1-K_C\right)}}\mathit{cos}{\delta }_{12}^{°}·\Delta {\delta }_{12}+{\displaystyle \frac{\Delta K_C}{\left(1-\Delta K_C\right)}}·{\displaystyle \frac{\left|V_1\right|\left|V_2\right|}{X_{12}}}\mathit{sin}{\delta }_{12}^{°}$$

(13)

where

$${\mathrm{T}}_{12}={\displaystyle \frac{\left|{\mathrm{V}}_1\right|\left|{\mathrm{V}}_2\right|}{{\mathrm{X}}_{12}\left(1-{\mathrm{K}}_{\mathrm{C}}\right)}}\cos {\delta }_{12}^{°} \mathrm{and} {\mathrm{K}}_{\mathrm{l}}={\displaystyle \frac{\left|{\mathrm{V}}_1\right|\left|{\mathrm{V}}_2\right|}{{\mathrm{X}}_{12}}}\sin {\delta }_{12}^{°}$$

(14)

When T₁₂ denotes the synchronizing coefficient and K₁ is a constant, the equation becomes as follows [18]:

$$\Delta P_{12}=T_{12}·\Delta {\delta }_{12}+{\displaystyle \frac{\Delta K_C}{\left(1-\Delta K_C\right)}}·K_l \mathrm{Where} \Delta {\delta }_{12}=\Delta {\delta }_1-\Delta {\delta }_2$$

(15)

When $\Delta {\delta }_1=2\pi \int \Delta f_1 dt$ and $\Delta {\delta }_2=2\pi \int \Delta f_2 dt$

$$\begin{gathered} \Delta {\delta }_{12}=2\pi {\displaystyle \int }\Delta f_1 dt-2\pi {\displaystyle \int }\Delta f_2 dt \\ =2\pi \left({\displaystyle \int }\Delta f_1 dt-{\displaystyle \int }\Delta f_2 dt\right) \end{gathered}$$

(16)

Take a LaPlace transform [18]:

$$\Delta P_{12}={\displaystyle \frac{2\pi T_{12}}{S}}\left[\Delta F_1\left(s\right)-\Delta F_2\left(s\right)\right]+{\displaystyle \frac{\Delta K_C}{\left(1-\Delta K_C\right)}}·K_l$$

(17)

The Taylor series was used to expand the second part of Equation (18), as shown in Equation (18) [18]

$${\displaystyle \frac{\Delta K_C}{\left(1-\Delta K_C\right)}}=\Delta K_c+\Delta K_c^2+\Delta K_c^3+\Delta K_c^4+\Delta K_c^5+\Delta K_c^6+\dots$$

(18)

$$\Delta P_{12}^{°}={\displaystyle \frac{2\pi T_{12}}{S}}\left[\Delta F_1\left(s\right)-\Delta F_2\left(s\right)\right]$$

(19)

Based on Equations (18) and (19), we can rewrite Equation (17) as follows [18]:

$$\Delta P_{12}=\Delta P_{12}^{°}+\left(\Delta K_c+\Delta K_c^2+\Delta K_c^3+\Delta K_c^4+\Delta K_c^5+\Delta K_c^6+\dots \right)·K_l$$

(20)

$$\mathrm{where} \Delta K_C\left(S\right)={\displaystyle \frac{K_{TCSC}}{1+s{T}_{TCSC}}}·\Delta Error \left(S\right)$$

(21)

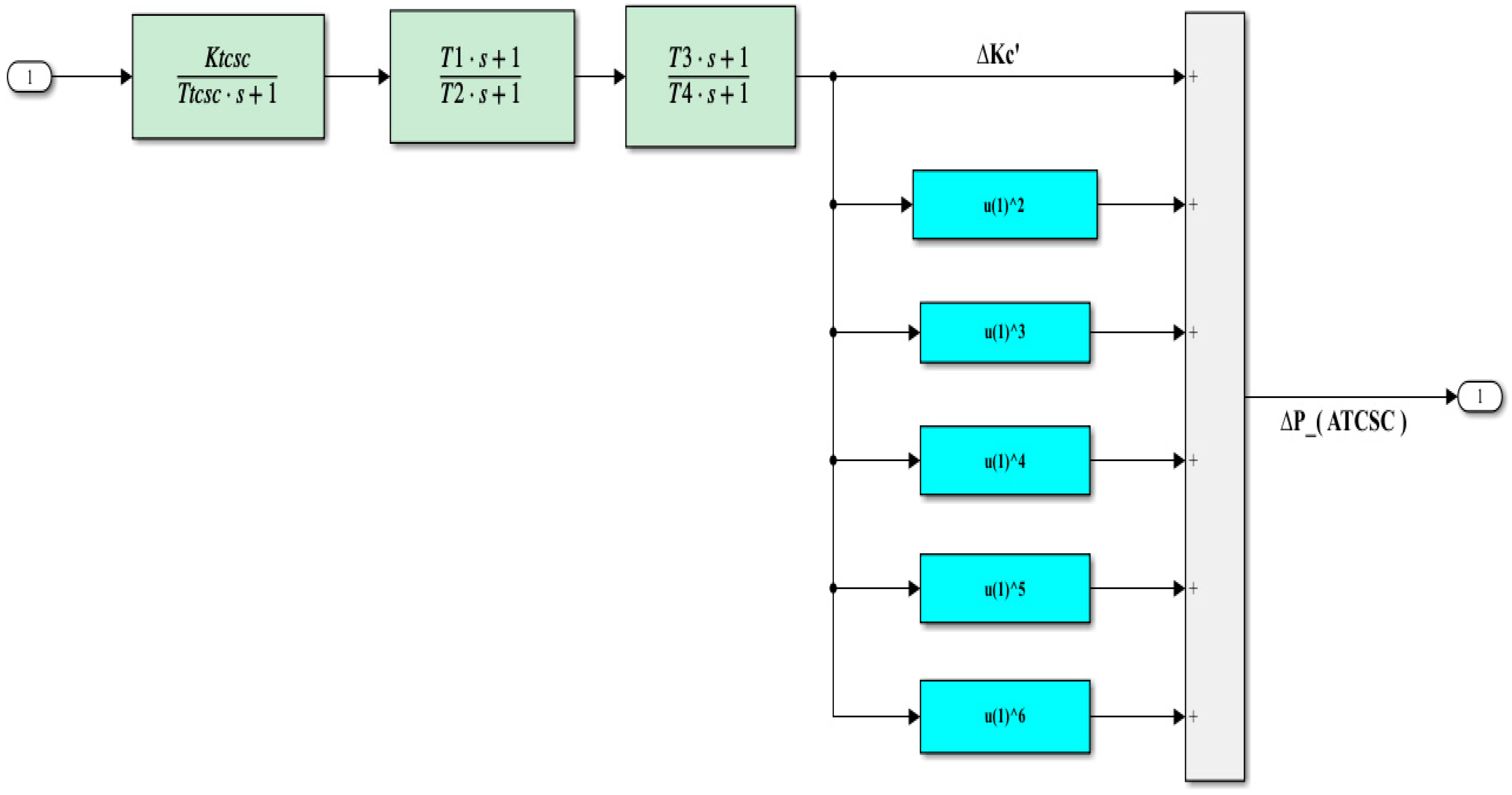
We used the first six terms of Equation (18) to increase the ATCSC’s effectiveness for power system stability. Figure 13 shows the $\Delta {\mathrm{P}}_{\mathrm{ATCSC}}$ structure with utilized lead-lag blocks [18].

$$\Delta P_{ATCSC}=\Delta K_c^{\prime }+\Delta K_c^{\prime 2}+\Delta K_c^{\prime 3}+\Delta {K^{\prime }}_c^4+\Delta K_c^{\prime 5}+\Delta K_c^{\prime 6}$$

(22)

where $\Delta K_C^{\prime }\left(S\right)={\displaystyle \frac{{K^{\prime }}_{TCSC}}{1+s{T}_{TCSC}}}·\Delta F\left(S\right)$.

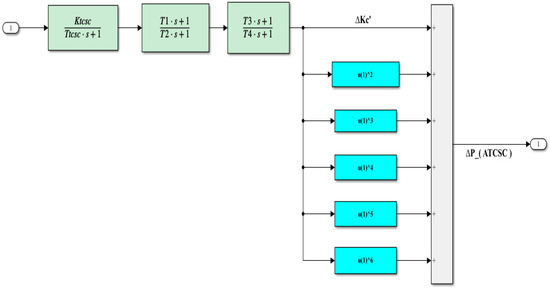
Figure 13. Structure for the ATCSC [18].

Depending on Equations (19) and (22), we can write the subsequent equation as follows [18]:

$$\Delta P_{12}=\Delta P_{12}^{°}+\Delta P_{ATCSC}$$

(23)

In this paper, when the ATCSC is connected between area-1 and the tie line, Equation (24) is used, but if it is connected to area-2, Equation (26) is used.

$$\Delta P_{12}=\Delta P_{12}^{°}+\Delta P_{ATCS{C}_{\Delta F1}}$$

(24)

$$\mathrm{where} \Delta K_{c_1}^{\prime }\left(S\right)={\displaystyle \frac{{K^{\prime }}_{TCS{C}_1}}{1+s{T}_{TCS{C}_1}}}·\Delta F_1\left(S\right)$$

(25)

$$\Delta P_{12}=\Delta P_{12}^{°}+\Delta {\mathrm{P}}_{{ \mathrm{ATCSC}}_{\Delta \mathrm{F}2}}$$

(26)

$$\mathrm{where} \Delta K_{c_2}^{\prime }\left(S\right)={\displaystyle \frac{{K^{\prime }}_{TCS{C}_2}}{1+s{T}_{TCS{C}_2}}}·\Delta F_2\left(S\right)$$

(27)

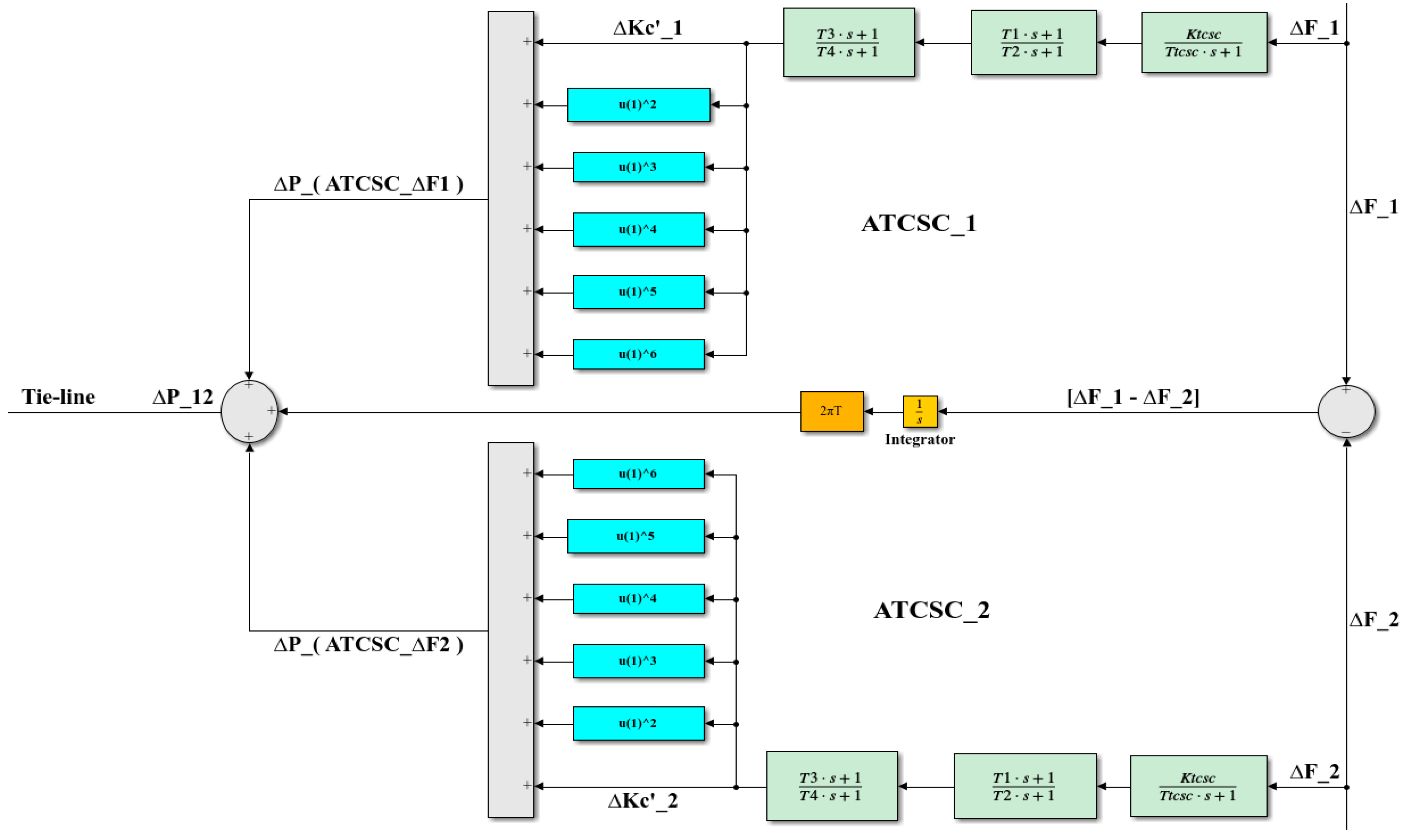
Figure 14 shows the structure to be used when there are two ATCSCs, one of which is connected to area-1 and the other is connected to area-2. For this case, we represent the ATCSCs with the following equation:

$$\Delta P_{12}=\Delta P_{12}^{°}+\Delta P_{ ATCS{C}_{\Delta F1}}+\Delta P_{ ATCS{C}_{\Delta F2}}$$

(28)

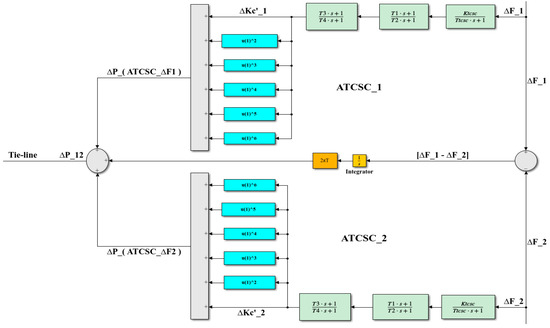
Figure 14. A proposed structure for two ATCSCs connected to two areas with a tie line.

2.2.4. Optimization Algorithm and Objective Function

The process of the SA algorithm involves a series of steps that transition from the present answer to a superior one, following certain criteria. It periodically accepts suboptimal solutions to ensure a wide exploration of the problem space and avoid becoming stuck at local optimal solutions [45]. The SA algorithm is a randomized search method derived from statistical mechanics [46]. By using the Integral of Time multiplied by the Absolute Error (ITAE) as a cost function, the efficiency of the power system can be significantly improved [47]. In this paper, ITAE is used as a cost function to reduce the error signal, including frequency deviation $\left(\Delta f_1,\Delta f_2\right)$, $\left(\Delta P_{ti{e}_{ 12}}\right)$, and terminal voltage deviation $\left(\Delta V_{t_1},\Delta V_{t_2}\right)$. Equation (29) illustrates this.

$$J_{ITAE}={{\displaystyle \int }}_{\mathrm{t}=0}^{t_{final}}t \left(\left|\Delta f_1\right|+\left|\Delta f_2\right|+\left|\Delta P_{ti{e}_{ 12}}\right|+\left|\Delta V_{t_1}\right|+\left|\Delta V_{t_2}\right|\right)dt$$

(29)

Parameters for both PID_AVR and ATCSC are defined by establishing a specific scenario that generates a disturbance in both areas (area-1, area-2). $\Delta P_{\mathrm{L}}=0.02 p.u$ represents the increase in load at time t = 0 s. The following range is defined to specify appropriate values for the controller parameters:

• ATCSC range: [0.5, 1 × 10⁻⁵]

$$\begin{gathered} K_{{TCSC}_{max}}\ge K_{TCSC}\ge K_{{TCSC}_{min}} \\ {T}_{{TCSC}_{max}}\ge T_{TCSC}\ge T_{{TCSC}_{min}} \\ {T}_{1_{max}}\ge T_1\ge T_{1_{min}} \\ {T}_{2_{max}}\ge T_2\ge T_{2_{min}} \\ {T}_{3_{max}}\ge T_3\ge T_{3_{min}} \\ {T}_{4_{max}}\ge T_4\ge T_{4_{min}} \end{gathered}$$

• PID_AVR range: [2, 0.01]

$$\begin{gathered} {K_p}_{max}\ge K_p\ge {K_p}_{min} \\ {K_i}_{max}\ge K_i\ge {K_i}_{min} \\ {K_i}_{max}\ge K_i\ge {K_i}_{min} \end{gathered}$$

3. Results and Discussion

This section delves into the simulations conducted on the power system, examining the effectiveness of the controllers in modifying the system’s dynamic response and presenting the findings from this simulation. An increase in load demand equal to $\Delta P_L=0.02 p.u$ is used in both areas of the power system model. Then, the IT2FSs-PID controller in LFC, the SA-PID controller in AVR, and SA-ATCSC are used to make the system more stable. Most of the simulations in this paper focus on this method. An additional ATCSC is added to a final case, and its impact on the power system is observed. The values of the power system modeling can be found in [48]. Table 6 shows the tuning parameter values for both ATCSC and PID_AVR.

Table 6. ATCSC and PID_AVR parameter values.

ATCSC Parameters	Tuning Values	PID Parameters	Tuning Values
KTCSC	0.48374	P1 1	1.06491
TTCSC	0.38333	I1	1.06491
T1	0.31167	D1	1.06491
T2	0.08869	P2 2	0.28211
T3	0.20292	I2	0.1
T4	0.09144	D2	0.1

¹ PID value of Area-1. ² PID value of Area-2.

3.1. Influence of Controllers on a Two-Area Interconnected Thermal Power System

Table 7 shows that the power system is unstable because the settling time values of $\Delta f_1$, $\Delta f_2$, $V_{t_1}$, $V_{t_1}$ and $\Delta P_{tie}$ are infinite. In this case, the LFC system did not use the IT2FSs-PID controller, and the tie line did not use TCSC or ATCSC. PID-SA exists in the AVR system, so according to Table 8, it is clear that frequency stability affects the terminal voltage stability.

Table 7. Dynamic performance of a power system without employing IT2FSs-PID, ATCSC, or TCSC.

Variation of Parameters	$\mathbf{\Delta }{\mathit{f}}_1$	$\mathbf{\Delta }{\mathit{f}}_2$	${\mathit{V}}_{{\mathit{t}}_1}$	${\mathit{V}}_{{\mathit{t}}_2}$	$\mathbf{\Delta }{\mathit{P}}_{\mathit{t}\mathit{i}\mathit{e}}$
Settling Time (s)	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$
Settling Min (Hz, P.u)	−2.56 × 104	−5.04 × 105	−3.28 × 102	−5.04 × 105	−2.85 × 104
Settling Max (Hz, P.u)	3.23 × 104	4.00 × 105	4.15 × 102	4.00 × 105	3.59 × 104
Rise Time (s)	-	-	0.1435	0.9591	-

Table 8. Sensitivity analysis of frequency deviation and power deviation.

Variation of Parameters		Settling Time (s)			Settling Max (Hz, P.u)			Settling Min (Hz, P.u)			${\mathit{J}}_{\mathit{I}\mathit{T}\mathit{A}\mathit{E}}$
		$\mathbf{\Delta }{\mathit{f}}_1$	$\mathbf{\Delta }{\mathit{f}}_2$	$\mathbf{\Delta }{\mathit{P}}_{\mathit{t}\mathit{i}\mathit{e}}$	$\mathbf{\Delta }{\mathit{f}}_1$	$\mathbf{\Delta }{\mathit{f}}_2$	$\mathbf{\Delta }{\mathit{P}}_{\mathit{t}\mathit{i}\mathit{e}}$	$\mathbf{\Delta }{\mathit{f}}_1$	$\mathbf{\Delta }{\mathit{f}}_2$	$\mathbf{\Delta }{\mathit{P}}_{\mathit{t}\mathit{i}\mathit{e}}$
Basic case		3.6633	8.4554	6.0172	0.0518	0.2949	0.0089	−0.67	−0.7875	−0.2674	4.36
$\Delta P_L$	−50%	4.8775	8.8251	6.0201	0.0494	0.2980	0.0089	−0.6572	−0.7841	−0.2654	4.363
	50%	3.6575	8.4494	6.0143	0.0543	0.2918	0.0090	−0.6829	−0.7918	−0.2693	4.359
$P_s$	−50%	3.6517	10.0034	5.2684	0.0332	0.3014	0.0060	−0.6785	−0.7758	−0.2599	5.023
	50%	4.7826	7.7287	6.63486	0.0691	0.2865	0.0157	−0.6622	−0.7976	−0.2736	3.892
$T_g$	−50%	2.9464	3.4156	2.8907	0.0061	0.0736	0.0022	−0.6552	−0.6977	−0.2660	2.39
	50%	8.5307	18.3991	11.9905	0.0940	0.4755	0.0328	−0.6805	−0.8563	−0.2686	14.51
$T_t$	−50%	3.1789	4.0247	2.9119	0.0067	0.0514	0.0023	−0.6391	−0.6776	−0.2610	2.409
	50%	7.2140	15.7777	10.2428	0.1165	0.4743	0.0271	−0.6857	−0.8657	−0.2600	11.47

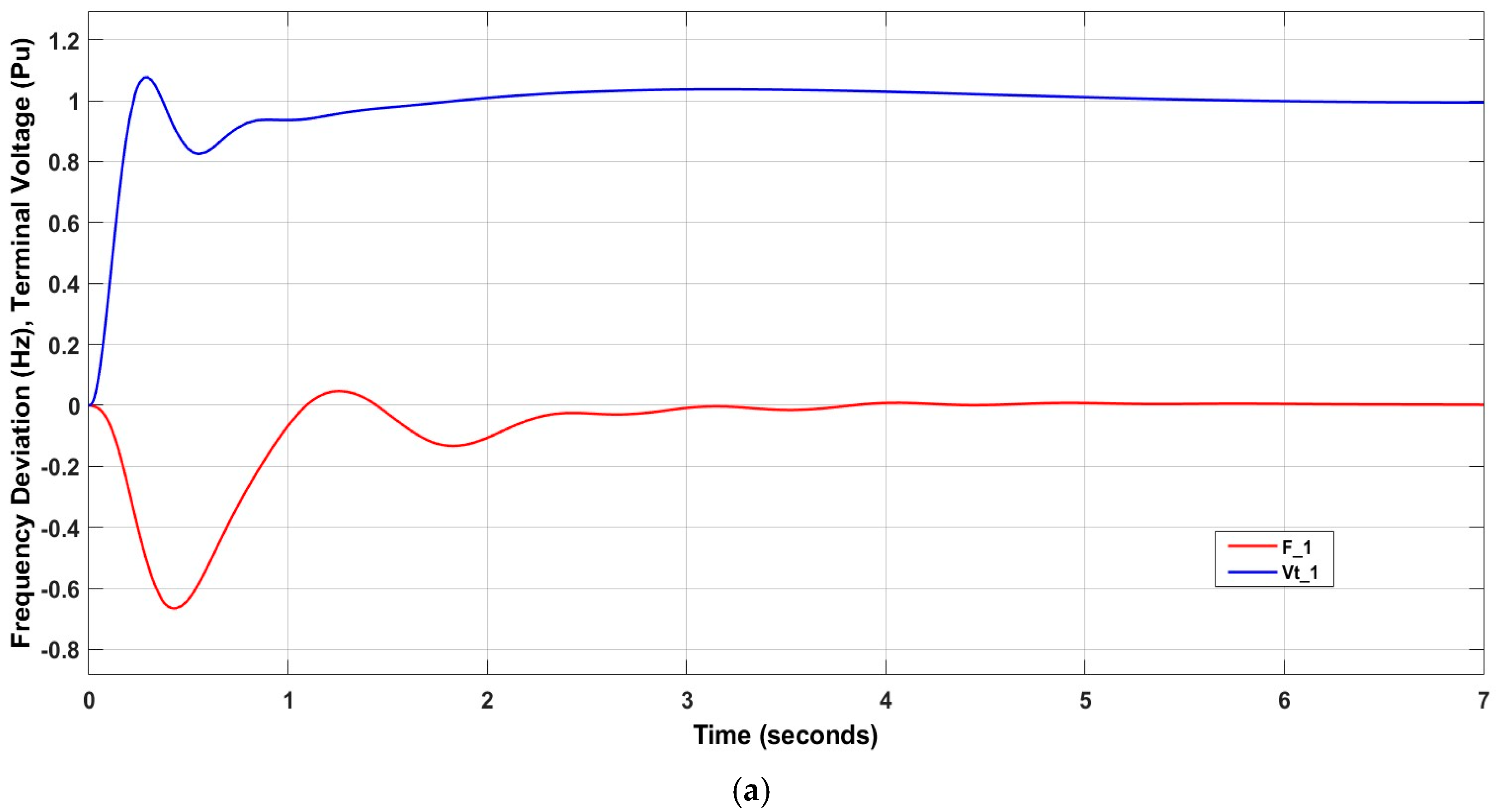
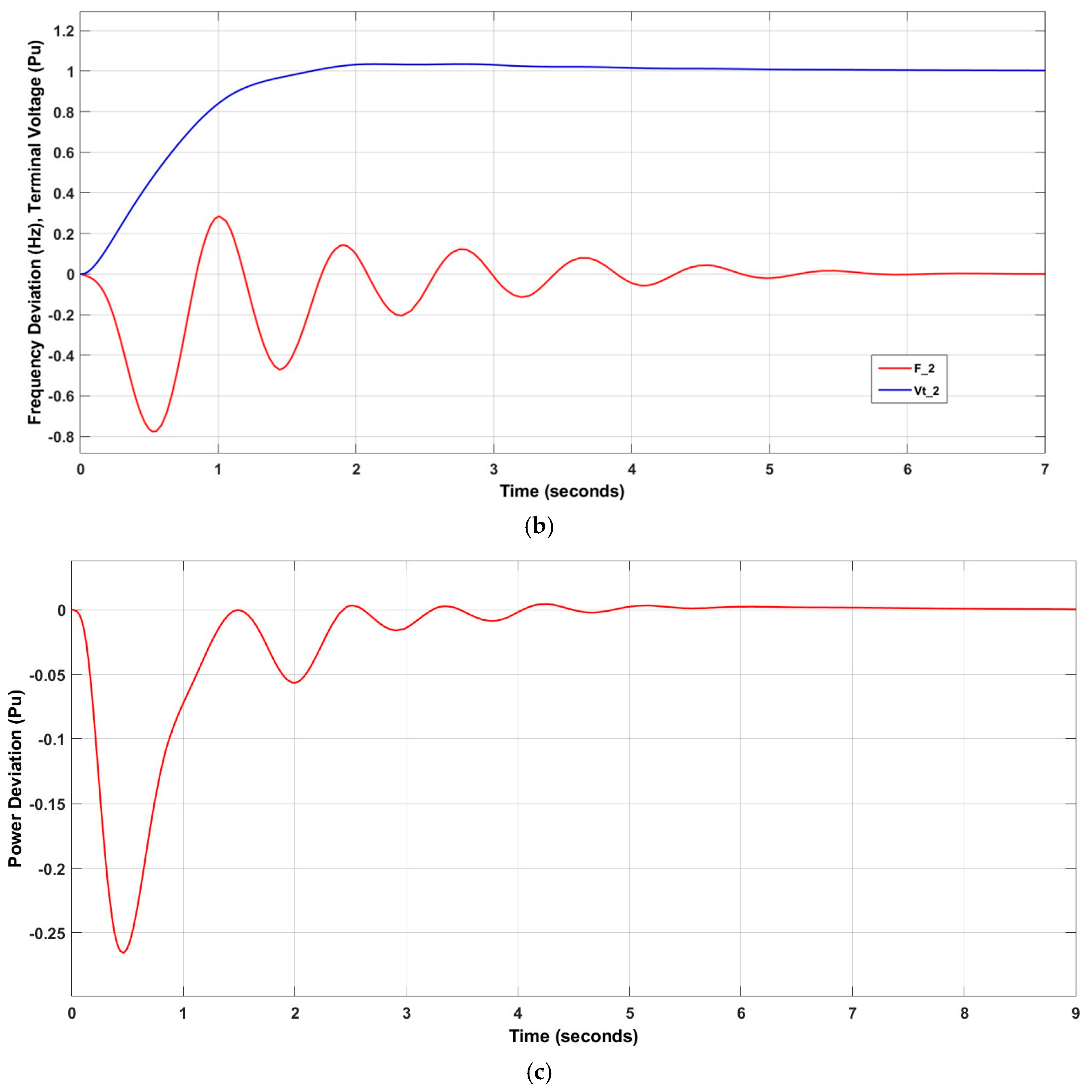
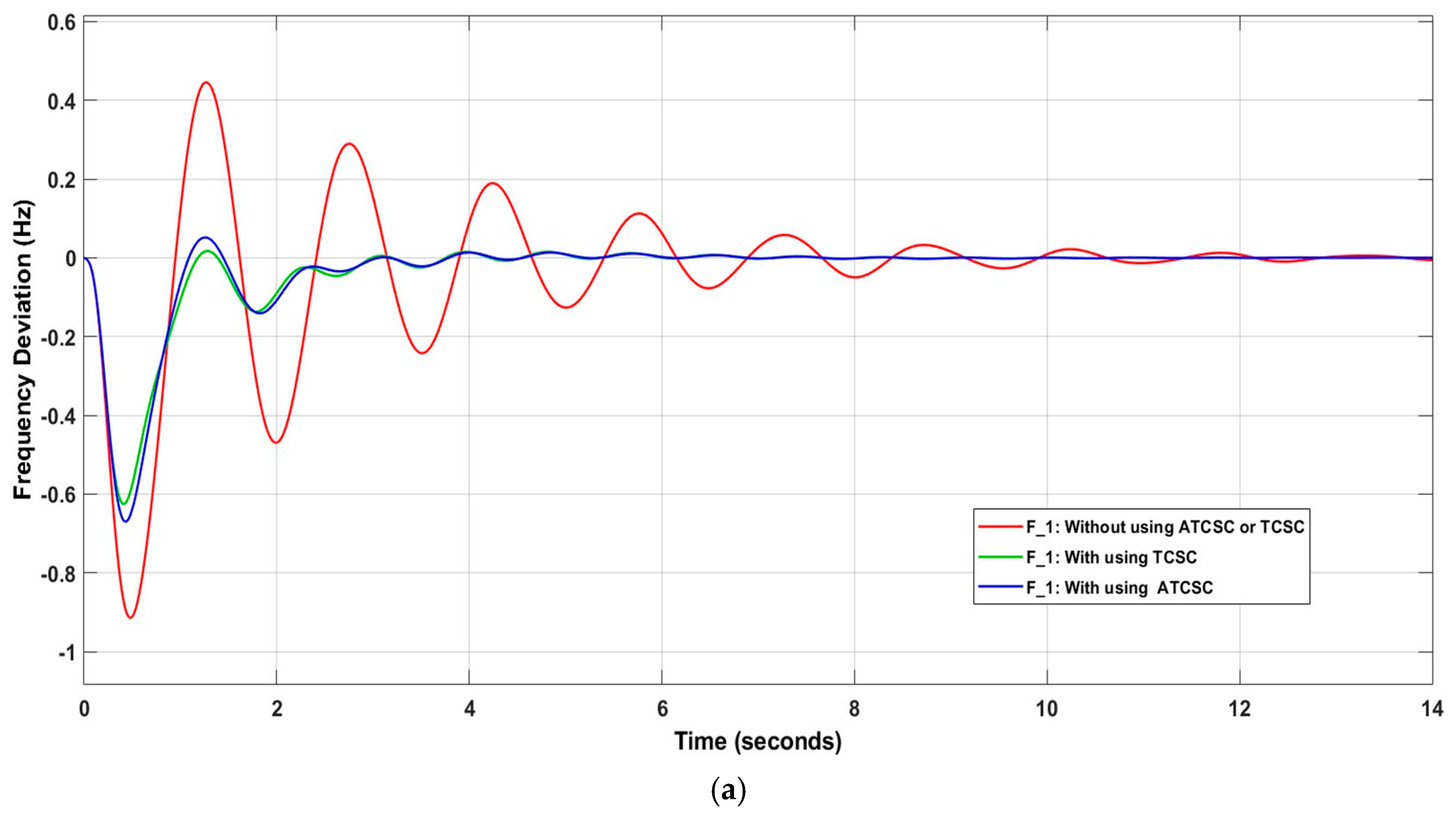
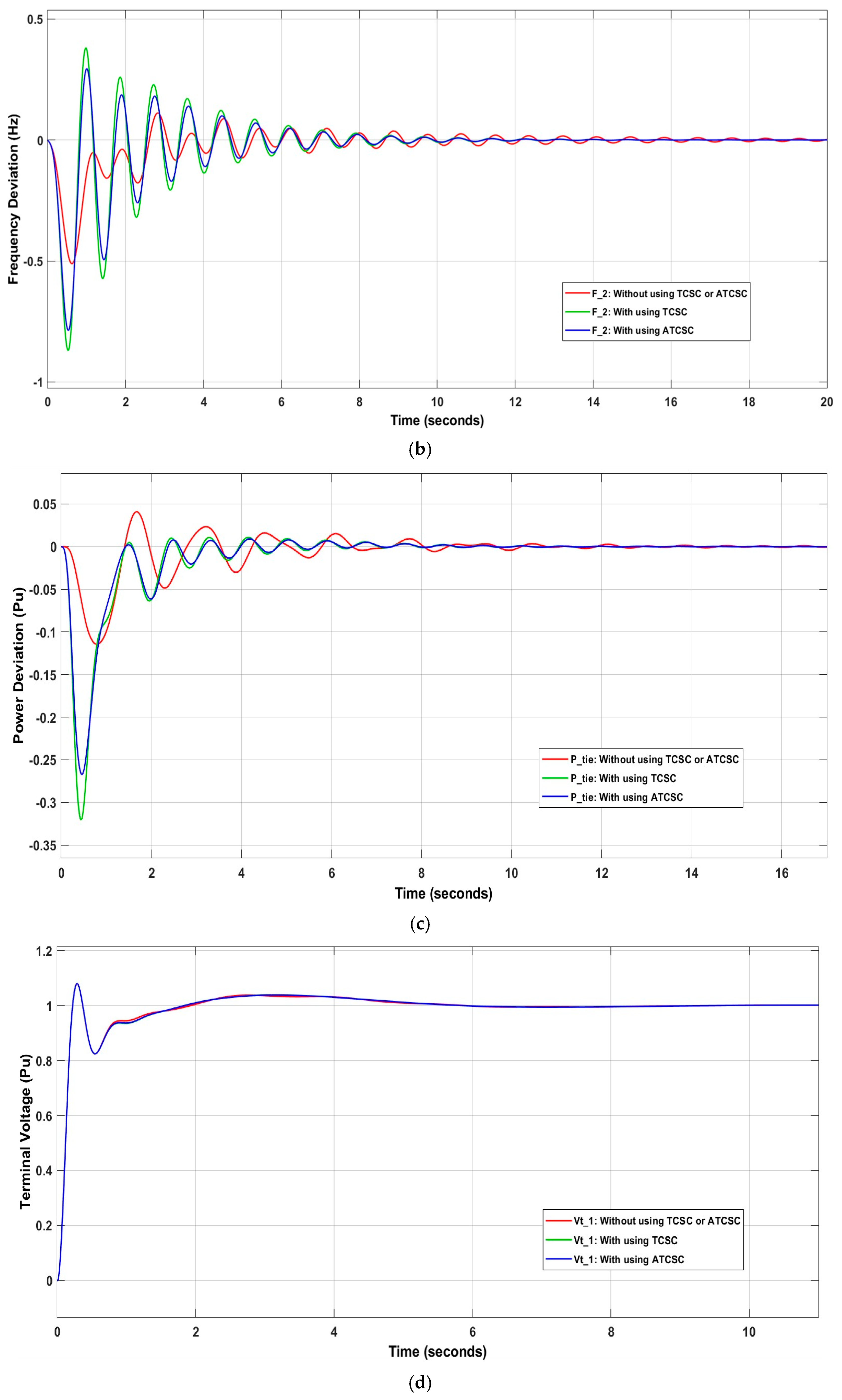
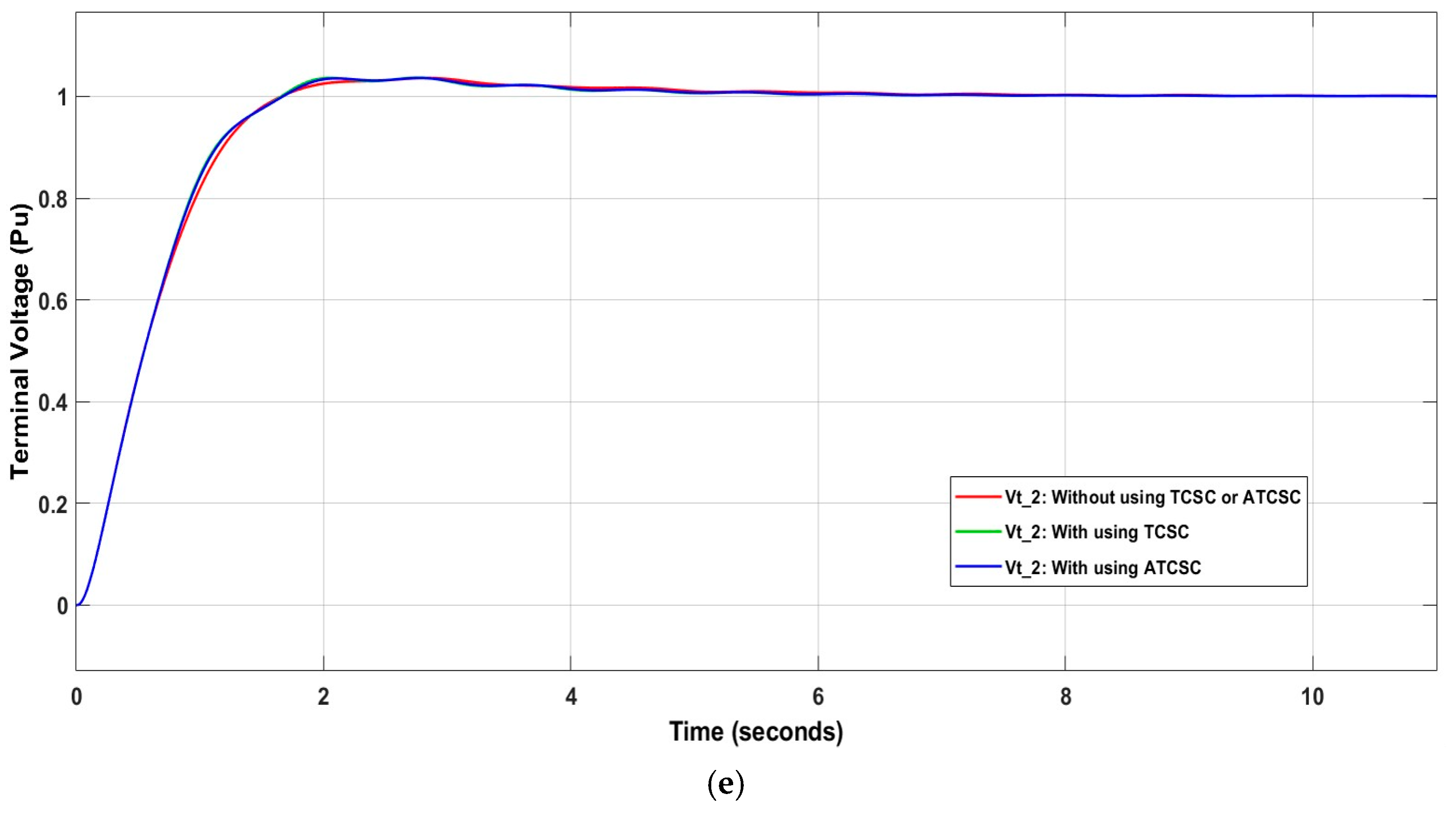
Applying the IT2FSs-PID controller and adding TCSC resulted in an improvement in system stability. The settling time value for $\Delta f_1$ decreased to 4.9236 s after using the controller, along with $\Delta f_2$ and $\Delta P_{tie}$. Using ATCSC instead of TCSC increased the stability of the power system. The $\Delta f_1$ value decreased to 3.6633 s, or 25.597%, and the value of $\Delta f_2$ decreased to 8.4554 s, or 4.349%. These are acceptable results for using ATCSC. Figure 15 shows the influence of the controllers on the power system.

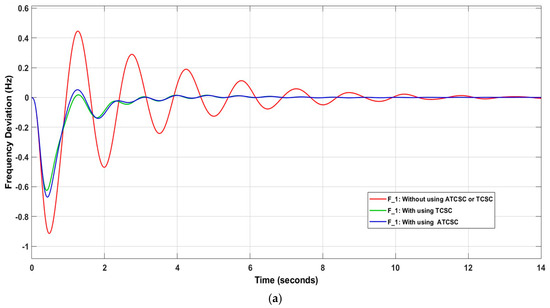
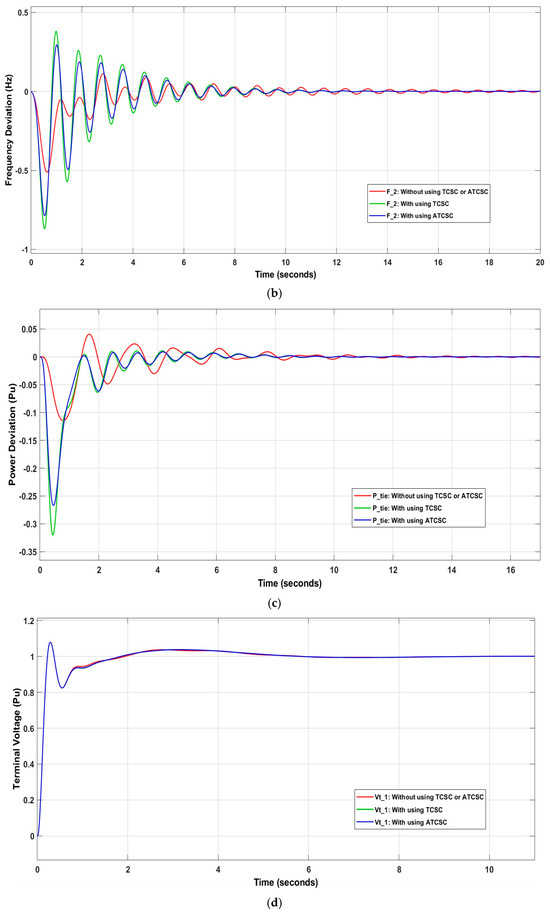
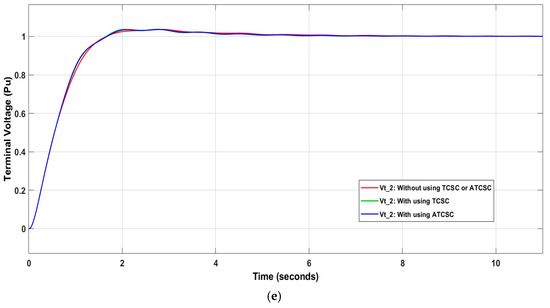
Figure 15. Influence of control system on (a) $\Delta f_1$; (b) $\Delta f_2$; (c) $\Delta P_{ti{e}_{ 12}}$; (d) $V_{t_1}$; (e) $V_{t_2}$.

3.2. Simulation of Case Studies

Three scenarios were used to verify the efficiency of the controllers. An increase in load demand equal to $\Delta P_L=0.02 p.u$ was used to cause a sudden disturbance in the power system. In the first scenario, the $\Delta P_L$ increases in two areas at time = 0 s. The second scenario is $\Delta P_L$ increase in area-1 only at time = 0 s. The final scenario involves an increase in $\Delta P_L$ in area-2 only at time = 0 s. According to Figure 16, the highest settling times for $\Delta f_1$ and $\Delta f_2$ in the second scenario were 4.8798 s and 8.8381 s, respectively, but the highest settling time for $\Delta P_{tie}$ occurred in the third scenario, with a time of 9.4659 s. In the three cases, settling max and settling min are close in the values of $\Delta f_1$ and $\Delta f_2$. However, as shown in Figure 16c, $\Delta P_{tie}$ is affected in cases 2 and 3. The $\Delta P_{tie}$ did not reach zero value because the $\Delta P_{tie}$ value during the optimization of the ATCSC parameters is insufficient. The solution is to optimize the ATCSC parameters, creating one $\Delta P_L$ in one area to increase the $\Delta P_{tie}$ value during the optimization. Moreover, applying the previous scenarios does not affect the terminal voltage.

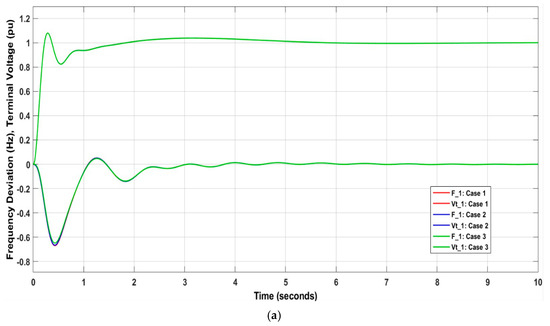
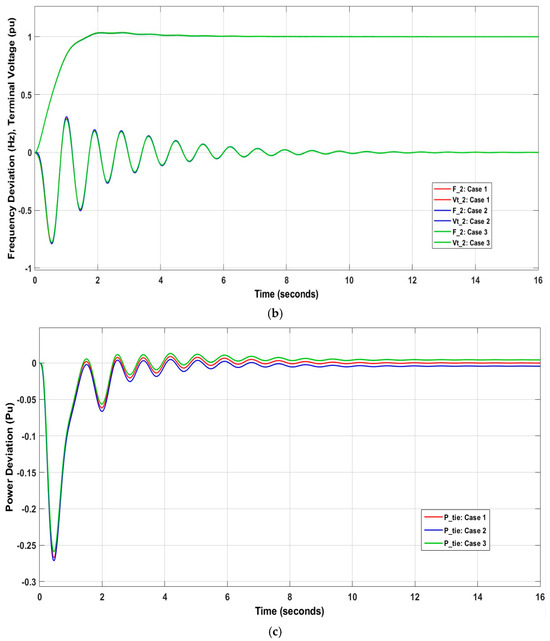
Figure 16. Influence of various scenarios on (a) $\Delta f_1 , V_{t_1}$; (b) $\Delta f_2 , V_{t_2}$; (c) $\Delta P_{{tie}_{12}}$.

3.3. Sensitivity Analysis

In this section, the controllers’ robustness was tested. The controllers were IT2FSs-PID for the LFC system, SA-PID for the AVR system, and ATCSC for the power in the tie line. The controllers’ robustness was tested by increasing the values of the following parameters: load disturbance $\left(\Delta P_L\right)$, synchronizing power coefficient $\left(P_s\right)$, governor time constant $\left(T_g\right)$, and turbine time constant $\left(T_t\right)$ by 50% and reducing by the same amount of the nominal value. The first scenario involves step load increases in two areas equal to $\Delta P_L=0.02 p.u$ at time = 0 s. The optimal parameter values of ATCSC and PID_AVR remain unchanged. The results in Table 8 and Table 9.

Table 9. Sensitivity analysis of terminal voltage.

Variation of Parameters		Settling Time (s)		Settling Max (P.u)		Settling Min (P.u)		Rise Time (s)
		${\mathit{V}}_{{\mathit{t}}_1}$	${\mathit{V}}_{{\mathit{t}}_2}$	${\mathit{V}}_{{\mathit{t}}_1}$	${\mathit{V}}_{{\mathit{t}}_2}$	${\mathit{V}}_{{\mathit{t}}_1}$	${\mathit{V}}_{{\mathit{t}}_2}$	${\mathit{V}}_{{\mathit{t}}_1}$	${\mathit{V}}_{{\mathit{t}}_2}$
Basic case		4.5285	3.8213	1.0797	1.0362	0.8240	0.9028	0.1435	0.9676
$\mathbf{\Delta }{\mathit{P}}_{\mathit{L}}$	−50%	4.5303	3.7909	1.0797	1.0351	0.8238	0.9033	0.1435	0.9719
	50%	4.5267	3.8478	1.0797	1.0374	0.8241	0.9024	0.1435	0.9633
${\mathit{P}}_{\mathit{s}}$	−50%	4.5238	3.9055	1.0796	1.0367	0.8239	0.9013	0.1435	0.9681
	50%	4.5351	3.7474	1.0797	1.0364	0.8239	0.9015	0.1435	0.9676
${\mathit{T}}_{\mathit{g}}$	−50%	4.5314	3.6810	1.0797	1.0371	0.8240	0.9017	0.1435	0.9880
	50%	4.5119	4.0927	1.0797	1.0421	0.8239	0.9035	0.14352	0.9484
${\mathit{T}}_{\mathit{t}}$	−50%	4.5314	3.6848	1.0797	1.0381	0.8241	0.9017	0.1435	0.9960
	50%	4.5170	4.1096	1.0797	1.0406	0.8239	0.9003	0.1435	0.9452

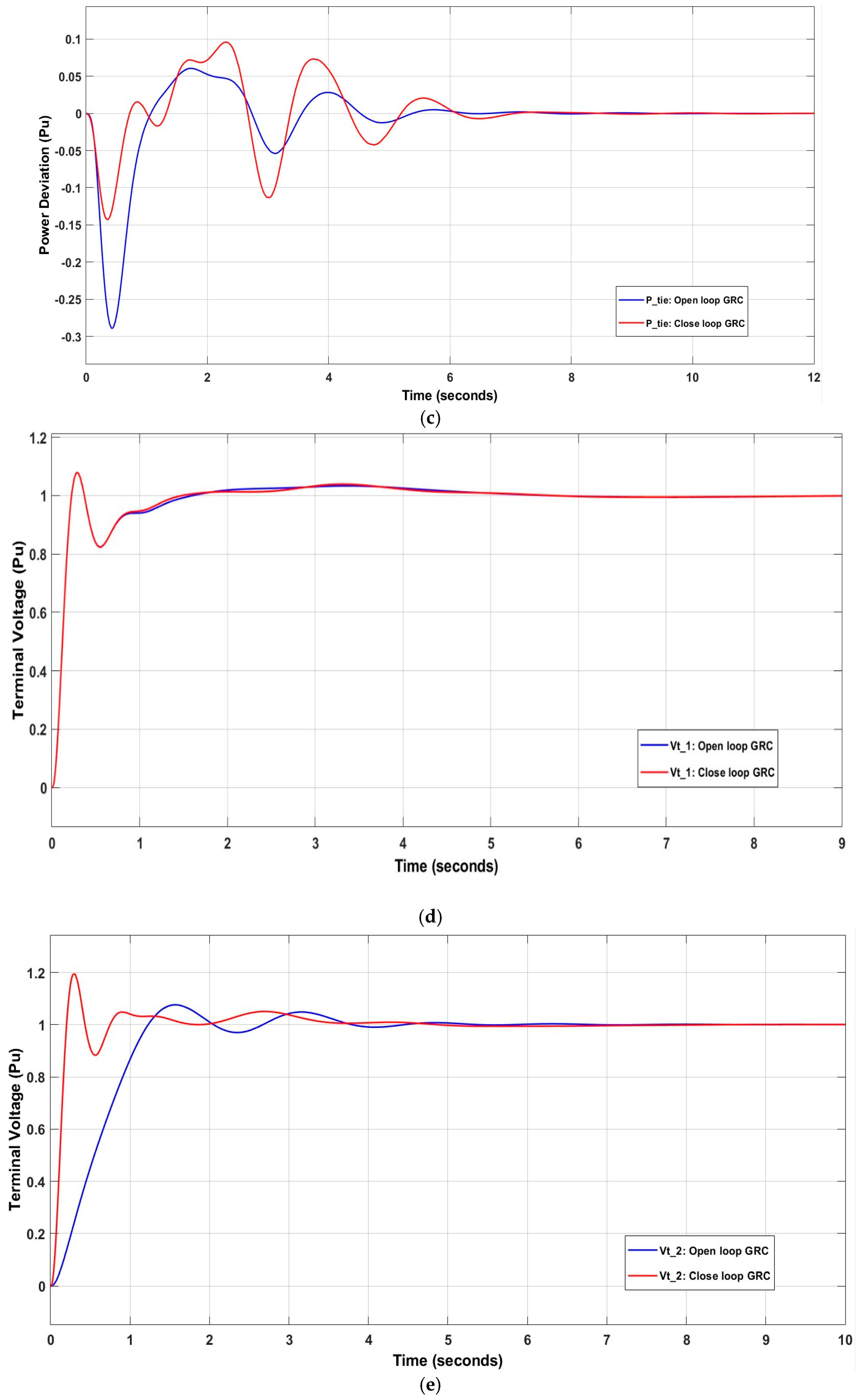
3.4. Improve the Two-Area Power System by Adding a Reheat Unit, Generation Rate Constraint (GRC), and Governing Dead Band (GDB) Nonlinearity

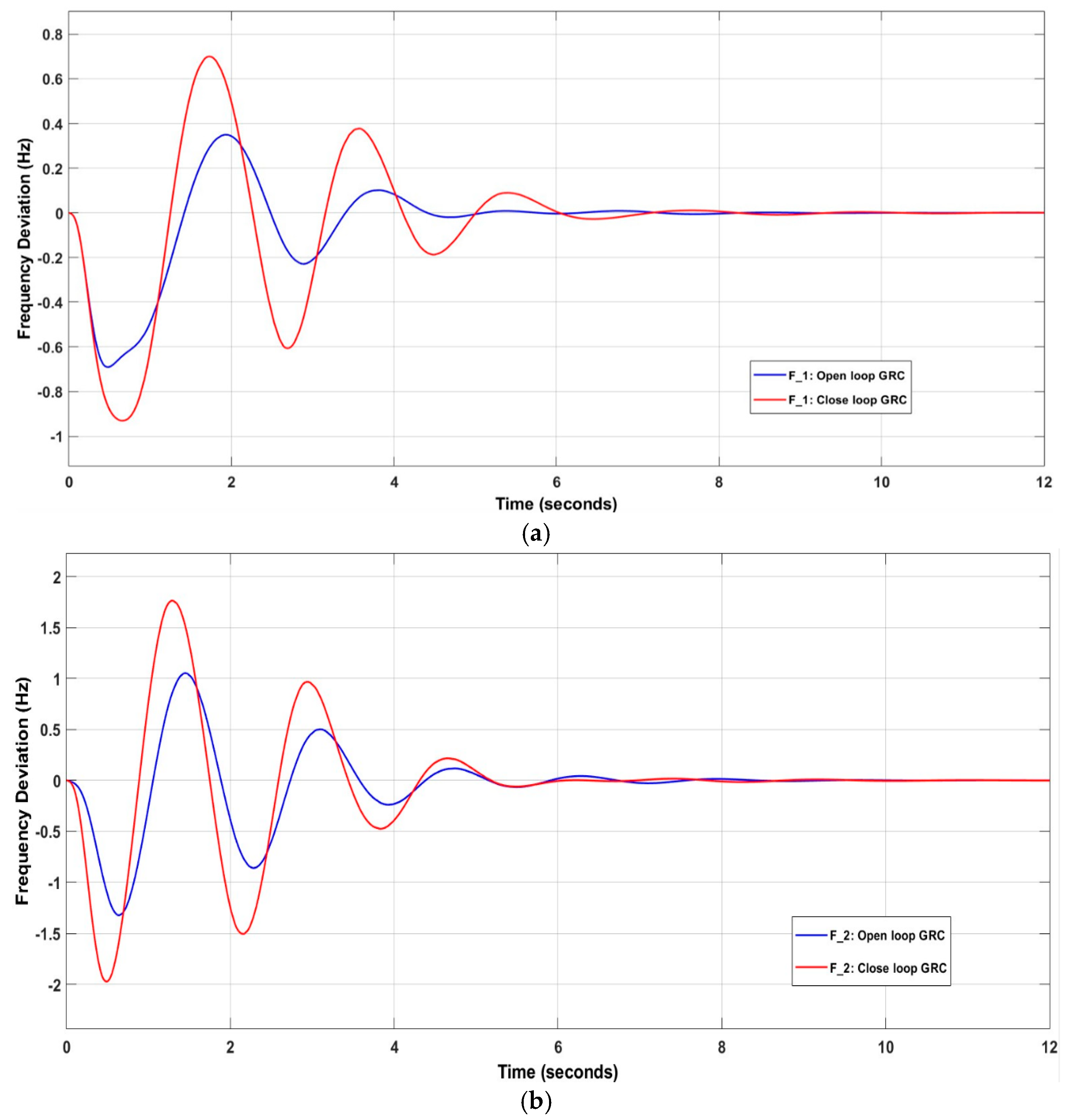
The settling times for $\Delta f_1$ and $\Delta P_{tie}$ in the open loop GRC case are superior to those in the closed loop GRC, being 4.8763 s and 5.2059 s, respectively, compared to 6.7316 s and 6.8915 s, respectively. However, $\Delta f_2$’s settling time in the closed loop condition is superior, with a time of 5.7252 s, compared to 6.4992 s for the open loop. The settling max for $\Delta f_1$,$\Delta f_2$, and $\Delta P_{tie}$ is higher in the closed loop GRC case than in the open loop GRC case. Similarly, the settling min for $\Delta f_1$ and $\Delta f_2$ is higher in the closed loop case, with values of −0.9277 p.u and −1.9534 p.u, respectively, except for $\Delta P_{tie}$, which has a larger value in the open loop case. The value of $\Delta P_{tie}$ is equal to −0.2885 p.u., compared to −0.1424 p.u in the closed loop GRC, as shown in Figure 17. Appendix A/Table A2 shows the system values after optimization.

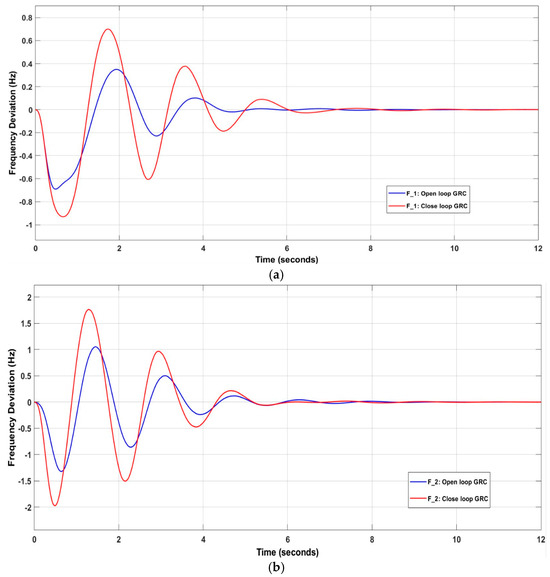
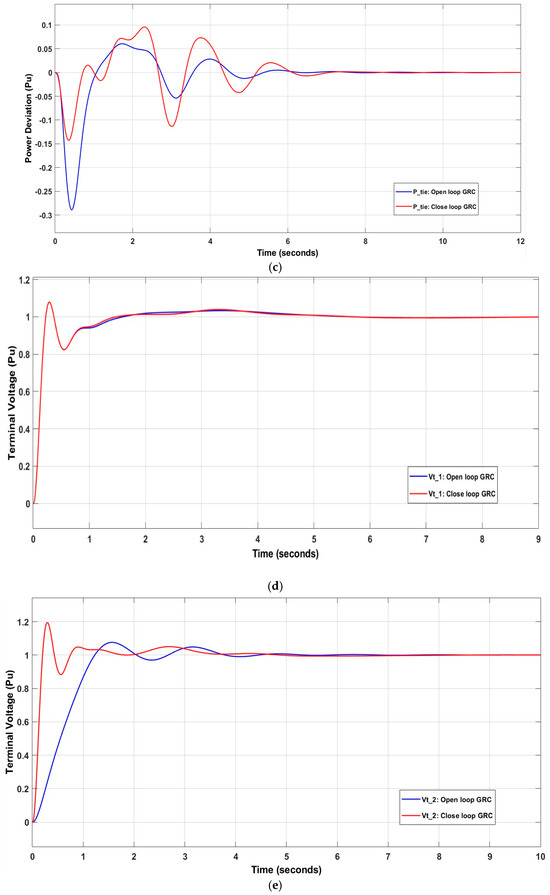
Figure 17. Effect of nonlinearity components on (a) $\Delta f_1$; (b) $\Delta f_2$; (c) $\Delta P_{ti{e}_{ 12}}$; (d) $V_{t_1}$; (e) $V_{t_2}$.

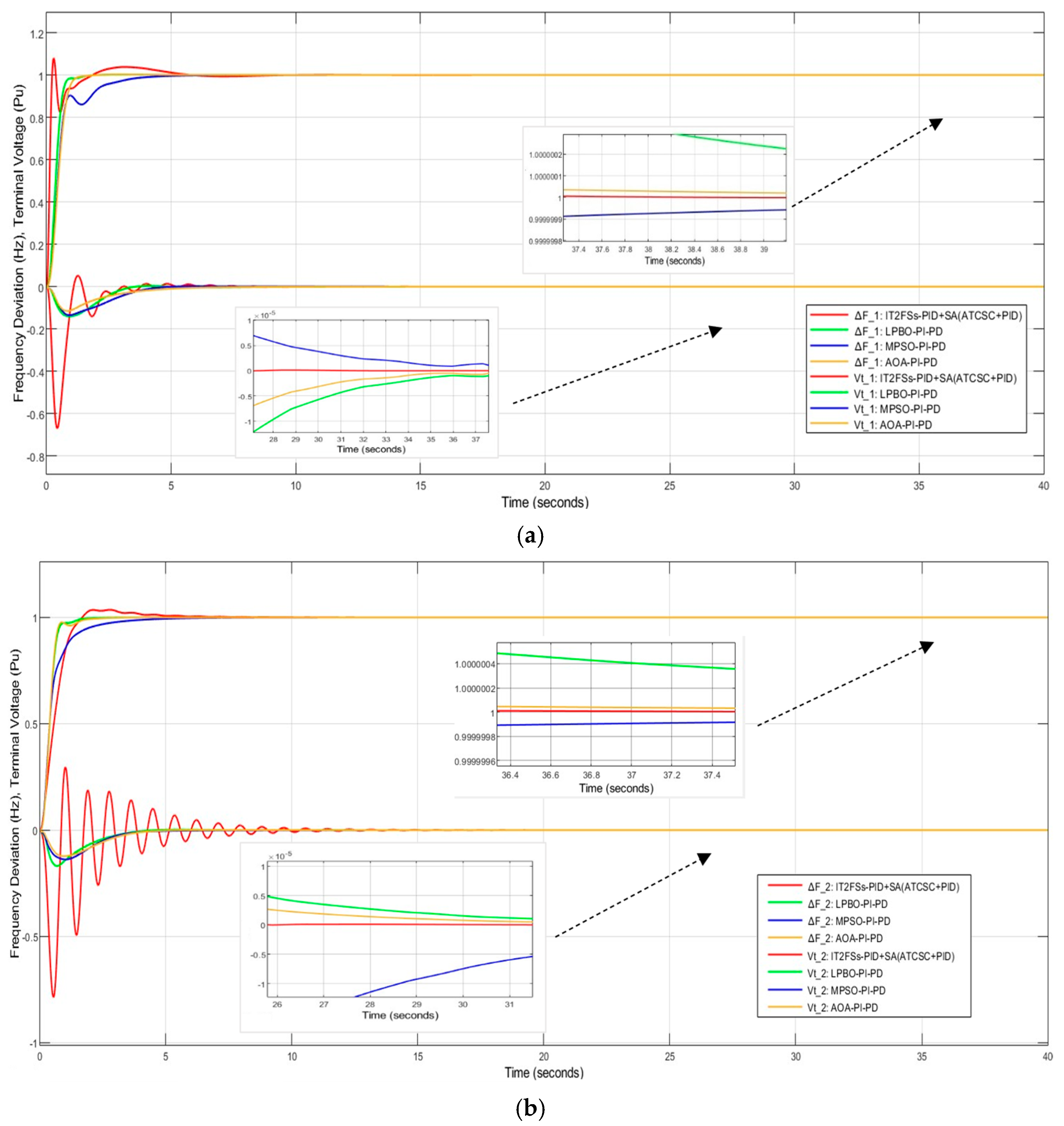
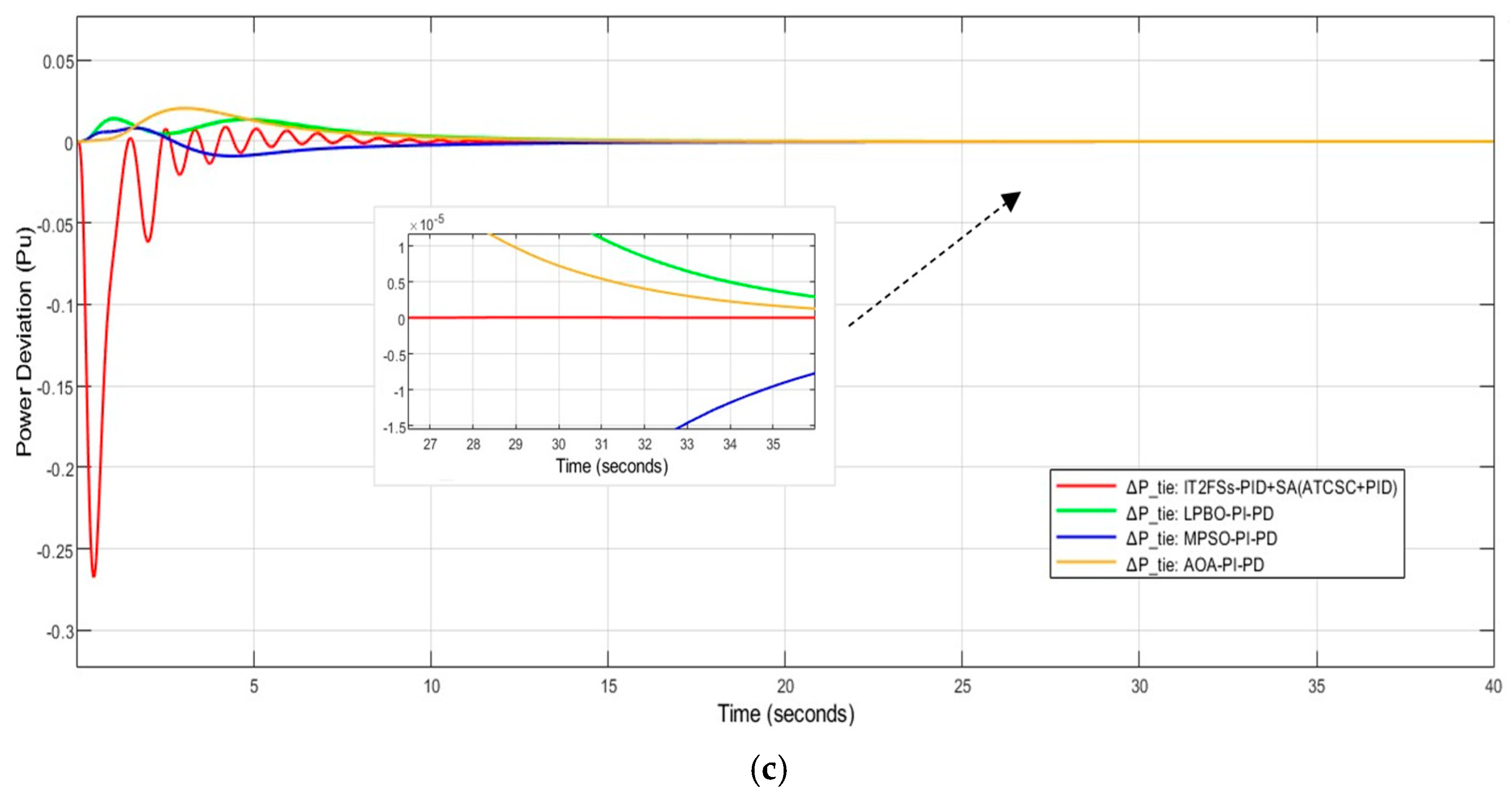
3.5. Comparison of IT2FSs-PID+SA (ATCSC+PID) with Other Strategies

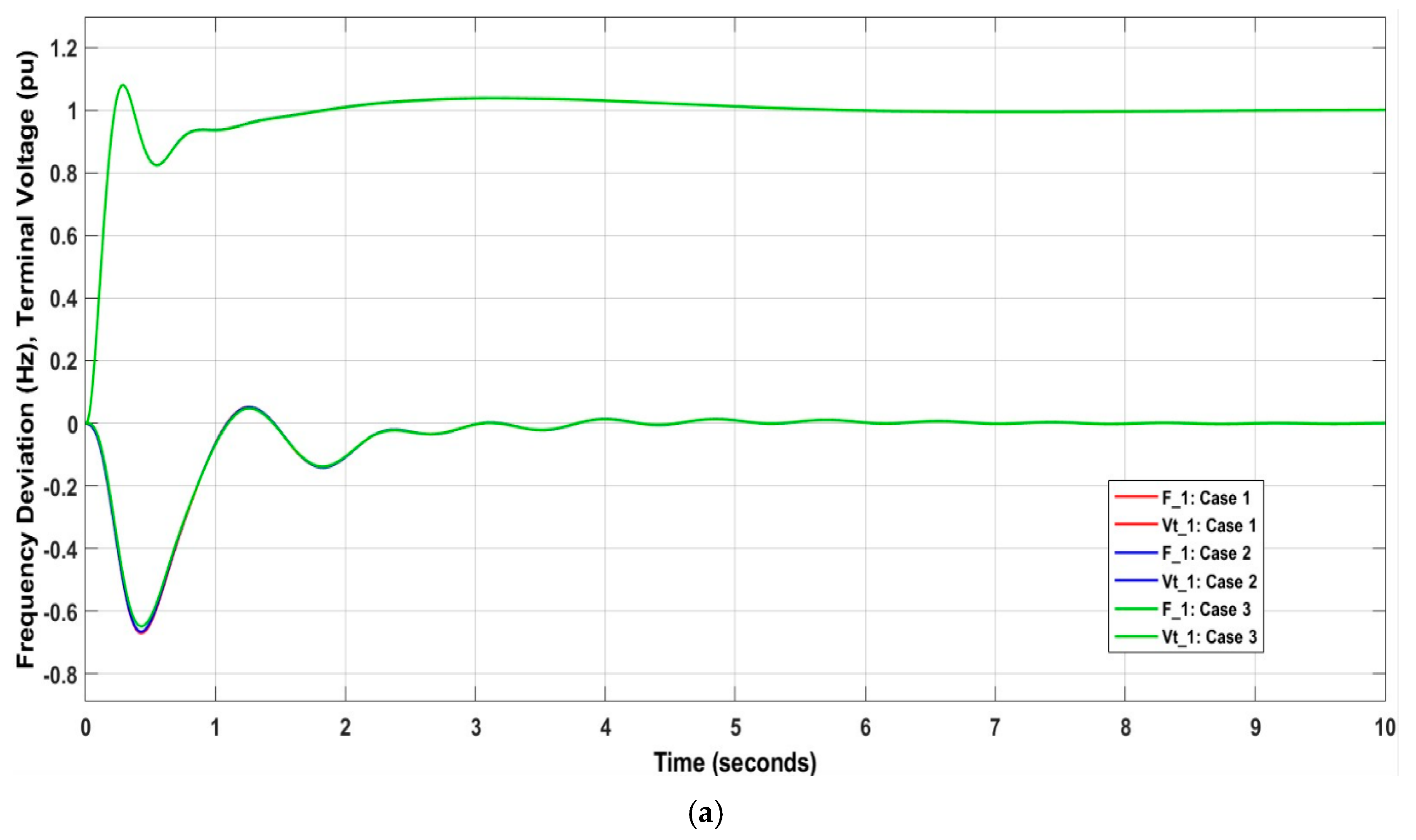
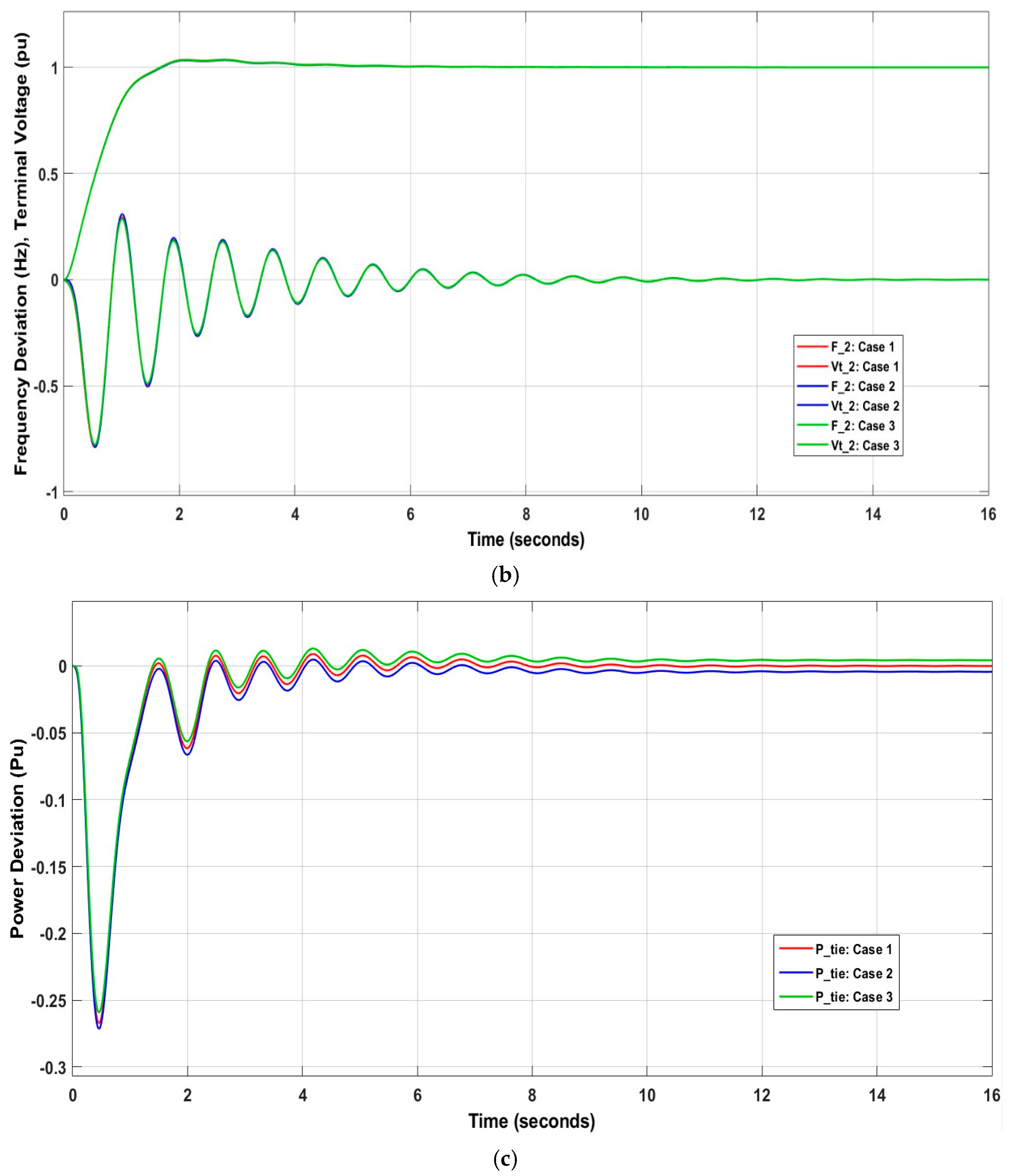
This section compares IT2FSs-PID+SA (ATCSC+PID) with other techniques used in the paper [48], utilizing the same model, LFC-AVR, in two areas with the same conditions. The paper also used the PI-PD controller, tuning its parameters using three algorithms: Modified Particle Swarm Optimization (MPSO), Learn Performance Based Behavior Optimization (LPBO), and the Archimedes Optimization Algorithm (AOA). The comparisons between the methods show that IT2FSs-PID+SA(ATCSC+PID) is better than the others. This is because the steady-state errors for $\Delta f_1$, $\Delta f_2$, $\Delta P_{tie}$, $V_{t_1}$, and $V_{t_2}$ go to zero faster. This is shown in Figure 18.

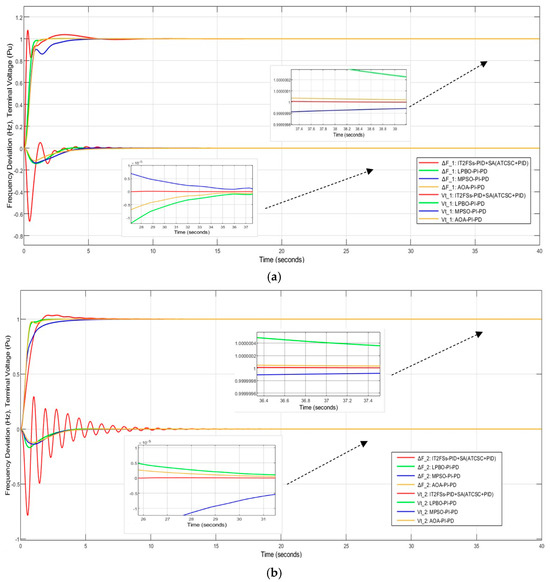
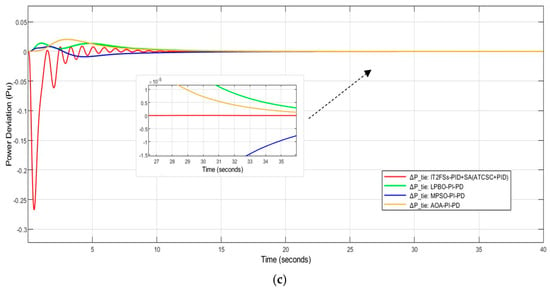
Figure 18. Influence of various techniques on (a) $\Delta f_1 , V_{t_1}$; (b) $\Delta f_2 , V_{t_2}$; (c) $\Delta P_{ti{e}_{ 12}}$.

3.6. Comparison Effect of Adding Another ATCSC to the Power System

Table 10 clearly illustrates the impact of the new ATCSC on area-2, demonstrating a decrease in the settling time for $\Delta f_2$ from 8.4554 s to 5.4895 s, and a similar decrease in the settling time for $\Delta P_{tie}$, from 6.0172 s to 3.9200 s. As a result, the impact of the new ATCSC on area-2 is greater than that of area-1 because of its connection to area-2. The results of settling max and min are close in the basic case, as well as when adding another ATCSC.

Table 10. Dynamic performance characteristics of a power system with one ATCSC and two ATCSCs of frequency and power.

Variation of Parameters	Settling Time (s)			Settling Max (Hz, P.u)			Settling Min (Hz, P.u)			JITAE
	$\mathbf{\Delta }{\mathit{f}}_1$	$\mathbf{\Delta }{\mathit{f}}_2$	$\mathbf{\Delta }{\mathit{P}}_{\mathit{t}\mathit{i}\mathit{e}}$	$\mathbf{\Delta }{\mathit{f}}_1$	$\mathbf{\Delta }{\mathit{f}}_2$	$\mathbf{\Delta }{\mathit{P}}_{\mathit{t}\mathit{i}\mathit{e}}$	$\mathbf{\Delta }{\mathit{f}}_1$	$\mathbf{\Delta }{\mathit{f}}_2$	$\mathbf{\Delta }{\mathit{P}}_{\mathit{t}\mathit{i}\mathit{e}}$
Including one ATCSC (Basic case)	3.6633	8.4554	6.0172	0.0518	0.2949	0.0089	−0.6700	−0.7875	−0.2674	4.36
Including two ATCSCs	3.6159	5.4895	3.9200	0.0469	0.2849	0.0045	−0.6662	−0.7770	−0.2656	3.02

Figure 19 shows the influence of the new ATCSC on the power system, with no noticeable effect on the values of settling time, settling max and min, and rising time, and their results are similar for terminal voltage.

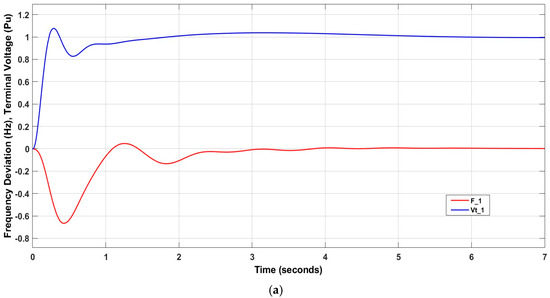
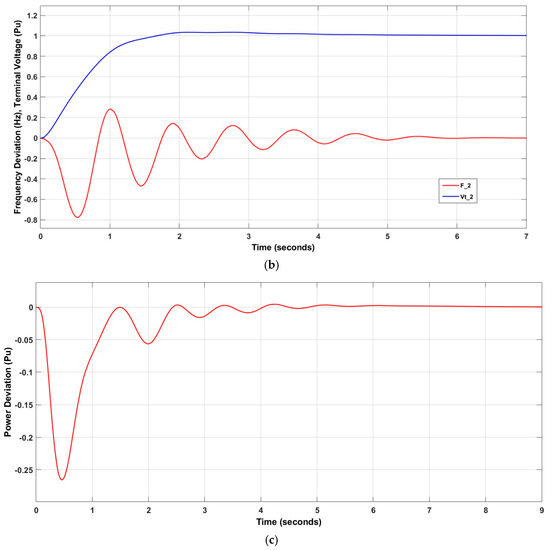
Figure 19. Influence of using two ATCSCs on (a) $\Delta f_1 , V_{t_1}$; (b) $\Delta f_2 , V_{t_2}$; (c) $\Delta P_{ti{e}_{ 12}}$.

4. Conclusions

This paper focused on the LFC-AVR model, utilizing the IT2FSs-PID controller for the LFC system and the PID controller for the AVR system. The ATCSC was added to the power system to enhance the dynamic efficiency of the system. Several experiments were conducted to prove the robustness of the controllers, including case study simulation, adding a reheat unit, GRC, and GDB to test the controllers in the power system. Also, after conducting the comparison, it became clear that IT2FSs-PID+SA (ATCSC+PID) is superior to other techniques in terms of the power system reaching a state of stability in the fastest time when disturbances occur. Finally, an ATCSC was added to validate its beneficial effects on the area it connects. The connection of an ATCSC to area-1 clearly demonstrated its effect, as the settling time for $\Delta f_1$ dropped to 3.6633 s, while $\Delta f_2$ experienced a decrease to 8.4554 s. Connecting the other ATCSC to the second region resulted in a decrease in the settling time value for $\Delta f_2$, from 8.4554 s to 5.489 s, while $\Delta f_1$ decreased from 3.6633 s to 3.6159 s. In future work, we will utilize T1FSs to adjust the PID parameters for LFC using real time simulation, utilize an alternative controller, such as an Integral Double Derivative (IDD), and optimize the controller parameters for a system that generates a disturbance value of 0.02 p.u in both areas at time = 0 sec to improve the result $\Delta P_{tie}$ in the simulation of case studies section.