An Improved Model for Five-Phase Induction Motor Based on Magnetic Noise Reduction Part I: Slot Opening Width
Abstract
:1. Introduction
2. Analytical Model of Electromagnetic Vibration
2.1. Electromagnetic Force Basis
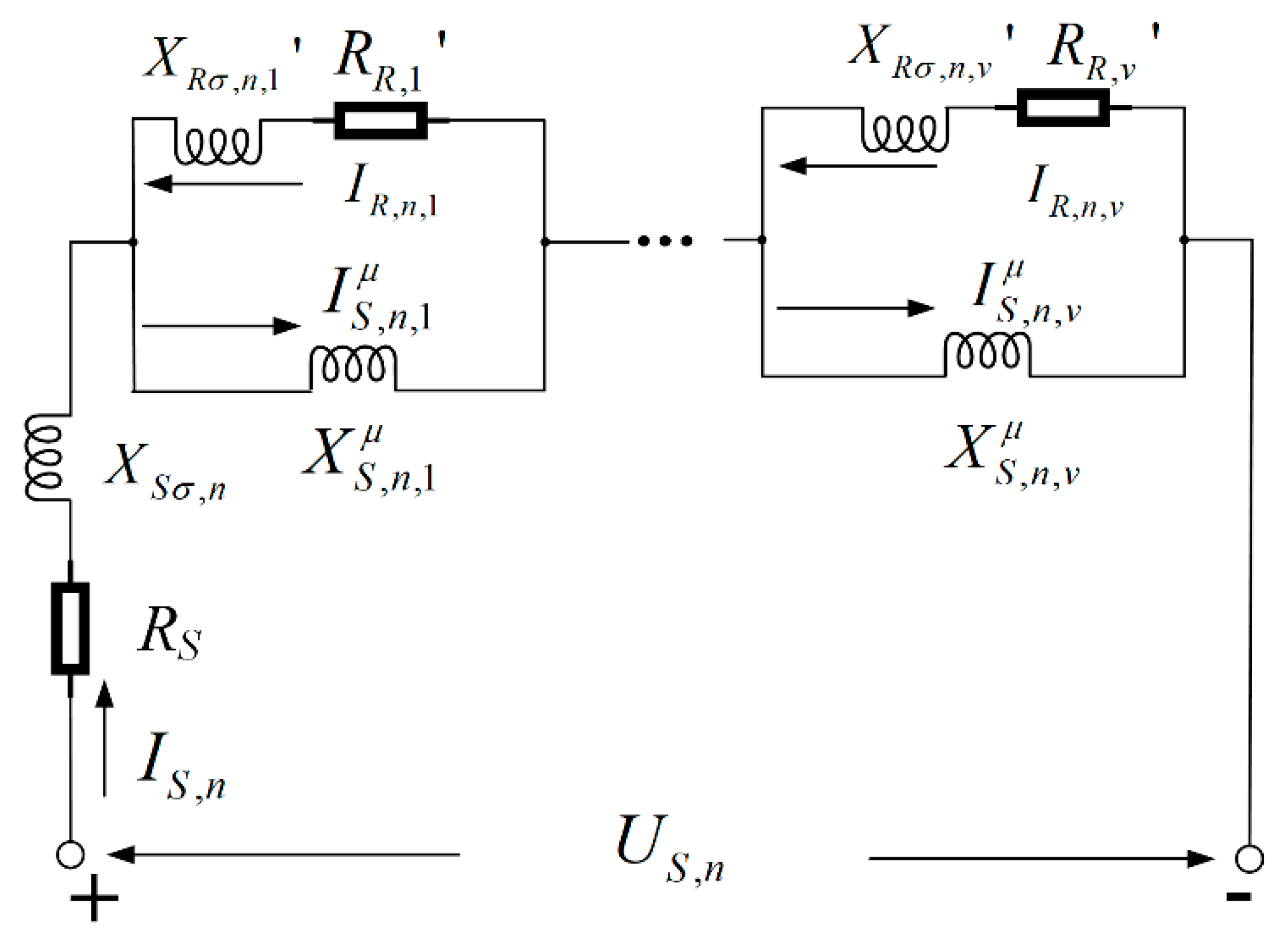
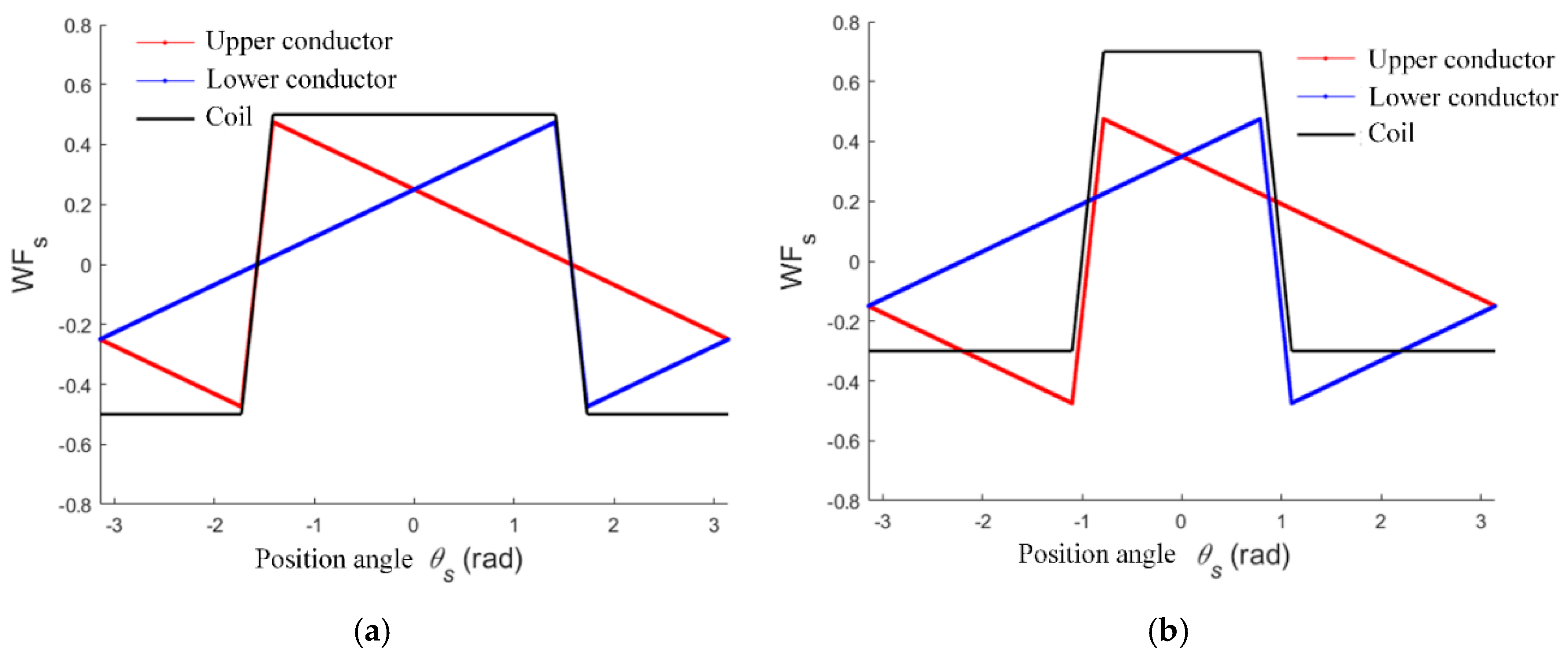
2.2. Current Computation
2.3. Analytical Calculation of Electromagnetic Force
2.4. Natural Frequency of Stator System
2.5. Vibration Characteristics
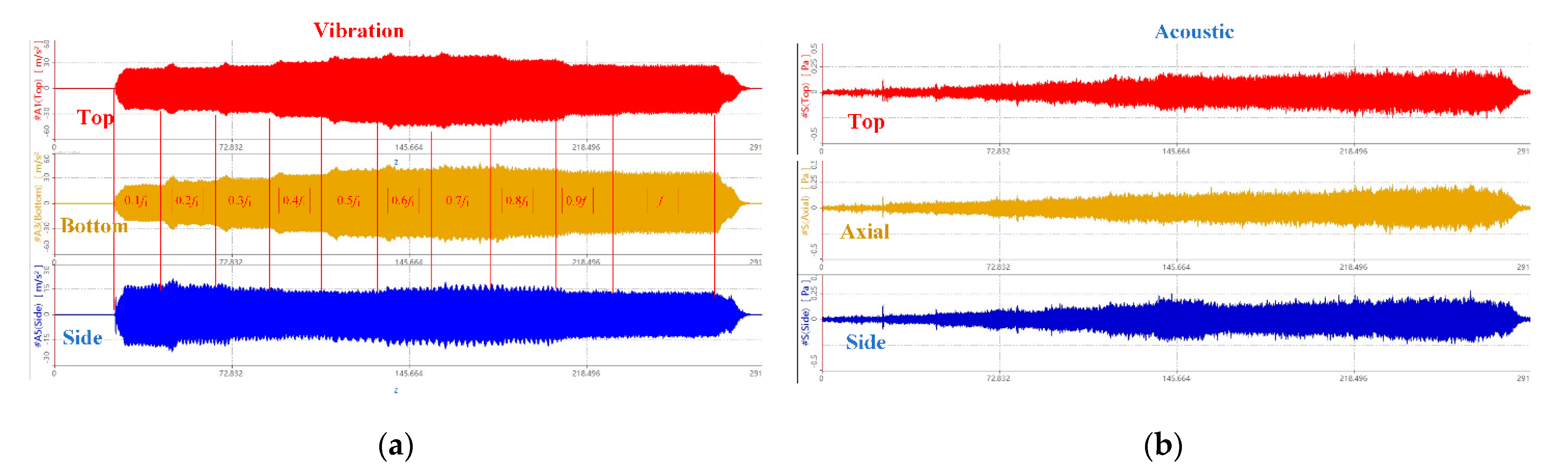
2.6. Model Validation
3. Magnetic Noise Radiation Calculation
3.1. Noise Radiation Model
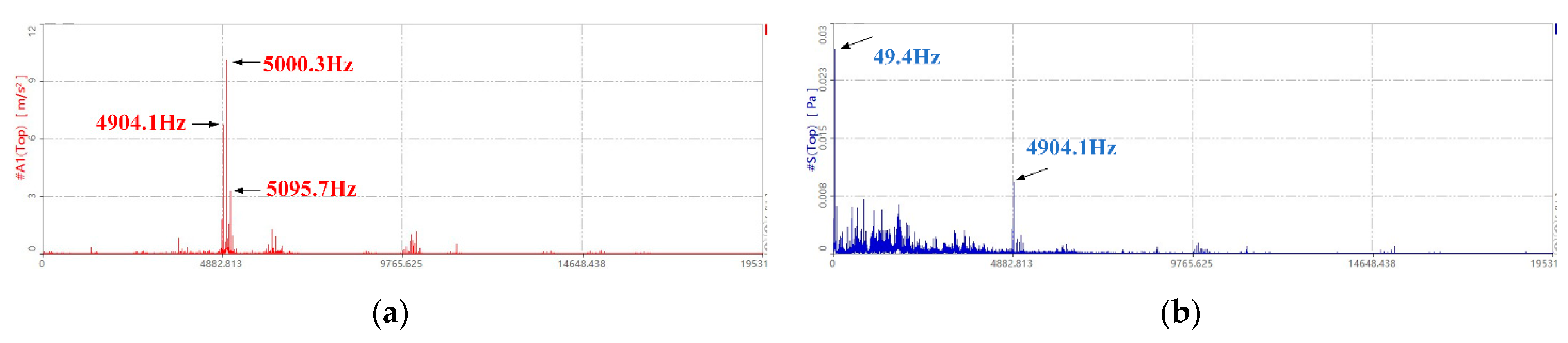
3.2. Noise Prediction Verification Experiment
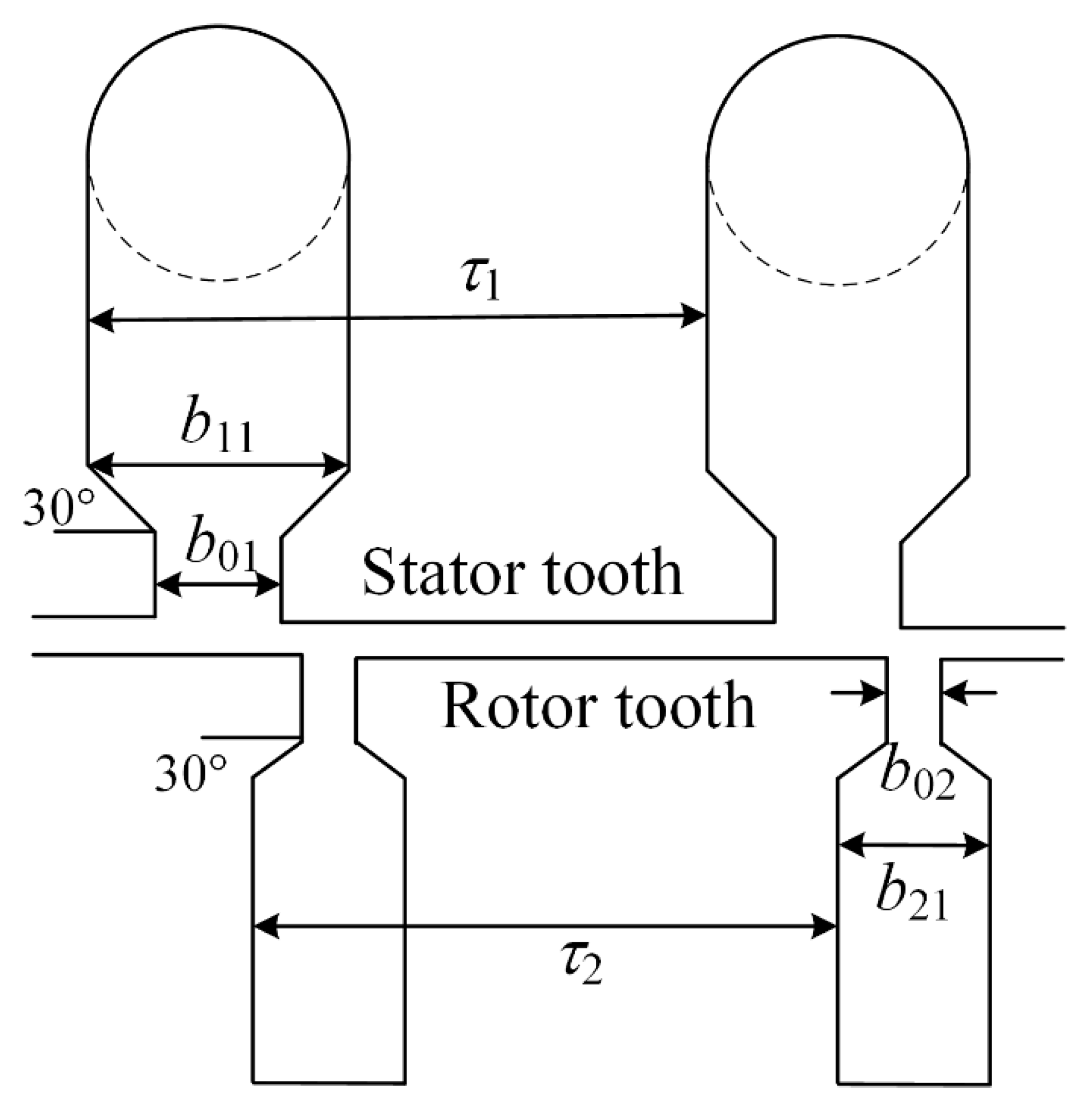
4. Low Noise Slot Opening Design
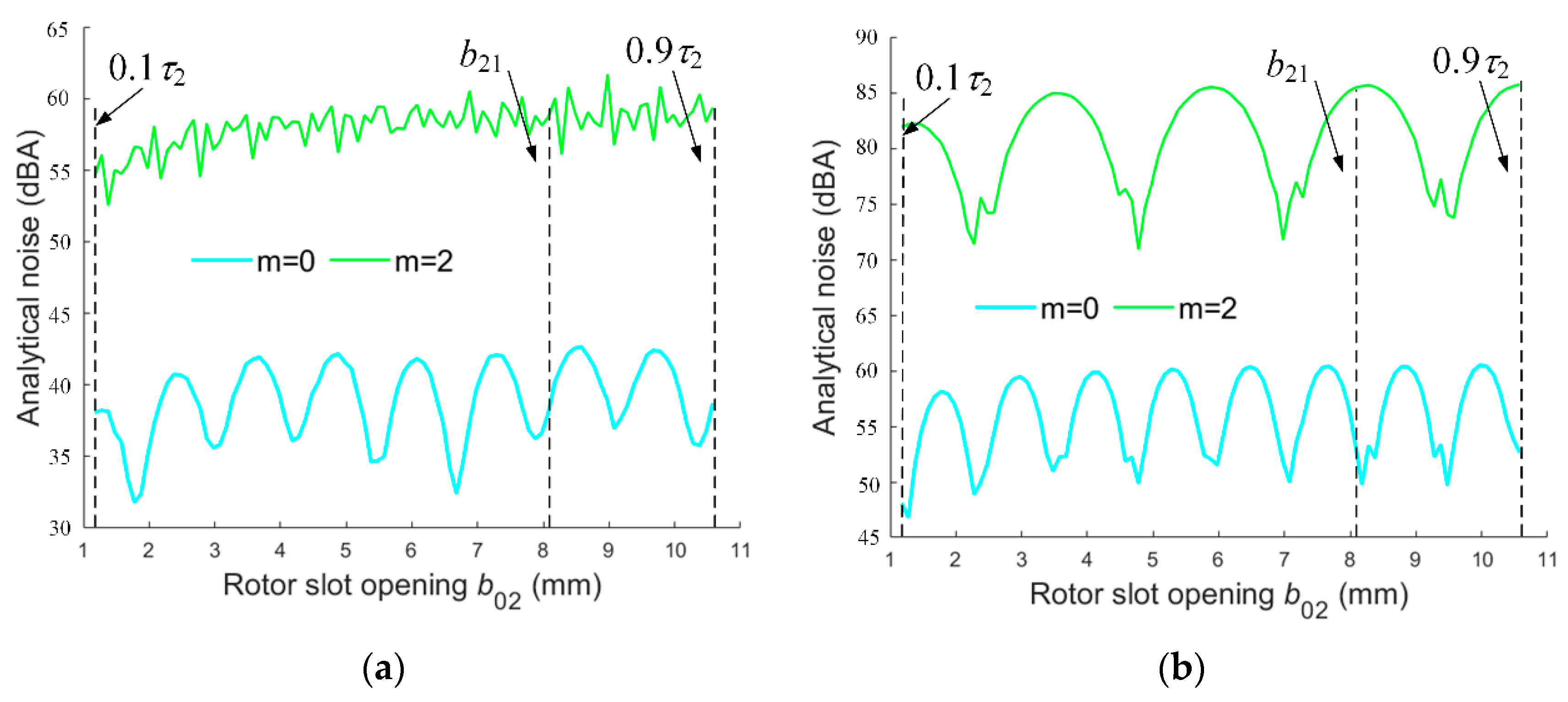
4.1. Low Noise Fundamental Analysis
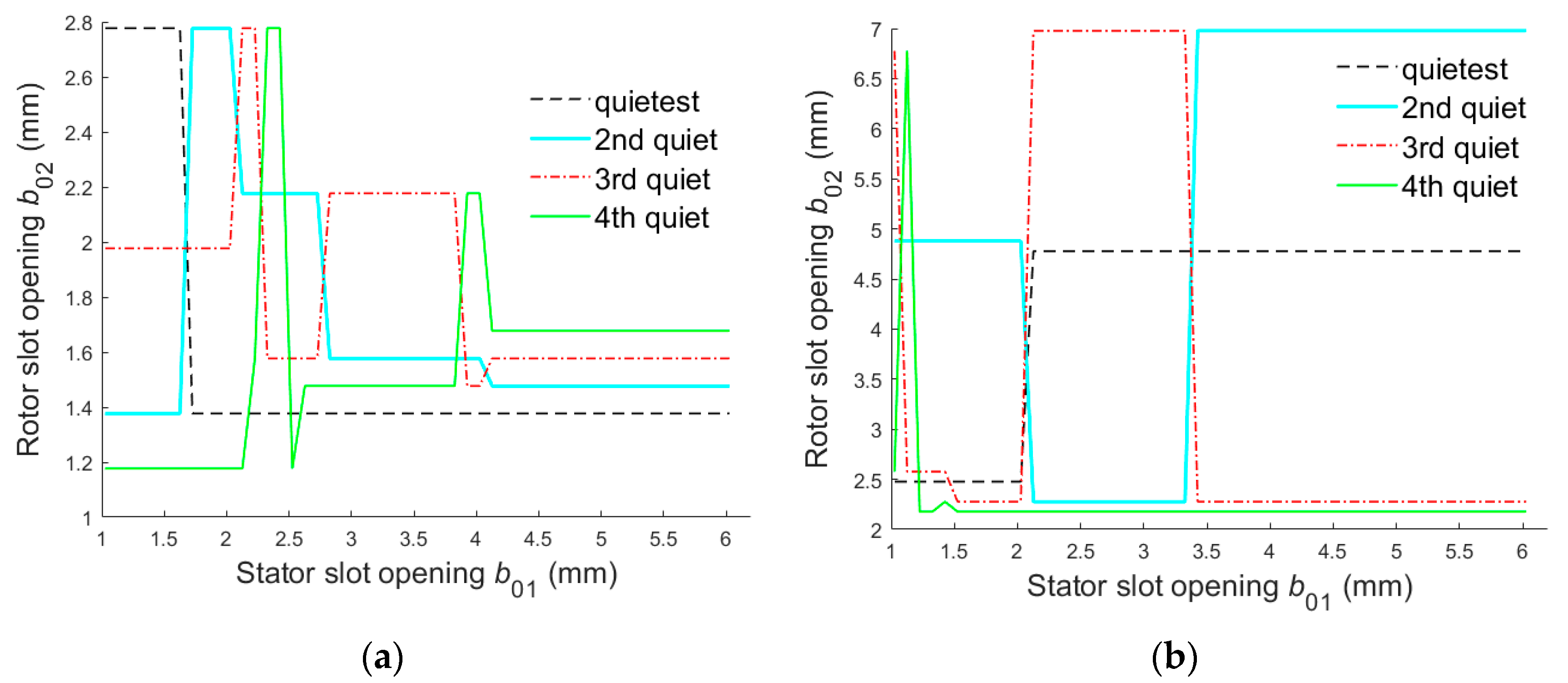
4.2. Slot Opening Width Schemes
- (1)
- The slip ratio changes linearly, ranging from 1 to 0.05.
- (2)
- In each case, five-phase sequential currents of the same amplitude are passed through the stator windings.
- (3)
- (4)
- Without the consideration of saturation, the air-gap permeability does not contain harmonic content caused by saturation.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Corton, R.; Sawezyn, H.; Belkhayat, D.; Brudny, J. Principe of Magnetic Noise Active Reduction Using Three Phase Systems Due to PWM Inverter Switching. In Proceedings of the 2nd International Seminar on Vibrations and Acoustic Noise of Electric Machinery (VANEM), Łódź, Poland, 1–3 June 2000; Volume 21. [Google Scholar]
- Cassoret, B.; Corton, R.; Roger, D.; Brudny, J.F. Magnetic Noise Reduction of Induction Machines. IEEE Trans. Power Electron. 2003, 18, 570–579. [Google Scholar] [CrossRef]
- Belkhayat, D.; Roger, D.; Brudny, J.F. Active Reduction of Magnetic Noise in Asynchronous Machine Controlled by Stator Current Harmonics. In Proceedings of the 1997 Eighth International Conference on (Conf. Publ. No. 444), Cambridge, UK, 1–3 September 1997. [Google Scholar]
- Liu, H.; Wang, D.; Yi, X.; Zhang, Y. A Unified Fault-tolerant Control for 15-phase Induction Machine Under Various Phase Failure Conditions. Proc. CSEE 2019, 39, 327–336. [Google Scholar]
- Cheng, Z.; Ruan, L.; Huang, S.; Yang, J. Research on Noise Reduction of 3.6 MW Evaporative Cooling Wind Motor Induced by Electromagnetic and Two-Phase Flow Resonance Based on Stator Optimization. Processes 2021, 9, 669. [Google Scholar] [CrossRef]
- Le Besnerais, J.; Lanfranchi, V.; Hecquet, M.; Romary, R.; Brochet, P. Optimal Slot Opening Width for Magnetic Noise Reduction in Induction Motors. IEEE Trans. Energy Convers. 2009, 24, 869–874. [Google Scholar] [CrossRef]
- Chen, Y. Analysis and Control of Motor Noise; Zhejiang University Press: Hangzhou, China, 1987; pp. 5–23. [Google Scholar]
- Shin, K.-H.; Bang, T.-K.; Kim, K.-H.; Hong, K.; Choi, J.-Y. Electromagnetic Analysis and Experimental Study to Optimize Force Characteristics of Permanent Magnet Synchronous Generator for Wave Energy Converter Using Subdomain Method. Processes 2021, 9, 1825. [Google Scholar] [CrossRef]
- Le Besnerais, J.; Lanfranchi, V.; Hecquet, M.; Brochet, P.; Friedrich, G. Acoustic Noise of Electromagnetic Origin in a Fractional-Slot Induction Machine. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2008, 27, 1033–1052. [Google Scholar] [CrossRef]
- Brudny, J.F. Modélisation de La Denture Des Machines Asynchrones. Phénomène de Résonance. J. Phys. III 1997, 7, 1009–1023. [Google Scholar] [CrossRef]
- Bossio, G.; De Angelo, C.; Solsona, J.; Garcia, G.; Valla, M.I. A 2-D Model of the Induction Machine: An Extension of the Modified Winding Function Approach. Energy Convers. IEEE Trans. 2004, 19, 144–150. [Google Scholar] [CrossRef]
- Belahcen, A. Vibrations of Rotating Electrical Machines Due to Magnetomechanical Coupling and Magnetostriction. IEEE Trans. Magn. 2006, 42, 971–974. [Google Scholar] [CrossRef]
- Hilgert, T.G.D.; Vandevelde, L.; Melkebeek, J.A.A. Numerical Analysis of the Contribution of Magnetic Forces and Magnetostriction to the Vibrations in Induction Machines. IET Sci. Meas. Technol. 2007, 1, 21–24. [Google Scholar] [CrossRef] [Green Version]
- Devillers, E.; Hecquet, M.; Le Besnerais, J.; Régniez, M. Tangential Effects on Magnetic Vibrations and Acoustic Noise of Induction Machines Using Subdomain Method and Electromagnetic Vibration Synthesis. In Proceedings of the 2017 IEEE International Electric Machines and Drives Conference (IEMDC), Miami, FL, USA, 21–24 May 2017; pp. 1–8. [Google Scholar]
- Gieras, J.F.; Chong, W.; Lai, J.C. Noise of Polyphase Electric Motors; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Alger, P.L. Induction Machines: Their Behavior and Uses. J. Clin. Investig. 1993, 91, 2314–2319. [Google Scholar]
- Timár, P.L. Noise and Vibration of Electrical Machines; Elsevier: Amsterdam, The Netherlands, 1989. [Google Scholar]
- Chen, S. Motor Design; Machinery Industry Press: Beijing, China, 2004; pp. 244–247. [Google Scholar]
- Hubert, A. Contribution à l’Étude des Bruits Acoustiques Générés Lors de l’Association Machines Électriques-Convertisseurs Statiques de Puissance. Application à la Machine Asynchrone. Ph.D. Thesis, Université de Technologie de Compiègne, Compiègne, France, 2000. [Google Scholar]
- Gojko, J.M.; Momir, D.D.; Aleksandar, O.B. Skew and Linear Rise of MMF across Slot Modelling-Winding Function Approach. IEEE Trans. Energy Convers. 1999, 14, 315–320. [Google Scholar] [CrossRef]
- Le Besnerais, J.; Lanfranchi, V.; Hecquet, M.; Brochet, P. Optimal Slot Numbers for Magnetic Noise Reduction in Variable-Speed Induction Motors. IEEE Trans. Magn. 2009, 45, 3131–3136. [Google Scholar] [CrossRef]
- Bao, X.; Cheng, Z.; Wang, H.; Di, C. Inductance Calculation of Eccentric Induction Motor Based on Modified Winding Function Approach. Trans. China Electrotech. Soc. 2016, 31, 8. [Google Scholar]
- Le Besnerais, J. Fast Prediction of Variable-Speed Acoustic Noise Due to Magnetic Forces in Electrical Machines. In Proceedings of the 2016 XXII International Conference on Electrical Machines (ICEM), Lausanne, Switzerland, 4–7 September 2016. [Google Scholar]
- Leissa, A.W.; Nordgren, R.P. Vibration of Shells. J. Appl. Mech. 1993, 41, 544. [Google Scholar] [CrossRef] [Green Version]
- Timar, P.L.; Lai, C.S.J. Acoustic Noise of Electromagnetic Origin in an Ideal Frequency-Converter-Driven Induction Motor. Electr. Power Appl. IEE Proc. 1994, 141, 341–346. [Google Scholar] [CrossRef]

| Symbol | Frequency fP | Force Wave Mode m | Remark |
|---|---|---|---|
| Pbelt | fn[k2Z2(1 − s)/p + l] | k2Z2 − 2m1pk1 + lp | l = 0, ±2 |
| Symbol | Value | Symbol | Value |
|---|---|---|---|
| Z1 | 30 | b02 | 1 mm |
| Z2 | 26 | b11 | 6.1 mm |
| p | 1 | b21 | 8.1 mm |
| PN | 4 kw | τ1 | πDi1/Z1 |
| f1 | 50 Hz | τ2 | πD2/Z2 |
| D1 | 175 mm | l1 | 106 mm |
| Di1 | 98 mm | l2 | 146 mm |
| D2 | 97.4 mm | l3 | 219 mm |
| b01 | 3.2 mm | - | - |
| fa,m | Mode a | RMSE | MAPE | ||
|---|---|---|---|---|---|
| Mode m | 1 | 2 | 3 | 330.1 | 4.38% |
| 0 | 8671 | 8961 | 9661 | ||
| (8338) | (8875) | (9806) | |||
| 1 | 2481 | 3763 | 4385 | ||
| (—) | (—) | (4554) | |||
| 2 | 2805 | 3667 | 4880 | ||
| (2403) | (3410) | (4939) | |||
| 3 | 5884 | 6197 | 6697 | ||
| (5432) | (6252) | (6954) | |||
| 4 | 10,582 | 10,736 | 11,031 | ||
| (10,151) | (11,302) | (—) | |||
| k1 | k2 | fP | m |
|---|---|---|---|
| 5 | 2 | fn(2Z2(1 − s)/p + 2) = 2570 Hz | 2Z2 − 10m1 + 2p = 4 |
| 8 | 3 | fn(8Z2(1 − s)/p + 2) = 3805 Hz | 3Z2 − 16m1 + 2p = 0 |
| 5 | 2 | fn(2Z2(1 − s)/p − 2) = 2325.8 Hz | 2Z2 − 10m1 − 2p = 0 |
| 8 | 3 | fn(6Z2(1 − s)/p − 2) = 3538.7 Hz | 3Z2 − 16m1 − 2p = −4 |
| 10 | 4 | fn(7Z2(1 − s)/p − 2) = 4751.6 Hz | 4Z2 − 20m1 − 2p = 2 |
| 5 | 2 | fn(2Z2(1 − s)/p) = 2425.8 Hz | 2Z2 − 10m1 = 2 |
| 8 | 3 | fn(3Z2(1 − s)/p) = 3638.7 Hz | 3Z2 − 16m1 = −2 |
| 10 | 4 | fn(4Z2(1 − s)/p) = 4851.6 Hz | 4Z2 − 20m1 = 4 |
| Symbol | Max | Min | Step |
|---|---|---|---|
| b01 | Max (1 − τ1/Max(k1), b11) | τ1/Max(k1) | 0.01 mm |
| b02 | Max (1 − τ1/Max(k2), b21) | τ2/Max(k2) | 0.01 mm |
| b01 | b02 of (37) | b02 of (38) |
|---|---|---|
| 0.1τ1 | 0.236τ2, 0.117τ2, 0.168τ2, 0.1τ2 | 0.211τ2, 0.414τ2, 0.576τ2, 0.219τ2 |
| 0.139τ1 | 0.236τ2, 0.117τ2, 0.168τ2, 0.1τ2 | 0.211τ2, 0.414τ2, 0.219τ2, 0.194τ2 |
| 0.178τ1 | 0.117τ2, 0.236τ2, 0.168τ2, 0.1τ2 | 0.211τ2, 0.414τ2, 0.194τ2, 0.185τ2 |
| 0.217τ1 | 0.117τ2, 0.185τ2, 0.236τ2, 0.134τ2 | 0.406τ2, 0.194τ2, 0.593τ2, 0.185τ2 |
| 0.256τ1 | 0.117τ2, 0.185τ2, 0.134τ2, 0.126τ2 | 0.406τ2, 0.194τ2, 0.593τ2, 0.185τ2 |
| 0.295τ1 | 0.117τ2, 0.134τ2, 0.185τ2, 0.126τ2 | 0.406τ2, 0.194τ2, 0.593τ2, 0.185τ2 |
| 0.334τ1 | 0.117τ2, 0.134τ2, 0.185τ2, 0.126τ2 | 0.406τ2, 0.593τ2, 0.194τ2, 0.185τ2 |
| 0.373τ1 | 0.117τ2, 0.134τ2, 0.185τ2, 0.126τ2 | 0.406τ2, 0.593τ2, 0.194τ2, 0.185τ2 |
| 0.412τ1 | 0.117τ2, 0.126τ2, 0.134τ2, 0.143τ2 | 0.406τ2, 0.593τ2, 0.194τ2, 0.185τ2 |
| 0.451τ1 | 0.117τ2, 0.126τ2, 0.134τ2, 0.143τ2 | 0.406τ2, 0.593τ2, 0.194τ2, 0.185τ2 |
| 0.49τ1 | 0.117τ2, 0.126τ2, 0.134τ2, 0.143τ2 | 0.406τ2, 0.593τ2, 0.194τ2, 0.185τ2 |
| 0.529τ1 | 0.117τ2, 0.126τ2, 0.134τ2, 0.143τ2 | 0.406τ2, 0.593τ2, 0.194τ2, 0.185τ2 |
| 0.568τ1 | 0.117τ2, 0.126τ2, 0.134τ2, 0.143τ2 | 0.406τ2, 0.593τ2, 0.194τ2, 0.185τ2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, H.; Zhao, J.; Xiong, Y.; Luo, X.; Zhang, Q. An Improved Model for Five-Phase Induction Motor Based on Magnetic Noise Reduction Part I: Slot Opening Width. Processes 2022, 10, 1496. https://doi.org/10.3390/pr10081496
Chen H, Zhao J, Xiong Y, Luo X, Zhang Q. An Improved Model for Five-Phase Induction Motor Based on Magnetic Noise Reduction Part I: Slot Opening Width. Processes. 2022; 10(8):1496. https://doi.org/10.3390/pr10081496
Chicago/Turabian StyleChen, Hansi, Jinghong Zhao, Yiyong Xiong, Xiangyu Luo, and Qingfei Zhang. 2022. "An Improved Model for Five-Phase Induction Motor Based on Magnetic Noise Reduction Part I: Slot Opening Width" Processes 10, no. 8: 1496. https://doi.org/10.3390/pr10081496
APA StyleChen, H., Zhao, J., Xiong, Y., Luo, X., & Zhang, Q. (2022). An Improved Model for Five-Phase Induction Motor Based on Magnetic Noise Reduction Part I: Slot Opening Width. Processes, 10(8), 1496. https://doi.org/10.3390/pr10081496






