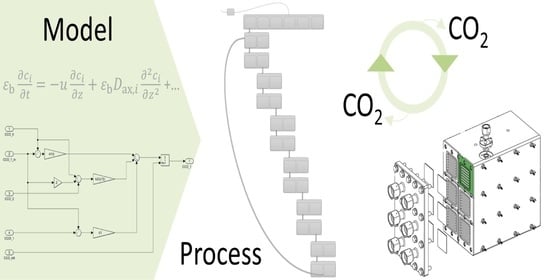
Numerical Simulation Approach for a Dynamically Operated Sorption-Enhanced Water-Gas Shift Reactor
Abstract
:1. Introduction
- 1.
- Providing synthesis gas (syngas) with a H2/CO ratio of approximately two for the subsequent Fischer–Tropsch synthesis.
- 2.
- Removing the by-product CO2 and refeeding it to the plasma reactor.
- pressurization (feed: reactants);
- reactive adsorption (feed: reactants);
- depressurization (no feed, often purged);
- regeneration (feed: purge gas).
2. SEWGS Model
2.1. Model Development
- Homogeneous distribution of uniformly sized catalyst and sorbent particles according to their weight fraction assumed as one phase
- Uniform gas distribution in the reaction chambers
- Isothermal conditions in the slits
- Negligible pressure drop in the slits
- Constant superficial velocity (which is only the case for sufficient dilution, [27])
- No gradients rectangular to flow direction
- Axial dispersion considered with axial dispersion coefficient
- External mass transfer limitations neglected (Maers criterion)
- Internal mass transfer limitations considered (Weisz–Prater criterion) and implemented with linear driving force (LDF) model (Glueckauf criterion)
- Equilibrium-based desorption of H2O and CO2.
2.2. Model Equations
2.3. Model Parameters
3. Numerical Simulation Approaches
3.1. Built-In Solver
3.2. Method-of-Lines (MoL)
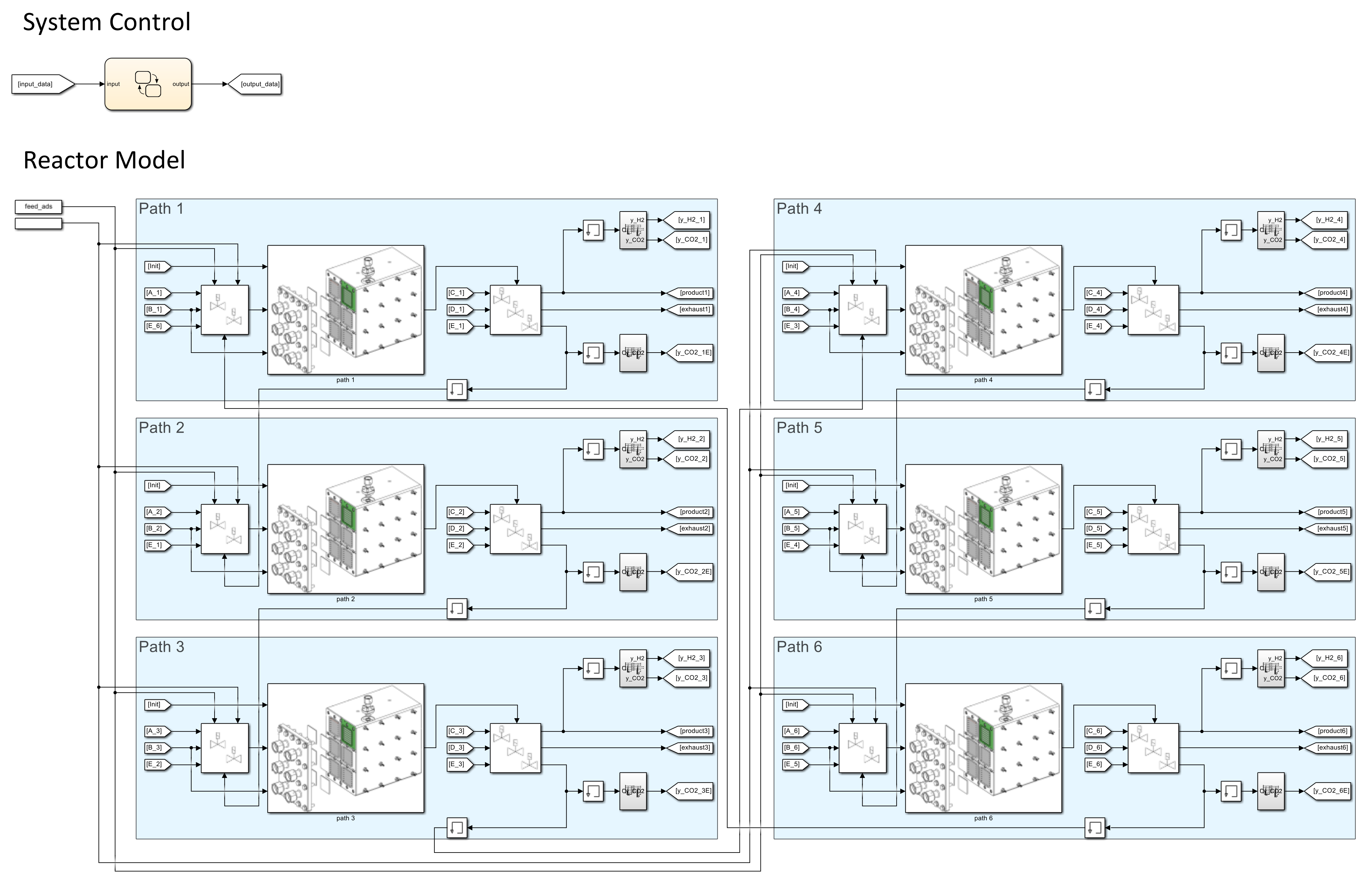
3.3. Simulink
3.3.1. Model Implementation and Data Structure
3.3.2. Solver Selection
3.3.3. Cyclic Process Design
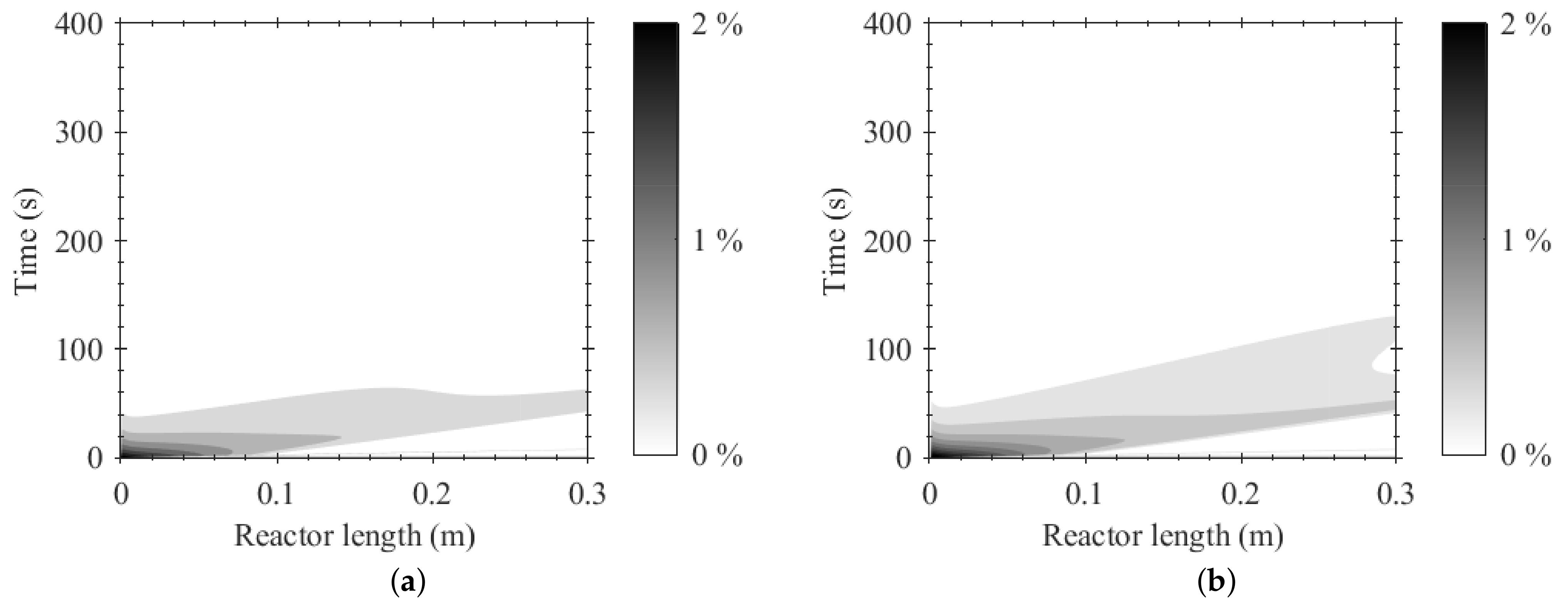
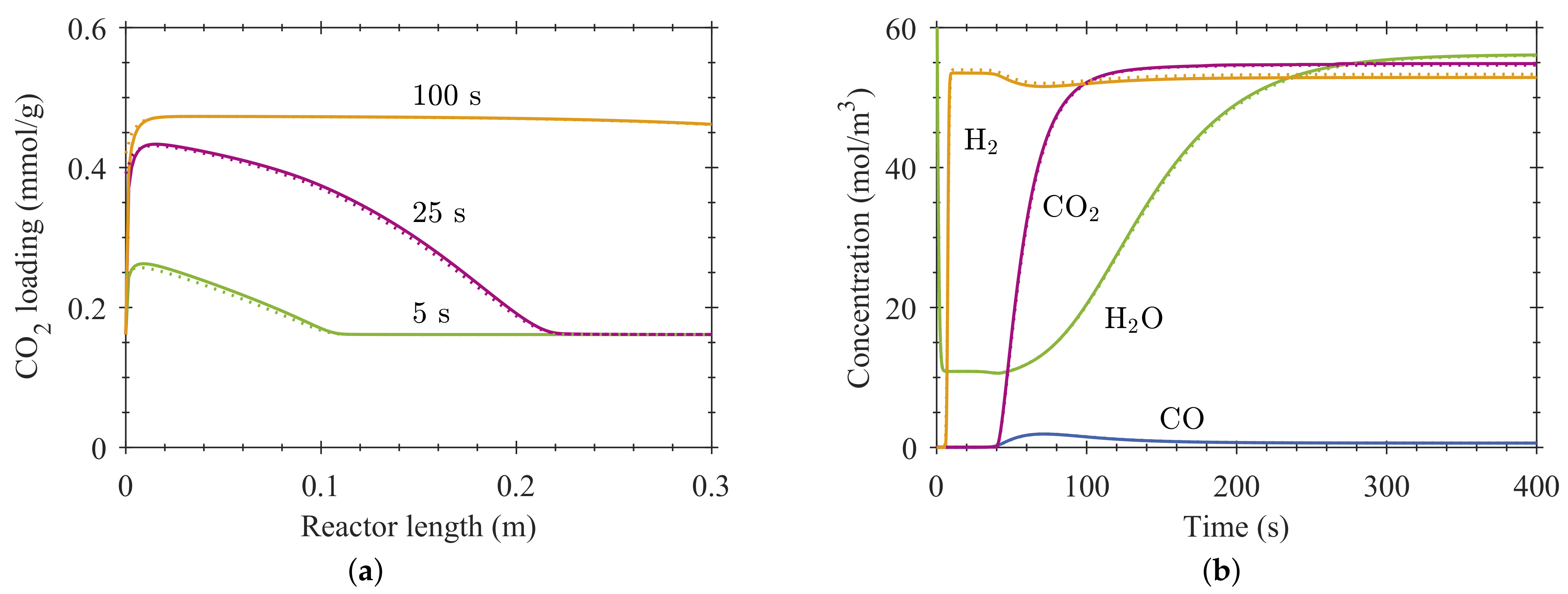
4. Results and Discussion
4.1. Reactive Adsorption
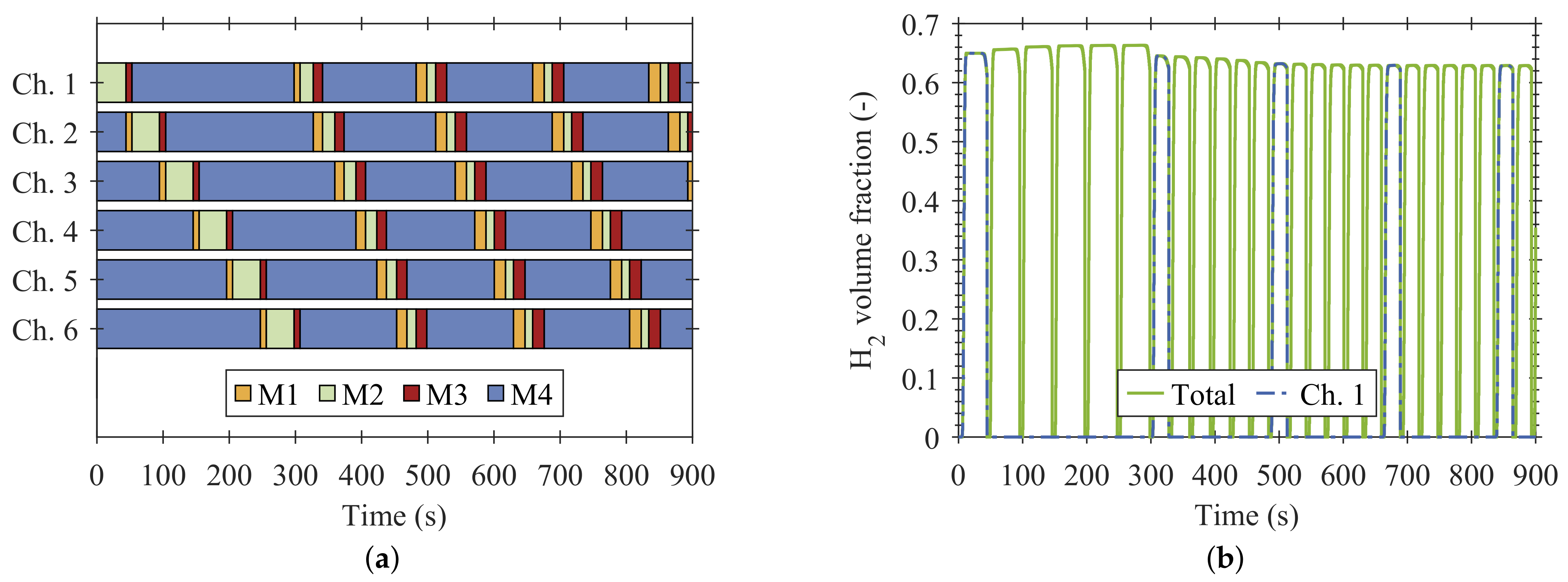
4.2. Process Design
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| The following abbreviations are used in this manuscript: | ||
| BFDM | Backward finite difference method of first order | |
| CFDM | Centered finite difference method of second order | |
| Ch. | Chamber | |
| CSTR | Continuously stirred tank reactor | |
| DAE | Differential algebraic equation | |
| DASOLV | Implicit backward differentiation formula solver in gPROMS | |
| DMES | Dimethyl ether synthesis | |
| FD | Finite Difference | |
| FEM | Finite elements method | |
| K-HTC | K2CO3-promoted hydrotalcite | |
| LDF | Linear driving force model | |
| M1-M4 | Mode 1-4 | |
| MoL | Method-of-lines | |
| ODE | Ordinary differential equation | |
| ode15s | Solver for stiff ODEs in MATLAB | |
| PDE | partial differential equation | |
| pdepe | Solver for systems of parabolic and elliptic PDEs in MATLAB | |
| PLC | Programmable logic controller | |
| PSA | Pressure swing adsorption | |
| PTSA | Pressure temperature swing adsorption | |
| SEWGS | Sorption-enhanced water–gas shift | |
| SMR | Steam-methane reforming | |
| TSA | Temperature swing adsorption | |
| WGS | Water–gas shift | |
| The following symbols are used in this manuscript: | ||
| activation energy change | () | |
| bed void fraction | (–) | |
| particle void fraction | (–) | |
| stoichiometric reaction coefficient | (–) | |
| bulk density | () | |
| adsorption rate | () | |
| pdepe diagonal matric | (–) | |
| bulk phase concentration | () | |
| particle void phase concentration | () | |
| axial dispersion coefficient | ( ) | |
| effective diffusion coefficient | ( ) | |
| gas mixture diffusion coefficient | ( ) | |
| activation energy | () | |
| equilibrium | (–) | |
| pdepe flux term coefficient | (–) | |
| volumetric flow rate at STP | () | |
| h | slit height | (mm) |
| standard reaction enthalpy | () | |
| i | species CO, H2O, CO2, H2, N2 | (–) |
| j | sorption site A, B, C | (–) |
| exchange rate coefficient 1 | () | |
| exchange rate coefficient 2 | () | |
| equilibrium constant | (–) | |
| Freundlich adsorption coefficient | () | |
| adsorption coefficient | () | |
| desorption coefficient | () | |
| desorption coefficient | () | |
| linear driving force coefficient | () | |
| frequency factor | () | |
| l | slit length | (mm) |
| tiny value exponent | (–) | |
| pdepe symmetry constant | (–) | |
| n | index variable | (–) |
| N | number of cells | (–) |
| Freundlich adsorption intensity | (–) | |
| O | approximation error | (–) |
| pdepe boundary coefficient | (–) | |
| (partial) pressure | (bar) | |
| pdepe boundary coefficient | (–) | |
| sorbent loading of species i on site j | () | |
| particle radius | (m) | |
| WGS reaction rate | ( ) | |
| R | gas constant | ( ) |
| pdepe source term coefficient | (–) | |
| t | time | () |
| T | temperature | () |
| u | gas velocity | () |
| v | dependent variable | (–) |
| w | slit width | (mm) |
| catalyst weight fraction | (–) | |
| volume fraction | (–) | |
| z | axial coordinate | () |
Appendix A
| MoL | pdepe | ||||||
|---|---|---|---|---|---|---|---|
| Number of Cells | 10 | 30 | 50 | 100 | 200 | 250 | 3000 |
| (-) | |||||||
| Computation Time | 0.04 | 0.22 | 0.27 | 4.96 | 46.81 | 90.93 | 12.19 |
| (min) | |||||||
References
- UN. COP26 Outcomes. In Proceedings of the UN Climate Change Conference at the SEC, Glasgow, UK, 31 October–13 November 2021. [Google Scholar]
- United Nations. Framework Convention on Climate Change. Adoption of the Paris Agreement. In Proceedings of the 21st Conference of the Parties, Paris, France, 30 November–11 December 2015. [Google Scholar]
- European Commission. A European Strategy for Low-Emission Mobility; EEA: Copenhagen, Denmark, 2020. [Google Scholar]
- Goede, A.P.H. CO2 neutral fuels. EPJ Web Conf. 2018, 189, 00010. [Google Scholar] [CrossRef] [Green Version]
- Rodrigues, A.E.; Madeira, L.M.; Wu, Y.J.; Faria, R. Sorption enhanced reaction processes. In Sustainable Chemistry Series; World Scientific: New Jersey, NJ, USA, 2018; Volume 1. [Google Scholar]
- Lee, C.H.; Lee, K.B. Application of one-body hybrid solid pellets to sorption-enhanced water gas shift reaction for high-purity hydrogen production. Int. J. Hydrogen Energy 2014, 39, 18128–18134. [Google Scholar] [CrossRef]
- Soria, M.A.; Rocha, C.; Tosti, S.; Mendes, A.; Madeira, L.M. COx free hydrogen production through water-gas shift reaction in different hybrid multifunctional reactors. Chem. Eng. J. 2019, 356, 727–736. [Google Scholar] [CrossRef]
- Stadler, T.J.; Barbig, P.; Kiehl, J.; Schulz, R.; Klövekorn, T.; Pfeifer, P. Sorption-Enhanced Water-Gas Shift Reaction for Synthesis Gas Production from Pure CO: Investigation of Sorption Parameters and Reactor Configurations. Energies 2021, 14, 355. [Google Scholar] [CrossRef]
- Zhu, X.; Li, S.; Shi, Y.; Cai, N. Recent advances in elevated-temperature pressure swing adsorption for carbon capture and hydrogen production. Prog. Energy Combust. Sci. 2019, 75, 100784. [Google Scholar] [CrossRef]
- Harrison, D.P. Sorption-Enhanced Hydrogen Production: A Review. Ind. Eng. Chem. Res. 2008, 47, 6486–6501. [Google Scholar] [CrossRef]
- Gazzani, M.; Macchi, E.; Manzolini, G. CO2 capture in integrated gasification combined cycle with SEWGS—Part A: Thermodynamic performances. Fuel 2013, 105, 206–219. [Google Scholar] [CrossRef]
- Schiesser, W.E. A Compendium of Partial Differential Equation Models: Method of Lines Analysis with MATLAB; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Lee, K.B.; Verdooren, A.; Caram, H.S.; Sircar, S. Chemisorption of carbon dioxide on potassium-carbonate-promoted hydrotalcite. J. Colloid Interface Sci. 2007, 308, 30–39. [Google Scholar] [CrossRef]
- Reijers, H.T.J.; Boon, J.; Elzinga, G.D.; Cobden, P.D.; Haije, W.G.; van den Brink, R.W. Modeling Study of the Sorption-Enhanced Reaction Process for CO2 Capture. I. Model Development and Validation. Ind. Eng. Chem. Res. 2009, 48, 6966–6974. [Google Scholar] [CrossRef] [Green Version]
- Najmi, B.; Bolland, O.; Colombo, K.E. A systematic approach to the modeling and simulation of a Sorption Enhanced Water Gas Shift (SEWGS) process for CO2 capture. Sep. Purif. Technol. 2016, 157, 80–92. [Google Scholar] [CrossRef]
- Karagöz, S.; Tsotsis, T.T.; Manousiouthakis, V.I. Multi-scale modeling and simulation of a novel membrane reactor (MR)/adsorptive reactor (AR) process. Chem. Eng. Process. Process. Intensif. 2019, 137, 148–158. [Google Scholar] [CrossRef]
- Di Giuliano, A.; Gallucci, K.; Giancaterino, F.; Courson, C.; Foscolo, P.U. Multicycle sorption enhanced steam methane reforming with different sorbent regeneration conditions: Experimental and modelling study. Chem. Eng. J. 2019, 377, 119874. [Google Scholar] [CrossRef]
- Van Kampen, J.; Boon, J.; Vente, J.; van Sint Annaland, M. Sorption enhanced dimethyl ether synthesis for high efficiency carbon conversion: Modelling and cycle design. J. CO2 Util. 2020, 37, 295–308. [Google Scholar] [CrossRef]
- Guffanti, S.; Visconti, C.G.; van Kampen, J.; Boon, J.; Groppi, G. Reactor modelling and design for sorption enhanced dimethyl ether synthesis. Chem. Eng. J. 2021, 404, 126573. [Google Scholar] [CrossRef]
- Guffanti, S.; Visconti, C.G.; Groppi, G. Model Analysis of the Role of Kinetics, Adsorption Capacity, and Heat and Mass Transfer Effects in Sorption Enhanced Dimethyl Ether Synthesis. Ind. Eng. Chem. Res. 2021, 60, 6767–6783. [Google Scholar] [CrossRef]
- Jang, H.M.; Lee, K.B.; Caram, H.S.; Sircar, S. High-purity hydrogen production through sorption enhanced water gas shift reaction using K2CO3-promoted hydrotalcite. Chem. Eng. Sci. 2012, 73, 431–438. [Google Scholar] [CrossRef]
- Aloisi, I.; Di Giuliano, A.; Di Carlo, A.; Foscolo, P.U.; Courson, C.; Gallucci, K. Sorption enhanced catalytic Steam Methane Reforming: Experimental data and simulations describing the behaviour of bi-functional particles. Chem. Eng. J. 2017, 314, 570–582. [Google Scholar] [CrossRef]
- Zheng, Y.; Shi, Y.; Li, S.; Yang, Y.; Cai, N. Elevated temperature hydrogen/carbon dioxide separation process simulation by integrating elementary reaction model of hydrotalcite adsorbent. Int. J. Hydrogen Energy 2014, 39, 3771–3779. [Google Scholar] [CrossRef]
- Boon, J.; Cobden, P.D.; van Dijk, H.; van Sint Annaland, M. High-temperature pressure swing adsorption cycle design for sorption-enhanced water—Gas shift. Chem. Eng. Sci. 2015, 122, 219–231. [Google Scholar] [CrossRef] [Green Version]
- Stankiewicz, A.I.; Moulijn, J.A. Process intensification: Transforming chemical engineering. Chem. Eng. Prog. 2000, 96, 22–34. [Google Scholar]
- Keil, F.J. Process intensification. Rev. Chem. Eng. 2018, 34, 135–200. [Google Scholar] [CrossRef] [Green Version]
- Di Giuliano, A.; Pellegrino, E. Numerical integration strategies of PFR dynamic models with axial dispersion and variable superficial velocity: The case of CO2 capture by a solid sorbent. Heliyon 2019, 5, e02040. [Google Scholar] [CrossRef] [PubMed]
- Choi, Y.; Stenger, H.G. Water gas shift reaction kinetics and reactor modeling for fuel cell grade hydrogen. J. Power Sources 2003, 124, 432–439. [Google Scholar] [CrossRef]
- Coenen, K.; Gallucci, F.; Hensen, E.; van Sint Annaland, M. Kinetic model for adsorption and desorption of H2O and CO2 on hydrotalcite-based adsorbents. Chem. Eng. J. 2019, 355, 520–531. [Google Scholar] [CrossRef]
- Moe, J.M. Design of water-gas shift reactors. Chem. Eng. Prog. 1962, 58, 8. [Google Scholar]
- Poling, B.E.; Prausnitz, J.M.; O’Connell, J.P. The Properties of Gases and Liquids, 5th ed.; McGraw-Hill: New York, NY, USA, 2001. [Google Scholar]
- Yang, R.T. Gas Separation by Adsorption Processes; Butterworths series in chemical engineering; Butterworths: Boston, MA, USA, 1987. [Google Scholar]
- MathWorks. Solve 1-D parabolic and elliptic PDEs—MATLAB pdepe. Available online: https://de.mathworks.com/help/matlab/ref/pdepe.html (accessed on 19 January 2022).
- Skeel, R.D.; Berzins, M. A Method for the Spatial Discretization of Parabolic Equations in One Space Variable. SIAM J. Sci. Stat. Comput. 1990, 11, 1–32. [Google Scholar] [CrossRef]
- Shampine, L.F.; Reichelt, M.W. The Matlab ODE suite. SIAM J. Sci. Comput. 1997, 18, 1–22. [Google Scholar] [CrossRef] [Green Version]
- Ukrainczyk, N.; Koenders, E.A.B. Numerical Model for Chloride Ingress in Cement Based Materials: Method of Lines Implementation for Solving Coupled Multi-species Diffusion with Binding. Comput. Mater. Civ. Eng. 2016, 1, 109–119. [Google Scholar]
- MathWorks. Simulink Product Description—MATLAB & Simulink. Available online: https://de.mathworks.com/help/simulink/gs/product-description.html (accessed on 19 January 2022).
- Puente León, F.; Jäkel, H. Signale und Systeme, 7th ed.; De Gruyter Studium, De Gruyter Oldenbourg: Berlin, Germany; Boston, MA, USA, 2019. [Google Scholar]
- MathWorks. Choose a Solver—MATLAB & Simulink. Available online: https://de.mathworks.com/help/simulink/ug/choose-a-solver.html (accessed on 19 January 2022).
- MathWorks. Overview of Stateflow Objects—MATLAB & Simulink. Available online: https://de.mathworks.com/help/stateflow/ug/overview-of-stateflow-objects.html (accessed on 19 January 2022).
- Bayrak, G.; Abrishamchian, F.; Vogel-Heuser, B. Effiziente Steuerungsprogrammierung durch automatische Modelltransformation von Matlab/Simulink/Stateflow nach IEC 61131-3. Autom. Prax. 2008, 50, 49–55. [Google Scholar]







| Reaction | Adsorption | Numerical Solution | Reference |
|---|---|---|---|
| - | CO2 on K-HTC | MATLAB: MoL (N = 500) / ode15s solver | [13] |
| SMR | CO2 on K-HTC | MATLAB: MoL / ode15s solver | [14] |
| WGS | CO2 on K-HTC | gPROMS: CFDM (N = 600) / DASOLV solver | [15] |
| WGS | CO2 | COMSOL Multiphysics: FEM | [16] |
| SMR | CO2 on CaO-mayenite | MATLAB: pdepe solver | [17] |
| DMES | H2O on LTA zeolite | MATLAB: MoL (N = 30) / ode15s solver | [18] |
| DMES | H2O on LTA zeolite 3A | gPROMS: BFDM (N = 60) / DASOLV solver | [19,20] |
| WGS | CO2 on K-HTC | MATLAB: MoL (N = 250) / ode15s solver | [21] |
| SMR | CO2 on CaO | MATLAB: pdepe solver | [22] |
| - | CO2 on K-HTC | gPROMS | [23] |
| General Parameters | |
|---|---|
| 1096 | |
| 100 | |
| Adsorption Parameters | |
| p | 8 bar |
| T | 250 |
| 2000 mL / | |
| Desorption Parameters | |
| p | 1 bar |
| T | 250 |
| 1000 mL / | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stadler, T.J.; Knoop, J.-H.; Decker, S.; Pfeifer, P. Numerical Simulation Approach for a Dynamically Operated Sorption-Enhanced Water-Gas Shift Reactor. Processes 2022, 10, 1160. https://doi.org/10.3390/pr10061160
Stadler TJ, Knoop J-H, Decker S, Pfeifer P. Numerical Simulation Approach for a Dynamically Operated Sorption-Enhanced Water-Gas Shift Reactor. Processes. 2022; 10(6):1160. https://doi.org/10.3390/pr10061160
Chicago/Turabian StyleStadler, Tabea J., Jan-Hendrik Knoop, Simon Decker, and Peter Pfeifer. 2022. "Numerical Simulation Approach for a Dynamically Operated Sorption-Enhanced Water-Gas Shift Reactor" Processes 10, no. 6: 1160. https://doi.org/10.3390/pr10061160
APA StyleStadler, T. J., Knoop, J.-H., Decker, S., & Pfeifer, P. (2022). Numerical Simulation Approach for a Dynamically Operated Sorption-Enhanced Water-Gas Shift Reactor. Processes, 10(6), 1160. https://doi.org/10.3390/pr10061160