Abstract
During methane extraction, the permeability of a coal seam is the vital factor affecting recovery. Although the permeability of a coal seam and its relationship with porosity have been studied in a few works, the calculation process of coal seam permeability is usually too simplistic or neglects the influence of microscopic fracture structures. Statistical research shows that the permeability of coal seams with the same porosity and different fracture structures is quite different. For the purpose of quantitatively investigating the contribution of fractures and pore structure in coal seams, a fractal permeability model considering the microstructure of coal seam fracture is established in this paper. The correctness of the model is verified by comparing with the previous research results. Then, the influence of the microscopic fracture structure on the equivalent permeability is analyzed. The simulation results show that the permeability of fractured coal is directly proportional to the fractal dimension of the fracture, the maximum fracture length and the azimuth. It is inversely proportional to the tortuous fractal dimension and the dip angle of the fracture surface. This conclusion provides the foundation for revealing the microstructure mechanisms of macroscopic seepage characteristics of coal seams, and implementing effective strategies to enhance gas recovery rates under different geological structures.
1. Introduction
As the main channel for gas migration in a reservoir, fracture length is unevenly distributed, with varying degrees of tortuosity and a complex structural distribution. The connection state of the coal pore-throat network will directly affect oil and gas recovery [1,2,3]. Moreover, the coal fracture network is also complex [4,5,6]; therefore, accurately exposing the connectivity of the reservoir structure and quantitatively investigating the interaction between the reservoir microstructure and the macroscopic behavior at the micro scale is the key to improving gas recovery [7,8,9,10]. In recent years, an increasing number of studies have demonstrated that fractures in unconventional reservoirs have distinct fractal characteristics and that fractal theory is better able to quantitatively characterize the distribution of fracture structure networks.
The application of fractal geometry in porous media has been studied more extensively by scholars. On the basis of the concepts of the geometric model of volume and surface fractal dimension, Deinert et al. [11,12] established a relationship between fluid saturation and capillary pressure. Later, on the basis of the fractal geometric theory, Xu et al. [13,14,15] explored the heat transfer properties and percolation behavior of fractal tree networks. In addition, Ishibashi et al. [16] explored the interaction law between fracture opening and seepage characteristics under different gas pressures and concluded that fracture permeability obeys a power-law distribution. On the basis of the fractal dimension of the pore space, Costa et al. [17] explored the relationship between the constant of the Kozeny-Carman equation and the porosity of the depth and derived the contribution of fractal permeability. Guarracino et al. [18] used the Sierpinski fractal model to predict hydraulic fracturing conductivity.
However, previous studies usually regard the fracture system as a simplified symmetric network or an empirical constant in the permeability model. Accurate and quantitative descriptions of seepage characteristics of different fracture network structures remain to be studied [19,20,21,22]. In this work, we established a permeability model, including fracture microstructures, such as fractal dimension of fracture dimension, fracture detour, fracture inclination, and fracture orientation, which does not contain empirical constants. In addition, the simulation results of the model are compared with the field-measured data, which has good consistency and verifies the correctness of the model. The internal relationship between the fracture macro permeability and micro-network structure is further analyzed.
2. Fractal Characterization of Coal Fracture Network
Statistics show that the length of coal fracture meets the fractal scaling law. Fractal theory defines the fractal power-law relation for fractals as [23,24,25]:
where is the single fracture length, , is the fracture number, is the fracture fractal dimension, for 2D space, . Therefore, Equation (1) can be simplified as:
Differentiating Equation (1), the number of fractures between l and l + dl in length can be expressed as:
Using Equation (3), the probability density function of the fracture is expressed as:
where is the total number of the fractures. Normalizing the probability density function yields:
Thus:
When the fracture network satisfies the fractal scaling law, fracture opening and the length of fracture satisfy the following relations [26,27]:
where is the reservoir matrix mechanical coefficient. The fractal dimension of the fracture length is:
where represents the dimension of the calculation domain, for the two-dimensional domain, . If , Equation (6) can be simplified as:
For natural fracture networks, the minimum length and the maximum length of the fractures usually satisfy . In additiont, on the basis of the porous media distribution law [28,29], the crack length and pore diameter are analogous. The total number of cracks for the reservoir is:
Combining Equations (9) and (10), we obtain:
Substituting Equation (11) into Equation (3), it can be determine that the fractal power law expression of fracture length in fractal fracture network is:
3. Fractal Permeability Model of Coal Fracture Network
In this section, we couple the fractal characteristic intrinsic constitutive equation derived above with the Hagen–Poiseuille equation and Darcy’s law to derive a comprehensive seepage model for the analysis of reservoir fracture structures. The cubic law of single fracture seepage is the basis of seepage theory of a fracture network because of its simplicity and accuracy. The flow rate for a single horizontal fracture is [30,31]:
where is gas hydrodynamic viscosity, is difference of pressure for a fracture, is length for a characterization unit. When considering the spatial orientation of fractures (as illustrated in Figure 1), the flow rate for single crack yields [32,33,34]:
where is the fracture azimuth angle and is the dip angle.
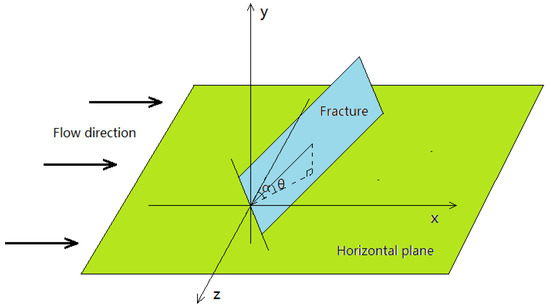
Figure 1.
Sketch map of the fracture azimuth.
Consequently, the total flow for all fractures in the analysis area (presented in Figure 2) can be obtained as:
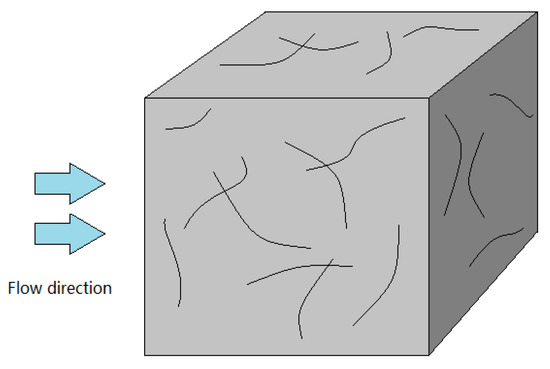
Figure 2.
Characterization unit of reservoir fracture structure.
The crack size satisfies [35,36]:
where is the throat tortuosity fractal dimension, is the length of the fracture in the fluid-flow direction.
Combining Equations (12), (15) and (17), we obtain:
On the basis of Darcy’s law:
where is the permeability of fractured coal. Simultaneous to Equations (17) and (18), the fractal permeability of fracture network is:
Figure 3 illustrates the process of developing the reservoir fractal permeability model. The coal microstructure is simplified as a combination of fractures. We then construct a permeability model on the basis of the basic theory of fractal geometry, which enables quantitative investigation of maximum pore size, throat tortuosity, and pore scale. In the 2D calculation domain: and .
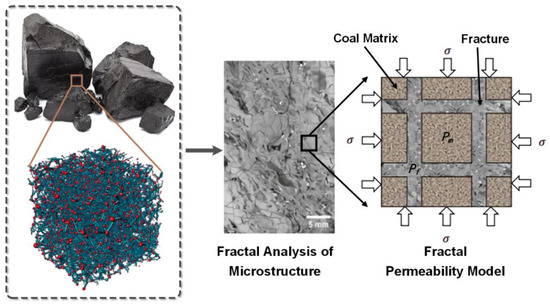
Figure 3.
Establishment of fractal permeability model.
4. Verification of the Permeability Model
The fractal dimension of the fracture length for 22 different natural fracture networks was calculated by Jafari and Babadagli [35] on the basis of the box-counting method, and then a fracture network of was constructed. The maximum length of the fracture was 2 m, and the fracture dip angle was 0. To verify the fractal fracture network model, the fractal model was compared with the above simulation results, as shown in Figure 4a. In addition, the simulation results of the fractal model in this paper were also compared with the seepage experimental results of rocks with different porosities [36] in order to further verify the rationality of the model, as shown in Figure 4b.
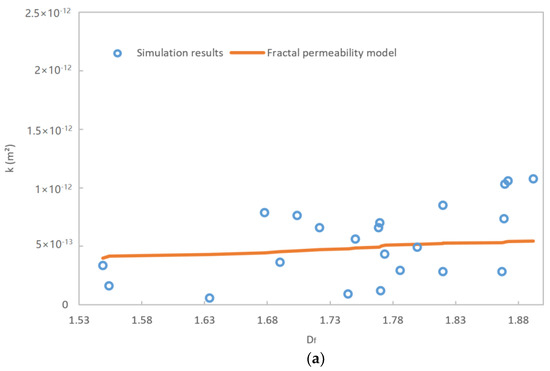
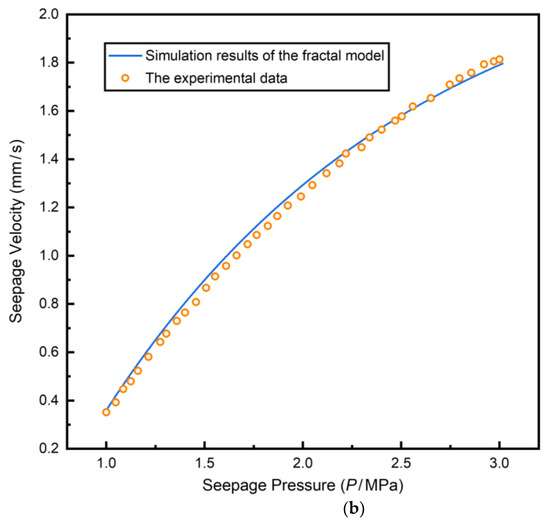
Figure 4.
Verification of the fractal permeability model. (a) Compared with the results of [35]; (b) Compared with the results of [36].
It is revealed in Figure 4 that the fractal permeability model proposed in this paper is in good agreement with the field permeability evolution results, verifying the accuracy of the fractal model.
5. Results and Discussion
The seepage network permeability is influenced by the microstructure parameters of fractures [37,38,39,40]. To discuss the impact of different structural parameters on reservoir permeability, we analyzed the influence mechanisms for microstructural parameters, including the fracture tortuosity fractal dimension, maximum fracture length, the azimuth angle of fracture, and the dip angle of fracture.
Figure 5 shows the curve of the permeability verified with DT. According to Figure 5, the permeability gradually decreases with increasing DT. This corresponds to the physical truth. Under the same inlet and outlet pressure difference, with increasing DT, the bending degree of the crack increases, so the fluid resistance through the fracture increases and the permeability decreases.
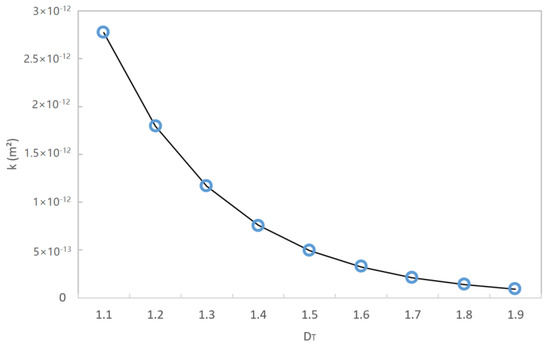
Figure 5.
Permeability variation with the increasing tortuosity fractal dimension.
The interaction between permeability and maximum fracture length is illustrated in Figure 6, i.e., k increases rapidly with increasing lmax. The main reason for this is that the total number of fractures decreases with the increasing length of a single fracture, and the small fractures tend to converge on several fractures, which reduces the flow resistance of the fluid.
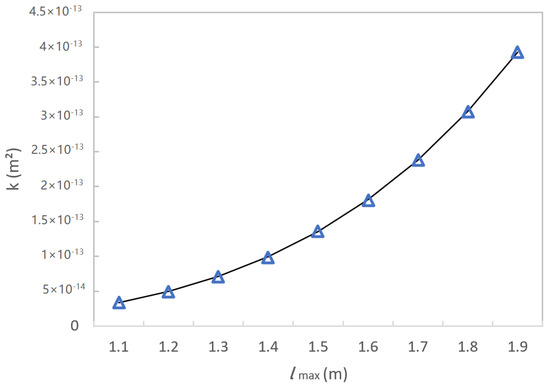
Figure 6.
Permeability variation with the increase of the maximum fracture length.
As illustrated in Figure 7, when the azimuth angle of fractures is constant, the permeability decreases with the increase in dip angle . When the dip angle is 0, the direction of the fluid flow is located on the fracture surface, and the resistance of the fluid flow is smallest, which is consistent with the physical truth. Furthermore, if the dip angle is constant, the permeability increases with the azimuth angle of fractures. When the fracture azimuth is , the direction of fracture coincides with the direction of the fluid flow, and the fluid resistance is smallest.
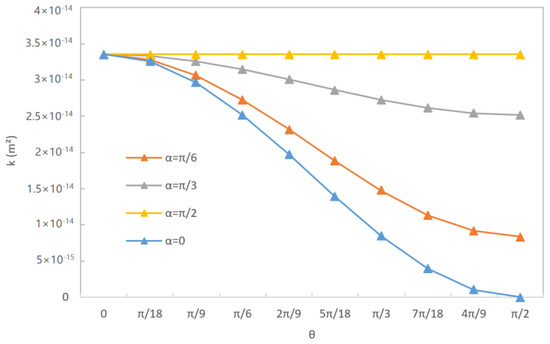
Figure 7.
Permeability variation with the increasing fracture azimuth.
6. Conclusions
To reveal the quantitative relationship between the macroscopic equivalent permeability and the micro-fracture structure of fractured coal, an equivalent permeability model, considering the microstructure of the fracture, is established on the basis of the fractal theory. The accuracy of the fractal permeability model is verified by comparing it with the previous simulation results.
Furthermore, by simulating the fluid flow in the fracture, the interactions of the microstructural parameters and permeability are studied, such as fracture fractal dimension, fracture tortuosity fractal dimension, maximum fracture length, dip angle of fracture, and azimuth angle of fracture. In this study, the calculation does not include the external force constraint and the process of coal deformation induced by adsorption and desorption in the gas flow. The evolution process of permeability and its effect on gas recovery under the combined effect of in situ stress and sorption–desorption-induced matrix deformation are interesting topics, and these will be our next work.
Author Contributions
Conceptualization, X.X.; methodology, X.X. and L.X.; validation, C.Y. and L.X.; formal analysis, X.X.; investigation, X.X. and C.Y.; resources, C.Y. and G.L.; data curation, X.X. and L.X.; writing—original draft preparation, X.X., C.Y. and G.L.; writing—review and editing, X.X. and G.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Open Research Fund of the State Key Laboratory of Coal Resources and Safe Mining, CUMT, No.SKLCRSM20KF007 and Innovation Training Program for Chinese College Students, No. 202110304040.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Arand, F.; Hesser, J. Accurate and efficient maximal ball algorithm for pore network extraction. Comput. Geosci. 2017, 101, 28–37. [Google Scholar] [CrossRef]
- Qin, X.; Zhou, Y.; Sasmito, A.P. An effective thermal conductivity model for fractal porous media with rough surfaces. Adv. Geo-Energy Res. 2019, 3, 149–155. [Google Scholar] [CrossRef]
- Bauer, B.; Cai, X.; Peth, S.; Schladitz, K.; Steidl, G. Variational-based segmentation of bio-pores in tomographic images. Comput. Geosci. 2017, 98, 1–8. [Google Scholar] [CrossRef]
- Li, Z.; Duan, Y.; Fang, Q.; Wei, M. A study of relative permeability for transient two-phase flow in a low permeability fractal porous medium. Adv. Geo-Energy Res. 2018, 2, 369–379. [Google Scholar] [CrossRef][Green Version]
- Zhao, X. The Study of Reconstruction Method of Digital Core and Pore Network Model. Ph.D. Thesis, China Petroleum University, Beijing, China, 2009. [Google Scholar]
- Li, K.; Kong, S.; Xia, P.; Wang, X. Microstructural characterisation of organic matter pores in coal-measure shale. Adv. Geo-Energy Res. 2020, 4, 372–391. [Google Scholar] [CrossRef]
- Raeini, A.Q.; Bijeljic, B.; Blunt, M.J. Generalized network modeling: Network extraction as a coarse-scale discretization of the void space of porous media. Phys. Rev. E 2017, 96, 013312. [Google Scholar] [CrossRef]
- Kelly, S.; El-Sobky, H.; Torres-Verdin, C.; Balhoff, M.T. Assessing the utility of FIB-SEM images for shale digital rock physics. Adv. Water Resour. 2016, 95, 302–316. [Google Scholar] [CrossRef]
- Zhang, T.Y.; Li, D.L.; Yang, J.Q.; Lu, D. A study of the effect of pore characteristic on permeability with a pore network model. Pet. Sci. Technol. 2013, 31, 1790–1796. [Google Scholar] [CrossRef]
- Starnonia, M.; Pokrajaca, D.; Neilson, J.E. Computation of fluid flow and pore-space properties estimation on micro CT images of rock samples. Comput. Geosci. 2017, 106, 118–129. [Google Scholar] [CrossRef]
- Deinert, M.; Parlange, J.Y.; Cady, K. Simplified thermodynamic model for equilibrium capillary pressure in a fractal porous medium. Phys. Rev. E 2005, 72, 041203. [Google Scholar] [CrossRef]
- Deinert, M.; Dathe, A.; Parlange, J.; Cady, K.B. Capillary pressure in a porous medium with distinct pore surface and pore volume fractal dimensions. Phys. Rev. E 2008, 77, 021203. [Google Scholar] [CrossRef] [PubMed]
- Xu, P.; Yu, B. The scaling laws of transport properties for fractal-like tree networks. J. Appl. Phys. 2006, 100, 104906. [Google Scholar] [CrossRef]
- Xu, P.; Yu, B.; Yun, M.; Zou, M. Heat conduction in fractal tree-like branched networks. Int. J. Heat Mass Transf. 2006, 49, 3746–3751. [Google Scholar] [CrossRef]
- Xu, P.; Yu, B.; Feng, Y.; Liu, Y. Analysis of permeability for the fractal-like tree network by parallel and series model. Phys. A Stat. Mech. Its Appl. 2006, 369, 884–894. [Google Scholar] [CrossRef]
- Ishibashi, T.; Watanabe, N.; Hirano, N.; Okamoto, A.; Tsuchiya, N. Beyond-laboratory-scale prediction for channeling flows through subsurface rock fractures with heterogeneous aperture distributions revealed by laboratory evaluation. J. Geophys. Res. Solid Earth 2015, 120, 106–124. [Google Scholar] [CrossRef]
- Costa, A. Permeability-porosity relationship: A reexamination of the Kozeny-Carman equation based on a fractal pore-space geometry assumption. Geophys. Res. Lett. 2006, 33, 87–94. [Google Scholar] [CrossRef]
- Guarracino, L. A fractal constitutive model for unsaturated flow in fractured hard rocks. J. Hydrol. 2006, 324, 154–162. [Google Scholar] [CrossRef]
- Majewska, Z.; Majewski, S.; Zietek, J. Swelling and acoustic emission behaviour of unconfined and confined coal during sorption of CO2. Int. J. Coal Geol. 2013, 117, 17–25. [Google Scholar] [CrossRef]
- Au, P.; Liu, J.S.; Leong, Y. Yield stress and microstructure of washed oxide suspensions at the isoelectric point: Experimental and model fractal structure. Rheol. Acta 2016, 55, 847–856. [Google Scholar] [CrossRef]
- Wang, C.G.; Liu, J.H.; Wei, M.Y. Controlling Effects of Gas Diffusion from Fractures to Matrixes in Coal on the Evolution of Local and Global Strains: Experimental Observations. Int. J. Coal Geol. 2016, 162, 74–84. [Google Scholar] [CrossRef]
- Karacan, C.O. Swelling-induced volumetric strains internal to a stressed coal associated with CO2 sorption. Int. J. Coal Geol. 2007, 72, 209–220. [Google Scholar] [CrossRef]
- Sahimi, M. Flow and Transport in Porous Media and Fractured Rock: From Classical Methods to Modern Approaches; John Wiley & Sons: New York, NY, USA, 2012. [Google Scholar]
- Bonnet, E.; Bour, O.; Odling, N.E.; Davy, P.; Main, I.G.; Cowie, P.; Berkowitz, B. Scaling of fracture systems in geological media. Rev. Geophys. 2001, 39, 347–383. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. The Fractal Geometry of Nature; Macmillan: New York, NY, USA, 1983. [Google Scholar]
- Hatton, C.; Main, I.; Meredith, P. Non-universal scaling of fracture length and opening displacement. Nature 1994, 367, 160–162. [Google Scholar] [CrossRef]
- Schultz, R.A.; Soliva, R.; Fossen, H.; Okubo, C.; Reeves, D.M. Dependence of displacement-length scaling relations for fractures and deformation bands on the volumetric changes across them. J. Struct. Geol. 2008, 30, 1405–1411. [Google Scholar] [CrossRef]
- Li, L.; Yu, B. Fractal analysis of the effective thermal conductivity of biological media embedded with randomly distributed vascular trees. Int. J. Heat Mass Tran. 2013, 67, 74–80. [Google Scholar] [CrossRef]
- Yu, B. Analysis of flow in fractal porous media. Appl. Mech. Rev. 2008, 61, 050801. [Google Scholar] [CrossRef]
- Khamforoush, M.; Shams, K.; Thovert, J.F.; Adler, P.M. Permeability and percolation of anisotropic three-dimensional fracture networks. Phys. Rev. E 2008, 77, 056307. [Google Scholar] [CrossRef]
- Nazridoust, K.; Ahmadi, G.; Smith, D.H. A new friction factor correlation for laminar, single-phase flows through rock fractures. J. Hydrol. 2006, 329, 315–328. [Google Scholar] [CrossRef]
- Miao, T.; Yu, B.; Duan, Y.; Fang, Q. A fractal analysis of permeability for fractured rocks. Int. J. Heat Mass Tran. 2015, 81, 75–80. [Google Scholar] [CrossRef]
- Liu, Y.; Ding, Z.; Qu, Y.; Zhao, C. The characterization of fracture orientation and the calculation of anisotropic permeability parameters of reservoirs. Acta Pet. Sin. 2011, 32, 842–846. [Google Scholar]
- Liu, R.; Li, B.; Jiang, Y.; Yu, L. A numerical approach for assessing effects of shear on equivalent permeability and nonlinear flow characteristics of 2-D fracture networks. Adv. Water Resour. 2018, 111, 289–300. [Google Scholar] [CrossRef]
- Jafari, A.; Babadagli, T. Effective fracture network permeability of geothermal reservoirs. Geothermics 2011, 40, 25–38. [Google Scholar] [CrossRef]
- Shi, X.Y.; Zhou, W.; Cai, Q.; Lu, X. Experimental study on nonlinear seepage characteristics and particle size gradation effect of fractured sandstones. Adv. Civ. Eng. 2018, 2018, 8640535. [Google Scholar] [CrossRef]
- Liu, Y.; Yu, B.; Xu, P.; Wu, J. Study of the effect of capillary pressure on permeability. Fractals 2007, 15, 55–62. [Google Scholar] [CrossRef]
- Miao, T.J.; Yang, S.; Long, Z.C.; Yu, B.M. Fractal analysis of permeability of dual-porosity media embedded with random fractures. Int. J. Heat Mass Transf. 2015, 88, 814–821. [Google Scholar] [CrossRef]
- Øren, P.E.; Bakke, S. Process based reconstruction of sandstones and prediction of transport properties. Transp. Porous Media 2002, 46, 311–343. [Google Scholar] [CrossRef]
- Liu, K.; Ostadhassan, M.; Zhou, J.; Gentzis, T.; Rezaee, R. Nanoscale pore structure characterization of the Bakken shale in the USA. Fuel 2017, 209, 567–578. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).