Abstract
Marcugini et al. proved, by computer-based proof, the unicity of the maximum (k,3)-arc in PG(2,7). In this paper, we show how the (15,3)-Arc in PG(2,7) may be described using only geometrical properties. The description we provide, believing it is novel, relies on the union of a conic and a complete external quadrangle.
MSC:
51E21; 51E21
1. Introduction and Motivation
A (k,n)−arc K in a projective plane PG(2,q) is a set of k points such that some n, but no n + 1 of them, are collinear. By writing the homogeneous coordinates of the k points of K as columns of a generator matrix, one obtains a projective linear [k,3,k−3]q code. Thus, (k,3)-arcs in PG(2,q) correspond to NMDS codes of dimension 3. Since its error-correcting capability increases with k, it is natural to determine the largest value of k for which a (k,3)-arc exists. Define m3(2,q) to be the maximum size of a (k,3)-arc in PG(2,q). In 1975, J. Thas [1] proved that if q > 3, then m3(2,q) ≤ 2q + 1. The projective plane of order seven is the dominant focus of this work. Our reason for deciding to conduct a detailed investigation of this special case is that PG(2,7) is the smallest projective plane of prime power such that the maximum (k,3)-arc, i.e., the (15,3)-Arc, is unique, up to projectivity, cf. [2,3], and the awareness that the unique (15,3)-Arc reveals interesting geometric descriptions, cf. [4,5,6,7,8]. The object of this paper is to show that the (15,3)-Arc of PG(2,7) may be described by means of geometrical properties only. An easy geometric description of the (15,3)-Arc in PG(2,7) is provided by considering the union of the vertices of a complete quadrangle with the conic for which the nine lines of the complete quadrangle are external lines.
2. The Description of the (15,3)-Arc in PG(2,7)
Let K be a (15,3)-Arc in PG(2,7). For each integer i such that 0 ≤ I ≤ 3, let us denote by ti = ti(K) the number of lines of PG(2,7) meeting K in exactly i points. The numbers ti are called the characters of K with respect to the lines, see [9]. By double counting the number of lines, the number of pairs (P,r), where P ∈ K and r is a line through P, and the number of pairs ((P, Q),r), where {P, Q} ⊂ K and r is the line through P and Q, we get the following equations:
Solving these equations, we obtain the characters of K with respect to the lines:
Therefore, we have six character vectors:
(t0,t1,t2,t3)∈{(7,15,0,35),(8,12,3,34),(9,9,6,33),(10,6,9,32),(11,3,12,31),(12,0,15,30)}.
Let P be a point of K. For each integer i such that 0 ≤ i ≤ 3, let us denote by vi = vi(P) the number of lines through P meeting K in exactly i points. The numbers vi are called the characters of P with respect to the lines, cf. [9]. By double counting the number of lines through P, the number of pairs (Q,r), where Q ∈ K − P and r is a line through P and Q, we get the following equations:
Solving these equations we obtain the characters of P with respect to the lines:
Since and we get . Therefore, we have two types of inner points:
(v1,v2,v3)∈{(0,2,6),(1,0,7)}.
Let Q be a point nonbelonging to K. For each integer i such that 0 ≤ i ≤ 3, let us denote by ui = ui(Q) the number of lines through Q meeting K in exactly i points. The numbers ui are called the characters of Q with respect to the lines, cf. [9]. By double counting the number of lines through Q, we get
Solving these equations we obtain the characters of Q with respect to the lines:
Therefore, we have eleven types of outer points:
(u0,u1,u2,u3)∈{(0,1,7,0),(0,2,5,1),(0,3,3,2),(0,4,1,3),(1,0,6,1),
(1,1,4,2),(1,2,2,3),(1,3,0,4),(2,0,3,3),(2,1,1,4),(3,0,0,5)}.
(1,1,4,2),(1,2,2,3),(1,3,0,4),(2,0,3,3),(2,1,1,4),(3,0,0,5)}.
In order to prove the unicity of the (15,3)-Arc in PG(2,7), we firstly prove that the character vector of a (15,3)-Arc in PG(2,7) is (12,0,15,30). We divide the proof into five steps.
Step 1. The nonexistence of a (15,3)-Arc in PG(2,7) with character vector (t0,t1,t2,t3) = (7,15,0,35).
Proof.
Let K be a (15,3)-Arc in PG(2,7) with character vector (t0,t1,t2,t3) = (7,15,0,35). Since t2 = 0, we have that u2 = v2 = 0, so the inner points are of type (1,0,7). The outer points are of types (u0,u1,u2,u3)∈{(1,3,0,4),(3,0,0,5)}. Let l denote a 0−line. Since the other six 0−lines meet l in outer points of type (3,0,0,5), we get that there are exactly 35 outer points of type (1,3,0,4) and exactly 7 points of type (3,0,0,5). The seven outer points of type (3,0,0,5) with the seven 0−lines has the structure of a Steiner triple system S(2,3,7), i.e., a Fano subplane of order two, a contradiction because PG(2,7) contains no Fano subplanes, cf. Lemma 7.2, page 154, of [9]. □
Step 2. The nonexistence of a (15,3)-Arc in PG(2,7) with character vector (t0,t1,t2,t3) = (8,12,3,34).
Proof.
Let K be a (15,3)-Arc in PG(2,7) with character vector (t0,t1,t2,t3) = (8,12,3,34). Since t2 = 3, we get that any two 2−lines meet in one inner point of type (0,2,6). Since t2 = 3, we have that 0 ≤ u2 ≤ 1, the outer points are of types (u0,u1,u2,u3) ∈ {(0,4,1,3),(1,3,0,4),(2,1,1,4),(3,0,0,5)}. Let x, y and z denote the number of outer points of type (0,4,1,3), (1,3,0,4) and (2,1,1,4), respectively, of a 1−line l1. By double counting the number of pairs (Q,r), where Q ∈ l1 and r is a i−line, I = 0,2,3, through Q, we get:
So, there are exactly 3 outer points of type (0,4,1,3). □
Moreover, let x and y denote the number of outer points of type (0,4,1,3) and (2,1,1,4), respectively, of a 2−line l2. By double counting the number of pairs (Q,r), where Q ∈ l2 and r is a i−line, I = 0,1,3, through Q, we get:
Since t2 = 3 and any two 2−lines meet in one inner point of type (0,2,6), we get that there are exactly 6 outer points of type (0,4,1,3), a contradiction.
Step 3. The nonexistence of a (15,3)-Arc in PG(2,7) with character vector (t0,t1,t2,t3) = (9,9,6,33).
Proof.
Let K be a (15,3)-Arc in PG(2,7) with character vector (t0,t1,t2,t3) = (9,9,6,33). Since a 2−line contains inner points of type (0,2,6) and t2 = 6, the six 2−lines with the six inner points of type (0,2,6) form either two disjoint triangles or one hexagon. If they form two triangles, P1, P3, P5 and P2, P4, P6 the lines P2h−1P2k, with h = 1,2,3, and k = 1,2,3 are nine 3−lines no three of which form a triangle with vertices Pi, I = 1,2, …, 6. If they form one hexagon with consecutive vertices, P1, P2, P3, P4, P5 and P6 the lines P2h−1P2k−1, and P2hP2k with h = 1,2,3, k = 1,2,3 and h ≠ k are 3−lines no three of which form a triangle with vertices Pi, I = 1,2, …, 6. Moreover, the outer points are of types
□
(u0,u1,u2,u3)∈{(0,3,3,2),(0,4,1,3),(1,2,2,3),(1,3,0,4),(2,0,3,3),(2,1,1,4),(3,0,0,5)}.
Let xij, i = u0, j = u1, denote the number of outer points of type (1,2,2,3), (1,3,0,4), (2,0,3,3), (2,1,1,4), (3,0,0,5) respectively, of a 0−line l0. By double counting the number of pairs (Q,r), where Q ∈ l0−K and r ≠ l0 is a i−line, I = 0,1,2,3, through Q, we get:
We get and .
Thus, .
If we get ⇒ .
If we get ⇒ .
If we get ⇒ .
If we get ⇒ .
If we get ⇒ .
If we get ⇒ .
If we get ⇒ .
Therefore, the 0−lines can be of type
Let xij, I = u0, j = u1, denote the number of outer points of type (0,3,3,2), (0,4,1,3), (1,2,2,3), (1,3,0,4), (2,1,1,4), respectively, of a 1−line l1. By double counting the number of pairs (Q,r), where Q∈l1−K and r≠l1 is a i−line, I = 0,1,2,3, through Q, we get:
By the first equation, we get . Thus, .
If we get ⇒ .
If we get ⇒ .
If we get ⇒ .
If we get ⇒ .
Therefore, the 1−lines can be of type
Now, let xij, I = u0, j = u1, denote the number of outer points of type (0,3,3,2), (0,4,1,3), (1,2,2,3), (2,0,3,3), (2,1,1,4), respectively, of a 2−line l2. By double counting the number of pairs (Q,r), where Q ∈ l2 − K and r ≠ l2 is a i−line, I = 0,1,2,3, through Q, we get:
Therefore, the 2−lines can be of type .
We note that .
Two 1−lines meet in an outer point.
We have two possibility: an outer point of type (0,3,3,2) exists or not.
If an outer point Q of type (0,3,3,2) exists, then the two 3−lines through Q contain six inner points of type (1,0,7). An outer point R of type (0,4,1,3) does not exist, otherwise the line QR would be a 3−line with an inner point of type (0,2,6), a contradiction. Let li and mi, i = 1,2,3, denote the 1−lines of type and the 2−lines of type through Q, respectively. Let us denote by M1, M2 and M3 the points of type (1,2,2,3) on m1, m2 and m3, respectively. Let us denote by n1, n2 and n3 the other three 2−lines on M1, M2 and M3, respectively. The 2−lines n1, n2 and n3 are of type , because they meet l1, l2 and l3 in nine points of type (2,1,1,4). Thus, there is another outer point R of type (0,3,3,2). Let rh denote the 1−lines through R, h = 1,2,3. The line QR is a 3−line with three inner points P1, P2 and P3 of type (1,0,7). Let pk denote the 1−line through Pk, k = 1,2,3. Let us denote by Lij the points of type (1,3,0,4) on the 1−lines li, j = 1,2,3. The eleven points Q, R, Lij with the nine 1−lines are contained in a dual affine plane structure DAG(2,3) embedded in PG(2,7). It follows that the three 1−lines pk meet in a unique point, a contradiction because they pairwise meet in the points M1, M2 and M3.
Therefore, an outer point of type (0,3,3,2) does not exist.
Thus, the 1−lines can be of type , and the 2−lines can be of type . Since every 2−line contains exactly three points of type (2,1,1,4), we have exactly 18 points of type (2,1,1,4). Let x, y and z be the number of 1−lines of type and , respectively. By double counting the number of 1−lines and the number of the pairs (Q,l) where Q is a point of type (2,1,1,4), l is a 1−line and Q ∈ l, we get . Multiply the first equation by −2 and add: y + 2z = 0. It follows that y = z = 0. Thus, the 1−lines are of type , an outer point of type (0,4,1,3) does not exist, and the 2−lines are of type . Thus, an outer point of type (2,0,3,3) does not exist.
Therefore, the 0−lines can be of type
Since every 0−line contains exactly one point of type (1,3,0,4), we have exactly 9 points of type (1,3,0,4). Since every 1−line contains exactly two points of type (1,2,2,3) and through any point of type (1,2,2,3) there pass two 1−lines, we have exactly 9 points of type (1,2,2,3). Thus, the number of points of type (3,0,0,5) is 6. By the 9 points of type (1,3,0,4) with the 9 1−lines we find an affine plane of order three AG(2,3) in which the incidences between the 9 points and the lines of one parallel class has been removed. It follows that the missing parallelism class is formed by three 3−lines of type which form a triangle with vertices points of type (0,2,6), a contradiction.
Step 4. The nonexistence of a (15,3)-Arc in PG(2,7) with character vector (t0,t1,t2,t3) = (10,6,9,32).
Proof.
Let K be a (15,3)-Arc in PG(2,7) with character vector (t0,t1,t2,t3) = (10,6,9,32). We have eleven types of outer points:
(u0,u1,u2,u3)∈{(0,1,7,0),(0,2,5,1),(0,3,3,2),(0,4,1,3),(1,0,6,1),
(1,1,4,2),(1,2,2,3),(1,3,0,4),(2,0,3,3),(2,1,1,4),(3,0,0,5)}.
(1,1,4,2),(1,2,2,3),(1,3,0,4),(2,0,3,3),(2,1,1,4),(3,0,0,5)}.
Since t2 = 9 and through any inner point of type (0,2,6) there are two 2−lines, we get that there are no outer points of type (u0,u1,u2,u3) ∈ . □
Let xij, i = u0, j = u1, denote the number of outer points of type (1,1,4,2), (1,2,2,3), (1,3,0,4), (2,0,3,3), (2,1,1,4), (3,0,0,5), respectively, of a 0−line l0. By double counting the number of pairs (Q,r), where Q ∈ l0 and r ≠ l0 is a i−line, I = 0,1,2,3, through Q, we get:
By the third equation, we have that .
If we get ⇒
Thus, , . Therefore,
If we get ⇒
Thus, , . Therefore, .
If we get ⇒ ,
Thus, and . Therefore,
Therefore, the 0−lines can be of type
Let xij, i = u0, j = u1, denote the number of outer points of type (0,3,3,2), (0,4,1,3), (1,1,4,2), (1,2,2,3), (1,3,0,4), (2,1,1,4), respectively, of a 1−line l1. By double counting the number of pairs (Q,r), where Q ∈ l1 and r ≠ l1 is a i−line, I = 0,1,2,3, through Q, we get:
The system of linear equation is equivalent to
Thus, , , . Therefore, Therefore, the 1−lines can be of type
Two 1−lines meet in an outer point.
We have two possibilities: an outer point of type (0,3,3,2) exists or not.
If an outer point Q of type (0,3,3,2) exists, then through Q there pass three 1−lines of type either or . A 1−line of type (1,1,0,0,0,5) does not exist because the other three 1−lines not through Q pass through the outer point R of type (0,4,1,3) and meet another 1−line in at most two outer points, a contradiction. Therefore, an outer point of type (0,4,1,3) does not exist and through Q there pass three 1−lines, l1, l2 and l3 of type . The other three 1−lines m1, m2 and m3 meet l1, l2 and l3 in points of type either (1,3,0,4) or (1,2,2,3). Thus, m1, m2 and m3 must contain two outer points of type (1,3,0,4) and one outer point of type (1,2,2,3), and they are of type . Now, we count the outer point types by the 1−line types. The pointset l1∪l2∪l3 consists of one point of type (0,3,3,2), the point Q, 12 points of type (2,1,1,4), 3 points of type (1,3,0,4) and 3 of type (1,2,2,3). The pointset (m1∪m2∪m3)−(l1∪l2∪l3) consists of 9 points of type (2,1,1,4) and 3 points of type (1,1,4,2). The types of the 11 outer points contained in no 1−lines remain to be determined. Since an outer point contained in no 1−lines is of type (u0,u1,u2,u3)∈{(2,0,3,3),(3,0,0,5)}, we have through it at least a pair of 0−lines. Each of the 0−lines pairs meet on points of type (u0,u1,u2,u3) ∈ {(2,0,3,3), (2,1,1,4), (3,0,0,5)}. Exactly 21 0−lines pairs meet on points of type (2,1,1,4). So, 24 0−lines pairs meet on points of type (u0,u1,u2,u3) ∈ {(2,0,3,3), (3,0,0,5)}. Let x and y denote the number of outer points of type (2,0,3,3) and (3,0,0,5), respectively. We get ⇒ , a contradiction.
Therefore, an outer point of type (0,3,3,2) does not exist.
Therefore, the 1−lines can be of type
Now, let xij, I = u0, j = u1, denote the number of outer points of type (0,4,1,3), (1,1,4,2), (1,2,2,3), (2,0,3,3), (2,1,1,4), respectively, of a 2−line l2. By double counting the number of pairs (Q,r), where Q ∈ l2 − K and r ≠ l2 is a i−line, I = 0,1,2,3, through Q, we get:
Taking into account the second equation, since 0 ≤ 4x0.4 ≤ 6 ⇒ .
The system of linear equation is equivalent to
If we get
Thus, and
If we get
Therefore, the 2−lines can be of type
.
Two 1−lines meet in an outer point.
We have two possibilities: an outer point of type (0,4,1,3) exists or not.
If an outer point Q of type (0,4,1,3) exists, then through Q there pass four 1−lines: three, l1, l2 and l3, of type and one, l, of type . The other two 1−lines not through Q, m1 and m2, are of type . Now, we count the outer point types by the 1−line types. The pointset l∪l1∪l2∪l3 consists of one point of type (0,4,1,3), the point Q, 16 points of type (2,1,1,4), 1 point of type (1,3,0,4), 1 point of type (1,1,4,2) and 6 of type (1,2,2,3). The pointset (m1∪m2) − (l∪l1∪l2∪l3) consists of 6 points of type (2,1,1,4). The types of the 11 outer points contained in no 1−lines remain to be determined. Since an outer point contained in no 1−lines is of type (u0,u1,u2,u3)∈{(2,0,3,3),(3,0,0,5)}, we have through it at least a pair of 0−lines. Each of the 0−lines pairs meet on points of type (u0,u1,u2,u3) ∈ {(2,0,3,3), (2,1,1,4), (3,0,0,5)}. Exactly 22 0−lines pairs meet on points of type (2,1,1,4). So, 23 0−lines pairs meet on points of type (u0,u1,u2,u3) ∈ {(2,0,3,3), (3,0,0,5)}. Let x and y denote the number of outer points of type (2,0,3,3) and (3,0,0,5), respectively. We get ⇒ . Thus, we have 5 outer points of type (2,0,3,3) and 6 outer points of type (3,0,0,5).
Therefore, the nine 2−lines can be of type
Since there is exactly one point of type (0,4,1,3), we have exactly one 2−line of type . Since there is exactly one point of type (1,1,4,2), we have exactly four 2−lines of type . It follows that the other four 2−lines are all of type .
Therefore, the ten 0−lines can be of type
Since there is exactly one point of type (1,1,4,2), there is exactly one 0−line of type
Since there is exactly one point of type (1,3,0,4), a 0−line of type does not exist, and there is exactly one 0−line of type
If there is exactly one 0−line of type and one of type , then the other eight 0−lines can be of type
Let us denote by x, y and z the number of 0−lines of type , and , respectively. Since there are exactly 6 points of type (1,2,2,3) and another 14 points of type (2,1,1,4), we get which has no solutions, a contradiction.
If there is exactly one 0−line of type and one of type , then the other eight 0−lines can be of type
Let us denote by x, y and z the number of 0−lines of type , and , respectively. Since there are exactly five points of type (1,2,2,3) and another 16 points of type (2,1,1,4), we get
If there is exactly one 0−line of type (1,1,0,0,3,3) and one of type , then the other eight 0−lines can be of type
Let us denote by x, y and z the number of 0−lines of type , (0,1,0,1,4,2) and , respectively. Since there are exactly five points of type (1,2,2,3), and another 16 points of type (2,1,1,4), we get
If there is exactly one 0−line of type and one of type , then the other eight 0−lines can be of type
Let us denote by x, y and z the number of 0−lines of type , and (0,2,0,1,2,3), respectively. Since there are exactly four points of type (1,2,2,3), and another 18 points of type (2,1,1,4), we get
If there is exactly one 0−line of type and one of type , then the other eight 0−lines can be of type
Let us denote by x, y and z the number of 0−lines of type , and , respectively. Since there are exactly four points of type (1,2,2,3), and another 18 points of type (2,1,1,4), we get
If there is exactly one 0−line of type and one of type , then the other eight 0−lines can be of type
Let us denote by x, y and z the number of 0−lines of type , and , respectively. Since there are exactly three points of type (1,2,2,3), and another 20 points of type (2,1,1,4), we get
If there is exactly one 0−line of type , then the other nine 0−lines can be of type
Let us denote by x, y and z the number of 0−lines of type , and , respectively. Since there are exactly six points of type (1,2,2,3), and another 20 points of type (2,1,1,4), we get
If there is exactly one 0−line of type , then the other nine 0−lines can be of type
Let us denote by x, y and z the number of 0−lines of type , and , respectively. Since there are exactly five points of type (1,2,2,3), and 22 points of type (2,1,1,4), we get
Therefore, an outer point of type (0,4,1,3) does not exist, and the 1−lines can be of type
and the 2−lines can be of type
The number of outer points of type (2,1,1,4) is 18 because every 1−line contains exactly 3 outer points of type (2,1,1,4). Let x, y and z denote the numbers of 2−lines of type , and , respectively. We get ⇒ we get . Thus, the 2−lines are of type . It follows that there are no outer points of type (1,1,4,2) and that the 1−lines are of type . There are exactly two outer points, P and Q, of type (1,3,0,4). The 3 1−lines through P meet the 3 1−lines through Q in different points of type (1,2,2,3). Therefore, there are exactly 9 outer points of type (1,2,2,3). There are exactly 6 outer points of type (2,0,3,3) and, so, 7 outer points of type (3,0,0,5).
Therefore, the 0−lines can be of type
Let x1, x2, x3, x4, x5 and x6 denote the numbers of 0−lines of type , , , , , and , respectively. We get which has no solutions, a contradiction.
Step 5. The nonexistence of a (15,3)-Arc in PG(2,7) with character vector (t0,t1,t2,t3) = (11,3,12,31).
Proof.
Let K be a (15,3)-Arc in PG(2,7) with character vector (t0,t1,t2,t3) = (11,3,12,31). We have ten types of outer points:
□
(u0,u1,u2,u3)∈{(0,1,7,0),(0,2,5,1),(0,3,3,2),(1,0,6,1),
(1,1,4,2),(1,2,2,3),(1,3,0,4),(2,0,3,3),(2,1,1,4),(3,0,0,5)}.
(1,1,4,2),(1,2,2,3),(1,3,0,4),(2,0,3,3),(2,1,1,4),(3,0,0,5)}.
We firstly prove that an outer point Q of type (0,1,7,0) does not exist. Suppose, on the contrary, that an outer point Q of type (0,1,7,0) exists. Since t1 = 3, there are exactly three inner points P1, P2 and P3 of type (1,0,7). The lines QP1, QP2 and QP3 are three 1−lines, a contradiction.
Let xij, i = u0, j = u1, denote the number of outer points of type (1,0,6,1), (1,1,4,2), (1,2,2,3), (1,3,0,4), (2,0,3,3), (2,1,1,4), (3,0,0,5), respectively, of a 0−line l0. By double counting the number of pairs (Q,r), where Q ∈ l0 and r ≠ l0 is a i−line, I = 0,1,2,3, through Q, we get:
By the second equation, we have that and .
If , we get
Thus, , . Therefore, .
If , we get
Thus, and . Therefore,
If ⇒ ⇒ ⇒ . Thus,
Therefore, the 0−lines can be of type
Let xij, i = u0, j = u1, denote the number of outer points of type (0,2,5,1), (0,3,3,2), (1,1,4,2), (1,2,2,3), (1,3,0,4), (2,1,1,4), respectively, of a 1−line l1. By double counting the number of pairs (Q,r), where Q ∈ l1 and r ≠ l1 is a i−line, I = 0,1,2,3, through Q, we get:
The system of linear equation is equivalent to
By the first equation, we have that and .
If we get .
Thus, . Therefore,
.
If , we get
Thus, . Therefore, .
If , we get
Thus, . Therefore, .
Therefore, the 1−lines can be of type
Two 1−lines meet in an outer point.
We have two possibilities: an outer point of type (0,3,3,2) exists or not.
If an outer point Q of type (0,3,3,2) exists, then through Q there pass three 1−lines, li, i ∈ {1,2,3}, of type . Let us denote by Li the point of type (1,1,4,2) on the 1−line li, i ∈ {1,2,3}. Let us denote by mij, j ∈ {1,2,3,4}, the four 2−lines through Li. Let us denote by Mih, h ∈ {1,2,3,4,5}, the five points of type (2,1,1,4) on the 1−line li, i ∈ {1,2,3}. Two of the eight 2−lines m1j and m2j, j ∈ {1,2,3,4}, meet l3 in the point L3 and the other six in six different points M3h, h ∈ {1,2,3,4,5}, a contradiction.
Therefore, an outer point of type (0,3,3,2) does not exist.
Thus, the 1−lines can be of type
We have two possibilities: an outer point of type (1,3,0,4) exists or not.
If an outer point Q of type (1,3,0,4) exists, then through Q there pass three 1−lines, l1, l2 and l3, of type . Now, we count the outer point types on the 1−lines. The pointset l1∪l2∪l3 consists of one point of type (1,3,0,4), the point Q, 12 points of type (2,1,1,4), 6 points of type (1,1,4,2). Two points of type (1,1,4,2) not on the same 1−line are joined by a 2−line. Thus the 0−lines have and . The 3−line through a point of type (1,0,6,1) meets l1, l2 and l3 in its inner points. A point of type (1,0,6,1) and Q are joined by a 0−line. Thus, the 0−line through Q contains at most two points of type (1,0,6,1) and there exist no 0−lines with and
Since there are 6 points of type (1,1,4,2), the number of 0−lines of type is 6. The other 5 0−lines are of type
Let x denote the number of 0−lines of type . Double counting the pairs (R,l), where R is a point of type (2,1,1,4), l is a 0−line of type and R ∈ l, we get 3x = 24, a contradiction.
Therefore, an outer point of type (1,3,0,4) does not exist.
Thus, the 1−lines can be of type .
Now, let xij, I = u0, j = u1, denote the number of outer points of type (0,2,5,1), (1,0,6,1), (1,1,4,2), (1,2,2,3), (2,0,3,3), (2,1,1,4), respectively, of a 2−line l2. By double counting the number of pairs (Q,r), where Q ∈ l2−K and r ≠ l2 is a i−line, I = 0,1,2,3, through Q, we get:
The third equation minus the first equation gives ⇒ .
Taking into account the second equation, we get .
⇒ .
The system of linear equation is equivalent to
Taking into account the second equation,
We get ⇒ .
If , we get
, a contradiction.
If , we get
, a contradiction.
If , we get
, a contradiction.
Thus, the character vector of a (15,3)-Arc in PG(2,7) is (12,0,15,30). Since t1 = 0, the inner points are of type (0,2,6) and the outer points are of type (u0,u1,u2,u3) ∈ {(1,0,6,1),(2,0,3,3),(3,0,0,5)}.
Let xij, i = u0, j = u1, denote the number of outer points of type (1,0,6,1), (2,0,3,3), (3,0,0,5), respectively, of a 0−line l0. By double counting the number of pairs (Q,r), where Q ∈ l0 and r≠l0 is a i−line, i = 0,2,3, through Q, we get:
We have that .
If , we get and
If , we get and
If , we get and
Thus, the 0−lines can be of type .
Let xij, i = u0, j = u1, denote the number of outer points of type (1,0,6,1), (2,0,3,3), respectively, of a 2−line l2. By double counting the number of pairs (Q,r), where Q ∈ l2 and r ≠ l2 is a i−line, i = 0,2,3, through Q, we get:
Thus, the 2−lines are of type , an outer point of type (1,0,6,1) does not exist, and the 0−lines are of type .
Let xij, i = u0, j = u1, denote the number of outer points of type (2,0,3,3), (3,0,0,5) respectively, of a 3−line l3. By double counting the number of pairs (Q,r), where Q ∈ l3 and r ≠ l3 is a i−line, i = 0,2,3, through Q, we get:
Thus, the 3−lines are of type .
Exactly 15 of the 2−lines pairs meet on points of type (0,2,6), the other 90 on points of type (2,0,3,3). So, we have exactly 30 points of type (2,0,3,3) and 12 points of type (3,0,0,5). This yields a self−dual configuration. Indeed, the set of the 2−lines in the dual plane is a (15,3)-Arc of PG(2,7).
Let X and Y denote two inner points such that the line joining X and Y is a 2−line l1. Let l2 and l3 denote the other two 2−lines through X and Y, respectively, different from l1.
If the point Z ∈ l2∩l3 does not belong to K then Z is of type (2,0,3,3). There is another 2−line through Z which meets the line l1 in a point Q0. Let P1 and P2 denote the two inner points of the 2−line Z Q0. Moreover let Qj, j = 1,2,3,4 denote the other four outer points of the 2−line Z Q0, different from Z and Q0. The points of K different from X, Y, Pi, I = 1,2, are one on each of the lines XZ and YZ, two on the lines PiQj, i = 1,2, j = 1,2,3,4, and one on the lines XPi and YPi, i = 1,2. Thus, the size of K is even, a contradiction.
Therefore, the point Z ∈ l2∩l3 belongs to K and the three 2−lines l1, l2 and l3 form a triangle with vertices X, Y and Z. It follows that there is a partition of the 2−line 15−set into 5 triangles.
Let P1 and P2 denote the two other inner points of a 3−line through X. Let P3 denote the other inner point of the 3−line YP2. Let P4 denote the other inner point of the 3−line XP3. If P4 is on the 3−line YP1, then the four 3−lines XP1P2, XP3P4, YP2P3, YP1P4 form a quadrangle with diagonal points X, Y and Z. If P4 is not on the 3−line YP1, then the 3−line P2P4 meets the 3−line P1P3 in the point Z, then the four 3−lines XP1P2, XP3P4, ZP2P4, ZP1P3 form a quadrangle with diagonal points X, Y and Z. Therefore, there exists a quadrangle of four 3−lines with diagonal points X, Y and Z. Since any quadrangle is projectively equivalent with the reference quadrangle R = {(0,0,1),(0,1,0),(1,0,0),(1,1,1)}, the construction and the uniqueness, up to projective equivalence, of the (15,3)-Arc K in PG(2,7) follows by observing that the other 8 points of K are exactly the complementary set of the union of the nine lines joining the seven points of the quadrangle.
We explicitly note that if one considers as blocks the 3−lines and the 3−sets of vertices of the 2−line triangles, then a Steiner triple system S(2,3,15) is obtained. It follows that the (15,3)-Arc K in PG(2,7) is an embedding of a Steiner triple system S(2,3,15) in PG(2,7).
The automorphism group of K is a group G72 of order 72 with 21 elements of order 2, 26 elements of order 3, 18 elements of order 4 and 6 elements of order 6, cf. [3].
For convenience we represent PG(2,7) as a set of orthogonal arrays of AG(2,7) with the intersection point of the members of each parallel class indicated to the right of the row array and at the bottom of the column array. We do this by using the Singer difference set defining PG(2,7) as the line at infinity , cf. [10]. The remaining lines of the plane are found by adding 1 to each point of the preceding line beginning with as and using addition modulo 57. Any quadrangle together with its three diagonal points is projectively equivalent with the reference quadrangle R = {0,1,2,16,51,52,53}, see Figure 1.
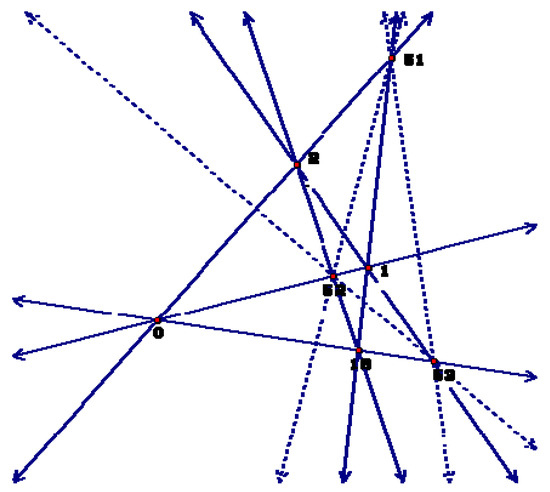
Figure 1.
The Reference quadrangle.
One can easily verify by the Singer representation, see Table 1, that the 8-set of points of the plane which are not in the nine lines joining these points is a conic C = {5,9,20,23,39,40,41,49}. Moreover, the set R∪C is, up to projective equivalence, the (15,3)-Arc of PG(2,7).

Table 1.
The Singer representation of PG(2,7).
3. Conclusions
The main contribution of this paper is the geometric construction of the (15,3)-Arc in PG(2,7), relying on the union of a conic and a complete external quadrangle. The construction has a particularly large automorphism group and a nice structure. This is in line with normal experience in all branches of finite geometry. Extremal (k,3)-arcs in PG(2,7) are shown to be vastly outnumbered by less interesting objects with no particular group or structure, cf. [3]. This leads us to conclude that except in a very small number of special cases, namely minimum and maximum cases, the question of geometric classification is neither feasible nor of particularly great interest.
Author Contributions
Investigation, S.I.; Writing–review & editing, M.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
We thank the anonymous referees whose reports have helped improve the presentation of the results of the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Thas, J.A. Some results concerning {(q+1)(n−1);n}-arcs and {(q+1)(n−1)+1;n}-arcs in finite projective planes of order q. J. Combin. Theory Ser. A 1975, 19, 228–232. [Google Scholar] [CrossRef]
- Ahmad, A.M.; Al-Mukhtar, A.S.H.; Faiyadh, M.S. Classification and Construction of (k,3)-Arcs on Projective Plane Over Galois Field GF(7). Ibn Al-Haitham J. Pure Appl. Sci. 2013, 26, 259–265. [Google Scholar]
- Marcugini, S.; Milani, A.; Pambianco, F. Classification of the (n,3)-arcs in PG(2,7). J. Geom. 2004, 80, 179–184. [Google Scholar] [CrossRef]
- Bouyukliev, I.; Cheon, E.J.; Maruta, T.; Okazaki, T. On the (29, 5)-Arcs in PG(2, 7) and Some Generalized Arcs in PG(2, q). Mathematics 2020, 8, 320. [Google Scholar] [CrossRef]
- Casse, L.R.A. (15;3)-arcs of S2,7. In Proceedings of the First Australian Conference on Combinatorial Math, Newcastle, 10–12 June 1972; pp. 193–196. [Google Scholar]
- Dodunekov, S.; Landgev, I. On near-MDS codes. J. Geom. 1995, 54, 30–43. [Google Scholar] [CrossRef]
- Yahya, N.Y.K. A Geometric Construction of Complete (k,r)-arcs in PG(2,7) and the Related projective [n,3,d]7 Codes. AL-Rafidain J. Comput. Sci. Math. 2018, 12, 24–40. [Google Scholar] [CrossRef][Green Version]
- Retkin, H.; Stein, E. On the symmetric (15,3)-arcs of the finite projective plane of order 7. Rend. Mater. 1965, 24, 392–399. [Google Scholar]
- Hirschfeld, J.W.P. Projective Geometries over Finite Fields, 2nd ed.; Clarendon Press: Oxford, UK, 1998. [Google Scholar]
- Singer, J. A theorem in finite projective geometry and some applications to number theory. Trans. Am. Math. Soc. 1968, 43, 377–385. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).