A Multi-Criteria Computer Package-Based Energy Management System for a Grid-Connected AC Nanogrid
Abstract
1. Introduction
- to smoothen the power exchanged with the utility;(be list format, and add the full bracket)
- to keep the SOC within secure thresholds;
- to apply energy curtailment to the PV power if required (when, for example, power injection into the utility network is not permitted by contract and there is a situation of high PV production, low local load and batteries fully charged);
- to guarantee a safety operation of the hybrid ESS in terms of power rating; and
- to maximize the revenue coming from energy trading with the utility.
- A new multi-criteria approach based on rules or knowledge is included in the EMS for controlling the operation of a NG.
- The hybrid combination of batteries and supercapacitors at the residential level in the considered grid-connected NG is quite interesting for increasing the lifespan of such infrastructure.
- The proposed package can be easily upgraded by including other rules or parameters in a very easy way. This fact is possible due to the powerful algebraic capabilities of Maple.
2. Nanogrid (NG) under Study
2.1. NG Modelling
2.1.1. Photovoltaic (PV) Array Model
2.1.2. Battery and Supercapacitor Models
3. Residential Nanogrid Energy Management System
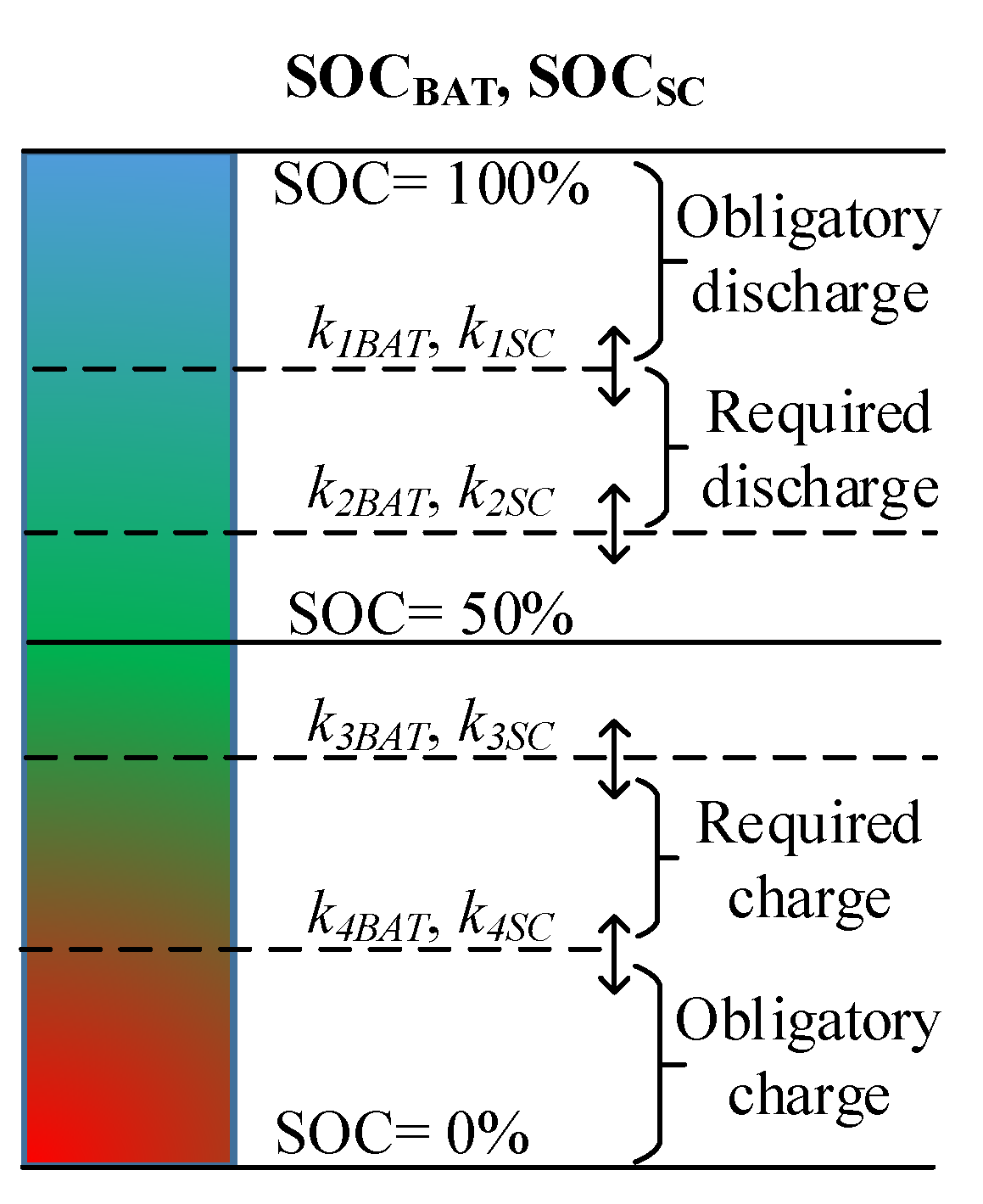
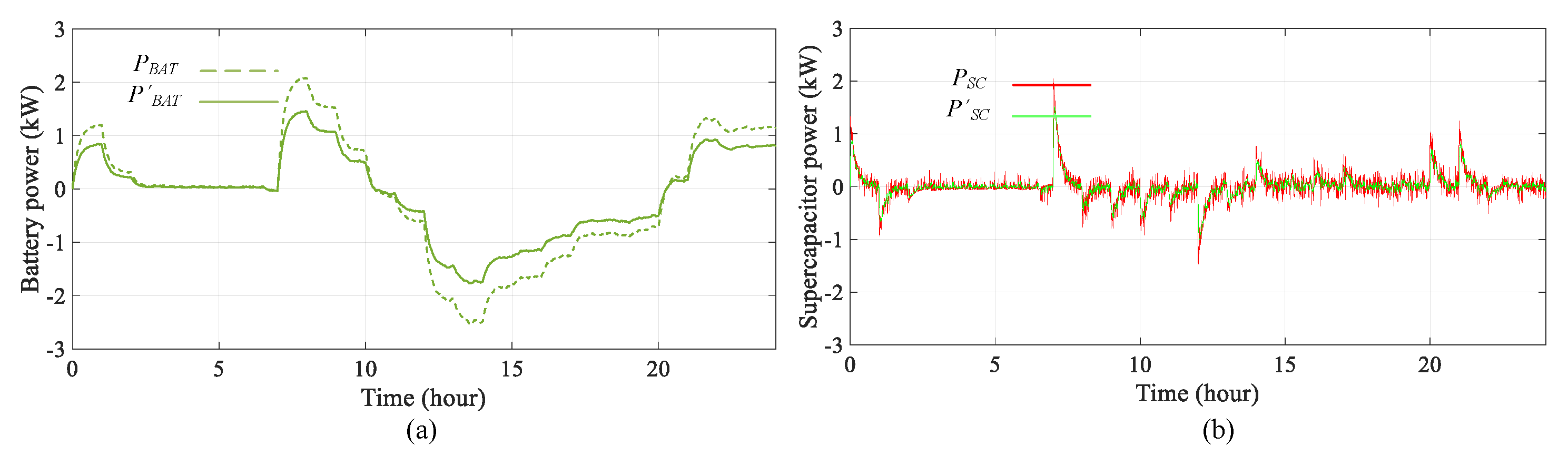
3.1. Hybrid Energy Storage System (HESS) Strategy and Constraints
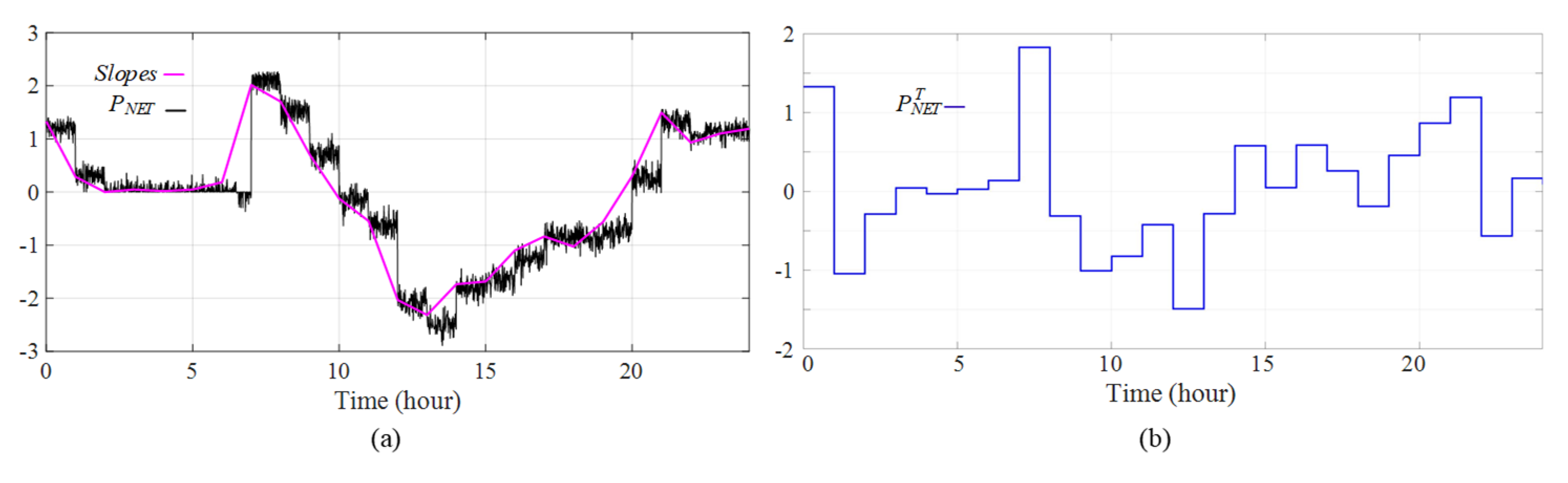
3.2. NG Net Power Trend
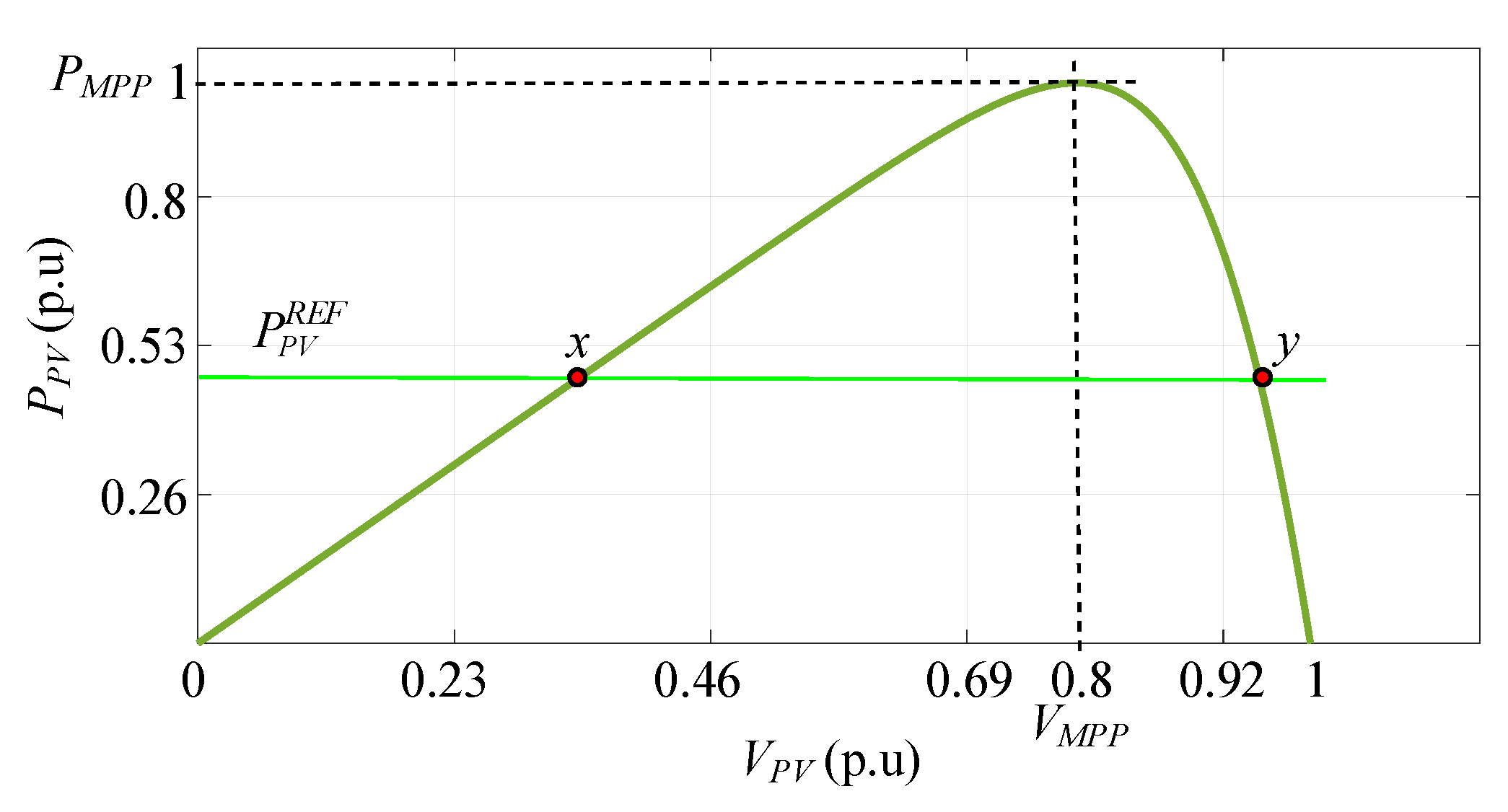
3.3. PV Power Regulation
3.4. Energy Price
3.5. Comtrol Rules
If (-battery discharged) and (-trends is slightly positive () and (-more power is required for PLOAD)) and (price is low) then the load will be supplied by the grid (50%, as the price is low) and by the battery (50%)(as we are not in the state of the battery “strongly discharged”).
4. The Associated Rule-Based Expert System (RBES)
4.1. Analysing the Structuring of the Information in the Tables
- SOCBAT:x1, x2, x3, x4, x5
- PTNET: y1, y2, y3, y4, y5
- PNET: z1, z2
- Price: u1, u2
4.2. Combinatorial Manual Grouping of the Information in the Tables
5. About the Inference Engine Chosen
5.1. A Brief Overview of the Algebraic Model for Logic
- Zn is considered instead of Z2 as the base field,
- the ideal <x12 − x1,x22 − x2,…,xm2 − xm> is substituted by ideal <x1n − x1,x2n − x2,…,xmn − xm>
- the polynomial translations of the logic connectives do change.
5.2. A Brief Overview of the Algebraic Model for RBES (Boolean Case)
- J is the polynomial ideal generated by the polynomial translation of the negation of the rules and integrity constraints, and
- K is the polynomial ideal generated by the polynomial translation of the negation of the given facts,
5.3. The Maple Implementation of the Algebraic Model for RBES
6. The Energy Management Nanogrid RBES Developed
6.1. Subsystem I
6.2. Subsystem II
6.3. Subsystem III
7. Simulations
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B. Subsystem I—Construction and Extracting Knowledge
Appendix C. Subystem I—Simplifying Knowledge Extraction
Appendix D. Subsystem I—Checking the Correctness of the Rules
Appendix E. Subsystem II—Extracting Knowledge
Appendix F. Subsystem III—Extracting Knowledge
Acronyms
| AC | Alternating Current |
| B2G, BAT2GRID | Battery to Grid |
| B2L, BAT2LOAD | Battery to Load |
| B2SC, BAT2SC | Battery to Supercapacitor |
| CAS | Computer Algebra System |
| DC | Direct Current |
| DER | Distributed Energy Resources |
| EMS | Energy Management System |
| ESS | Energy Storage System |
| G2B, GRID2BAT | Grid to Battery |
| G2L, GRID2LOAD | Grid to Load |
| G2SC, GRID2SC | Grid to Supercapacitor |
| GC | Grid-Connected |
| HESS | Hybrid Energy Storage System |
| LPF | Low-Pass Filter |
| MPP | Maximum Power Point |
| MG | Microgrid |
| MPPT | Maximum Power Point Tracking |
| N2B, NET2BAT | Surplus to Battery |
| N2G, NET2GRID | Surplus to Grid |
| NG | Nanogrid |
| P&O | Perturb and Observe |
| PV | Photovoltaic |
| PCC | Point of Common Coupling |
| RBES | Rule Based Expert System |
| RPP | Reference Power Point |
| RES | Renewable Energy Sources |
| RPPT | Reference Power Point Tracking |
| SA | Stand-Alone |
| STC | Standard Test Conditions |
| SOC | State of Charge |
| STS | Static Transfer Switch |
References
- European Commission. 2030 Climate & Energy Framework; European Commission: Brussels, Belgium; Available online: https://ec.europa.eu/clima/policies/strategies/2030_en#tab-0-0 (accessed on 24 November 2020).
- SETIS. Smart Electricity Grids. Available online: https://setis.ec.europa.eu/relatedjrc-activities/jrc-setis-reports/smart-electricity-grids (accessed on 3 April 2019).
- Lee, S.; Jin, H.; Vecchietti, L.F.; Hong, J.; Har, D. Short-Term Predictive Power Management of PV-Powered Nanogrids. IEEE Access 2020, 8, 147839–147857. [Google Scholar] [CrossRef]
- Sandgani, M.R.; Sirouspour, S. Energy Management in a Network of Grid-Connected Microgrids/Nanogrids Using Compromise Programming. IEEE Trans. Smart Grid 2018, 9, 2180–2191. [Google Scholar] [CrossRef]
- Ban, M.; Shahidehpour, M.; Yu, J.; Li, Z. A Cyber-Physical Energy Management System for Optimal Sizing and Operation of Networked Nanogrids With Battery Swapping Stations. IEEE Trans. Sustain. Energy 2019, 10, 491–502. [Google Scholar] [CrossRef]
- Luo, F.; Ranzi, G.; Wang, S.; Dong, Z.Y. Hierarchical Energy Management System for Home Microgrids. IEEE Trans Smart Grid 2019, 10, 5536–5546. [Google Scholar] [CrossRef]
- Farzaneh, H.; Shokri, M.; Kebriaei, H.; Aminifar, F. Robust Energy Management of Residential Nanogrids via Decentralized Mean Field Control. IEEE Trans. Sustain. Energy 2020, 11, 1995–2002. [Google Scholar] [CrossRef]
- Salazar, A.; Berzoy, A.; Song, W.; Velni, J.M. Energy Management of Islanded Nanogrids Through Nonlinear Optimization Using Stochastic Dynamic Programming. IEEE Trans. Ind. Appl. 2020, 56, 2129–2137. [Google Scholar] [CrossRef]
- Lee, S.; Lee, J.; Jung, H.; Cho, J.; Hong, J.; Lee, S.; Har, D. Optimal power management for nanogrids based on technical information of electric appliances. Energy Build. 2019, 191, 174–186. [Google Scholar] [CrossRef]
- Youssef, T.A.; Hariri, M.E.; Elsayed, A.T.; Mohammed, O.A. A DDS-Based Energy Management Framework for Small Microgrid Operation and Control. IEEE Trans. Ind. Inform. 2018, 14, 958–968. [Google Scholar] [CrossRef]
- Roncero-Clemente, C.; Gonzalez-Romera, E.; Barrero-González, F.; Milanés-Montero, M.I.; Romero-Cadaval, E. Power-Flow-Based Secondary Control for Autonomous Droop-Controlled AC Nanogrids with Peer-to-Peer Energy Trading. IEEE Access 2021, 9, 22339–22350. [Google Scholar] [CrossRef]
- Young, B.; Ertugrul, N.; Chew, H.G. Overview of optimal energy management for nanogrids (end-users with renewables and storage). In Proceedings of the 2016 Australasian Universities Power Engineering Conference (AUPEC), Brisbane, Australia, 25–28 September 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Bhosale, R.; Agarwal, V. Fuzzy Logic Control of the Ultracapacitor Interface for Enhanced Transient Response and Voltage Stability of a DC Microgrid. IEEE Trans. Ind. Appl. 2019, 55, 712–720. [Google Scholar] [CrossRef]
- Barricarte, J.J.; Martín, I.S.; Sanchis, P.; Marroyo, L. Energy management strategies for grid integration of microgrids based on renewable energy sources. In Proceedings of the 10th International Conference on Sustainable Energy Technology, Istambul, Turkey, 4–7 September 2011; pp. 4–7. [Google Scholar]
- Arcos-Aviles, D.; Espinosa, N.; Guinjoan, F.; Marroyo, L.; Sanchis, P. Improved fuzzy controller design for battery energy management in a grid connected microgrid. In Proceedings of the IECON 40th IEEE Annu. IEEE Industrial Electronics Society, Dallas, TX, USA, 29 October 2014; pp. 2128–2133. [Google Scholar]
- Arcos-Aviles, D.; Pascual, J.; Marroyo, L.; Sanchis, P.; Guinjoan, F. Fuzzy Logic-Based Energy Management System Design for Residential Grid-Connected Microgrids. IEEE Trans. Smart Grid 2018, 9, 530–543. [Google Scholar] [CrossRef]
- Ding, Y.; Wang, Z.; Liu, S.; Wang, X. Energy Management Strategy of PV Grid-Connected Household Nano-Grid System. In Proceedings of the 2019 IEEE Power & Energy Society General Meeting (PESGM), Atlanta, GA, USA, 4–8 August 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Ghiani, E.; Garau, M.; Celli, G.; Pilo, F.; Marongiu, G. Smart integration and aggregation of nanogrids: Benefits for users and DSO. In Proceedings of the 2017 IEEE Manchester PowerTech, Manchester, UK, 18–22 June 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Latifi, M.; Rastegarnia, A.; Khalili, A.; Bazzi, W.M.; Sanei, S. A Self-Governed Online Energy Management and Trading for Smart Micro/Nano-Grids. IEEE Trans. Ind. Electron. 2020, 67, 7484–7498. [Google Scholar] [CrossRef]
- Caldognetto, T.; Mion, E.; Bruschetta, M.; Simmini, F.; Carli, R.; Tenti, P. A Model Predictive Approach for Energy Management in Smart Buildings. In Proceedings of the 2019 21st European Conference on Power Electronics and Applications (EPE ’19 ECCE Europe), Genova, Italy, 3–5 September 2019; pp. P.1–P.10. [Google Scholar] [CrossRef]
- Roncero-Clemente, C.; González-Romera, E.; Romero-Cadaval, E.; Milanés-Montero, M.I.; Miñambres-Marcos, V. PSCAD/EMTDC model for photovoltaic modules with MPPT based on manufacturer specifications. In Proceedings of the 2013 International Conference-Workshop Compatibility and Power Electronics, Ljubljana, Slovenia, 5–7 June 2013; pp. 69–74. [Google Scholar] [CrossRef]
- Tremblay, O.; Dessaint, L.; Dekkiche, A. A Generic Battery Model for the Dynamic Simulation of Hybrid Electric Vehicles. In Proceedings of the 2007 IEEE Vehicle Power and Propulsion Conference, Arlington, TX, USA, 9–12 September 2007; pp. 284–289. [Google Scholar] [CrossRef]
- Miniguano, H.; Barrado, A.; Fernández, C.; Zumel, P.; Lázaro, A. A General Parameter Identification Procedure Used for the Comparative Study of Supercapacitors Models. Energies 2019, 12, 1776. [Google Scholar] [CrossRef]
- Kong, S.N.; Chin-Sien, M.; Yi-Ping, C.; Yao-Ching, H. Enhanced coulomb counting method for estimating state-of-charge and state-of-health of lithium-ion batteries. Appl. Energy 2009, 86, 1506–1511. [Google Scholar] [CrossRef]
- Ruiz-Cortés, M.; Romero-Cadaval, E.; Roncero-Clemente, C.; Barrero-González, F.; González-Romera, E. Energy management strategy to coordinate batteries and ultracapacitors of a hybrid energy storage system in a residential prosumer installation. In Proceedings of the 2017 International Young Engineers Forum (YEF-ECE), Almada, Portugal, 5 May 2017; pp. 30–35. [Google Scholar] [CrossRef]
- Ruiz-Cortés, M.; Romero-Cadaval, E.; Roncero-Clemente, C.; Barrero-González, F.; González-Romera, E. Comprehensive study of the benefits of integrating a sharing energy strategy between prosumers. In Proceedings of the IECON 2017—43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 29 October–1 November 2017; pp. 3609–3614. [Google Scholar] [CrossRef]
- Roncero-Clemente, C.; Vilhena, N.; Delgado-Gomes, V.; Romero-Cadaval, E.; Martins, J.F. Control and operation of a three-phase local energy router for prosumers in a smart community. IET Renew. Power Gener. 2020, 14, 560–570. [Google Scholar] [CrossRef]
- Roanes-Lozano, E.; Laita, L.M.; Roanes-Macías, E. A Groebner Bases Based Many-Valued Modal Logic Implementation in Maple. In AISC/Calculemus/MKM 2008, LNAI 5144; Autexier, S., Campbell, J., Rubio, J., Sorge, V., Suzuki, M., Wiedijk, F., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 170–183. [Google Scholar] [CrossRef]
- Roanes-Lozano, E.; Laita, L.M.; Hernando, A.; Roanes-Macías, E. An algebraic approach to rule based expert systems. Rev. R. Acad. Cien. Ser. A. Mat. 2010, 104, 19–40. [Google Scholar] [CrossRef]
- Buchberger, B. Bruno Buchberger’s PhD Thesis 1965: An algorithm for finding the basis elements of the residue class ring of a zero dimensional polynomial ideal. J. Symb. Comp. 2006, 41, 3–4. [Google Scholar] [CrossRef]
- Cox, D.; Little, J.; O’Shea, D. Ideals, Varieties, and Algorithms; Springer: Berlin/Heidelberg, Germany, 1992. [Google Scholar]
- Smodels Web Page. Available online: http://www.tcs.hut.fi/Software/smodels/ (accessed on 14 February 2021).
- Roanes-Lozano, E.; Alonso, J.A.; Hernando, A. An approach from answer set programming to decision making in a railway interlocking system. RACSAM 2014, 108, 973–987. [Google Scholar] [CrossRef]

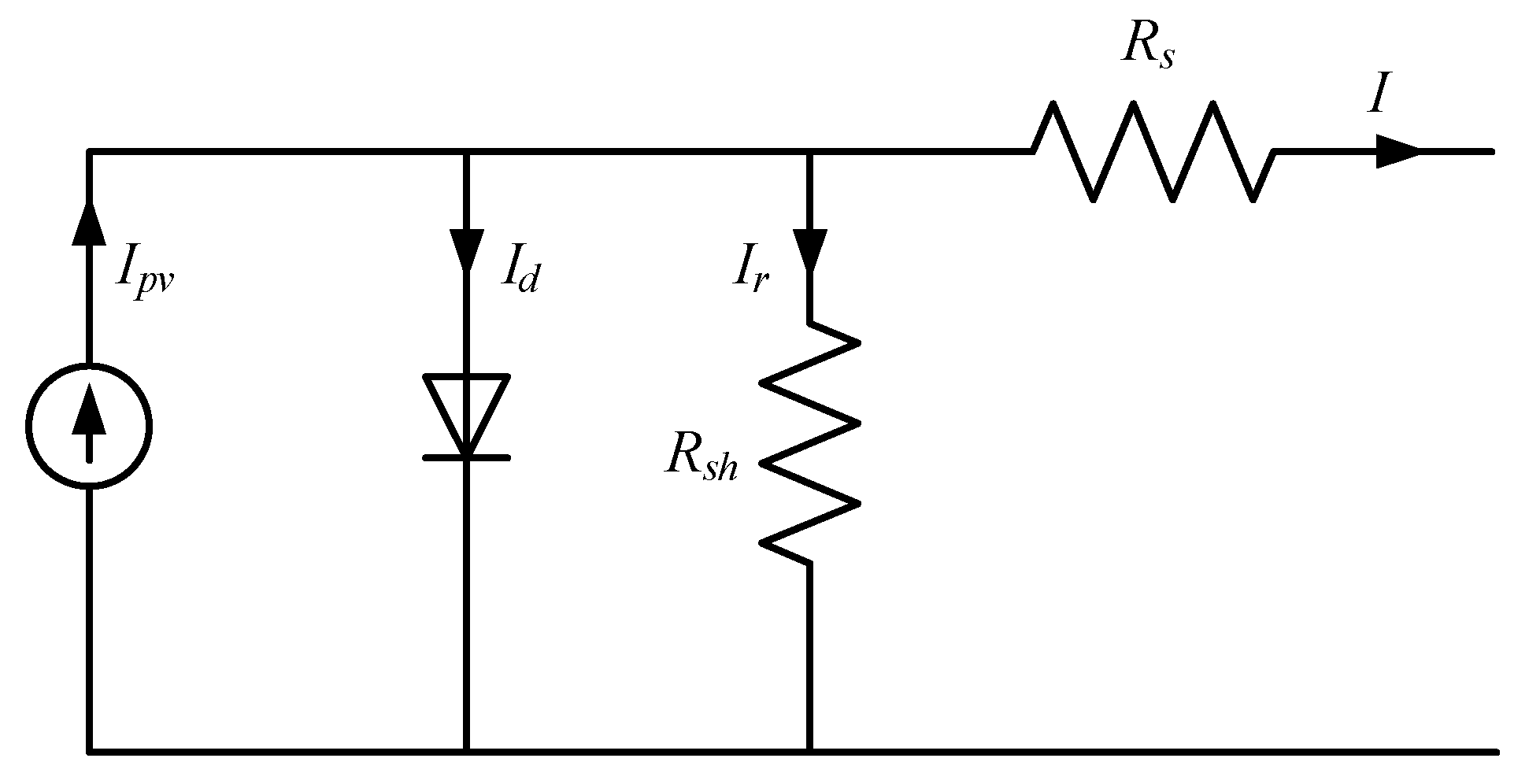
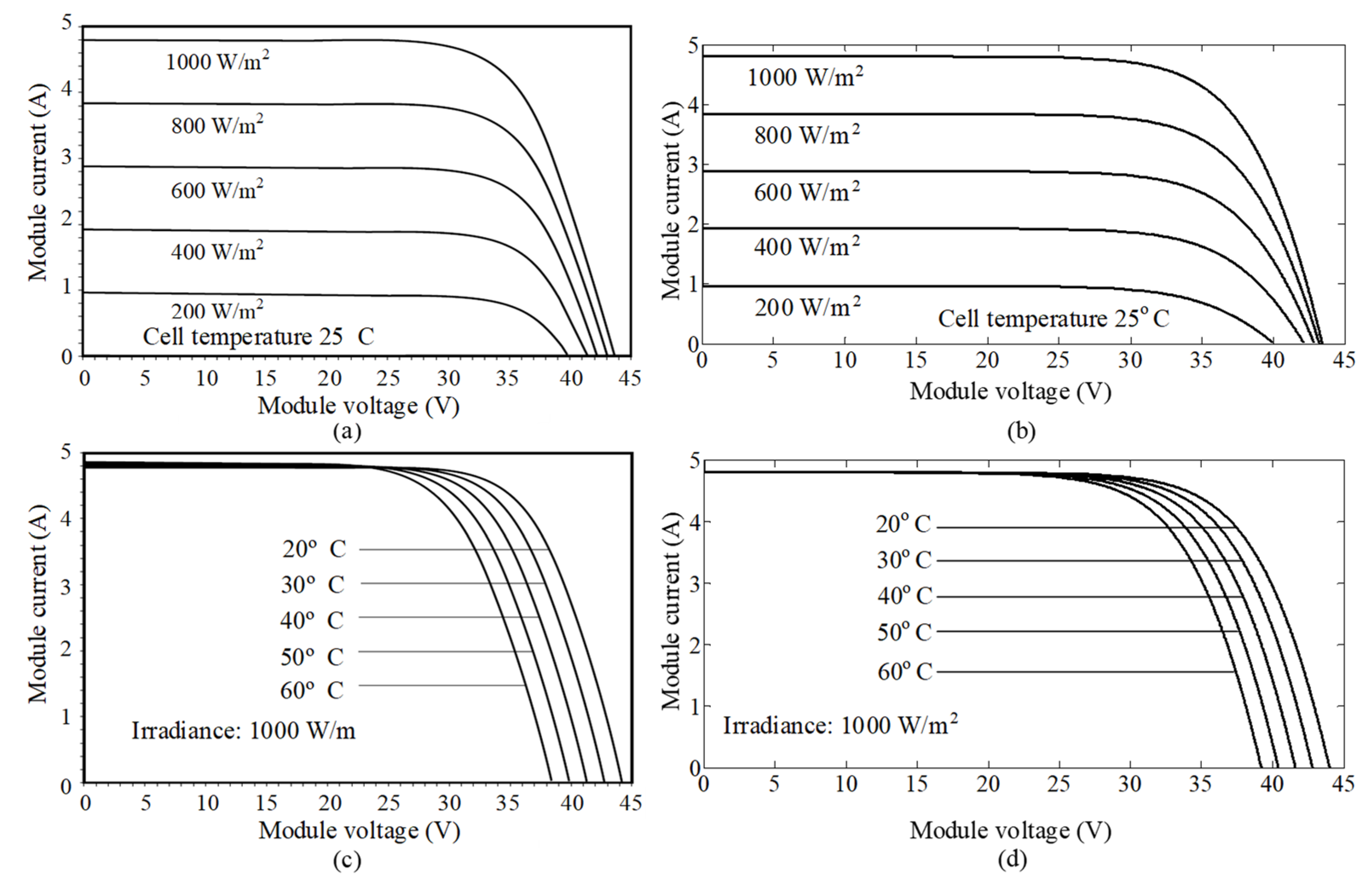


| Parameter | Description | Value |
|---|---|---|
| Pmpp (W) | Power at maximum power point | 150 |
| Vmpp (V) | Voltage at maximum power point | 34 |
| Voc (V) | Open circuit voltage | 43.4 |
| Isc (A) | Short circuit current | 4.8 |
| Consideration | |
|---|---|
| Power trend positive | |
| Power trend slightly positive | |
| Power trend null | |
| Power trend slightly negative | |
| Power trend negative |
(strongly charged) | B2L | N2G | B2L | N2G B2G | B2L B2G | N2G B2G | B2L B2G | N2G B2G | B2L B2G | N2G B2G |
(charged) | B2L | N2G | B2L B2G | N2G B2G | B2L B2G | N2G B2G | B2L B2G | N2G B2G | B2L B2G | N2G B2G |
| B2L | N2G | B2L | N2G | B2L B2G | N2G B2G | |||||
(intermediated) | G2L G2B | N2B | B2L | N2G B2G | B2L | N2G B2G | B2L B2G | N2G B2G | B2L | N2G B2G |
| B2L G2L | N2B | G2L | N2G | B2L | N2G | |||||
(discharged) | G2L G2B | N2B G2B | B2L | N2G | B2L | N2G N2B | B2L B2G | N2G B2G | G2L | N2G |
| B2L G2L | N2B | B2L G2L | N2B | B2L | N2G | |||||
(strongly discharged) | G2L G2B | N2B G2B | G2L G2B | N2B G2B | G2L G2B | N2B G2B | G2L G2B | N2B | G2L | N2B |
(strongly charged) | - | - | - | - | - | - | B2SC | B2SC | B2SC | B2SC |
(charged) | - | - | - | -- | - | - | B2SC | B2SC | B2SC | B2SC |
(intermediated) | - | - | - | - | - | B2SC | G2SC | B2SC | G2SC | |
(discharged) | - | - | - | - | - | - | G2SC | G2SC | G2SC | G2SC |
(strongly discharged) | - | - | - | - | - | - | G2SC | G2SC | G2SC | G2SC |
(strongly charged) | MPPT | RPPT | MPPT | RPPT | RPPT | RPPT | RPPT | RPPT | RPPT | RPPT |
(charged) | MPPT | RPPT | MPPT | RPPT | RPPT | RPPT | RPPT | RPPT | RPPT | RPPT |
(intermediated) | MPPT | MPPT | MPPT | RPPT | RPPT | RPPT | RPPT | RPPT | RPPT | RPPT |
(discharged) | MPPT | MPPT | MPPT | MPPT | MPPT | MPPT | MPPT | MPPT | MPPT | MPPT |
(strongly discharged) | MPPT | MPPT | MPPT | MPPT | MPPT | MPPT | MPPT | MPPT | MPPT | MPPT |
| TABLE NUMBER 6 | y1 | y2 | y3 | y4 | y5 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| u1 u2 | u1 u2 | u1 u2 | u1 u2 | u1 u2 | |||||||
| x1 | z1 ----- z2 | BAT 2 LOAD | NET 2 GRID | BAT 2 LOAD | NET2GRID BAT2GRID | BAT2LOAD BAT2GRID | NET2GRID BAT2GRID | BAT2LOAD BAT2GRID | NET2GRID BAT2GRID | BAT2LOAD BAT2GRID | NET2GRID BAT2GRID |
| x2 | z1 ----- z2 | BAT 2 LOAD | NET 2 GRID | BAT2LOAD BAT2GRID | NET2GRID BAT2GRID | BAT2LOAD BAT2GRID | NET2GRID BAT2GRID | BAT2LOAD BAT2GRID | NET2GRID BAT2GRID | BAT2LOAD BAT2GRID | NET2GRID BAT2GRID |
| BAT2LOAD | NET2GRID | BAT2LOAD | NET2GRID | BAT2LOAD BAT2GRID | NET2GRID BAT2GRID | ||||||
| x3 | z1 ----- z2 | GRID2LOAD GRID2BAT | NET 2 BAT | BAT2LOAD | NET2GRID BAT2GRID | BAT2LOAD | NET2GRID BAT2GRID | BAT2LOAD BAT2GRID | NET2GRID BAT2GRID | BAT 2 LOAD | NET2GRID BAT2GRID |
| BAT2LOAD GRID2LOAD | NET2BAT | GRID2LOAD | NET2GRID | BAT2LOAD | NET2GRID | ||||||
| x4 | z1 ------ z2 | GRID2LOAD GRID2BAT | NET2BAT GRID2BAT | BAT2LOAD | NET2GRID | BAT2LOAD | NET2GRID NET2BAT | BAT2LOAD BAT2GRID | NET2GRID BAT2GRID | GRID 2 LOAD | NET 2 GRID |
| BAT2LOAD GRID2LOAD | NET2BAT | BAT2LOAD GRID2LOAD | NET2BAT | BAT2LOAD | NET2GRID | ||||||
| x5 | z1 ------ z2 | GRID2LOAD GRID2BAT | NET2BAT GRID2BAT | GRID2LOAD GRID2BAT | NET2BAT GRID2BAT | GRID2LOAD GRID2BAT | NET2BAT GRID2BAT | GRID2LOAD GRID2BAT | NET 2 BAT | GRID 2 LOAD | NET 2 BAT |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roncero-Clemente, C.; Roanes-Lozano, E.; Barrero-González, F. A Multi-Criteria Computer Package-Based Energy Management System for a Grid-Connected AC Nanogrid. Mathematics 2021, 9, 487. https://doi.org/10.3390/math9050487
Roncero-Clemente C, Roanes-Lozano E, Barrero-González F. A Multi-Criteria Computer Package-Based Energy Management System for a Grid-Connected AC Nanogrid. Mathematics. 2021; 9(5):487. https://doi.org/10.3390/math9050487
Chicago/Turabian StyleRoncero-Clemente, Carlos, Eugenio Roanes-Lozano, and Fermín Barrero-González. 2021. "A Multi-Criteria Computer Package-Based Energy Management System for a Grid-Connected AC Nanogrid" Mathematics 9, no. 5: 487. https://doi.org/10.3390/math9050487
APA StyleRoncero-Clemente, C., Roanes-Lozano, E., & Barrero-González, F. (2021). A Multi-Criteria Computer Package-Based Energy Management System for a Grid-Connected AC Nanogrid. Mathematics, 9(5), 487. https://doi.org/10.3390/math9050487








