Remarks on the Local Irregularity Conjecture

Abstract

A locally irregular graph is a graph in which the end vertices of every edge have distinct degrees. A locally irregular edge coloring of a graph G is any edge coloring of G such that each of the colors induces a locally irregular subgraph of G. A graph G is colorable if it allows a locally irregular edge coloring. The locally irregular chromatic index of a colorable graph G, denoted by ${\chi }_{\mathrm{irr}}^{\prime }\left(G\right)$, is the smallest number of colors used by a locally irregular edge coloring of G. The local irregularity conjecture claims that all graphs, except odd-length paths, odd-length cycles and a certain class of cacti are colorable by three colors. As the conjecture is valid for graphs with a large minimum degree and all non-colorable graphs are vertex disjoint cacti, we study rather sparse graphs. In this paper, we give a cactus graph B which contradicts this conjecture, i.e., ${\chi }_{\mathrm{irr}}^{\prime }\left(B\right)=4$. Nevertheless, we show that the conjecture holds for unicyclic graphs and cacti with vertex disjoint cycles.

1. Introduction

All graphs mentioned in this paper are considered to be simple and finite. An edge coloring of a graph is neighbor sum distinguishing if any two neighboring vertices differ in the sum of the colors of the edges incident to them. This notion was first introduced in [1] and the following conjecture was proposed there.

Conjecture 1

(1-2-3 Conjecture). Every graph G without isolated edges admits a neighbor-sum-distinguishing edge coloring with the colors $\{1,2,3\}$.

This conjecture attracted a lot of interest [2,3,4,5,6] and for a survey we refer the reader to [7]. The best upper bound is that every graph without isolated edges admits a neighbor-sum-distinguishing edge coloring with five colors [8], but the 1-2-3 Conjecture remains open.

This variant of edge coloring and the 1-2-3 Conjecture motivated the introduction of similar variants of edge coloring. A locally irregular graph is any graph in which the two end vertices of every edge differ in degree. A locally irregular k-edge coloring, or k-liec for short, is any edge coloring of G with k colors such that every color induces a locally irregular subgraph of G. This variant of edge coloring was introduced in [9]. A third related edge coloring variant is the neighbor multiset-distinguishing edge coloring, where neighboring vertices must have assigned distinct multisets of colors on incident edges. In [10], it was established that every graph without isolated edges admits the neighbor multiset-distinguishing edge coloring with four colors. Notice that every locally irregular edge coloring is also a neighbor multiset-distinguishing edge coloring, but the reverse does not have to hold. In order to see that the reverse does not hold, consider the following graph with its edge coloring: G is a 2-path $abc$ and edges $ab$ and $bc$ are colored by 1 and 2, respectively. This is obviously not a locally irregular edge coloring but it is a neighbor multiset-distinguishing edge coloring as $\left\{1\right\},\{1,2\},\{1,2\}$ are the (multi)sets of colors at vertices a, b, c, respectively.

In this paper, we focus our attention on locally irregular edge colorings exclusively, and we say a graph is colorable if it admits such a coloring. The locally irregular chromatic index of a colorable graph $G,$ denoted by ${\chi }_{\mathrm{irr}}^{\prime }\left(G\right)$, is the smallest k, such that G admits a k-liec. In [9], the family of graphs $\mathfrak{T}$ has been defined as follows:

• $\mathfrak{T}$ contains the triangle $K_3$;
• if G is a graph from $\mathfrak{T}$, then a graph H obtained from G by identifying a vertex $v\in V\left(G\right)$ of degree $2,$ which belongs to a triangle of $G,$ with an end-vertex of an even length path or with an end vertex of an odd-length path such that the other end vertex of that path is identified with a vertex of a triangle, also belongs to $\mathfrak{T}$.

Note that every graph $G\in \mathfrak{T}$ has an odd size. A cactus graph is any graph in which cycles are pairwise edge disjoint. Notice that $\mathfrak{T}$ is a special family of cacti. Additionally, if we imagine triangles to be vertices and paths attached to vertices of a triangle as edges, we might informally say that G has tree-like structure. For the sake of simplicity, we define a broader family ${\mathfrak{T}}^{\prime }$ as the family obtained from $\mathfrak{T}$ by introducing to it all odd-length paths and all odd-length cycles. Notice that ${\mathfrak{T}}^{\prime }$ is a subclass of vertex-disjoint cactus graphs. It was established in [9] that a connected graph G is not colorable if and only if $G\in {\mathfrak{T}}^{\prime }$. Additionally, the following conjecture on the irregular chromatic index was proposed.

Conjecture 2

(Local Irregularity Conjecture). For every connected graph $G\notin {\mathfrak{T}}^{\prime }$, it holds that ${\chi }_{\mathrm{irr}}^{\prime }\left(G\right)\le 3.$

Let us mention some of the results related to Conjecture 2. For general graphs it was first established ${\chi }_{\mathrm{irr}}^{\prime }\left(G\right)\le 328$ [11], then it was lowered to ${\chi }_{\mathrm{irr}}^{\prime }\left(G\right)\le 220$ [12]. For some special classes of graphs Conjecture 2 is shown to hold, namely for trees [13], graphs with minimum degree at least ${10}^{10}$ [14], k-regular graphs where $k\ge {10}^7$ [9].

In this paper we will show that every unicyclic graph G which does not belong to ${\mathfrak{T}}^{\prime }$ admits a 3-liec, thus establishing that Conjecture 2 holds for unicyclic graphs. We will further extend this result to cactus graphs with vertex-disjoint cycles. Finally, we will provide an example of a colorable graph B with ${\chi }_{\mathrm{irr}}^{\prime }\left(B\right)=4$ showing that Conjecture 2 does not hold in general.

2. Revisiting the Trees

Since a unicyclic graph is obtained from a tree by adding a single edge to it, we first need to introduce the notation and several important results for trees from [13]. Additionally, we will establish several auxiliary results for trees, which will be useful throughout the paper.

First, a shrub is any tree rooted at a leaf. The only edge in a shrub G incident to the root we will call the root edge of G. An almost locally irregular k-edge coloring of a shrub $G,$ or k-aliec for short, is an edge coloring of G which is either k-liec or a coloring in which only the root edge is not locally irregular (notice that in this case the root edge is an isolated edge of its color, i.e., it is not adjacent to any other edge of the same color). A proper k-aliec is k-aliec which is not a k-liec. The following results for trees were established in [13].

Theorem 1.

Every shrub admits a 2-aliec.

Theorem 2.

For every colorable tree $T,$ it holds that ${\chi }_{\mathrm{irr}}^{\prime }\left(T\right)\le 3.$ Moreover, ${\chi }_{\mathrm{irr}}^{\prime }\left(T\right)\le 2$ if $\Delta \left(T\right)\ge 5.$

If an edge coloring uses at most three colors, we will denote those colors by $a,b,c.$ A 1-liec (resp. 2-liec, 3-liec) of a graph G will be denoted by ${\varphi }_a\left(G\right)$ (resp. ${\varphi }_{a,b}\left(G\right),$${\varphi }_{a,b,c}\left(G\right)$). A 2-aliec of a shrub G will be denoted by ${\varphi }_{a,b}\left(G\right)$ where a is the color of the root edge in G. Let $a,b,c,d$ be four colors, if ${\varphi }_{a,b}\left(G\right)$ is a 2-liec of G in colors a and $b,$ then 2-liec ${\varphi }_{c,d}\left(G\right)$ of G in colors c and d is obtained from ${\varphi }_{a,b}\left(G\right)$ by replacing colors a and b for c and d respectively, i.e., ${\varphi }_{c,d}\left(e\right)=c$ if and only if ${\varphi }_{a,b}\left(e\right)=a.$ Particularly, 2-(a)liec ${\varphi }_{b,a}\left(G\right)$ is called the inversion of the 2-(a)liec ${\varphi }_{a,b}\left(G\right),$ where colors a and b are replaced. Moreover, let ${\varphi }_{a,b,c}^i$ be an edge coloring of a graph $G_i$, for $i=1,\dots ,k,$ and let these graphs be pairwise edge disjoint, i.e., $E\left(G_i\right)\cap E\left(G_j\right)=\varnothing$ for any two distinct i and j. For a graph G such that $E\left(G\right)={\cup }_{i=1}^{k}E\left(G_i\right),$ by ${\sum }_{i=1}^k{\varphi }_{a,b,c}^i$ we will denote the edge coloring of G such that an edge e is colored by ${\varphi }_{a,b,c}^i\left(e\right)$ if and only if $e\in E\left(G_i\right).$

For any color of the edge coloring ${\varphi }_{a,b,c},$ say a, we define the a-degree of a vertex $v\in V\left(G\right)$ as the number of edges incident to v which are colored by a. The a-degree of a vertex v is denoted by $d_G^a\left(v\right).$ Assume that a vertex $v\in V\left(G\right)$ has k neighbors $w_1,\dots ,w_k$ such that each $v{w}_i$ is colored by $a.$ Then, the sequence $d_G^a\left(w_1\right),\dots ,d_G^a\left(w_k\right)$ is called the a-sequence of the vertex v. We usually assume that neighbors of v are denoted so that the a-sequence is non-increasing.

Throughout the paper we will use the technique of finding a 2-liec for trees introduced in [13]. Namely, if T is a tree with maximum degree 5 or more, then T admits a 2-liec according to Theorem 2. Otherwise, if the maximum degree of T is at most $4,$ let v be a vertex from T and $w_1,\dots ,w_k$ all the neighbors of v for $k\le 4.$ Notice that T consists of k shrubs $T_i$ starting at $v,$ let $T_i$ denote a shrub with the root edge $v{w}_i$ and let ${\varphi }_{a,b}^i$ denote a 2-aliec of $T_i$ which exists according to Theorem 1. Recall that ${\varphi }_{a,b}^i\left(v{w}_i\right)=a$ for every $i\le k.$ The coloring ${\varphi }_{a,b}={\sum }_{i=1}^k{\varphi }_{a,b}^i$ is called a shrub-based edge coloring of $T.$ We say that a shrub-based coloring ${\varphi }_{a,b}$ is inversion resistant if neither ${\varphi }_{a,b}$ is a 2-liec of T nor any of the colorings which can be obtained from ${\varphi }_{a,b}$ by color inversion in some of the shrubs $T_i.$ Let us now introduce the following lemma which stems from the technique used in [13].

Lemma 1.

Let T be a tree with $\Delta \left(T\right)\le 4$ and v a vertex from T of degree $k.$ Let $T_1,\dots ,T_k$ be all the shrubs of T rooted at v and let ${\varphi }_{a,b}^i$ be a 2-aliec of $T_i.$ If ${\varphi }_{a,b}^i$ is a 2-liec of $T_i$ for every $i=1,\dots ,k,$ then the shrub-based coloring ${\varphi }_{a,b}={\sum }_{i=1}^k{\varphi }_{a,b}^i$ can be inversion resistant in two cases only:

• If $d_T\left(v\right)=3$ and the a-sequence of v by ${\varphi }_{a,b}$ is $3,2,2$;
• If $d_T\left(v\right)=4$ and the a-sequence of v by ${\varphi }_{a,b}$ is $4,3,3,2$.

Proof. 

If $d_T\left(v\right)=1,$ then the shrub-based coloring of T equals ${\varphi }_{a,b}^1,$ which is 2-liec. If $d_T\left(v\right)=2,$ then ${\varphi }_{a,b}^1+{\varphi }_{b,a}^2$ would be a 2-liec of $T.$

If $d_T\left(v\right)=3,$ then the a-degree of v by ${\varphi }_{a,b}$ is $3,$ and inverting colors in one of the shrubs would decrease the a-degree of v to 2. Therefore, the a-sequence of v by ${\varphi }_{a,b}$ must contain 3 and $2.$ Considering the two possibilities $4,3,2,$ and $3,3,2$, we see that ${\varphi }_{a,b}^1+{\varphi }_{a,b}^2+{\varphi }_{b,a}^3$ would be 2-liec in both of them. The only remaining possibility is $3,2,2,$ and it is inversion resistant.

Finally, assume $d_T\left(v\right)=4.$ By a similar consideration as above, we see that the a-sequence of v by ${\varphi }_{a,b}$ must contain $4,$ $3,$ and $2.$ Therefore, we must consider the possibilities $4,4,3,2,$ then $4,3,3,2,$ then $4,3,2,2.$ It is easily seen that only in the case $4,3,3,2$, the shrub-based coloring ${\varphi }_{a,b}$ is inversion resistant. □

A spidey is a tree with radius at most two which consists of a central vertex u of degree at least 3 and the remaining vertices have degree at most 2 and are at distance at most 2 from u. Notice that every spidey is locally irregular, hence it admits a 1-liec. We say that a vertex v of a spidey G is a short leg if it is a leaf which is a neighbor of the central vertex of $G.$

Lemma 2.

Let H be a spidey with a short leg v and let K be a tree. Let G be a graph obtained from H and K by identifying the vertex v with a vertex from $K.$ Then, G admits a 3-liec such that all edges of $E\left(H\right)$ are colored by a same color.

Proof. 

Since H is a spidey, H admits a 1-liec, say ${\varphi }_c^0$. Assume first that a tree K is not colorable, i.e., K is an odd-length path. This implies there exists in K an edge $e_v$ incident with v, such that $K-e_v$ is a collection of even paths which, therefore, admits 2-liec ${\varphi }_{a,b}^1.$ The edge coloring ${\varphi }_{a,b,c}$ of G defined by

$${\varphi }_{a,b,c}\left(e\right)=\left\{\begin{array}{cc}c\hfill & \mathrm{if}e=e_v,\hfill \\ {\varphi }_{a,b}^1\left(e\right)\hfill & \mathrm{if}e\in E\left(K\right)\backslash \left\{e_v\right\},\hfill \\ {\varphi }_c^0\left(e\right)\hfill & \mathrm{if}e\in E\left(H\right),\hfill \end{array}\right.$$

is a 3-liec of $G.$

Assume now that K is a colorable tree. If K admits a 2-liec ${\varphi }_{a,b}^1,$ then ${\varphi }_c^0+{\varphi }_{a,b}^1$ is a 3-liec of G with the desired property. So, we may assume K is a colorable tree which does not admit a 2-liec. Theorem 2 implies $\Delta \left(K\right)\le 4.$ Let $d_K\left(v\right)=k\le 4$ and let $T_1,\dots ,T_k$ be all the shrubs of K rooted at $v.$ By Theorem 1, each shrub $T_i$ admits a 2-aliec ${\varphi }_{a,b}^i,$ where without loss of generality we may assume that ${\varphi }_{a,b}^i$ is a proper 2-aliec if and only if $i\le l.$ We distinguish the following four cases with respect to $l.$

• Case 1:$l\ge 3.$ Notice that $l\in \{3,4\}$ and $l\le k\le 4.$ If $l=3$ and $k=4,$ then ${\varphi }_{a,b}^1+{\varphi }_{a,b}^2+{\varphi }_{a,b}^3+{\varphi }_{b,a}^4$ would be a 2-liec of $K,$ a contradiction. Otherwise, the shrub-based coloring ${\varphi }_{a,b}={\sum }_{i=1}^k{\varphi }_{a,b}^i$ would be a 2-liec of $K,$ again a contradiction.
• Case 2:$l=2.$ If $k=2,$ then ${\varphi }_{a,b}^1+{\varphi }_{a,b}^2$ is a 2-liec of $K,$ a contradiction. If $k=3,$ then ${\varphi }_{a,b}^1+{\varphi }_{a,b}^2+{\varphi }_{b,a}^3$ is a 2-liec of $K,$ a contradiction. If $k=4,$ then let $w_1,\dots ,w_4$ be all the neighbors of v in $K.$ The shrub-based coloring ${\varphi }_{a,b}={\sum }_{i=1}^k{\varphi }_{a,b}^i$ is not a 2-liec only if the a-degree of $w_3$ or $w_4$ by ${\varphi }_{a,b}$ is $4.$ Without loss of generality we may assume that a-degree of $w_3$ by ${\varphi }_{a,b}$ is $4,$ but then ${\varphi }_{a,b}^1+{\varphi }_{a,b}^2+{\varphi }_{a,b}^3+{\varphi }_{b,a}^4$ is a 2-liec of $K,$ a contradiction.
• Case 3:$l=1.$ In this case, $T_1$ is the only shrub with a proper 2-aliec ${\varphi }_{a,b}^1.$ Let $w_1$ be the neighbor of v in $T_1,$ we define the coloring ${\varphi }_{a,b,c}^{\prime }$ of K as follows

  $${\varphi }_{a,b,c}^{\prime }\left(e\right)=\left\{\begin{array}{cc}c\hfill & \mathrm{if}e=v{w}_1,\hfill \\ \sum _{i=1}^k{\varphi }_{a,b}^i\left(e\right)\hfill & \mathrm{if}e\in E\left(K\right)\backslash \left\{v{w}_1\right\}.\hfill \end{array}\right.$$

  Notice that ${\varphi }_{a,b,c}^{\prime }$ is not a liec of $K,$ but ${\varphi }_c^0+{\varphi }_{a,b,c}^{\prime }$ is a 3-liec of $G=H+K$ with the desired property that all edges of H are colored by a same color, in this case c.
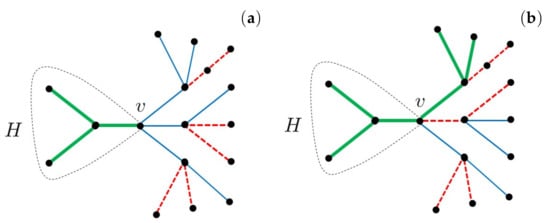
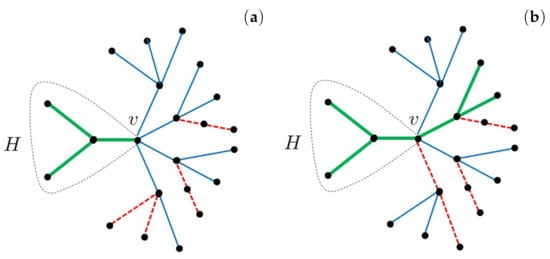
• Case 4:$l=0.$ Notice that in this case Lemma 1 applies on K and $v.$ Therefore, the only cases when K does not admit a 2-liec are: i) $d_K\left(v\right)=3$ and the a-sequence of v by the shrub-based coloring ${\varphi }_{a,b}={\sum }_{i=1}^k{\varphi }_{a,b}^i$ is $3,2,2,$ or ii) $d_K\left(v\right)=4$ and the a-sequence of v by ${\varphi }_{a,b}$ is $4,3,3,2.$ In the first case the coloring ${\varphi }_c^0+{\varphi }_{c,b}^1+{\varphi }_{b,a}^2+{\varphi }_{a,b}^3$ is a 3-liec of G such that $E\left(H\right)$ is colored by the same color c, as it is illustrated in Figure 1. In the other case, the coloring ${\varphi }_c^0+{\varphi }_{a,b}^1+{\varphi }_{c,b}^2+{\varphi }_{a,b}^3+{\varphi }_{b,a}^4$ is a 3-liec of G such that $E\left(H\right)$ is colored by a same color, as it is illustrated in Figure 2. □

Figure 1. A graph $G=H+K$ and a vertex v of degree 3 in $K:$ (a) the coloring ${\varphi }_c^0+{\varphi }_{a,b}^1+{\varphi }_{a,b}^2+{\varphi }_{a,b}^3$ is not a 3-liec of G; (b) the coloring ${\varphi }_c^0+{\varphi }_{c,b}^1+{\varphi }_{b,a}^2+{\varphi }_{a,b}^3$ is a 3-liec of $G.$

Figure 2. A graph $G=H+K$ and a vertex v of degree 4 in $K:$ (a) the coloring ${\varphi }_c^0+{\varphi }_{a,b}^1+{\varphi }_{a,b}^2+{\varphi }_{a,b}^3+{\varphi }_{a,b}^4$ is not a 3-liec of G, (b) the coloring ${\varphi }_c^0+{\varphi }_{a,b}^1+{\varphi }_{c,b}^2+{\varphi }_{a,b}^3+{\varphi }_{b,a}^4$ is a 3-liec of $G.$

3. Unicyclic Graphs

In this section, we will establish Conjecture 2 for unicyclic graphs. It is already known that there exist colorable unicyclic graphs which do not admit 2-liec, but require three colors in order for edge coloring to be locally irregular, namely cycles of length $4k+2,$ for $k\in \mathbb{N}$. We will show that such cycles are not an isolated family of unicyclic graphs that require three colors. The main result for unicyclic graphs is established through the following two lemmas in which we will consider separately cases whether the cycle of G is a triangle or not.

Lemma 3.

Let G be a unicyclic graph with the unique cycle being a triangle. If $G\notin {\mathfrak{T}}^{\prime },$ then ${\chi }_{\mathrm{irr}}^{\prime }\left(G\right)\le 3.$

Proof. 

Let $C=u_1{u}_2{u}_3$ be the triangle in G, let $T_i$ denote the connected component of $G-E\left(C\right)$ which contains $u_i.$ Since $G\notin {\mathfrak{T}}^{\prime },$ there must exist a vertex $u_i$ on C such that $T_i$ is not a pendant even length path, say it is $u_1.$ Let $G_1=T_1+u_1{u}_2$ and let $G_0=G-E\left(G_1\right).$ First notice that both $G_0$ and $G_1$ are trees and that $E\left(G\right)=E\left(G_0\right)\cup E\left(G_1\right).$ Since $T_1$ is not a pendant path of even length, it follows that $G_1$ is not an odd length path, hence it is colorable. Let ${\varphi }_{a,b,c}^1$ be a 3-liec of $G_1.$ Without loss of generality we may assume that ${\varphi }_{a,b,c}^1\left(u_1{u}_2\right)=c.$ Let H be the subgraph of $G_1$ induced by all edges incident to $u_1$ in $G_1.$ We may assume ${\varphi }_{a,b,c}^1\left(e\right)=c$ for every $e\in E\left(H\right),$ namely if $d_H\left(u_1\right)=2$ this follows from the local irregularity of ${\varphi }_{a,b,c}^1;$ otherwise, it follows from Lemma 2 applied on H and every component of $G_1-E\left(H\right)$ repeatedly.

Let us now consider the graph $G_0$ and notice that it is a shrub rooted at $u_1$ with the root edge $u_1{u}_3.$ By Theorem 1 there exists a 2-aliec ${\varphi }_{a,b}^0$ of $G_0.$ If ${\varphi }_{a,b}^0$ is a 2-liec, then ${\varphi }_{a,b,c}={\varphi }_{a,b}^0+{\varphi }_{a,b,c}^1$ is a 3-liec of G. Additionally, if ${\varphi }_{a,b}^0$ is a proper 2-aliec of $G_0$, then $G_1+u_1{u}_3$ is colorable and let ${\varphi }_{a,b,c}^2$ be a 3-liec of $G_1+u_1{u}_3$ such that ${\varphi }_{a,b,c}^2\left(e\right)=c$ for every edge $e\in E\left(H\right)\cup \left\{u_1{u}_3\right\}$ by Lemma 2. We define the edge coloring ${\varphi }_{a,b,c}$ of G as follows

$${\varphi }_{a,b,c}\left(e\right)=\left\{\begin{array}{cc}{\varphi }_{a,b}^0\left(e\right)\hfill & \mathrm{if}e\in E\left(G_0\right)\backslash \left\{u_1{u}_3\right\},\hfill \\ {\varphi }_{a,b,c}^1\left(e\right)\hfill & \mathrm{if}e\in E\left(G_1\right).\hfill \end{array}\right.$$

It is easily seen that ${\varphi }_{a,b,c}$ is a 3-liec of $G.$ □

Let us now consider unicyclic graphs with larger cycles.

Lemma 4.

Let G be a unicyclic graph with the unique cycle being of length at least four. If $G\notin {\mathfrak{T}}^{\prime },$ then ${\chi }_{\mathrm{irr}}^{\prime }\left(G\right)\le 3.$

Proof. 

If G is a cycle, then $G\notin {\mathfrak{T}}^{\prime }$ implies that G is an even-length cycle and hence admits a 3-liec. So, we may assume G is not a cycle, i.e., at least one vertex from the cycle of G is of degree at least three. Denote the cycle in G by $C=u_1{u}_2\cdots u_g$ with $g\ge 4.$ Without loss of generality we may assume that $u_1$ is the vertex with maximum degree among vertices from $C.$ We distinguish the following two cases with respect to $d_G\left(u_1\right).$

• Case 1:$d_G\left(u_1\right)\ge 4.$ Let $E_1$ denote the set of all edges incident to $u_1$ in G except the edge $u_1{u}_2$ and let H denote the subgraph of G induced by $E_1.$ The assumption $d_G\left(u_1\right)\ge 4$ implies $d_H\left(u_1\right)\ge 3,$ so H is a spidey in which every leg is short. Let $G_0$ be the connected component of $G-E_1$ which contains $u_2$ and let $G_1=G-E\left(G_0\right).$ Let $G_1^{\prime },\dots ,G_k^{\prime }$ be all connected components of $G_1-E\left(H\right).$ Each $G_i^{\prime }$ is a tree, so Lemma 2 can be applied to H and $K=G_i^{\prime },$ for every $i=1,\dots ,k$. We conclude that there exists a 3-liec ${\varphi }_{a,b,c}^1$ of $G_1$ such that ${\varphi }_{a,b,c}^1\left(e\right)=c$ for every $e\in E\left(H\right).$ On the other hand, $G_0$ is a shrub rooted at $u_1$ with the root edge $u_1{u}_2,$ so $G_0$ admits 2-aliec ${\varphi }_{a,b}^0$ according to Theorem 1.

If ${\varphi }_{a,b}^0$ is a 2-liec of $G_0,$ then ${\varphi }_{a,b,c}={\varphi }_{a,b}^0+{\varphi }_{a,b,c}^1$ is a 3-liec of $G.$ Additionally, if ${\varphi }_{a,b}^0$ is a proper 2-aliec of $G_0$, then $G_1+u_1{u}_2$ is colorable and let ${\varphi }_{a,b,c}^2$ be a 3-liec of $G_1+u_1{u}_2$ such that ${\varphi }_{a,b,c}^2=c$ for every edge $e\in E\left(H\right)\cup \left\{u_1{u}_2\right\}$ by Lemma 2. We define the edge coloring ${\varphi }_{a,b,c}$ of G as follows

$${\varphi }_{a,b,c}\left(e\right)=\left\{\begin{array}{cc}{\varphi }_{a,b}^0\left(e\right)\hfill & \mathrm{if}e\in E\left(G_0\right)\backslash \left\{u_1{u}_2\right\},\hfill \\ {\varphi }_{a,b,c}^1\left(e\right)\hfill & \mathrm{if}e\in E\left(G_1\right).\hfill \end{array}\right.$$

It is easily seen that thus defined ${\varphi }_{a,b,c}$ is a 3-liec of $G.$

• Case 2:$d_G\left(u_1\right)=3.$ Let $E_1$ be the set of all edges incident to $u_1$ in G and H a subgraph of G induced by $E_1.$ Let $G_0$ be the connected component of $G-E_1$ which contains $u_2$ and let $G_1=G-E\left(G_0\right).$ Similarly as in the previous case, there exists a 3-liec ${\varphi }_{a,b,c}^1$ of $G_1$ such that ${\varphi }_{a,b,c}\left(e\right)=c$ for every $e\in E\left(H\right).$ Notice that $d_G\left(u_2\right)\in \{2,3\},$ since $u_1$ is the vertex with maximum degree among vertices from $C.$ Now we distinguish two possibilities with regard to $d_G\left(u_2\right).$

If $d_G\left(u_2\right)=2,$ then $G_0$ is a shrub rooted in $u_2$ with the root edge $u_2{u}_3.$ According to Theorem 1, there exists a 2-aliec ${\varphi }_{a,b}^0$ of $G_0.$ If ${\varphi }_{a,b}^0$ is 2-liec of $G_0,$ then ${\varphi }_{a,b,c}={\varphi }_{a,b}^0+{\varphi }_{a,b,c}^1$ is a 3-liec of $G.$ Otherwise, ${\varphi }_{a,b,c}$ defined by

$${\varphi }_{a,b,c}\left(e\right)=\left\{\begin{array}{cc}c\hfill & \mathrm{if}e=u_2{u}_3,\hfill \\ {\varphi }_{a,b}^0\left(e\right)\hfill & \mathrm{if}e\in E\left(G_0\right)\backslash \left\{u_2{u}_3\right\},\hfill \\ {\varphi }_{a,b,c}^1\left(e\right)\hfill & \mathrm{if}e\in E\left(G_1\right),\hfill \end{array}\right.$$

is a 3-liec of $G.$

If $d_G\left(u_2\right)=3,$ then consider $G_0$ to be a tree rooted at $u_2$ which consists of two shrubs $G_0^{\prime }$ and $G_0^{\prime \prime },$ the first with the root edge $u_2{u}_3$ and the other with the root edge $u_2{v}_2,$ where $v_2$ is the only neighbor of $u_2$ which does not belong to the cycle C. Theorem 1 implies that there exist 2 aliecs ${\varphi }_{a,b}^{\prime }$ and ${\varphi }_{a,b}^{″}$ of $G_0^{\prime }$ and $G_0^{\prime \prime },$ respectively. If both ${\varphi }_{a,b}^{\prime }$ and ${\varphi }_{a,b}^{″}$ are a 2-liec of the respective shrub, then ${\varphi }_{a,b,c}={\varphi }_{a,b}^{\prime }+{\varphi }_{b,a}^{\prime \prime }+{\varphi }_{a,b,c}^1$ is a 3-liec of $G.$ If both ${\varphi }_{a,b}^{\prime }$ and ${\varphi }_{a,b}^{″}$ are a proper 2-aliec of the respective shrub, then ${\varphi }_{a,b,c}={\varphi }_{a,b}^{\prime }+{\varphi }_{a,b}^{\prime \prime }+{\varphi }_{a,b,c}^1$ is a 3-liec of $G.$ The only remaining possibility is that precisely one of ${\varphi }_{a,b}^{\prime }$ and ${\varphi }_{a,b}^{\prime \prime },$ say ${\varphi }_{a,b}^{\prime }$, is a proper 2-aliec of the respective shrub. In this case we define the coloring ${\varphi }_{a,b,c}^0$ of $G_0$ as follows

$${\varphi }_{a,b,c}^0\left(e\right)=\left\{\begin{array}{cc}c\hfill & \mathrm{if}e=u_2{u}_3,\hfill \\ {\varphi }_{a,b}^{\prime }\left(e\right)\hfill & \mathrm{if}e\in E\left(G_0^{\prime }\right)\backslash \left\{u_2{u}_3\right\},\hfill \\ {\varphi }_{a,b}^{\prime \prime }\left(e\right)\hfill & \mathrm{if}e\in E\left(G_0^{\prime \prime }\right).\hfill \end{array}\right.$$

Since $\left|V\left(C\right)\right|\ge 4,$ it is easily seen that ${\varphi }_{a,b,c}={\varphi }_{a,b,c}^0+{\varphi }_{a,b,c}^1$ is a 3-liec of $G.$ □

The previous two lemmas yield the following result.

Theorem 3.

Let G be a unicyclic graph. If $G\notin {\mathfrak{T}}^{\prime },$ then ${\chi }_{\mathrm{irr}}^{\prime }\left(G\right)\le 3.$

A natural question that arises is whether the bound ${\chi }_{\mathrm{irr}}^{\prime }\left(G\right)\le 3$ is tight, i.e., are there colorable unicyclic graphs which are not 2-colorable. The family of cycles of length $4k+2$ are such graphs, but this family is not an isolated case, there exist other unicyclic graphs which require three colors, for example, the graph from Figure 3. One can assure infinitely many such graphs, for example, by taking longer threads of suitable parity in the given graph.

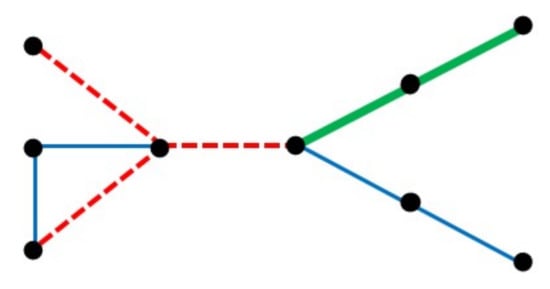
Figure 3. A colorable unicyclic graph distinct from cycle which requires 3 colors for locally irregular edge coloring.

4. Cacti with Vertex Disjoint Cycles

In this section, we will extend the result from the previous section to cacti with vertex disjoint cycles. We will also show that the result does not extend to all cacti by providing an example of a cactus graph with four cycles which is colorable, but requires 4 colors for a locally irregular edge coloring. This establishes that Conjecture 2 does not hold in general. We first need to introduce several useful notions in order to deal with cacti.

Let G be a cactus graph with at least two cycles, let C be a cycle in G and let u be a vertex from $C.$ We say that u is a root vertex of C if the connected component of $G-E\left(C\right)$ which contains u is a cyclic graph. A cycle C of G is a proper end cycle if $G-V\left(C\right)$ contains at most one cyclic connected component. Every cactus graph with vertex disjoint cycles contains at least two proper end cycles, given it is not a unicyclic graph.

Theorem 4.

Let G be a cactus graph with vertex disjoint cycles. If $G\notin {\mathfrak{T}}^{\prime },$ then ${\chi }_{\mathrm{irr}}^{\prime }\left(G\right)\le 3.$

Proof. 

The proof is by induction on the number of cycles in $G.$ If G is a unicyclic graph, then the claim holds by Theorem 3. Assume that the claim holds for all cacti with fewer than p cycles, where $p\ge 2$. Let G be a cactus graph with p cycles. We will show that G admits a 3-liec and this will establish the claim of the theorem. Let C be a proper end cycle of G, $u_1$ the root vertex of $C,$ and v the only neighbor of $u_1$ which belongs to the cyclic component of $G-E\left(C\right).$ Denote the other neighbors of $u_1$ by $u_2,\dots ,u_k$ so that $u_2$ and $u_3$ belong to the cycle C. In what follows, we distinguish two cases.

• Case 1:$d_G\left(u_1\right)=3$. Let $G_1$ be the connected component $G-u_{1}v$ which does not contain v and let $G_0=G-E\left(G_1\right).$ Let $G_0^{\prime }=G_0+u_1{u}_2$ and $G_1^{\prime }=G_1-u_1{u}_2.$

Suppose first that $G_0^{\prime }$ is colorable. Then, it admits a 3-liec ${\varphi }_{a,b,c}^0$ where the edges $u_1{u}_2$ and $u_{1}v$ must be colored by a same color, say color c. Notice that $G_1^{\prime }$ is a shrub rooted at $u_1$ with the root edge $u_1{u}_3.$ By Theorem 1, $G_1^{\prime }$ admits a 2-aliec ${\varphi }_{a,b}^1$. If ${\varphi }_{a,b}^1$ is a 2-liec of $G_1^{\prime }$, then ${\varphi }_{a,b,c}^0+{\varphi }_{a,b}^1$ is a 3-liec of $G.$ Otherwise, if ${\varphi }_{a,b}^1$ is a proper 2-aliec of $G_1,$ then the restriction of ${\varphi }_{a,b}^1$ to $G_1^{\prime \prime }=G_1^{\prime }-u_1{u}_3$ is a 2-liec of that graph. Notice that $G_0^{\prime \prime }=G_0^{\prime }+u_1{u}_3$ does not belong to ${\mathfrak{T}}^{\prime }$, so it is colorable and by induction hypothesis it admits a 3-liec ${\varphi }_{a,b,c}^{″}$ in which edges $u_1{u}_2$ and $u_1{u}_3$ must be colored by a same color (say color c) since $d_G\left(u_1\right)=3.$ Now, we infer that

$${\varphi }_{a,b,c}\left(e\right)=\left\{\begin{array}{cc}{\varphi }_{a,b}^1\left(e\right)& \mathrm{if}e\in E\left(G_1^{″}\right),\\ {\varphi }_{a,b,c}^{″}\left(e\right)& \mathrm{if}e\in E\left(G_0^{″}\right),\end{array}\right.$$

is a 3-liec of G.

Suppose now that $G_0^{\prime }$ is not colorable. Assume first $G_1$ is not colorable. Notice that $G_1$ is a unicyclic graph, so if the cycle of $G_1$ is a triangle, then the assumption that $G_0^{\prime }$ and $G_1$ are not colorable would imply $G\in \mathfrak{T}$, a contradiction. Otherwise, if $G_1$ is a unicyclic graph on a larger cycle, then it is not colorable only if it is an odd-length cycle. In this case let w be the only neighbor of $u_3$ distinct from $u_1,$ let $G_0^{″}=G_0^{\prime }+\{u_1{u}_3,u_{3}w\}$ and $G_1^{″}=G-E\left(G_0^{″}\right).$ Notice that by induction hypothesis $G_0^{″}$ is colorable and admits a 3-liec ${\varphi }_{a,b,c}^0$ for which we may assume ${\varphi }_{a,b,c}^0\left(u_{3}w\right)=a$ and ${\varphi }_{a,b,c}^0\left(u_1{u}_2\right)\in \{a,b\}.$ Additionally, notice that $G_1^{″}$ is an even length path, so it admits a 2-liec ${\varphi }_{b,c}^1$ where we may assume that the edge of $G_1^{″}$ incident to $u_2$ is colored by $c.$ Then ${\varphi }_{a,b,c}^0+{\varphi }_{b,c}^1$ is a 3-liec of $G.$

Suppose now that $G_1$ is colorable. Since $G_0^{\prime }$ is not colorable, the edge $u_1{u}_2$ of $G_0^{\prime }$ must belong to an even length path hanging at a vertex of a triangle in $G_0^{\prime },$ so the graph $G_0=G_0^{\prime }-u_1{u}_2$ contains an odd-length path hanging at a vertex of a triangle, which means $G_0\notin {\mathfrak{T}}^{\prime },$ so it is colorable. Therefore, by induction hypothesis $G_0$ admits a 3-liec ${\varphi }_{a,b,c}^0.$ Since $u_1$ is a leaf in $G_0$, we may assume that ${\varphi }_{a,b,c}^0\left(u_{1}v\right)=c.$ By Theorem 3, $G_1$ admits 3-liec ${\varphi }_{a,b,c}^1.$ Since the degree of $u_1$ in $G_1$ equals two, we may assume that the colors of edges $u_1{u}_2$ and $u_1{u}_3$ are from $\{a,b\}.$ Therefore, ${\varphi }_{a,b,c}^0+{\varphi }_{a,b,c}^1$ is a 3-liec of G.

• Case 2:$d_G\left(u_1\right)\ge 4.$ Let H be the subgraph of G induced by the set of all edges incident to $u_1$ in $G.$ Denote the connected components of $G-E\left(H\right)$ in the following way, let $G_0^{\prime }$ be the component which contains v and $G_1^{\prime }$ the component which contains $u_2$ and $u_3$. Additionally, let $G_1=G_1^{\prime }+u_1{u}_2$ and $G_0=G_0^{\prime }+u_{1}v.$ We may assume $G_0$ is colorable, as otherwise G would contain a proper end cycle which is a triangle with the root vertex of degree 3, which would reduce to the previous case. Let $G_2=G-(E\left(G_0\right)\cup E\left(G_1\right)\cup E\left(H\right))$ and $H^{\prime }=H-\{u_1{u}_2,u_{1}v\}.$

Suppose first that the tree $H^{\prime }+G_2$ is not colorable. This implies that it is an odd-length path. Notice that $H^{\prime }+G_2,$ as a shrub rooted at $u_3,$ admits a proper 2-aliec ${\varphi }_{a,b}^2,$ and since it is proper we have ${\varphi }_{a,b}^2\left(u_1{u}_4\right)=b.$ Since $G_0$ is colorable, by induction hypothesis it admits a 3-liec ${\varphi }_{a,b,c}^0,$ where we may assume ${\varphi }_{a,b,c}^0\left(u_{1}v\right)=a.$ Since $G_1$ is a shrub rooted at $u_1$ with the root edge $u_1{u}_2,$ it admits a 2-aliec ${\varphi }_{a,b}^1.$ If ${\varphi }_{a,b}^1$ is a proper 2-aliec of $G_1$, then

$${\varphi }_{a,b,c}\left(e\right)=\left\{\begin{array}{cc}c\hfill & \mathrm{if}e=u_1{u}_2\mathrm{or}{u}_1{u}_3,\hfill \\ ({\varphi }_{a,b,c}^0+{\varphi }_{a,b}^1+{\varphi }_{a,b}^2)\left(e\right)\hfill & \mathrm{if}e\in E\left(G\right)\backslash \{u_1{u}_2,u_1{u}_3\},\hfill \end{array}\right.$$

is a 3-liec of $G.$ Otherwise, if ${\varphi }_{a,b}^1$ is a 2-liec of $G_1,$ then let us consider the graph $G_0^{\prime \prime }=G_0+u_1{u}_3.$ It is colorable by the same argument as $G_0,$ so it admits a 3-liec ${\varphi }_{a,b,c}^{″}$ in which $u_1{u}_3$ and $u_{1}v$ must be colored by a same color, say c. Then

$${\varphi }_{a,b,c}\left(e\right)=\left\{\begin{array}{cc}{\varphi }_{a,b,c}^{\prime \prime }\left(e\right)\hfill & \mathrm{if}e\in E\left(G_0^{\prime \prime }\right),\hfill \\ ({\varphi }_{a,b}^1+{\varphi }_{a,b}^2)\left(e\right)\hfill & \mathrm{if}e\in E\left(G\right)\backslash E\left(G_0^{\prime \prime }\right),\hfill \end{array}\right.$$

is a 3-liec of $G.$

Suppose now that $H^{\prime }+G_2$ is a colorable tree, so it admits a 3-liec ${\varphi }_{a,b,c}^2.$ We may assume that ${\varphi }_{a,b,c}^2\left(e\right)=c$ for every $e\in E\left(H^{\prime }\right),$ as this follows either from $d_{H^{\prime }}\left(u_1\right)=2$ or from Lemma 2 applied to $H^{\prime }$ as a spidey and every connected component of $G_2$ as K. As for $G_0,$ recall that it is colorable, so by induction hypothesis, it has a 3-liec ${\varphi }_{a,b,c}^0$. Since $u_1$ is a leaf in $G_0,$ we may assume ${\varphi }_{a,b,c}^0\left(u_{1}v\right)=a.$ Let us now consider the graph $G_1.$ Recal that it is a shrub rooted at $u_1$ with the root edge $u_1{u}_2.$ Hence, by Theorem 1 the graph $G_1$ admits a 2-aliec ${\varphi }_{a,b}^1.$ If ${\varphi }_{a,b}^1$ is a 2-liec of $G_1,$ then ${\varphi }_{a,b,c}^0+{\varphi }_{b,a}^1+{\varphi }_{a,b,c}^2$ is a 3-liec of $G.$ Otherwise, we define $H^{\prime \prime }=H^{\prime }+u_1{u}_2$, and notice that $H^{″}$ is a spidey. According to Lemma 2, the graph $G_2^{\prime \prime }=H^{\prime \prime }+G_2$ admits a 3-liec ${\varphi }_{a,b,c}^{″}$ such that ${\varphi }_{a,b,c}^{\prime \prime }\left(e\right)=c$ for every $e\in E\left(H^{\prime \prime }\right).$ We conclude that

$${\varphi }_{a,b,c}\left(e\right)=\left\{\begin{array}{cc}{\varphi }_{a,b,c}^{\prime \prime }\left(e\right)\hfill & \mathrm{if}e\in E\left(G_2^{\prime \prime }\right),\hfill \\ ({\varphi }_{a,b,c}^0+{\varphi }_{a,b}^1)\left(e\right)\hfill & \mathrm{if}e\in E\left(G\right)\backslash E\left(G_2^{\prime \prime }\right),\hfill \end{array}\right.$$

is a 3-liec of $G.$ □

Let us now consider the so called bow-tie graph B shown in Figure 4. This is a cactus graph with four cycles, but in which cycles are not vertex disjoint. This graph is colorable and admits the 4-liec shown in Figure 4, but it does not admit a k-liec for $k\le 3$ since the two end vertices of the cut edge must have the degree three in the color of that edge. Hence, for the bow-tie graph B it holds that ${\chi }_{\mathrm{irr}}^{\prime }\left(B\right)=4.$ We conclude that Conjecture 2 does not hold in general.

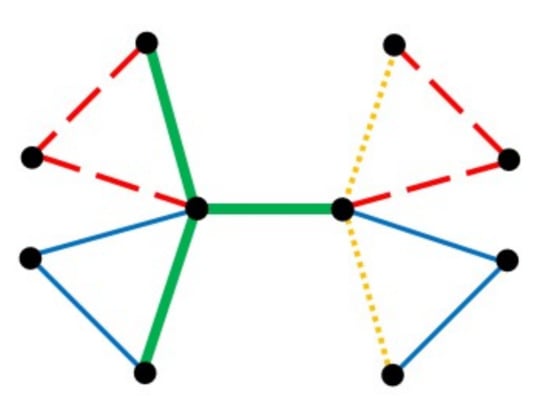
Figure 4. The bow-tie graph B and a 4-liec of it.

The consideration of the bow-tie graph gives rise to the following questions: are there any other graphs for which Conjecture 2 does not hold, do all colorable cacti admit a 4-liec, what is the thight upper bound on ${\chi }_{\mathrm{irr}}^{\prime }\left(G\right)$ of general graphs? We believe the following conjecture holds, which is a weaker form of the Local Irregularity Conjecture.

Conjecture 3.

Every connected graph G which does not belong to ${\mathfrak{T}}^{\prime }$ satisfies ${\chi }_{\mathrm{irr}}^{\prime }\left(G\right)\le 4.$

5. Concluding Remarks

It was established in [9] that a graph does not admit a locally irregular edge coloring if and only if it belongs to the family ${\mathfrak{T}}^{\prime }$. Additionally, it was further conjectured that all other graphs admit a locally irregular 3-edge coloring, see Conjecture 2. As the conjecture is valid for graphs with large minimum degree and all non-colorable graphs are vertex disjoint cacti, we took direction to study cacti.

In this paper we first consider trees to obtain an auxiliary result, then we considered unicyclic graphs and we established that every unicyclic graph $G\notin {\mathfrak{T}}^{\prime }$ admits a locally irregular 3-edge coloring as Conjecture 2 claims. Moreover, we have remarked that the bound 3 is tight also on a family of unicyclic graphs, distinct from cycles of the length $4k+2$, for which it was previously known.

We further extended the result to cacti with vertex disjoint cycles, showing that Conjecture 2 also holds for this class of graphs. Then we gave the so called bow-tie graph B in which cycles are not vertex disjoint, which is colorable and admits a 4-liec, but it does not admit a locally irregular 3-edge coloring. This graph is a counterexample for Conjecture 2. So the conjecture does not hold in general, but possibly this is a lonely counterexample. We concluded the paper by conjecturing that all colorable graphs admits a locally irregular 4-edge coloring.