Branched Continued Fraction Expansions of Horn’s Hypergeometric Function H₃ Ratios

Abstract

The paper deals with the problem of construction and investigation of branched continued fraction expansions of special functions of several variables. We give some recurrence relations of Horn hypergeometric functions $H_3.$ By these relations the branched continued fraction expansions of Horn’s hypergeometric function $H_3$ ratios have been constructed. We have established some convergence criteria for the above-mentioned branched continued fractions with elements in ${\mathbb{R}}^2$ and ${\mathbb{C}}^2.$ In addition, it is proved that the branched continued fraction expansions converges to the functions which are an analytic continuation of the above-mentioned ratios in some domain (here domain is an open connected set). Application for some system of partial differential equations is considered.

1. Introduction

Special functions with several variables (such as famous Appell, Lauricella, and Horn hypergeometric functions, etc.) appear in many areas of mathematics and its applications. Many authors have contributed works on this subject; we have mentioned a few: Res. [1,2,3,4]. In recent years, several authors have considered some interesting branched continued fraction expansions of the special functions of several variables (see [5,6,7,8,9,10]). In the paper, we construct the branched continued fraction expansions of Horn’s hypergeometric function $H_3$ ratios and investigate their convergence.

Horn hypergeometric function $H_3$ [11] is defined by double power series

$$H_3(a,b;c;\mathbf{z})=\sum _{m,n=0}^{\infty }\frac{{(a)}_{2m+n}{(b)}_n}{{(c)}_{m+n}}\frac{z_1^m}{m!}\frac{z_2^n}{n!},|z_1|<r,|z_2|<s,r+{\left(s-\frac{1}{2}\right)}^2=\frac{1}{4},$$

(1)

where a, b and c are complex constants, c is not equal to a non-positive integer, $\mathbf{z}=(z_1,z_2)\in {\mathbb{C}}^2,$ ${(·)}_k$ is the Pochhammer symbol defined for any complex number $\alpha$ and non-negative integers k by ${(\alpha )}_0=1$ and ${(\alpha )}_k=\alpha (\alpha +1)\dots (\alpha +k-1).$

Branched continued fractions are one of the multidimensional generalizations of continued fractions and are used, in particular, in numerical theory to express algebraic irrational numbers, in computational mathematics for the solution of systems of linear algebraical equations, in analysis for approximating functions of several variables [12,13,14].

Let $i(k)=(i_1,i_2,\dots ,i_k)$ be a multiindex and let

$$\mathcal{I}=\{i(k):i_r=1,2,1\le r\le k,k\ge 1\}$$

be a set of multiindices. Holomorphic functions of two complex variables $z_1$ and $z_2$ can be represented by various generalizations of continued fractions, in particular, branched continued fractions of the form

$$b_0(\mathbf{z})+\sum _{i_1=1}^2\frac{a_{i(1)}(\mathbf{z})}{b_{i(1)}(\mathbf{z})}\genfrac{}{}{0pt}{}{}{+}\sum _{i_2=1}^2\frac{a_{i(2)}(\mathbf{z})}{b_{i(2)}(\mathbf{z})}\genfrac{}{}{0pt}{}{}{+}\dots \genfrac{}{}{0pt}{}{}{+}\sum _{i_k=1}^2\frac{a_{i(k)}(\mathbf{z})}{b_{i(k)}(\mathbf{z})}\genfrac{}{}{0pt}{}{}{+}\dots ,$$

(2)

where the $b_0(\mathbf{z})$ and the elements $a_{i(k)}(\mathbf{z})$ and $b_{i(k)}(\mathbf{z}),$ $i(k)\in \mathcal{I},$ are certain polynomials (see [15,16]). Other constructions of branched continued fractions are considered in [9,17,18,19,20,21].

The paper is organized as follows. In Section 2, we construct the formal branched continued fraction expansions of the Horn’s hypergeometric function $H_3$ ratios. The construction of the expansions is based on the recurrence relations of the Horn hypergeometric functions $H_3.$ In Section 3, we derive some convergence criteria for the above-mentioned branched continued fractions. Here is also a proof that the branched continued fraction expansions converge to the functions which are an analytic continuation of Horn’s hypergeometric function $H_3$ ratios in some domain (here, domain is an open connected set). Finally, in Section 4, we consider the application for some system of partial differential equations.

2. Expansions

The problem of constructing the expansion of the ratio of hypergeometric series of one or several variables by means of a branched continued fraction is to obtain the simplest structure of a branched continued fraction expansion whose elements are simple polynomials. The various structures of the branched continued fractions have been given in [22] for ratios of contiguous hypergeometric series, in [5,23] for ratios of Lauricella hypergeometric functions, in [16,17] for ratios of Appell hypergeometric functions, and in [10] for ratios of Lauricella–Saran hypergeometric functions.

In the section, we will construct two formal expansions of the ratios of Horn hypergeometric functions $H_3$ by means of branched continued fractions of the form (2). The question of the convergence of branched continued fraction expansions to the ratios will be considered in Section 3.

2.1. Recurrence Relations of Horn Hypergeometric Functions $H_3$

To construct the expansion of the ratio of hypergeometric series of one or several variables, the recurrence relations between these series are used. Here, we give the necessary three- and four-term recurrence relations of Horn hypergeometric functions $H_3.$

By direct verification, the following recurrence relations hold

$$\begin{array}{cc}\hfill H_3(a,b;c;\mathbf{z})=& H_3(a+1,b;c;\mathbf{z})\hfill \\ \hfill & -\frac{2(a+1)}{c}{z}_1{H}_3(a+2,b;c+1;\mathbf{z})-\frac{b}{c}{z}_2{H}_3(a+1,b+1;c+1;\mathbf{z}),\hfill \end{array}$$

(3)

$$H_3(a,b;c;\mathbf{z})=H_3(a,b+1;c;\mathbf{z})-\frac{a}{c}{z}_2{H}_3(a+1,b+1;c+1;\mathbf{z}),$$

(4)

$$\begin{array}{cc}\hfill H_3(a,b;c;\mathbf{z})=& \frac{a}{2c}{H}_3(a+1,b;c+1;\mathbf{z})\hfill \\ \hfill & +\frac{b}{2c}{H}_3(a,b+1;c+1;\mathbf{z})+\frac{2c-a-b}{2c}{H}_3(a,b;c+1;\mathbf{z}),\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill H_3(a,b;c;\mathbf{z})=& H_3(a+1,b;c+1;\mathbf{z})-\frac{(2c-a)(a+1)}{c(c+1)}{z}_1{H}_3(a+2,b;c+2;\mathbf{z})\hfill \\ \hfill & -\frac{b(c-a)}{c(c+1)}{z}_2{H}_3(a+1,b+1;c+2;\mathbf{z}).\hfill \end{array}$$

(6)

Indeed, let us show, for example, the validity of the relation (6). We have

$$\begin{array}{cc}\hfill H_3(a,b;c;\mathbf{z})-& H_3(a+1,b;c+1;\mathbf{z})\hfill \\ \hfill =& \sum _{m,n=0}^{\infty }\frac{{(a)}_{2m+n}{(b)}_n}{{(c)}_{m+n}}\frac{z_1^m}{m!}\frac{z_2^n}{n!}-\sum _{m,n=0}^{\infty }\frac{{(a+1)}_{2m+n}{(b)}_n}{{(c+1)}_{m+n}}\frac{z_1^m}{m!}\frac{z_2^n}{n!}\hfill \\ \hfill =& \sum _{\begin{array}{c}m\ge 0,n\ge 0\\ m+n\ne 0\end{array}}\left(\frac{a}{c}-\frac{a+2m+n}{c+m+n}\right)\frac{{(a+1)}_{2m+n-1}{(b)}_n}{{(c+1)}_{m+n-1}}\frac{z_1^m}{m!}\frac{z_2^n}{n!}\hfill \\ \hfill =& -\sum _{\begin{array}{c}m\ge 0,n\ge 0\\ m+n\ne 0\end{array}}\frac{m(2c-a)+n(c-a)}{c(c+m+n)}\frac{{(a+1)}_{2m+n-1}{(b)}_n}{{(c+1)}_{m+n-1}}\frac{z_1^m}{m!}\frac{z_2^n}{n!}\hfill \\ \hfill =& -\frac{(2c-a)(a+1)}{c(c+1)}{z}_1\sum _{\begin{array}{c}m\ge 1,n\ge 0\end{array}}\frac{{(a+2)}_{2m+n-2}{(b)}_n}{{(c+2)}_{m+n-1}}\frac{z_1^{m-1}}{(m-1)!}\frac{z_2^n}{n!}\hfill \\ & -\frac{b(c-a)}{c(c+1)}{z}_2\sum _{\begin{array}{c}m\ge 0,n\ge 1\end{array}}\frac{{(a+1)}_{2m+n-1}{(b+1)}_{n-1}}{{(c+2)}_{m+n-1}}\frac{z_1^m}{m!}\frac{z_2^{n-1}}{(n-1)!}.\hfill \end{array}$$

Next, in view of Formula (1), we directly obtain the relation (6).

From the relations (3) and (4) it follows

$$\begin{array}{cc}\hfill H_3(a+1,b;c;\mathbf{z})=& H_3(a,b+1;c;\mathbf{z})+\frac{2(a+1)}{c}{z}_1{H}_3(a+2,b;c+1;\mathbf{z})\hfill \\ \hfill & +\frac{b-a}{c}{z}_2{H}_3(a+1,b+1;c+1;\mathbf{z}).\hfill \end{array}$$

(7)

2.2. Branched Continued Fraction Expansions

We set

$$R_k(a,b;c;\mathbf{z})=\frac{H_3(a,b;c;\mathbf{z})}{H_3(a+{\delta }_k^1,b+{\delta }_k^2;c+1;\mathbf{z})},k=1,2,$$

(8)

where ${\delta }_k^j$ is the Kronecker delta. Then from (6) it follows

$$R_1(a,b;c;\mathbf{z})=1-\frac{(2c-a)(a+1)z_1}{c(c+1)R_1(a+1,b;c+1;\mathbf{z})}-\frac{(c-a)b{z}_2}{c(c+1)R_2(a+1,b;c+1;\mathbf{z})}.$$

(9)

Use the relations (4), (5) and (7) gives

$$\begin{array}{cc}\hfill R_2(a+1,b;c;\mathbf{z})=& R_1(a,b+1;c;\mathbf{z})+\frac{b-a}{c}{z}_2+\frac{2(a+1)}{c}{z}_1\frac{H_3(a+2,b;c+1;\mathbf{z})}{H_3(a+1,b+1;c+1;\mathbf{z})}\hfill \\ \hfill =& R_1(a,b+1;c;\mathbf{z})+\frac{b-a}{c}{z}_2+4z_1{R}_2(a+1,b;c;\mathbf{z})\hfill \\ & -4z_1\left(\frac{b}{2c}+\frac{2c-a-b-1}{2c}\frac{H_3(a+1,b;c+1;\mathbf{z})}{H_3(a+1,b+1;c+1;\mathbf{z})}\right)\hfill \\ \hfill =& R_1(a,b+1;c;\mathbf{z})+\frac{b-a}{c}{z}_2+4z_1{R}_2(a+1,b;c;\mathbf{z})-\frac{2b}{c}{z}_1\hfill \\ \hfill & -\frac{2(2c-a-b-1)}{c}{z}_1\left(1-\frac{a+1}{c+1}{z}_2\frac{H_3(a+2,b+1;c+2;\mathbf{z})}{H_3(a+1,b+1;c+1;\mathbf{z})}\right)\hfill \\ \hfill =& 1-\frac{(2c-a)(a+1)z_1}{c(c+1)R_1(a+1,b+1;c+1;\mathbf{z})}-\frac{(c-a)(b+1)z_2}{c(c+1)R_2(a+1,b+1;c+1;\mathbf{z})}\hfill \\ \hfill & -\frac{2(2c-a-1)}{c}{z}_1+\frac{b-a}{c}{z}_2+4z_1{R}_2(a+1,b;c;\mathbf{z})\hfill \\ & +\frac{2(2c-a-b-1)(a+1)z_1{z}_2}{c(c+1)R_1(a+1,b+1;c+1;\mathbf{z})}\hfill \\ \hfill =& 1-\frac{2(2c-a-1)}{c}{z}_1+\frac{b-a}{c}{z}_2-\frac{(a+1)(2c-a-2(2c-a-b-1)z_2)z_1}{c(c+1)R_1(a+1,b+1;c+1;\mathbf{z})}\hfill \\ \hfill & -\frac{(c-a)(b+1)z_2}{c(c+1)R_2(a+1,b+1;c+1;\mathbf{z})}+4z_1{R}_2(a+1,b;c;\mathbf{z}).\hfill \end{array}$$

Hence

$$\begin{array}{c}(1-4z_1)R_2(a+1,b;c;\mathbf{z})=1-\frac{2(2c-a-1)}{c}{z}_1+\frac{b-a}{c}{z}_2\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-\frac{(a+1)(2c-a-2(2c-a-b-1)z_2)z_1}{c(c+1)R_1(a+1,b+1;c+1;\mathbf{z})}-\frac{(c-a)(b+1)z_2}{c(c+1)R_2(a+1,b+1;c+1;\mathbf{z})},\end{array}$$

that is

$$\begin{array}{c}(1-4z_1)R_2(a,b;c;\mathbf{z})=1-\frac{2(2c-a)}{c}{z}_1+\frac{b-a+1}{c}{z}_2\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-\frac{a(2c-a+1-2(2c-a-b)z_2)z_1}{c(c+1)R_1(a,b+1;c+1;\mathbf{z})}-\frac{(c-a+1)(b+1)z_2}{c(c+1)R_2(a,b+1;c+1;\mathbf{z})}.\end{array}$$

(10)

For convenience, we now write relations (9) and (10) as follows

$$\begin{array}{cc}(1-4z_1{\delta }_{i_0}^2)R_{i_0}(a,b;c;\mathbf{z})=\hfill & 1+\left(\frac{b-a+1}{c}{z}_2-\frac{2(2c-a)}{c}{z}_1\right){\delta }_{i_0}^2\hfill \\ \hfill & -\frac{(a+{\delta }_{i_0}^1)(2c-a+{\delta }_{i_0}^2-2(2c-a-b)z_2{\delta }_{i_0}^2)z_1}{c(c+1)R_1(a+{\delta }_{i_0}^1,b+{\delta }_{i_0}^2;c+1;\mathbf{z})}-\frac{(c-a+{\delta }_{i_0}^2)(b+{\delta }_{i_0}^2)z_2}{c(c+1)R_2(a+{\delta }_{i_0}^1,b+{\delta }_{i_0}^2;c+1;\mathbf{z})},\hfill \end{array}$$

(11)

where $i_0=1,2.$ Hence, for $i_1=1,2$ we obtain

$$\begin{array}{cc}\hfill (1-4z_1{\delta }_{i_1}^2)& R_{i_1}(a+{\delta }_{i_0}^1,b+{\delta }_{i_0}^2;c+1;\mathbf{z})\hfill \\ \hfill =& 1+\left(\frac{b-a+1-{\delta }_{i_0}^1+{\delta }_{i_0}^2}{c+1}{z}_2-\frac{2(2c-a+2-{\delta }_{i_0}^1)}{c+1}{z}_1\right){\delta }_{i_1}^2\hfill \\ \hfill & -\frac{(2c-a+2-{\delta }_{i_0}^1+{\delta }_{i_1}^2-2(2c-a-b+2-{\delta }_{i_0}^1-{\delta }_{i_0}^2)z_2{\delta }_{i_1}^2)(a+{\delta }_{i_0}^1+{\delta }_{i_1}^1)z_1}{(c+1)(c+2)R_1(a+{\delta }_{i_0}^1+{\delta }_{i_1}^1,b+{\delta }_{i_0}^2+{\delta }_{i_1}^2;c+2;\mathbf{z})}\hfill \\ \hfill & -\frac{(c-a+1-{\delta }_{i_0}^1+{\delta }_{i_1}^2)(b+{\delta }_{i_0}^2+{\delta }_{i_1}^2)z_2}{(c+1)(c+2)R_2(a+{\delta }_{i_0}^1+{\delta }_{i_1}^1,b+{\delta }_{i_0}^2+{\delta }_{i_1}^2;c+2;\mathbf{z})},\hfill \end{array}$$

(12)

and for each $k\ge 2$ and for $i_k=1,2$ we have

$$\begin{array}{cc}\hfill (1-4z_1{\delta }_{i_k}^2)& R_{i_k}\left(a+\sum _{r=0}^{k-1}{\delta }_{i_r}^1,b+\sum _{r=0}^{k-1}{\delta }_{i_r}^2;c+k;\mathbf{z}\right)\hfill \\ \hfill =& 1+\left(\frac{b-a+1+{\sum }_{r=0}^{k-1}({\delta }_{i_r}^2-{\delta }_{i_r}^1)}{c+k}{z}_2-\frac{2(2c-a+2k-{\sum }_{r=0}^{k-1}{\delta }_{i_r}^1)}{c+k}{z}_1\right){\delta }_{i_k}^2\hfill \\ \hfill & -\frac{(2c-a+k+{\sum }_{r=0}^k{\delta }_{i_r}^2-2z_2{\delta }_{i_k}^2(2c-a-b+k))(a+{\sum }_{r=0}^k{\delta }_{i_r}^1)z_1}{(c+k)(c+k+1)R_1(a+{\sum }_{r=0}^k{\delta }_{i_r}^1,b+{\sum }_{r=0}^k{\delta }_{i_r}^2;c+k+1;\mathbf{z})}\hfill \\ \hfill & -\frac{(c-a+{\sum }_{r=0}^k{\delta }_{i_r}^2)(b+{\sum }_{r=0}^k{\delta }_{i_r}^2)z_2}{(c+k)(c+k+1)R_2(a+{\sum }_{r=0}^k{\delta }_{i_r}^1,b+{\sum }_{r=0}^k{\delta }_{i_r}^2;c+k+1;\mathbf{z})}.\hfill \end{array}$$

(13)

Next, we will construct branched continued fraction expansions for $(1-4z_1{\delta }_{i_0}^2)R_{i_0}$ $(a,b;c;\mathbf{z}),$ where $i_0=1,2.$ Using relations (12) from (11) on the first step, for $i_0=1,2$ we obtain

$$\begin{array}{cc}\hfill (1-4z_1{\delta }_{i_0}^2)& R_{i_0}(a,b;c;\mathbf{z})\hfill \\ \hfill =& d_0(\mathbf{z})+\frac{c_1(\mathbf{z})}{d_1(\mathbf{z})+{\displaystyle \frac{c_{11}(\mathbf{z})}{R_1(a+2,b;c+1;\mathbf{z})}}+{\displaystyle \frac{c_{12}(\mathbf{z})}{(1-4z_1)R_2(a+1,b+1;c+1;\mathbf{z})}}}\hfill \\ \hfill & +\frac{c_2(\mathbf{z})}{d_2(\mathbf{z})+{\displaystyle \frac{c_{21}(\mathbf{z})}{R_1(a+1,b+1;c+1;\mathbf{z})}}+{\displaystyle \frac{c_{22}(\mathbf{z})}{(1-4z_1)R_2(a,b+2;c+1;\mathbf{z})}}},\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill d_0(\mathbf{z})& =1+\left(\frac{b+1-a}{c}{z}_2-\frac{2(2c-a)}{c}{z}_1\right){\delta }_{i_0}^2,\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill c_1(\mathbf{z})& =-\frac{(2c-a+{\delta }_{i_0}^2-2(2c-a-b)z_2{\delta }_{i_0}^2)(a+{\delta }_{i_0}^1)z_1}{c(c+1)},\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill c_2(\mathbf{z})& =-\frac{(c-a+{\delta }_{i_0}^2)(b+{\delta }_{i_0}^2)(1-4z_1)z_2}{c(c+1)},\hfill \end{array}$$

(16)

and for $k=1$ and for $i_1=1,2$

$$\begin{array}{cc}\hfill d_{i(k)}(\mathbf{z})& =1+\left(\frac{(b-a+1+{\sum }_{r=0}^{k-1}({\delta }_{i_r}^2-{\delta }_{i_r}^1))z_2}{c+k}-\frac{2(2c-a+k+{\sum }_{r=0}^{k-1}{\delta }_{i_r}^2)z_1}{c+k}\right){\delta }_{i_k}^2,\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill c_{i(k),1}(\mathbf{z})& =-\frac{(2c-a+k+{\sum }_{r=0}^k{\delta }_{i_r}^2-2(2c-a-b+k)z_2{\delta }_{i_k}^2)(a+{\sum }_{r=0}^k{\delta }_{i_r}^1)z_1}{(c+k)(c+k+1)},\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill c_{i(k),2}(\mathbf{z})& =-\frac{(c-a+{\sum }_{r=0}^k{\delta }_{i_r}^2)(b+{\sum }_{r=0}^k{\delta }_{i_r}^2)(1-4z_1)z_2}{(c+k)(c+k+1)}.\hfill \end{array}$$

(19)

Hence, applying recurrence relations (13) after n-th steps, we get

$$\begin{array}{c}(1-4z_1{\delta }_{i_0}^2)R_{i_0}(a,b,c;\mathbf{z})=d_0(\mathbf{z})+\sum _{i_1=1}^2\frac{c_{i(1)}(\mathbf{z})}{d_{i(1)}(\mathbf{z})}\genfrac{}{}{0pt}{}{}{+}\sum _{i_2=1}^2\frac{c_{i(2)}(\mathbf{z})}{d_{i(2)}(\mathbf{z})}\genfrac{}{}{0pt}{}{}{+}\dots \genfrac{}{}{0pt}{}{}{+}\sum _{i_{n-1}=1}^2\frac{c_{i(n-1)}(\mathbf{z})}{d_{i(n-1)}(\mathbf{z})}\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\genfrac{}{}{0pt}{}{}{+}\sum _{i_n=1}^2\frac{c_{i(n)}(\mathbf{z})}{(1-4z_1{\delta }_{i_n}^2)R_{i_n}(a+{\sum }_{r=0}^{n-1}{\delta }_{i_r}^1,b+{\sum }_{r=0}^{n-1}{\delta }_{i_r}^2;c+n;\mathbf{z})},\end{array}$$

(20)

where $d_0(\mathbf{z}),$ $c_1(\mathbf{z})$ and $d_2(\mathbf{z})$ are defined by (14)–(16), $d_{i(k)}(\mathbf{z}),$ $c_{i(k),1}(\mathbf{z})$ and $c_{i(k),2}(\mathbf{z})$, $i(k)\in \mathcal{I},$ $1\le k\le n-1,$ are defined by (17)–(19). In the right part (20) there are two different finite branched continued fractions: one for $i_0=1$ and the other for $i_0=2.$ Finally, by the relations (13), one obtains the branched continued fraction expansions for $i_0=1,2$

$$(1-4z_1{\delta }_{i_0}^2)R_{i_0}(a,b,c;\mathbf{z})\sim d_0(\mathbf{z})+\sum _{i_1=1}^2\frac{c_{i(1)}(\mathbf{z})}{d_{i(1)}(\mathbf{z})}\genfrac{}{}{0pt}{}{}{+}\sum _{i_2=1}^2\frac{c_{i(2)}(\mathbf{z})}{d_{i(2)}(\mathbf{z})}\genfrac{}{}{0pt}{}{}{+}\dots \genfrac{}{}{0pt}{}{}{+}\sum _{i_k=1}^2\frac{c_{i(k)}(\mathbf{z})}{d_{i(k)}(\mathbf{z})}\genfrac{}{}{0pt}{}{}{+}\dots ,$$

(21)

where the symbol∼denotes a formal expansion, $d_0(\mathbf{z}),$ $c_{i(k)}(\mathbf{z})$ and $d_{i(k)}(\mathbf{z}),$ $i(k)\in \mathcal{I},$ are defined by (14)–(19).

Remark 1.

In (21) there are two different branched continued fraction expansions: one for $i_0=1$ and the other for $i_0=2.$

Remark 2.

If $i_0=1,$ then

$$\begin{array}{cc}\hfill R_1(a,b,c;z_1,0)& =\frac{H_3(a,b;c;z_1,0)}{H_3(a+1,b;c+1;z_1,0)}\hfill \\ \hfill & =\frac{{}_2{F}_1(a/2,(a+1)/2;c;4z_1)}{{}_2{F}_1((a+1)/2,(a+2)/2;c+1;4z_1)}\hfill \\ \hfill & =1-\frac{e_1{z}_1}{1}\genfrac{}{}{0pt}{}{}{-}\frac{e_2{z}_1}{1}\genfrac{}{}{0pt}{}{}{-}\dots \genfrac{}{}{0pt}{}{}{-}\frac{e_k{z}_1}{1}\genfrac{}{}{0pt}{}{}{-}\dots ,|arg(z_1-1)|<\pi ,z_2=0,\hfill \end{array}$$

where ${}_2{F}_1(a,b;c;z)$ is a hypergeometric series, $e_k=(2c-a+k-1)(a+k)/((c+k-1)(c+k)),$ $k\ge 1,$ and, if $i_0=2,$ then

$$\begin{array}{cc}\hfill R_2(a,b,c;0,z_2)& =\frac{H_3(a,b;c;0,z_2)}{H_3(a,b+1;c+1;0,z_2)}\hfill \\ \hfill & =\frac{{}_2{F}_1(a,b;c;z_2)}{{}_2{F}_1(a,b+1;c+1;z_2)}\hfill \\ \hfill & =1+q_0{z}_2-\frac{p_1{z}_2}{1+q_1{z}_2}\genfrac{}{}{0pt}{}{}{-}\frac{p_2{z}_2}{1+q_2{z}_2}\genfrac{}{}{0pt}{}{}{-}\dots \genfrac{}{}{0pt}{}{}{-}\frac{p_k{z}_2}{1+q_k{z}_2}\genfrac{}{}{0pt}{}{}{-}\dots ,z_1=0,|z_2|>1,\hfill \end{array}$$

where $p_k=(c-a+k)(b+k)/((c+k-1)(c+k)),$ $q_{k-1}=(b-a+k)/(c+k-1),$ $k\ge 1.$ These are, on the one hand, two confluent branched continued fraction expansions and, on the other, two known continued fraction expansions, called respectively regular C-fraction [24] and general T-fraction [25] (more about it see [26,27,28,29]).

3. Convergence

Central to the theory of branched continued fractions is their problem of convergence. Various methods are used to prove the convergence of branched continued fractions, in particular, methods using the theorem on the continuation of convergence from an already known small domain to a larger [6,30], the value set technique for branched continued fraction [31], the even part of another branched continued fraction [32], the difference formula between its two approximants [33,34,35,36,37], and induction by dimension of a branched continued fraction [36,38,39].

In the section, we will set a some convergence criteria for branched continued fraction

$$d_0(\mathbf{z})+\sum _{i_1=1}^2\frac{c_{i(1)}(\mathbf{z})}{d_{i(1)}(\mathbf{z})}\genfrac{}{}{0pt}{}{}{+}\sum _{i_2=1}^2\frac{c_{i(2)}(\mathbf{z})}{d_{i(2)}(\mathbf{z})}\genfrac{}{}{0pt}{}{}{+}\dots \genfrac{}{}{0pt}{}{}{+}\sum _{i_k=1}^2\frac{c_{i(k)}(\mathbf{z})}{d_{i(k)}(\mathbf{z})}\genfrac{}{}{0pt}{}{}{+}\dots ,$$

(22)

where $d_0(\mathbf{z}),$ $c_{i(k)}(\mathbf{z})$ and $d_{i(k)}(\mathbf{z}),$ $i(k)\in \mathcal{I},$ defined by (14)–(19) with $i_0$ equals to 1 and/or $2.$

3.1. Definitions and Preliminaries

Let $Q_{i(k)}^{(n)}(\mathbf{z})$ denote the ‘tails’ of branched continued fraction (22), that is

$$Q_{i(n)}^{(n)}(\mathbf{z})=d_{i(n)}(\mathbf{z}),i(n)\in \mathcal{I},n\ge 1,$$

(23)

and

$$Q_{i(k)}^{(n)}(\mathbf{z})=d_{i(k)}(\mathbf{z})+\sum _{i_{k+1}=1}^2\frac{c_{i(k+1)}(\mathbf{z})}{d_{i(k+1)}(\mathbf{z})}\genfrac{}{}{0pt}{}{}{+}\sum _{i_{k+2}=1}^2\frac{c_{i(k+2)}(\mathbf{z})}{d_{i(k+2)}(\mathbf{z})}\genfrac{}{}{0pt}{}{}{+}\dots \genfrac{}{}{0pt}{}{}{+}\sum _{i_n=1}^2\frac{c_{i(n)}(\mathbf{z})}{d_{i(n)}(\mathbf{z})},$$

(24)

where $i(k)\in \mathcal{I},$ $1\le k\le n-1,$ $n\ge 2.$ It is clear that the following recurrence relations hold

$$Q_{i(k)}^{(n)}(\mathbf{z})=d_{i(k)}(\mathbf{z})+\sum _{i_{k+1}=1}^2\frac{c_{i(k+1)}(\mathbf{z})}{Q_{i(k+1)}^{(n)}(\mathbf{z})},i(k)\in \mathcal{I},1\le k\le n-1,n\ge 2.$$

(25)

If $f_n(\mathbf{z})$ denotes the n-th approximant of (22), then

$$\begin{array}{cc}\hfill f_n(\mathbf{z})& =d_0(\mathbf{z})+\sum _{i_1=1}^2\frac{c_{i(1)}(\mathbf{z})}{d_{i(1)}(\mathbf{z})}\genfrac{}{}{0pt}{}{}{+}\sum _{i_2=1}^2\frac{c_{i(2)}(\mathbf{z})}{d_{i(2)}(\mathbf{z})}\genfrac{}{}{0pt}{}{}{+}\dots \genfrac{}{}{0pt}{}{}{+}\sum _{i_n=1}^2\frac{c_{i(n)}(\mathbf{z})}{d_{i(n)}(\mathbf{z})}\hfill \\ & =d_0(\mathbf{z})+\sum _{i_1=1}^2\frac{c_{i(1)}(\mathbf{z})}{Q_{i(1)}^{(n)}(\mathbf{z})},n\ge 1.\hfill \end{array}$$

The branched continued fraction (22) is said to converge at $\mathbf{z}={\mathbf{z}}^0$ if its sequence of approximants $\left\{f_n({\mathbf{z}}^0)\right\}$ converges, and

$$\underset{n\to \infty }{lim}{f}_n({\mathbf{z}}^0)$$

is called its value.

The branched continued fraction (22), whose elements are functions of two variables in the certain domain $D,$ $D\subset {\mathbb{C}}^2,$ is called uniformly convergent on set $E,$ $E\subset D,$ if its sequence of approximants $\{f_n(\mathbf{z})\}$ converges uniformly on $E.$ When this occurs for an arbitrary set E such that $\overline{E}\subset D$ (here $\overline{E}$ is the closure of the set E) we say that the branched continued fraction converges uniformly on every compact subset of $D.$

If $Q_{i(k)}^{(n)}(\mathbf{z})\not\equiv 0$ for all $i(k)\in \mathcal{I},$ $1\le k\le n,$ $n\ge 1,$ then for each $m>n\ge 1$ the following formula is valid (see ([12], p. 28))

$$f_m(\mathbf{z})-f_n(\mathbf{z})={(-1)}^n\sum _{i_1=1}^2\frac{c_{i(1)}(\mathbf{z})}{Q_{i(1)}^{(m)}(\mathbf{z})Q_{i(1)}^{(n)}(\mathbf{z})}\dots \sum _{i_n=1}^2\frac{c_{i(n)}(\mathbf{z})}{Q_{i(n)}^{(m)}(\mathbf{z})Q_{i(n)}^{(n)}(\mathbf{z})}\sum _{i_{n+1}=1}^2\frac{c_{i(n+1)}(\mathbf{z})}{Q_{i(n+1)}^{(m)}(\mathbf{z})}.$$

(26)

Let

$$L(\mathbf{z})=\sum _{k,l=0}^{\infty }{a}_{k,l}{z}_1^k{z}_2^l,$$

where $a_{k,l}\in \mathbb{C},$ $k\ge 0,$ $l\ge 0,$ $\mathbf{z}\in {\mathbb{C}}^2,$ be a formal double power series at $\mathbf{z}=\mathbf{0}.$ Let $F(\mathbf{z})$ be function holomorphic in a neighbourhood of the origin $(\mathbf{z}=\mathbf{0}).$ Let the mapping $\Lambda :F(\mathbf{z})\to \Lambda (F)$ associate with $F(\mathbf{z})$ its Taylor expansion in a neighbourhood of the origin.

A sequence $\left\{F_n(\mathbf{z})\right\}$ of functions holomorphic at the origin is said to correspond at $\mathbf{z}=\mathbf{0}$ to a formal double power series $L(\mathbf{z})$ if

$$\underset{n\to \infty }{lim}\lambda \left(L-\Lambda (F_n)\right)=\infty ,$$

where $\lambda$ is the function defined as follows: $\lambda :\mathbb{L}\to {\mathbb{Z}}_{\ge 0}\cup \{\infty \}$; if $L(\mathbf{z})\equiv 0$ then $\lambda (L)=\infty ;$ if $L(\mathbf{z})\not\equiv 0$ then $\lambda (L)=m,$ where m is the smallest degree of homogeneous terms for which $a_{k,l}\ne 0,$ that is $m=k+l.$

If $\left\{F_n(\mathbf{z})\right\}$ corresponds at $\mathbf{z}=\mathbf{0}$ to a formal double power series $L(\mathbf{z}),$ then the order of correspondence of $F_n(\mathbf{z})$ is defined to be

$${\nu }_n=\lambda \left(L-\Lambda (F_n)\right).$$

By the definition of $\lambda ,$ the series $L(\mathbf{z})$ and $\Lambda (F_n)$ agree for all homogeneous terms up to and including degree $({\nu }_n-1).$

A branched continued fraction is said to correspond at $\mathbf{z}=\mathbf{0}$ to a formal double power series $L(\mathbf{z})$ if its sequence of approximants corresponds to $L(\mathbf{z}).$

3.2. Convergence of Branched Continued Fractions with Elements in ${\mathbb{R}}^2$

We will prove the following result.

Theorem 1.

Let (22) be a branched continued fraction with $d_0(\mathbf{z}),$ $c_{i(k)}(\mathbf{z}),$ and $d_{i(k)}(\mathbf{z}),$ $i(k)\in \mathcal{I},$ defined by (14)–(19) for $i_0=1,2,$ and such that

$$c\ge a\ge 0,2c\ge a+b,andb\ge 0.$$

(27)

Then for each $L>0$ the branched continued fraction (22) converges to a finite value $f(\mathbf{z})$ for each $\mathbf{z}\in D_L,$ where

$$D_L=\{\mathbf{z}\in {\mathbb{R}}^2:-L\le 2z_1\le z_2\le 0\},$$

(28)

and it converges uniformly on every compact subset of an interior of $D_L.$ If $f_n(\mathbf{z})$ denotes the n-th approximant of the branched continued fraction (22), then for each $n\ge 1$ and for each $L>0$

$$|f(\mathbf{z})-f_n(\mathbf{z})|\le \frac{{(2M)}^{n+1}}{{(1+2M)}^n}forall\mathbf{z}\in D_L,$$

(29)

where $M=L(1+2L)max\{(1+b)/c;1\}.$

Remark 3.

Just like for continued fraction, we adopt the convention that a branched continued fraction (22) and all of its approximants have value 1 at $\mathbf{z}=\mathbf{0}.$ If $z_1=0$ or $z_2=0$, then (22) is a confluent branched continued fraction, that is, a continued fraction (see Remark 2).

Proof of Theorem 1.

We will find the upper bound of $|f_m(\mathbf{z})-f_n(\mathbf{z})|$ for $m>n\ge 1$ and for $\mathbf{z}\in D_L.$ Let $\mathbf{z}$ be an arbitrary fixed point in (28). From (15), (16), (18), and (19) it is clear that for each $i(k)\in \mathcal{I}$ the elements $c_{i(k)}(\mathbf{z})$ of branched continued fraction (22) take non-negative values in the assumption of this theorem. In addition, use of relations (27) and inequalities in (28) to (17) for any $i(k)\in \mathcal{I}$ leads to

$$\begin{array}{cc}\hfill d_{i(k)}(\mathbf{z})& =1+\left(\frac{b+{\sum }_{r=0}^{k-1}({\delta }_{i_r}^2-{\delta }_{i_r}^1)+1-a}{c+k}{z}_2-\frac{2(2c-a+k+{\sum }_{r=0}^{k-1}{\delta }_{i_k}^2)}{c+k}{z}_1\right){\delta }_{i_r}^2\hfill \\ \hfill & =1-\left(\frac{2c-a+k+{\sum }_{r=0}^{k-1}{\delta }_{i_r}^2}{c+k}(2z_1-z_2)+\frac{2c+k+{\sum }_{r=0}^{k-1}{\delta }_{i_r}^1-b-1}{c+k}{z}_2\right){\delta }_{i_k}^2\hfill \\ \hfill & \ge 1.\hfill \end{array}$$

(30)

Also, let n be an arbitrary integer number, moreover, $n\ge 1.$ Using relations (25) and (30), by induction on k we show that the following inequalities are valid

$$Q_{i(k)}^{(n)}(\mathbf{z})\ge d_{i(k)}(\mathbf{z})\mathrm{for} \mathrm{all}i(k)\in \mathcal{I},1\le k\le n.$$

(31)

For $k=n$ and for each $i(n)\in \mathcal{I}$ inequalities (31) are obvious. By induction hypothesis that (31) hold for $k=r+1,$ where $r+1\le n,$ and for each $i(r+1)\in \mathcal{I},$ we prove (31) for $k=r$ and for all $i(r)\in \mathcal{I}.$ Indeed, use of relations (25) and (30) for any $i(r)\in \mathcal{I}$ lead to

$$\begin{array}{cc}\hfill Q_{i(r)}^{(n)}(\mathbf{z})& =d_{i(r)}(\mathbf{z})+\sum _{i_{r+1}=1}^2\frac{c_{i(r+1)}(\mathbf{z})}{Q_{i(r+1)}^{(n)}(\mathbf{z})}\hfill \\ & \ge d_{i(r)}(\mathbf{z}).\hfill \end{array}$$

From (30) and (31) it follows that $Q_{i(k)}^{(n)}(\mathbf{z})\ne 0$ for all $i(k)\in \mathcal{I},$ $1\le k\le n,$ $n\ge 1,$ and for all $\mathbf{z}\in D_L.$ Therefore, from (26) for each $m>n\ge 1$ and for each $\mathbf{z}\in D_L$ we get

$$\begin{array}{c}\hfill |f_m(\mathbf{z})-f_n(\mathbf{z})|\le \sum _{i_1=1}^2\frac{c_{i(1)}(\mathbf{z})}{Q_{i(1)}^{(r)}(\mathbf{z})}\dots \sum _{i_n=1}^2\frac{c_{i(n)}(\mathbf{z})}{Q_{i(n-1)}^{(n)}(\mathbf{z})Q_{i(n)}^{(n)}(\mathbf{z})}\sum _{i_{n+1}=1}^2\frac{c_{i(n+1)}(\mathbf{z})}{Q_{i(n)}^{(m)}(\mathbf{z})Q_{i(n+1)}^{(m)}(\mathbf{z})},\end{array}$$

(32)

where $r=m,$ if n is even, and $r=n,$ if n is odd.

Let’s estimate the elements $c_{i(k)}(\mathbf{z})$ for $i(k)\in \mathcal{I}$ and for $\mathbf{z}\in D_L.$ Let $\mathbf{z}$ be an arbitrary fixed point in (28). Then, using of relations (27) to (15) we get

$$\begin{array}{cc}\hfill c_1(\mathbf{z})& \le \frac{(2c-a+{\delta }_{i_0}^2+2{\delta }_{i_0}^2|z_2|(2c-a-b))(a+{\delta }_{i_0}^1)}{c(c+1)}|z_1|\hfill \\ & \le L(1+2L),\hfill \end{array}$$

and to (16) lead to

$$\begin{array}{cc}\hfill c_2(\mathbf{z})& \le L(1+2L)\frac{(c-a+1)(b+1)}{c(c+1)}\hfill \\ & \le L(1+2L)\frac{b+1}{c}.\hfill \end{array}$$

Next, from (18) and (19) for $k=1$ and for any $k\ge 2$ and $i(k-1)\in \mathcal{I},$ we have for $i_k=1$

$$\begin{array}{cc}\hfill c_{i(k),1}(\mathbf{z})& \le \frac{(2c-a+2k)(a+k+1)}{(c+k)(c+k+1)}|z_1|\hfill \\ & \le 2|z_1|\le L,\hfill \\ \hfill c_{i(k),2}(\mathbf{z})& \le \frac{(c-a+k)(b+k)}{(c+k)(c+k+1)}(1+4|z_1|)|z_2|\hfill \\ & \le L(1+2L)max\{(1+b)/(2+c);1\},\hfill \end{array}$$

and we obtain for $i_k=2$

$$\begin{array}{cc}\hfill c_{i(k),1}(\mathbf{z})& \le \frac{(2c-a+2k+1+2(2c-a-b+k)|z_2|)(a+k)}{(c+k)(c+k+1)}|z_1|\hfill \\ & \le 2|z_1|(1+2|z_2|)\hfill \\ & \le L(1+2L),\hfill \\ \hfill c_{i(k),2}(\mathbf{z})& \le \frac{(c-a+k+1)(b+k+1)}{(c+k)(c+k+1)}(1+4|z_1|)|z_2|\hfill \\ & \le L(1+2L)\frac{b+k+1}{c+k}\hfill \\ & <L(1+2L)max\{(1+b)/c;1\}.\hfill \end{array}$$

Thus, for all $i(k)\in \mathcal{I}$ and for all $\mathbf{z}\in D_L$

$$c_{i(k)}(\mathbf{z})\le L(1+2L)max\{(1+b)/c;1\}=M.$$

(33)

Let r be an arbitrary integer number, moreover $r\ge 2.$ By relations (25), (30), (31), and (33), for any $k,$ $1\le k\le r-1,$ and $i(k)\in \mathcal{I},$ and for any $\mathbf{z}\in D_L$ we have

$$\begin{array}{cc}\hfill \sum _{i_{k+1}=1}^2\frac{c_{i(k+1)}(\mathbf{z})}{Q_{i(k)}^{(r)}(\mathbf{z})Q_{i(k+1)}^{(r)}(\mathbf{z})}& ={\left(d_{i(k)}(\mathbf{z})+\sum _{i_{k+1}=1}^2\frac{c_{i(k+1)}(\mathbf{z})}{Q_{i(k+1)}^{(r)}(\mathbf{z})}\right)}^{-1}\sum _{i_{k+1}=1}^2\frac{c_{i(k+1)}(\mathbf{z})}{Q_{i(k+1)}^{(r)}(\mathbf{z})}\hfill \\ \hfill & \le \frac{2M}{1+2M}.\hfill \end{array}$$

(34)

Now, by a successive application of inequalities (34) and relations (30) and (33) to (32), for any $m>n\ge 1$ and for any $\mathbf{z}\in D_L$ we arrive at

$$\begin{array}{cc}\hfill |f_m(\mathbf{z})-f_n(\mathbf{z})|& \le {\left(\frac{2M}{1+2M}\right)}^n\sum _{i_1=1}^2\frac{c_{i(1)}(\mathbf{z})}{Q_{i(1)}^{(r)}(\mathbf{z})}\hfill \\ & \le \frac{{(2M)}^{n+1}}{{(1+2M)}^n},\hfill \end{array}$$

where $r=m,$ if n is even, and $r=n,$ if n is odd. It follows that the branched continued fraction (22) converges if $n\to \infty .$ Finally, passing to the limit at $m\to \infty ,$ we obtain the estimates (29). □

Remark 4.

It follows from the proof of Theorem 1 that for every nonzero $\mathbf{z}={\mathbf{z}}^0$ from (28) the (22) is a branched continued fraction with positive elements. This means that (see, ([12], p. 29))

$$f_{2n-2}({\mathbf{z}}^0)<f_{2n}({\mathbf{z}}^0)<f_{2n+1}({\mathbf{z}}^0)<f_{2n-1}({\mathbf{z}}^0),n\ge 1,$$

(here $f_0({\mathbf{z}}^0)=1$), so that the even and odd parts of (22) both converge to finite value $f({\mathbf{z}}^0).$ This system of inequalities expresses a so-called ‘fork property’ for branched continued fractions.

3.3. Convergence of Branched Continued Fractions with Elements in ${\mathbb{C}}^2$

We will prove a theorem.

Theorem 2.

Let (1) be a hypergeometric function $H_3$ with parameters $a,$ $b,$ and c satisfying

$$c\ge a\ge 0,c\ge b\ge 0.$$

(35)

If there exist positive numbers ${\lambda }_1,$ ${\lambda }_2,$ ${\mu }_1,$ ${\mu }_2,$ ${\nu }_1,$ ${\nu }_2,$ and ${\nu }_3$ such that

$$\frac{2{\nu }_1}{{\mu }_1}+\frac{{\nu }_2+4{\nu }_3}{{\mu }_2}\le 2(1-{\mu }_1),\frac{2{\nu }_1+4{\nu }_3}{{\mu }_1}+\frac{{\nu }_2+4{\nu }_3}{{\mu }_2}\le 2(1-2{\lambda }_1-2{\lambda }_2-{\mu }_2),$$

(36)

then:

(A) 

The branched continued fraction (22), where $d_0(\mathbf{z}),$ $c_{i(k)}(\mathbf{z})$ and $d_{i(k)}(\mathbf{z}),$ $i(k)\in \mathcal{I},$ defined by (14)–(19) for $i_0=1,$ converges uniformly on every compact subset of

$$\begin{array}{c}G=\{\mathbf{z}\in {\mathbb{C}}^2:2\mathrm{Re}(z_1)-\mathrm{Re}(z_2)<{\lambda }_1,\mathrm{Re}(z_2)<{\lambda }_2,\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}|z_1{z}_2|-\mathrm{Re}(z_1{z}_2)<{\nu }_3,|z_k|+\mathrm{Re}(z_k)<{\nu }_k,k=1,2\}\end{array}$$

(37)

to a function $f(\mathbf{z})$ holomorphic in $G.$

(B) 

The function $f(\mathbf{z})$ is an analytic continuation of

$$R_1(a,b,c;\mathbf{z})=\frac{H_3(a,b,c;\mathbf{z})}{H_3(a+1,b,c+1;\mathbf{z})}$$

in the domain $G.$

Remark 5.

If

$${\mu }_1=3/5,{\mu }_2=2/5,{\nu }_1=1/20,{\nu }_2=1/5,{\nu }_3=1/200,and{\lambda }_1={\lambda }_2=1/20,$$

(38)

then it is clear that the inequalities (36) hold. In addition, if $z_1=z_2=z,$ then the domain (37) can be written as

$$|y|<1/20,x<-10y^2+1/40,$$

where $x=\mathrm{Re}(z),$ $y=\mathrm{Im}(z).$

In our proof, we will use the auxiliary lemma derived from [5].

Lemma 1.

Let (22) be a branched continued fraction with $d_0(\mathbf{z}),$ $c_{i(k)}(\mathbf{z})$ and $d_{i(k)}(\mathbf{z}),$ $i(k)\in \mathcal{I},$ defined by (14)–(19) with $i_0=1,2.$ Let the elements $c_{i(k)}(\mathbf{z})$ and $d_{i(k)}(\mathbf{z}),$ $i(k)\in \mathcal{I},$ be the functions defined in some domain $D,$ $D\in {\mathbb{C}}^2.$ If there exists positive numbers ${\mu }_1$ and ${\mu }_2$ such that

$$\mathrm{Re}(d_{i(k-1)}(\mathbf{z}))\ge {\mu }_{i_{k-1}}and\sum _{i_k=1}^2\frac{|c_{i(k)}(\mathbf{z})|-\mathrm{Re}(c_{i(k)}(\mathbf{z}))}{2{\mu }_{i_k}}\le \mathrm{Re}(d_{i(k-1)}(\mathbf{z}))-{\mu }_{i_{k-1}}$$

for all $i(k)\in \mathcal{I},$ $k\ge 2,$ and for all $\mathbf{z}\in D,$ then for each $n\ge 1$

$$\mathrm{Re}(Q_{i(k)}^{(n)}(\mathbf{z}))\ge {\mu }_{i_k}for alli(k)\in \mathcal{I},1\le k\le n,andfor all\mathbf{z}\in D,$$

where $Q_{i(k)}^{(n)}(\mathbf{z}),$ $i(k)\in \mathcal{I},$ $1\le k\le n,$ $n\ge 1,$ defined by (23) and (24).

We note that the idea of proving Lemma 4.41 [27] is essentially used in proving this result. In addition, we will use the convergence continuation theorem, which immediately follows from Theorem 2.17 [12] (see also ([29], Theorem 24.2)).

Theorem 3.

Let $\left\{f_n(\mathbf{z})\right\}$ be a sequence of functions, holomorphic in the domain $D,$ $D\subset {\mathbb{C}}^2,$ which is uniform bounded on every compact subset of $D.$ Let the sequence converge at each point of the set $E,$ $E\subset D,$ which is the real neighborhood of the point ${\mathbf{z}}^0$ in $D,$ i.e.,

$$R({\mathbf{z}}^0,r)=\{\mathbf{z}\in {\mathbb{C}}^2:|\mathbf{z}-{\mathbf{z}}^0|<r,\mathrm{Im}(\mathbf{z})=\mathrm{Im}({\mathbf{z}}^0)\},r>0.$$

Then, $\left\{f_n(\mathbf{z})\right\}$ converges uniformly on every compact subset of D to a function holomorphic in $D.$

Proof of Theorem 2.

Let $\mathbf{z}$ be an arbitrary fixed point in (37). From (17) it is clear that $\mathrm{Re}(d_{i(k)}(\mathbf{z}))=1$ for each $i(k)\in \mathcal{I}$ such that $i_k=1.$ Moreover, use of relations (35) and inequalities in (37) for any $i(k)\in \mathcal{I}$ such that $i_k=2$ lead to

$$\begin{array}{cc}\hfill \mathrm{Re}(d_{i(k)}(\mathbf{z}))& =1-\frac{2c-a+k+{\sum }_{r=1}^{k-1}{\delta }_{i_r}^2}{c+k}\mathrm{Re}(2z_1-z_2)+\frac{2c+k+{\sum }_{r=1}^{k-1}{\delta }_{i_r}^1-b}{c+k}\mathrm{Re}(z_2)\hfill \\ \hfill & >1-2({\lambda }_1+{\lambda }_2).\hfill \end{array}$$

Now, for any $i(k)\in \mathcal{I}$ from (18) we have

$$\begin{array}{cc}\hfill |c_{i(k),1}(\mathbf{z})|-\mathrm{Re}(c_{i(k),1}(\mathbf{z}))=& \frac{(2c-a+k+{\sum }_{r=1}^k{\delta }_{i_r}^2)(a+{\sum }_{r=0}^k{\delta }_{i_r}^1)}{(c+k)(c+k+1)}(|z_1|+\mathrm{Re}(z_1))\hfill \\ & +\frac{2{\delta }_{i_k}^2(2c-a-b+k)(a+{\sum }_{r=0}^k{\delta }_{i_r}^1)}{(c+k)(c+k+1)}(|z_1{z}_2|-\mathrm{Re}(z_1{z}_2))\hfill \\ \hfill <& 2{\nu }_1+4{\delta }_{i_k}^2{\nu }_3\hfill \end{array}$$

and from (19)

$$\begin{array}{cc}\hfill |c_{i(k),2}(\mathbf{z})|-\mathrm{Re}(c_{i(k),2}(\mathbf{z}))& =\frac{(c-a+{\sum }_{r=1}^k{\delta }_{i_r}^2)(b+{\sum }_{r=1}^k{\delta }_{i_r}^2)}{(c+k)(c+k+1)}(|z_2|+\mathrm{Re}(z_2)+4(|z_1{z}_2|-\mathrm{Re}(z_1{z}_2)))\hfill \\ & <{\nu }_2+4{\nu }_3.\hfill \end{array}$$

Since, as follows from the inequalities (36) that ${\mu }_1<1$ and ${\mu }_2<1-2({\lambda }_1+{\lambda }_2),$ then for any $i(k)\in \mathcal{I}$ such that $i_k=1,$ we obtain

$$\begin{array}{cc}\hfill \sum _{i_{k+1}=1}^2\frac{|c_{i(k+1)}(\mathbf{z})|-\mathrm{Re}(c_{i(k+1)}(\mathbf{z}))}{{\mu }_{i_{k+1}}}& <\frac{2{\nu }_1}{{\mu }_1}+\frac{{\nu }_2+4{\nu }_3}{{\mu }_2}\hfill \\ & \le 2(1-{\mu }_1)\hfill \\ \hfill & =2(\mathrm{Re}(d_{i(k)}(\mathbf{z}))-{\mu }_1),\hfill \end{array}$$

and for any $i(k)\in \mathcal{I}$ such that $i_k=2,$ we get

$$\begin{array}{cc}\hfill \sum _{i_{k+1}=1}^2\frac{|c_{i(k+1)}(\mathbf{z})|-\mathrm{Re}(c_{i(k+1)}(\mathbf{z}))}{{\mu }_{i_{k+1}}}& <\frac{2{\nu }_1+4{\nu }_3}{{\mu }_1}+\frac{{\nu }_2+4{\nu }_3}{{\mu }_2}\hfill \\ & \le 2(1-2({\lambda }_1+{\lambda }_2)-{\mu }_2)\hfill \\ & <2(\mathrm{Re}(d_{i(k)}(\mathbf{z}))-{\mu }_2).\hfill \end{array}$$

Thus, by Lemma 1, for each $n\ge 1$ the following inequalities hold

$$\mathrm{Re}(Q_{i(k)}^{(n)}(\mathbf{z}))>{\mu }_{i_k}>0\mathrm{for} \mathrm{all}i(k)\in \mathcal{I},1\le k\le n,\mathrm{and}\mathrm{for} \mathrm{all}\mathbf{z}\in G,$$

(39)

where $Q_{i(k)}^{(n)}(\mathbf{z}),$ $i(k)\in \mathcal{I},$ $1\le k\le n,$ $n\ge 1,$ defined by (23) and (24). The approximants $f_n(\mathbf{z}),$ $n\ge 1,$ of (22) form a sequence of functions holomorphic in (37).

Let K is an arbitrary compact subset of (37). Then there exists an open ball around the origin with radius $r,$ containing $K.$ Using inequalities (39), for the arbitrary $\mathbf{z}\in K$ we obtain for any $n\ge 1$

$$\begin{array}{cc}\hfill |f_n(\mathbf{z})|& \le 1+\sum _{k=1}^2\frac{|c_k(\mathbf{z})|}{|Q_{i(k)}^{(n)}(\mathbf{z})|}\hfill \\ & <1+\frac{(2c-a)(a+1)}{c(c+1){\mu }_1}|z_1|+\frac{b(c-a)}{c(c+1){\mu }_2}(1+4|z_1|)|z_2|\hfill \\ & <1+\frac{(2c-a)(a+1)}{c(c+1){\mu }_1}r+\frac{b(c-a)}{c(c+1){\mu }_2}(1+4r)r\hfill \\ & =M(K),\hfill \end{array}$$

i.e., $\left\{f_n(\mathbf{z})\right\}$ is a uniformly bounded sequence on $K.$ Thus, the sequence is uniformly bounded on every compact subset of the domain (37).

It is clear that the elements of (22) satisfy the conditions of Theorem 1, and that the domain $D_L,$ where $D_L$ defined by (28), contains in G for each $L>0.$ It follows from Theorem 1 that (22) converges in $D_L,$ $D_L\subset G.$ Therefore by Theorem 3, the branched continued fraction (22) converges uniformly on compact subsets of G to a function $f(\mathbf{z})$ holomorphic in $G.$ This proves part (A).

Now, we prove the second statement of the theorem. We set

$$\begin{array}{cc}\hfill F_{i(n)}^{(n)}(\mathbf{z})& =(1-4z_1{\delta }_{i_n}^2)R_{i_n}\left(a+\sum _{r=0}^{n-1}{\delta }_{i_r}^1,b+\sum _{r=0}^{n-1}{\delta }_{i_r}^2;c+n;\mathbf{z}\right),i(n)\in \mathcal{I},n\ge 1,\hfill \end{array}$$

(40)

where the expression in the right-hand side is defined by (13), and

$$\begin{array}{c}\hfill F_{i(k)}^{(n)}(\mathbf{z})=d_{i(k)}(\mathbf{z})+\sum _{i_{k+1}=1}^2\frac{c_{i(k+1)}(\mathbf{z})}{d_{i(k+1)}(\mathbf{z})}\genfrac{}{}{0pt}{}{}{+}\sum _{i_{k+2}=1}^2\frac{c_{i(k+2)}(\mathbf{z})}{d_{i(k+2)}(\mathbf{z})}\genfrac{}{}{0pt}{}{}{+}\dots \genfrac{}{}{0pt}{}{}{+}\sum _{i_n=1}^2\frac{c_{i(n)}(\mathbf{z})}{F_{i(n)}^{(n)}(\mathbf{z})},\end{array}$$

where $i(k)\in \mathcal{I},$ $1\le k\le n-1,$ $n\ge 2.$ Then

$$\begin{array}{cc}\hfill F_{i(k)}^{(n)}(\mathbf{z})& =d_{i(k)}(\mathbf{z})+\sum _{i_{k+1}=1}^2\frac{c_{i(k)}(\mathbf{z})}{F_{i(k+1)}^{(n)}(\mathbf{z})}\mathrm{for} \mathrm{all}i(k)\in \mathcal{I},1\le k\le n-1,n\ge 2.\hfill \end{array}$$

(41)

From (13) and (20) it follows that for each $n\ge 1$

$$\begin{array}{cc}\hfill R_1(a,b,c;\mathbf{z})& =d_0(\mathbf{z})+\sum _{i_1=1}^2\frac{c_{i(1)}(\mathbf{z})}{d_{i(1)}(\mathbf{z})}\genfrac{}{}{0pt}{}{}{+}\sum _{i_2=1}^2\frac{c_{i(2)}(\mathbf{z})}{d_{i(2)}(\mathbf{z})}\genfrac{}{}{0pt}{}{}{+}\dots \genfrac{}{}{0pt}{}{}{+}\sum _{i_n=1}^2\frac{c_{i(n)}(\mathbf{z})}{d_{i(n)}(\mathbf{z})}\genfrac{}{}{0pt}{}{}{+}\sum _{i_{n+1}=1}^2\frac{c_{i(n+1)}(\mathbf{z})}{F_{i(n+1)}^{(n+1)}(\mathbf{z})}\hfill \\ \hfill & =d_0(\mathbf{z})+\sum _{i_1=1}^2\frac{c_{i(1)}(\mathbf{z})}{F_{i(1)}^{(n+1)}(\mathbf{z})}.\hfill \end{array}$$

Since $F_{i(k)}^{(n)}(\mathbf{0})=1$ and $Q_{i(k)}^{(n)}(\mathbf{0})=1$ for any $i(k)\in \mathcal{I},$ $1\le k\le n,$ $n\ge 1,$ then there exist $\Lambda (1/F_{i(k)}^{(n)})$ and $\Lambda (1/Q_{i(k)}^{(n)}),$ e.i. the $1/F_{i(k)}^{(n)}$ and $1/Q_{i(k)}^{(n)}$ have Taylor expansions in a neighbourhood of the origin. It is clear that $F_{i(k)}^{(n)}(\mathbf{z})\not\equiv 0$ and $Q_{i(k)}^{(n)}(\mathbf{z})\not\equiv 0$ for all indices. Taking into account (23), (25), (40), and (41) from (26) for each $n\ge 1$ one obtains

$$R_1(a,b,c;\mathbf{z})-f_n(\mathbf{z})={(-1)}^n\sum _{i_1=1}^2\frac{c_{i(1)}(\mathbf{z})}{F_{i(1)}^{(n+1)}(\mathbf{z})Q_{i(1)}^{(n)}(\mathbf{z})}\dots \sum _{i_n=1}^2\frac{c_{i(n)}(\mathbf{z})}{F_{i(n)}^{(n+1)}(\mathbf{z})Q_{i(n)}^{(n)}(\mathbf{z})}\sum _{i_{n+1}=1}^2\frac{c_{i(n+1)}(\mathbf{z})}{F_{i(n+1)}^{(n+1)}(\mathbf{z})}.$$

From this formula in a neighborhood of zero for any $n\ge 1$ we have

$$\Lambda (R_1)-\Lambda (f_n)=\sum _{\begin{array}{c}k+l\ge n\\ k\ge 0,l\ge 0\end{array}}{\alpha }_{k,l}^{(n)}{z}_1^k{z}_2^l,$$

where $a_{k,l}^{(n)},$ $k\ge 0,$ $l\ge 0,$ $k+l\ge n,$ are some coefficients. It follows that

$${\nu }_n=\lambda \left(\Lambda (R_1)-\Lambda (f_n)\right)=n$$

tends monotonically to ∞ as $n\to \infty .$

Thus, the branched continued fraction (22) corresponds at $\mathbf{z}=\mathbf{0}$ to a formal double power series $\Lambda (R_1).$

Let $\Delta$ be the neighborhood of the origin which contained in $G,$ where G is defined by (37), and in which

$$\Lambda (R_1)=\sum _{k,l=0}^{\infty }{\alpha }_{k,l}{z}_1^k{z}_2^l.$$

(42)

From part (A) it follows that the sequence $\left\{f_n(\mathbf{z})\right\}$ converges uniformly on each compact subset of the domain $\Delta$ to function $f(\mathbf{z}),$ which is holomorphic in $\Delta .$ Then according to Weierstrass’s theorem ([40], p. 288) for arbitrary $k+l,k\ge 0,l\ge 0,$ we have

$$\frac{{\partial }^{k+l}{f}_n(\mathbf{z})}{\partial z_1^k\partial z_2^l}\to \frac{{\partial }^{k+l}f(\mathbf{z})}{\partial z_1^k\partial z_2^l}\mathrm{as}n\to \infty$$

on each compact subset of the domain $\Delta .$ And now, according to the above proven, the expansion of each approximant $f_n(\mathbf{z}),n\ge 1,$ into formal double power series and series (42) agree for all homogeneous terms up to and including degree $(n-1).$ Then for arbitrary $k+l,k\ge 0,l\ge 0,$ we obtain

$$\underset{n\to \infty }{lim}\left(\frac{{\partial }^{k+l}{f}_n}{\partial z_1^k\partial z_2^l}(\mathbf{0})\right)=\frac{{\partial }^{k+l}f}{\partial z_1^k\partial z_2^l}(\mathbf{0})=k!l!{\alpha }_{k,l}.$$

Hence,

$$f(\mathbf{z})=\sum _{k,l=0}^{\infty }\frac{1}{k!l!}\left(\frac{{\partial }^{k+l}f}{\partial z_1^k\partial z_2^l}(\mathbf{0})\right)z_1^k{z}_2^l=\sum _{k,l=0}^{\infty }{\alpha }_{k,l}{z}_1^k{z}_2^l$$

for all $\mathbf{z}\in \Delta .$

Finally, by the principle of analytic continuation ([41], p. 53) follows part (B). □

Setting $a=0$ and replacing c by $c-1$ in Theorem 2, we obtain a corollary.

Corollary 1.

Let (1) be a hypergeometric function $H_3$ with parameters b and c satisfying inequalities $c-1\ge b\ge 0.$ If there exist positive numbers ${\lambda }_1,$ ${\lambda }_2,$ ${\mu }_1,$ ${\mu }_2,$ ${\nu }_1,$ ${\nu }_2,$ and ${\nu }_3$ such that (36) hold, then:

(A) 

The branched continued fraction

$$\frac{1}{1}\genfrac{}{}{0pt}{}{}{+}\sum _{i_1=1}^2\frac{c_{i(1)}(\mathbf{z})}{d_{i(1)}(\mathbf{z})}\genfrac{}{}{0pt}{}{}{+}\sum _{i_2=1}^2\frac{c_{i(2)}(\mathbf{z})}{d_{i(2)}(\mathbf{z})}\genfrac{}{}{0pt}{}{}{+}\dots \genfrac{}{}{0pt}{}{}{+}\sum _{i_k=1}^2\frac{c_{i(k)}(\mathbf{z})}{d_{i(k)}(\mathbf{z})}\genfrac{}{}{0pt}{}{}{+}\dots ,$$

(43)

where

$$c_1(\mathbf{z})=-\frac{2z_1}{c},c_2(\mathbf{z})=-\frac{b(1-4z_1)z_2}{c},$$

(44)

and for $i(k)\in \mathcal{I}$ and for $i_0=1$

$$\begin{array}{cc}\hfill d_{i(k)}(\mathbf{z})& =1+\left(\frac{(b+1+{\sum }_{r=0}^{k-1}({\delta }_{i_r}^2-{\delta }_{i_r}^1))z_2}{c-1+k}-\frac{2(2(c-1)+k+{\sum }_{r=0}^{k-1}{\delta }_{i_r}^2)z_1}{c-1+k}\right){\delta }_{i_k}^2,\hfill \end{array}$$

(45)

$$\begin{array}{cc}\hfill c_{i(k),1}(\mathbf{z})& =-\frac{(2(c-1)+k+{\sum }_{r=0}^k{\delta }_{i_r}^2-2(2(c-1)-b+k)z_2{\delta }_{i_k}^2){\sum }_{r=0}^k{\delta }_{i_r}^1{z}_1}{(c-1+k)(c+k)},\hfill \end{array}$$

(46)

$$\begin{array}{cc}\hfill c_{i(k),2}(\mathbf{z})& =-\frac{(c-1+{\sum }_{r=0}^k{\delta }_{i_r}^2)(b+{\sum }_{r=0}^k{\delta }_{i_r}^2)(1-4z_1)z_2}{(c-1+k)(c+k)},\hfill \end{array}$$

(47)

converges uniformly on every compact subset of (37) to a function $g(\mathbf{z})$ holomorphic in $G.$

(B) 

The function $g(\mathbf{z})$ is an analytic continuation of function $H_3(1,b,c;\mathbf{z})$ in the domain $G.$

Here it is suffices to note that if $g_n(\mathbf{z})$ denotes the n-th approximant of (43), then

$$g_1(\mathbf{z})=Q_0^{(0)}(\mathbf{z})=1$$

and

$$g_n(\mathbf{z})=\frac{1}{Q_0^{(n-1)}(\mathbf{z})}=\frac{1}{1}\genfrac{}{}{0pt}{}{}{+}\sum _{i_1=1}^2\frac{c_{i(1)}(\mathbf{z})}{Q_{i(1)}^{(n-1)}(\mathbf{z})},n\ge 2,$$

where $Q_{i(1)}^{(1)}(\mathbf{z})$ and $Q_{i(1)}^{(n-1)}(\mathbf{z}),$ $n\ge 3,$ are defined by (23) and (24), respectively. By analogy to proof of (39) it can be shown that

$$\mathrm{Re}(Q_0^{(n-1)}(\mathbf{z}))>{\mu }_1>0\mathrm{for} \mathrm{all}n\ge 1\mathrm{and}\mathrm{for} \mathrm{all}\mathbf{z}\in G,$$

where G is defined by (37). Hence $\left\{g_n(\mathbf{z})\right\}$ is a sequence of functions holomorphic in $G.$

The following theorem can be proved in much the same way as Theorem 2.

Theorem 4.

Let (1) be a hypergeometric function $H_3$ with parameters $a,$ $b,$ and c satisfying inequalities $c\ge a\ge 0$ and $c-1\ge b\ge 0.$ If there exist positive numbers ${\lambda }_1,$ ${\lambda }_2,$ ${\mu }_1,$ ${\mu }_2,$ ${\nu }_1,$ ${\nu }_2,$ and ${\nu }_3$ such that (36) hold, then:

(A) 

The branched continued fraction (22), where $d_0(\mathbf{z}),$ $c_{i(k)}(\mathbf{z})$ and $d_{i(k)}(\mathbf{z}),$ $i(k)\in \mathcal{I},$ defined by (14)–(19) for $i_0=2,$ converges uniformly on every compact subset of (37) to a function $f(\mathbf{z})$ holomorphic in $G.$

(B) 

The function $f(\mathbf{z})$ is an analytic continuation of function $(1-4z_1)R_2(a,b,c;\mathbf{z}),$where $R_2(a,b,c;\mathbf{z})$ is defined in (8), in the domain $G.$

4. Application

Horn hypergeometric functions (1) satisfies the system of partial differential equations (see ([1], Volume 1, p. 234))

$$\left\{\begin{array}{c}{\displaystyle z_1(1-4z_1)\frac{{\partial }^{2}u}{\partial z_1^2}+z_2(1-4z_1)\frac{{\partial }^{2}u}{\partial z_1\partial z_2}-z_2^2\frac{{\partial }^{2}u}{\partial z_2^2}+(c-(4a+6)z_1)\frac{\partial u}{\partial z_1}}\hfill \\ {\displaystyle -2(a+1)z_2\frac{\partial u}{\partial z_2}-a(a+1)u=0,}\hfill \\ {\displaystyle z_2(1-z_2)\frac{{\partial }^{2}u}{\partial z_2^2}+z_1(1-2z_2)\frac{{\partial }^{2}u}{\partial z_1\partial z_2}+(c-(a+b+1)z_2)\frac{\partial u}{\partial z_2}-2b{z}_1\frac{\partial u}{\partial z_1}-acu=0,}\hfill \end{array}\right.$$

(48)

in which $z_1$ and $z_2$ are the independent variables, $u=u(\mathbf{z})$ is an unknown function of $z_1$ and $z_2.$ If the conditions of Corollary 1 are satisfied, then the branched continued fraction (42) satisfies (48) in which $a=1.$ This means that the approximations of (42) can be used to approximate the solution of this system of partial differential equations in the domain (37).

For example, we set $b=1,$ $c=2$ and choose the parameters ${\mu }_1,$ ${\mu }_2,$ ${\nu }_1,$ ${\nu }_2,$ ${\nu }_3,$ ${\lambda }_1,$ and ${\lambda }_2,$ as in (38). Then from (44)–(47) we have the following approximations for $u(\mathbf{z}):$

$$g_1(\mathbf{z})=1,g_2(\mathbf{z})=\frac{1}{1}\genfrac{}{}{0pt}{}{}{+}\sum _{i_1=1}^2\frac{c_{i(1)}(\mathbf{z})}{d_{i(1)}(\mathbf{z})}=\frac{2-6z_1+z_2}{2-8z_1+6z_1^2+3z_1{z}_2},\mathrm{etc}.$$

The results of computation of the approximations $g_n(\mathbf{z}),$ $2\le n\le 9,$ for different values of $z_1$ and $z_2$ are given in Table 1.

Table 1. Values of $g_n(\mathbf{z})$ for different values of $z_1$ and $z_2.$

z	$(-0.1,-0.1)$	$(-1+0.04\mathit{i},-1+0.04\mathit{i})$	$(-2,-3)$
$g_2(\mathbf{z})$	0.8650519	$0.3681728+0.0096336i$	0.1833333
$g_3(\mathbf{z})$	0.8775636	$0.5305392+0.0063811i$	0.3995816
$g_4(\mathbf{z})$	0.8764257	$0.4639479+0.0090176i$	0.2694630
$g_5(\mathbf{z})$	0.8765262	$0.4876656+0.0077578i$	0.3250616
$g_6(\mathbf{z})$	0.8765262	$0.4786337+0.0083884i$	0.2964094
$g_7(\mathbf{z})$	0.8765262	$0.4819359+0.0080973i$	0.3099597
$g_8(\mathbf{z})$	0.8765262	$0.4806949+0.0082286i$	0.3032415
$g_9(\mathbf{z})$	0.8765262	$0.4811616+0.0081711i$	0.3065131

In view of table, the results of the approximation calculations in points $(-0.1,-0.1)$ and $(-2,-3)$ confirm the ‘fork property’ for branched continued fraction (43) (see Remark 4). At point $(-1+0.04i,-1+0.04i)$ it is clearly traced to what value the sequence of approximants of (43) coincides (see also Figure 1).

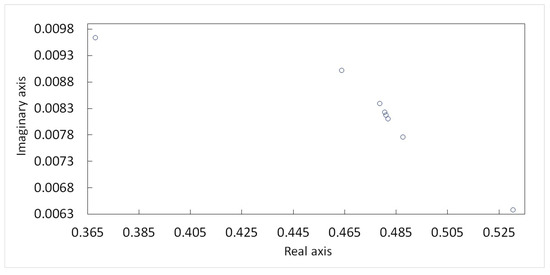
Figure 1. Dot plot for $g_n(\mathbf{z})$ in point $(-1+0.04i,-1+0.04i).$

5. Conclusions

In the paper, the branched continued fraction expansions of the Horn’s hypergeometric function $H_3$ ratios are constructed and investigated. This allows, in particular, to approximate this function by means of a branched continued fraction. The result is a generalization of the classical continued fraction expansions of the Gauss’s hypergeometric function ratios.

Branched continued fractions, being a multidimensional generalization of continued fractions, in comparison with multiple power series under certain conditions have wider convergence domain and endowed with the property of numerical stability. All this makes them an effective tool for approximating the analytical functions of several variables. The problem of studying the convergence of branched continued fractions is that the methods of studying the convergence of continued fractions are not transferred to the multidimensional case.

In the paper, we establish a convergence domain for the constructed expansions that is wider than the convergence domain of the corresponding Horn hypergeometric function $H_3$. However, in view of the convergence domains of continued fractions, the problem of studying a wider convergence domain and establishing estimates of the rate of convergence of the above-mentioned expansions still remains open.

The application of the obtained results is also an approximation of the solution of a certain system of partial differential equations, which can be used in applied problems in physics, astronomy, economics, and others. The calculation of the values of the approximants of the branched continued fraction expansion at the points of its convergence confirms the properties described above.

The proposed methods for constructing and studying the branched continued fraction expansions of the Horn’s hypergeometric function $H_3$ ratios can also be applied to construct the expansions of other relations of generalizations of the Gauss hypergeometric function.