Subordination Implications and Coefficient Estimates for Subclasses of Starlike Functions

Abstract

In the present paper, we consider various subclasses of star-like functions, which are defined by subordination and then we obtain several subordination implications related to these subclasses. Some coefficient bounds for functions belonging to some subclasses of star-like functions are also estimated. Moreover, we give some related connections of the outcomes stated here with those obtained earlier.

1. Introduction

Let $\mathbb{N}:=\left\{1,2,\dots \right\}$ and $\mathcal{A}$ be the class of functions of the form

$$f\left(z\right)=z+\sum _{n=2}^{\infty }{a}_n{z}^n$$

(1)

that are analytic in the open unit disk $\mathbb{U}=\left\{z\in \mathbb{C}:\left|z\right|<1\right\}$. Also, we denote by $\mathcal{S}$ the class of univalent functions in $\mathcal{A}$ and by ${\mathcal{S}}^{*}$ and $\mathcal{C}$, the popular categories of $\mathcal{S}$ including star-like functions regarding the origin and convex functions, respectively. Their geometric properties and diverse usages have attracted attention in this direction. Many of its categories have been extensively introduced and studied.

Ma and Minda [1] introduced different subclasses of star-like and convex functions using the concept of subordination. For this purpose, a univalent function $\varphi$ was considered with positive real part in $\mathbb{U}$, star-like with $\varphi \left(0\right)=1$ and ${\varphi }^{\prime }\left(0\right)>0$, which its region is symmetric respecting the real axis. They introduced the well-known classes as follows:

$${\mathcal{S}}^{*}\left(\varphi \right):=\left\{f\in \mathcal{A}:{\displaystyle \frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}}\prec \varphi \left(z\right)\right\}$$

and

$$\mathcal{C}\left(\varphi \right):=\left\{f\in \mathcal{A}:1+{\displaystyle \frac{z{f}^{″}\left(z\right)}{f^{\prime }\left(z\right)}}\prec \varphi \left(z\right)\right\},$$

where ≺ stands for the usual subordination for analytic functions in $\mathbb{U}$. Since $\varphi$ is a function with positive real part, all functions belonging to the classes $\mathcal{C}\left(\varphi \right)$ and ${\mathcal{S}}^{*}\left(\varphi \right)$ are convex functions and star-like functions, respectively. Also, it is well-known that the functions in ${\mathcal{S}}^{*}\left(\varphi \right)$ are univalent.

Choosing an appropriate function $\varphi$, it follows that the associated class ${\mathcal{S}}^{*}\left(\varphi \right)$ becomes one of the well-known classes of functions. For instance, the families ${\mathcal{S}}^{*}\left(\varphi \right)$ and $\mathcal{C}\left(\varphi \right)$ reduce to the classes ${\mathcal{S}}^{*}[A,B]:=(1+Az)/(1+Bz)$ and $\mathcal{C}[A,B]:=(1+Az)/(1+Bz)$ of the well-known Janowski star-like and Janowski convex functions for $-1\le B<A\le 1$, respectively. Setting $A=1-2\alpha$ and $B=-1$, where $0\le \alpha <1$, we obtain the categories ${\mathcal{S}}^{*}\left(\alpha \right)$ and $\mathcal{C}\left(\alpha \right)$ of the star-like andconvex functions of order$\alpha$, respectively. Individually, ${\mathcal{S}}^{*}:={\mathcal{S}}^{*}\left(0\right)$ and $\mathcal{C}:=\mathcal{C}\left(0\right)$.

Furthermore, for $\varphi \left(z\right)=\sqrt{1+z}$ we get the family ${\mathcal{S}}_l^{*}$ defined by Sokół and Stankiewicz [2], including functions f such that $w=z{f}^{\prime }\left(z\right)/f\left(z\right)$ lies in the region bounded by the right half of the lemniscate of Bernoulli given by $\left|w^2-1\right|<1$. Sokół [3] generalized this class by introducing a more general class ${\mathcal{S}}_{l_c}^{*}=:{\mathcal{S}}^{*}\left(\sqrt{1+cz}\right),c\in (0,1]$. Moreover, the properties of the class ${\mathcal{S}}_s^{*}:={\mathcal{S}}^{*}(1+sinz)$ such that the quantity $w=z{f}^{\prime }\left(z\right)/f\left(z\right)$ lies in an eight-shaped area in the right-half plane were studied by Cho et al. [4]. Raina and Sokół [5] studied the family ${\mathcal{S}}_{☾}^{*}:={\mathcal{S}}^{*}\left(q\right)$, where

$$q\left(z\right)=z+\sqrt{1+z^2}=1+\sum _{n=1}^{\infty }{B}_n{z}^n=1+z+\frac{z^2}{2}-\frac{z^4}{8}+\cdots ,z\in \mathbb{U}.$$

(2)

They have proved that $f\in {\mathcal{S}}_{☾}^{*}$ if and only if $z{f}^{\prime }\left(z\right)/f\left(z\right)\in \mathcal{R}$ where $\mathcal{R}:=\{z\in \mathbb{C}:\left|w^2-1\right|<2|w\left|\right\}$.

Lately, Kanas et al. [6] (see also [7,8]) defined the classes ${\mathcal{ST}}_{hpl}\left(s\right)$ and ${\mathcal{CV}}_{hpl}\left(s\right)$ by

$${\mathcal{ST}}_{hpl}\left(s\right)=:\left\{f\in \mathcal{A}:{\displaystyle \frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}}\prec {\mathfrak{q}}_s\left(z\right):=\frac{1}{{(1-z)}^s},0<s\le 1\right\}$$

and

$${\mathcal{CV}}_{hpl}\left(s\right):=\left\{f\in \mathcal{A}:1+{\displaystyle \frac{z{f}^{″}\left(z\right)}{f^{\prime }\left(z\right)}}\prec {\mathfrak{q}}_s\left(z\right):=\frac{1}{{(1-z)}^s},0<s\le 1\right\}.$$

Also, they obtained some geometric features in these categories.

The function

$$\begin{array}{cc}\hfill {\mathfrak{q}}_s\left(z\right)=\frac{1}{{(1-z)}^s}=e^{-slog(1-z)}& =1+\sum _{n=1}^{\infty }{B}_n{z}^n=1+\sum _{n=1}^{\infty }\frac{s(s+1)\cdots (s+n-1)}{n!}{z}^n\hfill \\ \hfill & =1+sz+\frac{s(s+1)}{2}{z}^2+\frac{s(s+1)(s+2)}{6}{z}^3+\cdots ,\hfill \end{array}$$

(3)

where the branch of the logarithm is determined by $q_s\left(0\right)=1$, maps $\mathbb{U}$ onto a domain bounded by the right branch of the hyperbola

$$H\left(s\right)=\left\{\rho e^{i\phi }:\rho =\frac{1}{{\left(2cos(\phi /s)\right)}^s},\left|\phi \right|<\frac{\pi s}{2}\right\}.$$

Moreover, ${\mathfrak{q}}_s\left(\mathbb{U}\right)$ is symmetric and star-like with respect to the real axis and ${\mathfrak{q}}_s\left(0\right)=1$. Also, ${\mathfrak{q}}_s^{\prime }\left(0\right)>0$ and ${\mathfrak{q}}_s$ has positive real part in $\mathbb{U}$. Thus, ${\mathfrak{q}}_s$ satisfies the family of Ma-Minda functions.

Furthermore, in a survey-cum-expository article [9] by Srivastava, it was indicated that the recent and future applications and importance of the classical q-calculus and the fractional q-calculus in geometric function theory of complex analysis motivate researchers to study many of these and other related subjects in this filed (see also [10,11,12]).

It is always interesting to find sufficient conditions such that certain class of analytic functions becomes close-to-convex, star-like or convex function. Such classes play an important role in various branches of applied mathematics and engineering sciences. Geometric properties of some special functions were recently examined by many authors, see for example [13,14,15,16,17] as well as in the references cited therein.

Motivated by the above mentioned works the aim of the present paper is to study various subordination implications or inclusion relationships for some subclasses of star-like functions associated with the class ${\mathcal{S}}^{*}\left(\varphi \right)$. We also estimate some coefficient bounds for function belonging to the class ${\mathcal{S}}^{*}\left(\varphi \right)$. Moreover, some relevant connections of the outcomes studied here with the result reported in earlier are given.

2. Subordination Implications

In this section, we conclude a sufficient condition consisting of subordination for the functions to be in the classes ${\mathcal{ST}}_{hpl}\left(s\right)$, ${\mathcal{S}}_{l_c}^{*}$ and others. In this paper, it is assumed that $\varphi$ is a univalent function in $\mathbb{U}$ with positive real part in $\mathbb{U}$ and $\varphi \left(0\right)=1$ so that it has series expansion as follows:

$$\begin{array}{c}\hfill \varphi \left(z\right)=1+B_{1}z+B_2{z}^2+B_3{z}^3+\cdots ,B_1\ne 0.\end{array}$$

(4)

To prove our main results, we require the following theorem on certain analytic functions, which is very important in this area.

Theorem 1. 

([18] [Theorem 2.2 (for $p=1$)]) Let ϕ be convex in $\mathbb{U}$ with $\varphi \left(0\right)=1$ and $\Re \left(\varphi \left(z\right)\right)>0$ in $\mathbb{U}$. Then

$$\mathcal{C}\left(\varphi \right)\subset {\mathcal{S}}^{*}\left(\varphi \right).$$

Theorem 2. 

Let $f\in \mathcal{A}$ given by (1) satisfy the subordination

$$1+\frac{z{f}^{″}\left(z\right)}{f^{\prime }\left(z\right)}\prec {\mathfrak{q}}_s\left(z\right)\left(z\in \mathbb{U}\right),$$

where ${\mathfrak{q}}_s$ is given by (3). Then

$$\frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}\prec {\mathfrak{q}}_s\left(z\right)\left(z\in \mathbb{U}\right).$$

In other words,

$${\mathcal{CV}}_{hpl}\left(s\right)\subset {\mathcal{ST}}_{hpl}\left(s\right).$$

Proof. 

Since ${\mathfrak{q}}_s$ is convex function according to Lemma 2.1 in [6], we obtain the required result from Theorem 1 with $\varphi =:{\mathfrak{q}}_s$. □

Theorem 3. 

Let $f\in \mathcal{A}$ given by (1) satisfy the subordination

$$1+\frac{z{f}^{″}\left(z\right)}{f^{\prime }\left(z\right)}\prec \sqrt{1+cz},c\in (0,1].$$

Then

$$\frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}\prec \sqrt{1+cz},c\in (0,1].$$

Proof. 

Since $\sqrt{1+cz},c\in (0,1]$ is convex function so we obtain the required result from Theorem 1 with $\varphi =:\sqrt{1+cz},c\in (0,1]$. □

Let us consider the function

$$\varphi \left(z\right)=1+{\displaystyle \frac{1}{2isin\delta }}log\left(\frac{1+e^{i\delta }z}{1+e^{-i\delta }z}\right)=1+\sum _{n=1}^{\infty }{B}_n\left(\delta \right)z^n\left(\pi /2\le \delta <\pi \right),$$

(5)

where

$$B_n\left(\delta \right)={(-1)}^{n-1}{\displaystyle \frac{sinn\delta }{nsin\delta }}\left(n\in \mathbb{N},\pi /2\le \delta <\pi \right).$$

Then it is clear that $\varphi$ satisfies the hypothesis of Theorem 1 [19]. Hence, we get the following result.

Theorem 4 

([20] (Theorem 3)). Let $f\in \mathcal{A}$ given by (1) satisfy the subordination

$$1+\frac{z{f}^{″}\left(z\right)}{f^{\prime }\left(z\right)}\prec \varphi \left(z\right)\left(z\in \mathbb{U}\right),$$

where ϕ is given by (5). Then

$$\frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}\prec \varphi \left(z\right)\left(z\in \mathbb{U}\right).$$

Let us consider the function

$$\varphi \left(z\right)={\left({\displaystyle \frac{1+cz}{1-z}}\right)}^{\frac{{\alpha }_1+{\alpha }_2}{2}}=1+\sum _{n=1}^{\infty }{\lambda }_n{z}^n\left(0<{\alpha }_1,{\alpha }_2\le 1,c=e^{i\pi \theta },\theta =\frac{{\alpha }_2-{\alpha }_1}{{\alpha }_2+{\alpha }_1}\right),$$

(6)

where

$${\lambda }_n=\sum _{k=1}^n\left(\genfrac{}{}{0pt}{}{n-1}{k-1}\right)\left(\genfrac{}{}{0pt}{}{({\alpha }_1+{\alpha }_2)/2}{k}\right){(1+c)}^k\left(n\in \mathbb{N}\right).$$

Then it is clear that $\varphi$ satisfies the hypothesis of Theorem 1 [21]. Hence, we obtain the following outcome.

Theorem 5. 

Let $f\in \mathcal{A}$ given by (1) satisfy the subordination

$$1+\frac{z{f}^{″}\left(z\right)}{f^{\prime }\left(z\right)}\prec \varphi \left(z\right)\left(z\in \mathbb{U}\right),$$

where ϕ is given by (6). Then

$$\frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}\prec \varphi \left(z\right)\left(z\in \mathbb{U}\right).$$

Remark 1. 

It is worthy to note that Theorem 5 gives an improvement of the results obtained by Kargar et al. ([22] [Lemma 2.1]) without the restriction $\left|z\right|\le \frac{1}{1+2cos(\theta /2)}.$

Let us consider the convex univalent function $\varphi$ defined by (5) in Theorem 1 and set

$$p\left(z\right)=1+{\displaystyle \frac{z{f}^{\prime \prime }\left(z\right)}{f^{\prime }\left(z\right)}}\mathrm{and}{\mathcal{B}}_{\delta }\left(z\right)={\displaystyle \frac{1}{2isin\delta }}log\left(\frac{1+z{e}^{i\delta }}{1+z{e}^{-i\delta }}\right)(\pi /2\le \delta <\pi ).$$

Since

$$p\left(0\right)=1\ne 0={\mathcal{B}}_{\delta }\left(0\right),$$

the relation

$$p\left(z\right)\prec {\mathcal{B}}_{\delta }\left(z\right)$$

does not hold. Thus, we get the following theorem, which is a correction of the results obtained by Kargar et al. ([19] [Theorem 2.1]).

Theorem 6. 

Let ${\delta }_0=1.24\dots$ denote the root of the equation

$$1+\frac{\delta -\pi }{2sin\delta }=0.$$

If ${\delta }_0\le \delta <\pi$, then $\mathcal{C}\left(\varphi \right)\subset {\mathcal{S}}^{*}\left(\varphi \right)$, where ϕ is given by (5).

In next result, we obtain that $q_0\left(z\right)=1+sinz$ is convex in $\left|z\right|<0.7948297394$.

Theorem 7. 

The function $q_0\left(z\right)=1+sinz$ is convex in |z| < 0.7948297394.

Proof. 

The function $q_0\left(z\right)=1+sinz$ is univalent in the unit disc [4]. For the proof that $q_0\left(z\right)$ is convex, let $z=r{\mathrm{e}}^{\mathrm{i}t}$ with $\left|z\right|=r<1,-\pi \le t\le \pi$. By computation we have

$$\mathcal{\Re }\left(1+\frac{z{q}_0^{″}\left(z\right)}{q_0^{\prime }\left(z\right)}\right)=\mathcal{\Re }\left(1-\frac{zsinz}{cosz}\right)\ge 1-\frac{\left|z\right||sinz|}{|cosz|}.$$

(7)

On the other hand, from ([4] [p. 5]) for $\omega \left(z\right)=z$ we have

$$|sinz|\le sinhr.$$

Also, it is a simple exercise to verify that

$$cosr\le |cosz|.$$

Now considering two above inequality with from (7), we get

$$\mathcal{\Re }\left(1+\frac{z{q}_0^{″}\left(z\right)}{q_0^{\prime }\left(z\right)}\right)\ge 1-\frac{\left|z\right||sinz|}{|cosz|}\ge 1-\frac{rsinhr}{cosr}>0,$$

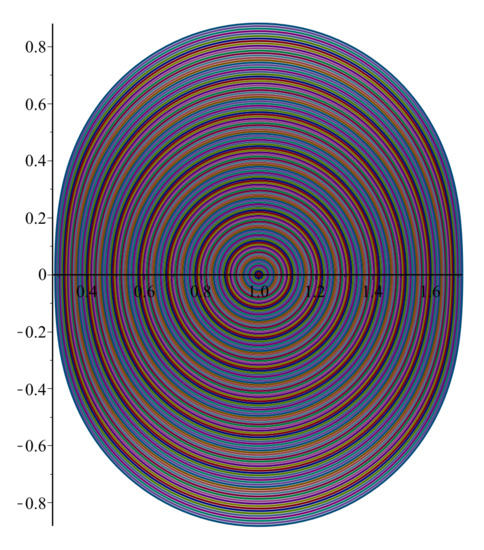
whenever $cosr-rsinhr>0$. Thus, the radius of star-likeness is the smallest positive root $r_0\in (0,1)$ of $cosr-rsinhr=0$, i.e., $r_0\approx 0.7948297394$, (see Figure 1). □

Figure 1. The image of $\left|z\right|<0.7948297394$ under $q_0\left(z\right)=1+sinz$.

3. The Classes ${\Sigma }^{\prime }$ and $\tilde{\Sigma }$

Let ${\Sigma }^{\prime }$ denote the family of meromorphic univalent functions g [23] defined in $\Delta =\left\{z\in \mathbb{C}:1<\left|z\right|<\infty \right\}$ with the following form:

$$g\left(z\right)=z+\sum _{n=0}^{\infty }\frac{b_n}{z^n}.$$

Let ${\mathcal{S}}^{\prime }\left(\varphi \right)$ denote the family of functions $g\in {\Sigma }^{\prime }$ satisfying

$$\frac{1}{z}\frac{g^{\prime }(1/z)}{g(1/z)}\prec \varphi \left(z\right)\left(z\in \mathbb{U}\right).$$

The mapping $f\left(z\right)\mapsto g\left(z\right):=1/f(1/z)$ establishes a one-to-one correspondence between functions in the families $\mathcal{S}$ and ${\Sigma }^{\prime }$ and therefore between functions in the families ${\mathcal{S}}^{*}\left(\varphi \right)$ and ${\mathcal{S}}^{\prime }\left(\varphi \right)$ because

$$\frac{z{g}^{\prime }\left(z\right)}{g\left(z\right)}=\frac{z{(1/f(1/z))}^{\prime }}{1/f(1/z)}=\frac{1}{z}\frac{f^{\prime }(1/z)}{f(1/z)},(z\in \Delta ).$$

(8)

Please note that if $g\in {\mathcal{S}}^{\prime }\left(\varphi \right)$, then there is a unique function $f\in {\mathcal{S}}^{*}\left(\varphi \right)$ with $g\left(z\right)=1/f(1/z).$

Let $\tilde{\Sigma }$ the family of meromorphic univalent functions h defined on the punctured unit disk ${\mathbb{U}}^{*}=\{z\in \mathbb{C}:0<\left|z\right|<1\}$ as follows:

$$h\left(z\right)=\frac{1}{z}+\sum _{n=0}^{\infty }{c}_n{z}^n.$$

Let $\tilde{\mathcal{S}}\left(\varphi \right)$ denote the family of functions $g\in \tilde{\Sigma }$ satisfying

$$-\frac{z{h}^{\prime }\left(z\right)}{h\left(z\right)}\prec \varphi \left(z\right)\left(z\in \mathbb{U}\right).$$

Then the mapping $f\left(z\right)\mapsto h\left(z\right):=1/f\left(z\right)$ establishes a one-to-one correspondence between functions in the classes $\mathcal{S}$ and $\tilde{\Sigma }$ and hence between functions in the classes ${\mathcal{S}}^{*}\left(\varphi \right)$ and $\tilde{\mathcal{S}}\left(\varphi \right)$, because

$$-\frac{z{h}^{\prime }\left(z\right)}{h\left(z\right)}=-\frac{z{(1/f\left(z\right))}^{\prime }}{1/f\left(z\right)}=\frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}\left(z\in \mathbb{U}\right).$$

(9)

Furthermore, the mapping $g\left(z\right)\mapsto h\left(z\right)=g(1/z)$ establishes a one-to-one correspondence between functions in the classes ${\Sigma }^{\prime }$ and $\tilde{\Sigma }$, and hence between functions in the families ${\mathcal{S}}^{\prime }\left(\varphi \right)$ and $\tilde{\mathcal{S}}\left(\varphi \right)$. In fact, the functions $g\in {\Sigma }^{\prime }$ and $h\left(z\right)=g(1/z)\in \tilde{\Sigma }$ have the same geometric properties. Recently, several authoress studied some different problems for an appropriate function $\varphi$ of the classes ${\mathcal{S}}^{*}\left(\varphi \right)$, ${\mathcal{S}}^{\prime }\left(\varphi \right)$ and $\tilde{\mathcal{S}}\left(\varphi \right)$ separately while according to the above mentioned issues only it is enough to investigate one of these classes.

Theorem 8 

([24] (Theorem 1)). Let ϕ be convex function in $\mathbb{U}$ with $\varphi \left(0\right)=1$. Define F by

$$F\left(z\right)=zexp\left({\int }_0^z{\displaystyle \frac{\varphi \left(x\right)-1}{x}}dx\right)\left(z\in \mathbb{U}\right).$$

The function $f\in {\mathcal{S}}^{*}\left(\varphi \right)$ if and only if for all $\left|s\right|\le 1$ and $\left|t\right|\le 1$,

$$\frac{sf\left(tz\right)}{tf\left(sz\right)}\prec \frac{sF\left(tz\right)}{tF\left(sz\right)}$$

holds.

Remark 2. 

For $t=1,s=0$, the relation $sf\left(tz\right)/tf\left(sz\right)\prec sF\left(tz\right)/tF\left(sz\right)$ is equivalent to $f\left(z\right)/z\prec F\left(z\right)/z$.

Referring to the proof of Theorem 1 in [25], we obtain the next lemma.

Lemma 1. 

Let ϕ be convex function in $\mathbb{U}$ with $\varphi \left(0\right)=1$. If $f\in {\mathcal{S}}^{*}\left(\varphi \right)$, then

$$log\left({\displaystyle \frac{f\left(z\right)}{z}}\right)\prec {\int }_0^z{\displaystyle \frac{\varphi \left(t\right)-1}{t}}dt\left(z\in \mathbb{U}\right).$$

Moreover,

$$\tilde{\varphi }\left(z\right)={\int }_0^z{\displaystyle \frac{\varphi \left(t\right)-1}{t}}dt\left(z\in \mathbb{U}\right)$$

is convex univalent.

By setting $\varphi =:{\mathfrak{q}}_s$ where ${\mathfrak{q}}_s$ is given (3) and taking $t=1,s=0$ in Theorem 8 and Lemma 1, we have the following results.

Theorem 9. 

The function $f\in {\mathcal{ST}}_{hpl}\left(s\right)$ if and only if

$$\frac{f\left(z\right)}{z}\prec exp\left({\int }_0^z{\displaystyle \frac{{\mathfrak{q}}_s\left(t\right)-1}{t}}dt\right)\left(z\in \mathbb{U}\right),$$

where ${\mathfrak{q}}_s$ is given by (3).

Theorem 10. 

If $f\in {\mathcal{ST}}_{hpl}\left(s\right)$, then

$$log\left({\displaystyle \frac{f\left(z\right)}{z}}\right)\prec {\int }_0^z{\displaystyle \frac{{\mathfrak{q}}_s\left(t\right)-1}{t}}dt\left(z\in \mathbb{U}\right),$$

where ${\mathfrak{q}}_s$ is given by (3). Moreover,

$$\widetilde{{\mathfrak{q}}_s}\left(z\right)={\int }_0^z{\displaystyle \frac{{\mathfrak{q}}_s\left(t\right)-1}{t}}dt\left(z\in \mathbb{U}\right)$$

is convex univalent.

By taking $\varphi \left(z\right)=:q_c\left(z\right)=\sqrt{1+cz},c\in (0,1]$ and setting $t=1,s=0$ in Theorem 8 and Lemma 1, we have next result.

Theorem 11. 

The function $f\in {\mathcal{S}}_{l_c}^{*}$ if and only if

$$\frac{f\left(z\right)}{z}\prec exp\left({\int }_0^z{\displaystyle \frac{q_c\left(t\right)-1}{t}}dt\right)\left(z\in \mathbb{U}\right),$$

where $q_c\left(z\right)=\sqrt{1+cz},c\in (0,1]$.

Theorem 12. 

If $f\in {\mathcal{S}}_{l_c}^{*}$, then

$$log\left({\displaystyle \frac{f\left(z\right)}{z}}\right)\prec {\int }_0^z{\displaystyle \frac{q_c\left(t\right)-1}{t}}dt\left(z\in \mathbb{U}\right),$$

where $q_c\left(z\right)=\sqrt{1+cz},c\in (0,1]$. Moreover,

$$\widetilde{q_c}\left(z\right)={\int }_0^z{\displaystyle \frac{q_c\left(t\right)-1}{t}}dt\left(z\in \mathbb{U}\right)$$

is convex univalent.

If we consider the function $\varphi$ defined in (5) and set $t=1,s=0$ in Theorem 8, then we have the following consequence.

Theorem 13. 

([20] (Theorem 1)). The function $f\in {\mathcal{S}}^{*}\left(\varphi \right)$ if and only if

$$\frac{f\left(z\right)}{z}\prec exp\left({\displaystyle \frac{1}{2isin\delta }}{\int }_0^z{\displaystyle \frac{1}{t}}log\left(\frac{1+e^{i\delta }t}{1+e^{-i\delta }t}\right)dt\right)\left(z\in \mathbb{U}\right),$$

where ϕ is given by (5).

If we consider the convex univalent function ([26] [Corollary 3.3])

$$\varphi \left(z\right)=1+{\displaystyle \frac{z}{1-\alpha z^2}}=1+z+\sum _{n=1}^{\infty }{\alpha }^n{z}^{2n+1}(0\le \alpha \le 3-2\sqrt{2})$$

(10)

and set $t=1,s=0$ in Theorem 8, then we have following consequence, which is a correction of the result obtained by Kargar et al. ([27] [Corollary 1.1]).

Theorem 14. 

The function $f\in {\mathcal{S}}^{*}\left(\varphi \right)$ if and only if

$$\frac{f\left(z\right)}{z}\prec exp\left({\int }_0^z\frac{1}{1-\alpha t^2}dt\right)\left(z\in \mathbb{U}\right),$$

where ϕ is given by (10).

If we consider the convex univalent function [28]

$$\varphi \left(z\right)=1+{\displaystyle \frac{\beta -\alpha }{\pi }}ilog\left(\frac{1-e^{2\pi i\frac{1-\alpha }{\beta -\alpha }}z}{1-z}\right)(0\le \alpha <1<\beta ;z\in \mathbb{U})$$

(11)

and set $t=1,s=0$ and also $f\left(z\right)=1/h\left(z\right)$ in Theorem 8, then we have the following consequence.

Theorem 15 

([29] (Theorem 1)). The function $f\in \tilde{\mathcal{S}}\left(\varphi \right)$ if and only if

$$\frac{f\left(z\right)}{z}\prec exp\left({\displaystyle \frac{\alpha -\beta }{\pi }}i{\int }_0^z{\displaystyle \frac{1}{t}}log\left(\frac{1-e^{2\pi i\frac{1-\alpha }{\beta -\alpha }}t}{1-t}\right)dt\right)\left(z\in \mathbb{U}\right)$$

holds, where ϕ is given by (11).

4. Coefficient Estimates

Finding the upper bounds for coefficients is sometimes extremely important in geometric function theory as it presents some properties of functions. For this goal, we need the following lemma due to Kuroki and Owa [28] (see also [30]).

Lemma 2. 

Let q be a convex function in $\mathbb{U}$ with form $q\left(z\right)=1+{\displaystyle \sum _{n=1}^{\infty }}{B}_n{z}^n.$ If function $f\in {\mathcal{S}}^{*}\left(q\right)$, then

$$\left|a_n\right|\le \frac{{\prod }_{k=2}^n\left(k-2+\left|B_1\right|\right)}{(n-1)!}\left(n=2,3,\cdots \right).$$

Remark 3. 

We note that

$$\frac{{\prod }_{k=2}^n\left(k-2+\left|B_1\right|\right)}{(n-1)!}=\prod _{k=2}^n\frac{k-2+\left|B_1\right|}{k-1}=\prod _{k=0}^{n-2}\frac{k+\left|B_1\right|}{k+1}=\frac{\left|B_1\right|}{n-1}\prod _{k=1}^{n-2}\left(1+\frac{\left|B_1\right|}{k}\right).$$

If we consider the function $\varphi$ defined in (5) and $B_1=B_1\left(\delta \right)=1$ in Lemma 2, then we have the following consequence.

Corollary 1 

([20] (Theorems 4)). Let $f\in {\mathcal{S}}^{*}\left(\varphi \right)$ where ϕ is given by (5). Then

$$\left|a_n\right|\le 1\left(n\in \mathbb{N}\right).$$

If we consider the function $\varphi$ defined in (6) and

$$B_1={\lambda }_1=\frac{(1+c)({\alpha }_1+{\alpha }_2)}{2}\left(0<{\alpha }_1,{\alpha }_2\le 1,c=e^{i\pi \theta },\theta =\frac{{\alpha }_2-{\alpha }_1}{{\alpha }_2+{\alpha }_1}\right)$$

in Lemma 2, then we have the following consequence, which is a correction of the result obtained by Kargar et al. ([22] [Theorem 3.2]).

Corollary 2. 

Let $f\in {\mathcal{S}}^{*}\left(\varphi \right)$ where ϕ is given by (6). Then

$$\left|a_n\right|\le \frac{{\prod }_{k=2}^n\left(k-2+\left|cos\frac{\pi \theta }{2}\right|\right)}{(n-1)!}\left(n=2,3,\cdots \right),$$

where ϕ is given by (6).

Note that the one-to-one correspondence (see (8)) between the classes ${\mathcal{S}}^{\prime }\left(\varphi \right)$ and ${\mathcal{S}}^{*}\left(\varphi \right)$ gives us the coefficient relation, $a_{n+2}=-b_n$ for $n=0,1,\cdots$. If we consider the function $\varphi$ defined in (11) and

$$B_1=\left|B_1\right|={\displaystyle \frac{2(\beta -\alpha )}{\pi }}sin{\displaystyle \frac{\pi (1-\alpha )}{\beta -\alpha }}$$

(12)

and also $g\left(z\right)=1/f(1/z)$ in Lemma 2, then we have the following consequence.

Corollary 3 

([31] (Theorem 1)). Let $g\in {\mathcal{S}}^{\prime }\left(\varphi \right)$ where ϕ is given by (11). Then

$$\left|b_0\right|=\left|a_2\right|\le {\displaystyle \frac{2(\beta -\alpha )}{\pi }}sin{\displaystyle \frac{\pi (1-\alpha )}{\beta -\alpha }}$$

and

$$\left|b_n\right|=\left|a_{n+2}\right|\le {\displaystyle \frac{2(\beta -\alpha )}{\left(n+1\right)\pi }}sin{\displaystyle \frac{\pi (1-\alpha )}{\beta -\alpha }}\prod _{k=1}^n\left(1+{\displaystyle \frac{2(\beta -\alpha )}{k\pi }}sin{\displaystyle \frac{\pi (1-\alpha )}{\beta -\alpha }}\right)\left(n\in \mathbb{N}\right).$$

We also note that the one-to-one correspondence (see (9)) between the classes $\tilde{\mathcal{S}}\left(\varphi \right)$ and ${\mathcal{S}}^{*}\left(\varphi \right)$ gives us the coefficient relation, $a_{n+2}=-c_n$ for $n=0,1,\cdots$. If we consider the function $\varphi$ defined in (11) with (12) and also $h\left(z\right)=1/f\left(z\right)$ in Lemma 2, then we have the following consequence.

Corollary 4 

([29] (Theorem 3)). Let $h\in \tilde{\mathcal{S}}\left(\varphi \right)$ where ϕ is given by (11). Then

$$\left|c_n\right|=\left|a_{n+2}\right|\le \prod _{k=0}^n\frac{k+{\displaystyle \frac{2(\beta -\alpha )}{\pi }}sin{\displaystyle \frac{\pi (1-\alpha )}{\beta -\alpha }}}{k+1}\left(n=0,1,\cdots \right).$$

If we consider the function $\varphi$ defined in (10) and $B_1=1$ in Lemma 2, then we have the following consequence, which is a more simple expression than given by Kargar et al. ([27] [Theorem 2.2]).

Corollary 5 

([27] (Theorem 2.2)). Let $f\in {\mathcal{S}}^{*}\left(\varphi \right)$ where ϕ is given by (10). Then

$$\left|a_n\right|\le 1\left(n=2,3,\cdots \right).$$

5. Conclusions

In the present paper, we obtain various subordination implications or inclusion relationships for a general class ${\mathcal{S}}^{*}\left(\varphi \right)$ of star-like functions considering some particular functions $\varphi \left(z\right)$. We also estimate some upper bounds for coefficients of functions belonging to the class ${\mathcal{S}}^{*}\left(\varphi \right)$. Moreover, we give some suitable relationships between the results presented here and those already studied.