Second Order Expansions for High-Dimension Low-Sample-Size Data Statistics in Random Setting

Abstract

We consider high-dimension low-sample-size data taken from the standard multivariate normal distribution under assumption that dimension is a random variable. The second order Chebyshev–Edgeworth expansions for distributions of an angle between two sample observations and corresponding sample correlation coefficient are constructed with error bounds. Depending on the type of normalization, we get three different limit distributions: Normal, Student’s t-, or Laplace distributions. The paper continues studies of the authors on approximation of statistics for random size samples.

1. Introduction

Let ${\overrightarrow{\mathrm{X}}}_1={(X_{11},\dots ,X_{1m})}^T,\dots ,{\overrightarrow{\mathrm{X}}}_k={(X_{k1},\dots ,X_{km})}^T$ be a random sample from m-dimensional population. The data set can be regarded as k vectors or points in m-dimensional space. Recently, there has been significant interest in a high-dimensional datasets when the dimension is large. In a high-dimensional setting, it is assumed that either (i) m tends to infinity and k is fixed, or (ii) both m and k tend to infinity. Case (i) is related to high-dimensional low sample size (HDLSS) data. One of the first results for HDLSS data appeared in Hall et al. [1]. It became the basis of research in mathematical statistics for the analysis of high-dimensional data, see, e.g., Fujikoshi et al. [2], which are an important part of the current data analysis fashionable area called Big data. Scientific areas where these settings have proven to be very useful include genetics and other types of cancer research, neuroscience, and also image and shape analysis. See a recent survey on HDLSS asymptotics and its applications in Aoshima et al. [3].

For examining the features of the data set, it is necessary to study the asymptotic behavior of three functions: the length $\parallel {\overrightarrow{\mathrm{X}}}_i\parallel$ of a m-dimensional observation vector, the distance $\parallel {\overrightarrow{\mathrm{X}}}_i-{\overrightarrow{\mathrm{X}}}_j\parallel$ between any two independent observation vectors, and the angle $\mathrm{ang}({\overrightarrow{\mathrm{X}}}_i,{\overrightarrow{\mathrm{X}}}_j)$ between these vectors at the population mean. Assuming that ${\overrightarrow{\mathrm{X}}}_i$’s are a sample from $N(0,I_m)$, it was shown in Hall et al. [1] that for HDLSS data the three geometric statistics satisfy the following relations:

$$\begin{array}{cc}\hfill \parallel {\overrightarrow{\mathrm{X}}}_i\parallel & =\sqrt{m}+{\mathcal{O}}_p(1),i=1,\dots ,k,\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill \parallel {\overrightarrow{\mathrm{X}}}_i-{\overrightarrow{\mathrm{X}}}_j\parallel & =\sqrt{2m}+{\mathcal{O}}_p(1),i,j=1,\dots k,i\ne j,\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill \mathrm{ang}({\overrightarrow{\mathrm{X}}}_i,{\overrightarrow{\mathrm{X}}}_j)& =\frac{1}{2}\pi +{\mathcal{O}}_p(m^{-1/2}),i,j=1,\dots k,i\ne j,\hfill \end{array}$$

(3)

where $\parallel ·\parallel$ is the Euclidean distance and ${\mathcal{O}}_p$ denotes the stochastic order. These interesting results imply that the data converge to the vertices of a deterministic regular simplex. These properties were extended for non-normal sample under some assumptions (see Hall et al. [1] and Aoshima et al. [3]). In Kawaguchi et al. [4], the relations (1)–(3) were refined by constructing second order asymptotic expansions for distributions of all three basic statistics. The refinements of (1) and (2) were achieved by using the idea of Ulyanov et al. [5] who obtained the computable error bounds of order $\mathcal{O}(m^{-1})$ for the chi-squared approximation of transformed chi-squared random variables with m degrees of freedom.

The aim of the present paper is to study approximation for the third statistic $\mathrm{ang}({\overrightarrow{\mathrm{X}}}_1,{\overrightarrow{\mathrm{X}}}_2)$ under generalized assumption that m is a realization of a random variable, say $N_n$, which represents the sample dimension and is independent of ${\overrightarrow{\mathrm{X}}}_1$ and ${\overrightarrow{\mathrm{X}}}_2$. This problem is closely related to approximations of statistics constructed from the random size samples, in particular, to this kind of problem for the sample correlation coefficient $R_m$.

The use of samples with random sample sizes has been steadily growing over the years. For an overview of statistical inferences with a random number of observations and some applications, see Esquível et al. [6] and the references cited therein. Gnedenko [7] considered the asymptotic properties of the distributions of sample quantiles for samples of random size. In Nunes et al. [8] and Nunes et al. [9], unknown sample sizes are assumed in medical research for analysis of one and more than one-way fixed effects ANOVA models to avoid false rejections, obtained when using the classical fixed size F-tests. Esquível et al. [6] considered inference for the mean with known and unknown variance and inference for the variance in the normal model. Prediction intervals for the future observations for generalized order statistics and confidence intervals for quantiles based on samples of random sizes are studied in Barakat et al. [10] and Al-Mutairi and Raqab [11], respectively. They illustrated their results with real biometric data set, the duration of remission of leukemia patients treated by one drug. The present paper continues studies of the authors on non-asymptotic analysis of approximations for statistics based on random size samples. In Christoph et al. [12], second order expansions for the normalized random sample sizes are proved, see below Propositions 1 and 2. These results allow for proving second order asymptotic expansions of random sample mean in Christoph et al. [12] and random sample median in Christoph et al. [13]. See also Chapters 1 and 9 in Fujikoshi and Ulyanov [14].

The structure of the paper is the following. In Section 2, we describe the relation between $\mathrm{ang}({\overrightarrow{\mathrm{X}}}_1,{\overrightarrow{\mathrm{X}}}_2)$ and $R_m$. We recall also previous approximation results proved for distributions of $\mathrm{ang}({\overrightarrow{\mathrm{X}}}_1,{\overrightarrow{\mathrm{X}}}_2)$ and $R_m$. Section 3 is on general transfer theorems, which allow us to construct asymptotic expansions for distributions of randomly normalized statistics on the base of approximation results for non-randomly normalized statistics and for the random size of the underlying sample, see Theorems 1 and 2. Section 4 contains the auxiliary lemmas. Some of them have independent interest. For example, Lemma 3 on the upper bounds for the negative order moments of a random variable having negative binomial distribution. We formulate and discuss main results in Section 5 and Section 6. In Theorems 3–8, we construct the second order Chebyshev–Edgeworth expansions for distributions of $\mathrm{ang}({\overrightarrow{\mathrm{X}}}_1,{\overrightarrow{\mathrm{X}}}_2)$ and $R_m$ in random setting. Depending on the type of normalization, we get three different limit distributions: Normal, Laplace, or Student’s t-distributions. All proofs are given in the Appendix A.

2. Sample Correlation Coefficient, Angle between Vectors and Their Normal Approximations

We slightly simplify notation. Let ${\overrightarrow{\mathrm{X}}}_m={(X_1,\dots ,X_m)}^T$ and ${\overrightarrow{\mathrm{Y}}}_m={(Y_1,\dots ,Y_m)}^T$ be two vectors from an m-dimensional normal distribution $N({0,\mathrm{I}}_m)$ with zero mean, identity covariance matrix ${\mathrm{I}}_m$ and the sample correlation coefficient

$$R_m=R_m({\overrightarrow{\mathrm{X}}}_m,{\overrightarrow{\mathrm{Y}}}_m)=\frac{{\sum }_{k=1}^m{X}_k{Y}_k}{\sqrt{{\sum }_{k=1}^m{X}_k^2{\sum }_{k=1}^m{Y}_k^2}}.$$

(4)

Under the null hypothesis $H_0$: {${\overrightarrow{\mathrm{X}}}_m$ and ${\overrightarrow{\mathrm{Y}}}_m$ are uncorrelated}, the so-called null density $p_{R_m}(y;n)$ of $R_m$ is given in Johnson, Kotz and Balakrishnan [15], Chapter 32, Formula (32.7):

$$p_{R_m}(y;m)=\frac{\mathsf{\Gamma }((m-1)/2)}{\sqrt{\pi }\mathsf{\Gamma }((m-2)/2)}{\left(1-y^2\right)}^{(m-4)/2}{\mathbb{I}}_{(-11)}(y)$$

for $m\ge 3$, where ${\mathbb{I}}_A(.)$ denotes indicator function of a set A.

• Note $\mu =\mathbb{E}{R}_m=0$ and ${\sigma }^2=\mathrm{Var}(R_m)=1/(m-1)$ for $m\ge 2$,
• $R_2$ is two point distributed with $P(R_2=-1)=P(R_2=1)=1/2$,
• $R_3$ is U-shaped with $p_{R_3}(y;3)=(1/\pi ){(1-y^2)}^{-1/2}{\mathbb{I}}_{(-1,1)}(y)$ and
• $R_4$ is uniform with density $p_{R_4}(y;4)=1/2{\mathbb{I}}_{(-1,1)}(y)$.
• Moreover, for $m\ge 5$, the density function $p_{R_m}(y;m)$ is unimodal.

Consider now the standardized correlation coefficient

$$\begin{array}{c}\hfill {\overline{R}}_m=\sqrt{m-c}{R}_m\end{array}$$

(5)

with some correcting real constant $c<m$ having density

$$\begin{array}{ccc}\hfill p_{{\overline{R}}_m}(y;m,c)& =& \frac{\mathsf{\Gamma }((m-1)/2)}{\sqrt{m-c}\sqrt{\pi }\mathsf{\Gamma }((m-2)/2)}{\left(1-\frac{y^2}{m-c}\right)}^{(m-4)/2}{\mathbb{I}}_{\{|r|<\sqrt{m-c}\}}(y),\hfill \end{array}$$

(6)

which converges with $c=\mathcal{O}(1)$ as $m\to \infty$ to the standard normal density

$$\phi (y)=\frac{{\displaystyle 1}}{{\displaystyle \sqrt{2\pi }}}{e}^{-y^2/2},y\in (-\infty \infty )$$

and by Konishi [16], Section 4, Formula (4.1) as $m\to \infty$:

$$\begin{array}{c}\hfill F_m^{*}(x,c):=P\left(\sqrt{m-c}{R}_m\le x\right)=\mathsf{\Phi }(x)+\frac{x^3+(2(c-1)-3)x}{4(m-c)}\phi (x)+\mathcal{O}(m^{-3/2}),\end{array}$$

(7)

where $\mathsf{\Phi }(x)={\int }_{-\infty }^x\phi (y)dy$ is the standard normal distribution function. Note that in Konishi [16] the sample size (in our case the dimension of vectors) is $m+1$ and $c=1+2\mathsf{\Delta }$ with Konishi’s correcting constant $\Delta$. Moreover, (7) follows from the more general Theorem 2.2 in the mentioned paper for independent components in the pairs $(X_k{Y}_k)$, $k=1,\dots ,m$.

In Christoph et al. [17], computable error bounds of approximations in (7) with $c=2$ and $c=2.5$ of order $\mathcal{O}(m^{-2})$ for all $m\ge 7$ are proved:

$${sup}_x\left|P\left(\sqrt{m-2.5}{R}_m\le x\right)-\mathsf{\Phi }(x)-\frac{x^3\phi (x)}{4(m-2.5)}\right|\le \frac{B_m}{{(m-2.5)}^2}\le \frac{B}{m^2}$$

(8)

and

$${sup}_x\left|P\left(\sqrt{m-2}{R}_m\le x\right)-\mathsf{\Phi }(x)-\frac{(x^3-x)\phi (x)}{4(m-2)}\right|\le \frac{B_m^{*}}{{(m-2)}^2}\le \frac{B^{*}}{m^2}$$

(9)

where for some $m\ge 7$ constants $B_m$ and $B_m^{*}$ are calculated and presented in Table 1 in Christoph et al. [17]: i.e., $B_7=1.875$, $B_7^{*}=2.083$ and $B_{50}=0.720$, $B_{50}^{*}=0.982$.

Usually, the asymptotic for ${\overline{R}}_m$ is (9), where $c=2$ since it is related to the t-distributed statistic $\sqrt{m-2}{R}_m/\sqrt{1-R_m^2}$. With the correcting constant $c=2.5$, one term in the asymptotic in (8) vanishes.

In order to use a transfer theorem from non-random to random dimension of the vectors, we prefer (7) with $c=0$. In a similar manner as proving (8) and (9) in Christoph et al. [17], one can verify the following inequalities for $m\ge 3$:

$$\begin{array}{c}\hfill {sup}_x\left|P\left(\sqrt{m}{R}_m\le x\right)-\mathsf{\Phi }(x)-\frac{{\displaystyle (x^3-5x)}}{{\displaystyle 4m}}\phi (x)\right|\le C_1{m}^{-2}.\end{array}$$

(10)

Let us consider now the connection between the correlation coefficient $R_m$ and the angle ${\theta }_m$ of the involved vectors ${\overrightarrow{\mathrm{X}}}_m,{\overrightarrow{\mathrm{Y}}}_m$:

$${\theta }_m=\mathrm{ang}({\overrightarrow{\mathrm{X}}}_m,{\overrightarrow{\mathrm{Y}}}_m).$$

(11)

Hall et al. [1] showed that under the given conditions

$${\theta }_m=\frac{1}{2}\pi +{\mathcal{O}}_p(m^{-1/2})\mathrm{as}m\to \infty ,$$

where ${\mathcal{O}}_p$ denotes the stochastic order. Since

$$cos{\theta }_m=\frac{\parallel {\overrightarrow{X}}_m{\parallel }^2+\parallel {\overrightarrow{Y}}_m{\parallel }^2-{\parallel {\overrightarrow{X}}_m-{\overrightarrow{Y}}_m\parallel }^2}{2\parallel {\overrightarrow{X}}_m\parallel \parallel {\overrightarrow{Y}}_m\parallel }=R_m({\overrightarrow{\mathrm{X}}}_m,{\overrightarrow{\mathrm{Y}}}_m)=R_m,$$

the computable error bounds for ${\theta }_m$ follows from computable error bounds for $R_m$.

For any fixed constant $c<m,$ and arbitrary x with $|x|<\sqrt{m-c}\pi /2$, we obtain for the angle ${\theta }_m:0<{\theta }_m<\pi$:

$$\begin{array}{cc}\hfill P\left(\sqrt{m-c}({\theta }_m-\pi /2)\le x\right)& =P\left({\theta }_m\le \pi /2+x/\sqrt{m-c}\right)\hfill \\ \hfill & =P\left(cos{\theta }_m\ge cos(\pi /2+x/\sqrt{m-c})\right)\hfill \\ \hfill & =P\left(R_m\ge -sin(x/\sqrt{m-c})\right)\hfill \\ \hfill & =P\left(\sqrt{m-c}{R}_m\le \sqrt{m-c}sin(x/\sqrt{m-c})\right)\hfill \end{array}$$

(12)

because $R_m$ is symmetric and $P(R_m\le x)=P(-R_m\le x)$.

Equation (12) shows the connection between the correlation coefficient $R_m$ and the angle ${\theta }_m$ among the vectors involved. In Christoph et al. [17], computable error bound of approximation in (8) are used to obtain similar bound for the approximation of the angle between two vectors, defined in (11). Here, the approximation (10) and (12) with $c=0$ lead for any $m\ge 3$ and for $|x|\le \pi \sqrt{m}/2$ to

$${sup}_x|P\left(\sqrt{m}({\theta }_m-\frac{\pi }{2})\le x\right)-\mathsf{\Phi }(x)-\frac{(1/3)x^3-5x}{4m}\phi (x)|\le C_1{m}^{-2}.$$

(13)

Many authors investigated limit theorems for the sums of random vectors when their dimension tends to infinity, see, e.g., Prokhorov [18]. In (6) and (7), the dimension m of the vectors ${\overrightarrow{\mathrm{X}}}_m$ and ${\overrightarrow{\mathrm{Y}}}_m$ tends to infinity.

Now, we consider the correlation coefficient of vectors ${\overrightarrow{\mathrm{X}}}_m$ and ${\overrightarrow{\mathrm{Y}}}_m$, where the non-random dimension m is replaced by a random dimension $N_n\in {\mathbb{N}}_{+}=\{1,2,\dots \}$ depending on some natural parameter $n\in {\mathbb{N}}_{+}$ and $N_n$ is independent of ${\overrightarrow{X}}_m$ and ${\overrightarrow{Y}}_m$ for any $m,n\in {\mathbb{N}}_{+}$. Define

$$R_{N_n}=\frac{{\sum }_{k=1}^{N_n}{X}_k{Y}_k}{\sqrt{{\sum }_{k=1}^{N_n}{X}_k^2{\sum }_{k=1}^{N_n}{Y}_k^2}}.$$

3. Statistical Models with a Random Number of Observations

Let $X_1,X_2,\dots \in \mathbb{R}=(-\infty \infty )$ and $N_1,N_2,\dots \in {\mathbb{N}}_{+}=\{1,2,\dots \}$ be random variables on the same probability space $\left(\mathsf{\Omega },\mathbb{A},\mathbb{P}\right)$. Let $N_n$ be a random size of the underlying sample, i.e., the random number of observations, which depends on parameter $n\in {\mathbb{N}}_{+}$. We suppose for each $n\in {\mathbb{N}}_{+}$ that $N_n\in {\mathbb{N}}_{+}$ is independent of random variables $X_1,X_2,\dots$ and $N_n\to \infty$ in probability as $n\to \infty$. Let $T_m:=T_m\left(X_1,\dots ,X_m\right)$ be some statistic of a sample with non-random sample size $m\in {\mathbb{N}}_{+}$. Define the random variable $T_{N_n}$ for every $n\in {\mathbb{N}}_{+}$:

$$T_{N_n}(\omega ):=T_{N_n(\omega )}\left(X_1(\omega ),\dots ,X_{N_n(\omega )}(\omega )\right),\omega \in \mathsf{\Omega },$$

i.e., $T_{N_n}$ is some statistic obtained from a random sample $X_1,X_2,\dots ,X_{N_n}$.

The randomness of the sample size may crucially change asymptotic properties of $T_{N_n}$, see, e.g., Gnedenko [7] or Gnedenko and Korolev [19].

3.1. Random Sums

Many models lead to random sums and random means

$$S_{N_n}={\sum }_{k=1}^{N_n}{X}_k\mathrm{and}{M}_{N_n}=\frac{1}{N_n}\sum _{k=1}^{N_n}{X}_k,.$$

(14)

A fundamental introduction to asymptotic distributions of random sums is given in Döbler [20].

It is worth mentioning that a suitable scaled factor by $S_{N_n}$ affects the type of limit distribution. In fact, consider random sum $S_{N_n}$ given in (14). For the sake of convenience, let $X_1,X_2,\dots$ be independent standard normal random variables and $N_n\in {\mathbb{N}}_{+}$ be geometrically distributed with $E(N_n)=n$ and independent of $X_1,X_2,\dots$. Then, one has

$$\begin{array}{cc}\hfill & \mathbb{P}\left(\frac{{\displaystyle 1}}{\sqrt{{\displaystyle N_n}}}{S}_{N_n}\le x\right)=\underset{-\infty }{\overset{x}{\int }}\frac{{\displaystyle 1}}{{\displaystyle \sqrt{2\pi }}}{e}^{-u^2/2}du\mathrm{for} \mathrm{all}n\in \mathbb{N},\end{array}$$

(15)

$$\begin{array}{cc}\hfill & \mathbb{P}\left(\frac{{\displaystyle 1}}{{\displaystyle \sqrt{\mathbb{E}(N_n)}}}{S}_{N_n}\le x\right)\to \underset{-\infty }{\overset{x}{\int }}\frac{{\displaystyle 1}}{{\displaystyle \sqrt{2}}}{e}^{-\sqrt{2}|u|}du\mathrm{as}n\to \infty ,\end{array}$$

(16)

$$\begin{array}{cc}\hfill & \mathbb{P}\left(\frac{{\displaystyle \sqrt{\mathbb{E}(N_n)}}}{{\displaystyle N_n}}{S}_{N_n}\le x\right)\to \underset{-\infty }{\overset{x}{\int }}{\left(2+u^2\right)}^{-3/2}du\mathrm{as}n\to \infty .\end{array}$$

(17)

We have three different limit distributions. The suitable scaled geometric sum $S_{N_n}$ is standard normal distributed or tends to the Laplace distribution with variance 1 depending on whether we take the random scaling factor $1/\sqrt{N_n}$ or the non-random scaling factor $1/\sqrt{\mathbb{E}{N}_n}$, respectively. Moreover, we get the Student distribution with two degrees of freedom as the limit distribution if we use scaling with the mixed factor $\sqrt{\mathbb{E}(N_n)}/N_n$. Similar results also hold for the normalized random mean $M_{N_n}=\frac{1}{N_n}{S}_{N_n}$.

Assertion (15) is obtained by conditioning and the stability of the normal law. Moreover, using Stein’s method, quantitative Berry–Esseen bounds in (15) and (16) for arbitrary centered random variables $X_1$ with $\mathbb{E}(|X_1{|}^3)<\infty$ were proved in (Chen et al. [21], Theorem 10.6), (Döbler [20] Theorems 2.5 and 2.7) and (Pike and Ren [22] Theorem 3), respectively. Statement (17) follows from (Bening and Korolev [23] Theorem 2.1).

First order asymptotic expansions are obtained for the distribution function of random sample mean and random sample median constructed from a sample with two different random sizes in Bening et al. [24] and in the conference paper Bening et al. [25]. The authors make use of the rate of convergence of $\mathbb{P}(N_n\le g_{n}x)$ to the limit distribution $H(x)$ with some $g_n\uparrow \infty$. In Christoph et al. [12], second order expansions for the normalized random sample sizes are proved, see below Propositions 1 and 2. These results allow for proving second order asymptotic expansions of random sample mean in Christoph et al. [12] and random sample median in Christoph et al. [13].

3.2. Transfer Proposition from Non-Random to Random Sample Sizes

Consider now the statistic $T_{N_n}=T_{N_n}\left({\overrightarrow{X}}_{N_n},{\overrightarrow{Y}}_{N_n}\right)$, where the dimension of the vectors ${\overrightarrow{X}}_{N_n},{\overrightarrow{Y}}_{N_n}$ is a random number $N_n\in {\mathbb{N}}_{+}$.

In order to avoid too long expressions and at the same time to preserve a necessary accuracy, we limit ourselves to obtaining limit distributions and terms of order $m^{-1}$ in the following non-asymptotic approximations with a bounds of order $m^{-a}$ for some $a>1$.

We suppose that the following condition on the statistic $T_m=T_m({\overrightarrow{X}}_m,{\overrightarrow{Y}}_m)$ with $\mathbb{E}{T}_m=0$ is met for a non-random sample size $m\in {\mathbb{N}}_{+}$:

Condition 1.

There exist differentiable bounded function$f_2(x)$with${sup}_x|x{f}_2^{\prime }(x)|<c_0$and real numbers$a>1$, $C_1>0$such that for all integer$m\ge 1$

$${sup}_x|\mathbb{P}\left(m^{\gamma }{T}_m\le x\right)-\mathsf{\Phi }(x)-m^{-1}{f}_2(x)|\le C_1{m}^{-a},$$

(18)

where$\gamma \in \{-1/2,0,1/2\}$.

Remark 1.

Relations (10) and (13) give the examples of statistics such that Condition 1 is met. For other examples of multivariate statistics of this kind, see Chapters 14–16 in Fujikoshi et al. [2].

Suppose that the limiting behavior of distribution functions of the normalized random size $N_n\in {\mathbb{N}}_{+}$ is described by the following condition.

Condition 2.

There exist a distribution function$H(y)$with$H(0+)=0$, a function of bounded variation$h_2(y)$, a sequence$0<g_n\uparrow \infty$and real numbers$b>0$and$C_2>0$such that for all integer$n\ge 1$

$$\left.\begin{array}{cc}{sup}_{y\ge 0}\left|\mathbb{P}\left(g_n^{-1}{N}_n\le y\right)-H(y)\right|\le C_2{n}^{-b},\hfill & 0<b\le 1\hfill \\ {sup}_{y\ge 0}\left|\mathbb{P}\left(g_n^{-1}{N}_n\le y\right)-H(y)-n^{-1}{h}_2(y)\right|\le C_2{n}^{-b},\hfill & b>1\hfill \end{array}\right\}$$

(19)

Remark 2.

In Propositions 1 and 2 below, we get the examples of discrete random variables $N_n$ such that Condition 2 is met.

Conditions 1 and 2 allow us to construct asymptotic expansions for distributions of randomly normalized statistics on the base of approximation results for normalized fixed-size statistics (see relation (18)) and for the random size of the underlying sample (see relation (19)). As a result, we obtain the following transfer theorem.

Theorem 1.

Let $|\gamma |\le K<\infty$ and both Conditions 1 and 2 be satisfied. Then, the following inequality holds for all $n\in {\mathbb{N}}_{+}$:

$${sup}_{x\in \mathbb{R}}|\mathbb{P}\left(g_n^{\gamma }{T}_{N_n}\le x\right)-G_n(x,1/g_n)|\le C_1\mathbb{E}\left(N_n^{-a}\right)+(C_3{D}_n+C_4)n^{-b},$$

(20)

$$G_n(x,1/g_n)={\int }_{1/g_n}^{\infty }\left(\mathsf{\Phi }(x{y}^{\gamma })+\frac{f_2(x{y}^{\gamma })}{g_{n}y}\right)d\left(H(y)+\frac{h_2(y)}{n}\right),$$

(21)

$$D_n=\underset{x}{sup}{\int }_{1/g_n}^{\infty }\left|\frac{{\displaystyle \partial }}{{\displaystyle \partial y}}\left(\mathsf{\Phi }(x{y}^{\gamma })+\frac{f_2(x{y}^{\gamma })}{y{g}_n}\right)\right|dy,$$

(22)

where $a>1,b>0,f_2(z),h_2(y)$ are given in (18) and (19). The constants $C_1,C_3,C_4$ do not depend on n.

Remark 3.

Later, we use only the cases $\gamma \in \{-1/2,0,1/2\}$.

Remark 4.

The domain $[1/g_n,\infty )$ of integration in (21) depends on $g_n$. Thus, it is not clear how $G_n(x,1/g_n)$ is represented as a polynomial in $g_n^{-1}$ and $n^{-1}$. To overcome this problem (see (26)), we prove the following theorem.

Theorem 2.

Under the conditions of Theorem 1 and the additional conditions on functions $H(.)$ and $h_2(.)$, depending on the convergence rate b in (19):

$$H(1/g_n)\le c_1{g}_n^{-b},b>0,$$

(23)

$$\left.\begin{array}{cc}i:\hfill & {\int }_0^{1/g_n}{y}^{-1}dH(y)\le c_2{g}_n^{-b+1},\hfill \\ ii:\hfill & h_2(0)=0and|h_2(1/g_n)|\le c_{3}n{g}_n^{-b},\hfill \\ iii:\hfill & {\int }_0^{1/g_n}{y}^{-1}|h_2(y)|dy\le c_{4}n{g}_n^{-b},\hfill \end{array}\right\}forb>1,$$

(24)

we obtain for the function $G_n(x,1/g_n)$ defined in (21):

$${sup}_x|G_n(x,1/g_n)-G_{n,2}(x)|\le C{g}_n^{-b}+{sup}_x\left(|I_1(x,n)|{\mathbb{I}}_{\{b<1\}}(b)+|I_2(x,n)|\right)$$

(25)

with

$$G_{n,2}(x)=\left\{\begin{array}{cc}\underset{0}{\overset{\infty }{\int }}\mathsf{\Phi }(x{y}^{\gamma })dH(y),\hfill & \hfill 0<b<1,\\ \underset{0}{\overset{\infty }{\int }}\mathsf{\Phi }(x{y}^{\gamma })dH(y)+\frac{{\displaystyle 1}}{{\displaystyle g_n}}\underset{0}{\overset{\infty }{\int }}\frac{{\displaystyle f_2(x{y}^{\gamma })}}{{\displaystyle y}}dH(y),\hfill & \hfill b=1\\ \underset{0}{\overset{\infty }{\int }}\mathsf{\Phi }(x{y}^{\gamma })dH(y)+\frac{{\displaystyle 1}}{{\displaystyle g_n}}\underset{0}{\overset{\infty }{\int }}\frac{{\displaystyle f_2(x{y}^{\gamma })}}{{\displaystyle y}}dH(y){\mathbb{I}}_{\{\gamma =0\}}(\gamma )+\frac{{\displaystyle 1}}{{\displaystyle n}}\underset{0}{\overset{\infty }{\int }}\mathsf{\Phi }(x{y}^{\gamma })d{h}_2(y),\hfill & \hfill b>1.\end{array}\right.$$

(26)

$$I_1(x,n)={\int }_{1/g_n}^{\infty }\frac{f_2(x{y}^{\gamma })}{g_{n}y}dH(y)forb\le 1and{I}_2(x,n)={\int }_{1/g_n}^{\infty }\frac{f_2(x{y}^{\gamma })}{g_{n}ny}d{h}_2(y)forb>1.$$

Remark 5.

The additional conditions (23) and (24) guarantee to extend the integration range from $[1/g_n,\infty )$ to $(0,\infty )$ of the integrals in (26).

Theorems 1 and 2 are proved in Appendix A.1.

4. Auxiliary Propositions and Lemmas

Consider the standardized correlation coefficient (5) having density (6) with correcting real constant $c=0$ and standardized angle $\sqrt{m}({\theta }_m-\pi /2)$, see (12). By (10) and (13) for $m\ge 3$, we have

$$\begin{array}{c}\hfill {sup}_x\left|P\left(\sqrt{m}{R}_m\le x\right)-\mathsf{\Phi }(x)-\frac{{\displaystyle (x^3-5x)}}{{\displaystyle 4m}}\phi (x)\right|\le C_1{m}^{-2},m\in {\mathbb{N}}_{+},\end{array}$$

(27)

and for the angle ${\theta }_m$ between the vectors for $|x|\le \pi \sqrt{m}/2$

$${sup}_x|P\left(\sqrt{m}({\theta }_m-\frac{\pi }{2})\le x\right)-\mathsf{\Phi }(x)-\frac{(1/3)x^3-5x}{4m}\phi (x)|\le C_1{m}^{-2},m\in {\mathbb{N}}_{+},$$

(28)

where (27) and (28) for $m=1$ and $m=2$ are trivial and $C_1$ does not depend on m.

Suppose $f_2(x;a)=(a{x}^3-5x)\phi (x)/4$ with $a=1$ or $a=1/3$ when (27) or (28) are considered. Since a product of polynomials in x with $\phi (x)$ is always bounded, numerical calculus leads to

$$\begin{array}{c}\hfill {sup}_x|x{f}_2^{\prime }(x;a)|={sup}_x|x(a{x}^4-(3a+5)x^2+5)|\phi (x)/4\le 0.4.\end{array}$$

Condition 1 of the transfer Theorem 1 to the statistics $R_m$ and ${\theta }_m$ are satisfied with $c_0=0.4$ and $a=2$.

Next, we estimate $D_n(x)$ defined in (22).

Lemma 1.

Let $g_n$ a sequence with $0<g_n\uparrow \infty$ as $n\to \infty$. Then, with some $0<c(\gamma ,a)<\infty$, we obtain with $a=1$ and $a=1/3$:

$$D_n=\underset{x}{sup}{\int }_{1/g_n}^{\infty }\left|\frac{{\displaystyle \partial }}{{\displaystyle \partial y}}\left(\mathsf{\Phi }(x{y}^{\gamma })+\frac{f_2(x{y}^{\gamma };a)}{y{g}_n}\right)\right|dy\le \frac{1}{2}+\frac{c(\gamma ,a)}{4}.$$

In the next subsection, we consider the cases when the random dimension $N_n$ is negative binomial distributed with success probability $1/n$.

4.1. Negative Binomial Distribution as Random Dimension of the Normal Vectors

Let the random dimension $N_n(r)$ of the underlying normal vectors be negative binomial distributed (shifted by 1) with parameters $1/n$ and $r>0$, having probability mass function

$$\mathbb{P}(N_n(r)=j)=\frac{\mathsf{\Gamma }(j+r-1)}{\mathsf{\Gamma }(j)\mathsf{\Gamma }(r)}{\left(\frac{1}{n}\right)}^r{\left(1-\frac{1}{n}\right)}^{j-1},j=1,2,\dots$$

(29)

with $\mathbb{E}(N_n(r))=r(n-1)+1$. Then, $\mathbb{P}(N_n(r)/g_n\le x)$ tends to the Gamma distribution function $G_{r,r}(x)$ with the shape and rate parameters $r>0$, having density

$$g_{r,r}(x)=\frac{r^r}{\mathsf{\Gamma }(r)}{x}^{r-1}{e}^{-rx}{\mathbb{I}}_{(0\infty )}(x),x\in \mathbb{R}.$$

(30)

If the statistic $T_m$ is asymptotically normal, the limit distribution of the standardized statistic $T_{N_n(r)}$ with random size $N_n(r)$ is Student’s t-distribution $S_{2r}(x)$ having density

$$s_{\nu }(x)=\frac{\mathsf{\Gamma }((\nu +1)/2)}{\sqrt{\nu \pi }\mathsf{\Gamma }(\nu /2)}{\left(1+\frac{x^2}{\nu }\right)}^{-(\nu +1)/2},\nu >0,x\in \mathbb{R},$$

(31)

with $\nu =2r$, see Bening and Korolev [23] or Schluter and Trede [26].

Proposition 1.

Let $r>0$, discrete random variable $N_n(r)$ have probability mass function (29) and $g_n:=\mathbb{E}{N}_n(r)=r(n-1)+1$. For $x>0$ and all $n\in \mathbb{N}$ there exists a real number $C_2(r)>0$ such that

$${sup}_{x\ge 0}\left|\mathbb{P}\left(\frac{N_n(r)}{g_n}\le x\right)-G_{r,r}(x)-\frac{h_{2;r}(x)}{n}\right|\le C_2(r)n^{-min\{r,2\}},$$

(32)

where

$$h_{2;r}(x)=\left\{\begin{array}{cc}0,\hfill & forr\le 1,\hfill \\ \frac{{\displaystyle g_{r,r}(x)\left((x-1)(2-r)+2Q_1\left(g_{n}x\right)\right)}}{{\displaystyle 2r}},\hfill & forr>1.\hfill \end{array}\right.$$

$$Q_1(y)=1/2-(y-[y])and[.]\mathit{denotes} \mathit{the} \mathit{integer} \mathit{part} \mathit{of} a \mathit{number}.$$

(33)

Figure 1 shows the approximation of $\mathbb{P}\left(N_n(r)\le (r(n-1)+1)x\right)$ by $G_{2,2}(x)$ and $G_{2,2}(x)+h_2(x)/n$.

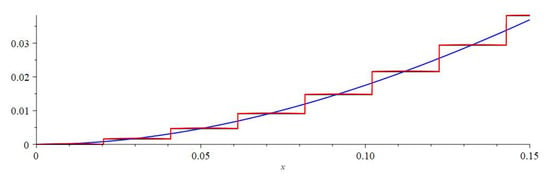
Figure 1. Distribution function $\mathbb{P}\left(N_n(r)\le (r(n-1)+1)x\right)$ (black line, almost covered by the red line), the limit law $G_{2,2}(x)$ (blue line) and the second approximation $G_{2,2}(x)+h_2(x)/n$ (red line) with $n=25$ and $r=2$.

Remark 6.

The convergence rate for $r\le 1$ is given in Bening et al. [24] or Gavrilenko et al. [27]. The Edgeworth expansion for $r>1$ is proved in Christoph et al. [12], Theorem 1. The jumps of the sample size $N_n(r)$ have an effect only on the function $Q_1(.)$ in the term $h_{2;r}(.)$.

The negative binomial random variable $N_n$ satisfies Condition 2 of the transfer Theorem 1 with $H(x)=G_{r,r}(x)$, $h_2(x)=h_{2;r}(x)$, $g_n=\mathbb{E}{N}_n(r)=r(n-1)+1$ and $b=min\{r2\}$.

Lemma 2.

In Theorem 2 the additional conditions (23) and (24) are satisfied with $H(x)=G_{r,r}(x)$, $h_2(x)=h_{2;r}(x)$, $g_n=\mathbb{E}{N}_n(r)=r(n-1)+1$ and $b=min\{r2\}$. Moreover, one has for $\gamma \in \{-1/2,0,1/2\}$ and $f_2(z;a)=(a{z}^3-5z)\phi (z)/4$, with $a=1$ or $a=1/3$:

$$|I_1(x,n)|=\left\{\begin{array}{cc}\left|{\int }_{1/g_n}^{\infty }\frac{{\displaystyle f_2(x{y}^{\gamma };a)}}{{\displaystyle g_{n}y}}d{G}_{r,r}(y)\right|\le c_5{g}_n^{-r}\hfill & r<1,\hfill \\ |{\int }_{1/n}^{\infty }\frac{{\displaystyle f_2(x{y}^{\gamma };a)}}{{\displaystyle ny}}d{G}_{1,1}(y)-n^{-1}{f}_2(x;a)lnn{\mathbb{I}}_{\{\gamma =0\}}(\gamma )|\le c_6{n}^{-1},\hfill & r=1,\hfill \end{array}\right.$$

(34)

$$|I_2(x,n)|=\left|{\int }_{1/g_n}^{\infty }\frac{{\displaystyle f_2(x{y}^{\gamma };a)}}{{\displaystyle g_{n}ny}}d{h}_{2;r}(y)\right|\le \left\{\begin{array}{cc}{c}_7{g}_n^{-r},\hfill & r>1,r\ne 2,\hfill \\ \left(c_7+c_{8}lnn{\mathbb{I}}_{\{\gamma =0\}}(\gamma )\right)g_n^{-2},\hfill & r=2.\hfill \end{array}\right.$$

(35)

Furthermore, we have

$$0\le g_n^{-1}-{(rn)}^{-1}\le (r-1){(rn)}^{-2}{e}^{-1/2}forr>1,n\ge 2.$$

(36)

In addition to the expansion of $N_n(r)$ a bound of $\mathbb{E}{(N_n(r))}^{-a}$ is required, where $m^{-a}$ is rate of convergence of Edgeworth expansion for $T_m$, see (18).

Lemma 3.

Let $r>0$, $\alpha >0$ and the random variable $N_n(r)$ is defined by (29). Then,

$$\mathbb{E}{\left(N_n(r)\right)}^{-\alpha }\le C(r)\left\{\begin{array}{cc}{n}^{-min\{r,\alpha \}},\hfill & r\ne \alpha \hfill \\ ln(n)n^{-\alpha },\hfill & r=\alpha \hfill \end{array}\right.$$

(37)

and the convergence rate in case $r=\alpha$ cannot be improved.

4.2. Maximum of n Independent Discrete Pareto Random Variables Is the Dimension of the Normal Vectors

Let $Y(s)\in \mathbb{N}$ be discrete Pareto II distributed with parameter $s>0$, having probability mass and distribution functions

$$\mathbb{P}(Y(s)=k)=\frac{s}{s+k-1}-\frac{s}{s+k}\mathrm{and}\mathbb{P}\left(Y(s)\le k\right)=\frac{k}{s+k},k\in \mathbb{N},$$

(38)

which is a particular class of a general model of discrete Pareto distributions, obtained by discretization continuous Pareto II (Lomax) distributions on integers, see Buddana and Kozubowski [28].

Now, let $Y_1(s),Y_2(s),\dots$, be independent random variables with the same distribution (38). Define for $n\in \mathbb{N}$ and $s>0$ the random variable

$$N_n(s)=\underset{1\le j\le n}{max}{Y}_j(s)\mathrm{with}\mathbb{P}(N_n(s)\le k)={\left(\frac{k}{s+k}\right)}^n,n\in \mathbb{N}.$$

(39)

It should be noted that the distribution of $N_n(s)$ is extremely spread out on the positive integers.

In Christoph et al. [12], the following Edgeworth expansion was proved:

Proposition 2.

Let the discrete random variable $N_n(s)$ have distribution function (39). For $x>0$, fixed $s>0$ and all $n\in \mathbb{N}$, then there exists a real number $C_3(s)>0$ such that

$$\underset{y>0}{sup}\left|\mathbb{P}\left(\frac{N_n(s)}{n}\le y\right)-H_s(y)-\frac{h_{2;s}(y)}{n}\right|\le \frac{C_3(s)}{n^2},$$

$$H_s(y)=e^{-s/y}and{h}_{2;s}(y)=s{e}^{-s/y}\left(s-1+2Q_1(ny)\right)/\left(2y^2\right),y>0$$

(40)

where $Q_1(y)$ is defined in (33).

Remark 7.

The continuous function $H_s(y)=e^{-s/y}{\mathbb{I}}_{(0\infty )}(y)$ with parameter $s>0$ is the distribution function of the inverse exponential random variable $W(s)=1/V(s)$, where $V(s)$ is exponentially distributed with rate parameter $s>0$. Both $H_s(y)$ and $\mathbb{P}(N_n(s)\le y)$ are heavy tailed with shape parameter 1.

Remark 8.

Therefore, $\mathbb{E}\left(N_n(s)\right)=\infty$ for all $n\in \mathbb{N}$ and $\mathbb{E}\left(W(s)\right)=\infty$. Moreover:

• First absolute pseudo moment ${\nu }_1={\int }_0^{\infty }x|d\left(\mathbb{P}\left(N_n(s)\le nx\right)-e^{-s/x}\right)|=\infty$,
• Absolute difference moment ${\chi }_u={\int }_0^{\infty }{x}^{u-1}|\mathbb{P}\left(N_n(s)\le nx\right)-e^{-s/x}|dx<\infty$
  for $1\le u<2$, see Lemma 2 in Christoph et al. [12].

On pseudo moments and some of their generalizations, see Chapter 2 in Christoph and Wolf [29].

Lemma 4.

In Transfer Theorem 2, the additional conditions (23) and (24) are satisfied with $H(y)=H_s(y)=e^{-s/y}$, $h_2(y)=h_{2;s}(y)=s{e}^{-s/y}\left(s-1+2Q_1(ny)\right)/\left(2y^2\right),y>0$, $g_n=n$ and $b=2$. Moreover, one has for $|\gamma |\le K<\infty$ and $f_2(z;a)=(a{z}^3-5z)\phi (z)/4$, with $a=1$ or $a=1/3$:

$$I_2(x,n)=\left|{\int }_{1/n}^{\infty }\frac{{\displaystyle f_2(x{y}^{\gamma };a)}}{{\displaystyle n^{2}y}}d{h}_{2;s}(y)\right|\le C(s)n^{-2}.$$

Lemma 5.

For random size $N_n(s)$ with probabilities (39) with reals $s\ge s_0>0$ and arbitrary small $s_0>0$ and $n\ge 1$, we have

$$\mathbb{E}{\left(N_n(s)\right)}^{-\alpha }\le C(s)n^{-\alpha }.$$

(41)

The Lemmas are proved in Appendix A.2.

5. Main Results

Consider the sample correlation coefficient $R_m=R_m({\overrightarrow{\mathrm{X}}}_m,{\overrightarrow{\mathrm{Y}}}_m)$, given in (4) and the two statistics $R_m^{*}=\sqrt{m}{R}_m$ and $R_m^{**}=m{R}_m$ which differ from $R_m$ by scaling factors. Hence, by (10),

$$\mathbb{P}(\sqrt{m}{R}_m\le x)=\mathbb{P}(R_m^{*}\le x)=\mathbb{P}\left(\frac{1}{\sqrt{m}}{R}_m^{**}\le x\right)=\mathsf{\Phi }(x)+\frac{{\displaystyle (x^3-5x)}}{{\displaystyle 4m}}\phi (x)+r(m)$$

(42)

with $|r(m)|\le C{m}^{-2}$.

Let ${\theta }_m$ be the angle between the vectors ${\overrightarrow{\mathrm{X}}}_m$ and ${\overrightarrow{\mathrm{Y}}}_m$. Contemplate the statistics ${\mathsf{\Theta }}_m={\theta }_m-\pi /2$, ${\mathsf{\Theta }}_m^{*}=\sqrt{m}({\theta }_m-\pi /2)$ and ${\mathsf{\Theta }}_m^{**}=m({\theta }_m-\pi /2)$ which differ only in scaling. Then, by (13),

$$\mathbb{P}(\sqrt{m}{\mathsf{\Theta }}_m\le x)=\mathbb{P}({\mathsf{\Theta }}_m^{*}\le x)=\mathbb{P}\left(\frac{1}{\sqrt{m}}{\mathsf{\Theta }}_m^{**}\le x\right)=\mathsf{\Phi }(x)+\frac{{\displaystyle \left((1/3)x^3-5x\right)}}{{\displaystyle 4m}}\phi (x)+r^{*}(m)$$

with $|r^{*}(m)|\le C{m}^{-2}$.

Consider now the statistics $R_{N_n}$, $R_{N_n}^{*}$ and $R_{N_n}^{**}$ as well as ${\mathsf{\Theta }}_{N_n}$, ${\mathsf{\Theta }}_{N_n}^{*}$ and ${\mathsf{\Theta }}_{N_n}^{**}$ when the vectors have random dimension $N_n$. The normalized statistics have different limit distributions as $n\to \infty$.

5.1. The Random Dimension $N_n=N_n(r)$ Is Negative Binomial Distributed

Let the random dimension $N_n(r)$ be negative binomial distributed with probability mass function (29) and $g_n=\mathbb{E}{N}_n(r)=r(n-1)+1$. “The negative binomial distribution is one of the two leading cases for count models, it accommodates the overdispersion typically observed in count data (which the Poisson model cannot)”, see Schluter and Trede [26].

It follows from Theorems 1 and 2 and Proposition 1 that if limit distributions for $\mathbb{P}\left(g_n^{\gamma }{N}_n{(r)}^{1/2-\gamma }{R}_{N_n(r)}\le x\right)$ for $\gamma \in \{1/2,0-1/2\}$ exist they are ${\int }_0^{\infty }\mathsf{\Phi }(x{y}^{\gamma })d{G}_{r,r}(y)$ with densities given bellow in the proof of the corresponding theorems:

$$\frac{r^r}{\sqrt{2\pi }\mathsf{\Gamma }(r)}{\int }_0^{\infty }{y}^{r-1/2}{e}^{-(x{y}^{\gamma }+ry)}dy=\left\{\begin{array}{cc}{s}_{2r}(x)=\frac{{\displaystyle \mathsf{\Gamma }(r+1/2)}}{{\displaystyle \sqrt{2r\pi }\mathsf{\Gamma }(r)}}{\left(1+\frac{{\displaystyle x^2}}{{\displaystyle 2r}}\right)}^{-(r+1/2)},\hfill & \gamma =1/2,\hfill \\ \phi (x)=\frac{{\displaystyle 1}}{{\displaystyle \sqrt{2\pi }}}{e}^{-x^2/2},\hfill & \gamma =0,\hfill \\ l_1(x)=\frac{{\displaystyle 1}}{{\displaystyle \sqrt{2}}}{e}^{-\sqrt{2}|x|},\mathrm{for}r=1,\hfill & \gamma =-1/2,\hfill \end{array}\right.$$

(43)

where in case $\gamma =-1/2$ for $r\ne 1$ generalized Laplace distributions occur.

5.1.1. Student’s t-Distribution

We start with the case $\gamma =1/2$ in Theorems 1 and 2. Consider the statistic ${\overline{R}}_{N_n(r)}=\sqrt{g_n}{R}_{N_n(r)}$. The limit distribution is the Student’s t-distribution $S_{2r}(x)$ with $2r$ degrees of freedom with density (31).

Theorem 3.

Let $r>0$ and (29) be the probability mass function of the random dimension $N_n=N_n(r)$ of the vectors under consideration. If the representation (42) for the statistic $R_m$ and the inequality (32) with $g_n=\mathbb{E}{N}_n(r)=r(n-1)+1$ hold, then there exists a constant $C_r$ such that for all $n\in {\mathbb{N}}_{+}$

$$\underset{x}{sup}\left|\mathbb{P}\left(\sqrt{g_n}{R}_{N_n(r)}\le x\right)-S_{2r;n}(x;1)\right|\le C_r\left\{\begin{array}{cc}{n}^{-min\{r,2\}},\hfill & r\ne 2,\hfill \\ ln(n)n^{-2},\hfill & r=2,\hfill \end{array}\right.$$

(44)

where

$$S_{2r;n}(x;a)=S_{2r}(x)+\frac{s_{2r}(x)}{rn}\left(a{x}^3-\frac{10rx+5x^3}{2r-1}+\frac{(2-r)(x^3+x)}{4(2r-1)}\right).$$

(45)

Moreover, the scaled angle ${\theta }_{N_n(r)}$ between the vectors ${\overrightarrow{\mathrm{X}}}_{N_n(r)}$ and ${\overrightarrow{\mathrm{Y}}}_{N_n(r)}$ allows the estimate

$${sup}_x\left|\mathbb{P}\left(\sqrt{g_n}({\theta }_{N_n(r)}-\pi /2)\le x\right)-S_{2r;n}(x;1/3)\right|\le C_r\left\{\begin{array}{cc}{n}^{-min\{r,2\}},\hfill & r\ne 2,\hfill \\ ln(n)n^{-2},\hfill & r=2,\hfill \end{array}\right.$$

where $S_{2r;n}(x;1/3)$ is given in (45) with $a=1/3$.

Figure 2 shows the advantage of the Chebyshev–Edgeworth expansion versus the limit law in approximating the empirical distribution function.

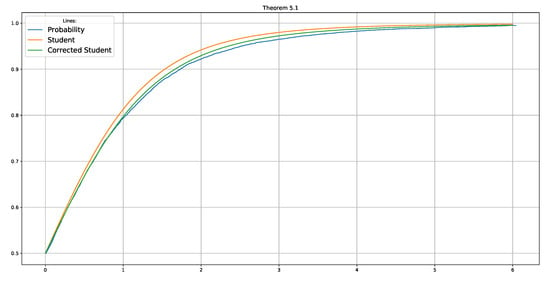
Figure 2. Empirical version of $\mathbb{P}\left(\sqrt{g_n}{R}_{N_n(r)}\le x\right)$ (blue line), limit Student law $S_{2r}(x)$ (orange line) and second approximation $S_{2r;n}(x;1)$ (green line) for the correlation coefficient for pairs of normal vectors with random dimension $N_{25}(2)$. Here, $x>0,n=25$ and $r=2$.

Remark 9.

The limit Student’s t-distribution $S_{2r}(x)$ is symmetric and a generalized hyperbolic distribution which can be written as a regularized incomplete beta function $I_z(a,b)$. For $x>0$:

$$S_{2r}(x)={\int }_{-\infty }^x{s}_{2r}(u)du=\frac{1}{2}\left(1+I_{2r/(x^2+2r)}(1/2,r)\right)and{I}_z(a,b)=\frac{\mathsf{\Gamma }(a+b)}{\mathsf{\Gamma }(a)\mathsf{\Gamma }(b)}{\int }_0^z{t}^{a-1}{(1-t)}^{b-1}.$$

Remark 10.

For integer values $\nu =2r\in \{1,2,\dots \}$ the Student’s t-distribution $S_{2r}(x)$ is computable in closed form:

$$the Cauchy law{S}_1(x)=\frac{1}{2}+\frac{1}{\pi }arctan(x),S_2(x)=\frac{1}{2}+\frac{x}{2\sqrt{2+x^2}},$$

$$S_3(x)=\frac{1}{2}+\frac{1}{\pi }\left(\frac{x}{\sqrt{3}(1+x^2/3)}+arctan(x/\sqrt{3})\right)and{S}_4(x)=\frac{1}{2}+\frac{27(x^2+3)x(2x^2+9)}{8{(3x^2+9)}^{5/2}}.$$

Remark 11.

If the dimension of the vectors has the geometric distribution $N_n(1)$, then asymptotic distribution of the sample coefficient is the Student law $S_2(x)$ with two degrees of freedom.

Remark 12.

The Cauchy limit distribution occurs when the dimension of the vectors has distribution $N_n(1/2)$.

Remark 13.

The Student’s t-distributions $S_{2r}(x)$ are heavy tailed and their moments of orders $\alpha \ge 2r$ do not exist.

5.1.2. Standard Normal Distribution

Let $\gamma =0$ in the Theorems 1 and 2 examining the statistics $R_{N_n(r)}^{*}$ and ${\mathsf{\Theta }}_{N_n(r)}^{*}=\sqrt{N_n(r)}({\theta }_{N_n(r)}-\pi /2)$.

Theorem 4.

Let $r>0$ and $N_n=N_n(r)$ be the random vector dimension having probability mass function (29). If the representation (42) for the statistic $R_m$ and the inequality (32) with $g_n=\mathbb{E}{N}_n(r)=r(n-1)+1$ hold, then there exists a constant $C_r$ such that for all $n\in {\mathbb{N}}_{+}$

$$\underset{x}{sup}\left|\mathbb{P}\left(\sqrt{N_n(r)}{R}_{N_n(r)}\le x\right)-{\mathsf{\Phi }}_{n;2}(x;1)\right|\le C_r\left\{\begin{array}{cc}{n}^{-min\{r,2\}},\hfill & r\ne 2,\hfill \\ ln(n)n^{-2},\hfill & r=2,\hfill \end{array}\right.$$

(46)

where

$${\mathsf{\Phi }}_{n;2}(x;a)=\mathsf{\Phi }(x)+\frac{\phi (x)}{n}\left(\frac{{\displaystyle (a{x}^3-5x)lnn}}{{\displaystyle 4}}{\mathbb{I}}_{\{r=1\}}(r)+\frac{\mathsf{\Gamma }(r-1)(a{x}^3-5x)}{4\mathsf{\Gamma }(r)}{\mathbb{I}}_{\{r>1\}}(r)\right).$$

(47)

Moreover, the scaled angle ${\theta }_{N_n(r)}^{*}$ between the vectors ${\overrightarrow{\mathrm{X}}}_{N_n(r)}$ and ${\overrightarrow{\mathrm{Y}}}_{N_n(r)}$ allows the estimate

$${sup}_x\left|\mathbb{P}\left(\sqrt{N_n(r)}({\theta }_{N_n(r)}-\pi /2)\le x\right)-{\mathsf{\Phi }}_{n;2}(x;1/3)\right|\le C_r\left\{\begin{array}{c}{n}^{-min\{r,2\}},r\ne 2,\hfill \\ ln(n)n^{-2},r=2,\hfill \end{array}\right.$$

where ${\mathsf{\Phi }}_{n;2}(x;1/3)$ is given in (47) with $a=1/3$.

Figure 3 shows that the second order Chebyshev–Edgeworth expansion approximates the empirical distribution function better than the limit normal distribution.

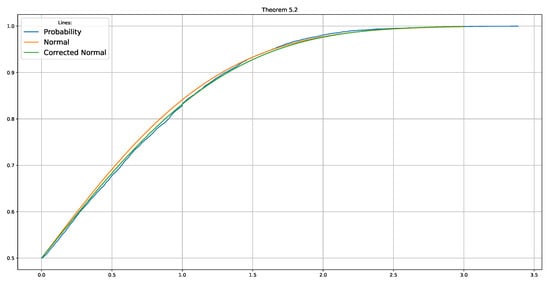
Figure 3. Empirical version of $\mathbb{P}\left(\sqrt{N_n(r)}{R}_{N_n(r)}\le x\right)$ (blue line), limit normal law $\mathsf{\Phi }(x)$ (orange line) and second approximation ${\mathsf{\Phi }}_{n;2}(x;1)$ (green line) for the correlation coefficient for pairs of normal vectors with random dimension $N_{25}(2)$. Here, $x>0,n=25$ and $r=2$.

Remark 14.

When the distribution function of a statistic $T_m$ without standardization tends to the standard normal distribution $\mathsf{\Phi }(x)$, i.e., $\mathbb{P}(T_m\le x)\to \mathsf{\Phi }(x)$, then the limit law for $\mathbb{P}(T_{N_n}\le x)$ remains the standard normal distribution $\mathsf{\Phi }(x)$.

5.1.3. Generalized Laplace Distribution

Finally, we use $\gamma =-1/2$ in Theorems 1 and 2 examining the statistic $g_n^{-1/2}{R}_{N_n(r)}^{**}$. Theorems 1 and 2 state that if there exists a limit distribution of $\mathbb{P}\left(g_n^{-1/2}{R}_{N_n}^{**}\le x\right)$ as $n\to \infty$ then it has to be a scale mixture of normal distributions with zero mean and gamma distribution:

$$L_r(x)={\int }_0^{\infty }\mathsf{\Phi }(x{y}^{-1/2})d{G}_{r,r}(y)$$

having density, see formula (A9) in the proof of Theorem 5:

$$l_r(x)=\frac{r^r}{\mathsf{\Gamma }(r)}{\int }_0^{\infty }\phi (x{y}^{-1/2})y^{r-3/2}{e}^{-ry}dy=\frac{2r^r}{\mathsf{\Gamma }(r)\sqrt{2\pi }}{\left(\frac{|x|}{\sqrt{2r}}\right)}^{r-1/2}{K}_{r-1/2}(\sqrt{2r}|x|).$$

(48)

where $K_{\alpha }(u)$ is the α-order Macdonald function or $\alpha$-order modified Bessel function of the third kind. See, e.g., Oldham et al. [30], Chapter 51, or Kotz et al. [31], Appendix, for properties of these functions.

For integer $r=1,2,3,\dots$ these densities $l_r(x)$, so-called Sargan densities, and their distribution functions are computable in closed forms:

$$\left.\begin{array}{ccc}{l}_1(x)=\frac{{\displaystyle 1}}{{\displaystyle \sqrt{2}}}{e}^{-\sqrt{2}|x|}\hfill & \mathrm{and}\hfill & L_1(x)=1-\frac{{\displaystyle 1}}{{\displaystyle 2}}{e}^{-\sqrt{2}|x|},x>0\hfill \\ l_2(x)=\left(\frac{{\displaystyle 1}}{{\displaystyle 2}}+|x|\right)e^{-2|x|}\hfill & \mathrm{and}\hfill & L_2(x)=1-\frac{{\displaystyle 1}}{{\displaystyle 2}}(1+x)e^{-2|x|},x>0\hfill \\ l_3(x)=\frac{{\displaystyle 3\sqrt{6}}}{{\displaystyle 16}}\left(1+\sqrt{6}|x|+2x^2\right)e^{-\sqrt{6}|x|})\hfill & \mathrm{and}\hfill & L_3(x)=1-\left(\frac{{\displaystyle 1}}{{\displaystyle 2}}+\frac{{\displaystyle 5\sqrt{6}x}}{{\displaystyle 16}}+\frac{{\displaystyle 3x^2}}{{\displaystyle 8}}\right)e^{-\sqrt{6}|x|},\hfill \end{array}\right\}$$

(49)

where $L_r(-x)=1-L_r(x)$ for $x\ge 0$.

The standard Laplace distribution is $L_1(x)$ with variance 1 and density $l_1(x)$ given in (49). Therefore, Sargans distributions are a kind of generalizations of the standard Laplace distribution.

Theorem 5.

Let $r=1,2,3$ and (29) be probability mass function of the random dimension $N_n=N_n(r)$ of the vectors under consideration. If the representation (42) for the statistic $R_m$ and the inequality (32) for $N_n(r)$ with $g_n=\mathbb{E}{N}_n(r)=r(n-1)+1$ hold, then there exists a constant $C_r$ such that for all $n\in {\mathbb{N}}_{+}$

$$\underset{x}{sup}\left|\mathbb{P}\left(g_n^{-1/2}{N}_n(r)R_{N_n(r)}\le x\right)-L_{n;2}(x;1)\right|\le C_r\left\{\begin{array}{cc}{n}^{-min\{r,2\}},\hfill & r\ne 2,\hfill \\ ln(n)n^{-2},\hfill & r=2,\hfill \end{array}\right.$$

(50)

where

$$L_{n;2}(x;a)=\left\{\begin{array}{cc}{L}_1(x),\hfill & r=1,\hfill \\ L_2(x)+\frac{{\displaystyle ax|x|-5x\sqrt{2}}}{{\displaystyle 2(n-1)+1}}{e}^{-2|x|},\hfill & r=2,\hfill \\ L_3(x)+\frac{{\displaystyle 27}}{{\displaystyle 24(n-1)+8}}\left(\frac{{\displaystyle a{x}^3}}{{\displaystyle \sqrt{2}}}-\frac{{\displaystyle 5x|x|}}{{\displaystyle 6}}-\frac{{\displaystyle 5x}}{{\displaystyle 6\sqrt{6}}}\right)e^{-\sqrt{6}|x|}\hfill \\ +\frac{{\displaystyle 9x}}{{\displaystyle 2n}}\left(\frac{{\displaystyle 1}}{{\displaystyle 12\sqrt{6}}}+\frac{{\displaystyle |x|}}{{\displaystyle 12}}-\frac{{\displaystyle x^2}}{{\displaystyle 6\sqrt{6}}}\right)e^{-\sqrt{6}|x|},\hfill & r=3.\hfill \end{array}\right.$$

(51)

For arbitrary $r>0$, the approximation rate is given by:

$$\underset{x}{sup}\left|\mathbb{P}\left(g_n^{-1/2}{N}_n(r)R_{N_n(r)}\le x\right)-L_r(x)\right|\le C_r{n}^{-min\{r1\}}.$$

Moreover, the scaled angle $N_n(r){\theta }_{N_n(r)}$ between the vectors ${\overrightarrow{\mathrm{X}}}_{N_n(r)}$ and ${\overrightarrow{\mathrm{Y}}}_{N_n(r)}$ allows the estimate

$${sup}_x\left|\mathbb{P}\left(g_n^{-1/2}{N}_n(r){\theta }_{N_n(r)}\le x\right)-L_{n;2}(x;1/3)\right|\le C_r\left\{\begin{array}{cc}{n}^{-min\{r,2\}},\hfill & r\ne 2,\hfill \\ ln(n)n^{-2},\hfill & r=2,\hfill \end{array}\right.$$

where $L_{n;2}(x;1/3)$ is given in (51) with $a=1/3$.

Figure 4 shows that the Chebyshev–Edgeworth expansion approaches the empirical distribution function better than the limit Laplace law.

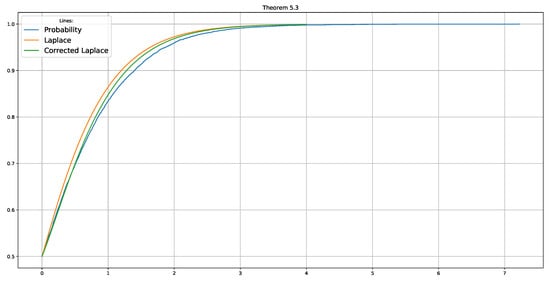
Figure 4. Empirical version of $\mathbb{P}\left(g_n^{-1/2}{N}_n(r)R_{N_n(r)}\le x\right)$ (blue line), limit Laplace law $L_r(x)$ (orange line) and second approximation $L_{n;2}(x;1)$ (green line) for the correlation coefficient for pairs of normal vectors with random dimension $N_{25}(2)$. Here, $x>0,n=25$ and $r=2$.

Remark 15.

One can find the distribution functions $L_r(x)$ for arbitrary $r>0$ with formula 1.12.1.3 in Prudnikov et al. [32]:

$$\begin{array}{cc}\hfill L_r(x)& =\frac{1}{2}+\frac{2r^r}{\sqrt{2\pi }\mathsf{\Gamma }(r)}{\int }_0^x{\left(\frac{|x|}{2r}\right)}^{r-1/2}{K}_{r-1/2}(\sqrt{2r}|x|)dx\hfill \\ \hfill & =\frac{1}{2}+\frac{x}{{(2r)}^{(r-1/2)/2}}\left(K_{r-1/2}(\sqrt{2r}x){\mathbf{L}}_{r-3/2}(\sqrt{2r}x)+K_{r-3/2}(\sqrt{2r}x){\mathbf{L}}_{r-1/2}(\sqrt{2r}x)\right).\hfill \end{array}$$

where ${\mathbf{L}}_{\alpha }(x)$ are the modified Struve functions of order α, for properties of modified Struve functions see, e.g., Oldham et al. [30], Section 57:13.

Remark 16.

The function (48) as density of a mixture of normal distributions with zero mean and random variance $W_r$ having gamma distribution $\mathbb{P}(W_r\le y)=G_{r,r}(y)$ is given also in Kotz et al. [31], Formula (4.1.32) with $\tau =r$, $\sigma =1/\sqrt{r}$, using Formula (A.0.4) with $\lambda =-r+3/2$ and the order-reflection formula $K_{-\alpha }(x)=K_{\alpha }(x)$. Such a variance gamma model is studied in Madan and Senata [33] for share market returns.

Remark 17.

A systematic exposition about the Laplace distribution and its numerous generalization and diverse applications one finds in the useful and interesting monography by Kotz et al. [31]. Here, these generalized Laplace distributions $L_1(x)$, $L_2(x)$ and $L_3(x)$ are the leading terms in the approximations of the sample correlation coefficient $R_{N_n(r)}^{**}$ of two Gaussian vectors with negative binomial distributed random dimension $N_n(r)$ and the angle ${\theta }_{N_n(r)}^{**}$ between these vectors.

Remark 18.

In Goldfeld and Quandt [34] and Missiakoulis [35] Sargans densities $l_r(x)$ and distribution functions $L_r(x)$ for arbitrary integer $r=1,2,3,\dots$ have been studied as an alternative to normal law in econometric models because they are computable in closed form, see also Kotz et al. [31], Section 4.4.3 and the references therein.

5.2. The Random Dimension $N_n=N_n(s)$ Is the Maximum of n Independent Discrete Pareto Random Variables

The random dimension $N_n(s)$ has probability mass function (39): Since $\mathbb{E}{N}_n(s)=\infty$ we choose $g_n=n$ and consider again the cases $\gamma =1/2$, $\gamma =0$ and $\gamma =-1/2$.

It follows from Theorems 1 and 2 and Proposition 2 that if limit distributions for $\mathbb{P}\left(g_n^{\gamma }{R}_{N_n(s)}\le x\right)$ for $\gamma \in \{1/2,0-1/2\}$ exist, they are ${\int }_0^{\infty }\mathsf{\Phi }(x{y}^{\gamma })d{H}_s(y)$ with densities given below in the proof of the corresponding theorems

$$\frac{s}{\sqrt{2\pi }}{\int }_0^{\infty }{y}^{-3/2}{e}^{-(x^2{y}^{2\gamma }/2+s/y)}dy=\left\{\begin{array}{cc}{l}_{1/\sqrt{s}}(x)=\frac{{\displaystyle \sqrt{2s}}}{{\displaystyle 2}}{e}^{-\sqrt{2s}|x|},\hfill & \gamma =1/2,\hfill \\ \phi (x)=\frac{{\displaystyle 1}}{{\displaystyle \sqrt{2\pi }}}{e}^{-x^2/2},\hfill & \gamma =0,\hfill \\ s_2^{*}(x;\sqrt{s})=\frac{{\displaystyle 1}}{{\displaystyle 2\sqrt{2s}}}{\left(1+\frac{{\displaystyle x^2}}{{\displaystyle 2s}}\right)}^{-3/2},\hfill & \gamma =-1/2,\hfill \end{array}\right.$$

(52)

where $s_2^{*}(x;\sqrt{s})$ is the density of the scaled Student’s t-distribution $S_2^{*}(x;\sqrt{s})$ with 2 degrees of freedom, see Definition B37 in Jackman [36], p.507. If Z has density $s_2^{*}(x;\sqrt{s})$ then $Z/\sqrt{s}$ has a classic Student’s t-distribution with two degrees of freedom.

5.2.1. Laplace Distribution

We start with the case $\gamma =1/2$ in Theorems 1 and 2. Consider the statistics $\sqrt{n}{R}_{N_n(s)}$ and $\sqrt{n}({\theta }_{N_n(s)}-\pi /2)$. The limit distribution is now the Laplace distribution

$$L_{1/\sqrt{s}}(x)=\frac{1}{2}+\frac{1}{2}\mathrm{sign}(x)\left(1-e^{-\sqrt{2s}|x|}\right)\mathrm{with} \mathrm{density}{l}_{1/\sqrt{s}}(x)=\frac{{\displaystyle \sqrt{2s}}}{{\displaystyle 2}}{e}^{-\sqrt{2s}|x|}.$$

Theorem 6.

Let $s>0$ and (39) be the probability mass function of the random dimension $N_n=N_n(s)$ of the vectors under consideration. If the representation (42) for the statistic $R_m$ and the inequality (32) with $g_n=n$ hold, then there exists a constant $C_s$ such that for all $n\in {\mathbb{N}}_{+}$

$$\underset{x}{sup}\left|\mathbb{P}\left(\sqrt{n}{R}_{N_n(s)}\le x\right)-L_{1/\sqrt{s};n}(x;a)\right|\le C_s{n}^{-2},$$

where

$$L_{1/\sqrt{s};n}(x;a)=L_{1/\sqrt{s}}(x)+\frac{l_{1/\sqrt{s}}(x)}{8sn}\left(a2s{x}^3-(4-s)x\left(1+\sqrt{2s}|x|\right)\right).$$

(53)

Moreover, the scaled angle ${\theta }_{N_n(s)}$ between the vectors ${\overrightarrow{\mathrm{X}}}_{N_n(s)}$ and ${\overrightarrow{\mathrm{Y}}}_{N_n(s)}$ allows the estimate

$${sup}_x\left|\mathbb{P}\left(\sqrt{n}({\theta }_{N_n(s)}-\pi /2)\le x\right)-L_{1/\sqrt{s};n}(x;1/3)\right|\le C_s{n}^{-2},$$

where $L_{1/\sqrt{s};n}(x;1/3)$ is given in (53) with $a=1/3$.

5.2.2. Standard Normal Distribution

Let $\gamma =0$ in the Theorems 1 and 2 examine the statistics $R_{N_n(s)}^{*}$ and ${\mathsf{\Theta }}_{N_n(s)}^{*}=\sqrt{N_n(s)}({\theta }_{N_n(s)}-\pi /2)$.

Theorem 7.

Let $s>0$ and $N_n=N_n(s)$ be the random vector dimension having probability mass function (39). If the representation (42) for the statistic $R_m$ and the inequality (32) with $g_n=n$ hold, then there exists a constant $C_s$ such that, for all $n\in {\mathbb{N}}_{+}$

$$\underset{x}{sup}\left|\mathbb{P}\left(\sqrt{N_n(s)}{R}_{N_n(s)}\le x\right)-\mathsf{\Phi }(x)-\frac{1}{4n}\phi (x)s^2(x^3-5x)\right|\le C_s{n}^{-2},$$

Moreover, the scaled angle ${\theta }_{N_n(s)}^{*}$ between the vectors ${\overrightarrow{\mathrm{X}}}_{N_n(s)}$ and ${\overrightarrow{\mathrm{Y}}}_{N_n(s)}$ allows the estimate

$${sup}_x\left|\mathbb{P}\left(\sqrt{N_n(s)}({\theta }_{N_n(s)}-\pi /2)\le x\right)-\mathsf{\Phi }(x)-\frac{1}{4n}\phi (x)s^2(\frac{1}{3}{x}^3-5x)\right|\le C_s{n}^{-2}.$$

5.2.3. Scaled Student’s t-Distribution

Finally, we use $\gamma =-1/2$ in Theorems 1 and 2 examining the statistics $n^{-1/2}{N}_n(s)R_{N_n(s)}$ and $n^{-1/2}{N}_n(s)({\theta }_{N_n(s)}-\pi /2)$. The limit Scaled Student’s t-Distribution $S_2^{*}(x;\sqrt{s})$ with two degrees of freedom is a scale mixture of the normal distribution with zero mean and mixing exponential distribution $1-e^{-sy},y\ge 0$, and it is representable in a closed form, see (A15) below in the proof of Theorem 8:

$$\begin{array}{cc}\hfill {\int }_0^{\infty }\mathsf{\Phi }(x/\sqrt{y})d{e}^{-s/y}& ={\int }_0^{\infty }\mathsf{\Phi }(x/\sqrt{y})s{y}^{-2}{e}^{-s/y}dy={\int }_0^{\infty }\mathsf{\Phi }(x\sqrt{z})s{e}^{-sz}dz\hfill \\ \hfill & ={\int }_0^{\infty }\mathsf{\Phi }(x\sqrt{z})d(1-e^{-sz)}dz=\frac{1}{2}+\frac{x/\sqrt{s}}{2\sqrt{2}\sqrt{1+x^2/(2s)}}=S_2^{*}(x)\hfill \end{array}$$

Theorem 8.

Let $s>0$ and $N_n=N_n(s)$ be the random vector dimension having probability mass function (39). If the representation (42) for the statistic $R_m$ and the inequality (32) with $g_n=n$ hold, then there exists a constant $C_s$ such that for all $n\in {\mathbb{N}}_{+}$

$$\underset{x}{sup}\left|\mathbb{P}\left(n^{-1/2}{N}_n(s)R_{N_n(s)}\le x\right)-S_{n;2}^{*}(x;1)\right|\le C_r{n}^{-2},$$

(54)

where

$$S_{n;2}^{*}(x;\sqrt{s};a)=S_2^{*}(x;\sqrt{s})+\frac{(15a+3s-18)x^3-6xs(6-s)}{4n{(x^2+2s)}^2}{s}_2^{*}(x;\sqrt{s})$$

(55)

Moreover, the scaled angle ${\theta }_{N_n(s)}^{*}$ between the vectors ${\overrightarrow{\mathrm{X}}}_{N_n(s)}$ and ${\overrightarrow{\mathrm{Y}}}_{N_n(s)}$ allows the estimate

$${sup}_x\left|\mathbb{P}\left(n^{-1/2}{N}_n(s){\theta }_{N_n(s)}\le x\right)-S_{n;2}(x;\sqrt{s};1/3)\right|\le C_s{n}^{-2},$$

where $S_{n;2}(x;\sqrt{s};1/3)$ is given in (55) with $a=1/3$.

Theorems 3 to 8 are proved in Appendix A.3.

6. Conclusions

The asymptotic distributions of the sample correlation coefficient of vectors with random dimensions are normal scale mixtures. From (43) and (52), one can conclude that random dimension and corresponding scaling have significant influence on limit distributions A scale mixture of a normal distribution change the tail behavior of the distribution. Students t-Distributions have polynomial tails, as one class of heavy-tailed distributions, they can be used to model heavy-tail returns data in finance. The Laplace distributions have heavier tails than normal distributions.

Appendix A.1. Proofs of Theorems 1 and 2

Proof of Theorem 1.

The proof follows along the similar arguments of the more general transfer Theorem 3.1 in Bening et al. [24]. Since in Theorem 3.1 in Bening et al. [24] the constant $\gamma$ has to be non-negative and in our Theorem 1, we also need $\gamma =-1/2$, therefore we repeat the proof. Conditioning on $N_n$, we have

$$\begin{array}{c}\hfill \mathbb{P}\left(g_n^{\gamma }{T}_{N_n}\le x\right)=\mathbb{P}\left(N_n^{\gamma }{T}_{N_n}\le x{(N_n/g_n)}^{\gamma }\right)={\sum }_{m=1}^{\infty }\mathbb{P}\left(m^{\gamma }{T}_m\le x{(m/g_n)}^{\gamma }\right)\mathbb{P}(N_n=m).\end{array}$$

Using now (18) with ${\mathsf{\Phi }}_m(z):=\mathsf{\Phi }(z)+m^{-1}{f}_2(z)$, we find

$$\begin{array}{cc}\hfill {\sum }_{m=1}^{\infty }& \left|\mathbb{P}\left(m^{\gamma }{T}_m\le x{(m/g_n)}^{\gamma }\right)-{\mathsf{\Phi }}_m(x{(m/g_n)}^{\gamma })\right|\mathbb{P}(N_n=m)\hfill \\ \hfill & \stackrel{(18)}{\le }{C}_1{\sum }_{m=1}^{\infty }{m}^{-a}\mathbb{P}(N_n=m)=C_1\mathbb{E}(N_n^{-a}).\hfill \end{array}$$

(A1)

Taking into account $\mathbb{P}\left(N_n/g_n<1/g_n\right)=\mathbb{P}\left(N_n<1\right)=0$, we obtain

$$\begin{array}{cc}\hfill {\sum }_{m=1}^{\infty }{\mathsf{\Phi }}_m(x{(m/g_n)}^{\gamma })\mathbb{P}(N_n=m)& =\mathbb{E}\left({\mathsf{\Phi }}_{N_n}(x{(N_n/g_n)}^{\gamma })\right)\hfill \\ \hfill & ={\int }_{1/g_n}^{\infty }{\mathsf{\Delta }}_n(x,y)d\mathbb{P}\left(\frac{N_n}{g_n}\le y\right)=G_n(x,1/g_n)+I_1,\hfill \end{array}$$

where ${\mathsf{\Delta }}_n(x,y):=\mathsf{\Phi }(x{y}^{\gamma })+f_2(x{y}^{\gamma })/(g_{n}y),$ $G_n(x,1/g_n)$ is defined in (21) and

$$I_1={\int }_{1/g_n}^{\infty }{\mathsf{\Delta }}_n(x,y)d\left(\mathbb{P}\left(\frac{N_n}{g_n}\le y\right)-H(y)-\frac{h_2(y){\mathbb{I}}_{\{b>1\}}(b)}{n}\right).$$

Estimating integral $I_1$, we use the integration by parts for Lebesgue–Stieltjes integrals, the boundedness of $f_2(z)$, say ${sup}_z|f_2(z)|\le c_1^{*}$, and estimates (19)

$$\begin{array}{cc}\hfill |I_1|& \le {sup}_x{\left.\underset{L\to \infty }{lim}|{\mathsf{\Delta }}_n(x,y)||\mathbb{P}\left(N_n/g_n\le y\right)-H(y)-n^{-1}{h}_2(y)\mathbb{I}\{b>1\}(b)|\right|}_{y=1/g_n}^{y=L}\hfill \\ \hfill & +{sup}_x{\int }_{1/g_n}^{\infty }\left|\frac{{\displaystyle \partial }}{{\displaystyle \partial y}}{\mathsf{\Delta }}_n(x,y)\right|\left|\mathbb{P}\left(N_n/g_n\le y\right)-H(y)-n^{-1}{h}_2(y){\mathbb{I}}_{\{b>1\}}(b)\right|dy\hfill \\ \hfill & \le (1+c_1^{*})C_2{n}^{-b}+C_2{D}_n{n}^{-b},\hfill \end{array}$$

where $D_n$ is defined in (22). Together with (A1), we obtain (20) and Theorem 1 is proved. □

Proof of Theorem 2.

Using (23), we find for $b>0$

$${\int }_0^{1/g_n}\mathsf{\Phi }(x{y}^{\gamma })dH(y)\le {\int }_0^{1/g_n}dH(y)=H(1/\sqrt{g_n})-H(0)\stackrel{(23)}{\le }{c}_1{g}_n^{-b}.$$

Let now $b>1$. Since $f_2(z)$ is supposed to be bounded, it follows from $|f_2(z)|\le c_1^{*}<\infty$ and (24i) that

$${\int }_0^{1/g_n}|f_2(x{y}^{\gamma })|y^{-1}dH(y)\le c_1^{*}{\int }_0^{1/g_n}{y}^{-1}dH(y)\stackrel{(24\mathrm{i})}{\le }{c}_1^{*}{c}_2{g}_n^{-b+1}.$$

Integration by parts, $|z|\phi (z)\le c^{*}={(2\pi e)}^{-1/2}$, (24ii) and (24iii) lead to

$$\left|{\int }_0^{1/g_n}\mathsf{\Phi }(x{y}^{\gamma })d{h}_2(y)\right|\le |h_2(1/g_n)|+\gamma c^{*}{\int }_0^{1/g_n}{y}^{-1}|h_2(y)|dy\le (c_3+\gamma c^{*}{c}_4)n{g}_n^{-b}.$$

Theorem 2 is proved. □

Appendix A.2. Proofs of Lemmas 1 to 5

Proof of Lemma 1.

To estimate $D_n$, we consider three cases:

$$D_n={sup}_x|D_n(x)|=max\{{sup}_{x>0}|D_n(x)|,{sup}_{x<0}|D_n(x)|,|D_n(0)|\}.$$

Let $x>0$. Since $\frac{{\displaystyle \partial }}{{\displaystyle \partial y}}\mathsf{\Phi }(x{y}^{\gamma })=\gamma x{y}^{\gamma -1}\phi (x{y}^{\gamma })\ge 0$, we find

$${\int }_{1/g_n}^{\infty }\left|\frac{{\displaystyle \partial }}{{\displaystyle \partial y}}\mathsf{\Phi }(x{y}^{\gamma })\right|dy={\int }_{1/g_n}^{\infty }\gamma x{y}^{\gamma -1}\phi (x{y}^{\gamma })dy={\int }_{x{g}_n^{-\gamma }}^{\infty }\phi (u)du=\mathsf{\Phi }(\infty )-\mathsf{\Phi }(x{g}_n^{-\gamma })\le 1/2.$$

Consider now $f_2(x{y}^{\gamma };a)=(a{(x{y}^{\gamma })}^3-5x{y}^{\gamma })\phi (x{y}^{\gamma })/4$ with $a=1$ or $a=1/3$. Then,

$$\frac{{\displaystyle \partial }}{{\displaystyle \partial y}}\left(\frac{f_2(x{y}^{\gamma };a)}{y}\right)=\frac{{\displaystyle Q_5(x{y}^{\gamma };a)}}{{\displaystyle 4y^2}},Q_5(z;a)=-(\gamma a{z}^5-((3a+5)\gamma -a)z^3+5(\gamma -1)z)\phi (z).$$

(A2)

Since ${sup}_z|Q_5(z;a)|\le c(\gamma ;a)<\infty$ and $g_n^{-1}{\int }_{1/g_n}^{\infty }{y}^{-2}dy=1$, inequality (29) holds for $x>0$. Taking into account $|D_n(x)|=|D_n(-x)|$ and $D_n(0)=0$, Lemma 1 is proved. □

Proof of Lemma 2.

Using (30), we find $G_{r,r}(1/g_n)\le c_1{g}_n^{-r}$ with $c_1=r^{r-1}/\mathsf{\Gamma }(r)$. For $r>1$, then ${\int }_0^{1/g_n}{y}^{-1}d{G}_{r,r}(y)\le c_2{g}_n^{-r+1}$ with $c_2=r^r/\left((r-1)\mathsf{\Gamma }(r)\right)$. Since $g_{r,r}(0)=0$, $h_{2;r}(0)=0$ and $g_n\le rn$ for $r>1$, then (24ii) and (24iii) hold with $c_3=c_r^{*}$ and $c_4=c_r^{*}/(r-1)$, where $c_r^{*}=\frac{{\displaystyle r^r}}{{\displaystyle 2r\mathsf{\Gamma }(r)}}{sup}_y\{e^{-ry}(|y-1||2-r|+1)\}<\infty$.

It remains to prove the bounds in (34) and (35). Let first $r<1$. With $c_1^{*}={sup}_z|f_2(z;a)|$, we find

$$|I_1(x,n)|\le \frac{c_1^{*}{r}^r}{g_n\mathsf{\Gamma }(r)}{\int }_{1/g_n}^{\infty }{y}^{r-2}dy\le \frac{c_1^{*}{r}^r}{(r-1)\mathsf{\Gamma }(r)}{g}_n^{-r}\mathrm{with}{c}_5=\frac{c_1^{*}{r}^r}{(r-1)\mathsf{\Gamma }(r)}.$$

If $r=1$ with $c_1^{**}={sup}_z\{|a{z}^2-5|\phi (z/\sqrt{2})\}$, we find $|f_2(z;a)|\le c_1^{**}|z|\phi (z/\sqrt{2})$ and

$$|I_1(x,n)|\le \frac{c_1^{**}|x|}{\sqrt{2\pi }n}{\int }_{1/n}^{\infty }{y}^{\gamma -1}{e}^{-(y+x^2{y}^{2\gamma }/4)}dy\mathrm{with}\gamma \in \{-1/2,0,1/2\}.$$

For $\gamma =1/2$ using $|x|{(1+x^2/4)}^{-1/2}\le 2$, we obtain

$$|I_1(x,n)|\le \frac{c_1^{**}|x|}{\sqrt{2\pi }n}{\int }_{1/n}^{\infty }{y}^{1/2-1}{e}^{-(1+x^2/4)y}dy\le \frac{c_1^{**}|x|\mathsf{\Gamma }(1/2)}{\sqrt{2\pi }{(1+x^2/4)}^{1/2}}{n}^{-1}\le c_6{n}^{-1},c_6=\sqrt{2}{c}_1^{**}.$$

If $\gamma =-1/2$, then Prudnikov et al. [37], formula 2.3.16.3, for $x\ne 0$ leads to

$$I_1(x,n)\le \frac{c_1^{**}|x|}{\sqrt{2\pi }n}{\int }_{1/n}^{\infty }{y}^{-1-1/2}{e}^{-(2y+x^2/(4y))}dy\le \frac{c_1^{**}|x|}{\sqrt{2\pi }n}\frac{2\sqrt{\pi }}{|x|}{e}^{-\sqrt{2}|x|}\le \frac{\sqrt{2}{c}_1^{**}}{n},c_6=\sqrt{2}{c}_1^{**}.$$

Finally, if $\gamma =0$, then $f_2(x{y}^{\gamma };a)=f_2(x;a)$ does not depend on y. Using now

$$0\le lnn-{\int }_{1/n}^1{y}^{-1}d{G}_{1,1}(y)={\int }_{1/n}^1\frac{1-e^{-y}}{y}dy\le 1\mathrm{and}{\int }_1^{\infty }{y}^{-1}d{G}_{1,1}(y)\le e^{-1},$$

then (34) for $r=1$ holds with $c_6=c_1^{*}(1+e^{-1})$.

Let $r>1$. Integration by parts for Lebesgue–Stieltjes integrals in $I_2(x,n)$ in (35) and (A2) lead to

$$I_2(x,n)\le \frac{1}{n{g}_n}\left(c_1^{*}{g}_n|h_{2;r}(1/g_n)|+{\int }_{1/g_n}^{\infty }\frac{|Q_5(x{y}^{\gamma };a)|}{4y^2}|h_{2;r}(y)|dy\right).$$

(A3)

Since $c(\gamma ;a)={sup}_z|Q_5(z;a)|<\infty$ and with above defined $c_r^{*}$, we find

$${\int }_{1/g_n}^{\infty }\frac{|h_{2;r}(y)|}{y^2}dy\le c_r^{*}{\int }_{1/g_n}^{\infty }{y}^{r-3}dy=\frac{c_r^{*}}{(2-r)}{g}_n^{-r+2}for1<r<2$$

and with $c_r^{**}=\frac{{\displaystyle r^{r-1}}}{{\displaystyle 2\mathsf{\Gamma }(r)}}{sup}_y\{(e^{-ry/2}(|y-1||2-r|+1)\}<\infty$, we obtain

$${\int }_{1/g_n}^{\infty }\frac{|h_{2;r}(y)|}{y^2}dy\le c_r^{**}{\int }_{1/g_n}^{\infty }{y}^{r-3}{e}^{-ry/2}dy\le \frac{c_r^{**}\mathsf{\Gamma }(r-2)}{{(r/2)}^{r-2}}\mathrm{for}r>2.$$

Hence, we obtain (35) for $r>1$, $r\ne 2$ with some constant $0<c_7<\infty$.

For $r=2$, the second integral in line above is an exponential integral. Therefore, we estimate the integral $I_2(x,n)$ in (35) more precisely like in estimating $I_1(x,n)$ above, taking into account the given function $f_2(z;a)$.

Using $|h_{2;2}(y)|\le 4y{e}^{-2y}$ and consider (A2), define $P_4(z;a)$ by $Q_5(z;a)=-z{P}_4(z;a)\phi (z/\sqrt{2})$ with $c_2^{*}={sup}_z|P_4(z;a)|\phi (z/\sqrt{2})<\infty$, we obtain in (A3)

$${\int }_{1/g_n}^{\infty }\frac{{\displaystyle |Q_5(x{y}^{\gamma })|}}{{\displaystyle 4y^2}}|h_{2;2}(y)|dy\le \frac{c_2^{*}|x|}{\sqrt{2\pi }}{\int }_{1/g_n}^{\infty }{y}^{\gamma -1}{e}^{-(2y+x^2{y}^{2\gamma }/4)}dy.$$

We estimate the latter integral in the same way as $I_1(x,n)$ for the two cases $\gamma =1/2$$\gamma =-1/2$ and find (35) for $r=2$ with some constants $0<c_7<\infty$.

In order to prove (35) for $r=2$ and $\gamma =0$, we consider for $\alpha >0$ the following inequalities:

$${\int }_{1/g_n}^{\infty }{y}^{-1}{e}^{-\alpha y}dy\left\{\begin{array}{c}\le {\int }_{1/g_n}^1{y}^{-1}dy+{\int }_1^{\infty }{e}^{-\alpha y}dy\le ln{g}_n+{\alpha }^{-1}{e}^{-\alpha },\hfill \\ \ge {\int }_{1/g_n}^1{y}^{-1}{e}^{-\alpha y}dy\ge e^{-\alpha }{\int }_{1/g_n}^1{y}^{-1}dy\ge e^{-\alpha }ln{g}_n\hfill \end{array}\right..$$

(A4)

The upper bound in (A4) leads to (35) for $r=2,\gamma =0$, too. The lower bound in (A4) shows that the $lnn$-term cannot be improved.

Bound (36) for $n\ge 2,r>1$ results from $0\le \frac{{\displaystyle 1}}{{\displaystyle g_n}}-\frac{{\displaystyle 1}}{{\displaystyle rn}}=\frac{{\displaystyle r-1}}{{\displaystyle r^2{n}^2(1-(r-1)/(rn)}}\le \frac{{\displaystyle 2(r-1)}}{{\displaystyle r^2{n}^2}}$. □

Proof of Lemma 3.

Let $r>0$. If $n=1$, then $\mathbb{P}(N_1(r)=1)=1$ and (37) holds with $C(r)=1$. Let $n\ge 2$ and $\alpha >0$

$$\mathbb{E}{\left(N_n(r)\right)}^{-\alpha }=\frac{1}{n^r}\left(1+{\sum }_{k=2}^{\infty }\frac{\mathsf{\Gamma }(k+r-1)}{k^{\alpha }\mathsf{\Gamma }(r)\mathsf{\Gamma }(k)}{\left(1-\frac{1}{n}\right)}^{k-1}\right).$$

It follows from the relations (49) and (50) with their corresponding bounds in the proof of Theorem 1 in Christoph et al. [12] that

$$\frac{\mathsf{\Gamma }(k+r-1)}{\mathsf{\Gamma }(r)\mathsf{\Gamma }(k)}=\frac{1}{(k+r-1)B(rk)}=\frac{k^{r-1}}{\mathsf{\Gamma }(r)}\left(1+R_1(k)\right),|R_1(k)|\le \frac{c_1(r)}{k}.$$

(A5)

For $x\ge k\ge 2$ using ${(1-1/n)}^x\le e^{-x/n}$, we find

$$\frac{k^{r-1}{(1-1/n)}^{k-1}}{k^{\alpha }}\le {\int }_k^{k+1}\frac{{\displaystyle x^r{(1-1/n)}^{x-2}}}{{\displaystyle {(x-1)}^{1+\alpha }}}dx\le 2^{3+\alpha }{\int }_k^{k+1}{x}^{r-3}{e}^{-x/n}dx.$$

Then, with $c_2(r)=2^{3+\alpha }(1+c_1(r))/\mathsf{\Gamma }(r)$, we obtain

$$\mathbb{E}{\left(N_n(r)\right)}^{-\alpha }\le c_2(r)n^{-r}{J}_r(n),\mathrm{where}{J}_r(n)={\int }_1^{\infty }{x}^{r-\alpha -1}{e}^{-x/n}dx=n^{r-\alpha }{\int }_{1/n}^{\infty }{y}^{r-\alpha -1}{e}^{-y}dy.$$

Since $J_r(n)\le {(\alpha -r)}^{-1}$ for $0<r<\alpha$, $J_r(n)\le n^{r-\alpha }\mathsf{\Gamma }(r-\alpha )$ for $r>\alpha$ and using (A4) with $r=\alpha$ $J_r(n)\le lnn+e^{-1}$, the upper bound (37) is proved.

Let $r=\alpha >0$. Considering the formula (A5), $0\le {\sum }_{k=2}^{\infty }{k}^{-1}|R_1(k)|\le c_1(r){\pi }^2/(6\mathsf{\Gamma }(r))<\infty$, ${\sum }_{(n)}:={\sum }_{k=2}^{n-1}{k}^{-1}\ge lnn-ln2$ and ${\sum }_{k=2}^{n-1}\frac{{\displaystyle 1-{(1-1/n)}^{k-1}}}{{\displaystyle k}}\le {\sum }_{k=2}^{n-1}\frac{{\displaystyle k-1}}{{\displaystyle kn}}\le 1$, we find:

$$\mathbb{E}{(N_n(r))}^{-r}\ge \frac{1}{n^r\mathsf{\Gamma }(r)}\left({\sum }_{k=2}^{n-1}\frac{1}{k}{\left(1-\frac{1}{n}\right)}^{k-1}-c_3\right)\ge \frac{1}{n^r\mathsf{\Gamma }(r)}\left({\sum }_{k=2}^{n-1}\frac{1}{k}-c_4\right)\ge \frac{1}{n^r\mathsf{\Gamma }(r)}\left(lnn-c_5\right),$$

where $c_3=c_1(r){\pi }^2/6$, $c_4=1+c_3$ and $c_5=c_4-ln2$. Hence, the $lnn$-term cannot be dropped. □

Proof of Lemma 4.

The upper bounds in the estimates (23) and (24) with $H_s(y)$, $h_{2;s}(y)$ and $I_2(x,n)$ given in (40) are $C(s)e^{-sn/2}$. For example, (24ii):

${\int }_0^{1/n}{y}^{-1}|h_{2;s}(y)|dy\le s(s+1)/2{\int }_0^{1/n}{y}^{-3}{e}^{-s/y}dy\le (s+1)/(2s){\int }_{sn}^{\infty }z{e}^{-z}dz\le (s+1)/(2s)e^{-sn/2}.$ □

Proof of Lemma 5.

Proceeding as in Bening et al. [24] using

$$\mathbb{P}(N_n(s)=k)={\left(\frac{k}{s+k}\right)}^n-{\left(\frac{k-1}{s+k-1}\right)}^n=sn{\int }_{k-1}^k\frac{x^{n-1}}{{(s+x)}^{n+1}}dx$$

and Formula 2.2.4.24 in Prudnikov et al. [37], p. 298, then

$$\mathbb{E}(N_n^{-\alpha })=sn\sum _{k=1}^{\infty }\frac{1}{k^{\alpha }}{\int }_{k-1}^k\frac{x^{n-1}}{{(s+x)}^{n+1}}dx\le sn{\int }_0^{\infty }\frac{x^{n-1-\alpha }}{{(s+x)}^{n+1}}dx=snB(n-\alpha ,1+\alpha ).$$

Using $B(n-\alpha ,1+\alpha )=\mathsf{\Gamma }(1+\alpha ){(n+1)}^{-1+\alpha }(1+R_1/n)$ with $|R_1|\le c<\infty$, we obtain (41). □

Appendix A.3. Proofs of Theorems 3 to 8

Proof of Theorem 3.

Since the additional assumptions (23) and (24) in the transfer Theorem 2 for the limit Gamma distribution $H(x)=G_{r,r}(x)$ of the normalized sample size $N_n(r)$ are satisfied by Lemma 2 with $b=r>0$ and by Lemma 3 for $\alpha =2$, it remains to calculate the integrals in (26). Define

$$\begin{array}{cc}\hfill J_1^{*}(x)& ={\int }_0^{\infty }\mathsf{\Phi }(x\sqrt{y})d{G}_{r,r}(y),J_2^{*}(x)={\int }_0^{\infty }\frac{a{(x\sqrt{y})}^3-5x\sqrt{y}\phi (x\sqrt{y})}{4y}d{G}_{r,r}(y),\mathrm{and}\hfill \\ \hfill J_3^{*}(x)& ={\int }_0^{\infty }\mathsf{\Phi }(x\sqrt{y})d{h}_{2;r}(y)\mathrm{with}{h}_{2;r}(y)=\left((y-1)(2-r)+2Q_1\left((r(n-1)+1)y\right)\right)\frac{g_{r,r}(y)}{2r},\hfill \end{array}$$

and $Q_1(y)=1/2-(y-[y])$. Then,

$$G_{2;n}(x;0)=J_1^{*}(x)+\frac{J_2^{*}(x)}{g_n}+\frac{J_3^{*}(x)}{n}\mathrm{with}{g}_n=\mathbb{E}{N}_n(r)=r(n-1)+1.$$

(A6)

Using formula 2.3.3.1 in Prudnikov et al. [37], p. 322, with $\alpha =r-1/2,r+1/2$, $p=1+x^2/(2r)$ and $q=1$:

$$M_{\alpha }(x)=\frac{r^r}{\mathsf{\Gamma }(r)\sqrt{2\pi }}\underset{0}{\overset{\infty }{\int }}{y}^{\alpha -1}{e}^{-(r+x^2/2)y}dy=\frac{\mathsf{\Gamma }(\alpha )r^{r-\alpha }}{\mathsf{\Gamma }(r)\sqrt{2\pi }}{\left(1+x^2/(2r)\right)}^{-\alpha }$$

(A7)

we calculate the integrals occurring in (A6). Consider

$$\begin{array}{cc}\hfill \frac{\partial }{\partial x}{J}_1^{*}(x)& ={\int }_0^{\infty }{y}^{1/2}\phi (x\sqrt{y})g_{r,r}(y)dy=\frac{r^r}{\mathsf{\Gamma }(r)\sqrt{2\pi }}{\int }_0^{\infty }{y}^{r-1/2}{e}^{-(r+x^2/2)y}dy\hfill \\ \hfill & =M_{r+1/2}(x)=s_{2r}(x)\mathrm{and}{J}_1^{*}(x)=S_{2r}(x).\hfill \end{array}$$

The integral $J_2^{*}(x)$ in (A6) we calculate again with (A7) using $M_{r-1/2}(x)=s_{2r}(x)(2r+x^2)/(2r-1)$ and $M_{r+1/2}(x)=s_{2r}(x)$

$$\begin{array}{cc}\hfill J_2^{*}(x)& :=\frac{r^r}{\sqrt{2\pi }\mathsf{\Gamma }(r)}{\int }_0^{\infty }\frac{1}{y}\left(a{x}^3{y}^{3/2}-5x{y}^{1/2}\right)y^{r-1}{e}^{-(r+x^2/2)y}dy\hfill \\ \hfill & =\left(a{x}^3{M}_{r+1/2}(x)-5x{M}_{r-1/2}(x)\right)=\left(a{x}^3-\frac{10rx+5x^3}{2r-1}\right)s_{2r}(x).\hfill \end{array}$$

The integral $J_3^{*}(x)$ in (A6) is the same as the integral $J_4(x)$ in the proof of Theorem 2 in Christoph et al. [12] with the estimate

$$\underset{x}{sup}\left|J_3^{*}(x)-\frac{(2-r)x(x^2+1)}{4r(2r-1)}{s}_{2r}(x)\right|\le c(r)n^{-r+1}.$$

With (36), we proved (44). □

Proof of Theorem 4.

By Lemma 2, the additional assumptions (23) and (24) in the transfer Theorem 2 are satisfied with the limit Gamma distribution $H(x)=G_{r,r}(x)$ of the normalized sample size $N_n(r)$ with $b=r>0$. In Transfer Theorem 1 for $T_{N_n}=\sqrt{N_n}{R}_{N_n}$, the right-hand side of (20) is estimated by Lemma 1 and Lemma 3 for $\alpha =2$ for the case $\gamma =0$. Then, we have by (21) with (35)

$$G_n(x,1/g_n)=\mathsf{\Phi }(x)\left(1-G_{r,r}(1/g_n)-n^{-1}{h}_{2;r}(1/g_n){\mathbb{I}}_{\{r>1\}}(r)\right)+\frac{f_2(x;a)}{g_n}{\int }_{1/g_n}^{\infty }\frac{1}{y}d{G}_{r,r}(y){\mathbb{I}}_{\{r>1\}}(r).$$

The estimates (23), (24i), (24ii), (34) and ${\int }_0^{\infty }{y}^{-1}d{G}_{r,r}(y)=r\mathsf{\Gamma }(r-1)/\mathsf{\Gamma }(r)$ for $r>1$ lead to (46) with ${\mathsf{\Phi }}_{n;2}(x;1)$ defined in (47). Thus, Theorem 4 is proved. □

Proof of Theorem 5.

By Lemma 2, the additional assumptions (23) and (24) in the transfer Theorem 2 are satisfied with the limit Gamma distribution $H(x)=G_{r,r}(x)$ of the normalized sample size $N_n(r)$ with $b=r>0$. In Transfer Theorem 1 for $T_{N_n}=g_n^{-1/2}{N}_n{R}_{N_n}$, the right-hand side of (20) is estimated by Lemma 1 and Lemma 3 for $\alpha =2$ for the case $\gamma =-1/2$. Then, we have in (25)

$$G_{2;n}(x;0)=J_{1;r}^{*}(x)+\left(\frac{J_{2;r}^{*}(x)}{g_n}+\frac{J_{3;r}^{*}(x)}{n}\right){\mathbb{I}}_{\{r>1\}}(r)\mathrm{with}{g}_n=\mathbb{E}{N}_n(r)=r(n-1)+1$$

(A8)

$$\begin{array}{cc}\hfill J_{1;r}^{*}(x)& ={\int }_0^{\infty }\mathsf{\Phi }(x/\sqrt{y})d{G}_{r,r}(y),J_{2;r}^{*}(x)={\int }_0^{\infty }\frac{(a{x}^3{y}^{-3/2}-5x{y}^{-1/2})\phi (x/\sqrt{y})}{4y}d{G}_{r,r}(y),\mathrm{and}\hfill \\ \hfill J_{3;r}^{*}(x)& ={\int }_0^{\infty }\mathsf{\Phi }(x/\sqrt{y})d{h}_{2;r}(y)\mathrm{with}{h}_{2;r}(y)=\left((y-1)(2-r)+2Q_1\left((r(n-1)+1)y\right)\right)\frac{g_{r,r}(y)}{2r}.\hfill \end{array}$$

Consider formula 2.3.16.1 in Prudnikov et al. [37], p. 444:

$$I_{\alpha }:={\int }_0^{\infty }{y}^{\alpha -1}{e}^{-py-q/y}dy=2{\left(\frac{q}{p}\right)}^{\alpha /2}{K}_{\alpha }(2\sqrt{pq})p>0,q>0,$$

where $K_{\alpha }(u)$ is the $\alpha$-order Macdonald function (or $\alpha$-order modified Bessel function of the second kind), see, e.g., Oldham et al. [30], Chapter 51, for properties of these functions.

Let us calculate the integral $J_{1;r}^{*}(x)$ occurring in (A8). Consider

$$\begin{array}{cc}\hfill \frac{d}{dx}{J}_{1;r}^{*}(x)& =\frac{r^r}{\sqrt{2\pi }\mathsf{\Gamma }(r)}{\int }_0^{\infty }{y}^{r-3/2}{e}^{-ry-(x^2/(2y)}dy\hfill \\ \hfill & =\frac{2r^r}{\sqrt{2\pi }\mathsf{\Gamma }(r)}{\left(\frac{|x|}{2r}\right)}^{r-1/2}{K}_{r-1/2}(\sqrt{2r}|x|)=:l_r(x).\hfill \end{array}$$

(A9)

If $\alpha =\pm 1/2,\pm 3/2,\pm 5/2,\dots$ the integral $I_{\alpha }$ and consequently $K_{\alpha }(x)$ are computable in closed-form expressions with formula 2.3.16.2 in Prudnikov et al. [37], p. 444:

$$I_m^{*}={\int }_0^{\infty }{y}^{m-1/2}{e}^{-py-q/y}dy={\left(-1\right)}^m\sqrt{\pi }\frac{{\partial }^m}{\partial p^m}\left(p^{-1/2}{e}^{-2\sqrt{pq}}\right),p>0,q>0,m=0,1,2,\dots$$

(A10)

and with formula 2.3.16.3 in Prudnikov et al. [37], p. 444:

$$I_{-m}^{*}={\int }_0^{\infty }{y}^{-m-1/2}{e}^{-py-q/y}dy={\left(-1\right)}^m\sqrt{\frac{\pi }{p}}\frac{{\partial }^m}{\partial q^m}{e}^{-2\sqrt{pq}},p>0,q>0,m=0,1,2,\dots$$

For $r=1,2,3$ using (A10) with $m=r-1$, we find

$$l_r(x)=\frac{d}{dx}{J}_{1,r}^{*}(x)=\frac{r^r}{\mathsf{\Gamma }(r)\sqrt{2\pi }}{\int }_0^{\infty }{y}^{r-3/2}{e}^{-ry-x^2/(2y)}dy=\frac{r^r}{\mathsf{\Gamma }(r)\sqrt{2\pi }}{I}_{r-1}^{*}$$

and we obtain the densities $l_r(x)$ in (49) with

$$I_m^{*}(x)==\left\{\begin{array}{cc}\sqrt{2\pi }\frac{{\displaystyle 1}}{{\displaystyle |x|}}{e}^{-\sqrt{2r}|x|},x\ne 0\hfill & m=-1,\hfill \\ \sqrt{\pi }{e}^{-\sqrt{2r}|x|},\hfill & m=0,\hfill \\ \sqrt{\pi }\left(\frac{{\displaystyle 1}}{{\displaystyle 2r^{3/2}}}+\frac{{\displaystyle |x|\sqrt{2}}}{{\displaystyle 2r}}\right)e^{-\sqrt{2r}|x|},\hfill & m=1,\hfill \\ \sqrt{\pi }\left(\frac{{\displaystyle 3}}{{\displaystyle 4r^{5/2}}}+\frac{{\displaystyle 3|x|\sqrt{2}}}{{\displaystyle 4r^2}}+\frac{{\displaystyle {|x|}^2}}{{\displaystyle 2r^{3/2}}}\right)e^{-\sqrt{2r}|x|},\hfill & m=2.\hfill \end{array}\right.$$

Consider now $J_{2;r}(x)$ for $r=2$ and $r=3$:

$$J_{2;r}^{*}(x)={\int }_0^{\infty }\frac{(a{x}^3{y}^{-3/2}-5x{y}^{-1/2})r^r{y}^{r-1}{e}^{-ry-x^2/(2y)}}{4y\sqrt{2\pi }\mathsf{\Gamma }(r)}dy=\frac{r^r}{4\sqrt{2\pi }\mathsf{\Gamma }(r)}\left(a{x}^3{I}_{r-3}^{*}(x)-5x{I}_{r-2}^{*}(x)\right).$$

Hence,

$$J_{2;2}^{*}(x)=\left(ax|x|-5x/\sqrt{2}\right)e^{-2|x|}\mathrm{and}{J}_{2;3}^{*}(x)=\frac{{\displaystyle 27}}{{\displaystyle 8}}\left(\frac{a{x}^3}{\sqrt{2}}-5x\left(\frac{1}{6\sqrt{6}}+\frac{|x|}{6}\right)\right)e^{-\sqrt{6}|x|}.$$

Integration by parts in the integral $J_{3;r}^{*}$ in (A8) leads to

$$\begin{array}{cc}\hfill J_{3;r}^{*}(x)& :={\int }_0^{\infty }\mathsf{\Phi }(x{y}^{-1/2})d(h_{2;r}(y))=\frac{x}{2}{\int }_0^{\infty }{y}^{-3/2}\phi (x{y}^{-1/2})h_{2;r}(y)dy\hfill \\ \hfill & =\frac{r^{r}x}{2r\mathsf{\Gamma }(r)\sqrt{2\pi }}{\int }_0^{\infty }{y}^{r-5/2}{e}^{-ry-x^2/(2y)}\left((y-1)(2-r)+2Q_1(g_{n}y)\right)dy,\hfill \\ \hfill & =\frac{r^{r-1}x}{2\mathsf{\Gamma }(r)\sqrt{2\pi }}{\int }_0^{\infty }{y}^{r-5/2}(y-1)(2-r)e^{-ry-x^2/(2y)}dy\hfill \\ \hfill & +\frac{r^{r-1}x}{\mathsf{\Gamma }(r)\sqrt{2\pi }}{\int }_0^{\infty }{y}^{r-5/2}{Q}_1(g_{n}y)e^{-ry-x^2/(2y)}dy=J_{3;r,1}(x)+J_{3;r,2}(x).\hfill \end{array}$$

Since $J_{3;2,1}(x)$ vanishes, we calculate $J_{3;3,1}(x)$:

$$J_{3;3,1}(x)=\frac{9x}{2\sqrt{2\pi }}(I_1^{*}(x)-I_2^{*}(x))=\frac{9x}{2}\left(\frac{{\displaystyle 1}}{{\displaystyle 12\sqrt{6}}}+\frac{{\displaystyle |x|}}{{\displaystyle 12}}-\frac{{\displaystyle {|x|}^2}}{{\displaystyle 6\sqrt{6}}}\right)e^{-\sqrt{6}|x|}.$$

It remains to estimate $J_{3;2,2}(x)$ and $J_{3;3,2}(x)$. The function $Q_1(y)$ is periodic with period 1:

$$Q_1(y)=Q_1(y+1)\mathrm{for} \mathrm{all}y\in \mathbb{R}\mathrm{and}{Q}_1(y):=1/2-y\mathrm{for}0\le y<1$$

It is right-continuous and has the jump 1 at every integer point y. The Fourier series expansion of $Q_1(y)$ at all non-integer points y is

$$Q_1(y)=1/2-(y-[y])={\sum }_{k=1}^{\infty }\frac{sin(2\pi ky)}{k\pi }y\ne [y],$$

(A11)

see formula 5.4.2.9 in Prudnikov et al. [37], p. 726, with $a=0$.

Using the Fourier series expansion (A11) of the periodic function $Q_1(y)$ and interchange sum and integral, we find

$$J_{3;r,2}^{*}=\frac{x}{\sqrt{2\pi }}{\sum }_{k=1}^{\infty }\frac{1}{k}{\int }_0^{\infty }{y}^{r-5/2}{e}^{-ry-x^2/(2y)}sin(2\pi k{g}_{n}y)dy.$$

(A12)

First, we consider $r=2$. Let $p>0$, $q>0$ and $b>0$ be some real constants. Formula 2.5.37.4 in Prudnikov et al. [37], p. 453 reads

$${\int }_0^{\infty }{y}^{-1/2}{e}^{-py-q/y}sin(by)dy=\sqrt{\frac{\pi }{p^2+b^2}}{e}^{-2\sqrt{q}{z}_{+}}\left(z_{+}sin(2\sqrt{q}{z}_{-})+z_{-}cos(2\sqrt{q}{z}_{-})\right).$$

(A13)

with $2z_{\pm }^2=\sqrt{p^2+b^2}\pm p$. Consider $z_{\pm }$ with $p=r$, $q=x^2/2$, $b=2\pi k{g}_n$, $k\ge 1$ and $n\ge 1$: Then,

$$\sqrt{\frac{\pi }{p^2+b^2}}=\sqrt{\frac{\pi }{r^2+{(2\pi k{g}_n)}^2}}\le \frac{\sqrt{\pi }}{2\pi k{g}_n},\sqrt{2}|x|z_{+}{e}^{-\sqrt{2}|x|z_{+}}\le e^{-1}\mathrm{and}0<z_{-}\le z_{+}$$

leads to

$$\begin{array}{cc}\hfill |J_{3;2,2}^{*}(x)|& \le \frac{2|x|}{\sqrt{2\pi }}{\sum }_{k=1}^{\infty }\frac{1}{k}\sqrt{\frac{\pi }{p^2+b^2}}{e}^{-2\sqrt{q}{z}_{+}}\left(z_{+}sin(2\sqrt{q}{z}_{-})+z_{-}cos(2\sqrt{q}{z}_{-})\right)\hfill \\ \hfill & \le \frac{2}{\sqrt{2\pi }}{\sum }_{k=1}^{\infty }\frac{1}{k}\frac{\sqrt{\pi }\sqrt{2}{e}^{-1}}{2\pi k{g}_n}=\frac{1}{2\pi e{g}_n}{\sum }_{k=1}^{\infty }\frac{1}{k^2}=\frac{\pi }{12e{g}_n}.\hfill \end{array}$$

Together with $g_n\ge n$, we find $n^{-1}|J_{3;2,2}^{*}(x)|\le C{n}^{-2}$.

Consider finally $J_{3;3,2}^{*}$ given in (A12). In order to estimate $J_{3;3,2}^{*}(x)$, we apply Leibniz’s rule for differentiation under the integral sign with respect to p in (A13) and obtain

$$\begin{array}{cc}\hfill {\int }_0^{\infty }{y}^{1/2}{e}^{-py-q/y}sin(by)dy& =\frac{\partial }{\partial p}\left\{\sqrt{\frac{\pi }{p^2+b^2}}{e}^{-2\sqrt{q}{z}_{+}}\left(z_{+}sin(2\sqrt{q}{z}_{-})+z_{-}cos(2\sqrt{q}{z}_{-})\right)\right\}.\hfill \end{array}$$

Simple calculation considering $\sqrt{q}=|x|/\sqrt{2}$ and ${|x|}^m{e}^{-\sqrt{2}|x|z_{+}}\le \frac{{\displaystyle m}}{{\displaystyle 2^{m/2}{z}_{+}}}\le \frac{{\displaystyle m}}{{\displaystyle 2^{m/2}{b}^m}}$ for $m=1,2$, leads to

$$|x|\frac{\partial }{\partial p}\left\{\sqrt{\frac{\pi }{p^2+b^2}}{e}^{-2\sqrt{q}{z}_{+}}\left(z_{+}sin(2\sqrt{q}{z}_{-})+z_{-}cos(2\sqrt{q}{z}_{-})\right)\right\}\le \frac{C}{b^2}=\frac{C}{{(2\pi k{g}_n)}^2}$$

and we find equation (A12) with $r=3$ that $n^{-1}|J_{3;3,2}^{*}|\le C{n}^{-3}$ and (50) is proved. The approximation (52) holds since Lemmas 1, 2, and 3 are valid for arbitrary $r>0$. Theorem 5 is proved. □

Proof of Theorem 6.

By Lemma 4, the additional assumptions (23) and (24) in the transfer Theorem 2 are satisfied with the limit inverse exponential distribution $H_s(y)$ and $h_{2;s}(y)$ given in (40), $g_n=n$ and $b=2$. In Transfer Theorem 1, the right-hand side of (20) is estimated by Lemma 1 and Lemma 5 for $\alpha =2$ for the case $\gamma =1/2$. Then, we have in (25) with (35)

$$G_{2;n}(x;0)=J_{1;s}^{*}(x)+n^{-1}{J}_{2;s}^{*}(x)+n^{-1}{J}_{3;s}^{*}(x),$$

$$\begin{array}{cc}\mathrm{where}{J}_{1;s}^{*}(x)={\int }_0^{\infty }\mathsf{\Phi }(x\sqrt{y})d{e}^{-s/y},& J_{2;s}^{*}(x)={\int }_0^{\infty }\frac{(a{x}^3{y}^{3/2}-5x\sqrt{y})\phi (x\sqrt{y})}{4y}d{e}^{-s/y},\\ \mathrm{and}{J}_{3;s}^{*}(x)={\int }_0^{\infty }\mathsf{\Phi }(x\sqrt{y})d{h}_{2;s}(y)& \mathrm{with}{h}_{2;s}(y)=s{e}^{-s/y}\left(s-1+2Q_1(ny)\right)/\left(2y^2\right).\end{array}$$

To obtain (53), we calculate the above integrals as in the proof of Theorem 5 in Christoph et al. [12]. Here, we use Formula 2.3.16.3 in Prudnikov et al. [37], p. 344 with $p=x^2/2>0$, $s>0$, $m=1,2$:

$${\int }_0^{\infty }\frac{e^{-x^{2}y/2}}{\sqrt{2\pi }{y}^{m-3/2}}d{H}_s(y)={\int }_0^{\infty }\frac{s{e}^{-x^{2}y/2-s/y}}{\sqrt{2\pi }{y}^{m+1/2}}dy={\left(-1\right)}^m\frac{s}{|x|}\frac{{\partial }^m}{\partial s^m}{e}^{-\sqrt{2s}|x|}.$$

(A14)

In the mentioned proof we obtained with (A14) for $m=1$

$${\int }_0^{\infty }\mathsf{\Phi }(x\sqrt{y})d{H}_s(y)=L_{1/\sqrt{s}}(x)$$

and with (A14) for $m=2$

$$n^{-1}\underset{x}{sup}\left|J_{3;s}^{*}(x)-\frac{(1-s)x(1+\sqrt{2s}|x|)}{8s}{l}_{1/\sqrt{s}}(x)\right|\le n^{-1}c(s)e^{-\sqrt{\pi sn}/2}\le C(s)n^{-2}.$$

Again using (A14) with $p=x^2/2>0$, $s>0$, $m=1,2$ we find

$$\begin{array}{cc}\hfill J_{2;s}(x)& =\frac{s}{\sqrt{2\pi }}{\int }_0^{\infty }(a{x}^3{y}^{-1-1/2}-5x{y}^{-2-1/2})e^{-(x^{2}y/2+s/y)}dy\hfill \\ \hfill & =\frac{2sa{x}^3-5x(\sqrt{2s}|x|+1)}{8s}{l}_{1/\sqrt{s}}(x).\hfill \end{array}$$

□

Proof of Theorem 7.

By Lemma 4, the additional assumptions (23) and (24) in Transfer Theorem 2 are satisfied with the limit inverse exponential distribution $H_s(y)$ and $h_{2;s}(y)$ given in (40), $g_n=n$ and $b=2$. In Transfer Theorem 1, the right-hand side of (20) is estimated by Lemma 1 and Lemma 5 for $\alpha =2$ in the case $\gamma =0$. Then, we have in (21) with (35)

$$G_n(x,1/n)=\mathsf{\Phi }(x)\left(1-e^{-sn}-n^{-1}{h}_{2;s}(1/n)\right)+\frac{f_2(x;a)}{n}{\int }_{1/n}^{\infty }\frac{1}{y}d{e}^{-s/y}.$$

The estimates (24i), (24ii) for $b=2$ and ${\int }_0^{\infty }{y}^{-1}d{e}^{-s/y}=s{\int }_0^{\infty }{y}^{-3}{e}^{-s/y}dy=s^2{\int }_0^{\infty }z{e}^{-z}dz=s^2$ lead to

$$\left|G_n(x,1/g_n)-\mathsf{\Phi }(x)-n^{-1}{s}^2{f}_2(x;a)\right|\le C_s{n}^{-2}$$

and Theorem 7 is proved. □

Proof of Theorem 8.

By Lemma 4, the additional assumptions (23) and (24) in Transfer Theorem 2 are satisfied with the limit inverse exponential distribution $H_s(y)$ and $h_{2;s}(y)$ given in (40), $g_n=n$ and $b=2$. In Transfer Theorem 1, the right-hand side of (20) is estimated by Lemma 1 and Lemma 5 for $\alpha =2$ in the case $\gamma =-1/2$. Then, we have in (21) with (35)

$$G_{2;n}(x;0)=J_{1;s}^{*}(x)+n^{-1}{J}_{2;s}^{*}(x)+n^{-1}{J}_{3;s}^{*}(x),$$

$$\begin{array}{cc}\hfill \mathrm{where}{J}_{1;s}^{*}(x)={\int }_0^{\infty }\mathsf{\Phi }(x{y}^{-1/2})d{e}^{-s/y},& J_{2;s}^{*}(x)={\int }_0^{\infty }\frac{(a{x}^3{y}^{-3/2}-5x{y}^{-1/2})\phi (x{y}^{-1/2})}{4y}d{e}^{-s/y},\hfill \\ \hfill \mathrm{and}{J}_{3;s}^{*}(x)={\int }_0^{\infty }\mathsf{\Phi }(x{y}^{-1/2})d{h}_{2;s}(y)& \mathrm{with}{h}_{2;s}(y)=s{e}^{-s/y}\left(s-1+2Q_1(ny)\right)/\left(2y^2\right).\hfill \end{array}$$

To obtain (54), we calculate the above integrals:

$$\begin{array}{cc}\hfill \frac{\partial }{\partial x}{\int }_0^{\infty }\mathsf{\Phi }(x\sqrt{y})d{e}^{-s/y}& =\frac{s}{\sqrt{2\pi }}{\int }_0^{\infty }{y}^{-3/2}{e}^{-(x^2/2+s)/y)}dy=\frac{s}{\sqrt{2\pi }}{\int }_0^{\infty }{z}^{1/2-1}{e}^{-(x^2/2+s)z)}dz\hfill \\ \hfill =\frac{{\displaystyle 1}}{{\displaystyle 2\sqrt{2s}}}{\left(1+\frac{{\displaystyle x^2}}{{\displaystyle 2s}}\right)}^{-3/2}& =s_2^{*}(x;\sqrt{s}),\mathrm{and}{\int }_0^{\infty }\mathsf{\Phi }(x\sqrt{y})d{e}^{-s/y}=S_2^{*}(x;\sqrt{s}).\hfill \end{array}$$

(A15)

Define $K=(s+x^2/2)$. With $z=K/y$ and $\mathsf{\Gamma }(\alpha )={\int }_0^{\infty }{z}^{\alpha -1}{e}^{-z}dz$, $\alpha >0$, we obtain

$$\begin{array}{cc}\hfill J_{2;s}^{*}(x)& =\frac{s}{4\sqrt{2\pi }}{\int }_0^{\infty }(a{x}^3{y}^{-9/2}-5x{y}^{-7/2})e^{-K/y}dy=\frac{s{K}^{-7/2}}{4\sqrt{2\pi }}{\int }_0^{\infty }(a{x}^3{z}^{5/2}-5x{z}^{3/2}K)e^{-z}dz\hfill \\ \hfill & =\frac{s{K}^{-7/2}}{4\sqrt{2\pi }}\left(a{x}^3\mathsf{\Gamma }(7/2)-5xK\mathsf{\Gamma }(5/2)\right)=\frac{1}{4{(x^2+2s)}^2}\left(15(a-1)x^3-30xs\right)s_2^{*}(x;\sqrt{s}).\hfill \end{array}$$

Integration by parts in $J_{3;s}^{*}(x)$ leads to

$$J_{3;s}^{*}(x)=\frac{x}{2\sqrt{2\pi }}{\int }_0^{\infty }{y}^{-3/2}{e}^{-x^2/(2y)}s{y}^{-2}{e}^{-s/y}\left((s-1)/2+Q_1(ny)\right)dy=J_{4;s}^{*}(x)+J_{5;s}^{*}(x),$$

where

$$J_{4;s}^{*}(x)=\frac{s(s-1)x}{4\sqrt{2\pi }}{\int }_0^{\infty }{y}^{-7/2}{e}^{-K/y}dy=\frac{s(s-1)x\mathsf{\Gamma }(5/2)}{4\sqrt{2\pi }{K}^{5/2}}=\frac{3(s-1)x}{4(x^2+2s)}{s}_2^{*}(x;\sqrt{s})$$

and using the Fourier series expansion (A11) of the periodic function $Q_1(y)$ and interchange sum and integral, we find

$$\begin{array}{cc}\hfill J_{5;s}^{*}(x)& =\frac{sx}{2\sqrt{2\pi }}{\int }_0^{\infty }{y}^{-7/2}{e}^{-K/y}{Q}_1(ny)dy=\frac{sx}{2\sqrt{2\pi }}{\sum }_{k=1}^{\infty }\frac{1}{k}{\int }_0^{\infty }{y}^{-7/2}{e}^{-K/y}sin(2\pi kny)dy\hfill \\ \hfill & =\frac{sx}{2\sqrt{2\pi }}{\sum }_{k=1}^{\infty }\frac{1}{k}{\int }_0^{\infty }{y}^{-7/2}{e}^{-K/y}sin(2\pi kny)dy.\hfill \end{array}$$

Integration by parts in the latter integral and $|x|/\sqrt{K}\le \sqrt{2}$ leads now to

$${sup}_x|J_{5;s}^{*}(x)|\le {sup}_x\frac{s|x|}{{(2\pi )}^{3/2}n}{\sum }_{k=1}^{\infty }\frac{1}{k^2}{\int }_0^{\infty }\left(\frac{7}{2}{y}^{-9/2}+K{y}^{11/2}\right)e^{-K/y}dy\le c_s{n}^{-1}$$

with $c_s=\frac{{\displaystyle s\sqrt{2}}}{{\displaystyle {(2\pi )}^{3/2}n}}\left(\frac{{\displaystyle 7\mathsf{\Gamma }(11/2)}}{{\displaystyle 2s^3}}+\frac{{\displaystyle \mathsf{\Gamma }(13/2)}}{{\displaystyle s^4}}\right)\frac{{\displaystyle {\pi }^2}}{{\displaystyle 6}}$ and Theorem 8 is proved. □