Wirelength of Enhanced Hypercube into Windmill and Necklace Graphs

Abstract

An embedding of an interconnection network into another is one of the main issues in parallel processing and computing systems. Congestion, dilation, expansion and wirelength are some of the parameters used to analyze the efficiency of an embedding in which resolving the wirelength problem reduces time and cost in the embedded design. Due to the potential topological properties of enhanced hypercube, it has become constructive in recent years, and a lot of research work has been carried out on it. In this paper, we use the edge isoperimetric problem to produce the exact wirelengths of embedding enhanced hypercube into windmill and necklace graphs.

1. Introduction

Graph theory is one of the most interesting branches of mathematics, with wide applications in the domain of computer science, leading to the choice of a network in the development of parallel computers on a commercial basis. An interconnection network can be modeled by a graph, in which processors and links between processors are denoted as vertices and edges of a graph, respectively. Interconnection network has many advantages and inherent applications in the field of system designs such as scheduling of multiprocessor systems and distributed systems. The problem of efficiently implementing a parallel algorithm developed for one network into another can be modeled by a graph-embedding problem [1]. A graph embedding of a guest graph G into a host graph H is defined by a bijective mapping f : $V(G)$→$V(H)$ together with a mapping $P_f$ which assigns to each edge $(u,v)$ of G a path between $f(u)$ and $f(v)$ in H [2].

An edge congestion of an embedding of G into H is the maximum number of edges of a graph G that are embedded on any single edge of H. Let $E{C}_f(e)$ denote the number of edges $(u,v)$ of graph G such that e is in a path $P_f((u,v))$ between $f(u)$ and $f(v)$ of H [2,3]. In other words,

$$E{C}_f(e)=\left|\{(u,v)\in E(G):e\in P_f((u,v))\}\right|.$$

The wirelength of an embedding f of G into H is computed by

$$W{L}_f(G,H)=\sum _{(u,v)\in E(G)}\mid P_f((u,v))\mid =\sum _{e\in E(H)}E{C}_f(e).$$

The wirelength of G into H is defined as

$$WL(G,H)=minW{L}_f(G,H)$$

where the minimum is taken over all embeddings f of G into H. The wirelength problem of a graph embedding emerges from VLSI designs [4], networks for parallel computer systems [5] and structural engineering [6,7].

Wirelength problems have been considered for enhanced hypercube into wounded lobsters [8], r-rooted complete binary tree [1], complete binary tree [9], caterpillar and path [10]. The wirelength of hypercubes into necklace, windmill and snake graphs have been examined in [11]. In this paper, we explore the exact wirelength of enhanced hypercube into necklace and windmill graphs and the main contributions are presented in Theorems 2, 3 and 4.

The rest of the paper is organized as follows. In Section 2, we study edge isoperimetric problem and 2-partition lemma. Enhanced hypercube and its properties will be discussed in Section 3. In Section 4, we compute the minimum wirelength of embedding enhanced hypercube into windmill and necklace graphs. Finally, Section 5 concludes the paper.

2. Edge Isoperimetric Problem

Consider an interesting NP-complete problem [12] namely combinatorial isoperimetric problem which optimizes or selects the best structure among several possibilities and arises naturally in communication engineering, computer science, physical sciences and mathematics [13]. The following two versions of the EIP of a graph G have been considered in the literature [14,15,16].

EIP (1): Find a subset of the vertices of a given graph such that the edge cut separating this subset from its complement has minimal size among all subsets of the same cardinality.

Mathematically, if for a given m, where m = $1,2,\dots ,\left|V\right|$, ${\theta }_G(m)$ = $\underset{A\subseteq V,\left|A\right|=m}{min}$$|{\theta }_G(A)|$, where ${\theta }_G(A)=\{(u,v)\in E:u\in A,v\notin A\}$, then the problem is to find $A\subseteq V$ such that $\left|A\right|$ = m and ${\theta }_G(m)$ = $|{\theta }_G(A)|$. Such subsets are called optimal with respect to EIP (1). If a set of vertices is optimal with respect to EIP (1), then it is trivial that its complement is also optimal to EIP (1).

EIP (2): Find a subset of the vertices of a given graph such that the number of edges in the subgraph induced by this subset is maximal among all induced subgraphs with the same number of vertices.

Mathematically, if for a given m, where m = $1,2,\dots ,\left|V\right|$, $I_G(m)$ = $\underset{A\subseteq V,\left|A\right|=m}{max}\left|I_G(A)\right|$, where $I_G(A)$ = $\left\{(u,v)\in E:u,v\in A\right\}$, then the problem is to find $A\subseteq V$ such that $\left|A\right|$ = m and $I_G(m)$ = $\left|I_G(A)\right|$. Such subsets are called optimal with respect to EIP (2).

Clearly, if a subset of vertices is optimal with respect to EIP (2), then its complement is also an optimal set only for regular graphs and moreover, if a subset of vertices is optimal with respect to EIP (2), it is also optimal with respect to EIP (1). In the case of non-regular graphs, if a subset of vertices is optimal with respect to EIP (2), it need not be optimal to EIP (1) and there is no specific condition to optimality [16].

We now state the congestion and partition lemmas which will be used to compute the exact wirelengths in our paper.

Lemma 1. 

(Congestion Lemma) [3] Let G be an r-regular graph and f be an embedding of G into H. Let S be an edge cut of H such that the removal of edges of S leaves H into two components $H_1$ and $H_2$ and let $G_1$= $G[f^{-1}(H_1)]$ and $G_2$= $G[f^{-1}(H_2)]$. Also S satisfies the following conditions:

(i) 

For every edge $(a,b)\in G_i$, $i=1,2,$$P_f((a,b))$ has no edges in S.

(ii) 

For every edge $(a,b)\in G$ with $a\in G_1$ and $b\in G_2$, $P_f((a,b))$ has exactly one edge in S.

(iii) 

$G_1$ is an optimal set.

Then $E{C}_f(S)$ is minimum and $E{C}_f(S)$ = $r|V(G_1)|-2|E(G_1)|.$

Lemma 2. 

(2-Partition Lemma) [17] Let $f:G\to H$ be an embedding. Let $[2E(H)]$ denote a collection of edges of H repeated exactly 2 times. Let $\{S_1,S_2,\dots ,S_m\}$ be a partition of $[2E(H)]$ such that each $S_i$ is an edge cut of H. Then

$$W{L}_f(G,H)=\frac{1}{2}\stackrel{m}{\sum _{i=1}}E{C}_f(S_i).$$

3. Properties of Enhanced Hypercubes

The hypercube $(Q_n)$ has received extensive attention in view of its regular structure, small diameter and good connection with a relatively small vertex degree [7,18]. As the effort to improve its efficiency, several variants of $Q_n$ have been proposed.

In many variants of hypercube, the topological structure of enhanced hypercube network $(Q_{n,k})$ is considered to be a significant topology due mainly to its reliability, efficiency and the fault tolerance of $Q_{n,k}$ are better than $Q_n$, which shows that the enhanced hypercube is an excellent choice of network topology to improve traffic distributions, bandwidth capabilities and performance in parallel processing computer systems [18].

Definition 1

([19]). The enhanced hypercube $Q_{n,k}$, $1\le k\le n-1$, is an $(n+1)$-regular graph with vertex set $V(Q_{n,k})$ = $V(Q_n)$ labeled as $\{0,1\dots ,2^n-1\}$ and edge set $E(Q_{n,k})=E(Q_n)\cup (x_1{x}_2\dots x_k{x}_{k+1}\dots x_n$, $x_1{x}_2\dots x_{k-1}{\overline{x}}_k{\overline{x}}_{k+1}\dots {\overline{x}}_n)$, $x_i=0or1$, $1\le i\le n$. The edges of $Q_n$ in $Q_{n,k}$ are called hypercube edges and the remaining edges of $Q_{n,k}$ are called complementary edges.

Remark 1.

$|V(Q_{n,k})|=2^n$ and $|E(Q_{n,k})|=(n+1)2^{n-1}$.

Theorem 1

([10]). For $1\le i\le 2^n$, $L_i$ = $\left\{0,1,\dots ,i-1\right\}$ is an optimal set in $Q_{n,k}$.

Lemma 3

([10]). For $1\le i\le 2^n$, $|E(Q_{n,k}[L_i])|$ = $|E(Q_n[L_i])|$+$⌊\frac{i}{2^{n-k+1}}⌋$$2^{n-k}$+${[x-2^{n-k}]}^{+}$ where x = $i-⌊\frac{i}{2^{n-k+1}}⌋2^{n-k+1}$ and

$${[x]}^{+}=\left\{\begin{array}{c}\begin{array}{ccc}0& :& x<0\\ x& :& x\ge 0.\end{array}\hfill \end{array}\right.$$

4. Computation of Wirelength

In this section, we compute the exact wirelength of enhanced hypercubes into windmill and necklace graphs. The basic definitions and results to obtain the minimum wirelength are explained as follows.

Lemma 4.

For i = $1,2,\dots ,n-1$, $Ncut{S}_i^{2^i}=\{2^i,2^i+1,\dots ,2^{i+1}-1\}$ is an optimal set in $Q_{n,k}$.

Proof. 

Define $\phi :Ncut{S}_i^{2^i}\to L_{2^i}$ by $\phi (2^i+p)$=p. Let the binary representation of $2^i+p$ be ${\alpha }_1{\alpha }_2\dots {\alpha }_n$. Then the binary representation of p is $\underset{(n-i)times}{\underbrace{00\dots 00}}{\alpha }_{n-i+1}\dots {\alpha }_n$. To show that $Q_{n,k}[Ncut{S}_i^{2^i}]$ is isomorphic to $Q_{n,k}[L_{2^i}]$, we discuss the following cases for $(x,y)\in E(Q_{n,k}[Ncut{S}_i^{2^i}])$.

Case 1. Let $(x,y)$ be the hypercube edge in $Q_{n,k}[Ncut{S}_i^{2^i}]$. Suppose the binary representations of x and y are

$$x={\alpha }_1{\alpha }_2\dots {\alpha }_{n-i}{\beta }_1{\beta }_2\dots {\beta }_k\dots {\beta }_i,$$

$$y={\alpha }_1{\alpha }_2\dots {\alpha }_{n-i}{\beta }_1{\beta }_2\dots {\overline{\beta }}_k\dots {\beta }_i.$$

Then,

$$\phi (x)=\underset{(n-i)times}{\underbrace{00\dots 00}}{\beta }_1{\beta }_2\dots {\beta }_k\dots {\beta }_i,$$

$$\phi (y)=\underset{(n-i)times}{\underbrace{00\dots 00}}{\beta }_1{\beta }_2\dots {\overline{\beta }}_k\dots {\beta }_i.$$

hence $(x,y)\in$$E(Q_{n,k}[Ncut{S}_i^{2^i}])$⇔ the binary representation of x and y differ in exactly one bit ⇔ the binary representation of $\phi (x)$ and $\phi (y)$ differ in exactly one bit ⇔$(\phi (x),\phi (y))\in$$E(Q_{n,k}[L_{2^i}])$.

Case 2. Let $(x,y)$ be the complementary edge in $Q_{n,k}[Ncut{S}_i^{2^i}]$. Suppose the binary representations of x and y are

$$x={\alpha }_1{\alpha }_2{\alpha }_3\dots {\alpha }_{n-i}{\alpha }_{n-i+1}\dots {\alpha }_{k-1}{\alpha }_k{\alpha }_{k+1}\dots {\alpha }_{n-1}{\alpha }_n,$$

$$y={\alpha }_1{\alpha }_2{\alpha }_3\dots {\alpha }_{n-i}{\alpha }_{n-i+1}\dots {\alpha }_{k-1}{\overline{\alpha }}_k{\overline{\alpha }}_{k+1}\dots {\overline{\alpha }}_{n-1}{\overline{\alpha }}_n.$$

Then,

$$\phi (x)=\underset{(n-i)times}{\underbrace{00\dots 00}}{\alpha }_{n-i+1}\dots {\alpha }_{k-1}{\alpha }_k{\alpha }_{k+1}\dots {\alpha }_n,$$

$$\phi (y)=\underset{(n-i)times}{\underbrace{00\dots 00}}{\alpha }_{n-i+1}\dots {\alpha }_{k-1}{\overline{\alpha }}_k{\overline{\alpha }}_{k+1}\dots {\overline{\alpha }}_n.$$

hence $(x,y)\in$$E(Q_{n,k}[Ncut{S}_i^{2^i}])$⇔ the binary representations of x and y differ from the $k^{th}$ to $n^{th}$ bits ⇔ the binary representations of $\phi (x)$ and $\phi (y)$ differ from the $k^{th}$ to $n^{th}$ bits ⇔$(\phi (x),\phi (y))\in$$E(Q_{n,k}[L_{2^i}])$. Hence $Q_{n,k}[Ncut{S}_i^{2^i}]$ and $Q_{n,k}[L_{2^i}]$ are isomorphic.

From the above cases and Theorem 1, we infer that $Ncut{S}_i^{2^i}$ is an optimal set in $Q_{n,k}$. □

The following result is an easy consequence of Lemma 4.

Lemma 5.

For i = $1,2,\dots ,n-1$, $Ncut{S}_i^{2^i-1}=\{2^i,2^i+1,\dots ,2^{i+1}-2\}$ is an optimal set in $Q_{n,k}$.

Definition 2.

[11] Let $K_{t_i}$ be a complete graph on $t_i$ vertices, $1\le i\le m$. Let $t_1=2^r$ and $t_i=2^{r+i-2}+1$ for all $2\le i\le m$ such that ${\displaystyle {\displaystyle \underset{i=1}{\overset{m}{\uplus }}}{K}_{t_i}}$ has one vertex $(s)$ as common. The resultant graph is called a windmill graph and is denoted by $WM(K_{t_1},K_{t_2},\dots ,K_{t_m})$.

Remark 2.

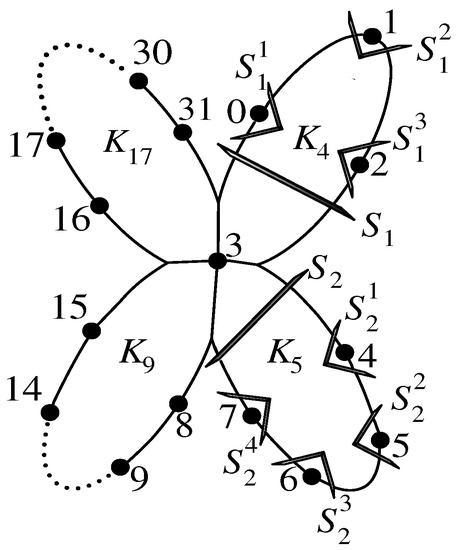
We denote $w_k$ = ${\displaystyle \sum _{i=1}^k}(t_i-1)+1$, $1\le k\le m$ and $w_0=t_0=0$. Then the windmill graph has $w_m=2^n$ vertices, see Figure 1.

Figure 1. The edge cuts of windmill $WM(K_4,K_5,K_9,K_{17})$.

Theorem 2.

The wirelength of $Q_{n,k}$ into $WM(K_{t_1},K_{t_2},\dots ,K_{t_m})$ is given by $WL(Q_{n,k},WM(K_{t_1},K_{t_2},\dots ,K_{t_m}))=\frac{1}{4}\{(n+1)(2^{n+1}+2^{m+r}-4)\}-{\displaystyle \sum _{i=1}^m}\left|E(Q_{n,k}\left[L_{t_i-1}\right])\right|.$

Proof. 

The proof is divided into three parts A, B, and C comprising of the embedding algorithm, proof of correctness, and computation of wirelength, respectively.

Part A:

Label the vertices of $Q_{n,k}$ by lexicographic order from 0 to $2^n-1$. Label the vertices of $K_{t_1}$ in $WM(K_{t_1},K_{t_2},\dots ,K_{t_m})$ as $0,1,2,\dots ,t_1-1$ such that $t_1-1$ is the label of common vertex s. For $2\le i\le m$, label the vertices of $K_{t_i}$ (except s) in $WM(K_{t_1},K_{t_2},\dots ,K_{t_m})$ as $w_{i-1}+j,j=0,1,2,\dots ,t_i-2$. Define an embedding f of $Q_{n,k}$ into $WM(K_{t_1},K_{t_2},\dots ,K_{t_m})$ given by $f(x)=x$.

Part B:

We assume that the labels represent the vertices to which they are assigned. Table 1 gives the notations for edge cuts of windmill graph as depicted in Figure 1.

Table 1. Edge cuts in windmill graph.

Cut Notation	Elements in the Cut	Range
$S_i$	$\{(w_1-1,x):x\in (V(K_{t_i})-\{w_1-1\})\}$	$1\le i\le m$
$S_i^j$	$\{(w_{i-1}+j-1,x):x\in (V(K_{t_i})-\{w_{i-1}+j-1\})\}$	$1\le i\le m$, $1\le j\le t_i-1$

Then {$S_i$: $1\le i\le m$} ∪ { $S_i^j$:$1\le i\le m$, $1\le j\le t_i-1$ } is a partition of $\left[2E(WM(K_{t_1},K_{t_2},\dots ,K_{t_m}))\right]$. The edge cut $S_i$ of $WM(K_{t_1},K_{t_2},\dots ,K_{t_m})$ disconnects $WM(K_{t_1},K_{t_2},\dots ,K_{t_m})$ into two components $X_i$ and $\overline{X_i}$ where $V(X_i)=\{w_{i-1},w_{i-1}+1,\dots ,w_{i-1}+t_i-2\}$. Let $G_i$ and $\overline{G_i}$ be the preimage of $X_i$ and $\overline{X_i}$ under f respectively. By Lemmas 4 & 5, $G_i$ is an optimal set and each $S_i$ satisfies conditions (i)–(iii) of the Congestion Lemma. Therefore, $E{C}_f(S_i)$ is minimum.

Similarly, the edge cut $S_i^j$ of $WM(K_{t_1},K_{t_2},\dots ,K_{t_m})$ disconnects $WM(K_{t_1},K_{t_2},\dots ,K_{t_m})$ into two components $X_i^j$ and $\overline{X_i^j}$ where $V(X_i^j)=\{w_{i-1}+j-1\}$. Let $G_i^j$ and $\overline{G_i^j}$ be the preimage of $X_i^j$ and $\overline{X_i^j}$ under f respectively. Since $G_i^j$ is an optimal set and each $S_i^j$ satisfies conditions $(i)-(iii)$ of the Congestion Lemma. Therefore, $E{C}_f(S_i^j)$ is minimum. The 2-Partition Lemma implies that $W{L}_f(Q_{n,k},WM(K_{t_1},K_{t_2},\dots ,K_{t_m})$ = $WL(Q_{n,k},WM(K_{t_1},K_{t_2},\dots ,K_{t_m})$.

Part C:

By Part B, we have $E{C}_f(S_i)=(n+1)(t_i-1)-2\left|E(Q_{n,k}\left[L_{t_i-1}\right])\right|$, $E{C}_f(S_i^j)=(n+1)$ for all $1\le i\le m$, $1\le j\le t_i-1$. Therefore, the wirelength of enhanced hypercube into windmill graph is given by $WL(Q_{n,k},WM(K_{t_1},K_{t_2},\dots ,K_{t_m})$ = $\frac{1}{2}{\displaystyle {\displaystyle \sum _{i=1}^m}}\{(n+1)(t_i-1)-2|E(Q_{n,k}\left[L_{t_i-1}\right])|\}+\frac{n+1}{2}(2^n-1)$ = $\frac{1}{4}\{(n+1)(2^{n+1}+2^{m+r}-4)\}-{\displaystyle {\displaystyle \sum _{i=1}^m}}\left|E(Q_{n,k}\left[L_{t_i-1}\right])\right|.$ □

Definition 3

([11]). Let $K_{1,m}$ be a star graph on $m+1$ vertices (say $v_0,v_1,\dots ,v_m$) and $K_{t_i}$ be complete graphs on $t_i$ vertices, $1\le i\le m$. Let $t_1=2^r$, $t_i=2^{r+i-2}$ for all $2\le i\le m-1$ and $t_m=2^{r+m-2}-1$ such that $K_{1,m}\uplus ({\displaystyle {\displaystyle \bigcup _{i=1}^m}}{K}_{t_i})$ has $v_i$ as common. The resultant graph is called a complete star necklace and is denoted by $SN(K_{1,m};K_{t_1},K_{t_2},\dots ,K_{t_m})$.

Remark 3.

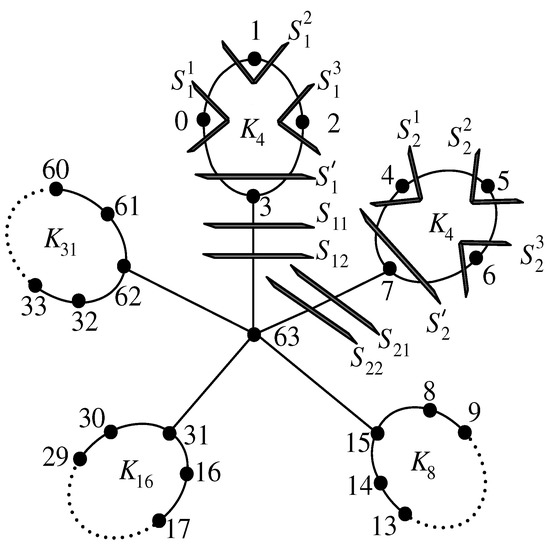
We denote $s_k$ = ${\displaystyle {\displaystyle \sum _{i=0}^k}}{t}_i$, $0\le k\le m$ where $t_0=0$. Then the complete star necklace has $s_m+1=2^n$ vertices, see Figure 2.

Figure 2. The edge cuts of complete star necklace $SN(K_{1,5};K_4,K_4,K_8,K_{16},K_{31})$.

Theorem 3.

$WL(Q_{n,k},SN(K_{1,m};K_{t_1}{K}_{t_2},\dots ,K_{t_m}))=\frac{1}{4}\{(n+1)(2^{n+1}+3·2^{m+r}-4m-8)\}-{\displaystyle {\displaystyle \sum _{i=1}^m}}\{2|E(Q_{n,k}\left[L_{t_i}\right])|+|E(Q_{n,k}\left[L_{t_i-1}\right])|\}.$

Proof. 

The proof technique is similar to Theorem 2 as divided into three parts A, B, and C.

Part A:

Label the vertices of $Q_{n,k}$ by lexicographic order from 0 to $2^n-1$. For $1\le i\le m$, label the vertices of $K_{t_i}$ in $SN(K_{1,m};K_{t_1},K_{t_2},\dots ,K_{t_m})$ as $s_{i-1}+j,j=0,1,2,\dots ,t_i-1$ such that $s_i-1$ is the label of $v_i$, and $v_0$ as $2^n-1$. Define an embedding f of $Q_{n,k}$ into $SN(K_{1,m};K_{t_1},K_{t_2},\dots ,K_{t_m})$ given by $f(x)=x$.

Part B:

We assume that the labels represent the vertices to which they are assigned. Table 2 gives the notations for edge cuts of complete star necklace graph as depicted in Figure 2.

Table 2. Edge cuts in complete star necklace graph.

Cut Notation	Elements in the Cut	Range
$S_{i1}$	$\{s_i-1,2^n-1\}$	$1\le i\le m$
$S_{i2}$	$\{s_i-1,2^n-1\}$	$1\le i\le m$
$S_i^{{}^{\prime }}$	$\{(s_i-1,x):x\in (V(K_{t_i})-\{s_i-1\})\}$	$1\le i\le m$
$S_i^j$	$\{(s_{i-1}+j-1,x):x\in (V(K_{t_i})-\{s_{i-1}+j-1\})\}$	$1\le i\le m$, $1\le j\le t_i-1$

Then {$S_{i1}$, $S_{i2}$, $S_i^{{}^{\prime }}$: $1\le i\le m$ } ∪ {$S_i^j$:$1\le i\le m$, $1\le j\le t_i-2$ } is a partition of $\left[2E(SN(K_{1,m};K_{t_1},K_{t_2},\dots ,K_{t_m}))\right]$. The edge cut $S_{i1}$ of $SN(K_{1,m};K_{t_1},K_{t_2},\dots ,K_{t_m})$ disconnects $SN(K_{1,m};K_{t_1},K_{t_2},\dots ,K_{t_m})$ into two components $X_i$ and $\overline{X_i}$ where $V(X_i)=\{s_{i-1},s_{i-1}+1,\dots ,s_i-1\}$. Let $G_i$ and $\overline{G_i}$ be the preimage of $X_i$ and $\overline{X_i}$ under f respectively. By Lemma 4, $G_i$ is an optimal set and each $S_{i1}$ satisfies conditions (i)–(iii) of the Congestion Lemma. Therefore, $E{C}_f(S_{i1})$ is minimum. Similarly, $E{C}_f(S_{i2})$ is minimum.

The edge cut $S_i^{{}^{\prime }}$ of $SN(K_{1,m};K_{t_1},K_{t_2},\dots ,K_{t_m})$ disconnects $SN(K_{1,m};K_{t_1},K_{t_2},\dots ,K_{t_m})$ into two components $X_i^{{}^{\prime }}$ and $\overline{X_i^{{}^{\prime }}}$ where $V(X_i^{{}^{\prime }})=\{s_{i-1},s_{i-1}+1,\dots ,s_i-2\}$. Let $G_i^{{}^{\prime }}$ and $\overline{G_i^{{}^{\prime }}}$ be the preimage of $X_i^{{}^{\prime }}$ and $\overline{X_i^{{}^{\prime }}}$ under f respectively. By Lemma 5, $G_i^{{}^{\prime }}$ is an optimal set and each $S_i^{{}^{\prime }}$ satisfies conditions (i)–(iii) of the Congestion Lemma. Therefore, $E{C}_f(S_i^{{}^{\prime }})$ is minimum.

The edge cut $S_i^j$ of $SN(K_{1,m};K_{t_1},K_{t_2},\dots ,K_{t_m})$ disconnects $SN(K_{1,m};K_{t_1},K_{t_2},\dots ,K_{t_m})$ into two components $X_i^j$ and $\overline{X_i^j}$ where $V(X_i^j)=\{s_{i-1}+j-1\}$. Let $G_i^j$ and $\overline{G_i^j}$ be the preimage of $X_i^j$ and $\overline{X_i^j}$ under f respectively. Since $G_i^j$ is an optimal set and each $S_i^j$ satisfies conditions $(i)-(iii)$ of the Congestion Lemma. Therefore, $E{C}_f(S_j^{{}^{\prime }})$ is minimum. The 2-Partition Lemma implies that $W{L}_f(Q_{n,k},SN(K_{1,m};K_{t_1},K_{t_2},\dots ,K_{t_m}))=WL(Q_{n,k},SN(K_{1,m};K_{t_1},K_{t_2},\dots ,K_{t_m}))$.

Part C:

By Part B, we have $E{C}_f(S_{i1})=E{C}_f(S_{i2})=(n+1)t_i-2\left|E(Q_{n,k}\left[L_{t_i}\right])\right|$, $E{C}_f(S_i^{{}^{\prime }})=(n+1)(t_i-1)-2\left|E(Q_{n,k}\left[L_{t_i-1}\right])\right|$, $E{C}_f(S_i^j)=(n+1)$ for all $1\le i\le m$, $1\le j\le t_i-1$. Therefore, the wirelength of enhanced hypercube into complete star necklace graph is given by $WL(Q_{n,k},SN(K_{1,m};K_{t_1},K_{t_2},\dots ,K_{t_m}))={\displaystyle \sum _{i=1}^m}\{(n+1)t_i-2|E(Q_{n,k}\left[L_{t_i}\right])|\}+\frac{1}{2}{\displaystyle \sum _{i=1}^m}\{(n+1)(t_i-1)-2|E(Q_{n,k}\left[L_{t_i-1}\right])|\}+\frac{n+1}{2}(2^n-m-1)=\frac{1}{4}\{(n+1)(2^{n+1}+3(2^{m+r})-4m-8)\}-{\displaystyle \sum _{i=1}^m}\{2|E(Q_{n,k}\left[L_{t_i}\right])|+|E(Q_{n,k}\left[L_{t_i-1}\right])|\}$. □

Definition 4

([11]). Let $K_m$ be a complete graph on m vertices (say $v_1,v_2,\dots ,v_m$) and $K_{t_i}$ be complete graphs on $t_i$ vertices, $1\le i\le m$. Let $t_1=2^r$ and $t_i=2^{r+i-2}$ for all $2\le i\le m$ such that $K_m\uplus ({\displaystyle \bigcup _{i=1}^m}{K}_{t_i})$ has $v_i$ as common. The resultant graph is called a circular necklace graph and is denoted by $CN(K_m;K_{t_1},K_{t_2},\dots ,K_{t_m})$.

Remark 4.

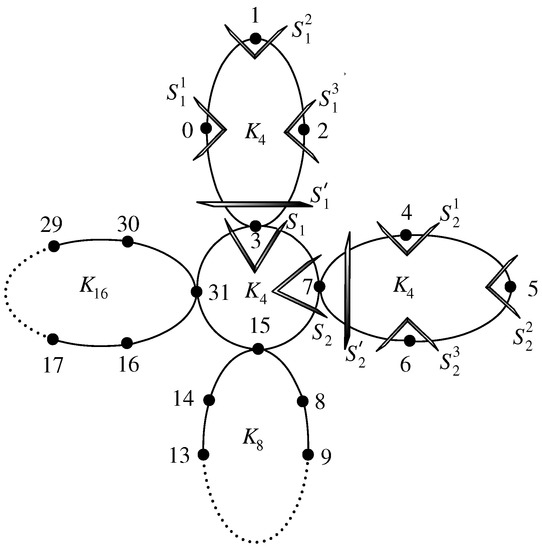
We denote $c_k$= ${\displaystyle \sum _{i=0}^k}{t}_i$, $0\le k\le m$ where $t_0=0$. Then the circular necklace has $c_m=2^n$ vertices, see Figure 3.

Figure 3. The edge cuts of circular necklace $CN(K_4;K_4,K_4,K_8,K_{16})$.

Theorem 4.

The wirelength of $Q_{n,k}$ into $CN(K_m;K_{t_1},K_{t_2},\dots ,K_{t_m})$ is given by $WL(Q_{n,k},CN(K_m;K_{t_1},K_{t_2},\dots ,K_{t_m}))=\frac{1}{2}\{(n+1)(2^{m+r}+2^n-2m)\}-{\displaystyle \sum _{i=1}^m}\{|E(Q_{n,k}\left[L_{t_i}\right])|+|E(Q_{n,k}\left[L_{t_i-1}\right])|\}.$

Proof. 

We label the vertices of $Q_{n,k}$ by lexicographic order from 0 to $2^n-1$. For $1\le i\le m$, label the vertices of $K_{t_i}$ in $CN(K_m;K_{t_1},K_{t_2},\dots ,K_{t_m})$ as $c_{i-1}+j,j=0,1,2,\dots ,t_i-1$ such that $c_i-1$ is the label of $v_i$. Define an embedding f of $Q_{n,k}$ into $CN(K_m;K_{t_1},K_{t_2},\dots ,K_{t_m})$ given by $f(x)=x$.

We assume that the labels represent the vertices to which they are assigned. Table 3 gives the notations for edge cuts of circular necklace graph as depicted in Figure 3.

Table 3. Edge cuts in circular necklace graph.

Cut Notation	Elements in the Cut	Range
$S_i$	$\{(c_i-1,x):x\in (V(K_m)-\{c_i-1\})\}$	$1\le i\le m$
$S_i^{{}^{\prime }}$	$\{(c_i-1,x):x\in (V(K_{t_i})-\{c_i-1\})\}$	$1\le i\le m$
$S_i^j$	$\{(c_{i-1}+j-1,x):x\in (V(K_{t_i})-\{c_{i-1}+j-1\})\}$	$1\le i\le m$, $1\le j\le t_i-1$

Then { $S_i$, $S_i^{{}^{\prime }}$:$1\le i\le m$ } ∪ { $S_i^j$:$1\le i\le m$, $1\le j\le t_i-2$ } is a partition of $\left[2E(CN(K_m;K_{t_1},K_{t_2},\dots ,K_{t_m}))\right]$. The edge cut $S_i$ of $CN(K_m;K_{t_1},K_{t_2},\dots ,K_{t_m})$ disconnects $CN(K_m;K_{t_1},K_{t_2},\dots ,K_{t_m})$ into two components $X_i$ and $\overline{X_i}$ where $V(X_i)=\{c_{i-1},c_{i-1}+1,\dots ,c_i-1\}$. Let $G_i$ and $\overline{G_i}$ be the preimage of $X_i$ and $\overline{X_i}$ under f respectively. By Lemma 4, $G_i$ is an optimal set and each $S_i$ satisfies conditions $(i)-(iii)$ of the Congestion Lemma. Therefore, $E{C}_f(S_i)$ is minimum.

The edge cut $S_i^{{}^{\prime }}$ of $CN(K_m;K_{t_1},K_{t_2},\dots ,K_{t_m})$ disconnects $CN(K_m;K_{t_1},K_{t_2},\dots ,K_{t_m})$ into two components $X_i^{{}^{\prime }}$ and $\overline{X_i^{{}^{\prime }}}$ where $V(X_i^{{}^{\prime }})=\{c_{i-1},c_{i-1}+1,\dots ,c_i-2\}$. Let $G_i^{{}^{\prime }}$ and $\overline{G_i^{{}^{\prime }}}$ be the preimage of $X_i^{{}^{\prime }}$ and $\overline{X_i^{{}^{\prime }}}$ under f respectively. By Lemma 5, $G_i^{{}^{\prime }}$ is an optimal set and each $S_i^{{}^{\prime }}$ satisfies conditions (i)–(iii) of the Congestion Lemma. Therefore, $E{C}_f(S_i^{{}^{\prime }})$ is minimum.

The edge cut $S_i^j$ of $CN(K_m;K_{t_1},K_{t_2},\dots ,K_{t_m})$ disconnects $CN(K_m;K_{t_1},K_{t_2},\dots ,K_{t_m})$ into two components $X_i^j$ and $\overline{X_i^j}$ where $V(X_i^j)=\{c_{i-1}+j-1\}$. Let $G_i^j$ and $\overline{G_i^j}$ be the preimage of $X_i^j$ and $\overline{X_i^j}$ under f respectively. Since $G_i^j$ is an optimal set and each $S_i^j$ satisfies conditions (i)–(iii) of the Congestion Lemma. Therefore $E{C}_f(S_j^{{}^{\prime }})$ is minimum. The 2-Partition Lemma implies that $W{L}_f(Q_{n,k},CN(K_m;K_{t_1},K_{t_2},\dots ,K_{t_m}))=WL(Q_{n,k},CN(K_m;K_{t_1},K_{t_2},\dots ,K_{t_m}))$.

Now, we have $E{C}_f(S_i)=(n+1)t_i-2\left|E(Q_{n,k}\left[L_{t_i}\right])\right|$, $E{C}_f(S_i^{{}^{\prime }})=(n+1)(t_i-1)-2\left|E(Q_{n,k}\left[L_{t_i-1}\right])\right|$, $E{C}_f(S_i^j)=(n+1)$ for all $1\le i\le m$, $1\le j\le t_i-1$. Therefore, the wirelength of enhanced hypercube into circular necklace graph is given by $WL(Q_{n,k},CN(K_m;K_{t_1},K_{t_2},\dots ,K_{t_m}))$ = $\frac{1}{2}{\displaystyle \sum _{i=1}^m}\{(n+1)t_i-2|E(Q_{n,k}\left[L_{t_i}\right])|\}+\frac{1}{2}{\displaystyle \sum _{i=1}^m}\{(n+1)(t_i-1)-2|E(Q_{n,k}\left[L_{t_i-1}\right])|\}+\frac{n+1}{2}(2^n-m)$ = $\frac{1}{2}\{(n+1)(2^{m+r}+2^n-2m)\}-{\displaystyle \sum _{i=1}^m}\{|E(Q_{n,k}\left[L_{t_i}\right])|+|E(Q_{n,k}\left[L_{t_i-1}\right])|\}.$ □

5. Conclusions

In this paper, we have computed the minimum wirelength of embedding enhanced hypercube into host graph such as windmill and necklace graphs by partitioning the edge set of the host graph. On comparing with the wirelength of hypercube into windmill and necklace graphs, we found that the computation varies by degree of enhanced hypercube. The results obtained in this paper would build a great impact on parallel computing systems. Furthermore, it would be an interesting line of research to compute the wirelength of general r-regular graph into windmill and necklace graphs.