Categorical Structures in Rough Set Theory and Information Systems

Abstract

Using the concept of category, we provide some insight into and prove an intrinsic property of the category AprS of approximation spaces and continuous functions. We also introduce rough closure and rough interior operators to characterize clopen topologies. Our main result proves the equivalence of several categories, including the category of equivalence relations and relation-preserving functions, the category of rough interior spaces and continuous functions, the category of rough closure spaces and continuous functions, and the category AprS. This work provides a deeper understanding of the interplay among rough set theory, information systems, and category theory.

1. Introduction

Rough set theory (RST), introduced by Pawlak [1], is intrinsically a study of an equivalence relation [2]. The theory originates from the concept of an approximation space $⟨U,t⟩$, where U is a universe of objects and t is an equivalence relation on U. From the topological point of view, the Pawlak lower and upper approximations correspond, respectively, to the interior and closure functions in a clopen topology (a topology $\mathcal{T}$ on a set is called a clopen topology if every member of $\mathcal{T}$ is both open and closed) with the base (a base $\mathcal{B}$ for a topological space $(U,\mathcal{T})$ is a set of open sets such that every member of $\mathcal{T}$ can be expressed as a union of members of $\mathcal{B}$; we say that the base generates the topology $\mathcal{T}$). the set of all distinct t-equivalence classes. Consequently, there exists a natural bijection between the clopen topologies on a set U and the approximation spaces over U.

On the other hand, categories are rich algebraic structures that provide a unified framework for abstraction. Recently, Borzooei et al. [3] considered the class of approximation spaces and discussed some categories of lower, upper, and natural approximations without using many topological structures of spaces. However, their approach, which deliberately avoids deep topological machinery, has limitations in deriving more powerful categorical results. The need for a categorical framework grounded in topology is growing.

The classical Pawlak model offers a foundational framework for reasoning about uncertainty and indiscernibility, but its reliance on equivalence relations imposes a rigid partition structure, which is inadequate for dynamic or complex data. To address these limitations, rough set theory has expanded beyond equivalence-based granulations. One major direction replaces equivalence relations with arbitrary binary relations, tolerance relations, or neighborhood systems [4], enabling more flexible representations of similarity and proximity. Notable developments include generalized approximation spaces based on overlapping subset neighborhoods and overlapping containment rough neighborhoods. In fact, a rich interplay with topology has emerged. Topological tools, open sets, $\delta$-open sets, and covering-based neighborhoods have been used to generate new rough models and to analyze arbitrary relations [5]. Concepts such as separation axioms and covering properties further refine granularity and relational structure. Together, these relational and topological generalizations demonstrate the field’s evolution toward more adaptable and mathematically integrated frameworks.

Against this backdrop, a rigorous categorical foundation for the classical equivalence-based setting remains essential. This work addresses this need by developing a topological interpretation of the standard rough set model. We advance this direction by systematically exploiting the topological structures inherent in rough set theory. In particular, we define the category AprS of approximation spaces and continuous functions. By introducing the notions of rough closure and rough interior operators, we provide an operator-theoretic characterization of clopen topologies. This framework reveals the intrinsic topological structure underlying Pawlak’s model and establishes a stable categorical foundation from which broader generalizations can be developed in a systematic and unified manner. Our overarching goal is to achieve a coherent categorical interpretation of rough set theory.

Our main result establishes the equivalence of four categories: the category AprS of approximation spaces and continuous functions; the category Equiv of equivalence relations and relation-preserving functions; the category of rough interior spaces and continuous functions; and the category of rough closure spaces and continuous functions.

We organize the paper as follows. Section 2 presents the necessary preliminaries, including approximation spaces, information systems, and basic topological notions. In particular, we review closure and interior operators and equivalent characterizations of continuity, which serve as foundational tools for later sections. In Section 3, we introduce rough closure and rough interior operators and show that they yield an operator-theoretic characterization of clopen topologies. We study minimal clopen neighborhoods, analyze union- and intersection-preserving operators, and characterize continuity between clopen spaces via these rough operators. Section 4 defines several categories that naturally arise from the rough set theory, including categories of approximation spaces, equivalence relations, rough closure spaces, and rough interior spaces. We prove that these categories are mutually equivalent, providing structurally identical perspectives on rough approximations. We also examine the connection between approximation spaces and information systems by introducing a subcategory of information systems with non-expansive O–A–D homomorphisms and constructing functors linking it to the category of approximation spaces. Section 5 reviews related categorical approaches to rough sets and compares our framework with existing ones, highlighting key conceptual and structural differences. Finally, Section 6 concludes with remarks on the significance of established categorical equivalences and outlines directions for future research, including further applications of categorical methods to rough set theory and information systems.

More precisely, we provide the following conceptual flowchart of the paper (Figure 1).

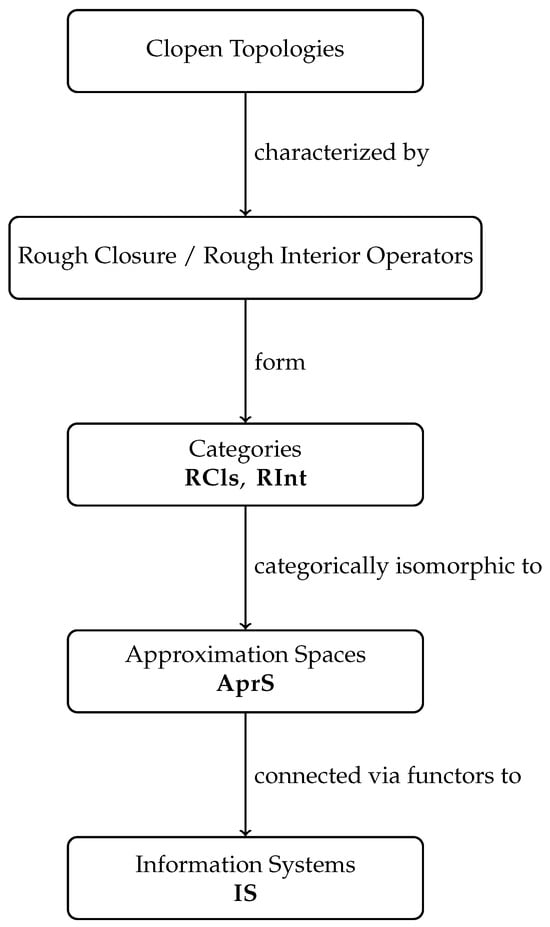
Figure 1. The diagram presents the conceptual structure of the paper in a top-down manner. Clopen topologies are characterized by rough closure and interior operators. These operators naturally form the categories $\mathbf{RCls}$ and $\mathbf{RInt}$, which have been shown to be categorically isomorphic to the category of approximation spaces $\mathbf{AprS}$. Approximation spaces are linked to information systems $\mathbf{IS}$ through appropriate functors.

2. Preliminaries

This section recalls the basic concepts and notations that will be used throughout this paper. We begin with the fundamental notion of equivalence relations and their induced structures, then review essential set-theoretic operators, closure and interior spaces, topological spaces and continuity, and finally, approximation spaces and information systems in the context of rough set theory.

We shall denote the power set of a set U (i.e., the set of all subsets of U) by $2^U$. A function $c:2^U\to 2^U$ from the power set of U to itself is also called an operator on U. The dual of the operator $c:2^U\to 2^U$ is the operator $i:2^U⟶2^U$ defined by

$$i\left(X\right)=U\setminus c(U\setminus X)$$

(1)

and hence

$$c\left(X\right)=U\setminus i(U\setminus X).$$

(2)

For an equivalence relation t on U and an element $u\in U$, we denote by ${\left[u\right]}_t$ the t-equivalence class of u, i.e., ${\left[u\right]}_t=\{u^{\prime }\in U\mid (u,u^{\prime })\in t\}$. The set of all distinct t-equivalence classes, denoted $U/t$, is a partition of U and is called the quotient set of U modulo t.

2.1. Images and Preimages

Assume that $f:U\to V$ is a function from a set U to a set V. We shall use the notations $f^{\to }\left(A\right)$ and $f^{\leftarrow }\left(B\right)$ to denote, respectively, the image of $A\subseteq U$ and the preimage of $B\subseteq V$ under the function f.

The preimage operator commutes with all basic set operations. Specifically, for any $B\subseteq V$, the preimage of B is the complement of the preimage of the complement of B as follows:

$$f^{\leftarrow }\left(B\right)=U\setminus f^{\leftarrow }(V\setminus B)$$

(3)

and hence

$$f^{\leftarrow }(V\setminus B)=U\setminus f^{\leftarrow }\left(B\right).$$

(4)

These properties will be useful when studying continuity and approximations.

2.2. Closure and Interior Spaces

A closure operator on a set U is a function $c:2^U⟶2^U$ from the power set $2^U$ of U into itself that satisfies the following four conditions (known as the Kuratowski closure axioms): $c(\varnothing )=\varnothing$ (it preserves the empty set), $X\subseteq c\left(X\right)$ (it is extensive), $c\left(c\right(X\left)\right)=c\left(X\right)$ (it is idempotent), and $c(X\cup Y)=c\left(X\right)\cup c\left(Y\right)$ (it preserves binary unions) for every $X,Y\in 2^U$. The pair $(U,c)$ is called a closure space.

The notion of an interior operator is dual to that of a closure operator. An interior operator on U is a function $i:2^U⟶2^U$ that satisfies the dual interior axioms (called the Kuratowski interior axioms) as follows: $i\left(U\right)=U$ (it preserves the total space), $i\left(X\right)\subseteq X$ (it is intensive), $i\left(i\right(X\left)\right)=i\left(X\right)$ (it is idempotent), and $i(X\cap Y)=i\left(X\right)\cap i\left(Y\right)$ (it preserves binary intersections) for every $X,Y\in 2^U$. The pair $(U,i)$ is called an interior space. The following lemma relates closure and interior operators via preimages.

Lemma 1.

Let $(U,c_U)$ and $(V,c_V)$ be closure spaces. Assume that $i_U$ and $i_V$ are the interior operators corresponding to $c_U$ and $c_V$, respectively, and that f is a function from U to V. The following statements are equivalent.

(1) 

For each subset B of V, $c_U(f^{\leftarrow }\left(B\right))\subseteq f^{\leftarrow }\left(c_V\left(B\right)\right)$.

(2) 

For each subset B of V, $f^{\leftarrow }\left(i_V\left(B\right)\right)\subseteq i_U\left(f^{\leftarrow }\left(B\right)\right)$.

The proof is provided in Appendix B.

2.3. Topological Spaces and Continuity

A topological space $(U,\mathcal{T})$ can be described equivalently in terms of closure, interior, or neighborhood systems. For a subset $A\subseteq U$, $\mathrm{cl}\left(A\right)$ and $\mathrm{int}\left(A\right)$ represent the closure of A and the interior of A, respectively. The closure function

$$A⟼\mathrm{cl}\left(A\right):=\cap \{K\subseteq U\mid U\setminus K\in \mathcal{T},A\subseteq K\}$$

(5)

associated with each subset $A\subseteq U$, with its closure $\mathrm{cl}\left(A\right)$ satisfying the Kuratowski closure axioms.

Dually, the interior function

$$A⟼\mathrm{int}\left(A\right):=\cup \{G\in \mathcal{T}\mid G\subseteq A\}$$

satisfies the Kuratowski interior axioms.

A set N in $(U,\mathcal{T})$ is a neighborhood of a point $u\in U$ if and only if (shortened iff) N contains an open set to which u belongs, i.e., $u\in \mathrm{int}\left(N\right)$. The set of all neighborhoods of u is called the neighborhood system of u and is denoted by $\mathcal{N}\left(u\right)$. The neighborhood function

$$u⟼\mathcal{N}\left(u\right)=\{N\subseteq U\mid u\in \mathrm{int}(N\left)\right\}$$

(6)

satisfies the four neighborhood axioms [6]. It is an easy fact that for each subset $A\subseteq U$, a point $u\in \mathrm{cl}\left(A\right)$ iff $A\cap N\ne \varnothing$ for every neighborhood N of u for closure operators. We therefore have the following.

$$\mathrm{cl}\left(A\right)=\{u\in U\mid N\cap A\ne \varnothing ,\forall N\in \mathcal{N}(u\left)\right\}\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{l}\mathrm{l}A\subseteq U.$$

(7)

Topologies are usually given in terms of open sets. As is well known [6,7], a topological space can be equivalently defined by a closure space, or an interior space, or a neighborhood function. This leads us to study the topological structure from different points of view.

A localized form of continuity in terms of neighborhoods may be stated as follows.

Definition 1.

Let U and V be topological spaces. A function $f:U\to V$ is continuous at $u\in U$, iff for each neighborhood M of $f\left(u\right)$ there is a neighborhood N of u such that $f^{\to }\left(N\right)\subseteq M$. We say $f:U\to V$ is continuous if f is continuous at every $u\in U$.

Proposition 1

([6]). Assume that U and V are topological spaces, and that f is a function from U into V. The following statements are equivalent.

(1) 

The function f is continuous.

(2) 

The preimage of each open set is open.

(3) 

For each $A\subseteq U$, the image of its closure is contained in the closure of its image.

(4) 

For each $B\subseteq V$, the closure of its preimage is contained in the preimage of its closure.

2.4. Approximation Spaces

An approximation space is a pair $⟨U,t⟩$ where U is a universe and t is an equivalence relation on U. The upper and lower approximations, ${\overline{apr}}_t\left(X\right)$ and ${\underline{apr}}_t\left(X\right)$, of a set $A\subseteq U$ are defined, respectively, as follows [1]:

$${\overline{apr}}_t\left(A\right)=\bigcup _{u\in U}\{{\left[u\right]}_t\mid {\left[u\right]}_t\cap A\ne \varnothing \}$$

(8)

$${\underline{apr}}_t\left(A\right)=U\setminus {\overline{apr}}_t(U\setminus A)=\bigcup _{u\in U}\{{\left[u\right]}_t\mid {\left[u\right]}_t\subseteq A\}.$$

(9)

The upper approximation operator ${\overline{apr}}_t:2^U⟶2^U$ is a closure operator and satisfies

$${\overline{apr}}_t(\bigcup _{A\in \mathcal{A}}A)=\bigcup _{A\in \mathcal{A}}{\overline{apr}}_t\left(A\right)$$

(10)

for all $\mathcal{A}\subseteq 2^U$, i.e., the upper approximation operator ${\overline{apr}}_t:2^U⟶2^U$ is union preserving (a union-preserving operator on a set U is a function $J:2^U⟶2^U$ if it satisfies the property: $J({\displaystyle \bigcup _{A\in \mathcal{A}}}A)={\displaystyle \bigcup _{A\in \mathcal{A}}}J\left(A\right)$ for all $\mathcal{A}\subseteq 2^U$.). The upper and lower approximation operators satisfy

$${\overline{apr}}_t\left({\underline{apr}}_t\left(A\right)\right)={\underline{apr}}_t\left(A\right)\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{l}\mathrm{l}A\subseteq U,$$

(11)

or equivalently,

$${\underline{apr}}_t\left({\overline{apr}}_t\left(A\right)\right)={\overline{apr}}_t\left(A\right)\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{l}\mathrm{l}A\subseteq U$$

(12)

The last two equations imply that for every $A\subseteq U$,

$${\overline{apr}}_t\left(A\right)=A⟺{\underline{apr}}_t\left(A\right)=A.$$

(13)

Lemma 2.

If $⟨U,t⟩$ is an approximation space then the set of all subsets X of U for which ${\overline{apr}}_t\left(X\right)=X$ is the same as the set of all subsets X of U for which ${\underline{apr}}_t\left(X\right)=X$. In other words, the topology

$$\begin{array}{ccc}\hfill {\mathcal{T}}_t& =& \{X\subseteq U\mid {\overline{apr}}_t(U\setminus X)=U\setminus X\}\hfill \\ & =& \{X\subseteq U\mid {\underline{apr}}_t\left(X\right)=X\}\hfill \\ & =& \{X\subseteq U\mid {\overline{apr}}_t\left(X\right)=X\}\hfill \end{array}$$

is clopen.

Proof. 

Since, in a given approximation space $⟨U,t⟩$, the upper and lower approximation operators are dual and the upper approximation satisfies the Kuratowski closure axioms, it follows that

$$\begin{array}{ccc}\hfill {\mathcal{T}}_t& =& \{X\subseteq U\mid {\overline{apr}}_t(U\setminus X)=U\setminus X\}\hfill \\ & =& \{X\subseteq U\mid {\underline{apr}}_t\left(X\right)=X\}\hfill \end{array}$$

is a topology on U. It follows immediately from (13) that

$$\{X\subseteq U\mid {\underline{apr}}_t\left(X\right)=X\}=\{X\subseteq U\mid {\overline{apr}}_t\left(X\right)=X\}$$

is clopen. □

2.5. Information Systems

As rough set theory is applied to data analysis, an approximation space is usually induced from information systems. According to [1], an information system (also called knowledge representation systems, data tables, or attribute–value systems) is defined as a tuple $T=(U,A,\{D_a\mid a\in A\},\{f_a\mid a\in A\})$, where U is a nonempty finite set, called the universe; A is a nonempty finite set of primitive attributes; for each $a\in A$, $D_a$ is the domain of values for a; and for each $a\in A$, $f_a:U\to D_a$ is the information function for the attribute a. To simplify the presentation, we can identify each attribute a with its information function and set $D={\bigcup }_{a\in A}{D}_a$. Then, an information system is simply a triplet $(U,A,D)$, where A is a set of functions from U to D. Given an information system $(U,A,D)$ and a subset of attributes $B\subseteq A$, the indiscernibility relation with respect to B is defined as $ind\left(B\right)=\left\{\right(x,y)\mid x,y\in U,a(x)=a(y)\forall a\in B\}.$ Obviously, for each $B\subseteq A$, $⟨U,ind\left(B\right)⟩$ is an approximation space. In particular, we can associate with each information system $(U,A,D)$ its finest approximation space $⟨U,t_A⟩$, where $t_A=ind\left(A\right)$. On the other hand, given an approximation space $⟨U,t⟩$, we can (somewhat trivially) associate with it a single-attribute information system $(U,\left\{a_t\right\},D)$, where $D=U/t$ is the quotient set of U modulo t and $a_t:U\to D,u\mapsto {\left[u\right]}_t$.

In [8], homomorphisms between information systems are introduced. Given two information systems $T_1=(U_1,A_1,D_1)$ and $T_2=(U_2,A_2,D_2)$, an O-A-D homomorphism from $T_1$ to $T_2$ is a triple of functions $h=(h_O,h_A,h_D)$, where

• $h_O:U_1\to U_2$ is the object mapping.
• $h_A:A_1\to A_2$ is the attribute mapping.
• $h_D:D_1\to D_2$ is the domain mapping.

such that

$$h_D\left(a\left(x\right)\right)=h_A\left(a\right)\left(h_O\left(x\right)\right)$$

(14)

for any $a\in A_1$ and $x\in U_1$.

The definitions of categories and functors are defined in Appendix A.

Remark 1.

From a categorical standpoint, information systems and their associated rough structures are unified by the notion of granulation. The equivalence of the proposed categories demonstrates that rough approximations, topological structures, and equivalence relations encode the same informational content at different levels of abstraction.

In this sense, the categorical framework does not replace information systems but rather clarifies their structural essence, enabling principled transformations and deeper theoretical insight.

3. Characterizations of Clopen Topologies

In this section, we restrict our study to clopen topological spaces. Unless otherwise stated, we shall assume throughout that $(U,\mathcal{T})$ is a clopen topological space. To better understand its structure, we begin with the notion of minimal clopen neighborhoods, then move on to continuous functions between such spaces, and finally connect these ideas to closure operators that naturally arise in rough set theory.

3.1. Minimal Clopen Neighborhoods

Recall [9] that an Alexandrov space is a topological space in which arbitrary intersections of open sets are open, or equivalently, every point has a minimal open neighborhood including it. It is clear that clopen topological spaces are Alexandrov spaces. Thus, in a given clopen topological space $(U,\mathcal{T})$, every point has a minimal clopen neighborhood including it. We shall show that for every $u\in U$, $\mathrm{cl}\left(\right\{u\left\}\right)$ is the minimal clopen neighborhood of u.

We now show that for every $u\in U$, the set $\mathrm{cl}\left(\right\{u\left\}\right)$ serves as this minimal clopen neighborhood. From (5), we have for each $u\in U$,

$$\begin{array}{ccc}\hfill \mathrm{cl}\left(\right\{u\left\}\right)& =& \cap \{K\in \tau \mid \{u\}\subseteq K\}\hfill \\ & =& \cap \{K\in \tau \mid u\in K\}\hfill \end{array}$$

(15)

and $u\in \mathrm{cl}\left(\right\{u\left\}\right)$. Hence $\mathrm{cl}\left(\right\{u\left\}\right)$ is the minimal clopen neighborhood of u. Consequently, the neighborhood system $\mathcal{N}\left(u\right)$ of u is the set of all supersets of $\mathrm{cl}\left(\right\{u\left\}\right)$. Namely,

$$\mathcal{N}\left(u\right)=\{N\subseteq U\mid N\supseteq \mathrm{cl}(\left\{u\right\}\left)\right\}$$

(16)

We next show that for $u,u^{\prime }\in U$, $\mathrm{cl}\left(\right\{u\left\}\right)$ and $\mathrm{cl}\left(\left\{u^{\prime }\right\}\right)$ are either identical or have no elements in common. On the contrary, assume that

$$\mathrm{cl}\left(\left\{u^{\prime }\right\}\right)\ne \mathrm{cl}\left(\left\{u\right\}\right)\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{cl}\left(\left\{u^{\prime }\right\}\right)\cap \mathrm{cl}\left(\left\{u\right\}\right)\ne \varnothing$$

It follows that $\mathrm{cl}\left(\left\{u^{\prime }\right\}\right)\cap \mathrm{cl}\left(\left\{u\right\}\right)$ is a nonempty clopen subset of $\mathrm{cl}\left(\right\{u\left\}\right)$ and so $u\notin \mathrm{cl}\left(\left\{u^{\prime }\right\}\right)\cap \mathrm{cl}\left(\left\{u\right\}\right)$. We have

$$\begin{array}{ccc}\hfill u& \in & \mathrm{cl}\left(\left\{u\right\}\right)\setminus (\mathrm{cl}\left(\left\{u^{\prime }\right\}\right)\cap \mathrm{cl}\left(\left\{u\right\}\right))\hfill \\ & =& \mathrm{cl}\left(\left\{u\right\}\right)\cap (U\setminus \mathrm{cl}\left(\left\{u^{\prime }\right\}\right)\subseteq \mathrm{cl}\left(\left\{u\right\}\right);\hfill \end{array}$$

consequently, the set $\mathrm{cl}\left(\left\{u\right\}\right)\setminus (\mathrm{cl}\left(\left\{u^{\prime }\right\}\right)\cap \mathrm{cl}\left(\left\{u\right\}\right))$ includes u and is a clopen subset of $\mathrm{cl}\left(\right\{u\left\}\right)$. This is impossible since $\mathrm{cl}\left(\right\{u\left\}\right)$ is a minimal clopen set including u. Therefore, $\mathrm{cl}\left(\right\{u\left\}\right)$ and $\mathrm{cl}\left(\left\{u^{\prime }\right\}\right)$ are either identical or have no elements in common. We thus obtain

Proposition 2.

Let $(U,\mathcal{T})$ be a clopen topological space. For a subset A of U, $\mathrm{cl}\left(A\right)$ denotes the closure of A in $(U,\mathcal{T})$. Then the following properties hold:

(1) 

For each $u\in U$, $\mathrm{cl}\left(\right\{u\left\}\right)$ is the minimal clopen neighborhood of u.

(2) 

For $u,u^{\prime }\in U$, $\mathrm{cl}\left(\right\{u\left\}\right)$ and $\mathrm{cl}\left(\left\{u^{\prime }\right\}\right)$ are either identical or disjointed.

Since, in a given clopen topological space $(U,\mathcal{T})$, the closure $\mathrm{cl}\left(\right\{u\left\}\right)$ of a singleton $\left\{u\right\}$ is a minimal clopen set including u it follows that if $u^{\prime }\notin \mathrm{cl}\left(\left\{u\right\}\right)$ then $\mathrm{cl}\left(\left\{u^{\prime }\right\}\right)$ and $\mathrm{cl}\left(\right\{u\left\}\right)$ have no elements in common. This gives

$$\mathrm{cl}\left(\left\{u\right\}\right)=\{u^{\prime }\in U\mid \mathrm{cl}\left(\left\{u^{\prime }\right\}\right)=\mathrm{cl}\left(\left\{u\right\}\right)\}$$

(17)

From (7), (16), and (17), we obtain for every $A\subseteq U$,

$$\begin{array}{ccc}\hfill \mathrm{cl}\left(A\right)& =& \{u\in U\mid \mathrm{cl}(\left\{u\right\})\cap A\ne \varnothing \}\hfill \\ & =& \bigcup _{u\in U}\{\mathrm{cl}\left(\left\{u\right\}\right)\mid \mathrm{cl}\left(\left\{u\right\}\right)\cap A\ne \varnothing \}\hfill \end{array}$$

(18)

We clearly have, for any $\mathcal{A}\subseteq 2^U$,

$$\mathrm{cl}\left(\bigcup _{A\in \mathcal{A}}A\right)=\bigcup _{A\in \mathcal{A}}\mathrm{cl}\left(A\right),$$

(19)

i.e., the closure function $\mathrm{cl}:2^U⟶2^U$ is union preserving.

Lemma 3.

Let $(U,\mathcal{T})$ be a clopen topological space. For a subset A of U, $\mathrm{cl}\left(A\right)$ denotes the closure of A in $(U,\mathcal{T})$. Then the closure function $A⟼\mathrm{cl}\left(A\right)$ is union preserving and satisfies the Kuratowski closure axioms.

3.2. Continuous Functions Between Clopen Topological Spaces

Having established the structure of minimal clopen neighborhoods, we now turn to the behavior of functions between clopen spaces. The continuity of a function $f:U\to V$ can be characterized in terms of these closures. Assume that $(U,\mathcal{T})$ and $(V,\tau )$ are clopen topological spaces, and that f is a function from U to V. Denote by ${\mathrm{cl}}_U$ and ${\mathrm{cl}}_V$ the closure functions in $(U,\mathcal{T})$ and in $(V,\tau )$, respectively. For each $u\in U$ and $v\in V$, let ${\mathcal{N}}_1\left(u\right)$ and ${\mathcal{N}}_2\left(v\right)$ be the neighborhood systems of u in $(U,\mathcal{T})$ and of v in $(V,\tau )$, respectively. Then, from (16), we obtain

$$\begin{array}{ccc}\hfill & & {\mathcal{N}}_1\left(u\right)=\{N\subseteq U\mid N\supseteq {\mathrm{cl}}_U\left(\left\{u\right\}\right)\}\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{l}\mathrm{l}u\in U\hfill \\ & & {\mathcal{N}}_2\left(v\right)=\{M\subseteq V\mid M\supseteq {\mathrm{cl}}_V\left(\left\{v\right\}\right)\}\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{l}\mathrm{l}v\in V.\hfill \end{array}$$

(20)

According to Definition 1, $f:U\to V$ is continuous, iff

$$f^{\to }\left({\mathrm{cl}}_U\left(\left\{u\right\}\right)\right)\subseteq {\mathrm{cl}}_V\left(\left\{f\left(u\right)\right\}\right)\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{c}\mathrm{h}u\in U.$$

(21)

We note in connection with (17) that

$$\begin{array}{ccc}\hfill & & f^{\to }\left({\mathrm{cl}}_U\left(\left\{u\right\}\right)\right)\subseteq {\mathrm{cl}}_V\left(\left\{f\left(u\right)\right\}\right)\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{c}\mathrm{h}u\in U\hfill \\ & ⟺& \mathrm{f}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{l}\mathrm{l}u,u^{\prime }\in U,\hfill \\ & & {\mathrm{cl}}_U\left(\left\{u\right\}\right)={\mathrm{cl}}_U\left(\left\{u^{\prime }\right\}\right)\mathrm{implies}{\mathrm{cl}}_V\left(\left\{f\left(u\right)\right\}\right)={\mathrm{cl}}_V\left(\left\{f\left(u^{\prime }\right)\right\}\right)\hfill \end{array}$$

(22)

This, together with Lemma 1 and Proposition 1, gives the following:

Proposition 3.

Assume that $(U,\mathcal{T})$ and $(V,\tau )$ are clopen topological spaces, and that f is a function from U to V. Let ${\mathrm{cl}}_U$ and ${\mathrm{cl}}_V$ denote the closure functions in $(U,\mathcal{T})$ and in $(V,\tau )$, respectively. Assume that ${\mathrm{int}}_U$ and ${\mathrm{int}}_V$ are the interior functions in $(U,\mathcal{T})$ and in $(V,\tau )$, respectively. The following statements are equivalent.

(1) 

The function f is continuous.

(2) 

For each $u\in U$, $f^{\to }\left({\mathrm{cl}}_U\left(\left\{u\right\}\right)\right)\subseteq {\mathrm{cl}}_V\left(\left\{f\left(u\right)\right\}\right)$.

(3) 

For all $u,u^{\prime }\in U$, ${\mathrm{cl}}_U\left(\left\{u\right\}\right)={\mathrm{cl}}_U\left(\left\{u^{\prime }\right\}\right)$ implies ${\mathrm{cl}}_V\left(\left\{f\left(u\right)\right\}\right)={\mathrm{cl}}_V\left(\left\{f\left(u^{\prime }\right)\right\}\right)$.

(4) 

The preimage of each open set is open.

(5) 

For each $B\subseteq V$, ${\mathrm{cl}}_U\left(f^{\leftarrow }\left(B\right)\right)\subseteq f^{\leftarrow }\left({\mathrm{cl}}_V\left(B\right)\right)$.

(6) 

For each $B\subseteq V$, $f^{\leftarrow }\left({\mathrm{int}}_V\left(B\right)\right)\subseteq {\mathrm{int}}_U\left(f^{\leftarrow }\left(B\right)\right)$.

In other words, continuity can be equivalently expressed in several ways, including the preservation of closures of singletons, the preservation of open sets under preimages, and compatibility with interior operators. These equivalences are summarized in Proposition 3, which provides a robust characterization of continuous functions between clopen spaces.

3.3. Clopen Topologies and Rough Closure Operators

Note that a union-preserving operator preserves empty unions and binary unions. Thus, any extensive, idempotent, and union-preserving operator $c_U:2^U⟶2^U$ on a given set U is a closure operator and defines the topology $\{X\subseteq U\mid C_U(U\setminus X)=U\setminus X\}$ on U. We establish the following equivalent condition of a clopen topology.

Proposition 4.

Let U be a given set. Assume that $c_U:2^U⟶2^U$ is an extensive and idempotent union-preserving operator, and that $i_U:2^U⟶2^U$ its dual interior operator. Let

$$\mathcal{T}=\{X\subseteq U\mid C_U(U\setminus X)=U\setminus X\}$$

(23)

Then $\mathcal{T}$ is a clopen topology iff

$$c_U\left(X\right)\subseteq U\setminus c_U(U\setminus c_U\left(X\right))foreachX\subseteq U,$$

(24)

or equivalently,

$$i_U\left(X\right)\supseteq U\setminus i_U(U\setminus i_U\left(X\right))foreachX\subseteq U.$$

(25)

Proof. 

We have seen that $\mathcal{T}$ is a topology. Consequently, $\mathcal{T}$ is a clopen topology iff

$$\{X\subseteq U\mid i_U\left(X\right)=X\}=\{X\subseteq U\mid c_U\left(X\right)=X\}$$

(26)

Since $c_U:2^U⟶2^U$ is extensive, it is easily seen from (1) that $i_U:2^U⟶2^U$ is intensive. This gives

$$i_U\left(A\right)\subseteq A\subseteq c_U\left(A\right)\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{c}\mathrm{h}A\subseteq U$$

(27)

We first show that (24) and (25) are equivalent. From (1) and (2), we have

$$\begin{array}{ccc}\hfill & & c_U\left(A\right)\subseteq U\setminus c_U(U\setminus c_U\left(A\right))\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{c}\mathrm{h}A\subseteq U\hfill \\ & ⟺& c_U(U\setminus c_U\left(A\right))\subseteq U\setminus c_U\left(A\right)\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{c}\mathrm{h}A\subseteq U\hfill \\ & ⟺& c_U\left(i_U(U\setminus A)\right)\subseteq i_U(U\setminus A)\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{c}\mathrm{h}A\subseteq U\hfill \\ & ⟺& c_U\left(i_U\left(A\right)\right)\subseteq i_U\left(A\right)\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{c}\mathrm{h}A\subseteq U\hfill \\ & ⟺& U\setminus i_U(U\setminus i_U\left(A\right))\subseteq i_U\left(A\right)\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{c}\mathrm{h}A\subseteq U\hfill \end{array}$$

(28)

Assume that $\mathcal{T}$ is a clopen topology. From (26), we obtain for every $A\in 2^U$

$$c_U\left(A\right)=A⟺i_U\left(A\right)=A$$

(29)

Since $c_U:2^U⟶2^U$ is idempotent, we have for every $A\in 2^U$, $c_U\left(A\right)=c_U\left(c_U\left(A\right)\right)$; by the clopen property, $c_U\left(c_U\left(A\right)\right)$ must be open; therefore, from (1), (2), and (29), we obtain

$$\begin{array}{ccc}\hfill c_U\left(A\right)& =& c_U\left(c_U\left(A\right)\right)\hfill \\ & =& i_U\left(c_U\left(A\right)\right)\hfill \\ & =& U\setminus c_U(U\setminus c_U\left(A\right)))\hfill \end{array}$$

This proves that $c_U\left(A\right)\subseteq U\setminus c_U(U\setminus c_U\left(A\right))$.

Conversely, assume that (24) holds.

(1) If $c_U\left(X\right)=X$, then from (1) and (24), we have

$$\begin{array}{ccc}\hfill c_U\left(X\right)& \subseteq & U\setminus c_U(U\setminus c_U\left(X\right))\hfill \\ & =& U\setminus c_U(U\setminus X)\hfill \\ & =& i_U\left(X\right)\hfill \end{array}$$

Hence, from (27), we obtain $i_U\left(X\right)=X$.

(2) If $i_U\left(X\right)=X$, then from (2) and (24), we have

$$\begin{array}{ccc}\hfill i_U\left(X\right)& \supseteq & U\setminus i_U(U\setminus i_U\left(X\right))\hfill \\ & =& U\setminus i_U(U\setminus X)\hfill \\ & =& c_U\left(X\right)\hfill \end{array}$$

Hence, from (27), we obtain $c_U\left(X\right)=X$. This proves (29). Consequently, $\mathcal{T}$ is a clopen topology. This completes the proof. □

Proposition 4 motivates us to define the notions of rough closure operators and rough interior operators as follows:

Definition 2.

Let U be a given set. An extensive and idempotent union-preserving operator $c_U:2^U⟶2^U$ on U will be called a rough closure operator on U if it satisfies

$$c_U\left(X\right)\subseteq U\setminus c_U(U\setminus c_U\left(X\right))foreachX\subseteq U.$$

The pair $(U,c_U)$ is called a rough closure space. Dually, an intensive and idempotent intersection-preserving operator (an intersection-preserving operator on a set U is a function $M:2^U⟶2^U$ if its dual operator is union preserving). $i_U:2^U⟶2^U$ on U will be called a rough interior operator on U if it satisfies

$$i_U\left(X\right)\supseteq U\setminus i_U(U\setminus i_U\left(X\right))foreachX\subseteq U.$$

The pair $(U,i_U)$ is called a rough interior space.

For a given set U, it follows from Proposition 4 and Definition 2 that any rough closure operator $c_U:2^U⟶2^U$ defines the clopen topology

$$\{X\subseteq U\mid c_U(U\setminus X)=U\setminus X\}=\{X\subseteq U\mid c_U\left(X\right)=X\}.$$

on U. Conversely, let $(U,\mathcal{T})$ be a given clopen topological space. Since the closure function $\mathrm{cl}:2^U⟶2^U$ in $(U,\mathcal{T})$ satisfies the Kuratowski closure axioms, it follows from (19) that $\mathrm{cl}:2^U⟶2^U$ is a rough closure operator on U. Accordingly, a clopen topological space $(U,\mathcal{T})$ can be equivalently defined by a rough closure space, or a rough interior space.

4. Some Categories Equivalent to the Category Clop

In this section, we define the category $\mathbf{AprS}$ of approximation spaces and continuous functions, the category Equiv of equivalence relations and relation-preserving functions, the category RCls of rough closure spaces and continuous functions, and the category RInt of rough interior spaces and continuous functions. We prove that Equiv, AprS, RCls, and RInt are mutually equivalent. Furthermore, we define the category $\mathbf{IS}$ of information systems and O-A-D homomorphisms. We establish the relationship between IS and AprS by considering a subcategory NeIS of information systems non-expansive O-A-D homomorphisms.

Given a clopen topological space $(U,\mathcal{T})$, let

$$S\left(u\right)=\mathrm{cl}\left(\right\{u\left\}\right)\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{c}\mathrm{h}u\in U.$$

(30)

Then the relation

$$t:=\{(u,u^{\prime })\in U\times U\mid S\left(u\right)=S\left(u^{\prime }\right)\}$$

(31)

is an equivalence relation on U, called the kernel relation of S. From (17), we obtain

$${\left[u\right]}_t=\mathrm{cl}\left(\left\{u\right\}\right)\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{c}\mathrm{h}u\in U$$

(32)

This gives

$$t=\bigcup _{u\in U}\mathrm{cl}\left(\left\{u\right\}\right)\times \mathrm{cl}\left(\left\{u\right\}\right)\subseteq U\times U.$$

(33)

This section demonstrates that the category of clopen topological spaces is not isolated, but rather equivalent to multiple other categories, each offering a different perspective on the same underlying structure.

4.1. The Category of Approximation Spaces

For a given set U, it follows from (18), (19), and (32) that every clopen topological space $(U,\mathcal{T})$ becomes an approximation space $⟨U,t⟩$ via the restriction of its closure function $\mathrm{cl}:2^U⟶2^U$ to the set of singletons:

$$t=\bigcup _{u\in U}\mathrm{cl}\left(\left\{u\right\}\right)\times \mathrm{cl}\left(\left\{u\right\}\right)\subseteq U\times U.$$

Conversely, it follows from Lemma 2 that every approximation space $⟨U,t⟩$ determines a clopen topology on U via its upper approximation operator ${\overline{apr}}_t:2^U⟶2^U$. This establishes a bijective correspondence between clopen topologies on U, and approximation spaces $⟨U,t⟩$. Accordingly, a clopen topological space $(U,\mathcal{T})$ can be equivalently defined as an approximation space $⟨U,t⟩$. Hence from statement (2) of Proposition 3, we obtain the following:

Proposition 5.

Define the category  AprS  with objects’ approximation spaces $⟨U,t⟩$, where U is a set and t is an equivalence relation on U. Morphisms $f:⟨U,t⟩\to ⟨V,s⟩$ are continuous functions, i.e., functions $f:U\to V$ such that

$$f^{\to }\left({\left[u\right]}_t\right)\subseteq {\left[f\left(u\right)\right]}_{s}forallu\in U.$$

(34)

Then the categories  AprS  and  Clop  are isomorphic.

4.2. The Category of Equivalence Relations

Rydeheard and Burstall [10] considered the category Rel whose objects are pairs of the form $(U,R)$ where U and R are sets such that R is a binary relation on U, i.e., $R\subseteq U\times U$, and whose morphisms $f:(U,R)\to (V,S)$ are relation-preserving functions; that is, functions $f:U\to V$ such that

$$(u,u^{\prime })\in R\mathrm{implies}(f\left(u\right),f\left(u^{\prime }\right))\in S.$$

(35)

Considering the category Rel, we can define a second category Equiv of equivalence relations and relation-preserving functions, which is the subcategory of Rel with objects being ordered pairs $(U,t)$, where U is a set and t is an equivalence relation on U, and morphisms $f:(U,t)\to (V,s)$ are relation-preserving functions.

From § 4.1 and statement (2) of Proposition 3, we obtain the following:

Proposition 6.

The categories  Equiv  and  Clop  are isomorphic.

4.3. The Categories of Rough Closure and Rough Interior Spaces

Let us define the category RCls as the category whose objects are rough closure spaces $(U,c_U)$, where U is a set and $c_U$ is a rough closure operator on U. Morphisms $f:(U,c_U)\to (V,c_V)$ are continuous functions, i.e., functions $f:U\to V$ such that

$$f^{\to }\left(c_U\left(\left\{u\right\}\right)\right)\subseteq c_V\left(\left\{f\left(u\right)\right\}\right)\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{l}\mathrm{l}u\in U.$$

(36)

or equivalently, $c_U(f^{\leftarrow }\left(Y\right))\subseteq f^{\leftarrow }\left(c_V\left(Y\right)\right)$ for all $Y\subseteq V$.

As it is shown in § 3.3, a clopen topological space $(U,\mathcal{T})$ can be equivalently defined as a rough closure space $(U,c_U)$. Hence from statement (2) of Proposition 3, we obtain the following:

Proposition 7.

The categories  RCls  and  Clop  are isomorphic.

Of course, since rough closure spaces and rough interior spaces are equivalent concepts. The category of rough interior spaces RInt has rough interior spaces as its objects. Morphisms $f:(U,i_U)\to (V,i_V)$ are continuous functions; i.e., functions $f:U\to V$ such that

$$f^{\leftarrow }\left(i_V\left(Y\right)\right)\subseteq i_U\left(f^{\leftarrow }\left(Y\right)\right)\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{l}\mathrm{l}Y\subseteq V.$$

(37)

Proposition 8.

The categories RInt  and  Clop  are isomorphic.

4.4. The Category of Information Systems

The category of information systems $\mathbf{IS}$ has information systems as its objects and O-A-D homomorphisms as its morphisms. We say that an O-A-D homomorphism is non-expansive if its attribute mapping is onto it. To establish the relationship between $\mathbf{IS}$ and $\mathbf{AprS}$, we consider a subcategory $\mathbf{NeIS}$ whose objects are information systems and morphisms are non-expansive O-A-D homomorphisms. Then, it is easy to see that, if $h=(h_O,h_A,h_D)$ is a non-expansive O-A-D homomorphism between information systems $(U,A_1,D_1)$ and $(V,A_2,D_2)$, then $h_O$ is a relation-preserving function between approximation space $⟨U,t_{A_1}⟩$ and $⟨V,t_{A_2}⟩$ by using (14). Hence, we can define a functor

$$H:\mathbf{NeIS}\to \mathbf{AprS}$$

by setting $H\left((U,A,D)\right)=⟨U,t_A⟩$ and

$$H(h:(U,A_1,D_1)\to (V,A_2,D_2))=h_O:⟨U,t_{A_1}⟩\to ⟨V,t_{A_2}⟩.$$

On the other hand, let $f:⟨U,t⟩\to ⟨V,s⟩$ be a relation-preserving function. Then, we can define a non-expansive O-A-D homomorphism $h_f=(h_O,h_A,h_D):(U,\left\{a_t\right\},U/t)\to (V,\left\{a_s\right\},V/s)$ by setting $h_O=f$, $h_A\left(a_t\right)=a_s$, and $h_D\left({\left[u\right]}_t\right)={\left[f\left(u\right)\right]}_s$ for any ${\left[u\right]}_t\in U/t$. It is obvious that $h_f$ is non-expansive and satisfies the homomorphic condition (14). Thus, we can define a functor

$$H^{\prime }:\mathbf{AprS}\to \mathbf{NeIS}$$

by setting $H^{\prime }\left(⟨U,t⟩\right)=(U,\left\{a_t\right\},U/t)$ and

$$H^{\prime }(f:⟨U,t⟩\to ⟨V,s⟩)=h_f:(U,\left\{a_t\right\},U/t)\to (V,\left\{a_s\right\},V/s).$$

We can see that

$$H\circ H^{\prime }={\mathbf{1}}_{\mathbf{AprS}}$$

but $H^{\prime }\circ H={\mathbf{1}}_{\mathbf{NeIS}}$ does not hold. This means that an information system is more informative than the finest approximation space derived from it. Indeed, we can usually induce the same approximation space from several different information systems by using different sets of attributes, and this is the main idea of attribute reduction in rough set theory.

Together, these categories, $\mathbf{Equiv}$, $\mathbf{AprS}$, $\mathbf{RCIs}$, $\mathbf{RInt}$, and $\mathbf{IS}$, are equivalent to $\mathbf{Clop}$, showing that clopen topologies can be studied from multiple perspectives: relational, algebraic, and informational.

4.5. Practical Applications

The equivalence of $\mathbf{Equiv}$, $\mathbf{AprS}$, $\mathbf{RCIs}$, $\mathbf{RInt}$, and $\mathbf{IS}$ allows us to switch between relational, algebraic, and topological languages depending on the problem. The study of these categories offers several possible practical benefits:

• Attribute Reduction and Feature Selection
  The functorial relationship between IS and AprS formalizes the process of attribute reduction by demonstrating that different attribute sets can induce isomorphic approximation spaces. This provides a principle, category-theoretic justification for feature selection algorithms. Formally, a subset $B\subseteq A$ of attributes constitutes a reduct if the induced approximation space $⟨U,\mathrm{ind}\left(B\right)⟩$ is isomorphic to $⟨U,\mathrm{ind}\left(A\right)⟩$ in the category AprS [11]. Practically, this enables the systematic identification of minimal attribute sets that preserve the original classification power, facilitating efficient preprocessing and dimensionality reduction without compromising approximation capability [12]. The functor $H^{\prime }:\mathbf{AprS}\to \mathbf{NeIS}$, which maps multiple information systems to the same approximation space, justifies algorithmic searches for minimal isomorphic representations, ensuring that the underlying knowledge, encoded topologically, remains invariant during the reduction process [13].
• Data Integration and System Interoperability
  Morphisms in Equiv and AprS define rigorous, structure-preserving transformations between heterogeneous data sources. A morphism $f:⟨U,t⟩\to ⟨V,s⟩$ guarantees that objects indistinguishable in the source domain remain indistinguishable in the target domain, thereby maintaining classification consistency during data migration [14,15]. This formalism finds critical application in database schema mapping, ontology alignment, federated databases, multi-source data fusion, and knowledge graph transformation [16]. The framework serves as a powerful validation tool: if a proposed data mapping fails to be continuous, it indicates a potential distortion of the original indiscernibility classes, signaling the risks of classification errors and guiding the design of more robust integration pipelines [17].
• Topological Analysis of Discrete Data
  The isomorphism between AprS and Clop enables the powerful application of topological methods to discrete datasets structured via equivalence relations. Since the induced clopen topologies are Alexandrov spaces, tools from algebraic topology—such as homology and persistent homology—can be employed to analyze global connectivity and shape in discrete settings [18,19]. This connection yields concrete analytical benefits: topological connectedness corresponds to irreducible data clusters, allowing the decomposition of datasets into independent, lossless components for optimized storage and processing [20]. Furthermore, equivalence classes form minimal clopen neighborhoods, defining sets of topologically indistinguishable objects for robust, neighborhood-based classification. The rough closure operator, defined as $c_U\left(X\right)=\bigcup \{E\in U/\theta :E\cap X\ne \varnothing \}$, provides a natural mechanism for approximate query matching by identifying all objects that share equivalence classes with query elements [21].
• Formal Specification of Knowledge-Preserving Mappings
  The categorical framework provides an explicit, mathematical definition for what it means for a mapping between systems to “preserve knowledge.” This formalism guides the principled design of interoperable software in domains such as ontology alignment, database schema mapping, and knowledge graph transformation [22]. The correspondence between rough closure operators and clopen topologies offers a systematic methodology for engineers to construct application-specific approximation models by designing appropriate union-preserving operators [23]. Crucially, the equivalence demonstrates that four distinct mathematical representations—equivalence relations (Equiv), approximation operators (AprS), closure operators (RCls), and interior operators (RInt)—encode identical informational content, allowing practitioners to select the most convenient or efficient representation for their specific task with guaranteed semantic consistency [24].
• Algorithmic Optimization and Efficient Computation
  The mathematical properties, revealed by the categorical equivalence, directly enable practical algorithm design and optimization for large-scale data processing. The union-preserving property of rough closure operators, expressed as $c_U\left({\bigcup }_{i=1}^n{A}_i\right)={\bigcup }_{i=1}^n{c}_U\left(A_i\right)$, permits the parallel computation of approximations and supports efficient incremental updates, significantly enhancing scalability [25]. Propositional characterizations of continuity provide multiple equivalent verification conditions, allowing algorithm designers to select the most computationally efficient method to ensure structure preservation in data transformations [21]. The representational flexibility afforded by the framework allows practitioners to leverage equivalence relations for database normalization, approximation operators for boundary region analysis, closure operators for topological reasoning, or interior operators for definability analysis, with results seamlessly transferring across these perspectives [26]. This flexibility underpins optimization strategies that search for minimal isomorphic representations, improving both storage efficiency and processing speed in practical implementations [27].

The established categorical equivalence provides a rigorous mathematical foundation that effectively bridges abstract theory and practical application. By facilitating seamless transitions between relational, algebraic, and topological perspectives, it delivers principled mechanisms for attribute reduction, novel methodologies for the topological analysis of discrete data, formal specifications for designing knowledge-preserving systems, and optimized algorithms for large-scale data processing [28]. This unified framework demonstrates that rough set theory, when interpreted through a categorical lens, offers not only profound mathematical insight but also directly applicable, operational tools for addressing contemporary, data-driven challenges across science and engineering [29].

5. Related Works

While rough set theory has been extensively studied from diverse perspectives, a limited number of works have investigated its structure from a categorical perspective. In [3], three categories of approximations, denoted by $\underline{\mathbf{Apr}}\mathbf{S}$, $\overline{\mathbf{Apr}}\mathbf{S}$, and $\mathbf{AprS}$, are defined. Objects of the three categories, as well as our definition of $\mathbf{AprS}$, are all approximation spaces. However, the corresponding morphisms preserve not only the underlying equivalence relation but also lower and/or upper approximations. These morphisms are called lower/upper transformations, although they are simply morphisms instead of natural transformations in the sense of category theory. More precisely, let $⟨U,t⟩$ and $⟨V,s⟩$ be two approximation spaces. Then, a function $f:U\to V$ is called a lower and upper natural transformation if it satisfies, for any $X\subseteq U$,

$${\underline{apr}}_s\left(f^{\to }\left(X\right)\right)=f^{\to }({\underline{apr}}_t\left(X\right))$$

and

$${\overline{apr}}_s\left(f^{\to }\left(X\right)\right)=f^{\to }\left({\overline{apr}}_t\left(X\right)\right),$$

respectively. In addition, f is simply a natural transformation if it is both a lower and upper natural transformation. It is shown that a lower natural transformation preserves equivalence classes ([3], Proposition 2.4). On the other hand, they also proved that a mapping is an upper natural transformation iff it preserves equivalence classes ([3], Theorem 3.4). This indicates that a lower natural transformation is automatically an upper natural transformation, although it is generally not the case. Because a function-preserving equivalence class is necessarily relation-preserving (but not conversely), the categories introduced in [3] impose a much stricter restriction on morphisms than ours. As a result, all three categories in [3] are subcategories of $\mathbf{AprS}$ (or equivalently, $\mathbf{RCls}$ or $\mathbf{RInt}$) in this paper.

Unlike the categories defined in [3] and this paper, categories of rough sets also exist where the objects are not limited to approximation spaces. The earliest categorical analysis of rough sets is the category ROUGHdefined in [30]. Objects of ROUGH are triples $⟨R,t,X⟩$, where $⟨R,t⟩$ is an approximation space and $X\subseteq U$. Let ${\overline{\mathcal{X}}}_t$ and ${\underline{\mathcal{X}}}_t$ denote the quotient sets of ${\overline{apr}}_t\left(X\right)$ and ${\underline{apr}}_t\left(X\right)$, respectively. Then, a morphism $f:⟨R,t,X⟩\to ⟨V,s,Y⟩$ in ROUGH is a map $f:{\overline{\mathcal{X}}}_t\to {\overline{\mathcal{Y}}}_s$ such that $f^{\to }\left({\underline{\mathcal{X}}}_t\right)\subseteq {\underline{\mathcal{Y}}}_s$. Thus, morphisms of ROUGH must preserve lower approximations.

Yet another category of rough sets is based on the algebraic interpretation of rough sets [31]. A pair $(U,\mathbf{B})$ is called a rough universe in [31], where U is the domain and B is a subalgebra of the power set Boolean algebra $(2^U,\cup ,-,\varnothing )$. Any pair $(X_1,X_2)$ such that $X_1,X_2\in \mathbf{B}$ and $X_1\subseteq X_2$ is an I-rough set of $(U,\mathbf{B})$. Then, the category RSC has all I-rough sets as its objects and a morphism $f:(X_1,X_2)\to (Y_1,Y_2)$ is simply a function $f:X_2\to Y_2$ such that $f^{\to }\left(X_1\right)\subseteq Y_1$ [32]. While ROUGH and RSC appear different at first glance, they are shown to be equivalent in [32].

A subcategory of ROUGH, called $\xi$-ROUGH, is defined to have the same objects as ROUGH, but its morphisms must satisfy the additional condition of preserving the boundary region. That is, $f:⟨R,t,X⟩\to ⟨V,s,Y⟩$ is a morphism of $\xi$-ROUGH if it is a morphism of ROUGH satisfying $f^{\to }({\overline{\mathcal{X}}}_t-{\underline{\mathcal{X}}}_t)\subseteq ({\overline{\mathcal{Y}}}_s-{\underline{\mathcal{Y}}}_s)$. Analogously, $\xi$-RSC is the subcategory of RSC with the same collection of objects and its morphisms $f:(X_1,X_2)\to (Y_1,Y_2)$ are RSC morphisms satisfying $f^{\to }(X_2-X_1)\subseteq (Y_2-Y_1)$. It is shown that $\xi$-ROUGH and $\xi$-RSC are equivalent and both are equivalent to Set², whose objects are pairs of sets $(X_1,X_2)$ and morphisms are pairs of functions $(f,g):(X_1,X_2)\to (Y_1,Y_2)$ where $f:X_1\to Y_1$ and $g:X_2\to Y_2$. The result shows that the role of approximation spaces has become hardly visible in the categories of algebraic rough sets. By contrast, our categories of approximation spaces, rough closure spaces, and rough interior spaces arise from a topological interpretation of rough sets. Hence, approximation spaces and continuous functions between them play the major role in such categories. In some sense, this means that categories based on $\xi$-rough sets somewhat lose structural information behind the construction of rough approximations.

6. Conclusions

By introducing the concepts of rough closure and rough interior operators, and leveraging the power of functors, we have established the categorical equivalence of

• The category of approximation spaces and continuous functions.
• The category of equivalence relations and relation-preserving functions.
• The category of all rough interior spaces and continuous functions.
• The category of rough closure spaces and continuous functions.

Our approach of using information systems to characterize the category of approximation space and its subcategory gives rise to a deeper insight of the interplay among rough set theory, information systems, and category theory. It gives us not only a better understanding of the rough set theory structures in the context of category theory but also the relationships of different categories arising from some topological tools. By using the concepts of categories, one can derive further useful properties and applications of rough set theory. Category theory provides a powerful, uniform language for describing how mathematical structures transform via structure-preserving maps. It allows us to articulate the preservation of structural behavior across different domains. However, the abstract nature of category theory, which deliberately ignores the specific sets, operations, and axioms defining the objects, means that a deep understanding of the underlying technical details remains crucial. This knowledge is essential for exploring the full implications of the proven results and for driving further theoretical developments and applications. We plan to pursue these promising research directions in future work.