An Approach to the Total Least Squares Method for Symmetric Triangular Fuzzy Numbers

Abstract

The total least squares method has a broad applicability in many fields. It is also useful in fuzzy data analysis. In this paper, we study the method of total least squares for fuzzy variables. The regression parameters are considered to be crisp. First, we find a formula for the distance between an arbitrary pair of triangular fuzzy numbers and the set described by the regression relation. Second, we develop a new approach to total least squares for data that are modeled as symmetric triangular fuzzy numbers. To illustrate the theoretical results obtained in the paper, some numerical examples are presented.

1. Introduction

The least squares method (LS) and the total least squares method (TLS) have been widely discussed in many papers. Various approaches have been developed, and numerous practical applications have been discovered. As the study of fuzzy regression has advanced, the use of LS and TLS methods together with fuzzy numbers has been discussed. In this article, we focus on the TLS technique. In the following lines, we mention some results obtained in various works. These results are part of a broader framework within which this article can also be included.

Some exponential fitting models and TLS techniques with applications in a fairly large number of environmental problems, such as watershed rainfall-runoff modeling and forecasting water consumption in certain regions of Earth, are shown in [1]. In [2] are presented some generalizations of TLS that are mainly based on the addition of constraints and the use of regularization and weighted norms. There are books that focus on the TLS procedure [3,4]. These books bring forward discussions ranging from basic concepts to numerous generalizations and applications. In [5], an algorithm for the TLS method is presented, and the relation between LS and TLS is discussed. In [6], some orthogonal regression approaches are presented. Moreover, these approaches are compared from theoretical and practical points of view. The utility of orthogonal regression for the study of seismic hazard is emphasized. In [7], the generalization of the TLS method is discussed, and its importance in various domains such as system theory and signal processing is highlighted. In [8], three methods of regression, namely Chi-square regression, general orthogonal regression and weighted total least squares, are used for the topic of earthquake magnitude conversion. In [9], a new algorithm that is based on a regularized loss function is employed to deal with the orthogonal regression problem. In [10], orthogonal regression is discussed in relation to eruption data of a geyser. In [11], a MATLAB 7.0 (R14) routine for TLS is used to describe the economies of a group of four East European countries. In [12], a MATLAB 7.11 (R2010b) toolbox for problems related to TLS is presented. In [13], real estate prices are studied, and it is proved that TLS is better than ordinary least squares when using the Hedonic Price Model. In [14], there is given a fuzzy regression model based on least squares, where independent variables are crisp, and the response variables are L-R fuzzy numbers. The L-R representation of a fuzzy number is discussed in [15]. To analyze environmental effects in the process of modeling complex systems from the field of systems science, [16] discusses some fuzzy regression models that use, among other types of fuzzy numbers, symmetric triangular fuzzy numbers. In [17], numerous papers from the field of fuzzy regression analysis are systematically discussed. In [18], triangular fuzzy numbers are used to study some characteristics of logistics centers. In [19], a neuro-fuzzy inference system is used in a fuzzy regression model with trapezoidal fuzzy outputs. In [20], fuzzy regression is employed to study technological developments. In [21], there is presented a comparison between ordinary least squares and fuzzy least squares in the framework of a simulation experiment regarding pharmacokinetic parameters. Taking into account the uncertainty theory [22], two linear regression methods are discussed in [23]: an uncertain total least squares estimation and an uncertain robust total least squares estimation. In [23], work with uncertain variables is performed considering the expected value of an uncertain variable [22]. In [24], orthogonal least squares is used to develop an orthogonal least squares learning algorithm. In [25], the TLS method is improved by considering constrained TLS parameter optimization. In [26], an orthogonal least squares-based fuzzy filter with a small computational load is proposed. It is used in analysis of lung sounds. The work in this field is continued in [27]. Paper [28] discusses methods that use deep learning and regression in fuzzy logic systems, focusing on accuracy and interpretability. In [29,30], quadratic programming is considered for use in fuzzy regression models. In [31], various approaches to fuzzy least squares and fuzzy orthogonal least squares are investigated. In [32,33], fuzzy regression is used to study some aquifer systems. In [32], a relation between some drought indices and the observed water table in two geographical areas is established. In [33], fuzzy regression is employed to deal with uncertainty when monitoring some biological quality elements in six Greek lakes. TLS regression was also proved useful in Geodesy [34,35]. In [34], an errors-in-observations model is used with a TLS algorithm. In [36], fuzzy regression is considered for real estate price prediction. In [37], the orthogonal least squares method is modified, and it is applied to a fault detection depollution problem. In [38], there is developed a regression model that can be used for triangular and other types of fuzzy numbers. A fuzzy least squares model is given in [39]. In [39], the least squares technique is used for general fuzzy data, and an application for data modeled as triangular fuzzy numbers is also presented.

This paper is organized as follows. Some concepts and formulas from previous works are presented in Section 2. We consider the approach from [39] regarding the definition of the distance between two fuzzy numbers. This definition uses the parameterization of a fuzzy number [40]. In Section 3 we analyze the distances from a certain triangular fuzzy number to each element of a particular set of triangular fuzzy numbers, and we identify the element from the set for which the smallest distance is obtained. This smallest distance is regarded as the distance between that certain triangular fuzzy number and the considered set. Section 4 contains the main theoretical results, and it is divided into several subsections. In Section 4.1, we give a method for calculating the sum of squared distances from some triangular fuzzy numbers to a particular set of triangular fuzzy numbers. This particular set of fuzzy numbers, which we can call the fuzzy regression set, replaces the regression line that appears when only real numbers are used. In Section 4.2, we consider the special case of symmetric triangular fuzzy numbers. This subsection contains theoretical results regarding the parameters that define the fuzzy regression set. The possible cases that can be encountered in applications are systematically discussed in Section 4.3. In Section 4.4, the steps of the algorithm are presented. To illustrate the viability of the method, some numerical examples are provided in Section 5. Some comments are given in Section 6. Section 7 contains the conclusions.

2. Preliminaries—Materials and Methods

We consider the definition of a fuzzy number as given in [39]. We denote a triangular fuzzy number by $\tilde{X}=\left(x,\underset{\_}{x},\overline{x}\right)$, where $x$ is the real value at which the membership function takes the value 1, $\underset{\_}{x}$ is the left spread, and $\overline{x}$ is the right spread. We have $x\in ℝ$ and $\underset{\_}{x},\overline{x}\in \left(0,\infty \right)$. The membership function of $\tilde{X}$ is

$$X: ℝ\to \left[0,1\right], X\left(t\right)=\left\{\begin{array}{l}{\displaystyle \frac{1}{\underset{\_}{x}}}\left(t-x+\underset{\_}{x}\right),t\in \left[x-\underset{\_}{x},x\right)\hfill \\ 1,t=x\hfill \\ {\displaystyle \frac{1}{\overline{x}}}\left(-t+x+\overline{x}\right),t\in \left(\left.x,x+\overline{x}\right]\right.\hfill \\ 0,t\in \left(-\infty ,x-\underset{\_}{x}\right)\cup \left(x+\overline{x},\infty \right).\hfill \end{array}\right.$$

For $\alpha \in \left[0,1\right]$, the $\alpha$-cut is $\mathit{X}\left(\alpha \right)=\left[\underset{\_}{X}\left(\alpha \right),\overline{X}\left(\alpha \right)\right]$, where $\underset{\_}{X}\left(\alpha \right)=x-\underset{\_}{x}+\underset{\_}{x}\alpha$ and $\overline{X}\left(\alpha \right)=x+\overline{x}-\overline{x}\alpha$ [39,40]. If $\underset{\_}{x}=\overline{x}$, then we obtain a symmetric triangular fuzzy number [16], which can be denoted by $\left(x,\underset{\_}{x},\underset{\_}{x}\right)$.

Let $\left(\tilde{F},\tilde{G}\right)$ be a pair of triangular fuzzy numbers, where $\tilde{F}=\left(f,\underset{\_}{f},\overline{f}\right)$, $\tilde{G}=\left(g,\underset{\_}{g},\overline{g}\right)$.

We consider the set $\tilde{\mathit{L}}=\left\{\left(\tilde{X},\tilde{Y}\right)\left|\tilde{Y}=a\tilde{X}+b\right.\right\}$, where $\tilde{X},\tilde{Y}$ are triangular fuzzy numbers and $a\in ℝ-\left\{0\right\}$, $b\in ℝ$. The operations involving fuzzy numbers follow the general rules discussed in [15,39,40]. The two possible situations for the sign of $a$ will be treated separately, because this sign influences the form of the elements belonging to the set $\tilde{\mathit{L}}$. We use the metric that is considered in [39]. We have [39]

$${\delta }^2\left(\tilde{F},\tilde{X}\right)={{\displaystyle \int }}_0^1{\left(\underset{\_}{F}\left(\alpha \right)-\underset{\_}{X}\left(\alpha \right)\right)}^{2}d\alpha +{{\displaystyle \int }}_0^1{\left(\overline{F}\left(\alpha \right)-\overline{X}\left(\alpha \right)\right)}^{2}d\alpha ,$$

$${\delta }^2\left(\tilde{G},\tilde{Y}\right)={{\displaystyle \int }}_0^1{\left(\underset{\_}{G}\left(\alpha \right)-\underset{\_}{Y}\left(\alpha \right)\right)}^{2}d\alpha +{{\displaystyle \int }}_0^1{\left(\overline{G}\left(\alpha \right)-\overline{Y}\left(\alpha \right)\right)}^{2}d\alpha$$

and

$$d^2\left(\left(\tilde{F},\tilde{G}\right),\left(\tilde{X},\tilde{Y}\right)\right)={\delta }^2\left(\tilde{F},\tilde{X}\right)+{\delta }^2\left(\tilde{G},\tilde{Y}\right).$$

3. On Distance from a Triangular Fuzzy Number to a Certain Set of Fuzzy Numbers

Proposition 1.

If $\tilde{F}=\left(f,\underset{\_}{f},\overline{f}\right)$, $\tilde{G}=\left(g,\underset{\_}{g},\overline{g}\right)$ and $a\in \left(0,\infty \right)$, then there exists a unique element $\left({\tilde{X}}^{•},{\tilde{Y}}^{•}\right)\in \tilde{\mathit{L}}$ such that

$$d^2\left(\left(\tilde{F},\tilde{G}\right),\left({\tilde{X}}^{•},{\tilde{Y}}^{•}\right)\right)\le d^2\left(\left(\tilde{F},\tilde{G}\right),\left(\tilde{X},\tilde{Y}\right)\right),$$

 for all $\left(\tilde{X},\tilde{Y}\right)\in \tilde{\mathit{L}}$.

Moreover, we have

$${\tilde{X}}^{•}=\left(x^{•},{\underset{\_}{x}}^{•},{\overline{x}}^{•}\right)\mathrm{and}{\tilde{Y}}^{•}=a{\tilde{X}}^{•}+b,$$

where

$$x^{•}={\displaystyle \frac{1}{a^2+1}}\left(f+ag-ab\right),$$

$${\underset{\_}{x}}^{•}={\displaystyle \frac{1}{a^2+1}}\left(\underset{\_}{f}+a\underset{\_}{g}\right),$$

$${\overline{x}}^{•}={\displaystyle \frac{1}{a^2+1}}\left(\overline{f}+a\overline{g}\right).$$

Proof. 

The proof is given in Appendix A. □

Proposition 2.

If $\tilde{F}=\left(f,\underset{\_}{f},\overline{f}\right)$, $\tilde{G}=\left(g,\underset{\_}{g},\overline{g}\right)$ and $a\in \left(-\infty ,0\right)$, then there exists a unique element $\left({\tilde{X}}^{\circ },{\tilde{Y}}^{\circ }\right)\in \tilde{\mathit{L}}$ such that

$$d^2\left(\left(\tilde{F},\tilde{G}\right),\left({\tilde{X}}^{\circ },{\tilde{Y}}^{\circ }\right)\right)\le d^2\left(\left(\tilde{F},\tilde{G}\right),\left(\tilde{X},\tilde{Y}\right)\right),$$

for all $\left(\tilde{X},\tilde{Y}\right)\in \tilde{\mathit{L}}$.

Moreover, we have

$${\tilde{X}}^{\circ }=\left(x^{\circ },{\underset{\_}{x}}^{\circ },{\overline{x}}^{\circ }\right)\mathrm{and}{\tilde{Y}}^{\circ }=a{\tilde{X}}^{\circ }+b,$$

where

$$x^{\circ }={\displaystyle \frac{1}{a^2+1}}\left(f+ag-ab\right),$$

$${\underset{\_}{x}}^{\circ }={\displaystyle \frac{1}{a^2+1}}\left(\underset{\_}{f}-a\overline{g}\right),$$

$${\overline{x}}^{\circ }={\displaystyle \frac{1}{a^2+1}}\left(\overline{f}-a\underset{\_}{g}\right).$$

Proof. 

The proof is given in Appendix A. □

If $\tilde{X}=\left(x,\underset{\_}{x},\underset{\_}{x}\right)$ is a symmetric triangular fuzzy number, then its membership function is

$$X:ℝ\to \left[0,1\right],X\left(t\right)=\left\{\begin{array}{l}{\displaystyle \frac{1}{\underset{\_}{x}}}\left(t-x+\underset{\_}{x}\right),t\in \left[x-\underset{\_}{x},x\right)\hfill \\ 1,t=x\hfill \\ {\displaystyle \frac{1}{\underset{\_}{x}}}\left(-t+x+\underset{\_}{x}\right),t\in \left(\left.x,x+\underset{\_}{x}\right]\right.\hfill \\ 0,t\in \left(-\infty ,x-\underset{\_}{x}\right)\cup \left(x+\underset{\_}{x},\infty \right).\hfill \end{array}\right.$$

In this case, $\tilde{X}=\left(x,\underset{\_}{x},\underset{\_}{x}\right)$ has the $\alpha$-cut $\mathit{X}\left(\alpha \right)=\left[\underset{\_}{X}\left(\alpha \right),\overline{X}\left(\alpha \right)\right]$, where $\underset{\_}{X}\left(\alpha \right)=x-\underset{\_}{x}+\underset{\_}{x}\alpha$, $\overline{X}\left(\alpha \right)=x+\underset{\_}{x}-\underset{\_}{x}\alpha$ and $\alpha \in \left[0,1\right]$.

In Proposition 1, if $\left(\tilde{F},\tilde{G}\right)$ is a pair of symmetric triangular fuzzy numbers, we obtain

$${\underset{\_}{x}}^{•}={\overline{x}}^{•}={\displaystyle \frac{1}{a^2+1}}\left(\underset{\_}{f}+a\underset{\_}{g}\right).$$

In Proposition 2, if $\left(\tilde{F},\tilde{G}\right)$ is a pair of symmetric triangular fuzzy numbers, we obtain

$${\underset{\_}{x}}^{\circ }={\overline{x}}^{\circ }={\displaystyle \frac{1}{a^2+1}}\left(\underset{\_}{f}-a\underset{\_}{g}\right).$$

4. Total Least Squares for Symmetric Triangular Fuzzy Numbers

4.1. Preliminary Results

Let $\left({\tilde{F}}_i,{\tilde{G}}_i\right)$, $i=\overline{1,n}$, be $n$ pairs of triangular fuzzy numbers, where ${\tilde{F}}_i=\left(f_i,{\underset{\_}{f}}_i,{\overline{f}}_i\right)$ and ${\tilde{G}}_i=\left(g_i,{\underset{\_}{g}}_i,{\overline{g}}_i\right)$. For all $i=\overline{1,n}$, we have

$${\mathit{F}}_i\left(\alpha \right)=\left[{\underset{\_}{F}}_i\left(\alpha \right),{\overline{F}}_i\left(\alpha \right)\right],\mathrm{where}{\underset{\_}{F}}_i\left(\alpha \right)=f_i-{\underset{\_}{f}}_i+{\underset{\_}{f}}_i\alpha ,{\overline{F}}_i\left(\alpha \right)=f_i+{\overline{f}}_i-{\overline{f}}_i\alpha$$

and

$${\mathit{G}}_i\left(\alpha \right)=\left[{\underset{\_}{G}}_i\left(\alpha \right),{\overline{G}}_i\left(\alpha \right)\right],\mathrm{where}{\underset{\_}{G}}_i\left(\alpha \right)=g_i-{\underset{\_}{g}}_i+{\underset{\_}{g}}_i\alpha ,{\overline{G}}_i\left(\alpha \right)=g_i+{\overline{g}}_i-{\overline{g}}_i\alpha .$$

Let us recall that $\tilde{\mathit{L}}=\left\{\left(\tilde{X},\tilde{Y}\right)\left|\tilde{Y}=a\tilde{X}+b\right.\right\}$, where $\tilde{X},\tilde{Y}$ are triangular fuzzy numbers and $a\in ℝ-\left\{0\right\}$. We consider the sum

$$D^2\left(a,b\right)={\displaystyle {\displaystyle \sum }_{i=1}^n}{d}^2\left(\left({\tilde{F}}_i,{\tilde{G}}_i\right),\tilde{\mathit{L}}\right)=\left\{\begin{array}{l}{\displaystyle {\displaystyle \sum }_{i=1}^n}{d}^2\left(\left({\tilde{F}}_i,{\tilde{G}}_i\right),\left({\tilde{X}}_i^{•},{\tilde{Y}}_i^{•}\right)\right),\mathrm{if}a\in \left(0,\infty \right)\hfill \\ {\displaystyle {\displaystyle \sum }_{i=1}^n}{d}^2\left(\left({\tilde{F}}_i,{\tilde{G}}_i\right),\left({\tilde{X}}_i^{\circ },{\tilde{Y}}_i^{\circ }\right)\right), \mathrm{if}a\in \left(-\infty ,0\right).\hfill \end{array}\right.$$

For every $\left({\tilde{F}}_i,{\tilde{G}}_i\right)$, $i=\overline{1,n}$, the pair $\left({\tilde{X}}_i^{•},{\tilde{Y}}_i^{•}\right)$ is given by Proposition 1, and the pair $\left({\tilde{X}}_i^{\circ },{\tilde{Y}}_i^{\circ }\right)$ is given by Proposition 2. The following two propositions give formulas for $D^2\left(a,b\right)$.

Proposition 3.

Consider the set $\tilde{\mathit{L}}=\left\{\left(\tilde{X},\tilde{Y}\right)\left|\tilde{Y}=a\tilde{X}+b\right.\right\}$, where $\tilde{X},\tilde{Y}$ are triangular fuzzy numbers and $a\in \left(0,\infty \right)$. If ${\tilde{F}}_i=\left(f_i,{\underset{\_}{f}}_i,{\overline{f}}_i\right)$ and ${\tilde{G}}_i=\left(g_i,{\underset{\_}{g}}_i,{\overline{g}}_i\right)$, for all $i=\overline{1,n}$, then

$$\begin{gathered} D^2\left(a,b\right)={\displaystyle \frac{1}{a^2+1}}{\displaystyle {\displaystyle \sum }_{i=1}^n}\left\{2{\left(a{f}_i+b-g_i\right)}^2+\right. \\ +\left(a{f}_i+b-g_i\right)\left[\left(-a{\underset{\_}{f}}_i+{\underset{\_}{g}}_i\right)+\left(a{\overline{f}}_i-{\overline{g}}_i\right)\right]+ \\ \left.+{\displaystyle \frac{1}{3}}\left[{\left(-a{\underset{\_}{f}}_i+{\underset{\_}{g}}_i\right)}^2+{\left(a{\overline{f}}_i-{\overline{g}}_i\right)}^2\right]\right\}. \end{gathered}$$

Proof. 

The proof is given in Appendix A. □

Proposition 4.

Consider the set $\tilde{\mathit{L}}=\left\{\left(\tilde{X},\tilde{Y}\right)\left|\tilde{Y}=a\tilde{X}+b\right.\right\}$, where $\tilde{X},\tilde{Y}$ are triangular fuzzy numbers and $a\in \left(-\infty ,0\right)$. If ${\tilde{F}}_i=\left(f_i,{\underset{\_}{f}}_i,{\overline{f}}_i\right)$ and ${\tilde{G}}_i=\left(g_i,{\underset{\_}{g}}_i,{\overline{g}}_i\right)$, for all $i=\overline{1,n}$, then

$$\begin{gathered} D^2\left(a,b\right)={\displaystyle \frac{1}{a^2+1}}{\displaystyle {\displaystyle \sum }_{i=1}^n}\left\{2{\left(a{f}_i+b-g_i\right)}^2+\right. \\ +\left(a{f}_i+b-g_i\right)\left[\left(a{\overline{f}}_i+{\underset{\_}{g}}_i\right)-\left(a{\underset{\_}{f}}_i+{\overline{g}}_i\right)\right]+ \\ \left.+{\displaystyle \frac{1}{3}}\left[{\left(a{\overline{f}}_i+{\underset{\_}{g}}_i\right)}^2+{\left(a{\underset{\_}{f}}_i+{\overline{g}}_i\right)}^2\right]\right\}. \end{gathered}$$

Proof. 

The proof is given in Appendix A. □

4.2. Theoretical Results on the Total Least Squares for Symmetric Triangular Fuzzy Numbers

Let $\left({\tilde{F}}_i,{\tilde{G}}_i\right)$, $i=\overline{1,n}$, be $n$ pairs of symmetric triangular fuzzy numbers, where ${\tilde{F}}_i=\left(f_i,{\underset{\_}{f}}_i,{\underset{\_}{f}}_i\right)$ and ${\tilde{G}}_i=\left(g_i,{\underset{\_}{g}}_i,{\underset{\_}{g}}_i\right)$.

For all $i=\overline{1,n}$, we have

$${\mathit{F}}_i\left(\alpha \right)=\left[{\underset{\_}{F}}_i\left(\alpha \right),{\overline{F}}_i\left(\alpha \right)\right],{\underset{\_}{F}}_i\left(\alpha \right)=f_i-{\underset{\_}{f}}_i+{\underset{\_}{f}}_i\alpha ,{\overline{F}}_i\left(\alpha \right)=f_i+{\underset{\_}{f}}_i-{\underset{\_}{f}}_i\alpha$$

and

$${\mathit{G}}_i\left(\alpha \right)=\left[{\underset{\_}{G}}_i\left(\alpha \right),{\overline{G}}_i\left(\alpha \right)\right],{\underset{\_}{G}}_i\left(\alpha \right)=g_i-{\underset{\_}{g}}_i+{\underset{\_}{g}}_i\alpha ,{\overline{G}}_i\left(\alpha \right)=g_i+{\underset{\_}{g}}_i-{\underset{\_}{g}}_i\alpha .$$

We must find the parameters $a\in ℝ-\left\{0\right\}$ and $b\in ℝ$, which define the set $\tilde{\mathit{L}}=\left\{\left(\tilde{X},\tilde{Y}\right)\left|\tilde{Y}=a\tilde{X}+b\right.\right\}$, such that

$$D^2\left(a,b\right)={\displaystyle {\displaystyle \sum }_{i=1}^n}{d}^2\left(\left({\tilde{F}}_i,{\tilde{G}}_i\right),\tilde{\mathit{L}}\right)$$

is minimized. In other words, the optimization problem to be solved is

$$\underset{\left(a,b\right)\in {ℝ}^{*}\times ℝ}{\min }{D}^2\left(a,b\right).$$

Proposition 5.

If $a\in \left(0,\infty \right)$ and ${\tilde{F}}_i=\left(f_i,{\underset{\_}{f}}_i,{\underset{\_}{f}}_i\right)$, ${\tilde{G}}_i=\left(g_i,{\underset{\_}{g}}_i,{\underset{\_}{g}}_i\right)$, for all $i=\overline{1,n}$, then

$$D^2\left(a,b\right)={\displaystyle \frac{2}{a^2+1}}{\displaystyle {\displaystyle \sum }_{i=1}^n}\left[{\left(a{f}_i+b-g_i\right)}^2+{\displaystyle \frac{1}{3}}{\left(a{\underset{\_}{f}}_i-{\underset{\_}{g}}_i\right)}^2\right].$$

Proof. 

Taking into account the equalities ${\underset{\_}{f}}_i={\overline{f}}_i$ and ${\underset{\_}{g}}_i={\overline{g}}_i$, for all $i=\overline{1,n}$, the result follows from Proposition 3. □

Proposition 6.

If $a\in \left(-\infty ,0\right)$ and ${\tilde{F}}_i=\left(f_i,{\underset{\_}{f}}_i,{\underset{\_}{f}}_i\right)$, ${\tilde{G}}_i=\left(g_i,{\underset{\_}{g}}_i,{\underset{\_}{g}}_i\right)$, for all $i=\overline{1,n}$, then

$$D^2\left(a,b\right)={\displaystyle \frac{2}{a^2+1}}{\displaystyle {\displaystyle \sum }_{i=1}^n}\left[{\left(a{f}_i+b-g_i\right)}^2+{\displaystyle \frac{1}{3}}{\left(a{\underset{\_}{f}}_i+{\underset{\_}{g}}_i\right)}^2\right].$$

Proof. 

Taking into account the equalities ${\underset{\_}{f}}_i={\overline{f}}_i$ and ${\underset{\_}{g}}_i={\overline{g}}_i$, for all $i=\overline{1,n}$, the result follows from Proposition 4. □

Proposition 7.

Let $\left({\tilde{F}}_i,{\tilde{G}}_i\right)$, $i=\overline{1,n}$, $n\ge 2$, be $n$ pairs of symmetric triangular fuzzy numbers, where ${\tilde{F}}_i=\left(f_i,{\underset{\_}{f}}_i,{\underset{\_}{f}}_i\right)$ and ${\tilde{G}}_i=\left(g_i,{\underset{\_}{g}}_i,{\underset{\_}{g}}_i\right)$. It is assumed that the relation

$${\left({\alpha }_2^{•}\right)}^2+{\beta }_2^2\ne 0$$

is true, where

$${\alpha }_2^{•}={\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i{g}_i+{\displaystyle \frac{1}{3}}{\displaystyle {\displaystyle \sum }_{i=1}^n}{\underset{\_}{f}}_i{\underset{\_}{g}}_i-{\displaystyle \frac{1}{n}}\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right) ,$$

$${\beta }_2={\displaystyle {\displaystyle \sum }_{i=1}^n}\left(f_i^2-g_i^2\right)+{\displaystyle \frac{1}{n}}\left[{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)}^2-{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)}^2\right]+{\displaystyle \frac{1}{3}}{\displaystyle {\displaystyle \sum }_{i=1}^n}\left({{\underset{\_}{f}}_i}^2-{{\underset{\_}{g}}_i}^2\right).$$

The inequality

$${\alpha }_2^{•}>0$$

is a necessary and sufficient condition for the existence and unicity of a pair $\left({\widehat{a}}^{•},{\widehat{b}}^{•}\right)$ such that

$$\underset{\left(a,b\right)\in {ℝ}_{+}^{*}\times ℝ}{\min }{D}^2\left(a,b\right)=D^2\left({\widehat{a}}^{•},{\widehat{b}}^{•}\right).$$

Moreover, the following relations hold:

$${\widehat{a}}^{•}={\displaystyle \frac{-{\beta }_2+\sqrt{{\beta }_2^2+4{\left({\alpha }_2^{•}\right)}^2}}{2{\alpha }_2^{•}}},$$

$${\widehat{b}}^{•}={\displaystyle \frac{1}{n}}\left[\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)-{\widehat{a}}^{•}\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)\right].$$

Proof. 

According to Proposition 5, if $a\in \left(0,\infty \right)$, we have

$$\begin{gathered} D^2\left(a,b\right)={\displaystyle \frac{2}{a^2+1}}{\displaystyle {\displaystyle \sum }_{i=1}^n}\left[{\left(a{f}_i+b-g_i\right)}^2+{\displaystyle \frac{1}{3}}{\left(a{\underset{\_}{f}}_i-{\underset{\_}{g}}_i\right)}^2\right]= \\ ={\displaystyle {\displaystyle \sum }_{i=1}^n}\left[2·{\displaystyle \frac{{\left(a{f}_i+b-g_i\right)}^2}{a^2+1}}+{\displaystyle \frac{2}{3}}{\displaystyle \frac{{\left(a{\underset{\_}{f}}_i-{\underset{\_}{g}}_i\right)}^2}{a^2+1}}\right]. \end{gathered}$$

We obtain

$$\begin{gathered} {\displaystyle \frac{\partial D^2}{\partial a}}\left(a,b\right)={\displaystyle {\displaystyle \sum }_{i=1}^n}\left[2·{\displaystyle \frac{2f_i\left(a{f}_i+b-g_i\right)\left(a^2+1\right)-{\left(a{f}_i+b-g_i\right)}^{2}2a}{{\left(a^2+1\right)}^2}}+\right. \\ \left.+{\displaystyle \frac{2}{3}}·{\displaystyle \frac{2{\underset{\_}{f}}_i\left(a{\underset{\_}{f}}_i-{\underset{\_}{g}}_i\right)\left(a^2+1\right)-{\left(a{\underset{\_}{f}}_i-{\underset{\_}{g}}_i\right)}^{2}2a}{{\left(a^2+1\right)}^2}}\right]= \\ ={\displaystyle {\displaystyle \sum }_{i=1}^n}\left[4·{\displaystyle \frac{\left(a{f}_i+b-g_i\right)\left(f_i{a}^2+f_i-a^2{f}_i-ab+a{g}_i\right)}{{\left(a^2+1\right)}^2}}+\right. \\ \left.+{\displaystyle \frac{4}{3}}·{\displaystyle \frac{\left(a{\underset{\_}{f}}_i-{\underset{\_}{g}}_i\right)\left({\underset{\_}{f}}_i{a}^2+{\underset{\_}{f}}_i-a^2{\underset{\_}{f}}_i+a{\underset{\_}{g}}_i\right)}{{\left(a^2+1\right)}^2}}\right]= \\ ={\displaystyle \frac{4}{{\left(a^2+1\right)}^2}}{\displaystyle {\displaystyle \sum }_{i=1}^n}\left[\left(a{f}_i+b-g_i\right)\left(f_i-ab+a{g}_i\right)+{\displaystyle \frac{1}{3}}\left(a{\underset{\_}{f}}_i-{\underset{\_}{g}}_i\right)\left({\underset{\_}{f}}_i+a{\underset{\_}{g}}_i\right)\right] . \end{gathered}$$

(1)

Further, we can obtain

$$\begin{gathered} {\displaystyle \frac{\partial D^2}{\partial a}}\left(a,b\right)={\displaystyle \frac{4}{{\left(a^2+1\right)}^2}}{\displaystyle {\displaystyle \sum }_{i=1}^n}\left\{\left[a{f}_i+\left(b-g_i\right)\right]\left[f_i-a\left(b-g_i\right)\right]+{\displaystyle \frac{1}{3}}\left(a{\underset{\_}{f}}_i-{\underset{\_}{g}}_i\right)\left({\underset{\_}{f}}_i+a{\underset{\_}{g}}_i\right)\right\}= \\ ={\displaystyle \frac{4}{{\left(a^2+1\right)}^2}}{\displaystyle {\displaystyle \sum }_{i=1}^n}\left[a{f}_i^2-a^2{f}_i\left(b-g_i\right)+\right.\left(b-g_i\right)f_i-a{\left(b-g_i\right)}^2+ \\ \left.+{\displaystyle \frac{1}{3}}\left(a{{\underset{\_}{f}}_i}^2+a^2{\underset{\_}{f}}_i{\underset{\_}{g}}_i-{\underset{\_}{f}}_i{\underset{\_}{g}}_i-a{{\underset{\_}{g}}_i}^2\right)\right]= \\ ={\displaystyle \frac{4}{{\left(a^2+1\right)}^2}}{\displaystyle {\displaystyle \sum }_{i=1}^n}\left\{a^2\left[-f_i\left(b-g_i\right)+{\displaystyle \frac{1}{3}}{\underset{\_}{f}}_i{\underset{\_}{g}}_i\right]\right.+ \\ \left.+a\left[f_i^2-{\left(b-g_i\right)}^2+{\displaystyle \frac{1}{3}}\left({{\underset{\_}{f}}_i}^2-{{\underset{\_}{g}}_i}^2\right)\right]+\left[f_i\left(b-g_i\right)-{\displaystyle \frac{1}{3}}{\underset{\_}{f}}_i{\underset{\_}{g}}_i\right]\right\}. \end{gathered}$$

Thus we can write

$${\displaystyle \frac{\partial D^2}{\partial a}}\left(a,b\right)={\displaystyle \frac{4}{{\left(a^2+1\right)}^2}}\left({\alpha }_1^{•}\left(b\right)·a^2+{\beta }_1\left(b\right)·a-{\alpha }_1^{•}\left(b\right)\right) ,$$

(2)

where

$${\alpha }_1^{•}\left(b\right)={\displaystyle {\displaystyle \sum }_{i=1}^n}\left[-f_i\left(b-g_i\right)+{\displaystyle \frac{1}{3}}{\underset{\_}{f}}_i{\underset{\_}{g}}_i\right],$$

(3)

$${\beta }_1\left(b\right)={\displaystyle {\displaystyle \sum }_{i=1}^n}\left[f_i^2-{\left(b-g_i\right)}^2+{\displaystyle \frac{1}{3}}\left({{\underset{\_}{f}}_i}^2-{{\underset{\_}{g}}_i}^2\right)\right].$$

(4)

We also obtain

$${\displaystyle \frac{\partial D^2}{\partial b}}\left(a,b\right)={\displaystyle \frac{4}{a^2+1}}{\displaystyle {\displaystyle \sum }_{i=1}^n}\left(a{f}_i+b-g_i\right).$$

(5)

Using (2), we can write

$$\begin{gathered} {\displaystyle \frac{{\partial }^2{D}^2}{\partial a^2}}\left(a,b\right)={\displaystyle \frac{4}{{\left(a^2+1\right)}^4}}· \\ ·\left[\left(2{\alpha }_1^{•}\left(b\right)·a+{\beta }_1\left(b\right)\right){\left(a^2+1\right)}^2-\left({\alpha }_1^{•}\left(b\right)·a^2+{\beta }_1\left(b\right)·a-{\alpha }_1^{•}\left(b\right)\right)4a\left(a^2+1\right)\right] . \end{gathered}$$

(6)

Using (1), we obtain

$$\begin{gathered} {\displaystyle \frac{{\partial }^2{D}^2}{\partial a\partial b}}\left(a,b\right)={\displaystyle \frac{4}{{\left(a^2+1\right)}^2}}{\displaystyle {\displaystyle \sum }_{i=1}^n}\left[f_i-ab+a{g}_i-a\left(a{f}_i+b-g_i\right)\right]= \\ ={\displaystyle \frac{4}{{\left(a^2+1\right)}^2}}{\displaystyle {\displaystyle \sum }_{i=1}^n}\left(f_i-ab+a{g}_i-a^2{f}_i-ab+a{g}_i\right)= \\ ={\displaystyle \frac{4}{{\left(a^2+1\right)}^2}}{\displaystyle {\displaystyle \sum }_{i=1}^n}\left(f_i-2ab+2a{g}_i-a^2{f}_i\right)= \\ ={\displaystyle \frac{4}{{\left(a^2+1\right)}^2}}{\displaystyle {\displaystyle \sum }_{i=1}^n}\left[-a^2{f}_i-2a\left(b-g_i\right)+f_i\right]. \end{gathered}$$

Using (5), we obtain

$$\begin{gathered} {\displaystyle \frac{{\partial }^2{D}^2}{\partial b\partial a}}\left(a,b\right)=4{\displaystyle {\displaystyle \sum }_{i=1}^n}{\displaystyle \frac{f_i\left(a^2+1\right)-\left(a{f}_i+b-g_i\right)2a}{{\left(a^2+1\right)}^2}}= \\ ={\displaystyle \frac{4}{{\left(a^2+1\right)}^2}}\left[\left(a^2+1\right)\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)-2a{\displaystyle {\displaystyle \sum }_{i=1}^n}\left(a{f}_i+b-g_i\right)\right]= \\ ={\displaystyle \frac{4}{{\left(a^2+1\right)}^2}}{\displaystyle {\displaystyle \sum }_{i=1}^n}\left[a^2{f}_i+f_i-2a^2{f}_i-2a\left(b-g_i\right)\right]= \\ ={\displaystyle \frac{4}{{\left(a^2+1\right)}^2}}{\displaystyle {\displaystyle \sum }_{i=1}^n}\left[-a^2{f}_i-2a\left(b-g_i\right)+f_i\right]. \end{gathered}$$

We can conclude that

$${\displaystyle \frac{{\partial }^2{D}^2}{\partial a\partial b}}\left(a,b\right)={\displaystyle \frac{{\partial }^2{D}^2}{\partial b\partial a}}\left(a,b\right)={\displaystyle \frac{4}{{\left(a^2+1\right)}^2}}\left[\left(a^2+1\right)\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)-2a{\displaystyle {\displaystyle \sum }_{i=1}^n}\left(a{f}_i+b-g_i\right)\right] .$$

(7)

From (5), we obtain

$${\displaystyle \frac{{\partial }^2{D}^2}{\partial b^2}}\left(a,b\right)={\displaystyle \frac{4n}{a^2+1}}.$$

(8)

Consider the system

$$\left\{\begin{array}{l}{\displaystyle \frac{\partial D^2}{\partial a}}\left(a,b\right)=0\hfill \\ {\displaystyle \frac{\partial D^2}{\partial b}}\left(a,b\right)=0\hfill \end{array}\right.$$

(9)

and the Hessian matrix

$$H_{D^2}^{•}\left(a,b\right)=\left(\begin{array}{cc}{\displaystyle \frac{{\partial }^2{D}^2}{\partial a^2}}\left(a,b\right)& {\displaystyle \frac{{\partial }^2{D}^2}{\partial a\partial b}}\left(a,b\right)\\ {\displaystyle \frac{{\partial }^2{D}^2}{\partial b\partial a}}\left(a,b\right)& {\displaystyle \frac{{\partial }^2{D}^2}{\partial b^2}}\left(a,b\right)\end{array}\right).$$

Using relation (5), the equation

$${\displaystyle \frac{\partial D^2}{\partial b}}\left(a,b\right)=0$$

gives

$${\displaystyle {\displaystyle \sum }_{i=1}^n}\left(a{f}_i+b-g_i\right)=0 .$$

(10)

Thus, we successively obtain

$$a{\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i+nb-{\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i=0,$$

$$a{\displaystyle \frac{1}{n}}{\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i+b-{\displaystyle \frac{1}{n}}{\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i=0$$

and

$$b={\displaystyle \frac{1}{n}}{\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i-a{\displaystyle \frac{1}{n}}{\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i={\displaystyle \frac{1}{n}}\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i-a{\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right).$$

(11)

We obtain

$$b{\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i={\displaystyle \frac{1}{n}}\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)-a{\displaystyle \frac{1}{n}}{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)}^2$$

(12)

and

$$ab{\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i=a{\displaystyle \frac{1}{n}}{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)}^2-a^2{\displaystyle \frac{1}{n}}\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right) .$$

(13)

Using (11), we also have

$$\begin{gathered} {\displaystyle {\displaystyle \sum }_{i=1}^n}\left[-f_i\left(b-g_i\right)\right]=-b\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)+\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i{g}_i\right)= \\ =-{\displaystyle \frac{1}{n}}\left[\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)-a\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)\right]\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)+{\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i{g}_i= \\ ={\displaystyle \frac{1}{n}}\left[-\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)+a{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)}^2\right]+{\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i{g}_i \end{gathered}$$

(14)

and

$$\begin{gathered} {\displaystyle {\displaystyle \sum }_{i=1}^n}{\left(b-g_i\right)}^2={\displaystyle {\displaystyle \sum }_{i=1}^n}\left(b^2+g_i^2-2b{g}_i\right)= \\ =n{b}^2+\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i^2\right)-2b\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)= \\ ={\displaystyle \frac{1}{n}}\left[{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)}^2+a^2{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)}^2-2a\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)\right]+ \\ +\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i^2\right)-2{\displaystyle \frac{1}{n}}\left[\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)-a\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)\right]\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)= \\ ={\displaystyle \frac{1}{n}}{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)}^2+a^2{\displaystyle \frac{1}{n}}{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)}^2-2a{\displaystyle \frac{1}{n}}\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)+ \\ +\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i^2\right)-2{\displaystyle \frac{1}{n}}{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)}^2+2{\displaystyle \frac{1}{n}}a\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)= \\ =-{\displaystyle \frac{1}{n}}{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)}^2+a^2{\displaystyle \frac{1}{n}}{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)}^2+\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i^2\right) . \end{gathered}$$

(15)

Using relation (1), the equation

$${\displaystyle \frac{\partial D^2}{\partial a}}\left(a,b\right)=0$$

becomes

$${\displaystyle \frac{4}{{\left(a^2+1\right)}^2}}{\displaystyle {\displaystyle \sum }_{i=1}^n}\left[\left(a{f}_i+b-g_i\right)\left(f_i-ab+a{g}_i\right)+{\displaystyle \frac{1}{3}}\left(a{\underset{\_}{f}}_i-{\underset{\_}{g}}_i\right)\left({\underset{\_}{f}}_i+a{\underset{\_}{g}}_i\right)\right]=0 .$$

Thus,

$$\begin{gathered} {\displaystyle {\displaystyle \sum }_{i=1}^n}\left[\left(a{f}_i+b-g_i\right)f_i+\left(a{f}_i+b-g_i\right)a{g}_i+{\displaystyle \frac{1}{3}}\left(a{\underset{\_}{f}}_i-{\underset{\_}{g}}_i\right)\left({\underset{\_}{f}}_i+a{\underset{\_}{g}}_i\right)\right]- \\ -ab{\displaystyle {\displaystyle \sum }_{i=1}^n}\left(a{f}_i+b-g_i\right)=0 . \end{gathered}$$

(16)

Using (16) and (10), we can write

$${\displaystyle {\displaystyle \sum }_{i=1}^n}\left[\left(a{f}_i+b-g_i\right)f_i+\left(a{f}_i+b-g_i\right)a{g}_i+{\displaystyle \frac{1}{3}}\left(a{\underset{\_}{f}}_i-{\underset{\_}{g}}_i\right)\left({\underset{\_}{f}}_i+a{\underset{\_}{g}}_i\right)\right]=0 ,$$

which is equivalent to

$$\begin{gathered} {\displaystyle {\displaystyle \sum }_{i=1}^n}\left[a{f}_i^2\right.-f_i{g}_i+a^2{f}_i{g}_i-a{g}_i^2+ \\ \left.+{\displaystyle \frac{1}{3}}\left(a{{\underset{\_}{f}}_i}^2+a^2{\underset{\_}{f}}_i{\underset{\_}{g}}_i-{\underset{\_}{f}}_i{\underset{\_}{g}}_i-a{{\underset{\_}{g}}_i}^2\right)\right]+b\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)+ab\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)=0 . \end{gathered}$$

(17)

Using (12) and (13), from (17) we obtain

$$\begin{gathered} {\displaystyle {\displaystyle \sum }_{i=1}^n}\left[a{f}_i^2\right.-f_i{g}_i+a^2{f}_i{g}_i-a{g}_i^2+ \\ \left.+{\displaystyle \frac{1}{3}}\left(a{{\underset{\_}{f}}_i}^2+a^2{\underset{\_}{f}}_i{\underset{\_}{g}}_i-{\underset{\_}{f}}_i{\underset{\_}{g}}_i-a{{\underset{\_}{g}}_i}^2\right)\right]+ \\ +{\displaystyle \frac{1}{n}}\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)-a{\displaystyle \frac{1}{n}}{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)}^2+ \\ +a{\displaystyle \frac{1}{n}}{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)}^2-a^2{\displaystyle \frac{1}{n}}\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)=0 , \end{gathered}$$

which gives

$$\begin{gathered} a^2\left[{\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i{g}_i+{\displaystyle \frac{1}{3}}{\displaystyle {\displaystyle \sum }_{i=1}^n}{\underset{\_}{f}}_i{\underset{\_}{g}}_i-{\displaystyle \frac{1}{n}}\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)\right]+ \\ +a\left[{\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i^2-{\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i^2+{\displaystyle \frac{1}{3}}{\displaystyle {\displaystyle \sum }_{i=1}^n}{{\underset{\_}{f}}_i}^2-{\displaystyle \frac{1}{3}}{\displaystyle {\displaystyle \sum }_{i=1}^n}{{\underset{\_}{g}}_i}^2-{\displaystyle \frac{1}{n}}{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)}^2+{\displaystyle \frac{1}{n}}{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)}^2\right]- \\ -\left[{\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i{g}_i+{\displaystyle \frac{1}{3}}{\displaystyle {\displaystyle \sum }_{i=1}^n}{\underset{\_}{f}}_i{\underset{\_}{g}}_i-{\displaystyle \frac{1}{n}}\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)\right]=0. \end{gathered}$$

(18)

Relation (18) can be written as

$${\alpha }_2^{•}{a}^2+{\beta }_{2}a-{\alpha }_2^{•}=0 ,$$

(19)

where

$${\alpha }_2^{•}={\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i{g}_i+{\displaystyle \frac{1}{3}}{\displaystyle {\displaystyle \sum }_{i=1}^n}{\underset{\_}{f}}_i{\underset{\_}{g}}_i-{\displaystyle \frac{1}{n}}\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right) ,$$

(20)

$${\beta }_2={\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i^2-{\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i^2+{\displaystyle \frac{1}{3}}{\displaystyle {\displaystyle \sum }_{i=1}^n}{{\underset{\_}{f}}_i}^2-{\displaystyle \frac{1}{3}}{\displaystyle {\displaystyle \sum }_{i=1}^n}{{\underset{\_}{g}}_i}^2-{\displaystyle \frac{1}{n}}{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)}^2+{\displaystyle \frac{1}{n}}{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)}^2.$$

(21)

The discriminant of Equation (19) is

$${\Delta }^{•}={\beta }_2^2+4{\left({\alpha }_2^{•}\right)}^2 ,$$

which is a nonnegative real number.

Equation (19) has at least one real solution, and $b$ can be obtained from (11). Let $\left(a^{•},b^{•}\right)$ be a generic solution, from $ℝ\times ℝ,$ of system (9).

Using Formula (2) and the fact that $\left(a^{•},b^{•}\right)$ verifies the first equation of system (9), we obtain

$${\alpha }_1^{•}\left(b^{•}\right)·{\left(a^{•}\right)}^2+{\beta }_1\left(b^{•}\right)·a^{•}-{\alpha }_1^{•}\left(b^{•}\right)=0 .$$

(22)

Using (6) and (22), we obtain

$${\displaystyle \frac{{\partial }^2{D}^2}{\partial a^2}}\left(a^{•},b^{•}\right)={\displaystyle \frac{4}{{\left[{\left(a^{•}\right)}^2+1\right]}^2}}\left(2{\alpha }_1^{•}\left(b^{•}\right)·a^{•}+{\beta }_1\left(b^{•}\right)\right) .$$

(23)

The pair $\left(a^{•},b^{•}\right)$ fulfills relations (10)–(15), because it is a solution of system (9). Using (3) and (14), we obtain

$$\begin{gathered} {\alpha }_1^{•}\left(b^{•}\right)={\displaystyle {\displaystyle \sum }_{i=1}^n}\left[-f_i\left(b^{•}-g_i\right)+{\displaystyle \frac{1}{3}}{\underset{\_}{f}}_i{\underset{\_}{g}}_i\right]= \\ =-{\displaystyle \frac{1}{n}}\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)+a^{•}{\displaystyle \frac{1}{n}}{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)}^2+{\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i{g}_i+{\displaystyle \frac{1}{3}}{\displaystyle {\displaystyle \sum }_{i=1}^n}{\underset{\_}{f}}_i{\underset{\_}{g}}_i . \end{gathered}$$

(24)

Using (4) and (15), we obtain

$$\begin{gathered} {\beta }_1\left(b^{•}\right)={\displaystyle {\displaystyle \sum }_{i=1}^n}\left[f_i^2-{\left(b^{•}-g_i\right)}^2+{\displaystyle \frac{1}{3}}\left({{\underset{\_}{f}}_i}^2-{{\underset{\_}{g}}_i}^2\right)\right]= \\ ={\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i^2+{\displaystyle \frac{1}{n}}{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)}^2-{\left(a^{•}\right)}^2{\displaystyle \frac{1}{n}}{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)}^2-{\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i^2+{\displaystyle \frac{1}{3}}{\displaystyle {\displaystyle \sum }_{i=1}^n}\left({{\underset{\_}{f}}_i}^2-{{\underset{\_}{g}}_i}^2\right) . \end{gathered}$$

(25)

Using (23)–(25), we obtain

$$\begin{gathered} {\displaystyle \frac{{\partial }^2{D}^2}{\partial a^2}}\left(a^{•},b^{•}\right)={\displaystyle \frac{4}{{\left[{\left(a^{•}\right)}^2+1\right]}^2}}· \\ ·\left[-2a^{•}{\displaystyle \frac{1}{n}}\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)+2{\left(a^{•}\right)}^2{\displaystyle \frac{1}{n}}{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)}^2+2a^{•}{\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i{g}_i+2a^{•}{\displaystyle \frac{1}{3}}{\displaystyle {\displaystyle \sum }_{i=1}^n}{\underset{\_}{f}}_i{\underset{\_}{g}}_i+\right. \\ \left.+{\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i^2+{\displaystyle \frac{1}{n}}{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)}^2-{\left(a^{•}\right)}^2{\displaystyle \frac{1}{n}}{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)}^2-{\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i^2+{\displaystyle \frac{1}{3}}{\displaystyle {\displaystyle \sum }_{i=1}^n}\left({{\underset{\_}{f}}_i}^2-{{\underset{\_}{g}}_i}^2\right) \right]= \\ ={\displaystyle \frac{4}{{\left[{\left(a^{•}\right)}^2+1\right]}^2}}· \\ ·\left\{{\left(a^{•}\right)}^2{\displaystyle \frac{1}{n}}{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)}^2+2a^{•}\left[-{\displaystyle \frac{1}{n}}\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)+{\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i{g}_i+{\displaystyle \frac{1}{3}}{\displaystyle {\displaystyle \sum }_{i=1}^n}{\underset{\_}{f}}_i{\underset{\_}{g}}_i\right]+\right. \\ \left.+{\displaystyle \frac{1}{n}}{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)}^2+{\displaystyle {\displaystyle \sum }_{i=1}^n}\left(f_i^2-g_i^2\right)+{\displaystyle \frac{1}{3}}{\displaystyle {\displaystyle \sum }_{i=1}^n}\left({{\underset{\_}{f}}_i}^2-{{\underset{\_}{g}}_i}^2\right) \right\} \end{gathered}$$

Thus, we can write

$${\displaystyle \frac{{\partial }^2{D}^2}{\partial a^2}}\left(a^{•},b^{•}\right)={\displaystyle \frac{4}{{\left[{\left(a^{•}\right)}^2+1\right]}^2}}\left[{\gamma }_1·{\left(a^{•}\right)}^2+2{\alpha }_2^{•}{a}^{•}+{\gamma }_2\right] ,$$

(26)

where

$${\gamma }_1={\displaystyle \frac{1}{n}}{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)}^2 ,$$

(27)

$${\gamma }_2={\displaystyle \frac{1}{n}}{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)}^2+{\displaystyle {\displaystyle \sum }_{i=1}^n}\left(f_i^2-g_i^2\right)+{\displaystyle \frac{1}{3}}{\displaystyle {\displaystyle \sum }_{i=1}^n}\left({{\underset{\_}{f}}_i}^2-{{\underset{\_}{g}}_i}^2\right) .$$

(28)

Taking into account (21), (27) and (28), we remark that

$${\beta }_2={\gamma }_2-{\gamma }_1 .$$

(29)

Using (19) and (29), we obtain

$${\alpha }_2^{•}·{\left(a^{•}\right)}^2+{\gamma }_2{a}^{•}-{\gamma }_1{a}^{•}-{\alpha }_2^{•}=0 .$$

(30)

Thus, we have

$${\alpha }_2^{•}·{\left(a^{•}\right)}^3+{\gamma }_2·{\left(a^{•}\right)}^2-{\gamma }_1·{\left(a^{•}\right)}^2-{\alpha }_2^{•}{a}^{•}=0$$

and

$${\gamma }_1·{\left(a^{•}\right)}^2={\alpha }_2·{\left(a^{•}\right)}^3+{\gamma }_2·{\left(a^{•}\right)}^2-{\alpha }_2{a}^{•} .$$

We obtain

$$\begin{gathered} {\gamma }_1·{\left(a^{•}\right)}^2+2{\alpha }_2^{•}{a}^{•}+{\gamma }_2={\alpha }_2^{•}·{\left(a^{•}\right)}^3+{\gamma }_2·{\left(a^{•}\right)}^2-{\alpha }_2^{•}{a}^{•}+2{\alpha }_2^{•}{a}^{•}+{\gamma }_2= \\ ={\alpha }_2^{•}·{\left(a^{•}\right)}^3+{\gamma }_2·{\left(a^{•}\right)}^2+{\alpha }_2^{•}{a}^{•}+{\gamma }_2={\alpha }_2^{•}{a}^{•}\left[{\left(a^{•}\right)}^2+1\right]+{\gamma }_2\left[{\left(a^{•}\right)}^2+1\right]= \\ =\left[{\left(a^{•}\right)}^2+1\right]\left({\alpha }_2^{•}{a}^{•}+{\gamma }_2\right)=\left[{\left(a^{•}\right)}^2+1\right]\left({\alpha }_2^{•}{a}^{•}+{\beta }_2+{\gamma }_1\right). \end{gathered}$$

Finally, taking into account (26), we have

$$\begin{gathered} {\displaystyle \frac{{\partial }^2{D}^2}{\partial a^2}}\left(a^{•},b^{•}\right)={\displaystyle \frac{4}{{\left[{\left(a^{•}\right)}^2+1\right]}^2}}\left[{\gamma }_1·{\left(a^{•}\right)}^2+2{\alpha }_2^{•}{a}^{•}+{\gamma }_2\right]= \\ ={\displaystyle \frac{4}{{\left(a^{•}\right)}^2+1}}\left({\alpha }_2^{•}{a}^{•}+{\beta }_2+{\gamma }_1\right)={\displaystyle \frac{4}{{\left(a^{•}\right)}^2+1}}\left[{\alpha }_2^{•}{a}^{•}+{\beta }_2+{\displaystyle \frac{1}{n}}{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)}^2\right]. \end{gathered}$$

(31)

Using (10), which is verified by $\left(a^{•},b^{•}\right)$, and (7), we obtain

$${\displaystyle \frac{{\partial }^2{D}^2}{\partial a\partial b}}\left(a^{•},b^{•}\right)={\displaystyle \frac{{\partial }^2{D}^2}{\partial b\partial a}}\left(a^{•},b^{•}\right)={\displaystyle \frac{4}{{\left(a^{•}\right)}^2+1}}{\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i .$$

(32)

From (8), we have

$${\displaystyle \frac{{\partial }^2{D}^2}{\partial b^2}}\left(a^{•},b^{•}\right)={\displaystyle \frac{4n}{a^2+1}} .$$

(33)

From (31)–(33) the Hessian matrix becomes

$$H_{D^2}^{•}\left(a^{•},b^{•}\right)={\displaystyle \frac{4}{{\left(a^{•}\right)}^2+1}}\left(\begin{array}{cc}{\alpha }_2^{•}{a}^{•}+{\beta }_2+{\displaystyle \frac{1}{n}}{\left({\displaystyle {\displaystyle {\displaystyle \sum }_{i=1}^n}}{f}_i\right)}^2& {\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\\ {\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i& n\end{array}\right)={\displaystyle \frac{4}{{\left(a^{•}\right)}^2+1}}{K}_{D^2}^{•}\left(a^{•},b^{•}\right) .$$

We have

$$\begin{gathered} {\Delta }_1\left(a^{•},b^{•}\right)={\alpha }_2^{•}{a}^{•}+{\beta }_2+{\displaystyle \frac{1}{n}}{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)}^2 , \\ {\Delta }_2\left(a^{•},b^{•}\right)=\det \left(K_{D^2}\left(a^{•},b^{•}\right)\right)=n\left({\alpha }_2^{•}{a}^{•}+{\beta }_2\right). \end{gathered}$$

Since $a^{•}$ verifies Equation (19), we can write

$$\begin{gathered} {\alpha }_2^{•}·{\left(a^{•}\right)}^2+{\beta }_2{a}^{•}-{\alpha }_2^{•}=0 \\ \Rightarrow a^{•}\left({\alpha }_2^{•}{a}^{•}+{\beta }_2\right)={\alpha }_2^{•} \\ \Rightarrow {\alpha }_2^{•}{a}^{•}+{\beta }_2={\displaystyle \frac{{\alpha }_2^{•}}{a^{•}}} . \end{gathered}$$

Thus, ${\Delta }_1\left(a^{•},b^{•}\right)$ and ${\Delta }_2\left(a^{•},b^{•}\right)$ are both strictly positive if and only if ${\alpha }_2^{•}$ and $a^{•}$ have the same sign.

If ${\alpha }_2^{•}>0$, Equation (19) has two distinct solutions, namely

$$a_{1,2}^{•}={\displaystyle \frac{-{\beta }_2\pm \sqrt{{\beta }_2^2+4{\left({\alpha }_2^{•}\right)}^2}}{2{\alpha }_2^{•}}} ,$$

from which only one is strictly positive.

If ${\alpha }_2^{•}>0$, let ${\widehat{a}}^{•}$ be the unique strictly positive solution of (19), namely

$${\widehat{a}}^{•}={\displaystyle \frac{-{\beta }_2+\sqrt{{\beta }_2^2+4{\left({\alpha }_2^{•}\right)}^2}}{2{\alpha }_2^{•}}} .$$

Thus,

$$\underset{\left(a,b\right)\in {ℝ}_{+}^{*}\times ℝ}{\min }{D}^2\left(a,b\right)=D^2\left({\widehat{a}}^{•},{\widehat{b}}^{•}\right) ,$$

where ${\widehat{b}}^{•}$ is obtained from (11) as

$${\widehat{b}}^{•}={\displaystyle \frac{1}{n}}\left[\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)-{\widehat{a}}^{•}\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)\right] .$$

If ${\alpha }_2^{•}=0$, Equation (19) has the solution $a^{•}=0$, which is not in ${ℝ}_{+}^{*}$. □

Proposition 8.

Let $\left({\tilde{F}}_i,{\tilde{G}}_i\right)$, $i=\overline{1,n}$, $n\ge 2$, be $n$ pairs of symmetric triangular fuzzy numbers, where ${\tilde{F}}_i=\left(f_i,{\underset{\_}{f}}_i,{\underset{\_}{f}}_i\right)$ and ${\tilde{G}}_i=\left(g_i,{\underset{\_}{g}}_i,{\underset{\_}{g}}_i\right)$. It is assumed that the relation

$${\left({\alpha }_2^{\circ }\right)}^2+{\beta }_2^2\ne 0$$

is true, where

$${\alpha }_2^{\circ }={\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i{g}_i-{\displaystyle \frac{1}{3}}{\displaystyle {\displaystyle \sum }_{i=1}^n}{\underset{\_}{f}}_i{\underset{\_}{g}}_i-{\displaystyle \frac{1}{n}}\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right) ,$$

$${\beta }_2={\displaystyle {\displaystyle \sum }_{i=1}^n}\left(f_i^2-g_i^2\right)+{\displaystyle \frac{1}{n}}\left[{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)}^2-{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)}^2\right]+{\displaystyle \frac{1}{3}}{\displaystyle {\displaystyle \sum }_{i=1}^n}\left({{\underset{\_}{f}}_i}^2-{{\underset{\_}{g}}_i}^2\right) .$$

The inequality

$${\alpha }_2^{\circ }<0$$

is a necessary and sufficient condition for the existence and unicity of a pair $\left({\widehat{a}}^{\circ },{\widehat{b}}^{\circ }\right)$ such that

$$\underset{\left(a,b\right)\in {ℝ}_{-}^{*}\times ℝ}{\min }{D}^2\left(a,b\right)=D^2\left({\widehat{a}}^{\circ },{\widehat{b}}^{\circ }\right) .$$

Moreover, the following relations hold:

$${\widehat{a}}^{\circ }={\displaystyle \frac{-{\beta }_2+\sqrt{{\beta }_2^2+4{\left({\alpha }_2^{\circ }\right)}^2}}{2{\alpha }_2^{\circ }}} ,$$

$${\widehat{b}}^{\circ }={\displaystyle \frac{1}{n}}\left[\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)-{\widehat{a}}^{\circ }\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)\right] .$$

Proof. 

According to Proposition 6, if $a\in \left(-\infty ,0\right)$, we have

$$\begin{gathered} D^2\left(a,b\right)={\displaystyle \frac{2}{a^2+1}}{\displaystyle {\displaystyle \sum }_{i=1}^n}\left[{\left(a{f}_i+b-g_i\right)}^2+{\displaystyle \frac{1}{3}}{\left(a{\underset{\_}{f}}_i+{\underset{\_}{g}}_i\right)}^2\right]= \\ ={\displaystyle {\displaystyle \sum }_{i=1}^n}\left[2·{\displaystyle \frac{{\left(a{f}_i+b-g_i\right)}^2}{a^2+1}}+{\displaystyle \frac{2}{3}}·{\displaystyle \frac{{\left(a{\underset{\_}{f}}_i+{\underset{\_}{g}}_i\right)}^2}{a^2+1}}\right]. \end{gathered}$$

We obtain

$$\begin{gathered} {\displaystyle \frac{\partial D^2}{\partial a}}\left(a,b\right)={\displaystyle {\displaystyle \sum }_{i=1}^n}\left[2·{\displaystyle \frac{2f_i\left(a{f}_i+b-g_i\right)\left(a^2+1\right)-{\left(a{f}_i+b-g_i\right)}^{2}2a}{{\left(a^2+1\right)}^2}}+\right. \\ \left.+{\displaystyle \frac{2}{3}}·{\displaystyle \frac{2{\underset{\_}{f}}_i\left(a{\underset{\_}{f}}_i+{\underset{\_}{g}}_i\right)\left(a^2+1\right)-{\left(a{\underset{\_}{f}}_i+{\underset{\_}{g}}_i\right)}^{2}2a}{{\left(a^2+1\right)}^2}}\right]= \\ ={\displaystyle {\displaystyle \sum }_{i=1}^n}\left[4·{\displaystyle \frac{\left(a{f}_i+b-g_i\right)\left(f_i{a}^2+f_i-a^2{f}_i-ab+a{g}_i\right)}{{\left(a^2+1\right)}^2}}+\right. \\ \left.+{\displaystyle \frac{4}{3}}·{\displaystyle \frac{\left(a{\underset{\_}{f}}_i+{\underset{\_}{g}}_i\right)\left({\underset{\_}{f}}_i{a}^2+{\underset{\_}{f}}_i-a^2{\underset{\_}{f}}_i-a{\underset{\_}{g}}_i\right)}{{\left(a^2+1\right)}^2}}\right]= \\ ={\displaystyle \frac{4}{{\left(a^2+1\right)}^2}}{\displaystyle {\displaystyle \sum }_{i=1}^n}\left[\left(a{f}_i+b-g_i\right)\left(f_i-ab+a{g}_i\right)+{\displaystyle \frac{1}{3}}\left(a{\underset{\_}{f}}_i+{\underset{\_}{g}}_i\right)\left({\underset{\_}{f}}_i-a{\underset{\_}{g}}_i\right)\right] \end{gathered}$$

(34)

Further, we can obtain

$$\begin{gathered} {\displaystyle \frac{\partial D^2}{\partial a}}\left(a,b\right)={\displaystyle \frac{4}{{\left(a^2+1\right)}^2}}{\displaystyle {\displaystyle \sum }_{i=1}^n}\{\left[a{f}_i+\left(b-g_i\right)\right]\left[f_i-a\left(b-g_i\right)\right] \\ +{\displaystyle \frac{1}{3}}\left(a{\underset{\_}{f}}_i+{\underset{\_}{g}}_i\right)\left({\underset{\_}{f}}_i-a{\underset{\_}{g}}_i\right)\}= \\ ={\displaystyle \frac{4}{{\left(a^2+1\right)}^2}}{\displaystyle {\displaystyle \sum }_{i=1}^n}\left[a{f}_i^2-a^2{f}_i\left(b-g_i\right)+\right.\left(b-g_i\right)f_i-a{\left(b-g_i\right)}^2+ \\ \left.+{\displaystyle \frac{1}{3}}\left(a{{\underset{\_}{f}}_i}^2-a^2{\underset{\_}{f}}_i{\underset{\_}{g}}_i+{\underset{\_}{f}}_i{\underset{\_}{g}}_i-a{{\underset{\_}{g}}_i}^2\right)\right]= \\ ={\displaystyle \frac{4}{{\left(a^2+1\right)}^2}}{\displaystyle {\displaystyle \sum }_{i=1}^n}\left\{a^2\left[-f_i\left(b-g_i\right)-{\displaystyle \frac{1}{3}}{\underset{\_}{f}}_i{\underset{\_}{g}}_i\right]\right.+ \\ \left.+a\left[f_i^2-{\left(b-g_i\right)}^2+{\displaystyle \frac{1}{3}}\left({{\underset{\_}{f}}_i}^2-{{\underset{\_}{g}}_i}^2\right)\right]+\left[f_i\left(b-g_i\right)+{\displaystyle \frac{1}{3}}{\underset{\_}{f}}_i{\underset{\_}{g}}_i\right]\right\}. \end{gathered}$$

Thus, we can write

$${\displaystyle \frac{\partial D^2}{\partial a}}\left(a,b\right)={\displaystyle \frac{4}{{\left(a^2+1\right)}^2}}\left({\alpha }_1^{\circ }\left(b\right)·a^2+{\beta }_1\left(b\right)·a-{\alpha }_1^{\circ }\left(b\right)\right),$$

(35)

where

$${\alpha }_1^{\circ }\left(b\right)={\displaystyle {\displaystyle \sum }_{i=1}^n}\left[-f_i\left(b-g_i\right)-{\displaystyle \frac{1}{3}}{\underset{\_}{f}}_i{\underset{\_}{g}}_i\right],$$

(36)

$${\beta }_1\left(b\right)={\displaystyle {\displaystyle \sum }_{i=1}^n}\left[f_i^2-{\left(b-g_i\right)}^2+{\displaystyle \frac{1}{3}}\left({{\underset{\_}{f}}_i}^2-{{\underset{\_}{g}}_i}^2\right)\right] .$$

(37)

We also obtain

$${\displaystyle \frac{\partial D^2}{\partial b}}\left(a,b\right)={\displaystyle \frac{4}{a^2+1}}{\displaystyle {\displaystyle \sum }_{i=1}^n}\left(a{f}_i+b-g_i\right) .$$

(38)

Using (35), we can write

$$\begin{gathered} {\displaystyle \frac{{\partial }^2{D}^2}{\partial a^2}}\left(a,b\right)={\displaystyle \frac{4}{{\left(a^2+1\right)}^4}}· \\ ·\left[\left(2{\alpha }_1^{\circ }\left(b\right)·a+{\beta }_1\left(b\right)\right){\left(a^2+1\right)}^2-\left({\alpha }_1^{\circ }\left(b\right)·a^2+{\beta }_1\left(b\right)·a-{\alpha }_1^{\circ }\left(b\right)\right)4a\left(a^2+1\right)\right]. \end{gathered}$$

(39)

Using (34), we obtain

$$\begin{gathered} {\displaystyle \frac{{\partial }^2{D}^2}{\partial a\partial b}}\left(a,b\right)={\displaystyle \frac{4}{{\left(a^2+1\right)}^2}}{\displaystyle {\displaystyle \sum }_{i=1}^n}\left[f_i-ab+a{g}_i-a\left(a{f}_i+b-g_i\right)\right]= \\ ={\displaystyle \frac{4}{{\left(a^2+1\right)}^2}}{\displaystyle {\displaystyle \sum }_{i=1}^n}\left(f_i-ab+a{g}_i-a^2{f}_i-ab+a{g}_i\right)= \\ ={\displaystyle \frac{4}{{\left(a^2+1\right)}^2}}{\displaystyle {\displaystyle \sum }_{i=1}^n}\left(f_i-2ab+2a{g}_i-a^2{f}_i\right)= \\ ={\displaystyle \frac{4}{{\left(a^2+1\right)}^2}}{\displaystyle {\displaystyle \sum }_{i=1}^n}\left[-a^2{f}_i-2a\left(b-g_i\right)+f_i\right]. \end{gathered}$$

From (38), we obtain

$$\begin{gathered} {\displaystyle \frac{{\partial }^2{D}^2}{\partial b\partial a}}\left(a,b\right)=4{\displaystyle {\displaystyle \sum }_{i=1}^n}{\displaystyle \frac{f_i\left(a^2+1\right)-\left(a{f}_i+b-g_i\right)2a}{{\left(a^2+1\right)}^2}}= \\ ={\displaystyle \frac{4}{{\left(a^2+1\right)}^2}}\left[\left(a^2+1\right)\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)-2a{\displaystyle {\displaystyle \sum }_{i=1}^n}\left(a{f}_i+b-g_i\right)\right]= \\ ={\displaystyle \frac{4}{{\left(a^2+1\right)}^2}}{\displaystyle {\displaystyle \sum }_{i=1}^n}\left[a^2{f}_i+f_i-2a^2{f}_i-2a\left(b-g_i\right)\right]= \\ ={\displaystyle \frac{4}{{\left(a^2+1\right)}^2}}{\displaystyle {\displaystyle \sum }_{i=1}^n}\left[-a^2{f}_i-2a\left(b-g_i\right)+f_i\right]. \end{gathered}$$

We can conclude that

$${\displaystyle \frac{{\partial }^2{D}^2}{\partial a\partial b}}\left(a,b\right)={\displaystyle \frac{{\partial }^2{D}^2}{\partial b\partial a}}\left(a,b\right)={\displaystyle \frac{4}{{\left(a^2+1\right)}^2}}\left[\left(a^2+1\right)\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)-2a{\displaystyle {\displaystyle \sum }_{i=1}^n}\left(a{f}_i+b-g_i\right)\right] .$$

(40)

From (38), we obtain

$${\displaystyle \frac{{\partial }^2{D}^2}{\partial b^2}}\left(a,b\right)={\displaystyle \frac{4n}{a^2+1}} .$$

(41)

Consider the system

$$\left\{\begin{array}{l}{\displaystyle \frac{\partial D^2}{\partial a}}\left(a,b\right)=0\hfill \\ {\displaystyle \frac{\partial D^2}{\partial b}}\left(a,b\right)=0\hfill \end{array}\right.$$

(42)

and the Hessian matrix

$$H_{D^2}^{\circ }\left(a,b\right)=\left(\begin{array}{cc}{\displaystyle \frac{{\partial }^2{D}^2}{\partial a^2}}\left(a,b\right)& {\displaystyle \frac{{\partial }^2{D}^2}{\partial a\partial b}}\left(a,b\right)\\ {\displaystyle \frac{{\partial }^2{D}^2}{\partial b\partial a}}\left(a,b\right)& {\displaystyle \frac{{\partial }^2{D}^2}{\partial b^2}}\left(a,b\right)\end{array}\right) .$$

Using relation (38), the equation

$${\displaystyle \frac{\partial D^2}{\partial b}}\left(a,b\right)=0$$

gives

$${\displaystyle {\displaystyle \sum }_{i=1}^n}\left(a{f}_i+b-g_i\right)=0 .$$

(43)

Taking into account (10) and (43), note that using the same reasoning as in (11)–(15), we can write the following relations:

$$b={\displaystyle \frac{1}{n}}{\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i-a{\displaystyle \frac{1}{n}}{\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i={\displaystyle \frac{1}{n}}\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i-a{\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right) ,$$

(44)

$$b{\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i={\displaystyle \frac{1}{n}}\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)-a{\displaystyle \frac{1}{n}}{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)}^2 ,$$

(45)

$$ab{\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i=a{\displaystyle \frac{1}{n}}{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)}^2-a^2{\displaystyle \frac{1}{n}}\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right) ,$$

(46)

$${\displaystyle {\displaystyle \sum }_{i=1}^n}\left[-f_i\left(b-g_i\right)\right]={\displaystyle \frac{1}{n}}\left[-\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)+a{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)}^2\right]+{\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i{g}_i ,$$

(47)

$${\displaystyle {\displaystyle \sum }_{i=1}^n}{\left(b-g_i\right)}^2=-{\displaystyle \frac{1}{n}}{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)}^2+a^2{\displaystyle \frac{1}{n}}{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)}^2+\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i^2\right) .$$

(48)

Using relation (34), the equation

$${\displaystyle \frac{\partial D^2}{\partial a}}\left(a,b\right)=0$$

becomes

$${\displaystyle {\displaystyle \sum }_{i=1}^n}\left[\left(a{f}_i+b-g_i\right)\left(f_i-ab+a{g}_i\right)+{\displaystyle \frac{1}{3}}\left(a{\underset{\_}{f}}_i+{\underset{\_}{g}}_i\right)\left({\underset{\_}{f}}_i-a{\underset{\_}{g}}_i\right)\right]=0 .$$

Thus,

$$\begin{gathered} {\displaystyle {\displaystyle \sum }_{i=1}^n}\left[\left(a{f}_i+b-g_i\right)f_i+\left(a{f}_i+b-g_i\right)a{g}_i+{\displaystyle \frac{1}{3}}\left(a{\underset{\_}{f}}_i+{\underset{\_}{g}}_i\right)\left({\underset{\_}{f}}_i-a{\underset{\_}{g}}_i\right)\right]- \\ -ab{\displaystyle {\displaystyle \sum }_{i=1}^n}\left(a{f}_i+b-g_i\right)=0 . \end{gathered}$$

(49)

Using (49) and (43), we can write

$${\displaystyle {\displaystyle \sum }_{i=1}^n}\left[\left(a{f}_i+b-g_i\right)f_i+\left(a{f}_i+b-g_i\right)a{g}_i+{\displaystyle \frac{1}{3}}\left(a{\underset{\_}{f}}_i+{\underset{\_}{g}}_i\right)\left({\underset{\_}{f}}_i-a{\underset{\_}{g}}_i\right)\right]=0 ,$$

which is equivalent to

$$\begin{gathered} {\displaystyle {\displaystyle \sum }_{i=1}^n}\left[a{f}_i^2-f_i{g}_i+a^2{f}_i{g}_i-a{g}_i^2+\right. \\ \left.+{\displaystyle \frac{1}{3}}\left(a{{\underset{\_}{f}}_i}^2-a^2{\underset{\_}{f}}_i{\underset{\_}{g}}_i+{\underset{\_}{f}}_i{\underset{\_}{g}}_i-a{{\underset{\_}{g}}_i}^2\right)\right]+b\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)+ab\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)=0 . \end{gathered}$$

(50)

Using (45) and (46), from (50) we obtain

$$\begin{gathered} {\displaystyle {\displaystyle \sum }_{i=1}^n}\left[a{f}_i^2-f_i{g}_i+a^2{f}_i{g}_i-a{g}_i^2+\right. \\ \left.+{\displaystyle \frac{1}{3}}\left(a{{\underset{\_}{f}}_i}^2-a^2{\underset{\_}{f}}_i{\underset{\_}{g}}_i+{\underset{\_}{f}}_i{\underset{\_}{g}}_i-a{{\underset{\_}{g}}_i}^2\right)\right]+ \\ +{\displaystyle \frac{1}{n}}\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)-a{\displaystyle \frac{1}{n}}{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)}^2+ \\ +a{\displaystyle \frac{1}{n}}{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)}^2-a^2{\displaystyle \frac{1}{n}}\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)=0 , \end{gathered}$$

which gives

$$\begin{gathered} a^2\left[{\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i{g}_i-{\displaystyle \frac{1}{3}}{\displaystyle {\displaystyle \sum }_{i=1}^n}{\underset{\_}{f}}_i{\underset{\_}{g}}_i-{\displaystyle \frac{1}{n}}\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)\right]+ \\ +a\left[{\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i^2-{\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i^2+{\displaystyle \frac{1}{3}}{\displaystyle {\displaystyle \sum }_{i=1}^n}{{\underset{\_}{f}}_i}^2-{\displaystyle \frac{1}{3}}{\displaystyle {\displaystyle \sum }_{i=1}^n}{{\underset{\_}{g}}_i}^2-{\displaystyle \frac{1}{n}}{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)}^2+{\displaystyle \frac{1}{n}}{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)}^2\right]- \\ -\left[{\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i{g}_i-{\displaystyle \frac{1}{3}}{\displaystyle {\displaystyle \sum }_{i=1}^n}{\underset{\_}{f}}_i{\underset{\_}{g}}_i-{\displaystyle \frac{1}{n}}\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)\right]=0 . \end{gathered}$$

(51)

Relation (51) can be written as

$${\alpha }_2^{\circ }{a}^2+{\beta }_{2}a-{\alpha }_2^{\circ }=0 ,$$

(52)

where

$${\alpha }_2^{\circ }={\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i{g}_i-{\displaystyle \frac{1}{3}}{\displaystyle {\displaystyle \sum }_{i=1}^n}{\underset{\_}{f}}_i{\underset{\_}{g}}_i-{\displaystyle \frac{1}{n}}\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right) ,$$

(53)

$${\beta }_2={\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i^2-{\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i^2+{\displaystyle \frac{1}{3}}{\displaystyle {\displaystyle \sum }_{i=1}^n}{{\underset{\_}{f}}_i}^2-{\displaystyle \frac{1}{3}}{\displaystyle {\displaystyle \sum }_{i=1}^n}{{\underset{\_}{g}}_i}^2-{\displaystyle \frac{1}{n}}{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)}^2+{\displaystyle \frac{1}{n}}{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)}^2.$$

(54)

The discriminant of Equation (52) is

$${∆}^{\circ }={\beta }_2^2+4{\left({\alpha }_2^{\circ }\right)}^2 ,$$

which is a nonnegative real number.

Equation (52) has at least one real solution, and $b$ can be obtained from (44). Let $\left(a^{\circ },b^{\circ }\right)$ be a generic solution, from $ℝ\times ℝ$, of system (42).

Using Formula (35) and the fact that $\left(a^{\circ },b^{\circ }\right)$ verifies the first equation of system (42), we obtain

$${\alpha }_1^{\circ }\left(b^{\circ }\right)·{\left(a^{\circ }\right)}^2+{\beta }_1\left(b^{\circ }\right)·a^{\circ }-{\alpha }_1^{\circ }\left(b^{\circ }\right)=0 .$$

(55)

Using (39) and (55), we obtain

$${\displaystyle \frac{{\partial }^2{D}^2}{\partial a^2}}\left(a^{\circ },b^{\circ }\right)={\displaystyle \frac{4}{{\left[{\left(a^{\circ }\right)}^2+1\right]}^2}}\left(2{\alpha }_1^{\circ }\left(b^{\circ }\right)·a^{\circ }+{\beta }_1\left(b^{\circ }\right)\right) .$$

(56)

The pair $\left(a^{\circ },b^{\circ }\right)$ satisfies relations (43)–(48), because it is a solution of system (42). Using (36) and (47), we obtain

$$\begin{gathered} {\alpha }_1^{\circ }\left(b^{\circ }\right)={\displaystyle {\displaystyle \sum }_{i=1}^n}\left[-f_i\left(b^{\circ }-g_i\right)-{\displaystyle \frac{1}{3}}{\underset{\_}{f}}_i{\underset{\_}{g}}_i\right]= \\ =-{\displaystyle \frac{1}{n}}\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)+a^{\circ }{\displaystyle \frac{1}{n}}{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)}^2+{\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i{g}_i-{\displaystyle \frac{1}{3}}{\displaystyle {\displaystyle \sum }_{i=1}^n}{\underset{\_}{f}}_i{\underset{\_}{g}}_i . \end{gathered}$$

(57)

Using (37) and (48), we obtain

$$\begin{gathered} {\beta }_1\left(b^{\circ }\right)={\displaystyle {\displaystyle \sum }_{i=1}^n}\left[f_i^2-{\left(b^{\circ }-g_i\right)}^2+{\displaystyle \frac{1}{3}}\left({{\underset{\_}{f}}_i}^2-{{\underset{\_}{g}}_i}^2\right)\right]= \\ ={\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i^2+{\displaystyle \frac{1}{n}}{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)}^2-{\left(a^{\circ }\right)}^2{\displaystyle \frac{1}{n}}{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)}^2-{\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i^2+{\displaystyle \frac{1}{3}}{\displaystyle {\displaystyle \sum }_{i=1}^n}\left({{\underset{\_}{f}}_i}^2-{{\underset{\_}{g}}_i}^2\right) . \end{gathered}$$

(58)

Using (56)–(58), we obtain

$$\begin{gathered} {\displaystyle \frac{{\partial }^2{D}^2}{\partial a^2}}\left(a^{\circ },b^{\circ }\right)={\displaystyle \frac{4}{{\left[{\left(a^{\circ }\right)}^2+1\right]}^2}}· \\ ·\left[-2a^{\circ }{\displaystyle \frac{1}{n}}\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)+2{\left(a^{\circ }\right)}^2{\displaystyle \frac{1}{n}}{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)}^2+2a^{\circ }{\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i{g}_i-2a^{\circ }{\displaystyle \frac{1}{3}}{\displaystyle {\displaystyle \sum }_{i=1}^n}{\underset{\_}{f}}_i{\underset{\_}{g}}_i+\right. \\ \left.+{\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i^2+{\displaystyle \frac{1}{n}}{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)}^2-{\left(a^{\circ }\right)}^2{\displaystyle \frac{1}{n}}{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)}^2-{\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i^2+{\displaystyle \frac{1}{3}}{\displaystyle {\displaystyle \sum }_{i=1}^n}\left({{\underset{\_}{f}}_i}^2-{{\underset{\_}{g}}_i}^2\right) \right]= \\ ={\displaystyle \frac{4}{{\left[{\left(a^{\circ }\right)}^2+1\right]}^2}}· \\ ·\left\{{\left(a^{\circ }\right)}^2{\displaystyle \frac{1}{n}}{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)}^2+2a^{\circ }\left[-{\displaystyle \frac{1}{n}}\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)+{\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i{g}_i-{\displaystyle \frac{1}{3}}{\displaystyle {\displaystyle \sum }_{i=1}^n}{\underset{\_}{f}}_i{\underset{\_}{g}}_i\right]+\right. \\ \left.+{\displaystyle \frac{1}{n}}{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)}^2+{\displaystyle {\displaystyle \sum }_{i=1}^n}\left(f_i^2-g_i^2\right)+{\displaystyle \frac{1}{3}}{\displaystyle {\displaystyle \sum }_{i=1}^n}\left({{\underset{\_}{f}}_i}^2-{{\underset{\_}{g}}_i}^2\right) \right\}. \end{gathered}$$

Thus, we can write

$${\displaystyle \frac{{\partial }^2{D}^2}{\partial a^2}}\left(a^{\circ },b^{\circ }\right)={\displaystyle \frac{4}{{\left[{\left(a^{\circ }\right)}^2+1\right]}^2}}\left[{\gamma }_1·{\left(a^{\circ }\right)}^2+2{\alpha }_2^{\circ }{a}^{\circ }+{\gamma }_2\right] ,$$

(59)

where

$${\gamma }_1={\displaystyle \frac{1}{n}}{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)}^2 ,$$

(60)

$${\gamma }_2={\displaystyle \frac{1}{n}}{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)}^2+{\displaystyle {\displaystyle \sum }_{i=1}^n}\left(f_i^2-g_i^2\right)+{\displaystyle \frac{1}{3}}{\displaystyle {\displaystyle \sum }_{i=1}^n}\left({{\underset{\_}{f}}_i}^2-{{\underset{\_}{g}}_i}^2\right) .$$

(61)

Taking into account (54), (60) and (61), we can remark that

$${\beta }_2={\gamma }_2-{\gamma }_1 .$$

(62)

Using (52) and (62), we obtain

$${\alpha }_2^{\circ }·{\left(a^{\circ }\right)}^2+{\gamma }_2{a}^{\circ }-{\gamma }_1{a}^{\circ }-{\alpha }_2^{\circ }=0 .$$

(63)

Thus, we have

$${\alpha }_2^{\circ }·{\left(a^{\circ }\right)}^3+{\gamma }_2·{\left(a^{\circ }\right)}^2-{\gamma }_1·{\left(a^{\circ }\right)}^2-{\alpha }_2^{\circ }{a}^{\circ }=0$$

and

$${\gamma }_1·{\left(a^{\circ }\right)}^2={\alpha }_2^{\circ }·{\left(a^{\circ }\right)}^3+{\gamma }_2·{\left(a^{\circ }\right)}^2-{\alpha }_2^{\circ }{a}^{\circ } .$$

We obtain

$$\begin{gathered} {\gamma }_1·{\left(a^{\circ }\right)}^2+2{\alpha }_2^{\circ }{a}^{\circ }+{\gamma }_2={\alpha }_2^{\circ }·{\left(a^{\circ }\right)}^3+{\gamma }_2·{\left(a^{\circ }\right)}^2-{\alpha }_2^{\circ }{a}^{\circ }+2{\alpha }_2^{\circ }{a}^{\circ }+{\gamma }_2= \\ ={\alpha }_2^{\circ }·{\left(a^{\circ }\right)}^3+{\gamma }_2·{\left(a^{\circ }\right)}^2+{\alpha }_2^{\circ }{a}^{\circ }+{\gamma }_2={\alpha }_2^{\circ }{a}^{\circ }\left[{\left(a^{\circ }\right)}^2+1\right]+{\gamma }_2\left[{\left(a^{\circ }\right)}^2+1\right]= \\ =\left[{\left(a^{\circ }\right)}^2+1\right]\left({\alpha }_2^{\circ }{a}^{\circ }+{\gamma }_2\right)=\left[{\left(a^{\circ }\right)}^2+1\right]\left({\alpha }_2^{\circ }{a}^{\circ }+{\beta }_2+{\gamma }_1\right). \end{gathered}$$

Finally, taking into account (59), we have

$$\begin{gathered} {\displaystyle \frac{{\partial }^2{D}^2}{\partial a^2}}\left(a^{\circ },b^{\circ }\right)={\displaystyle \frac{4}{{\left[{\left(a^{\circ }\right)}^2+1\right]}^2}}\left[{\gamma }_1·{\left(a^{\circ }\right)}^2+2{\alpha }_2^{\circ }{a}^{\circ }+{\gamma }_2\right]= \\ ={\displaystyle \frac{4}{{\left(a^{\circ }\right)}^2+1}}\left({\alpha }_2^{\circ }{a}^{\circ }+{\beta }_2+{\gamma }_1\right)={\displaystyle \frac{4}{{\left(a^{\circ }\right)}^2+1}}\left[{\alpha }_2^{\circ }{a}^{\circ }+{\beta }_2+{\displaystyle \frac{1}{n}}{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)}^2\right] . \end{gathered}$$

(64)

Using (43), which is verified by $\left(a^{\circ },b^{\circ }\right)$ and (40), we obtain

$${\displaystyle \frac{{\partial }^2{D}^2}{\partial a\partial b}}\left(a^{\circ },b^{\circ }\right)={\displaystyle \frac{{\partial }^2{D}^2}{\partial b\partial a}}\left(a^{\circ },b^{\circ }\right)={\displaystyle \frac{4}{{\left(a^{\circ }\right)}^2+1}}{\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i .$$

(65)

From (41), we have

$${\displaystyle \frac{{\partial }^2{D}^2}{\partial b^2}}\left(a^{\circ },b^{\circ }\right)={\displaystyle \frac{4n}{{\left(a^{\circ }\right)}^2+1}} .$$

(66)

From (64)–(66), the Hessian matrix becomes

$$H_{D^2}^{\circ }\left(a^{\circ },b^{\circ }\right)={\displaystyle \frac{4}{{\left(a^{\circ }\right)}^2+1}}\left(\begin{array}{cc}{\alpha }_2^{\circ }{a}^{\circ }+{\beta }_2+{\displaystyle \frac{1}{n}}{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)}^2& {\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\\ {\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i& n\end{array}\right)={\displaystyle \frac{4}{{\left(a^{\circ }\right)}^2+1}}{K}_{D^2}^{\circ }\left(a^{\circ },b^{\circ }\right) .$$

We have

$$\begin{gathered} {\Delta }_1\left(a^{\circ },b^{\circ }\right)={\alpha }_2^{\circ }{a}^{\circ }+{\beta }_2+{\displaystyle \frac{1}{n}}{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)}^2 , \\ {\Delta }_2\left(a^{\circ },b^{\circ }\right)=\det \left(K_{D^2}^{\circ }\left(a^{\circ },b^{\circ }\right)\right)=n\left({\alpha }_2^{\circ }{a}^{\circ }+{\beta }_2\right). \end{gathered}$$

Since $a^{\circ }$ verifies Equation (52), we can write

$$\begin{gathered} {\alpha }_2^{\circ }·{\left(a^{\circ }\right)}^2+{\beta }_2{a}^{\circ }-{\alpha }_2^{\circ }=0 \\ \Rightarrow a^{\circ }\left({\alpha }_2^{\circ }{a}^{\circ }+{\beta }_2\right)={\alpha }_2^{\circ } \\ \Rightarrow {\alpha }_2^{\circ }{a}^{\circ }+{\beta }_2={\displaystyle \frac{{\alpha }_2^{\circ }}{a^{\circ }}} . \end{gathered}$$

Thus ${\Delta }_1\left(a^{\circ },b^{\circ }\right)$ and ${\Delta }_2\left(a^{\circ },b^{\circ }\right)$ are both strictly positive if and only if ${\alpha }_2^{\circ }$ and $a^{\circ }$ have the same sign.

If ${\alpha }_2^{\circ }<0$, Equation (52) has two distinct solutions, namely

$$a_{1,2}^{\circ }={\displaystyle \frac{-{\beta }_2\pm \sqrt{{\beta }_2^2+4{\left({\alpha }_2^{\circ }\right)}^2}}{2{\alpha }_2^{\circ }}} ,$$

from which only one is strictly negative.

If ${\alpha }_2^{\circ }<0$, let ${\widehat{a}}^{\circ }$ be the unique strictly negative solution of (52), namely

$${\widehat{a}}^{\circ }={\displaystyle \frac{-{\beta }_2+\sqrt{{\beta }_2^2+4{\left({\alpha }_2^{\circ }\right)}^2}}{2{\alpha }_2^{\circ }}} .$$

Thus,

$$\underset{\left(a,b\right)\in {ℝ}_{-}^{*}\times ℝ}{\min }{D}^2\left(a,b\right)=D^2\left({\widehat{a}}^{\circ },{\widehat{b}}^{\circ }\right) ,$$

where ${\widehat{b}}^{\circ }$ is obtained from (44) as

$${\widehat{b}}^{\circ }={\displaystyle \frac{1}{n}}\left[\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)-{\widehat{a}}^{\circ }\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)\right] .$$

If ${\alpha }_2^{\circ }=0$, Equation (52) has the solution $a^{\circ }=0$, which is not in ${ℝ}_{-}^{*}$. □

Proposition 9.

The following relation holds:

$${\alpha }_2^{\circ }<{\alpha }_2^{•}.$$

Proof. 

Using Formulas (20) and (53) from Proposition 7 and Proposition 8, respectively, we obtain

$$\begin{gathered} {\alpha }_2^{•}-{\alpha }_2^{\circ }=-{\displaystyle \frac{1}{n}}\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)+{\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i{g}_i+{\displaystyle \frac{1}{3}}{\displaystyle {\displaystyle \sum }_{i=1}^n}{\underset{\_}{f}}_i{\underset{\_}{g}}_i- \\ -\left[-{\displaystyle \frac{1}{n}}\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)+{\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i{g}_i-{\displaystyle \frac{1}{3}}{\displaystyle {\displaystyle \sum }_{i=1}^n}{\underset{\_}{f}}_i{\underset{\_}{g}}_i\right]={\displaystyle \frac{2}{3}}{\displaystyle {\displaystyle \sum }_{i=1}^n}{\underset{\_}{f}}_i{\underset{\_}{g}}_i . \end{gathered}$$

We obtain ${\alpha }_2^{•}-{\alpha }_2^{\circ }>0$, since ${\underset{\_}{f}}_i,{\underset{\_}{g}}_i\in \left(0,\infty \right)$ for all $i=\overline{1,n}$. □

Proposition 10.

If $a^{•}\in \left(0,\infty \right)$, then

$$D^2\left(a^{•},b^{•}\right)={\displaystyle \frac{2}{{\left(a^{•}\right)}^2+1}}\left[{\alpha }_3·{\left(a^{•}\right)}^2-2{\alpha }_2^{•}{a}^{•}+{\alpha }_3-{\beta }_2\right],$$

where

$${\alpha }_3={\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i^2-{\displaystyle \frac{1}{n}}{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)}^2+{\displaystyle \frac{1}{3}}{\displaystyle {\displaystyle \sum }_{i=1}^n}{{\underset{\_}{f}}_i}^2.$$

Proof. 

Using Proposition 5 together with relations (14) and (15), we obtain

$$\begin{gathered} D^2\left(a^{•},b^{•}\right)={\displaystyle \frac{2}{{\left(a^{•}\right)}^2+1}}{\displaystyle {\displaystyle \sum }_{i=1}^n}\left\{{\left[a^{•}{f}_i+\left(b-g_i\right)\right]}^2+{\displaystyle \frac{1}{3}}{\left(a^{•}{\underset{\_}{f}}_i-{\underset{\_}{g}}_i\right)}^2\right\}= \\ ={\displaystyle \frac{2}{{\left(a^{•}\right)}^2+1}}{\displaystyle {\displaystyle \sum }_{i=1}^n}\left[{\left(a^{•}\right)}^2{f}_i^2+{\left(b-g_i\right)}^2+2a^{•}{f}_i\left(b-g_i\right)+{\displaystyle \frac{1}{3}}{\left(a^{•}\right)}^2{{\underset{\_}{f}}_i}^2+{\displaystyle \frac{1}{3}}{{\underset{\_}{g}}_i}^2-{\displaystyle \frac{2}{3}}{a}^{•}{\underset{\_}{f}}_i{\underset{\_}{g}}_i\right]= \\ ={\displaystyle \frac{2}{{\left(a^{•}\right)}^2+1}}\left[{\left(a^{•}\right)}^2{\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i^2-{\displaystyle \frac{1}{n}}{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)}^2\right.+{\displaystyle \frac{1}{n}}{\left(a^{•}\right)}^2{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)}^2+{\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i^2+ \\ +{\displaystyle \frac{2a^{•}}{n}}\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)-{\displaystyle \frac{2{\left(a^{•}\right)}^2}{n}}{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)}^2-2a^{•}{\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i{g}_i+ \\ \left.+{\displaystyle \frac{1}{3}}{\left(a^{•}\right)}^2{\displaystyle {\displaystyle \sum }_{i=1}^n}{{\underset{\_}{f}}_i}^2+{\displaystyle \frac{1}{3}}{\displaystyle {\displaystyle \sum }_{i=1}^n}{{\underset{\_}{g}}_i}^2-{\displaystyle \frac{2}{3}}{a}^{•}{\displaystyle {\displaystyle \sum }_{i=1}^n}{\underset{\_}{f}}_i{\underset{\_}{g}}_i\right]= \\ ={\displaystyle \frac{2}{{\left(a^{•}\right)}^2+1}}\left\{{\left(a^{•}\right)}^2\left[{\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i^2-{\displaystyle \frac{1}{n}}{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)}^2+{\displaystyle \frac{1}{3}}{\displaystyle {\displaystyle \sum }_{i=1}^n}{{\underset{\_}{f}}_i}^2\right]-\right. \\ -2a^{•}\left[{\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i{g}_i+{\displaystyle \frac{1}{3}}{\displaystyle {\displaystyle \sum }_{i=1}^n}{\underset{\_}{f}}_i{\underset{\_}{g}}_i-{\displaystyle \frac{1}{n}}\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)\right]- \\ \left.-{\displaystyle \frac{1}{n}}{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)}^2+{\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i^2+{\displaystyle \frac{1}{3}}{\displaystyle {\displaystyle \sum }_{i=1}^n}{{\underset{\_}{g}}_i}^2\right\} \end{gathered}$$

 □

Proposition 11.

If $a^{\circ }\in \left(-\infty ,0\right)$ then

$$D^2\left(a^{\circ },b^{\circ }\right)={\displaystyle \frac{2}{{\left(a^{\circ }\right)}^2+1}}\left[{\alpha }_3·{\left(a^{\circ }\right)}^2-2{\alpha }_2^{\circ }{a}^{\circ }+{\alpha }_3-{\beta }_2\right].$$

Proof. 

Using Proposition 6 together with relations (47) and (48), we have

$$\begin{gathered} D^2\left(a^{\circ },b^{\circ }\right)={\displaystyle \frac{2}{{\left(a^{\circ }\right)}^2+1}}{\displaystyle {\displaystyle \sum }_{i=1}^n}\left[{\left(a^{\circ }{f}_i+b-g_i\right)}^2+{\displaystyle \frac{1}{3}}{\left(a^{\circ }{\underset{\_}{f}}_i+{\underset{\_}{g}}_i\right)}^2\right]= \\ ={\displaystyle \frac{2}{{\left(a^{\circ }\right)}^2+1}}{\displaystyle {\displaystyle \sum }_{i=1}^n}\left[{\left(a^{\circ }\right)}^2{f}_i^2+{\left(b-g_i\right)}^2+2a^{\circ }{f}_i\left(b-g_i\right)+{\displaystyle \frac{1}{3}}{\left(a^{\circ }\right)}^2{{\underset{\_}{f}}_i}^2+{\displaystyle \frac{1}{3}}{{\underset{\_}{g}}_i}^2+{\displaystyle \frac{2}{3}}{a}^{\circ }{\underset{\_}{f}}_i{\underset{\_}{g}}_i\right]= \\ ={\displaystyle \frac{2}{{\left(a^{\circ }\right)}^2+1}}\left[{\left(a^{\circ }\right)}^2{\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i^2-{\displaystyle \frac{1}{n}}{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)}^2\right.+{\displaystyle \frac{1}{n}}{\left(a^{\circ }\right)}^2{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)}^2+{\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i^2+ \\ +{\displaystyle \frac{2a^{\circ }}{n}}\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)-{\displaystyle \frac{2{\left(a^{\circ }\right)}^2}{n}}{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)}^2-2a^{\circ }{\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i{g}_i+ \\ \left.+{\displaystyle \frac{1}{3}}{\left(a^{\circ }\right)}^2{\displaystyle {\displaystyle \sum }_{i=1}^n}{{\underset{\_}{f}}_i}^2+{\displaystyle \frac{1}{3}}{\displaystyle {\displaystyle \sum }_{i=1}^n}{{\underset{\_}{g}}_i}^2+{\displaystyle \frac{2}{3}}{a}^{\circ }{\displaystyle {\displaystyle \sum }_{i=1}^n}{\underset{\_}{f}}_i{\underset{\_}{g}}_i\right]= \\ ={\displaystyle \frac{2}{{\left(a^{\circ }\right)}^2+1}}\left\{{\left(a^{\circ }\right)}^2\left[{\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i^2-{\displaystyle \frac{1}{n}}{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)}^2+{\displaystyle \frac{1}{3}}{\displaystyle {\displaystyle \sum }_{i=1}^n}{{\underset{\_}{f}}_i}^2\right]-\right. \\ -2a^{\circ }\left[{\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i{g}_i-{\displaystyle \frac{1}{3}}{\displaystyle {\displaystyle \sum }_{i=1}^n}{\underset{\_}{f}}_i{\underset{\_}{g}}_i-{\displaystyle \frac{1}{n}}\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)\right]- \\ \left.-{\displaystyle \frac{1}{n}}{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)}^2+{\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i^2+{\displaystyle \frac{1}{3}}{\displaystyle {\displaystyle \sum }_{i=1}^n}{{\underset{\_}{g}}_i}^2\right\} \end{gathered}$$

 □

4.3. Concluding Theoretical Discussion

In this part of the article, we analyze the possibilities that arise when solving the optimization problem

$$\underset{\left(a,b\right)\in {ℝ}^{*}\times ℝ}{\min }{D}^2\left(a,b\right),$$

which is stated at the beginning of Section 4.2.

In accordance with Proposition 9, the inequalities ${\alpha }_2^{•}<0$ and ${\alpha }_2^{\circ }>0$ cannot be simultaneously true. Moreover, ${\alpha }_2^{•}$ and ${\alpha }_2^{\circ }$ cannot be both equal to zero.

By considering Propositions 7–11, a structured theoretical discussion will have to include certain cases that are split into subcases. The division into cases is related to ${\beta }_2$ while the possibilities for ${\alpha }_2^{•}$ and ${\alpha }_2^{\circ }$ are studied in subcases.

Case 1.

Consider the situation in which ${\beta }_2\in ℝ-\left\{0\right\}$.

Subcase 1.1.

${\alpha }_2^{•}>0$, ${\alpha }_2^{\circ }>0$.

According to relation (53) and Proposition 9, the inequalities ${\alpha }_2^{•}>0$ and ${\alpha }_2^{\circ }>0$ are simultaneously true if and only if

$${\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i{g}_i-{\displaystyle \frac{1}{n}}\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)>{\displaystyle \frac{1}{3}}{\displaystyle {\displaystyle \sum }_{i=1}^n}{\underset{\_}{f}}_i{\underset{\_}{g}}_i.$$

Using Propositions 7 and 8, we can conclude that $\left({\widehat{a}}^{•},{\widehat{b}}^{•}\right)$ is the solution for the optimization problem, where $\left({\widehat{a}}^{•},{\widehat{b}}^{•}\right)$ is obtained in Proposition 7.

Subcase 1.2.

${\alpha }_2^{•}>0$, ${\alpha }_2^{\circ }=0$.

The relations ${\alpha }_2^{\circ }=0$ and ${\alpha }_2^{•}>0$ are simultaneously true if and only if

$${\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i{g}_i-{\displaystyle \frac{1}{n}}\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)={\displaystyle \frac{1}{3}}{\displaystyle {\displaystyle \sum }_{i=1}^n}{\underset{\_}{f}}_i{\underset{\_}{g}}_i.$$

Taking again into account Propositions 7 and 8, the solution is $\left({\widehat{a}}^{•},{\widehat{b}}^{•}\right)$.

Subcase 1.3.

${\alpha }_2^{•}>0$,${\alpha }_2^{\circ }<0$.

The inequalities ${\alpha }_2^{•}>0$ and ${\alpha }_2^{\circ }<0$ are simultaneously true if and only if

$$\left|{\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i{g}_i-{\displaystyle \frac{1}{n}}\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)\right|<{\displaystyle \frac{1}{3}}{\displaystyle {\displaystyle \sum }_{i=1}^n}{\underset{\_}{f}}_i{\underset{\_}{g}}_i.$$

We consider the pairs $\left({\widehat{a}}^{•},{\widehat{b}}^{•}\right)$ and $\left({\widehat{a}}^{\circ },{\widehat{b}}^{\circ }\right)$ from Proposition 7 and Proposition 8, respectively.

The solution is $\left({\widehat{a}}^{•},{\widehat{b}}^{•}\right)$ when $D^2\left({\widehat{a}}^{•},{\widehat{b}}^{•}\right)<D^2\left({\widehat{a}}^{\circ },{\widehat{b}}^{\circ }\right)$.

The solution is $\left({\widehat{a}}^{\circ },{\widehat{b}}^{\circ }\right)$ when $D^2\left({\widehat{a}}^{\circ },{\widehat{b}}^{\circ }\right)<D^2\left({\widehat{a}}^{•},{\widehat{b}}^{•}\right)$.

If there exists a set of data such that $D^2\left({\widehat{a}}^{•},{\widehat{b}}^{•}\right)=D^2\left({\widehat{a}}^{\circ },{\widehat{b}}^{\circ }\right)$, then both $\left({\widehat{a}}^{•},{\widehat{b}}^{•}\right)$ and $\left({\widehat{a}}^{\circ },{\widehat{b}}^{\circ }\right)$ can be taken as solutions.

Subcase 1.4.

${\alpha }_2^{•}=0$,${\alpha }_2^{\circ }<0.$

The relations ${\alpha }_2^{•}=0$ and ${\alpha }_2^{\circ }<0$ are simultaneously true if and only if

$${\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i{g}_i-{\displaystyle \frac{1}{n}}\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)=-{\displaystyle \frac{1}{3}}{\displaystyle {\displaystyle \sum }_{i=1}^n}{\underset{\_}{f}}_i{\underset{\_}{g}}_i.$$

Taking into account Propositions 7 and 8, the solution is $\left({\widehat{a}}^{\circ },{\widehat{b}}^{\circ }\right)$.

Subcase 1.5.

${\alpha }_2^{•}<0$, ${\alpha }_2^{\circ }<0$.

The inequalities ${\alpha }_2^{•}<0$ and ${\alpha }_2^{\circ }<0$ are simultaneously true if and only if

$${\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i{g}_i-{\displaystyle \frac{1}{n}}\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)<-{\displaystyle \frac{1}{3}}{\displaystyle {\displaystyle \sum }_{i=1}^n}{\underset{\_}{f}}_i{\underset{\_}{g}}_i.$$

According to Propositions 7 and 8, the solution is $\left({\widehat{a}}^{\circ },{\widehat{b}}^{\circ }\right)$.

Case 2.

Consider the situation in which ${\beta }_2=0$.

Subcase 2.1.

${\alpha }_2^{•}>0$, ${\alpha }_2^{\circ }>0$.

From relation

$${\widehat{a}}^{•}={\displaystyle \frac{-{\beta }_2+\sqrt{{\beta }_2^2+4{\left({\alpha }_2^{•}\right)}^2}}{2{\alpha }_2^{•}}},$$

which is given in Proposition 7, we obtain

$${\widehat{a}}^{•}=1.$$

We have

$$\begin{gathered} H_{D^2}^{•}\left(1,{\widehat{b}}^{•}\right)=2\left(\begin{array}{cc}{\alpha }_2^{•}+{\displaystyle \frac{1}{n}}{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)}^2& {\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\\ {\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i& n\end{array}\right)=2K_{D^2}^{•}\left(1,{\widehat{b}}^{•}\right), \\ {\Delta }_1\left(1,{\widehat{b}}^{•}\right)={\alpha }_2^{•}+{\displaystyle \frac{1}{n}}{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)}^2>0, \\ {\Delta }_2\left(1,{\widehat{b}}^{•}\right)=\det \left(K_{D^2}\left(1,{\widehat{b}}^{•}\right)\right)=n{\alpha }_2^{•}>0. \end{gathered}$$

From Proposition 10, we obtain

$$D^2\left(1,{\widehat{b}}^{•}\right)=2{\alpha }_3-2{\alpha }_2^{•}.$$

Since $a^{\circ }$ must be strictly negative, in Proposition 8 we retain the stationary point

$$\left(a^{\circ },b^{\circ }\right)=\left(-1,b^{\circ }\right).$$

Note that, in Proposition 8, the determinant ${\Delta }_2\left(-1,b^{\circ }\right)$ is strictly negative.

From Proposition 11, we obtain

$$D^2\left(-1,b^{\circ }\right)=2{\alpha }_3+2{\alpha }_2^{\circ }.$$

By using the inequalities ${\alpha }_2^{•}>0$ and ${\alpha }_2^{\circ }>0$ we can write

$$D^2\left(1,{\widehat{b}}^{•}\right)<D^2\left(-1,b^{\circ }\right).$$

In conclusion, the solution for the optimization problem is $\left({\widehat{a}}^{•},{\widehat{b}}^{•}\right)$, where

$${\widehat{a}}^{•}=1, {\widehat{b}}^{•}={\displaystyle \frac{1}{n}}\left[\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)-\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)\right].$$

Subcase 2.2.

${\alpha }_2^{•}>0$, ${\alpha }_2^{\circ }=0$.

As in Subcase 2.1, from Proposition 7 we have ${\widehat{a}}^{•}=1$.

From Proposition 10, we obtain

$$D^2\left(1,{\widehat{b}}^{•}\right)=2{\alpha }_3-2{\alpha }_2^{•} .$$

If $a^{\circ }\in \left(-\infty ,0\right)$, ${\alpha }_2^{\circ }=0$, ${\beta }_2=0$, from Proposition 11 we obtain

$$D^2\left(a^{\circ },b^{\circ }\right)={\displaystyle \frac{2}{{\left(a^{\circ }\right)}^2+1}}\left[{\alpha }_3·{\left(a^{\circ }\right)}^2+{\alpha }_3\right]=2{\alpha }_3.$$

We have

$$D^2\left(1,{\widehat{b}}^{•}\right)<D^2\left(a^{\circ },b^{\circ }\right)$$

and we can conclude that the solution is

$${\widehat{a}}^{•}=1, {\widehat{b}}^{•}={\displaystyle \frac{1}{n}}\left[\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)-\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)\right].$$

Subcase 2.3.

${\alpha }_2^{•}>0$, ${\alpha }_2^{\circ }<0.$

As in Subcase 2.1, we obtain ${\widehat{a}}^{•}=1$ and

$$D^2\left(1,{\widehat{b}}^{•}\right)=2{\alpha }_3-2{\alpha }_2^{•}.$$

Using the formula

$${\widehat{a}}^{\circ }={\displaystyle \frac{-{\beta }_2+\sqrt{{\beta }_2^2+4{\left({\alpha }_2^{\circ }\right)}^2}}{2{\alpha }_2^{\circ }}},$$

which is given in Proposition 8, we obtain ${\widehat{a}}^{\circ }=-1$.

We have

$$\begin{gathered} H_{D^2}^{\circ }\left(-1,{\widehat{b}}^{\circ }\right)=2\left(\begin{array}{cc}-{\alpha }_2^{\circ }+{\displaystyle \frac{1}{n}}{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)}^2& {\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\\ {\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i& n\end{array}\right)=2K_{D^2}^{\circ }\left(-1,{\widehat{b}}^{\circ }\right), \\ {\Delta }_1\left(-1,{\widehat{b}}^{\circ }\right)=-{\alpha }_2^{\circ }+{\displaystyle \frac{1}{n}}{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)}^2>0, \\ {\Delta }_2\left(-1,{\widehat{b}}^{\circ }\right)=\det \left(K_{D^2}^{\circ }\left(-1,{\widehat{b}}^{\circ }\right)\right)=-n{\alpha }_2^{\circ }>0. \end{gathered}$$

Using Proposition 11, we obtain

$$D^2\left(-1,{\widehat{b}}^{\circ }\right)=2{\alpha }_3+2{\alpha }_2^{\circ }.$$

We have

$$D^2\left(-1,{\widehat{b}}^{\circ }\right)-D^2\left(1,{\widehat{b}}^{•}\right)=2\left({\alpha }_2^{•}+{\alpha }_2^{\circ }\right)=2\left({\alpha }_2^{•}-\left|{\alpha }_2^{\circ }\right|\right).$$

If ${\alpha }_2^{•}-\left|{\alpha }_2^{\circ }\right|>0,$ we obtain $D^2\left(-1,{\widehat{b}}^{\circ }\right)>D^2\left(1,{\widehat{b}}^{•}\right)$ and the solution is

$${\widehat{a}}^{•}=1, {\widehat{b}}^{•}={\displaystyle \frac{1}{n}}\left[\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)-\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)\right].$$

If ${\alpha }_2^{•}-\left|{\alpha }_2^{\circ }\right|<0$, the solution is

$${\widehat{a}}^{\circ }=-1, {\widehat{b}}^{\circ }={\displaystyle \frac{1}{n}}\left[\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)+\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)\right].$$

If ${\alpha }_2^{•}=\left|{\alpha }_2^{\circ }\right|$, we obtain $D^2\left(-1,{\widehat{b}}^{\circ }\right)=D^2\left(1,{\widehat{b}}^{•}\right)$.

Subcase 2.4.

${\alpha }_2^{•}=0$, ${\alpha }_2^{\circ }<0.$

As in Subcase 2.3, from Proposition 8 we obtain ${\widehat{a}}^{\circ }=-1$.

From Proposition 11, we have

$$D^2\left(-1,{\widehat{b}}^{\circ }\right)=2{\alpha }_3+2{\alpha }_2^{\circ }.$$

If $a^{•}\in \left(0,\infty \right)$, from Proposition 10 we obtain

$$D^2\left(a^{•},b^{•}\right)={\displaystyle \frac{2}{{\left(a^{•}\right)}^2+1}}\left[{\alpha }_3·{\left(a^{•}\right)}^2+{\alpha }_3\right]=2{\alpha }_3.$$

We have

$$D^2\left(-1,{\widehat{b}}^{\circ }\right)<D^2\left(a^{•},b^{•}\right).$$

The solution is

$${\widehat{a}}^{\circ }=-1, {\widehat{b}}^{\circ }={\displaystyle \frac{1}{n}}\left[\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)+\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)\right].$$

Subcase 2.5.

${\alpha }_2^{•}<0$, ${\alpha }_2^{\circ }<0$.

From Proposition 8, we obtain ${\widehat{a}}^{\circ }=-1$.

We have

$$D^2\left(-1,{\widehat{b}}^{\circ }\right)=2{\alpha }_3+2{\alpha }_2^{\circ }.$$

Using Proposition 7, we retain the stationary point $\left(a^{•},b^{•}\right)=\left(1,b\right)$. Note that, in Proposition 7, the determinant ${\Delta }_2\left(1,b^{•}\right)$ is strictly negative.

From Proposition 10, we have

$$D^2\left(1,b^{•}\right)=2{\alpha }_3-2{\alpha }_2^{•}.$$

We obtain

$$D^2\left(-1,{\widehat{b}}^{\circ }\right)<D^2\left(1,b^{•}\right).$$

The solution is $\left({\widehat{a}}^{\circ },{\widehat{b}}^{\circ }\right)$, where

$${\widehat{a}}^{\circ }=-1, {\widehat{b}}^{\circ }={\displaystyle \frac{1}{n}}\left[\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)+\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)\right].$$

4.4. The Final Form of the Algorithm

Consider the following formulas:

$$\begin{gathered} {\alpha }_2^{•}={\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i{g}_i-{\displaystyle \frac{1}{n}}\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)+{\displaystyle \frac{1}{3}}{\displaystyle {\displaystyle \sum }_{i=1}^n}{\underset{\_}{f}}_i{\underset{\_}{g}}_i , \\ {\alpha }_2^{\circ }={\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i{g}_i-{\displaystyle \frac{1}{n}}\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)-{\displaystyle \frac{1}{3}}{\displaystyle {\displaystyle \sum }_{i=1}^n}{\underset{\_}{f}}_i{\underset{\_}{g}}_i , \\ {\alpha }_3={\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i^2-{\displaystyle \frac{1}{n}}{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)}^2+{\displaystyle \frac{1}{3}}{\displaystyle {\displaystyle \sum }_{i=1}^n}{{\underset{\_}{f}}_i}^2, \\ {\beta }_2={\displaystyle {\displaystyle \sum }_{i=1}^n}\left(f_i^2-g_i^2\right)+{\displaystyle \frac{1}{n}}\left[{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)}^2-{\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)}^2\right]+{\displaystyle \frac{1}{3}}{\displaystyle {\displaystyle \sum }_{i=1}^n}\left({{\underset{\_}{f}}_i}^2-{{\underset{\_}{g}}_i}^2\right), \\ {\widehat{a}}^{•}={\displaystyle \frac{-{\beta }_2+\sqrt{{\beta }_2^2+4{\left({\alpha }_2^{•}\right)}^2}}{2{\alpha }_2^{•}}},{\widehat{b}}^{•}={\displaystyle \frac{1}{n}}\left[\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)-{\widehat{a}}^{•}\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)\right], \\ {\widehat{a}}^{\circ }={\displaystyle \frac{-{\beta }_2+\sqrt{{\beta }_2^2+4{\left({\alpha }_2^{\circ }\right)}^2}}{2{\alpha }_2^{\circ }}},{\widehat{b}}^{\circ }={\displaystyle \frac{1}{n}}\left[\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{g}_i\right)-{\widehat{a}}^{\circ }\left({\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_i\right)\right], \\ {D}^2\left({\widehat{a}}^{•},{\widehat{b}}^{•}\right)={\displaystyle \frac{2}{{\left({\widehat{a}}^{•}\right)}^2+1}}\left[{\alpha }_3·{\left({\widehat{a}}^{•}\right)}^2-2{\alpha }_2^{•}{\widehat{a}}^{•}+{\alpha }_3-{\beta }_2\right], \\ {D}^2\left({\widehat{a}}^{\circ },{\widehat{b}}^{\circ }\right)={\displaystyle \frac{2}{{\left({\widehat{a}}^{\circ }\right)}^2+1}}\left[{\alpha }_3·{\left({\widehat{a}}^{\circ }\right)}^2-2{\alpha }_2^{\circ }{\widehat{a}}^{\circ }+{\alpha }_3-{\beta }_2\right] \end{gathered}$$

The results obtained in the paper can be summarized as follows.

• ${\beta }_2\in ℝ-\left\{0\right\}$;

  1.1

  $0<{\alpha }_2^{\circ }<{\alpha }_2^{•}$. The solution is $\left({\widehat{a}}^{•},{\widehat{b}}^{•}\right)$.

  1.2

  $0={\alpha }_2^{\circ }<{\alpha }_2^{•}$. The solution is $\left({\widehat{a}}^{•},{\widehat{b}}^{•}\right)$.

  1.3

  ${\alpha }_2^{\circ }<0<{\alpha }_2^{•}$;

  1.3.1.

  $D^2\left({\widehat{a}}^{•},{\widehat{b}}^{•}\right)<D^2\left({\widehat{a}}^{\circ },{\widehat{b}}^{\circ }\right)$. The solution is $\left({\widehat{a}}^{•},{\widehat{b}}^{•}\right)$.

  1.3.2.

  $D^2\left({\widehat{a}}^{•},{\widehat{b}}^{•}\right)=D^2\left({\widehat{a}}^{\circ },{\widehat{b}}^{\circ }\right)$. The solutions are: $\left({\widehat{a}}^{•},{\widehat{b}}^{•}\right)$, $\left({\widehat{a}}^{\circ },{\widehat{b}}^{\circ }\right)$.

  1.3.3.

  $D^2\left({\widehat{a}}^{•},{\widehat{b}}^{•}\right)>D^2\left({\widehat{a}}^{\circ },{\widehat{b}}^{\circ }\right)$. The solution is $\left({\widehat{a}}^{\circ },{\widehat{b}}^{\circ }\right)$.

  1.4

  ${\alpha }_2^{\circ }<{\alpha }_2^{•}=0$. The solution is $\left({\widehat{a}}^{\circ },{\widehat{b}}^{\circ }\right)$.

  1.5

  ${\alpha }_2^{\circ }<{\alpha }_2^{•}<0$. The solution is $\left({\widehat{a}}^{\circ },{\widehat{b}}^{\circ }\right)$.

• ${\beta }_2=0$;

  2.1

  $0<{\alpha }_2^{\circ }<{\alpha }_2^{•}$. The solution is $\left(1,{\widehat{b}}^{•}\right)$.

  2.2.

  $0={\alpha }_2^{\circ }<{\alpha }_2^{•}$. The solution is $\left(1,{\widehat{b}}^{•}\right)$.

  2.3.

  ${\alpha }_2^{\circ }<0<{\alpha }_2^{•}$;

  2.3.1.

  $\left|{\alpha }_2^{\circ }\right|<{\alpha }_2^{•}$. The solution is $\left(1,{\widehat{b}}^{•}\right)$.

  2.3.2.

  $\left|{\alpha }_2^{\circ }\right|={\alpha }_2^{•}$. The solutions are: $\left(1,{\widehat{b}}^{•}\right)$, $\left(-1,{\widehat{b}}^{\circ }\right)$.

  2.3.3.

  $\left|{\alpha }_2^{\circ }\right|>{\alpha }_2^{•}$. The solution is $\left(-1,{\widehat{b}}^{\circ }\right)$.

  2.4.

  ${\alpha }_2^{\circ }<{\alpha }_2^{•}=0$. The solution is $\left(-1,{\widehat{b}}^{\circ }\right)$.

  2.5.

  ${\alpha }_2^{\circ }<{\alpha }_2^{•}<0$. The solution is $\left(-1,{\widehat{b}}^{\circ }\right)$.

5. Numerical Examples

In this section, we consider some numerical examples.

Example 1.

Let $\left({\tilde{F}}_i,{\tilde{G}}_i\right)$, $i=\overline{1,3}$, be pairs of symmetric triangular fuzzy numbers, where ${\tilde{F}}_1=\left(3,2,2\right)$, ${\tilde{F}}_2=\left(5,1,1\right)$, ${\tilde{F}}_3=\left(12,3,3\right)$, ${\tilde{G}}_1=\left(2,1,1\right)$, ${\tilde{G}}_2=\left(9,3,3\right)$, ${\tilde{G}}_3=\left(7,4,4\right)$. We organize some of the calculations in Table A1; see Appendix B. Using the formulas from Section 4.4, we obtain ${\alpha }_2^{•}=20.66667$, ${\alpha }_2^{\circ }=9.33333$, ${\alpha }_3=49.33333$ and ${\beta }_2=14.66667$. Therefore, we have ${\widehat{a}}^{•}=0.70625$, ${\widehat{b}}^{•}=1.29166$ and ${\widehat{a}}^{\circ }=0.48603$, ${\widehat{b}}^{\circ }=2.75976$. This example fits in Subcase 1.1. The solution is $\left({\widehat{a}}^{•},{\widehat{b}}^{•}\right)=\left(0.70625,1.29166\right)$. We can write the relation

$$\tilde{Y}=0.70625\tilde{X}+1.29166.$$

Thus, we have

$$\tilde{\mathit{L}}=\left\{\left(\tilde{X},\tilde{Y}\right)\left|\tilde{Y}=0.70625\tilde{X}+1.29166\right.\right\}$$

Moreover, we obtain $D^2\left({\widehat{a}}^{•},{\widehat{b}}^{•}\right)=40.14164$.

Fuzzy numbers can be characterized using certain crisp values, one of which is the possibilistic mean value [41]. The possibilistic mean value of a symmetric triangular fuzzy number $\tilde{X}=\left(x,\underset{\_}{x},\underset{\_}{x}\right)$ is $\overline{M}\left(\tilde{X}\right)=x$; see [41]. Therefore, for ${\tilde{F}}_i=\left(f_i,{\underset{\_}{f}}_i,{\underset{\_}{f}}_i\right)$ and ${\tilde{G}}_i=\left(g_i,{\underset{\_}{g}}_i,{\underset{\_}{g}}_i\right)$, we have $\overline{M}\left({\tilde{F}}_i\right)=f_i$ and $\overline{M}\left({\tilde{G}}_i\right)=g_i$, $i=\overline{1,3}$.

Various graphical representations are used in works that study fuzzy numbers. In [42], a pair of fuzzy interval numbers is described using a rectangle. In [43], a fuzzy number is represented by a line segment. More precisely, in [43] the output values of a regression model are triangular fuzzy numbers that are represented by vertical line segments. Graphical representations related to the topic of fuzzy regression can also be found in [44,45,46].

Instead of a rectangle, we use a schematic representation formed by two intersecting line segments. We consider an arbitrary pair $\left({\tilde{F}}_i,{\tilde{G}}_i\right)$, where ${\tilde{F}}_i=\left(f_i,{\underset{\_}{f}}_i,{\underset{\_}{f}}_i\right)$, ${\tilde{G}}_i=\left(g_i,{\underset{\_}{g}}_i,{\underset{\_}{g}}_i\right)$, $i=\overline{1,3}$.

In the plane ${ℝ}^2$, we choose a closed horizontal line segment and a closed vertical line segment, as follows. The horizontal line segment has the endpoints $\left(f_i-{\underset{\_}{f}}_i,g_i\right)$ and $\left(f_i+{\underset{\_}{f}}_i,g_i\right)$. The vertical line segment has the endpoints $\left(f_i,g_i-{\underset{\_}{g}}_i\right)$ and $\left(f_i,g_i+{\underset{\_}{g}}_i\right)$.

The pair $\left({\tilde{F}}_i,{\tilde{G}}_i\right)$ can be represented by the geometric shape formed by these two segments. Notably, the horizontal line segment and the vertical line segment intersect at point $\left(\overline{M}\left({\tilde{F}}_i\right),\overline{M}\left({\tilde{G}}_i\right)\right)$.

In the plane ${ℝ}^2$, we consider the line

$$\mathit{L}=\left\{\left(x,y\right)\in {ℝ}^2\left|y={\widehat{a}}^{•}x+{\widehat{b}}^{•}\right.\right\}.$$

If $\left(\tilde{F},\tilde{G}\right)\in \tilde{\mathit{L}}$, where $\tilde{F}=\left(f,\underset{\_}{f},\overline{f}\right)$, $\tilde{G}=\left(g,\underset{\_}{g},\overline{g}\right)$, then $\left(f,g\right)\in \mathit{L}$. On the other hand, there are pairs $\left(\tilde{F},\tilde{G}\right)$ such that $\left(f,g\right)\in \mathit{L}$ and $\left(\tilde{F},\tilde{G}\right)\notin \tilde{\mathit{L}}$.

Figure 1 shows the line $\mathit{L}$ and the representations of the pairs $\left({\tilde{F}}_i,{\tilde{G}}_i\right)$, $i=\overline{1,3}$.

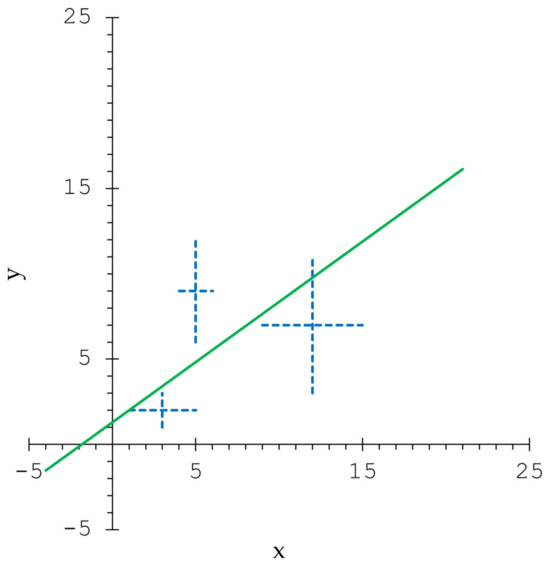
Figure 1. The line $\mathit{L}$ and the representations of the pairs $\left({\tilde{F}}_i,{\tilde{G}}_i\right)$, $i=\overline{1,3}$.

In [11] it is emphasized that the regression relationship does not change even if the roles of the real variables are reversed. To see if this also happens in the case of symmetric triangular fuzzy variables, we consider the pairs $\left({\tilde{G}}_i,{\tilde{F}}_i\right)$, $i=\overline{1,3}$. We use again the results from Section 4.4. After reversing the roles of the fuzzy variables, it can be seen that ${\alpha }_2^{•}$ and ${\alpha }_2^{\circ }$ do not change their values, and ${\beta }_2$ only changes its sign. As in the case of regression for real numbers, we can obtain the relation

$$\tilde{X}={\displaystyle \frac{1}{{\widehat{a}}^{•}}}\tilde{Y}+{\displaystyle \frac{1}{n}}\left[\left({\displaystyle {\displaystyle \sum }_{i=1}^3}{f}_i\right)-{\displaystyle \frac{1}{{\widehat{a}}^{•}}}\left({\displaystyle {\displaystyle \sum }_{i=1}^3}{g}_i\right)\right] ,$$

that is

$$\tilde{Y}={\widehat{a}}^{•}\tilde{X}+{\displaystyle \frac{1}{n}}\left[\left({\displaystyle {\displaystyle \sum }_{i=1}^3}{g}_i\right)-{\widehat{a}}^{•}\left({\displaystyle {\displaystyle \sum }_{i=1}^3}{f}_i\right)\right]$$

or

$$\tilde{Y}={\widehat{a}}^{•}\tilde{X}+{\widehat{b}}^{•}.$$

Just like in the model for real data, the regression relation actually remains unchanged if the roles of the fuzzy variables are reversed. This kind of reasoning also works in the other theoretical subcases.

Example 2.

Let $\left({\tilde{F}}_i,{\tilde{G}}_i\right)$, $i=\overline{1,4}$, be pairs of symmetric triangular fuzzy numbers, where ${\tilde{F}}_1=\left(5,3,3\right)$, ${\tilde{F}}_2=\left(10,25,25\right)$, ${\tilde{F}}_3=\left(14,8,8\right)$, ${\tilde{F}}_4=\left(19,4,4\right)$, ${\tilde{G}}_1=\left(3,1,1\right)$, ${\tilde{G}}_2=\left(12,8,8\right)$, ${\tilde{G}}_3=\left(13,30,30\right)$, ${\tilde{G}}_4=\left(21,7,7\right)$. Using Table A2 from Appendix B, we have ${\alpha }_2^{•}=285$, ${\alpha }_2^{\circ }=-29$, ${\alpha }_3=344$, ${\beta }_2=-156.75$. Therefore ${\widehat{a}}^{•}=1.31212$, ${\widehat{b}}^{•}=-3.49548$ and ${\widehat{a}}^{\circ }=-5.58425$, ${\widehat{b}}^{\circ }=79.26097$. We obtain $D^2\left({\widehat{a}}^{•},{\widehat{b}}^{•}\right)=253.5896$ and $D^2\left({\widehat{a}}^{\circ },{\widehat{b}}^{\circ }\right)=677.6136$. This example corresponds to Subcase 1.3. We obtain the solution $\left({\widehat{a}}^{•},{\widehat{b}}^{•}\right)=\left(1.31212,-3.49548\right)$.

Example 3.

Let $\left({\tilde{F}}_i,{\tilde{G}}_i\right)$, $i=\overline{1,3}$, be pairs of symmetric triangular fuzzy numbers, where ${\tilde{F}}_1=\left(2,4,4\right)$, ${\tilde{F}}_2=\left(4,3,3\right)$, ${\tilde{F}}_3=\left(5,5,5\right)$, ${\tilde{G}}_1=\left(3,2,2\right)$, ${\tilde{G}}_2=\left(6,1,1\right)$, ${\tilde{G}}_3=\left({\displaystyle \frac{9}{4}},\sqrt{{\displaystyle \frac{283}{8}}},\sqrt{{\displaystyle \frac{283}{8}}}\right)$. Using Table A3 from Appendix B, we obtain ${\alpha }_2^{•}={\displaystyle \frac{11+5\sqrt{35.375}}{3}}$, ${\alpha }_2^{\circ }=-{\displaystyle \frac{11+5\sqrt{35.375}}{3}}$, ${\alpha }_3={\displaystyle \frac{64}{3}}$, ${\beta }_2=0$. Thus we have ${\widehat{a}}^{•}=1$, ${\widehat{b}}^{•}={\displaystyle \frac{1}{12}}$ and ${\widehat{a}}^{\circ }=-1$, ${\widehat{b}}^{\circ }={\displaystyle \frac{89}{12}}$. Further, we obtain $D^2\left({\widehat{a}}^{•},{\widehat{b}}^{•}\right)=D^2\left({\widehat{a}}^{\circ },{\widehat{b}}^{\circ }\right)=15.5077$. This example falls into Subcase 2.3, when the relation $\left|{\alpha }_2^{\circ }\right|={\alpha }_2^{•}$ is true.

In the plane ${ℝ}^2$, we consider the lines

$${\mathit{L}}_{\mathbf{1}}=\left\{\left(x,y\right)\left|y={\widehat{a}}^{•}x+{\widehat{b}}^{•}\right.\right\},$$

$${\mathit{L}}_{\mathbf{2}}=\left\{\left(x,y\right)\left|y={\widehat{a}}^{\circ }x+{\widehat{b}}^{\circ }\right.\right\}.$$

Figure 2 shows the lines ${\mathit{L}}_{\mathbf{1}}$, ${\mathit{L}}_{\mathbf{2}}$ and the representations of the pairs $\left({\tilde{F}}_i,{\tilde{G}}_i\right)$, $i=\overline{1,3}$.

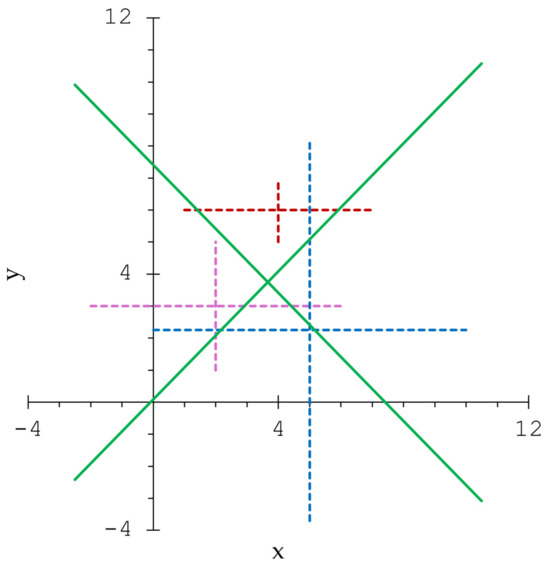
Figure 2. The lines ${\mathit{L}}_{\mathbf{1}}$, ${\mathit{L}}_{\mathbf{2}}$ and the representations of the pairs $\left({\tilde{F}}_i,{\tilde{G}}_i\right)$, $i=\overline{1,3}$.

Example 4.

Let $\left({\tilde{F}}_i,{\tilde{G}}_i\right)$, $i=\overline{1,3}$, be pairs of symmetric triangular fuzzy numbers, where ${\tilde{F}}_1=\left(3,2,2\right)$, ${\tilde{F}}_2=\left(5,1,1\right)$, ${\tilde{F}}_3=\left(12,3,3\right)$, ${\tilde{G}}_1=\left(2,8,8\right)$, ${\tilde{G}}_2=\left(9,2,2\right)$, ${\tilde{G}}_3=\left(7,9,9\right)$. Some intermediate calculations are given in Table A4, Appendix B. We obtain ${\alpha }_2^{•}=30$, ${\alpha }_2^{\circ }=0$, ${\alpha }_3=49.33333$, ${\beta }_2=-26.33333$. Therefore, we have ${\widehat{a}}^{•}=1.53096$, ${\widehat{b}}^{•}=-4.20641$. This example illustrates Subcase 1.2. The solution is $\left({\widehat{a}}^{•},{\widehat{b}}^{•}\right)=\left(1.53096,-4.20641\right)$, for which $D^2\left({\widehat{a}}^{•},{\widehat{b}}^{•}\right)=59.47562$.

6. Discussion

In the broad field of regression analysis, this paper falls into the area of methods that use fuzzy numbers. In this article, the method of total least squares is adapted for symmetric triangular fuzzy numbers. Triangular fuzzy numbers are often used in the literature. Moreover, if $\mathit{X}\left(\alpha \right)=\left[\underset{\_}{X}\left(\alpha \right),\overline{X}\left(\alpha \right)\right]$ is the $\alpha$-cut of a triangular fuzzy number, then the functions $\underset{\_}{X}\left(\alpha \right)$ and $\overline{X}\left(\alpha \right)$ are defined on the compact interval $\left[0,1\right]$ and have certain properties that are highlighted in [39]. In the regression model for real numbers, the regression relationship does not change, even if the roles of the variables are reversed [11,47]. We remark that this phenomenon also occurs in the case of the method for fuzzy data: the same regression relationship is obtained regardless of whether the data $\left({\tilde{F}}_i,{\tilde{G}}_i\right)$, $i=\overline{1,n}$, or the data $\left({\tilde{G}}_i,{\tilde{F}}_i\right)$, $i=\overline{1,n}$, are considered. So, from this point of view, the results obtained in this paper are consistent with results from previous works.

In [39], the least squares method for fuzzy data is discussed. Considering what was discussed there, in this article the total least squares method for symmetric triangular fuzzy variables is approached. At the same time, this paper finds its place next to other works, such as [23,25,37], which study the use of regression in a framework marked by uncertainty.

7. Conclusions

The total least squares algorithm is a useful tool in the field of regression. In this paper, the total least squares method is used for an optimization model in which the data are modeled as symmetric triangular fuzzy numbers. In this way, the scope of the total least squares algorithm is widened from applications that use real data to applications that take into account the uncertainty described by fuzzy numbers. This paper contains general theoretical results, discussions on some particular cases and the systematic presentation of the steps of the final algorithm, and in this way it tries to offer a comprehensive work on the considered topic. To test the theoretical results, some numerical examples are discussed.