Computing the Matrix G of Multi-Dimensional Markov Chains of M/G/1 Type

Abstract

We consider Md-M/G/1 processes, which are irreducible discrete-time Markov chains consisting of two components. The first component is a nonnegative integer vector, while the second component indicates the state (or phase) of the external environment. The level of a state is defined by the minimum value in its first component. The matrix G of the process represents the conditional probabilities that, starting from a given state of a certain level, the Markov chain will first reach a lower level in a specific state. This study aims to develop an effective algorithm for computing matrices $G$ for Md-M/G/1 processes.

1. Introduction

Multi-dimensional Markov chains of M/G/1 type (Md-M/G/1) are the natural extensions of the classical Markov chains of M/G/1 type [1,2]. They are discrete-time Markov processes with state space $X={\mathbb{Z}}_{+}^M\times J$, where ${\mathbb{Z}}_{+}$ is the set of nonnegative integers and $J=\{1,2,\dots ,n\}$ [3,4,5,6]. The number $n$ of the elements in the set $J$ can be finite or infinite. The probability of transition from a state $(k,i)$ with $k\ge 1$ to states $(n,j)$ may depend on $i,j$, and $n-k$ but not on the specific values of $k$ and $n.$ The one-step transitions of Md-M/G/1 processes from a state $(k,i)$ are limited to states $(n,j)$ such that $k-n\le 1,$ where the vector $1$ consists of all 1s. Md-QBD processes are a specific type of multi-dimensional Markov chain of M/G/1 type, where one-step transitions from $(k,i)$ to states $(n,j)$ are allowed only if $-1\le k-n\le 1$ [3,5,6,7]. Md-M/G/1 processes are Markov chains of M/G/1 type with the level $l$ consisting of states $(k_1,k_2,\dots ,k_M,j)$, for which condition $\min k_m=l$ holds.

The matrix $G$ is a key characteristic of Markov chains of M/G/1 type. Each element of this matrix represents the conditional probabilities that, starting from a specific state at a given level, the process will first appear at a lower level in a particular state. It has been shown in [8] that the matrix $G$ can be expressed in terms of matrices of order $n$, called the sector exit probabilities. A system of equations was created for these matrices, and an algorithm to find its minimal nonnegative solution was proposed.

For the Md-M/G/1 processes, the concept of the state sectors has been introduced in [8]. It has been shown that the matrix $G$ can be expressed in terms of matrices of order $n$ representing the sector exit probabilities. A system of equations was developed for these matrices, and an algorithm for solving it was proposed. However, it remains unclear whether the set of matrices of sector exit probabilities constitutes the minimal nonnegative solution to this system.

This study builds upon the work presented in [8]. We demonstrate that the family of matrices representing the sector exit probabilities is the minimal nonnegative solution to the system established in [8]. Additionally, we introduce a new iterative algorithm for computing blocks of order $n$ of the matrix $G$. Section 2 reviews the relevant results obtained in [8]. Section 3 focuses on the joint distribution of the sector exit times and the number of sectors crossed. Section 4 establishes the minimality property of the matrices of the sector exit probabilities. In Section 5, we introduce our new iterative algorithm for computing the matrix $G.$ Finally, Section 6 presents our concluding remarks.

We use bold capital letters to denote matrices and bold lowercase letters to denote vectors. Unless otherwise stated, all vectors in this paper have integer components and the length $M$. For any vector $x$, we use the notation $x_i$ for the $i\mathrm{th}$ component of $x$. For vectors $x=(x_1,x_2,\dots ,x_M)$ and $y=(y_1,y_2,\dots ,y_M)$, $x\ge y$ means that $x_j\ge y_j$ for all $j$, and $x\le y$ means that $x_j\le y_j$ for all $j$. Functions $\mathcal{l}(x)$ and $\mathsf{\Delta }(x)$ are defined, respectively, as $\mathcal{l}(x)=\min x_m$ and $\mathsf{\Delta }(x)=x-\mathcal{l}(x)1$. Given a vector $w\ge 1$, we define sets $Z(w),$$X(w)$ and $X^c(w)$ as $Z(w)=\{n\in Z_{+}^N|n\ge w\}$, $X(w)=Z(w)\times J$, and $X^c(w)=X\backslash X(w)$. We refer to the sets of the form $X(w)$ as the sectors.

2. Multi-Dimensional Process of M/G/1 Type

Let $\xi (t)=(\alpha (t),\beta (t))$ be an irreducible multi-dimensional Markov chain of M/G/1 type on the state space $X={\mathbb{Z}}_{+}^M\times J$, and $p_{k,n}(i,j)$ denote the probability of a one-step transition from $(k,i)$ to $(n,j)$. We assume that the transition probability matrix $P$, partitioned into blocks $P_{k,n}=[p_{k,n}(i,j)]$ ($i,j\in J)$, for all $k\ge 1$, satisfies the following properties:

$$P_{k,n}=\left\{\begin{array}{cc}{Q}_{n-k},& k-n\le 1,\\ O,& \mathrm{otherwise},\end{array}\right.$$

(1)

where $Q_r=[q_r(i,j)]$ $(i,j\in J)$, $r\ge -1$, are nonnegative square matrices such that $Q={\displaystyle {\sum }_{r\ge -1}{Q}_r}$ is a stochastic matrix. Process $\xi (t)$ is the Markov chain of M/G/1 type, with the level $l$ consisting of states $(n,j)$ such that $\min n_i=l$. We refer to this process as an M-dimensional Markov chain of M/G/1 type $(M\mathrm{d}-\mathrm{M}/\mathrm{G}/1)$.

The level $l$ of a multi-dimensional process of M/G/1 type consists of states $(n,j)$ such that $\min n_i=l$. For instance, consider the state space $X$ of a $2\mathrm{d}-\mathrm{M}/\mathrm{G}/1$ process, which is divided into subsets $\left\{k\right\}\times J$, $k\in {\mathbb{Z}}_{+}^2$, as illustrated in Figure 1. Solid lines represent the boundaries of the process levels. The states of the sector $X(3,1)$ belong to the gray-colored subsets.

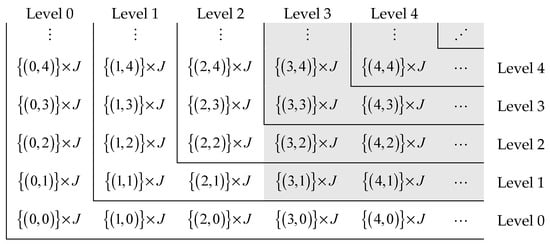
Figure 1. The levels and sector $X(3,1)$ of a 2d-M/G/1 process.

The transition matrix of a multi-dimensional Markov chain of M/G/1 type has a block Hessenberg form

$$P=\left[\begin{array}{lllll}{B}_0\hfill & B_1\hfill & B_2\hfill & B_3\hfill & \cdots \hfill \\ A_{-1}\hfill & A_0\hfill & A_1\hfill & A_2\hfill & \ddots \hfill \\ O\hfill & A_{-1}\hfill & A_0\hfill & A_1\hfill & \ddots \hfill \\ O\hfill & O\hfill & A_{-1}\hfill & A_0\hfill & \ddots \hfill \\ ⋮\hfill & \ddots \hfill & \ddots \hfill & \ddots \hfill & \ddots \hfill \end{array}\right]$$

(2)

where blocks $B_k$ and $A_k$ are nonnegative square matrices, such that ${\displaystyle {\sum }_{k=0}^{\infty }{B}_k}$ and ${\displaystyle {\sum }_{k=-1}^{\infty }{A}_k}$ are stochastic matrices. Each state $(n,j)$ of a level $l$ can be characterized by the triple $(l,\alpha ,j)$, where $\alpha =n-l1$ is an element of the set $\mathcal{N}$ defined as

$$\mathcal{N}=\{({\alpha }_1,\dots ,{\alpha }_M)\in {\mathbb{Z}}_{+}^M|\min {\alpha }_m=0\}.$$

Hence, entries of the matrices $B_k$ and $A_k$ can be indexed by the elements of the set $\mathcal{N}\times J$. As it follows from (1), the matrices $A_k$, partitioned into blocks $A_{k,\alpha ,\beta }=[a_k((\alpha ,i),(\beta ,j))]$ $(i,j\in J)$ of order $n$, can be represented as

$$A_{k,\alpha ,\beta }=Q_{\beta -\alpha +k1}, \alpha ,\beta \in \mathcal{N}, k\ge -1.$$

For any level $l\ge 1$, the entry $g((\alpha ,i),(\beta ,j))$ of the matrix $G$ represents the probability that, starting from the state $(\alpha +l1,i)$ of the level $l$, the chain will first appear at the level $l-1$ in state $(\beta +(l-1)1,j)$. The matrix $G$ is the minimal nonnegative solution to the equation ([1])

$$G={\displaystyle \sum _{v=0}^{\infty }{A}_{v-1}{G}^v}$$

(3)

Equation (3) can be transformed into the following system for the blocks $G_{\alpha ,\beta }=[g((\alpha ,i),(\beta ,j))]$ $(i,j\in J)$ of the matrix $G$:

$$G_{\alpha ,\beta }=Q_{\beta -\alpha -1}+{\displaystyle \sum _{\delta \in \mathcal{N}}{Q}_{\delta -\alpha }}{G}_{\delta ,\beta }+{\displaystyle \sum _{l=1}^{\infty }{\displaystyle \sum _{\delta \in \mathcal{N}}{Q}_{\delta +l1-\alpha }}}$$

$${\displaystyle \sum _{{\gamma }_1,\dots ,{\gamma }_l\in \mathcal{N}}{G}_{\delta ,{\gamma }_1}{G}_{{\gamma }_1,{\gamma }_2}\dots G_{{\gamma }_{l-1},{\gamma }_l}{G}_{{\gamma }_l,\beta }}, \alpha ,\beta \in \mathcal{N}.$$

(4)

Let the set $\mathit{\epsilon }$ be defined as

$$\mathit{\epsilon }=\{\beta \in {\mathbb{Z}}_{+}^M|\min {\beta }_m=-1\}.$$

(5)

For any vectors $w\ge 1$ and $\beta \in \mathit{\epsilon }$, the entry $f_{\beta }(i,j)$ of the matrix of the sector exit probabilities $F_{\beta }$ represents the probability that, starting in the state $(w,i)$, the process $\xi (t)$ reaches the set $X^c(w)$ by hitting the state $(w+\beta ,j)$ ([8]). It implies that the matrix $F={\displaystyle {\sum }_{\beta \in \mathit{\epsilon }}{F}_{\beta }}$ is substochastic.

The family of matrices $F_{\beta }$, $\beta \in \mathit{\epsilon }$, and the matrix $G$ uniquely define each other, since we have the following equalities

$$F_{\beta }=G_{0,\beta +1}, \beta \in \mathit{\epsilon },$$

(6)

$$G_{\alpha ,\beta }={\displaystyle \sum _{v=1}^{\infty }{\displaystyle \sum _{({\epsilon }_1,\dots ,{\epsilon }_v)\in {\mathrm{E}}_{\alpha ,\beta -1}^{(v)}}{F}_{{\epsilon }_1}{F}_{{\epsilon }_2}\cdots F_{{\epsilon }_v}}}, \alpha ,\beta \in \mathcal{N},$$

(7)

where ${\mathrm{E}}_{\alpha ,\gamma }^{(v)}$ is the set of all v−tuples $({\epsilon }_1,\dots ,{\epsilon }_v)\in {\mathit{\epsilon }}^v$ satisfying $\alpha +{\epsilon }_1\ge 0,$ $\alpha +{\epsilon }_1+{\epsilon }_2\ge 0,$…, $\alpha +{\epsilon }_1+\dots +{\epsilon }_{v-1}\ge 0$, $\alpha +{\epsilon }_1+\dots +{\epsilon }_v=\gamma$.

As shown in [8], the matrices $F_{\beta }$, $\beta \in \mathit{\epsilon }$, satisfy the following system:

$$F_{\beta }=Q_{\beta }+{\displaystyle \sum _{\alpha \ge 0}{Q}_{\alpha }}{\displaystyle \sum _{v=1}^{\infty }{\displaystyle \sum _{({\epsilon }_1,\dots ,{\epsilon }_v)\in {\mathrm{E}}_{\alpha ,\beta }^{(v)}}{F}_{{\epsilon }_1}{F}_{{\epsilon }_2}\cdots F_{{\epsilon }_v}}}, \beta \in \mathit{\epsilon }.$$

(8)

We will demonstrate that the family $F_{\beta }$, $\beta \in \mathit{\epsilon }$, is the minimal nonnegative solution to the system (8) in the set of families $Y_{\beta }$, $\beta \in \mathit{\epsilon }$, of nonnegative matrices.

3. The Joint Distribution of the Sector Exit Times and the Number of Sectors Crossed

Let us define the sequence of passage times as follows:

$${\theta }_0=0,{\theta }_{k+1}=\min \{t>{\theta }_k|\xi (t)\in X^c(\alpha ({\theta }_k)\},k\ge 0.$$

We say that at time $t$, the process $\xi (t)=(\alpha (t),\beta (t))$ is in the sector $X(r)$ if conditions ${\theta }_k\le t<{\theta }_{k+1}$ and $\alpha ({\theta }_k)=r$ are met. The difference ${\sigma }_k={\theta }_{k+1}-{\theta }_k$ represents the time the process spends in the sector $X(\alpha ({\theta }_k)\}$. We define the sector $X(w)$ exit time as the moment ${\tau }_w$ when the process leaves the sector $X(w)$,

$${\tau }_w=\min \{t\ge 0|\xi (t)\in X^c(w)\}.$$

Additionally, we define the number of sectors visited along a path to $X^c(w)$ as

$${\kappa }_w=\max \{k\ge 0|{\theta }_k\le {\tau }_w\}.$$

If an initial state $\xi (0)$ of the process belongs to $X^c(w)$, then we have ${\tau }_w=0$ and ${\kappa }_w=0$. If $\xi (0)=(k,i)$ with $k\ge w$, then at the first hitting time of $X^c(w)$, the process exits the sector $X(\alpha ({\theta }_{{\kappa }_w-1}))$ and enters the sector $X(\alpha ({\theta }_{{\kappa }_w}))$, which implies equality ${\tau }_w={\theta }_{{\kappa }_w}$. The set $X^c(w)$ is reached at the moment of transition from the set $X_0(\alpha ({\theta }_{{\kappa }_w-1}))\cap X_0(w)$ to the state $\xi ({\theta }_{{\kappa }_w})\in X_{-1}(\alpha ({\theta }_{{\kappa }_w-1}))\cap X_{-1}(w)$.

For vectors $w\ge 1$, $k\in X(w)$, and $n\in X^c(w)$, we define matrices ${\Phi }_{k,n}^{(v)}(w)=[{\phi }_{(k,i),(r,j)}^{(v)}(w)]$ $(i,j\in J)$, ${\Phi }_{k,n}(w)=[{\phi }_{(k,i),(n,j)}(w)]$ $(i,j\in J)$, ${\overline{\Phi }}_{k,n}^{(s,v)}(w)=[{\overline{\phi }}_{(k,i),(r,j)}^{(s,v)}(w)]$ $(i,j\in J)$, and ${\overline{\Phi }}_{k,n}^{(s)}(w)=[{\overline{\phi }}_{(k,i),(n,j)}^{(s)}(w)]$ $(i,j\in J)$ as follows.

The element ${\phi }_{(k,i),(n,j)}^{(v)}(w)$ of the matrix ${\Phi }_{k,n}^{(v)}(w)$ is the conditional probability that the process $\xi (t)$, starting in the state $(k,i)\in X(w)$, reaches the set $X^c(w)$ by hitting the state $(n,j)$ after passing through exactly $v$ sectors,

$${\phi }_{(k,i),(n,j)}^{(v)}(w)=\mathbb{P}\{{\kappa }_w=v,\xi ({\theta }_{{\kappa }_w})=(n,j)|\xi (0)=(k,i)\}$$

$$=\mathbb{P}\{{\kappa }_w=v,\xi ({\tau }_w)=(n,j)|\xi (0)=(k,i)\} .$$

(9)

The element ${\phi }_{(k,i),(n,j)}(w)$ of the matrix ${\Phi }_{k,n}(w)$ is the conditional probability that the process $\xi (t)$ will eventually hit the set $X^c(w)$ in the state $(n,j)$, given that it starts in the state $(k,i)$,

$${\phi }_{(k,i),(n,j)}(w)=\mathbb{P}\{{\kappa }_w<\infty ,\xi ({\theta }_{{\kappa }_w})=(n,j)|\xi (0)=(k,i)\}$$

$$=\mathbb{P}\{{\tau }_w<\infty ,\xi ({\tau }_w)=(n,j)|\xi (0)=(k,i)\} .$$

(10)

The element ${\overline{\phi }}_{(k,i),(r,j)}^{(s,v)}(w)$ of the matrix ${\overline{\Phi }}_{k,n}^{(s,v)}(w)$ is the conditional probability that the process $\xi (t)$, starting in the state $(k,i)\in X(w)$, reaches the set $X^c(w)$ by hitting the state $(n,j)$ after no more than $s$ transition steps, and passing through exactly $v$ sectors,

$${\overline{\phi }}_{(k,i),(n,j)}^{(s,v)}(w)=\mathbb{P}\{{\kappa }_w=v,{\theta }_{{\kappa }_w}\le s,\xi ({\theta }_{{\kappa }_w})=(n,j)|\xi (0)=(k,i)\}$$

$$=\mathbb{P}\{{\kappa }_w=v,{\tau }_w\le s,\xi ({\tau }_w)=(n,j)|\xi (0)=(k,i)\} .$$

(11)

The element ${\overline{\phi }}_{(k,i),(n,j)}^{(s)}(w)$ of the matrix ${\overline{\Phi }}_{k,n}^{(s)}(w)$ is the conditional probability that the process $\xi (t)$ will hit the set $X^c(w)$ in the state $(n,j)$ after no more than $s$ transition steps, given that it starts in the state $(k,i)$,

$${\overline{\phi }}_{(k,i),(n,j)}^{(s)}(w)=\mathbb{P}\{{\theta }_{{\kappa }_w}\le s,\xi ({\theta }_{{\kappa }_w})=(n,j)|\xi (0)=(k,i)\}$$

$$=\mathbb{P}\{{\tau }_w\le s,\xi ({\tau }_w)=(n,j)|\xi (0)=(k,i)\} .$$

(12)

It is easy to see that the matrices ${\Phi }_{k,n}(w)$, ${\Phi }_{k,n}^{(v)}(w)$, ${\overline{\Phi }}_{k,n}^{(s)}(w)$, and ${\overline{\Phi }}_{k,n}^{(s,v)}(w)$ satisfy the following relations

$${\Phi }_{k,n}(w)={\displaystyle \sum _{v=1}^{\infty }{\Phi }_{k,n}^{(v)}(w)}, {\overline{\Phi }}_{k,n}^{(s)}(w)={\displaystyle \sum _{v=1}^{\infty }{\overline{\Phi }}_{k,n}^{(s,v)}(w)},$$

(13)

$$\underset{s\to \infty }{\lim }{\overline{\Phi }}_{k,n}^{(s,v)}(w)={\Phi }_{k,n}^{(v)}(w), \underset{s\to \infty }{\lim }{\overline{\Phi }}_{k,n}^{(s)}(w)={\Phi }_{k,n}(w).$$

(14)

For each $l\ge 0$, any path of $\xi (t)$ leading from a state $(k,i)\in X_l(w)$ to a state $(n,j)\in X^c(w)$ must successively visit sets $X_{l-1}(w),X_{l-2}(w),\dots ,X_0(w),X_{-1}(w)$, which will require visiting at least $l+1$ sectors. Therefore, we have

$${\Phi }_{k,n}^{(v)}(w)=O$$

(15)

for all $k\in Z_l(w)$, $n\in Z_{-1}(w)$, and $v\le l$. Additionally, it is impossible to visit $v$ sectors without taking at least $v$ transition steps, which implies that

$${\overline{\Phi }}_{k,n}^{(s,v)}(w)=O,$$

(16)

for all $k\in Z_l(w)$, $n\in Z_{-1}(w)$, and $s<v\le l$.

The transition probabilities away from the boundary are spatially homogeneous, indicating that for any vector $k\ge w\ge 1$ and any vector $n\in Z_{-1}(w)$, the probabilities ${\phi }_{(k,i),(n,j)}(w)$ may depend on $i,j,$ $k-w$, and $n-w$, but not on the specific values of $k$, $n$ and $w$, i.e.,

$${\Phi }_{k,n}(w)={\Phi }_{k-w+1,n-w+1}(1), {\overline{\Phi }}_{k,n}^{(s)}(w)={\overline{\Phi }}_{k-w+1,n-w+1}^{(s)}(1).$$

This means that the matrices ${\Phi }_{k,n}(w)$ and ${\overline{\Phi }}_{k,n}^{(s)}(w)$ may be expressed as

$${\Phi }_{k,n}(w)={\Psi }_{k-w,n-w}, {\overline{\Phi }}_{k,n}^{(s)}(w)={\overline{\Psi }}_{k-w,n-w}^{(s).}$$

Here, for vectors $\alpha \ge 0$ and $\beta \in \mathit{\epsilon }$, the matrices ${\Psi }_{\alpha ,\beta }=[{\psi }_{(\alpha ,i),(\beta ,j)}]$ $(i,j\in J)$ and ${\overline{\Psi }}_{\alpha ,\beta }^{(s)}=[{\overline{\psi }}_{(\alpha ,i),(\beta ,j)}^{(s)}]$ $(i,j\in J)$ are defined as

$${\Psi }_{\alpha ,\beta }={\Phi }_{w+\alpha ,w+\beta }(w), {\overline{\Psi }}_{\alpha ,\beta }^{(s)}={\overline{\Phi }}_{w+\alpha ,w+\beta }^{(s)}(w)$$

(17)

independently of the vector $w\ge 1$. Vectors $\alpha$ and $\beta$ in (17) satisfy conditions $w+\alpha \ge w$ and $w+\beta \in Z_{-1}(w)$. Therefore, the index $\alpha$ of matrices ${\Psi }_{\alpha ,\beta }$ and ${\overline{\Psi }}_{\alpha ,\beta }^{(s)}$ is a nonnegative vector and its index $\beta$ belongs to the set $\mathit{\epsilon }$. We refer to the matrices ${\Psi }_{\alpha ,\beta }$ as the matrices of the first passage probabilities.

It was demonstrated in [8] that for all $\alpha \ge 0$ and $\beta \in \mathit{\epsilon }$, the matrices ${\Psi }_{\alpha ,\beta }$ satisfy the system

$${\Psi }_{\alpha ,\beta }=Q_{\beta -\alpha }+{\displaystyle \sum _{\gamma \ge 0}{Q}_{\gamma -\alpha }}{\Psi }_{\gamma ,\beta }.$$

In the next theorem, we obtain a similar property for the matrices ${\overline{\Psi }}_{\alpha ,\beta }^{(s)}$.

Theorem 1.

The matrices ${\overline{\Psi }}_{\alpha ,\beta }^{(s)}$ satisfy the system

$${\overline{\Psi }}_{\alpha ,\beta }^{(1)}=Q_{\beta -\alpha }, {\overline{\Psi }}_{\alpha ,\beta }^{(s)}=Q_{\beta -\alpha }+{\displaystyle \sum _{\gamma \ge 0}{Q}_{\gamma -\alpha }}{\overline{\Psi }}_{\gamma ,\beta }^{(s-1)}, s\ge 2, \alpha \ge 0,\beta \in \mathit{\epsilon }.$$

(18)

Proof of Theorem 1.

We will initially demonstrate the validity of the following formulae for all values of $k\in Z(w)$ and $n\in Z_{-1}(w)$:

$${\overline{\Phi }}_{k,n}^{(1)}(w)=P_{k,n}, {\overline{\Phi }}_{k,n}^{(s)}(w)=P_{k,n}+{\displaystyle \sum _{r\ge w}{P}_{k,r}}{\overline{\Phi }}_{k,n}^{(s-1)}(w), s\ge 2.$$

(19)

The first formula, in (19), is straightforward. The second formula adheres to the law of total probability, accounting for all possible process states following the first transition. Consider two states: $(k,i)\in X(w)$ and $(n,j)\in X_{-1}(w)$. The state $(n,j)$ can be reached from the state $(k,i)$ after a single transition, which contributes the term $P_{k,n}$ to the second formula in (19). Additionally, the first transition can lead the process to some state $(r,j)$ with $r\ge w$. To reach the set $X_{-1}(w)$ from state $(r,j)$, the process $\xi (t)$ must necessarily hit the state $(n,j)\in X_{-1}(w)$ within no more than $s-1$ transition steps. This contributes to the second term on the right-hand side of (19). Equation (18) for the matrices ${\overline{\Psi }}_{\alpha ,\beta }$ is derived from (19) using Formulas (1) and (17). □

4. Minimality Property of the Sector Exit Probabilities

Matrices of the sector exit probabilities were defined in [8] as the $F_{\beta }={\Psi }_{0,\beta }$, $\beta \in \mathit{\epsilon }$. Entries of the matrix $F_{\beta }=[f_{\beta }(i,j)]$ $(i,j\in J)$ determine the transition probabilities of the embedded Markov chain $\xi ({\theta }_k)$, since for $k\ge 1$, we have

$$\mathbb{P}\{{\theta }_k<\infty ,\xi ({\theta }_k)=(n,j)|\xi ({\theta }_{k-1})=(k,i)\}$$

$$=\mathbb{P}\{{\tau }_k<\infty ,\xi ({\tau }_k)=(n,j)|\xi (0)=(k,i)\}=f_{n-k}(i,j).$$

(20)

We define matrices $F_{\beta }^{(s)}=[f_{\beta }^{(s)}(i,j)]$ $(i,j\in J)$, $\beta \in \mathit{\epsilon }$, as $F_{\beta }^{(s)}={\overline{\Psi }}_{0,\beta }^{(s)}$. These matrices determine the transition probabilities of the Markov process $(\xi ({\theta }_k),{\sigma }_k)$ as

$$\mathbb{P}\{\xi ({\theta }_k)=(n,j),{\sigma }_k\le s|\xi ({\theta }_{k-1})=(k,i)\}$$

$$=\mathbb{P}\{{\tau }_k\le s,\xi ({\tau }_k)=(n,j)|\xi (0)=(k,i)\}=f_{n-k}^{(s)}(i,j)$$

(21)

for all $k\ge 1$ and $s=1,2,\dots$. From (20) and (21), it follows that the matrices $F_{\beta }$ and $F_{\beta }^{(s)}$ are related as

$$\underset{s\to \infty }{\lim }{F}_{\beta }^{(s)}=F_{\beta }, \beta \in \mathit{\epsilon }.$$

(22)

As a direct consequence of Theorem 1, we can derive the following property of the matrices $F_{\beta }^{(s)}={\overline{\Psi }}_{0,\beta }^{(s)}$:

$$F_{\beta }^{(1)}=Q_{\beta }, F_{\beta }^{(s)}=Q_{\beta }+{\displaystyle \sum _{\gamma \ge 0}{Q}_{\gamma }}{\overline{\Psi }}_{\gamma ,\beta }^{(s-1)}, \mathrm{for} s\ge 2\mathrm{and} \beta \in \mathit{\epsilon }.$$

(23)

Neuts has demonstrated in [1] that in one-dimensional cases—when the equality $G=F_{-1}$ holds—the matrix $G$ is the minimal nonnegative solution of (3). We will show that similar results are also held in multi-dimensional cases. The proof is based on inequalities that we will derive in Lemma 1.

Lemma 1.

The matrices $F_{\beta }^{(s)}$ satisfy the following inequalities

$$F_{\beta }^{(s)}\le Q_{\beta }+{\displaystyle \sum _{\gamma \ge 0}{Q}_{\alpha }}{\displaystyle \sum _{v=1}^{\infty }{\displaystyle \sum _{({\epsilon }_1,\dots ,{\epsilon }_v)\in {\mathrm{E}}_{\gamma ,\beta }^{(v)}}{F}_{{\epsilon }_1}^{(s-1)}{F}_{{\epsilon }_2}^{(s-1)}\cdots F_{{\epsilon }_v}^{(s-1)}}}, s\ge 2, \beta \in \mathit{\epsilon }.$$

(24)

Proof of Lemma 1.

For any vectors $w\ge 1$, $(k,i)\in X(w)$, and $(n,j)\in X^c(w)$, the element ${\overline{\phi }}_{(k,i),(r,j)}^{(s,v)}(w)$ of the matrix ${\overline{\Phi }}_{k,n}^{(s,v)}(w)$ is the conditional probability that the process $\xi (t)$, starting in the state $(k,i)$, reaches the set $X^c(w)$ by hitting the state $(n,j)$ after no more than $s$ transition steps and passing through exactly $v$ sectors. To hit the set $X^c(w)$, starting in a state $(k,i)\in X(w)$ and passing through exactly one sector is only possible if that single crossed sector is the set $X(k)$. Therefore, we have the equalities

$${\overline{\Phi }}_{k,n}^{(s,1)}(w)={\overline{\Phi }}_{k,n}^{(s,1)}(k)={\overline{F}}_{n-k}^{(s)}, s\ge 1.$$

(25)

Let the sets ${\mathrm{T}}_{k,n}^{(u)}(w)$ be defined as the set of all $u-$ tuples $(r_1,\dots ,r_u)\in Z{(w)}^u$ satisfying $r_1\in Z_{-1}(k)$, $r_2\in Z_{-1}(r_1)$,…, $r_u\in Z_{-1}(r_{u-1})$, $n\in Z_{-1}(r_u)$. Hitting the set $X^c(w)$ after no more than $s$ transition steps is only possible if the total number of steps taken in the crossed sectors does not exceed $s$. It implies the following inequality

$${\overline{\Phi }}_{k,n}^{(s,v)}(w)={\displaystyle \sum _{(r_1,\dots ,r_{v-1})\in {\mathrm{T}}_{k,n}^{(v-1)}(w)}{\displaystyle \sum _{\begin{array}{c}{s}_1,\dots ,s_v\ge 1\\ s_1+\dots +s_v\le s\end{array}}{\overline{\Phi }}_{k,r_1}^{(s_1,1)}(k)}}{\overline{\Phi }}_{r_1,r_2}^{(s_2,1)}(r_1)\cdots {\overline{\Phi }}_{r_{v-2},r_{v-1}}^{(s_{v-1},1)}(r_{v-2}){\overline{\Phi }}_{r_{v-1},n}^{(s_v,1)}(r_{v-1})$$

$$\le {\displaystyle \sum _{(r_1,\dots ,r_{v-1})\in {\mathrm{T}}_{k,n}^{(v-1)}(w)}{\displaystyle \sum _{1\le s_1\le s}\cdots {\displaystyle \sum _{1\le s_v\le s}{\overline{\Phi }}_{k,r_1}^{(s_1,1)}(k){\overline{\Phi }}_{r_1,r_2}^{(s_2,1)}(r_1)\cdots {\overline{\Phi }}_{r_{v-2},r_{v-1}}^{(s_{v-1},1)}}(r_{v-2}){\overline{\Phi }}_{r_{v-1},n}^{(s_v,1)}(r_{v-1})}}$$

$$={\displaystyle \sum _{(r_1,\dots ,r_{v-1})\in {\mathrm{T}}_{k,n}^{(v-1)}(w)}{\overline{\Phi }}_{k,r_1}^{(s,1)}{\overline{\Phi }}_{r_1,r_2}^{(s,1)}(r_1)\cdots {\overline{\Phi }}_{r_{v-2},r_{v-1}}^{(s,1)}(r_{v-2}){\overline{\Phi }}_{r_{v-1},n}^{(s,1)}(r_{v-1})}$$

$$={\displaystyle \sum _{(r_1,\dots ,r_{v-1})\in {\mathrm{T}}_{k,n}^{(v-1)}(w)}{F}_{r_1-k}^{(s)}{F}_{r_2-r_1}^{(s)}\cdots F_{r_{v-1}-r_{v-2}}^{(s)}{F}_{n-r_{v-1}}^{(s)}}.$$

(26)

Let us introduce, in (26), new variables $\gamma =k-w\ge 0$, $\beta =n-w\in \mathit{\epsilon }$, ${\epsilon }_1=r_1-k$, ${\epsilon }_2=r_2-r_1$, …, ${\epsilon }_{v-1}=r_{v-1}-r_{v-2},$ ${\epsilon }_v=n-r_{v-1}$. Since $(r_1,\dots ,r_{v-1})\in T_{k,n}^{(v-1)}(w)$, it is clear that the v-tuple (${\epsilon }_1,\dots ,{\epsilon }_v$) belongs to the set ${\mathrm{E}}_{\gamma ,\beta }^{(v)}$. Using these variables and Formula (17), we can obtain from (26) the inequality

$${\overline{\Psi }}_{\gamma ,\beta }^{(s)}\le {\displaystyle \sum _{v=1}^{\infty }{\displaystyle \sum _{({\epsilon }_1,\dots ,{\epsilon }_v)\in {\mathrm{E}}_{\gamma ,\beta }^{(v)}}{F}_{{\epsilon }_1}^{(s)}{F}_{{\epsilon }_2}^{(s)}\cdots F_{{\epsilon }_v}^{(s)}}}.$$

(27)

The statement of Lemma 1 follows from (23) and (27). □

Let matrices $X_{\beta }(k)$, $\beta \in \mathit{\epsilon }$, $k\ge 1$, be defined as

$$X_{\beta }(1)=Q_{\beta },$$

(28)

$$X_{\beta }(k+1)=Q_{\beta }+{\displaystyle \sum _{\alpha \ge 0}{Q}_{\alpha }}{\displaystyle \sum _{v=1}^{\infty }{\displaystyle \sum _{({\epsilon }_1,\dots ,{\epsilon }_v)\in {\mathrm{E}}_{\alpha ,\beta }^{(v)}}{X}_{{\epsilon }_1}(k)\cdots X_{{\epsilon }_v}}(k)}, k\ge 1.$$

(29)

It has been shown in [8] that for each $\beta \in \mathit{\epsilon }$, the sequence $X_{\beta }(k)$, $k\ge 1$, entry-wise monotonically converges to matrix $X_{\beta }$. The family of matrices $X_{\beta },$ $\beta \in \mathit{\epsilon }$, is the minimal solution of system (8) in the set of families $Y_{\beta }$, $\beta \in \mathit{\epsilon }$, of nonnegative matrices. In the following theorem, we will demonstrate that the equality $X_{\beta }=F_{\beta }$ holds for all $\beta \in \mathit{\epsilon }$.

Theorem 2.

The family of matrices of the sector exit probabilities $F_{\beta }$, $\beta \in \mathit{\epsilon }$, is the minimal solution of the system (8) in the set of families of nonnegative matrices $Y_{\beta }$, $\beta \in \mathit{\epsilon }$. For each $\beta \in \mathit{\epsilon }$, the sequence $X_{\beta }(k)$, $k\ge 1$, entry-wise monotonically converges to matrix $F_{\beta }$.

Proof of Theorem 2.

At first, we prove by induction that matrices $X_{\beta }(k)$ defined by (28)–(29) satisfy $X_{\beta }(k)\ge F_{\beta }^{(k)}$ for all $\beta \in \mathit{\epsilon }$ and for all $k\ge 1$. Since $X_{\beta }(1)=Q_{\beta }$ and $F_{\beta }^{(1)}=Q_{\beta }$, we know that $X_{\beta }(1)\ge F_{\beta }^{(1)}$. Let us assume that $X_{\beta }(k)\ge F_{\beta }^{(k)}$ for some $k$ and for all $\beta \in \mathit{\epsilon }.$ Then, using (29), we obtain

$$X_{\beta }(k+1)=Q_{\beta }+{\displaystyle \sum _{\alpha \ge 0}{Q}_{\alpha }}{\displaystyle \sum _{v=1}^{\infty }{\displaystyle \sum _{({\epsilon }_1,\dots ,{\epsilon }_v)\in {\mathrm{E}}_{\alpha ,\beta }^{(v)}}{X}_{{\epsilon }_1}(k)\cdots X_{{\epsilon }_v}}(k)}$$

$$\ge Q_{\beta }+{\displaystyle \sum _{\alpha \ge 0}{Q}_{\alpha }}{\displaystyle \sum _{v=1}^{\infty }{\displaystyle \sum _{({\epsilon }_1,\dots ,{\epsilon }_v)\in {\mathrm{E}}_{\alpha ,\beta }^{(v)}}{F}_{{\epsilon }_1}^{(k)}{F}_{{\epsilon }_3}^{(k)}\cdots F_{{\epsilon }_v}^{(k)}}}\ge F_{\beta }^{(k+1)},$$

(30)

which proves the induction step. The sequence $X_{\beta }(k)$, $k\ge 1$, entry-wise monotonically converges to matrix $X_{\beta }$ and the sequence $F_{\beta }^{(k)}$, $k\ge 1$, converges to matrix $F_{\beta }$ [8]. This implies the following inequalities for limiting matrices $X_{\beta }$ and $F_{\beta }$:

$$X_{\beta }=\underset{k\to \infty }{\lim }{X}_{\beta }(k)\ge \underset{k\to \infty }{\lim }{F}_{\beta }^{(k)}=F_{\beta }, \beta \in \mathit{\epsilon }.$$

Since both families $X_{\beta }$, $\beta \in \mathit{\epsilon }$, and $F_{\beta }$, $\beta \in \mathit{\epsilon }$, are solutions of the system (8), and the family $X_{\beta },$ $\beta \in \mathit{\epsilon }$, is the minimal nonnegative solution of (8), and the inequalities $X_{\beta }\ge F_{\beta }$ hold for all $\beta \in \mathit{\epsilon },$ we necessarily have equality $X_{\beta }=F_{\beta }$ for all $\beta \in \mathit{\epsilon }$. □

5. Computing the Matrix G

Any vector $\alpha \in {\mathbb{Z}}_{+}^M$ can be represented as $\alpha =\delta +k1$, where $\delta =\mathsf{\Delta }(\alpha )$ and $k=\mathcal{l}(\alpha ).$ It was shown in [8] that the matrices of the first passage probabilities possess the following properties

$${\Psi }_{\alpha ,\epsilon }={\displaystyle \sum _{v=1}^{\infty }{\displaystyle \sum _{({\epsilon }_1,\dots ,{\epsilon }_v)\in {\mathrm{E}}_{\alpha ,\epsilon }^{(v)}}{F}_{{\epsilon }_1}{F}_{{\epsilon }_2}\cdots F_{{\epsilon }_v}}}, \alpha \in {\mathbb{Z}}_{+}^M, \epsilon \in \mathit{\epsilon },$$

(31)

$${\Psi }_{\delta +k1,\epsilon }={\displaystyle \sum _{{\gamma }_1,\dots ,{\gamma }_k\in \mathcal{N}}{\Psi }_{\delta ,{\gamma }_1-1}{\Psi }_{{\gamma }_1,{\gamma }_2-1}\dots {\Psi }_{{\gamma }_{k-1},{\gamma }_k-1}{\Psi }_{{\gamma }_k,\epsilon }}, \delta \in \mathcal{N}, \epsilon \in \mathit{\epsilon }, k\ge 1.$$

(32)

In Theorem 3 we show that decomposition (32) is a special case of more general results for nonnegative matrices of the form (31).

Theorem 3.

Let $Y_{\epsilon }$, $\epsilon \ge -1$, be a family of nonnegative matrices such that $Y_{\epsilon }=O$ for all $\epsilon \notin \mathit{\epsilon },$ and let each entry of the matrix series

$$Z_{\alpha ,\beta }={\displaystyle \sum _{v=1}^{\infty }{\displaystyle \sum _{{\epsilon }_1,\dots ,{\epsilon }_v\in {\mathrm{E}}_{\alpha ,\beta -1}^{(v)}}{Y}_{{\epsilon }_1}{Y}_{{\epsilon }_2}\cdots Y_{{\epsilon }_v}}}, \alpha \in {\mathbb{Z}}_{+}^M, \beta \in \mathcal{N},$$

(33)

be convergent. Then, matrices $Z_{\alpha ,\beta }$ satisfy the following system

$$Z_{\alpha ,\beta }=Y_{\beta -\alpha -1}+{\displaystyle \sum _{\begin{array}{c}\epsilon \in \mathit{\epsilon }\\ \mathcal{l}(\alpha +\epsilon )=0\end{array}}{Y}_{\epsilon }}{Z}_{\alpha +\epsilon ,\beta }+{\displaystyle \sum _{i=1}^{\infty }{\displaystyle \sum _{\begin{array}{c}\epsilon \in \mathit{\epsilon }\\ \mathcal{l}(\alpha +\epsilon )=i\end{array}}{Y}_{\epsilon }}}$$

$${\displaystyle \sum _{{\gamma }_1,\dots ,{\gamma }_i\in \mathcal{N}}{Z}_{\alpha +\epsilon ,{\gamma }_1-1}{Z}_{{\gamma }_1,{\gamma }_2-1}}\cdots Z_{{\gamma }_{i-1},{\gamma }_i-1}{Z}_{{\gamma }_i,\beta }, \alpha \in {\mathbb{Z}}_{+}^M, \beta \in \mathcal{N}.$$

(34)

For each vector $\alpha \in {\mathbb{Z}}_{+}^M$ such that $\mathcal{l}(\alpha )\ge 1$,  matrices $Z_{\alpha ,\beta }$, $\beta \in \mathcal{N}$, can be decomposed as

$$Z_{\alpha ,\beta }={\displaystyle \sum _{{\gamma }_1,\dots ,{\gamma }_{\mathcal{l}(\alpha )}\in \mathcal{N}}{Z}_{\mathsf{\Delta }(\alpha ),{\gamma }_1}{Z}_{{\gamma }_1,{\gamma }_2}\dots Z_{{\gamma }_{\mathcal{l}(\alpha )-1},{\gamma }_{\mathcal{l}(\alpha )}}{Z}_{{\gamma }_{\mathcal{l}(\alpha )},\beta }}$$

(35)

Proof of Theorem 3.

It was shown in [7] (Lemma 1), that for $\delta ,\beta \in \mathcal{N}$ and $k\ge 1$, the sets ${\mathrm{E}}_{\delta +k1,\beta -1}^{(v)}$, $v\ge 1,$ can be decomposed in terms of the cartesian products of sets ${\mathrm{E}}_{\gamma ,\epsilon }^{(u)}$, $\gamma \in \mathcal{N}$, $\epsilon \in \mathit{\epsilon },$ as

$${\mathrm{E}}_{\delta +k1,\beta -1}^{(v)}={\displaystyle \underset{\begin{array}{c}{u}_1,\dots ,u_{k+1}\ge 1\\ u_1+\dots +u_{k+1}=v\end{array}}{\cup } {\displaystyle \underset{{\gamma }_1,\dots ,{\gamma }_k\in \mathcal{N}}{\cup }{\mathrm{E}}_{\delta ,{\gamma }_1-1}^{(u_1)}\times {\mathrm{E}}_{{\gamma }_1,{\gamma }_2-1}^{(u_2)}\times \dots \times {\mathrm{E}}_{{\gamma }_{k-1},{\gamma }_k-1}^{(u_k)}\times }{\mathrm{E}}_{{\gamma }_k,\beta -1}^{(u_{k+1})}}$$

(36)

It follows from (33) and (35) that the matrix $Z_{\delta +k1,\beta }$ can be represented as follows:

$$Z_{\delta +k1,\beta }={\displaystyle \sum _{v=1}^{\infty }{\displaystyle \sum _{\begin{array}{c}{u}_1,\dots ,u_{k+1}\ge 1\\ u_1+\dots +u_{k+1}=v\end{array}}{\displaystyle \sum _{{\gamma }_1,\dots ,{\gamma }_k\in \mathcal{N}}({\displaystyle \sum _{({\epsilon }_{1,1},\dots ,{\epsilon }_{1,u_1})\in {\mathrm{E}}_{\delta ,{\gamma }_1-1}^{(u_1)}}{Y}_{{\epsilon }_{1,1}}\cdots Y_{{\epsilon }_1,u_1})}}}}$$

$$({\displaystyle \sum _{({\epsilon }_{2,1},\dots ,{\epsilon }_{2,u_2})\in {\mathrm{E}}_{{\gamma }_1,{\gamma }_2-1}^{(u_2)}}{Y}_{{\epsilon }_{2,1}}\cdots Y_{{\epsilon }_{2,u_2}})}\dots ({\displaystyle \sum _{({\epsilon }_{k,1},\dots ,{\epsilon }_{k,u_k})\in {\mathrm{E}}_{{\gamma }_{k-1},{\gamma }_k-1}^{(u_k)}}{Y}_{{\epsilon }_{k.1}}\cdots Y_{{\epsilon }_{k,u_k}})}$$

$$({\displaystyle \sum _{({\epsilon }_{k+1,1},\dots ,{\epsilon }_{k+1,u_{k+1}})\in {\mathrm{E}}_{{\gamma }_k,\beta }^{(u_{k+1})}}{F}_{{\epsilon }_{k+1,1}}\cdots Y_{{\epsilon }_{k+1,u_{k+1}}})}$$

$$={\displaystyle \sum _{{\gamma }_1,\dots ,{\gamma }_k\in \mathcal{N}}[{\displaystyle \sum _{u_1=1}^{\infty }({\displaystyle \sum _{({\epsilon }_{1,1},\dots ,{\epsilon }_{1,u_1})\in {\mathrm{E}}_{\delta ,{\gamma }_1-1}^{(u_1)}}{Y}_{{\epsilon }_{1,1}}\cdots Y_{{\epsilon }_1,u_1})}}}$$

$${\displaystyle \sum _{u_2=1}^{\infty }({\displaystyle \sum _{({\epsilon }_{2,1},\dots ,{\epsilon }_{2,u_2})\in {\mathrm{E}}_{{\gamma }_1,{\gamma }_2-1}^{(u_2)}}{Y}_{{\epsilon }_{2,1}}\cdots Y_{{\epsilon }_{2,u_2}})}\dots }$$

$${\displaystyle \sum _{u_k=1}^{\infty }({\displaystyle \sum _{({\epsilon }_{k,1},\dots ,{\epsilon }_{k,u_k})\in {\mathrm{E}}_{{\gamma }_{k-1},{\gamma }_k-1}^{(u_k)}}{Y}_{{\epsilon }_{k,1}}\cdots Y_{{\epsilon }_{k,u_k}})}}$$

$${\displaystyle \sum _{u_{k+1}=1}^{\infty }({\displaystyle \sum _{({\epsilon }_{k+1,1},\dots ,{\epsilon }_{k+1,u_{k+1}})\in {\mathrm{E}}_{{\gamma }_k,\beta -1}^{(u_{k+1})}}{Y}_{{\epsilon }_{k+1.1}}{Y}_{{\epsilon }_{k+1,2}}\cdots Y_{{\epsilon }_{k+1,u_{k+1}}})}}]$$

(37)

After applying (33) to each sum inside the square brackets in (37), we obtain

$$Z_{\delta +k1,\beta }={\displaystyle \sum _{{\gamma }_1,\dots ,{\gamma }_k\in \mathcal{N}}{Z}_{\delta ,{\gamma }_1}{Z}_{{\gamma }_1,{\gamma }_2}\dots Z_{{\gamma }_{k-1},{\gamma }_k}{Z}_{{\gamma }_k,\beta }},$$

which can be rewritten as (35).

It follows from the definition of the set ${\mathrm{E}}_{\alpha ,\beta }^{(v)}$, that isolating in (33) the first component of the $v$-tuple ${\epsilon }_1,\dots ,{\epsilon }_v$, the matrix $Z_{\alpha ,\beta }$ can be transformed as

$$Z_{\alpha ,\beta }={\displaystyle \sum _{i=1}^{\infty }{\displaystyle \sum _{({\epsilon }_1,\dots ,{\epsilon }_i)\in {\mathrm{E}}_{\alpha ,\beta -1}^{(i)}}{Y}_{{\epsilon }_1}\cdots Y_{{\epsilon }_i}}}$$

$$=Y_{\beta -\alpha -1}+{\displaystyle \sum _{\begin{array}{c}\epsilon \in \mathit{\epsilon }\\ \alpha +\epsilon \ge 0\end{array}}{Y}_{\epsilon }}{\displaystyle \sum _{w=1}^{\infty }{\displaystyle \sum _{({\epsilon }_1,\dots ,{\epsilon }_w)\in {\mathrm{E}}_{\alpha +\epsilon ,\beta -1}^{(w)}}{Y}_{{\epsilon }_1}\cdots Y_{{\epsilon }_w}}}=Y_{\beta -\alpha -1}+{\displaystyle \sum _{\begin{array}{c}\epsilon \in \mathit{\epsilon }\\ \alpha +\epsilon \ge 0\end{array}}{Y}_{\epsilon }}{Z}_{\alpha +\epsilon ,\beta }.$$

From here, using Formula (35), we obtain

$$Z_{\alpha ,\beta }=Y_{\beta -\alpha -1}+{\displaystyle \sum _{\begin{array}{c}\epsilon \in \mathit{\epsilon }\\ \mathcal{l}(\alpha +\epsilon )=0\end{array}}{Y}_{\epsilon }}{Z}_{\alpha +\epsilon ,\beta }$$

$$+{\displaystyle \sum _{i=1}^{\infty }{\displaystyle \sum _{\begin{array}{c}\epsilon \in \mathit{\epsilon }\\ \mathcal{l}(\alpha +\epsilon )=i\end{array}}{Y}_{\epsilon }}}{\displaystyle \sum _{{\gamma }_1,\dots ,{\gamma }_i\in \mathcal{N}}{Z}_{\mathsf{\Delta }(\alpha +\epsilon ),{\gamma }_1}{Z}_{{\gamma }_1,{\gamma }_2}}\cdots Z_{{\gamma }_{i-1},{\gamma }_i}{Z}_{{\gamma }_i,\beta },$$

which proves Formula (34). □

Let us define matrices $G_{\alpha ,\beta }(k)$ as

$$G_{\alpha ,\beta }(k)={\displaystyle \sum _{v=1}^{\infty }{\displaystyle \sum _{({\epsilon }_1,\dots ,{\epsilon }_v)\in {\mathrm{E}}_{\alpha ,\beta -1}^{(v)}}{X}_{{\epsilon }_1}(k)\cdots X_{{\epsilon }_v}}(k)}, \alpha ,\beta \in \mathcal{N}, k\ge 1.$$

(38)

For each $\epsilon \in \mathit{\epsilon }$, the sequence $X_{\epsilon }(k)$, $k\ge 1$, is entry-wise monotonically increasing and converges to the matrix $F_{\epsilon }$ ([8]). This implies that for all $\alpha ,\beta \in \mathcal{N}$, the sequence $G_{\alpha ,\beta }(k),$ $k\ge 1$, is also entry-wise monotonically increasing and converges to the matrix $G_{\alpha ,\beta }$ given by (7).

It follows from Theorem 3 that matrices $Z_{\alpha ,\beta }=G_{\alpha ,\beta }(k)$ satisfy the system

$$G_{\alpha ,\beta }(k)=X_{\beta -1-\alpha }(k)+{\displaystyle \sum _{\begin{array}{c}\epsilon \in \mathit{\epsilon }\\ \mathcal{l}(\alpha +\epsilon )=0\end{array}}{X}_{\epsilon }(k)}{G}_{\alpha +\epsilon ,\beta }(k)$$

$$+{\displaystyle \sum _{i=1}^{\infty }{\displaystyle \sum _{\begin{array}{c}\epsilon \in \mathit{\epsilon }\\ \mathcal{l}(\alpha +\epsilon )=i\end{array}}{X}_{\epsilon }(k)}}{\displaystyle \sum _{{\gamma }_1,\dots ,{\gamma }_i\in \mathcal{N}}{G}_{\mathsf{\Delta }(\alpha +\epsilon ),{\gamma }_1}(k)G_{{\gamma }_1,{\gamma }_2}(k)}\cdots G_{{\gamma }_{i-1},{\gamma }_i}(k)G_{{\gamma }_i,\beta }(k).$$

(39)

Using decomposition (35), we can rewrite Equation (29) as

$$X_{\epsilon }(k+1)=Q_{\epsilon }+{\displaystyle \sum _{\alpha \ge 0}{Q}_{\alpha }}{G}_{\alpha ,\epsilon +1}(k)=Q_{\epsilon }+{\displaystyle \sum _{\delta \in \mathcal{N}}{\displaystyle \sum _{l=0}^{\infty }{Q}_{\delta +l1}{G}_{\delta +l1,\epsilon +1}(k)}}$$

$$=Q_{\epsilon }+{\displaystyle \sum _{\delta \in \mathcal{N}}{Q}_{\delta }{G}_{\delta ,\epsilon +1}(k)}+{\displaystyle \sum _{\delta \in \mathcal{N}}{\displaystyle \sum _{l=1}^{\infty }{Q}_{\delta +l1}}}$$

$${\displaystyle \sum _{{\gamma }_1,\dots ,{\gamma }_l\in \mathcal{N}}{G}_{\delta ,{\gamma }_1}(k)G_{{\gamma }_1,{\gamma }_2}(k)\cdots G_{{\gamma }_{l-1},{\gamma }_l}(k)G_{{\gamma }_l,\epsilon +1}(k)}.$$

(40)

When using the iterative algorithm (28) and (29) to solve the system (8), a key challenge is the enumeration of elements of the set ${\mathrm{E}}_{\alpha ,\beta }^{(v)}$. In the subsequent theorem, we will show how to avoid these calculations.

Theorem 4.

Let matrices $V_{\epsilon }(k)$, $\epsilon \in \mathit{\epsilon }$, and $W_{\alpha ,\beta }(k)$, $\alpha ,\beta \in \mathcal{N}$, $k\ge 0$, be defined as

$$W_{\alpha ,\beta }(0)=O, \alpha ,\beta \in \mathcal{N};$$

(41)

$$V_{\epsilon }(k+1)=Q_{\epsilon }+{\displaystyle \sum _{\delta \in \mathcal{N}}{Q}_{\delta }{W}_{\delta ,\epsilon +1}(k)}+{\displaystyle \sum _{\delta \in \mathcal{N}}{\displaystyle \sum _{l=1}^{\infty }{Q}_{\delta +l1}}}$$

$${\displaystyle \sum _{{\gamma }_1,\dots ,{\gamma }_l\in \mathcal{N}}{W}_{\delta ,{\gamma }_1}(k)W_{{\gamma }_1,{\gamma }_2}(k)\cdots W_{{\gamma }_{l-1},{\gamma }_l}(k)W_{{\gamma }_l,\epsilon +1}(k)}, \epsilon \in \mathit{\epsilon },$$

(42)

$$W_{\alpha ,\beta }(k+1)=V_{\beta -\alpha -1}(k+1)+{\displaystyle \sum _{\begin{array}{c}\epsilon \in \mathit{\epsilon }\\ \mathcal{l}(\alpha +\epsilon )=0\end{array}}{V}_{\epsilon }(k+1)}{W}_{\alpha +\epsilon ,\beta }(k)+{\displaystyle \sum _{i=1}^{\infty }{\displaystyle \sum _{\begin{array}{c}\epsilon \in \mathit{\epsilon }\\ \mathcal{l}(\alpha +\epsilon )=i\end{array}}{V}_{\epsilon }(k+1)}}$$

$${\displaystyle \sum _{{\gamma }_1,\dots ,{\gamma }_i\in \mathcal{N}}{W}_{\mathsf{\Delta }(\alpha +\epsilon ),{\gamma }_1}(k)W_{{\gamma }_1,{\gamma }_2}(k)}\cdots W_{{\gamma }_{i-1},{\gamma }_i}(k)W_{{\gamma }_i,\beta }(k), \alpha ,\beta \in \mathcal{N}, k\ge 0.$$

(43)

Then, for each $k\ge 1$, matrices $V_{\epsilon }(k)$ and $W_{\alpha ,\beta }(k)$ satisfy the following inequalities

$$X_{\epsilon }(k-1)\le V_{\epsilon }(k)\le X_{\epsilon }(k), \epsilon \in \mathit{\epsilon }; G_{\alpha ,\beta }(k-1)\le W_{\alpha ,\beta }(k)\le G_{\alpha ,\beta }(k), \alpha ,\beta \in \mathcal{N}.$$

(44)

Proof of Theorem 4.

The proof is based on the fact that the sequences $X_{\epsilon }(k)$, $k\ge 1$, and $G_{\alpha ,\beta }(k)$, $\alpha ,\beta \in \mathcal{N}$, are entry-wise monotonically increasing.

First, we will demonstrate that for all vectors $\epsilon \in \mathit{\epsilon }$ and $\alpha ,\beta \in \mathcal{N}$, the sequences $V_{\epsilon }(k),$ $k\ge 1,$ and $W_{\alpha ,\beta }(k)$, $k\ge 1$, satisfy $V_{\epsilon }(k)\le X_{\epsilon }(k)$, $W_{\alpha ,\beta }(k)\le G_{\alpha ,\beta }(k)$. Since $V_{\epsilon }(1)=Q_{\epsilon }=X_{\epsilon }(1)$ and

$$W_{\alpha ,\beta }(1)=X_{\beta -1-\alpha }(1)\le {\displaystyle \sum _{v=1}^{\infty }{\displaystyle \sum _{({\epsilon }_1,\dots ,{\epsilon }_v)\in {\mathrm{E}}_{\alpha ,\beta -1}^{(v)}}{X}_{{\epsilon }_1}(1)\cdots X_{{\epsilon }_v}}(1)}=G_{\alpha ,\beta }(1),$$

we know that $V_{\epsilon }(1)\le X_{\epsilon }(1)$ and $W_{\alpha ,\beta }(1)\le G_{\alpha ,\beta }(1)$. Let us assume that $V_{\epsilon }(k)\le X_{\epsilon }(k)$ and $W_{\alpha ,\beta }(k)\le G_{\alpha ,\beta }(k)$ for some $k$ and for all $\epsilon \in \mathit{\epsilon }$, $\alpha ,\beta \in \mathcal{N}$. Then, it follows from (42) and (40) that the following inequality holds:

$$V_{\epsilon }(k+1)=Q_{\epsilon }+{\displaystyle \sum _{\delta \in \mathcal{N}}{Q}_{\delta }{W}_{\delta ,\epsilon +1}(k)}+{\displaystyle \sum _{\delta \in \mathcal{N}}{\displaystyle \sum _{l=1}^{\infty }{Q}_{\delta +l1}}}$$

$${\displaystyle \sum _{{\gamma }_1,\dots ,{\gamma }_l\in \mathcal{N}}{W}_{\delta ,{\gamma }_1}(k)W_{{\gamma }_1,{\gamma }_2}(k)\cdots W_{{\gamma }_{l-1},{\gamma }_l}(k)W_{{\gamma }_l,\epsilon +1}(k)})$$

$$\le Q_{\epsilon }+{\displaystyle \sum _{\delta \in \mathcal{N}}{Q}_{\delta }{G}_{\delta ,\epsilon +1}(k)}+{\displaystyle \sum _{\delta \in \mathcal{N}}{\displaystyle \sum _{l=1}^{\infty }{Q}_{\delta +l1}}}$$

$${\displaystyle \sum _{{\gamma }_1,\dots ,{\gamma }_l\in \mathcal{N}}{G}_{\delta ,{\gamma }_1}(k)G_{{\gamma }_1,{\gamma }_2}(k)\dots G_{{\gamma }_{l-1},{\gamma }_l}(k)G_{{\gamma }_l,\epsilon +1}(k)}=X_{\epsilon }(k+1).$$

(45)

Using (43), inequality (45), and (39), we obtain

$$W_{\alpha ,\beta }(k+1)=V_{\beta -1-\alpha }(k+1)+{\displaystyle \sum _{\begin{array}{c}\epsilon \in \mathit{\epsilon }\\ \mathcal{l}(\alpha +\epsilon )=0\end{array}}{V}_{\epsilon }(k+1)}{W}_{\alpha +\epsilon ,\beta }(k)+{\displaystyle \sum _{i=1}^{\infty }{\displaystyle \sum _{\begin{array}{c}\epsilon \in \mathit{\epsilon }\\ \mathcal{l}(\alpha +\epsilon )=i\end{array}}{V}_{\epsilon }(k+1)}}$$

$${\displaystyle \sum _{{\gamma }_1,\dots ,{\gamma }_i\in \mathcal{N}}{W}_{\mathsf{\Delta }(\alpha +\epsilon ),{\gamma }_1}(k)W_{{\gamma }_1,{\gamma }_2}(k)}\cdots W_{{\gamma }_{i-1},{\gamma }_i}(k)W_{{\gamma }_i,\beta }(k)$$

$$\le X_{\beta -1-\alpha }(k+1)+{\displaystyle \sum _{\begin{array}{c}\epsilon \in \mathit{\epsilon }\\ \mathcal{l}(\alpha +\epsilon )=0\end{array}}{X}_{\epsilon }(k+1)}{G}_{\alpha +\epsilon ,\beta }(k+1)+{\displaystyle \sum _{i=1}^{\infty }{\displaystyle \sum _{\begin{array}{c}\epsilon \in \mathit{\epsilon }\\ \mathcal{l}(\alpha +\epsilon )=i\end{array}}{X}_{\epsilon }(k+1)}}$$

$${\displaystyle \sum _{{\gamma }_1,\dots ,{\gamma }_i\in \mathcal{N}}{G}_{\mathsf{\Delta }(\alpha +\epsilon ),{\gamma }_1}(k+1)G_{{\gamma }_1,{\gamma }_2}(k+1)}\cdots G_{{\gamma }_{i-1},{\gamma }_i}(k+1)G_{{\gamma }_i,\beta }(k+1)=G_{\alpha ,\beta }(k+1),$$

which proves the induction step. Therefore, $V_{\epsilon }(k)\le X_{\epsilon }(k)$ and $W_{\alpha ,\beta }(k)\le G_{\alpha ,\beta }(k)$ for all $k\ge 1$ and for all $\epsilon \in \mathit{\epsilon }$, $\alpha ,\beta \in \mathcal{N}$.

Let us demonstrate that for all $\epsilon \in \mathit{\epsilon }$ and $\alpha ,\beta \in \mathcal{N}$, the sequences $Y_{\epsilon }(k),$ $k\ge 1$, and $W_{\alpha ,\beta }(k)$, $k\ge 1$, satisfy $X_{\epsilon }(k-1)\le V_{\epsilon }(k)$, $G_{\alpha ,\beta }(k-1)\le W_{\alpha ,\beta }(k)$. Since $V_{\epsilon }(1)=Q_{\epsilon }\ge X_{\epsilon }(0)=O$ and

$$W_{\alpha ,\beta }(1)=X_{\beta -1-\alpha }(1)\ge G_{\alpha ,\beta }(0)=O,$$

we know that $V_{\epsilon }(1)\ge X_{\epsilon }(0)$ and $W_{\alpha ,\beta }(1)\ge G_{\alpha ,\beta }(0)$. Let us assume that $V_{\epsilon }(k)\ge X_{\epsilon }(k-1)$ and $W_{\alpha ,\beta }(k)\ge G_{\alpha ,\beta }(k-1)$ for some $k$ and for all $\epsilon \in \mathit{\epsilon }$, $\alpha ,\beta \in \mathcal{N}$. The following inequality follows from (42) and (40):

$$V_{\epsilon }(k+1)=Q_{\epsilon }+{\displaystyle \sum _{\delta \in \mathcal{N}}{Q}_{\delta }{W}_{\delta ,\epsilon +1}(k)}+{\displaystyle \sum _{\delta \in \mathcal{N}}{\displaystyle \sum _{l=1}^{\infty }{Q}_{\delta +l1}}}$$

$${\displaystyle \sum _{{\gamma }_1,\dots ,{\gamma }_l\in \mathcal{N}}{W}_{\delta ,{\gamma }_1}(k)W_{{\gamma }_1,{\gamma }_2}(k)\cdots W_{{\gamma }_{l-1},{\gamma }_l}(k)W_{{\gamma }_l,\epsilon +1}(k)})$$

$$\ge Q_{\epsilon }+{\displaystyle \sum _{\delta \in \mathcal{N}}{Q}_{\delta }{G}_{\delta ,\epsilon +1}(k-1)}+{\displaystyle \sum _{\delta \in \mathcal{N}}{\displaystyle \sum _{l=1}^{\infty }{Q}_{\delta +l1}}}$$

$${\displaystyle \sum _{{\gamma }_1,\dots ,{\gamma }_l\in \mathcal{N}}{G}_{\delta ,{\gamma }_1}(k-1)G_{{\gamma }_1,{\gamma }_2}(k-1)\dots G_{{\gamma }_{l-1},{\gamma }_l}(k-1)G_{{\gamma }_l,\epsilon +1}(k-1)}=X_{\epsilon }(k).$$

By applying this inequality along with the equalities (43) and (39), we can derive the following results:

$$W_{\alpha ,\beta }(k+1)=V_{\beta -1-\alpha }(k+1)+{\displaystyle \sum _{\begin{array}{c}\epsilon \in \mathit{\epsilon }\\ \mathcal{l}(\alpha +\epsilon )=0\end{array}}{V}_{\epsilon }(k+1)}{W}_{\alpha +\epsilon ,\beta }(k)+{\displaystyle \sum _{i=1}^{\infty }{\displaystyle \sum _{\begin{array}{c}\epsilon \in \mathit{\epsilon }\\ \mathcal{l}(\alpha +\epsilon )=i\end{array}}{V}_{\epsilon }(k+1)}}$$

$${\displaystyle \sum _{{\gamma }_1,\dots ,{\gamma }_i\in \mathcal{N}}{W}_{\mathsf{\Delta }(\alpha +\epsilon ),{\gamma }_1}(k)W_{{\gamma }_1,{\gamma }_2}(k)}\cdots W_{{\gamma }_{i-1},{\gamma }_i}(k)W_{{\gamma }_i,\beta }(k)$$

$$\ge X_{\beta -1-\alpha }(k)+{\displaystyle \sum _{\begin{array}{c}\epsilon \in \mathit{\epsilon }\\ \mathcal{l}(\alpha +\epsilon )=0\end{array}}{X}_{\epsilon }(k)}{G}_{\alpha +\epsilon ,\beta }(k)+{\displaystyle \sum _{i=1}^{\infty }{\displaystyle \sum _{\begin{array}{c}\epsilon \in \mathit{\epsilon }\\ \mathcal{l}(\alpha +\epsilon )=i\end{array}}{X}_{\epsilon }(k)}}$$

$${\displaystyle \sum _{{\gamma }_1,\dots ,{\gamma }_i\in \mathcal{N}}{G}_{\mathsf{\Delta }(\alpha +\epsilon ),{\gamma }_1}(k)G_{{\gamma }_1,{\gamma }_2}(k)}\cdots G_{{\gamma }_{i-1},{\gamma }_i}(k)G_{{\gamma }_i,\beta }(k)=G_{\alpha ,\beta }(k),$$

which prove the induction step. Thus, $V_{\epsilon }(k)\ge X_{\epsilon }(k-1)$ and $W_{\alpha ,\beta }(k)\ge G_{\alpha ,\beta }(k-1)$ for all $k\ge 1$ and for all $\epsilon \in \mathit{\epsilon }$, $\alpha ,\beta \in \mathcal{N}$. □

Given that the sequences $X_{\epsilon }(k)$, $k\ge 1$, and $G_{\alpha ,\beta }(k),$ $k\ge 1$, are entry-wise monotonically increasing, we can derive the following inequalities based on Theorem 4:

$$O=X_{\epsilon }(0)\le V_{\epsilon }(1)\le X_{\epsilon }(1)\le V_{\epsilon }(2)\le X_{\epsilon }(2)\le V_{\epsilon }(3)\le X_{\epsilon }(3)\le \dots$$

(46)

for all $\epsilon \in \mathit{\epsilon }$, and

$$O=G_{\alpha ,\beta }(0)\le W_{\alpha ,\beta }(1)\le G_{\alpha ,\beta }(1)\le W_{\alpha ,\beta }(2)\le G_{\alpha ,\beta }(2)\le W_{\alpha ,\beta }(3)\le G_{\alpha ,\beta }(3)\dots$$

(47)

for all $\alpha ,\beta \in \mathcal{N}$. Since the sequence $X_{\epsilon }(k)$, $k\ge 1$, converges to the matrix $F_{\epsilon }$, and the sequence $G_{\alpha ,\beta }(k),$ $k\ge 1$, converges to the matrix $G_{\alpha ,\beta }$, the inequalities (46) and (47) lead to the conclusion presented in Corollary 1.

Corollary 1.

For each $\epsilon \in \mathit{\epsilon }$, the sequence $V_{\epsilon }(k)$, $k\ge 1$, is entry-wise monotonically increasing and converges to the matrix $F_{\epsilon }$. For each $\alpha ,\beta \in \mathcal{N}$, the sequence $W_{\alpha ,\beta }(k)$, $k\ge 1,$ is entry-wise monotonically increasing and converges to the matrix $G_{\alpha ,\beta }$.

Consequently, Theorem 4 outlines the new algorithm for computing the matrices of the sector exit probabilities and the matrix $G$. Passing in the equalities (42) and (43) to the limit as $k$ tends to infinity, and using Corollary 1, we obtain a system of equations for matrices $F_{\epsilon }$ and $G_{\alpha ,\beta }$.

Corollary 2.

Matrices $F_{\epsilon }$ and $G_{\alpha ,\beta }$ satisfy the following system:

$$F_{\epsilon }=Q_{\epsilon }+{\displaystyle \sum _{\delta \in \mathcal{N}}{Q}_{\delta }{G}_{\delta ,\epsilon +1}}+{\displaystyle \sum _{\delta \in \mathcal{N}}{\displaystyle \sum _{l=1}^{\infty }{Q}_{\delta +l1}}}$$

$${\displaystyle \sum _{{\gamma }_1,\dots ,{\gamma }_l\in \mathcal{N}}{G}_{\delta ,{\gamma }_1}{G}_{{\gamma }_1,{\gamma }_2}\cdots G_{{\gamma }_{l-1},{\gamma }_l}{G}_{{\gamma }_l,\epsilon +1}}, \epsilon \in \mathit{\epsilon };$$

(48)

$$G_{\alpha ,\beta }=F_{\beta -1-\alpha }+{\displaystyle \sum _{\begin{array}{c}\epsilon \in \mathit{\epsilon }\\ \mathcal{l}(\alpha +\epsilon )=0\end{array}}{F}_{\epsilon }}{G}_{\alpha +\epsilon ,\beta }+{\displaystyle \sum _{i=1}^{\infty }{\displaystyle \sum _{\begin{array}{c}\epsilon \in \mathit{\epsilon }\\ \mathcal{l}(\alpha +\epsilon )=i\end{array}}{F}_{\epsilon }}}$$

$${\displaystyle \sum _{{\gamma }_1,\dots ,{\gamma }_i\in \mathcal{N}}{G}_{\mathsf{\Delta }(\alpha +\epsilon ),{\gamma }_1}{G}_{{\gamma }_1,{\gamma }_2}}\cdots G_{{\gamma }_{i-1},{\gamma }_i}{G}_{{\gamma }_i,\beta }, \alpha ,\beta \in \mathcal{N}.$$

(49)

Please note, if $\alpha =0$, all sums in Equation (49) will equal zero, since $\mathcal{l}(\epsilon )=-1$ for all $\epsilon \in \mathit{\epsilon }$. Therefore, in these cases, Equation (49) has the form $G_{0,\beta }=F_{\beta -1}$, $\beta \in \mathcal{N}$. Consequently, Equations (48) and (49) outline the relationships between the blocks $F_{\epsilon }=G_{0,\epsilon +1}$, $\epsilon \in \mathit{\epsilon }$, of the matrix $G$ and all its other blocks.

6. Conclusions

Matrices of the sector exit probabilities $F_{\epsilon }$ were introduced in [8] as a means of calculating the matrix $G$ of multi-dimensional processes of M/G/1 type using matrices of order $n$. A system of Equations (28) and (29) for the matrices $F_{\epsilon }$ was obtained, and an algorithm for calculating its minimal nonnegative solution was proposed. However, the question remained whether the family of matrices $F_{\epsilon }$, $\epsilon \in \mathit{\epsilon }$, was a minimal nonnegative solution to the system (28) and (29). In Theorem 2, we gave a positive answer to this question. The algorithm proposed in [8] was difficult to apply due to the need to enumerate the elements of the set ${\mathrm{E}}_{\alpha ,\beta }^{(v)}$. In Section 5, we demonstrated that the matrices $F_{\epsilon }$ and blocks $G_{\alpha ,\beta }$ of the matrix $G$ satisfied the system (48) and (49), and provided an algorithm outlined in Equations (41) and (43) for solving this system. This algorithm successfully avoided the challenges associated with the enumeration of the elements of the set ${\mathrm{E}}_{\alpha ,\beta }^{(v)}$ in the algorithm introduced in [8].

In multi-dimensional cases, both families of the matrices $F_{\epsilon }$ and $G_{\alpha ,\beta }$ are infinite, leading to a system with infinitely many equations. Managing systems with infinitely many equations and unknown infinite matrices is not feasible. Therefore, future research should concentrate on developing a method for selecting an appropriate truncation approximation.