Impact of Vertical Magnetic Field on Onset of Instability of a Casson Fluid Saturated Porous Layer: A Nonlinear Theory

Abstract

This study examines the stability and instability of a Casson fluid in a horizontal porous medium with magnetic effect using linear and global theories. Both linear and nonlinear analyses are conducted using the normal modes. The study proves that the linear and nonlinear stability thresholds coincide. Two different methodologies were used to solve the system of equations. The eigenvalue problem for linear and global theories were solved using a Galerkin scheme and bvp4c routine in MATLAB. The results show that the Casson parameter destabilizes the flow, while the solutal Rayleigh number and Darcy number stabilize it.

1. Introduction

Chocolate, a popular product worldwide, is made of cocoa beans, sugar, and milk powder. During chocolate processing, rheological behaviour is one of the salient features that needs to be checked. The rheological features of chocolate are generally influenced by the ingredients used to make chocolate and chocolate production technology. Hence, controlling the characteristics of chocolate is essential [1,2,3,4]. The perfect mathematical flow model is essential for the illustration of the characteristics of chocolate. Casson fluid model is one of the important models that are used to study the characteristics of chocolate [5,6].

Aghighi et al. [7] have studied the stability theory of convection in Casson fluids numerically. They showed the influence of the yield stress on convective motion and heat transfer. Aghighi et al. [8] have investigated the RBC of viscoplastic fluid in a trapezoidal enclosure, where they used Galerkin’s method to simultaneously solve differential equations. Urvashi Gupta et al. [9] have discussed the thermohaline convection of Casson nanofluid under different boundaries, and have obtained the algebraic expressions for the solution of system for all cases. Internally heated convection of Casson nanofluid has been studied by Urvashi Gupta et al. [10], and have shown their results using neutral curves and found that the internal heat source destabilizes the Casson nanofluid layer. Haldar et al. [11] examined the steady boundary layer flow of a non-Newtonian Casson fluid over a power-law stretching sheet. Recently, Ramesh and Misbah [12] made an attempt to study the hydromagnetic flow of Casson fluid. They used temporal stability to investigate the Poiseuille flow of a Casson fluid. Reddy et al. [13] studied the thermohaline instability of a Casson fluid, and they presented the algebraic expressions for the solution of system by using Galerkin’s method. Very recently, Reddy et al. [14] investigated the onset of instability of Casson fluid in porous slab with dissipative effect.

The aim of the present analysis is to study the thermal convection in Casson fluids with magnetic effect [15]. Casson fluid is one type of non-Newtonian fluids, where a lot of research articles on the thermal convection in Newtonian fluids [16,17,18] whereas only a few research articles are found on the thermal convection in non-Newtonian fluids. These fluids have complex flow behavior, hence to analyze the properties of these fluids researchers suggested different types of models such as the power–law model [19], Jeffrey model [20], Maxwell model [21], and other viscoplastic fluid models. In non-Newtonian fluids, viscoplastic fluids are of a special type, which flows only when yield stress is less than the applied stresses. In order to study the flow behavior of such types of fluids, rheological models such as Herschel–Bulkley [22], the Bingham model [23], and the Casson model [24] have been developed by researchers.

The present work is an extension of the work done by Reddy et al. [13] by considering the effect of magnetic field. The paper is organized as follows: Section 2 discusses the governing equations. Section 3 and Section 4 cover the linear and nonlinear theories, respectively, and Section 5 presents the outcomes of results. The paper concludes with a discussion of the findings.

2. Basic Equations

This work examines the porous medium confined between two horizontal infinite planes with distance d. A (non-Newtonian) Casson fluid is considered inside the medium. Horizontal axes denoted by x and y, and the vertical axes by z. The bottom surface is held at temperature $T_0+\Delta T$ and concentration at $C_0+\Delta C$, while the upper surface is at temperature $T_0$, concentration at $C_0$, respectively (see Figure 1). The model operates under the following assumptions:

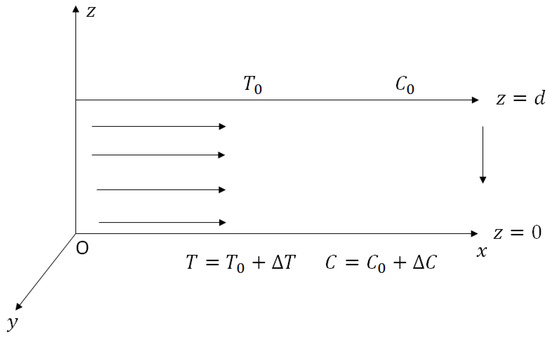
Figure 1. Geometrical representation of the flow.

• Brinkmann’s law is used to characterize the flow of the fluid.
• Oberbeck–Boussinesq approximation, i.e., variation of density considered with body force term only.
• Density varies linearly with temperature and concentration, i.e.,

  $$\rho ={\rho }_0(1-{\alpha }_1(T-T_0)+{\alpha }_2(C-C_0)).$$
  Density of the solute is greater than the density of the solvent.
• Local thermal equilibrium is assumed between solid and fluid phases.
• Viscous dissipation is negligible.

The stress tensor of Casson fluid is considered as

$$\begin{array}{c}\hfill {\tau }_{ij}=\left\{\begin{array}{cc}2\left({\mu }_B+{\displaystyle \frac{p_z}{\sqrt{2\pi }}}\right)e_{ij}\hfill & \mathrm{if}\pi <{\pi }_c;\hfill \\ 2\left({\mu }_B+{\displaystyle \frac{p_z}{\sqrt{2{\pi }_c}}}\right)e_{ij}\hfill & \mathrm{if}\pi >{\pi }_c.\hfill \end{array}\right.\end{array}$$

(1)

where

$$\left\{\begin{array}{c}{\mu }_B-\mathrm{dynamic}\mathrm{viscosity},p_z-\mathrm{yield}\mathrm{shear}\mathrm{stress},\hfill \\ e_{ij}-\mathrm{rate}\mathrm{of}\mathrm{deformation}\mathrm{tensor},\pi =e_{ij}{e}_{ij},\hfill \\ {\pi }_c-\mathrm{critical}\mathrm{value}\mathrm{of}\pi .\hfill \end{array}\right.$$

Casson fluid’s yield stress $p_z$ mathematically in terms of Casson parameter $\beta$ can be expressed as

$$p_z={\displaystyle \frac{{\mu }_c\sqrt{2\pi }}{\beta }}.$$

The viscosity of Casson fluid is expressed as follows:

$$\mu =({\mu }_c+{\displaystyle \frac{p_z}{\sqrt{2\pi }}});\pi <{\pi }_c.$$

From above equations the viscosity of the fluid is given by

$$\mu ={\mu }_c(1+{\displaystyle \frac{1}{\beta }}).$$

According to assumption of the present problem, energy balance equation that describes the temperature field’s behavior is given as

$$\sigma {\displaystyle \frac{\partial T}{\partial t}}+\left(\mathbf{u}·\nabla \right)T=\chi {\nabla }^{2}T$$

The governing mathematical equations for a binary Casson fluid layer, which is heated and soluted from below are (after using Equation (1))

$$\begin{array}{cc}\hfill & \nabla ·\mathbf{u}=0,\hfill \\ \hfill & {\displaystyle \frac{{\rho }_0}{\varphi }}{\displaystyle \frac{\partial \mathbf{u}}{\partial t}}=-\nabla p+{\rho }_0{\alpha }_1\left(T-T_0\right)g{\widehat{e}}_z-{\rho }_0{\alpha }_2\left(C-C_0\right)g{\widehat{e}}_z-{\displaystyle \frac{\mu }{\kappa }}\mathbf{u}\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill & +{\mu }_e\left(1+{\displaystyle \frac{1}{\beta }}\right){\nabla }^2\mathbf{u}+{\sigma }_1({\mathbf{u}}^{*}\times B_0{\widehat{e}}_z)\times B_0{\widehat{e}}_z,\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill & \sigma {\displaystyle \frac{\partial T}{\partial t}}+\left(\mathbf{u}·\nabla \right)T=\chi {\nabla }^{2}T,\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\partial C}{\partial t}}+\left(\mathbf{u}·\nabla \right)C={\chi }_c{\nabla }^{2}C,\hfill \end{array}$$

(5)

with

$$\begin{array}{cc}\hfill & \mathbf{u}=0,T=1,C=1\mathrm{on}z=0,\hfill \\ \hfill & \mathbf{u}=0,T=0,C=0\mathrm{on}z=1.\hfill \end{array}$$

(6)

where

$$\left\{\begin{array}{c}\mathbf{u}=(u,v,w)-\mathrm{fluid}\mathrm{velocity},{\alpha }_1-\mathrm{thermal}\mathrm{expansion}\mathrm{coefficient},\hfill \\ {\rho }_0-\mathrm{reference}\mathrm{density},{\alpha }_2-\mathrm{solutal}\mathrm{density}\mathrm{coefficient},\hfill \\ \mu -\mathrm{dynamic}\mathrm{viscosity},{\mu }_e-\mathrm{effective}\mathrm{viscosity},\hfill \\ \varphi -\mathrm{porosity},\beta ={\displaystyle \frac{{\mu }_B\sqrt{2\pi }}{p_z}}-\mathrm{Casson}\mathrm{fluid}\mathrm{parameter},B_0-\mathrm{magnetic}\mathrm{field},\hfill \\ p-\mathrm{pressure},T-\mathrm{temperature},C-\mathrm{concentration},\hfill \\ \sigma -\mathrm{heat}\mathrm{capacity}\mathrm{ratio},{\sigma }_1-\mathrm{electric}\mathrm{conductivity},\hfill \\ \chi -\mathrm{thermal}\mathrm{diffusivity},{\chi }_c-\mathrm{mass}\mathrm{diffusivity}.\hfill \end{array}\right.$$

Let us define

$$\begin{array}{cccccc}\hfill & x=x^{*}d,\hfill & \hfill y& =y^{*}d,\hfill & \hfill z& =z^{*}d,\hfill \\ \hfill & u={\displaystyle \frac{\chi }{d}}{u}^{*},\hfill & \hfill v& ={\displaystyle \frac{\chi }{d}}{v}^{*},\hfill & \hfill w& ={\displaystyle \frac{\chi }{d}}{w}^{*},\hfill \\ \hfill & t={\displaystyle \frac{\sigma d^2}{\chi }}{t}^{*},\hfill & \hfill T& =\Delta T{T}^{*}.\hfill \end{array}$$

Then from (2)–(6), the following equations are obtained

$$\begin{array}{cc}\hfill & \nabla ·\mathbf{u}=0,\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{Va}}{\displaystyle \frac{\partial \mathbf{u}}{\partial t}}=-\nabla p+RaT{\widehat{e}}_z-RsC{\widehat{e}}_z-\mathbf{u}+Da\left(1+{\displaystyle \frac{1}{\beta }}\right){\nabla }^2\mathbf{u}+H{a}^2[(\mathbf{u}\times {\widehat{e}}_z)\times {\widehat{e}}_z],\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\partial T}{\partial t}}+\left(\mathbf{u}·\nabla \right)T={\nabla }^{2}T,\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\partial C}{\partial t}}+\left(\mathbf{u}·\nabla \right)C={\displaystyle \frac{1}{Le}}{\nabla }^{2}C,\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill & \mathbf{u}=T=C=0\mathrm{on}z=0,1.\hfill \end{array}$$

(11)

where

$$\left\{\begin{array}{c}Va={\displaystyle \frac{{\rho }_0\xi \kappa }{\varphi \mu \sigma d^2}}-\mathrm{Vadasz}\mathrm{number},\hfill \\ Da={\displaystyle \frac{{\mu }_e\kappa }{\mu d^2}}-\mathrm{Darcy}\mathrm{number},\hfill \\ Ra={\displaystyle \frac{{\rho }_{0}d{\alpha }_1\kappa \Delta T}{\xi \mu }}-\mathrm{Thermal}\mathrm{Rayleigh}\mathrm{number},\hfill \\ H{a}^2={\displaystyle \frac{{\sigma }_1{B}_0^{2}K}{\mu }}-\mathrm{Hartmann}\mathrm{number},\hfill \\ Rs={\displaystyle \frac{{\rho }_{0}d{\alpha }_1\kappa \Delta C}{\xi \mu }}-\mathrm{Solute}\mathrm{Rayleigh}\mathrm{number},\hfill \\ Le={\displaystyle \frac{{\xi }_c\sigma }{\xi }}-\mathrm{Lewis}\mathrm{number}.\hfill \end{array}\right.$$

Basic State

The basic flow is assumed as

$$\begin{array}{c}\hfill u_b=0,T_b=1-z,C_b=1-z.\end{array}$$

(12)

where the subscript b indicates for basic state.

3. Linear Instability

Minor perturbation for basic flow is applied as

$$\begin{array}{c}\hfill \mathbf{u}=u_b+\mathbf{U},p=P_b+P,T=T_b+\theta ,C=C_b+\Phi .\end{array}$$

(13)

By putting above equations into Equations (7)–(10), the following equations are obtained

$$\begin{array}{cc}\hfill & \nabla .\mathbf{U}=0,\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{Va}}{\displaystyle \frac{\partial \mathbf{U}}{\partial t}}=-\nabla p+Ra\theta {\widehat{e}}_z-Rs\Phi {\widehat{e}}_z-\mathbf{U}+Da\left(1+{\displaystyle \frac{1}{\beta }}\right){\nabla }^2\mathbf{U}+H{a}^2[(\mathbf{U}\times {\widehat{e}}_z)\times {\widehat{e}}_z],\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\partial \theta }{\partial t}}+\mathbf{U}.\nabla T_b+u_b.\nabla \theta ={\nabla }^2\theta ,\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\partial \Phi }{\partial t}}+\mathbf{U}.\nabla C_b+u_b.\nabla \Phi ={\displaystyle \frac{1}{Le}}{\nabla }^2\Phi ,\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill & \mathbf{U}=0,\theta =0,\Phi =0\mathrm{on}z=0,1.\hfill \end{array}$$

(18)

After removing the pressure (by taking double curl of Equation (15)),

$$\begin{array}{cc}\hfill & \left({\displaystyle \frac{1}{Va}}{\displaystyle \frac{\partial }{\partial t}}+1-\left(1+{\displaystyle \frac{1}{\beta }}\right)Da{\nabla }^2\right){\nabla }^{2}w-Ra{\nabla }_h^2\theta +Rs{\nabla }_h^2\Phi +H{a}^2{D}^{2}w=0,\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\partial \theta }{\partial t}}-w={\nabla }^2\theta ,\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\partial \Phi }{\partial t}}-w={\displaystyle \frac{1}{Le}}{\nabla }^2\Phi ,\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill & \mathbf{U}=0,\theta =0,\Phi =0\mathrm{on}z=0,1.\hfill \end{array}$$

(22)

The solution in terms of normal modes is considered as

$$\begin{array}{c}\hfill (w,\theta )=\left(W\left(z\right),\theta \left(z\right)\right)e^{i(lx+my-\omega t)},\end{array}$$

(23)

where $q=\sqrt{l^2+m^2}$ is wave number and $\omega$ is growth rate.

On using Equation (23), Equations (19)–(22) become

$$\begin{array}{cc}\hfill & \left({\displaystyle \frac{1}{Va}}i\omega +1-\left(1+{\displaystyle \frac{1}{\beta }}\right)Da(D^2-q^2)\right)(D^2-q^2)W+Ra{q}^2\theta -Rs{q}^2\Phi +H{a}^2{D}^{2}w=0,\hfill \end{array}$$

(24)

$$\begin{array}{cc}\hfill & i\omega \theta -W=(D^2-q^2)\theta ,\hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill & i\omega \Phi -W={\displaystyle \frac{1}{Le}}(D^2-q^2)\theta ,\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill & W=\theta =\Phi =0:z=0,1.\hfill \end{array}$$

(27)

One Term Galerkin Method

The solution can be chosen in the form of

$$\begin{array}{c}\hfill \left(W,\theta ,\Phi \right)=\left(W_0,{\theta }_0,{\Phi }_0\right)sin\pi z.\end{array}$$

(28)

By substituting Equation (28) in (24)–(26),

$$\begin{array}{c}\hfill \left(\begin{array}{ccc}{\displaystyle \frac{i\omega {\delta }^2}{Va}}+{\delta }^2+{\delta }^{4}Da\left(1+{\displaystyle \frac{1}{\beta }}\right)+H{a}^2{\pi }^2& -Ra{q}^2& Rs{q}^2\\ -1& i\omega +{\delta }^2& 0\\ -1& 0& i\omega +{\displaystyle \frac{{\delta }^2}{Le}}\end{array}\right)\left(\begin{array}{c}{W}_0\\ {\theta }_0\\ C_0\end{array}\right)=\left(\begin{array}{c}0\\ 0\\ 0\end{array}\right),\end{array}$$

(29)

where ${\delta }^2={\pi }^2+q^2$.

The classical stability analysis on Equation (29) is now floowed. Hence, the analytical expression of the stationary thermal Rayleigh number, $R{a}_{sc}$, and oscillatory thermal Rayleigh number, $R{a}_{oc}$, are obtained in the following form

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill & R{a}_{sc}={\displaystyle \frac{{\delta }_{sc}^4}{q_{sc}^2}}+Da\left(1+{\displaystyle \frac{1}{\beta }}\right){\displaystyle \frac{{\delta }_{sc}^6}{q_{sc}^2}}+{\displaystyle \frac{{\delta }_{sc}^2}{q_{sc}^2}}H{a}^2{\pi }^2+LeRs,\hfill \\ \hfill & R{a}_{oc}={\displaystyle \frac{{\eta }_1\left({\eta }_2(1+Le){\delta }_{oc}^2+LeVa\beta Rs{q}_{oc}^2\right)}{Va\beta L{e}^2{q}_{oc}^2{\eta }_2}},\hfill \end{array}\right.\end{array}$$

where

$$\left\{\begin{array}{c}{\eta }_1=H{a}^{2}LeVa\beta {\pi }^2+Leva\beta {\delta }_{oc}^2+\left(\beta +DaLeVa(1+\beta )\right){\delta }_{oc}^4,\hfill \\ {\eta }_2=H{a}^{2}Va\beta {\pi }^2+va\beta {\delta }_{oc}^2+\left(\beta +DaVa(1+\beta )\right){\delta }_{oc}^4.\hfill \end{array}\right.$$

For Newtonian fluid, in the absence of Brinkmann law, magnetic field and concentration ($Da=0,Rs=0$), the above stationary Rayleigh number reduces to $R{a}_{sc}={\displaystyle \frac{{\delta }_{sc}^4}{q_{sc}^2}}$ with the critical values $R{a}_{sc}^c=4{\pi }^2$ and $q_{sc}^c=\pi$, which agrees with the results of Horton and Rogers [25] and Lapwood [26] for the onset of convection in a porous layer.

4. Nonlinear Instability

The energy functional is defined as

$$\begin{array}{c}\hfill E\left(t\right)={\displaystyle \frac{1}{2Va}}{\Vert \mathbf{U}\Vert }^2+{\displaystyle \frac{{\xi }_1}{2}}{\Vert \theta \Vert }^2+{\displaystyle \frac{{\xi }_2}{2}}{\Vert \Phi \Vert }^2.\end{array}$$

(30)

Here, ${\xi }_1$ and ${\xi }_2$ are positive coupling parameters. Now we multiply Equation (15) by $\mathbf{U}$, Equation (16) by $\theta$ and Equation (17) by $\Phi$, integrating over V,

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{2Va}}{\displaystyle \frac{d}{dt}}{\Vert \mathbf{U}\Vert }^2=-{\Vert \mathbf{U}\Vert }^2-\left(1+{\displaystyle \frac{1}{\beta }}\right)Da{\Vert \nabla \mathbf{U}\Vert }^2+Ra<\theta ,w>-Rs<\Phi ,w>\hfill \\ \hfill & +H{a}^2\left({\Vert \mathbf{U}\Vert }^2-{\Vert W\Vert }^2\right),\hfill \end{array}$$

(31)

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{2}}{\displaystyle \frac{d}{dt}}{\Vert \theta \Vert }^2+<\left(\mathbf{U}.\nabla T_b\right),\theta >=-{\Vert \nabla \theta \Vert }^2,\hfill \end{array}$$

(32)

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{2}}{\displaystyle \frac{d}{dt}}{\Vert \Phi \Vert }^2+<\left(\mathbf{U}.\nabla C_b\right),\Phi >=-{\displaystyle \frac{1}{Le}}{\Vert \nabla \Phi \Vert }^2.\hfill \end{array}$$

(33)

Differentiating Equation (30) with respect to t and using Equations (31)–(33),

$$\begin{array}{c}\hfill {\displaystyle \frac{dE}{dt}}=I-D,\end{array}$$

(34)

where

$$\begin{array}{cc}\hfill & I=-{\xi }_1<\left(\mathbf{U}.\nabla T_b\right),\theta >-{\xi }_2<\left(\mathbf{U}.\nabla C_b\right),\Phi >+Ra<\theta ,w>-Rs<\Phi ,w>,\hfill \end{array}$$

(35)

$$\begin{array}{cc}\hfill & D={\Vert \mathbf{U}\Vert }^2+\left(1+{\displaystyle \frac{1}{\beta }}\right){Da\Vert \nabla \mathbf{U}\Vert }^2+{\xi }_1{\Vert \nabla \theta \Vert }^2+{\xi }_2{\displaystyle \frac{1}{Le}}{\Vert \nabla \Phi \Vert }^2\hfill \\ \hfill & +H{a}^2\left({\Vert U\Vert }^2+{\Vert W\Vert }^2\right).\hfill \end{array}$$

(36)

From Equations (34)–(36), (by using Poincare inequality), we get,

$$\begin{array}{c}\hfill {\displaystyle \frac{dE}{dt}}\le -2{\pi }^2(1-m)E,\end{array}$$

(37)

where

$$\begin{array}{c}\hfill m=ma{x}_H\left({\displaystyle \frac{I}{D}}\right),\end{array}$$

(38)

and $H=\left\{\left(\mathbf{U},\Phi \right)\in L^2\left(V\right):\nabla .\mathbf{U}=0,W=\Phi =0\mathrm{at}z=0,1\right\}$.

On integrating Equation (37), confirms $E\left(t\right)\to 0$ as $t\to \infty$ for $0<m<1$. Here, we choose $m=1$,

$$\begin{array}{cc}\hfill & -2\mathbf{U}-2\left(1+{\displaystyle \frac{1}{\beta }}\right)Da{\nabla }^2\mathbf{U}-{\xi }_1\nabla T_b\theta -{\xi }_2\nabla C_b\Phi +Ra<\theta ,w>\hfill \\ \hfill & -Rs<\Phi ,w>-2H{a}^2\left(U+V\right)=\nabla \lambda ,\hfill \end{array}$$

(39)

$$\begin{array}{cc}\hfill & -{\xi }_1<\mathbf{U}·\nabla T_b,\theta >+Raw+2{\xi }_1{\nabla }^2\theta =0,\hfill \end{array}$$

(40)

$$\begin{array}{cc}\hfill & -{\xi }_2<\mathbf{U}·\nabla C_b,\Phi >+Rsw+{\displaystyle \frac{2}{Le}}{\xi }_2{\nabla }^2\Phi =0,\hfill \end{array}$$

(41)

where $\lambda$ is a Lagrange multiplier. Taking the third component of curl of curl of Equation (39),

$$\begin{array}{cc}\hfill & 2Da\left(1+{\displaystyle \frac{1}{\beta }}\right){\nabla }^{4}w+2{\nabla }^{2}w-\left({\xi }_1{\displaystyle \frac{d{T}_b}{dz}}+Ra\right){\nabla }_h^2\theta \hfill \\ \hfill & +\left(Rs-{\xi }_2{\displaystyle \frac{d{C}_b}{dz}}\right){\nabla }_h^2\Phi +2H{a}^2{D}^{2}W=0,\hfill \end{array}$$

(42)

$$\begin{array}{cc}\hfill & -{\xi }_1<\mathbf{U}·\nabla T_b,\theta >+Ra\theta w+2{\xi }_1{\nabla }^2\theta =0,\hfill \end{array}$$

(43)

$$\begin{array}{cc}\hfill & -{\xi }_2<\mathbf{U}·\nabla C_b,\Phi >+Rsw+{\displaystyle \frac{2}{Le}}{\xi }_2{\nabla }^2\Phi =0.\hfill \end{array}$$

(44)

On using Equation (23) in Equations (42) and (44),

$$\begin{array}{cc}\hfill & 2\left(1+{\displaystyle \frac{1}{\beta }}\right)Da{\left(D^2-q^2\right)}^{2}W+2\left(D^2-q^2\right)W-\left(Ra-{\xi }_1{\displaystyle \frac{d{T}_b}{dz}}\right)q^2\theta \hfill \\ \hfill & +\left(Ra-{\xi }_1{\displaystyle \frac{d{C}_b}{dz}}\right)q^{2}C+2H{a}^2{D}^{2}W=0,\hfill \end{array}$$

(45)

$$\begin{array}{cc}\hfill & 2{\xi }_1\left(D^2-q^2\right)\theta +RaW-{\xi }_1{\displaystyle \frac{d{T}_b}{dz}}W=0,\hfill \end{array}$$

(46)

$$\begin{array}{cc}\hfill & 2{\xi }_2\left(D^2-q^2\right)\Phi +RsW-{\xi }_2{\displaystyle \frac{d{C}_b}{dz}}W=0.\hfill \end{array}$$

(47)

Solution Methodology

The eigenvalue problem specified by Equations (45)–(47) with (27) is solved using the bvp4c in MATLAB R2024b. For obtaining a non-trivial solution to the eigenvalue problem, the normalization condition ${\theta }^{\prime }\left(0\right)=1$ is considered. With this normalization condition, the eigenvalue of Rayleigh number is established. The wave number and critical Rayleigh number are acquired using index-linked instructions in MATLAB. For achieving higher-order accuracy, the comparative and conclusive tolerances are set to ${10}^{-6}$ and ${10}^{-10}$, respectively.

5. Discussion

The numerical results and discussions are shown in this section. The present analysis is aimed to analyze the nonlinear magnetoconvection of Casson fluid in a horizontal porous slab. Table 1 shows the linear and nonlinear critical Rayleigh numbers for different values of $Da$ with $\beta =0.2$, $H{a}^2=0.2$, and $Rs=5$. It is observed from this table that the linear and nonlinear thresholds coincide. Hence, the linear instability analysis predicts the beginning of convective motion accurately.

Table 1. Comparison between the linear and the nonlinear stability critical $Ra$ for $H{a}^2=0.2$; $\beta =0.2$; $Rs=5$.

	$\mathit{Le}=0.5$		$\mathit{Le}=1$		$\mathit{Le}=1.5$
$\mathit{Da}$	Linear	Nonlinear	Linear	Nonlinear	Linear	Nonlinear
$0.1$	$446.7422$	$446.7422$	$449.2422$	$449.2422$	$451.7422$	$451.7422$
$0.2$	$841.5326$	$841.5326$	$844.0326$	$844.0326$	$846.5326$	$846.5326$
$0.3$	$1236.1409$	$1236.1409$	$1238.6409$	$1238.6409$	$1241.1409$	$1241.1409$
$0.4$	$1630.6998$	$1630.6998$	$1633.1998$	$1633.1998$	$1635.6998$	$1635.6998$
$0.5$	$2025.2384$	$2025.2384$	$2027.7384$	$2027.7384$	$2030.2384$	$2030.2384$
$0.6$	$2419.7665$	$2419.7665$	$2422.2665$	$2422.2665$	$2424.7665$	$2424.7665$
$0.7$	$2814.2887$	$2814.2887$	$2816.7887$	$2816.7887$	$2819.2887$	$2819.2887$
$0.8$	$3208.8071$	$3208.8071$	$3211.3071$	$3211.3071$	$3213.8071$	$3213.8071$
$0.9$	$3603.3230$	$3603.3230$	$3605.8230$	$3605.8230$	$3608.3230$	$3608.3230$
1	$3997.8370$	$3997.8370$	$4000.3370$	$4000.3370$	$4002.8370$	$4002.8370$

In Table 2, Table 3 and Table 4, the effect of $Rs$ on linear instability is shown and the existence of stationary or oscillatory instability sets in. From these tables, it is clear that stationary stability sets in for the case $Le\le 1$ for all values of $Rs$. For $Le>1$, there exist a $R{s}^{*}$ such that the convection arises via an oscillatory mode for $Rs>R{s}^{*}$. Moreover, the stabilizing effect of the solute Rayleigh number ($Rs$) observed in these tables indicates that adding a solute to a fluid can enhance its stability against convective instabilities. This finding can be utilized in applications such as the cooling of electronic components or the operation of geothermal power plants, where the presence of dissolved salts can affect the convective stability of the fluids. Furthermore, both $R{a}_{sc}^c$ and $R{a}_{oc}^c$ increasing functions of $H{a}^2$ indicate the stabilizing effect of the Hartmann number.

Table 2. Critical $Ra$ with various values of $Rs$ and $Va=10$; $Da=0.5$; $\beta =0.5$; $Le=0.5$.

	${\mathit{Ha}}^2=0.5$			${\mathbf{Ha}}^2=0.6$
$\mathit{Rs}$	${\mathit{Ra}}_{\mathit{sc}}^{\mathit{c}}$	${\mathit{Ra}}_{\mathit{oc}}^{\mathit{c}}$	Instability	${\mathit{Ra}}_{\mathit{sc}}^{\mathit{c}}$	${\mathit{Ra}}_{\mathit{oc}}^{\mathit{c}}$	Instability
0	1045.046	3529.793	Stationary	1047.935	3538.485	Stationary
100	1095.046	3635.714	Stationary	1097.935	3644.391	Stationary
200	1145.046	3741.635	Stationary	1147.935	3750.297	Stationary
300	1195.046	3847.556	Stationary	1197.935	3856.203	Stationary
400	1245.046	3953.477	Stationary	1247.935	3962.109	Stationary
500	1295.046	4059.398	Stationary	1297.935	4068.015	Stationary
600	1345.046	4165.319	Stationary	1347.935	4173.921	Stationary
700	1395.046	4271.240	Stationary	1397.935	4279.827	Stationary
800	1445.046	4377.161	Stationary	1447.935	4385.733	Stationary
900	1495.046	4483.082	Stationary	1497.935	4491.639	Stationary
1000	1545.046	4589.003	Stationary	1547.935	4597.545	Stationary

Table 3. Critical $Ra$ with various values of $Rs$ and $Va=10$; $Da=0.5$; $\beta =0.5$; $Le=1$.

	${\mathit{Ha}}^2=0.5$			${\mathit{Ha}}^2=0.6$
$\mathit{Rs}$	${\mathit{Ra}}_{\mathit{sc}}^{\mathit{c}}$	${\mathit{Ra}}_{\mathit{oc}}^{\mathit{c}}$	Instability	${\mathit{Ra}}_{\mathit{sc}}^{\mathit{c}}$	${\mathit{Ra}}_{\mathit{oc}}^{\mathit{c}}$	Instability
0	1045.046	2221.647	Stationary	1047.935	2227.434	Stationary
100	1145.046	2321.647	Stationary	1147.935	2327.434	Stationary
200	1245.046	2421.647	Stationary	1247.935	2427.434	Stationary
300	1345.046	2521.647	Stationary	1347.935	2527.434	Stationary
400	1445.046	2621.647	Stationary	1447.935	2627.434	Stationary
500	1545.046	2721.647	Stationary	1547.935	2727.434	Stationary
600	1645.046	2821.647	Stationary	1647.935	2827.434	Stationary
700	1745.046	2921.647	Stationary	1747.935	2927.434	Stationary
800	1845.046	3021.647	Stationary	1847.935	3027.434	Stationary
900	1945.046	3121.647	Stationary	1947.935	3127.434	Stationary
1000	2045.046	3221.647	Stationary	2047.935	3227.434	Stationary

Table 4. Critical $Ra$ with various values of $Rs$ and $Va=10$; $Da=0.5$; $\beta =0.5$; $Le=2$.

	${\mathit{Ha}}^2=0.5$			${\mathit{Ha}}^2=0.6$
$\mathit{Rs}$	${\mathit{Ra}}_{\mathit{sc}}^{\mathit{c}}$	${\mathit{Ra}}_{\mathit{oc}}^{\mathit{c}}$	Instability	${\mathit{Ra}}_{\mathit{sc}}^{\mathit{c}}$	${\mathit{Ra}}_{\mathit{oc}}^{\mathit{c}}$	Instability
550	2145.046	2150.618	Stationary	2147.938	2155.001	Stationary
551	2147.046	2151.589	Stationary	2149.938	2155.970	Stationary
552	2149.0464	2152.559	Stationary	2151.938	2156.941	Stationary
553	2151.0464	2153.530	Stationary	2153.938	2157.911	Stationary
554	2153.046	2154.501	Stationary	2155.938	2158.882	Stationary
555	2155.046	2155.471	Stationary	2157.938	2159.852	Stationary
556	2157.046	2156.441	Oscillatory	2159.938	2160.823	Stationary
557	2159.046	2157.411	Oscillatory	2161.938	2161.793	Oscillatory
558	2161.046	2158.382	Oscillatory	2163.938	2162.7642	Oscillatory
559	2163.046	2159.352	Oscillatory	2165.938	2163.734	Oscillatory
560	2165.046	2160.322	Oscillatory	2167.938	2164.705	Oscillatory

Figure 2 shows the effect of Casson parameter on stationary convection. It is obvious from this graph that as $\beta$ increases, the critical $R{a}_{sc}$ is observed to decrease and the $\beta$ has a destabilizing effect on the system, which implies that a fluid with a higher $\beta$ will be more prone to convective instabilities. And also, the graphical results in Figure 2 are an illustration of the change in critical $R{a}_{sc}$ as a function of $Da$ (Darcy number), for different values of $Le$. From this graph, it is observed that the critical $R{a}_{sc}$ is increasing as $Da$ increases. In other words, $Da$ has stabilizing nature on the flow, i.e., the presence of a porous medium can also enhance the stability of the fluid against convective instabilities.

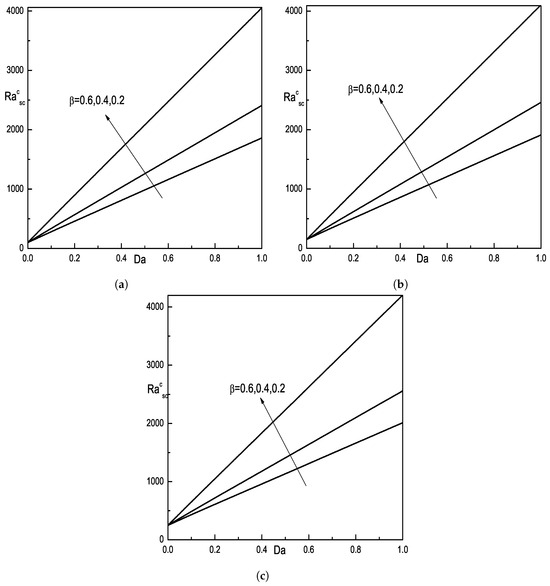
Figure 2. Plot of $R{a}_{sc}^c$ versus Darcy number and $\beta$ and for fixed value of $Va=10$; $Rs=100$; $H{a}^2=0.5$; (a) $Le=0.5$; (b) $Le=1$; (c) $Le=2$.

Figure 3 shows the variation of critical $R{a}_{oc}$ with Darcy number and Casson parameter for the fixed values of $Va=10$, $Rs=100$, $H{a}^2=0.5$. From this figure, it is observed that the critical $R{a}_{oc}$ decreases as $\beta$ increases. Hence, $\beta$ has a destabilizing effect on the system. It is also identified that the enhancement of critical $R{a}_{oc}$ with $Da$, indicating that the $Da$ has a stabilizing effect on the system.

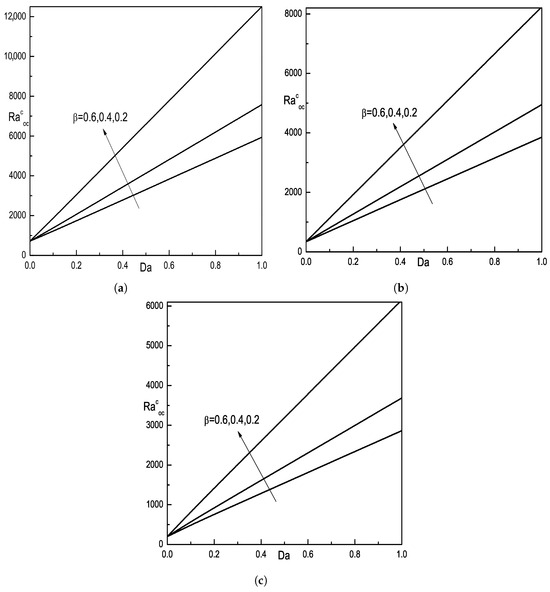
Figure 3. Plot of $R{a}_{oc}^c$ versus Darcy number and $\beta$ and for fixed value of $Va=10$; $Rs=100$; $H{a}^2=0.5$; (a) $Le=0.5$; (b) $Le=1$; (c) $Le=2$.

The decreasing nature of the Vadasz number on oscillatory convection is displayed in Figure 4. Moreover, the change of threshold $R{a}_{oc}$ with $Le$ is illustrated in this figure. The Lewis number has a destabilizing nature on oscillatory instability.

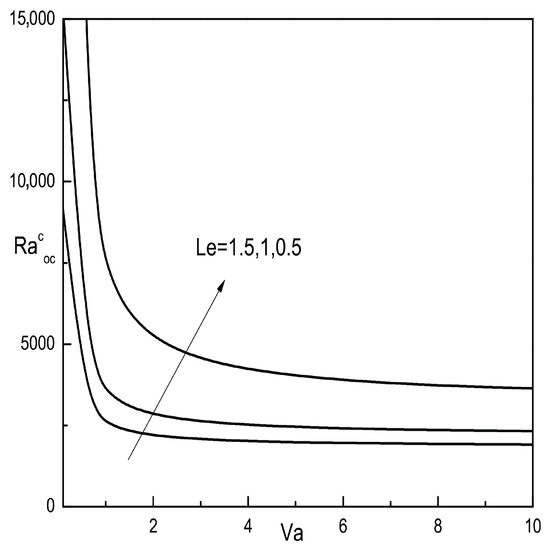
Figure 4. Plot of $R{a}_{sc}^c$ versus Vadasz number and $Le$ and for fixed value of $Da=0.5$; $Rs=100$; $H{a}^2=0.5$; $\beta =0.5$.

6. Conclusions

In this paper, linear analysis and nonlinear analysis of a Casson fluid in a porous layer with magnetic field are analyzed. Both linear and nonlinear theories have been studied. In linear and nonlinear analyses, the critical Rayleigh number is calculated. The eigenvalue problem for linear instability is solved by the Galerkin scheme, whereas the eigenvalue problem for nonlinear instability is solved numerically by using the bvp4c routine in MATLAB. The study shows that the linear and nonlinear theory thresholds coincide. The Casson parameter has a destabilizing nature on the flow, while Darcy number and and solutal Rayleigh number have a stabilizing nature on the flow.