Abstract
Flight delays during extreme weather events exhibit spatio-temporal propagation and cascading effects, posing serious challenges to the resilience of aviation systems. Existing prediction approaches often neglect dynamic dependencies across flight chains and struggle to model sparse extreme events. This study develops a data-driven framework that explicitly models delay propagation paths, incorporates historical scenario retrieval to capture rare disruption patterns, and integrates meteorological, airport operational, and flight-specific information through multi-source fusion. Using U.S. flight operations and weather records, the framework demonstrates clear advantages over established baselines in extreme-delay scenarios, achieving a MAE of 3.23 min, an RMSE of 6.25 min, and an R2 of 0.92—improving by 8.8%, 26.0%, and 5.75% compared to the best benchmark. Ablation studies confirm the contribution of the propagation modeling, historical retrieval, and multi-source integration modules, while cross-airport evaluations reveal consistent accuracy at both major hubs (e.g., Atlanta, Chicago O’Hare) and regional airports (e.g., Kona, Anchorage). These findings demonstrate that the proposed framework enables reliable forecasting of delay propagation under complex weather conditions, providing valuable support for proactive departure management and enhancing the resilience of aviation operations.
Keywords:
flight delay prediction; extreme delays; flight chain propagation; Temporal Fusion Transformer; data sparsity; aviation operations MSC:
68T07
1. Introduction
With the rapid recovery of global air transport, the continuous expansion of aviation networks has established flight delays as a critical challenge, significantly compromising operational efficiency and passenger experience [1]. According to the Bureau of Transportation Statistics (BTS), delays occur with particularly high frequency under exceptional operational scenarios—such as extreme weather, peak traffic periods, and temporary airport closures—where they exhibit characteristics of nonlinear propagation and cascading propagation. Beyond tropospheric weather, space weather can also affect aviation through impacts on GNSS (Global Navigation Satellite System)-based navigation and communication systems. These effects, though less frequent, can cause significant disruptions to air traffic operations, particularly for high-latitude and long-haul routes where reliance on satellite-based navigation is critical [2]. This pattern substantially erodes the overall stability and resilience of the aviation system.
As the initial phase in flight operations, departure delays often propagate downstream effects through flight chains (networks of consecutive flight legs operated by the same aircraft) across both temporal and spatial dimensions [3]. This propagation unfolds via two primary mechanisms. First, temporal propagation occurs when a delay on one leg reduces the turnaround buffer for subsequent flights within the same aircraft rotation, increasing the likelihood of accumulated or cascading delays throughout the day. Second, because a single aircraft typically serves multiple airports, spatial propagation enables an initial delay at one airport to extend to other regions of the network, disrupting airport operations on a broader geographic scale. Such propagation can trigger large-scale cascading disruptions throughout the flight network. Hence, accurate and efficient prediction of departure delays serves not only as a cornerstone for enhancing airport operational efficiency but also as a critical enabler for intelligent decision-making in air traffic management systems. Currently, the DMAN (Departure Management System)—a core component of the A-CDM (Airport Collaborative Decision Making) framework—has been widely deployed to optimize departure efficiency [4]. However, when confronted with highly uncertain and operationally complex extreme scenarios, conventional DMAN systems still exhibit substantial limitations in prediction accuracy and dynamic adaptability.
Confronted with these conditions, three persistent deficiencies emerge in the current literature: (i) sequence-based models implicitly assume dense and regularly sampled data [5]; (ii) graph-oriented approaches aggregate effects at the airport level, overlooking individual flight chain dynamics [6]; and (iii) extreme delay records are commonly treated as outliers to be discarded, depriving the model of the very examples it most needs to learn robust behavior [7].
To address these gaps, this study explores a flight chain prediction framework that integrates historical operational data with extreme weather contexts. Rather than treating extreme delays as anomalies or applying post hoc propagation rules, we incorporate preceding delay effects and weather-driven disturbances directly into the model input, enabling dynamic adaptation to real-time operational disruptions. Our goal is to enhance the resilience of predictive models under sparse data and high-impact scenarios by explicitly capturing the temporal and structural dependencies that define flight delay propagation.
The contributions of this work are as follows:
- (1)
- Extreme Delay as Reference Exemplars: Unlike conventional approaches that discard extreme delays as outliers, we repurpose them as reference exemplars through similarity retrieval. This design alleviates the data sparsity in extreme weather scenarios and allows the model to learn from rare but high-impact disruptions rather than discarding them.
- (2)
- Learnable Delay Propagation Mechanism: We explicitly model the “preceding delay × exponential time decay” as a learnable feature and feed it directly into the model. Enabling end-to-end optimization of delay propagation effects.
- (3)
- Integrated Prediction Framework: Building upon the Temporal Fusion Transformer, we develop an integrated architecture that comprises a historical retrieval module for rare-delay cases, a multi-source channel-attention embedding fusion module (MS-CA-EFM) to integrate different types of feature embeddings, and a flight chain delay-propagation module that embeds flight chain dependencies.
- (4)
- Empirical Validation Across Diverse Conditions: Our experiments on U.S. flight data demonstrate consistent performance improvements across airports with varying traffic densities, meteorological conditions, and operational complexities, with MAE (Mean Absolute Error) of 3.23 min, RMSE (Root Mean Square Error) of 6.25 min, and R2 of 0.92—improving by 8.8%, 26.0%, and 5.75% compared to the best benchmark.
The remainder of the paper is organized as follows. Section 2 reviews related work on flight delay prediction and propagation. Section 3 describes the proposed TFT-DCP (Temporal Fusion Transformer—Dynamic Chain Propagation) framework, including the data processing workflow, feature encoding, and model architecture. Section 4 presents the experimental setup, benchmark comparisons, ablation studies, and cross-airport evaluations. Section 5 concludes the paper by summarizing the key findings, discussing limitations, and outlining directions for future research.
2. Literature Review
The increasing complexity of global air transportation systems has positioned flight delays, particularly extreme disruptions, as a critical research focus in air traffic management. Early studies primarily relied on statistical models and parametric inference to estimate delay probabilities. For example, Wesonga [8] developed a parametric framework using Entebbe International Airport data to quantify probabilities of ground delays and airborne holdings, revealing threshold-sensitive delay distributions.
With the rise in data-driven methodologies, machine learning and deep learning techniques have become prevalent in operational delay modeling. Early work focused on delay classification using models such as Random Forests (RF), Support Vector Machines (SVM), and Neural Networks, later evolving into time series models like LSTM (Long Short-Term Memory). Kim [9] applied LSTM to airport sequence modeling, while Gui [10] integrated ADS-B, weather, and schedule data, comparing LSTM and RF, and demonstrating RF’s robustness in sparse data settings. Yu [11] further proposed a DBN-SVR ensemble showing reliable generalization in large-scale datasets.
Researchers soon began to recognize the importance of external influence factors—such as meteorological conditions, flight chain dependencies, and airport network interactions—in shaping delay outcomes. Qu [12] and Li [13] employed CNN-based architectures to fuse spatiotemporal features from weather and operations, while Shi [14] and Lian [15] introduced metaheuristic optimization to improve training and prediction efficiency. Guo [16] enhanced RF with the Maximal Information Coefficient for more effective feature selection.
Recent advancements focus increasingly on attention mechanisms and bidirectional modeling architectures to capture deeper temporal and contextual dependencies. Mamdouh [17] used attention-BiLSTM with SMOTE to address class imbalance, whereas Khan [18] developed parallel-serial ELM frameworks for multi-label IATA delay classification. Forecast horizons have also been extended significantly; Kim and Park [19], for instance, explored prediction windows ranging from 2 to 48 h. Zeng et al. [20] further extended this trend by developing a multimodal spatial-temporal network (MST-WA) that integrates weather imagery and network topology to enhance terminal area flow prediction, while Fang et al. [21] proposed an attention-enhanced graph convolutional LSTM (AGC-LSTM) that explicitly models spatial dependencies within sector traffic flow.
Given the cascading nature of delays, understanding their propagation along flight chains is now regarded as essential for improving prediction accuracy and intervention strategies. Cai [22] introduced Dynamic Graph Convolutional Networks (DGCNs) to model airport network disruptions using temporal and adaptive spatial modules. Rebollo and Balakrishnan [23] defined network-level delay state variables, using RF for system-wide forecasts. Meanwhile, Li and Jing [24] proposed a spatiotemporal Random Forest combining complex network features with LSTM-extracted temporal dependencies. Evler [25] took a system-level approach, jointly modeling aircraft recovery and turnaround operations to track and quantify delay propagation paths.
Despite these advances, individual flight-level delay prediction remains challenging, particularly due to irregularly sampled, multivariate time series caused by incomplete or asynchronous observations. To address this, current efforts diverge into two main lines:
- (1)
- Imputation-based methods, such as GRU-D [26], use missingness masks and time-gap encoding, but often introduce distributional distortions;
- (2)
- Non-imputation models, such as Shukla’s mTAN [27] and Hajisafi’s WaveGNN [28], directly embed irregular observations through multi-scale attention or graph-based dynamics.
In the aviation domain, Liu [29] leveraged adaptive bi-directional GNNs to mitigate ground-handling data gaps and validated their operational feasibility.
Nevertheless, three persistent limitations remain:
- (1)
- Deep models often assume dense, regularly sampled inputs, which are incompatible with sparse and incomplete flight logs;
- (2)
- Graph-based approaches tend to aggregate delays at the airport level, overlooking micro-level flight chain interactions;
- (3)
- Extreme delays, while rare, are frequently discarded during training due to class imbalance or noise suppression.
Unlike prior work that applies chain rules as post-processing steps or discards extremes as anomalies, TFT-DCP embeds the time-decayed influence of upstream delays as a learnable feature directly inside the Transformer, and repurposes extreme delays as reference exemplars via similarity retrieval, thereby simultaneously closing all three gaps within a single training objective.
3. Data and Methodology
To address the challenges of delay propagation under extreme weather scenarios, this study proposes a chain-aware, data-driven prediction framework. As shown in Figure 1, the framework is designed to integrate three key factors that jointly influence flight departure delays:
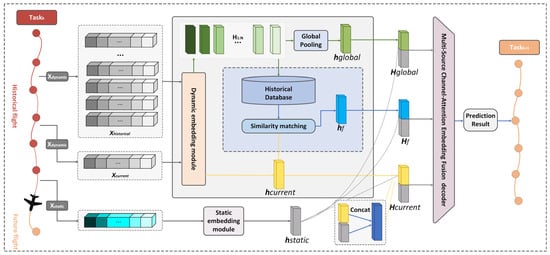
Figure 1.
The architecture of the TFT-DCP.
- Temporal flight chain dependencies: capturing how upstream delays propagate across flight legs;
- External disruptions: incorporating meteorological and airport operational data to model real-time conditions;
- Sparse and irregular observations: enabling robust prediction even under limited or irregular flight records.
The model consists of a historical retrieval module for rare-delay cases, a delay-propagation module that embeds flight chain dependencies, and a multi-source attention-based decoder to fuse meteorological, flight, and airport information. This architecture is designed not merely for performance but to support resilient decision-making in operationally complex environments.
The following subsections introduce the datasets and preprocessing steps used to support this framework.
3.1. Data
This study employs 2023–2024 U.S. airline flight operations data as the core dataset, encompassing flight numbers, departure and arrival airports, scheduled and actual times, along with other relevant attributes. Flight and airport records are sourced from the Bureau of Transportation Statistics (BTS) Airline On-Time Performance Database, while meteorological data originate from NOAA’s (National Oceanic and Atmospheric Administration) Local Climatological Data (LCD) system.
3.1.1. Analysis of Flight Departure Delay Time Characteristics
Departure delay is defined as the difference between actual and scheduled departure times [30]. Figure 2 summarizes the overall distribution of departure delays in the U.S. during 2023. Most flights depart on time or with only minor delays. According to FAA (Federal Aviation Administration) standards, short delays (16–30 min) and medium delays (31–60 min) account for 17.17% and 14.65% of flights, respectively. In contrast, delays exceeding 180 min occur in only 6.52% of cases, highlighting their statistical rarity but potential operational severity.
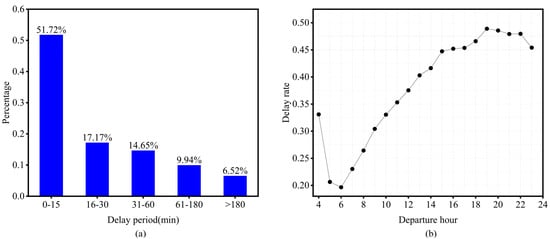
Figure 2.
Flight departure delay time characteristics. (a) Distribution of flight delays by delay duration. (b) Variation of hourly departure delay rate throughout the day.
Temporal analysis of delay occurrence reveals a clear diurnal pattern. As shown in Figure 2b, departure delays are lowest in the early morning hours (4:00–6:00), when airport utilization is minimal. However, as the day progresses and traffic density increases, delays gradually intensify, especially after the morning peak. The highest delay rates occur during the late afternoon and evening hours (16:00–20:00), indicating that system congestion and cumulative propagation from earlier disruptions play a major role.
This cyclical behavior reflects the spatiotemporal heterogeneity of delay propagation in large-scale aviation networks. The interaction between daily flight scheduling patterns, airport capacity, and weather conditions—particularly in the afternoon when convective weather is more likely—leads to significantly higher variability in operational outcomes.
Such temporal characteristics not only impact individual flights but also influence delay propagation across flight chains, as aircraft arriving late from one segment often cause subsequent departures to be delayed. Therefore, capturing these regularities is critical in designing a robust prediction framework.
3.1.2. Extreme Delay Definition and Identification
In this study, we define extreme delays as departure delays exceeding 180 min. This threshold follows the approach of Du et al. [1], which treats cancelled flights as equivalent to delays of at least 180 min for the purpose of delay propagation analysis. The rationale for this definition is twofold: it captures the operational severity of such events, and it provides a consistent basis for identifying high-impact disruptions across datasets.
To identify extreme delay events, we analyzed U.S. flight operations data from the year 2024, calculating the daily and weekly frequencies of flights exceeding this threshold [31]. The results, shown in Figure 3, reveal several distinct peaks, each corresponding to a known extreme weather event. These include:
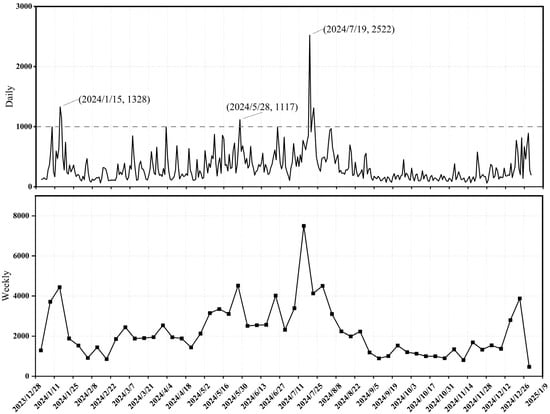
Figure 3.
Extreme delays (daily and weekly) in the US in 2024.
13–16 January 2024: A major winter storm affecting large parts of North America, with 1328 extreme delays recorded on 15 January alone [32];
28–29 May 2024: Severe wind and hail storms across the South Plains, resulting in 1117 extreme delays on 28 May [33];
18–20 July 2024: Prolonged high-pressure conditions in the same region caused 2522 extreme delays on 19 July [34].
These cases highlight the coupling between meteorological extremes and delay spikes, where local or regional weather systems can induce cascading disruptions across multiple airports.
Importantly, these events serve not only as case studies but also as critical inputs for evaluating model performance under high-stress conditions. By integrating such extreme scenarios into the model’s training and testing pipeline, we aim to improve its ability to generalize and respond to rare but impactful disruptions.
This empirical identification process lays the foundation for scenario-specific validation of the prediction framework and also reinforces the importance of weather-aware, chain-aware modeling strategies—especially when extreme delays may propagate rapidly through the network.
3.1.3. Data Processing Workflow
To ensure the effectiveness of delay prediction under real-world conditions—especially those involving extreme weather and interdependent flight operations—this study implements a structured data processing pipeline. The design emphasizes three core objectives:
- (1)
- Preserving extreme delay events;
- (2)
- Capturing airport-level operational states to reflect congestion and capacity changes;
- (3)
- Aligning multi-source features, including meteorological and flight chain information, for consistent model input.
The approach enables more precise modeling of temporal dependencies in flight delays through the following stages, which form an integrated pipeline where each stage builds upon the output of the previous step:
- Step 1: Anomaly Detection
Flight operation data often contains outliers or irregular entries caused by equipment failure, data transmission issues, or unexpected operational disruptions. To distinguish genuine extreme delays from erroneous records, we apply an unsupervised clustering algorithm for anomaly detection.
Importantly, delays flagged as statistically extreme are not removed, but retained intentionally, as they may represent valid high-impact events (e.g., storm-induced ground stops). This approach ensures that the model learns to handle rare, disruptive conditions rather than ignoring them. The output of this stage—cleaned but complete delay records including extreme events—serves as input for the subsequent data cleaning process.
- Step 2: Data Cleaning
Given the heterogeneity of data sources, different cleaning strategies are applied:
Flight data: Records with critical missing attributes or confirmed cancellations (for which no delay propagation can be modeled) are removed. Features with high missingness are discarded.
Meteorological data: short gaps are interpolated linearly over time; For longer gaps, two complementary strategies are applied depending on the weather condition. During non-extreme periods, missing records are replaced using the same-hour historical averages to maintain temporal consistency. In contrast, during extreme-weather periods, missing meteorological values are complemented using spatially adjacent observations from nearby weather stations to preserve the integrity of abnormal meteorological patterns. To ensure model stability and convergence, we implemented a two-stage normalization process: (1) Categorical Feature Encoding: Categorical features such as airport codes and tail numbers were transformed into numerical representations using James-Stein encoding. (2) Min-Max Normalization: All numerical features were normalized to the [0, 1] range using Min-Max scaling. All normalization parameters were derived exclusively from the training set.
This stage ensures data completeness while preserving the integrity of extreme events identified in Step 1. The cleaned dataset then feeds into the feature extraction process, where operational metrics can be reliably computed.
- Step 3: Airport Status Feature Extraction
Using the cleaned data, we derive key metrics from scheduled flight information to holistically characterize airport operational states:
Historical peak capacity: Maximum number of hourly departures handled, quantifying infrastructure capacity;
Cumulative departure delay (past hour): Total delay minutes in the previous hour;
Operational density: Number of scheduled departures within the current hour;
Real-time utilization rate: Ratio of current operational density to historical peak capacity.
These metrics dynamically capture fluctuations in airport workload across time windows, providing critical inputs for delay prediction models.
- Step 4: Multi-source Data Integration
We construct a unified input structure through spatiotemporal alignment and feature consolidation. This stage coordinates the previously processed data streams into a coherent format: Flight-centric data fusion, integrating flight operations, airport status, and meteorological data into a single record per flight:
where components represent airport status indicators, meteorological features, and flight-specific attributes, where i represents the index of individual flight records (i = 1, 2, …, N), with N denoting the total number of flights in the dataset; ai, bi, and fi denote the airport status, meteorological, and flight-specific feature vectors, respectively, for the i-th flight.
Prediction task definition: In this study, a prediction task is defined as a group of flights that share the same origin airport, destination airport, and scheduled departure time. This grouping strategy structures the input data into similar operational contexts. Flights within the same task encounter comparable environment characteristics and temporal conditions—such as specific weather patterns.
By learning from these groups of analogous flights, the model can mitigate the challenges of data sparsity and irregular sampling. Consequently, each prediction task represents a shared operational scenario for a given origin–destination pair under specific temporal conditions, forming a robust foundation for training and prediction:
Let Tj denote the j task. Where j represents the index of prediction tasks (j = 1, 2, …, J), with J denoting the total number of prediction tasks in the dataset; Tj represents the j-th prediction task grouping flights with identical origin airport O, destination airport D, and scheduled departure time t. Flight records with identical attributes are assigned to the same task.
This unified representation forms the input to our predictive model, where both external disturbances and chain-based propagation can be modeled explicitly.
3.1.4. Flight Chain Data Architecture
One of the most critical features of flight operations is that aircraft follow predetermined chains of flight legs, typically operating multiple segments within a single day. A delay at the beginning of this chain can propagate to later flights, resulting in cascading disruptions. To capture this behavior, we reconstruct the complete operational trajectories of individual aircraft using flight chain modeling.
- (1)
- Chain Construction Protocol
Each aircraft is uniquely identified by its tail number, and its daily operations are grouped based on this identifier and the flight date. By sorting these records in chronological order, we reconstruct the sequence of flight legs—forming a flight chain for each aircraft on each day:
where k represents the index of flight chains (k = 1, 2, …, K), with K denoting the total number of flight chains in the dataset, each Ck represents the k-th flight chains comprising sequential flight legs operated by the same aircraft on date D. This structure enables the explicit modeling of intra-aircraft temporal dependencies, which are not captured in airport-level aggregation approaches.
- (2)
- Delay Propagation Encoding
To model how delays propagate across these chains, we define a dedicated input feature called Late-aircraft-delay. For each flight in a chain (except the first), this value is computed based on the actual delay in the previous leg, adjusted by a time-decay factor to account for the recovery potential between flights. Figure 4 presents a real-world delay propagation sequence derived from the same-aircraft operations of tail number 191NV on January 1, 2023. The aircraft performed four consecutive flights (BNA–PGD–LEX–PGD–BNA) on that day. The first leg from BNA to PGD departed 13 min late and arrived 30 min late. Due to a short turnaround interval of about 35 min, the subsequent leg from PGD to LEX departed 30 min late, and the following legs exhibited similar delay magnitudes without full recovery.
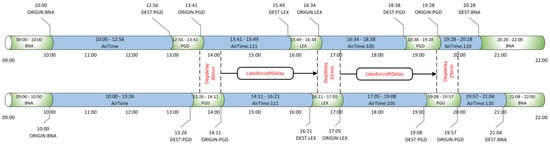
Figure 4.
Flight chain delay propagation mechanism.
This sequence demonstrates how limited turnaround buffers amplify temporal dependency between successive flights: when an upstream leg incurs a significant delay, downstream legs operated by the same aircraft tend to inherit part of the disruption.
The processing pipeline yields a dataset comprising 145,167 flight chains. Each chain consists of sequential flight legs, represented as:
3.2. Prediction Model
This section details the architecture of the proposed TFT-DCP model. To address the challenges of delay prediction in flight chain structures under extreme and sparse operational conditions, we extend the Temporal Fusion Transformer (TFT) [35] framework with three key innovations: A multi-source attentional embedding fusion decoder, Temporal Convolutional Networks (TCNs) [36] enhanced with gated residual connections, and a dynamic chain propagation mechanism incorporating embedded historical retrieval. These components collectively form the Temporal Fusion Transformer with Dynamic Chain Propagation for departure delay prediction.
3.2.1. Feature Encoding
The feature encoding module is designed to extract meaningful representations from flight, airport, and weather data. These features are divided into two categories: dynamic features and static features. Static features represent time-invariant attributes that characterize the operational context of a flight. These features are directly derived from the published flight schedule and airport data, remaining constant from the initial planning phase through execution. Examples include the origin and destination airport index, scheduled departure and arrival times.
In contrast, dynamic features capture time-varying operational states. These features are computed from continuously updated data streams, including actual flight operations, airport-level aggregates, and real-time meteorological observations. Unlike static features, these features evolve with the operational environment, allowing the model to capture real-time fluctuations, the cascading effects of upstream disruptions, and the dynamics of extreme weather scenarios. A detailed breakdown of the features used in this study, along with their sources and categorization, is provided in Table 1.

Table 1.
Flight data classification features.
- (1)
- Dynamic Feature Embedding
Dynamic features are encoded using a Temporal Convolutional Network (TCN), which leverages dilated causal convolutions to capture temporal dependencies. This process generates per-flight embedding vectors, as follows:
Each flight’s dynamic input sequence is transformed into an embedding vector representing its historical operational pattern. These are then aggregated into a global representation, which serves as one of the core inputs to the downstream prediction framework.
- (2)
- Static Feature Embedding
Static features are encoded via a Gated Residual Network (GRN) to produce static embedding vectors. The GRN computation is defined by Equations (7)–(10):
Here, ELU (Exponential Linear Unit) denotes the Exponential Linear Unit activation function [37]; W and b represent the weight matrices and bias terms for the respective gates; γ is the input from the previous layer; σ denotes the Sigmoid activation function; ⊙ represents the element-wise (Hadamard) product; and LayerNorm (Layer Normalization) [38] refers to layer normalization. The GRN adaptively regulates information flow through gated mechanisms and incorporates residual connections to mitigate the vanishing gradient problem, thereby producing the static embedding vectors hstatic.
3.2.2. Embedded Historical Retrieval
Flight delays caused by extreme weather are relatively rare but operationally significant. Traditional models often underperform in these scenarios due to the limited number of similar samples available during training. To address this challenge, we design an embedded historical retrieval mechanism that allows the model to dynamically reference historically similar flights during inference.
This module consists of three main steps:
- Step 1: Creation of the Historical Database
A reference database is constructed using embedding vectors from previously observed flights. After each day’s predictions are completed, the learned dynamic representations (from the TCN encoder in Section 3.2.1) are stored and indexed. To enhance robustness under disruption scenarios, the historical database additionally incorporates extreme-weather cases observed over the past five years (2019–2023). Each vector captures the temporal context of the flight, including operational and weather-related characteristics:
This allows the model to maintain an up-to-date memory of diverse delay scenarios—especially those involving high-impact or rare disruptions.
- Step 2: Similarity-Based Retrieval
When predicting delays for a new flight, the model computes the cosine similarity between the current flight’s embedding and all historical vectors in the database.
The top-k most similar records are selected. A weight μi is assigned to each retrieved record based on its similarity score, indicating its relevance to the current flight’s context.
Equations (12) and (13) formalize the similarity computation and weighting process.
- Step 3: Historical Fusion
The selected historical embeddings are aggregated into a reference vector using a weighted average, ensuring that both operationally similar and high-impact past examples contribute to the prediction.
This reference vector is then combined with the current flight’s embedding to produce an enriched representation that reflects both recent observations and relevant historical context.
Equations (14) and (15) define the fusion mechanism.
The historical retrieval module is differentiable, allowing gradients to propagate through operations. During backpropagation, the prediction loss generates gradients that flow through the fused representation, combining the current flight embedding and the retrieved historical embedding.
The gradient is distributed between the current and historical embeddings according to the fusion coefficient, ensuring that both real-time and historical information contribute to learning. The portion assigned to the historical embedding is further propagated to individual historical records based on their relevance weights.
These weights are computed via a softmax function over cosine similarity scores, providing a differentiable path for gradients to reach the similarity computations. The gradients also propagate into the TCN encoder that generates the embeddings, enabling joint optimization of the encoder and retrieval mechanism.
This end-to-end gradient flow allows the model to continuously refine its embedding space and retrieval weights, improving its ability to identify relevant historical patterns and enhancing prediction accuracy under rare or extreme delay scenarios.
By integrating these historical patterns, the model becomes more robust in low-data and high-variance conditions, particularly when confronted with extreme delays caused by weather or cascading operational failures. This capability is essential for maintaining prediction accuracy during rare but critical disruptions.
3.2.3. Multi-Source Channel-Attention Embedding Fusion Module
In real-world flight operations, delays are rarely caused by a single factor. Instead, they often arise from the joint influence of multiple heterogeneous sources, including airport congestion, meteorological disruptions, and residual upstream delays. To effectively capture this complexity, we implement a multi-source channel-attention embedding fusion module (MS-CA-EFM).
This module enables the model to dynamically assess and integrate different types of feature embeddings based on their relative importance at each moment. It consists of three main stages:
- (1)
- Multi-Source Feature Concatenation
Vector-space alignment is first performed on hierarchical embeddings. The static embedding is concatenated with (a) the global dynamic embedding, (b) the reference dynamic embedding, and (c) the dynamic embedding of the flight to be predicted, yielding vectors Hcurrent (target flight), Hf (reference), and Hglobal (global). This preserves multi-source information while enabling effective attention computation.
- (2)
- Channel-Attention Fusion
To capture channel-wise contribution variances, a channel-attention architecture (Figure 5) fuses the embeddings [39]:
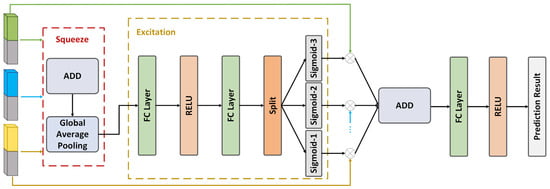
Figure 5.
Multi-source Channel Attention-based Embedding Fusion Module.
Step 1. Element-wise summation generates an aggregated vector:
Step 2. Global average pooling extracts channel-wise statistics:
Step 3. With a reduction ratio r, two fully connected layers model channels dependencies:
where and are the weight matrices. The output A is partitioned into three segments, each activated by a sigmoid function to generate the respective weight vectors:
Step 4. Apply channel-wise weighting:
Step 5. Sum the weighted embeddings to obtain the fused representation:
- (3)
- Residual Enhancement and Prediction
To reduce information loss and accelerate convergence, the fused vector is processed with a residual connection and LayerNorm. The normalized vector is then passed through a fully connected layer, followed by ReLU activation to produce the predicted delay.
By adaptively learning the relative importance of each information source, this module enhances the model’s robustness and interpretability, especially in the presence of conflicting signals or incomplete data. It serves as a critical bridge between low-level feature encoding and high-level flight delay prediction.
3.2.4. Flight Chain Delay Propagation Module
Multiple factors contribute to flight delays and cancellations—including severe weather, air-traffic control restrictions, and operational disruptions. Among these, delays in preceding flights are identified as one of the most critical causes [40,41].
Unlike prior work that treats flight chain propagation as a static rule or a post hoc correction, TFT-DCP is the first to explicitly model the term “preceding delay × exponential time decay” as a learnable feature and feed it directly into the Transformer, thereby endowing the model with an inductive bias for dynamic chain dependencies during training.
This module explicitly models the propagation effects of upstream delays on subsequent flights, establishing delay-propagation paths within flight chains to address the conventional neglect of inter-flight dependencies. The core procedure comprises the following:
Let {F1, F2, …, FN} denote the set of preceding flights, {yprev,1, yprev,2, …, yprev, N} each predecessor’s delay duration, and {Δt1, Δt2, …, ΔtN} the time interval between each preceding flight and the current flight. An exponential decay function computes the time-decayed weights:
where β is the decay coefficient modulating the influence of the time interval. Using the weights σ from Equation (23), the predecessor delays are aggregated to generate the current flight’s propagated-delay feature:
The attenuation coefficient β is defined as a learnable model parameter. During training, β is optimized through backpropagation as part of the end-to-end learning process. Specifically, after each forward pass, the prediction loss L (MSE) generates gradients with respect to β through the chain rule:
The final term captures how the time-decay weight σ changes with β within the exponential function. These gradients are then used in gradient-descent updates so that β converges to values that minimize the overall prediction error. In practice, β is initialized to 1.0 and adaptively adjusted during training to represent the effective recovery rate of the system. Our experiments show that β converges to 0.73–0.89 across different weather conditions. This mechanism enables the model to automatically learn context-specific temporal decay patterns under different operational and meteorological conditions.
This mechanism captures dynamic dependencies among flights within the chain, significantly enhancing overall delay-prediction performance and rectifying the oversight of inter-flight dependencies in conventional approaches.
3.2.5. Computational Complexity Analysis
The proposed TFT-DCP model extends the base Temporal Fusion Transformer by introducing three modules:
- (1)
- Embedded Historical Retrieval Module
The computational cost arises primarily from the cosine similarity computation between the current embedding hcurrent and the top-k historical embeddings hi, followed by a softmax normalization. Both operations scale linearly with the embedding dimension d and the number of retrieved records k, yielding a time complexity of O(k·d).
- (2)
- Multi-Source Channel-Attention Embedding Fusion Module
This module integrates representations from three heterogeneous information sources (hglobal, hf and hcurrent) through a channel-attention mechanism. Its complexity is primarily determined by the channel-wise operations. The element-wise summation (Equation (16)), global average pooling (Equation (17)), and channel-wise weighting (Equation (21)) each have a complexity of O(B × C × d), where B is the batch size, C is the number of channels (C = 3), and d is the embedding dimension. Since B is typically considered a constant during complexity analysis, the effective complexity simplifies to O(d). The channel attention operations (Equations (18) and (19)) involve only low-dimensional transformations due to the channel reduction ratio, resulting in negligible additional complexity.
- (3)
- Flight Chain Delay Propagation Module
The delay propagation module computes the exponential weighting across N preceding flight legs within the same chain. The complexity is O(N) for each flight, as the decay weight σi and the weighted sum yprop are calculated sequentially. Given that N (the chain length) is typically small (N < 6), this cost is negligible compared to the transformer-based temporal encoding.
Overall, the proposed modules introduce only linear overhead with respect to the number of retrieved records (k), source streams (C), and flight-chain length (N). Moreover, each module enhances interpretability: historical retrieval explicitly identifies analogous delay scenarios, fusion quantifies source contributions, and delay-decay models temporal propagation strength—thereby improving robustness without compromising efficiency or explainability.
4. Results
This section details the input features, evaluation metrics, and baseline models, together with experimental results demonstrating the predictive performance of the proposed TFT-DCP model.
4.1. Input Features
To enhance the model’s ability to predict flight delays, flight attributes are categorized into static and dynamic features. This division enables better adaptation to the modeling requirements posed by heterogeneous data types (Table 1). Static features provide context about each flight’s scheduled characteristics, such as the airport category or scheduled departure time. These features help the model distinguish between different flight categories and operational baselines. Dynamic features, by contrast, reflect the real-time operational environment. They include both observed values, such as actual taxi-out time or upstream delay, and forecasted inputs, such as scheduled weather or predicted airport density. This structure enables the model to recognize temporal patterns and detect abnormal conditions, especially under extreme scenarios. By combining these features, the model receives a comprehensive view of each flight’s current condition, operational history, and environmental context. These input categories align directly with the encoding, retrieval, and fusion modules introduced in Section 3.2.
4.2. Experimental Environment and Settings
4.2.1. Computational Environment
A flight chain delay-prediction system was developed and evaluated under laboratory conditions using real flight, airport, and meteorological datasets. All experiments were implemented in Python 3.11.10 on a Windows 11 platform. The computing hardware comprised an Intel Core i7-12700H processor (2.3 GHz) and an NVIDIA GeForce RTX 3060 Laptop GPU. Model development and training were conducted in PyCharm 2023.2.1 with PyTorch 2.5.1, leveraging CUDA 12.6 for accelerated computation.
4.2.2. Hyperparameter Configuration and Experimental Design
The model was trained on the complete 2023 U.S. airline dataset, with temporal partitioning where data from January to October 2023 were used for training and November-December 2023 for validation. The test set consisted of periods in 2024 corresponding to the identified extreme weather events (13–16 January, 28–29 May, and 18–20 July), as shown in Figure 3. Extensive tuning yielded the following optimal hyperparameters: learning rate = 0.001, dropout rate = 0.1, hidden dimension = 128, batch size = 256, and sequence length = 14.
Three sets of experiments were conducted to evaluate the effectiveness of the proposed approach:
- (1)
- Benchmark Comparison: Performance was contrasted with classical time-series forecasting models to demonstrate the superiority of the proposed method.
- (2)
- Ablation Study: Component-level ablations were performed to assess the indispensability of each architectural module.
- (3)
- Cross-Airport Evaluation: Predictive accuracy was analyzed across different airports to verify robustness under diverse operational environments.
4.2.3. Evaluation Metrics
The model’s performance is assessed using three standard indicators: Mean Absolute Error (MAE), Root Mean Square Error (RMSE), and the coefficient of determination (R2). They are defined as follows:
All evaluations are conducted on de-normalized data to present the results in their original scale.
4.3. Experimental Validation
To validate the efficacy and superiority of the proposed TFT-DCP model for flight-delay prediction, we designed three experimental groups:
- (1)
- Benchmark comparisons against classical time-series models to verify performance advantages;
- (2)
- Ablation studies evaluating the essential contribution of each component;
- (3)
- Cross-airport analyses assessing robustness under diverse operational conditions.
4.3.1. Baseline-Model Comparison
For a comprehensive performance assessment, the following canonical predictors were selected as baselines:
Historical Average (HA): Forecasts future values by averaging historical observations from identical time windows. While simple and stable, it cannot address non-periodic fluctuations.
Long Short-Term Memory (LSTM) [42]: A specialized recurrent neural network capable of modelling long-range dependencies.
Temporal Convolutional Network (TCN): Captures local dependencies in sequence data through stacked convolutions with extended receptive fields, offering an alternative to RNNs.
Informer [43]: A Transformer-based forecasting architecture optimized for long-sequence time-series prediction.
Temporal Fusion Transformer (TFT): A transformer-based framework that explicitly handles heterogeneous data sources.
All models were trained and evaluated on the identical dataset with uniform training protocols to ensure fair comparison. Results are in Table 2.

Table 2.
Comparative experiment.
The proposed TFT-DCP outperforms the traditional model (HA), deep-learning baselines (LSTM, TCN, Informer), and the original TFT across all metrics. Relative to the best baseline (TFT), TFT-DCP reduces MAE and RMSE by 8.8% and 26.0%, respectively, and improves R2 by 5.75%.
Table 3 presents a detailed comparison of model performance across three representative meteorological scenarios—Winter Storm, Convective Weather, and High-Pressure Event—and two operational periods (Normal and Peak Disruption).

Table 3.
Comparison across three meteorological scenarios.
Across all scenarios, TFT-DCP consistently outperforms both the baseline TFT and Informer models, achieving lower MAE and RMSE and higher R2. This consistency demonstrates the model’s robustness under varying levels of operational stress.
To validate the reliability of the observed performance improvements, we conducted paired t-tests between the proposed TFT-DCP and the best baseline (TFT) across 100 randomly sampled test subsets. The results show that the improvements in MAE (3.23 and 3.54), RMSE (6.25 and 8.45), and R2 (0.92 and 0.87) are statistically significant, with p-values < 0.001 for all metrics. The corresponding 95% confidence intervals for the performance differences are [−0.38, −0.24] for MAE, [−2.45, −1.95] for RMSE, and [0.045, 0.061] for R2, confirming that the observed gains are statistically robust and unlikely to arise from random variation.
Figure 6 provides a visual comparison of model performance under extreme-delay scenarios. The bottom panel displays the actual delay trajectory (black line), while the upper three panels show the predictions made by TCN (red), TFT (blue), and the proposed TFT-DCP model (green).
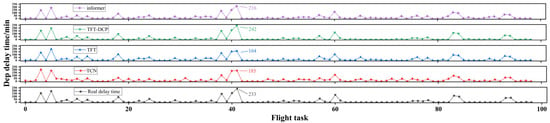
Figure 6.
Flight departure delay prediction results.
Among the three models, TFT-DCP demonstrates the closest alignment with real delay patterns, particularly during the peak disruption period. Its predicted maximum delay reaches 242 min, which nearly matches the ground truth. In contrast, TCN and TFT exhibit substantial deviations from the actual delay peaks.
Overall, TFT-DCP achieves a prediction error of only 9 min, compared to 185 min for TCN and 164 min for TFT. These results highlight the model’s effectiveness in capturing the dynamic characteristics of extreme delay propagation and its robustness under volatile operational conditions.
4.3.2. Ablation Study
Table 4 presents the results of the ablation study assessing the contribution of each key module to the overall performance of the proposed TFT-DCP model. Experiment 1, which excludes all core modules, achieves the worst performance with an MAE of 3.86 min, RMSE of 7.62 min, and R2 of 0.79. Introducing the Dynamic Embedding Module in Experiment 2 significantly improves accuracy (MAE reduced to 3.51 min; R2 increased to 0.85), demonstrating its effectiveness in capturing temporal dynamics. Experiment 3, which further incorporates the Embedded Historical Data Retrieval Module, achieves additional gains (MAE of 3.36 min, RMSE of 6.47 min, and R2 of 0.87), highlighting the importance of leveraging historical extreme delay patterns. Finally, Experiment 4 integrates all modules—including the MS-CA-EF (Multi-Source Channel-Attention Embedding Fusion) Module and the Flight Chain Module—resulting in the best performance (MAE of 3.23 min, RMSE of 6.25 min, R2 of 0.92). These results clearly validate the contribution of each module, and more importantly, illustrate the synergistic effect of combining delay propagation modeling with historical memory and multi-source fusion, particularly under high-impact disruption scenarios.

Table 4.
Comparative experiment.
4.3.3. Comparative Performance Analysis Across Airports
To further assess the model’s generalizability across different airport environments, we analyze prediction errors in terms of MAE and RMSE across all test-set airports.
As shown in Figure 7, the model demonstrates overall accuracy: most airports exhibit MAE values between 3 and 6 min, indicating reliable capture of primary delay patterns. However, RMSE values are often higher, with notable differences between MAE and RMSE at certain airports—suggesting that a small number of extreme delay outliers significantly increase error variance.
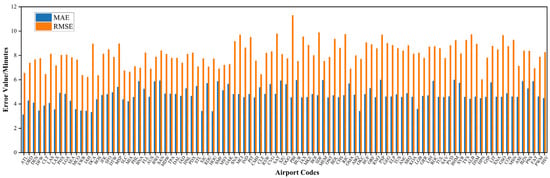
Figure 7.
Prediction performance at different airports.
At major high-traffic hubs such as Atlanta (ATL), Chicago O’Hare (ORD), and Dallas/Fort Worth (DFW), the model achieves consistently low error values, and the MAE-RMSE gap remains narrow, reflecting stable operations and fewer extreme disruptions.
In contrast, airports like Kona (KOA), Anchorage (ANC), and San Juan (SJU) show much wider MAE-RMSE discrepancies. This suggests that sporadic extreme delay events—often driven by geographic remoteness, weather instability, or infrastructure limitations—contribute to sharp spikes in prediction error.
Despite these challenges, the model maintains predictive performance across most airports. These results not only validate the model’s predictive performance but also underscore its transferability, reflecting its ability to generalize across airports with different traffic densities, meteorological patterns, and operational complexities. These results underscore the robust generalization capability of the TFT-DCP model and its resilience to localized disruption patterns under complex real-world conditions.
5. Conclusions
To address the intertwined challenges of data sparsity, extreme delays, and dynamic flight chain dependencies in departure-delay prediction, this study proposes TFT-DCP—a flight chain prediction model based on an enhanced Temporal Fusion Transformer framework. In contrast to traditional methods that either discard extreme delays as outliers or apply chain-propagation as post hoc corrections, TFT-DCP incorporates the decaying influence of upstream delays as a learnable embedding during training. This design enables the model to inherently learn dynamic chain-dependent structures and respond to complex propagation effects.
Guided by aviation operational logic, we develop a structured data processing pipeline that includes anomaly filtering, task-specific imputation, and flight-task grouping to accurately reconstruct flight chains and retain rare but critical delay cases. The proposed model integrates historical retrieval, multi-scale temporal learning, a feature fusion module, and flight chain propagation into the architecture. Extensive experiments confirm the superiority of TFT-DCP over baselines, and cross-airport evaluations highlight its transferability and robustness across diverse airport types, traffic volumes, and meteorological conditions. This confirms the model’s potential as a scalable and deployable solution for enhancing departure management and traffic flow coordination under extreme delay scenarios.
These findings indicate that TFT-DCP has the potential to enhance the DMAN and A-CDM framework. With accurate delay forecasts, air traffic controllers and airport operators can proactively coordinate resources, adapt departure strategies, and mitigate cascading delays, improving systemic efficiency and passenger satisfaction.
Future extensions will aim to incorporate real-time airspace constraints and ground-resource availability into the model input space. Additionally, future extensions could incorporate space weather indices to examine indirect impacts on delay propagation via navigation/communication degradation, especially on high-latitude and long-haul routes where GNSS systems are most vulnerable to space weather effects. In addition, the integration of networks will allow for modeling inter-airport delay propagation at a regional and national scale, supporting a network-wide situational awareness framework.
Author Contributions
Conceptualization, J.G. and J.L.; methodology, J.L.; software, J.L.; validation, J.Y. and Z.R.; formal analysis, J.L.; investigation, J.Y., Y.Y.; resources, J.G. and Y.Y.; data curation, Y.Y.; writing—original draft preparation, J.L.; writing—review and editing, J.G. and Z.R.; visualization, J.L.; supervision, J.G.; project administration, J.G.; funding acquisition, J.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key R&D Program of China (grant number 2024YFB2605201), the Special Funding for Basic Scientific Research Business Expenses of Central Universities (grant number PHD2023-041), and the Civil Aviation Education Talent Project (grant number MHJY2025002, MHJY2025003). The APC was funded by the authors.
Data Availability Statement
These data were derived from the following resources available in the public domain: Bureau of Transportation Statistics (https://www.transtats.bts.gov/, accessed on 28 October 2025) and National Centers for Environmental Information (https://www.ncdc.noaa.gov/, accessed on 28 October 2025).
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| DMAN | Departure Management |
| A-CDM | Airport Collaborative Decision Making |
| TFT | Temporal Fusion Transformer |
| TFT-DCP | Temporal Fusion Transformer with Dynamic Chain Propagation |
| TCN | Temporal Convolutional Network |
| GRN | Gated Residual Network |
| MS-CA-EFM | Multi-Source Channel-Attention Embedding Fusion Module |
| MAE | Mean Absolute Error |
| RMSE | Root Mean Square Error |
| R2 | Coefficient of Determination |
| HA | Historical Average |
| LSTM | Long Short-Term Memory |
| FAA | Federal Aviation Administration |
| BTS | Bureau of Transportation Statistics |
| NOAA | National Oceanic and Atmospheric Administration |
| LCD | Local Climatological Data |
| ELU | Exponential Linear Unit |
| LayerNorm | Layer Normalization |
References
- Du, W.B.; Zhang, M.Y.; Zhang, Y.; Cao, X.B.; Zhang, J. Delay causality network in air transport systems. Transp. Res. Part E Logist. Transp. Rev. 2018, 118, 466–476. [Google Scholar] [CrossRef]
- Xue, D.; Wu, L.; Xu, T.; Wu, C.L.; Wang, Z.; He, Z. Space weather effects on transportation systems: A review of current understanding and future outlook. Space Weather 2024, 22, e2024SW004055. [Google Scholar] [CrossRef]
- Qu, J.; Wu, S.; Zhang, J. Flight delay propagation prediction based on deep learning. Mathematics 2023, 11, 494. [Google Scholar] [CrossRef]
- Zheng, Y.; Miao, J.; Le, N.; Jiang, Y.; Li, Y. Intelligent airport collaborative decision making (A-CDM) system. In Proceedings of the 2019 IEEE 1st International Conference on Civil Aviation Safety and Information Technology (ICCASIT), Kunming, China, 17–19 October 2019; pp. 616–620. [Google Scholar] [CrossRef]
- Xu, N.; Kosma, C.; Vazirgiannis, M. TimeGNN: Temporal dynamic graph learning for time series forecasting. In Proceedings of the International Conference on Complex Networks and Their Applications, Cham, Switzerland, 28–30 November 2023; Springer Nature: Cham, Switzerland, 2023; pp. 87–99. [Google Scholar] [CrossRef]
- Sun, X.; Wandelt, S.; Zanin, M. Worldwide air transportation networks: A matter of scale and fractality? Transp. A Transp. Sci. 2017, 13, 607–630. [Google Scholar] [CrossRef]
- Henriques, R.; Feiteira, I. Predictive modelling: Flight delays and associated factors, Hartsfield–Jackson Atlanta International Airport. Procedia Comput. Sci. 2018, 138, 638–645. [Google Scholar] [CrossRef]
- Wesonga, R.; Nabugoomu, F.; Jehopio, P. Parameterized framework for the analysis of probabilities of aircraft delay at an airport. J. Air Transp. Manag. 2012, 23, 1–4. [Google Scholar] [CrossRef]
- Kim, Y.J.; Choi, S.; Briceno, S.; Mavris, D. A deep learning approach to flight delay prediction. In Proceedings of the 2016 IEEE/AIAA 35th Digital Avionics Systems Conference (DASC), Sacramento, CA, USA, 25–29 September 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Gui, G.; Liu, F.; Sun, J.; Yang, J.; Zhou, Z.; Zhao, D. Flight delay prediction based on aviation big data and machine learning. IEEE Trans. Veh. Technol. 2019, 69, 140–150. [Google Scholar] [CrossRef]
- Yu, B.; Guo, Z.; Asian, S.; Wang, H.; Chen, G. Flight delay prediction for commercial air transport: A deep learning approach. Transp. Res. Part E Logist. Transp. Rev. 2019, 125, 203–221. [Google Scholar] [CrossRef]
- Qu, J.; Zhao, T.; Ye, M.; Li, J.; Liu, C. Flight delay prediction using deep convolutional neural network based on fusion of meteorological data. Neural Process. Lett. 2020, 52, 1461–1484. [Google Scholar] [CrossRef]
- Li, Q.; Guan, X.; Liu, J. A CNN-LSTM framework for flight delay prediction. Expert Syst. Appl. 2023, 227, 120287. [Google Scholar] [CrossRef]
- Shi, T.; Lai, J.; Gu, R.; Wei, Z. An improved artificial neural network model for flights delay prediction. Int. J. Pattern Recognit. Artif. Intell. 2021, 35, 2159027. [Google Scholar] [CrossRef]
- Lian, G.; Zhang, Y.; Desai, J.; Xing, Z.; Luo, X. Predicting taxi-out time at congested airports with optimization--based support vector regression methods. Math. Probl. Eng. 2018, 2018, 7509508. [Google Scholar] [CrossRef]
- Guo, Z.; Yu, B.; Hao, M.; Wang, W.; Jiang, Y.; Zong, F. A novel hybrid method for flight departure delay prediction using random forest regression and maximal information coefficient. Aerosp. Sci. Technol. 2021, 116, 106822. [Google Scholar] [CrossRef]
- Mamdouh, M.; Ezzat, M.; Hefny, H. Improving flight delays prediction by developing attention-based bidirectional LSTM network. Expert Syst. Appl. 2024, 238, 121747. [Google Scholar] [CrossRef]
- Khan, W.A.; Chung, S.H.; Eltoukhy, A.E.E.; Khurshid, F. A novel parallel series data-driven model for IATA-coded flight delays prediction and features analysis. J. Air Transp. Manag. 2024, 114, 102488. [Google Scholar] [CrossRef]
- Kim, S.; Park, E. Prediction of flight departure delays caused by weather conditions adopting data-driven approaches. J. Big Data 2024, 11, 11. [Google Scholar] [CrossRef]
- Zeng, Y.; Hu, M.; Chen, H.; Yuan, L.; Alam, S.; Xue, D. Improved air traffic flow prediction in terminal areas using a multimodal spatial–temporal network for weather-aware (MST-WA) model. Adv. Eng. Inform. 2024, 62, 102935. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, S.; Zhang, L.; Jiang, W.; Alam, S.; Xue, D. Short-term multi-step-ahead sector-based traffic flow prediction based on the attention-enhanced graph convolutional LSTM network (AGCLSTM). Transp. Res. Part C Emerg. Technol. 2024, 160, 104461. [Google Scholar] [CrossRef]
- Cai, K.; Li, Y.; Fang, Y.P.; Zhu, Y. A deep learning approach for flight delay prediction through time-evolving graphs. IEEE Trans. Intell. Transp. Syst. 2021, 23, 11397–11407. [Google Scholar] [CrossRef]
- Rebollo, J.J.; Balakrishnan, H. Characterization and prediction of air traffic delays. Transp. Res. Part C Emerg. Technol. 2014, 44, 231–241. [Google Scholar] [CrossRef]
- Li, Q.; Jing, R. Flight delay prediction from spatial and temporal perspective. Expert Syst. Appl. 2022, 205, 117662. [Google Scholar] [CrossRef]
- Evler, J.; Lindner, M.; Fricke, H.; Schultz, M. Integration of turnaround and aircraft recovery to mitigate delay propagation in airline networks. Comput. Oper. Res. 2022, 138, 105602. [Google Scholar] [CrossRef]
- Che, Z.; Purushotham, S.; Cho, K.; Sontag, D.; Liu, Y. Recurrent neural networks for multivariate time series with missing values. Sci. Rep. 2018, 8, 6085. [Google Scholar] [CrossRef] [PubMed]
- Shukla, S.N.; Marlin, B.M. Multi-time attention networks for irregularly sampled time series. arXiv 2021, arXiv:2101.10318. [Google Scholar] [CrossRef]
- Hajisafi, A.; Siampou, M.D.; Azarijoo, B.; Shahabi, C. WaveGNN: Modeling irregular multivariate time series for accurate predictions. arXiv 2024, arXiv:2412.10621. [Google Scholar] [CrossRef]
- Liu, C.; Chen, Y.R.; Wang, H.; Zhang, Y.; Dai, X.; Luo, Q.; Chen, L. Airport flight ground service time prediction with missing data using graph convolutional neural network imputation and bidirectional sliding mechanism. Appl. Soft Comput. 2023, 133, 109941. [Google Scholar] [CrossRef]
- Wang, D.; Sherry, L.; Xu, N.; Larson, M. Statistical comparison of passenger trip delay and flight delay metrics. Transp. Res. Rec. 2008, 2052, 72–78. [Google Scholar] [CrossRef]
- Bombelli, A.; Sallan, J.M. Analysis of the effect of extreme weather on the US domestic air network: A delay and cancellation propagation network approach. J. Transp. Geogr. 2023, 107, 103541. [Google Scholar] [CrossRef]
- January 13–16, 2024 North American Winter Storm. Available online: https://en.wikipedia.org/wiki/January_13%E2%80%9316,_2024_North_American_winter_storm (accessed on 29 June 2025).
- Destructive Wind and Giant Hail Impact the South Plains. Available online: https://www.weather.gov/lub/events-2024-20240528-storms (accessed on 29 June 2025).
- Thursday Webinar Briefing. Available online: https://www.weather.gov/media/tbw/dssbriefs/ThursdayWebinar.pdf (accessed on 29 June 2025).
- Lim, B.; Arık, S.Ö.; Loeff, N.; Pfister, T. Temporal fusion transformers for interpretable multi-horizon time series forecasting. Int. J. Forecast. 2021, 37, 1748–1764. [Google Scholar] [CrossRef]
- Bai, S.; Kolter, J.Z.; Koltun, V. An empirical evaluation of generic convolutional and recurrent networks for sequence modeling. arXiv 2018, arXiv:1803.01271. [Google Scholar] [CrossRef]
- Clevert, D.A.; Unterthiner, T.; Hochreiter, S. Fast and accurate deep network learning by exponential linear units (ELUs). arXiv 2015, arXiv:1511.07289. [Google Scholar]
- Ba, J.L.; Kiros, J.R.; Hinton, G.E. Layer normalization. arXiv 2016, arXiv:1607.06450. [Google Scholar] [CrossRef]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 7132–7141. [Google Scholar] [CrossRef]
- Gopalakrishnan, K.; Balakrishnan, H. Control and optimization of air traffic networks. Annu. Rev. Control Robot. Auton. Syst. 2021, 4, 397–424. [Google Scholar] [CrossRef]
- Wang, Y.; Li, M.Z.; Gopalakrishnan, K.; Liu, T. Timescales of delay propagation in airport networks. Transp. Res. Part E Logist. Transp. Rev. 2022, 161, 102687. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond efficient transformer for long sequence time-series forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 2–9 February 2021; Volume 35, pp. 11106–11115. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).