Joint Antenna Selection and Transmit Power Optimization for UAV-Assisted Relaying in Cognitive Radio IoT Networks

Abstract

In this paper, we study a cognitive relay Internet of Things (IoT) network aided by an unmanned aerial vehicle (UAV) equipped with multiple antennas. The UAV performs relaying for secondary communication under stringent interference constraints imposed by the primary network. To address the outage probability floor problem caused by strong interference channels, we propose a novel joint antenna selection and transmit power optimization scheme for Rician fading channels. By using the time-sharing condition and the Lagrangian dual method, the nonconvex mixed-integer optimization problem is efficiently solved to obtain the optimal solution. Additionally, a closed-form asymptotic lower bound on the outage probability is derived for Rayleigh fading channels, providing valuable performance insights. Numerical results demonstrate that the proposed joint optimization scheme significantly outperforms existing works.

1. Introduction

As the number of Internet of Things (IoT) applications and devices grows exponentially, radio spectrum resources become increasingly scarce. In this context, the combination of cognitive radio (CR) and relaying is considered for spectrum sharing in long-range IoT communications [1]. In [2,3,4,5,6], cognitive relay networks have been investigated as an efficient method to extend transmission range and enhance network coverage while maintaining interference to primary users at an acceptable level. In [2], the outage performance of antenna selection schemes was analyzed for cognitive relay networks. In [3], an optimal precoder design scheme was proposed for non-regenerative multiple-input multiple-output (MIMO) cognitive relay systems. In [4], beamforming and power control schemes were proposed for cognitive two-way relay networks. In [5], a spectrum-sharing scheme was proposed for time-switching simultaneous wireless information and power transfer (SWIPT) receivers, where secondary users can exchange information and perform energy harvesting as a reward for providing relay assistance to primary users. In [6], the outage performance of this spectrum-sharing scheme was further analyzed for power-splitting SWIPT receivers and multi-antenna-equipped primary users.

Meanwhile, to address the challenge of signal blockage due to geographical constraints in terrestrial communication systems, unmanned aerial vehicles (UAVs) have been employed as mobile relays in the CR networks [7,8,9,10,11,12]. In [7], a power control algorithm was proposed for UAV-assisted cognitive relay networks with energy harvesting capability. In [8], a virtual multiple-input multiple-output transmission scheme was proposed for UAV-enabled cognitive relay networks. In [9], security and reliability tradeoff performance was analyzed under consideration of multiple cognitive UAV relays. In [10], closed-form expressions for the secrecy outage probability and the non-zero secret capacity probability were derived for UAV-assisted cognitive relay networks with energy harvesting, and their asymptotic behaviors were analyzed. In [11], the closed-form secrecy outage probability was derived and analyzed for cognitive UAV relay networks under a Nakagami-m channel. In [12], an iterative algorithm was proposed to optimize trajectory and transmit power in UAV-based cognitive relay NOMA networks. However, the schemes proposed in [2,3,4,5,6,7,8,9,10,11,12] suffer from the outage probability floor problem, where the outage probability is the performance metric for slow-fading channels, which correspond to the scenario where a hovering UAV performs relaying. In other words, the outage probability is saturated at a specific signal-to-noise ratio point; i.e., the outage probability cannot be smaller than a floor value.

The problem of the outage probability floor becomes significantly severe when the air-to-ground channel gain between the UAV and the primary destination (PD) is too high. Therefore, it is a major obstacle to the use of UAVs and thus must be addressed. To overcome this challenge, this paper proposes a scheme that jointly optimizes antenna selection and transmit power to minimize the outage probability under Rician fading channels. On the other hand, in the existing works [2,10,11], the transmit power and antenna selection were optimized separately rather than jointly. Specifically, the transmit power was determined solely by considering the interference channel, while antenna selection was determined solely based on the secondary communication channel. In the literature, power adaptation schemes were proposed in [13,14] to minimize the outage probability in device-to-device (D2D) networks. However, these schemes are not applicable to cognitive relay networks, as relay nodes were not considered.

The main contributions of our work are as follows.

• First, in order to mitigate the outage probability floor problem of the cognitive relay networks, we formulate a problem to minimize the outage probability by jointly optimizing antenna selection and transmit power of the relaying UAV under Rician fading channels. Since the formulated problem is a mixed-integer programming problem, it is nonconvex and difficult to solve. However, by exploiting the time-sharing condition and the Lagrangian dual method, the optimal solution is efficiently obtained by jointly considering both the interference channel and the secondary communication channel for the transmit power and antenna selection. On the other hand, in the existing works [2,10,11], the transmit power and the antenna selection are determined by the interference channel and the secondary communication channel, respectively.
• Second, for Rayleigh fading channels, by deriving a closed-form asymptotic lower bound on the secondary outage probability, a new insight is obtained into the proposed scheme. Specifically, it is revealed that the proposed scheme achieves this lower-bound performance while the existing scheme cannot, which implies that the proposed scheme effectively minimizes the outage probability, thereby enhancing the system reliability.

2. System Model and Problem Formulation

2.1. System Model

We consider a cognitive decode-and-forward relay network as depicted in Figure 1. The secondary source (SS), the secondary destination (SD), and the UAV coexist with a primary network. In this network, the SS communicates with the SD via the UAV. The primary network consists of a primary source (PS) and a PD. The UAV is equipped with N antennas to maximize communication capability during its limited flight duration, whereas all other nodes are equipped with a single antenna. Due to the payload and battery constraints of the UAV, we assume that it is equipped with a single RF chain; thus, it must select one antenna from the N available antennas for each transmission.

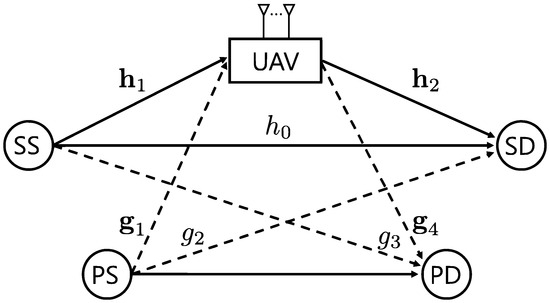
Figure 1. UAV-assisted cognitive relay networks.

Let $h_0$, $g_2$, and $g_3$ represent the channel power gains from the SS to the SD, from the PS to the SD, and from the SS to the PD, respectively. Furthermore, let ${\mathbf{h}}_1\in {\mathbb{R}}^N$, ${\mathbf{h}}_2\in {\mathbb{R}}^N$, ${\mathbf{g}}_1\in {\mathbb{R}}^N$, and ${\mathbf{g}}_4\in {\mathbb{R}}^N$ denote the row vectors with their ith elements $h_{1i}$, $h_{2i}$, $g_{1i}$, and $g_{4i}$, corresponding to the channel power gains from the SS to the ith antenna of the UAV, from the ith antenna of the UAV to the SD, from the PS to the ith antenna of the UAV, and from the ith antenna of the UAV to the PD, respectively.

All channels are assumed to undergo independent Rician fading. As a result, all vector elements within each vector ${\mathbf{h}}_1$, ${\mathbf{h}}_2$, ${\mathbf{g}}_1$, and ${\mathbf{g}}_4$ are modeled as independent and identically distributed (i.i.d.) random variables. For every channel power gain $y\in \{h_0,h_1,h_2,g_1,g_2,g_3,g_4\}$, the probability density function (PDF) is given as

$$\begin{array}{cc}\hfill f_y\left(x\right)& =A_y{e}^{-[K_y+A_{y}x]}{I}_0\left(2\sqrt{K_y{A}_{y}x}\right)\hfill \\ \hfill & \stackrel{\left(a\right)}{=}{A}_y{e}^{-[K_y+A_{y}x]}\sum _{k=0}^{\infty }{\displaystyle \frac{{\left(K_y{A}_{y}x\right)}^k}{{(k!)}^2}},\hfill \end{array}$$

(1)

where $K_y$ is the Rician K-factor, ${\mathsf{\Omega }}_y=\mathbb{E}\left[y\right]$, $\mathbb{E}[·]$ is the expectation operation, $I_0(·)$ is the zero-order modified Bessel function of the first kind, and

$$\begin{array}{cc}\hfill A_y=& {\displaystyle \frac{K_y+1}{{\mathsf{\Omega }}_y}}.\hfill \end{array}$$

(2)

Here, $f_{h_1}\left(x\right)$, $f_{h_2}\left(x\right)$, $f_{g_1}\left(x\right)$, and $f_{g_4}\left(x\right)$ denote the PDFs of a generic element of the channel vectors ${\mathbf{h}}_1$, ${\mathbf{h}}_2$, ${\mathbf{g}}_1$, and ${\mathbf{g}}_4$, respectively, since all their elements are i.i.d. The equality (a) follows from ([15], Equation (2.3.32)). In particular, when $K_y=0$, the Rician fading reduces to Rayleigh fading, and the PDF $f_y\left(x\right)$ in (1) simplifies to

$$\begin{array}{cc}\hfill f_y^{\prime }\left(x\right)\triangleq f_y\left(x\right){|}_{K_y=0}& ={\displaystyle \frac{1}{{\mathsf{\Omega }}_y}}{e}^{-x/{\mathsf{\Omega }}_y}.\hfill \end{array}$$

(3)

We assume that all the instantaneous channel power gains are known at the UAV, which operates under a time-division duplex (TDD) protocol allowing channel reciprocity-based channel estimation [16]. Thanks to channel reciprocity, the UAV can estimate its own local channel power gains, i.e., ${\mathbf{h}}_1$, ${\mathbf{h}}_2$, ${\mathbf{g}}_1$, and ${\mathbf{g}}_4$, from pilot signals sent by the primary and secondary nodes. The other channel power gains, i.e., $h_0$, $g_2$, and $g_3$, are estimated at the SS and SD and fed back to the UAV. If the coordination with the primary nodes is absent, the UAV may acquire the channel power gains through a learning process [17].

In this system, the UAV is considered to operate in half-duplex mode, meaning it cannot transmit and receive signals simultaneously. Therefore, the secondary relay transmission requires two separate time slots. During the first time slot, the SS transmits its message to the UAV and the SD with a target rate $R_t$. The received signal-to-interference–noise ratios (SINRs) at the SD and the UAV are, respectively, given by

$$\begin{array}{cc}\hfill {\eta }_0& ={\displaystyle \frac{p_1{h}_0}{{\sigma }^2+p_0{g}_2}},\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill {\eta }_1& ={\displaystyle \frac{p_1{h}_{1i^{*}}}{{\sigma }^2+p_0{g}_{1i^{*}}}},\hfill \end{array}$$

(5)

where $p_0$ is the transmit power of the PS, $p_1$ is the transmit power of the SS, and

$$\begin{array}{c}\hfill i^{*}=\underset{i}{\arg \max }{\displaystyle \frac{p_1{h}_{1i}}{{\sigma }^2+p_0{g}_{1i}}}.\end{array}$$

(6)

In (6), the receive antenna of the UAV is selected as the one with the maximum SINR. Then, by using the random variable transformation formula [18], the cumulative distribution functions (CDFs) of ${\eta }_0$ and ${\eta }_1$ are, respectively, given as

$$\begin{array}{cc}\hfill F_0\left(\eta \right)=& 1-{\int }_{x={\displaystyle \frac{\eta {\sigma }^2}{p_1}}}^{\infty }{\int }_{y=0}^{{\displaystyle \frac{p_{1}x}{p_0\eta }}-{\displaystyle \frac{{\sigma }^2}{p_0}}}{f}_{g_2}\left(y\right)f_{h_0}\left(x\right)dydx,\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill F_1\left(\eta \right)=& {\left[1-{\int }_{x={\displaystyle \frac{\eta {\sigma }^2}{p_1}}}^{\infty }{\int }_{y=0}^{{\displaystyle \frac{p_{1}x}{p_0\eta }}-{\displaystyle \frac{{\sigma }^2}{p_0}}}{f}_{g_1}\left(y\right)f_{h_1}\left(x\right)dydx\right]}^N.\hfill \end{array}$$

(8)

During the second time slot, the data rate at the SD takes one of two forms depending on the value of ${\eta }_1$. Specifically, if ${\displaystyle \frac{1}{2}}{\log }_2(1+{\eta }_1)<R_t$, as the UAV cannot successfully decode the message received from the SS, it does not transmit any signals, i.e., $p_2\left(\mathit{s}\right)=0$, where $\mathit{s}$ and $p_2\left(\mathit{s}\right)$ denote the instantaneous channel state $\mathit{s}=[h_0,{\mathbf{h}}_1,{\mathbf{h}}_2,{\mathbf{g}}_1$$,g_2,{\mathbf{g}}_4]$ and the UAV’s transmit power adapted to $\mathit{s}$, respectively. In this case, since the SD receives signals only from the SS, the data rate is given by

$$\begin{array}{c}\hfill {\displaystyle \frac{1}{2}}{\log }_2(1+{\eta }_0).\end{array}$$

(9)

On the other hand, if ${\displaystyle \frac{1}{2}}{\log }_2(1+{\eta }_1)\ge R_t$, the UAV can successfully decode the message received from the SS and transmits the decoded message to the SD. Then, the received SINR at the SD is given by

$$\begin{array}{c}\hfill {\eta }_2={\displaystyle \frac{p_2\left(\mathit{s}\right)h_{2j\left(\mathit{s}\right)}}{{\sigma }^2+p_0{g}_2}},\end{array}$$

(10)

where $j\left(\mathit{s}\right)$ is the index of the UAV’s transmit antenna which is selected according to $\mathit{s}$. In this case, by using maximal-ratio combining (MRC) between the SS → SD link signal and the SS → UAV → SD link signal, the data rate is given by

$$\begin{array}{c}\hfill {\displaystyle \frac{1}{2}}{\log }_2(1+\min ({\eta }_1,{\eta }_0+{\eta }_2)).\end{array}$$

(11)

Therefore, the overall data rate during the second time slot, including both described cases, is given by

$$\begin{array}{c}\hfill R_s=\left\{\begin{array}{cc}{\displaystyle \frac{1}{2}}{\log }_2(1+{\eta }_0),\hfill & \mathrm{if}{\displaystyle \frac{1}{2}}{\log }_2(1+{\eta }_1)<R_t,\hfill \\ {\displaystyle \frac{1}{2}}{\log }_2(1+\min ({\eta }_1,{\eta }_0+{\eta }_2)),\hfill & \mathrm{if}{\displaystyle \frac{1}{2}}{\log }_2(1+{\eta }_1)\ge R_t,\hfill \end{array}\right.\end{array}$$

(12)

Then, the outage probability of the secondary network is given by

$$\begin{array}{cc}\hfill {\mathcal{O}}_s=& Pr\{R_s<R_t\}\hfill \\ \hfill =& \mathrm{Pr}({\eta }_1<{\eta }_t,{\eta }_0<{\eta }_t)+\mathrm{Pr}({\eta }_1\ge {\eta }_t,{\eta }_0+{\eta }_2<{\eta }_t)\hfill \\ \hfill \stackrel{\left(b\right)}{=}& F_0\left({\eta }_t\right)F_1\left({\eta }_t\right)+E_{\mathit{s}}\left[\chi \right],\hfill \end{array}$$

(13)

where $I\left(x\right)$ is an indicator function that equals 1 if condition x is true and 0 otherwise,

$$\begin{array}{cc}\hfill {\eta }_t& =2^{2R_t}-1,\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill \chi & =I({\eta }_1\ge {\eta }_t)I({\eta }_0+{\eta }_2<{\eta }_t).\hfill \end{array}$$

(15)

The equality (b) follows from the fact that the probability of an event is equal to the expected value of its indicator function.

2.2. Problem Formulation

In this paper, we consider a scenario where the UAV hovers and performs relaying to establish a CR network between low-mobility ground secondary nodes subject to the interference power constraint at the PD. Furthermore, due to the finite battery capacity of the UAV, efficient use of the constrained power is crucial. Therefore, assuming a slow-fading channel [19], we address the outage probability minimization problem under transmit power and interference power constraints, which is formulated as follows:

$$\begin{array}{cc}\hfill \underset{j\left(\mathit{s}\right),p_2\left(\mathit{s}\right)}{min}& F_0\left({\eta }_t\right)F_1\left({\eta }_t\right)+E_{\mathit{s}}\left[\chi \right]\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill \mathrm{s}.\mathrm{t}.& E_{\mathit{s}}\left[p_2\left(\mathit{s}\right)g_{4j\left(\mathit{s}\right)}\right]\le Q_p\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill & 0\le p_2\left(\mathit{s}\right)\le Q_{\mathrm{UAV}}\hfill \end{array}$$

(18)

where $Q_p$ is the average interference power threshold at the PD and $Q_{\mathrm{UAV}}$ is the instantaneous transmit power threshold at the UAV. Since the SS does not know the instantaneous values of $\mathit{s}$, its transmit power $p_1$ cannot be adapted to $\mathit{s}$ and thus is set as

$$\begin{array}{c}\hfill p_1=\min \left({\displaystyle \frac{Q_p}{{\mathsf{\Omega }}_{g_3}}},Q_{\mathrm{SS}}\right)\end{array}$$

(19)

which is determined from constraints on the transmit power at the SS, i.e., $p_1\le Q_{\mathrm{SS}}$, and on the interference power at the PD, i.e., $p_1{\mathsf{\Omega }}_{g_3}\le Q_p$.

3. Closed-Form Expressions for SINR CDFs

In this section, we present closed-form expressions for the SINR CDFs $F_0\left(\eta \right)$ in (7) and $F_1\left(\eta \right)$ in (8), which are essential for accurate evaluation of the outage probability ${\mathcal{O}}_s$ in (13).

3.1. Rician Fading Channels

The CDF of ${\eta }_0$, i.e., $F_0\left(\eta \right)$ in (7), can be derived as follows:

$$\begin{array}{cc}\hfill F_0\left(\eta \right)=& 1-{\int }_{x={\displaystyle \frac{\eta {\sigma }^2}{p_1}}}^{\infty }{\int }_{y=0}^{{\displaystyle \frac{p_{1}x}{p_0\eta }}-{\displaystyle \frac{{\sigma }^2}{p_0}}}{f}_{g_2}\left(y\right)f_{h_0}\left(x\right)dydx,\hfill \\ \hfill =& 1-{\int }_{x={\displaystyle \frac{\eta {\sigma }^2}{p_1}}}^{\infty }{A}_{g_2}{e}^{-K_{g_2}}\sum _{k=0}^{\infty }{\displaystyle \frac{{\left(K_{g_2}{A}_{g_2}\right)}^k}{{(k!)}^2}}\left({\int }_{y=0}^{{\displaystyle \frac{p_{1}x}{p_0\eta }}-{\displaystyle \frac{{\sigma }^2}{p_0}}}{e}^{-A_{g_2}y}{y}^{k}dy\right)f_{h_0}\left(x\right)dx,\hfill \\ \hfill \stackrel{\left(c\right)}{=}& 1-{\int }_{x={\displaystyle \frac{\eta {\sigma }^2}{p_1}}}^{\infty }{A}_{g_2}{e}^{-K_{g_2}}\sum _{k=0}^{\infty }{\displaystyle \frac{{\left(K_{g_2}{A}_{g_2}\right)}^k}{{(k!)}^2}}{\left(A_{g_2}\right)}^{-k-1}\gamma \left(k+1,{\displaystyle \frac{K_{g_2}+1}{{\mathsf{\Omega }}_{g_2}{p}_0}}\left({\displaystyle \frac{p_{1}x}{\eta }}-{\sigma }^2\right)\right)f_{h_0}\left(x\right)dx,\hfill \\ \hfill =& 1-A_{h_0}{A}_{g_2}{e}^{-K_{h_0}-K_{g_2}}\sum _{k=0}^{\infty }\sum _{n=0}^{\infty }{\displaystyle \frac{{\left(K_{h_0}{A}_{h_0}\right)}^k}{{(k!)}^2}}{\displaystyle \frac{{\left(K_{g_2}{A}_{g_2}\right)}^k}{{(k!)}^2}}{\left(A_{g_2}\right)}^{-k-1}\hfill \\ \hfill & \times {\int }_{x={\displaystyle \frac{\eta {\sigma }^2}{p_1}}}^{\infty }{e}^{-A_{h_0}x}{x}^n\gamma \left(k+1,{\displaystyle \frac{K_{g_2}+1}{{\mathsf{\Omega }}_{g_2}{p}_0}}\left({\displaystyle \frac{p_{1}x}{\eta }}-{\sigma }^2\right)\right)dx,\hfill \\ \hfill \stackrel{\left(d\right)}{=}& 1-A_{h_0}{A}_{g_2}{e}^{-K_{h_0}-K_{g_2}}\sum _{k=0}^{\infty }\sum _{n=0}^{\infty }{\displaystyle \frac{{\left(K_{h_0}{A}_{h_0}\right)}^k}{{(k!)}^2}}{\displaystyle \frac{{\left(K_{g_2}{A}_{g_2}\right)}^k}{{(k!)}^2}}{\left(A_{g_2}\right)}^{-k-1}{e}^{-{\displaystyle \frac{A_{h_0}\eta }{p_1}}{\sigma }^2}{\left({\displaystyle \frac{\eta }{p_1}}\right)}^{n+1}\hfill \\ \hfill & \times {\int }_{t=0}^{\infty }{e}^{-{\displaystyle \frac{A_{h_0}\eta }{p_1}}t}{\left(t+{\sigma }^2\right)}^n\gamma \left(k+1,{\displaystyle \frac{K_{g_2}+1}{{\mathsf{\Omega }}_{g_2}{p}_0}}t\right)dt,\hfill \\ \hfill =& 1-A_{h_0}{A}_{g_2}{e}^{-K_{h_0}-K_{g_2}}\sum _{k=0}^{\infty }\sum _{n=0}^{\infty }\sum _{m=0}^n{\displaystyle \frac{{\left(K_{h_0}{A}_{h_0}\right)}^k}{{(k!)}^2}}{\displaystyle \frac{{\left(K_{g_2}{A}_{g_2}\right)}^k}{{(k!)}^2}}{\left(A_{g_2}\right)}^{-k-1}{e}^{-{\displaystyle \frac{A_{h_0}\eta }{p_1}}{\sigma }^2}{\left({\displaystyle \frac{\eta }{p_1}}\right)}^{n+1}\hfill \\ \hfill & \times {\sigma }^{2(n-m)}\left({\displaystyle \genfrac{}{}{0pt}{}{n}{m}}\right){\int }_{t=0}^{\infty }{e}^{-{\displaystyle \frac{A_{h_0}\eta }{p_1}}t}{t}^m\gamma \left(k+1,{\displaystyle \frac{K_{g_2}+1}{{\mathsf{\Omega }}_{g_2}{p}_0}}t\right)dt,\hfill \\ \hfill \stackrel{\left(e\right)}{=}& 1-A_{h_0}{A}_{g_2}{e}^{-K_{h_0}-K_{g_2}}\sum _{k=0}^{\infty }\sum _{n=0}^{\infty }\sum _{m=0}^n{\displaystyle \frac{{\left(K_{h_0}{A}_{h_0}\right)}^k}{{(k!)}^2}}{\displaystyle \frac{{\left(K_{g_2}{A}_{g_2}\right)}^k}{{(k!)}^2}}{\left(A_{g_2}\right)}^{-k-1}{e}^{-{\displaystyle \frac{A_{h_0}\eta }{p_1}}{\sigma }^2}{\left({\displaystyle \frac{\eta }{p_1}}\right)}^{n+1}\hfill \\ \hfill & \times {\sigma }^{2(n-m)}\left({\displaystyle \genfrac{}{}{0pt}{}{n}{m}}\right){\displaystyle \frac{{\left(\frac{K_{g_2}+1}{{\mathsf{\Omega }}_{g_2}{p}_0}\right)}^{k+1}\mathsf{\Gamma }(k+m+2)}{(k+1){(\frac{K_{g_2}+1}{{\mathsf{\Omega }}_{g_2}{p}_0}+\frac{A_{h_0}\eta }{p_1})}^{k+m+2}}}\hfill \\ \hfill & \times {}_{2}F_1\left(1,k+m+2;k+2;{\displaystyle \frac{p_1(K_{g_2}+1)}{p_1(K_{g_2}+1)+{\mathsf{\Omega }}_{g_2}{p}_0{A}_{h_0}\eta }}\right),\hfill \end{array}$$

(20)

where $\gamma (·,·)$ is the lower incomplete gamma function ([20], Equation (8.350.1)), $\mathsf{\Gamma }(·)$ is the gamma function ([20], Equation (8.310.1)), and ${}_{2}F_1(·,·;·;·)$ is the Gauss hypergeometric function ([20], Equation (9.100)). The equalities (c) and (e) follow from ([20], Equation (3.351.1)) and ([20], Equation (6.455.2)), respectively. The equality (d) is derived by substituting the variable $t={\displaystyle \frac{p_{1}x}{\eta }}-{\sigma }^2$. In a similar manner, the CDF of ${\eta }_1$, i.e., $F_1\left(\eta \right)$ in (8), can be derived as follows:

$$\begin{array}{cc}\hfill F_1\left(\eta \right)=& [1-A_{h_1}{A}_{g_1}{e}^{-K_{h_1}-K_{g_1}}\sum _{k=0}^{\infty }\sum _{n=0}^{\infty }\sum _{m=0}^n{\displaystyle \frac{{\left(K_{h_1}{A}_{h_1}\right)}^k}{{(k!)}^2}}{\displaystyle \frac{{\left(K_{g_1}{A}_{g_1}\right)}^k}{{(k!)}^2}}{\left(A_{g_1}\right)}^{-k-1}{e}^{-{\displaystyle \frac{A_{h_1}\eta }{p_1}}{\sigma }^2}{\left({\displaystyle \frac{\eta }{p_1}}\right)}^{n+1}\hfill \\ \hfill & \times {\sigma }^{2(n-m)}\left({\displaystyle \genfrac{}{}{0pt}{}{n}{m}}\right){\displaystyle \frac{{\left(\frac{K_{g_1}+1}{{\mathsf{\Omega }}_{g_1}{p}_0}\right)}^{k+1}\mathsf{\Gamma }(k+m+2)}{(k+1){(\frac{K_{g_1}+1}{{\mathsf{\Omega }}_{g_1}{p}_0}+\frac{A_{h_1}\eta }{p_1})}^{k+m+2}}}\hfill \\ \hfill & \times {}_{2}F_1\left(1,k+m+2;k+2;{\displaystyle \frac{p_1(K_{g_1}+1)}{p_1(K_{g_1}+1)+{\mathsf{\Omega }}_{g_1}{p}_0{A}_{h_1}\eta }}\right){]}^N.\hfill \end{array}$$

(21)

3.2. Rayleigh Fading Channels

In particular, when $K_y=0$ (i.e., Rayleigh fading), $F_0\left(\eta \right)$ in (7) and $F_1\left(\eta \right)$ in (8) can be derived as follows, respectively:

$$\begin{array}{cc}\hfill F_0^{\prime }\left(\eta \right)\triangleq F_0\left(\eta \right){|}_{K_{h_0}=K_{g_2}=0}& =1-{\int }_{x={\displaystyle \frac{\eta {\sigma }^2}{p_1}}}^{\infty }{\int }_{y=0}^{{\displaystyle \frac{p_{1}x}{p_0\eta }}-{\displaystyle \frac{{\sigma }^2}{p_0}}}{f}_{g_2}^{\prime }\left(y\right)f_{h_0}^{\prime }\left(x\right)dydx\hfill \\ & =1-{\displaystyle \frac{p_1{\mathsf{\Omega }}_{h_0}{e}^{-\left(\eta {\sigma }^2\right)/\left(p_1{\mathsf{\Omega }}_{h_0}\right)}}{\eta p_0{\mathsf{\Omega }}_{g_2}+p_1{\mathsf{\Omega }}_{h_0}}},\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill F_1^{\prime }\left(\eta \right)\triangleq F_1\left(\eta \right){|}_{K_{h_1}=K_{g_1}=0}& ={\left[1-{\int }_{x={\displaystyle \frac{\eta {\sigma }^2}{p_1}}}^{\infty }{\int }_{y=0}^{{\displaystyle \frac{p_{1}x}{p_0\eta }}-{\displaystyle \frac{{\sigma }^2}{p_0}}}{f}_{g_1}^{\prime }\left(y\right)f_{h_1}^{\prime }\left(x\right)dydx\right]}^N\hfill \\ & ={\left[1-{\displaystyle \frac{p_1{\mathsf{\Omega }}_{h_1}{e}^{-\left(\eta {\sigma }^2\right)/\left(p_1{\mathsf{\Omega }}_{h_1}\right)}}{\eta p_0{\mathsf{\Omega }}_{g_1}+p_1{\mathsf{\Omega }}_{h_1}}}\right]}^N.\hfill \end{array}$$

(23)

In this Rayleigh case, the CDFs are given in closed-form expressions without the gamma and hypergeometric functions, which significantly simplifies computation compared to the Rician case.

4. Joint Antenna Selection and Power Adaptation

The problem (16) is a mixed-integer programming problem that is nonconvex and difficult to solve. Nevertheless, due to the continuous distributions of the channel power gains, by following the proof of ([21], Th. 2), it can be verified that the problem (16) satisfies the so-called “time-sharing” condition and thus has zero duality gap. Hence, the optimal solution can be obtained by the Lagrangian dual method. By introducing the dual variable $\lambda \ge 0$ associated with the constraint in (17), the Lagrange dual function of problem (16) can be expressed as follows:

$$\begin{array}{cc}\hfill f\left(\lambda \right)=\underset{j\left(\mathit{s}\right),p_2\left(\mathit{s}\right)}{min}& E_{\mathit{s}}\left[\chi \right]+\lambda (E_{\mathit{s}}\left[p_2\left(\mathit{s}\right)g_{4j\left(\mathit{s}\right)}\right]-Q_p)\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& \left(18\right).\hfill \end{array}$$

(24)

4.1. Optimizing $j\left(\mathit{s}\right)$ and $p_2\left(\mathit{s}\right)$ for Given $\lambda$

The optimal solution to the problem (24) can be obtained by the dual decomposition method [22] as in the following theorem.

Theorem 1.

$$\begin{array}{cc}\hfill & j^{*}\left(\mathit{s}\right)=arg\underset{j\in \mathcal{M}}{min}{X}_j{g}_{4j}\hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill & p_2^{*}\left(\mathit{s}\right)=\left\{\begin{array}{cc}{X}_{j^{*}\left(\mathit{s}\right)},\hfill & \mathit{if}{\eta }_t\le {\eta }_1,M>0,Y_1\le {\displaystyle \frac{1}{\lambda }}\hfill \\ 0,\hfill & \mathit{otherwise}\hfill \end{array}\right.\hfill \end{array}$$

(26)

where ${\left[x\right]}^{+}$ denotes $\max (0,x)$, M is the cardinality of $\mathcal{M}$,

$$\begin{array}{cc}\hfill Y_1& =\left\{\begin{array}{cc}{X}_{j^{*}\left(\mathit{s}\right)}{g}_{4j^{*}\left(\mathit{s}\right)},\hfill & \mathit{if}M>0\hfill \\ 0,\hfill & \mathit{if}M=0\hfill \end{array}\right.\hfill \end{array}$$

(27)

$$\begin{array}{cc}\hfill X_j& ={\displaystyle \frac{{[{\eta }_t({\sigma }^2+p_0{g}_2)-p_1{h}_0]}^{+}}{h_{2j}}},\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill \mathcal{M}& =\left\{j\right|X_j\le Q_{\mathrm{UAV}},1\le j\le N\}.\hfill \end{array}$$

(29)

Proof. 

See Appendix A.   □

In (28), $X_j$ corresponds to the UAV’s transmit power required to achieve R with the jth transmit antenna. In (29), $\mathcal{M}$ is the set of antenna indices where the required power value $X_j$ satisfies the constraint in (18), i.e., $X_j\le Q_{\mathrm{UAV}}$. In (25), the transmit antenna is selected among $\mathcal{M}$ to minimize the interference power received at the PD. In (26), when $M=0$, since the target rate $R_t$ cannot be achieved, i.e., $X_j>Q_{\mathrm{UAV}}$ for $\forall j\in \{1,2,\dots ,N\}$, the transmit power of the UAV is zero. In (27), $Y_1$ is the received interference power at the PD.

Note that the antenna selection $j^{*}\left(\mathit{s}\right)$ in (25) and the transmit power $p_2^{*}\left(\mathit{s}\right)$ in (26) are jointly optimized to minimize the interference power at the PD while ensuring the target rate $R_t$ at the SD. Consequently, under the average interference power constraint in (17), the secondary outage probability ${\mathcal{O}}_s$ in (13) is minimized, thereby optimizing the average secondary performance. On the other hand, in existing works [2,10,11], the antenna selection $j\left(\mathit{s}\right)$ and the transmit power $p_2\left(\mathit{s}\right)$ are determined solely by the secondary communication channels ${\mathbf{h}}_2$ and the interference channel ${\mathbf{g}}_4$, respectively, which results in a significant degradation of the secondary outage performance.

From (26), it is observed that the optimal transmit power $p_2^{*}\left(\mathit{s}\right)$ is a function of the dual variable $\lambda$, which determines whether the UAV transmits signals or not. Since the UAV does not transmit signals in the case of $Y_1>{\displaystyle \frac{1}{\lambda }}$ in (26), the outage probability ${\mathcal{O}}_s$ in (13) with the proposed scheme $j^{*}\left(\mathit{s}\right)$ in (25) and $p_2^{*}\left(\mathit{s}\right)$ in (26), which is denoted as ${\mathcal{O}}_s^{*}\left(\lambda \right)$, is an increasing function of $\lambda$. On the other hand, the average interference power at the PD with the proposed scheme $j^{*}\left(\mathit{s}\right)$ in (25) and $p_2^{*}\left(\mathit{s}\right)$ in (26) is a decreasing function of $\lambda$ and is denoted as follows:

$$\begin{array}{c}\hfill I_p\left(\lambda \right)=E_{\mathit{s}}\left[p_2^{*}\left(\mathit{s}\right)g_{4j^{*}\left(\mathit{s}\right)}\right].\end{array}$$

(30)

Therefore, $\lambda$ determines the tradeoff between the outage performance of the secondary network and the average interference power received at the PD.

4.2. Asymptotic Closed-Form Solution

In (26), the optimal solution for $p_2\left(\mathit{s}\right)$ is obtained as an explicit function of the dual variable $\lambda$. However, determining the specific $\lambda$ that satisfies the complementary slackness condition generally requires iterative search, which may incur significant computational burden.

To alleviate the computational complexity, the asymptotic behavior of $\lambda$ is examined. Owing to the zero-duality-gap property of (16) ([21], Th. 2), the optimal dual variable $\lambda$, which is denoted as ${\lambda }^{*}$, satisfies the complementary slackness condition:

$$\begin{array}{c}\hfill {\lambda }^{*}(I_p\left(\lambda \right)-Q_p)=0.\end{array}$$

(31)

This condition implies that ${\lambda }^{*}=0$ as $Q_p\to \infty$. Then, substituting $\lambda =0$ into (26) yields an asymptotic closed-form solution as follows:

$$\begin{array}{c}\hfill {\overline{p}}_2\left(\mathit{s}\right)=\left\{\begin{array}{cc}{X}_{j^{*}\left(\mathit{s}\right)},\hfill & \mathrm{if}{\eta }_t\le {\eta }_1,M>0\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.\end{array}$$

(32)

4.3. Optimizing the Dual Variable $\lambda$

We now determine the dual variable $\lambda$ corresponding to the constraint (17). When $j^{*}\left(\mathit{s}\right)$ in (25) and ${\overline{p}}_2\left(\mathit{s}\right)$ in (32) satisfy $E_{\mathit{s}}\left[p_2\left(\mathit{s}\right)g_{4j\left(\mathit{s}\right)}\right]\le Q_p$ in (17), i.e., $I_p\left(0\right)\le Q_p$, the optimal value of $\lambda$ is given by ${\lambda }^{*}=0$ since this satisfies the complementary slackness condition in (31). Then, $j^{*}\left(\mathit{s}\right)$ in (25) and ${\overline{p}}_2\left(\mathit{s}\right)$ in (32) become the optimal solution. Otherwise, since $I_p\left(\lambda \right)$ in (30) is a monotonically decreasing function of $\lambda$, the optimal value ${\lambda }^{*}$ satisfying (31) can be efficiently obtained by the bisection method, solving

$$\begin{array}{c}\hfill I_p\left(\lambda \right)=Q_p.\end{array}$$

(33)

Here, the evaluation of the average interference power $I_p\left(\lambda \right)$ in (30) under the Rician fading channel involves complicated integrals over the Rician PDFs, which significantly increases computational complexity. However, when the channels undergo Rayleigh fading, we can obtain the following tractable expression for $I_p\left(\lambda \right)$ in (30). When $K_y=0$ for $\forall y\in \{h_0,h_1,h_2,g_1,g_2,g_3,g_4\}$, $I_p\left(\lambda \right)$ in (30) can be derived in a single-integral form as follows:

$$\begin{array}{cc}\hfill I_p\left(\lambda \right){|}_{K_y=0}& =E_{\mathit{s}}\left[p_2^{*}\left(\mathit{s}\right)g_{4j^{*}\left(\mathit{s}\right)}\right]{|}_{K_y=0}\hfill \\ \hfill & \stackrel{\left(f\right)}{=}(1-F_1^{\prime }\left({\eta }_t\right)){\int }_{x_2=0}^{\infty }{f}_{Y_2}\left(x_2\right){\int }_{x_1=0}^{{\displaystyle \frac{1}{\lambda }}}{x}_1{f}_{Y_1}\left(x_1\right|Y_2=x_2)d{x}_{1}d{x}_2\hfill \\ \hfill & =(1-F_1^{\prime }\left({\eta }_t\right)){\int }_{x_2=0}^{\infty }{f}_{Y_2}\left(x_2\right)\sum _{m=1}^N{L}_1(L_2+L_3)d{x}_2\hfill \end{array}$$

(34)

where

$$\begin{array}{cc}{f}_{Y_1}\left(x_1\right|Y_2=x_2)\hfill & =\sum _{m=1}^{N}m{L}_1\left({\displaystyle \frac{{\mathsf{\Omega }}_{h_2}}{{\mathsf{\Omega }}_{g_4}{x}_2+{\mathsf{\Omega }}_{h_2}{x}_1}}+{\displaystyle \frac{1}{Q_{\mathrm{UAV}}{\mathsf{\Omega }}_{g_4}}}\right)\hfill \\ & \times {\left({\displaystyle \frac{{\mathsf{\Omega }}_{g_4}{x}_2}{{\mathsf{\Omega }}_{g_4}{x}_2+{\mathsf{\Omega }}_{h_2}{x}_1}}\right)}^m{e}^{-m{\displaystyle \frac{{\mathsf{\Omega }}_{g_4}{x}_2+{\mathsf{\Omega }}_{h_2}{x}_1}{Q_{\mathrm{UAV}}{\mathsf{\Omega }}_{h_2}{\mathsf{\Omega }}_{g_4}}}},\hfill \end{array}$$

(35)

$$\begin{array}{cc}\hfill Y_2& ={\eta }_t{\sigma }^2+{\eta }_t{p}_0{g}_2-p_1{h}_0,\hfill \end{array}$$

(36)

$$\begin{array}{cc}\hfill f_{Y_2}\left(x\right)& =\left\{\begin{array}{c}{\displaystyle \frac{e^{\frac{x-{\eta }_t{\sigma }^2}{p_1{a}_0}}}{{\eta }_t{p}_0{\mathsf{\Omega }}_{g_2}+p_1{\mathsf{\Omega }}_{h_0}}},x<{\eta }_t{\sigma }^2\hfill \\ {\displaystyle \frac{e^{-\frac{x-{\eta }_t{\sigma }^2}{{\eta }_t{p}_0{\mathsf{\Omega }}_{g_2}}}}{{\eta }_t{p}_0{\mathsf{\Omega }}_{g_2}+p_1{\mathsf{\Omega }}_{h_0}}},x\ge {\eta }_t{\sigma }^2\hfill \end{array}\right.\hfill \end{array}$$

(37)

$$\begin{array}{cc}\hfill & L_1=\left({\displaystyle \genfrac{}{}{0pt}{}{N}{m}}\right){\left(1-e^{-{\displaystyle \frac{x_2}{{\mathsf{\Omega }}_{h_2}{Q}_{\mathrm{UAV}}}}}\right)}^{N-m},\hfill \end{array}$$

(38)

$$\begin{array}{c}{L}_2=-{\displaystyle \frac{1}{\lambda }}{\left({\displaystyle \frac{{\mathsf{\Omega }}_{g_4}{x}_2}{{\mathsf{\Omega }}_{g_4}{x}_2+\frac{{\mathsf{\Omega }}_{h_2}}{\lambda }}}\right)}^m{e}^{-m{\displaystyle \frac{{\mathsf{\Omega }}_{g_4}{x}_2+\frac{{\mathsf{\Omega }}_{h_2}}{\lambda }}{Q_{\mathrm{UAV}}{\mathsf{\Omega }}_{h_2}{\mathsf{\Omega }}_{g_4}}}},\hfill \end{array}$$

(39)

$$\begin{array}{cc}{L}_3\hfill & ={\int }_{x_1=0}^{{\displaystyle \frac{1}{\lambda }}}{\left({\displaystyle \frac{{\mathsf{\Omega }}_{g_4}{x}_2}{{\mathsf{\Omega }}_{g_4}{x}_2+{\mathsf{\Omega }}_{h_2}{x}_1}}\right)}^m{e}^{-m{\displaystyle \frac{{\mathsf{\Omega }}_{g_4}{x}_2+{\mathsf{\Omega }}_{h_2}{x}_1}{Q_{\mathrm{UAV}}{\mathsf{\Omega }}_{h_2}{\mathsf{\Omega }}_{g_4}}}}d{x}_1\hfill \\ & ={\displaystyle \frac{Q_{\mathrm{UAV}}{\mathsf{\Omega }}_{g_4}}{m}}{(-{\displaystyle \frac{m{x}_2}{Q_{\mathrm{UAV}}{\mathsf{\Omega }}_{h_2}}})}^m[\sum _{k=1}^{m-1}{\displaystyle \frac{(m-1-k)!}{(m-1)!}}\left({\displaystyle \frac{e^{A_1}}{A_1^{m-k}}}-{\displaystyle \frac{e^{A_2}}{A_2^{m-k}}}\right)\hfill \\ \hfill & +{\displaystyle \frac{1}{(m-1)!}}(\mathrm{Ei}\left(A_2\right)-\mathrm{Ei}\left(A_1\right))],\hfill \end{array}$$

(40)

$$\begin{array}{cc}\hfill & A_1=-{\displaystyle \frac{m{x}_2}{Q_{\mathrm{UAV}}{\mathsf{\Omega }}_{h_2}}}-{\displaystyle \frac{m}{Q_{\mathrm{UAV}}{\mathsf{\Omega }}_{g_4}\lambda }},\hfill \end{array}$$

(41)

$$\begin{array}{cc}\hfill & A_2=-{\displaystyle \frac{m{x}_2}{Q_{\mathrm{UAV}}{\mathsf{\Omega }}_{h_2}}},\hfill \end{array}$$

(42)

$$\begin{array}{cc}\hfill & \mathrm{Ei}\left(x\right)={\int }_{-\infty }^x{t}^{-1}{e}^{t}dt.\hfill \end{array}$$

(43)

The equality (f) follows from the random variable transformation formula [18] by introducing a new random variable $Y_2$ in (36), which represents the signal power that the SD is required to receive from the UAV in order to achieve the target rate $R_t$. Since $Y_2$ appears in the numerator of Equation (28), the expectation operation can be transformed into an integral with respect to $Y_2$, as shown in equality (f). In (35), $f_{Y_1}\left(x_1\right|Y_2=x_2)$ is the conditional PDF of $Y_1$ given that $Y_2=x_2$ and $K_y=0$ for $\forall y\in \{h_0,h_1,h_2,g_1,g_2,g_3,g_4\}$. In (37), $f_{Y_2}\left(x\right)$ is the PDF of $Y_2$ in (36). In (43), $\mathrm{Ei}\left(x\right)$ is the exponential integral function.

4.4. Complexity Analysis

Algorithm 1 summarizes the procedure to compute the solution $j^{*}\left(\mathit{s}\right)$ in (25) and $p_2^{*}\left(\mathit{s}\right)$ in (26). The value of $\lambda$ can be determined by the gradient method [23]. The complexity of Algorithm 1 is primarily determined by steps 3 and 4, since $X_j$ in (28) must be computed for each of the N antennas, resulting in a computational complexity of $\mathcal{O}\left(N\right)$ per iteration. Regarding step 7, let T denote the number of iterations in the gradient method, where T is directly related to the desired accuracy of the solution. Consequently, the overall computational complexity of the algorithm scales as $\mathcal{O}\left(NT\right)$.

Algorithm 1 Joint Antenna Selection and Transmit Power Optimization Algorithm

1: Initialize the dual variable $\lambda$. 2: repeat  3:     Compute $j^{*}\left(\mathit{s}\right)$ according to (25). 4:     Compute $p_2^{*}\left(\mathit{s}\right)$ according to (26). 5:     Compute $I_p\left(\lambda \right)$ according to (30). 6:     Update the Lagrangian multiplier $\lambda$ via the gradient method. 7: until Convergence

5. Closed-Form Outage Lower Bound for Rayleigh Fading Channels

In this section, we present a closed-form asymptotic lower bound on the outage probability for Rayleigh fading channels, which facilitates the analysis of outage performance. Because ${\mathcal{O}}_s^{*}\left(\lambda \right)$ is a monotonically increasing function of $\lambda \ge 0$, its minimum value (i.e., the asymptotic lower bound) is attained when $\lambda =0$. When $K_y=0$ for $\forall y\in \{h_0,h_1,h_2,g_1,g_2,g_3,g_4\}$, this asymptotic lower bound can be obtained by substituting $j^{*}\left(\mathit{s}\right)$ in (25) and ${\overline{p}}_2\left(\mathit{s}\right)$ in (32) into ${\mathcal{O}}_s$ in (13) as follows:

$$\begin{array}{c}\hfill {\mathcal{O}}_s^{*}\left(0\right){|}_{K_y=0}=F_0^{\prime }\left({\eta }_t\right)F_1^{\prime }\left({\eta }_t\right)+L_4,\end{array}$$

(44)

where

$$\begin{array}{cc}\hfill L_4& =E_{\mathit{s}}\left[I({\eta }_1\ge {\eta }_t)I\left({\eta }_0+{\displaystyle \frac{{\overline{p}}_2\left(\mathit{s}\right)h_{2j^{*}\left(\mathit{s}\right)}}{{\sigma }^2+p_0{g}_2}}<{\eta }_t\right)\right]{|}_{K_y=0}\hfill \\ \hfill & \stackrel{\left(g\right)}{=}{E}_{\mathit{s}}\left[I({\eta }_1\ge {\eta }_t)I\left({\overline{p}}_2\left(\mathit{s}\right)h_{2j^{*}\left(\mathit{s}\right)}<Y_2\right)\right]{|}_{K_y=0}\hfill \\ \hfill & =(1-F_1^{\prime }\left({\eta }_t\right)){\int }_{x=0}^{\infty }{f}_{Y_2}\left(x\right)\mathrm{Pr}\left({\displaystyle \frac{x}{h_{2j^{*}\left(\mathit{s}\right)}}}>Q_{\mathrm{UAV}}\right)dx\hfill \\ \hfill & \stackrel{\left(h\right)}{=}(1-F_1^{\prime }\left({\eta }_t\right)){\int }_{x=0}^{\infty }{f}_{Y_2}\left(x\right)\prod _{j=1}^N\left[\mathrm{Pr}\left({\displaystyle \frac{x}{h_{2j}}}>Q_{\mathrm{UAV}}\right)\right]dx\hfill \\ \hfill & =(1-F_1^{\prime }\left({\eta }_t\right)){\int }_{x=0}^{\infty }{f}_{Y_2}\left(x\right){\left[1-e^{-{\displaystyle \frac{x}{{\mathsf{\Omega }}_{h_2}{Q}_{\mathrm{UAV}}}}}\right]}^{N}dx\hfill \end{array}$$

$$\begin{array}{cc}\hfill & \stackrel{\left(i\right)}{=}(1-F_1^{\prime }\left({\eta }_t\right))\sum _{n=0}^N\left({\displaystyle \genfrac{}{}{0pt}{}{N}{n}}\right){(-1)}^n{\displaystyle \frac{Q_{\mathrm{UAV}}{\mathsf{\Omega }}_{h_2}{e}^{-\frac{n{\eta }_t{\sigma }^2}{Q_{\mathrm{UAV}}{\mathsf{\Omega }}_{h_2}}}}{{\eta }_t{p}_0{\mathsf{\Omega }}_{g_2}+{\mathsf{\Omega }}_{h_0}{p}_1}}\hfill \\ \hfill & \times \left[{\displaystyle \frac{p_1{\mathsf{\Omega }}_{h_0}\left(e^{\frac{n{p}_1{\mathsf{\Omega }}_{h_0}-Q_{\mathrm{UAV}}{\mathsf{\Omega }}_{h_2}}{p_1{\mathsf{\Omega }}_{h_0}{Q}_{\mathrm{UAV}}{\mathsf{\Omega }}_{h_2}}{\eta }_t{\sigma }^2}-1\right)}{n{p}_1{\mathsf{\Omega }}_{h_0}-Q_{\mathrm{UAV}}{\mathsf{\Omega }}_{h_2}}}+{\displaystyle \frac{{\eta }_t{p}_0{\mathsf{\Omega }}_{g_2}}{n{\eta }_t{p}_0{\mathsf{\Omega }}_{g_2}+Q_{\mathrm{UAV}}{\mathsf{\Omega }}_{h_2}}}\right],\hfill \end{array}$$

(45)

The equality (g) follows by substituting Equations (4) and (36). The equality (h) follows from the fact that the probability that the optimal antenna does not satisfy the transmit power threshold $Q_{\mathrm{UAV}}$ is equivalent to the probability that all antennas simultaneously fail to satisfy $Q_{\mathrm{UAV}}$. The equality (i) follows by substituting Equation (37), expanding the power term using the binomial theorem, and integrating the resulting summation of exponentials term by term. As the asymptotic lower bound in (44) is provided in closed form, this enables efficient evaluation of the outage probability lower bound.

6. Numerical Results

In this section, numerical results are presented to evaluate the performance behaviors of the proposed scheme. For the performance evaluation, we set $R=1\mathrm{bits}/\mathrm{s}/\mathrm{Hz}$, ${\sigma }^2=3.98\times {10}^{-12}$, $p_0=20$ dBm, $Q_{\mathrm{SS}}=Q_{\mathrm{UAV}}$, and $N=1,8$. The channel power gains are modeled as ${\mathsf{\Omega }}_{h_i}=({10}^{-3}/d_{h_i}^3)\mathrm{for}i\in \{0,1,2\}$ and ${\mathsf{\Omega }}_{g_j}=({10}^{-3}/d_{g_j}^3)\mathrm{for} j\in \{1,2,3,4\}$ [24,25], where $d_{h_i}$ and $d_{g_j}$ denote the distances associated with channels $h_i$ and $g_j$, respectively. For performance comparison, we also consider the conventional scheme [2,10,11] as follows:

$$\begin{array}{cc}\hfill j\left(\mathit{s}\right)& =arg\underset{j}{max}{h}_{2j},\hfill \end{array}$$

(46)

$$\begin{array}{cc}\hfill p_2\left(\mathit{s}\right)& =\min \left({\displaystyle \frac{Q_p}{g_{4j\left(\mathit{s}\right)}}},Q_{\mathrm{UAV}}\right).\hfill \end{array}$$

(47)

Figure 2 illustrates the secondary outage probability ${\mathcal{O}}_s$ as a function of the UAV transmit power threshold $Q_{\mathrm{UAV}}$ for $Q_p=-70$ dBm, $K_y=1$, $d_{h_1}=d_{h_2}=100$, $d_{h_0}=d_{g_1}=d_{g_2}=150$, and $d_{g_3}=d_{g_4}=100,110,120,130$. Contrary to the expectation that outage probability would continuously decrease with increasing $Q_{\mathrm{UAV}}$, the results demonstrate the existence of a floor value, implying that the secondary outage probability saturates beyond a certain transmit power. This phenomenon arises due to the interference constraint (17) imposed by the PD. Importantly, through joint antenna selection and transmit power optimization (proposed scheme), this floor value can be significantly lowered compared to the conventional scheme. Furthermore, as the distance $d_{g_3}=d_{g_4}$ increases, i.e., when the SS and UAV are located farther from the PD, the floor value of the secondary outage probability ${\mathcal{O}}_s$ decreases. Figure 3 presents the secondary outage probability ${\mathcal{O}}_s$ as a function of the interference power threshold $Q_p$ at the PD. Simulation parameters are set to $Q_{\mathrm{SS}}=Q_{\mathrm{UAV}}=30$ dBm, $K_y=1$, $d_{h_1}=d_{h_2}=100$, $d_{h_0}=150$, $d_{g_1}=d_{g_2}=d_{g_3}=200$, and $d_{g_4}=70,80,90,100$. In this scenario, the outage probability monotonically decreases as $Q_p$ increases, since relaxed interference constraints enable higher secondary transmit powers. Notably, the proposed scheme achieves a substantial reduction in outage probability compared to the conventional approach across all tested parameter ranges, demonstrating the effectiveness of joint antenna selection and power optimization in mitigating secondary outages under stringent interference limits.

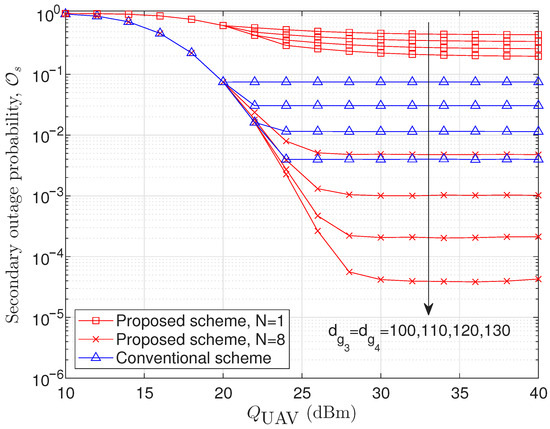
Figure 2. Secondary outage probability ${\mathcal{O}}_s$ versus $Q_{\mathrm{UAV}}$. $Q_p=-70$ dBm, $K_y=1$, $d_{h_1}=d_{h_2}=100$, $d_{h_0}=d_{g_1}=d_{g_2}=150$, and $d_{g_3}=d_{g_4}=100,110,120,130$.

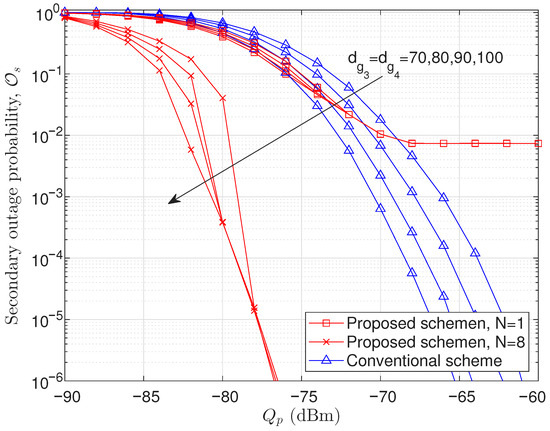
Figure 3. Secondary outage probability ${\mathcal{O}}_s$ versus $Q_p$. $Q_{\mathrm{SS}}=Q_{\mathrm{UAV}}=30$ dBm, $K_y=1$, $d_{h_1}=d_{h_2}=100$, $d_{h_0}=150$, $d_{g_1}=d_{g_2}=d_{g_3}=200$, and $d_{g_4}=70,80,90,100$.

Figure 4 and Figure 5 illustrate the secondary outage probability ${\mathcal{O}}_s$ for the Rayleigh fading scenario, where $K_y=0$, while other simulation parameters remain identical to those in Figure 2 and Figure 3, respectively. Since the simulation environments are nearly the same except for the Rician K-factor, the trend of the outage probability exhibited in Figure 4 and Figure 5 is similar to those observed in Figure 2 and Figure 3. However, unlike Figure 2 and Figure 3, Figure 4 and Figure 5 include the closed-form asymptotic lower bound on the outage probability, which is derived for the Rayleigh fading scenario in (44). In Figure 4, it is observed that the conventional scheme fails to achieve the asymptotic lower bound at the floor region of the outage probability, indicating a performance gap due to suboptimal antenna selection and power allocation. In contrast, the proposed scheme successfully attains this lower bound, demonstrating its effectiveness in minimizing outage probability even at the floor. Figure 5 shows the outage probability ${\mathcal{O}}_s$ versus the interference power threshold $Q_p$ at the PD. As $Q_p$ increases, the secondary outage probability of the proposed scheme approaches the asymptotic lower bound, reflecting its capability to optimally manage interference and minimize outages under relaxed constraints. In contrast, the conventional scheme remains unable to reach this lower bound, highlighting its inferior performance even as interference constraints are loosened.

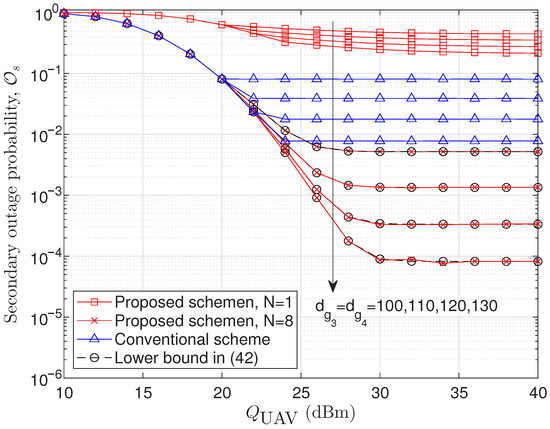
Figure 4. Secondary outage probability ${\mathcal{O}}_s$ versus $Q_{\mathrm{UAV}}$. $Q_p=-70$ dBm, $K_y=0$, $d_{h_1}=d_{h_2}=100$, $d_{h_0}=d_{g_1}=d_{g_2}=150$, and $d_{g_3}=d_{g_4}=100,110,120,130$.

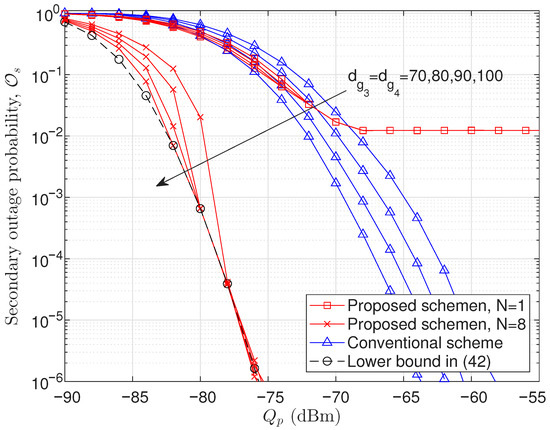
Figure 5. Secondary outage probability ${\mathcal{O}}_s$ versus $Q_p$. $Q_{\mathrm{SS}}=Q_{\mathrm{UAV}}=30$ dBm, $K_y=1$, $d_{h_1}=d_{h_2}=100$, $d_{h_0}=150$, $d_{g_1}=d_{g_2}=d_{g_3}=200$, and $d_{g_4}=70,80,90,100$.

Through Figure 2, Figure 3, Figure 4 and Figure 5, the contributions of the two optimization factors, i.e., antenna selection and transmit power, can be clearly identified in terms of outage performance improvement. Specifically, by comparing the proposed schemes with $N=8$ and $N=1$, the performance improvement achieved by the antenna selection optimization can be observed. Furthermore, by comparing the proposed scheme with $N=8$ against the conventional scheme, the performance improvement resulting from the transmit power optimization can be confirmed. As we can observe in Figure 2, Figure 3, Figure 4 and Figure 5, the antenna selection optimization plays a more dominant role than the transmit power optimization in improving the outage performance, because it increases the diversity order of the system, leading to a steeper decay slope of the outage probability curve.

7. Conclusions

In this paper, we have proposed a joint antenna selection and power adaptation scheme for the relaying UAV to minimize the outage probability of secondary networks. By jointly optimizing antenna selection and transmit power over fading states, the proposed scheme significantly improves secondary outage performance compared to conventional approaches that determine these parameters separately. In contrast, existing works determine antenna selection and transmit power using only partial channel state information, resulting in significantly degraded secondary performance. We have also derived a closed-form asymptotic lower bound on the secondary outage probability for Rayleigh fading channels and demonstrated through analysis and simulation that the proposed scheme approaches this bound. Finally, simulation results show that the performance gain becomes more pronounced as the SS and UAV move farther from the PD.