A Novel Integrated Fuzzy Analytic Hierarchy Process with a 4-Tuple Hedge Algebra Semantics for Assessing the Level of Digital Transformation of Enterprises

Abstract

Hedge algebra is a powerful and flexible tool for handling linguistic information, enabling precise quantitative computations and enhancing the effectiveness of multi-criteria decision-making (MCDM). This study proposes a novel integrated fuzzy MCDM approach that combines an enhanced fuzzy analytic hierarchy process (EFAHP) with a 4-tuple hedge algebra semantics model to assess digital transformation in retail enterprises. In this approach, the EFAHP method is integrated with hedge algebra to determine the priorities of pillars and criteria while providing a rigorous mathematical mechanism to transform ambiguous linguistic evaluations into numerical values. This transformation leverages the semantic structure of linguistic variable domains and incorporates fuzziness measures for both atomic words and intensity-modifying words (hedges). Furthermore, a new consistency index formula is introduced to evaluate the reliability of the EFAHP results, with validation being limited to the case study dataset. The 4-tuple hedge algebra semantic model is then employed to assess and rank the digital transformation levels of retail enterprises in Vietnam. Finally, a sensitivity analysis verifies the robustness of the proposed approach by illustrating how variations in pillar and criterion weights influence enterprise rankings.

1. Introduction

In daily experts’ or organizations’ operations, decision-making (DM) plays a crucial role and has thus garnered significant attention from researchers across various disciplines [1,2,3,4,5,6,7,8,9]. However, DM is becoming increasingly complex due to the involvement of multiple criteria, numerous stakeholders, and the inherent difficulty in evaluating these criteria, especially when qualitative factors are expressed using linguistic (L) words of variables. In this context, multiple-criteria group decision-making (MCGDM) methods, designed to handle information articulated in words, have emerged as essential tools across various domains, including management, engineering, logistics, healthcare, and public policy. A major challenge in MCGDM lies in effectively modeling and processing qualitative information, which is often ambiguous, imprecise, and subjective, particularly when expressed by L-variables’ words [10].

Computing with words (CWW), introduced by Zadeh, is a paradigm for computing and reasoning based on the information expressed by natural L-words [11]. Over the past decades, CWW has gained significant attention among researchers in the field of fuzzy set theory [12,13,14,15]. To enable automated reasoning, computing, or DM using L-expressions, it is crucial to construct approximate models capable of processing L-information while preserving the semantic meaning of the words in a way that aligns with human cognitive processes [16]. However, this presents a considerable challenge due to the inherently vague and uncertain nature of L-data.

A key challenge in DM involving L-information is how to establish a reliable formalism that can deal with L-data while preserving their inherent semantics. Ho et al. [16] suggest mathematically formalizing the L-domains to become the so-called hedge algebras (HAs) and to quantify them. In the context of CWW applied to DM, two fundamental problems emerge: how one can deal with L-data as mathematical or computational objects, and how to effectively process them. The L-computation typically uses fuzzy sets to model the semantics of words to solve DM problems [12]. However, the output fuzzy sets of the computational procedures usually do not match the existing fuzzy sets originally defined to represent the given words [17]. This misalignment can lead to information loss and decrease the outputs’ accuracy. To address this issue, Herrera et al. [12] proposed a 2-tuple L-representation model, considered as the symbolic approach, which symbolically encodes the semantics of L-words. This model assumes a predefined ordered L-scale and maps each L-word to a numerical scale’s value that facilitates computation [1,3,9,12,15]. Despite its advantages, this mapping can still lead to information loss, particularly when semantic granularity is high. Most studies assume that L-scales are linearly ordered. In applications, experts rely on the order of their L-words to make their decisions. However, computational processes are required to deal with the quantitative semantics of L-words, which are not directly derivable from ordinal scales alone. This limitation highlights a critical gap in current models: the lack of a formal connection between qualitative and quantitative (numerical) representations of L-information. Bridging this gap is essential to improve the accuracy, interpretability, and semantic consistency of the L-computation.

To deal with the L-data, the studies [16,18] introduced the theory of hedge algebra (HA), which establishes an axiomatic mathematical framework to handle the L-domains and quantify their words’ semantics. This is achieved by formally defining a semantic mapping that associates each L-word with a suitable corresponding numerical value. The HA theory serves as a powerful and practical tool for representing and processing the multifaceted semantics of L-words. It has been successfully applied in various fields, including fuzzy control [19], L-summarization [20], decision support systems [21], and MCGDM [2]. Building upon the 2-tuple L-representation model for MCGDM problems, a 4-tuple semantic model based on HA was proposed in [2]. In the 2-tuple approach, the words in the L-scale are semantically increasingly arranged, say {$l_0,l_1$, …, $l_n$}; the desired MCGDM will compute based on the L-labels’ indices. That is, these indices must be, in this context, considered as the numeric semantics of the L-labels $l_i$s. It can be observed that the syntactic and semantic relationships among such L-words are relatively weak, as the indices merely represent their ordinal positions within the L-scale. However, the semantics of L-words inherently encompass richer characteristics beyond mere ordering. Neglecting these deeper semantic features results in a significant loss of information that would otherwise be preserved during the structuring phase of linguistic DM problems.

To overcome this constraint, Nguyen et al. [2] proposed the 4-tuple semantic model (x, $S_{\left(k\right)}\left(x\right)$, ϑ(x), r) where x is an L-word, $S_{\left(k\right)}\left(x\right),$ is its fuzzy interval representing the quantitative semantic range of x, ϑ(x) is its quantitative value, and r is a reference value such that both ϑ(x) and r belong to $S_{\left(k\right)}\left(x\right)$. The difference between ϑ(x) and r, referred to as the semantic deviation, indicates the extent to which the meaning of x diverges from the reference. This model allows conventional mathematical operations (e.g., average, weighted average) to be directly applied to L-words via their quantitative values, thereby enhancing the flexibility and computational efficiency of processing L-information compared with the traditional fuzzy set-based or symbolic methods. Nevertheless, in the applications [2,22], the authors did not propose any method for determining the weights of the criteria. Instead, subjective expert-assigned weights were adopted, which may lead to bias in judgment and low reproducibility of results. This limitation highlights a methodological gap in existing studies that employ the 4-tuple semantic representation but do not systematically address the weighting process, which is a crucial factor in MCGDM. To address this weakness, this study integrates the 4-tuple semantic model into the EFAHP framework, which enables the derivation of data-driven and linguistically grounded weights rather than purely subjective ones. In addition, a new consistency index (CI) is proposed to evaluate the internal reliability of pairwise comparisons, ensuring greater robustness and methodological transparency in the weighting process. This integration not only enhances the objectivity of MCGDM analysis but also strengthens the semantic interpretability of expert judgments.

Today, digital transformation is regarded as an inevitable trend to enhance business competitiveness and achieve sustainable development [23]. Several studies have highlighted the critical role of digital transformation in strengthening supply chain management [24], improving the business environment [25], increasing production efficiency [26], promoting sustainable development in enterprises [27], enhancing the efficiency of technological innovation in enterprises [28], and improving ESG performance [29,30]. However, there are currently few studies that propose models for assessing the level of digital transformation in enterprises. Such assessment is inherently complex, as it requires the consideration of multiple evaluation criteria [31]. Therefore, evaluating the digital transformation level of enterprises can be regarded as an MCGDM problem [23].

The remainder of this paper is organized as follows. Section 2 provides an overview of HAs and L-scoring based on the 4-tuple semantics model and introduces the EFAHP method. Section 3 develops an HA-based EFAHP approach, integrating the 4-tuple semantic model to address the MCGDM problem. Section 4 applies the proposed HA-based EFAHP method to a real-world case study, evaluating the level of digital transformation in Vietnamese enterprises and demonstrating its effectiveness. To assess the model’s reliability, Section 5 presents both a sensitivity analysis and a comparative analysis, in which the fuzzy set-based FAHP-FTOPSIS method is employed to systematically examine the stability and consistency of the final rankings of digital transformation levels among small- and medium-sized enterprises (SMEs) in the retail sector. Finally, Section 6 concludes the paper.

2. Preliminaries

2.1. Hedge Algebras and the 4-Tuple Semantic Model

The theory of HAs was initially introduced in [16] and has since been significantly expanded in subsequent studies [2,18,19,20,21,22]. This theory uncovers both the qualitative and the quantitative structures that are inherently embedded in the L-domains of the L-variables. The HA theory offers a formal and unified framework, based on which one can handle the L-words’ qualitative and quantitative semantics in a unified axiomatic formalism. This section presents the core concepts and fundamental HA knowledge for constructing an L-scale, which reflect the natural semantics of L-words represented by a 4-tuple semantic model useful for the study:

2.1.1. The Concept of the Hedge Algebras

Let us consider the L-variable AGE, whose domain consists of the words generated from two primary generators or primitive words, e.g., “young” and “old”, by means of L-hedges. For example, let us consider two hedges “very” and “little”; the words generated by applying these hedges to the generators “young” and “old” include “very young”, “little young”, “very old”, “very very old”, and so on. These words are semantically comparable, e.g., very young ≤ young ≤ little young ≤ old ≤ very old ≤ very very old. There are many hedges in a natural language (NL), say, in English, such as more (M), very (V), and extremely (E), whose function is to increase the semantic tendency of the word “old” of AGE above, called its atomic word. In contrast, the hedges rather (R) and little (L) decrease it, e.g., a person of R_old is younger than the other person of old. Moreover, we have $LR\_old\le old$ and $L\_old\le R\_old\le old$. The latter implies that $L$ modify the semantics of a word more strongly than $R$, and we write $R\le L$. Similarly, we observe also that $old\le M\_old\le V\_old\le E\_old$, which justify that $M\le V\le E$. The semantic relations among the hedges L, R, M, V, and E are shown in Table 1.

Table 1. Semantic ordering and converse relations among hedges in the HA of AGE.

Hedges	L	R	M	V	E
L	=	>	><	><	><
R	<	=	><	><	><
M	><	><	=	<	<
V	><	><	>	=	<
E	><	><	>	>	=

><: The notation means that the related hedges, h and k, are semantically converse, i.e., for every primitive word $a$, $ha\le a$ if and only if $ka\ge a.$

Thus, we observe that every word domain must contain a semantic order-based structure, which suggests the introduction of the following definition:

Definition 1.

An HA of an L-variable $X$ is defined in [32] as follows:

$$AX = (X\mathrm{,} G\mathrm{,} \mathit{Є}\mathrm{,} H\mathrm{,} \mathit{\partial }\mathrm{,} Ф\mathrm{,} \le )$$

in which:

• $X$ is the set of L-words of the variable $X$, called the word domain of $X$$;$
• G = {$g^{-}$,  $g^{+}$} is the set of the $X$’s generators representing, respectively, the negative and positive primary word;
• Є = {0, W, 1} is the set of constants interpreted as the smallest, the neutral, and the largest word in $X$, satisfying the ordering 0 < $g^{-}$ < W < $g^{+}$ < 1;
• H = $H^{-}\cup H^{+}$, where $H^{-}$ and $H^{+}$, are the sets of negative and positive hedges applied to the $X$’s words to generate new words from a given one of the L-variable $X;$
• ∂ and Ф are specific artificial operators that determine, respectively, the supremum and infimum of a subset of the word domain $X$;
• ≤ is a semantic ordering relation defined on $X$.

When a hedge acts on a non-constant word, a new word is induced. For example, Temperature is an L-variable. For two generators G = {“cold”, “hot”}, Є = {0, W, 1}, where W = {“medium”}, 0 = “extremely cold”, 1 = “extremely hot”, and H = {“little”, “very”}. $X_{\left(2\right)}$ is the set of words of variable Temperature created from “cold” and “hot” using the hedges “little” and “very”, $X_{\left(2\right)}$ = {“extremely cold”, “cold”, “medium”, “hot”, “extremely hot”} $\cup$ {“little cold”, “very cold”, “little hot”, “very hot”}. Note that $X_{\left(\mathrm{k}\right)}$ denotes the set of words that have the word lengths less than or equal to k. Each term x in $X$ can be represented as the string representation, i.e., either x = c or x = $h_m\dots h_{1c}$, in which c $\in$ {$c^{-}$, $c^{+}$} $\cup$ G and $h_j\in$ H, j = 1, …, m. All the words generated from x by using the hedges in H can be abbreviated as H(x).

Let $H^{-}$ be the set {h_−q, h_−q+1, …, h₋₁} whose hedges do decrease the semantics of the $X$’s generators and, therefore, are called the negative hedges, whereas let $H^{+}$ be the set {h₁, h₂, …, h_p} whose hedges do increase the $X$’s generators and, therefore, are called the positive hedges. We assume h_−q < h_−q+1 < … < h₋₁, and h₁ < h₂ < … < h_p, where h < h’ means that h’ modifies a given word more strongly than h does. Then, for every $x\in X$, from $hx\le x$ and $h\in H^{+}$, we derive h_px $\le$ h_p−1x $\le$ … $\le$ h₁x $\le$ h₋₁x $\le$ h₋₂x $\le$ … $\le$ h_−qx; and from $hx\ge x$ and $h\in H^{+}$, we derive h_px $\ge$ h_p−1x $\ge$ … $\ge$ h₁x $\ge$ h₋₁x $\ge$ h₋₂x $\ge$ … $\ge$ h_−qx.

For every x ∈ $X$, H(x) denotes the set of all words u ∈ $X$ generated from x by applying any sequence of hedges of H. Formally, this is expressed by:

$$H\left(x\right)=\{u\mathit{\in }X|u=h_n{h}_{n-1}\dots h_{1}x\mathrm{,}{h}_i\mathit{\in }H\mathrm{,}1\le i\le n\mathrm{,}\forall n\ge 1\}$$

H(x) plays a significant semantic role because it can describe the fuzziness of the word x: the larger the set H(x), the more fuzziness of the word x. We can imagine the size of H(x) to be viewed as the fuzziness measure (FM) of $x$, denoted by fɱ(x). This suggests the introduction of the following definition of the words’ fuzziness:

Definition 2

[18]. Let $AX$ = ($X$, G, Є, H, ∂, Ф, ≤) be a linear complete hedge algebra (ComHA) of the given L-variable $X$. A mapping fɱ: $X$⟶ [0, 1] is said to be an FM of $X$ if the following conditions are satisfied:

(i) fɱ is complete in the sense that fɱ(g⁻) + fɱ(g⁺) = 1, and $\sum _{h\in H}fɱ\left(hu\right)=fɱ\left(u\right)$, for ∀u ∈ $X$;

(ii) fɱ(x) = 0, for all x satisfying H(x) = {x}. Particularly, fɱ(0) = fɱ(W) = fɱ(1) = 0;

(iii) ∀x, y ∈ $X$, ∀h ∈ H; the ratio $\mu \left(h\right)={\displaystyle \frac{fɱ\left(hx\right)}{fɱ\left(x\right)}}={\displaystyle \frac{fɱ\left(hy\right)}{fɱ\left(y\right)}}$ is independent from x and y and is referred to as the FM of the hedge h, denoted by $\mu \left(h\right)$.

The main properties of the FMs for words and hedges are as follows:

Proposition 1

[18]. Given the FM of words and the FM of hedges defined in Definition 2, we have:

(i) fɱ(g⁻) + fɱ(g⁺) = 1 and $\sum _{h\in H}fɱ\left(hx\right)=fɱ\left(x\right)$;

(ii) $\sum _{j=-q}^{-1}\mu \left(h_j\right)=\alpha$, $\sum _{j=1}^p\mu \left(h_j\right)=\beta$, where α, β > 0 and α + β = 1;

(iii) Σ_x∈ $\sum _{x\in X_k}fɱ\left(x\right)=1$, $X_{\left(k\right)}$ is the set of words in $X$ = H(G) of length k;

(iv) fɱ(hx) = μ(h)fɱ(x), and for all x∈ Lim(X), fɱ(x) = 0;

(v) Let fɱ(g⁻), fɱ(g⁺) and μ(h),$\forall$ h ∈ H, be known. Then, for each x = $h_n$…$h_1{g}^{\epsilon }$, $\epsilon$ ∈ {−, +}, the fɱ(x) is calculated as fɱ($h_n$…$h_1{g}^{\epsilon }$) = μ($h_n$)μ($h_{n-1}$)… μ(h₁) fɱ($g^{\epsilon }$).

2.1.2. Quantitative Theory of the Linear Complete Hedge Algebra

In HA theory, the numeric semantics of words is defined by any isomorphic mapping from a given word domain into [0, 1], the normalized domain of its respective numeric variable. It is formally defined as follows:

Definition 3

[18]. Let $AX$ = ($X$, G, Є, H, ∂, Ф, ≤) be a linear ComHA. A mapping ϑ: $X$ ⟶ [0, 1] is called a semantically quantifying mapping of $AX$ if it satisfies the following conditions:

(i) ϑ is a one-to-one (1-1) mapping from $X$ into [0, 1] such that ϑ(0) = 0 and ϑ(1) = 1, and the semantic order on $X$, is preserved; for all x, y ∈ $X$, if x < y, then ϑ(x) < ϑ(y);

(ii) ϑ is continuous for all x ∈$X$, ϑ(Фx) = infimum ϑ($X$(x) and ϑ(∂x) = supremum ϑ(H(x)).

Thus, the completeness of an HA means that, for every word set H(x), there are always the upper limit and lower limit of the words sets H(x)s.

Similarly, as the algebraic sign of the numbers of the classical analytic mathematics, the $X$’s L-words also have their algebraic signs defined as follows, called the sign function:

Definition 4

[18]. The sign function ζg: $X$⟶ {−1, 0, 1} is a mapping defined recursively as follows, where h, h’ ∈ H and с ∈ {с⁻, с⁺}:

(i) ζg(с⁻) = −1, ζg(с⁺) = +1;

(ii) ζg(hс) = −ζg(с) if hс < с, and ζg(hс) = +ζg(с) if hс > с;

(iii) ζg(h’hx) = 0 if h’hx = hx; ζg(h’hx) = −ζg(hx), if h’hx≠ hx and h’ is negative with respect to h; otherwise, ζg(h’hx) = ζg(hx), if h’hx≠ hx and h’ is positive with respect to h;

(iv) ζg(h’hx) = 0, if h’hx = hx.

There is a closed relation between the sign function and the semantic order of hx and x:

Proposition 2

[18]. For any hedge h and word x, the given sign function ζg(hx) allows us to compare hx and x as follows: if ζg(hx) = +1, then hx > x; if ζg(hx) = −1, then hx < x; if ζg(hx) = 0, then hx = x.

The word sets H(x)s have the following properties:

H(x) $\cap$ H(y) $=\varnothing ,$ for x ∉ H(x) and y ∉ H(y) and 0 ≤ H(x) ≤ 1. Moreover:

if ζg(h_px) = +1, then H(h_−qx) ≤ H(h_−q+1x) ≤ … ≤ H(h₋₁x) ≤ x ≤ H(h₁x) ≤ H(h₂x) ≤ … ≤ H(h_px);

if ζg(h_px) = −1, then H(h_qx) ≥ H(h_−q+1x) ≥ … ≥ H(h₋₁x) ≥ x ≥ H(h₁x) ≥ H(h₂x) ≥ … ≥ H(h_px).

A significant concept of nature language’s words is their numeric semantics, which we can formalize as a semantically quantifying mapping as follows:

Definition 5

[18]. Let $AX$ = ($X$, G, Є, H, ∂, Ф, ≤) be a free linear ComHA and fɱ be an FM on $X$. A mapping ϑ: $X$ ⟶ [0, 1] is said to be induced by fɱ if it is recursively defined as follows:

(i) ϑ(W) = θ = fɱ(g⁻), ϑ(g⁻) = θ − αfɱ(g⁻) = βfɱ(g⁻), ϑ(g⁺) = θ +αfɱ(g⁺);

(ii) ϑ(h_jx) = ϑ(x) + ζg$\left(h_{j}x\right)\left\{\sum _{i=\zeta g\left(j\right)}^{j-\zeta g\left(j\right)}\mu \left(h_i\right)fɱ\left(x\right)-\omega \left(h_{j}x\right)\mu \left(h_{j}x\right)fɱ\left(x\right)\right\}$ for all j, where −q ≤ j ≤ p, j≠ 0, and $\omega \left(h_{j}x\right)={\displaystyle \frac{1}{2}}\left[1+\zeta g\left(h_{j}x\right)\zeta g\left(h_p{h}_{j}x\right)(\beta -\alpha )\right]$;

(iii) ϑ(Фg⁻) = 0, ϑ(∂g⁻) = θ = ϑ(Фg⁺), ϑ(∂g⁺) = 1, and for all j, −q ≤ j ≤ p,

ϑ(Ф$h_{j}x$) = ϑ(x)+ ζg$\left(h_{j}x\right)\left\{\sum _{i=\zeta g\left(j\right)}^{j-\zeta g\left(j\right)}\mu \left(h_i\right)fɱ\left(x\right)\right\}-{\displaystyle \frac{1}{2}}\left(1-\zeta g\left(h_{j}x\right)\right)\mu \left(h_i\right)fɱ(x)$,

ϑ(∂$h_{j}x$) = ϑ(x)+ ζg$\left(h_{j}x\right)\left\{\sum _{i=\zeta g\left(j\right)}^{j-\zeta g\left(j\right)}\mu \left(h_i\right)fɱ\left(x\right)\right\}+{\displaystyle \frac{1}{2}}\left(1+\zeta g\left(h_{j}x\right)\right)\mu \left(h_i\right)fɱ(x)$.

It can be shown that this definition satisfies the requirements of a semantic quantification function and guarantees that the resulting values are densely distributed over the interval [0, 1].

2.2. Linguistic Scale with Its Words’ Semantics Represented by 4-Tuple

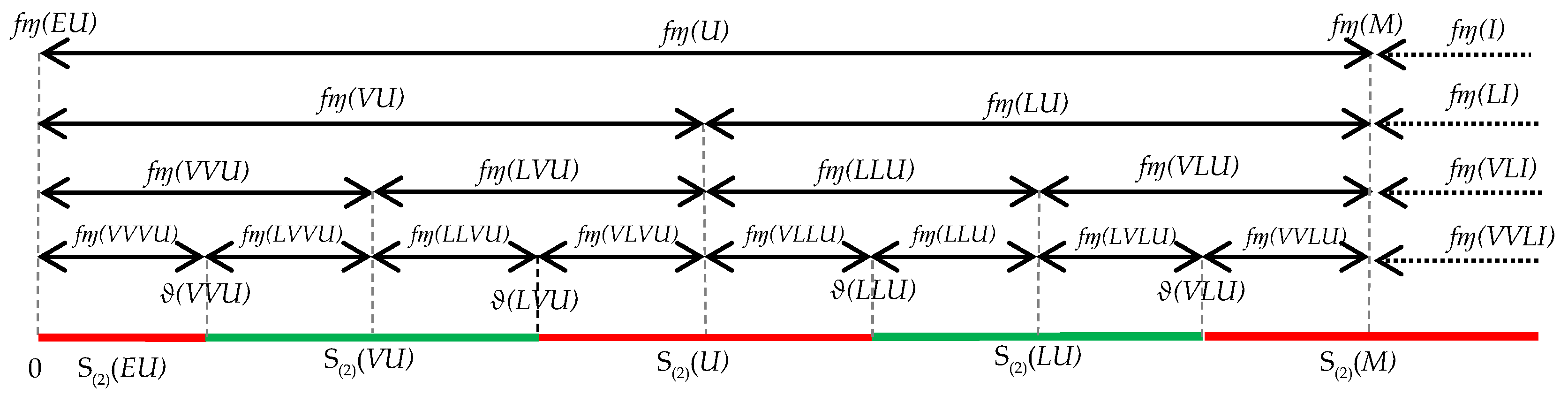
Another aspect of the L-words’ quantitative semantics is the concept of the similarity interval of the words of the given word set $X$_(k) = {x $\in$ $X$: |x| ≤ k}, the set of words whose lengths are at most $k$. Assume ϑ to be an $X$’s semantic quantification function and the system of the $x$’s intervals; {$S_{\left(k\right)}(x$): x $\in$ $X$_(k)}, forms a partition of [0, 1], the normalized numerical domain of its respective numeric variable, so that each interval $S_{\left(k\right)}\left(x\right)$ contains a unique value ϑ(x) of the set {ϑ(x): x $\in$ $X$_(k)}. The interval $S_{\left(k\right)}\left(x\right)$ is called the k-similarity interval of x. The collection {$S_{\left(k\right)}(x$): ∀x $\in$ $X$_(k)} is referred to as the k-similarity interval system defined by $X$_(k). The method constructing this interval system can be found in [2]. Figure 1 is an example illustrating a similarity interval system of $X$₍₂₎.

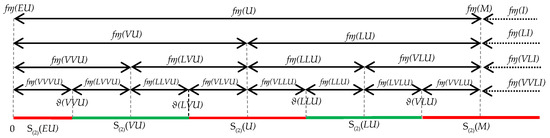
Figure 1. An illustration of constructing the 2-similarity interval of the L-word set $X_{(2)}$, $S_{\left(2\right)}$.

To construct the similarity interval system S_(k) for the word set $X$_(k) in the case of a HA with two generators and two hedges, first of all, we generate the words set with length exactly k+2, $X$_k+2, compute the FM for all x $\in$ $X$_k+2, and arrange them linearly from left to right, following the order of their words. The similarity intervals corresponding to 0 and 1 are the first and the last among the fuzzy intervals of $X$_k+2, respectively. The fuzzy similarity interval of word x $\in$$X$_(k) is defined by concatenating two fuzziness intervals in $X$_k+2, one of which has an endpoint equal to the quantitative value ϑ(x).

Nguyen et al. [2] developed a 4-tuple semantic representation model of L-scales, where the semantics of words are expressed by using 4-tuples. This method aims to capture the nuanced meanings of ambiguous L-words and is especially useful for solving MCGDM problems, as described below:

Definition 6

[2]. Given an L-variable $X$ and its normalized numeric reference domain [0, 1], the 4-tuple semantic representation of $X$ is:

$$(x,S_{\left(k\right)}(x),\vartheta (x),r)$$

(1)

where:

• x $\in$ Dom ($X$): is a linguistic word;
• $S_{\left(k\right)}\left(x\right)$ ⊆ [0, 1]: is the similarity interval of x for the given $X$_k;
• ϑ(x): is the numeric quantitative semantics of x;
• r $\in S_{\left(k\right)}\left(x\right)$: is a reference value within the similarity interval.

When (ϑ(x) − r) is the semantic deviation between the word and the reference value r; r = ϑ(x), the 4-tuple is the semantic representation of the L-word x.

Definition 7

[2]. Let $AX$ = ($X$, G, Є, H, ∂, Ф, ≤) be a free linear HA for the L-variable $X$. A totally ordered word set T = $\left\{t_0,\dots ,t_g\right\}$ ⊆ $X$ is called a superior-closed L-scale at specificity level k if:

(i) ∀$t$∈ T, |$t$|$\le k$, and ∃ $t$∈ T such that |t| = k;

(ii) $g^{-}$, $g^{+},$ 0, W, 1∈ T;

(iii) if y = hx∈ T then x∈ T.

Since $AX$ is a free HA and $X$ is countably infinite, T ⊆ $X$ means that the qualitative semantics of its words should be considered in the context of $X$. Thus, the 4-tuple semantic representations must be defined over the full algebra A$X$ (see Section 2.1).

Condition (i): Ensures specificity level is maintained;

Condition (ii): Ensures inclusion of the core vague words of the L-variable, serving as the base for generating other words;

Condition (iii): Supports superior-closed.

However, since T lacks computational structure, a semantic L-scale using a 4-tuple semantic representation model of L-words will accompany it. This enhanced version is termed the 4-tuple semantic L-scale.

Definition 8

[2]. A 4-tuple semantic L-scale with specificity level k, associated with a given L-scale T that satisfies Definition 7, is defined as a set of 4-tuples:

$$T_{\vartheta ,k}=\left\{\right(t,S_{\left(k\right)}\left(t\right),\mathsf{\vartheta }\left(t\right),r_t)\text{:} t\in \mathrm{T},r_t\in S_{\left(k\right)}\left(t\right)\}$$

(i) For every $t$  ∈ T, ($t$, $S$_(k)(t), ϑ(t), $r$_t) forms a valid 4-tuple semantic representation, where $S$_(k)(t)⊆ [0, 1] denotes the interval semantics of $t$; ϑ(t)∈ [0, 1] denotes the numeric quantitative semantics of t as defined in Definition 6;

(ii) The intervals $S$  _(k)(t), for all t∈ T, partition the domain [0, 1] such that each $S$_(k)(t) represents a similarity region corresponding to t. That is, elements of $S$_(k)(t) are considered semantically similar to t to a degree determined by the specificity level k;

(iii) For any t, t′ ∈ T, if t ≤ t’ then $S$_(k)(t) ≤ $S$_(k’)(t’);

(iv) ϑ(t) ∈ $S$_(k)(t) for all t  ∈ T.

Proposition 3

[2]. Let T be a superior-closed L-scale with the specificity level k, constructed based on a given HA: $AX$ = ($X$, G, Є, H, ∂, Ф, ≤). For the given fuzziness parameters of its L-variable $X$, the set:$T_{\vartheta }$ = {($t$, $S$_(k)(t), ϑ(t), $r$_t): $t$ ∈ T, $r$_t ∈ $S$_(k)(t)} satisfies the following fundamental properties:

(i) $T_{\vartheta }$ constitutes a 4-tuple semantic L-scale associated with T;

(ii) Each interval $S$_(k)(t) is defined and computed based on the semantic structure of the words of $AX,$ as follows:

$${\mathrm{S}}_{\left(\mathrm{k}\right)}\left(t\right)={\mathrm{S}}_{\left(\mathrm{L}\right)}\left(t\right)\cup {\mathrm{S}}_{\left(\mathrm{R}\right)}\left(t\right)\mathrm{and}{\mathrm{S}}_{\left(\mathrm{k}\right)}\left(t\right)=\cup \left\{\mathrm{T}\right(X)\in X_{\mathrm{k}+2}\text{\&} \mathrm{T}\left(X\right)\subseteq \left(\mathsf{\vartheta }\right(t_{L,p_L+1}),\mathsf{\vartheta }(t_{R,p_R+1})\left)\right\}$$

(2)

2.3. The Generalized Fuzzy AHP Method

The extent analysis method on fuzzy AHP, introduced by Chang [33], has gained widespread adoption in MCDM due to its ability to model hierarchical structures and incorporate expert judgments under uncertainty. However, several limitations have been identified in the literature. Specifically, Wang et al. [34] observed that Chang’s method may irrationally assign zero weights to relevant criteria, which can potentially lead to the selection of suboptimal alternatives. Furthermore, its applicability is restricted to normalized triangular fuzzy numbers.

To overcome these shortcomings, Hue et al. [35] proposed an enhanced fuzzy AHP method that utilized generalized triangular fuzzy numbers (GTFNs) along with a centroid index to more accurately derive the priority weights of the criteria. This refined approach improves the reliability of the ranking process for alternatives by adopting a structured, step-by-step procedure, as follows:

• Step 1: Define the GTFNs comparison matrix

$$\mathrm{F}={\left({\stackrel{⃛}{\mathcal{x}}}_{\mathcal{i}\mathcal{j}}\right)}_{nxn}=\left[\begin{array}{cccc}(1,1,1;{\mathcal{w}}_{11})& ({\mathcal{a}}_{12},{\mathcal{b}}_{12},{\mathcal{c}}_{12};{\mathcal{w}}_{12})& \dots & ({\mathcal{a}}_{1n},{\mathcal{b}}_{1n},{\mathcal{c}}_{1n};{\mathcal{w}}_{1n})\\ ({\mathcal{a}}_{21},{\mathcal{b}}_{21},{\mathcal{c}}_{21};{\mathcal{w}}_{21})& (1,1,1;{\mathcal{w}}_{22})& \dots & ({\mathcal{a}}_{2n},{\mathcal{b}}_{2n},{\mathcal{c}}_{2n};{\mathcal{w}}_{2n})\\ \dots & \dots & \dots & \dots \\ ({\mathcal{a}}_{n1},{\mathcal{b}}_{n1},{\mathcal{c}}_{n1};{\mathcal{w}}_{n1})& ({\mathcal{a}}_{n2},{\mathcal{b}}_{n2},{\mathcal{c}}_{n2};{\mathcal{w}}_{n2})& \dots & (1,1,1;{\mathcal{w}}_{nm})\end{array}\right]$$

where: ${\stackrel{⃛}{\mathcal{x}}}_{\mathcal{i}\mathcal{j}}=\left({\mathcal{a}}_{\mathcal{i}\mathcal{j}},{\mathcal{b}}_{\mathcal{i}\mathcal{j}},{\mathcal{c}}_{\mathcal{i}\mathcal{j}};{\mathcal{w}}_{\mathcal{i}\mathcal{j}}\right)$, ${\stackrel{⃛}{\mathcal{x}}}_{\mathcal{i}\mathcal{j}}^{-1}=\left({{\displaystyle \frac{1}{\mathcal{c}}}}_{\mathcal{i}\mathcal{j}},{{\displaystyle \frac{1}{\mathcal{b}}}}_{\mathcal{i}\mathcal{j}},{{\displaystyle \frac{1}{\mathcal{a}}}}_{\mathcal{i}\mathcal{j}};{\mathcal{w}}_{\mathcal{i}\mathcal{j}}\right)for\mathcal{i},\mathcal{j}=1,\dots ,nand\mathcal{i}\ne \mathcal{j}$.

• Step 2: Calculate the fuzzy synthetic extents

The fuzzy synthetic extent, ${\mathcal{S}}_{\mathcal{i}}$, is calculated as follows:

$$\begin{array}{l}{\mathcal{S}}_{\mathcal{i}}=({\mathcal{g}}_{\mathcal{i}},{\mathcal{h}}_{\mathcal{i}},{\mathcal{k}}_i;\min ({\mathcal{w}}_{\mathcal{i}\mathcal{j}}\left)\right)\\ =\left(\begin{array}{c}{\displaystyle \frac{\sum _{\mathcal{j}=1}^n{\mathcal{a}}_{\mathcal{i}\mathcal{j}}}{\sum _{\mathcal{j}=1}^n{\mathcal{a}}_{\mathcal{i}\mathcal{j}+}{\sum }_{\mathcal{k}=1,\mathcal{k}\ne \mathcal{i}}^n\sum _{\mathcal{j}=1}^n{\mathcal{c}}_{\mathcal{k}\mathcal{j}}}},{\displaystyle \frac{\sum _{\mathcal{j}=1}^n{\mathcal{b}}_{\mathcal{i}\mathcal{j}}}{{\sum }_{\mathcal{i}=1}^n\sum _{\mathcal{j}=1}^n{\mathcal{b}}_{\mathcal{i}\mathcal{j}}}},{\displaystyle \frac{\sum _{\mathcal{j}=1}^n{\mathcal{c}}_{\mathcal{i}\mathcal{j}}}{\sum _{\mathcal{j}=1}^n{\mathcal{c}}_{\mathcal{i}\mathcal{j}+}{\sum }_{\mathcal{k}=1,\mathcal{k}\ne \mathcal{i}}^n\sum _{\mathcal{j}=1}^n{\mathcal{a}}_{\mathcal{k}\mathcal{j}}}};\min \left({\mathcal{w}}_{\mathcal{i}\mathcal{j}}\right)\end{array}\right)\end{array}$$

(3)

where: $\sum _{\mathcal{j}=1}^n{M}_{{\mathcal{g}}_{\mathcal{i}}}^{\mathcal{j}}=\left(\sum _{\mathcal{j}=1}^n{\mathcal{a}}_{\mathcal{i}\mathcal{j},}\sum _{\mathcal{j}=1}^n{\mathcal{b}}_{\mathcal{i}\mathcal{j}},\sum _{\mathcal{j}=1}^n{\mathcal{c}}_{\mathcal{i}\mathcal{j},}\min \left({\mathcal{w}}_{\mathcal{i}\mathcal{j}}\right)\right),\mathcal{i},\mathcal{j}=1,2,\dots ,n$.

Next, compute the centroid indices of the fuzzy synthetic extents ${\mathcal{S}}_{\mathcal{i}}$ using the approach proposed by Dat et al. [36]. Let ${\mathcal{S}}_1$, ${\mathcal{S}}_2$, …, ${\mathcal{S}}_n$ be the fuzzy synthetic extent values. The centroid point of each fuzzy number ${\mathcal{S}}_i$, denoted as ${\mathrm{C}}_{\mathrm{i}}$ = (${\overline{\mathcal{x}}}_{{\mathcal{S}}_{\mathcal{i}}},{\overline{\mathcal{y}}}_{{\mathcal{S}}_{\mathcal{i}}}$), for $\mathcal{i}$ = 1, 2, …, n, can be calculated as follows:

$${\overline{\mathcal{x}}}_{{\mathcal{S}}_{\mathcal{i}}}=({\mathcal{g}}_{\mathcal{i}}+{\mathcal{h}}_{\mathcal{i}}+{\mathcal{k}}_i)/3;{\overline{\mathcal{y}}}_{{\mathcal{S}}_{\mathcal{i}}}=min\left({\mathcal{w}}_{\mathcal{i}\mathcal{j}}\right)/3$$

(4)

The distance between each centroid point ${\mathrm{C}}_{\mathrm{i}}$ = (${\overline{\mathcal{x}}}_{{\mathcal{S}}_{\mathcal{i}}},{\overline{\mathcal{y}}}_{{\mathcal{S}}_{\mathcal{i}}}$), for $\mathcal{i}$ = 1, 2, …, n, and the minimum point G = (${\mathcal{x}}_{min},{\mathcal{y}}_{min}$), where ${\mathcal{x}}_{min}=\min \left({\mathcal{g}}_{\mathcal{i}}\right)\mathrm{a}\mathrm{n}\mathrm{d}{\mathcal{y}}_{min}=\mathrm{m}\mathrm{i}\mathrm{n}\left({\mathcal{w}}_{\mathcal{i}\mathcal{j}}\right)$, is calculated as follows:

$$D\left({\mathcal{S}}_{\mathcal{i}},G\right)=\sqrt{({\overline{\mathcal{x}}}_{{\mathcal{S}}_{\mathcal{i}}}-{\mathcal{x}}_{min}{)}^2+({\overline{\mathcal{y}}}_{{\mathcal{S}}_{\mathcal{i}}}-{\displaystyle \frac{\omega }{3}}{\mathcal{y}}_{min}{)}^2}$$

(5)

• Step 3: Determine the weight vector W = ${({\mathcal{w}}_1,\dots ,{\mathcal{w}}_n)}^{\mathrm{T}}$ corresponding to the fuzzy comparison matrix, where:

$${\mathcal{w}}_i={\displaystyle \frac{D\left({\mathcal{S}}_{\mathcal{i}},C_{\mathcal{i}}\right)}{\sum _{\mathcal{i}=1}^{n}D({\mathcal{S}}_{\mathcal{i}},C_{\mathcal{i}}))}}={\displaystyle \frac{\sqrt{({\overline{\mathcal{x}}}_{{\mathcal{S}}_{\mathcal{i}}}-{\mathcal{x}}_{min}{)}^2+({\overline{\mathcal{y}}}_{{\mathcal{S}}_{\mathcal{i}}}-\frac{\omega }{3}{\mathcal{y}}_{min}{)}^2}}{\sum _{\mathcal{i}=1}^n\sqrt{({\overline{\mathcal{x}}}_{{\mathcal{S}}_{\mathcal{i}}}-{\mathcal{x}}_{min}{)}^2+({\overline{\mathcal{y}}}_{{\mathcal{S}}_{\mathcal{i}}}-\frac{\omega }{3}{\mathcal{y}}_{min}{)}^2}}}, wherei=1,\dots ,n$$

(6)

3. A New Integrated EFAHP Method Based on 4-Tuple HA Semantics

Although the generalized fuzzy AHP method proposed by Hue et al. [35] represents a significant advancement in addressing key limitations of traditional fuzzy AHP, particularly those associated with Chang’s extent analysis [33], it still exhibits notable academic shortcomings. Specifically, the method remains constrained by the subjectivity involved in assigning fuzzy sets to L-words on the evaluation scale. These limitations are further exacerbated by the reliance on centroid-based defuzzification techniques, the limited expressive power of its fuzzy modeling, and the absence of consistency verification in experts’ judgments. Such shortcomings highlight the need to incorporate more advanced semantic frameworks, such as HA and 4-tuple semantics models, which enable decision-makers to express their evaluations using natural language words enriched with qualitative semantics. This integration improves both the intuitiveness and cognitive alignment of the assessment process, thereby enhancing the accuracy and reliability of DM outcomes. The proposed method is implemented through the following step-by-step procedure:

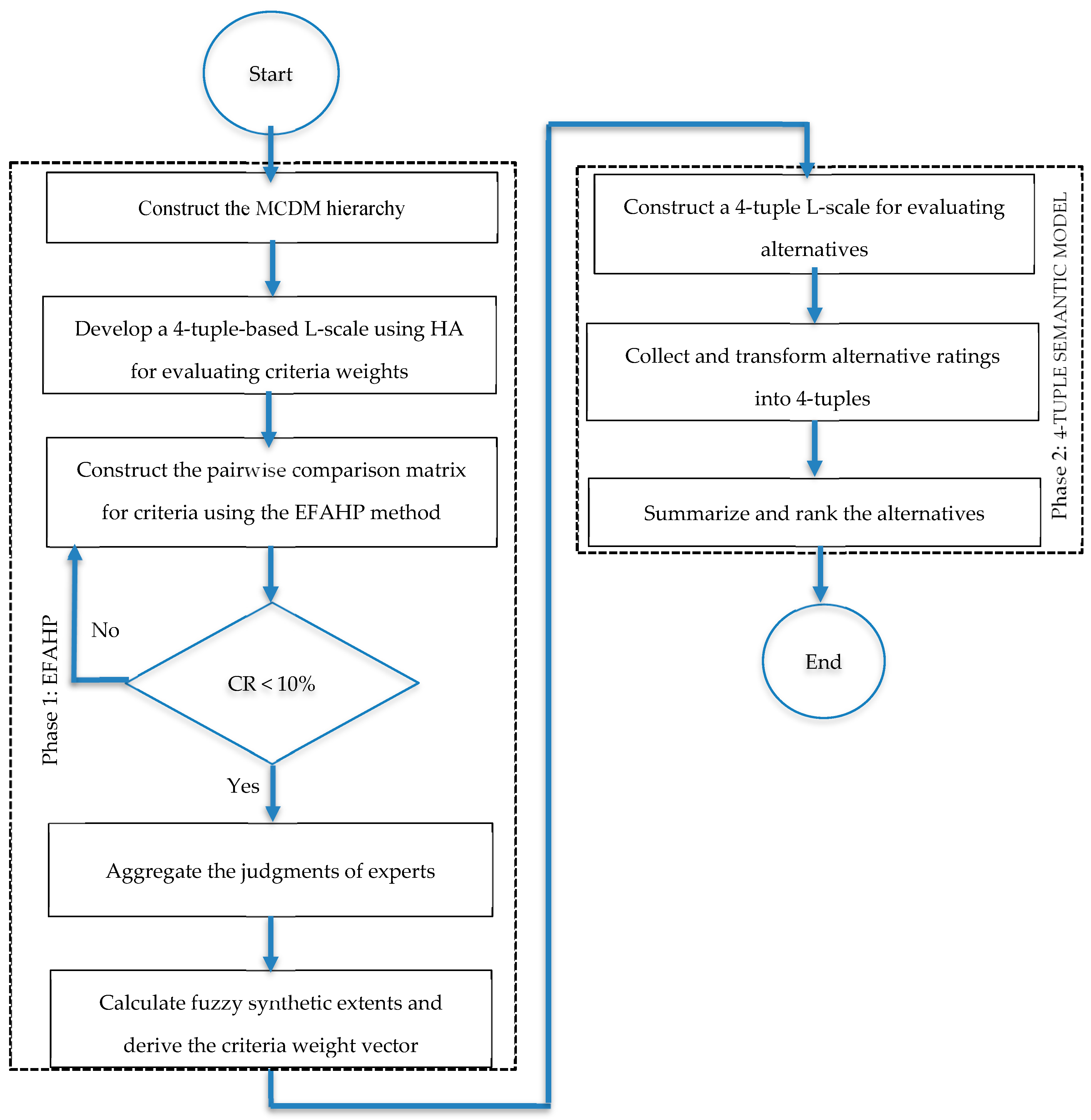
The proposed framework (Figure 2) adopts a two-phase process for MCDM under L-uncertainty. In Phase 1, the decision problem is structured into a hierarchy of goals, criteria, and sub-criteria. Expert judgments, expressed through a 4-tuple HA L-scale, are processed within the EFAHP framework. A new consistency index ensures coherent pairwise comparisons, and consistent evaluations are aggregated to derive criteria weights. In Phase 2, alternatives are assessed using the same 4-tuple scale, transforming L-word ratings into quantitative values that are combined with the weights to compute final scores and rankings. This framework integrates the structural rigor of the EFAHP method with the semantic precision of HAs, enabling a comprehensive and linguistically grounded evaluation of digital transformation readiness in Vietnam’s retail enterprises.

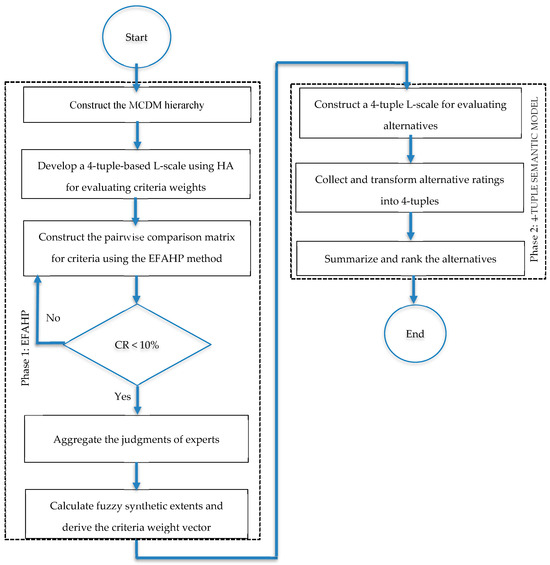
Figure 2. Flowchart of the proposed model.

• Step 1. Designing the hierarchical structure for the decision goal

The application of EFAHP requires the prior construction of a well-defined hierarchical structure centered around a clearly articulated decision goal. At the top level, the overall objective is specified; the second level comprises the relevant evaluation criteria, and the bottom level consists of the available decision alternatives. This hierarchical structuring process involves the integration of theoretical frameworks with expert knowledge elicitation to ensure both the logical consistency and the contextual relevance of the DM model.

• Step 2. Construction of a 4-tuple-based L-scale using HA for criteria weight evaluation

To assess the relative importance of the criteria, the DM experts reached a consensus to construct a linear ComHA. This process involves defining the FMs of atomic words and hedges and establishing a set of L-words, with the maximum word length in the word domain being equal to k as follows:

Let a linear ComHA $AX$ = ($X$, G, Є, H, ∂, Ф, ≤) be given, where G = {g⁻, g⁺} is the set of atomic words, Є = {0, W, 1} is the set of L-constants, and H = $H^{-}\cup$ $H^{+}$, where $H^{-}$= {h_−q, h_−q+1, …, h₋₁} is the set of the q negative hedges and $H^{+}$= {h₁, h₂, …, h_p} is the set of the p positive hedges.

The FMs of the atomic words are denoted by fɱ(g⁻) and fɱ(g⁺), where fɱ(g⁺) =1− fɱ(g⁻). The FMs of hedges are denoted by $\mu$(h_−q), $\mu$(h_−q+1), …, $\mu$(h₋₁), $\mu$(h₁), …, $\mu ($h_p), which satisfy the constraint: $\mu \left(h_p\right)=1-\sum _{i=-q}^{p-1}\mu \left(h_i\right)$.

The constructed ComHA $AX$ is then employed to develop an L-scale, whose words form the word set $X$_(k) and are represented in words of the 4-tuple semantic model.

Example 1.

Let us consider a linear ComHA $AX$ = ($X$, G, Є, H, ∂, Ф, ≤) of the L-variable “Criteria” with: G = (“Unimportant”, “Important”), Є = (“Extremely Unimportant”, “Medium”, “Extremely Important”), H = $H^{-}\cup$ $H^{+}$= (“Little”, “Very”), where the L-words are Unimportant, Important, Extremely Unimportant, Medium, and Extremely Important, combined with the hedges Little and Very. These are abbreviated as U, I, EU, M, EI, L, and V. According to Proposition 1, the FMs of atomic words and hedges can be defined as follows:

These parameters are determined based on expert knowledge or empirical data relevant to the intended application context.

For example, in the context of assessing the level of digital transformation in Vietnamese enterprises, the DM experts agreed on the following FMs:

$$f\mathit{ɱ}(\mathrm{U}) = 0.489, f\mathit{ɱ}(\mathrm{I}) = 1 - f\mathit{ɱ}(\mathrm{U}); \mathit{\mu }\left(V\right) = 0.472, \mathit{\mu }\left(L\right) = 1 - \mathit{\mu }\left(V\right)$$

These values satisfy the constraints μ(V) < μ(L) and Conditions (i) and (ii) as specified in Proposition 1.

Loop step: For i = 1, …, k − 1, for every word x of length i, and for every hedge h, the value fɱ(hx) is computed as: fɱ(hx) = μ(h)fɱ(x).

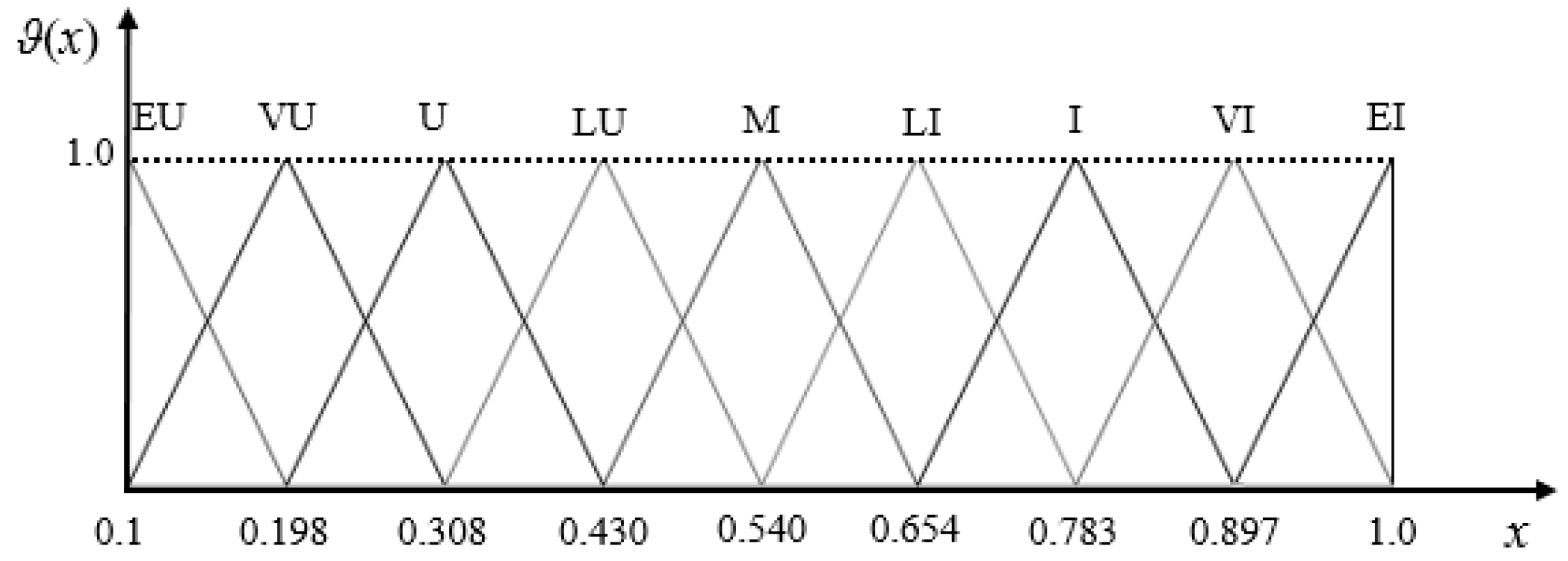
For instance, with k = 2, the FMs of L-words with a length not exceeding 2 are computed to Proposition 1. The word set $X$₍₂₎ is ordered as follows:

L = {Extremely Unimportant < Very Unimportant < Unimportant < Little Unimportant < Medium < Little Important < Important < Very Important < Extremely Important}.

For brevity, we denote the words in L as: L = {EU, VU, U, LU, M, LI, I, VI, EI}.

The corresponding fuzzy meanings of these words are summarized in Table 2.

Table 2. Fuzziness measures of L-words in $X$₍₂₎.

L-scale	EU	VU	U	LU	M	LI	I	VI	EI
FMs	0	0.231	0.489	0.258	0.000	0.270	0.511	0.241	0

To address practical problems effectively, we must quantify the semantics of words. In fuzzy logic, because words are represented by fuzzy sets, their quantitative semantics can be computed using a fuzzy set defuzzification method. In the HA framework, the numeric semantics of L-variables is defined through a quantifying mapping, denoted by ϑ(x), as defined in Definition 5.

This allows us to compute the semantic quantification value ϑ(x) for every word x ∈ X_(k) in the L-scale of the variable “Criteria”. These values are then rescaled from the interval [0, 1] to [0.1, 1] to avoid division by zero when calculating inverse values in the pairwise comparison matrix used in Step 3.

Example 2.

Let us revisit the HA associated with the variable Criteria in Example 1. The FMs of the words and hedges of Criteria are: fɱ(U) = 0.489 and fɱ(I) = 1 − fɱ(U). Thus, we have: μ(V) = 0.472, μ(L) = 1 − μ(V), and q = p =1.

Using Definition 5, the semantic quantification values ϑ(x) are computed for the L-words x ∈ X_(k) in the L-scale of the variable “Criteria”, as shown in Table 3.

Table 3. Semantic quantification values of the words in the L-scale ($X$_(k).

L-scale	EU	VU	U	LU	M	LI	I	VI	EI
ϑ(x)	0.1	0.198	0.308	0.430	0.540	0.654	0.783	0.897	1

Applying Equation (2), we calculate the interval semantics $S$_(k)(x) of the words x$\in$$X$_(k) in L-scale S.

Example 3.

Let us revisit the HA associated with the variable “Criteria” in Examples 1 and 2, where fɱ(U) = 0.489, fɱ(I) = 1 − fɱ(U); μ(V) = 0.472, μ(L) = 1 − μ(V), and q = p =1, k =2. The semantic quantification values of the nine words are in Table 1 and Table 2. Using Equation (2), we calculate the interval semantics S₍₂₎(x) for each x ∈ $X$₍₂₎ in the L-scale S as follows:

$S$₍₂₎(EU) = [0.1, 0.146), $S$₍₂₎(VU) = [0.146, 0.256), $S$₍₂₎(U) = [0.256, 0.366), $S$₍₂₎(LU) = [0.366, 0.488), $S$₍₂₎(M) = [0.488, 0.594), $S$₍₂₎(LI) = [0.594, 0.722), $S$₍₂₎(I) = [0.722, 0.837), $S$₍₂₎(VI) = [0.837, 0.952), $S$₍₂₎(EI) = [0.952, 1].

Finally, we define the L-scale L, with the semantics of its words represented by a 4-tuple semantic: L = {(x, $\mathrm{S}$_(k)(x), ϑ(x), $r$_x): x$\in$$X$_(k), $r$_x$\in$$\mathrm{S}$_(k)(x)}.

Example 4

. Let us revisit the HA associated with the variable “Criteria” in Examples 1 to 3, where: fɱ(U) = 0.489, fɱ(I) = 1 − fɱ(U); μ(V) = 0.472, μ(L) = 1 − μ(V), and q = p =1. The semantic quantification values and similarity intervals of the nine L-words are provided in Table 1, Table 2 and Table 3. Applying Definition 8, we obtain an L-scale L, whose semantics are represented by a 4-tuple semantic as follows:

L = {(EU, [0.1, 0.146), 0.1, r1), (VU, [0.146, 0.256), 0.198, r2), (U, [0.256, 0.366), 0.308, r3), (LU, [0.366, 0.488), 0.430, r4), (M, [0.488, 0.594), 0.540, r5), (LI, [0.594, 0.722), 0.655, r6), (I, [0.722, 0.837), 0.783, r7), (VI, [0.837, 0.952), 0.898, r8), (EI, [0.952, 1], 1, r9)}.

• Step 3. Establishing the pairwise comparison matrix for the criteria and checking its consistency

Experts use the L-words x $\in$ $X$_(k) from the L-scale L in Step 2 (Example 4) to express the relative importance of criteria through pairwise comparison matrices. This is performed using matrix A, defined in Equation (7), across all criteria in the hierarchical structure.

It is important to note that, for each criterion i, its importance relative to itself is considered equal. Thus, $x_{ij}$ = $M$, the neutral element in the ComHA. Let $x_{ij}$ denote the linguistic comparison value provided by the $d^{th}$ expert, representing the relative importance of the ith criterion with respect to the $j^{th}$criterion in relation to the overall objective.

$$A={\left(x_{ij}\right)}_{nxn}=\left(\begin{array}{cccc}M& x_{12}& \dots & x_{1n}\\ 1/x_{21}& M& \dots & x_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ 1/x_{n1}& 1/x_{n2}& \dots & M\end{array}\right)$$

(7)

In the traditional FAHP method [33,35], pairwise comparisons between the $i^{th}$ and $j^{th}$ criteria that are considered equally important are typically represented using numerical values, such as the triangular fuzzy number (1, 1, 1) or the GTFN (1, 1, 1; 1), to eliminate ambiguity. In contrast, the proposed method employs the L-word “M” from the L-scale L (defined in Example 4), which corresponds to the neutral element “W” in ComHA, to represent equal importance. This approach provides a more flexible and fuzzy representation of the concept of “equality”, thereby capturing the inherent imprecision of natural language expressions such as approximately equal, almost the same, and equal.

Construct a GTFN comparison matrix by converting the semantic quantitative value ϑ(x) of a word x$\in$$X$_(k) from the L-scale L (defined in Example 4) into a GTFN, as illustrated in Equation (8) below:

$$\mathrm{B}={\left(a_{ij}\right)}_{n\mathrm{x}n}=\left[\begin{array}{cccc}(L_{11},C_{11},R_{11};{\omega }_{11})& (L_{12},C_{12},R_{12};{\omega }_{12})& \dots & (L_{1n},C_{1n},R_{1n;}{\omega }_{1n})\\ ({{\displaystyle \frac{1}{R}}}_{21},{{\displaystyle \frac{1}{C}}}_{21},{{\displaystyle \frac{1}{L}}}_{21}{;\omega }_{21})& (L_{22},C_{22},R_{22};{\omega }_{22})& \dots & (L_{2n},C_{2n},R_{2n};{\omega }_{2n})\\ \dots & \dots & \dots & \dots \\ ({{\displaystyle \frac{1}{R}}}_{n1},{{\displaystyle \frac{1}{C}}}_{n1},{{\displaystyle \frac{1}{L}}}_{n1};{\omega }_{n1})& ({{\displaystyle \frac{1}{R}}}_{n2},{{\displaystyle \frac{1}{C}}}_{n2},{{\displaystyle \frac{1}{L}}}_{n2};{\omega }_{nn})& \dots & (L_{nn},C_{nn},R_{nn};{\omega }_{nn})\end{array}\right]$$

(8)

where: $a_{ij}=(L_{ij},C_{ij},R_{ij};{\omega }_{ij})$, $a_{ij}^{-1}=\left({{\displaystyle \frac{1}{R}}}_{ij},{{\displaystyle \frac{1}{C}}}_{ij},{{\displaystyle \frac{1}{L}}}_{ij};{\omega }_{ij}\right),fori,j=1,\dots ,nandi\ne j$.

• Table 4 presents the GTFNs used to compare the importance between two criteria in this study.
  Table 4. GTFNs for comparing the importance between two criteria.

  Order	L-Words	GTFN Based on HA	Reciprocal GTFN Based on HA
  1	EU	(0.1, 0.1, 0.198; 0.7)	(1/0.198, 1/0.1, 1/0.1; 0.7)
  2	VU	(0.1, 0.198, 0.308; 0.7)	(1/0.308, 1/0.198, 1/0.1; 0.7)
  3	U	(0.198, 0.308, 0.430; 0.8)	(1/0.430, 1/0.308, 1/0.198; 0.8)
  4	LU	(0.308, 0.430, 0.540; 0.8)	(1/0.540, 1/0.430, 1/0.308; 0.8)
  5	M	(0.430, 0.540, 0.654; 1.0)	(1/0.654, 1/0.540, 1/0.430; 1.0)
  6	LI	(0.540, 0.654, 0.783; 0.9)	(1/0.783, 1/0.654, 1/0.540; 0.9)
  7	I	(0.654, 0.783, 0.897; 0.9)	(1/0.897, 1/0.783, 1/0.654; 0.9)
  8	VI	(0.783, 0.897, 1; 1.0)	(1, 1/0.897, 1/0.783; 1.0)
  9	EI	(0.897, 1, 1; 1.0)	(1, 1, 1/0.897; 1.0)

Traditional FAHP methods typically represent pairwise comparisons of equally important criteria using fixed numerical values, such as the TFN (1, 1, 1) or GTFN (1, 1, 1; 1). Although computationally convenient, this approach fails to capture the intrinsic vagueness of natural language expressions such as approximately equal or almost the same, often resulting in oversimplified consistency evaluations. The proposed method introduces a significant advancement by incorporating the neutral L-word “M” from the L-scale to represent equality. Through semantic quantification, this neutral element is mapped into a numerical value, thereby embedding L-semantics directly into the consistency assessment process. Unlike the CI (Saaty) formulation, which relies solely on crisp or GTFNs, the revised formula integrates the semantic fuzziness of HAs, producing a consistency measure that is both more sensitive and more faithful to human L-reasoning.

This innovation addresses one of the core limitations of conventional FAHP approaches by ensuring that subtle inconsistencies in expert judgments can be more effectively identified. Moreover, the integration of HA semantics enhances both the interpretability and methodological rigor of the consistency check, making the framework particularly robust for MCGDM under L-uncertainty.

The consistency of each pairwise comparison matrix is assessed by calculating the consistency ratio (CR), as shown in Equation (9) below:

$$CR={\displaystyle \frac{CI}{RI}}$$

(9)

where CI is the consistency index. In this study, the new consistency index is defined in Equation (10):

$$CI={\displaystyle \frac{{\lambda }_{max-}(n-\left(1-M\right))}{(n-\left(1-M\right))}}$$

(10)

Here, ${\lambda }_{max}$denotes the maximum eigenvalue, $n$ is the number of criteria, and $M$ represents the semantic quantification of the neutral element in the ComHA. Unlike Saaty’s original formulation, where the numerator and denominator are fixed by the numerical values n and (n − 1), the revised formula integrates the semantic fuzziness of HAs (1 − M). This integration yields a consistency measure that is more sensitive and better aligned with human L-reasoning. By leveraging the semantic richness of HAs and introducing the neutral L-word “M” as the representation of equality, the proposed method embeds semantic quantification directly into the mathematical consistency framework. This adjustment ensures that the model better reflects the nuanced and imprecise nature of human L-reasoning, thereby overcoming one of the main limitations of traditional FAHP approaches that rely exclusively on crisp data. Embedding HA-based semantics into the CI formulation not only improves interpretability but also strengthens methodological rigor in handling uncertainty. The random index (RI) values used for this study are provided in Table 5.

Table 5. Random index values.

n	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
RI	0.00	0.00	0.58	0.90	1.12	1.24	1.32	1.41	1.45	1.49	1.51	1.54	1.56	1.57	1.59

If the CR of the $d^{th}$ pairwise comparison matrix is greater than or equal to 0.10 (CR $\ge 0.10)$, it indicates inconsistency in the expert’s judgments. In such a case, the $d^{th}$ expert will be asked to re-evaluate the matrix to ensure that the revised CR satisfies (CR < 0.10).

• Step 4. Aggregating the judgments provided by experts

The aggregated pairwise comparison matrix C is obtained by averaging the ratings from d experts. This is shown in Equation (11):

$$C=({{\stackrel{⃛}{a}}_{ij})}_{n\mathrm{x}n}=\left(\begin{array}{cccc}{\stackrel{⃛}{a}}_{11}& {\stackrel{⃛}{a}}_{12}& \dots & {\stackrel{⃛}{a}}_{1n}\\ {\stackrel{⃛}{a}}_{21}& {\stackrel{⃛}{a}}_{22}& \dots & {\stackrel{⃛}{a}}_{2n}\\ ⋮& ⋮& ⋮& ⋮\\ {\stackrel{⃛}{a}}_{n1}& {\stackrel{⃛}{a}}_{n2}& \dots & {\stackrel{⃛}{a}}_{nn}\end{array}\right)$$

(11)

where ${\stackrel{⃛}{a}}_{ij}$ =$\left({\displaystyle \frac{\sum _{t=1}^d{L}_{ij}}{d}},{\displaystyle \frac{\sum _{t=1}^d{C}_{ij}}{d}},{\displaystyle \frac{\sum _{t=1}^d{R}_{ij}}{d}};{\displaystyle \frac{\sum _{t=1}^d{\omega }_{ij}}{d}}\right)$; let $t=1,\dots ,d;i,j=1,\dots ,n$.

• Step 5. Calculating fuzzy synthetic extent values and the weight vector of criteria

The fuzzy synthetic extent values ${\mathbb{P}}_i$ are computed using the normalization Equation (12) as follows:

$$\begin{array}{l}{\mathbb{P}}_i=({\mathbb{D}}_{\mathtt{i}},{\mathbb{K}}_{\mathtt{i}},{\mathbb{T}}_{\mathtt{i}};\mathrm{m}\mathrm{i}\mathrm{n}\left({\omega }_{\mathtt{i}\mathtt{j}}\right))\\ =\left(\begin{array}{c}{\displaystyle \frac{\sum _{\mathtt{i}\mathtt{j}=1}^n{L}_{\mathtt{i}\mathtt{j}}}{\sum _{\mathtt{j}=1}^n{L}_{\mathtt{i}\mathtt{j}+}{\sum }_{\mathtt{k}=1,\mathtt{k}\ne \mathtt{i}}^n\sum _{\mathtt{j}=1}^n{R}_{\mathtt{k}\mathtt{j}}}},{\displaystyle \frac{\sum _{\mathtt{j}=1}^n{C}_{\mathtt{i}\mathtt{j}}}{{\sum }_{\mathtt{i}=1}^n\sum _{\mathtt{j}=1}^n{C}_{\mathtt{i}\mathtt{j}}}},{\displaystyle \frac{\sum _{\mathtt{j}=1}^n{R}_{\mathtt{i}\mathtt{j}}}{\sum _{\mathtt{j}=1}^n{R}_{\mathtt{i}\mathtt{j}+}{\sum }_{\mathtt{k}=1,\mathtt{k}\ne \mathtt{i}}^n\sum _{\mathtt{j}=1}^n{L}_{\mathtt{k}\mathtt{j}}}};\min \left({\omega }_{\mathtt{i}\mathtt{j}}\right)\end{array}\right)\end{array}$$

(12)

Let ${\mathbb{P}}_1$, ${\mathbb{P}}_2$, …, ${\mathbb{P}}_n$ denote the fuzzy synthetic extent values. The centroid corresponding to each fuzzy number ${\mathbb{P}}_i$ is given by m_i = (${\overline{u}}_{{\mathbb{P}}_{\mathtt{i}}},{\overline{v}}_{{\mathbb{P}}_{\mathtt{i}}}$), for $i$ =1, 2, …, $n$, and is calculated using the following expression:

$${\overline{u}}_{{\mathbb{P}}_i}=({\mathbb{D}}_{\mathtt{i}}+{\mathbb{K}}_{\mathtt{i}}+{\mathbb{T}}_{\mathtt{i}})/3;{\overline{v}}_{{\mathbb{P}}_i}=min\left({\omega }_{\mathtt{i}\mathtt{j}}\right)/3$$

(13)

The separation between each centroid point m_i = (${\overline{u}}_{{\mathbb{P}}_{\mathtt{i}}},{\overline{v}}_{{\mathbb{P}}_{\mathtt{i}}}$) and the reference point Ꞓ = ($u_{min},v_{min}$) is computed using Equation (14)

$$D\left({\mathbb{P}}_i,\mathrm{Ꞓ}\right)=\sqrt{({\overline{u}}_{{\mathbb{P}}_i}-u_{min}{)}^2+({\overline{v}}_{{\mathbb{P}}_{\mathtt{i}}}-{\displaystyle \frac{\psi }{3}}{v}_{min}{)}^2,}$$

(14)

where: $u_{min}=\min \left({\mathbb{D}}_{\mathtt{i}}\right),v_{min}=\mathrm{m}\mathrm{i}\mathrm{n}\left({\omega }_{\mathtt{i}\mathtt{j}}\right)$.

Finally, the weight vector Ƭ = (${\mathcal{w}}_1$, …,${\mathcal{w}}_n$)^T corresponding to the fuzzy comparison matrix is computed as follows:

$${\mathcal{w}}_i={\displaystyle \frac{D\left({\mathbb{P}}_i,{\mathrm{Ꞓ}}_i\right)}{\sum _{i=1}^{n}D\left({\mathbb{P}}_i,{\mathrm{Ꞓ}}_i\right)}}={\displaystyle \frac{\sqrt{({\overline{u}}_{{\mathbb{P}}_i}-u_{min}{)}^2+({\overline{v}}_{{\mathbb{P}}_{\mathtt{i}}}-\frac{\psi }{3}{v}_{min}{)}^2}}{\sum _{i=1}^n\sqrt{({\overline{u}}_{{\mathbb{P}}_i}-u_{min}{)}^2+({\overline{v}}_{{\mathbb{P}}_{\mathtt{i}}}-\frac{\psi }{3}{v}_{min}{)}^2}}},i=1,\dots ,n$$

(15)

• Step 6. Constructing a 4-tuple scale for evaluating alternatives

To evaluate the alternatives with respect to the criteria, the DM experts reached a consensus to construct a linear ComHA. This involves defining the FMs of atomic words and hedges and establishing sets of L-words with the maximum word length in the word domain equal to k as follows:

Let a linear ComHA $AX$ = ($X$, G, Є, H, ∂, Ф, ≤) be given, where G = {g⁻, g⁺} is the set of atomic words, Є = {0, W, 1} is the of L-constants, and H = $H^{-}\cup H^{+}$, where $H^{-}$ = {h_−q, h_−q+1, …, h₋₁} is the set of the q negative hedges and $H^{+}$= {h₁, h₂, …, h_p} is the set of the p positive hedges.

The FMs of the atomic words are denoted by fɱ(g⁻) and fɱ(g⁺), where fɱ(g⁺) =1− fɱ(g⁻). The FMs of hedges are denoted by $\mu$(h_−q), $\mu$(h_−q+1), …, $\mu$(h₋₁), $\mu$(h₁), …, $\mu ($h_p), which satisfy the constraint: $\mu \left(h_p\right)=1-\sum _{i=-q}^{p-1}\mu \left(h_i\right)$. The constructed ComHA $AX$ is then used to generate an L-scale, where each L-word in the form $X$_(k) is represented using the 4-tuple semantic model.

A semantic quantification mapping (SQM) function (as defined in Definition 5) is used to compute the semantic quantification values ϑ(x) for each word x$\in$$X$_(k).

Using Equation (2), the interval semantics $(S$_(k)(x)) of the words x$\in$$X$_(k) is calculated.

Finally, Definitions 6 and 8 are applied to obtain the L-scale Z, where each word is represented as a 4-tuple:

$$\mathrm{Z}=\left\{\right(x,{\mathrm{S}}_{\left(\mathrm{k}\right)}\left(x\right),\mathsf{\vartheta }\left(x\right),r_x):x\in X_{\left(\mathrm{k}\right)},r_x\in {\mathrm{S}}_{\left(\mathrm{k}\right)}\left(x\right)\}$$

• Step 7. Collecting and transforming alternatives ratings into 4-tuple semantic representations

Experts use the L-words x$\in$$X$_(k), obtained from the L-scale in Step 6, to represent the scores of the m alternatives across n evaluation criteria. These scores are organized in a decision matrix D, as shown in Equation (16):

$$D={\left(u_{ij}\right)}_{m\mathrm{x}n}\left(\begin{array}{cccc}{u}_{11}& u_{12}& \dots & u_{1n}\\ u_{21}& u_{22}& \dots & u_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ u_{m1}& u_{m2}& \dots & u_{mn}\end{array}\right)$$

(16)

where $u_{ij}$ denotes the score of the $i^{th}$ alternative with respect to the $j^{th}$ criterion.

Based on Definition 6, the L-ratings of the alternatives, as provided by the experts, are then transformed into 4-tuple semantic representations of the form (x, $\mathrm{S}$_(k)(x), ϑ(x), r).

• Step 8. Summarize and rank alternatives

The arithmetic mean of the 4-tuples is used to aggregate the experts’ ratings for the alternatives with respect to each evaluation criterion as follows:

Given a set T_S of p L-words, each is represented as a 4-tuple: (x_i, S_(k)(x_i), ϑ(x_i), r_i), i = 1, …, p. The aggregation function $g$using arithmetic mean is defined as:

$$g\left(\left(x_1,{\mathrm{S}}_{\left(\mathrm{k}\right)}\left(x_1\right),v\left(x_1\right),r_1\right),\dots ,\left(x_p,{\mathrm{S}}_{\left(\mathrm{k}\right)}\left(x_p\right),v\left(x_p\right),r_p\right)\right)=\mathsf{\Delta }({\displaystyle \frac{\sum _{j=1}^p{r}_j}{p}})$$

(17)

where ${\displaystyle \frac{\sum _{j=1}^p{r}_j}{p}}$$\in$$\mathrm{S}$_(k)(x).

The weighted arithmetic mean is then applied to the 4-tuple semantic representations to aggregate the final evaluation scores for each alternative as follows:

Given an L-word set T_S with p L-words, each is represented as a 4-tuple: (x_i, S_(k)(x_i), ϑ(x_i), r_i), i = 1, …, p. The aggregation function p, using the weighted arithmetic mean, is defined as:

$$g((x_1,{\mathrm{S}}_{\left(\mathrm{k}\right)}(x_1),v(x_1),r_1),\dots ,(x_p,{\mathrm{S}}_{\left(\mathrm{k}\right)}(x_p),v(x_p),r_p))=\mathsf{\Delta }(\sum _{j=1}^p{w}_j{r}_j),$$

(18)

subject to:

$$\sum _{j=1}^p{w}_j=1;$$

where the result of the aggregation is a 4-tuple: (s, S(k)(x), v(x), $\sum _{j=1}^p{w}_j{r}_j$), and $\sum _{j=1}^p{w}_j{r}_j$$\in$ S(k)(x).

Finally, the alternatives are ranked based on their total scores in ascending order (i.e., the alternative with the highest score will be ranked first).

4. Implementation of the Integrated EFAHP Method Using 4-Tuple HA Semantic

This section applies the proposed integrated EFAHP method, based on 4-tuple HA semantics, to evaluate the digital transformation levels of small- and medium-sized enterprises (SMEs) in the retail sector. In Vietnam, the retail sector is one of the sectors most directly and profoundly affected by digital transformation due to shifts in consumer behavior and the adoption of modern business models. The assessment is conducted using a set of criteria issued by the Ministry of Information and Communications of Vietnam, comprising seven pillars and 34 criteria, as detailed in Table 6.

Table 6. Criteria for evaluating the digital transformation level of retail SMEs in vietnam.

Pillars	Criteria
Strategic orientation (P1)	Leaders understand digital transformation in their business domain (P1.1)
	Digital transformation is recognized as a strategic priority (P1.2)
	Budget is allocated for innovation and internal transformation initiatives (P1.3)
	Digital tools and analytics are used to support strategic decisions (P1.4)
Customer experience and multichannel sales (P2)	Digital tools enhance marketing, distribution, and sales for customer experience and competitiveness (P2.1)
	Digital transformation improves service and customer experience (P2.2)
	Customer relationship management systems are integrated to expand functionality and capabilities (P2.3)
	Data analytics support performance measurement (P2.4)
	Digital solutions enable sales forecasting and strategic adjustments (P2.5)
Supply chain integration (P3)	Digital tools support performance evaluation and forecasting (P3.1)
	Digital transformation enhances supply chain forecasting and management (P3.2)
	Digital solutions align budgeting with business planning (P3.3)
	Digital technologies enable flexible and responsive supply chains (P3.4)
	Digital transformation promotes automation in production processes (P3.5)
	Digital applications improve efficiency and automate inventory management (P3.6)
	Digital systems support data-driven decision-making in operations (P3.7)
Internal operations: finance, planning, human resource, legal (P4)	Digital transformation supports economic efficiency and decision-making (P4.1)
	Digital transformation enhances human resource management automation and transparency (P4.2)
	Digital tools aid in identifying and assessing business risks (P4.3)
Information systems and data governance (P5)	Digital transformation keeps businesses aligned with technology trends (P5.1)
	Emerging digital technologies improve cost and business management efficiency (P5.2)
	Digital solutions allow flexible integration with new technologies (P5.3)
	Resources are allocated to upgrade digital information systems (P5.4)
	Processes and policies are in place to support digital transformation (P5.5)
Risk management and cybersecurity (P6)	The enterprise is fully aware of cybersecurity and data risks in digital transformation (P6.1)
	The system monitors, evaluates, and mitigates information systems related risks (P6.2)
	The system automatically detects and alerts cybersecurity threats (P6.3)
	Incident response procedures for information technology and cybersecurity are in place (P6.4)
Human and organizational capabilities (P7)	Digital transformation personnel adapt quickly and positively to change (P7.1)
	The organization has a structure adaptable to internal and external changes (P7.2)
	Personnel possess adequate knowledge, skills, and experience (P7.3)
	Policies attract and retain competent information technology staff for long-term commitment (P7.4)
	Internal training programs are effectively implemented to improve employee’s competencies (P7.5)
	Real-time data sharing supports integrated and effective enterprise management (P7.6)

The data used in this study were collected through expert interviews and a survey assessing the digital transformation levels of retail SMEs in Vietnam. Four experts, each with extensive experience in retail research and management, were invited to independently evaluate the importance weights of the pillars and criteria. In addition, 16 retail SMEs were randomly selected to collect secondary data on their digital transformation status through a structured questionnaire. The computational procedure is summarized as follows:

4.1. Construction of a 4-Tuple L-Scale Based on HA for Evaluating Criteria Weights

Based on Definition 1 to 4, the experts agreed to construct a linear ComHA and determine fuzzy parameters for the evaluation criteria. Sets of L-words with the maximum word length in the word domain equal to k = 2 were employed, as shown in Table 7. In this context, each HA utilizes only one positive hedge and one negative hedge, where the negative hedge is defined as fɱ(g⁻) = 1 − fɱ(g⁺), μ(h−₁) = 1 − μ(h₁).

Table 7. HA and fuzzy parameter settings.

L-Variable	ComHA	Atomic Words		Constant Words			Hedge		Fuzzy Measure
		g−	g+	0	W	1	${\mathit{h}}_{-1}$	${\mathit{h}}_1$	fɱ (g−)	$\mathit{\mu }({\mathit{h}}_{-1}$)
Criteria	Åχ	U	I	EU	M	EI	L	V	0.489	0.528

Using Definition 5, the semantic quantification values ϑ(x) are computed for the L-words x$\in$$X$_(k) (k = 2) in the L-scale of the variable “Criteria”, as illustrated in Table 4 and Figure 3 below:

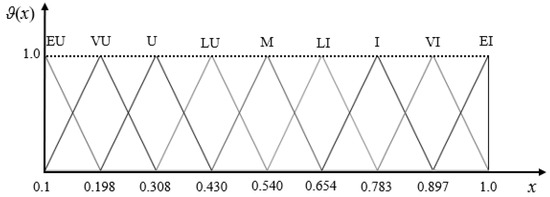
Figure 3. Numerical semantic quantitative values of the L-words.

By applying Equation (2), the interval semantics $(S$₍₂₎(x)) of the L-words x$\in$$X$₍₂₎ in the L-scale can be calculated. Furthermore, using Definition 6 and 8, the L-scale L is constructed with its L-word being represented as a 4-tuple, as presented in Example 4.

4.2. Aggregation of Expert Judgments Using the Arithmetic Mean Method

Using Equation (7), four experts independently constructed an L- pairwise comparison matrix by employing L-words x$\in$$X$₍₂₎, derived from the L-scale L (as presented in Example 4 or Table 4). These L-words are used to represent the relative importance among the criteria within the hierarchical structure. Using Equation (8) and Table 4, GTFN comparison decision matrices are constructed. To ensure the reliability of these matrices, Equations (9) and (10) are applied to calculate the CR of each pairwise comparison matrix. In this study, all CR values are below 0.1 (CR < 10%), indicating a satisfactory level of consistency across all matrices. Subsequently, using Equation (11), the GTFN comparison matrices derived from the evaluations provided by the four experts are aggregated. The final aggregated fuzzy comparison results are presented in Table 8, Table 9, Table 10, Table 11, Table 12, Table 13, Table 14 and Table 15 below:

Table 8. Averaged fuzzy comparison matrix for the seven pillars.

Pillars	P1	P2	P3	P4	P5	P6	P7
P1	(0.430, 0.540, 0.654; 1)	(0.687, 0.812, 0.923; 0.9)	(0.837, 0.952, 1.069; 1)	(0.601, 0.715, 0.837; 0.9)	(0.894, 1.003, 1.069; 1)	(0.629, 0.747, 0.866; 0.9)	(0.455, 0.570, 0.690; 0.8)
P2	(1.086, 1.236, 1.465; 0.9)	(0.430, 0.540, 0.654; 1)	(0.626, 0.751, 0.869; 0.9)	(0.715, 0.847, 0.991; 0.8)	(0.712, 0.842, 0.998; 0.9)	(0.772, 0.909, 1.091; 0.9)	(0.311, 0.425, 0.546; 0.8)
P3	(0.946, 1.060, 1.208; 1)	(1.155, 1.340, 1.609; 0.9)	(0.430, 0.540, 0.654; 1)	(0.547, 0.655, 0.741; 1)	(0.542, 0.662, 0.776; 0.9)	(0.485, 0.603, 0.716; 0.8)	(0.713, 0.891, 1.111; 0.7)
P4	(1.208, 1.425, 1.708; 0.9)	(1.155, 1.375, 1.738; 0.8)	(1.396, 1.639, 2.022; 1)	(0.430, 0.540, 0.654; 1)	(0.541, 0.658, 0.780; 0.9)	(0.602, 0.719, 0.834; 0.9)	(0.369, 0.485, 0.597; 0.8)
P5	(0.946, 1.003, 1.126; 1)	(1.081, 1.279, 1.532; 0.9)	(1.299, 1.564, 1.926; 0.9)	(1.299, 1.546, 1.889; 0.9)	(0.430, 0.540, 0.654; 1)	(0.397, 0.514, 0.629; 0.8)	(0.369, 0.483, 0.602; 0.8)
P6	(1.167, 1.362, 1.627; 0.9)	(1.091, 1.317, 1.611; 0.9)	(1.495, 1.823, 2.406; 0.8)	(1.230, 1.443, 1.745; 0.9)	(1.627, 2.007, 2.668; 0.8)	(0.430, 0.540, 0.654; 1)	(0.369, 0.485, 0.597; 0.8)
P7	(1.483, 1.808, 2.319; 0.8)	(1.944, 2.587, 3.799; 0.8)	(1.663, 2.401, 4.154; 0.7)	(1.690, 2.088, 2.786; 0.8)	(1.745, 2.238, 3.118; 0.8)	(1.690, 2.088, 2.786; 0.8)	(0.430, 0.540, 0.654; 1)
Expert 1: CR = 0.04		Expert 2: CR = 0.048		Expert 3: CR = 0.037		Expert 4: CR = 0.054

Table 9. Averaged fuzzy comparison matrix for Pillar 1: strategic orientation.

P1	P1.1	P1.2	P1.3	P1.4
P1.1	(0.430, 0.540, 0.654; 1)	(0.712, 0.834, 0.964; 1)	(0.483, 0.602, 0.719; 0.9)	(0.369, 0.483, 0.602; 0.8)
P1.2	(1.072, 1.245, 1.477; 1)	(0.430, 0.540, 0.654; 1)	(0.575, 0.690, 0.802; 1)	(0.483, 0.602, 0.719; 1)
P1.3	(1.443, 1.745, 2.238; 0.9)	(1.293, 1.524, 1.863; 1)	(0.430, 0.540, 0.654; 1)	(1.277, 1.528, 1.852; 0.9)
P1.4	(1.745, 2.238, 3.118; 0.8)	(1.443, 1.745, 2.238; 1)	(0.540, 0.654, 0.783; 0.9)	(0.430, 0.540, 0.654; 1)
Expert 1: CR = 0.02		Expert 2: CR = 0.024	Expert 3: CR = 0.017	Expert 4: CR = 0.041

Table 10. The averaged fuzzy comparison matrix for Pillar 2: customer experience and multichannel sales.

P2	P2.1	P2.2	P2.3	P2.4	P2.5
P2.1	(0.430, 0.540, 0.654; 1)	(0.690, 0.808, 0.920; 1)	(0.629, 0.747, 0.866; 0.9)	(0.658, 0.780, 0.894; 1)	(0.626, 0.751, 0.869; 0.9)
P2.2	(1.098, 1.258, 1.483; 1)	(0.430, 0.540, 0.654; 1)	(0.837, 0.952, 1.069; 1)	(0.974, 1.101, 1.271; 0.9)	(0.540, 0.654, 0.783; 0.9)
P2.3	(1.167, 1.362, 1.627; 0.9)	(0.946, 1.060, 1.208; 1)	(0.430, 0.540, 0.654; 1)	(0.601, 0.715, 0.837; 0.9)	(0.712, 0.842, 0.998; 0.9)
P2.4	(1.126, 1.299, 1.546; 1)	(0.805, 0.923, 1.044; 1)	(1.208, 1.425, 1.708; 0.9)	(0.430, 0.540, 0.654; 1)	(0.886, 1.011, 1.184; 0.9)
P2.5	(1.155, 1.340, 1.609; 0.9)	(1.277, 1.528, 1.852; 0.9)	(1.081, 1.279, 1.532; 0.9)	(0.937, 1.107, 1.305; 0.9)	(0.430, 0.540, 0.654; 1)
Expert 1: CR = 0.01		Expert 2: CR = 0.018	Expert 3: CR = 0.013		Expert 4: CR = 0.028

Table 11. Averaged fuzzy comparison matrix for Pillar 3: supply chain integration.

P3	P3.1	P3.2	P3.3	P3.4	P3.5	P3.6	P3.7
P3.1	(0.430, 0.540, 0.654; 1.0)	(1.455, 1.760, 2.325; 0.8)	(1.000, 1.129, 1.277; 1.0)	(1.052, 1.238, 1.470; 0.9)	(0.783, 0.897, 1.000; 1.0)	(1.000, 1.118, 1.277; 1.0)	(0.569, 0.687, 0.812; 0.9)
P3.2	(0.513, 0.635, 0.744; 0.8)	(0.430, 0.540, 0.654; 1.0)	(0.780, 0.894, 0.974; 0.9)	(0.458, 0.569, 0.687; 0.9)	(0.540, 0.654, 0.783; 0.9)	(0.512, 0.634, 0.747; 0.8)	(0.872, 1.074, 1.361; 0.8)
P3.3	(0.783, 0.886, 1.000; 1.0)	(1.029, 1.126, 1.299; 0.9)	(0.430, 0.540, 0.654; 1.0)	(1.318, 1.611, 2.124; 0.8)	(0.514, 0.629, 0.747; 0.9)	(0.626, 0.751, 0.869; 0.9)	(0.515, 0.631, 0.744; 0.8)
P3.4	(0.744, 0.871, 1.024; 0.9)	(1.465, 1.771, 2.206; 0.8)	(0.654, 0.772, 0.908; 0.8)	(0.430, 0.540, 0.654; 1.0)	(0.747, 0.859, 0.920; 0.9)	(0.546, 0.658, 0.773; 0.9)	(0.808, 0.920, 0.974; 0.9)
P3.5	(1.000, 1.114, 1.277; 1.0)	(1.277, 1.528, 1.852; 0.9)	(1.098, 1.627, 2.007; 0.9)	(1.098, 1.201, 1.402; 0.9)	(0.430, 0.540, 0.654; 1.0)	(1.414, 1.868, 2.486; 0.7)	(0.600, 0.723, 0.834; 0.8)
P3.6	(0.783, 0.895, 1.000; 1.0)	(1.402, 1.682, 2.157; 0.8)	(1.155, 1.340, 1.609; 0.9)	(1.333, 1.586, 1.944; 0.9)	(1.493, 2.807, 2.905; 0.7)	(0.430, 0.540, 0.654; 1.0)	(0.840, 0.949, 1.000; 1.0)
P3.7	(1.236, 1.465, 1.771; 0.9)	(1.172, 1.401, 1.807; 0.8)	(1.414, 1.704, 2.175; 0.8)	(1.029, 1.098, 1.258; 0.9)	(1.270, 1.498, 1.895; 0.8)	(1.000, 1.057, 1.196; 1.0)	(0.430, 0.540, 0.654; 1.0)
Expert 1: CR = 0.063		Expert 2: CR = 0.032		Expert 3: CR = 0.037		Expert 4: CR = 0.062

Table 12. Averaged fuzzy comparison matrix for Pillar 4: internal operations.

P4	P4.1	P4.2	P4.3
P4.1	(0.430, 0.540, 0.654; 1.0)	(0.629, 0.747, 0.866; 0.9)	(0.626, 0.751, 0.869; 0.9)
P4.2	(1.167, 1.362, 1.627; 0.9)	(0.430, 0.540, 0.654; 1.0)	(0.430, 0.540, 0.654; 1.0)
P3.3	(1.155, 1.340, 1.609; 0.9)	(1.528, 1.852, 2.324; 1.0)	(0.430, 0.540, 0.654; 1.0)
Expert 1: CR = 0.033	Expert 2: CR = 0.02	Expert 3: CR = 0.01	Expert 4: CR = 0.018

Table 13. Averaged fuzzy comparison matrix for Pillar 5: information systems and data governance.

P5	P5.1	P5.2	P5.3	P5.4	P5.5
P5.1	(0.430, 0.540, 0.654; 1.0)	(0.812, 0.923, 1.000; 1.0)	(0.719, 0.840, 0.949; 0.9)	(0.513, 0.626, 0.751; 1.0)	(0.626, 0.751, 0.869; 0.9)
P5.2	(1.000, 1.086, 1.236; 1.0)	(0.430, 0.540, 0.654; 1.0)	(0.458, 0.569, 0.687; 0.9)	(1.086, 1.236, 1.465; 0.9)	(0.259, 0.369, 0.483; 0.7)
P5.3	(1.057, 1.196, 1.403; 0.9)	(1.465, 1.771, 2.206; 0.9)	(0.430, 0.540, 0.654; 1.0)	(0.339, 0.458, 0.569; 0.9)	(0.375, 0.483, 0.600; 0.7)
P5.4	(1.340, 1.609, 1.970; 0.8)	(0.687, 0.812, 0.923; 1.0)	(1.771, 2.206, 3.017; 0.9)	(0.430, 0.540, 0.654; 1.0)	(0.684, 0.810, 0.969; 0.9)
P5.5	(0.769, 0.907, 1.055; 0.9)	(1.771, 2.206, 3.017; 0.9)	(1.528, 1.852, 2.324; 1.0)	(1.121, 1.342, 1.613; 0.9)	(0.430, 0.540, 0.654; 1.0)
Expert 1: CR = 0.034		Expert 2: CR = 0.014	Expert 3: CR = 0.046		Expert 4: CR = 0.041

Table 14. Averaged fuzzy comparison matrix for Pillar 6: risk management and cybersecurity.

P6	P6.1	P6.2	P6.3	P6.4
P6.1	(0.430, 0.540, 0.654; 1.0)	(0.569, 0.687, 0.812; 1.0)	(0.690, 0.808, 0.920; 0.9)	(0.751, 0.869, 0.974; 0.8)
P6.2	(1.236, 1.465, 1.771; 1.0)	(0.430, 0.540, 0.654; 1.0)	(0.575, 0.684, 0.773; 0.9)	(0.575, 0.684, 0.773; 1.0)
P6.3	(1.098, 1.258, 1.483; 0.9)	(1.333, 1.558, 1.903; 0.9)	(0.430, 0.540, 0.654; 1.0)	(1.277, 1.528, 1.852; 0.9)
P6.4	(1.029, 1.155, 1.340; 0.8)	(1.333, 1.558, 1.903; 1.0)	(0.540, 0.654, 0.783; 0.9)	(0.430, 0.540, 0.654; 1.0)
Expert 1: CR = 0.015		Expert 2: CR = 0.023	Expert 3: CR = 0.038	Expert 4: CR = 0.035

Table 15. Averaged fuzzy comparison matrix for Pillar 7: human and organizational capabilities.

P7	P7.1	P7.2	P7.3	P7.4	P7.5	P7.6
P7.1	(0.430, 0.540, 0.654; 1.0)	(0.514, 0.629, 0.747; 0.9)	(1.000, 1.129, 1.277; 1.0)	(0.840, 0.949, 1.000; 1.0)	(0.654, 0.783, 0.897; 0.9)	(0.783, 0.897, 1.000; 1.0)
P7.2	(1.362, 1.627, 2.007; 0.9)	(0.430, 0.540, 0.654; 1.0)	(0.458, 0.569, 0.687; 0.9)	(0.662, 0.776, 0.892; 0.9)	(0.654, 0.783, 0.897; 0.9)	(0.719, 0.834, 0.920; 0.9)
P7.3	(0.783, 0.886, 1.000; 1.0)	(1.465, 1.771, 2.206; 0.9)	(0.430, 0.540, 0.654; 1.0)	(0.540, 0.654, 0.783; 0.9)	(0.458, 0.569, 0.687; 0.9)	(0.427, 0.541, 0.658; 0.8)
P7.4	(1.000, 1.057, 1.196; 1.0)	(1.138, 1.321, 1.564; 0.8)	(1.277, 1.528, 1.852; 0.9)	(0.430, 0.540, 0.654; 1.0)	(0.369, 0.485, 0.597; 0.8)	(0.430, 0.540, 0.654; 1.0)
P7.5	(1.114, 1.277, 1.528; 0.9)	(1.114, 1.277, 1.528; 0.9)	(1.690, 1.771, 2.206; 0.9)	(1.690, 2.088, 2.786; 0.8)	(0.430, 0.540, 0.654; 1.0)	(0.458, 0.569, 0.687; 0.9)
P7.6	(1.000, 1.114, 1.277; 1.0)	(1.098, 1.230, 1.443; 0.9)	(1.546, 1.889, 2.437; 0.8)	(1.528, 1.852, 2.324; 1.0)	(1.465, 1.771, 2.206; 0.9)	(0.430, 0.540, 0.654; 1.0)
Expert 1: CR = 0.049		Expert 2: CR = 0.043		Expert 3: CR = 0.051	Expert 3: CR = 0.045

4.3. Determining the Fuzzy Synthetic Extent and Weight Vectors of Pillars and Criteria

Using Equations (12)–(15), the fuzzy synthetic extent values and the weight vectors of the pillars, along with their corresponding criteria, were calculated and are summarized in Table 16 and Table 17 below:

Table 16. The fuzzy synthetic extent values of the pillars and criteria.

Pillars	Fuzzy Synthetic Extent	Criteria	Fuzzy Synthetic Extent
P1	(0.07, 0.10, 0.14; 0.70)	P1.1	(0.10, 0.15, 0.21; 0.80)
		P1.2	(0.14, 0.19, 0.26; 0.80)
		P1.3	(0.25, 0.33, 0.43; 0.80)
		P1.4	(0.24, 0.32, 0.43; 0.80)
P2	(0.07, 0.10, 0.15; 0.70)	P2.1	(0.11, 0.15, 0.20; 0.90)
		P2.2	(0.15, 0.19, 0.24; 0.90)
		P2.3	(0.15, 0.19, 0.25; 0.90)
		P2.4	(0.17, 0.22, 0.28; 0.90)
		P2.5	(0.19, 0.25, 0.31; 0.90)
P3	(0.07, 0.11, 0.15; 0.70)	P3.1	(0.11, 0.14, 0.19; 0.70)
		P3.2	(0.07, 0.10, 0.13; 0.70)
		P3.3	(0.09, 0.12, 0.16; 0.70)
		P3.4	(0.09, 0.12, 0.17; 0.70)
		P3.5	(0.12, 0.17, 0.23; 0.70)
		P3.6	(0.13, 0.19, 0.24; 0.70)
		P3.7	(0.13, 0.17, 0.23; 0.70)
P4	(0.09, 0.13, 0.18; 0.70)	P4.1	(0.18, 0.25, 0.32; 0.90)
		P4.2	(0.23, 0.30, 0.38; 0.90)
		P4.3	(0.37, 0.45, 0.55; 0.90)
P5	(0.09, 0.13, 0.18; 0.70)	P5.1	(0.11, 0.15, 0.20; 0.70)
		P5.2	(0.11, 0.15, 0.21; 0.70)
		P5.3	(0.13, 0.18, 0.24; 0.70)
		P5.4	(0.18, 0.24, 0.33; 0.70)
		P5.5	(0.21, 0.28, 0.37; 0.70)
P6	(0.12, 0.17, 0.24; 0.70)	P6.1	(0.14, 0.19, 0.25; 0.80)
		P6.2	(0.17, 0.22, 0.29; 0.80)
		P6.3	(0.26, 0.32, 0.41; 0.80)
		P6.4	(0.20, 0.26, 0.33; 0.80)
P7	(0.18, 0.26, 0.37; 0.70)	P7.1	(0.10, 0.14, 0.17; 0.80)
		P7.2	(0.10, 0.14, 0.19; 0.80)
		P7.3	(0.10, 0.14, 0.18; 0.80)
		P7.4	(0.11, 0.15, 0.20; 0.80)
		P7.5	(0.16, 0.21, 0.28; 0.80)
		P7.6	(0.17, 0.23, 0.30; 0.80)

Table 17. The weight vector of the pillars and criteria.

Pillars	Weight Score	Criteria	Weight Score
P1	0.10	P1.1	0.11
		P1.2	0.16
		P1.3	0.37
		P1.4	0.36
P2	0.10	P2.1	0.11
		P2.2	0.18
		P2.3	0.18
		P2.4	0.24
		P2.5	0.29
P3	0.11	P3.1	0.14
		P3.2	0.10
		P3.3	0.12
		P3.4	0.12
		P3.5	0.16
		P3.6	0.18
		P3.7	0.17
P4	0.12	P4.1	0.15
		P4.2	0.26
		P4.3	0.59
P5	0.12	P5.1	0.13
		P5.2	0.14
		P5.3	0.17
		P5.4	0.25
		P5.5	0.31
P6	0.16	P6.1	0.15
		P6.2	0.20
		P6.3	0.39
		P6.4	0.27
P7	0.28	P7.1	0.12
		P7.2	0.13
		P7.3	0.12
		P7.4	0.14
		P7.5	0.23
		P7.6	0.27

4.4. Developing a 4-Tuple Scale for Evaluating Alternatives Regarding the Digital Transformation Level of Retail SMEs in Vietnam

The scale used to assess the current digital transformation status of retail SMEs in Vietnam is divided into five levels, as shown in Table 18. Each level corresponds to a specific pillar or component index.

Table 18. L-scale for evaluating alternatives.

Order	L-Words	The Quantitative Semantic Values of the L-Words x (ϑ(x))	Similarity Intervals of the L-Words x (S(1)(x))
1	Extremely Low (EL)	0.1	[0.1, 0.219)
2	Low (L)	0.336	[0.219, 0.450)
3	Medium (M)	0.566	[0.450, 0.675)
4	High (H)	0.781	[0.675, 0.889)
5	Extremely High (EH)	1	[0.889, 1]

Using Definitions 1 to 4, the experts agreed to construct a linear ComHA $AX$ = ($X$, G, Є, H, ∂, Ф, ≤), incorporating fuzzy parameters for evaluating alternatives. The scale was built based on a maximum word length of k = 1, defined as: G = {Low, High}, Є = {Extremely Low, Medium, Extremely High}, fɱ(Low) = 0.518, μ(Little) = 0.495. The resulting L-scale for evaluating alternatives consists of five L-words ordered as: Z₍₁₎ = {Extremely Low < Low < Medium < High < Extremely High}. This set is abbreviated as: Z₍₁₎ = {EL, L, M, H, EH}.

The SQM function defined in Definition 5 is used compute the semantic quantification values ϑ(x) for each word x$\in$$X$₍₁₎ in the L-scale, as summarized in Table 18.

Using Equation (2), the interval semantics $(S$₍₁₎(x)) of the words x$\in$$X$₍₁₎ in the L-scale is presented in Table 18.

By applying Definition 6 and 8, an L-scale Z is constructed in which the semantics of each word is represented by a 4-tuple as follows:

Z = {(EL, [0.1, 0.219), 0.1, r1), (L, [0.219, 0.450), 0.336, r2), (M, [0.450, 0.675), 0.566, r3), (H, [0.675, 0.889), 0.430, r4), (EH, [0.889, 1], 1, r5)}.

4.5. Collecting and Transforming Ratings of Alternatives’ Digital Transformation Levels into 4-Tuple Semantic Representations

Using Equation (16) and Table 18, the ratings provided by 16 retail SMEs for each criterion were collected. These ratings were then transformed into 4-tuple semantic representations by applying Definitions 6 and 8, as illustrated in Table A1 in the Appendix.

4.6. Aggregated Results and Rankings of Retail SMEs’ Digital Transformation Levels in Vietnam

The aggregated ratings for each criterion were calculated using Equation (17), while Equation (18) was applied to compute the final scores representing the overall digital transformation levels of the 16 retail SMEs in Vietnam. The resulting rankings are presented in Table 19 below.

Table 19. Weighted assessment results for the digital transformation levels of retail SMEs in Vietnam.

Pillars	Criteria	Enterprises
		E1	E2	E3	E4	E5	E6	E7	E8
P1	P1.1	0.009	0.006	0.004	0.004	0.009	0.004	0.001	0.004
	P1.2	0.005	0.009	0.005	0.009	0.009	0.002	0.005	0.002
	P1.3	0.012	0.021	0.004	0.012	0.004	0.012	0.004	0.012
	P1.4	0.012	0.012	0.012	0.004	0.004	0.004	0.012	0.004
P2	P2.1	0.006	0.006	0.004	0.004	0.004	0.004	0.009	0.004
	P2.2	0.006	0.006	0.002	0.011	0.002	0.006	0.002	0.011
	P2.3	0.002	0.006	0.006	0.015	0.006	0.002	0.002	0.006
	P2.4	0.008	0.008	0.002	0.008	0.008	0.008	0.019	0.014
	P2.5	0.010	0.003	0.003	0.003	0.024	0.010	0.017	0.010
P3	P3.1	0.005	0.005	0.001	0.001	0.005	0.005	0.005	0.005
	P3.2	0.004	0.004	0.004	0.004	0.001	0.001	0.001	0.006
	P3.3	0.001	0.004	0.001	0.004	0.004	0.004	0.004	0.010
	P3.4	0.004	0.001	0.004	0.004	0.004	0.004	0.010	0.001
	P3.5	0.002	0.006	0.002	0.010	0.002	0.002	0.002	0.006
	P3.6	0.002	0.002	0.002	0.002	0.006	0.006	0.015	0.002
	P3.7	0.006	0.002	0.002	0.002	0.006	0.002	0.014	0.002
P4	P4.1	0.006	0.006	0.006	0.006	0.002	0.006	0.002	0.006
	P4.2	0.011	0.003	0.003	0.003	0.011	0.011	0.011	0.018
	P4.3	0.024	0.024	0.007	0.024	0.024	0.007	0.024	0.024
P5	P5.1	0.006	0.002	0.002	0.002	0.002	0.006	0.002	0.009
	P5.2	0.006	0.010	0.002	0.006	0.006	0.006	0.006	0.002
	P5.3	0.007	0.007	0.007	0.016	0.007	0.007	0.002	0.002
	P5.4	0.011	0.003	0.011	0.025	0.018	0.011	0.011	0.018
	P5.5	0.013	0.021	0.021	0.030	0.021	0.013	0.013	0.013
P6	P6.1	0.008	0.014	0.008	0.008	0.008	0.014	0.002	0.014
	P6.2	0.003	0.011	0.011	0.011	0.003	0.011	0.011	0.011
	P6.3	0.022	0.006	0.006	0.006	0.022	0.006	0.022	0.006
	P6.4	0.015	0.025	0.004	0.004	0.015	0.015	0.025	0.004
P7	P7.1	0.019	0.019	0.011	0.011	0.011	0.019	0.003	0.011
	P7.2	0.012	0.020	0.020	0.012	0.012	0.020	0.003	0.012
	P7.3	0.019	0.019	0.011	0.011	0.011	0.011	0.011	0.011
	P7.4	0.013	0.022	0.013	0.022	0.013	0.022	0.004	0.004
	P7.5	0.022	0.036	0.022	0.036	0.036	0.036	0.006	0.036
	P7.6	0.042	0.042	0.007	0.007	0.025	0.042	0.007	0.025
Pillars	Criteria	Enterprises
		E9	E10	E11	E12	E13	E14	E15	E16
P1	P1.1	0.001	0.001	0.004	0.004	0.001	0.004	0.004	0.004
	P1.2	0.005	0.005	0.009	0.013	0.005	0.005	0.009	0.002
	P1.3	0.021	0.012	0.012	0.021	0.004	0.004	0.012	0.012
	P1.4	0.028	0.004	0.020	0.012	0.004	0.012	0.020	0.004
P2	P2.1	0.006	0.004	0.009	0.006	0.001	0.004	0.006	0.001
	P2.2	0.006	0.002	0.002	0.002	0.011	0.006	0.002	0.006
	P2.3	0.002	0.006	0.002	0.002	0.011	0.006	0.002	0.011
	P2.4	0.002	0.008	0.008	0.002	0.008	0.008	0.008	0.008
	P2.5	0.010	0.010	0.010	0.010	0.024	0.017	0.003	0.010
P3	P3.1	0.005	0.008	0.001	0.008	0.005	0.005	0.005	0.008
	P3.2	0.006	0.006	0.001	0.001	0.001	0.006	0.004	0.006
	P3.3	0.007	0.004	0.004	0.001	0.004	0.007	0.004	0.007
	P3.4	0.004	0.004	0.007	0.004	0.004	0.010	0.007	0.004
	P3.5	0.002	0.006	0.006	0.006	0.010	0.010	0.006	0.006
	P3.6	0.002	0.011	0.006	0.006	0.006	0.006	0.002	0.006
	P3.7	0.006	0.010	0.006	0.002	0.002	0.006	0.006	0.006
P4	P4.1	0.006	0.002	0.011	0.011	0.002	0.011	0.002	0.011
	P4.2	0.011	0.003	0.011	0.011	0.011	0.018	0.003	0.011
	P4.3	0.007	0.024	0.007	0.007	0.024	0.024	0.024	0.007
P5	P5.1	0.006	0.009	0.002	0.002	0.006	0.002	0.009	0.006
	P5.2	0.010	0.002	0.006	0.006	0.002	0.002	0.006	0.002
	P5.3	0.007	0.007	0.002	0.007	0.007	0.007	0.007	0.007
	P5.4	0.003	0.018	0.003	0.003	0.003	0.003	0.003	0.011
	P5.5	0.013	0.013	0.013	0.004	0.013	0.004	0.021	0.013
P6	P6.1	0.002	0.002	0.014	0.014	0.008	0.008	0.008	0.002
	P6.2	0.018	0.011	0.011	0.011	0.003	0.011	0.011	0.011
	P6.3	0.006	0.022	0.036	0.022	0.006	0.022	0.006	0.022
	P6.4	0.015	0.025	0.025	0.025	0.015	0.015	0.015	0.004
P7	P7.1	0.003	0.003	0.003	0.003	0.003	0.003	0.003	0.003
	P7.2	0.020	0.012	0.003	0.012	0.012	0.003	0.012	0.003
	P7.3	0.011	0.003	0.003	0.003	0.011	0.003	0.011	0.011
	P7.4	0.013	0.013	0.004	0.013	0.004	0.013	0.004	0.004
	P7.5	0.022	0.022	0.006	0.022	0.022	0.022	0.022	0.022
	P7.6	0.007	0.007	0.007	0.007	0.025	0.007	0.007	0.025

Table 20 presents the aggregated results and corresponding rankings of 16 retail SMEs, based on their weighted digital transformation scores. These scores were obtained by aggregating fuzzy ratings across all criteria, as detailed in the evaluation matrix shown in Table 19 and Table 20. Each enterprise’s performance is represented as a 4-tuple semantic model (x, $\mathrm{S}$_(k)(x), ϑ(x), r). The results indicate that Enterprise E2 ranks highest in words of digital transformation readiness, with a final score of 0.393, followed by Enterprise E1 (0.352), Enterprise E5 (0.345), and Enterprise E6 (0.338). Enterprise E3 recorded the lowest level of digital transformation, with a score of 0.232, indicating a significant gap in digital capabilities compared with top-performing enterprises. Notably, although most enterprises share the same L-word “L” (Low) and similar semantic intervals [0.219,0.450), the ranking differentiation is effectively captured through the crisp score r, showcasing the sensitivity of the 4-tuple semantic in distinguishing subtle differences in digital maturity.

Table 20. Aggregated scores and rankings for the digital transformation levels of retail SMEs in Vietnam.

Enterprises	Final Score	4-Tuple Semantic Model				Ranking
		x	S(k)(x)	ϑ(x)	r
E1	0.352	L	[0.219, 0.450)	0.336	0.352	2
E2	0.393	L	[0.219, 0.450)	0.336	0.393	1
E3	0.232	L	[0.219, 0.450)	0.336	0.232	16
E4	0.338	L	[0.219, 0.450)	0.336	0.338	5
E5	0.345	L	[0.219, 0.450)	0.336	0.345	3
E6	0.338	L	[0.219, 0.450)	0.336	0.338	4
E7	0.288	L	[0.219, 0.450)	0.336	0.288	10
E8	0.325	L	[0.219, 0.450)	0.336	0.325	6
E9	0.296	L	[0.219, 0.450)	0.336	0.296	8
E10	0.301	L	[0.219, 0.450)	0.336	0.301	7
E11	0.277	L	[0.219, 0.450)	0.336	0.277	13
E12	0.283	L	[0.219, 0.450)	0.336	0.283	11
E13	0.277	L	[0.219, 0.450)	0.336	0.277	12
E14	0.295	L	[0.219, 0.450)	0.336	0.295	9
E15	0.277	L	[0.219, 0.450)	0.336	0.277	14
E16	0.276	L	[0.219, 0.450)	0.336	0.276	15

This proves particularly useful in domains where linguistic evaluations are common and quantitative gaps may be narrow. From the aggregated weight distribution, it can be observed that certain criteria under Pillar 7 (human and organizational capabilities) and Pillar 4 (internal operations) have relatively higher influence due to their larger assigned weights (e.g., P7.6 with weight 0.27 and P4.3 with weight 0.59). This suggests that investment in human capital, training, and digital literacy remains a key driver in successful digital transformation initiatives among Vietnamese retail enterprises. Furthermore, the analysis highlights noticeable variation among enterprises in implementing specific digital capabilities, such as data-driven sales forecasting (P2.4), supply chain automation (P3.4), and risk management mechanisms (P6.2), which correspond to higher-performing entities.

5. Sensitivity Analysis and Discussion

5.1. Sensitivity Analysis

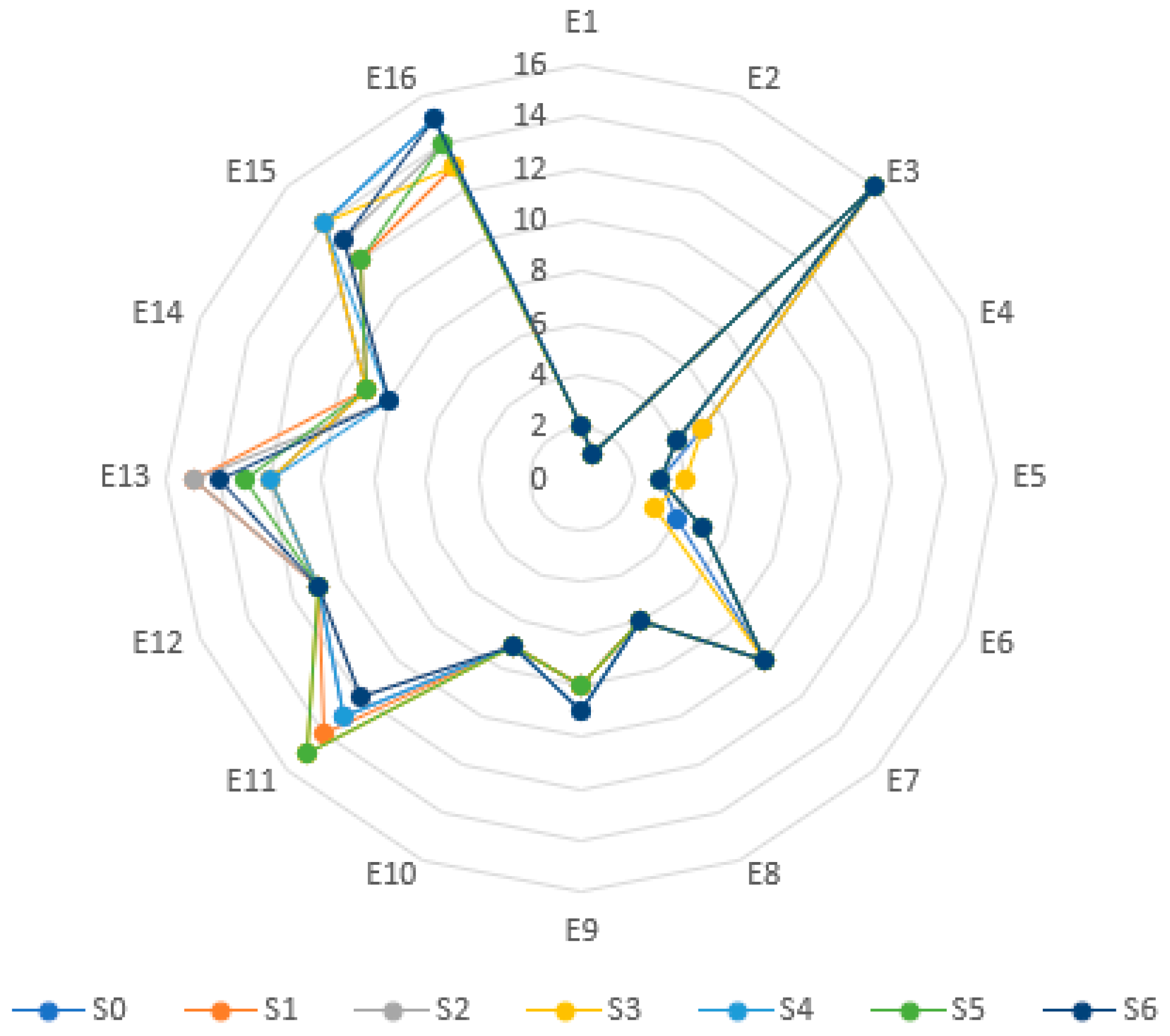
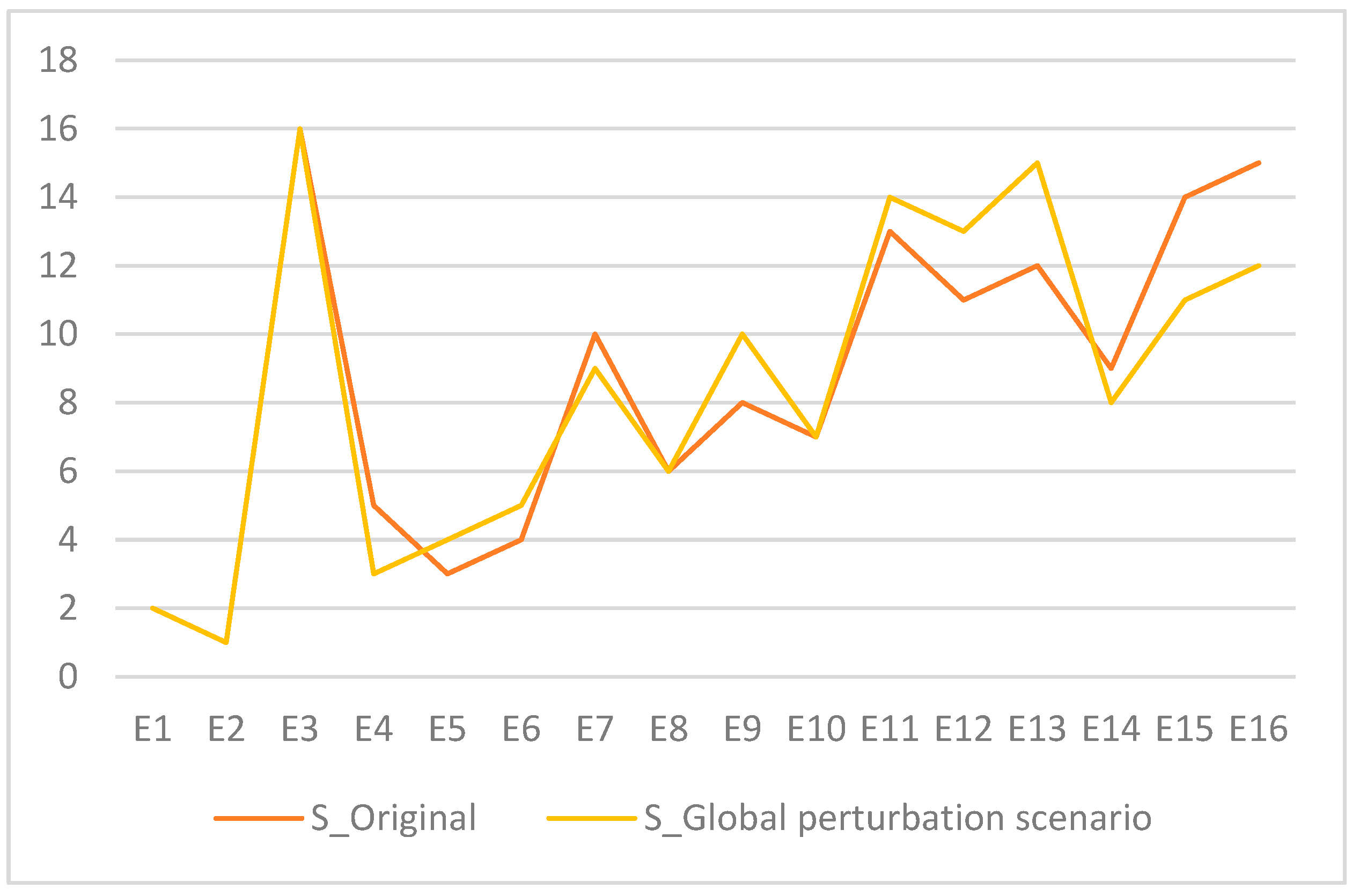
In this study, sensitivity analysis was performed by systematically adjusting the pairwise comparison values among the seven pillars used to evaluate the digital transformation levels of 16 retail SMEs in Vietnam. Specifically, in Scenarios S0 through S6, the relative importance of each pillar (P1 to P7) over the remaining six pillars was increased by one level on the L-scale presented in Table 4. For instance, in Scenario 1 (S1), the relative weight of Pillar 1 (Strategic orientation) was increased by one level compared with Pillars 2 through 7. This procedure was then repeated individually for each subsequent pillar (P2 through P7), allowing for an isolated assessment of how prioritizing each pillar affects the final ranking outcomes. The results of the sensitivity analysis are summarized in Table 21 and Figure 4, as presented below.

Table 21. Final scores and rankings following sensitivity analysis.

Enterprises	S0 (Original)		S1		S2		S3		S4		S5		S6
	Final Score	Ranking	Final Score	Ranking	Final Score	Ranking	Final Score	Ranking	Final Score	Ranking	Final Score	Ranking	Final Score	Ranking
E1	0.352	2	0.350	2	0.350	2	0.356	2	0.352	2	0.352	2	0.351	2
E2	0.393	1	0.389	1	0.390	1	0.400	1	0.391	1	0.392	1	0.391	1
E3	0.232	16	0.233	16	0.231	16	0.235	16	0.230	16	0.232	16	0.231	16
E4	0.338	5	0.344	4	0.336	4	0.338	5	0.337	4	0.340	4	0.337	4
E5	0.345	3	0.346	3	0.343	3	0.347	4	0.344	3	0.345	3	0.344	3
E6	0.338	4	0.335	5	0.334	5	0.347	3	0.336	5	0.337	5	0.336	5
E7	0.288	10	0.290	10	0.290	10	0.281	10	0.289	10	0.288	10	0.290	10
E8	0.325	6	0.325	6	0.323	6	0.326	6	0.325	6	0.326	6	0.324	6
E9	0.296	8	0.296	8	0.295	9	0.293	8	0.295	9	0.296	8	0.296	9
E10	0.301	7	0.305	7	0.303	7	0.298	7	0.301	7	0.302	7	0.302	7
E11	0.277	13	0.277	14	0.282	12	0.271	15	0.277	13	0.276	15	0.279	12
E12	0.283	11	0.281	11	0.285	11	0.281	11	0.283	11	0.282	11	0.284	11
E13	0.277	12	0.276	15	0.275	15	0.276	12	0.278	12	0.277	13	0.277	14
E14	0.295	9	0.294	9	0.296	8	0.290	9	0.297	8	0.295	9	0.296	8
E15	0.277	14	0.280	12	0.278	13	0.273	14	0.276	14	0.278	12	0.277	13
E16	0.276	15	0.278	13	0.275	14	0.274	13	0.276	15	0.277	14	0.276	15

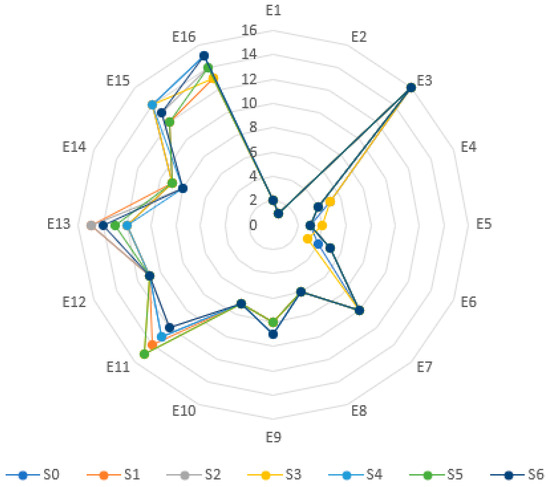
Figure 4. Sensitivity analysis single-criterion perturbation.

As shown in Table 21 and Figure 4, the results demonstrate a high level of stability in the final rankings, even when the pairwise comparison values were systematically adjusted within a reasonable range. The top-performing Enterprise E2 consistently retained its first-place position across all scenarios, with its final score varying marginally between 0.389 and 0.400. Similarly, the second-ranked Enterprise E1 exhibited minimal variation in both its final scores and ranks, retaining its position throughout all six scenarios. Notably, the lowest-ranked Enterprise E3 also demonstrated complete rank stability. These findings indicate that the evaluation model possesses strong robustness against changes in pillar prioritization, suggesting that the framework is not overly sensitive to subjective adjustments in weighting.

The sensitivity analysis results, illustrated in Figure 5, provide compelling evidence of the robustness and reliability of the proposed EFAHP–4-tuple HA model. Under a systematic perturbation scenario, in which all pairwise comparison values were uniformly increased by one level, the model consistently preserved the overall ranking structure, thereby validating the soundness of the methodology.

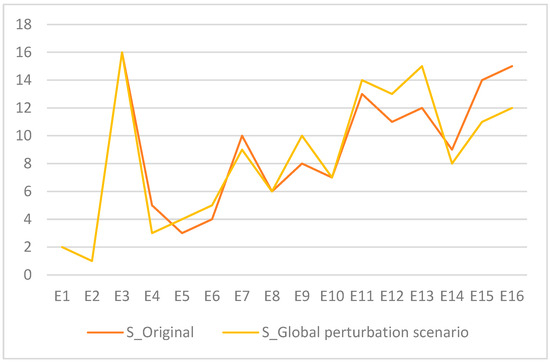
Figure 5. Sensitivity analysis global perturbation scenario.

The sensitivity analysis shows strong stability at the top and bottom rankings, with leading enterprises (E2, E1) and the lowest-ranked one (E3) being unchanged, demonstrating the model’s ability to consistently identify outstanding and weak performers. Fluctuations occurred mainly among mid-tier enterprises, reflecting the model’s refined discriminatory power, as illustrated by the resolution of ties among E11, E13, and E15. Some shifts, such as E16 improving and E13 declining by three ranks, indicate sensitivity to specific pillar weights. Overall, EFAHP with 4-tuple HA balances robustness and sensitivity, effectively handling linguistic vagueness while ensuring resilient decision-making outcomes.

5.2. A Comparative Analysis

In this subsection, a comparative analysis is conducted to evaluate the effectiveness and robustness of the proposed methodology. To enhance the reliability of the results, the fuzzy set-based FAHP-FTOPSIS method is applied, allowing a systematic comparison of ranking stability and decision consistency, in line with sensitivity analysis principles commonly used in MCDM. A detailed numerical comparison of the final prioritization results from both the FAHP-FTOPSIS and the proposed EFAHP–4-tuple HA semantics model is summarized in Table 22.

Table 22. Final scores and ranks from FAHP + FTOPSIS and the proposed method.

Enterprises	FAHP + FTOPSIS		The Proposed Method
	Score	Ranking	Score	Ranking
E1	0.581	4	0.352	2
E2	0.701	1	0.393	1
E3	0.521	11	0.232	16
E4	0.518	12	0.338	5
E5	0.476	13	0.345	3
E6	0.608	2	0.338	4
E7	0.339	16	0.288	10
E8	0.605	3	0.325	6
E9	0.548	8	0.296	8
E10	0.472	14	0.301	7
E11	0.565	7	0.277	13
E12	0.565	6	0.283	11
E13	0.439	15	0.277	12
E14	0.572	5	0.295	9
E15	0.526	10	0.277	14
E16	0.541	9	0.276	15

Table 22 presents the total scores and corresponding ranks of each enterprise. The comparative analysis between the fuzzy set-based FAHP-FTOPSIS and the EFAHP–4-tuple HA semantics model highlights differences in discriminatory power and consistency. Both methods consistently identify top performers, with E2 being ranked first and E9 being ranked eighth in both approaches, showing convergence in recognizing high-performing and stable mid-tier enterprises. However, disparities appear among mid-range enterprises due to the distinct semantic representations of linguistic assessments. For example, E6 and E8 are ranked second and third by FAHP-FTOPSIS but fourth and sixth by the proposed method, while E7 improves from sixteenth to tenth, indicating a more nuanced differentiation.

Overall, the EFAHP–4-tuple HA model demonstrates greater stability at the top ranks and refined sensitivity in the mid-range, preserving semantic integrity and reducing information distortion compared with conventional fuzzy methods. This makes it a robust and semantically faithful tool for assessing the digital transformation readiness of retail enterprises in Vietnam.

6. Conclusions

This study proposed a novel integrated fuzzy MCDM framework that combines the EFAHP method with the 4-tuple HA semantics model to evaluate the digital transformation readiness of retail enterprises in Vietnam. The proposed method offers several advantages: it provides a richer semantic representation of L-information, introduces a new consistency index tailored to handle HA-based judgments, and demonstrates strong robustness against linguistic vagueness. The empirical application to 16 retail enterprises confirms its effectiveness in integrating qualitative and quantitative expert opinions while maintaining internal consistency and interpretability. However, the approach also has certain limitations. Its validation is case-specific, relying on a relatively small expert pool and a single-country dataset, which may constrain the generalizability of the findings.

Future research should focus on validating the framework with larger and more diverse datasets across multiple sectors, as well as comparing its performance with other advanced fuzzy MCDM methods. Extending the model to incorporate dynamic digital transformation indicators and embedding it into intelligent decision support systems could further enhance its applicability in real-world decision-making contexts.