Multiplicative Fractional Hermite–Hadamard-Type Inequalities in G-Calculus

Abstract

This paper extends Hermite–Hadamard-type inequalities to the fractional multiplicative framework of G-calculus. Using multiplicative Riemann–Liouville fractional integrals, we introduce a notion of multiplicative convexity and establish fractional Hermite–Hadamard, midpoint, and trapezoidal inequalities for $GG$-convex functions. Examples and graphical illustrations are provided to demonstrate the applicability of our results and further highlight the role of fractional multiplicative analysis in broadening traditional integral inequalities.

1. Introduction

In 1967, Robert Katz and Michael Grossman introduced the first framework of what is now known as non-Newtonian calculus, specifically referred to here as geometric calculus. By 1970, they had expanded this concept into an infinite family of calculi, each fundamentally distinct from the classical calculus developed by Newton and Leibniz. Each of these non-Newtonian systems includes four key operations: a gradient (representing an average rate of change), a derivative, an averaging operator, and an integral. For every such calculus, there exists a specific set of functions that exhibit a constant derivative. Due to the foundational contributions made by Grossman and Katz [1], we refer to one of these systems as multiplicative calculus. Its primary operations are accordingly named the multiplicative derivative and the multiplicative integral. For further reading on the foundations and applications of multiplicative calculus, we direct the reader to the works of Grossman and Katz [1], Stanley [2], Bashirov et al. [3], and Boruah and Hazarika [4,5].

The complete mathematical description of multiplicative calculus was rigorously provided by Georgiev and Zennir [6] through a novel arithmetic system built on elementary operations, defined as follows:

Let ${\mathbb{R}}_{*}=\left\{{\varkappa }_{*}:{\varkappa }_{*}=exp\left\{\varkappa \right\},\varkappa \in \mathbb{R}\right\}$. The basic arithmetic operations in the multiplicative sense $\mathfrak{u},\mathfrak{v}\in {\mathbb{R}}_{*}$, are given by

• $\mathfrak{u}\oplus \mathfrak{v}=exp\left\{ln\left(\mathfrak{u}\right)+ln\left(\mathfrak{v}\right)\right\}=\mathfrak{u}\mathfrak{v}$;
• $\mathfrak{u}\ominus \mathfrak{v}=exp\left\{ln\left(\mathfrak{u}\right)-ln\left(\mathfrak{v}\right)\right\}={\displaystyle \frac{\mathfrak{u}}{\mathfrak{v}}}$;
• $\mathfrak{u}\odot \mathfrak{v}=exp\left\{ln\left(\mathfrak{u}\right).ln\left(\mathfrak{v}\right)\right\}={\mathfrak{u}}^{ln\left(\mathfrak{v}\right)}$;
• $\mathfrak{u}\oslash \mathfrak{v}=exp\left\{{\displaystyle \frac{ln\left(\mathfrak{u}\right)}{ln\left(\mathfrak{v}\right)}}\right\}={\mathfrak{u}}^{{\displaystyle \frac{1}{ln\left(\mathfrak{v}\right)}}}$, with $\mathfrak{v}\ne 1$.

Remark 1. 

$\left({\mathbb{R}}_{*},\oplus \right)$ and $\left({\mathbb{R}}_{*},\odot \right)$ are abelian groups, and ${\mathbb{R}}_{*}$ is a field according to the operations ⊕ and ⊙. We note also that in ${\mathbb{R}}_{*}$, the multiplicative zero and multiplicative unit are $0_{*}=1$ and $1_{*}=e$, respectively.

In the framework of multiplicative calculus, there are two principal types of calculi. The first, known as geometric calculus, was introduced by Grossman and Katz in [1], where they defined the multiplicative derivative as

$${\displaystyle \frac{{\mathrm{d}}_{*}\mathfrak{h}\left(\varkappa \right)}{{\mathrm{d}}_{*}\varkappa }}=\underset{\mathfrak{k}\to 0}{lim}{\left({\displaystyle \frac{\mathfrak{h}\left(\varkappa +\mathfrak{k}\right)}{\mathfrak{h}\left(\varkappa \right)}}\right)}^{{\displaystyle \frac{1}{\mathfrak{k}}}}.$$

a definition based on proportional variation of the independent variable. Later, Grossman [7] proposed an alternative definition of the multiplicative derivative, given by

$${\displaystyle \frac{{\mathrm{d}}_{*}\mathfrak{h}\left(\varkappa \right)}{{\mathrm{d}}_{*}\varkappa }}=\underset{\mathfrak{k}\to 1}{lim}{\left({\displaystyle \frac{\mathfrak{h}\left(\varkappa \mathfrak{k}\right)}{\mathfrak{h}\left(\varkappa \right)}}\right)}^{{\displaystyle \frac{1}{ln\mathfrak{k}}}},$$

which is now referred to as the bigeometric derivative, as it replaces arithmetic increments with geometric ones. To avoid ambiguity, Boruah and Hazarika [5] adopted the term G-calculus to denote the multiplicative calculus built upon the bigeometric derivative. Throughout the rest of this paper, although the term “multiplicative” may occasionally be used, all references to concepts such as the multiplicative derivative and integral are to be understood strictly within the framework of G-calculus.

Fractional calculus, which extends the classical notions of differentiation and integration to arbitrary real or complex orders, has emerged as a powerful tool for modeling systems with memory, hereditary effects, and non-local dynamics. Unlike integer-order operators, fractional derivatives capture the global evolution of a process, making them particularly suitable for describing anomalous diffusion, viscoelasticity, and other complex phenomena. Among the various definitions of fractional integrals, the Riemann–Liouville fractional integrals are among the most prominent and widely used. Introduced in the 19th century, the Riemann–Liouville fractional integral provides a natural generalization of repeated integration and serves as a foundational concept in the theory of fractional calculus. Its definition, based on the convolution of a power-law kernel with a given function, not only preserves key analytical properties but also facilitates the derivation of corresponding fractional differential operators. Due to their mathematical elegance and broad applicability, Riemann–Liouville integrals have become a standard reference in both theoretical investigations and practical applications across physics, engineering, and applied mathematics.

It is worth emphasizing that, in recent years, geometric calculus has witnessed substantial advances in the development of multiplicative versions of classical fractional integral operators. Notably, researchers have formulated multiplicative analogues of several well-known operators, including the Riemann–Liouville fractional integral [8], tempered fractional integrals [9], Hadamard fractional integrals [10], Katugampola fractional integrals [11], conformable fractional integrals [12], fractional integrals with exponential kernels [13], and even $AB$-fractional integrals [14], all adapted to the multiplicative setting. These contributions have significantly enriched non-Newtonian analysis, providing a natural framework for modeling phenomena governed by relative rather than absolute changes.

Within the framework of G-calculus, Bas et al. [15] recently introduced the concept of multiplicative Riemann–Liouville fractional integrals, constructed via repeated multiplicative integration, as follows:

Definition 1 

([15]). Let $\mathcal{D}\subset {\mathbb{R}}_{*}$ and $\mathfrak{h}:\mathcal{D}\to {\mathbb{R}}_{*}$. Then, the left- and right-sided multiplicative Riemann–Liouville fractional integrals of order $\alpha >0$ are defined by the following:

$${}_{*}\mathcal{R}_{{\mathfrak{a}}^{+}}^{\alpha }\mathfrak{h}\left(\mathfrak{u}\right)=exp\left\{{\displaystyle \frac{1}{\Gamma \left(\alpha \right)}}\underset{\mathfrak{a}}{\stackrel{\mathfrak{u}}{\int }}{\left(ln\mathfrak{u}-ln\mathfrak{v}\right)}^{\alpha -1}{\displaystyle \frac{ln\mathfrak{h}\left(\mathfrak{v}\right)}{\mathfrak{v}}}\mathrm{d}\mathfrak{v}\right\},\mathfrak{u}>\mathfrak{a},$$

(1)

and

$${}_{*}\mathcal{R}_{{\mathfrak{b}}^{-}}^{\alpha }\mathfrak{h}\left(\mathfrak{u}\right)=exp\left\{{\displaystyle \frac{1}{\Gamma \left(\alpha \right)}}\underset{\mathfrak{u}}{\stackrel{\mathfrak{b}}{\int }}{\left(ln\mathfrak{v}-ln\mathfrak{u}\right)}^{\alpha -1}{\displaystyle \frac{ln\mathfrak{h}\left(\mathfrak{v}\right)}{\mathfrak{v}}}\mathrm{d}\mathfrak{v}\right\},\mathfrak{u}<\mathfrak{b},$$

(2)

respectively.

The multiplicative Riemann–Liouville fractional integrals motivate a natural extension of fractional calculus to multiplicative settings. While classical fractional calculus models memory effects in additive processes, many phenomena in biology, finance, and information theory evolve through relative rather than absolute changes. Fractional multiplicative integrals provide a suitable framework for such contexts, preserving key properties like semigroup structure and compatibility with multiplicative derivatives.

Integral inequalities play a fundamental role in various areas of mathematical analysis and its applications, particularly in establishing bounds, approximations, and stability results. In the context of multiplicative calculus, classical integral inequalities must be reinterpreted and reformulated to align with the new operations of multiplicative integration and differentiation. A central result in this field is the Hermite–Hadamard inequality, which states that if the function $\mathfrak{h}$ is convex on $[\mathfrak{a},\mathfrak{b}]$, then the following inequalities are satisfied:

$$\mathfrak{h}\left(\frac{\mathfrak{a}+\mathfrak{b}}{2}\right)\le \frac{1}{\mathfrak{b}-\mathfrak{a}}\underset{\mathfrak{a}}{\stackrel{\mathfrak{b}}{\int }}\mathfrak{h}\left(\varkappa \right)\mathrm{d}\varkappa \le \frac{\mathfrak{h}\left(\mathfrak{a}\right)+\mathfrak{h}\left(\mathfrak{b}\right)}{2}.$$

(3)

These inequalities serve as a fundamental tool in numerical analysis and approximation theory, particularly in establishing error bounds for quadrature rules and integral approximations.

In [16], Kirmaci proved the following result concerning the left inequality in (3):

Theorem 1 

([16]). Consider a differentiable mapping $\mathfrak{h}:I\subset \mathbb{R}\to \mathbb{R}$ such that $\mathfrak{h}\in L_1[\mathfrak{a},\mathfrak{b}]$, with $\mathfrak{a}$, $\mathfrak{b}\in I$ and $\mathfrak{a}<\mathfrak{b}$. If $\left|{\mathfrak{h}}^{\prime }\right|$ exhibits convexity on $[\mathfrak{a},\mathfrak{b}]$, then

$$\left|\mathfrak{h}\left(\frac{\mathfrak{a}+\mathfrak{b}}{2}\right)-\frac{1}{\mathfrak{b}-\mathfrak{a}}\underset{\mathfrak{a}}{\stackrel{\mathfrak{b}}{\int }}\mathfrak{h}\left(\varkappa \right)\mathrm{d}\varkappa \right|\le \frac{\mathfrak{b}-\mathfrak{a}}{8}\left(\left|{\mathfrak{h}}^{\prime }\left(\mathfrak{a}\right)\right|+\left|{\mathfrak{h}}^{\prime }\left(\mathfrak{b}\right)\right|\right).$$

In [17], Dragomir and Agarwal obtained the following result pertaining to the right inequality in (3):

Theorem 2 

([17]). Consider a differentiable mapping $\mathfrak{h}:I\subset \mathbb{R}\to \mathbb{R}$ such that $\mathfrak{h}\in L_1[\mathfrak{a},\mathfrak{b}]$, with $\mathfrak{a}$, $\mathfrak{b}\in I$ and $\mathfrak{a}<\mathfrak{b}$. If $\left|{\mathfrak{h}}^{\prime }\right|$ exhibits convexity on $[\mathfrak{a},\mathfrak{b}]$, then the following inequality holds:

$$\left|\frac{\mathfrak{h}\left(\mathfrak{a}\right)+\mathfrak{h}\left(\mathfrak{b}\right)}{2}-\frac{1}{\mathfrak{b}-\mathfrak{a}}\underset{\mathfrak{a}}{\stackrel{\mathfrak{b}}{\int }}\mathfrak{h}\left(\varkappa \right)\mathrm{d}\varkappa \right|\le \frac{\mathfrak{b}-\mathfrak{a}}{8}\left(\left|{\mathfrak{h}}^{\prime }\left(\mathfrak{a}\right)\right|+\left|{\mathfrak{h}}^{\prime }\left(\mathfrak{b}\right)\right|\right).$$

Hermite–Hadamard-type inequalities have been widely investigated in the mathematical literature. For foundational results and further developments, the reader may refer to [18,19,20,21], which explore various generalizations and applications of these inequalities.

In this work, we focus on adapting key integral inequalities, including Hermite–Hadamard, midpoint, and trapezoidal types, to the multiplicative fractional framework. By doing so, we provide a new perspective on these classical results and open the door to further research in non-Newtonian analysis, numerical approximation, and optimization within this alternative calculus setting.

This paper is organized as follows. In Section 2, we review some basic definitions and key results from G-calculus that will be used throughout this paper. Section 3 begins with an exploration of the multiplicative analogues of classical quadrature rules, such as the midpoint and trapezoidal formulas. We then introduce and discuss the appropriate notion of convexity within the framework of multiplicative calculus. Based on these foundations, Section 4 presents multiplicative fractional version of Hermite–Hadamard inequality, as well as midpoint- and trapezoid-type inequalities, extending well-known results from classical analysis to the framework of G-calculus. A numerical example with graphical representations is presented in Section 5. Finally, Section 6 provides some applications of the derived results, illustrating their relevance and potential for further research.

2. Elements of G-Calculus

To lay the groundwork for our study, we first recall the basic definitions and central results from G-calculus that will play a crucial role in our analysis.

Definition 2 

([6]). For a function $\mathrm{f}:{\mathbb{R}}_{*}\to \mathbb{R}$, the associated multiplicative function $\mathfrak{f}:{\mathbb{R}}_{*}\to {\mathbb{R}}_{*}$ is defined by

$$\mathfrak{f}\left(\varkappa \right)=exp\left\{\mathrm{f}\left(ln\left(\varkappa \right)\right)\right\},\varkappa \in {\mathbb{R}}_{*}.$$

Table 1 lists some examples of the multiplicative versions of some well-known functions.

Table 1. Example of multiplicative functions.

$\mathbf{f}\left(\mathit{\varkappa }\right)$	$\mathfrak{f}\left(\mathit{\varkappa }\right)$
$\varkappa$	${\varkappa }_{*}=\varkappa$
${\varkappa }^k$	${\varkappa }^{k_{*}}=exp\left\{{\left(ln\varkappa \right)}^k\right\}$, $k\ge 0$
$exp\left(\varkappa \right)$	$exp{\left(\varkappa \right)}_{*}=exp\left(\varkappa \right)$
$ln\left(\varkappa \right)$	$ln{\left(\varkappa \right)}_{*}=ln\left(\varkappa \right)$
$cos\left(\varkappa \right)$	${cos}_{*}\left(\varkappa \right)=exp\left\{cos\left(ln\varkappa \right)\right\}$
$P\left(\varkappa \right)={\displaystyle \sum _{i=0}^n{\mathfrak{c}}_i{\varkappa }^i}$	$\mathcal{P}\left(\varkappa \right)={\displaystyle \prod _{i=0}^n{\mathfrak{c}}_{i_{*}}}\odot {\varkappa }^{i_{*}}$, where ${\mathfrak{c}}_{i_{*}}=e^{{\mathfrak{c}}_i}$

Definition 3 

([6]). Let $\mathcal{D}\subseteq {\mathbb{R}}_{*}$. The function $\mathfrak{f}:\mathcal{D}\to {\mathbb{R}}_{*}$ is said to be a continuous multiplicative function at the point ${\varkappa }_0\in \mathcal{D}$, if $exp\left\{\mathrm{f}\left(ln\left(\varkappa \right)\right)\right\}$ is continuous at ${\varkappa }_0$. The function $\mathfrak{f}$ is said to be a continuous multiplicative function on $\mathcal{D}$ if it is continuous at any point of $\mathcal{D}$. In this case, we denote $\mathfrak{f}\in {\mathcal{C}}_{*}\left(\mathcal{D}\right)$.

Definition 4 

([6]). Let $\mathcal{D}\subset {\mathbb{R}}_{*}$ and $\mathrm{f}:\mathcal{D}\to {\mathbb{R}}_{*}$ be a differentiable function. Then, $\mathfrak{f}$ is multiplicatively differentiable (∗-differentiable), and the multiplicative derivative (∗-derivative) of $\mathfrak{f}$ at $\varkappa \in \mathcal{D}$ is defined by the following:

$$\begin{array}{cc}\hfill {\displaystyle \frac{{\mathrm{d}}_{*}\mathfrak{f}\left(\varkappa \right)}{{\mathrm{d}}_{*}\varkappa }}={\mathfrak{f}}^{*}\left(\varkappa \right)=& \underset{\mathfrak{k}\to 0_{*}}{lim}\left(\left[\mathfrak{f}*\left(\varkappa \oplus \mathfrak{k}\right)\ominus \mathfrak{f}\left(\varkappa \right)\right]\oslash \mathfrak{k}\right)\hfill \\ \hfill =& \underset{\mathfrak{k}\to 1}{lim}exp\left\{{\displaystyle \frac{ln\mathfrak{f}\left(\mathfrak{k}\varkappa \right)-ln\mathfrak{f}\left(\varkappa \right)}{ln\left(\mathfrak{k}\right)}}\right\}\hfill \\ \hfill =& \underset{\mathfrak{k}\to 1}{lim}exp\left\{{\displaystyle \frac{\varkappa \mathfrak{k}{\mathfrak{f}}^{\prime }\left(\varkappa \mathfrak{k}\right)}{\mathfrak{f}\left(\varkappa \mathfrak{k}\right)}}\right\}\hfill \\ \hfill =& exp\left\{\varkappa {\displaystyle \frac{{\mathfrak{f}}^{\prime }\left(\varkappa \right)}{\mathfrak{f}\left(\varkappa \right)}}\right\}.\hfill \end{array}$$

Proposition 1 

([6]). Let $\mathfrak{f},\mathfrak{g}:\mathcal{D}\subseteq {\mathbb{R}}_{*}\to {\mathbb{R}}_{*}$ be ∗-differentiable functions on $\mathcal{D}$. Then, the following properties hold:

• ${\left(\mathfrak{c}\odot \mathfrak{f}\right)}^{*}\left(\varkappa \right)=\mathfrak{c}\odot {\mathfrak{f}}^{*}\left(\varkappa \right)={\left({\mathfrak{f}}^{*}\left(\varkappa \right)\right)}^{ln\left(\mathfrak{c}\right)}$, $\mathfrak{c}\in {\mathbb{R}}_{*}$;
• ${\left(\mathfrak{f}\oplus \mathfrak{g}\right)}^{*}\left(\varkappa \right)={\mathfrak{f}}^{*}\left(\varkappa \right)\oplus {\mathfrak{g}}^{*}\left(\varkappa \right)={\mathfrak{f}}^{*}\left(\varkappa \right){\mathfrak{g}}^{*}\left(\varkappa \right)$;
• ${\left(\mathfrak{f}\odot \mathfrak{g}\right)}^{*}\left(\varkappa \right)=\left[{\mathfrak{f}}^{*}\left(\varkappa \right)\odot \mathfrak{g}\left(\varkappa \right)\right]\oplus \left[\mathfrak{f}\left(\varkappa \right)\odot {\mathfrak{g}}^{*}\left(\varkappa \right)\right]={\left({\mathfrak{f}}^{*}\left(\varkappa \right)\right)}^{ln\left(\mathfrak{g}\left(\varkappa \right)\right)}{\left({\mathfrak{g}}^{*}\left(\varkappa \right)\right)}^{ln\left(\mathfrak{f}\left(\varkappa \right)\right)}$;
• ${\left(\mathfrak{f}\oslash \mathfrak{g}\right)}^{*}\left(\varkappa \right)=\left(\left[{\mathfrak{f}}^{*}\left(\varkappa \right)\odot \mathfrak{g}\left(\varkappa \right)\right]\ominus \left[\mathfrak{f}\left(\varkappa \right)\odot {\mathfrak{g}}^{*}\left(\varkappa \right)\right]\right)\oslash {\mathfrak{g}}^{2_{*}}\left(\varkappa \right)={\left({\displaystyle \frac{{\left(\mathfrak{g}\left(\varkappa \right)\right)}^{{\mathfrak{f}}^{*}\left(\varkappa \right)}}{{\left(\mathfrak{f}\left(\varkappa \right)\right)}^{{\mathfrak{g}}^{*}\left(\varkappa \right)}}}\right)}^{{\displaystyle \frac{1}{{\left(ln\left(\mathfrak{g}\left(\varkappa \right)\right)\right)}^2}}}$;
• $\left(\mathfrak{f}\circ \mathfrak{g}\right)\left(\varkappa \right)={\mathfrak{g}}^{*}\left(\varkappa \right)\odot {\mathfrak{f}}^{*}\left(\mathfrak{g}\left(\varkappa \right)\right)={\left({\mathfrak{f}}^{*}\left(\mathfrak{g}\left(\varkappa \right)\right)\right)}^{ln\left({\mathfrak{g}}^{*}\left(\varkappa \right)\right)}$.

Proposition 2 

([6]). [(Multiplicative Tests for Monotonicity)]

• A ∗-differentiable function $\mathfrak{f}:[\mathfrak{a},\mathfrak{b}]\to {\mathbb{R}}_{*}$ is said to be ∗-increasing on $[\mathfrak{a},\mathfrak{b}]$, if ${\mathfrak{f}}^{*}\left(\varkappa \right)\ge 1$ for all $\varkappa \in [\mathfrak{a},\mathfrak{b}]$.
• If ${\mathfrak{f}}^{*}\left(\varkappa \right)\le 1$ for all $\varkappa \in [\mathfrak{a},\mathfrak{b}]$, then $\mathfrak{f}$ is ∗-decreasing on $[\mathfrak{a},\mathfrak{b}]$.

Definition 5 

([6]). Suppose that $\mathfrak{f}:\mathcal{D}\subseteq {\mathbb{R}}_{*}\to {\mathbb{R}}_{*}$ is a function satisfying $\mathfrak{f}\in {\mathcal{C}}_{*}^n$, $n\in \mathbb{N}$ with $n\ge 2$. The multiplicative differential ${\mathrm{d}}_{*}\varkappa$ is given by

$${\mathrm{d}}_{*}\varkappa =exp\left\{\mathrm{d}\left(ln\varkappa \right)\right\}=exp\left\{{\displaystyle \frac{\mathrm{d}\varkappa }{\varkappa }}\right\}$$

and

$${\mathrm{d}}_{*}\mathfrak{f}\left(\varkappa \right)=exp\left\{\mathrm{d}\left(ln\mathfrak{f}\left(\varkappa \right)\right)\right\}=exp\left\{{\displaystyle \frac{{\mathfrak{f}}^{\prime }\left(\varkappa \right)}{\mathfrak{f}\left(\varkappa \right)}}\mathrm{d}\varkappa \right\}.$$

Definition 6 

([6]). Let $\mathfrak{f}:\left[\mathfrak{a},\mathfrak{b}\right]\subset {\mathbb{R}}_{*}\to {\mathbb{R}}_{*}$ be a function such that $\mathfrak{f}\in {\mathcal{C}}_{*}\left[\mathfrak{a},\mathfrak{b}]\right)$. Then, $\mathfrak{f}$ is ∗-integrable (integrable in the multiplicative sense), and its multiplicative integral is expressed as follows:

$$\underset{\mathfrak{a}}{\stackrel{\mathfrak{b}}{{\int }_{*}}}\mathfrak{f}\left(\varkappa \right)\odot {\mathrm{d}}_{*}\varkappa =exp\left\{\underset{\mathfrak{a}}{\stackrel{\mathfrak{b}}{\int }}{\displaystyle \frac{ln\mathfrak{f}\left(\varkappa \right)}{\varkappa }}\mathrm{d}\varkappa \right\}.$$

Proposition 3 

([6]). Let $\mathfrak{f},\mathfrak{g}:[\mathfrak{a},\mathfrak{b}]\subseteq {\mathbb{R}}_{*}\to {\mathbb{R}}_{*}$ be ∗-integrable functions on $[\mathfrak{a},\mathfrak{b}]$ and $\mathfrak{u},\mathfrak{v}\in {\mathbb{R}}_{*}$. Then, the following properties hold:

• $\underset{\mathfrak{a}}{\stackrel{\mathfrak{a}}{{\int }_{*}}}\mathfrak{f}\left(\varkappa \right)\odot {\mathrm{d}}_{*}\varkappa =0_{*}=1$;
• $\underset{\mathfrak{a}}{\stackrel{\mathfrak{b}}{{\int }_{*}}}\left(\mathfrak{u}\odot \mathfrak{f}\left(\varkappa \right)\oplus \mathfrak{v}\odot \mathfrak{g}\left(\varkappa \right)\right)\odot {\mathrm{d}}_{*}\varkappa =\mathfrak{u}\odot \left(\underset{\mathfrak{a}}{\stackrel{\mathfrak{b}}{{\int }_{*}}}\mathfrak{f}\left(\varkappa \right)\odot {\mathrm{d}}_{*}\varkappa \right)\oplus \mathfrak{v}\odot \left(\underset{\mathfrak{a}}{\stackrel{\mathfrak{b}}{{\int }_{*}}}{\mathfrak{g}}_{*}\left(\varkappa \right)\odot {\mathrm{d}}_{*}\varkappa \right)$;
• $\underset{\mathfrak{a}}{\stackrel{\mathfrak{b}}{{\int }_{*}}}\mathfrak{f}\left(\varkappa \right)\odot {\mathrm{d}}_{*}\varkappa =\underset{\mathfrak{a}}{\stackrel{\mathfrak{c}}{{\int }_{*}}}\mathfrak{f}\left(\varkappa \right)\odot {\mathrm{d}}_{*}\varkappa \oplus \underset{\mathfrak{c}}{\stackrel{\mathfrak{b}}{{\int }_{*}}}\mathfrak{f}\left(\varkappa \right)\odot {\mathrm{d}}_{*}\varkappa$;
• $\underset{\mathfrak{a}}{\stackrel{\mathfrak{b}}{{\int }_{*}}}{\left(\mathfrak{f}\left(\varkappa \right)\right)}^k\odot {\mathrm{d}}_{*}\varkappa ={\left(\underset{\mathfrak{a}}{\stackrel{\mathfrak{b}}{{\int }_{*}}}\mathfrak{f}\left(\varkappa \right)\odot {\mathrm{d}}_{*}\varkappa \right)}^k$.

Proposition 4. 

Let $\mathfrak{f}:\mathcal{D}\subset {\mathbb{R}}_{*}\to {\mathbb{R}}_{*}$ be a ∗-integrable function, and $\mathfrak{g}:\mathcal{D}\subset {\mathbb{R}}_{*}\to {\mathbb{R}}_{*}$ be a differentiable function. Then, one has

$$\underset{\mathfrak{a}}{\stackrel{\mathfrak{b}}{{\int }_{*}}}\mathfrak{f}\left(\mathfrak{g}\left(\varkappa \right)\right)\odot {\mathrm{d}}_{*}\left(\mathfrak{g}\left(\varkappa \right)\right)=exp\left\{\underset{\mathfrak{a}}{\stackrel{\mathfrak{b}}{\int }}ln\left(\mathfrak{f}\left(\mathfrak{g}\left(\varkappa \right)\right)\right){\displaystyle \frac{{\mathfrak{g}}^{\prime }\left(\varkappa \right)}{\mathfrak{g}\left(\varkappa \right)}}\mathrm{d}\varkappa \right\}.$$

Proposition 5 

([6]). [(Multiplicative absolute value)] For $\mathcal{E}\in {\mathbb{R}}_{*}$, the ∗-absolute value (multiplicative absolute value) is defined as follows:

$${\left|\mathcal{E}\right|}_{*}=\left\{\begin{array}{cc}\mathcal{E},\hfill & \mathit{if}\mathcal{E}\ge 1,\hfill \\ {\displaystyle \frac{1}{\mathcal{E}}},\hfill & \mathit{if}0<\mathcal{E}<1.\hfill \end{array}\right.$$

Remark 2.  

The relation between the classical absolute value and the multiplicative one is given by

$$\left|ln\left(\mathcal{E}\right)\right|\le ln{\left|\mathcal{E}\right|}_{*}.$$

Proposition 6 

([6]). [(Multiplicative triangle inequality)] For $\mathcal{E},\mathcal{F}\in {\mathbb{R}}_{*}$, the multiplicative triangle inequality, which is also known as the ∗-triangle inequality, is expressed as

$${\left|\mathcal{E}\mathcal{F}\right|}_{*}\le {\left|\mathcal{E}\right|}_{*}{\left|\mathcal{F}\right|}_{*}.$$

3. Quadrature and Convexity in Multiplicative Calculus

With the necessary background provided, we now turn our attention to the multiplicative analogues of classical quadrature rules and explore the corresponding notion of convexity in this new framework.

Before illustrating some multiplicative quadrature rules, we begin by recalling the ∗-arclength of a piecewise smooth curve, which is defined as follows:

Definition 7 

([22]). Let $\mathfrak{h}:[\mathfrak{a},\mathfrak{b}]\subset {\mathbb{R}}_{*}\to {\mathbb{R}}_{*}$ be a ∗-continous and ∗-differentiable on $[\mathfrak{a},\mathfrak{b}]$. Then, the ∗-arclength of $\mathfrak{h}$ on $[\mathfrak{a},\mathfrak{b}]$ is given by

$$\underset{\mathfrak{a}}{\stackrel{\mathfrak{b}}{{\int }_{*}}}{\left[1_{*}\oplus {\left({\mathfrak{h}}^{*}\left(\varkappa \right)\right)}^{2_{*}}\right]}^{{{\displaystyle \frac{1}{2}}}_{*}}\odot {\mathrm{d}}_{*}\varkappa =\underset{\mathfrak{a}}{\stackrel{\mathfrak{b}}{{\int }_{*}}}exp\left\{{\displaystyle \frac{1+{\left(ln\left({\mathfrak{h}}^{*}\left(\varkappa \right)\right)\right)}^2}{2}}\right\}\odot {\mathrm{d}}_{*}\varkappa ,$$

where we have used the fact that ${\mathfrak{g}}^{k_{*}}=exp\left\{{\left(ln\left(\mathfrak{g}\right(\varkappa \left)\right)\right)}^k\right\}$ for all $k\in \mathbb{R}$ [6].

Proposition 7. 

From Definition 7, it is natural to require that the ∗-distance between two points $\mathfrak{c}$ and $\mathfrak{d}$ corresponds precisely to the ∗-arclength of the ∗-segment joining them. In this context, the length of the interval $[\mathfrak{a},\mathfrak{b}]$ is given by $exp\left\{ln\left(\mathfrak{b}\right)-ln\left(\mathfrak{a}\right)\right\}$.

Proposition 7 enables us to introduce multiplicative analogues of classical quadrature rules, such as the multiplicative midpoint and trapezoidal formulas.

3.1. Multiplicative Quadrature Rules

We begin this subsection by introducing the multiplicative counterparts of classical quadrature rules, including the midpoint and trapezoidal formulas, adapted to the framework of multiplicative calculus.

3.1.1. Multiplicative Midpoint Formula

Definition 8. 

Let $\mathfrak{h}:[\mathfrak{a},\mathfrak{b}]\subset {\mathbb{R}}_{*}\to {\mathbb{R}}_{*}$ be ∗-integrable on $[\mathfrak{a},\mathfrak{b}]$. The multiplicative midpoint formula denoted by ${\mathcal{M}}_{*}\left(\mathfrak{h}\right)$ is defined as

$$\begin{array}{cc}\hfill {\mathcal{I}}_{*}\left(\mathfrak{h}\right)={\left(\underset{\mathfrak{a}}{\stackrel{\mathfrak{b}}{{\int }_{*}}}\mathfrak{h}\left(\varkappa \right)\odot {\mathrm{d}}_{*}\varkappa \right)}^{{\displaystyle \frac{1}{ln\left(\mathfrak{b}\right)-ln\left(\mathfrak{a}\right)}}}\simeq {\mathcal{M}}_{*}\left(\mathfrak{h}\right)=& exp\left\{\mathrm{h}\left({\displaystyle \frac{ln\left(\mathfrak{a}\right)+ln\left(\mathfrak{b}\right)}{2}}\right)\right\}=exp\left\{\mathrm{h}\left(ln\sqrt{\mathfrak{a}\mathfrak{b}}\right)\right\}=\mathfrak{h}\left(\sqrt{\mathfrak{a}\mathfrak{b}}\right).\hfill \end{array}$$

Proposition 8. 

The multiplicative midpoint formula has degree of precision 1, that is, it is exact for all multiplicative polynomials of degree at most 1.

Proof. 

1- 

Multiplicative polynomial of degree 0: Let $\mathfrak{h}\left(\varkappa \right)=1_{*}$. Then,

$${\mathcal{I}}_{*}\left(1_{*}\right)={\left(\underset{\mathfrak{a}}{\stackrel{\mathfrak{b}}{{\int }_{*}}}{1}_{*}\odot {\mathrm{d}}_{*}\varkappa \right)}^{{\displaystyle \frac{1}{ln\left(\mathfrak{b}\right)-ln\left(\mathfrak{a}\right)}}}=exp{\left\{ln\left(\mathfrak{b}\right)-ln\left(\mathfrak{a}\right)\right\}}^{{\displaystyle \frac{1}{ln\left(\mathfrak{b}\right)-ln\left(\mathfrak{a}\right)}}}=1_{*}.$$

(4)

On the other hand, we have

$${\mathcal{M}}_{*}\left(1_{*}\right)=\mathfrak{h}\left(\sqrt{\mathfrak{a}\mathfrak{b}}\right)=1_{*}.$$

Thus, the multiplicative midpoint formula is at least of order 0.

2- 

Multiplicative polynomial of degree 1: Let $\mathfrak{h}\left(\varkappa \right)={\varkappa }_{*}=\varkappa$. Then,

$${\mathcal{I}}_{*}\left({\varkappa }_{*}\right)={\left(\underset{\mathfrak{a}}{\stackrel{\mathfrak{b}}{{\int }_{*}}}{\varkappa }_{*}\odot {\mathrm{d}}_{*}\varkappa \right)}^{{\displaystyle \frac{1}{ln\left(\mathfrak{b}\right)-ln\left(\mathfrak{a}\right)}}}=exp{\left\{{\displaystyle \frac{{\left[ln\left(\mathfrak{b}\right)\right]}^2-{\left[ln\left(\mathfrak{a}\right)\right]}^2}{2}}\right\}}^{{\displaystyle \frac{1}{ln\left(\mathfrak{b}\right)-ln\left(\mathfrak{a}\right)}}}=\sqrt{\mathfrak{a}\mathfrak{b}}.$$

(5)

On the other hand, we have

$${\mathcal{M}}_{*}\left({\varkappa }_{*}\right)=\mathfrak{h}\left(\sqrt{\mathfrak{a}\mathfrak{b}}\right)=\sqrt{\mathfrak{a}\mathfrak{b}}.$$

Thus, the multiplicative midpoint formula is at least of order 1.

3- 

Multiplicative polynomial of degree 2: Let $\mathfrak{h}\left(\varkappa \right)={\varkappa }^{2_{*}}=exp\left\{{\left(ln\varkappa \right)}^2\right\}$. Then, we have

$${\mathcal{I}}_{*}\left({\varkappa }^{2_{*}}\right)={\left(\underset{\mathfrak{a}}{\stackrel{\mathfrak{b}}{{\int }_{*}}}{\varkappa }^{2_{*}}\odot {\mathrm{d}}_{*}\varkappa \right)}^{{\displaystyle \frac{1}{ln\left(\mathfrak{b}\right)-ln\left(\mathfrak{a}\right)}}}=exp{\left\{{\displaystyle \frac{{\left[ln\left(\mathfrak{b}\right)\right]}^3-{\left[ln\left(\mathfrak{a}\right)\right]}^3}{3}}\right\}}^{{\displaystyle \frac{1}{ln\left(\mathfrak{b}\right)-ln\left(\mathfrak{a}\right)}}}=exp\left\{{\displaystyle \frac{{\left[ln\left(\mathfrak{a}\right)\right]}^2+\left[ln\left(\mathfrak{a}\right)ln\left(\mathfrak{b}\right)\right]+{\left[ln\left(\mathfrak{b}\right)\right]}^2}{3}}\right\}.$$

(6)

On the other hand, we have

$${\mathcal{M}}_{*}\left({\varkappa }^{2_{*}}\right)=\mathfrak{h}\left(\sqrt{\mathfrak{a}\mathfrak{b}}\right)=exp\left\{{\left(ln\sqrt{\mathfrak{a}\mathfrak{b}}\right)}^2\right\}=exp\left\{{\left({\displaystyle \frac{ln\mathfrak{a}+ln\mathfrak{b}}{2}}\right)}^2\right\}=exp\left\{{\displaystyle \frac{{\left[ln\left(\mathfrak{a}\right)\right]}^2+2\left[ln\left(\mathfrak{a}\right)ln\left(\mathfrak{b}\right)\right]+{\left[ln\left(\mathfrak{b}\right)\right]}^2}{4}}\right\}.$$

Since ${\mathcal{M}}_{*}\left({\varkappa }^{2_{*}}\right)\ne {\mathcal{I}}_{*}\left({\varkappa }^{2_{*}}\right)$, the multiplicative midpoint formula is not exact for multiplicative polynomials of degree 2. Therefore, the formula is indeed of order 1.

The proof is completed. □

3.1.2. Multiplicative Trapezium Formula

Definition 9. 

Let $\mathfrak{h}:[\mathfrak{a},\mathfrak{b}]\subset {\mathbb{R}}_{*}\to {\mathbb{R}}_{*}$ be ∗-integrable on $[\mathfrak{a},\mathfrak{b}]$. The multiplicative trapezoid formula denoted by ${\mathcal{T}}_{*}\left({\mathfrak{h}}_{*}\right)$ is defined as

$$\begin{array}{cc}\hfill {\mathcal{I}}_{*}\left(\mathfrak{h}\right)={\left(\underset{\mathfrak{a}}{\stackrel{\mathfrak{b}}{{\int }_{*}}}\mathfrak{h}\left(\varkappa \right)\odot {\mathrm{d}}_{*}\varkappa \right)}^{{\displaystyle \frac{1}{ln\left(\mathfrak{b}\right)-ln\left(\mathfrak{a}\right)}}}\simeq \mathcal{T}\left(\mathfrak{h}\right)=exp\left\{{\displaystyle \frac{\mathrm{h}\left(ln\left(\mathfrak{a}\right)\right)+\mathrm{h}\left(ln\left(\mathfrak{b}\right)\right)}{2}}\right\}=& \sqrt{\mathfrak{h}\left(\mathfrak{a}\right)\mathfrak{h}\left(\mathfrak{b}\right)}.\hfill \end{array}$$

Proposition 9. 

The multiplicative trapezium formula has degree of precision 1, that is, it is exact for all multiplicative polynomials of degree at most 1.

Proof. 

1- 

Multiplicative polynomial of degree 0: For $\mathfrak{h}\left(\varkappa \right)=1_{*}$, we have

$${\mathcal{T}}_{*}\left(1_{*}\right)=\sqrt{\mathfrak{h}\left(\mathfrak{a}\right)\mathfrak{h}\left(\mathfrak{b}\right)}=\sqrt{e^2}=1_{*},$$

which is equal to ${\mathcal{I}}_{*}\left(1_{*}\right)$ given by (4). Thus, the multiplicative trapezium formula is at least of order 0.

2- 

Multiplicative polynomial of degree 1: For $\mathfrak{h}\left(\varkappa \right)={\varkappa }_{*}=\varkappa$, we have

$${\mathcal{T}}_{*}\left({\varkappa }_{*}\right)=\sqrt{\mathfrak{h}\left(\mathfrak{a}\right)\mathfrak{h}\left(\mathfrak{b}\right)}=\sqrt{\mathfrak{a}\mathfrak{b}},$$

which is equal to ${\mathcal{I}}_{*}\left({\varkappa }_{*}\right)$ given by (5). Thus, the multiplicative trapezium formula is at least of order 1.

3- 

Multiplicative polynomial of degree 2: Let $\mathfrak{h}\left(\varkappa \right)={\varkappa }^{2_{*}}=exp\left\{{\left(ln\varkappa \right)}^2\right\}$. Then, we have

$${\mathcal{T}}_{*}\left({\varkappa }^{2_{*}}\right)=\sqrt{\mathfrak{h}\left(\mathfrak{a}\right)\mathfrak{h}\left(\mathfrak{b}\right)}=\sqrt{exp\left\{{\left(ln\left(\mathfrak{a}\right)\right)}^2+{\left(ln\left(\mathfrak{b}\right)\right)}^2\right\}}=exp\left\{{\displaystyle \frac{{\left(ln\left(\mathfrak{a}\right)\right)}^2+{\left(ln\left(\mathfrak{b}\right)\right)}^2}{2}}\right\}.$$

Since ${\mathcal{T}}_{*}\left({\varkappa }^{2_{*}}\right)\ne {\mathcal{I}}_{*}\left({\varkappa }^{2_{*}}\right)$, the multiplicative trapezium formula is not exact for multiplicative polynomials of degree 2. Therefore, the formula is indeed of order 1.

Thus, the proof is completed. □

3.2. Convexity in the Framework of Multiplicative Calculus

Having established the key quadrature formulas, we now define and analyze the appropriate notion of convexity in the context of multiplicative calculus, which will serve as a foundation for deriving the main results in the next section.

Let us begin by recalling the definition and some properties of $GA$- and $GG$-convex functions.

Definition 10 

([23]). A function $\mathfrak{h}:\mathbb{R}\to {\mathbb{R}}_{*}$ is said to be $GA$-convex on $[\mathfrak{a},\mathfrak{b}]\subset \mathbb{R}$, if the following inequality,

$$\mathfrak{h}\left({\varkappa }^{\mathsf{\ell }}{\varpi }^{(1-\mathsf{\ell })}\right)\le \mathsf{\ell }\mathfrak{h}\left(\varkappa \right)+\left(1-\mathsf{\ell }\right)\mathfrak{h}\left(\varpi \right),$$

holds true for all $\varkappa ,\varpi \in [\mathfrak{a},\mathfrak{b}]$ and all $\mathsf{\ell }\in [0,1]$.

Definition 11 

([23]). A function $\mathfrak{h}:{\mathbb{R}}_{*}\to {\mathbb{R}}_{*}$ is said to be $GG$-convex on $[\mathfrak{a},\mathfrak{b}]\subset {\mathbb{R}}_{*}$, if the following inequality,

$$\mathfrak{h}\left({\varkappa }^{\mathsf{\ell }}{\varpi }^{(1-\mathsf{\ell })}\right)\le {\left(\mathfrak{h}\left(\varkappa \right)\right)}^{\mathsf{\ell }}{\left(\mathfrak{h}\left(\varpi \right)\right)}^{\left(1-\mathsf{\ell }\right)},$$

holds true for all $\varkappa ,\varpi \in [\mathfrak{a},\mathfrak{b}]$ and all $\mathsf{\ell }\in [0,1]$.

Remark 3 

([23]). A function $\mathfrak{h}:I\subset {\mathbb{R}}_{*}\to {\mathbb{R}}_{*}$ is $GG$-convex on I if and only if $ln\circ \mathfrak{h}$ is $GA$-convex on I.

Remark 4 

([24]). Every real analytic function $\mathfrak{h}\left(\varkappa \right)={\displaystyle \sum _{n=0}^{\infty }}{\mathfrak{c}}_n{\varkappa }^n$ with non-negative coefficients ${\mathfrak{c}}_n$ is $GG$-convex on $(0,\mathit{R})$, where $\mathit{R}$ denotes the radius of convergence. Thus, we have the following examples of $GG$-convex functions:

• Every polynomial $P\left(\varkappa \right)$ with non-negative coefficients is a $GG$-convex function on $[0,\infty )$;
• $\mathfrak{h}\left(\varkappa \right)=exp\left\{\varkappa \right\}$ is $GG$-convex on $(0,\infty )$;
• $\mathfrak{h}\left(\varkappa \right)=ln\left({\displaystyle \frac{1}{1-\varkappa }}\right)$ is $GG$-convex on $(0,1)$;
• $\mathfrak{h}\left(\varkappa \right)={\displaystyle \frac{1+\varkappa }{1-\varkappa }}$ is $GG$-convex on $(0,1)$.

We now turn our attention to the concept of convexity within the framework of multiplicative calculus.

Definition 12. 

A function $\mathfrak{h}$ is deemed to be multiplicatively convex (called in what follows ∗-convex) on $[\mathfrak{a},\mathfrak{b}]\subset {\mathbb{R}}_{*}$ if for all $\varkappa ,\varpi \in [\mathfrak{a},\mathfrak{b}]$ and $\mathsf{\ell }\in [0,1]$, the inequality

$$\mathfrak{h}\left({\mathsf{\ell }}_{*}{\times }_{*}\varkappa {+}_{*}{(1-\mathsf{\ell })}_{*}\times \varpi \right)\le {\mathsf{\ell }}_{*}{\times }_{*}\mathfrak{h}\left(\varkappa \right){+}_{*}{(1-\mathsf{\ell })}_{*}{\times }_{*}\mathfrak{h}\left(\varpi \right)$$

(7)

holds, where ${\mathfrak{c}}_{*}=exp\left\{\mathfrak{c}\right\}$.

Remark 5. 

By rewriting inequality (7) using standard operations, we see that ∗-convexity coincides precisely with $GG$-convexity.

Proposition 10. 

Let $\mathfrak{h}$ be a twice ∗-differentiable function. If ${\mathfrak{h}}^{**}\ge 0_{*}$, (i.e., ${\mathfrak{h}}^{**}\ge 1$) on $[\mathfrak{a},\mathfrak{b}]\subset {\mathbb{R}}_{*}$, then $\mathfrak{h}$ is ∗-convex on $[\mathfrak{a},\mathfrak{b}]$.

Proof. 

Let ${\mathfrak{h}}^{**}\ge 0_{*}$; then, ${\mathfrak{h}}^{*}$ is ∗-increasing. So, from the multiplicative Lagrange Theorem [6], we have, for $\mu ={\varkappa }^{\mathsf{\ell }}{\varpi }^{(1-\mathsf{\ell })}$ with $\mathsf{\ell }\in [0,1]$,

$${\left({\displaystyle \frac{\mathfrak{h}\left(\mu \right)}{\mathfrak{h}\left(\varkappa \right)}}\right)}^{{\displaystyle \frac{1}{ln\left(\mu \right)-ln\left(\varkappa \right)}}}\le {\left({\displaystyle \frac{\mathfrak{h}\left(\varpi \right)}{\mathfrak{h}\left(\mu \right)}}\right)}^{{\displaystyle \frac{1}{ln\left(\varpi \right)-ln\left(\mu \right)}}},$$

which can be written as

$${\left({\displaystyle \frac{\mathfrak{h}\left(\mu \right)}{\mathfrak{h}\left(\varkappa \right)}}\right)}^{ln\left(\varpi \right)-ln\left(\mu \right)}\le {\left({\displaystyle \frac{\mathfrak{h}\left(\varpi \right)}{\mathfrak{h}\left(\mu \right)}}\right)}^{ln\left(\mu \right)-ln\left(\varkappa \right)}.$$

(8)

Expanding and rearranging, (8) yields

$${\left(\mathfrak{h}\left(\mu \right)\right)}^{ln\left(\varpi \right)-ln\left(\varkappa \right)}\le {\left(\mathfrak{h}\left(\varkappa \right)\right)}^{ln\left(\varpi \right)-ln\left(\mu \right)}{\left(\mathfrak{h}\left(\varpi \right)\right)}^{ln\left(\mu \right)-ln\left(\varkappa \right)}.$$

Finally, we obtain

$$\begin{array}{cc}\hfill \mathfrak{h}\left({\varkappa }^{\mathsf{\ell }}{\varpi }^{(1-\mathsf{\ell })}\right)=\mathfrak{h}\left(\mu \right)\le & {\left(\mathfrak{h}\left(\varkappa \right)\right)}^{{\displaystyle \frac{ln\left(\varpi \right)-ln\left(\mu \right)}{ln\left(\varpi \right)-ln\left(\varkappa \right)}}}{\left(\mathfrak{h}\left(\varpi \right)\right)}^{{\displaystyle \frac{ln\left(\mu \right)-ln\left(\varkappa \right)}{ln\left(\varpi \right)-ln\left(\varkappa \right)}}}\hfill \\ \hfill =& {\left(\mathfrak{h}\left(\varkappa \right)\right)}^{{\displaystyle \frac{ln\left(\frac{\varpi }{\mu }\right)}{ln\left(\frac{\varpi }{\varkappa }\right)}}}{\left(\mathfrak{h}\left(\varpi \right)\right)}^{{\displaystyle \frac{ln\left(\frac{\mu }{\varkappa }\right)}{ln\left(\frac{\varpi }{\varkappa }\right)}}}\hfill \\ \hfill =& {\left(\mathfrak{h}\left(\varkappa \right)\right)}^{\mathsf{\ell }}{\left(\mathfrak{h}\left(\varpi \right)\right)}^{\left(1-\mathsf{\ell }\right)}.\hfill \end{array}$$

Thus, the implication ${\mathfrak{h}}^{**}\ge 0_{*}\Rightarrow$$\mathfrak{h}$ is $GG$-convex has been proved. □

Proposition 10 provides a simpler way to verify that a given function is $GG$-convex, as illustrated in the following proposition.

Proposition 11. 

For $k\in (-\infty ,0]\cup [1,\infty )$, the function $\mathfrak{h}\left(\varkappa \right)={\varkappa }_{*}^k$ is $GG$-convex on $[1,\infty )$.

Proof. 

Consider the function $\mathfrak{h}:[1,\infty )\to {\mathbb{R}}_{*}$, defined by $\mathfrak{h}\left(\varkappa \right)={\varkappa }^{k_{*}}$ with $k\in (-\infty ,0]\cup [1,\infty )$. Then, the first-order multiplicative derivative is given by

$${\mathfrak{h}}^{*}\left(\varkappa \right)={\left(exp\left\{{\left(ln\left(\varkappa \right)\right)}^k\right\}\right)}^{*}=exp\left\{\varkappa \frac{{\left(exp\left\{{\left(ln\left(\varkappa \right)\right)}^k\right\}\right)}^{\prime }}{exp\left\{{\left(ln\left(\varkappa \right)\right)}^k\right\}}\right\}=exp\left\{k{\left(ln\left(\varkappa \right)\right)}^{k-1}\right\}=e^k\odot {\varkappa }^{{(k-1)}_{*}},$$

and the second-order multiplicative derivative is expressed as

$${\mathfrak{h}}^{**}\left(\varkappa \right)={\left(e^k\odot {\varkappa }^{{(k-1)}_{*}}\right)}^{*}=e^k\odot e^{k-1}\odot {\varkappa }^{{(k-2)}_{*}}=exp\left\{k(k-1){\left(ln\varkappa \right)}^{k-2}\right\}.$$

Now, since $k\in (-\infty ,0]\cup [1,\infty )$, and $\varkappa \ge 1$, then

$$k(k-1){\left(ln\varkappa \right)}^{k-2}\ge 0.$$

Consequently, we have

$$exp\left\{k(k-1){\left(ln\varkappa \right)}^{k-2}\right\}\ge 1,\mathrm{which}\mathrm{is}\mathrm{equivalent}\mathrm{to}{\mathfrak{h}}^{**}\left(\varkappa \right)\ge 0_{*}.$$

The proof is completed. □

4. Multiplicative Hermite–Hadamard-Type Inequalities

Building on the previous section, we now derive multiplicative versions of important integral inequalities, extending classical results such as Hermite–Hadamard, midpoint, and trapezoid-type inequalities to the non-Newtonian setting.

4.1. Multiplicative Hermite–Hadamard Inequality

We start by presenting multiplicative versions of the classical Hermite–Hadamard inequality, which plays a central role in the derivation of other related inequalities.

Theorem 3. 

Let $\mathfrak{h}:[\mathfrak{a},\mathfrak{b}]\subset {\mathbb{R}}_{*}\to {\mathbb{R}}_{*}$ be an ∗-integrable multiplicative function. If $\mathfrak{h}$ is $GG$-convex on $[\mathfrak{a},\mathfrak{b}]$, then the following Hermite–Hadamard inequality for multiplicative integrals holds:

$$\mathfrak{h}\left(\sqrt{\mathfrak{a}\mathfrak{b}}\right)\le {\left[\left({}_{*}\mathcal{R}_{{\sqrt{\mathfrak{a}\mathfrak{b}}}^{+}}^{\alpha }\mathfrak{h}\left(\mathfrak{b}\right)\right)\left({}_{*}\mathcal{R}_{{\sqrt{\mathfrak{a}\mathfrak{b}}}^{-}}^{\alpha }\mathfrak{h}\left(\mathfrak{a}\right)\right)\right]}^{\frac{2^{\alpha -1}\Gamma (\alpha +1)}{{(ln\mathfrak{b}-ln\mathfrak{a})}^{\alpha }}}\le \sqrt{\mathfrak{h}\left(\mathfrak{a}\right)\mathfrak{h}\left(\mathfrak{b}\right)},$$

(9)

where ${}_{*}\mathcal{R}_{a^{+}}^{\alpha }$ and ${}_{*}\mathcal{R}_{b^{-}}^{\alpha }$ are defined as in (1) and (2), respectively.

Proof. 

Let $\mathfrak{u}={\mathfrak{a}}^{\frac{\mathsf{\ell }}{2}}{\mathfrak{b}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}$ and $\mathfrak{v}={\mathfrak{a}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}{\mathfrak{b}}^{\frac{\mathsf{\ell }}{2}}$. Then, from the ∗-convexity of $\mathfrak{h}$, we have

$$\mathfrak{h}\left(\sqrt{\mathfrak{a}\mathfrak{b}}\right)=\mathfrak{h}\left(\sqrt{\mathfrak{u}\mathfrak{v}}\right)\le \sqrt{\mathfrak{h}\left(\mathfrak{u}\right)\mathfrak{h}\left(\mathfrak{v}\right)}=\sqrt{\mathfrak{h}\left({\mathfrak{a}}^{\frac{\mathsf{\ell }}{2}}{\mathfrak{b}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}\right)\mathfrak{h}\left({\mathfrak{a}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}{\mathfrak{b}}^{\frac{\mathsf{\ell }}{2}}\right)}.$$

(10)

By applying the logarithmic function, we obtain the following from inequality (10):

$$ln\left(\mathfrak{h}\left(\sqrt{\mathfrak{a}\mathfrak{b}}\right)\right)\le {\displaystyle \frac{ln\left(\mathfrak{h}\left({\mathfrak{a}}^{\frac{\mathsf{\ell }}{2}}{\mathfrak{b}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}\right)\right)+ln\left(\mathfrak{h}\left({\mathfrak{a}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}{\mathfrak{b}}^{\frac{\mathsf{\ell }}{2}}\right)\right)}{2}}.$$

(11)

By multiplying both sides of (11) by ${\mathsf{\ell }}^{\alpha -1}$, then integrating the resulting inequality with respect to ℓ over $[0,1]$, we obtain

$$\begin{array}{cc}\hfill ln\left(\mathfrak{h}\left(\sqrt{\mathfrak{a}\mathfrak{b}}\right)\right)\le & {\displaystyle \frac{\alpha }{2}}\underset{0}{\stackrel{1}{\int }}\left[ln\left(\mathfrak{h}\left({\mathfrak{a}}^{\frac{\mathsf{\ell }}{2}}{\mathfrak{b}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}\right)\right)+ln\left(\mathfrak{h}\left({\mathfrak{a}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}{\mathfrak{b}}^{\frac{\mathsf{\ell }}{2}}\right)\right)\right]{\mathsf{\ell }}^{\alpha -1}\mathrm{d}\mathsf{\ell }\hfill \\ \hfill =& {\displaystyle \frac{\alpha }{2^{1-\alpha }}}\left[\underset{\sqrt{\mathfrak{a}\mathfrak{b}}}{\stackrel{\mathfrak{b}}{\int }}{\left(ln\mathfrak{b}-ln\varkappa \right)}^{\alpha -1}{\displaystyle \frac{ln\left(\mathfrak{h}\left(\varkappa \right)\right)}{\varkappa {\left(ln\mathfrak{b}-ln\mathfrak{a}\right)}^{\alpha }}}\mathrm{d}\varkappa +\underset{\mathfrak{a}}{\stackrel{\sqrt{\mathfrak{a}\mathfrak{b}}}{\int }}{\left(ln\varkappa -ln\mathfrak{a}\right)}^{\alpha -1}{\displaystyle \frac{ln\left(\mathfrak{h}\left(\varkappa \right)\right)}{\varkappa {\left(ln\mathfrak{b}-ln\mathfrak{a}\right)}^{\alpha }}}\mathrm{d}\varkappa \right]\hfill \\ \hfill =& {\displaystyle \frac{\alpha }{2^{1-\alpha }}}\left[\underset{\sqrt{\mathfrak{a}\mathfrak{b}}}{\stackrel{\mathfrak{b}}{\int }}{\displaystyle \frac{ln\left(\mathfrak{h}{\left(\varkappa \right)}^{\frac{{\left(ln\mathfrak{b}-ln\varkappa \right)}^{\alpha -1}}{{\left(ln\mathfrak{b}-ln\mathfrak{a}\right)}^{\alpha }}}\right)}{\varkappa }}\mathrm{d}\varkappa +\underset{\mathfrak{a}}{\stackrel{\sqrt{\mathfrak{a}\mathfrak{b}}}{\int }}{\displaystyle \frac{ln\left(\mathfrak{h}{\left(\varkappa \right)}^{\frac{{\left(ln\varkappa -ln\mathfrak{a}\right)}^{\alpha -1}}{{\left(ln\mathfrak{b}-ln\mathfrak{a}\right)}^{\alpha }}}\right)}{\varkappa }}\mathrm{d}\varkappa \right].\hfill \end{array}$$

(12)

Applying the exponential function to both sides of (12) yields

$$\begin{array}{cc}\hfill \mathfrak{h}\left(\sqrt{\mathfrak{a}\mathfrak{b}}\right)\le & exp\left\{{\displaystyle \frac{\alpha }{2^{1-\alpha }}}\left[\underset{\sqrt{\mathfrak{a}\mathfrak{b}}}{\stackrel{\mathfrak{b}}{\int }}{\displaystyle \frac{ln\left(\mathfrak{h}{\left(\varkappa \right)}^{\frac{{\left(ln\mathfrak{b}-ln\varkappa \right)}^{\alpha -1}}{{\left(ln\mathfrak{b}-ln\mathfrak{a}\right)}^{\alpha }}}\right)}{\varkappa }}\mathrm{d}\varkappa +\underset{\mathfrak{a}}{\stackrel{\sqrt{\mathfrak{a}\mathfrak{b}}}{\int }}{\displaystyle \frac{ln\left(\mathfrak{h}{\left(\varkappa \right)}^{\frac{{\left(ln\varkappa -ln\mathfrak{a}\right)}^{\alpha -1}}{{\left(ln\mathfrak{b}-ln\mathfrak{a}\right)}^{\alpha }}}\right)}{\varkappa }}\mathrm{d}\varkappa \right]\right\}\hfill \\ \hfill =& {\left[\left(\underset{\sqrt{\mathfrak{a}\mathfrak{b}}}{\stackrel{\mathfrak{b}}{{\int }_{*}}}\mathfrak{h}{\left(\varkappa \right)}^{\frac{{\left(ln\mathfrak{b}-ln\varkappa \right)}^{\alpha -1}}{{\left(ln\mathfrak{b}-ln\mathfrak{a}\right)}^{\alpha }}}\odot {\mathrm{d}}_{*}\varkappa \right)\left(\underset{\mathfrak{a}}{\stackrel{\sqrt{\mathfrak{a}\mathfrak{b}}}{{\int }_{*}}}\mathfrak{h}{\left(\varkappa \right)}^{\frac{{\left(ln\varkappa -ln\mathfrak{a}\right)}^{\alpha -1}}{{\left(ln\mathfrak{b}-ln\mathfrak{a}\right)}^{\alpha }}}\odot {\mathrm{d}}_{*}\varkappa \right)\right]}^{\frac{\alpha }{2^{1-\alpha }}}\hfill \\ \hfill =& {\left[\left(\underset{\sqrt{\mathfrak{a}\mathfrak{b}}}{\stackrel{\mathfrak{b}}{{\int }_{*}}}\mathfrak{h}{\left(\varkappa \right)}^{{\left(ln\mathfrak{b}-ln\varkappa \right)}^{\alpha -1}}\odot {\mathrm{d}}_{*}\varkappa \right)\left(\underset{\mathfrak{a}}{\stackrel{\sqrt{\mathfrak{a}\mathfrak{b}}}{{\int }_{*}}}\mathfrak{h}{\left(\varkappa \right)}^{{\left(ln\varkappa -ln\mathfrak{a}\right)}^{\alpha -1}}\odot {\mathrm{d}}_{*}\varkappa \right)\right]}^{\frac{2^{\alpha -1}\alpha }{{\left(ln\mathfrak{b}-ln\mathfrak{a}\right)}^{\alpha }}}\hfill \\ \hfill =& exp\left\{{\displaystyle \frac{2^{\alpha -1}\Gamma (\alpha +1)}{{\left(ln\mathfrak{b}-ln\mathfrak{a}\right)}^{\alpha }}}\left[{\displaystyle \frac{1}{\Gamma \left(\alpha \right)}}\underset{\sqrt{\mathfrak{a}\mathfrak{b}}}{\stackrel{\mathfrak{b}}{\int }}{\left(ln\mathfrak{b}-ln\varkappa \right)}^{\alpha -1}{\displaystyle \frac{ln\mathfrak{h}\left(\varkappa \right)}{\varkappa }}\mathrm{d}\varkappa +{\displaystyle \frac{1}{\Gamma \left(\alpha \right)}}\underset{\mathfrak{a}}{\stackrel{\sqrt{\mathfrak{a}\mathfrak{b}}}{\int }}{\left(ln\varkappa -ln\mathfrak{a}\right)}^{\alpha -1}{\displaystyle \frac{ln\mathfrak{h}\left(\varkappa \right)}{\varkappa }}\mathrm{d}\varkappa \right]\right\}\hfill \\ \hfill =& {\left[\left({}_{*}\mathcal{R}_{{\sqrt{\mathfrak{a}\mathfrak{b}}}^{+}}^{\alpha }\mathfrak{h}\left(\mathfrak{b}\right)\right)\left({}_{*}\mathcal{R}_{{\sqrt{\mathfrak{a}\mathfrak{b}}}^{-}}^{\alpha }\mathfrak{h}\left(\mathfrak{a}\right)\right)\right]}^{\frac{2^{\alpha -1}\Gamma (\alpha +1)}{{(ln\mathfrak{b}-ln\mathfrak{a})}^{\alpha }}}.\hfill \end{array}$$

(13)

The ∗-convexity of $\mathfrak{h}$ implies

$$\sqrt{\mathfrak{h}\left({\mathfrak{a}}^{\frac{\mathsf{\ell }}{2}}{\mathfrak{b}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}\right)\mathfrak{h}\left({\mathfrak{a}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}{\mathfrak{b}}^{\frac{\mathsf{\ell }}{2}}\right)}\le \sqrt{\mathfrak{h}{\left(\mathfrak{a}\right)}^{\frac{\mathsf{\ell }}{2}}\mathfrak{h}{\left(\mathfrak{b}\right)}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}\mathfrak{h}{\left(\mathfrak{a}\right)}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}\mathfrak{h}{\left(\mathfrak{b}\right)}^{\frac{\mathsf{\ell }}{2}}}=\sqrt{\mathfrak{h}\left(\mathfrak{a}\right)\mathfrak{h}\left(\mathfrak{b}\right)}.$$

(14)

By applying the logarithmic function, inequality (14) yields

$${\displaystyle \frac{ln\left(\mathfrak{h}\left({\mathfrak{a}}^{\frac{\mathsf{\ell }}{2}}{\mathfrak{b}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}\right)\right)+ln\left(\mathfrak{h}\left({\mathfrak{a}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}{\mathfrak{b}}^{\frac{\mathsf{\ell }}{2}}\right)\right)}{2}}\le ln\left(\sqrt{\mathfrak{h}\left(\mathfrak{a}\right)\mathfrak{h}\left(\mathfrak{b}\right)}\right).$$

(15)

By multiplying both sides of (15) by ${\mathsf{\ell }}^{\alpha -1}$, integrating with respect to ℓ over $[0,1]$ and applying the exponential function, we obtain

$${\left[\left({}_{*}\mathcal{R}_{{\sqrt{\mathfrak{a}\mathfrak{b}}}^{+}}^{\alpha }\mathfrak{h}\left(\mathfrak{b}\right)\right)\left({}_{*}\mathcal{R}_{{\sqrt{\mathfrak{a}\mathfrak{b}}}^{-}}^{\alpha }\mathfrak{h}\left(\mathfrak{a}\right)\right)\right]}^{\frac{2^{\alpha -1}\Gamma (\alpha +1)}{{(ln\mathfrak{b}-ln\mathfrak{a})}^{\alpha }}}\le \sqrt{\mathfrak{h}\left(\mathfrak{a}\right)\mathfrak{h}\left(\mathfrak{b}\right)}.$$

(16)

Inequality (9) may be obtained by combining (13) and (16). □

Corollary 1. 

By setting $\alpha =1$, Theorem 3 yields the following Hermite–Hadamard inequality:

$$\mathfrak{h}\left(\sqrt{\mathfrak{a}\mathfrak{b}}\right)\le {\left(\underset{\mathfrak{a}}{\stackrel{\mathfrak{b}}{{\int }_{*}}}\mathfrak{h}\left(\varkappa \right)\odot {\mathrm{d}}_{*}\varkappa \right)}^{{\displaystyle \frac{1}{ln\mathfrak{b}-ln\mathfrak{a}}}}\le \sqrt{\mathfrak{h}\left(\mathfrak{a}\right)\mathfrak{h}\left(\mathfrak{b}\right)},$$

which was obtained by Dragomir in ([25], Theorem 3).

4.2. Multiplicative Midpoint-Type Inequalities

Building on the results obtained for the Hermite–Hadamard inequality, we now derive midpoint-type inequalities in the multiplicative setting, offering refined bounds under suitable convexity assumptions.

Lemma 1. 

Let $\mathfrak{h}:[\mathfrak{a},\mathfrak{b}]\subset {\mathbb{R}}_{*}\to {\mathbb{R}}_{*}$ be a ∗-differentiable function with ${\mathfrak{h}}^{*}\in L\left([\mathfrak{a},\mathfrak{b}]\right)$ with $\mathfrak{a}\le \mathfrak{b}$. Then, the following multiplicative identity holds:

$$\begin{array}{cc}\hfill {\displaystyle \frac{\mathfrak{h}\left(\sqrt{\mathfrak{a}\mathfrak{b}}\right)}{{\left[\left({}_{*}\mathcal{R}_{{\sqrt{\mathfrak{a}\mathfrak{b}}}^{+}}^{\alpha }\mathfrak{h}\left(\mathfrak{b}\right)\right)\left({}_{*}\mathcal{R}_{{\sqrt{\mathfrak{a}\mathfrak{b}}}^{-}}^{\alpha }\mathfrak{h}\left(\mathfrak{a}\right)\right)\right]}^{\frac{2^{\alpha -1}\Gamma (\alpha +1)}{{(ln\mathfrak{b}-ln\mathfrak{a})}^{\alpha }}}}}=& \sqrt{\underset{0}{\stackrel{1}{{\int }_{*}}}{\left[{\mathfrak{h}}^{*}\left({\mathfrak{a}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}{\mathfrak{b}}^{\frac{\mathsf{\ell }}{2}}\right)\right]}^{{\mathsf{\ell }}^{\alpha }}\odot {\mathrm{d}}_{*}\left({\mathfrak{a}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}{\mathfrak{b}}^{\frac{\mathsf{\ell }}{2}}\right)}\hfill \\ \hfill & \ominus \sqrt{\underset{0}{\stackrel{1}{{\int }_{*}}}{\left[{\mathfrak{h}}^{*}\left({\mathfrak{a}}^{\frac{\mathsf{\ell }}{2}}{\mathfrak{b}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}\right)\right]}^{{\mathsf{\ell }}^{\alpha }}\odot {\mathrm{d}}_{*}\left({\mathfrak{a}}^{\frac{\mathsf{\ell }}{2}}{\mathfrak{b}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}\right)}.\hfill \end{array}$$

Proof. 

Let

$$\mathcal{I}={\mathcal{I}}_1\ominus {\mathcal{I}}_2,$$

(17)

where

$${\mathcal{I}}_1=\sqrt{\underset{0}{\stackrel{1}{{\int }_{*}}}{\left[{\mathfrak{h}}^{*}\left({\mathfrak{a}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}{\mathfrak{b}}^{\frac{\mathsf{\ell }}{2}}\right)\right]}^{{\mathsf{\ell }}^{\alpha }}\odot {\mathrm{d}}_{*}\left({\mathfrak{a}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}{\mathfrak{b}}^{\frac{\mathsf{\ell }}{2}}\right)}$$

and

$${\mathcal{I}}_2=\sqrt{\underset{0}{\stackrel{1}{{\int }_{*}}}{\left[{\mathfrak{h}}^{*}\left({\mathfrak{a}}^{\frac{\mathsf{\ell }}{2}}{\mathfrak{b}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}\right)\right]}^{{\mathsf{\ell }}^{\alpha }}\odot {\mathrm{d}}_{*}\left({\mathfrak{a}}^{\frac{\mathsf{\ell }}{2}}{\mathfrak{b}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}\right)}.$$

By using Proposition 4 along with properties of multiplicative differentiation and integration, we have for ${\mathcal{I}}_1$

$$\begin{array}{cc}\hfill {\mathcal{I}}_1=& \sqrt{\underset{0}{\stackrel{1}{{\int }_{*}}}{\left[{\mathfrak{h}}^{*}\left({\mathfrak{a}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}{\mathfrak{b}}^{\frac{\mathsf{\ell }}{2}}\right)\right]}^{{\mathsf{\ell }}^{\alpha }}\odot {\mathrm{d}}_{*}\left({\mathfrak{a}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}{\mathfrak{b}}^{\frac{\mathsf{\ell }}{2}}\right)}\hfill \\ \hfill =& exp\left\{{\displaystyle \frac{1}{2}}\underset{0}{\stackrel{1}{\int }}{\displaystyle \frac{ln\mathfrak{b}-ln\mathfrak{a}}{2}}ln{\left({\mathfrak{h}}^{*}\left({\mathfrak{a}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}{\mathfrak{b}}^{\frac{\mathsf{\ell }}{2}}\right)\right)}^{{\mathsf{\ell }}^{\alpha }}\mathrm{d}\mathsf{\ell }\right\}\hfill \\ \hfill =& exp\left\{{\displaystyle \frac{1}{4}}\underset{0}{\stackrel{1}{\int }}\left(ln\mathfrak{b}-ln\mathfrak{a}\right){\mathsf{\ell }}^{\alpha }ln\left({\mathfrak{h}}^{*}\left({\mathfrak{a}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}{\mathfrak{b}}^{\frac{\mathsf{\ell }}{2}}\right)\right)\mathrm{d}\mathsf{\ell }\right\}\hfill \\ \hfill =& exp\left\{{\displaystyle \frac{1}{2}}\underset{\mathfrak{a}}{\stackrel{\sqrt{\mathfrak{a}\mathfrak{b}}}{\int }}{\left(2{\displaystyle \frac{ln\varkappa -ln\mathfrak{a}}{ln\mathfrak{b}-ln\mathfrak{a}}}\right)}^{\alpha }{\displaystyle \frac{ln\left({\mathfrak{h}}^{*}\left(\varkappa \right)\right)}{\varkappa }}\mathrm{d}\varkappa \right\}\hfill \\ \hfill =& exp\left\{{\displaystyle \frac{1}{2}}\underset{\mathfrak{a}}{\stackrel{\sqrt{\mathfrak{a}\mathfrak{b}}}{\int }}{\left(2{\displaystyle \frac{ln\varkappa -ln\mathfrak{a}}{ln\mathfrak{b}-ln\mathfrak{a}}}\right)}^{\alpha }{\left(ln\mathfrak{h}\right)}^{\prime }\left(\varkappa \right)\mathrm{d}\varkappa \right\}\hfill \\ \hfill =& exp\left\{2^{\alpha -1}{\left.{\left({\displaystyle \frac{ln\varkappa -ln\mathfrak{a}}{ln\mathfrak{b}-ln\mathfrak{a}}}\right)}^{\alpha }\left(ln\mathfrak{h}\right)\left(\varkappa \right)\right|}_{\mathfrak{a}}^{\sqrt{\mathfrak{a}\mathfrak{b}}}-{\displaystyle \frac{2^{\alpha -1}\alpha }{{\left(ln\mathfrak{b}-ln\mathfrak{a}\right)}^{\alpha }}}\underset{\mathfrak{a}}{\stackrel{\sqrt{\mathfrak{a}\mathfrak{b}}}{\int }}{\left(ln\varkappa -ln\mathfrak{a}\right)}^{\alpha -1}{\displaystyle \frac{ln\mathfrak{h}\left(\varkappa \right)}{\varkappa }}\mathrm{d}\varkappa \right\}\hfill \\ \hfill =& exp\left\{{\displaystyle \frac{ln\mathfrak{h}\left(\sqrt{\mathfrak{a}\mathfrak{b}}\right)}{2}}-{\displaystyle \frac{2^{\alpha -1}\Gamma (\alpha +1)}{{\left(ln\mathfrak{b}-ln\mathfrak{a}\right)}^{\alpha }}}\left({\displaystyle \frac{1}{\Gamma \left(\alpha \right)}}\underset{\mathfrak{a}}{\stackrel{\sqrt{\mathfrak{a}\mathfrak{b}}}{\int }}{\left(ln\varkappa -ln\mathfrak{a}\right)}^{\alpha -1}{\displaystyle \frac{ln\mathfrak{h}\left(\varkappa \right)}{\varkappa }}\mathrm{d}\varkappa \right)\right\}\hfill \\ \hfill =& {\displaystyle \frac{\sqrt{\mathfrak{h}\left(\sqrt{\mathfrak{a}\mathfrak{b}}\right)}}{{\left({}_{*}\mathcal{R}_{{\sqrt{\mathfrak{a}\mathfrak{b}}}^{-}}^{\alpha }\mathfrak{h}\left(\mathfrak{a}\right)\right)}^{\frac{2^{\alpha -1}\Gamma (\alpha +1)}{{(ln\mathfrak{b}-ln\mathfrak{a})}^{\alpha }}}}}.\hfill \end{array}$$

(18)

Similarly,

$$\begin{array}{cc}\hfill {\mathcal{I}}_2=& \sqrt{\underset{0}{\stackrel{1}{{\int }_{*}}}{\left[{\mathfrak{h}}^{*}\left({\mathfrak{a}}^{\frac{\mathsf{\ell }}{2}}{\mathfrak{b}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}\right)\right]}^{{\mathsf{\ell }}^{\alpha }}\odot {\mathrm{d}}_{*}\left({\mathfrak{a}}^{\frac{\mathsf{\ell }}{2}}{\mathfrak{b}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}\right)}\hfill \\ \hfill =& exp\left\{{\displaystyle \frac{1}{2}}\underset{0}{\stackrel{1}{\int }}{\displaystyle \frac{ln\mathfrak{a}-ln\mathfrak{b}}{2}}ln{\left({\mathfrak{h}}^{*}\left({\mathfrak{a}}^{\frac{\mathsf{\ell }}{2}}{\mathfrak{b}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}\right)\right)}^{{\mathsf{\ell }}^{\alpha }}\mathrm{d}\mathsf{\ell }\right\}\hfill \\ \hfill =& exp\left\{{\displaystyle \frac{1}{4}}\underset{0}{\stackrel{1}{\int }}\left(ln\mathfrak{a}-ln\mathfrak{b}\right){\mathsf{\ell }}^{\alpha }ln\left({\mathfrak{h}}^{*}\left({\mathfrak{a}}^{\frac{\mathsf{\ell }}{2}}{\mathfrak{b}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}\right)\right)\mathrm{d}\mathsf{\ell }\right\}\hfill \\ \hfill =& exp\left\{{\displaystyle \frac{1}{2}}\underset{\sqrt{\mathfrak{a}\mathfrak{b}}}{\stackrel{\mathfrak{b}}{\int }}{\left(2{\displaystyle \frac{ln\mathfrak{b}-ln\varkappa }{ln\mathfrak{b}-ln\mathfrak{a}}}\right)}^{\alpha }{\displaystyle \frac{ln\left({\mathfrak{h}}^{*}\left(\varkappa \right)\right)}{\varkappa }}\mathrm{d}\varkappa \right\}\hfill \\ \hfill =& exp\left\{{\displaystyle \frac{1}{2}}\underset{\sqrt{\mathfrak{a}\mathfrak{b}}}{\stackrel{\mathfrak{b}}{\int }}{\left(2{\displaystyle \frac{ln\varkappa -ln\mathfrak{a}}{ln\mathfrak{b}-ln\mathfrak{a}}}\right)}^{\alpha }{\left(ln\mathfrak{h}\right)}^{\prime }\left(\varkappa \right)\mathrm{d}\varkappa \right\}\hfill \\ \hfill =& exp\left\{{\left.2^{\alpha -1}{\left({\displaystyle \frac{ln\mathfrak{b}-ln\varkappa }{ln\mathfrak{b}-ln\mathfrak{a}}}\right)}^{\alpha }\left(ln\mathfrak{h}\right)\left(\varkappa \right)\right|}_{\sqrt{\mathfrak{a}\mathfrak{b}}}^{\mathfrak{b}}+{\displaystyle \frac{2^{\alpha -1}\alpha }{{\left(ln\mathfrak{b}-ln\mathfrak{a}\right)}^{\alpha }}}\underset{\sqrt{\mathfrak{a}\mathfrak{b}}}{\stackrel{\mathfrak{b}}{\int }}{\left(ln\mathfrak{b}-ln\varkappa \right)}^{\alpha -1}{\displaystyle \frac{ln\mathfrak{h}\left(\varkappa \right)}{\varkappa }}\mathrm{d}\varkappa \right\}\hfill \\ \hfill =& exp\left\{-{\displaystyle \frac{ln\mathfrak{h}\left(\sqrt{\mathfrak{a}\mathfrak{b}}\right)}{2}}+{\displaystyle \frac{2^{\alpha -1}\Gamma (\alpha +1)}{{\left(ln\mathfrak{b}-ln\mathfrak{a}\right)}^{\alpha }}}\left({\displaystyle \frac{1}{\Gamma \left(\alpha \right)}}\underset{\sqrt{\mathfrak{a}\mathfrak{b}}}{\stackrel{\mathfrak{b}}{\int }}{\left(ln\mathfrak{b}-ln\varkappa \right)}^{\alpha -1}{\displaystyle \frac{ln\mathfrak{h}\left(\varkappa \right)}{\varkappa }}\mathrm{d}\varkappa \right)\right\}\hfill \\ \hfill =& {\displaystyle \frac{{\left({}_{*}\mathcal{R}_{{\sqrt{\mathfrak{a}\mathfrak{b}}}^{+}}^{\alpha }\mathfrak{h}\left(\mathfrak{b}\right)\right)}^{\frac{2^{\alpha -1}\Gamma (\alpha +1)}{{(ln\mathfrak{b}-ln\mathfrak{a})}^{\alpha }}}}{\sqrt{\mathfrak{h}\left(\sqrt{\mathfrak{a}\mathfrak{b}}\right)}}}.\hfill \end{array}$$

(19)

The result can be obtained by replacing (18) and (19) in (17). Thus, the proof is completed. □

Theorem 4. 

Let $\mathfrak{h}$ be as in Lemma 1. If ${\left|{\mathfrak{h}}^{*}\right|}_{*}$ is $GG$-convex, then the following multiplicative midpoint inequality holds:

$${\left|{\displaystyle \frac{\mathfrak{h}\left(\sqrt{\mathfrak{a}\mathfrak{b}}\right)}{{\left[\left({}_{*}\mathcal{R}_{{\sqrt{\mathfrak{a}\mathfrak{b}}}^{+}}^{\alpha }\mathfrak{h}\left(\mathfrak{b}\right)\right)\left({}_{*}\mathcal{R}_{{\sqrt{\mathfrak{a}\mathfrak{b}}}^{-}}^{\alpha }\mathfrak{h}\left(\mathfrak{a}\right)\right)\right]}^{\frac{2^{\alpha -1}\Gamma (\alpha +1)}{{(ln\mathfrak{b}-ln\mathfrak{a})}^{\alpha }}}}}\right|}_{*}\le {\left[{\left|{\mathfrak{h}}^{*}\left(\mathfrak{a}\right)\right|}_{*}{\left|{\mathfrak{h}}^{*}\left(\mathfrak{b}\right)\right|}_{*}\right]}^{\frac{ln\mathfrak{b}-ln\mathfrak{a}}{4(\alpha +1)}}.$$

Proof. 

Taking the ∗-absolute value on both sides of the equality given in Lemma 1, and then applying the ∗-triangle inequality, we obtain

$$\begin{array}{cc}\hfill & {\left|{\displaystyle \frac{\mathfrak{h}\left(\sqrt{\mathfrak{a}\mathfrak{b}}\right)}{{\left[\left({}_{*}\mathcal{R}_{{\sqrt{\mathfrak{a}\mathfrak{b}}}^{+}}^{\alpha }\mathfrak{h}\left(\mathfrak{b}\right)\right)\left({}_{*}\mathcal{R}_{{\sqrt{\mathfrak{a}\mathfrak{b}}}^{-}}^{\alpha }\mathfrak{h}\left(\mathfrak{a}\right)\right)\right]}^{\frac{2^{\alpha -1}\Gamma (\alpha +1)}{{(ln\mathfrak{b}-ln\mathfrak{a})}^{\alpha }}}}}\right|}_{*}\hfill \\ \hfill \le & {\left|\sqrt{\underset{0}{\stackrel{1}{{\int }_{*}}}{\left[{\mathfrak{h}}^{*}\left({\mathfrak{a}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}{\mathfrak{b}}^{\frac{\mathsf{\ell }}{2}}\right)\right]}^{{\mathsf{\ell }}^{\alpha }}\odot {\mathrm{d}}_{*}\left({\mathfrak{a}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}{\mathfrak{b}}^{\frac{\mathsf{\ell }}{2}}\right)}\right|}_{*}\times {\left|\sqrt{\underset{0}{\stackrel{1}{{\int }_{*}}}{\left({\mathfrak{h}}^{*}\left({\mathfrak{a}}^{\frac{\mathsf{\ell }}{2}}{\mathfrak{b}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}\right)\right)}^{{\mathsf{\ell }}^{\alpha }}\odot {\mathrm{d}}_{*}\left({\mathfrak{a}}^{\frac{\mathsf{\ell }}{2}}{\mathfrak{b}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}\right)}\right|}_{*}\hfill \\ \hfill =& {\left|exp\left\{{\displaystyle \frac{ln\mathfrak{b}-ln\mathfrak{a}}{4}}\underset{0}{\stackrel{1}{\int }}{\mathsf{\ell }}^{\alpha }ln\left({\mathfrak{h}}^{*}\left({\mathfrak{a}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}{\mathfrak{b}}^{\frac{\mathsf{\ell }}{2}}\right)\right)\mathrm{d}\mathsf{\ell }\right\}\right|}_{*}\times {\left|exp\left\{{\displaystyle \frac{ln\mathfrak{a}-ln\mathfrak{b}}{4}}\underset{0}{\stackrel{1}{\int }}{\mathsf{\ell }}^{\alpha }ln\left({\mathfrak{h}}^{*}\left({\mathfrak{a}}^{\frac{\mathsf{\ell }}{2}}{\mathfrak{b}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}\right)\right)\mathrm{d}\mathsf{\ell }\right\}\right|}_{*}\hfill \\ \hfill =& exp\left\{{\displaystyle \frac{ln\mathfrak{b}-ln\mathfrak{a}}{4}}\left(\left|\underset{0}{\stackrel{1}{\int }}{\mathsf{\ell }}^{\alpha }ln\left({\mathfrak{h}}^{*}\left({\mathfrak{a}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}{\mathfrak{b}}^{\frac{\mathsf{\ell }}{2}}\right)\right)\mathrm{d}\mathsf{\ell }\right|+\left|\underset{0}{\stackrel{1}{\int }}{\mathsf{\ell }}^{\alpha }ln\left({\mathfrak{h}}^{*}\left({\mathfrak{a}}^{\frac{\mathsf{\ell }}{2}}{\mathfrak{b}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}\right)\right)\mathrm{d}\mathsf{\ell }\right|\right)\right\}\hfill \\ \hfill \le & exp\left\{{\displaystyle \frac{ln\mathfrak{b}-ln\mathfrak{a}}{4}}\left(\underset{0}{\stackrel{1}{\int }}{\mathsf{\ell }}^{\alpha }\left|ln\left({\mathfrak{h}}^{*}\left({\mathfrak{a}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}{\mathfrak{b}}^{\frac{\mathsf{\ell }}{2}}\right)\right)\right|\mathrm{d}\mathsf{\ell }+\underset{0}{\stackrel{1}{\int }}{\mathsf{\ell }}^{\alpha }\left|ln\left({\mathfrak{h}}^{*}\left({\mathfrak{a}}^{\frac{\mathsf{\ell }}{2}}{\mathfrak{b}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}\right)\right)\right|\mathrm{d}\mathsf{\ell }\right)\right\}\hfill \\ \hfill =& exp\left\{{\displaystyle \frac{ln\mathfrak{b}-ln\mathfrak{a}}{4}}\left(\underset{0}{\stackrel{1}{\int }}{\mathsf{\ell }}^{\alpha }ln{\left|{\mathfrak{h}}^{*}\left({\mathfrak{a}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}{\mathfrak{b}}^{\frac{\mathsf{\ell }}{2}}\right)\right|}_{*}\mathrm{d}\mathsf{\ell }+\underset{0}{\stackrel{1}{\int }}{\mathsf{\ell }}^{\alpha }ln{\left|{\mathfrak{h}}^{*}\left({\mathfrak{a}}^{\frac{\mathsf{\ell }}{2}}{\mathfrak{b}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}\right)\right|}_{*}\mathrm{d}\mathsf{\ell }\right)\right\}.\hfill \end{array}$$

(20)

Using the $GG$-convexity of ${\left|{\mathfrak{h}}^{*}\right|}_{*}$, (20) yields

$$\begin{array}{cc}\hfill & {\left|{\displaystyle \frac{\mathfrak{h}\left(\sqrt{\mathfrak{a}\mathfrak{b}}\right)}{{\left[\left({}_{*}\mathcal{R}_{{\sqrt{\mathfrak{a}\mathfrak{b}}}^{+}}^{\alpha }\mathfrak{h}\left(\mathfrak{b}\right)\right)\left({}_{*}\mathcal{R}_{{\sqrt{\mathfrak{a}\mathfrak{b}}}^{-}}^{\alpha }\mathfrak{h}\left(\mathfrak{a}\right)\right)\right]}^{\frac{2^{\alpha -1}\Gamma (\alpha +1)}{{(ln\mathfrak{b}-ln\mathfrak{a})}^{\alpha }}}}}\right|}_{*}\hfill \\ \hfill \le & exp\left\{{\displaystyle \frac{ln\mathfrak{b}-ln\mathfrak{a}}{4}}\left(\underset{0}{\stackrel{1}{\int }}{\mathsf{\ell }}^{\alpha }\left[{\displaystyle \frac{1-\mathsf{\ell }}{2}}ln{\left|{\mathfrak{h}}^{*}\left(\mathfrak{a}\right)\right|}_{*}+{\displaystyle \frac{\mathsf{\ell }}{2}}ln{\left|{\mathfrak{h}}^{*}\left(\mathfrak{b}\right)\right|}_{*}\right]\mathrm{d}\mathsf{\ell }+\underset{0}{\stackrel{1}{\int }}{\mathsf{\ell }}^{\alpha }\left[{\displaystyle \frac{\mathsf{\ell }}{2}}ln{\left|{\mathfrak{h}}^{*}\left(\mathfrak{a}\right)\right|}_{*}+{\displaystyle \frac{1-\mathsf{\ell }}{2}}ln{\left|{\mathfrak{h}}^{*}\left(\mathfrak{b}\right)\right|}_{*}\right]\mathrm{d}\mathsf{\ell }\right)\right\}\hfill \\ \hfill =& exp\left\{{\displaystyle \frac{ln\mathfrak{b}-ln\mathfrak{a}}{4}}\underset{0}{\stackrel{1}{\int }}{\mathsf{\ell }}^{\alpha }\left[ln{\left|{\mathfrak{h}}^{*}\left(\mathfrak{a}\right)\right|}_{*}+ln{\left|{\mathfrak{h}}^{*}\left(\mathfrak{b}\right)\right|}_{*}\right]\mathrm{d}\mathsf{\ell }\right\}\hfill \\ \hfill =& exp\left\{{\displaystyle \frac{ln\mathfrak{b}-ln\mathfrak{a}}{4(\alpha +1)}}\left(ln{\left|{\mathfrak{h}}^{*}\left(\mathfrak{a}\right)\right|}_{*}+ln{\left|{\mathfrak{h}}^{*}\left(\mathfrak{b}\right)\right|}_{*}\right)\right\}\hfill \\ \hfill =& {\left({\left|{\mathfrak{h}}^{*}\left(\mathfrak{a}\right)\right|}_{*}{\left|{\mathfrak{h}}^{*}\left(\mathfrak{b}\right)\right|}_{*}\right)}^{\frac{ln\mathfrak{b}-ln\mathfrak{a}}{4(\alpha +1)}}.\hfill \end{array}$$

This completes the proof. □

Corollary 2. 

If we attempt to take $\alpha =1$, Theorem 4 yields the following multiplicative midpoint-type inequality:

$$\mathfrak{h}\left(\sqrt{\mathfrak{a}\mathfrak{b}}\right){\left(\underset{\mathfrak{a}}{\stackrel{\mathfrak{b}}{{\int }_{*}}}\mathfrak{h}\left(\varkappa \right)\odot \mathrm{d}\varkappa \right)}^{{\displaystyle \frac{1}{ln\mathfrak{a}-ln\mathfrak{b}}}}\le {\left({\left|{\mathfrak{h}}^{*}\left(\mathfrak{a}\right)\right|}_{*}{\left|{\mathfrak{h}}^{*}\left(\mathfrak{b}\right)\right|}_{*}\right)}^{\frac{ln\mathfrak{b}-ln\mathfrak{a}}{8}}.$$

Theorem 5. 

Let $\mathfrak{h}$ be as in Lemma 1. If ${\left(ln{\left|{\mathfrak{h}}^{*}\right|}_{*}\right)}^{\mathfrak{q}}$ is $GA$-convex for $\mathfrak{q}>1$, then the following multiplicative midpoint inequality holds:

$${\left|{\displaystyle \frac{\mathfrak{h}\left(\sqrt{\mathfrak{a}\mathfrak{b}}\right)}{{\left[\left({}_{*}\mathcal{R}_{{\sqrt{\mathfrak{a}\mathfrak{b}}}^{+}}^{\alpha }\mathfrak{h}\left(\mathfrak{b}\right)\right)\left({}_{*}\mathcal{R}_{{\sqrt{\mathfrak{a}\mathfrak{b}}}^{-}}^{\alpha }\mathfrak{h}\left(\mathfrak{a}\right)\right)\right]}^{\frac{2^{\alpha -1}\Gamma (\alpha +1)}{{(ln\mathfrak{b}-ln\mathfrak{a})}^{\alpha }}}}}\right|}_{*}\le {\left({\left|{\mathfrak{h}}^{*}\left(\mathfrak{a}\right)\right|}_{*}{\left|{\mathfrak{h}}^{*}\left(\mathfrak{b}\right)\right|}_{*}\right)}^{\frac{ln\mathfrak{b}-ln\mathfrak{a}}{2^{\frac{\mathfrak{q}+2}{\mathfrak{q}}}{\left(\alpha \mathfrak{p}+1\right)}^{\frac{1}{\mathfrak{p}}}}},$$

where $\mathfrak{p}\mathfrak{q}=\mathfrak{p}+\mathfrak{q}$.

Proof. 

By using Hölder inequality, inequality (20) gives

$$\begin{array}{cc}\hfill & {\left|{\displaystyle \frac{\mathfrak{h}\left(\sqrt{\mathfrak{a}\mathfrak{b}}\right)}{{\left[\left({}_{*}\mathcal{R}_{{\sqrt{\mathfrak{a}\mathfrak{b}}}^{+}}^{\alpha }\mathfrak{h}\left(\mathfrak{b}\right)\right)\left({}_{*}\mathcal{R}_{{\sqrt{\mathfrak{a}\mathfrak{b}}}^{-}}^{\alpha }\mathfrak{h}\left(\mathfrak{a}\right)\right)\right]}^{\frac{2^{\alpha -1}\Gamma (\alpha +1)}{{(ln\mathfrak{b}-ln\mathfrak{a})}^{\alpha }}}}}\right|}_{*}\hfill \\ \hfill \le & exp\left\{{\displaystyle \frac{ln\mathfrak{b}-ln\mathfrak{a}}{4}}{\left(\underset{0}{\stackrel{1}{\int }}{\mathsf{\ell }}^{\alpha \mathfrak{p}}\mathrm{d}\mathsf{\ell }\right)}^{{\displaystyle \frac{1}{\mathfrak{p}}}}\left[{\left(\underset{0}{\stackrel{1}{\int }}{\left(ln{\left|{\mathfrak{h}}^{*}\left({\mathfrak{a}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}{\mathfrak{b}}^{\frac{\mathsf{\ell }}{2}}\right)\right|}_{*}\right)}^{\mathfrak{q}}\mathrm{d}\mathsf{\ell }\right)}^{{\displaystyle \frac{1}{\mathfrak{q}}}}+{\left(\underset{0}{\stackrel{1}{\int }}{\left(ln{\left|{\mathfrak{h}}^{*}\left({\mathfrak{a}}^{\frac{\mathsf{\ell }}{2}}{\mathfrak{b}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}\right)\right|}_{*}\right)}^{\mathfrak{q}}\mathrm{d}\mathsf{\ell }\right)}^{{\displaystyle \frac{1}{\mathfrak{q}}}}\right]\right\}.\hfill \end{array}$$

(21)

Since ${\left(ln{\left|{\mathfrak{h}}^{*}\right|}_{*}\right)}^{\mathfrak{q}}$ is $GA$-convex, inequality (21) yields

$$\begin{array}{cc}\hfill & {\left|{\displaystyle \frac{\mathfrak{h}\left(\sqrt{\mathfrak{a}\mathfrak{b}}\right)}{{\left[\left({}_{*}\mathcal{R}_{{\sqrt{\mathfrak{a}\mathfrak{b}}}^{+}}^{\alpha }\mathfrak{h}\left(\mathfrak{b}\right)\right)\left({}_{*}\mathcal{R}_{{\sqrt{\mathfrak{a}\mathfrak{b}}}^{-}}^{\alpha }\mathfrak{h}\left(\mathfrak{a}\right)\right)\right]}^{\frac{2^{\alpha -1}\Gamma (\alpha +1)}{{(ln\mathfrak{b}-ln\mathfrak{a})}^{\alpha }}}}}\right|}_{*}\hfill \\ \hfill \le & exp\left\{{\displaystyle \frac{ln\mathfrak{b}-ln\mathfrak{a}}{4{\left(\alpha \mathfrak{p}+1\right)}^{\frac{1}{\mathfrak{p}}}}}\left[\begin{array}{c}{\left(\underset{0}{\stackrel{1}{\int }}\left[{\displaystyle \frac{1-\mathsf{\ell }}{2}}{\left(ln{\left|{\mathfrak{h}}^{*}\left(\mathfrak{a}\right)\right|}_{*}\right)}^{\mathfrak{q}}+{\displaystyle \frac{\mathsf{\ell }}{2}}{\left(ln{\left|{\mathfrak{h}}^{*}\left(\mathfrak{b}\right)\right|}_{*}\right)}^{\mathfrak{q}}\right]\mathrm{d}\mathsf{\ell }\right)}^{{\displaystyle \frac{1}{\mathfrak{q}}}}\hfill \\ +{\left(\underset{0}{\stackrel{1}{\int }}\left[{\displaystyle \frac{\mathsf{\ell }}{2}}{\left(ln{\left|{\mathfrak{h}}^{*}\left(\mathfrak{a}\right)\right|}_{*}\right)}^{\mathfrak{q}}+{\displaystyle \frac{1-\mathsf{\ell }}{2}}{\left(ln{\left|{\mathfrak{h}}^{*}\left(\mathfrak{b}\right)\right|}_{*}\right)}^{\mathfrak{q}}\right]\mathrm{d}\mathsf{\ell }\right)}^{{\displaystyle \frac{1}{\mathfrak{q}}}}\hfill \end{array}\right]\right\}\hfill \\ \hfill =& exp\left\{{\displaystyle \frac{ln\mathfrak{b}-ln\mathfrak{a}}{2{\left(\alpha \mathfrak{p}+1\right)}^{\frac{1}{\mathfrak{p}}}}}{\left({\displaystyle \frac{{\left(ln{\left|{\mathfrak{h}}^{*}\left(\mathfrak{a}\right)\right|}_{*}\right)}^{\mathfrak{q}}+{\left(ln{\left|{\mathfrak{h}}^{*}\left(\mathfrak{b}\right)\right|}_{*}\right)}^{\mathfrak{q}}}{4}}\right)}^{{\displaystyle \frac{1}{\mathfrak{q}}}}\right\}\hfill \\ \hfill \le & exp\left\{{\displaystyle \frac{ln\mathfrak{b}-ln\mathfrak{a}}{2^{\frac{\mathfrak{q}+2}{\mathfrak{q}}}{\left(\alpha \mathfrak{p}+1\right)}^{\frac{1}{\mathfrak{p}}}}}\left[ln{\left|{\mathfrak{h}}^{*}\left(\mathfrak{a}\right)\right|}_{*}+ln{\left|{\mathfrak{h}}^{*}\left(\mathfrak{b}\right)\right|}_{*}\right]\right\}\hfill \\ \hfill =& {\left({\left|{\mathfrak{h}}^{*}\left(\mathfrak{a}\right)\right|}_{*}{\left|{\mathfrak{h}}^{*}\left(\mathfrak{b}\right)\right|}_{*}\right)}^{\frac{ln\mathfrak{b}-ln\mathfrak{a}}{2^{\frac{\mathfrak{q}+2}{\mathfrak{q}}}{\left(\alpha \mathfrak{p}+1\right)}^{\frac{1}{\mathfrak{p}}}}},\hfill \end{array}$$

where we have used the fact that ${\mathcal{E}}^{\mathfrak{q}}+{\mathcal{F}}^{\mathfrak{q}}\le {\left(\mathcal{E}+\mathcal{F}\right)}^{\mathfrak{q}}$ for $\mathcal{E},\mathcal{F}>0$ and $\mathfrak{q}>1$. This completes the proof. □

Theorem 6. 

Let $\mathfrak{h}$ be as in Lemma 1. If ${\left(ln{\left|{\mathfrak{h}}^{*}\right|}_{*}\right)}^{\mathfrak{q}}$ is $GA$-convex for $\mathfrak{q}>1$, then the following multiplicative midpoint inequality holds:

$${\left|{\displaystyle \frac{\mathfrak{h}\left(\sqrt{\mathfrak{a}\mathfrak{b}}\right)}{{\left[\left({}_{*}\mathcal{R}_{{\sqrt{\mathfrak{a}\mathfrak{b}}}^{+}}^{\alpha }\mathfrak{h}\left(\mathfrak{b}\right)\right)\left({}_{*}\mathcal{R}_{{\sqrt{\mathfrak{a}\mathfrak{b}}}^{-}}^{\alpha }\mathfrak{h}\left(\mathfrak{a}\right)\right)\right]}^{\frac{2^{\alpha -1}\Gamma (\alpha +1)}{{(ln\mathfrak{b}-ln\mathfrak{a})}^{\alpha }}}}}\right|}_{*}\le {\left({\left|{\mathfrak{h}}^{*}\left(\mathfrak{a}\right)\right|}_{*}{\left|{\mathfrak{h}}^{*}\left(\mathfrak{b}\right)\right|}_{*}\right)}^{\frac{ln\mathfrak{b}-ln\mathfrak{a}}{2^{2+\frac{1}{\mathfrak{q}}}(\alpha +1)}\left(\frac{1+{(\alpha +1)}^{\frac{1}{\mathfrak{q}}}}{{\left(\alpha +2\right)}^{\frac{1}{\mathfrak{q}}}}\right)}.$$

Proof. 

By using power mean inequality, inequality (20) gives

$$\begin{array}{cc}\hfill & {\left|{\displaystyle \frac{\mathfrak{h}\left(\sqrt{\mathfrak{a}\mathfrak{b}}\right)}{{\left[\left({}_{*}\mathcal{R}_{{\sqrt{\mathfrak{a}\mathfrak{b}}}^{+}}^{\alpha }\mathfrak{h}\left(\mathfrak{b}\right)\right)\left({}_{*}\mathcal{R}_{{\sqrt{\mathfrak{a}\mathfrak{b}}}^{-}}^{\alpha }\mathfrak{h}\left(\mathfrak{a}\right)\right)\right]}^{\frac{2^{\alpha -1}\Gamma (\alpha +1)}{{(ln\mathfrak{b}-ln\mathfrak{a})}^{\alpha }}}}}\right|}_{*}\hfill \\ \hfill \le & exp\left\{{\displaystyle \frac{ln\mathfrak{b}-ln\mathfrak{a}}{4}}{\left(\underset{0}{\stackrel{1}{\int }}{\mathsf{\ell }}^{\alpha }\mathrm{d}\mathsf{\ell }\right)}^{1-{\displaystyle \frac{1}{\mathfrak{q}}}}\left[\begin{array}{c}{\left(\underset{0}{\stackrel{1}{\int }}{\mathsf{\ell }}^{\alpha }{\left(ln{\left|{\mathfrak{h}}^{*}\left({\mathfrak{a}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}{\mathfrak{b}}^{\frac{\mathsf{\ell }}{2}}\right)\right|}_{*}\right)}^{\mathfrak{q}}\mathrm{d}\mathsf{\ell }\right)}^{{\displaystyle \frac{1}{\mathfrak{q}}}}\hfill \\ +{\left(\underset{0}{\stackrel{1}{\int }}{\mathsf{\ell }}^{\alpha }{\left(ln{\left|{\mathfrak{h}}^{*}\left({\mathfrak{a}}^{\frac{\mathsf{\ell }}{2}}{\mathfrak{b}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}\right)\right|}_{*}\right)}^{\mathfrak{q}}\mathrm{d}\mathsf{\ell }\right)}^{{\displaystyle \frac{1}{\mathfrak{q}}}}\hfill \end{array}\right]\right\}.\hfill \end{array}$$

(22)

Since ${\left(ln{\left|{\mathfrak{h}}^{*}\right|}_{*}\right)}^{\mathfrak{q}}$ is $GA$-convex, inequality (21) yields

$$\begin{array}{cc}\hfill & {\left|{\displaystyle \frac{\mathfrak{h}\left(\sqrt{\mathfrak{a}\mathfrak{b}}\right)}{{\left[\left({}_{*}\mathcal{R}_{{\sqrt{\mathfrak{a}\mathfrak{b}}}^{+}}^{\alpha }\mathfrak{h}\left(\mathfrak{b}\right)\right)\left({}_{*}\mathcal{R}_{{\sqrt{\mathfrak{a}\mathfrak{b}}}^{-}}^{\alpha }\mathfrak{h}\left(\mathfrak{a}\right)\right)\right]}^{\frac{2^{\alpha -1}\Gamma (\alpha +1)}{{(ln\mathfrak{b}-ln\mathfrak{a})}^{\alpha }}}}}\right|}_{*}\hfill \\ \hfill \le & exp\left\{{\displaystyle \frac{ln\mathfrak{b}-ln\mathfrak{a}}{4{\left(\alpha +1\right)}^{1-\frac{1}{\mathfrak{q}}}}}\left[\begin{array}{c}{\left(\underset{0}{\stackrel{1}{\int }}{\mathsf{\ell }}^{\alpha }\left[{\displaystyle \frac{1-\mathsf{\ell }}{2}}{\left(ln{\left|{\mathfrak{h}}^{*}\left(\mathfrak{a}\right)\right|}_{*}\right)}^{\mathfrak{q}}+{\displaystyle \frac{\mathsf{\ell }}{2}}{\left(ln{\left|{\mathfrak{h}}^{*}\left(\mathfrak{b}\right)\right|}_{*}\right)}^{\mathfrak{q}}\right]\mathrm{d}\mathsf{\ell }\right)}^{{\displaystyle \frac{1}{\mathfrak{q}}}}\hfill \\ +{\left(\underset{0}{\stackrel{1}{\int }}{\mathsf{\ell }}^{\alpha }\left[{\displaystyle \frac{\mathsf{\ell }}{2}}{\left(ln{\left|{\mathfrak{h}}^{*}\left(\mathfrak{a}\right)\right|}_{*}\right)}^{\mathfrak{q}}+{\displaystyle \frac{1-\mathsf{\ell }}{2}}{\left(ln{\left|{\mathfrak{h}}^{*}\left(\mathfrak{b}\right)\right|}_{*}\right)}^{\mathfrak{q}}\right]\mathrm{d}\mathsf{\ell }\right)}^{{\displaystyle \frac{1}{\mathfrak{q}}}}\hfill \end{array}\right]\right\}\hfill \\ \hfill =& exp\left\{{\displaystyle \frac{ln\mathfrak{b}-ln\mathfrak{a}}{4{(\alpha +1)}^{1-\frac{1}{\mathfrak{q}}}}}\left[{\left({\displaystyle \frac{{\left(ln{\left|{\mathfrak{h}}^{*}\left(\mathfrak{a}\right)\right|}_{*}\right)}^{\mathfrak{q}}+(\alpha +1){\left(ln{\left|{\mathfrak{h}}^{*}\left(\mathfrak{b}\right)\right|}_{*}\right)}^{\mathfrak{q}}}{2(\alpha +1)(\alpha +2)}}\right)}^{{\displaystyle \frac{1}{\mathfrak{q}}}}+{\left({\displaystyle \frac{(\alpha +1){\left(ln{\left|{\mathfrak{h}}^{*}\left(\mathfrak{a}\right)\right|}_{*}\right)}^{\mathfrak{q}}+{\left(ln{\left|{\mathfrak{h}}^{*}\left(\mathfrak{b}\right)\right|}_{*}\right)}^{\mathfrak{q}}}{2(\alpha +1)(\alpha +2)}}\right)}^{{\displaystyle \frac{1}{\mathfrak{q}}}}\right]\right\}\hfill \\ \hfill \le & exp\left\{{\displaystyle \frac{ln\mathfrak{b}-ln\mathfrak{a}}{2^{2+\frac{1}{\mathfrak{q}}}(\alpha +1)}}\left({\displaystyle \frac{1+{(\alpha +1)}^{\frac{1}{\mathfrak{q}}}}{{\left(\alpha +2\right)}^{\frac{1}{\mathfrak{q}}}}}\right)\left[ln{\left|{\mathfrak{h}}^{*}\left(\mathfrak{a}\right)\right|}_{*}+ln{\left|{\mathfrak{h}}^{*}\left(\mathfrak{b}\right)\right|}_{*}\right]\right\}\hfill \\ \hfill =& {\left({\left|{\mathfrak{h}}^{*}\left(\mathfrak{a}\right)\right|}_{*}{\left|{\mathfrak{h}}^{*}\left(\mathfrak{b}\right)\right|}_{*}\right)}^{\frac{ln\mathfrak{b}-ln\mathfrak{a}}{2^{2+\frac{1}{\mathfrak{q}}}(\alpha +1)}\left(\frac{1+{(\alpha +1)}^{\frac{1}{\mathfrak{q}}}}{{\left(\alpha +2\right)}^{\frac{1}{\mathfrak{q}}}}\right)},\hfill \end{array}$$

where we have used the fact that ${\mathcal{E}}^{\mathfrak{q}}+{\mathcal{F}}^{\mathfrak{q}}\le {\left(\mathcal{E}+\mathcal{F}\right)}^{\mathfrak{q}}$ for $\mathcal{E},\mathcal{F}>0$ and $\mathfrak{q}>1$. This completes the proof. □

4.3. Multiplicative Trapezoid-Type Inequalities

In this subsection, we extend our analysis to trapezoid-type inequalities, establishing multiplicative analogues that mirror their classical counterparts and complement the midpoint-type results.

Lemma 2. 

Let $\mathfrak{h}:[\mathfrak{a},\mathfrak{b}]\subset {\mathbb{R}}_{*}\to {\mathbb{R}}_{*}$ be a ∗-differentiable function with ${\mathfrak{h}}^{*}\in L\left([\mathfrak{a},\mathfrak{b}]\right)$ with $\mathfrak{a}\le \mathfrak{b}$. Then, the following multiplicative identity holds:

$$\begin{array}{cc}\hfill {\displaystyle \frac{\sqrt{\mathfrak{h}\left(\mathfrak{a}\right)\mathfrak{h}\left(\mathfrak{b}\right)}}{{\left[\left({}_{*}\mathcal{R}_{{\sqrt{\mathfrak{a}\mathfrak{b}}}^{+}}^{\alpha }\mathfrak{h}\left(\mathfrak{b}\right)\right)\left({}_{*}\mathcal{R}_{{\sqrt{\mathfrak{a}\mathfrak{b}}}^{-}}^{\alpha }\mathfrak{h}\left(\mathfrak{a}\right)\right)\right]}^{\frac{2^{\alpha -1}\Gamma (\alpha +1)}{{(ln\mathfrak{b}-ln\mathfrak{a})}^{\alpha }}}}}=& \sqrt{\underset{0}{\stackrel{1}{{\int }_{*}}}{\left({\mathfrak{h}}^{*}\left({\mathfrak{a}}^{\frac{\mathsf{\ell }}{2}}{\mathfrak{b}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}\right)\right)}^{1-{\mathsf{\ell }}^{\alpha }}\odot {\mathrm{d}}_{*}\left({\mathfrak{a}}^{\frac{\mathsf{\ell }}{2}}{\mathfrak{b}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}\right)}\hfill \\ \hfill & \ominus \sqrt{\underset{0}{\stackrel{1}{{\int }_{*}}}{\left({\mathfrak{h}}^{*}\left({\mathfrak{a}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}{\mathfrak{b}}^{\frac{\mathsf{\ell }}{2}}\right)\right)}^{1-{\mathsf{\ell }}^{\alpha }}\odot {\mathrm{d}}_{*}\left({\mathfrak{a}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}{\mathfrak{b}}^{\frac{\mathsf{\ell }}{2}}\right)}.\hfill \end{array}$$

Proof. 

Let

$$\mathcal{J}={\mathcal{J}}_1\ominus {\mathcal{J}}_2,$$

(23)

with

$${\mathcal{J}}_1=\sqrt{\underset{0}{\stackrel{1}{{\int }_{*}}}{\left({\mathfrak{h}}^{*}\left({\mathfrak{a}}^{\frac{\mathsf{\ell }}{2}}{\mathfrak{b}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}\right)\right)}^{1-{\mathsf{\ell }}^{\alpha }}\odot {\mathrm{d}}_{*}\left({\mathfrak{a}}^{\frac{\mathsf{\ell }}{2}}{\mathfrak{b}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}\right)}$$

and

$${\mathcal{J}}_2=\sqrt{\underset{0}{\stackrel{1}{{\int }_{*}}}{\left({\mathfrak{h}}^{*}\left({\mathfrak{a}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}{\mathfrak{b}}^{\frac{\mathsf{\ell }}{2}}\right)\right)}^{1-{\mathsf{\ell }}^{\alpha }}\odot {\mathrm{d}}_{*}\left({\mathfrak{a}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}{\mathfrak{b}}^{\frac{\mathsf{\ell }}{2}}\right)}.$$

By using Proposition 4 along with properties of multiplicative differentiation and integration, we obtain for ${\mathcal{J}}_1$

$$\begin{array}{cc}\hfill {\mathcal{J}}_1=& \sqrt{\underset{0}{\stackrel{1}{{\int }_{*}}}{\left({\mathfrak{h}}^{*}\left({\mathfrak{a}}^{\frac{\mathsf{\ell }}{2}}{\mathfrak{b}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}\right)\right)}^{1-{\mathsf{\ell }}^{\alpha }}\odot {\mathrm{d}}_{*}\left({\mathfrak{a}}^{\frac{\mathsf{\ell }}{2}}{\mathfrak{b}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}\right)}\hfill \\ \hfill =& exp\left\{{\displaystyle \frac{1}{2}}\underset{0}{\stackrel{1}{\int }}{\displaystyle \frac{ln\mathfrak{a}-ln\mathfrak{b}}{2}}ln{\left({\mathfrak{h}}^{*}\left({\mathfrak{a}}^{\frac{\mathsf{\ell }}{2}}{\mathfrak{b}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}\right)\right)}^{1-{\mathsf{\ell }}^{\alpha }}\mathrm{d}\mathsf{\ell }\right\}\hfill \\ \hfill =& exp\left\{{\displaystyle \frac{1}{4}}\underset{0}{\stackrel{1}{\int }}\left(ln\mathfrak{a}-ln\mathfrak{b}\right)\left(1-{\mathsf{\ell }}^{\alpha }\right)ln\left({\mathfrak{h}}^{*}\left({\mathfrak{a}}^{\frac{\mathsf{\ell }}{2}}{\mathfrak{b}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}\right)\right)\mathrm{d}\mathsf{\ell }\right\}\hfill \\ \hfill =& exp\left\{{\displaystyle \frac{1}{2}}\underset{\sqrt{\mathfrak{a}\mathfrak{b}}}{\stackrel{\mathfrak{b}}{\int }}\left(1-2{\left({\displaystyle \frac{ln\mathfrak{b}-ln\varkappa }{ln\mathfrak{b}-ln\mathfrak{a}}}\right)}^{\alpha }\right){\displaystyle \frac{ln\left({\mathfrak{h}}^{*}\left(\varkappa \right)\right)}{\varkappa }}\mathrm{d}\varkappa \right\}\hfill \\ \hfill =& exp\left\{{\displaystyle \frac{1}{2}}\underset{\sqrt{\mathfrak{a}\mathfrak{b}}}{\stackrel{\mathfrak{b}}{\int }}\left(1-2{\left({\displaystyle \frac{ln\mathfrak{b}-ln\varkappa }{ln\mathfrak{b}-ln\mathfrak{a}}}\right)}^{\alpha }\right){\left(ln\mathfrak{h}\right)}^{\prime }\left(\varkappa \right)\mathrm{d}\varkappa \right\}\hfill \\ \hfill =& exp\left\{{\displaystyle \frac{1}{2}}{\left.\left(1-2{\left({\displaystyle \frac{ln\mathfrak{b}-ln\varkappa }{ln\mathfrak{b}-ln\mathfrak{a}}}\right)}^{\alpha }\right)\left(ln\mathfrak{h}\right)\left(\varkappa \right)\right|}_{\sqrt{\mathfrak{a}\mathfrak{b}}}^{\mathfrak{b}}-{\displaystyle \frac{2^{\alpha -1}\alpha }{{\left(ln\mathfrak{b}-ln\mathfrak{a}\right)}^{\alpha }}}\underset{\sqrt{\mathfrak{a}\mathfrak{b}}}{\stackrel{\mathfrak{b}}{\int }}{\left(ln\mathfrak{b}-ln\varkappa \right)}^{\alpha -1}{\displaystyle \frac{ln\mathfrak{h}\left(\varkappa \right)}{\varkappa }}\mathrm{d}\varkappa \right\}\hfill \\ \hfill =& exp\left\{{\displaystyle \frac{ln\mathfrak{h}\left(\mathfrak{b}\right)}{2}}-{\displaystyle \frac{2^{\alpha -1}\Gamma (\alpha +1)}{{\left(ln\mathfrak{b}-ln\mathfrak{a}\right)}^{\alpha }}}\left({\displaystyle \frac{1}{\Gamma \left(\alpha \right)}}\underset{\sqrt{\mathfrak{a}\mathfrak{b}}}{\stackrel{\mathfrak{b}}{\int }}{\left(ln\mathfrak{b}-ln\varkappa \right)}^{\alpha -1}{\displaystyle \frac{ln\mathfrak{h}\left(\varkappa \right)}{\varkappa }}\mathrm{d}\varkappa \right)\right\}\hfill \\ \hfill =& {\displaystyle \frac{\sqrt{\mathfrak{h}\left(\mathfrak{b}\right)}}{{\left({}_{*}\mathcal{R}_{{\sqrt{\mathfrak{a}\mathfrak{b}}}^{+}}^{\alpha }\mathfrak{h}\left(\mathfrak{b}\right)\right)}^{\frac{2^{\alpha -1}\Gamma (\alpha +1)}{{(ln\mathfrak{b}-ln\mathfrak{a})}^{\alpha }}}}}.\hfill \end{array}$$

(24)

Similarly,

$$\begin{array}{cc}\hfill {\mathcal{J}}_2=& \sqrt{\underset{0}{\stackrel{1}{{\int }_{*}}}{\left[{\mathfrak{h}}^{*}\left({\mathfrak{a}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}{\mathfrak{b}}^{\frac{\mathsf{\ell }}{2}}\right)\right]}^{1-{\mathsf{\ell }}^{\alpha }}\odot {\mathrm{d}}_{*}\left({\mathfrak{a}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}{\mathfrak{b}}^{\frac{\mathsf{\ell }}{2}}\right)}\hfill \\ \hfill =& exp\left\{{\displaystyle \frac{1}{2}}\underset{0}{\stackrel{1}{\int }}{\displaystyle \frac{ln\mathfrak{b}-ln\mathfrak{a}}{2}}ln{\left({\mathfrak{h}}^{*}\left({\mathfrak{a}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}{\mathfrak{b}}^{\frac{\mathsf{\ell }}{2}}\right)\right)}^{1-{\mathsf{\ell }}^{\alpha }}\mathrm{d}\mathsf{\ell }\right\}\hfill \\ \hfill =& exp\left\{{\displaystyle \frac{1}{4}}\underset{0}{\stackrel{1}{\int }}\left(ln\mathfrak{b}-ln\mathfrak{a}\right)\left(1-{\mathsf{\ell }}^{\alpha }\right)ln\left({\mathfrak{h}}^{*}\left({\mathfrak{a}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}{\mathfrak{b}}^{\frac{\mathsf{\ell }}{2}}\right)\right)\mathrm{d}\mathsf{\ell }\right\}\hfill \\ \hfill =& exp\left\{{\displaystyle \frac{1}{2}}\underset{\mathfrak{a}}{\stackrel{\sqrt{\mathfrak{a}\mathfrak{b}}}{\int }}\left(1-{\left(2{\displaystyle \frac{ln\varkappa -ln\mathfrak{a}}{ln\mathfrak{b}-ln\mathfrak{a}}}\right)}^{\alpha }\right){\displaystyle \frac{ln\left({\mathfrak{h}}^{*}\left(\varkappa \right)\right)}{\varkappa }}\mathrm{d}\varkappa \right\}\hfill \\ \hfill =& exp\left\{{\displaystyle \frac{1}{2}}\underset{\mathfrak{a}}{\stackrel{\sqrt{\mathfrak{a}\mathfrak{b}}}{\int }}\left(1-{\left(2{\displaystyle \frac{ln\varkappa -ln\mathfrak{a}}{ln\mathfrak{b}-ln\mathfrak{a}}}\right)}^{\alpha }\right){\left(ln\mathfrak{h}\right)}^{\prime }\left(\varkappa \right)\mathrm{d}\varkappa \right\}\hfill \\ \hfill =& exp\left\{{\left.{\displaystyle \frac{1}{2}}\left(1-{\left(2{\displaystyle \frac{ln\varkappa -ln\mathfrak{a}}{ln\mathfrak{b}-ln\mathfrak{a}}}\right)}^{\alpha }\right)\left(ln\mathfrak{h}\right)\left(\varkappa \right)\right|}_{\mathfrak{a}}^{\sqrt{\mathfrak{a}\mathfrak{b}}}+{\displaystyle \frac{2^{\alpha -1}\alpha }{{\left(ln\mathfrak{b}-ln\mathfrak{a}\right)}^{\alpha }}}\underset{\mathfrak{a}}{\stackrel{\sqrt{\mathfrak{a}\mathfrak{b}}}{\int }}{\left(ln\varkappa -ln\mathfrak{a}\right)}^{\alpha -1}{\displaystyle \frac{ln\mathfrak{h}\left(\varkappa \right)}{\varkappa }}\mathrm{d}\varkappa \right\}\hfill \\ \hfill =& exp\left\{-{\displaystyle \frac{ln\mathfrak{h}\left(\mathfrak{a}\right)}{2}}+{\displaystyle \frac{2^{\alpha -1}\Gamma (\alpha +1)}{{\left(ln\mathfrak{b}-ln\mathfrak{a}\right)}^{\alpha }}}\left({\displaystyle \frac{1}{\Gamma \left(\alpha \right)}}\underset{\mathfrak{a}}{\stackrel{\sqrt{\mathfrak{a}\mathfrak{b}}}{\int }}{\left(ln\varkappa -ln\mathfrak{a}\right)}^{\alpha -1}{\displaystyle \frac{ln\mathfrak{h}\left(\varkappa \right)}{\varkappa }}\mathrm{d}\varkappa \right)\right\}\hfill \\ \hfill =& {\displaystyle \frac{{\left({}_{*}\mathcal{R}_{{\sqrt{\mathfrak{a}\mathfrak{b}}}^{-}}^{\alpha }\mathfrak{h}\left(\mathfrak{a}\right)\right)}^{\frac{2^{\alpha -1}\Gamma (\alpha +1)}{{(ln\mathfrak{b}-ln\mathfrak{a})}^{\alpha }}}}{\sqrt{\mathfrak{h}\left(\mathfrak{a}\right)}}}.\hfill \end{array}$$

(25)

The result can be obtained by replacing (24) and (25) in (23). Thus, the proof is completed. □

Theorem 7. 

Let $\mathfrak{h}$ be as in Lemma 2. If ${\mathfrak{h}}^{*}$ is $GG$-convex, then the following multiplicative trapezium inequality holds:

$${\left|{\displaystyle \frac{\sqrt{\mathfrak{h}\left(\mathfrak{a}\right)\mathfrak{h}\left(\mathfrak{b}\right)}}{{\left[\left({}_{*}\mathcal{R}_{{\sqrt{\mathfrak{a}\mathfrak{b}}}^{+}}^{\alpha }\mathfrak{h}\left(\mathfrak{b}\right)\right)\left({}_{*}\mathcal{R}_{{\sqrt{\mathfrak{a}\mathfrak{b}}}^{-}}^{\alpha }\mathfrak{h}\left(\mathfrak{a}\right)\right)\right]}^{\frac{2^{\alpha -1}\Gamma (\alpha +1)}{{(ln\mathfrak{b}-ln\mathfrak{a})}^{\alpha }}}}}\right|}_{*}\le {\left({\left|{\mathfrak{h}}^{*}\left(\mathfrak{a}\right)\right|}_{*}{\left|{\mathfrak{h}}^{*}\left(\mathfrak{b}\right)\right|}_{*}\right)}^{\frac{\alpha \left(ln\mathfrak{b}-ln\mathfrak{a}\right)}{4(\alpha +1)}}.$$

Proof. 

We first take the ∗-absolute value of both sides of the equality from Lemma 2, and then apply the ∗-triangle inequality to obtain

$$\begin{array}{cc}\hfill & {\left|{\displaystyle \frac{\sqrt{\mathfrak{h}\left(\mathfrak{a}\right)\mathfrak{h}\left(\mathfrak{b}\right)}}{{\left[\left({}_{*}\mathcal{R}_{{\sqrt{\mathfrak{a}\mathfrak{b}}}^{+}}^{\alpha }\mathfrak{h}\left(\mathfrak{b}\right)\right)\left({}_{*}\mathcal{R}_{{\sqrt{\mathfrak{a}\mathfrak{b}}}^{-}}^{\alpha }\mathfrak{h}\left(\mathfrak{a}\right)\right)\right]}^{\frac{2^{\alpha -1}\Gamma (\alpha +1)}{{(ln\mathfrak{b}-ln\mathfrak{a})}^{\alpha }}}}}\right|}_{*}\hfill \\ \hfill =& {\left|\sqrt{\underset{0}{\stackrel{1}{{\int }_{*}}}{\left({\mathfrak{h}}^{*}\left({\mathfrak{a}}^{\frac{\mathsf{\ell }}{2}}{\mathfrak{b}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}\right)\right)}^{1-{\mathsf{\ell }}^{\alpha }}\odot {\mathrm{d}}_{*}\left({\mathfrak{a}}^{\frac{\mathsf{\ell }}{2}}{\mathfrak{b}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}\right)}\right|}_{*}\times {\left|\sqrt{\underset{0}{\stackrel{1}{{\int }_{*}}}{\left({\mathfrak{h}}^{*}\left({\mathfrak{a}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}{\mathfrak{b}}^{\frac{\mathsf{\ell }}{2}}\right)\right)}^{1-{\mathsf{\ell }}^{\alpha }}\odot {\mathrm{d}}_{*}\left({\mathfrak{a}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}{\mathfrak{b}}^{\frac{\mathsf{\ell }}{2}}\right)}\right|}_{*}\hfill \\ \hfill =& {\left|exp\left\{\underset{0}{\stackrel{1}{\int }}{\displaystyle \frac{ln\mathfrak{a}-ln\mathfrak{b}}{4}}ln{\left({\mathfrak{h}}^{*}\left({\mathfrak{a}}^{\frac{\mathsf{\ell }}{2}}{\mathfrak{b}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}\right)\right)}^{1-{\mathsf{\ell }}^{\alpha }}\mathrm{d}\mathsf{\ell }\right\}\right|}_{*}\times {\left|exp\left\{\underset{0}{\stackrel{1}{\int }}{\displaystyle \frac{ln\mathfrak{b}-ln\mathfrak{a}}{4}}ln{\left({\mathfrak{h}}^{*}\left({\mathfrak{a}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}{\mathfrak{b}}^{\frac{\mathsf{\ell }}{2}}\right)\right)}^{1-{\mathsf{\ell }}^{\alpha }}\mathrm{d}\mathsf{\ell }\right\}\right|}_{*}\hfill \\ \hfill =& exp\left\{\left|\underset{0}{\stackrel{1}{\int }}{\displaystyle \frac{ln\mathfrak{a}-ln\mathfrak{b}}{4}}ln{\left({\mathfrak{h}}^{*}\left({\mathfrak{a}}^{\frac{\mathsf{\ell }}{2}}{\mathfrak{b}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}\right)\right)}^{1-{\mathsf{\ell }}^{\alpha }}\mathrm{d}\mathsf{\ell }\right|+\left|\underset{0}{\stackrel{1}{\int }}{\displaystyle \frac{ln\mathfrak{b}-ln\mathfrak{a}}{4}}ln{\left({\mathfrak{h}}^{*}\left({\mathfrak{a}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}{\mathfrak{b}}^{\frac{\mathsf{\ell }}{2}}\right)\right)}^{1-{\mathsf{\ell }}^{\alpha }}\mathrm{d}\mathsf{\ell }\right|\right\}\hfill \\ \hfill \le & exp\left\{{\displaystyle \frac{ln\mathfrak{b}-ln\mathfrak{a}}{4}}\left(\underset{0}{\stackrel{1}{\int }}\left(1-{\mathsf{\ell }}^{\alpha }\right)\left|ln\left({\mathfrak{h}}^{*}\left({\mathfrak{a}}^{\frac{\mathsf{\ell }}{2}}{\mathfrak{b}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}\right)\right)\right|\mathrm{d}\mathsf{\ell }+\underset{0}{\stackrel{1}{\int }}\left(1-{\mathsf{\ell }}^{\alpha }\right)\left|ln\left({\mathfrak{h}}^{*}\left({\mathfrak{a}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}{\mathfrak{b}}^{\frac{\mathsf{\ell }}{2}}\right)\right)\right|\mathrm{d}\mathsf{\ell }\right)\right\}\hfill \\ \hfill =& exp\left\{{\displaystyle \frac{ln\mathfrak{b}-ln\mathfrak{a}}{4}}\left(\underset{0}{\stackrel{1}{\int }}\left(1-{\mathsf{\ell }}^{\alpha }\right)\left[ln{\left|{\mathfrak{h}}^{*}\left({\mathfrak{a}}^{\frac{\mathsf{\ell }}{2}}{\mathfrak{b}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}\right)\right|}_{*}+ln{\left|{\mathfrak{h}}^{*}\left({\mathfrak{a}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}{\mathfrak{b}}^{\frac{\mathsf{\ell }}{2}}\right)\right|}_{*}\right]\mathrm{d}\mathsf{\ell }\right)\right\}.\hfill \end{array}$$

(26)

Using the $GG$-convexity of ${\left|{\mathfrak{h}}^{*}\right|}_{*}$, (26) yields

$$\begin{array}{cc}\hfill & {\left|{\displaystyle \frac{\sqrt{\mathfrak{h}\left(\mathfrak{a}\right)\mathfrak{h}\left(\mathfrak{b}\right)}}{{\left[\left({}_{*}\mathcal{R}_{{\sqrt{\mathfrak{a}\mathfrak{b}}}^{+}}^{\alpha }\mathfrak{h}\left(\mathfrak{b}\right)\right)\left({}_{*}\mathcal{R}_{{\sqrt{\mathfrak{a}\mathfrak{b}}}^{-}}^{\alpha }\mathfrak{h}\left(\mathfrak{a}\right)\right)\right]}^{\frac{2^{\alpha -1}\Gamma (\alpha +1)}{{(ln\mathfrak{b}-ln\mathfrak{a})}^{\alpha }}}}}\right|}_{*}\hfill \\ \hfill \le & exp\left\{{\displaystyle \frac{ln\mathfrak{b}-ln\mathfrak{a}}{4}}\left(\underset{0}{\stackrel{1}{\int }}\left(1-{\mathsf{\ell }}^{\alpha }\right)\mathrm{d}\mathsf{\ell }\right)\left(ln{\left|{\mathfrak{h}}^{*}\left(\mathfrak{a}\right)\right|}_{*}+ln{\left|{\mathfrak{h}}^{*}\left(\mathfrak{b}\right)\right|}_{*}\right)\right\}\hfill \\ \hfill =& exp\left\{{\displaystyle \frac{\alpha \left(ln\mathfrak{b}-ln\mathfrak{a}\right)}{4(\alpha +1)}}\left[ln{\left|{\mathfrak{h}}^{*}\left(\mathfrak{a}\right)\right|}_{*}+ln{\left|{\mathfrak{h}}^{*}\left(\mathfrak{b}\right)\right|}_{*}\right]\right\}\hfill \\ \hfill =& {\left({\left|{\mathfrak{h}}^{*}\left(\mathfrak{a}\right)\right|}_{*}{\left|{\mathfrak{h}}^{*}\left(\mathfrak{b}\right)\right|}_{*}\right)}^{\frac{\alpha \left(ln\mathfrak{b}-ln\mathfrak{a}\right)}{4(\alpha +1)}}.\hfill \end{array}$$

The proof is completed. □

Corollary 3. 

If we attempt to take $\alpha =1$, Theorem 7 yields the following multiplicative midpoint-type inequality:

$$\sqrt{\mathfrak{h}\left(\mathfrak{a}\right)\mathfrak{h}\left(\mathfrak{b}\right)}{\left(\underset{\mathfrak{a}}{\stackrel{\mathfrak{b}}{{\int }_{*}}}\mathfrak{h}\left(\varkappa \right)\odot \mathrm{d}\varkappa \right)}^{{\displaystyle \frac{1}{ln\mathfrak{a}-ln\mathfrak{b}}}}\le {\left({\left|{\mathfrak{h}}^{*}\left(\mathfrak{a}\right)\right|}_{*}{\left|{\mathfrak{h}}^{*}\left(\mathfrak{b}\right)\right|}_{*}\right)}^{\frac{ln\mathfrak{b}-ln\mathfrak{a}}{8}}.$$

Theorem 8. 

Let $\mathfrak{h}$ be as in Lemma 2. If ${\left(ln{\left|{\mathfrak{h}}^{*}\right|}_{*}\right)}^{\mathfrak{q}}$ is $GA$-convex for $\mathfrak{q}>1$, then the following multiplicative trapezium inequality holds:

$${\left|{\displaystyle \frac{\sqrt{\mathfrak{h}\left(\mathfrak{a}\right)\mathfrak{h}\left(\mathfrak{b}\right)}}{{\left[\left({}_{*}\mathcal{R}_{{\sqrt{\mathfrak{a}\mathfrak{b}}}^{+}}^{\alpha }\mathfrak{h}\left(\mathfrak{b}\right)\right)\left({}_{*}\mathcal{R}_{{\sqrt{\mathfrak{a}\mathfrak{b}}}^{-}}^{\alpha }\mathfrak{h}\left(\mathfrak{a}\right)\right)\right]}^{\frac{2^{\alpha -1}\Gamma (\alpha +1)}{{(ln\mathfrak{b}-ln\mathfrak{a})}^{\alpha }}}}}\right|}_{*}\le {\left({\left|{\mathfrak{h}}^{*}\left(\mathfrak{a}\right)\right|}_{*}{\left|{\mathfrak{h}}^{*}\left(\mathfrak{b}\right)\right|}_{*}\right)}^{\frac{ln\mathfrak{b}-ln\mathfrak{a}}{4^{1+\frac{1}{\mathfrak{q}}}}\left(1+3^{{\displaystyle \frac{1}{\mathfrak{q}}}}\right){\left(\frac{1}{\alpha }B\left({\displaystyle \frac{1}{\alpha }},\mathfrak{p}+1\right)\right)}^{{\displaystyle \frac{1}{\mathfrak{p}}}}},$$

where $\mathfrak{p}\mathfrak{q}=\mathfrak{p}+\mathfrak{q}$, and $B(.,.)$ denotes the Beta function.

Proof. 

By using Hölder inequality, inequality (26) gives

$$\begin{array}{cc}\hfill & {\left|{\displaystyle \frac{\sqrt{\mathfrak{h}\left(\mathfrak{a}\right)\mathfrak{h}\left(\mathfrak{b}\right)}}{{\left[\left({}_{*}\mathcal{R}_{{\sqrt{\mathfrak{a}\mathfrak{b}}}^{+}}^{\alpha }\mathfrak{h}\left(\mathfrak{b}\right)\right)\left({}_{*}\mathcal{R}_{{\sqrt{\mathfrak{a}\mathfrak{b}}}^{-}}^{\alpha }\mathfrak{h}\left(\mathfrak{a}\right)\right)\right]}^{\frac{2^{\alpha -1}\Gamma (\alpha +1)}{{\left(ln\mathfrak{b}-ln\mathfrak{a}\right)}^{\alpha }}}}}\right|}_{*}\hfill \\ \hfill \le & exp\left\{{\displaystyle \frac{ln\mathfrak{b}-ln\mathfrak{a}}{4}}{\left(\underset{0}{\stackrel{1}{\int }}{\left(1-{\mathsf{\ell }}^{\alpha }\right)}^{\mathfrak{p}}\mathrm{d}\mathsf{\ell }\right)}^{{\displaystyle \frac{1}{\mathfrak{p}}}}\left[{\left(\underset{0}{\stackrel{1}{\int }}{\left(ln{\left|{\mathfrak{h}}^{*}\left({\mathfrak{a}}^{\frac{\mathsf{\ell }}{2}}{\mathfrak{b}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}\right)\right|}_{*}\right)}^{\mathfrak{q}}\mathrm{d}\mathsf{\ell }\right)}^{{\displaystyle \frac{1}{\mathfrak{q}}}}+{\left(\underset{0}{\stackrel{1}{\int }}{\left(ln{\left|{\mathfrak{h}}^{*}\left({\mathfrak{a}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}{\mathfrak{b}}^{\frac{\mathsf{\ell }}{2}}\right)\right|}_{*}\right)}^{\mathfrak{q}}\mathrm{d}\mathsf{\ell }\right)}^{{\displaystyle \frac{1}{\mathfrak{q}}}}\right]\right\}\hfill \\ \hfill =& exp\left\{{\displaystyle \frac{ln\mathfrak{b}-ln\mathfrak{a}}{4}}{\left({\displaystyle \frac{1}{\alpha }}B\left({\displaystyle \frac{1}{\alpha }},\mathfrak{p}+1\right)\right)}^{{\displaystyle \frac{1}{\mathfrak{p}}}}\left[{\left(\underset{0}{\stackrel{1}{\int }}{\left(ln{\left|{\mathfrak{h}}^{*}\left({\mathfrak{a}}^{\frac{\mathsf{\ell }}{2}}{\mathfrak{b}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}\right)\right|}_{*}\right)}^{\mathfrak{q}}\mathrm{d}\mathsf{\ell }\right)}^{{\displaystyle \frac{1}{\mathfrak{q}}}}+{\left(\underset{0}{\stackrel{1}{\int }}{\left(ln{\left|{\mathfrak{h}}^{*}\left({\mathfrak{a}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}{\mathfrak{b}}^{\frac{\mathsf{\ell }}{2}}\right)\right|}_{*}\right)}^{\mathfrak{q}}\mathrm{d}\mathsf{\ell }\right)}^{{\displaystyle \frac{1}{\mathfrak{q}}}}\right]\right\}.\hfill \end{array}$$

(27)

From the $GA$-convexity of ${\left(ln{\left|{\mathfrak{h}}^{*}\right|}_{*}\right)}^{\mathfrak{q}}$, inequality (27) yields

$$\begin{array}{cc}\hfill & {\left|{\displaystyle \frac{\sqrt{\mathfrak{h}\left(\mathfrak{a}\right)\mathfrak{h}\left(\mathfrak{b}\right)}}{{\left[\left({}_{*}\mathcal{R}_{{\sqrt{\mathfrak{a}\mathfrak{b}}}^{+}}^{\alpha }\mathfrak{h}\left(\mathfrak{b}\right)\right)\left({}_{*}\mathcal{R}_{{\sqrt{\mathfrak{a}\mathfrak{b}}}^{-}}^{\alpha }\mathfrak{h}\left(\mathfrak{a}\right)\right)\right]}^{\frac{2^{\alpha -1}\Gamma (\alpha +1)}{{(ln\mathfrak{b}-ln\mathfrak{a})}^{\alpha }}}}}\right|}_{*}\hfill \\ \hfill \le & exp\left\{{\displaystyle \frac{ln\mathfrak{b}-ln\mathfrak{a}}{4}}{\left({\displaystyle \frac{1}{\alpha }}B\left({\displaystyle \frac{1}{\alpha }},\mathfrak{p}+1\right)\right)}^{{\displaystyle \frac{1}{\mathfrak{p}}}}\left[\begin{array}{c}{\left(\underset{0}{\stackrel{1}{\int }}\left[{\displaystyle \frac{\mathsf{\ell }}{2}}{\left(ln{\left|{\mathfrak{h}}^{*}\left(\mathfrak{a}\right)\right|}_{*}\right)}^{\mathfrak{q}}+\left(1-\frac{\mathsf{\ell }}{2}\right){\left(ln{\left|{\mathfrak{h}}^{*}\left(\mathfrak{b}\right)\right|}_{*}\right)}^{\mathfrak{q}}\right]\mathrm{d}\mathsf{\ell }\right)}^{{\displaystyle \frac{1}{\mathfrak{q}}}}\hfill \\ +{\left(\underset{0}{\stackrel{1}{\int }}\left[\left(1-\frac{\mathsf{\ell }}{2}\right){\left(ln{\left|{\mathfrak{h}}^{*}\left(\mathfrak{a}\right)\right|}_{*}\right)}^{\mathfrak{q}}+{\displaystyle \frac{\mathsf{\ell }}{2}}{\left(ln{\left|{\mathfrak{h}}^{*}\left(\mathfrak{b}\right)\right|}_{*}\right)}^{\mathfrak{q}}\right]\mathrm{d}\mathsf{\ell }\right)}^{{\displaystyle \frac{1}{\mathfrak{q}}}}\hfill \end{array}\right]\right\}\hfill \\ \hfill =& exp\left\{{\displaystyle \frac{ln\mathfrak{b}-ln\mathfrak{a}}{4}}{\left({\displaystyle \frac{1}{\alpha }}B\left({\displaystyle \frac{1}{\alpha }},\mathfrak{p}+1\right)\right)}^{{\displaystyle \frac{1}{\mathfrak{p}}}}\left[{\left({\displaystyle \frac{{\left(ln{\left|{\mathfrak{h}}^{*}\left(\mathfrak{a}\right)\right|}_{*}\right)}^{\mathfrak{q}}+3{\left(ln{\left|{\mathfrak{h}}^{*}\left(\mathfrak{b}\right)\right|}_{*}\right)}^{\mathfrak{q}}}{4}}\right)}^{{\displaystyle \frac{1}{\mathfrak{q}}}}+{\left({\displaystyle \frac{3{\left(ln{\left|{\mathfrak{h}}^{*}\left(\mathfrak{a}\right)\right|}_{*}\right)}^{\mathfrak{q}}+{\left(ln{\left|{\mathfrak{h}}^{*}\left(\mathfrak{b}\right)\right|}_{*}\right)}^{\mathfrak{q}}}{4}}\right)}^{{\displaystyle \frac{1}{\mathfrak{q}}}}\right]\right\}\hfill \\ \hfill \le & exp\left\{{\displaystyle \frac{ln\mathfrak{b}-ln\mathfrak{a}}{4^{1+\frac{1}{\mathfrak{q}}}}}\left(1+3^{{\displaystyle \frac{1}{\mathfrak{q}}}}\right){\left({\displaystyle \frac{1}{\alpha }}B\left({\displaystyle \frac{1}{\alpha }},\mathfrak{p}+1\right)\right)}^{{\displaystyle \frac{1}{\mathfrak{p}}}}\left[ln{\left|{\mathfrak{h}}^{*}\left(\mathfrak{a}\right)\right|}_{*}+ln{\left|{\mathfrak{h}}^{*}\left(\mathfrak{b}\right)\right|}_{*}\right]\right\}\hfill \\ \hfill =& {\left({\left|{\mathfrak{h}}^{*}\left(\mathfrak{a}\right)\right|}_{*}{\left|{\mathfrak{h}}^{*}\left(\mathfrak{b}\right)\right|}_{*}\right)}^{\frac{ln\mathfrak{b}-ln\mathfrak{a}}{4^{1+\frac{1}{\mathfrak{q}}}}\left(1+3^{{\displaystyle \frac{1}{\mathfrak{q}}}}\right){\left(\frac{1}{\alpha }B\left({\displaystyle \frac{1}{\alpha }},\mathfrak{p}+1\right)\right)}^{{\displaystyle \frac{1}{\mathfrak{p}}}}},\hfill \end{array}$$

where we have used the fact that ${\mathcal{E}}^{\mathfrak{q}}+{\mathcal{F}}^{\mathfrak{q}}\le {\left(\mathcal{E}+\mathcal{F}\right)}^{\mathfrak{q}}$ for $\mathcal{E},\mathcal{F}>0$ and $\mathfrak{q}>1$. This completes the proof. □

Theorem 9. 

Let $\mathfrak{h}$ be as in Lemma 2. If ${\left(ln{\mathfrak{h}}^{*}\right)}^{\mathfrak{q}}$ is $GA$-convex for $\mathfrak{q}>1$, then the following multiplicative trapezium inequality holds:

$${\left|{\displaystyle \frac{\sqrt{\mathfrak{h}\left(\mathfrak{a}\right)\mathfrak{h}\left(\mathfrak{b}\right)}}{{\left[\left({}_{*}\mathcal{R}_{{\sqrt{\mathfrak{a}\mathfrak{b}}}^{+}}^{\alpha }\mathfrak{h}\left(\mathfrak{b}\right)\right)\left({}_{*}\mathcal{R}_{{\sqrt{\mathfrak{a}\mathfrak{b}}}^{-}}^{\alpha }\mathfrak{h}\left(\mathfrak{a}\right)\right)\right]}^{\frac{2^{\alpha -1}\Gamma (\alpha +1)}{{(ln\mathfrak{b}-ln\mathfrak{a})}^{\alpha }}}}}\right|}_{*}\le {\left({\left|{\mathfrak{h}}^{*}\left(\mathfrak{a}\right)\right|}_{*}{\left|{\mathfrak{h}}^{*}\left(\mathfrak{b}\right)\right|}_{*}\right)}^{\frac{ln\mathfrak{b}-ln\mathfrak{a}}{4^{1+\frac{1}{\mathfrak{q}}}}\left(1+3^{{\displaystyle \frac{1}{\mathfrak{q}}}}\right){\left(\frac{\alpha }{\alpha +1}\right)}^{1-{\displaystyle \frac{1}{\mathfrak{q}}}}}.$$

Proof. 

By using power mean inequality, inequality (26) gives

$$\begin{array}{cc}\hfill & {\left|{\displaystyle \frac{\sqrt{\mathfrak{h}\left(\mathfrak{a}\right)\mathfrak{h}\left(\mathfrak{b}\right)}}{{\left[\left({}_{*}\mathcal{R}_{{\sqrt{\mathfrak{a}\mathfrak{b}}}^{+}}^{\alpha }\mathfrak{h}\left(\mathfrak{b}\right)\right)\left({}_{*}\mathcal{R}_{{\sqrt{\mathfrak{a}\mathfrak{b}}}^{-}}^{\alpha }\mathfrak{h}\left(\mathfrak{a}\right)\right)\right]}^{\frac{2^{\alpha -1}\Gamma (\alpha +1)}{{(ln\mathfrak{b}-ln\mathfrak{a})}^{\alpha }}}}}\right|}_{*}\hfill \\ \hfill \le & exp\left\{{\displaystyle \frac{ln\mathfrak{b}-ln\mathfrak{a}}{4}}{\left(\underset{0}{\stackrel{1}{\int }}\left(1-{\mathsf{\ell }}^{\alpha }\right)\mathrm{d}\mathsf{\ell }\right)}^{1-{\displaystyle \frac{1}{\mathfrak{q}}}}\left[\begin{array}{c}{\left(\underset{0}{\stackrel{1}{\int }}\left(1-{\mathsf{\ell }}^{\alpha }\right){\left(ln{\left|{\mathfrak{h}}^{*}\left({\mathfrak{a}}^{\frac{\mathsf{\ell }}{2}}{\mathfrak{b}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}\right)\right|}_{*}\right)}^{\mathfrak{q}}\mathrm{d}\mathsf{\ell }\right)}^{{\displaystyle \frac{1}{\mathfrak{q}}}}\hfill \\ +{\left(\underset{0}{\stackrel{1}{\int }}\left(1-{\mathsf{\ell }}^{\alpha }\right){\left(ln{\left|{\mathfrak{h}}^{*}\left({\mathfrak{a}}^{\left(1-\frac{\mathsf{\ell }}{2}\right)}{\mathfrak{b}}^{\frac{\mathsf{\ell }}{2}}\right)\right|}_{*}\right)}^{\mathfrak{q}}\mathrm{d}\mathsf{\ell }\right)}^{{\displaystyle \frac{1}{\mathfrak{q}}}}\hfill \end{array}\right]\right\}\hfill \end{array}$$

(28)

By using the $GA$-convexity of ${\left(ln{\left|{\mathfrak{h}}^{*}\right|}_{*}\right)}^{\mathfrak{q}}$, inequality (28) yields

$$\begin{array}{cc}\hfill & {\left|{\displaystyle \frac{\sqrt{\mathfrak{h}\left(\mathfrak{a}\right)\mathfrak{h}\left(\mathfrak{b}\right)}}{{\left[\left({}_{*}\mathcal{R}_{{\sqrt{\mathfrak{a}\mathfrak{b}}}^{+}}^{\alpha }\mathfrak{h}\left(\mathfrak{b}\right)\right)\left({}_{*}\mathcal{R}_{{\sqrt{\mathfrak{a}\mathfrak{b}}}^{-}}^{\alpha }\mathfrak{h}\left(\mathfrak{a}\right)\right)\right]}^{\frac{2^{\alpha -1}\Gamma (\alpha +1)}{{(ln\mathfrak{b}-ln\mathfrak{a})}^{\alpha }}}}}\right|}_{*}\hfill \\ \hfill \le & exp\left\{{\displaystyle \frac{ln\mathfrak{b}-ln\mathfrak{a}}{4}}{\left({\displaystyle \frac{\alpha }{\alpha +1}}\right)}^{1-{\displaystyle \frac{1}{\mathfrak{q}}}}\left[\begin{array}{c}{\left(\underset{0}{\stackrel{1}{\int }}\left(1-\mathsf{\ell }\right)\left[{\displaystyle \frac{\mathsf{\ell }}{2}}{\left(ln{\left|{\mathfrak{h}}^{*}\left(\mathfrak{a}\right)\right|}_{*}\right)}^{\mathfrak{q}}+\left(1-{\displaystyle \frac{\mathsf{\ell }}{2}}\right){\left(ln{\left|{\mathfrak{h}}^{*}\left(\mathfrak{b}\right)\right|}_{*}\right)}^{\mathfrak{q}}\right]\mathrm{d}\mathsf{\ell }\right)}^{{\displaystyle \frac{1}{\mathfrak{q}}}}\hfill \\ +{\left(\underset{0}{\stackrel{1}{\int }}\left(1-\mathsf{\ell }\right)\left[{\displaystyle \frac{\mathsf{\ell }}{2}}{\left(ln{\left|{\mathfrak{h}}^{*}\left(\mathfrak{a}\right)\right|}_{*}\right)}^{\mathfrak{q}}+\left(1-{\displaystyle \frac{\mathsf{\ell }}{2}}\right){\left(ln{\left|{\mathfrak{h}}^{*}\left(\mathfrak{b}\right)\right|}_{*}\right)}^{\mathfrak{q}}\right]\mathrm{d}\mathsf{\ell }\right)}^{{\displaystyle \frac{1}{\mathfrak{q}}}}\hfill \end{array}\right]\right\}\hfill \\ \hfill =& exp\left\{{\displaystyle \frac{ln\mathfrak{b}-ln\mathfrak{a}}{4}}{\left({\displaystyle \frac{\alpha }{\alpha +1}}\right)}^{1-{\displaystyle \frac{1}{\mathfrak{q}}}}\left[{\left({\displaystyle \frac{{\left(ln{\left|{\mathfrak{h}}^{*}\left(\mathfrak{a}\right)\right|}_{*}\right)}^{\mathfrak{q}}+3{\left(ln{\left|{\mathfrak{h}}^{*}\left(\mathfrak{b}\right)\right|}_{*}\right)}^{\mathfrak{q}}}{4}}\right)}^{{\displaystyle \frac{1}{\mathfrak{q}}}}+{\left({\displaystyle \frac{3{\left(ln{\left|{\mathfrak{h}}^{*}\left(\mathfrak{a}\right)\right|}_{*}\right)}^{\mathfrak{q}}+{\left(ln{\left|{\mathfrak{h}}^{*}\left(\mathfrak{b}\right)\right|}_{*}\right)}^{\mathfrak{q}}}{4}}\right)}^{{\displaystyle \frac{1}{\mathfrak{q}}}}\right]\right\}\hfill \\ \hfill \le & exp\left\{{\displaystyle \frac{ln\mathfrak{b}-ln\mathfrak{a}}{4^{1+\frac{1}{\mathfrak{q}}}}}\left(1+3^{{\displaystyle \frac{1}{\mathfrak{q}}}}\right){\left({\displaystyle \frac{\alpha }{\alpha +1}}\right)}^{1-{\displaystyle \frac{1}{\mathfrak{q}}}}\left[ln{\left|{\mathfrak{h}}^{*}\left(\mathfrak{a}\right)\right|}_{*}+ln{\left|{\mathfrak{h}}^{*}\left(\mathfrak{b}\right)\right|}_{*}\right]\right\}\hfill \\ \hfill =& {\left({\left|{\mathfrak{h}}^{*}\left(\mathfrak{a}\right)\right|}_{*}{\left|{\mathfrak{h}}^{*}\left(\mathfrak{b}\right)\right|}_{*}\right)}^{\frac{ln\mathfrak{b}-ln\mathfrak{a}}{4^{1+\frac{1}{\mathfrak{q}}}}\left(1+3^{{\displaystyle \frac{1}{\mathfrak{q}}}}\right){\left(\frac{\alpha }{\alpha +1}\right)}^{1-{\displaystyle \frac{1}{\mathfrak{q}}}}},\hfill \end{array}$$

where we have used the fact that ${\mathcal{E}}^{\mathfrak{q}}+{\mathcal{F}}^{\mathfrak{q}}\le {\left(\mathcal{E}+\mathcal{F}\right)}^{\mathfrak{q}}$ for $\mathcal{E},\mathcal{F}>0$ and $\mathfrak{q}>1$. This completes the proof. □

5. Illustrative Example

In this section, we validate the coherence of our findings by means of a numerical example and its accompanying graphical illustration within the multiplicative framework.

Example 1.  

Consider the function $\mathfrak{h}$ defined on the interval $[\mathfrak{a},\mathfrak{b}]=[1,2]$ by

$$\mathfrak{h}\left(\varkappa \right)={\varkappa }^{3_{*}}\oslash exp\left\{3\right\}.$$

Its multiplicative (i.e., ∗-) derivative is given by ${\mathfrak{h}}^{*}\left(\varkappa \right)={\varkappa }^{2_{*}}$, which, by Proposition 11, is $GG$-convex on $[1,2]$. This $GG$-convexity guarantees that $\mathfrak{h}$ satisfies the key hypothesis needed to apply our main results.

By applying Theorem 4 and Theorem 7, we obtain the following midpoint and trapezium inequalities:

$${\left|exp\left\{{\displaystyle \frac{{\left(ln2\right)}^3}{24}}-{\displaystyle \frac{({\alpha }^2+3\alpha +8){(ln2)}^3}{24({\alpha }^2+3\alpha +2)}}\right\}\right|}_{*}\le exp\left\{{\displaystyle \frac{{\left(ln2\right)}^3}{4(\alpha +1)}}\right\}$$

(29)

and

$${\left|exp\left\{{\displaystyle \frac{{\left(ln2\right)}^3}{6}}-{\displaystyle \frac{({\alpha }^2+3\alpha +8){(ln2)}^3}{24({\alpha }^2+3\alpha +2)}}\right\}\right|}_{*}\le exp\left\{{\displaystyle \frac{\alpha {\left(ln2\right)}^3}{4(\alpha +1)}}\right\},$$

(30)

respectively.

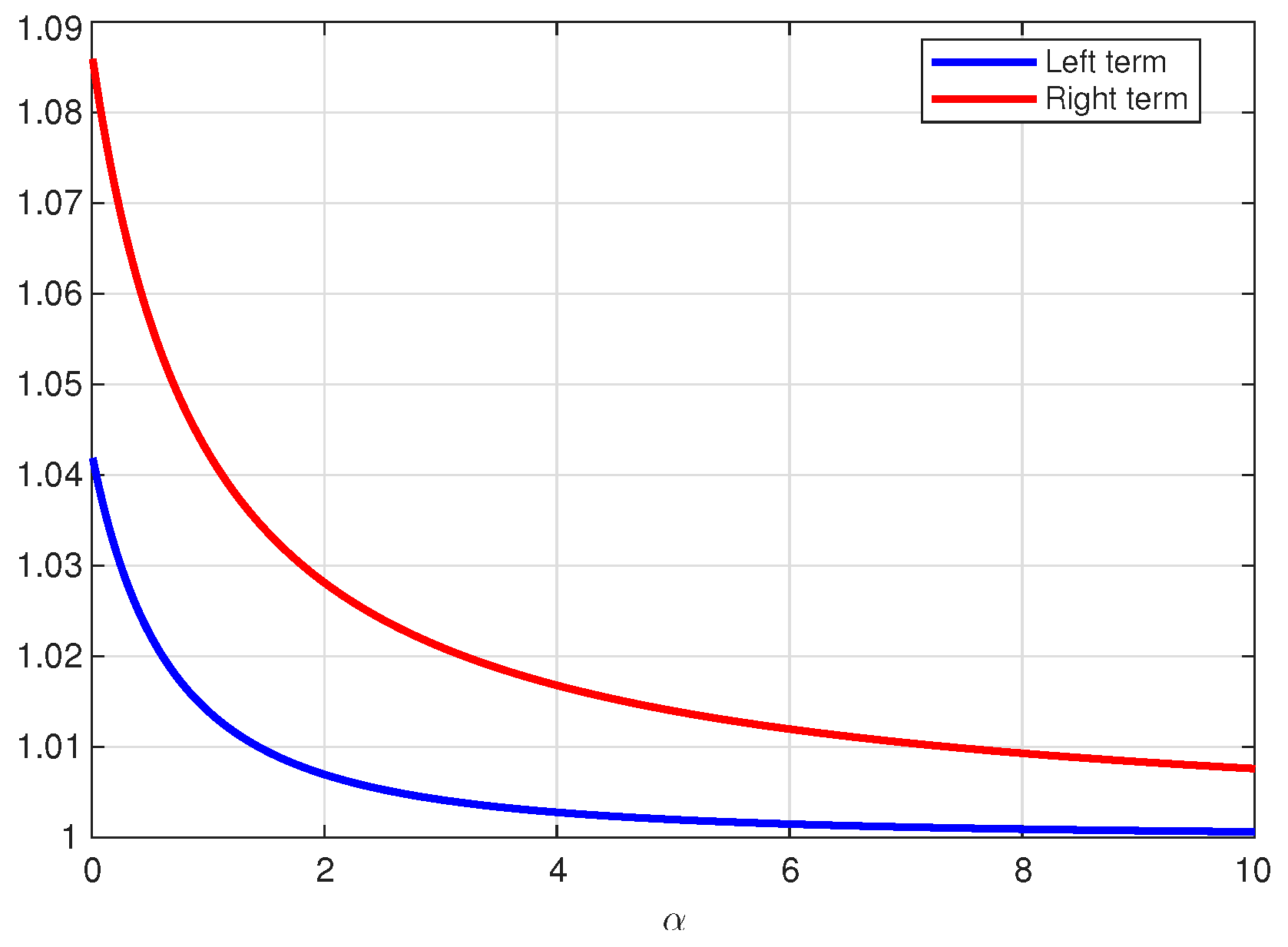
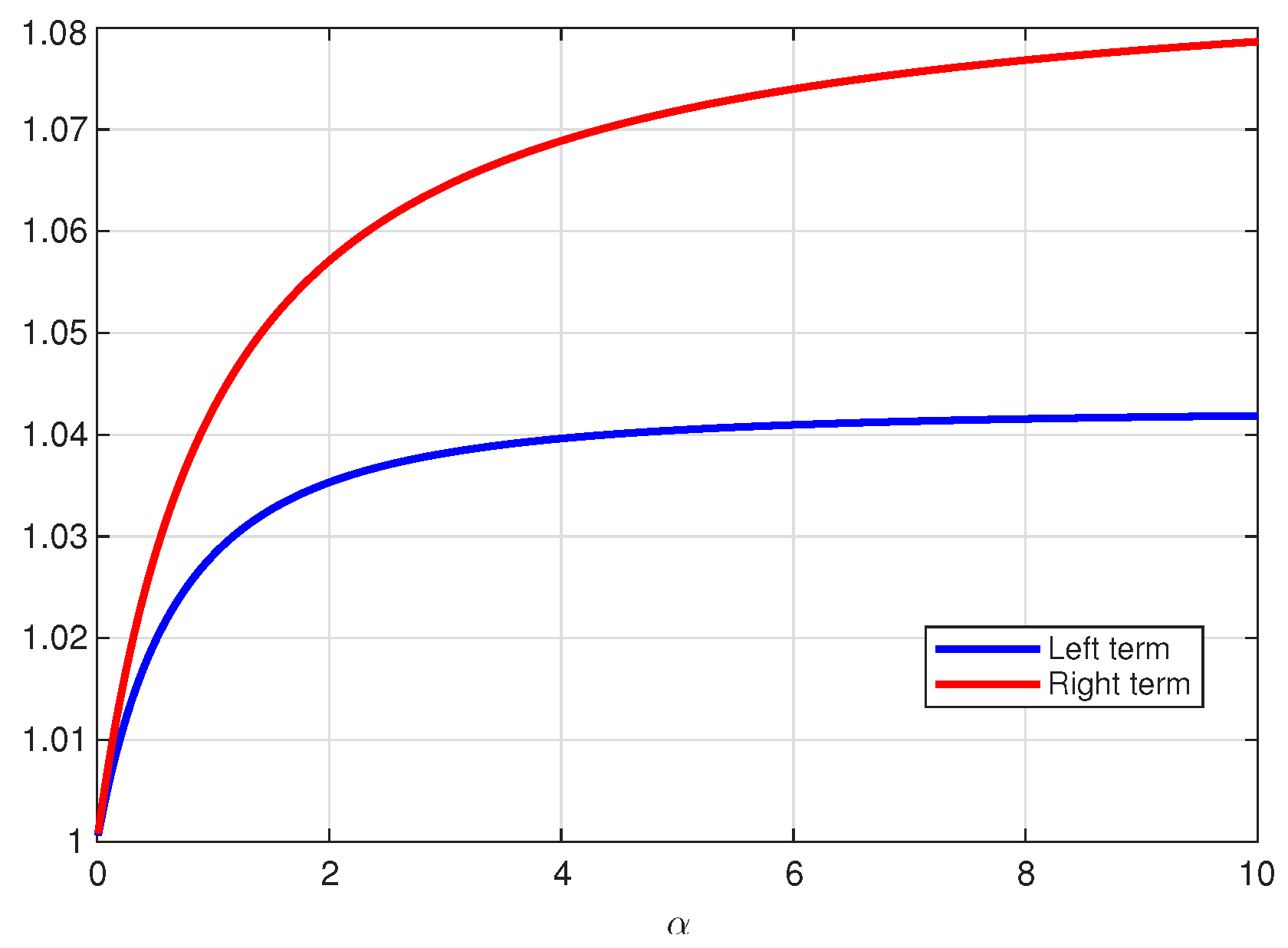
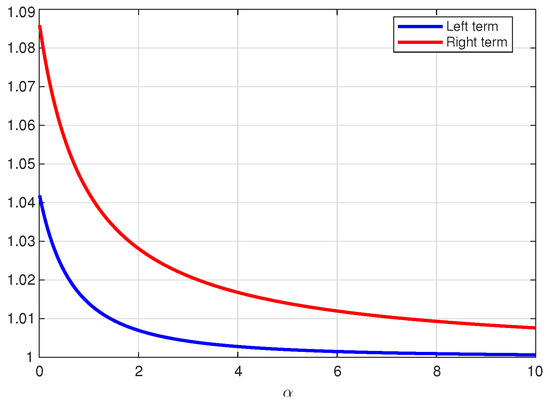
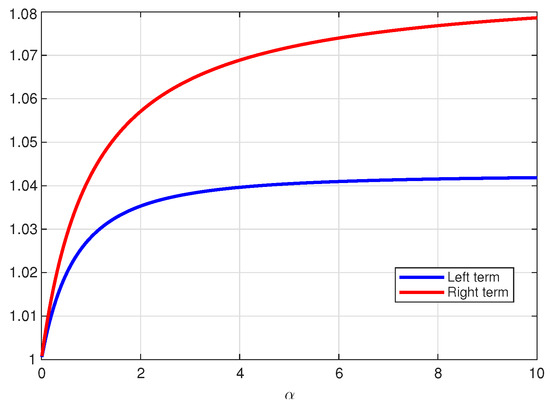
Figure 1 illustrates the left- and right-hand sides of inequality (29) for $\alpha \in (0,10]$, while Figure 2 shows those of inequality (30) over the same range of α. In both cases, the right-hand side consistently exceeds the left-hand side throughout the interval, thereby providing numerical confirmation of the theoretical results.

Figure 1. Multiplicative fractional midpoint inequality (29).

Figure 2. Multiplicative fractional trapezium inequality (30).

6. Practical Applications

To illustrate the relevance and utility of the obtained results, we present some applications of the multiplicative integral inequalities developed earlier in this paper.

We begin by recalling the definitions of some classical means: the arithmetic mean $\mathcal{A}(\mathfrak{a},\mathfrak{b})={\displaystyle \frac{\mathfrak{a}+\mathfrak{b}}{2}}$, the geometric mean $\mathcal{G}(\mathfrak{a},\mathfrak{b})=\sqrt{\mathfrak{a}\mathfrak{b}}$, the logarithmic mean $\mathcal{L}\left(\mathfrak{a},\mathfrak{b}\right)={\displaystyle \frac{\mathfrak{b}-\mathfrak{a}}{ln\mathfrak{b}-ln\mathfrak{a}}}$, and the p-logarithmic mean ${\mathcal{L}}_p(\mathfrak{a},\mathfrak{b})={\left({\displaystyle \frac{{\mathfrak{b}}^{p+1}-{\mathfrak{a}}^{p+1}}{(p+1)(\mathfrak{b}-\mathfrak{a})}}\right)}^{{\displaystyle \frac{1}{p}}}$ for $\mathfrak{a}\ne \mathfrak{b}$ and $p\in \mathbb{R}\setminus \left\{0\right\}$.

Proposition 12. 

Let $\mathfrak{a},\mathfrak{b}\in {\mathbb{R}}_{*}$ with $1<\mathfrak{a}<\mathfrak{b}$ and $k\ge 2$. Then, one has

$$exp\left\{{\left(ln\mathcal{G}\left(\mathfrak{a},\mathfrak{b}\right)\right)}^k-{\mathcal{L}}_k^k\left(ln\mathfrak{a},ln\mathfrak{b}\right)\right\}\le {\left({\mathfrak{a}}^{k{\left(ln\mathfrak{a}\right)}^{k-2}}{\mathfrak{b}}^{k{\left(ln\mathfrak{b}\right)}^{k-2}}\right)}^{\frac{ln\mathfrak{b}-ln\mathfrak{a}}{8}}.$$

Proof. 

The desired result follows by applying Corollary 2 to the function $\mathfrak{h}\left(\varkappa \right)={\varkappa }^{k_{*}}$, for which the multiplicative integral is

$${\left(\underset{\mathfrak{a}}{\stackrel{\mathfrak{b}}{\int }}\mathfrak{h}\left(\varkappa \right)\odot d_{*}\varkappa \right)}^{\frac{1}{ln\mathfrak{a}-ln\mathfrak{b}}}=exp\left\{-{\mathcal{L}}_k^k\left(ln\mathfrak{a},ln\mathfrak{b}\right)\right\},$$

and whose multiplicative derivative is ${\mathfrak{h}}^{*}\left(\varkappa \right)=e^k\odot {\varkappa }^{{(k-1)}_{*}}=exp\left\{k{\left(ln\varkappa \right)}^{k-1}\right\}={\varkappa }^{k{\left(ln\varkappa \right)}^{k-2}}$. □

Proposition 13. 

Let $\mathfrak{a},\mathfrak{b}\in {\mathbb{R}}_{*}$ with $0<\mathfrak{a}<\mathfrak{b}$. Then, one has

$$exp\left\{\mathcal{A}\left(\mathfrak{a},\mathfrak{b}\right)-\mathcal{L}\left(\mathfrak{a},\mathfrak{b}\right)\right\}\le exp\left\{\left(\mathfrak{a}+\mathfrak{b}\right){\displaystyle \frac{ln\mathfrak{b}-ln\mathfrak{a}}{8}}\right\}.$$

Proof. 

The desired result follows by applying Corollary 2 to the function $\mathfrak{h}\left(\varkappa \right)=exp\left\{\varkappa \right\}$, for which the multiplicative integral is given by

$${\left(\underset{\mathfrak{a}}{\stackrel{\mathfrak{b}}{\int }}\mathfrak{h}\left(\varkappa \right)\odot d_{*}\varkappa \right)}^{\frac{1}{ln\mathfrak{a}-ln\mathfrak{b}}}=exp\left\{{\displaystyle \frac{\mathfrak{b}-\mathfrak{a}}{ln\mathfrak{a}-ln\mathfrak{b}}}\right\}=exp\left\{-\mathcal{L}\left(\mathfrak{a},\mathfrak{b}\right)\right\},$$

and whose multiplicative derivative is ${\mathfrak{h}}^{*}\left(\varkappa \right)=exp\left\{\varkappa \right\}$. □

7. Conclusions

In conclusion, this work successfully extends key integral inequalities, such as Hermite–Hadamard, midpoint, and trapezoid-type estimates, to the context of fractional G-calculus. By adapting classical tools to this non-Newtonian framework and introducing an appropriate concept of convexity, we have shown that many familiar results can be reformulated and applied in a multiplicative setting. These findings open up several promising directions for future research, including the study of other types of inequalities, the investigation of alternative notions of convexity, and the development of numerical methods tailored to this new calculus. This work thus lays the foundation for further exploration into non-Newtonian analysis and its broader mathematical implications.