OGK Approach for Accurate Mean Estimation in the Presence of Outliers

Abstract

This paper proposes a new family of robust estimators of means, depending on the Orthogonalized Gnanadesikan–Kettenring (OGK) covariance matrix. These estimators are computationally feasible and robust replacements of the Minimum Covariance Determinant (MCD) estimator in survey sampling contexts involving auxiliary information. With the growing popularity of outliers in environmental data, as in the case of measuring solar radiation, conventional estimators like the sample mean or the Ordinary Least Squares (OLS) regression-based estimators are both biased and unreliable. The suggested OGK-based exponential-type estimators combine robust measures of location and dispersion and have a considerable advantage in the estimation of the population mean when auxiliary variables such as temperature are highly correlated with the variable of interest. The MSE property of OGK-based estimators is also obtained through a detailed theoretical derivation with the expressions of optimal weights. Performance was further proved using real-world and simulated data on solar radiation, as well as by demonstrating lower MSEs and higher PREs in comparison to MCD-based estimators. These results show that OGK-based estimators are highly efficient and robust in actual and artificially contaminated situations and hence are a good option in robust survey sampling and environmental data analysis.

1. Introduction

A survey is the basic first step of most research projects, as it is the most acceptable method of collecting primary data. Surveys can be conducted in different ways, e.g., face-to-face interviews, telephonic interactions, mailed questionnaires, group discussions, or in the form of digital media, which is growing in popularity. They are widely applicable in many disciplines such as education, healthcare, labor economics, consumer behavior, business analytics, and environmental studies. No matter the mode, the utility of a survey is highly dependent on the quality and reliability of the data collection process. Ill-constructed surveys can lead to deceiving or erroneous conclusions. Thus, it is necessary to properly design and thoroughly develop a strategy for efficiency and precision. Auxiliary information (additional variables related to the main variable of interest) can be used to increase the precision of a survey. When used properly, such auxiliary variables can substantially enhance the estimation of study parameters, and the results will be more solid and representative of the characteristics of the underlying population.

Estimating population parameters, such as the mean of a particular study variable, is a major objective of any statistical analysis, particularly in environmental and energy-related research studies; see [1,2,3,4]. One of the problems we address in our research is how to solve this issue using powerful statistical techniques that provide accurate estimates despite the presence of outliers, which is quite common in environmental data, such as those obtained on solar radiation.

Solar radiation is a key indicator of renewable energy systems and agriculture, as well as climate modeling (Mirbolouki et al. [5]). Nevertheless, sensor failures, atmospheric irregularities, or erroneous recordings may often cause observational solar radiation data to contain outliers. This can bias conventional estimators, such as the sample mean or traditional regression-based methods. This difficulty is even more acute in the presence of auxiliary data, which may be exploited in an attempt to increase the effectiveness of the estimation process using design- and model-aided methods.

With data contamination, especially outliers, the widely used Ordinary Least Squares (OLS)-based mean estimation method turns out to be unreliable. In most cases, biased and inefficient estimates are obtained. To overcome this, Kadilar et al. [6] proposed the replacement of the standard OLS estimator with the Huber-M robust regression estimator, which initiated a line of research on the need to achieve robustness in mean estimators. Continuing in this line, Zaman and Bulut [7] proposed a family of ratio-type estimators based on other robust regression techniques, further improving results on contaminated data. The idea was subsequently extended by Ali et al. [8] to accommodate sensitive study variables, and Zaman [9] developed another estimator class that achieved efficiency levels comparable to classical regression estimators. Zaman et al. [10] later added bivariate auxiliary information to the framework, and Zaman et al. [11] introduced a new application of robust regression coefficients to Hartley–Ross-type estimators. Transitioning to a larger statistical background, Alomair and Shahzad [12] worked out a sound framework in the neutrosophic context, which is precisely applicable to sensitive data applications. Subzar et al. [13] further added robust estimation methods to settings involving rare and clustered data. The typical weakness of these contributions, however, is that although the regression coefficients are more robust, the remaining components, including those of variance, location, and measures of scatter, still use traditional methods; thus, they are not as robust. This observation inspired Zaman and Bulut [14] to develop the Minimum Covariance Determinant (MCD)-based [15] mean estimation, a robust and high-breakdown alternative to multivariate location and scatter estimation. Based on the mentioned innovation, Zaman and Bulut [14] became the first authors to adopt strong covariance structures, such as MCD and MVE, within the framework of stratified random sampling. Shahzad et al. [16] also extended this work by developing imputation-based mean estimators in the context of missing data scenarios, relying on aspects of MCD. Closely related, a new type of robust ratio estimators with MCD was proposed by Bulut and Zaman [17]. Although MCD is very robust, it is computationally expensive and inefficient when confronted with strongly correlated or data that do not follow an elliptical distribution (Croux and Haesbroeck [18]). In dealing with these issues, Maronna and Zamar [19] proposed a computationally tractable, affine-equivariant, and robust alternative: the Orthogonalized Gnanadesikan–Kettenring (OGK) covariance matrix and location estimator. The present research builds upon the work by Bulut and Zaman [17] by replacing MCD with OGK in the mean estimation frameworks, thereby offering a strategic addition to the body of knowledge in the robust survey sampling field.

The motivation of this study is both theoretical and practical. We want to build and compare OGK- and MCD-based mean estimators in a scenario using temperature as auxiliary information to estimate the population mean of solar radiation. The issue lies with the survey sampling framework but has been extended to handle multivariate robust estimation using real-world environmental data. Such a combination is both methodologically novel and essential regarding modern data-based decision-making in sustainability and environmental monitoring.

The rest of this paper is organized in a manner that strategically unravels the theory, empirical validation, and implications of using OGK instead of MCD in the estimation of robust mean in the presence of outliers. Section 2 presents a background review of robust estimation techniques with a particular focus on the theoretical basis of the MCD covariance matrix and a review of MCD-based mean estimators and their applicability in the outlier setting. Section 3 presents the proposed family of OGK-based mean estimators, their mathematical construction, and the calculation of their MSE. Section 4 illustrates an empirical assessment that consists of both empirical data, i.e., data gathered on solar radiation, and a well-planned simulation study. The results are also extensively discussed in this section. Lastly, Section 5 presents the conclusion of this article, and also describes possible future research and application directions.

2. Bulut and Zaman [17] MCD-Based Estimators

Over the past decades, the statistical community has focused more on the design of robust procedures related to the estimation of the mean with a special interest in contaminated data or high-dimensional data. While classical estimators are efficient in an ideal case, they are sensitive to extreme observations or structural noise that may severely distort the results. It is of special concern in environmental and energy data, especially in the case of solar radiation, which is frequently measured in uncontrolled field conditions, where outliers tend to occur.

The availability of auxiliary information in survey sampling is not a new phenomenon and is well known to improve the precision of estimators. Early contributions by Cochran [20] and Sarndal et al. [21] were instrumental to the inclusion of additional variables into mean estimation. However, this idea was later improved due to the use of regression-type and ratio-type estimators that work well when the relationship between the variables is strong, but fail in the case of outliers (Koc and Koc [22]; Singh et al. [23]). To overcome this robustness shortcoming, robust multivariate estimators of location and scatter have become popular. One of them is the MCD, proposed by Rousseeuw [15]. MCD is robust to contamination in multivariate data as it has a high breakdown point and is affine-equivariant.

A well-known robust approach to estimating the location vector and the covariance matrix of multivariate data is the so-called MCD estimator, which is also very competitive in cases that involve outliers. In a bivariate setting with study variable y and auxiliary variable x, like in survey sampling and model-assisted estimation, the MCD estimator selects a subset of the observations of fixed size h (say, about 75 percent of the data) whose classical covariance matrix has a minimal determinant. The assumption is that this subset has no outliers and is representative of the underlying population structure. In particular, given a data set ${\left\{(x_i,y_i)\right\}}_{i=1}^n$, the MCD procedure seeks to find the subset $H\subset \{1,2,\dots ,n\}$ with $\left|H\right|=h$ such that the corresponding empirical covariance matrix involved

$${\widehat{\Xi }}_H={\displaystyle \frac{1}{h}}\sum _{i\in H}({\mathbf{z}}_i-{\overline{\mathbf{z}}}_H){({\mathbf{z}}_i-{\overline{\mathbf{z}}}_H)}^{\top },$$

has the minimum possible determinant, where ${\mathbf{z}}_i={(x_i,y_i)}^{\top }$, and ${\overline{\mathbf{z}}}_H$ is the mean vector of the subset H. The accompanying robust estimate of the location is

$${\widehat{\mathit{\mu }}}_{\mathrm{MCD}}={\overline{\mathbf{z}}}_H={\displaystyle \frac{1}{h}}\sum _{i\in H}{\mathbf{z}}_i,$$

and the strong covariance matrix is ${\widehat{\Xi }}_{\mathrm{MCD}}$, optionally reweighed with the full sample for the sake of efficiency. This method has a high breakdown of 50 percent, which implies that it is not affected by more than half the data being outliers. The MCD estimator is also affine-equivariant and guarantees the validity of multivariate estimators like Mahalanobis distances even in the face of contamination. The MCD gives a valid joint estimate of the central tendency and dispersion of the variables x and y when applied to the variables. This is why it is a great tool for robust regression, high-leverage detection, and mean estimation within sample surveys where auxiliary information is used to increase precision.

Using MCD methodology-based characteristics, Bulut and Zaman [17] classified following estimators:

$$J_{mc{d}_1}={\displaystyle \frac{{\widehat{\mu }}_{mc{d}_y}+{\widehat{\Phi }}_{mc{d}_{yx}}({\mu }_{mc{d}_x}-{\widehat{\mu }}_{mc{d}_x})}{\left({\widehat{\mu }}_{mc{d}_x}\right)}}\left({\mu }_{mc{d}_x}\right)$$

$$J_{mc{d}_2}={\displaystyle \frac{{\widehat{\mu }}_{mc{d}_y}+{\widehat{\Phi }}_{mc{d}_{yx}}({\mu }_{mc{d}_x}-{\widehat{\mu }}_{mc{d}_x})}{({\widehat{\mu }}_{mc{d}_x}+C_{mc{d}_x})}}({\mu }_{mc{d}_x}+C_{mc{d}_x})$$

$$J_{mc{d}_3}={\displaystyle \frac{{\widehat{\mu }}_{mc{d}_y}+{\widehat{\Phi }}_{mc{d}_{yx}}({\mu }_{mc{d}_x}-{\widehat{\mu }}_{mc{d}_x})}{({\widehat{\mu }}_{mc{d}_x}+{\beta }_{2mc{d}_x})}}({\mu }_{mc{d}_x}+{\beta }_{2mc{d}_x})$$

$$J_{mc{d}_4}={\displaystyle \frac{{\widehat{\mu }}_{mc{d}_y}+{\widehat{\Phi }}_{mc{d}_{yx}}({\mu }_{mc{d}_x}-{\widehat{\mu }}_{mc{d}_x})}{({\beta }_{2mc{d}_x}{\widehat{\mu }}_{mc{d}_x}+C_{mc{d}_x})}}({\beta }_{2mc{d}_x}{\mu }_{mc{d}_x}+C_{mc{d}_x})$$

$$J_{mc{d}_5}={\displaystyle \frac{{\widehat{\mu }}_{mc{d}_y}+{\widehat{\Phi }}_{mc{d}_{yx}}({\mu }_{mc{d}_x}-{\widehat{\mu }}_{mc{d}_x})}{(C_{mc{d}_x}{\widehat{\mu }}_{mc{d}_x}+{\beta }_{2mc{d}_x})}}(C_{mc{d}_x}{\mu }_{mc{d}_x}+{\beta }_{2mc{d}_x})$$

In general form,

$$J_{mc{d}_i}={\displaystyle \frac{{\widehat{\mu }}_{mc{d}_y}+{\widehat{\Phi }}_{mc{d}_{yx}}({\mu }_{mc{d}_x}-{\widehat{\mu }}_{mc{d}_x})}{(A_{mc{d}_i}{\widehat{\mu }}_{mc{d}_x}+B_{mc{d}_i})}}(A_{mc{d}_i}{\mu }_{mc{d}_x}+B_{mc{d}_i})fori=1,2,...,5$$

where $({\mu }_{mc{d}_x},{\mu }_{mc{d}_y})$ denotes the population averages and $({\widehat{\mu }}_{mc{d}_x},{\widehat{\mu }}_{mc{d}_y})$ denotes the sample averages under SRS. The variances of these sample averages, i.e., $({\widehat{\mu }}_{mc{d}_x},{\widehat{\mu }}_{mc{d}_y})$, are $V\left({\widehat{\mu }}_{mc{d}_x}\right)=\theta {\sigma }_{mc{d}_x}^2$ and $V\left({\widehat{\mu }}_{mc{d}_y}\right)=\theta {\sigma }_{mc{d}_y}^2$. Further, $A_{mc{d}_i}$ and $B_{mc{d}_i}$ are either (0,1) or some other known population measures, such as $C_{mc{d}_x}$, the coefficient of variation; ${\beta }_{2mc{d}_x}$, the coefficient of kurtosis; or ${\widehat{\Phi }}_{mc{d}_{yx}}$, the MCD-based robust regression coefficient. The MSE of Bulut and Zaman’s [17] family of estimators is given below:

$$MSE\left(J_{mc{d}_i}\right)=\theta [{\sigma }_{mc{d}_y}^2+g_i^2{\sigma }_{mc{d}_x}^2+2{\Phi }_{mc{d}_{yx}}{k}_{mc{d}_i}{\sigma }_{mc{d}_x}^2+{\Phi }_{mc{d}_{yx}}^2{\sigma }_{mc{d}_x}^2-2k_{mc{d}_i}{\sigma }_{mc{d}_{yx}}-2{\Phi }_{mc{d}_{yx}}{\sigma }_{mc{d}_{yx}}]$$

where $k_{mc{d}_i}={\displaystyle \frac{A_{mc{d}_i}{\mu }_{mc{d}_y}}{A_{mc{d}_i}{\mu }_{mc{d}_x}+B_{mc{d}_i}}}$, and $\theta =({\displaystyle \frac{1-f}{n}})$ for i = 1, 2, …, 5. Further, ${\sigma }_{mc{d}_y}^2$ and ${\sigma }_{mc{d}_x}^2$ are the variances of Y and X, respectively.

However, the computational complexity of MCD and the instability of MCD when applied to highly multicollinear data or data with nearly singular covariance matrices have encouraged researchers to find alternatives (Croux and Haesbroeck [18]). The OGK estimator suggested by Maronna and Zamar [19] is an interesting solution in this endeavor. OGK breaks the process of estimating covariance via robust univariate scale estimation and robust correlation structures, hence being both efficient and robust. The applicability of the OGK in high-dimensional or environmental data applications has been recently shown (Hubert et al. [24]), but it has not been explored in survey sampling or auxiliary-based mean estimation. More recently, the literature has also focused on combining robust covariance estimators with model-assisted estimation algorithms under non-ideal circumstances. As an example, Dagdoug et al. [25] argue about the benefits of using auxiliary data alongside strong modeling in finite populations, whereas Alameddine et al. [26] explored robust covariances-based diagnostics in the multivariate abnormality detection of environmental data.

Nevertheless, there still is a gap in the strategic research: the comparative performance of OGK and MCD in mean estimation frameworks, which exploit auxiliary information in the presence of outlier contamination, has not been studied in detail yet. In future sections, our contribution is a direct answer to this gap since we not only apply both OGK and MCD estimators to real-world environmental data but also consider their MSE and relative efficiency in estimating mean solar radiation with temperature as an auxiliary variable.

3. OGK and Proposed Estimators

The OGK provides an effective and powerful methodology to estimate the location vector and the covariance matrix when the variable of interest in a study y is considered together with an auxiliary variable x, which is often the case in survey sampling and regression modeling. In contrast to classical estimators that are quite sensitive to outliers, the OGK method uses robust univariate statistics and an orthogonalization procedure to provide reliability even in the case of data contamination. Given bivariate data ${\left\{(x_i,y_i)\right\}}_{i=1}^n$, the procedure then begins by calculating robust location estimates ${\tilde{\mu }}_x=\mathrm{median}\left(x\right)$ and ${\tilde{\mu }}_y=\mathrm{median}\left(y\right)$, and robust scale estimates $s_x=\mathrm{MAD}\left(x\right)$ and $s_y=\mathrm{MAD}\left(y\right)$. The interdependence between x and y is estimated with the Gnanadesikan–Kettenring identity:

$${\widehat{\varpi }}_{xy}={\displaystyle \frac{1}{4}}\left[s^2(x+y)-s^2(x-y)\right],$$

with a robust estimator of the variance $s^2(·)$, e.g., squared MAD or scaleTau2. The following are the first robust covariance matrices:

$$V=\left[\begin{array}{cc}{s}_x^2& {\widehat{\varpi }}_{xy}\\ {\widehat{\varpi }}_{xy}& s_y^2\end{array}\right].$$

The orthogonalization of this matrix is performed through eigen-decomposition, $V=E\upsilon E^{\top }$, so that the data can be transformed to uncorrelated space. Within such a changed space, strong estimates of the location vector ${\tilde{\mathit{\mu }}}_Z={({\tilde{\mu }}_{Z_x},{\tilde{\mu }}_{Z_y})}^{\top }$ and variances $(s_{Z_x}^2,s_{Z_y}^2)$ are obtained. The last strongly placed estimate in the initial space is obtained by

$${\widehat{\mathit{\mu }}}_{\mathrm{OGK}}=E{\tilde{\mathit{\mu }}}_Z,$$

and the strong covariance matrix is as follows:

$${\widehat{\Xi }}_{\mathrm{OGK}}=E·\mathrm{diag}(s_{Z_x}^2,s_{Z_y}^2)·E^{\top }.$$

This is a robust estimator in that the location and scatter parameters of study variable y, when measured in relation to auxiliary variable x, will be unwavering and reliable despite the heavy-tail distribution or the existence of outliers. The OGK is recommended for its computational efficiency and robust breakdown performance, and is specifically suited to survey analysis, robust regression modeling, and environmental data analysis, where auxiliary information is important in enhancing inference accuracy.

The present article uses OGK’s characteristics, which are available through the CovOgk() function within the rrcov package of the R language version 4.5.0 and which have been directly applied to pairs of auxiliary and study variables. This effective estimation method delivers a combination of location vectors and scatter matrices, which are very resistant to outliers. Unlike MCD and MVE, OGK is not based on subsampling and is much faster than affine equivariance. Its credibility is also supported by theoretical strength aspects, such as a restricted influence measure, a discontinuity of about 25%, low gross-error sensitivity, and a finite rejection point. These attributes make OGK very attractive when surveying contaminated data.

Proposed OGK-Based Mean Estimators

Taking motivation from Bulut and Zaman [17] and Koyuncu [27], we propose the following class of estimators:

$$P_{og{k}_i}=\left[g_1{\widehat{\mu }}_{og{k}_y}+g_2{\left({\displaystyle \frac{{\widehat{\mu }}_{og{k}_x}}{{\mu }_{og{k}_x}}}\right)}^{\psi }\right]\mathsf{exp}\left[{\displaystyle \frac{A_{og{k}_i}({\mu }_{og{k}_x}-{\widehat{\mu }}_{og{k}_x})}{A_{og{k}_i}({\mu }_{og{k}_x}+{\widehat{\mu }}_{og{k}_x})+2B_{og{k}_i}}}\right],$$

(1)

where $\psi$ is a suitable real number, and $g_1$ and $g_2$ are suitable weights. $({\mu }_{og{k}_x},{\mu }_{og{k}_y})$ denotes the population averages and $({\widehat{\mu }}_{og{k}_x},{\widehat{\mu }}_{og{k}_y})$ denotes the OGK-based sample averages under SRS. The variances of these sample averages, i.e., $({\widehat{\mu }}_{og{k}_x},{\widehat{\mu }}_{og{k}_y})$, are $V\left({\widehat{\mu }}_{og{k}_x}\right)=\theta {\sigma }_{og{k}_x}^2$ and $V\left({\widehat{\mu }}_{og{k}_y}\right)=\theta {\sigma }_{og{k}_y}^2$. Further, $A_{og{k}_i}$ and $B_{og{k}_i}$ are either (0,1) or some known population measures based on OGK, namely, $C_{og{k}_x}$, the coefficient of variation, and ${\beta }_{2og{k}_x}$, the coefficient of kurtosis. A set of new estimators generated from (1) is listed in Table 1. Expressing (1) in terms of $e_{og{k}_y}$ and $e_{og{k}_x}$, we have

$$P_{og{k}_i}=\left[g_1{\mu }_{og{k}_y}(1+e_{og{k}_y})+g_2{(1+e_{og{k}_x})}^{\psi }\right]\mathsf{exp}\left[{\displaystyle \frac{-{\mu }_{og{k}_x}{e}_{og{k}_x}{A}_{og{k}_i}}{A_{og{k}_i}(2{\mu }_{og{k}_x}+{\mu }_{og{k}_x}{e}_{og{k}_x})+2B_{og{k}_i}}}\right].$$

(2)

Table 1. Proposed OGK estimators.

Estimators	$\mathit{\psi }$	${\mathit{A}}_{{\mathit{ogk}}_{\mathit{i}}}$	${\mathit{B}}_{{\mathit{ogk}}_{\mathit{i}}}$
$P_{og{k}_1}$	1	1	1
$P_{og{k}_2}$	1	1	$C_{og{k}_x}$
$P_{og{k}_3}$	1	1	${\beta }_{2og{k}_x}$
$P_{og{k}_4}$	1	${\beta }_{2og{k}_x}$	$C_{og{k}_x}$
$P_{og{k}_5}$	1	$C_{og{k}_x}$	${\beta }_{2og{k}_x}$

The Taylor approximation yields

$$P_{og{k}_i}=\left[g_1{\mu }_{og{k}_y}(1+e_{og{k}_y})+g_2\left(1+\psi e_{og{k}_x}+{\displaystyle \frac{\psi (\psi -1)}{2}}{e}_{og{k}_x}^2\right)\right]\left\{1-{\displaystyle \frac{q_{og{k}_x}}{2}}{e}_{og{k}_x}+{\displaystyle \frac{3}{8}}{q}_{og{k}_x}^2{e}_{og{k}_x}^2+\cdots \right\},$$

(3)

where $q_{og{k}_x}={\displaystyle \frac{A_{og{k}_i}{\mu }_{og{k}_x}}{A_{og{k}_i}{\mu }_{og{k}_x}+B_{og{k}_i}}}$. Simplifying (3) and retaining the second-order terms in e yields

$$\begin{array}{cc}\hfill P_{og{k}_i}-{\mu }_{og{k}_y}& ={\mu }_{og{k}_y}(g_1-1)+g_1{\mu }_{og{k}_y}{e}_{og{k}_y}+\left(g_2+g_2\psi e_{og{k}_x}+g_2{\displaystyle \frac{\psi (\psi -1)}{2}}{e}_{og{k}_x}^2\right)\hfill \\ \hfill & -g_1{\displaystyle \frac{q_{og{k}_x}}{2}}{\mu }_{og{k}_y}{e}_{og{k}_x}-g_1{\displaystyle \frac{q_{og{k}_x}}{2}}{\mu }_{og{k}_y}{e}_{og{k}_x}{e}_{og{k}_y}-g_2{\displaystyle \frac{q_{og{k}_x}}{2}}{e}_{og{k}_x}-g_2{\displaystyle \frac{q_{og{k}_x}}{2}}\psi e_{og{k}_x}^2\hfill \\ \hfill & +{\displaystyle \frac{3}{8}}{g}_1{q}_{og{k}_x}^2{\mu }_{og{k}_y}{e}_{og{k}_x}^2+{\displaystyle \frac{3}{8}}{g}_2{q}_{og{k}_x}^2{e}_{og{k}_x}^2.\hfill \end{array}$$

(4)

The MSE of $P_{og{k}_i}$, at its first-order approximation, is given by

$$\mathrm{MSE}\left(P_{og{k}_i}\right)=\left[{\mu }_{og{k}_y}^2{g}_1^2{\lambda }_A+g_2^2{\lambda }_B+{\mu }_{og{k}_y}^2{g}_1{\lambda }_D+{\mu }_{og{k}_y}{g}_2{\lambda }_G+{\mu }_{og{k}_y}^2+{\mu }_{og{k}_y}{g}_1{g}_2{\lambda }_F\right],$$

(5)

where

$$\begin{array}{cc}\hfill {\lambda }_A& =\left(1+\theta \left({\displaystyle \frac{{\sigma }_{og{k}_y}^2}{{\mu }_{og{k}_y}^2}}+q_{og{k}_x}^2{\displaystyle \frac{{\sigma }_{og{k}_x}^2}{{\mu }_{og{k}_x}^2}}-2q_{og{k}_x}{\displaystyle \frac{{\sigma }_{og{k}_{yx}}}{{\mu }_{og{k}_y}{\mu }_{og{k}_x}}}\right)\right),\hfill \\ \hfill {\lambda }_B& =\left(1+{\psi }^2+q_{og{k}_x}^2+\psi (\psi -1)-2q_{og{k}_x}\psi \right)\theta {\displaystyle \frac{{\sigma }_{og{k}_x}^2}{{\mu }_{og{k}_x}^2}},\hfill \\ \hfill {\lambda }_D& =\left(q_{og{k}_x}\theta {\displaystyle \frac{{\sigma }_{og{k}_{yx}}}{{\mu }_{og{k}_y}{\mu }_{og{k}_x}}}-2-{\displaystyle \frac{3}{4}}{q}_{og{k}_x}^2\theta {\displaystyle \frac{{\sigma }_{og{k}_x}^2}{{\mu }_{og{k}_x}^2}}\right),\hfill \\ \hfill {\lambda }_G& =\left(\left(q_{og{k}_x}\psi -{\displaystyle \frac{3}{4}}{q}_{og{k}_x}^2-\psi (\psi -1)\right)\theta {\displaystyle \frac{{\sigma }_{og{k}_x}^2}{{\mu }_{og{k}_x}^2}}-2\right),\hfill \\ \hfill {\lambda }_F& =\left(2+2(\psi -q_{og{k}_x})\theta {\displaystyle \frac{{\sigma }_{og{k}_{yx}}}{{\mu }_{og{k}_y}{\mu }_{og{k}_x}}}+\left(2q_{og{k}_x}^2+\psi (\psi -1)-2\psi q_{og{k}_x}\right)\theta {\displaystyle \frac{{\sigma }_{og{k}_x}^2}{{\mu }_{og{k}_x}^2}}\right).\hfill \end{array}$$

The values of $g_1$ and $g_2$ that minimize $\mathrm{MSE}\left(P_{og{k}_i}\right)$ are

$$g_1={\displaystyle \frac{{\lambda }_G{\lambda }_F-2{\lambda }_D{\lambda }_B}{(4{\lambda }_B{\lambda }_A-{\lambda }_F^2)}},g_2={\mu }_{og{k}_y}{\displaystyle \frac{{\lambda }_D{\lambda }_F-2{\lambda }_G{\lambda }_A}{(4{\lambda }_A{\lambda }_B-{\lambda }_F^2)}}.$$

(6)

By substituting the optimal values of ${\lambda }^s$, we obtain the minimum MSE of $P_{og{k}_i}$:

$${\mathrm{MSE}}_{min}\left(P_{og{k}_i}\right)={\mu }_{og{k}_y}^2\left[1-{\displaystyle \frac{{\lambda }_B{\lambda }_D^2-{\lambda }_D{\lambda }_F{\lambda }_G+{\lambda }_A{\lambda }_G^2}{(4{\lambda }_B{\lambda }_A-{\lambda }_F^2)}}\right].$$

(7)

The suggested OGK-based mean estimators with the use of auxiliary information are the first and central contribution to the field of survey sampling. Although the MCD estimator has previously been used in mean estimators by Bulut and Zaman [17], and other researchers have considered the use of Minimum Volume Ellipsoid (MVE) covariance matrices, no previous research has formally applied an OGK robust covariance matrix. This is remarkable considering that OGK has been shown to have an advantage in terms of computational efficiency, interpretability, and affine equivariance, especially in high-dimensional or non-elliptical distributions (Maronna and Zamar [19]). This work extends beyond a simple replacement of MCD with OGK—it introduces a structurally different methodology, which is more robust to outliers and less computationally intensive. Notably, the proposed methodology applies OGK beyond its classical uses in multiple variables to the survey estimation means and is therefore an innovative move in effective statistical practice in contaminated or partially misspecified data. Hence, the proposed work is an important and non-incremental improvement on the previous literature.

4. Numerical Illustration

4.1. Solar Radiation Data (Population-1)

Solar radiation is a core variable in climate models and renewable energy research and is subject to variability because of cloud cover, atmospheric dust, sensor shading, and measurement anomalies. In contrast, temperature tends to show a high and steady linear relationship with solar radiation because of diurnal solar variations (Mirbolouki et al. [5]). In line with the objectives of this study, we employed an environmental dataset in which temperature serves as the auxiliary variable and solar radiation is the study variable of interest. These data are available from the open access site Kaggle. One of the most important features of testing the performance of robust mean estimators is how they estimate the mean on real data, which in most cases is usually noisy and irregular and may contain outliers. To fulfill these requirements, we replaced the last five observations of the data with outliers. The scatter plot of the data, highlighting five outliers, is provided in Figure 1.

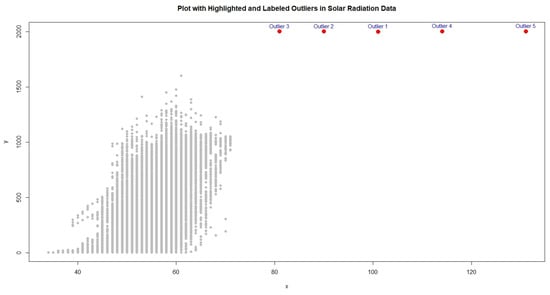
Figure 1. Scatter plot for Population-1.

4.2. Simulation Study (Population-2)

Real data give ecological validity, but a controlled simulation is also needed to test the robustness of the OGK and MCD estimators in a controlled way under conditions of known contamination. In the present work, we consider a bivariate normal population N = 1000 with a strong linear correlation between auxiliary variable x and study variable y by drawing a joint distribution:

$$\left(\begin{array}{c}X\\ Y\end{array}\right)\sim \mathcal{N}\left(\left(\begin{array}{c}{\mu }_x\\ {\mu }_y\end{array}\right),\left(\begin{array}{cc}{\vartheta }_x^2& r{\vartheta }_x{\vartheta }_y\\ r{\vartheta }_x{\vartheta }_y& {\vartheta }_y^2\end{array}\right)\right)$$

We set the parameters as follows:

• ${\mu }_x=15$, ${\mu }_y=0.15$;
• ${\vartheta }_x=6$, ${\vartheta }_y=0.05$;
• $r=0.8$.

In order to simulate contamination, we randomly selected a percentage $ϵ$ of the units (e.g., $10\%$) and change their value of Y by substituting it with extreme values. The contaminated values are characterized by

$$Y_i^{*}=\left\{\begin{array}{cc}{Y}_i,\hfill & \mathrm{with}\mathrm{probability}1-ϵ\hfill \\ Y_i+{\Theta }_i,\hfill & \mathrm{with}\mathrm{probability}ϵ\hfill \end{array}\right.\mathrm{where}{\Theta }_i\sim \mathcal{N}(0.2,0.{01}^2)$$

This formulation injects anomalously high values in the data by mimicking irregular conditions. Therefore, the simulation guarantees that both the OGK and MCD estimators are tested on realistic but controlled data irregularities, and we are able to study MSE and relative efficiency in the case of contamination. The scatter plot of the data is provided in Figure 2.

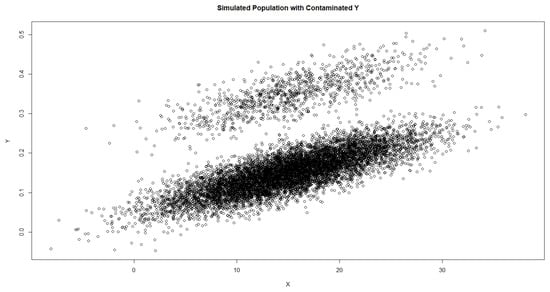
Figure 2. Scatter Plot for Population-2.

4.3. Interpretation

The MSE and PRE based on real and simulated populations are presented in Table 2, Table 3, Table 4 and Table 5. Table 2, Table 3, Table 4 and Table 5 are interpreted as follows:

Table 2. MSE using solar radiation data.

i	Population-1
$J_{mc{d}_1}$	$7.999097\times {10}^{-4}$
$J_{mc{d}_2}$	$7.995695\times {10}^{-4}$
$J_{mc{d}_3}$	$6.966328\times {10}^{-4}$
$J_{mc{d}_4}$	$7.032661\times {10}^{-4}$
$J_{mc{d}_5}$	$6.966328\times {10}^{-4}$
$P_{og{k}_1}$	$3.416565\times {10}^{-5}$
$P_{og{k}_2}$	$3.427384\times {10}^{-5}$
$P_{og{k}_3}$	$1.366556\times {10}^{-4}$
$P_{og{k}_4}$	$3.416570\times {10}^{-5}$
$P_{og{k}_5}$	$1.366556\times {10}^{-4}$

Table 3. PRE using solar radiation data.

i	${\mathit{J}}_{{\mathit{mcd}}_1}$	${\mathit{J}}_{{\mathit{mcd}}_2}$	${\mathit{J}}_{{\mathit{mcd}}_3}$	${\mathit{J}}_{{\mathit{mcd}}_4}$	${\mathit{J}}_{{\mathit{mcd}}_5}$
$P_{og{k}_1}$	2341.2691	2333.8785	585.3473	2341.2655	585.3473
$P_{og{k}_2}$	2340.2733	2332.8859	585.0984	2340.2698	585.0984
$P_{og{k}_3}$	2038.9863	2032.5499	509.7728	2038.9832	509.7728
$P_{og{k}_4}$	2058.4012	2051.9036	514.6267	2058.3981	514.6267
$P_{og{k}_5}$	2038.9863	2032.5499	509.7728	2038.9832	509.7728

Table 4. MSE using simulation data.

i	Population-2
$J_{mc{d}_1}$	$8.983728\times {10}^{-6}$
$J_{mc{d}_2}$	$9.104253\times {10}^{-6}$
$J_{mc{d}_3}$	$4.566413\times {10}^{-6}$
$J_{mc{d}_4}$	$3.841712\times {10}^{-6}$
$J_{mc{d}_5}$	$4.060548\times {10}^{-6}$
$P_{og{k}_1}$	$9.229949\times {10}^{-7}$
$P_{og{k}_2}$	$9.866356\times {10}^{-7}$
$P_{og{k}_3}$	$3.652275\times {10}^{-6}$
$P_{og{k}_4}$	$9.423510\times {10}^{-7}$
$P_{og{k}_5}$	$3.726288\times {10}^{-6}$

Table 5. PRE using simulation study.

i	${\mathit{J}}_{{\mathit{mcd}}_1}$	${\mathit{J}}_{{\mathit{mcd}}_2}$	${\mathit{J}}_{{\mathit{mcd}}_3}$	${\mathit{J}}_{{\mathit{mcd}}_4}$	${\mathit{J}}_{{\mathit{mcd}}_5}$
$P_{og{k}_1}$	973.3237	910.5416	245.9762	953.3314	241.0906
$P_{og{k}_2}$	986.3817	922.7574	249.2762	966.1212	244.3250
$P_{og{k}_3}$	494.7387	462.8267	125.0293	484.5767	122.5459
$P_{og{k}_4}$	416.2224	389.3749	105.1868	407.6731	103.0976
$P_{og{k}_5}$	439.9317	411.5549	111.1786	430.8954	108.9703

• Table 2 presents the MSE of estimators $J_{mc{d}_i}$ and $P_{og{k}_i}$ ($i=1,\dots ,5$) on real data regarding solar radiation. Among the MCD-type estimators, with the lowest MSEs were found to be $J_{mc{d}_3}$, $J_{mc{d}_4}$, and $J_{mc{d}_5}$, which were about $6.966\times {10}^{-4}$, demonstrating greater robustness and reduced variability. On the contrary, the OGK-type estimators have smaller MSEs in general, with the lowest MSEs being as low as $3.416\times {10}^{-5}$, especially in the case of $P_{og{k}_1}$ and $P_{og{k}_2}$. This implies that exponential-type estimators $P_{og{k}_i}$, which are built in OGK-based robust covariance structures, are much more precise than MCD-type estimators when real-world data are provided, comprising solar radiation and auxiliary temperature variables.
• Table 3 contains the values of PRE related to the MSE of estimators presented in Table 2. The findings demonstrate conclusively that the $P_{og{k}_i}$ estimators, particularly, $P_{og{k}_1}$, $P_{og{k}_2}$, and $P_{og{k}_4}$, are more efficient in terms of their PRE values (e.g., 2341.2691 and 2340.2733) compared with those of the baseline estimator family $J_{mc{d}_i}$. Even though $J_{mc{d}_3}$ and $J_{mc{d}_5}$ also performed well in the middle range of PREs, they still did not outperform OGK-type counterparts. These results evidence the strategic benefit of the proposed estimators $P_{og{k}_i}$ in the application of environmental data.
• Table 4 shows the results of the MSE obtained via simulation, considering real-world contamination and structural variance replication. Simulation further establishes the excellent performance of $P_{og{k}_i}$ estimators, which once again prove to have lesser MSE values when compared to their respective $J_{mc{d}_i}$ estimators. Specifically, the MSEs reported by $P_{og{k}_1}$, $P_{og{k}_2}$, and $P_{og{k}_4}$ are so low (in the range of the order of ${10}^{-7}$) that their reliability is justified in controlled experiments. OGK-type estimators perform best compared to any of the MCD-type estimators, although $J_{mc{d}_4}$ and $J_{mc{d}_5}$ are the best MCD-type estimators. These results indicate that the proposed estimators not only work well on real data but they are also highly robust in simulated conditions with outlier contamination.
• Table 5 gives the PREs of the same estimators, in the simulated environment, given in Table 4. These are consistent with the MSE results, as $P_{og{k}_1}$, $P_{og{k}_2}$, and $P_{og{k}_4}$ are consistently superior with their values being above 970, supporting their efficiency superiority. The MCD-type estimators, including $J_{mc{d}_4}$ and $J_{mc{d}_5}$, follow with fairly high PREs, yet they are not as efficient as their OGK-type counterparts. On the whole, the simulation demonstrates that exponential-type estimators built with OGK robust covariance matrices are highly precise and efficient with artificially injected data irregularities, which points at the relevance of the approach in a diversity of robust survey sampling settings.

Real and simulated data indicate that OGK-type estimators with robust location and covariance matrices are superior to MCD-type estimators both in terms of MSE and PRE. These results are also visualize in Figure 3 and Figure 4.

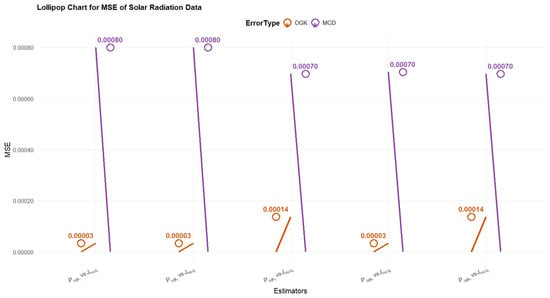
Figure 3. Performance comparison using Population-1.

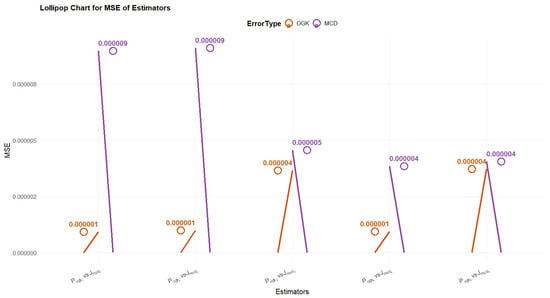
Figure 4. Performance comparison using Population-4.

5. Conclusions and Future Recommendations

This research work is part of the current development of powerful statistical approaches in survey sampling, especially when dealing with environmental data that are prone to contamination. The integration of the OGK robust covariance matrix resulted in a new family of mean estimators that effectively integrates auxiliary information in the presence of outliers. As shown through rigorous theoretical development and empirical evaluation, the OGK-based estimators outperformed the corresponding MCD-based ones in terms of smaller MSEs and larger PREs. In contrast to classical estimators based on the classical covariance structure and highly susceptible to unusual measurements, the OGK-based framework is resistant to outliers, computationally more stable, and affine-equivariant. It is especially appropriate for real-world datasets, which are often extreme and non-normal, e.g., solar radiation measurements. The simulation results also play a part in determining the reliability and scalability of the estimators with regard to the performance of the proposed estimators. Notably, the given estimators are not only theoretically novel but also may be practically useful in areas where plentiful auxiliary variables, such as temperature, can be found and are closely linked with the variable under study. The possibility to utilize such information with the help of strong and computationally effective tools creates new possibilities to increase the quality of inference in both observational and designed surveys. On the whole, this paper validates the fact that the OGK framework is a strategic alternative of MCD to use in the modern estimation of statistical mean in the presence of uncertainty and contamination.

Further, the current article presents a new OGK-based mean estimation method utilizing auxiliary data; future research can consider multivariate median-type estimators to contribute to the increased robustness of the measure under nonparametric or heavy-contamination conditions. Also, the utilization of other well-known methods, such as RFCH [28], RMVN [28], Det-MCD [24], and Sign Covariance Matrix [29], to survey sampling mean estimation may be promising to extract comparisons. Although we still focused on robust covariance-based mean estimators, an alternative approach, such as Least Trimmed Squares (LTS) [30,31], might be considered in future research to assess the performance of mean estimation. Moreover, future studies may also further work on the issue of combining OGK-based estimation with machine learning models for adaptive bandwidth decisions or nonlinear modeling, or using L-Comoments robust covariance matrix [32] to generalize the method to multivariate or stratified sampling designs.