Abstract
Pseudospectral methods are effective tools for solving optimal control problems, but they result in large-scale nonlinear programming (NLP) problems that are computationally demanding. A major bottleneck is the repeated evaluation of the objective function, system dynamics, path constraints, and their derivatives. This paper presents an approach to accelerating these computations using Graphics Processing Units (GPUs). We offload the evaluation of the NLP functions and their first and second derivatives to the GPU by developing custom CUDA kernels that exploit the parallelism in the discretized problem structure. The effectiveness of this method is demonstrated on a low-thrust interplanetary trajectory optimization problem. A comparison with a CPU implementation shows that the GPU-accelerated approach reduces the overall computational time. This work demonstrates the potential of GPU acceleration and provides a foundation for future research into fully GPU-native optimal control solvers.
MSC:
49M37; 49M25; 65K05
1. Introduction
Optimal control is a cornerstone of many modern engineering practices, including aerospace [1], chemistry [2], and biology [3], providing a systematic framework for designing trajectories [4] and control strategies [5] that optimize mission performance. Specifically, in the field of aerospace engineering, trajectory optimization, a key application of optimal control, is crucial for a wide range of missions, including launch vehicle ascent [6], satellite orbit transfers [7], interplanetary travel [8], and atmospheric entry, descent, and landing [9,10]. The primary objective is often to minimize fuel consumption, reduce flight time, or maximize payload mass, subject to complex system dynamics and operational constraints. The resulting optimal control problems are typically high-dimensional and nonlinear, posing significant computational challenges.
In general terms, methods for solving optimal control problems are classified as either indirect or direct approaches [1,11]. Indirect methods, based on Pontryagin’s Minimum Principle, provide necessary conditions for optimality and transform the original problem into a two- or multi-point boundary value problem (TPBVP). Although indirect methods can produce highly accurate solutions, they require the analytical derivation of the optimality conditions and a good initial guess due to their small radius of convergence [12].
Direct methods, in contrast, discretize the state and control variables, transcribing the continuous optimal control problem into a finite-dimensional nonlinear programming (NLP) problem. This NLP can then be solved using well-established numerical optimization algorithms, such as SNOPT [13] and IPOPT [14]. Direct methods are generally more robust, have a larger radius of convergence, and are more readily applicable to complex problems with path constraints. Among the various direct methods, pseudospectral collocation [15,16,17,18,19,20] has become a leading approach for trajectory optimization in aerospace and robotics. In these methods, the continuous-time problem is transcribed into an NLP by approximating the states and controls with global polynomials and enforcing the dynamics at Gaussian quadrature nodes [21]. This approach yields spectral convergence for smooth problems, allowing the solution to be approximated accurately with fewer collocation points.
For problems with long time horizons or complex dynamics, representing the state and control variables requires a large number of time points, creating challenges for both indirect and direct methods. In indirect methods, long durations lead to high sensitivity of the terminal state with respect to the initial costate guess, making the convergence of shooting methods difficult [12]. To mitigate this difficulty, techniques such as homotopy [12] and multiple shooting have been studied, and artificial intelligence has been explored to provide good initial costate estimates [22]. For direct methods, substantial work has also focused on computational efficiency. Prior studies have exploited the sparse structure of the resulting NLPs to accelerate the computation. For example, Patterson and Rao [23] derived closed-form expressions for the objective gradient, constraint Jacobian, and Hessian in a Radau pseudospectral transcription, showing that leveraging the sparsity in derivative computations substantially reduces the computational time. Mesh refinement techniques [24,25,26] provide another effective strategy by automatically detecting intervals where variables change rapidly and by placing denser mesh points in those regions while keeping other areas sparse. As a result, high accuracy is achieved with a relatively small number of mesh points, reducing the computational burden.
More recently, researchers have leveraged graphics processing units (GPUs) to accelerate scientific computing tasks, including optimal control solvers. For instance, an efficient GPU-based algorithm was developed for analyzing the dynamic response of fluid-saturated porous media, improving finite-element assembly and iterative solution efficiency for very large models [27]. For heat transfer, GPU-accelerated finite-difference methods have been applied to three-layer conduction problems, demonstrating stability and convergence [28]. In numerical linear algebra, an alternative GPU algorithm for very large sparse LU factorization employed a divide-and-conquer strategy to handle limited GPU memory while maintaining scalability [29]. In computational biology, GPU-accelerated Monte Carlo simulations enabled efficient modeling of cardiac hybrid cellular automata [30]. For robotics, GPU acceleration of convex approximations has allowed near-real-time multi-agent trajectory optimization by reformulating collision constraints into large unconstrained quadratic programs [31]. In applied mathematics, splitting schemes for differential matrix equations have been parallelized on GPUs, yielding significant speedups for Lyapunov and Riccati solvers [32]. In computational fluid dynamics, Roccon [33] reported a GPU port of a multi-phase Navier–Stokes pseudospectral code using OpenACC and cuFFT, achieving significant speedups by offloading fast Fourier transform (FFT)–based differentiation to the GPU. In the optimal control community, several efforts have similarly exploited GPU parallelism for trajectory optimization. Adabag et al. [34] introduced MPCGPU, a real-time nonlinear Model Predictive Control (MPC) solver that builds and solves the Karush–Kuhn–Tucker (KKT) linear system on the GPU using a custom parallel preconditioned conjugate gradient algorithm, thereby demonstrating faster linear solves than a CPU solver on large sparse problems. Similarly, Jeon et al. [35] presented CusADi, a GPU extension of the CasADi framework that automatically generates CUDA kernels for batched optimal control problem evaluation, reporting speedups over CPU-based MPC on parallel hardware. Collectively, these works show that GPUs can substantially reduce the computational time for pseudospectral methods and for the numerical solution of large-scale optimal control problems. Building on these advances, our work introduces custom CUDA kernels for pseudospectral collocation that explicitly exploit the inherent parallelism and sparsity of the discretized optimal control problem to achieve significant improvements over CPU-based solvers.
This paper presents a straightforward approach to accelerating pseudospectral methods for optimal control using GPUs. We offload the computationally intensive parts of the NLP formulation, including the evaluation of the objective function, system dynamics, path constraints, and their first and second derivatives, to the GPU. By designing CUDA kernels that exploit parallelism in the discretized problem structure, we reduce the time required to solve large-scale trajectory optimization problems. Numerical experiments demonstrate the effectiveness of our GPU-accelerated approach for Hessian evaluation, which is often one of the most time-consuming components in second-order optimization methods for large-scale NLPs. Although the NLP solver itself remains CPU-based, numerical experiments show that our GPU-accelerated approach achieves speedups compared to a CPU-only implementation. The proposed method provides a practical way to leverage GPU computing for optimal control problems requiring fine discretizations or involving complex dynamics. The primary contributions of this work are (i) a practical strategy to offload the expensive function evaluation phase of a direct method for optimal control problems, designed to leverage the GPU capabilities and the sparsity structure of the problem; (ii) a quantitative assessment of the speedup for each function type and for the overall solution process, providing a reference for practical deployment of GPU-accelerated direct methods; and (iii) a practical spacecraft trajectory optimization example demonstrating the applicability of the developed GPU-accelerated pseudospectral method to real aerospace problems.
The remainder of this paper is organized as follows. Section 2 details the mathematical formulation of the optimal control problem, the pseudospectral discretization method, and our GPU acceleration strategy. Section 3 presents a numerical case study of a low-thrust interplanetary trajectory optimization problem, comparing the performance of our GPU-accelerated implementation with that of a traditional CPU-based approach. Finally, Section 4 discusses the results, highlights the benefits and limitations of the proposed method, and outlines directions for future work.
2. Pseudospectral Method with GPU Acceleration
This section outlines the mathematical formulation of the optimal control problem, the pseudospectral discretization technique used to transcribe it into a nonlinear programming problem, and our strategy for accelerating the solution using GPUs.
2.1. Optimal Control Problem Formulation
We consider a general single-phase optimal control problem formulated as follows:
where is the state vector, is the control vector, F is the cost functional, defines the system dynamics, and represents path constraints. We assume that the functions , and are twice continuously differentiable with respect to all arguments in the interior of the feasible domain, which is necessary for NLP algorithms that use second-derivative information. This framework can be extended to multi-phase optimal control problems by applying the hardware acceleration to each phase independently.
2.2. Pseudospectral Discretization
To solve the optimal control problem numerically, we employ the Legendre–Gauss– Radau (LGR) pseudospectral method. Compared with the Legendre–Gauss (LG) and Legendre–Gauss–Lobatto (LGL) methods, the LGR method allows for a simpler implementation with comparable accuracy [21]. However, other choices are also suitable, and the GPU acceleration strategy described below is also applicable to other direct methods, such as LG and LGL pseudospectral methods, with only minor modifications.
To accommodate potentially free initial and final times, the time interval is linearly mapped to the normalized domain via
This transformation converts the original problem into an equivalent one on the fixed interval ; and are treated as optimization variables in the discretized NLP when they are not fixed. The system dynamics and cost are scaled accordingly:
where .
To handle complex dynamics and improve solution accuracy, the normalized interval is partitioned into M subintervals for , with and . Within each subinterval, the pseudospectral method transcribes the continuous-time problem into a finite-dimensional problem, and the results from all subintervals are assembled into a single large-scale NLP.
For each subinterval k, the state and control variables are approximated using -th degree Lagrange polynomials. These polynomials are based on a set of interpolation points, , in the canonical interval , to which the subinterval time is mapped. The approximations are given by
where and are the variable values at the interpolation points, and are the Lagrange basis polynomials. The subinterval time is mapped to . The points are the LGR collocation points [17,18], and is a non-collocated endpoint.
The time derivative of the state at a collocation point is approximated using a differentiation matrix [17,18]. This process transforms the differential equation into a set of algebraic constraints for each subinterval:
for , with . To ensure a continuous trajectory, the state vectors are linked at the subinterval boundaries, such that for . This continuity is enforced by using a single NLP variable for the state at the endpoint of subinterval k and the start point of subinterval .
The integral cost function is approximated by summing the quadrature approximations from each subinterval, and path constraints are enforced at each collocation point. The continuous problem is thus converted into a large, sparse NLP. The decision variables of this NLP are the discrete state and control vectors for all subintervals, , along with the initial and final times, , if they are free.
The pseudospectral discretization transcribes the continuous optimal control problem into the following finite-dimensional NLP problem:
Here and collect all discrete state and control variables, respectively; represents the LGR quadrature weights; and , . This finite-dimensional NLP can be solved using standard optimization algorithms.
2.3. GPU Acceleration
The discretization process transforms the continuous optimal control problem into a large-scale, sparse NLP. Solving this NLP is computationally expensive, as the problem size (in terms of decision variables and constraints) is directly proportional to the number of subintervals M and collocation points . Efficient solution of the NLP typically uses second-order optimization methods, which are preferred for their fast convergence. These solvers, regardless of the specific algorithm (active-set, interior-point, etc.), generally consist of three layers:
- Function Evaluation: Evaluation of the objective function, constraints, and their derivatives, including the Jacobian and the Hessian of the Lagrangian;
- NLP Algorithm: An iterative algorithm that updates the decision variables based on the function evaluations to find an optimal solution;
- Linear Algebra Solver: A solver for the KKT linear systems that arise in each iteration of the NLP solver, often involving factorization of large sparse symmetric indefinite matrices.
Among these layers, the function evaluation and linear algebra solver are the most computationally demanding [36]. In this work, we focus on accelerating the function evaluation layer using GPUs. Consequently, the NLP algorithm and linear algebra solver were not modified, as they require complex data structures and control flow that are not well suited for GPU execution without significant redesign. Thus, we adopt a hybrid CPU-GPU approach, where the function evaluations are offloaded to the GPU, and the NLP solver and linear algebra solver remain CPU-based. Our hybrid approach offers a pragmatic solution, accelerating the computationally intensive parts while leveraging the maturity and robustness of established CPU-based solvers.
The structure of the discretized problem is well suited to parallel computation because the calculations for each collocation point are largely independent. As shown in Equations (11)–(13), the objective function F, the dynamics function , and the path constraint function can be evaluated independently at each collocation point . Similarly, the first and second derivatives of these functions with respect to the state and control variables are independent across collocation points. This parallelism aligns well with the architecture of modern GPUs. Our approach is to offload the computationally demanding parts of the NLP solution process to the GPU. Specifically, we use the following strategies for evaluating the objective function, constraints, and their derivatives:
- Objective Function Evaluation: The integral cost function is approximated as a sum over all subintervals and collocation points. The contribution to the cost from each collocation point is computed in parallel. These values are then summed efficiently using parallel reduction techniques on the GPU to obtain the total cost.
- Dynamics and Path Constraint Evaluation: To evaluate the system dynamics and path constraints in parallel, we assign the calculations for each collocation point to a separate GPU thread. This allows for simultaneous computation of all dynamics and path constraints, reducing evaluation time. The matrix multiplications on the left-hand side of Equation (10) are less computationally demanding and are performed on the CPU using sparse matrix operations.
- Jacobian and Hessian Computation: Second-order optimization methods require the construction of the constraint Jacobian and the Hessian of the Lagrangian. The sparsity patterns of these matrices are fixed and can be determined beforehand. The first and second derivatives of the objective and constraint functions are independent for each collocation point, except for the terms involving matrix multiplication in the dynamics. We compute these derivatives in parallel on the GPU, with each thread calculating the derivatives for a single collocation point. This computation is performed sparsely, using pre-generated expressions for each nonzero entry in the Jacobian and Hessian. Since the differentiation matrix is sparse and fixed for a given discretization, the first derivatives of the matrix multiplication terms are handled by memory copy operations, and their second derivatives are zero.
By utilizing the parallel processing capabilities of GPUs, we accelerate the evaluation of the objective function, constraints, and their derivatives. This acceleration is especially effective for large-scale optimal control problems with complex dynamics and constraints, where the computational benefits of parallelism outweigh the overhead of data transfer between the CPU and GPU and kernel launch times. Since the memory usage is , where is the total number of collocation points, the required data easily fit into modern GPUs for practical values of N.
3. Numerical Experiment
3.1. Low-Thrust Trajectory Optimization Problem
To evaluate the proposed GPU-accelerated pseudospectral method, we applied it to a low-thrust trajectory optimization problem that was previously studied by Jiang et al. [37]. The objective is to minimize the fuel consumption for a spacecraft transferring between two orbits using low-thrust propulsion. We used the modified equinoctial elements (MEEs) to describe the spacecraft’s orbit. The MEEs are defined as [38]
where a is the semi-major axis, e is the eccentricity, i is the inclination, is the right ascension of the ascending node, is the argument of perigee, and is the true anomaly. When the spacecraft is subject only to central gravitation from a central celestial body such as the Sun, the five elements a, e, i, , and remain constant. To account for the change in mass due to fuel consumption, the spacecraft’s mass m was included as a state variable. The complete state vector is . The control vector is , where , , and are the radial, tangential, and normal components of the thrust vector, respectively.
The equations of motion for a spacecraft under central gravitation and low-thrust propulsion, expressed in MEE, are given by [38]
where , , and are the components of thrust acceleration. The auxiliary variables are and . Additionally, is the gravitational parameter of the central body, is the specific impulse of the thruster, and is the standard gravitational acceleration, 9.80665 m/s2.
The optimization problem is formulated as follows:
where is the maximum allowable thrust magnitude and represents the system dynamics defined by Equations (17)–(22).
3.2. Problem Setup
3.2.1. Initial and Final Conditions
The initial and final conditions for the low-thrust trajectory optimization problem are specified in Table 1. The problem considers a rendezvous maneuver from the Earth to Venus, where the spacecraft’s boundary position and velocity match those of the respective planets. The spacecraft’s initial mass is 1500 kg, while the final mass is free; maximizing the final mass is equivalent to minimizing fuel consumption. The initial epoch is 7 October 2005 00:00:00 (coordinate time), and the total transfer time is fixed at 1000 days. The spacecraft is equipped with a low-thrust propulsion system that provides a maximum thrust of 0.33 N and has a specific impulse of 3800 s. The Sun’s gravitational parameter is m3/s2.

Table 1.
Initial and final conditions for the low-thrust transfer problem.
3.2.2. Problem Discretization Parameters
The LGR pseudospectral method and GPU acceleration strategy described in Section 2 were used to discretize and solve the low-thrust trajectory optimization problem. To assess the computational benefits of our approach, we performed a series of tests comparing the GPU-accelerated implementation with a CPU-only baseline. The problem was solved using different numbers of subintervals (M), ranging from 64 to 4096, with collocation points per subinterval. This setup allowed us to analyze how performance scales with the size of the resulting NLP problem.
3.2.3. Initial Guess Generation
An initial guess is needed to start the optimization process. For the MEE states, the guess was generated by linearly interpolating between the initial and final conditions. The initial guess for the mass was set to its initial value of 1500 kg for the entire trajectory. The control inputs were initialized to at all times. This straightforward initial guess provides a reasonable starting point for the optimization algorithm to converge to an optimal solution. The method is robust against initial guesses, and simple initial guesses such as linear interpolation or zero controls typically lead to convergence.
3.2.4. Software Implementation
The pseudospectral method was implemented in C++, with the GPU-accelerated components developed using the NVIDIA CUDA framework. The resulting NLP was solved using IPOPT [14], a solver well-suited to large-scale nonlinear optimization. The HSL MA57 solver [39] handled the underlying sparse linear algebra operations. For comparison, a CPU-only baseline version was also implemented, which executed its parallel components using Single Instruction, Multiple Data (SIMD) instructions through the Eigen library [40].
3.2.5. Hardware Environment
The numerical experiments were conducted on a laptop equipped with an Intel Core i9-13900HX CPU, an NVIDIA GeForce RTX 4060 Laptop GPU, and 64 GB of RAM.
3.3. Performance Analysis
3.3.1. Solution Accuracy
In all test cases reported below, the solver converged to solutions that satisfied the first-order optimality conditions. We verified the accuracy using two checks:
- For a given number of subintervals M, the CPU and GPU solutions agreed with at least 10 significant digits in the objective value J, as computed by both implementations.
- Solutions computed with different numbers of subintervals agreed with the value reported by Jiang et al. [37] with a relative error of less than 0.01% in the objective value J.
Reference plots of the orbit and thrust profile obtained with subintervals are shown in Figure 1 and Figure 2, respectively. The spacecraft departs from the Earth’s orbit and spirals inward to reach Venus. The thrust profile exhibits a bang–bang structure, which is typical for low-thrust optimal control problems.
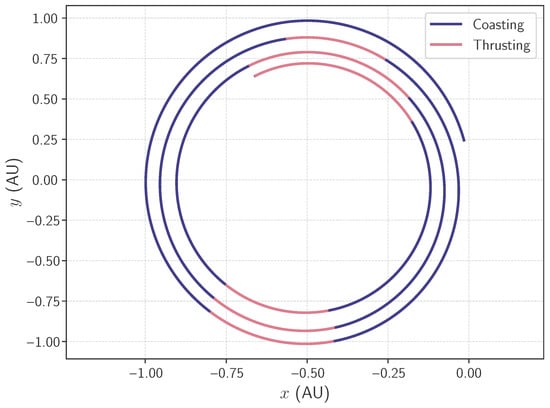
Figure 1.
Optimal trajectory for the Earth-to Venus-problem with subintervals. The trajectory is projected onto the x-y plane.
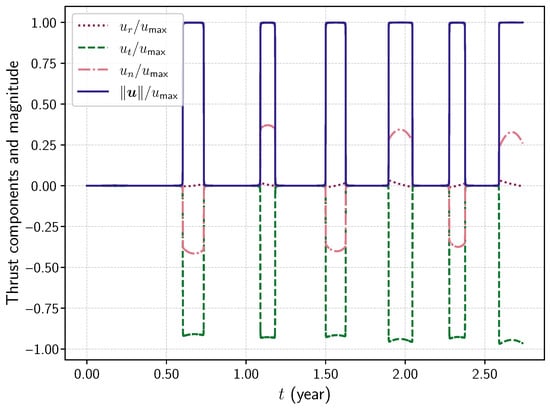
Figure 2.
Optimal thrust profile for the Earth-to-Venus problem with subintervals. The thrust magnitude is normalized by the maximum thrust .
3.3.2. Time Breakdown
To provide a detailed analysis of computational performance, we measured the average time required for each major component of the NLP evaluation: objective function evaluation, constraint evaluation, Jacobian computation, and Hessian computation. These measurements were taken for both the CPU and GPU implementations for different numbers of subintervals M.
The speedup for each component is calculated as the ratio of CPU time to GPU time, . Table 2 reports the computational times in seconds and the corresponding speedups for each component, while Figure 3 illustrates the ratios. The results indicate that GPU acceleration provides a significant speedup for Hessian evaluation, whereas the other components are slower on the GPU. Hessian evaluation is the most computationally intensive part of the NLP evaluation and benefits most from parallel execution. In contrast, the other components require less computation, so kernel launch and data transfer overhead dominate, incurring a latency on the order of tens of microseconds and negating the benefits for functions with very short CPU evaluation times. These results highlight the value of GPU parallelism for second-order NLP solvers, where efficient Hessian evaluation is critical to performance.

Table 2.
CPU and GPU runtimes (in seconds) and their ratios for different M.
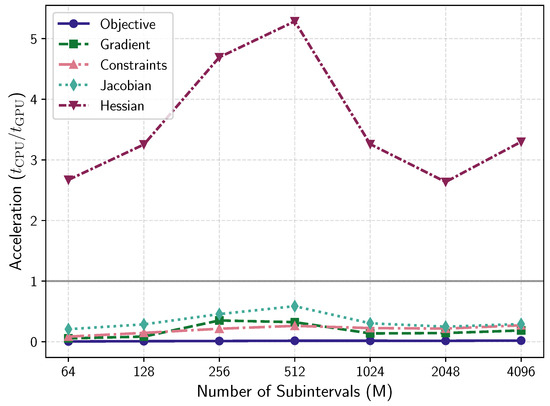
Figure 3.
Acceleration ratios for key NLP evaluation components (objective, gradient, constraint, Jacobian, Hessian) as a function of the number of subintervals M. Values greater than 1 indicate a speedup using GPU acceleration.
3.3.3. Overall Performance
Based on the time breakdowns, we tested two GPU offloading strategies:
- Full Offload: All components (objective function, gradient, constraints, Jacobian, and Hessian) are computed on the GPU.
- Heterogeneous Offload: Only the Hessian evaluation is offloaded to the GPU, while the other components are computed on the CPU.
The overall computational time for solving the NLP with IPOPT was measured for both strategies and compared to the CPU-only baseline. The results are shown in Figure 4.
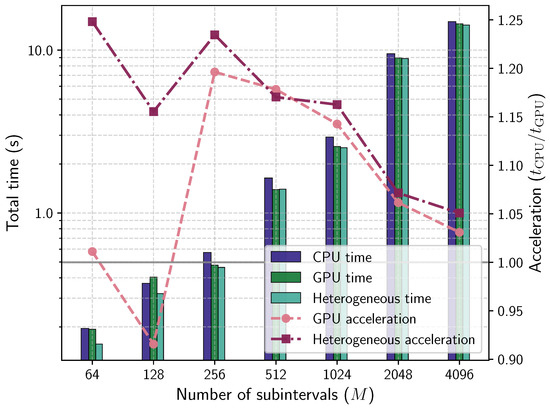
Figure 4.
Overall acceleration ratio using the CPU-only implementation as the baseline. Three configurations are shown: CPU-only (baseline), full GPU (objective, constraints, first and second derivatives offloaded), and heterogeneous (only Hessian offloaded). Values greater than 1 indicate a speedup using GPU acceleration.
For problems with small sizes, the Heterogeneous Offload strategy provided a modest speedup over the CPU baseline, while the Full Offload strategy was slower due to the overhead of data transfer between the CPU and GPU and the kernel launch times. As the problem size increased, both GPU strategies showed improved performance compared to the CPU baseline. For large problems, the dominant computational cost shifted to the linear algebra operations for the KKT system, such as the LDLT factorization and backsolve, which are performed on the CPU and have a complexity greater than . The time required for these operations increased with problem size, reducing the relative impact of the GPU-accelerated components. As a result, the overall acceleration ratios for both GPU strategies decreased for the largest problems.
4. Discussion and Conclusions
This work introduced a GPU-accelerated pseudospectral method for large-scale optimal control problems, focusing on the evaluation of objective functions, system dynamics, path constraints, and their derivatives. Numerical experiments on a low-thrust interplanetary trajectory optimization problem demonstrated that GPU acceleration yields substantial speedups, especially for the most computationally intensive components such as Hessian evaluation. The proposed framework enables the efficient solution of optimal control problems and supports advanced mission design and analysis in aerospace and related fields.
Future research will focus on developing fully GPU-native optimal control solvers, including GPU-based sparse linear algebra and interior-point methods, to further reduce data transfer overhead and improve scalability. This would involve creating custom GPU kernels for the core NLP algorithm and linear algebra layers. Additionally, investigating the energy efficiency of GPU-accelerated solvers compared to CPU-only implementations could provide valuable insights for real-time embedded systems, such as those used in MPC applications.
Author Contributions
Conceptualization, Y.Z. and F.J.; Methodology, Y.Z. and F.J.; Software, Y.Z.; Validation, Y.Z. and F.J.; Formal analysis, Y.Z. and F.J.; Investigation, Y.Z. and F.J.; Resources, Y.Z. and F.J.; Data curation, Y.Z.; Writing—original draft, Y.Z.; Writing—review and editing, Y.Z. and F.J.; Visualization, Y.Z.; Supervision, F.J.; Project administration, F.J.; Funding acquisition, F.J. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (Grant No. 12472355).
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Acknowledgments
The authors thank Arthur Gabriel for helping to refine the language. During the preparation of this manuscript, the authors also used ChatGPT (https://chatgpt.com) to improve readability. The authors have reviewed and edited all content and take full responsibility for the publication.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CPU | Central processing unit |
| GPU | Graphics processing unit |
| CUDA | Compute Unified Device Architecture |
| NLP | Nonlinear programming |
| TPBVP | Two-point boundary value problem |
| FFT | Fast Fourier transform |
| MPC | Model predictive control |
| KKT | Karush–Kuhn–Tucker |
| LG | Legendre–Gauss |
| LGR | Legendre–Gauss–Radau |
| LGL | Legendre–Gauss–Lobatto |
| MEE | Modified equinoctial element |
| AU | Astronomical unit |
| SIMD | Single instruction, multiple data |
References
- Betts, J.T. Survey of Numerical Methods for Trajectory Optimization. J. Guid. Control Dyn. 1998, 21, 193–207. [Google Scholar] [CrossRef]
- Andres-Martinez, O.; Palma-Flores, O.; Ricardez-Sandoval, L. Optimal control and the Pontryagin’s principle in chemical engineering: History, theory, and challenges. AIChE J. 2022, 68, e17777. [Google Scholar] [CrossRef]
- Baleanu, D.; Jajarmi, A.; Sajjadi, S.; Mozyrska, D. A new fractional model and optimal control of a tumor-immune surveillance with non-singular derivative operator. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 083127. [Google Scholar] [CrossRef] [PubMed]
- Kelly, M. An Introduction to Trajectory Optimization: How to Do Your Own Direct Collocation. SIAM Rev. 2017, 59, 849–904. [Google Scholar] [CrossRef]
- Wang, J.; Cui, N.; Wei, C. Optimal Rocket Landing Guidance Using Convex Optimization and Model Predictive Control. J. Guid. Control Dyn. 2019, 42, 1078–1092. [Google Scholar] [CrossRef]
- Benedikter, B.; Zavoli, A.; Colasurdo, G.; Pizzurro, S.; Cavallini, E. Convex Approach to Three-Dimensional Launch Vehicle Ascent Trajectory Optimization. J. Guid. Control Dyn. 2021, 44, 1116–1131. [Google Scholar] [CrossRef]
- Gao, Y. Near-Optimal Very Low-Thrust Earth-Orbit Transfers and Guidance Schemes. J. Guid. Control Dyn. 2007, 30, 529–539. [Google Scholar] [CrossRef]
- Quarta, A.A.; Mengali, G.; Bassetto, M.; Niccolai, L. Optimal Interplanetary Trajectories for Sun-facing Ideal Diffractive Sails. Astrodynamics 2023, 7, 285–299. [Google Scholar] [CrossRef]
- Lu, P.; Sandoval, S.; Davami, C. Fast and Robust Optimization of Full Trajectory from Entry Through Powered Descent. J. Guid. Control Dyn. 2024, 47, 203–216. [Google Scholar] [CrossRef]
- Li, W.; Song, Y.; Cheng, L.; Gong, S. Closed-Loop Deep Neural Network Optimal Control Algorithm and Error Analysis for Powered Landing under Uncertainties. Astrodynamics 2023, 7, 211–228. [Google Scholar] [CrossRef]
- Ottesen, D.; Russell, R.P. Direct-to-Indirect Mapping for Optimal Low-Thrust Trajectories. Astrodynamics 2024, 8, 27–46. [Google Scholar] [CrossRef]
- Haberkorn, T.; Martinon, P.; Gergaud, J. Low Thrust Minimum-Fuel Orbital Transfer: A Homotopic Approach. J. Guid. Control Dyn. 2004, 27, 1046–1060. [Google Scholar] [CrossRef]
- Gill, P.E.; Murray, W.; Saunders, M.A. SNOPT: An SQP Algorithm for Large-Scale Constrained Optimization. SIAM J. Optim. 2002, 12, 979–1006. [Google Scholar] [CrossRef]
- Wächter, A.; Biegler, L.T. On the Implementation of an Interior-Point Filter Line-Search Algorithm for Large-Scale Nonlinear Programming. Math. Program. 2006, 106, 25–57. [Google Scholar] [CrossRef]
- Benson, D.A.; Huntington, G.T.; Thorvaldsen, T.P.; Rao, A.V. Direct Trajectory Optimization and Costate Estimation via an Orthogonal Collocation Method. J. Guid. Control Dyn. 2006, 29, 1435–1440. [Google Scholar] [CrossRef]
- Benson, D. A Gauss Pseudospectral Transcription for Optimal Control. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2005. [Google Scholar]
- Garg, D.; Patterson, M.A.; Francolin, C.; Darby, C.L.; Huntington, G.T.; Hager, W.W.; Rao, A.V. Direct trajectory optimization and costate estimation of finite-horizon and infinite-horizon optimal control problems using a Radau pseudospectral method. Comput. Optim. Appl. 2011, 49, 335–358. [Google Scholar] [CrossRef]
- Kameswaran, S.; Biegler, L.T. Convergence rates for direct transcription of optimal control problems using collocation at Radau points. Comput. Optim. Appl. 2008, 41, 81–126. [Google Scholar] [CrossRef]
- Elnagar, G.; Kazemi, M.; Razzaghi, M. The pseudospectral Legendre method for discretizing optimal control problems. IEEE Trans. Autom. Control 1995, 40, 1793–1796. [Google Scholar] [CrossRef]
- Fahroo, F.; Ross, I.M. Costate Estimation by a Legendre Pseudospectral Method. J. Guid. Control Dyn. 2001, 24, 270–277. [Google Scholar] [CrossRef]
- Garg, D.; Patterson, M.; Hager, W.W.; Rao, A.V.; Benson, D.A.; Huntington, G.T. A Unified Framework for the Numerical Solution of Optimal Control Problems Using Pseudospectral Methods. Automatica 2010, 46, 1843–1851. [Google Scholar] [CrossRef]
- Wu, D.; Cheng, L.; Gong, S.; Baoyin, H. Low-Thrust Trajectory Optimization with Averaged Dynamics Using Analytical Switching Detection. J. Guid. Control Dyn. 2024, 47, 1135–1149. [Google Scholar] [CrossRef]
- Patterson, M.A.; Rao, A.V. Exploiting Sparsity in Direct Collocation Pseudospectral Methods for Solving Optimal Control Problems. J. Spacecr. Rocket. 2012, 49, 354–377. [Google Scholar] [CrossRef]
- Betts, J.T. Practical Methods for Optimal Control and Estimation Using Nonlinear Programming, Second Edition, 2nd ed.; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2010. [Google Scholar] [CrossRef]
- Jain, S.; Tsiotras, P. Trajectory optimization using multiresolution techniques. J. Guid. Control Dyn. 2008, 31, 1424–1436. [Google Scholar] [CrossRef]
- Fornberg, B. A Practical Guide to Pseudospectral Methods; Cambridge Monographs on Applied and Computational Mathematics, Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Lin, W.; Zhou, Q.; Chen, X.; Shi, W.; Ai, J. An Efficient GPU-Accelerated Algorithm for Solving Dynamic Response of Fluid-Saturated Porous Media. Mathematics 2025, 13, 181. [Google Scholar] [CrossRef]
- Murúa, N.; Coronel, A.; Tello, A.; Berres, S.; Huancas, F. GPU Accelerating Algorithms for Three-Layered Heat Conduction Simulations. Mathematics 2024, 12, 3503. [Google Scholar] [CrossRef]
- Chen, J.; Zhu, P. An Alternate GPU-Accelerated Algorithm for Very Large Sparse LU Factorization. Mathematics 2023, 11, 3149. [Google Scholar] [CrossRef]
- Treml, L.M.; Bartocci, E.; Gizzi, A. Modeling and Analysis of Cardiac Hybrid Cellular Automata via GPU-Accelerated Monte Carlo Simulation. Mathematics 2021, 9, 164. [Google Scholar] [CrossRef]
- Rastgar, F.; Masnavi, H.; Shrestha, J.; Kruusamäe, K.; Aabloo, A.; Singh, A.K. GPU Accelerated Convex Approximations for Fast Multi-Agent Trajectory Optimization. IEEE Robot. Autom. Lett. 2021, 6, 3303–3310. [Google Scholar] [CrossRef]
- Mena, H.; Pfurtscheller, L.M.; Stillfjord, T. GPU Acceleration of Splitting Schemes Applied to Differential Matrix Equations. Numer. Algorithms 2020, 83, 395–419. [Google Scholar] [CrossRef]
- Roccon, A. A GPU-ready Pseudo-Spectral Method for Direct Numerical Simulations of Multiphase Turbulence. Procedia Comput. Sci. 2024, 240, 17–30. [Google Scholar] [CrossRef]
- Adabag, E.; Atal, M.; Gerard, W.; Plancher, B. MPCGPU: Real-Time Nonlinear Model Predictive Control through Preconditioned Conjugate Gradient on the GPU. In Proceedings of the 2024 IEEE International Conference on Robotics and Automation (ICRA), Yokohama, Japan, 13–17 May 2024; pp. 9787–9794. [Google Scholar] [CrossRef]
- Jeon, S.H.; Hong, S.; Lee, H.J.; Khazoom, C.; Kim, S. CusADi: A GPU Parallelization Framework for Symbolic Expressions and Optimal Control. IEEE Robot. Autom. Lett. 2025, 10, 899–906. [Google Scholar] [CrossRef]
- Diehl, M.; Ferreau, H.J.; Haverbeke, N. Efficient Numerical Methods for Nonlinear MPC and Moving Horizon Estimation. In Nonlinear Model Predictive Control: Towards New Challenging Applications; Magni, L., Raimondo, D.M., Allgöwer, F., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 391–417. [Google Scholar] [CrossRef]
- Jiang, F.; Baoyin, H.; Li, J. Practical Techniques for Low-Thrust Trajectory Optimization with Homotopic Approach. J. Guid. Control Dyn. 2012, 35, 245–258. [Google Scholar] [CrossRef]
- Walker, M.J.H.; Ireland, B.; Owens, J. A Set of Modified Equinoctial Orbit Elements. Celest. Mech. 1985, 36, 409–419. [Google Scholar] [CrossRef]
- Gould, N.I.M.; Scott, J.A. A Numerical Evaluation of HSL Packages for the Direct Solution of Large Sparse, Symmetric Linear Systems of Equations. ACM Trans. Math. Softw. 2004, 30, 300–325. [Google Scholar] [CrossRef]
- Guennebaud, G.; Jacob, B. Eigen v3. 2010. Available online: http://eigen.tuxfamily.org (accessed on 1 October 2025).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).