New Results on the Computation of Periods of IETs

Abstract

We introduce a novel technique for computing the periods of $(d,k)$-IETs based on Rauzy induction $\mathcal{R}$. Specifically, we establish a connection between the set of periods of an interval exchange transformation (IET) T and those of the IET $T^{\prime }$ obtained either by applying the Rauzy operator $\mathcal{R}$ to T or by considering the Poincaré first return map. Rauzy matrices play a central role in this correspondence whenever T lies in the domain of $\mathcal{R}$ (Theorem 4). Furthermore, Theorem 6 addresses the case when T is not in the domain of $\mathcal{R}$, while Theorem 5 deals with IETs having associated reducible permutations. As an application, we characterize the set of periods of oriented 3-IETs (Theorem 8), and we also propose a general framework for studying the periods of $(d,k)$-IETs. Our approach provides a systematic method for determining the periods of non-transitive IETs. In general, given an IET with d discontinuities, if Rauzy induction allows us to descend to another IET whose periodic components are already known, then the main theorems of this paper can be applied to recover the set of periods of the original IET. This method has been also applied to obtain the set of periods of all $(2,k)$-IETs and some $(3,k)$-IETs, $k\ge 1$. Several open problems are presented at the end of the paper.

1. Introduction

Given $d\in \mathbb{N}=\{1,2,3,\dots \}$ and a real positive number ℓ, a d-IET is an injective map $T:D\subset (0,\ell )\to (0,\ell )$ such that

(i):

D is the union of d pairwise disjoint open intervals, $D={\bigcup }_{i=1}^d{I}_i$, with $I_i=(a_i,a_{i+1})$, $0=a_1<a_2<a_3<\dots <a_{d+1}=\ell$;

(ii):

${T|}_{I_i}$ is an affine map of constant slope equals to 1 or $-1$, $i=1,2,\dots ,d$.

When the slope of T is negative in the family of intervals $\mathcal{F}=\{I_{f_1},I_{f_2},\dots ,I_{f_k}\}$, $k\le d$, we say that T is an interval exchange transformation of d intervals with k flips or a (d,k)-IET; otherwise, we say that T is an interval exchange transformation of d intervals without flips or an oriented interval exchange transformation of d intervals. We will say that T is a proper$(d,k)$-IET if the points $a_i$, $2\le i\le d$, are not false discontinuities.

The orbit of $x\in (0,\ell )$, generated by T, is the set

$${\mathcal{O}}_T\left(x\right)=\{T^m\left(x\right):m\mathrm{is}\mathrm{an}\mathrm{integer}\mathrm{and}{T}^m\left(x\right)\mathrm{makes}\mathrm{sense}\},$$

where $T^0=\mathrm{Id}$, $T^{-1}$ is the inverse map of T, and $T^{\pm n}=T^{\pm }\circ T^{\pm (n-1)}$ for any $n\in \mathbb{N}$. Moreover, ${\mathcal{O}}_T\left(0\right)=\left\{0\right\}\cup {\mathcal{O}}_T\left({lim}_{x\to 0^{+}}T\left(x\right)\right)$ and ${\mathcal{O}}_T(\ell )=\{\ell \}\cup {\mathcal{O}}_T\left({lim}_{x\to {\ell }^{-}}T\left(x\right)\right)$. We say that $x\in D$ is periodic if there is $m\in \mathbb{N}$ such that $T^m\left(x\right)=x$ and $T^i\left(x\right)\ne x$ for all $0<i<m$. In that case m is the period of x. When $m=1$ we have fixed points. By $\mathrm{Per}\left(T\right)$ we denote the set of all the periods of periodic points of T. T is said to be minimal if ${\mathcal{O}}_T\left(x\right)$ is dense in $[0,\ell ]$ for any $x\in [0,\ell ]$, while T is transitive if it has a dense orbit in $[0,\ell ]$. This notion of minimality is equal to say that T is transitive and it does not have finite orbits, see (Remark 1, [1]).

The points from ${\left\{a_i\right\}}_{i=2}^d$ are called singular points of T; also, 0 and ℓ are the endpoints of T. We define

$$w_1=w_1^{+}=\underset{x\to 0^{+}}{lim}T\left(x\right),w_{d+1}=w_{d+1}^{-}=\underset{x\to {\ell }^{-}}{lim}T\left(x\right),$$

$$w_j^{+}=\underset{x\to a_j^{+}}{lim}T\left(x\right)\mathrm{and}{w}_j^{-}=\underset{x\to a_j^{-}}{lim}T\left(x\right)\mathrm{for}\mathrm{any}2\le j\le d.$$

Let $w_r\in \{w_r^{+},w_r^{-}\}$, $2\le r\le d$. If there exist $r,s\in \{1,2,\dots ,d+1\}$, $2\le r\le d$, and $p\ge 0$ such that $\mathcal{C}=\{a_r,w_r,T\left(w_r\right),\dots ,T^p\left(w_r\right)=a_s\}$ then $\mathcal{C}$ is said to be a saddle connection. We denote by $\mathcal{S}$ the set of saddle points, that is, $\mathcal{S}=\{x\in [0,\ell ]:x\in \mathcal{C}\mathrm{for}\mathrm{some}\mathrm{saddle}\mathrm{connection}\mathcal{C}\}$. Note that any IET always has trivial saddle connections containing 0 and ℓ, so $0,\ell \in \mathcal{S}$. However, any IET which does not have other saddle connections is minimal, see (Corollary 14.5.12, p.474, [2]) and (Th. 3, [3]).

Interval exchange transformations have been studied due to their intrinsic interest and their applications in different research areas, for example surface flows, Teichmüller flows, continued fraction expansions and polygonal billiards; see [1] and references therein.

The study of the set of periods of continuous functions on the interval has a long tradition, tracing back to the celebrated Sharkovsky’s Theorem which provides the solution when the maps are continuous [4,5]. Numerous works have extended this topic by considering alternative phase spaces or by considering non-autonomous dynamical systems. A comprehensive review on this subject can be found in [6].

Studying this problem for IETs is a natural extension of Sharkovsky’s framework. In particular, the present authors initiated this classification for 2-IETs in [7], and for certain specific cases of 3-IETs. As far as we know, the question of computing the periods of IETs has been only considered in [7] with a direct approach. In this paper, we introduce the matrix of periods to try to obtain the set of periods of general IETs relating them with the transformed ones by the Rauzy operator.

An additional motivation was the problem proposed by Misiurewicz, see [8], which consists in characterizing all possible sets of periods of periodic orbits of interval maps $f:[0,1/2)\cup (1/2,1]\to [0,1]$ such that f is continuous and strictly increasing on $[0,1/2)$, and continuous and strictly decreasing on $(1/2,1]$. This setting allows us to characterize the set of periods of 2-IETs. The resulting classification is as follows (see (Th. 7, [7])):

Theorem 1.

Let T be a 2-IET, let $n\ge 0$ be an integer and let A be one of the following sets: ∅, $\{n+1\}$, $\{n+1,2(n+1\left)\right\}$, $\left\{n+1,2(n+1),n+2,2(n+2)\right\}$. Then, $\mathrm{Per}\left(T\right)=A$ for some of the above sets.

Conversely, given an above set A, there exists a 2-IET, T, with $\mathrm{Per}\left(T\right)=A$.

The main goal of this paper is to provide a new technique for computing periods of IETs, based on the fact that it is possible to relate the periods sets of any IET and the periods of its induced maps by the Rauzy operator, see below Theorems 4–6. As a consequence of this connection, we apply these general results in order to give a complete description of the set of periods that oriented 3-IETs can have, see Theorem 8; as another application of this investigation, we will also analyze the flipped IETs of a particular non oriented Rauzy class.

The paper is organized as follows. In Section 2, we introduce the Rauzy induction operator $\mathcal{R}$, which allows us to relate the periods sets of any IET T and the periods of its induced maps $T^{\left(k\right)}$ by means of $\mathcal{R}$ and certain matrices of periods $P\left(T\right),P\left(T^{\left(k\right)}\right)$. This connection will be clarified in Section 3 by means of Theorems 4–6. Then, we will analyze the case of 2-IETs in Section 4. Although Theorem 1 gives a full answer to the characterization of periods for 2-IETs, we devote a section to this class of maps to show the reader the strength of the new approach by Rauzy induction because in (Th. 7, [7]), the analysis was practically direct. In Section 5, we will study the case referring to 3-IETs. We characterize in Theorem 8 the possible sets of periods for oriented 3-IETs, and in the rest of the section we illustrate the new technique with a class of non-oriented IETs.

This paper can be viewed as a continuation of the study begun in [7]. Now, we have presented a new technique, based on the Rauzy induction, and in a general framework, for computing periods of $(d,k)$-IETs.

2. Folklore Results

In this section, we introduce the way of codifying IETs and some known results that we need in the following, concerning the Rauzy induction and in relation with a certain matrix of periods $P\left(T\right)$.

2.1. Coordinates in the Set of IETs

An easy way to work with IETs is introducing coordinates, which allow us to identify any IET with a couple of data $(\lambda ,\pi )$, where $\lambda$ is a vector of positive entries and $\pi$ is a (signed) permutation. We follow [1] for the notation and terminology. To do that, for $d\in \mathbb{N}$, there exists a natural injection between the set of d-IETs and ${\mathcal{C}}_d={\Lambda }^d\times S_d^{\sigma }$, where ${\mathbb{R}}_{+}=(0,\infty )$, ${\Lambda }^d$ is the cone ${\mathbb{R}}_{+}^d$ and $S_d^{\sigma }$ is the set of signed permutations. A signed permutation is an injective map $\pi :N_d=\{1,2,\dots ,d\}\to N_d^{\sigma }=\{-d,-(d-1),\dots ,-1,1,2,\dots ,d\}$ such that $\left|\pi \right|:N_d\to N_d$ is bijective, that is, a standard permutation; a non standard permutation will be a signed permutation $\pi$, thus holding $\pi \left(i\right)<0$ for some i. As in the case of standard permutations, $\pi$ will be represented by the tuple $(\pi \left(1\right),\pi \left(2\right),\dots ,\pi \left(d\right))\in {\left(N_d^{\sigma }\right)}^d.$ Let T be an d-IET like in the preceding initial section; then, its associated coordinates in ${\mathcal{C}}_d$ are $(\lambda ,\pi )$, defined by

• ${\lambda }_i=a_{i+1}-a_i$ for all $i\in N_d$.
• $\pi \left(i\right)$ is positive (resp. negative) if ${T|}_{I_i}$ has slope 1 (resp. $-1$). Moreover $\left|\pi \right(i\left)\right|$ is the position of the interval $T\left(I_i\right)$ in the set ${\left\{T\left(I_i\right)\right\}}_{i=1}^d$ taking into account the usual order in $\mathbb{R}$.

Conversely, given a pair $(\lambda ,\pi )\in {\mathcal{C}}_d$ we can associate to it a unique d-IET, $T:D\subset [0,\ell ]\to [0,\ell ]$, where

• $\ell =\left|\lambda \right|:={\sum }_{i=1}^d{\lambda }_i$;
• $I_1=(0,{\lambda }_1)$;
• $I_i=({\sum }_{j=1}^{i-1}{\lambda }_j,{\sum }_{j=1}^i{\lambda }_j)$ for any $1<i\le d$;
• ${T|}_{I_i}\left(x\right)=\left({\sum }_{j=1}^{\left|\pi \right|\left(i\right)-{\displaystyle \frac{\sigma \left(\pi \right(i\left)\right)+1}{2}}}{\lambda }_{{\left|\pi \right|}^{-1}\left(j\right)}\right)+\sigma \left(\pi \left(i\right)\right)\left[x-\left({\sum }_{j=1}^{i-1}{\lambda }_j\right)\right],$ for any $1\le i\le d$, where $\sigma \left(z\right)$ denotes the sign of $z\in \mathbb{R}\setminus \left\{0\right\},$ namely, $\sigma \left(z\right)={\displaystyle \frac{z}{\left|z\right|}}.$

These coordinates allow us to make the identification $T=(\lambda ,\pi )$. For a fixed permutation $\pi ,$ we can consider the Lebesgue measure of the cone ${\Lambda }^d$ on the set of d-IETs having associated permutation $\pi$.

A permutation $\pi :N_d\to N_d^{\sigma }$ is said to be irreducible if $\left|\pi \right(\{1,2,\dots t\}\left)\right|\ne \{1,2,\dots ,t\}$ for any $1\le t<d$. The set of irreducible permutations is denoted by $S_d^{\sigma ,\ast }$. We will write $S_d^{\sigma ,+}$ to denote the set of permutations, $\pi \in S_d^{\sigma }$, satisfying $\left|\pi \right|\left(d\right)\ne d$. Observe that $S_d^{\sigma ,\ast }\subset S_d^{\sigma ,+}\subset S_d^{\sigma }$. It is easily seen that if $(\lambda ,\pi )$ is a minimal d-IET (not necessarily oriented), then $\pi$ is irreducible.

2.2. Rauzy Induction

In most situations, the generalized Rauzy induction is an operator in the set of IETs which sends any $T:D\subset [0,\ell ]\to [0,\ell ]$ to its first return map on some subinterval $[0,{\ell }^{\prime }]⊊[0,\ell ].$ We pass to give a formalization of this operator, by means of the maps a and b defined on $S_d^{\sigma }$. In the final part of this subsection, we investigate the relationship between the Rauzy induction and the existence of minimal IETs with flips (see Theorem 2).

Let $x\in \mathbb{R}\setminus \left\{0\right\}$. Recall that the sign of x is denoted by $\sigma \left(x\right).$ The generalized Rauzy maps were introduced by Nogueira in [9] (cf. also [10]) and are $a,b:S_d^{\sigma ,+}\to S_d^{\sigma },$ where $a\left(\pi \right)$ and $b\left(\pi \right)$ are the permutations defined by

$$a\left(\pi \right)\left(i\right)=\left\{\begin{array}{cc}\pi \left(i\right)\hfill & \mathrm{if}\left|\pi \left(i\right)\right|\le \left|\pi \left(d\right)\right|-{\displaystyle \frac{1-\sigma \left(\pi \right(d\left)\right)}{2}},\hfill \\ \sigma \left(\pi \left(d\right)\right)\sigma \left(\pi \left(i\right)\right)(|\pi \left(d\right)|+{\displaystyle \frac{1+\sigma \left(\pi \right(d\left)\right)}{2}})\hfill & \mathrm{if}\left|\pi \right(i\left)\right|=d,\hfill \\ \sigma \left(\pi \right(i\left)\right)\left(\right|\pi \left(i\right)|+1)\hfill & \mathrm{otherwise},\hfill \end{array}\right.$$

(1)

and

$$b\left(\pi \right)\left(i\right)=\left\{\begin{array}{cc}\pi \left(i\right)\hfill & \mathrm{if}i\le {\left|\pi \right|}^{-1}\left(d\right)+{\displaystyle \frac{{\sigma \left(\pi \right(\left|\pi \right|}^{-1}\left(d\right)\left)\right)-1}{2}},\hfill \\ {\sigma \left(\pi \right(\left|\pi \right|}^{-1}\left(d\right)\left)\right)\pi \left(d\right)\hfill & \mathrm{if}i={\left|\pi \right|}^{-1}\left(d\right)+{\displaystyle \frac{{\sigma \left(\pi \right(\left|\pi \right|}^{-1}\left(d\right)\left)\right)-1}{2}}+1,\hfill \\ \pi (i-1)\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(2)

Together with these maps, we also define the generalized Rauzy matrices associated to a permutation $\pi \in S_d^{\sigma ,+}$, $M_a\left(\pi \right)$ and $M_b\left(\pi \right)$. Given $1\le i,j\le d$, $E_{i,j}$ denotes the $d\times d$ matrix having zeros in all the positions except for the position $(i,j)$ which is equal to 1, and ${\mathrm{Id}}_d$ denotes the $d\times d$ identity matrix. The definitions of $M_a\left(\pi \right)$ and $M_b\left(\pi \right)$ are

$$\begin{array}{ccc}\hfill M_a\left(\pi \right)& =& {\mathrm{Id}}_d+E_{{d,\left|\pi \right|}^{-1}\left(d\right)};\hfill \\ \hfill M_b\left(\pi \right)& =& \left(\sum _{i=1}^{{\left|\pi \right|}^{-1}\left(d\right)}{E}_{i,i}\right)+E_{{d,\left|\pi \right|}^{-1}\left(d\right)+{\displaystyle \frac{1+{\sigma \left(\pi \right(\left|\pi \right|}^{-1}\left(d\right)\left)\right)}{2}}}+\left(\sum _{i={\left|\pi \right|}^{-1}\left(d\right)}^{d-1}{E}_{i,i+1}\right).\hfill \end{array}$$

(3)

We are now ready to present formally the generalized Rauzy operator $\mathcal{R}$. Let

$$\mathcal{D}=\{(\lambda ,\pi )\in {\Lambda }^d\times S_d^{\sigma }:{\lambda }_d\ne {\lambda }_{{\left|\pi \right|}^{-1}\left(d\right)}\};$$

then

$$\begin{array}{ccc}\hfill \mathcal{R}:\mathcal{D}\subset {\Lambda }^d\times S_d^{\sigma }& ⟶& {\Lambda }^d\times S_d^{\sigma }\hfill \\ \hfill T=(\lambda ,\pi )& \to & T^{\prime }=({\lambda }^{\prime },{\pi }^{\prime })\hfill \end{array}$$

is defined by

$$T^{\prime }=({\lambda }^{\prime },{\pi }^{\prime })=\left\{\begin{array}{cc}\left(M_a{\left(\pi \right)}^{-1}\lambda ,a\left(\pi \right)\right)\hfill & \mathrm{if}{\lambda }_{{\left|\pi \right|}^{-1}\left(d\right)}<{\lambda }_d,\hfill \\ \left(M_b{\left(\pi \right)}^{-1}\lambda ,b\left(\pi \right)\right)\hfill & \mathrm{if}{\lambda }_{{\left|\pi \right|}^{-1}\left(d\right)}>{\lambda }_d.\hfill \end{array}\right.$$

If $T^{\prime }$ is obtained from T by means of the operator $a,$T is said to be of type a, otherwise T is of type b. In any case, $T^{\prime }$ is the Poincaré first return map induced by T on $[0,{\ell }^{\prime }],$ with ${\ell }^{\prime }=\ell -min\{{\lambda }_d,{\lambda }_{{\left|\pi \right|}^{-1}\left(d\right)}\}$, see (Proposition 5, [3]). In Figure 1 and Figure 2 we draw IETs and the induced ones by mean of the generalized Rauzy operator.

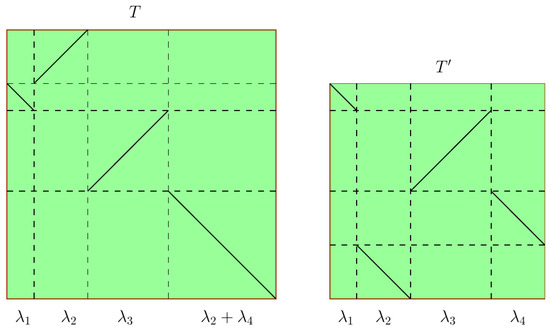
Figure 1. (Left): A $(4,2)$-IET of type a (notice that the length of second interval is smaller than the length of the fourth one) with associated irreducible permutation $(-3,4,2,-1)$, the minus signs indicate the presence of flips in the first and fourth intervals. (Right): The $(4,3)$-IET induced by the Rauzy operator, with associated irreducible permutation $(-4,-1,3,-2)$. In this case, $T^{\prime }$ is also of type a since ${\lambda }_1<{\lambda }_4$, and we have three flips.

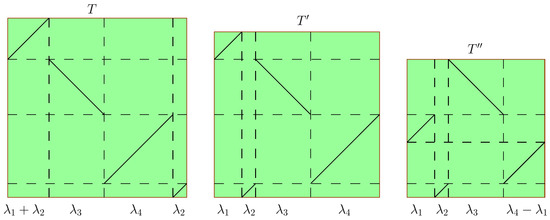
Figure 2. (Left): A $(4,1)$-IET, T, of type b (the length of the first interval is bigger than the length of the last one) with associated irreducible permutation $(4,-3,2,1)$. (Middle): The type a $(4,1)$-IET, $T^{\prime }$, induced by the Rauzy operator, with associated irreducible permutation $(4,1,-3,2)$. (Right): The $(4,1)$-IET induced by the Rauzy operator, $T^{″}$, with associated irreducible permutation $(3,1,-4,2)$.

The operators a and b induce in the set $S_d^{\sigma ,\ast }$ a directed graph structure whose vertices are all the points from $S_d^{\sigma ,\ast }$ and the directed edges are arrows labelled by a and b. Given $\pi ,{\pi }^{\prime }\in S_d^{\sigma ,\ast },$ there exists an arrow labelled by a (resp. b) from $\pi$ to ${\pi }^{\prime }$ if and only if $a\left(\pi \right)={\pi }^{\prime }$ (resp. $b\left(\pi \right)={\pi }^{\prime }$). An IET T follows the path $v=(v_1,v_2,v_3,\dots )\in {\{a,b\}}^L$, $L\in \mathbb{N}\cup \{\infty \}$, if ${\mathcal{R}}^k\left(T\right)$ is of type $v_{k+1}$ for all $k\ge 0.$

The following result guarantees minimality for IETs, see (Th. A, [3]).

Theorem 2.

Let T be an IET. If all the iterates by the Rauzy operator exist, ${\mathcal{R}}^k\left(T\right)=({\lambda }^k,{\pi }^k)$, $k\in \mathbb{N}$, and ${\pi }^k$ is irreducible, then T does not have saddle connections and T is minimal.

Thus, in order to have periodic orbits, we need to arrive, after finitely many times operating $\mathcal{R}$, to reach either an IET with reducible permutation, or an IET which is not in the domain of $\mathcal{R}$, which is the length of the last interval and the one that is placed in the last position coincide.

2.3. Periodic and Transitive Components of an IET: The Matrix of Periods $P\left(T\right)$

It is well known that IETs decompose into periodic and minimal components [2,9,11,12]. This decomposition is essential to analyze the set of periods. Each periodic component has either two or one associated periods depending on whether it reverses the orientation or not. An open interval J is said to be rigid if all positive iterates $T^m$ are defined; that is, these iterates do not contain discontinuity points. When a rigid interval J does not admit any other rigid interval containing it, then we say that J is a maximal rigid interval.

Remark 1.

Observe that for any maximal rigid interval J there is a minimal positive integer m such that $T^m\left(J\right)=J$ and then all points in J have either period $2m$ or m. Both periods exist when ${\left(T^m\right)}^{\prime }\left(x\right)=-1$ for any $x\in J$, and only m if ${\left(T^m\right)}^{\prime }\left(x\right)=1$ for any $x\in J$.

Let J be a maximal rigid interval and let m be positive as above. Then ${\bigcup }_{j=0}^{m-1}{T}^j\left(J\right)$ is said to be a periodic component of T. Notice that for each interval $T^j\left(J\right)$, $0\le j\le m-1$, there exists an interval $I_{i_j}$ from the definition of the IET T such that $T^j\left(J\right)$ is contained in $I_{i_j}$. A transitive component of T is a non-empty set $M\subseteq \mathrm{Dom}\left(T\right)$ such that $M=\mathrm{Cl}\left({\mathcal{O}}_T\left(x\right)\right)$ for some $x\in M$ (here, $\mathrm{Cl}\left(W\right)$ denotes the topological closure of the set W). The following results are relevant for us.

Lemma 1.

Let O be either a periodic or a transitive component of an IET, T. Then, the boundary points of O are in $\mathcal{S}$, that is, they are saddle points.

Proof. 

See (Th. 3.2 and Lemma 3.1, [13]) and (Sect. 14.5.9, [2]). □

Theorem 3

(Nogueira, Pires, Troubetzkoy). The numbers $d_{\mathrm{per}}$ of periodic components and $d_{\mathrm{tran}}$ of transitive components of an d-IET satisfy the inequality $d_{\mathrm{per}}+2d_{\mathrm{tran}}\le d$.

Proof. 

See (Theorem A and Lemma 3.1, [13]). □

We are mainly interested in periodic components. For an IET, $T:D={\bigcup }_{i=1}^d{I}_i\subset (0,\ell )\to (0,\ell )$, having periodic components, we denote them by $O_j$, $1\le j\le d_{\mathrm{per}}\le d$. Moreover, we label the components taking into account the following rule: If $1\le i<j\le d_{\mathrm{per}}$, then there exist points $x\in O_i$ such that $x<y$ for any $y\in O_j$.

A given periodic component $O_j$ can be decomposed into finitely many connected open intervals ${\left\{J_l^j\right\}}_{l=1}^{p_j}$. For any interval $I_i$, exchanged by T, let ${\left\{I_{i,l}\right\}}_{l=1}^{p_{i,j}}$ be the components of $O_j$ included in $I_i$. Observe then that ${\sum }_{i=1}^d{p}_{i,j}=p_j$, being $p_{i,j}$ the number of connected components of $O_j$ lying in $I_i$, and $p_j$ the number of connected open intervals in $O_j$.

Now we are ready to define the $d\times d_{\mathrm{per}}$ matrix of periods $P\left(T\right)$. If

$$P\left(T\right)={\left(a_{i,j}\right)}_{\begin{array}{c}1\le i\le d\\ 1\le j\le d_{\mathrm{per}}\end{array}},$$

then $a_{i,j}$ is the number of connected components of $O_j$ in the interval $I_i$. To fix ideas, let us give an example. If $T=(\lambda ,\pi )$, with $\ell =1$, $\lambda =(1/3,1/3,1/3)$, and $\pi =(-3,2,-1)$, we have $O_1=(0,1/3)\cup (2/3,1)$, $O_2=(1/3,2/3)$, $d_{\mathrm{per}}=2$, and $P\left(T\right)$ is the $3\times 2$ matrix given by $P\left(T\right)=\left(\begin{array}{cc}1& 0\\ 0& 1\\ 1& 0\end{array}\right).$

Observe that if an IET T has only transitive components then $P\left(T\right)$ is not defined. Conversely, if we assume the existence of $P\left(T\right)$ for an IET T then T has at least one periodic component.

3. The Behavior of the Matrix of Periods P(T) Under Rauzy Operators

In this section we fix an IET, T, and we apply the Rauzy operator (if possible) to obtain $T^{\prime }$. We are mainly concerned in obtaining the relationship between the matrices $P\left(T\right)$ and $P\left(T^{\prime }\right)$. At least, we know from (Corollary 5.6, [13]) that the number of periodic (also the transitive) components of T and $T^{\prime }$ coincide.

Theorem 4.

Let $T=(\lambda ,\pi )$ and let $T^{\prime }=\mathcal{R}\left(T\right)=({\lambda }^{\prime },{\pi }^{\prime })$. Then

$$P\left(T^{\prime }\right)=M_i{\left(\pi \right)}^{-1}P\left(T\right),$$

with T being of type $i\in \{a,b\}$.

Proof. 

We will prove $M_i\left(\pi \right)P\left(T^{\prime }\right)=P\left(T\right)$. Assume first that T is of type a; then, ${\lambda }_{{\left|\pi \right|}^{-1}\left(d\right)}<{\lambda }_d$ and the intervals of T and $T^{\prime }$ are respectively $\{I_1,I_2,\dots ,I_d\}$ and $\{I_1^{\prime }=I_1,I_2^{\prime }=I_2,\dots ,I_{d-1}^{\prime }=I_{d-1},I_d^{\prime }=I_d\setminus (\ell -{\lambda }_{{\left|\pi \right|}^{-1}\left(d\right)},\ell )\}$.

Observe that any periodic component, $O_i$, in $I_{{\left|\pi \right|}^{-1}\left(d\right)}$ is continued in $(\ell -{\lambda }_{{\left|\pi \right|}^{-1}\left(d\right)},\ell )$ by T. When we obtain $T^{\prime }$, we remove these periodic components and then, in order to compute $P\left(T^{\prime }\right)$, we replace the d-th row of $P\left(T\right)$ with the difference between d-th row and the ${\left|\pi \right|}^{-1}\left(d\right)$-th row. In other words, we obtain $P\left(T\right)$ from $P\left(T^{\prime }\right)$ by adding to the d-th row the ${\left|\pi \right|}^{-1}\left(d\right)$-th row. Thus

$$P\left(T\right)=({\mathrm{Id}}_d+E_{{d,\left|\pi \right|}^{-1}\left(d\right)})P\left(T^{\prime }\right)=M_a\left(\pi \right)P\left(T^{\prime }\right).$$

Assume that T is of type b; then, ${\lambda }_d<{\lambda }_{{\left|\pi \right|}^{-1}\left(d\right)}$ and the intervals of T and $T^{\prime }$ are $\{I_1,I_2,\dots ,I_{d-1},I_d\}$ and $\{I_1^{\prime },I_2^{\prime },\dots ,I_{d-1}^{\prime },I_d^{\prime }\}$, respectively, with the following relationship. If $\sigma \left(\pi \left({\left|\pi \right|}^{-1}\left(d\right)\right)\right)<0$, we have

(a)

$I_i^{\prime }=I_i$ for any $i<{\left|\pi \right|}^{-1}\left(d\right)$,

(b)

$I_{{\left|\pi \right|}^{-1}\left(d\right)}^{\prime }=(a_{{\left|\pi \right|}^{-1}\left(d\right)},a_{{\left|\pi \right|}^{-1}\left(d\right)}+{\lambda }_d)$,

(c)

$I_{{\left|\pi \right|}^{-1}\left(d\right)+1}^{\prime }=(a_{{\left|\pi \right|}^{-1}\left(d\right)}+{\lambda }_d,a_{{\left|\pi \right|}^{-1}\left(d\right)+1})$,

(d)

$I_{l+1}^{\prime }=I_l$ for any ${\left|\pi \right|}^{-1}\left(d\right)+1\le l\le d-1$.

On the contrary, if $\sigma \left(\pi \left({\left|\pi \right|}^{-1}\left(d\right)\right)\right)>0$:

(a)

$I_i^{\prime }=I_i$ for any $i<{\left|\pi \right|}^{-1}\left(d\right)$,

(b)

$I_{{\left|\pi \right|}^{-1}\left(d\right)}^{\prime }=(a_{{\left|\pi \right|}^{-1}\left(d\right)},a_{{\left|\pi \right|}^{-1}\left(d\right)+1}-{\lambda }_d)$,

(c)

$I_{{\left|\pi \right|}^{-1}\left(d\right)+1}^{\prime }=(a_{{\left|\pi \right|}^{-1}\left(d\right)+1}-{\lambda }_d,a_{{\left|\pi \right|}^{-1}\left(d\right)+1})$,

(d)

$I_{l+1}^{\prime }=I_l$ for any ${\left|\pi \right|}^{-1}\left(d\right)+1\le l\le d-1$.

In any case, when we pass from T to $T^{\prime }$, we are removing the connected components of periodic components of any $O_j$ contained in $I_d$. Let us call $P\left(T\right)=\left(p_{i,j}\right)$ and $P\left(T^{\prime }\right)=\left(p_{i,j}^{\prime }\right)$. Observe that, in this case, we are splitting the interval $I_{{\left|\pi \right|}^{-1}\left(d\right)}$ into two intervals $I_{{\left|\pi \right|}^{-1}\left(d\right)}^{\prime }$ and $I_{{\left|\pi \right|}^{-1}\left(d\right)+1}^{\prime }$, and we remove $I_d$. In view of the above relationship between the intervals of T and $T^{\prime }$, we have

• $p_{r,j}=p_{r,j}^{\prime }$ for any $r<{\left|\pi \right|}^{-1}\left(d\right)$,
• $p_{r,j}=p_{r+1,j}^{\prime }$ for any ${\left|\pi \right|}^{-1}\left(d\right)+2\le r\le d-1$.
• If ${\sigma \left(\pi \right(\left|\pi \right|}^{-1}\left(d\right)\left)\right)<0,$ then $p_{{\left|\pi \right|}^{-1}\left(d\right),j}^{\prime }=p_{d,j}$ and $p_{{\left|\pi \right|}^{-1}\left(d\right)+1,j}^{\prime }=p_{{\left|\pi \right|}^{-1}\left(d\right),j}-p_{d,j}$. From here, $p_{{\left|\pi \right|}^{-1}\left(d\right),j}=p_{{\left|\pi \right|}^{-1}\left(d\right)+1,j}^{\prime }+p_{{\left|\pi \right|}^{-1}\left(d\right),j}^{\prime }$.
• If ${\sigma \left(\pi \right(\left|\pi \right|}^{-1}\left(d\right)\left)\right)>0$, now $p_{{\left|\pi \right|}^{-1}\left(d\right),j}^{\prime }=p_{{\left|\pi \right|}^{-1}\left(d\right),j}-p_{d,j}$ and $p_{{\left|\pi \right|}^{-1}\left(d\right)+1,j}^{\prime }=p_{d,j}$. Also, $p_{{\left|\pi \right|}^{-1}\left(d\right),j}=p_{{\left|\pi \right|}^{-1}\left(d\right),j}^{\prime }+p_{{\left|\pi \right|}^{-1}\left(d\right)+1,j}^{\prime }$.

As a consequence, according to the definition of matrix $M_b\left(\pi \right)$, we can write

$$M_b\left(\pi \right)P\left(T^{\prime }\right)=P\left(T\right).$$

□

We now analyze the matrix of periods when $T=(\lambda ,\pi ):(0,\ell )\to (0,\ell )$, being $\pi$ a reducible permutation. In this case, there exists a minimal $k<d$ such that $\left|\pi \right|\left(\right\{1,2,\dots ,k\left\}\right)=\{1,2,\dots ,k\}$. In this case, the dynamics of T splits into the dynamics of two simpler IETs: $T_1$ and $T_2$, which we will analyze next. Let $T_1{=T|}_{{\bigcup }_{i=1}^k{I}_i}$, ${\ell }_1={\sum }_{i=1}^k{\lambda }_i$, ${\ell }_2={\sum }_{i=k+1}^d{\lambda }_i=\ell -{\ell }_1$, and $T_2:(0,{\ell }_2)\to (0,{\ell }_2)$, $T_2\left(x\right)=T(x+{\ell }_1)-{\ell }_1$. It is easy to see that $T_1$ and $T_2$ are IETs verifying the following result.

Theorem 5.

Let $T=(\lambda ,\pi ):(0,\ell )\to (0,\ell )$ with π being reducible and let $T_1$ and $T_2$ be defined as above with associated matrices of periods $P\left(T_1\right)$ and $P\left(T_2\right)$. Assume that $T_1$ and $T_2$ have $d_1\le k$ and $d_2\le d-k$ periodic components, respectively. Then

(a)

$T_1=({\lambda }^1,{\pi }^1)$ with ${\lambda }_i^1={\lambda }_i$ and ${\pi }_i^1={\pi }_i$ for any $1\le i\le k$.

(b)

$T_2=({\lambda }^2,{\pi }^2)$ with ${\lambda }_i^2={\lambda }_{i+k}$ and ${\pi }_i^2=\sigma \left({\pi }_{i+k}\right)\left(\right|{\pi }_{i+k}|-k)$ for any $1\le i\le d-k$.

(c)

The matrix of periods of T is

$$P\left(T\right)=\left(\begin{array}{cc}P\left(T_1\right)& {\mathbf{0}}_{k,d_2}\\ {\mathbf{0}}_{d-k,d_1}& P\left(T_2\right)\end{array}\right),$$

where ${\mathbf{0}}_{l,m}$ denotes the $l\times m$ zero matrix for any naturals l and m.

Proof. 

Items (a) and (b) are easy consequences of the reducible structure of T. In order to prove (c), observe that any periodic component from $T_1$ is a periodic component of T and the distribution of the connected components on ${\bigcup }_{i=1}^d{I}_i$ coincides with the distribution of those of T. Then, the disposition of the $d_1$ first columns is proved.

For any $A\subset \mathbb{R}$ and $u\in \mathbb{R}$ we write $A\pm u:=\{x\pm u:x\in A\}$. Observe that the intervals exchanged by $T_2$ are $J_i=I_{i+k}-{\ell }_1$, $1\le i\le d-k$. Also, if $A\subset I_i$, $k+1\le i\le d$, is a connected component of a periodic component of T then $A-{\ell }_1$ is a connected component of a periodic component of $T_2$ in $J_i$. This relation among connected components of periodic components of T and $T_2$ ensures that the columns from $d_1+1$ to $d_1+d_2$ fit the theorem. □

Also, it is interesting to analyze the situation of an IET $T=(\lambda ,\pi )$, which is not in the domain of $\mathcal{R}$, in which case ${\lambda }_{{\left|\pi \right|}^{-1}\left(d\right)}={\lambda }_d$, and we assume here that $\pi$ is irreducible. We can not apply the Rauzy induction; however, we are allowed to see what is the behaviour of the first return map to $I^{\prime }={\bigcup }_{i=1}^{d-1}{I}_i$. Specifically, $T^{\prime }:I^{\prime }\to I^{\prime }$ is defined by $T^{\prime }\left(x\right)=T\left(x\right)$ if $x\in I^{\prime }\setminus I_{{\left|\pi \right|}^{-1}\left(d\right)}$ and $T^{\prime }\left(x\right)=T\left(T\left(x\right)\right)$ otherwise. Realize that $T^{\prime }$ is an IET of $d-1$ intervals. Figure 3 illustrates this procedure.

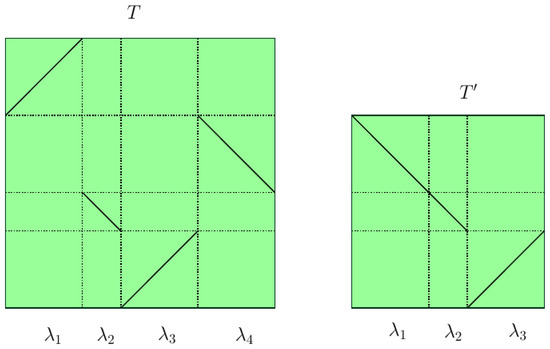
Figure 3. The figure on the left depicts a $(4,2)$-IET with an associated irreducible permutation $(4,-2,1,-3)$. On the right, we show the first return map to the interval $(0,{\lambda }_1+{\lambda }_2+{\lambda }_3)$, which is a $(3,2)$-IET with a reducible associated permutation $(-3,-2,1)$. Moreover, the induced map $T^{\prime }$ exhibits a false discontinuity.

Moreover, it holds

Theorem 6.

Let $T=(\lambda ,\pi )$ be a $(d,k)$-IET, $d\ge k\ge 0$, with π irreducible and $T\notin \mathrm{Dom}\left(\mathcal{R}\right)$, and let $T^{\prime }=({\lambda }^{\prime },{\pi }^{\prime })$ be the first return map of T to $I^{\prime }={\bigcup }_{i=1}^{d-1}{I}_i$. Then

(a)

${\lambda }_i^{\prime }={\lambda }_i$, $1\le i\le d-1$.

(b)

${\pi }^{\prime }\left(i\right)=\pi \left(i\right)$ for any $1\le i\le d-1$, $i\ne {\left|\pi \right|}^{-1}\left(d\right)$.

(c)

${\pi }^{\prime }{\left(\right|\pi |}^{-1}\left(d\right))=\pi \left(d\right)$.

(d)

The matrix of periods of T is

$$P\left(T\right)=\left(\begin{array}{c}P\left(T^{\prime }\right)\\ u\end{array}\right),$$

where u is a copy of the ${\left|\pi \right|}^{-1}\left(d\right)$ row of $P\left(T^{\prime }\right)$.

Proof. 

Item (a) is obvious. Observe that $T^{\prime }{=T|}_{{\bigcup }_{i=1}^{d-1}{I}_i}$; then ${\pi }^{\prime }\left(i\right)=\pi \left(i\right)$ for any $i<d$ with $i\ne {\left|\pi \right|}^{-1}\left(d\right)$. However, if $\pi \left(j\right)\in \{-d,d\}$ then $T^{\prime }\left(I_j\right)=T\left(I_d\right)$ and ${\pi }^{\prime }\left(j\right)=\pi \left(d\right)$. Then, items (b) and (c) follow.

Now, observe that any connected component of a periodic component of $T^{\prime }$ is a connected component of a periodic component of T and its orbit, by T, is the same of the orbit by $T^{\prime }$ if it does not hit $T^{-1}\left(I_d\right)$. In other case, the orbit of this component has as many components in $I_d$ as the ones located in $T^{-1}\left(I_d\right)$ and then (d) follows. □

Inverse and Conjugate

Let $T=(\lambda ,\pi )$ be an $(d,k)$-IET and consider its inverse $T^{-1}=({\lambda }^i,{\pi }^i)$. Also, we define the homeomorphism $h:[0,1]\to [0,1]$, $h\left(x\right)=1-x$, which holds $h^2=\mathrm{Id}$. We define the conjugated map of T by means of h, $T^h$, as $T^h:=h\circ T\circ h^{-1}$. $T^h$ is also an IET (since h is an isometry), and we write $T^h=({\lambda }^h,{\pi }^h)$.

Theorem 7

(Th. 5, [7]). Let $T=(\lambda ,\pi )$ be a $(d,k)$-IET. Then

(a)

$T^{-1}=({\lambda }^i,{\pi }^i)$, with ${\lambda }_j^i={\lambda }_{{\left|\pi \right|}^{-1}\left(j\right)}$ and ${\pi }^i\left(j\right)=\sigma \left(\pi \left(|{\pi }^{-1}|\left(j\right)\right)\right){\left|\pi \right|}^{-1}\left(j\right)$, $1\le j\le d.$

(b)

$T^h=({\lambda }^h,{\pi }^h)$, with ${\lambda }_j^h={\lambda }_{d+1-j}$ and ${\pi }^h\left(j\right)=\sigma \left(\pi (d+1-j)\right)(d+1-|\pi \left|(d+1-j)\right)$, $1\le j\le d$.

(c)

$\mathrm{Per}\left(T\right)=\mathrm{Per}\left(T^{-1}\right)=\mathrm{Per}\left(T^h\right)$.

4. Revisiting the Computation of Periods for $\mathbf{2}$-IETs

We introduce the Rauzy-classes. Roughly speaking, it consists of subgraphs whose vertices are (irreducible) permutations and we put an arrow, labelled by $j\in \{a,b\}$, from $\pi$ to $\tilde{\pi }$ if T is of type j. For instance, if $\pi =(-3,1,-2)$ and $\tilde{\pi }=(2,-3,1)$, we have $\pi \stackrel{b}{\to }\tilde{\pi }$. In the case of 2-IETs with irreducible permutations, the relations are summarized as follows:

$${}^a⥀(2,1){⥁}^b{⥁}^b(2,-1){\to }^a(-1,-2){}^a⥀(-2,1){\to }^b(-1,-2)(-2,-1)$$

Unless otherwise will stated, we assume in this section that $\ell =1$.

4.1. 2-IETs with Associate Permutations ${\pi }_1=(-2,1)$ and ${\pi }_2=(2,-1)$

The following result, see (Corollary 2, [7]), simplifies the study since these two permutations will generate the same sets of periods.

Lemma 2.

Let $T=(\lambda ,\pi )$ with ${\pi }_2=(2,-1)$ and $\lambda =({\lambda }_1,{\lambda }_2)$. Then $T^{-1}=({\lambda }^i,{\pi }^i)$ with ${\pi }^i=(-2,1)={\pi }_1$ and ${\lambda }^i=({\lambda }_2,{\lambda }_1)$ and $\mathrm{Per}\left(T\right)=\mathrm{Per}\left(T^{-1}\right)$.

We will study IETs with permutation ${\pi }_1=(-2,1)$. Let $T=(\lambda ,{\pi }_1)$; then, according to the relations shown above, we can eventually apply n times the operator a and finally we would apply b to obtain ${\mathcal{R}}^{n+1}\left(T\right)=T^{(n+1)}=({\lambda }^{(n+1)},(-1,-2))$. Perhaps, it can occur initially that T has type b, in which case $n=0$. Observe that $P\left(T^{(n+1)}\right)=\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right)$. Taking into account that $M_a\left((-2,1)\right)=\left(\begin{array}{cc}1& 0\\ 1& 1\end{array}\right)$ and $M_b\left((-2,1)\right)=\left(\begin{array}{cc}1& 1\\ 1& 0\end{array}\right)$, from Theorem 4 we obtain

$$P\left(T\right)=M_a{\left((-2,1)\right)}^n{M}_b\left((-2,1)\right)P\left(T^{(n+1)}\right)=\left(\begin{array}{cc}1& 0\\ n& 1\end{array}\right)\left(\begin{array}{cc}1& 1\\ 1& 0\end{array}\right)=\left(\begin{array}{cc}1& 1\\ n+1& n\end{array}\right).$$

(4)

Therefore, from the definition of $P\left(T\right)$, we have two periodic components, $O_1$ and $O_2$. The first one, $O_1$, has one connected component in $I_1$ and $n+1$ connected components in $I_2$; then, by Remark 1, we receive $n+2$ as a period of T, and since the IET returns by reversing the orientation, we add the double, that is, $2(n+2)$. For the second periodic component, $O_2$, we have one connected component in $I_1$ and n connected components in $I_2$, thus we obtain $n+1$ and also $2(n+1)$ as periods. Finally, we summarize the above information in the form of the following proposition.

Proposition 1.

Let $T=(\lambda ,{\pi }_1)$, with ${\pi }_1=(-2,1)$ and $\lambda =({\lambda }_1,{\lambda }_2)$. Assume that ${\mathcal{R}}^{n+1}\left(T\right)=({\lambda }^{(n+1)},(-1,-2))$ after applying the Rauzy operator n ($n\ge$0) times having type a and a final time having type b. Then,

$$\mathrm{Per}\left(T\right)=\{n+1,n+2,2(n+1),2(n+2\left)\right\}.$$

Remark 2.

In the above study, realize that the number of periodic components and the corresponding connected components coincide with the direct study remarked in (Remark 4, [7]). Moreover, note that n in Proposition 1 satisfies

$$n<{\displaystyle \frac{{\lambda }_2}{{\lambda }_1}}<n+1.$$

Indeed, from the proof of (Theorem 6, [7]), all points of $\mathrm{Dom}\left(T\right)$ are periodic, so if ${\ell }_j$ denotes the length of the rigid interval $J_j$ which produces $O_j$, $j\in \{1,2\}$, it holds ${\ell }_1+{\ell }_2={\lambda }_1$ and $(n+1){\ell }_1+n{\ell }_2={\lambda }_2$, with ${\lambda }_1+{\lambda }_2=1$. From the above equalities it is straightforward to see that $n<{\displaystyle \frac{{\lambda }_2}{{\lambda }_1}}={\displaystyle \frac{(n+1){\ell }_1+n{\ell }_2}{{\ell }_1+{\ell }_2}}<n+1$.

On the other hand, following with IETs of the form $T=(\lambda ,{\pi }_1)$, observe that, after applying n times the operator a, we could arrive to a 2-IET ${\mathcal{R}}^n\left(T\right)=T^{\left(n\right)}=({\lambda }^{\left(n\right)},(-2,1))$ with ${\lambda }_1^{\left(n\right)}={\lambda }_2^{\left(n\right)}$ and then we cannot again apply the operator $\mathcal{R}$. In this case, being ${\left(T^{\left(n\right)}\right)}^4=\mathrm{Id}$, $O_1=(0,{\lambda }_1)\cup ({\lambda }_1,1)$ the unique component periodic of T, and using Theorem 4, we find

$$P\left(T^{\left(n\right)}\right)=\left(\begin{array}{c}1\\ 1\end{array}\right)\mathrm{and}P\left(T\right)=M_a{\left((-2,1)\right)}^{n}P\left(T^{\left(n\right)}\right)=\left(\begin{array}{cc}1& 0\\ n& 1\end{array}\right)\left(\begin{array}{c}1\\ 1\end{array}\right)=\left(\begin{array}{c}1\\ n+1\end{array}\right).$$

(5)

Analyzing this matrix, in an analogous way to Proposition 1, we obtain

Proposition 2.

Let $T=(\lambda ,{\pi }_1)$, with ${\pi }_1=(-2,1)$ and $\lambda =({\lambda }_1,{\lambda }_2)$. Assume that ${\mathcal{R}}^n\left(T\right)=({\lambda }^{\left(n\right)},(-1,-2))$ with ${\lambda }_1^{\left(n\right)}={\lambda }_2^{\left(n\right)}$ after applying n times the Rauzy operator a. Then,

$$\mathrm{Per}\left(T\right)=\{n+2,2(n+2\left)\right\}.$$

Remark 3.

Note that in this case ${\displaystyle \frac{{\lambda }_2}{{\lambda }_1}}=n+1$.

Corollary 1.

Let $T=(\lambda ,{\pi }_1)$ be a 2-IET, with ${\pi }_1=(-2,1)$ and $\lambda =({\lambda }_1,{\lambda }_2)$. Then, $\mathrm{Per}\left(T\right)\ne \varnothing$ and this set of periods can be either $\{m,2m\}$ for some $m\in \mathbb{N},m\ge 2$, or $\{n,n+1,2n,2(n+1\left)\right\}$ for some $n\in \mathbb{N}$.

Proof. 

We distinguish cases according to the application of the Rauzy operator $\mathcal{R}$.

(1)

If $T\notin \mathrm{Dom}\left(\mathcal{R}\right)$, this implies that ${\lambda }_1={\lambda }_2$, and then it is easily seen that $T^2=(\lambda ,(-1,-2))$, therefore $\mathrm{Per}\left(T\right)=\{2,4\}$.

(2)

If $T\in \mathrm{Dom}\left(\mathcal{R}\right)$, in turn the following can occur:

(2.i)

We can apply n times the operator a and to arrive to an IET $T^{\left(n\right)}=(({\lambda }_1^n,{\lambda }_2^n),(-2,1))$, with ${\lambda }_1^n={\lambda }_2^n$. Then, from Proposition 2 we have $\mathrm{Per}\left(T\right)=\{n+2,2(n+2\left)\right\}.$ (Note that if T itself does not belong to the domain of $\mathcal{R}$, its set of periods is compatible with this case, considering that $n=0$.)

(2.ii)

Since we cannot produce an infinite path $a^{\infty }=aaa\dots$ because if we repeat the Rauzy process to T infinitely many times, by force in some moment we will have ${\lambda }_1^k>{\lambda }_2^k$ and then $T^{\left(k\right)}$ will be of type b. In this case, therefore, we find the finite path $a^{n}b$, and Proposition 1 enables us to state that $\mathrm{Per}\left(T\right)=\{n+1,n+2,2(n+1),2(n+2\left)\right\}$ for some $n\ge 0$.

□

Remark 4.

According to the constructions of T in Propositions 1 and 2, the converse for Corollary 1 also holds: given a set of periods A of the form $\{m,2m\}$, $m\ge 2$, or $\{n,n+1,2n,2(n+1\left)\right\}$, $n\ge 1$, there exists the corresponding 2-IET $T=(\lambda ,{\pi }_1)$ such that $\mathrm{Per}\left(T\right)=A$.

For the permutation ${\pi }_2=(2,-1)$, from Lemma 2 we know that the set of periods of $T=(\lambda ,{\pi }_2)=(({\lambda }_1,{\lambda }_2),{\pi }_2)$ must be equal to that of $T^{-1}=(({\lambda }_2,{\lambda }_1),{\pi }_1)$. Nevertheless, for the sake of completeness, given $T=(\lambda ,{\pi }_2)$, let us mention that

• After applying n ($n\ge 0)$ times the operator b followed by the operator a, we obtain ${\mathcal{R}}^{n+1}\left(T\right)=T^{(n+1)}=({\lambda }^{(n+1)},(-1,-2))$; then $P\left(T^{(n+1)}\right)=\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right)$, and therefore

  $$P\left(T\right)=M_b{\left((2,-1)\right)}^n{M}_a\left((2,-1)\right)P\left(T^{(n+1)}\right)=\left(\begin{array}{cc}1& n\\ 0& 1\end{array}\right)\left(\begin{array}{cc}1& 0\\ 1& 1\end{array}\right)=\left(\begin{array}{cc}n+1& n\\ 1& 1\end{array}\right).$$
  In this way,

  $$\mathrm{Per}\left(T\right)=\{n+1,n+2,2(n+1),2(n+2\left)\right\},$$

  and we have $n<{\displaystyle \frac{{\lambda }_1}{{\lambda }_2}}<n+1$.
• If after applying n times the operator b we could arrive to a 2-IET ${\mathcal{R}}^n\left(T\right)=T^{\left(n\right)}=({\lambda }^{\left(n\right)},(2,-1))$ with ${\lambda }_1^{\left(n\right)}={\lambda }_2^{\left(n\right)}$, then we cannot apply again the operator $\mathcal{R}$. However,

  $$\begin{array}{c}\hfill P\left(T^{\left(n\right)}\right)=\left(\begin{array}{c}1\\ 1\end{array}\right)\mathrm{and}P\left(T\right)=M_a{\left((2,-1)\right)}^{n}P\left(T^{\left(n\right)}\right)=\left(\begin{array}{cc}1& n\\ 0& 1\end{array}\right)\left(\begin{array}{c}1\\ 1\end{array}\right)=\left(\begin{array}{c}n+1\\ 1\end{array}\right),\end{array}$$

  and the analysis of this matrix yields

  $$\mathrm{Per}\left(T\right)=\{n+2,2(n+2\left)\right\},$$

  with ${\displaystyle \frac{{\lambda }_1}{{\lambda }_2}}=n+1.$

4.2. 2-IETs with Associate Permutation ${\pi }_3=(2,1)$

In this case, after applying operators a and b to $T=(\lambda ,{\pi }_3)$, we always obtain again ${\pi }_3$, an irreducible permutation; then, if we assume that T has periodic components, after a finite number of iterates we would reach ${\mathcal{R}}^k\left(T\right)=T^{\left(k\right)}=({\lambda }^k,{\pi }^k)$ with ${\pi }^k=(2,1)$, ${\lambda }^k=({\lambda }_1^k,{\lambda }_2^k)$ and ${\lambda }_1^k={\lambda }_2^k$. Otherwise by Theorem 2, T would be minimal, without periodic points. Then $P\left(T^{\left(k\right)}\right)=\left(\begin{array}{c}1\\ 1\end{array}\right)$. This means, according to the first return Poincaré map, that $T^{\left(k\right)}$ has only a periodic component and so is the case for $T=(\lambda ,{\pi }_3)$. Moreover, since T is a rational rotation it has only one period, let us say q, and then the periodic component $O_1$ of T decomposes in q connected components of length ${\displaystyle \frac{{\lambda }_1+{\lambda }_2}{q}}$, which are distributed in the following way: ${\displaystyle \frac{{\lambda }_1}{{\lambda }_1+{\lambda }_2}}q$ in $I_1$ and ${\displaystyle \frac{{\lambda }_2}{{\lambda }_1+{\lambda }_2}}q$ in $I_2$. Therefore

$$P\left(T\right)=\left(\begin{array}{c}{\displaystyle \frac{{\lambda }_1}{{\lambda }_1+{\lambda }_2}}q\\ {\displaystyle \frac{{\lambda }_2}{{\lambda }_1+{\lambda }_2}}q\end{array}\right).$$

(6)

Example 1.

For instance, if we apply consecutively n times the operator a followed by m applications of operator b, and ${\lambda }_1^k={\lambda }_2^k$ with $k=n+m$, taking into account that $M_a\left({\pi }_3\right)=\left(\begin{array}{cc}1& 0\\ 1& 1\end{array}\right)$ and $M_b\left({\pi }_3\right)=\left(\begin{array}{cc}1& 1\\ 0& 1\end{array}\right),$ we have $P\left(T\right)={\left(M_a\left({\pi }_3\right)\right)}^n{\left(M_b\left({\pi }_3\right)\right)}^m\left(\begin{array}{c}1\\ 1\end{array}\right)=\left(\begin{array}{c}1+m\\ 1+n+nm\end{array}\right),$ so $\mathrm{Per}\left(T\right)=\{2+m+n+nm\}.$ Note that if we put $S_{n,m}:=\{2+m+n+nm:n,m\in \mathbb{N}\}$, and we denote by $\mathbb{I}$ and $\mathbb{P}$ the set of odd numbers and even numbers, respectively, since $2+m+n+nm=(n+1)(m+1)+1$, we obtain $S_{n,m}=\left(\mathbb{I}\setminus \{1,3\}\right)\cup \left(\mathbb{P}\setminus \{2q:2q-1\mathrm{is}\mathrm{prime}\}\right)$. This implies that all the numbers of $S_{n,m}$ can be derived as periods of an oriented 2-IET $T=(\lambda ,{\pi }_3)$ whenever the application of the Rauzy process to the path $a^n{b}^m$ leads to another IET $T^{(n+m)}$ with ${\lambda }_1^{n+m}={\lambda }_2^{n+m}$.

To end the section, let us emphasize that all the results obtained for 2-IETs via the matrix of periods $P\left(T\right)$ are consistent with the findings already presented in [7].

5. Study of the Set of Periods of $\mathbf{3}$-IETs via the Matrix $\mathbf{P}\left(\mathbf{T}\right)$

We are going to show how to apply Theorems 4–6 to 3-IETs. We split this section in the study of oriented IETs and a particular non-oriented Rauzy class. It should be noted that a comprehensive study of all permutations is extensive; it suffices to illustrate the application of the main results in specific cases. Nevertheless, the oriented case is completely covered for 3-IETs, which is an improvement over the results established in [7].

5.1. Oriented 3-IETs

The Rauzy class of orientable 3-IETs is the following:

$$\begin{array}{ccccc}\hfill {⥁}^b(2,3,1)& \stackrel{a}{\leftrightarrow }& (3,2,1)\hfill & \stackrel{b}{\leftrightarrow }& (3,1,2){⥀}^a\end{array}$$

The application of Theorem 4 requires the computation of the Rauzy matrices $M_a$ and $M_b$. We introduce them in the following Claim.

$$M_a\left((2,3,1)\right)=\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 1& 1\end{array}\right),M_b\left((2,3,1)\right)=\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 1\\ 0& 0& 1\end{array}\right),M_a\left((3,2,1)\right)=\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 1& 0& 1\end{array}\right),$$

$$M_b\left((3,2,1)\right)=\left(\begin{array}{ccc}1& 1& 0\\ 0& 0& 1\\ 0& 1& 0\end{array}\right),M_a\left((3,1,2)\right)=\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 1& 0& 1\end{array}\right),M_b\left((3,1,2)\right)=\left(\begin{array}{ccc}1& 1& 0\\ 0& 0& 1\\ 0& 1& 0\end{array}\right).$$

Let us fix first an IET $T=(\lambda ,\pi )$ with periodic components; in order to obtain the periods we need that the orbit of T, by $\mathcal{R}$, finishes in an IET ${\mathcal{R}}^k\left(T\right)=T^{\left(k\right)}=({\lambda }^k,{\pi }^k)$, where ${\pi }^k$ belongs to this Rauzy class, but $T^{\left(k\right)}$ is not in the domain of $\mathcal{R}$, that is, ${\lambda }_d^k={\lambda }_{|{\pi }^k{|}^{-1}\left(d\right)}^k$, where we write ${\lambda }^k=({\lambda }_1^k,{\lambda }_2^k,{\lambda }_3^k),$ with $d=3$. Then, the following possibilities arise:

(a)

${\pi }^k=(2,3,1)$ with ${\lambda }_2^k={\lambda }_3^k$. In this case, the Poincaré map of $T^{\left(k\right)}$ is a rational rotation with only one periodic component, matrix of periods $\left(\begin{array}{c}r\\ s\end{array}\right)$ by Equation (6), and period $p=r+s$. Then, Theorem 6 implies $P\left(T^{\left(k\right)}\right)=\left(\begin{array}{c}r\\ s\\ s\end{array}\right)$ and $r+2s=q.$ In this case, by Theorem 4, we have $P\left(T\right)=M_v\left(\pi \right)P\left(T^{\left(k\right)}\right)$ for some $v\in {\{a,b\}}^k$, and then the set of periods of T has cardinality 1 and can be computed depending on $\pi$ and the followed Rauzy path v.

(b)

${\pi }^k=(3,2,1)$ with ${\lambda }_1^k={\lambda }_3^k$. In this case, its Poincaré map is the identity map with a false discontinuity and with two periodic component, thus the periodic components are $O_1=(0,{\lambda }_1^k)\cup (1-{\lambda }_1^k,1),O_2=({\lambda }_1^k,1-{\lambda }_1^k)$, and $P\left(T^{\left(k\right)}\right)=\left(\begin{array}{cc}1& 0\\ 0& 1\\ 1& 0\end{array}\right)$ by Theorem 6. Consequently, $\mathrm{Per}\left(T\right)$ contains two elements.

For example, if the initial IET $T=(\lambda ,\pi )$, with $\pi =(3,2,1),$ is following the Rauzy path made with $2r\ge 2$ consecutive applications of operator b continued by $2s\ge 2$ applications of operator a, then

$$\begin{array}{ccc}\hfill P\left(T\right)& =& {\left[M_b\left((3,2,1)\right)M_b\left((3,1,2)\right)\right]}^r{\left[M_a\left((3,2,1)\right)M_a\left((2,3,1)\right)\right]}^{s}P\left({\mathcal{R}}^{2r+2s}\left(T\right)\right)\hfill \\ & =& \left(\begin{array}{ccc}1& r& r\\ 0& 1& 0\\ 0& 0& 1\end{array}\right)\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ s& s& 1\end{array}\right)\left(\begin{array}{cc}1& 0\\ 0& 1\\ 1& 0\end{array}\right)=\left(\begin{array}{cc}rs+r+1& rs+r\\ 0& 1\\ s+1& s\end{array}\right)\hfill \end{array}$$

thus $\mathrm{Per}\left(T\right)=\{rs+r+s+2,rs+r+s+1\}=\left\{\right(r+1\left)\right(s+1)+1,(r+1\left)\right(s+1\left)\right\}.$ As a curiosity, realize that this class of two consecutive natural numbers contains all the pairs $(2n,2n+1)$ with $n\ge 2$, and the pairs $(2m+1,2m)$ whenever $2m+1$ is not prime and $m\ge 4.$

(c)

${\pi }^k=(3,1,2)$ with ${\lambda }_1^k={\lambda }_3^k$. In this case, the Poincaré map is a rational rotation with only one periodic component and matrix of periods $\left(\begin{array}{c}r\\ s\end{array}\right)$, whose period, say q, is equal to $q=r+s$. By Theorem 6, $P\left(T^{\left(k\right)}\right)=\left(\begin{array}{c}r\\ s\\ r\end{array}\right)$ with $2r+s=q+s;$ again, we obtain only one period for T whose value will depend on the Rauzy path made to arrive from T to $T^{\left(k\right)}$.

To finish this section we are going to prove a deeper result. In particular we can give the complete characterization of periods for oriented 3-IETs.

Theorem 8.

Let $T=(\lambda ,\pi )$ be an oriented 3-IET, then $\mathrm{Per}\left(T\right)$ is one of the following sets:

$$\varnothing ,\left\{p\right\},\{1,p\},\{p,p+1\},\mathrm{for}\mathrm{some}p\in \mathbb{N}.$$

Conversely, for any one of the previous sets, let us say A, we can build an oriented 3-IET, T, such that $\mathrm{Per}\left(T\right)=A$.

Proof. 

Observe that $\pi$ is one of the following six permutations:

$${\pi }_1=(1,2,3),{\pi }_2=(1,3,2),{\pi }_3=(2,1,3),{\pi }_4=(2,3,1),{\pi }_5=(3,1,2),{\pi }_6=(3,2,1).$$

If $\pi$ is reducible, then $\pi \in \{{\pi }_1,{\pi }_2,{\pi }_3\}$, and we can ensure the existence of periods. It is easy to realize that $\mathrm{Per}\left(T\right)=\left\{1\right\}$ for ${\pi }_1$, and $\mathrm{Per}\left(T\right)=\left\{1\right\}$ or $\mathrm{Per}\left(T\right)=\{1,p\}$ for some $p\in \mathbb{N}$ when $\pi ={\pi }_2$ or $\pi ={\pi }_3$. Also, it is a simple task to build 3-IETs T having associated reducible permutations and with set of periods $\left\{1\right\}$ or $\{1,p\}$ for all $p\in \mathbb{N}.$

The IETs associated to permutations ${\pi }_4$ and ${\pi }_5$ are rotation circles with one false discontinuity. Then, either $\mathrm{Per}\left(T\right)=\varnothing$ or $\mathrm{Per}\left(T\right)=\left\{p\right\}$ for some $p\in \mathbb{N}$. Conversely, we can find a rotation of the circle with period p and adding a false discontinuity in order to obtain a 3-IET T such that either $\mathrm{Per}\left(T\right)=\varnothing$ or $\mathrm{Per}\left(T\right)=\left\{p\right\}$ regardless of the number p is chosen.

Finally, it remains to analyze 3-IETs $T=(\lambda ,\pi )$ with $\pi ={\pi }_6=(3,2,1)$. If $\mathrm{Per}\left(T\right)=\varnothing$, there is nothing to study. So, we assume that $\mathrm{Per}\left(T\right)\ne \varnothing$. If T is not in the domain of $\mathcal{R}$, we have shown above that $P\left(T\right)=\left(\begin{array}{cc}1& 0\\ 0& 1\\ 1& 0\end{array}\right)$ and then $\mathrm{Per}\left(T\right)=\{1,2\}$ (although this set can be computed directly if we notice that ${\lambda }_1={\lambda }_3$). If, in exchange, $T\in \mathrm{Dom}\left(\mathcal{R}\right)$, we compute $\mathcal{R}\left(T\right)=T^{\prime }=({\lambda }^{\prime },{\pi }^{\prime })$ and the following two possibilities arise, depending on whether T has type a or type b:

(a)

${\pi }^{\prime }=(2,3,1)$, $T^{\prime }=({\lambda }^{\prime },{\pi }^{\prime })$. In this case, $T^{\prime }$ is a rotation of the circle with a false discontinuity, let us say $c:={\lambda }_1^{\prime }$. We denote by S this rotation (deleting the discontinuity at c). Notice that $\mathrm{Per}\left(T^{\prime }\right)\ne \varnothing$, otherwise $\mathrm{Per}\left(S\right)=\varnothing$, so S and T would be minimal without periodic orbits, in contradiction with the initial hypothesis imposed to T. Realize that S is an orientable 2-IET with a unique periodic component (see Section 4.2). Note that c is in the interior of this component and the orbit, by S, split this component into two periodic components of $T^{\prime }$, both of them having the same number of connected components; then, we easily obtain that

$$\begin{array}{c}\hfill P\left(S\right)=\left(\begin{array}{c}r\\ s\end{array}\right),\mathrm{and}P\left(T^{\prime }\right)=\left(\begin{array}{cc}{r}_1& r_1-1\\ r_2& r_2+1\\ s& s\end{array}\right)\mathrm{with}{r}_1+r_2=r\ge 1,s\ge 1,r_1\ge 1.\end{array}$$

Now by applying Theorem 4 and Claim 2:

$$P\left(T\right)=M_a(3,2,1)P\left(T^{\prime }\right)=\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 1& 0& 1\end{array}\right)\left(\begin{array}{cc}{r}_1& r_1-1\\ r_2& r_2+1\\ s& s\end{array}\right)=\left(\begin{array}{cc}{r}_1& r_1-1\\ r_2& r_2+1\\ r_1+s& r_1-1+s\end{array}\right)$$

and then $\mathrm{Per}\left(T\right)=\{2r_1+r_2+s,2r_1+r_2+s-1\}=\{r+r_1+s,r+r_1+s-1\}$ or

$$\mathrm{Per}\left(T\right)=\{p,p+1\}\mathrm{with}p\ge 2.$$

(b)

${\pi }^{\prime }=(3,1,2)$, $T^{\prime }=({\lambda }^{\prime },{\pi }^{\prime })$. Again $T^{\prime }$ is a rotation of the circle with a false discontinuity, $c:=1-{\lambda }_3^{\prime }$. If S denotes the rotation containing c in its domain, reasoning as in (a), S splits its unique periodic component into two periodic components of $T^{\prime }$, both of them having the same number of connected components, so

$$\begin{array}{c}\hfill P\left(S\right)=\left(\begin{array}{c}r\\ s\end{array}\right)\mathrm{and}P\left(T^{\prime }\right)=\left(\begin{array}{cc}r& r\\ s_1& s_1-1\\ s_2& s_2+1\end{array}\right)\mathrm{with}{s}_1+s_2=s\ge 1,r\ge 1,s_1\ge 1.\end{array}$$

Theorem 4 and Claim 2 give

$$P\left(T\right)=M_b(3,2,1)P\left(T^{\prime }\right)=\left(\begin{array}{ccc}1& 1& 0\\ 0& 0& 1\\ 0& 1& 0\end{array}\right)\left(\begin{array}{cc}r& r\\ s_1& s_1-1\\ s_2& s_2+1\end{array}\right)=\left(\begin{array}{cc}r+s_1& r+s_1-1\\ s_2& s_2+1\\ s_1& s_1-1\end{array}\right),$$

therefore $\mathrm{Per}\left(T\right)=\{2s_1+s_2+r,2s_1+s_2+r-1\}$ or

$$\mathrm{Per}\left(T\right)=\{p,p+1\}\mathrm{with}p\ge 2.$$

In order to finish the proof, we need to complete the converse part. Note first that we have shown above that the set of periods $\left\{p\right\}$ and $\{1,p\}$, $p\in \mathbb{N}$, can be easily realized by means of reducible permutations. Also $\left\{p\right\}$ is the period set of a rational rotation by including a false discontinuity.

It only remains to give 3-IETs $T=(\lambda ,\pi )$ with set of periods $\{p,p+1\}$, $p\ge 2$. This case can be easily built following this route: take a rational rotation (2-IET) S with matrix of periods $\left(\begin{array}{c}r\\ s\end{array}\right)$ and induce in it a false discontinuity c in the first interval of continuity of S. Then, we obtain a 3-IET $T=(\lambda ,\pi )$ with $\pi =(2,3,1)$; observe that we can adequately choose c in order to have $T\in \mathrm{Dom}\left(\mathcal{R}\right)$ and T of type a. Under these premises, $P\left(T\right)=\left(\begin{array}{cc}{r}_1& r_1-1\\ r_2& r_2+1\\ s& s\end{array}\right)\mathrm{with}{r}_1+r_2=r\ge 1,s\ge 1,r_1\ge 1,$ and $P\left(T^{\prime }\right)=M_a^{-1}(2,3,1)P\left(T\right)=\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& -1& 1\end{array}\right)\left(\begin{array}{cc}{r}_1& r_1-1\\ r_2& r_2+1\\ s& s\end{array}\right)=\left(\begin{array}{cc}{r}_1& r_1-1\\ r_2& r_2+1\\ s-r_2& s-r_2-1\end{array}\right)$ $\mathrm{then}$ Per(T′) = {s + r₁, s + r₁ − 1}. $\mathrm{Since} \mathrm{we} \mathrm{can} \mathrm{take}$ s, r, _r1 ≥ 1$, \mathrm{even} \mathrm{with} s>r, \mathrm{we} \mathrm{obtain} \mathrm{that}$ T′$\mathrm{can} \mathrm{be} \mathrm{adequately} \mathrm{chosen} \mathrm{to} \mathrm{have}$ Per(T′) = {p, p + 1}$\mathrm{for} \mathrm{any}$ p ≥ 1. □

Claim 3.

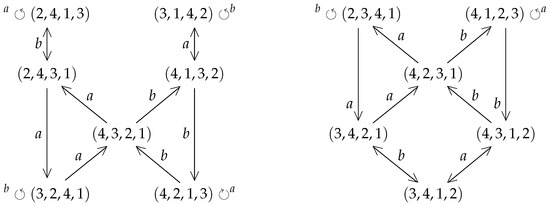
For orientable 4-IETs, there exist two Rauzy classes, which we illustrate in Figure 4. The class on the right can be studied by reducing it to 3-IETs, as any permutation has false discontinuities, and by applying Theorems 4–6. However, the other class (the one on the left) has no false discontinuities, and the range of possible paths that an IET can take through the Rauzy operator is infinite. Thus, formulating a global theorem is certainly complicated, but the techniques presented in this paper allow us to analyze individually any case that may arise.

Figure 4. Representation of the two Rauzy classes in ${\mathcal{O}}_4$.

5.2. The Class of $(-3,-2,1)$

This subsection is devoted to show the powerful of our study about the computation of periods of IETS via the period matrix $P\left(T\right)$. Due the numerous cases for general 3-IETs, namely, $3!\times 2^3=48$ permutations, we have restricted our attention to a singular Rauzy class.

In particular, we take into account the Rauzy-class introduced in Figure 5. Observe that, by Theorem 7, the study of the periods of these permutations also gives the periods of another Rauzy class, the one of vertices: $(3,-2,-1)$, $(2,3,-1)$, $(3,-1,-2)$, $(-2,-1,-3)$ and $(-1,-3,-2)$, since these permutations are the inverse and conjugated of the ones appearing in Figure 5.

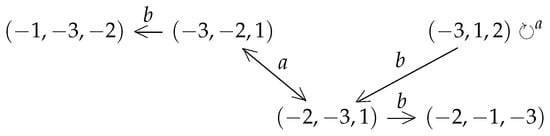
Figure 5. A Rauzy class of non-oriented 3-IETs.

We are going to show how to apply Theorems 4–6 to the Rauzy class introduced in Figure 5. We focus on those irreducible permutations appearing in Figure 5: $(-3,-2,1),(-2,-3,1),$ and $(-3,1,2).$

5.2.1. Permutation $\pi =(-3,-2,1)$

Observe that we have a false discontinuity and then the result is a consequence of the results in Section 4.1. If we remove the false discontinuity we obtain a 2-IET with associated permutation $(-2,1)$. Let $T=(\lambda ,\pi )$ and $T_2$ the IET obtained from T by removing the false discontinuity c.

(A) Assume first that, according to (4), see also Proposition 1 and Corollary 1, $T_2$ has associated matrix of periods $P\left(T_2\right)=\left(\begin{array}{cc}1& 1\\ n+1& n\end{array}\right)$ and two periodic components, $O_1$ and $O_2$, with $n\ge 0$; then the matrix of periods of T, and the set $\mathrm{Per}\left(T\right)$, are one of the following:

(a)

If $c\in \mathrm{Bd}{O}_1\cap \mathrm{Bd}{O}_2$ (c is a saddle point of $T_2$ by Lemma 1), then:

$$P\left(T\right)=\left(\begin{array}{cc}1& 0\\ 0& 1\\ n+1& n\end{array}\right)\mathrm{and}\mathrm{Per}\left(T\right)=\{n+2,n+1,2(n+2),2(n+1)\}.$$

(b)

If $c\in O_1$ and its period, by T, is $n+2$, then c is placed in the middle of one connected component of $O_1$ and each one of these components split into two pieces by the orbit of c. Then:

$$P\left(T\right)=\left(\begin{array}{cc}1& 0\\ 1& 1\\ 2(n+1)& n\end{array}\right)\mathrm{and}\mathrm{Per}\left(T\right)=\{2(n+2),n+1,2(n+1)\}.$$

(c)

Assume that $c\in O_1$ and that its period, by T, is $2(n+2)$. Denote by $I_1^j$, $1\le j\le n+2$, the connected components of $O_1$ (for $T_2$) labelled satisfying $c\in I_1^1$, $T\left(I_1^j\right)=I_1^{j+1}$ for any $1\le j\le n+1$, and $T\left(I_1^{n+2}\right)=I_1^1$. Observe that the orbit of c visits each one of the connected components of $O_1$ twice and this orbit divides these components into three pieces (left, middle, and right because in each component we have one point of order $n+2$): $I_1^j=I_1^{j,l}\cup I_1^{j,m}\cup I_1^{j,r}$. Note now the following relations:

$$\begin{array}{ccccc}T\left(I_1^{1,l}\right)=I_1^{2,r},& & T\left(I_1^{j,l}\right)=I_1^{j+1,l},2\le j\le n+1,& & T\left(I_1^{n+2,l}\right)=I_1^{1,l},\\ T\left(I_1^{1,r}\right)=I_1^{2,l},& & T\left(I_1^{j,r}\right)=I_1^{j+1,r},2\le j\le n+1,& & T\left(I_1^{n+2,r}\right)=I_1^{1,r},\\ & & T\left(I_1^{j,m}\right)=I_1^{j+1,m},1\le j\le n+1,& & T\left(I_1^{n+2,m}\right)=I_1^{1,m}.\end{array}$$

Hence, the periodic component $O_1$ from $T_2$ gives two periodic components, $O_1^{\prime }$ and $O_2^{\prime }$, of T (being $O_2^{\prime }$ the connected component giving the movement of the middle intervals $I_1^{j,m}$, $1\le j\le n+2$), and $O_3^{\prime }=O_2$ remains as a periodic component of T. Finally, we obtain the matrix of periods and the set of periods depending on if $c\in \mathrm{Bd}\left(I_1^{1,l}\right)$ or $c\in \mathrm{Bd}\left(I_1^{1,r}\right)$. They are respectively

$$P\left(T\right)=\left(\begin{array}{ccc}1& 0& 0\\ 1& 1& 1\\ 2(n+1)& n+1& n\end{array}\right),\mathrm{Per}\left(T\right)=\{2(n+2),n+2,n+1,2(n+1)\}\mathrm{and}$$

$$P\left(T\right)=\left(\begin{array}{ccc}1& 1& 0\\ 1& 0& 1\\ 2(n+1)& n+1& n\end{array}\right)\mathrm{and}\mathrm{Per}\left(T\right)=\{2(n+2),n+2,n+1,2(n+1)\}.$$

(d)

If $c\in O_2$ and its period, by T, is $n+1$, then c is in the middle of one connected component of $O_2$ and all the components of $O_2$ are split into two pieces by the orbit of c in such a way that in $O_1^{\prime }=O_1$ we find intervals of the form $(0,\delta )$ in $I_1$, $({\lambda }_1+{\lambda }_2,\delta )$ and $(1-\delta ,\delta )$ in $I_3$, for some $\delta >0$; whereas in $(I_1\cup I_2)\cap O_2^{\prime }$ we find the intervals $(\delta ,c)\cup (c,{\lambda }_1+{\lambda }_2)$ which are reversed by T when we return to $I_1\cup I_2$. Thus, we have

$$P\left(T\right)=\left(\begin{array}{cc}1& 1\\ 0& 1\\ n+1& 2n\end{array}\right)\mathrm{and}\mathrm{Per}\left(T\right)=\{n+2,2(n+2),2(n+1)\}.$$

(e)

If the period of c in $O_2$, under T, is $2(n+1)$, then we make an argument similar to the one in the previous item (c) and we have two possibilities:

$$P\left(T\right)=\left(\begin{array}{ccc}1& 1& 0\\ 0& 1& 1\\ n+1& 2n& n\end{array}\right)\mathrm{or}P\left(T\right)=\left(\begin{array}{ccc}1& 1& 1\\ 0& 1& 0\\ n+1& 2n& n\end{array}\right),$$

whose associate periods sets are, in both cases:

$$\mathrm{Per}\left(T\right)=\{n+2,2(n+2),2(n+1),n+1,2(n+1\left)\right\}.$$

(B) If, according to (5) (see also Proposition 2 and Corollary 1), we assume that $T_2$ has an associated matrix of periods $P\left(T_2\right)=\left(\begin{array}{c}1\\ n+1\end{array}\right),$ then the period matrix of T is one of the following:

(a)

If the period of c, by T, is $n+2$, then we have again a unique periodic component, and

$$P\left(T\right)=\left(\begin{array}{c}1\\ 1\\ 2(n+1)\end{array}\right)\mathrm{with}\mathrm{Per}\left(T\right)=\left\{2(n+2)\right\}.$$

(b)

If the period of c, by T, is $2(n+2)$, a new periodic component $O_2^{\prime }$ appears composed by “middle” intervals having c and its iterates in their boundary, thus

$$P\left(T\right)=\left(\begin{array}{cc}1& 0\\ 1& 1\\ 2(n+1)& n+1\end{array}\right)\mathrm{or}P\left(T\right)=\left(\begin{array}{cc}1& 1\\ 1& 0\\ 2(n+1)& n+1\end{array}\right).$$

In both cases $\mathrm{Per}\left(T\right)=\left\{2\right(n+2),n+2\}.$

(C) Finally, if T is not in the domain of $\mathcal{R}$ then $P\left(T\right)=\left(\begin{array}{cc}1& 0\\ 0& 1\\ 1& 0\end{array}\right)$ and $\mathrm{Per}\left(T\right)=\{1,2,4\}$.

Theorem 9.

Let $T=(\lambda ,\pi )$ be a 3-IET with $\pi =(-3,-2,1)$. Then, $P\left(T\right)$ is one of the following matrices:

$$\begin{array}{ccc}& & \left(\begin{array}{cc}1& 0\\ 0& 1\\ n+1& n\end{array}\right),\left(\begin{array}{cc}1& 0\\ 1& 1\\ 2(n+1)& n\end{array}\right),\left(\begin{array}{ccc}1& 0& 0\\ 1& 1& 1\\ 2(n+1)& n+1& n\end{array}\right),\left(\begin{array}{ccc}1& 1& 0\\ 1& 0& 1\\ 2(n+1)& n+1& n\end{array}\right),\hfill \\ & & \left(\begin{array}{cc}1& 1\\ 0& 1\\ n+1& 2n\end{array}\right),\left(\begin{array}{ccc}1& 1& 0\\ 0& 1& 1\\ n+1& 2n& n\end{array}\right),\left(\begin{array}{ccc}1& 1& 1\\ 0& 1& 0\\ n+1& 2n& n\end{array}\right),\left(\begin{array}{cc}1& \\ 1& \\ 2(n+1)\end{array}\right),\hfill \\ & & \left(\begin{array}{cc}1& 0\\ 1& 1\\ 2(n+1)& n+1\end{array}\right),\left(\begin{array}{cc}1& 1\\ 1& 0\\ 2(n+1)& n+1\end{array}\right),\left(\begin{array}{cc}1& 0\\ 0& 1\\ 1& 0\end{array}\right),n\ge 0.\hfill \end{array}$$

Corollary 2.

Let $T=(\lambda ,\pi )$ be a 3-IET with $\pi =(-3,-2,1)$. Then, $\mathrm{Per}\left(T\right)=A$ being A one of the following sets for some $n\ge 0$:

• $\{n+2,n+1,2(n+2),2(n+1\left)\right\}$
• $\left\{2\right(n+2),n+1,2(n+1\left)\right\}$
• $\{n+2,2(n+2),2(n+1\left)\right\}$
• $\left\{2\right(n+2\left)\right\}$
• $\left\{2\right(n+2),n+2\}$

Proof. 

Observe that the period sets computed in this section are

• $\{n+2,n+1,2(n+2),2(n+1\left)\right\}$
• $\left\{2\right(n+2),n+1,2(n+1\left)\right\}$
• $\{n+2,2(n+2),2(n+1\left)\right\}$
• $\left\{2\right(n+2\left)\right\}$
• $\left\{2\right(n+2),n+2\}$
• $\{1,2,4\}$.

Then, it is easy to abstract these periods sets in the ones of the statement. □

5.2.2. IETs Associated to the Permutation $\pi =(-2,-3,1)$

Let $T=(\lambda ,\pi )$ with $\pi =(-2,-3,1)$; now we have three possibilities:

• T is not in the domain of $\mathcal{R}$. In this case $P\left(T\right)$ is one of the following:

  $$\left(\begin{array}{cc}1& 1\\ 1& 0\\ 1& 0\end{array}\right),\left(\begin{array}{cc}1& 0\\ 1& 1\\ 1& 1\end{array}\right),\left(\begin{array}{c}1\\ 1\\ 1\end{array}\right),$$

  in the situations ${\lambda }_1>{\lambda }_2={\lambda }_3$, ${\lambda }_1<{\lambda }_2={\lambda }_3$ and ${\lambda }_1={\lambda }_2={\lambda }_3$, respectively. A graphical example of each one of this cases is depicted in Figure 6.
  

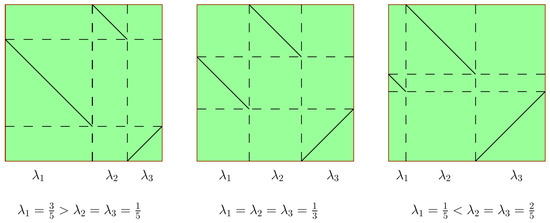  Figure 6. IETs with associated permutation $\pi =(-2,-3,1)$ for which the operator $\mathcal{R}$ is not defined.
• We can apply b to T and $\mathcal{R}\left(T\right)=({\lambda }^{\prime },(-2,-1,-3))$. Observe first that $P\left(\mathcal{R}\right(T\left)\right)$ is one of the following matrices:

  $$\left(\begin{array}{cc}1& 0\\ 1& 0\\ 0& 1\end{array}\right),\left(\begin{array}{ccc}1& 0& 0\\ 1& 1& 0\\ 0& 0& 1\end{array}\right),\left(\begin{array}{ccc}1& 1& 0\\ 1& 0& 0\\ 0& 0& 1\end{array}\right),$$

  depending if ${\lambda }_1^{\prime }={\lambda }_2^{\prime }$, ${\lambda }_1^{\prime }<{\lambda }_2^{\prime }$ or ${\lambda }_1^{\prime }>{\lambda }_2^{\prime }$, respectively. Figure 7 represents the last case.
  

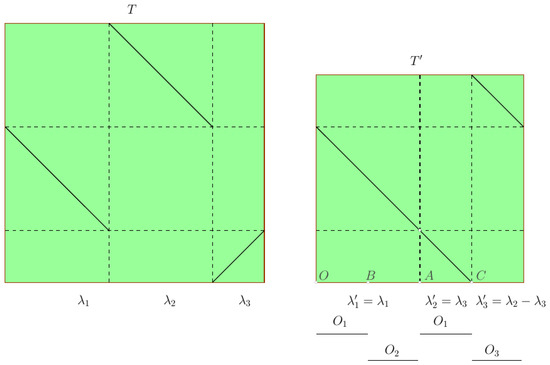  Figure 7. IET T with associated permutation $\pi =(-2,-3,1)$ on the left. On the right we have $T^{\prime }$ with the connected components $O_1=(O,B)\cup (A,C)$, $O_2=(B,A)\subset I_1^{\prime }$ and $O_3=I_3^{\prime }$.
  Consequently, by Theorem 4, $P(T)=M_b((-2,-3,1))P(\mathcal{R}(T))=\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 1\\ 0& 1& 0\end{array}\right)P\left(\mathcal{R}\left(T\right)\right)$ and $P\left(T\right)$ is one of the following matrices:

  $$\left(\begin{array}{cc}1& 0\\ 1& 1\\ 1& 0\end{array}\right),\left(\begin{array}{ccc}1& 0& 0\\ 1& 1& 1\\ 1& 1& 0\end{array}\right),\left(\begin{array}{ccc}1& 1& 0\\ 1& 0& 1\\ 1& 0& 0\end{array}\right).$$
• We can apply a to T and $\mathcal{R}\left(T\right)=({\lambda }^{\prime },(-3,-2,1))$. In this case, $P\left(T^{\prime }\right)$ is one of the matrices listed in Theorem 9. Also $P\left(T\right)=M_a\left((-2,-3,1)\right)P\left(T^{\prime }\right)=\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 1& 1\end{array}\right)P\left(T^{\prime }\right)$. Then, $P\left(T\right)$ is one of the following matrices:

  $$\begin{array}{c}\hfill \left(\begin{array}{cc}1& 0\\ 0& 1\\ n+1& n+1\end{array}\right),\left(\begin{array}{cc}1& 0\\ 1& 1\\ 2n+3& n+1\end{array}\right),\left(\begin{array}{ccc}1& 0& 0\\ 1& 1& 1\\ 2n+3& n+2& n+1\end{array}\right),\left(\begin{array}{ccc}1& 1& 0\\ 1& 0& 1\\ 2n+3& n+1& n+1\end{array}\right),\\ \hfill \left(\begin{array}{cc}1& 1\\ 0& 1\\ n+1& 2n+1\end{array}\right),\left(\begin{array}{ccc}1& 1& 0\\ 0& 1& 1\\ n+1& 2n+1& n+1\end{array}\right),\left(\begin{array}{ccc}1& 1& 1\\ 0& 1& 0\\ n+1& 2n+1& n\end{array}\right),\left(\begin{array}{c}1\\ 1\\ 2n+3\end{array}\right),\\ \hfill \left(\begin{array}{cc}1& 0\\ 1& 1\\ 2n+3& n+2\end{array}\right),\left(\begin{array}{cc}1& 1\\ 1& 0\\ 2n+3& n+1\end{array}\right),\left(\begin{array}{cc}1& 0\\ 0& 1\\ 1& 1\end{array}\right).\end{array}$$

Finally

Theorem 10.

Let $T=(\lambda ,\pi )$ be a 3-IET with $\pi =(-2,-3,1)$. Then, $P\left(T\right)$ is one of the following matrices:

$$\begin{array}{ccc}& & \left(\begin{array}{cc}1& 1\\ 1& 0\\ 1& 0\end{array}\right),\left(\begin{array}{cc}1& 0\\ 1& 1\\ 1& 1\end{array}\right),\left(\begin{array}{c}1\\ 1\\ 1\end{array}\right),\left(\begin{array}{cc}1& 0\\ 1& 1\\ 1& 0\end{array}\right),\left(\begin{array}{ccc}1& 0& 0\\ 1& 1& 1\\ 1& 1& 0\end{array}\right),\left(\begin{array}{ccc}1& 1& 0\\ 1& 0& 1\\ 1& 0& 0\end{array}\right),\left(\begin{array}{cc}1& 0\\ 0& 1\\ n+1& n+1\end{array}\right),\hfill \\ & & \left(\begin{array}{cc}1& 0\\ 1& 1\\ 2n+3& n+1\end{array}\right),\left(\begin{array}{ccc}1& 0& 0\\ 1& 1& 1\\ 2n+3& n+2& n+1\end{array}\right),\left(\begin{array}{ccc}1& 1& 0\\ 1& 0& 1\\ 2n+3& n+1& n+1\end{array}\right),\hfill \\ & & \left(\begin{array}{cc}1& 1\\ 0& 1\\ n+1& 2n+1\end{array}\right),\left(\begin{array}{ccc}1& 1& 0\\ 0& 1& 1\\ n+1& 2n+1& n+1\end{array}\right),\left(\begin{array}{ccc}1& 1& 1\\ 0& 1& 0\\ n+1& 2n+1& n\end{array}\right),\hfill \\ & & \left(\begin{array}{c}1\\ 1\\ 2n+3\end{array}\right),\left(\begin{array}{cc}1& 0\\ 1& 1\\ 2n+3& n+2\end{array}\right),\left(\begin{array}{cc}1& 1\\ 1& 0\\ 2n+3& n+1\end{array}\right),\left(\begin{array}{cc}1& 0\\ 0& 1\\ 1& 1\end{array}\right).\hfill \end{array}$$

As a consequence of these matrices of periods, we obtain

Corollary 3.

Let $T=(\lambda ,\pi )$ be a 3-IET with $\pi =\left\{\right(-2,-3,1\left)\right\}$. Then, $\mathrm{Per}\left(T\right)=A$, being A one of the following sets:

• $\{1,2,3\}$
• $\{2,3,4\}$
• $\left\{3\right\}$
• $\{1,2,3,4\}$
• $\{n+2,2n+4\}$
• $\{n+2,2n+4,2n+5\}$
• $\{n+2,2n+4,n+3,2n+6,2n+5\}$
• $\{n+2,2n+4,2n+3\}$
• $\{n+1,2n+2,n+2,2n+4,2n+3\}$
• $\{2n+5\}$
• $\{2n+5,n+3,2n+6\}$
• $\{2n+5,n+2,2n+4\}$

Note that we have seventeen matrices of periods while only twelve sets of periods. This is because for some different matrices we obtain the same sets of periods. This is the case for example for the first and fourth matrices.

5.2.3. Permutation $\pi =(-3,1,2)$

Let $T=(\lambda ,\pi )=(\lambda ,(-3,1,2\left)\right)$. Observe that T is a $(2,1)$-IET with a false discontinuity and associate permutation $(-2,1)$, let us denote it by $T_2$. We could repeat the arguments of Section 5.2.1 where we have explained how to obtain the matrices of periods. For the sake of simplicity we will obtain solely the set of periods of T. We avoid computing the period matrices because they are not needed in what follows. In Section 5.2.1, we performed this computation because they were required in Section 5.2.2.

Observe that the orbits of T and $T_2$ coincide except for the one of the false discontinuity c, let us say that the period of c is p. This orbit is not an orbit of T and eventually, if T has not other orbits of period p then $\mathrm{Per}\left(T\right)=\mathrm{Per}\left(T_2\right)\setminus \left\{p\right\}$. In another case, $\mathrm{Per}\left(T\right)=\mathrm{Per}\left(T_2\right)$.

Recall that the matrix of periods of $T_2$, see (4) and (5), is one of

$$A=\left(\begin{array}{cc}1& 1\\ n+1& n\end{array}\right),B=\left(\begin{array}{c}1\\ n+1\end{array}\right),n\ge 0.$$

If $P\left(T_2\right)=A$ then $T_2$ has infinitely many orbits of periods $2(n+2)$ and $2(n+1)$, only one orbit of period $n+2$ and another one of period $n+1$ (the one corresponding to the middle point of the connected components of the periodic components). Then, depending on the location of the false discontinuity, $\mathrm{Per}\left(T\right)$ is one of the following:

• $\left\{2\right(n+1),2(n+2),n+1,n+2\},$
• $\left\{2\right(n+1),2(n+2),n+2\},$
• $\left\{2\right(n+1),2(n+2),n+1\}.$

If $P\left(T_2\right)=B$ then $T_2$ has infinitely many orbits of periods $2(n+2)$ and only one orbit of period $n+2$ (the one corresponding to the middle point of the connected components of the periodic component). Then, depending on the location of the false discontinuity, $\mathrm{Per}\left(T\right)$ is one of the following:

• $\left\{2\right(n+2),n+2\},$
• $\left\{2\right(n+2\left)\right\}.$

Therefore, we have proved the following:

Corollary 4.

Let $T=(\lambda ,\pi )$ be a 3-IET with $\pi =(-3,1,2)$. Then, $\mathrm{Per}\left(T\right)$ is one of the following sets:

• $\left\{2\right(n+1),2(n+2),n+1,n+2\},$
• $\left\{2\right(n+1),2(n+2),n+2\},$
• $\left\{2\right(n+1),2(n+2),n+1\},$
• $\left\{2\right(n+2),n+2\},$
• $\left\{2\right(n+2\left)\right\}.$

To finish this subsection, we present in Table 1 the corresponding matrices $P\left(T\right)$ to the reducible permutations of the Rauzy class appearing in Figure 5. In the first row, the matrices correspond with the cases ${\lambda }_2<{\lambda }_3$, ${\lambda }_2>{\lambda }_3,$ and ${\lambda }_2={\lambda }_3$, respectively; whereas, the row for $(-2,-1,-3)$ reflects the cases ${\lambda }_1<{\lambda }_2$, ${\lambda }_1>{\lambda }_2,$ and ${\lambda }_1={\lambda }_2$, respectively.

Table 1. Matrices of periods associated to reducible permutations in Figure 5.

$\mathit{\pi }$	$\mathit{P}\left(\mathit{T}\right)=(\mathit{\lambda },\mathit{\pi }))$
$(-1,-3,-2)$	$\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 1& 1\end{array}\right)$, $\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 1\\ 0& 1& 0\end{array}\right)$ or $\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 1& 0\end{array}\right)$
$(-2,-1,-3)$	$\left(\begin{array}{ccc}1& 0& 0\\ 1& 1& 0\\ 0& 0& 1\end{array}\right)$, $\left(\begin{array}{ccc}1& 1& 0\\ 1& 0& 0\\ 0& 0& 1\end{array}\right)$ or $\left(\begin{array}{ccc}1& 0& 0\\ 1& 0& 0\\ 0& 1& 0\end{array}\right)$

5.3. The Class of $(-3,2,-1)$, Third Class

In this class, if $T=(\lambda ,\pi )$ with $\pi =(-3,2,-1),$ we have three possibilities:

• T is not in the domain of $\mathcal{R}$ because ${\lambda }_1={\lambda }_3$; then, $P\left(T\right)=\left(\begin{array}{cc}1& 0\\ 0& 1\\ 1& 0\end{array}\right),$ and $\mathrm{Per}\left(T\right)=\{1,2\}$.
• T is in the domain of $\mathcal{R}$ and we obtain $\mathcal{R}\left(T\right)=T^{\prime }=({\lambda }^{\prime },{\pi }^{\prime })$ by means of a, with ${\pi }^{\prime }=(1,3,-2)$. Observe that, according to the results of Section 4.1, there exists $n\ge 0$ such that either $P\left(\mathcal{R}\right(T\left)\right)$ is $\left(\begin{array}{ccc}1& 0& 0\\ 0& n+1& n\\ 0& 1& 1\end{array}\right)$ or $\left(\begin{array}{ccc}1& 0& 0\\ 0& n+1& 0\\ 0& 1& 0\end{array}\right)$. In this case, we obtain, respectively, $P\left(T\right)=M_a\left((-3,2,1)\right)P\left(\mathcal{R}\left(T\right)\right)$ is $\left(\begin{array}{ccc}1& 0& 0\\ 0& n+1& n\\ 1& 1& 1\end{array}\right)\mathrm{or}\left(\begin{array}{ccc}1& 0& 0\\ 0& n+1& 0\\ 1& 1& 0\end{array}\right)$ and, respectively, the following periods: $\{2,n+2,2(n+2),n+1,2(n+1\left)\right\}$ and $\{2,n+2,2(n+2\left)\right\}$.
• T is in the domain of $\mathcal{R}$ and we obtain $\mathcal{R}\left(T\right)$ by means of b and ${\pi }^{\prime }=(1,-3,2)$. Observe that again Section 4.1 gives the existence of $n\ge 0$ such that either $P\left(\mathcal{R}\right(T\left)\right)$ is $\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 1\\ 0& n+1& n\end{array}\right)$ or $\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& n+1& 0\end{array}\right)$. In this case, we obtain, respectively, $P\left(T\right)=M_b\left((-3,2,1)\right)P\left(\mathcal{R}\left(T\right)\right)$ is either $\left(\begin{array}{ccc}1& 1& 1\\ 0& n+1& n\\ 1& 0& 0\end{array}\right)\mathrm{or}\left(\begin{array}{ccc}1& 1& 0\\ 0& n+1& 0\\ 1& 0& 0\end{array}\right)$ and, respectively, the following period sets: $\{2,n+2,2n+4,n+1,2n+2\}$ and $\{2,n+2,2n+4\}$ (doubling the second period if n is even).

6. Conclusions

In this paper, we have presented a new mechanism for computing the set of periods of non-transitive interval exchange transformations; see Theorems 4–6. This procedure is related with the so-called Rauzy induction process. In this way, we have determined all the sets of periods that an oriented 3-IET can exhibit, Theorem 8; additionally, with this technique we have been able to revisit the case of 2-IETs, oriented or not, and we have checked that our approach gives the same results as those presented in [7].

Evidently, a full characterization of the set of periods for a general $(d,k)$-IETS is far from being achieved, even for the case of non-oriented $(3,k)$-IETs the casuistry increases rapidly, as we have shown with the elements of the Rauzy class given in Figure 5. Nevertheless, the results presented enable the computation of the periods for any specific $(n,k)$-IET without transitive components, even though to provide a comprehensive description of all possible periods for an arbitrary IET remains a complex task.

In any case, if we have an IET with d discontinuities, and we are able, by the effect of operators a and b involved in the Rauzy induction, to descend until another IET whose periodic components are already known, by using the main theorems of this paper we will be able to determine the periods of the initial IET.