Abstract
Padé approximants are computational tools customarily employed for resumming divergent Stieltjes series. However, they become ineffective or even fail when applied to Stieltjes series whose moments do not satisfy the Carleman condition. Differently from Padé, Levin-type transformations incorporate important structural information on the converging factors of a typical Stieltjes series. For example, the computational superiority of Weniger’s -transformation over Wynn’s epsilon algorithm is ultimately based on the fact that Stieltjes series converging factors can always be represented as inverse factorial series. In the present paper, the converging factors of an important class of superfactorially divergent Stieltjes series are investigated via an algorithm developed one year ago from the first-order difference equation satisfied by the Stieltjes series converging factors. Our analysis includes the analytical derivation of the inverse factorial representation of the moment ratio sequence of the series under investigation, and demonstrates the numerical effectiveness of our algorithm, together with its implementation ease. Moreover, a new perspective on the converging factor representation problem is also proposed by reducing the recurrence relation to a linear Cauchy problem whose explicit solution is provided via Faà di Bruno’s formula and Bell’s polynomials.
MSC:
40-08; 40A05; 40A30
1. Introduction
Stieltjes series are fundamental tools in mathematical physics and continue to receive considerable attention. For instance, the factorially divergent perturbation expansion of the energy eigenvalue of the -symmetric Hamiltonian has been proved to be Stieltjes [1,2], as conjectured ten years earlier [3]. More recently, it was shown that even the character of the celebrated Bessel solution of Kepler’s equation [4] belongs to the Stieltjes family [5].
The present paper constitutes the follow-up of a previous work on the study of the convergence factors of Stieltjes series [6]. A well-established general convergence theory based on Padé approximants already exists for Stieltjes series. For example, if the moment sequence of a given Stieltjes series satisfies Carleman’s condition, then sequences of its diagonal or near-diagonal Padé approximants are guaranteed to converge to the Stieltjes function that generates the series itself (see, for instance, Baker and Graves-Morris [7]). This has consecrated Padé approximants as the main computational tool for the resummation of Stieltjes series. However, Padé approximants are subject to intrinsic limitation, especially when dealing with wildly divergent series (e.g., such that Carleman’s condition is not satisfied). This led to the development of new types of sequence transformations for summing divergent series. Among them, Levin-type transformations [8,9,10] proved to be particularly effective and powerful, in some cases outperforming Padé-based methods, such as Wynn’s epsilon algorithm [11]. Within the last four decades, an important literature has been produced, especially on nonlinear and nonregular sequence transformations [9,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28].
About fifteen years ago, Ernst Joachim Weniger and I embarked on a challenging research project. We believed that a solid theoretical understanding of Levin-type sequence transformations—perhaps even a comprehensive convergence theory—could offer a valid alternative to Padé approximants for summing divergent Stieltjes series, particularly where Padé-based methods fail. Reference [28] demonstrated the remarkable computational effectiveness of Weniger’s -transformation [9]. This specific Levin-type transformation not only successfully resummed the celebrated Euler series (a paradigm of factorial divergence) but did it with convergence rates greater than Padé. The proof in [28] relied on an inverse factorial expansion for Euler series converging factors, discovered a few years before [29]. Factorial series are often overlooked mathematical objects, largely unknown to non-specialists. Weniger’s merits include unearthing them while developing his -transformation.
Ernst Joachim Weniger passed away on 10 August 2022. Two years later, his contributions and legacy were celebrated in Ref. [6], where a constructive proof that converging factors of typical Stieltjes series can always be expressed through inverse factorial series was proposed. This proof was cast as an algorithm based on a first-order difference equation, which has been shown to be satisfied by the convergent factors of any Stieltjes series [6]. The present paper directly builds upon that tribute, providing a significant continuation of our work. Specifically, the algorithm proposed in [6] is here tested on a class of Stieltjes series with superfactorial moment growth. Weniger’s -transformation has previously succeeded in resumming extremely divergent perturbation expansions, closely related to this class of Stieltjes series [30,31,32,33]. In some of these cases, Padé approximants often proved to be ineffective, as seen with the Rayleigh–Schrödinger perturbation series for the sextic anharmonic oscillator, or even failed in the more challenging octic case [34].
In Section 2, the main definitions and properties of Stieltjes series and Stieltjes functions are briefly reviewed, together with a résumé of Ref. [6]. In Section 3, the class of superfactorially divergent series is presented, and the inverse factorial representation of the moment ratio sequence is analytically found. Section 4 illustrates some examples of application of our algorithm to show its effectiveness and its ease of implementation. Finally, in Section 5 the converging factor representation problem is reformulated from a different perspective by transforming the recurrence relation of [6] into a linear Cauchy problem, whose explicit solution is obtained using Faà di Bruno’s formula together with the use of Bell’s polynomials ([35], Section 3.3).
For an improved readability, the most technical parts have been relegated to appendices.
2. Stieltjes Series Converging Factors, Factorial Series and the Moment Problem
Consider a nondecreasing, real-valued function defined for , possessing infinitely many points of increase. This ensures that the associated measure, say , is positive on . It will be assumed that all of its moments, defined as
are finite. The formal power series
is called a Stieltjes series. Such a series turns out to be asymptotic, in the sense of Poincaré, for , to the function defined by
which is analytic in the complex plane cut along the negative real axis (i.e., and is called the Stieltjes function.
The probably best known example of a Stieltjes series is the Euler series [36], characterised by the moment sequence and asymptotic to the Euler integral,
which has the form given in Equation (3), with the measure .
Given a sequence of moments , is the corresponding Stieltjes function uniquely determined? And, if so, is it possible to decode the asymptotic series into Equation (2) to retrieve the correct value of F? The solution of such a fundamental problem, which is known as the Stieltjes moment problem, depends on the growth rate of the moments. Carleman’s condition represents an important sufficient criterion to assess unicity to the moment problem. In particular, the Stieltjes moment problem is determinate if the series
diverges.
Any Stieltjes function can be expressed as the sum of the nth-order partial sum of the associated asympotic series (2) and of a truncation error which has itself the form of a Stieltjes integral (see for example ([9], Theorem 13-1)). More precisely, we have
and the truncation error term can always be recast as follows:
where the function
will be called the mth-order converging factor [37,38]. (Actually, the definition of the converging factor used here sligthly differs from the classical definition by a factor of z. This has been done to make the subsequent calculations easier.)
From Equation (7), it appears that if reasonable estimates of the converging factor could be achieved without resorting to the numerical evaluation of the integral into Equation (8), then the numerical evaluation of via its asymptotics would be, in principle, possible. The search for techniques aimed at estimating convergence factors plays a role of pivotal importance in decoding divergent asymptotic series. In [6] it has been shown that, given a Stieltjes series, the converging factor in Equation (8) can always be represented as an inverse factorial series. Our proof was ultimately based on (i) the fact that must satisfy the following first-order difference equation [6]:
and (ii) that inverse factorial series constitute natural tools for solving difference equations, similarly as inverse power series are used to solve differential equations. For the reader’s convenience, the basic definitions and properties of factorial series will now be briefly recalled, although extensive reviews can be found, for instance, in [6,28]. More interested and motivated readers are encouraged to go through the Weniger paper [25], where a hystorical account of his re-discovery of factorial series can be found, together with a list of their most important computational features. For the scope of the present paper, it is sufficient to limit ourselves to the following key points:
- (i)
- Let be a complex function of a complex variable x. A factorial series representation of is an expansion of the following type:where the symbol denotes the Pochhammer symbol. In the following, it will be assumed .
- (ii)
- Compared to inverse power series, factorial series often possess superior convergence properties. For example, consider the divergent sequence and construct the following two infinite series:andThe power series diverges for all , whereas the factorial series converges for all . In other words, it may happen that a given function possessing a representation in terms of a divergent asymptotic series also possesses a representation as a convergent factorial series.More precisely, based on the following asymptotics,it is possible to prove that the factorial series into Equation (10) converges if and only if the associated Dirichlet series, i.e.,converges too (see, for example, ([39], p. 262) or ([40], p. 167)).
- (iii)
- Factorial series admit useful integral representations. Starting fromand on inserting into Equation (10), after interchanging integration and summation, the following integral representation is found ([41], Section I on p. 244):where the function turns out to beNote that the function can be thought of as a truncated Mellin transform of the function , in terms of which the expanding coefficients into Equation (10) take on the following form:where the symbol denotes the kth-order derivative of the function . In other words, is nothing but the generating function of the sequence .
The main results of the algorithm derived in Ref. [6] will now be briefly recalled. The idea consisted in searching the solution of the difference Equation (9) in the form of the following inverse factorial series:
where is a real nonnegative parameter and denotes a sequence which is independent of m. For the sake of simplicity, it will be assumed that henceforth. What has been found in Ref. [6] is that the expanding coefficients s can be obtained in a very easy way if the moment ratio sequence admits itself an inverse factorial expansion, i.e.,
In particular, the following recurrence relation holds [6]:
where the sequence is given by
or, equivalently, by
In Ref. [6], Equations (20)–(23) have been applied to re-derive and further generalize (to any ) the result found in [29] as far as the converging factor of the Euler series is concerned. In the next section, they will be employed to find the inverse factorial series representation of the converging factor of an important class of superfactorial divergent Stieltjes series, which can be thought as suitable generalizations of the Euler series.
3. A Class of Superfactorially Divergent Stieltjes Series
The class of Stieltjes series under investigation are characterised by the following moment sequence:
where and . The Euler series corresponds to the choice . Asymptotic series of Equation (24) play a role of pivotal importance in theoretical as well as mathematical physics. They are strictly related to the theory of quantum anharmonic oscillators. In two seminal papers, Bender and Wu [42,43] showed that the Rayleigh–Schrödinger perturbative expansion of the energy levels of the Hamiltonian
with , is asymptotically dominated by the Stieltjes series in Equation (24), with . The summability of such asymptotic series was also addressed in 1993 by Weniger et al. [33] through a series of important numerical experiments aimed at comparing the retrieving performances of Levin-type nonlinear transformations with those of Padé approximants as far as the computation of the energy levels of quartic, sextic and octic oscillators was concerned. In particular, they also considered the numerical resummation of Stieltjes series of the type in Equation (24) for and for some integer values of . In particular, it was found that both Levin’s and Weniger’s transformations were able to correctly decode the series when , whereas Padé approximants failed to achieve the task already when , i.e., when the Carleman condition in Equation (5) is not satisfied.
In the present section, the inverse factorial estimate of the converging factor of the Stieltjes series of Equation (24) will be obtained by applying the algorithm of [6]. Our analysis will be carried out for any values of and q, while it will be set that in all subsequent calculations, as said above. In order for the algorithm in Section 2 to be applied, it is mandatory to find the inverse factorial expansion of the moment ratio sequence for the class of Stieltjes series defined by Equation (24), which can be recast as follows:
On expanding the right side of Equation (26) as a sum of partial fractions of the form
it is not difficult to prove that (see Appendix A)
The subsequent step consists in using Waring’s formula ([41], Equation (3) on p. 77), namely
which, together with Equations (27) and (28), after some algebra, leads to Equation (20) with the following expanding coefficient sequence (see Appendix B):
It should be noted how the mathematical structure of the right side of Equation (30) is nothing but the th-order forward difference of the kth-degree polynomial , i.e.,
where the forward difference operator is defined as . In particular, since is a kth-order polynomial, it follows at once that
The above result can be extended to deal with the most general inverse factorial expansion of the moment ratio. In fact, it is not difficult to show that, in order to deal with , it is sufficient to recast Equation (26) as follows:
and then to proceed similarly as we did for the case . The final result, which is given without proof, is the following:
with the expanding coefficient sequence now being given by
4. Numerical Results
In the present section, a few examples concerning the numerical estimation of the converging factors of some of the divergent superfactorial Stieltjes series analysed in the previous section will be presented. Our attention will be directed to a series of important numerical experiments carried out in 1993 by Weniger et al. [33]. (In order to facilitate the comparison with the original results, in the present section the same notations employed in [33] will be employed.) In particular, our computational targets are two Stieltjes integrals, namely
and
It is not difficult to show that both integrals into Equations (36) and (37) can be recast in the form of Equation (3). For the first integral, it is sufficient to change the integration variable from t to and to let , so to have
with the measure being given by
so that
corresponding to the pair within the model of Equation (24). More importantly, the mth-order converging factor can be analytically evaluated for any in terms of hypergeometric functions (and the result has also been obtained via Wolfram Mathematica),
Similar results hold also for the Stieltjes integral , which can be recast as
where now and
so that
corresponding to . Similarly as happened for , the converging factor of can also be found exactly, although the resulting expression is quite complicated and annoying.
Our algorithm will now be tested starting from by focusing our attention on the relative error obtained when the mth-order converging factor into Equation (41) is evaluated through the following truncated inverse factorial series:
Figure 1 shows the behaviour of the relative error, defined as
related to the converging factor defined by Equation (41), as far as the integral is concerned, for (dashed curve), (dotted curve) and (solid curve).
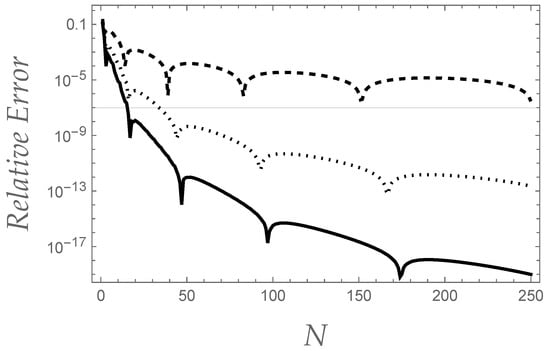
Figure 1.
The behaviour of the relative error related to the converging factor defined by Equation (41), as far as the integral is concerned, for (dashed curve), (dotted curve) and (solid curve).
It can be appreciated how the inverse factorial series representation of appears to converge as , with the convergence rate becoming larger and larger upon increasing the order m, as might be expected from Equation (3) and from the general considerations about inverse factorial series recalled at the beginning of Section 2.
Even more interesting are the numerical results obtained as far as the estimate of the converging factor of the Stieltjes integral is concerned, results that are shown in Figure 2.
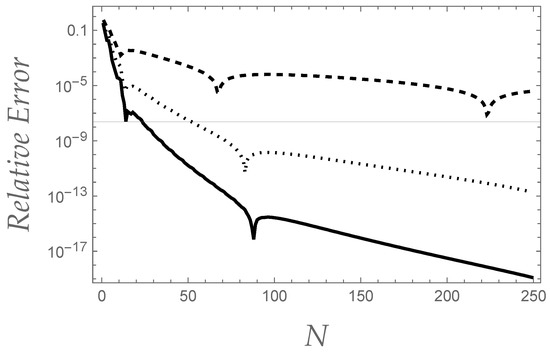
Figure 2.
The behaviour of the relative error related to the converging factor of the integral for (dashed curve), (dotted curve) and (solid curve).
In particular, it should be noted how, for both cases, the performances of our algorithm (e.g., for what concerns the order of magnitude of the relative error as a function of the factorial series truncation order) are comparable, despite the fact that choosing or determines the validity or not of Carleman’s condition, respectively. As was put into evidence in Ref. [33], such a circumstance greatly influences the numerical performances of Padé approximants in retrieving the correct values of as well as , while it does not affect the retrieving action of Levin’s, as well as Weniger’s, transformations [33]. These preliminary results corroborate our feeling about the robustness of Levin-type transformations in resumming superfactorially divergent Stieltjes series. The final part of the present paper is aimed at exploring further properties of the key role played by the factorial expansion of converging factors, and at giving some general guidelines for future estimations of the related convergence rates.
5. On the Integral Representation of the Converging Factors for
In the present section, some of the results found in Section 3 will now be re-derived in a completely different way, on employing the integral representation of the factorial series of Equation (16). We are convinced that what is going to be presented could reveal something of a certain importance in future in order for the convergence features of Levin-type nonlinear transformations in resumming superfactorially divergent Stieltjes series to be explored, similarly to what has been found for the Euler series [28]. In Section 3, the starting point of our convergence analysis was just the truncated Mellin transform representation of the Euler series converging factor, obtained from the results published in [29]. The same results will now be re-derived within a few steps, using the recurrence relation in Equation (9) for the converging factor together with Equation (24) written for , i.e.,
On taking Equation (16) into account, the following integral equation for the generating function is obtained:
On integrating by parts the first integral, we obtain
with the superscript denoting derivation with respect to t. Finally, on substituting from Equation (49) into Equation (48), our integral equation is transformed into the following first-order Cauchy problem for :
whose solution is
that leads to ([28], Equation (5.17)). (The reader should be aware of the fact that in [28] the quantity is instead of z.)
It is then natural to ask whether similar results could also be found for the pairs , following the same strategy. For the sake of simplicity, only the cases and will now be detailed. A conjecture, which we thought to be valid for , will be proposed as an open problem at the end of the paper.
Consider now the case . From Equation (24) we have which, once substituted into Equation (9), gives
that can also be recast as follows:
Similarly as done for the Euler series, to solve the difference equation, the integral representation in Equation (16) will now be used, together with the two relationships
that can be proved again via partial integration. Substitution from Equation (54) into Equation (53) gives the following integral equation for the function :
which leads to the Cauchy problem
On letting , straigthforward algebra transforms Equation (56) into
whose solution is . Accordingly, we have
It is not difficult to check how, after substituting from Equation (58) into Equation (18), the whole sequence so generated coincides with the sequence obtained through the recursive algorithm into Equations (21) and (23), for any z.
The case is particularly intriguing, due to the fact that when Carleman’s condition is not satisfied and Padé approximants are no longer able to decode the associated Stieltjes series. As far as Equation (9) is concerned, we have
which can be recast as follows:
On recalling Equation (54) and on taking into account that
after some algebra it is possible to show that the function must satisfy the following Cauchy problem:
that, on letting , transforms into
whose explicit solution is given by
The above results would suggest that a factorial expansion of the converging factor could be costructed also for . In Appendix C, a possible strategy for the case is outlined, from which we conjecture that the generating function can always be recast as follows:
with the function being the solution of the th-order Cauchy problem
In particular, the extraction of the sequence could be done directly through Equation (18), without explicitly solving Equation (66). To this end, it is sufficient to note that, thanks to Equation (65), the sequence can be generated through
and so on, where the sequence is achievable via recurrence as follows:
starting from the initial values given in Equation (66).
In particular, it should be noted that, due to the above recursive definition, the derivatives satisfy the following property:
where the symbol denotes Kronecker’ symbol. Equation (69) greatly simplifies Equation (67), which can be given in closed-form terms by using Faà di Bruno’s formula, as shown in Appendix D; i.e.,
where the symbol denotes the partial Bell polynomial ([35], Section 3.3). In particular, on substituting from Equation (69) into Equation (70) and on taking Equation (18) into account, the following expression for the expanding coefficients of the inverse factorial series into Equation (19) is obtained:
Since the conjecture into Equations (65) and (66) has not yet been proved (cujus rei demonstrationem mirabilem sane detexi, hanc marginis exiguitas non caperet), several numerical checks have been carried out to give a partial validation of Equation (71). To this end, numerical comparisons with the brute force-based recursive algorithm of Equations (20)–(23), together with Equation (30) evaluated at , have been performed for . In particular, we noticed that the evaluation of Bell’s polynomials through the native Mathematica command BellY unfortunately still represents a considerable numerical bottleneck.
The following measure,
is able to generate, for , all moments in Equation (24). Moreover, on again employing Wolfram Mathematica, it is possible to express the corresponding mth-order converging factor in closed form as follows:
where the symbol denotes Meijer G-functions, whose evaluation is available, up to arbitrarily high precision, on the Wolfram Mathematica platform.
Similarly as we did in Section 4, the behaviour of the converging factor relative error defined by Equations (45) and (46) will now be briefly analysed for a couple of values of and for values of the converging factor order m larger than those of Section 4. Moreover, in all subsequent simulations the parameter z has been set to the unity, which is considerably smaller than the values used to compute the converging factors of as well as of , in order to make the corresponding experiments numerically harder.
Figure 3 shows the relative error behaviour of the converging factor into Equation (73), evaluated for and for the order values (dashed curve), (dotted curve) and (solid curve).
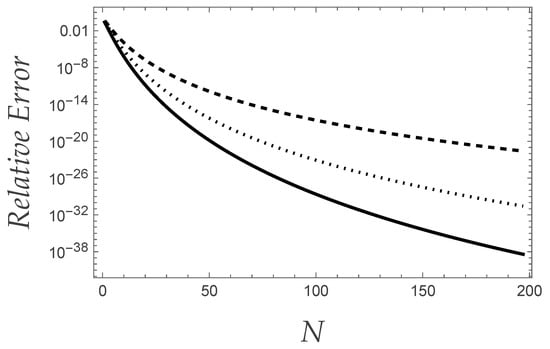
Figure 3.
The behaviour of the relative error related to the converging factor defined by Equation (73) for and for (dashed curve), (dotted curve) and (solid curve). The value of z has been set to the unity.
It can be appreciated how, with respect to the case previously analysed, the error behaviour turns out to be strictly monotonic, the sort of resonances that appeared in Figure 1 and Figure 2 being no longer present. Similar considerations can be made as far as the error behaviour evaluated for , which is shown in Figure 4.
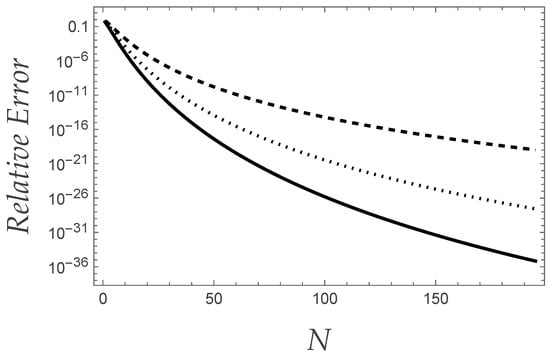
Figure 4.
The behaviour of the relative error related to the converging factor defined by Equation (73) for and for (dashed curve), (dotted curve) and (solid curve). The value of z has been set to the unity.
6. Conclusions
In the present paper, we explored the converging factors for a class of Stieltjes series exhibiting superfactorial divergence using the algorithm developed in [6]. We successfully demonstrated the numerical effectiveness of the algorithm and its ease of implementation. Our algorithm proved to be robust in estimating converging factors, even for series whose moments do not satisfy Carleman’s condition, where Padé approximants largely fail.
We also introduced novel theoretical perspectives on the converging factor representation problem. By reducing the recurrence relation satisfied by the converging factor to a linear Cauchy problem, we provided explicit solutions using the Faà di Bruno formula and Bell’s polynomials. This could help to develop new strategies for future theoretical explorations of Levin-type sequence transformation convergence features. In particular, the integral representations of the converging factor obtained for the class of Stieltjes series investigated here are expected to be instrumental in estimating the convergence rates of Weniger’s -transformation for this class of divergent series, similar to what has been done for the Euler series [28].
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
I wish to thank one of the anonymous reviewers for their accurate revision of my paper and Turi Maria Spinozzi for his useful comments and help.
Conflicts of Interest
The author declares no conflicts of interest.
Appendix A. Proof of Equation (28)
Proof.
The proof is elementary. First of all, it is worth letting , so that Equation (27) becomes
so that the ℓth-order expanding coefficient into Equation (28) can be obtained through
or, after simplyfing and rearranging,
As far as the two products in the denominator are concerned, we have
and, similarly,
Appendix B. Proof of Equation (30)
Appendix C. Proving Equation (66) for ν = 4
Proof.
By proceeding similarly as for and , it is not difficult to recast the difference equation into Equation (9) as follows:
Then, on again using Equations (54) and (61), and after taking into account that
long but straightforward algebra leads to the following differential equation for :
which has to be solved together with the initial conditions
Once again, this differential equation simplifies by letting , which transforms the Cauchy problem of Equations (A12) and (A13) into
□
References
- Grecchi, V.; Maioli, M.; Martinez, A. Padé summability of the cubic oscillator. J. Phys. A 2009, 42, 425208. [Google Scholar] [CrossRef]
- Grecchi, V.; Martinez, A. The spectrum of the cubic oscillator. Commun. Math. Phys. 2013, 319, 479–500. [Google Scholar] [CrossRef][Green Version]
- Bender, C.M.; Weniger, E.J. Numerical evidence that the perturbation expansion for a non-Hermitian PT-symmetric Hamiltonian is Stieltjes. J. Math. Phys. 2001, 42, 2167–2183. [Google Scholar] [CrossRef]
- Colwell, P. Solving Kepler’s Equation over Three Centuries; Willmann-Bell: Richmond, VA, USA, 1993. [Google Scholar]
- Borghi, R. On the Bessel Solution of Kepler’s Equation. Mathematics 2024, 12, 154. [Google Scholar] [CrossRef]
- Borghi, R. Factorial Series Representation of Stieltjes Series Converging Factors. Mathematics 2024, 12, 2330. [Google Scholar] [CrossRef]
- Baker, G.A., Jr.; Graves-Morris, P. Padé Approximants, 2nd ed.; Cambridge U.P.: Cambridge, UK, 1996. [Google Scholar]
- Levin, D. Development of non-linear transformations for improving convergence of sequences. Int. J. Comput. Math. B 1973, 3, 371–388. [Google Scholar] [CrossRef]
- Weniger, E.J. Nonlinear sequence transformations for the acceleration of convergence and the summation of divergent series. Comput. Phys. Rep. 1989, 10, 189–371. [Google Scholar] [CrossRef]
- Weniger, E.J. Mathematical properties of a new Levin-type sequence transformation introduced by Čížek, Zamastil, and Skála. I. Algebraic theory. J. Math. Phys. 2004, 45, 1209–1246. [Google Scholar] [CrossRef]
- Wynn, P. On a device for computing the em(Sn) transformation. Math. Tables Aids Comput. 1956, 10, 91–96. [Google Scholar] [CrossRef]
- Brezinski, C. Accélération de la Convergence en Analyse Numérique; Springer: Berlin/Heidelberg, Germany, 1977. [Google Scholar]
- Brezinski, C. Algorithmes d’Accélération de la Convergence–Étude Numérique; Éditions Technip: Paris, France, 1978. [Google Scholar]
- Brezinski, C.; Redivo Zaglia, M. Extrapolation Methods; North-Holland: Amsterdam, The Netherlands, 1991. [Google Scholar]
- Sidi, A. Practical Extrapolation Methods; Cambridge U. P.: Cambridge, UK, 2003. [Google Scholar]
- Wimp, J. Sequence Transformations and Their Applications; Academic Press: New York, NY, USA, 1981. [Google Scholar]
- Homeier, H.H. Analytical and numerical studies of the convergence behavior of the j transformation. J. Comput. Appl. Math. 1996, 69, 81–112. [Google Scholar] [CrossRef]
- Brezinski, C.; Redivo Zaglia, M.; Weniger, E.J. Approximation and extrapolation of convergent and divergent sequences and series (CIRM, Luminy–France, 2009). Appl. Numer. Math. 2010, 60, 1183–1464. [Google Scholar] [CrossRef]
- Weniger, E.J. An introduction to the topics presented at the conference “Approximation and extrapolation of convergent and divergent sequences and series” CIRM Luminy: September 28, 2009–October 2, 2009. Appl. Numer. Math. 2010, 60, 1184–1187. [Google Scholar] [CrossRef]
- Aksenov, S.V.; Savageau, M.A.; Jentschura, U.D.; Becher, J.; Soff, G.; Mohr, P.J. Application of the combined nonlinear-condensation transformation to problems in statistical analysis and theoretical physics. Comput. Phys. Commun. 2003, 150, 1–20. [Google Scholar] [CrossRef]
- Bornemann, F.; Laurie, D.; Wagon, S.; Waldvogel, J. The SIAM 100-Digit Challenge: A Study in High-Accuracy Numerical Computing; Society of Industrial Applied Mathematics: Philadelphia, PA, USA, 2004. [Google Scholar]
- Gil, A.; Segura, J.; Temme, N.M. Numerical Methods for Special Functions; SIAM: Philadelphia, PA, USA, 2007. [Google Scholar]
- Caliceti, E.; Meyer-Hermann, M.; Ribeca, P.; Surzhykov, A.; Jentschura, U.D. From useful algorithms for slowly convergent series to physical predictions based on divergent perturbative expansions. Phys. Rep. 2007, 446, 1–96. [Google Scholar] [CrossRef]
- Temme, N.M. Numerical aspects of special functions. Acta Numer. 2007, 16, 379–478. [Google Scholar] [CrossRef]
- Weniger, E.J. Summation of divergent power series by means of factorial series. Appl. Numer. Math. 2010, 60, 1429–1441. [Google Scholar] [CrossRef]
- Gil, A.; Segura, J.; Temme, N.M. Basic methods for computing special functions. In Recent Advances in Computational and Applied Mathematics; Simos, T.E., Ed.; Springer: Dordrecht, The Netherlands, 2011; pp. 67–121. [Google Scholar]
- Trefethen, L.N. Approximation Theory and Approximation Practice; SIAM: Philadelphia, PA, USA, 2013. [Google Scholar]
- Borghi, R.; Weniger, E.J. Convergence analysis of the summation of the factorially divergent Euler series by Padé approximants and the delta transformation. Appl. Numer. Math. 2015, 94, 149–178. [Google Scholar] [CrossRef]
- Borghi, R. Asymptotic and factorial expansions of Euler series truncation errors via exponential polynomials. Appl. Numer. Math. 2010, 60, 1242–1250. [Google Scholar] [CrossRef]
- Weniger, E.J. A convergent renormalized strong coupling perturbation expansion for the ground state energy of the quartic, sextic, and octic anharmonic oscillator. Ann. Phys. 1996, 246, 133–165. [Google Scholar] [CrossRef]
- Weniger, E.J. Construction of the strong coupling expansion for the ground state energy of the quartic, sextic and octic anharmonic oscillator via a renormalized strong coupling expansion. Phys. Rev. Lett. 1996, 77, 2859–2862. [Google Scholar] [CrossRef]
- Weniger, E.J.; Čížek, J.; Vinette, F. Very accurate summation for the infinite coupling limit of the perturbation series expansions of anharmonic oscillators. Phys. Lett. A 1991, 156, 169–174. [Google Scholar] [CrossRef]
- Weniger, E.J.; Čížek, J.; Vinette, F. The summation of the ordinary and renormalized perturbation series for the ground state energy of the quartic, sextic, and octic anharmonic oscillators using nonlinear sequence transformations. J. Math. Phys. 1993, 34, 571–609. [Google Scholar] [CrossRef]
- Graffi, S.; Grecchi, V. Borel summability and indeterminacy of the Stieltjes moment problem: Application to the anharmonic oscillators. J. Math. Phys. 1978, 19, 1002–1006. [Google Scholar] [CrossRef]
- Comtet, L. Advanced Combinatorics; D. Reidel: Dordrecht, The Netherlands, 1974. [Google Scholar]
- Euler, L. Institutiones Calculi Differentialis Cum eius Usu in Analysi Finitorum ac Doctrina Serierum. Pars II.1. De Transformatione Serierum; Academia Imperialis Scientiarum Petropolitana: St. Petersburg, Russia, 1755. [Google Scholar]
- Airey, J.R. The “converging factor” in asymptotic series and the calculation of Bessel, Laguerre and other functions. Philos. Mag. 1937, 24, 521–552. [Google Scholar] [CrossRef]
- Dingle, R.B. Asymptotic Expansions: Their Derivation and Interpretation; Academic Press: London, UK, 1973. [Google Scholar]
- Knopp, K. Theorie und Anwendung der Unendlichen Reihen; Springer: Berlin/Heidelberg, Germany, 1964. [Google Scholar]
- Landau, E. Über Die Grundlagen der Theorie der Fakultätenreihen. Sitzungsb. Königl. Bay. Akad. Wissensch. München Math.-Phys. Kl. 1906, 36, 151–218. [Google Scholar]
- Nielsen, N. Die Gammafunktion; Chelsea: New York, NY, USA, 1965. [Google Scholar]
- Bender, C.M.; Wu, T.T. Anharmonic oscillator. Phys. Rev. 1969, 184, 1231–1260. [Google Scholar] [CrossRef]
- Bender, C.M.; Wu, T.T. Anharmonic oscillator. II. A study in perturbation theory in large order. Phys. Rev. D 1973, 7, 1620–1636. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).