Appointment Scheduling Considering Outpatient Unpunctuality Under Telemedicine Services

Abstract

Patient unpunctuality substantially complicates appointment scheduling in integrated telemedicine–traditional outpatient systems. The current research frequently ignores behavioral distinctions between telemedicine patients and outpatients, while neglecting to measure the intangible burden on physicians from service mode switches. To address these gaps, this study incorporates patient heterogeneity and introduces two novel cost metrics. Specifically, we implement penalties for service-mode switching and penalties for consecutive telemedicine sessions. We develop a Stochastic Mixed-Integer Programming (SMIP) model. This stochastic model is transformed into a deterministic Mixed-Integer Linear Programming (MILP) formulation via Sample Average Approximation (SAA). Linearization techniques enhance computational efficiency. In numerical experiments, the dual-penalty model yields balanced schedules with moderate patient mix, reducing physician overtime by 62.5% and service mode switches by 55% compared to baseline approaches. Sensitivity analysis confirms that narrowing outpatient unpunctuality ranges significantly reduces patient waiting and overtime, while raising telemedicine patient proportions bolsters system stability at the cost of increased physician idle time. These insights offer actionable guidance for healthcare institutions managing integrated online–offline services.

1. Introduction

Rapid advances in information technology have profoundly transformed service industry operations, establishing remote services as a key method for enhancing efficiency and accessibility. Within healthcare, telemedicine optimizes resource allocation by overcoming geographical and temporal constraints [1,2,3]. The statistics indicate that approximately 74% of U.S. patients choose this convenient option, particularly benefiting underserved communities [4]. Telemedicine has consequently become essential to outpatient care systems.

Nevertheless, incorporating telemedicine into conventional outpatient scheduling introduces new complexities and challenges, despite its significant promise and rising adoption. Current research on integrated scheduling models exhibits two critical limitations that hinder their practical effectiveness in real-world hybrid settings. First, they typically fail to recognize crucial behavioral differences between telemedicine patients and outpatients. A common but flawed assumption presumes both groups share similar unpunctuality patterns. This assumption overlooks the reality that telemedicine patients, often constrained by standardized digital platforms and protocols, typically exhibit strict adherence to scheduled times, while outpatient arrivals are subject to significant random deviations. Such behavioral variation remains largely unaddressed. Second, and more critically, existing models focus mainly on easily measured time costs, such as patient waiting time, physician idle time, and overtime, while neglecting the “non-quantifiable burden” frequent switching between outpatient and telemedicine duties imposes on physicians. This switching cost, though challenging to measure precisely, critically impacts genuine operational efficiency and physician satisfaction in hybrid service environments. Meanwhile, previous research has failed to account for the operational reality that healthcare institutions’ core service capacity remains oriented toward outpatients, where consecutive telemedicine may impede outpatients’ timely access to services. To bridge critical gaps in the existing literature, we develop a novel SMIP framework. This model jointly quantifies patient heterogeneity while incorporating operational penalties for service mode switching and consecutive telemedicine.

This study makes three primary contributions. First, it addresses the oversight of behavioral differences in telemedicine–outpatient integration by creating an innovative SMIP model. This model explicitly captures heterogeneity in unpunctuality between telemedicine patients and outpatients. The approach introduces two new non-measurable cost metrics: penalties for service mode switching and penalties for consecutive telemedicine sessions. It combines these with patient waiting time, physician idle time, and overtime to create a multi-dimensional objective. This provides a more holistic reflection of true operational costs in hybrid settings. Second, an efficient solution framework based on SAA is proposed. This framework converts the stochastic program into a deterministic MILP through scenario sampling. Linearization techniques are designed to manage quadratic terms and nonlinear constraints, substantially improving computational efficiency. Finally, systematic numerical experiments uncover crucial managerial insights, offering healthcare institutions practical strategies for configuring parameters to coordinate online and offline services effectively.

The paper is structured as follows: Section 2 reviews the literature on outpatient scheduling and telemedicine integration. Section 3 details the problem formulation and presents the SMIP model. Section 4 elaborates on the SAA solution methodology. Section 5 discusses numerical experiment design and management insights. Section 6 concludes and suggests future research avenues.

2. Literature Review

2.1. Traditional Outpatient Appointment Scheduling

Traditional studies typically assume perfect patient punctuality as an ideal condition, concentrating on managing service time variability through appointment interval adjustments. This approach seeks to balance patient waiting durations against physician idle periods [5,6,7,8]. Although computationally straightforward, such models inadequately represent common real-world uncertainties like random patient arrivals, frequently leading to suboptimal outcomes in clinical settings [9]. Research advancements reveal that patient tardiness critically undermines schedule reliability [10,11,12]. Consequently, scholarly focus has transitioned toward stochastic optimization frameworks. These models integrate probability distributions for service durations and arrival time fluctuations, utilizing techniques such as scenario analysis, robust optimization, or stochastic programming to address unpredictability [13,14]. Notable contributions include Jiang et al. [15], who proposed a stochastic recursive model for scheduling unpunctual patients but treated all patients as behaviorally homogeneous, ignoring heterogeneity in punctuality patterns. Meanwhile, Homem-de-Mello et al. [16] developed a simulation–optimization method using Monte Carlo gradient estimation, yet overlooked the operational costs of frequent schedule disruptions caused by no-shows or tardiness. Dogru et al. [17] strengthened disruption management via Depth-First Search and SAA, Li et al. [18] combined a Real-Time Sequencing Strategy and a Biased Random Key Genetic Algorithm to reduce both waiting times and resource expenses, but their method is limited in applicability to hybrid care systems. Zhou et al. [19] optimized weighted completion times but omitted telemedicine integration entirely. Collectively, while these works improved modeling realism, they universally ignored behavioral distinctions between patient types and neglected non-temporal costs, gaps our study directly addresses through patient-heterogeneity modeling and switching penalties.

2.2. Appointment Scheduling Incorporating Telemedicine

Empirical evidence confirms telemedicine’s significant potential to lower healthcare expenses, decrease patient wait times, and enhance resource efficiency [20,21,22,23,24]. Consequently, researchers have modeled telemedicine as either a distinct service channel or patient category. For instance, Qiao et al. [25] optimized teleconsultation systems under variable arrival rates but assumed identical unpunctuality distributions for all patients, disregarding telemedicine’s inherent punctuality advantage. Ji et al. [26] applied two-stage robust optimization for physician–patient matching, yet failed to account for physician fatigue induced by alternating service modes. Huang et al. [27] prioritized multi-disciplinary scheduling involving both telemedicine and outpatients, whereas Shen et al. [28] incorporated no-show behavior to optimize timing for multi-server hybrid systems but lacked mechanisms to penalize frequent service-switching. Guo et al. [29] unified offline/online scheduling via capacity control but reductively positioned telemedicine as a gap-filler for physician idle time, underestimating its operational weight. Critically, existing studies presume uniform patient behavior and ignore the intangible burden of service-mode switches on clinicians, yielding schedules that are theoretically efficient but clinically impractical.

Diverging from this literature, our work explicitly models telemedicine patients’ strict punctuality versus outpatients’ stochastic deviations, introduces novel penalties for service-switching and consecutive telemedicine sessions, and integrates these non-temporal costs with classical time-based objectives. Numerical tests confirm our model produces schedules that harmonize time efficiency with practical viability.

2.3. Appointment Scheduling with Mathematical Programming Methods

Mathematical programming, particularly MILP, has been proven to be a powerful and widely applied method for solving complex appointment scheduling problems [30]. MILP models excel at formulating decisions involving binary choices and continuous variables within a unified framework of linear objectives and constraints. This capability makes them highly suitable for optimizing schedules that must balance conflicting objectives while adhering to operational rules and resource constraints [31]. The deterministic form of MILP, derived from stochastic models via techniques such as SAA, enables efficient solving using commercial solvers like GUROBI or CPLEX, even for realistically sized problems. In the specific context of outpatient appointment scheduling, MILP provides a rigorous foundation for capturing the combinatorial aspects of patient sequencing. For instance, Wu et al. [32] derived a deterministic MILP for the multi-physician appointment scheduling problem using the SAA method and further strengthened the formulation by exploiting problem-specific characteristics. Shen et al. [33] developed a MILP model incorporating both initial and follow-up appointments and proposed an enhanced Progressive Hedging Algorithm (PHA) approach. In contrast, our model formulates a SMIP model based on differences in patient behavior and service time uncertainty, subsequently converting the stochastic program into a deterministic MILP via scenario sampling.

3. Problem Formulation

This section introduces a stochastic scheduling model for single-physician clinics managing both outpatients and telemedicine patients exhibiting tardiness. System notation is established to characterize operational features. Given uncertainties in service durations and patient arrival deviations (early/late arrivals), the problem is formulated as a SMIP model.

Traditionally, physicians conducted only in-person consultations. When clinics introduce telemedicine services, physicians must manage two distinct patient groups during fixed shifts: outpatients with random arrival time variations and strictly punctual telemedicine patients adhering to standardized protocols. The study examines how clinic managers allocate these heterogeneous patient types to discrete time slots for individual physicians. Specifically, hospital administrators assign $T$ total patients to consecutive time slots $t\in \mathcal{T}=\{\mathrm{1,2},\dots ,\mathrm{T}\}$, each of fixed duration $L$. Telemedicine and outpatient proportions are denoted ${\rho }^{\mathrm{e}}$ and ${\rho }^{\mathrm{o}}$, respectively, satisfying ${\rho }^{\mathrm{o}}+{\rho }^{\mathrm{e}}=1$. Binary decision variables $x_t^{\mathrm{e}}$ and $x_t^{\mathrm{o}}$ indicate telemedicine or outpatient assignment to slot $t$. This design is grounded in observations of actual hospital appointment scheduling workflows. At the beginning of the scheduling cycle, administrators first finalize the complete patient list, including patient types (telemedicine patient or outpatient), and then assign these patients to predefined fixed time slots. Once the assignment results are notified to patients, appointments become effectively locked and their sequence cannot be altered. This approach aligns with real-world operational requirements by directly binding service modes to time slots, thereby avoiding patient notification conflicts that may arise from dynamic resequencing. Due to operational disruptions caused by frequent service mode switches, a switching penalty is incurred whenever the service mode changes between consecutive time slots $t-1$ and $t$. This penalty is activated/signified by the binary variable $y_t=1$. Conversely, consecutive telemedicine assignments incur a continuity penalty, triggered by variable $z_t=1$ when both time slots $t-1$ and $t$ serve telemedicine patients. Uncertainties are modeled through scenarios $k\in \mathcal{K}=\{1,2,\dots ,K\}$. Service times for telemedicine and outpatients in slot $t$ under scenario $k$ are represented by $v_{k,t}^{\mathrm{e}}$ and $v_{k,t}^{\mathrm{o}}$, while $A_t$ denotes the slot’s planned start time. For each time slot $t$ and scenario $k$, the telemedicine service time $v_{k,t}^{\mathrm{e}}$ and the outpatient service time $v_{k,t}^{\mathrm{o}}$ are independently sampled from their respective probability distributions. This implies that even for the same time slot assigned to the same service mode, the generated service times may differ across scenarios. Simultaneously, the total service times under different patient type combinations exhibit variations across scenarios. We capture this stochasticity by generating a sufficiently large number of scenarios, ensuring the statistical robustness of the objective function’s estimation of expected costs. Outpatient unpunctuality $u_{k,t}$ (where $u_{k,t}>0$ indicates lateness, $u_{k,t}<0$ indicates earliness) yields actual arrival time $A_t+u_{k,t}$, contrasting with telemedicine patients’ exact arrival at $A_t$. The actual service commencement time is $S_{k,t}$, with $w_{k,t}^{\mathrm{e}}$ and $w_{k,t}^{\mathrm{o}}$ capturing telemedicine and outpatient waiting times, respectively. Physician idle time per slot is $I_{k,t}$, while $O_k$ denotes overall overtime under scenario $k$. Figure 1, Figure 2 and Figure 3 demonstrate how early, late, and punctual arrivals of outpatients affect waiting times, idle times, and overtime.

Figure 1. Outpatient early arrival.

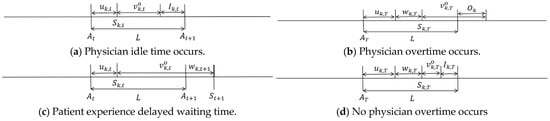
Figure 2. Outpatient late arrival.

Figure 3. Outpatient punctual arrival.

The variables, parameters, and sets involved in this study are detailed in Table 1.

Table 1. Model notation.

Sets and Parameters	Description
$t\in \mathcal{T}=\{\mathrm{1,2},\dots ,T\}$	Set of time slots
$k\in \mathcal{K}=\{\mathrm{1,2},\dots ,\mathrm{K}\}$	Set of scenarios
$L$	Fixed length of a time slot
$A_t$	Planned start time of the $t$-th time slot
${\rho }^{\mathrm{e}}$	Proportion of telemedicine patients scheduled
${\rho }^{\mathrm{o}}$	Proportion of outpatients scheduled
$v_{k,t}^{\mathrm{e}}$	Service time for telemedicine patient assigned to slot $t$ in scenario $k$
$v_{k,t}^{\mathrm{o}}$	Service time for outpatient assigned to slot $t$ in scenario $k$
$u_{k,t}$	Unpunctuality of outpatient assigned to slot $t$ in scenario $k$
$\alpha , \beta , \gamma , \delta ,\eta$	Weight coefficients
Decision Variables	Description
$x_t^{\mathrm{e}}$	Binary variable, 1 if slot $t$ assigned to telemedicine patient, else 0
$x_t^{\mathrm{o}}$	Binary variable, 1 if slot $t$ assigned to outpatient, else 0
$S_{k,t}$	Continuous variable, actual service start time for patient in slot $t$, scenario $k$
$w_{k,t}^{\mathrm{e}}$	Continuous variable, waiting time of telemedicine patient in slot $t$, scenario $k$
$w_{k,t}^{\mathrm{o}}$	Continuous variable, waiting time of outpatient in slot $t$, scenario $k$
$I_{k,t}$	Continuous variable, physician idle time in slot $t$, scenario $k$
$O_k$	Continuous variable, physician overtime in scenario $k$
$y_t$	Binary variable, 1 if the service status switches between time slots $t-1$ and $t$, else 0
$z_t$	Binary variable, 1 if both slots $t-1$ and $t$ are assigned to telemedicine patients, else 0

An illustrative example helps elucidate the problem description and parameter settings while enabling clear comprehension of Figure 1, Figure 2 and Figure 3. Consider a single physician handling two consecutive fixed 10 min time slots (scheduled start times: Slot 1 at $A_1=0$, Slot 2 at $A_2=10$), assigning one outpatient (Slot 1) and one telemedicine patient (Slot 2). In situation 1 (Early Outpatient), the outpatient in Slot 1 arrives 3 min early but due to the time slot boundary constraint still starts service at ${S_1=A}_1=0$ (patient waiting 3 min), with a service time of 8 min, resulting in 2 min of physician idle time; the telemedicine patient in Slot 2 strictly adheres to the time slot boundary constraint, starting service at ${S_2=A}_2=10$ with a service time of 11 min, causing 1 min of physician overtime, and this sequence triggers the service switching penalty. In situation 2 (Late Outpatient), the outpatient in Slot 1 arrives late by $u_1=4$ min, starting service at ${S_1=A}_1+u_1=4$ (physician waiting 4 min), with a service time of 9 min; this causes the telemedicine patient in Slot 2 to be delayed to ${S_2=S}_1+9=13$ (patient waiting 3 min), with a service time of 10 min, incurring 3 min of physician overtime, also triggering the switching penalty. In situation 3 (Punctual Outpatient), the outpatient in Slot 1 starts service at ${S_1=A}_1=0$ with a service time of 6 min, resulting in 4 min of physician idle time; the telemedicine patient in Slot 2 starts service at ${S_2=A}_2=10$ with a service time of 11 min, causing 1 min of physician overtime, and also triggers the switching penalty, demonstrating how early outpatient arrivals cause patient waiting (situation 1), late arrivals lead to physician waiting and cascading delays (situation 2), and service time variations produce idle time (situation 3).

The SMIP formulation for the appointment scheduling problem considering outpatient unpunctuality under telemedicine services is as follows:

$$\min \left[E\left[\alpha \sum _{t\in \mathcal{T}}\left(x_t^{\mathrm{e}}{w}_{k,t}^{\mathrm{e}}+x_t^{\mathrm{o}}{w}_{k,t}^{\mathrm{o}}\right)+\beta \sum _{t\in \mathcal{T}}{I}_{k,t}+\gamma O_k\right]+\delta \sum _{t\in \mathcal{T}}{y}_t+\eta \sum _{t\in \mathcal{T}}{z}_t\right]$$

(1)

s.t.

$$x_t^{\mathrm{e}}+x_t^{\mathrm{o}}=1,\forall t\in \mathcal{T}$$

(2)

$$\sum _{t\in \mathcal{T}}{x}_t^{\mathrm{e}}=T{\rho }^{\mathrm{e}}$$

(3)

$$\sum _{t\in \mathcal{T}}{x}_t^{\mathrm{o}}=T{\rho }^{\mathrm{o}}$$

(4)

$$S_{k,t}\ge A_t,\forall k\in \mathcal{K},t\in \mathcal{T}$$

(5)

$$S_{k,t}\ge S_{k,t-1}+x_{t-1}^{\mathrm{e}}{v}_{k,t-1}^{\mathrm{e}}+x_{t-1}^{\mathrm{o}}{v}_{k,t-1}^{\mathrm{o}},\forall k\in \mathcal{K},t=\{2,\dots ,T\}$$

(6)

$$S_{k,t}\ge A_t+x_t^{\mathrm{o}}{u}_{k,t},\forall k\in \mathcal{K},t\in \mathcal{T}$$

(7)

$$w_{k,t}^{\mathrm{e}}\ge S_{k,t}-A_t,\forall k\in \mathcal{K},t\in \mathcal{T}$$

(8)

$$w_{k,t}^{\mathrm{o}}\ge S_{k,t}-\left(A_t+u_{k,t}\right),\forall k\in \mathcal{K},t\in \mathcal{T}$$

(9)

$$I_{k,t}\ge \left(A_t+L\right)-\left(S_{k,t}+x_t^{\mathrm{e}}{v}_{k,t}^{\mathrm{e}}+x_t^{\mathrm{o}}{v}_{k,t}^{\mathrm{o}}\right),\forall k\in \mathcal{K},t\in \mathcal{T}$$

(10)

$$O_k\ge \left(S_{k,T}+x_t^{\mathrm{e}}{v}_{k,T}^{\mathrm{e}}+x_t^{\mathrm{o}}{v}_{k,T}^{\mathrm{o}}\right)-TL,\forall k\in \mathcal{K}$$

(11)

$$y_t\ge \left(x_{t-1}^{\mathrm{o}}{x}_t^{\mathrm{e}}\right)+\left(x_{t-1}^{\mathrm{e}}{x}_t^o\right),\forall t=\{2,\dots ,T\}$$

(12)

$$z_t\ge x_{t-1}^{\mathrm{e}}{x}_t^{\mathrm{e}},\forall t=\{2,\dots ,T\}$$

(13)

$$x_t^{\mathrm{e}},x_t^{\mathrm{o}},y_t,z_t\in \left\{\mathrm{0,1}\right\},{y_1,z}_1=0,\forall t\in \mathcal{T}$$

(14)

$$S_{k,t},w_{k,t}^{\mathrm{e}},w_{k,t}^{\mathrm{o}},I_{k,t},O_k\ge 0,\forall k\in \mathcal{K},t\in \mathcal{T}$$

(15)

The objective function (1) minimizes the total expected cost, which includes expenses associated with patient waiting time, physician idle time, overtime, service mode switching penalties, and continuity penalties for consecutive telemedicine sessions. Assignment constraint (2) mandates that each time slot receives exactly one patient, while constraints (3) and (4) govern the required proportions of telemedicine and outpatient appointments. Temporal dependencies are enforced through several constraints: service initiation cannot precede a slot’s scheduled start time (constraint (5)), the current patient’s service must begin after the previous patient’s service completion (constraint (6)), and outpatient services cannot start before their actual arrival (constraint (7)). Constraints (8) through (11) compute patient waiting durations, physician idle periods, and overtime hours. Penalty triggers are determined by constraints (12) and (13), which identify service mode switches and consecutive telemedicine assignments. Finally, constraints (14) and (15) restrict the decision variables to their defined domains and non-negativity requirements.

4. Solution Approach

Solving stochastic programs directly is difficult because service time randomness and outpatient scheduling uncertainty create substantial complexity. This study uses the Sample Average Approximation method to manage this difficulty. SAA creates several independent and identically distributed random scenarios through Monte Carlo sampling. These scenarios approximate the mathematical expectation term in the original stochastic program using the sample mean. This process converts the complex SMIP model into a simpler deterministic MILP model [34,35].

Specifically, $K$ independent scenarios (denoted $k\in \mathcal{K}=\{\mathrm{1,2},\dots ,\mathrm{K}\}$) are first sampled from the joint probability distribution of service times ($v_{k,t}^{\mathrm{e}}$, $v_{k,t}^{\mathrm{o}}$) and outpatient unpunctuality deviations ($u_{k,t}$). Subsequently, the expected cost $E[\cdot ]$ in the objective function (1) is replaced by the average cost across these $K$ scenarios, resulting in the deterministic approximate objective shown in equation (16):

$$\min \left[{\displaystyle \frac{1}{K}}\sum _{k=1}^K\left[\alpha \sum _{t\in \mathcal{T}}\left(x_t^{\mathrm{e}}{w}_{k,t}^{\mathrm{e}}+x_t^{\mathrm{o}}{w}_{k,t}^{\mathrm{o}}\right)+\beta \sum _{t\in \mathcal{T}}{I}_{k,t}+\gamma O_k\right]+\delta \sum _{t\in \mathcal{T}}{y}_t+\eta \sum _{t\in \mathcal{T}}{z}_t\right]$$

(16)

Constraints (12) and (13) contain quadratic terms. They are linearized as follows:

$$y_t\ge x_{t-1}^{\mathrm{o}}+x_t^{\mathrm{e}}-1,\forall t=\{2,\dots ,T\}$$

(17)

$$y_t\ge x_{t-1}^{\mathrm{e}}+x_t^o-1,\forall t=\{2,\dots ,T\}$$

(18)

$$y_t\le x_{t-1}^{\mathrm{o}},\forall t=\{2,\dots ,T\}$$

(19)

$$y_t\le x_t^{\mathrm{e}},\forall t=\{2,\dots ,T\}$$

(20)

$$z_t\ge x_{t-1}^{\mathrm{e}}+x_t^{\mathrm{e}}-1,\forall t=\{2,\dots ,T\}$$

(21)

$$z_t\le x_{t-1}^{\mathrm{e}},\forall t=\{2,\dots ,T\}$$

(22)

$$z_t\le x_t^{\mathrm{e}},\forall t=\{2,\dots ,T\}$$

(23)

Furthermore, objective function (16) contains quadratic terms $x_t^{\mathrm{e}}{w}_{k,t}^{\mathrm{e}}$ and $x_t^{\mathrm{o}}{w}_{k,t}^{\mathrm{o}}$. Since $x_t^{\mathrm{e}}$, $x_t^{\mathrm{o}}$ are binary, methods from Ross [36] and Pelletier et al. [37] are applied. Introduce auxiliary decision variables $p_{k,t}^{\mathrm{e}}$, $p_{k,t}^{\mathrm{o}}$ to replace $x_t^{\mathrm{e}}{w}_{k,t}^{\mathrm{e}}$ and $x_t^{\mathrm{o}}{w}_{k,t}^{\mathrm{o}}$ in the objective, linearizing it. Add the constraints:

$$p_{k,t}^{\mathrm{e}}\ge w_{k,t}^{\mathrm{e}}-M\left(1-x_t^{\mathrm{e}}\right),\forall k\in \mathcal{K},t\in \mathcal{T}$$

(24)

$$p_{k,t}^{\mathrm{e}}\le w_{k,t}^{\mathrm{e}},\forall k\in \mathcal{K},t\in \mathcal{T}$$

(25)

$$p_{k,t}^{\mathrm{e}}\le M{x}_t^{\mathrm{e}},\forall k\in \mathcal{K},t\in \mathcal{T}$$

(26)

$$p_{k,t}^{\mathrm{e}}\ge 0,\forall k\in \mathcal{K},t\in \mathcal{T}$$

(27)

$$p_{k,t}^{\mathrm{o}}\ge w_{k,t}^{\mathrm{o}}-M\left(1-x_t^{\mathrm{o}}\right),\forall k\in \mathcal{K},t\in \mathcal{T}$$

(28)

$$p_{k,t}^{\mathrm{o}}\le w_{k,t}^{\mathrm{o}},\forall k\in \mathcal{K},t\in \mathcal{T}$$

(29)

$$p_{k,t}^{\mathrm{o}}\le M{x}_t^{\mathrm{o}},\forall k\in \mathcal{K},t\in \mathcal{T}$$

(30)

$$p_{k,t}^{\mathrm{o}}\ge 0,\forall k\in \mathcal{K},t\in \mathcal{T}$$

(31)

Here, $M$ is a sufficiently large positive constant.

The model is thus transformed into a more tractable MILP:

$$\min \left[{\displaystyle \frac{1}{K}}\sum _{k=1}^K\left[\alpha \sum _{t\in \mathcal{T}}\left(p_{k,t}^{\mathrm{e}}+p_{k,t}^{\mathrm{o}}\right)+\beta \sum _{t\in \mathcal{T}}{I}_{k,t}+\gamma O_k\right]+\delta \sum _{t\in \mathcal{T}}{y}_t+\eta \sum _{t\in \mathcal{T}}{z}_t\right]$$

(32)

s.t., (2)–(11), (14), (15), (17)–(31).

5. Numerical Studies

We conducted comprehensive numerical testing to verify the performance of our novel single-doctor appointment scheduling framework, which integrates telehealth capabilities while accommodating patient unpunctuality. The foundational experiment outlined in Section 5.2 examines how outpatient unpunctuality influences the hybrid scheduling system by comparing four distinct penalty-based approaches. This comparison assesses each approach’s impact on critical operational measures. Subsequent sensitivity analyses explore four pivotal parameters. Relative to our baseline configuration, we systematically examine how modifying these parameters affects both the global objective function and specific performance indicators, ultimately revealing how parametric adjustments govern schedule design evolution.

5.1. Data Settings

Data was sourced from a large hospital in Nanjing, establishing a real-world case study. We model a standard half-day outpatient session (e.g., 8:00 a.m.–12:00 p.m.) by dividing time into fixed 10 min slots, yielding 24 consecutive slots. Telemedicine patient service durations follow a log-normal distribution (mean: 10 min, SD: 3 min), truncated to [1, 20] minutes for practicality. Outpatient service times adhere to a log-normal distribution (mean: 8 min, SD: 1.5 min), truncated to [1, 15] minutes. Outpatient arrival deviations are represented by a truncated normal distribution (mean: 0 min, SD: 2.5 min) bounded at $\pm L/3$ ($\pm 3.333$ min), while telemedicine patients exhibit perfect punctuality. Patient proportions are fixed at ${\rho }^e=0.5$ (telemedicine) and ${\rho }^o=0.5$ (outpatient). To prevent the impact of cost parameters on the results, we set the cost ratios as $\alpha :\beta :\gamma :\delta :\eta =1:1:1:1:1$. The linearized stochastic mixed-integer programming model is solved using GUROBI 10.0.1 on an Intel Core i7-12700 CPU @ 2.11 GHz, configured with a 0.05% optimality gap tolerance and a 3000 s runtime limit.

5.2. Ablation Study

The sample size $K$ affects the accuracy of the Sample Average Approximation (SAA) method. To determine an appropriate $K$ value, we tested a range of sample sizes, including $K=20, 30, 40, 50, 60, 70, ..., 180.$ For each $K$ value, we ran the model multiple times using the GUROBI solver, calculated and recorded the average optimal objective value and the solution time. The results are presented in Table 2. Analysis of Table 2 data reveals that when the sample size $K$ reaches 100, the obtained average optimal objective value stabilizes with significantly reduced fluctuations. This indicates that using 100 scenarios is sufficient to adequately capture the stochasticity within the model, and the SAA solution exhibits good convergence at this sample size. Simultaneously, $K = 100$ provides a reasonable balance point between computational efficiency and estimation accuracy. Based on this stability analysis and efficiency consideration, we fixed the sample size $K$ at 100 for all subsequent numerical experiments.

Table 2. The impact of sample size K on scheduling outcomes.

Sample Size (K)	Objective Value	Solution Time
20	67.15	1.6
30	68.03	4.4
40	69.60	7.3
50	70.79	14.7
60	70.30	21.8
70	71.72	35.7
80	70.33	23.8
90	72.11	76.4
100	71.32	41.6
110	71.49	151.4
120	71.75	158.7
130	71.09	179.8
140	71.45	299.2
150	71.92	300.9
160	71.13	317.1
170	71.55	398.9
180	71.45	416.9

We assessed four scheduling approaches to isolate penalty mechanism effects. The Base model minimized only temporal costs (patient waiting time, physician idle time, overtime). Adding penalties for service-mode switches created the Base + Switch model. The Base + Consecutive model incorporated penalties for consecutive telemedicine sessions. The Full model combined both switch and consecutive penalties.

We executed all models using baseline parameters over 100 scenarios while averaging performance metrics to minimize variability. Figure 4 and Figure 5 present core performance metrics (average patient waiting time per slot, physician idle time, and physician overtime) and representative scheduling configurations, where circles denote telemedicine patients and crosses indicate outpatients. Figure 4 indicates remarkably stable physician idle times across scheduling methods. This consistency arises from constraints of total patient load, service duration distributions, and fixed session length, exhibiting minimal responsiveness to penalty designs. Conversely, Figure 5 reveals significant differences in how patient wait times and physician overtime react to distinct penalty schemes.

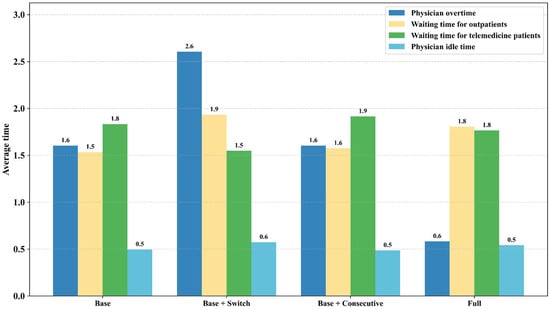
Figure 4. Performance metrics analysis for four scheduling models.

Figure 5. Scheduling schemes and performance metrics comparison analysis.

Analysis of Figure 4 and Figure 5a reveals that compared to the Base model, the Full model exhibits greater fluctuations in average patient waiting time but significantly reduces physician overtime by 62.5% and service-mode switches by 55%. This outcome stems from the inherent equilibrium logic of the dual-penalty mechanism. Simultaneously penalizing both service switching and consecutive telemedicine sessions drives the system toward a hybrid scheduling approach, preventing the frequent service changes characteristic of the Base model’s disregard for switching costs. However, the interplay between arrival variations and service time unpredictability within outpatient clusters may cause pronounced waiting time surges and irregular idle time allocation during specific intervals. Comparison of Figure 4 with Figure 5b indicates that the Full model achieves a substantial reduction in concentrated telemedicine assignments while maintaining comparable time efficiency metrics. The Base + Switch model’s exclusive focus on minimizing switches enforces extensive homogeneous blocks, whereas the Full model’s integrated constraints strategically incorporate outpatient appointments. This configuration retains the cognitive load reduction benefit of the Base + Switch model while using dispersed scheduling to absorb uncertainty. Simultaneously, Figure 4 and Figure 5c demonstrate that relative to the Base + Consecutive model, the Full model achieves superior switch reduction while preventing operational risks from prolonged telemedicine sequences. The Base + Consecutive model aggressively scatters telemedicine patients among outpatient slots to minimize its penalty, generating substantially more service switches. Although this fragmented scheduling marginally improves time utilization, elevated switch frequency intensifies physician workload. Conversely, the Full model attains enhanced equilibrium through coordinated penalties: its schedule permits limited consecutive telemedicine sessions while tactically incorporating outpatient appointments to restrict block length. This structure maintains fewer switches than the Base + Consecutive model and prevents telemedicine concentration, thereby respecting healthcare facilities’ outpatient-centric capacity and establishing an optimal compromise between temporal efficiency and practical workflow integration.

5.3. Sensitivity Analysis

5.3.1. Impact of Time Slot Length

To investigate the impact of time slot length $L$ on Full model performance and scheduling schemes, experiments were conducted varying $L$ from 8 to 14 min in 1 min increments, keeping other base parameters constant. The average total waiting time of telemedicine patients, average total waiting time of outpatients, average total physician idle time, and average overtime across all time slots under 100 scenarios, as well as the characteristics of the scheduling schemes, are shown in Figure 6, where circles denote telemedicine patients and crosses indicate outpatients.

Figure 6. Performance metrics and scheduling schemes under different time slot lengths.

Figure 6a demonstrates that patient waiting times and physician overtime generally decline as slot length $L$ increases, whereas physician idle time rises. Extended time slots offer enhanced buffering capacity, effectively accommodating uncertainties stemming from service time fluctuations and patient unpunctuality. These larger buffers mitigate waiting time accumulation for subsequent patients caused by service overruns or early/late arrivals, while also lowering the probability of compulsory overtime. This buffering improvement, however, involves a trade-off: reduced compactness in time utilization. Physicians completing services early may need to wait for the next slot’s scheduled start time under longer slot configurations, directly elevating idle time. Consequently, selecting $L$ represents a critical mechanism for balancing uncertainty absorption against time-use efficiency. Figure 6b further reveals $L$’s influence on optimal scheduling approaches. Excessively short (e.g., 8 min) time slots lead to significant delays and waiting times for late-arriving outpatients, prompting the system to prioritize clustering all telemedicine patients before scheduling outpatients. Conversely, for long time slots ($L=12–14$ min), the substantial per-slot buffering effectively minimizes waiting times and overtime caused by unpunctuality or service time variability. Consequently, temporal costs become negligible, and the schedule optimization is dominated by the penalty terms. Moderate slot lengths (e.g., 9–10 min), especially near the 10 min baseline, yield schedules exhibiting greater hybridity and flexibility (illustrated in Figure 5c), characterized by more evenly interspersed telemedicine and outpatient appointments. This approach capitalizes on the adequate buffering afforded by medium slots while preserving the necessary flexibility to optimize patient sequencing.

5.3.2. Impact of Unpunctuality Range

Patient tardiness represents a primary driver of scheduling uncertainty. To evaluate its effects within the Full model, we varied the outpatient unpunctuality range $u$ as specific proportions of the fixed 10 min time slot ($L$): $L/2$ ($\pm 5$ min), $L/3$ ($\pm 3.333$ min, baseline), $L/4$ ($\pm 2.5$ min), and $L/5$ ($\pm 2$ min). All remaining parameters maintained their baseline values. Outcomes are presented in Figure 7.

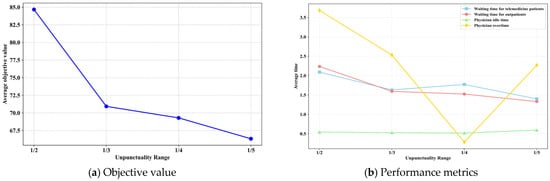
Figure 7. Impact of different unpunctuality ranges on results.

Figure 7a shows that reducing the outpatient unpunctuality range has a significantly positive effect on the optimization objective. Figure 7b indicates that as the unpunctuality range narrows, waiting times for both patient types and physician overtime decrease synchronously, while physician idle time increases slightly. This occurs because reduced $u$ means outpatient actual arrival times deviate less significantly from planned slot start times $A_t$, allowing the system to schedule service start times $S_t$ more precisely. This substantially reduces cascading effects caused by earliness or lateness. Specifically, reduced lateness lowers the risk of waiting accumulation for subsequent patients and physician overtime; reduced earliness effectively avoids long waiting times for early patients. Meanwhile, if outpatients arrive on time or are slightly late, the physician may finish service before the slot ends, creating idle fragments. Although physician idle time increases mildly, overall system efficiency is substantially optimized.

5.3.3. Impact of Telemedicine Patient Proportion

This section analyzes the impact of the telemedicine patient proportion ${\rho }^e$ on the objective value and system performance metrics. Keeping other base parameters constant, ${\rho }^e$ was varied from $0.1$ to $0.9$ in $0.1$ increments. The results are shown in Figure 8.

Figure 8. Impact of different telemedicine patient proportions on results.

Figure 8 indicates a steady decline in the overall objective value as the proportion of telemedicine patients ${\rho }^e$ rises. Synchronous reductions occur in waiting times for both patient groups and physician overtime, whereas physician idle time grows. This trend stems from telemedicine patients’ strict punctuality and the greater predictability of their service start times $S_{k,t}$ compared to outpatients, whose schedules are subject to more variables. Consequently, elevating the telemedicine patient ratio introduces greater stability into the scheduling system. The presence of these reliable, standardized-service patients throughout the schedule effectively diminishes disruptions and accumulated uncertainty resulting from outpatient tardiness and service time fluctuations. Lowered risks of delays directly ease patient waiting, while improved service start time predictability decreases the likelihood of appointments running beyond scheduled hours. Simultaneously, the rise in idle time arises from two linked factors: telemedicine’s inherent efficiency and reduced time variability minimize concealed idle periods within slots previously caused by early service completion and diminished overall uncertainty, particularly in arrivals, allows the system to scale back implicit buffers designed to accommodate outpatient unpunctuality. In this more predictable setting, the freed time becomes more visible as idle segments. Thus, boosting the share of telemedicine patients essentially harnesses the stability these services provide to improve the scheduling system’s manageability and operational efficiency.

5.3.4. Impact of Weighting Coefficients

In this subsection, we analyze the impact of the cost weighting coefficients. Under the condition that the Full model and basic parameters remain unchanged, we systematically adjusted the combinations of weights for different cost components in the objective function. As shown in Table 3, the weight configurations significantly altered the balance of system performance metrics. When solely increasing the weighting coefficient $\alpha$ for outpatient waiting time, the total waiting time for outpatients (Total $w^o$) across all time slots significantly decreases; however, the total waiting time for telemedicine patients (Total $w^e$) and physician overtime (Total $O$) increase. Conversely, reducing $\alpha$ leads to a surge in outpatient waiting time while a physician’s total idle time (Total $I$) approaches 0. Increasing the idle time weighting coefficient $\beta$ completely eliminates physician idle time but elevates outpatient waiting time, whereas decreasing $\beta$ increases physician idle time accompanied by rising overtime. Elevating the overtime weighting coefficient $\gamma$ effectively controls physician overtime at the cost of marginally increasing waiting times for both patient types; reducing $\gamma$ significantly worsens over time. Increasing the service-switching penalty weight $\delta$ reduces telemedicine patient waiting time but exacerbates physician overtime and outpatient waiting time. Raising the consecutive telemedicine penalty weight $\eta$ increases the telemedicine patient waiting time. Simultaneously increasing both $\delta$ and $\eta$ reduces waiting times for both patient types yet intensifies physician overtime and idle time. These outcomes reveal core conflicts: minimizing outpatient waiting time exacerbates telemedicine patient waiting, as evidenced by the inverse relationship when adjusting $\alpha$, confirming that the two waiting time metrics are competing indicators; a systematic trade-off exists between total patient waiting time and physician workload indicators, specifically the sum of idle time and overtime. Furthermore, the regulatory intensity of $\alpha$ on outpatient waiting time significantly surpasses that of $\eta$ on telemedicine waiting. This provides managers with a priority configuration basis whereby optimizing patient waiting times requires coordinated adjustment of $\alpha$ and $\beta$, while safeguarding in-person services necessitates emphasis on $\eta$.

Table 3. The results for different combinations of weighting coefficients.

Weighting Coefficients	Objective Value	$\mathbf{Total} {\mathit{w}}^{\mathit{e}}$	$\mathbf{Total} {\mathit{w}}^{\mathit{o}}$	$\mathbf{Total} \mathit{I}$	$\mathbf{Total} \mathit{O}$
$\alpha :\beta :\gamma :\delta :\eta =1:1:1:1:1$	72.44	21.2	21.7	13.0	0.6
$\alpha :\beta :\gamma :\delta :\eta =0.5:1:1:1:1$	44.07	32.2	24.9	0.0	0.5
$\alpha :\beta :\gamma :\delta :\eta =2:1:1:1:1$	105.73	15.1	17.7	19.7	2.5
$\alpha :\beta :\gamma :\delta :\eta =1:0.5:1:1:1$	62.24	14.0	19.7	20.2	2.5
$\alpha :\beta :\gamma :\delta :\eta =1:2:1:1:1$	72.52	32.0	23.4	0.0	1.1
$\alpha :\beta :\gamma :\delta :\eta =1:1:0.5:1:1$	71.42	17.1	22.3	14.4	3.1
$\alpha :\beta :\gamma :\delta :\eta =1:1:2:1:1$	73.30	22.1	21.3	12.1	0.4
$\alpha :\beta :\gamma :\delta :\eta =1:1:1:0.5:1$	66.01	22.9	19.8	11.3	0.6
$\alpha :\beta :\gamma :\delta :\eta =1:1:1:2:1$	78.32	16.3	25.4	15.2	3.4
$\alpha :\beta :\gamma :\delta :\eta =1:1:1:1:0.5$	68.39	18.4	22.5	14.4	2.6
$\alpha :\beta :\gamma :\delta :\eta =1:1:1:1:2$	77.74	23.1	20.4	11.6	0.6
$\alpha :\beta :\gamma :\delta :\eta =0.5:0.5:0.5:1:1$	43.80	21.3	22.7	13.0	0.5
$\alpha :\beta :\gamma :\delta :\eta =1:1:1:2:2$	128.20	19.6	19.1	14.0	2.5

6. Conclusions

This study developed a SMIP model to address patient unpunctuality challenges in telemedicine-integrated outpatient scheduling while accounting for service time uncertainty. The model was converted into a MILP via SAA and solved to global optimality using the GUROBI solver. The numerical results reveal that, firstly, integrating both service-switching penalties and consecutive-telemedicine penalties achieves an effective balance between operational viability and temporal efficiency. The resulting schedules prevent excessive grouping of identical patient types (which avoids switching costs) while eliminating extreme fragmentation (which minimizes continuity penalties). Second, systems maximize buffer utilization by blending telemedicine and outpatients when time slots are moderately sized; however, prioritizing all telemedicine appointments first becomes optimal when slots are either extremely short or long. Additionally, narrowing the range of outpatient tardiness substantially decreases waiting-time cascades and clinician overtime exposure. Crucially, the sensitivity analysis of weighting coefficients reveals that outpatient and telemedicine waiting times are competing objectives, while a systematic trade-off exists between total patient waiting time and physician workload. Healthcare administrators can enforce punctuality policies through reminder systems and late-arrival protocols, such as restricting outpatient tardiness to within one-fifth of the time slot duration. Increasing the proportion of telemedicine patients also mitigates disruptions from outpatient arrivals and service variability. Although this elevates observable physician idle time, it methodically reduces scheduling instability. Simultaneously, rational configuration of time slot lengths and optimization of weighting coefficients further enhance overall hospital operational efficiency.

Although the current model accommodates heterogeneous unpunctuality patterns and stochastic service durations, future research should examine dynamic scheduling in multi-physician settings and develop prediction models for telemedicine patient punctuality using historical data, which will further enhance scheduling accuracy. Strategic interactions between clinicians and patients regarding timing deviations also warrant exploration through game-theoretic frameworks.