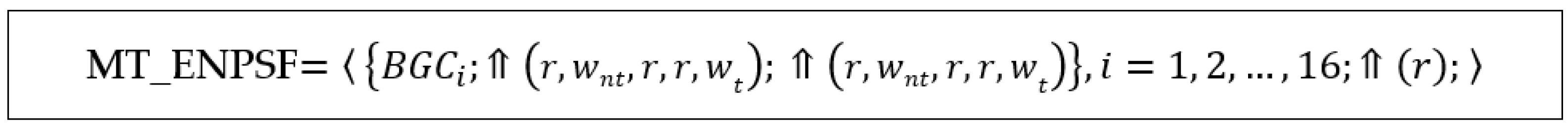Near-Optimal Multirun March Memory Test Algorithms for Neighborhood Pattern-Sensitive Faults in Random-Access Memories

Abstract

This research paper addresses the problem of testing N × 1 random-access memories (RAMs) in which complex models of unlinked static neighborhood pattern-sensitive faults (NPSFs) are considered. Specifically, two well-known fault models are addressed: the classical NPSF model that includes only memory faults sensitized by transition write operations and an extended NPSF model that covers faults sensitized by transition write operations as well as faults sensitized by non-transition writes or read operations. For these NPSF models, near-optimal multirun march memory tests suitable for implementation in embedded self-test logic are proposed. Each of the two new memory tests completely covers the NPSF model considered. The assessment of optimality is based on the fact that for any group of cells corresponding to the NPSF model, the state graph is completely covered and each arc is traversed only once, which means that the graph is of the Eulerian type. However, we say that these memory tests are near-optimal and not optimal because some additional write operations are required for data background changes. A characteristic of a memory test algorithm where multiple data backgrounds are applied is that the test data is always correlated with the address of the accessed location. For easy implementation in embedded self-test logic, the proposed tests use 4 × 4 memory initialization patterns rather than the more difficult-to-implement 3 × 3 patterns, as is the case with other currently known near-optimal memory tests.

1. Introduction

As shown in the International Roadmap for Devices and Systems (IRDS) edited by the IEEE Computer Society or in works such as [1,2,3], in a System on a Chip (SoC) or Network on a Chip (NoC), the memory part has a growing share, currently covering 75–85% of the integrated area. Therefore, in the production of reliable integrated circuits at competitive costs, efficient testing of the memory part is a very important requirement.

In this paper, the authors address the issue of testing $N\times 1$ RAMs with regard to the complex fault model of static unlinked neighborhood NPSFs as a subclass of the coupling fault (CF) model [4,5]. According to the classification of memory faults, as presented for example in [2,6,7,8], the “static fault” class refers to those faults sensitized by performing at most one memory operation, while the “dynamic fault” class refers to those faults sensitized by two or more operations performed sequentially. According to the same taxonomy presented in [6] or [7], for example, CFs are said to be unlinked when they do not influence each other. In this paper, the class of static unlinked CFs is addressed.

The CF model reflects imperfections in the memory cell area that cause two or more cells to influence each other in their operation [2,3]. Depending on the number of cells involved in a memory fault, there are several classes of coupling faults, such as two-cell coupling, three-cell coupling, four-cell coupling, or five-cell coupling. In the two-cell CF model, it is considered that the cells involved in a CF can be anywhere in the memory [9]. In this way, this model also addresses memory faults [6]. For more complex $k$-cell CF models, where $k\ge 3$, it is assumed that the cells involved in a memory fault are physically adjacent [5,10,11]. It is therefore necessary to know the memory structure, or more precisely the correspondence between logical addresses and physical addresses, in the form of row and column addresses. This realistic limitation allows the complexity of these fault models to be more easily managed [12,13,14]. For these complex CF models, testing is usually performed with additional integrated architectures called built-in self-test (BIST) logic [15,16,17,18,19,20].

Regarding the $k$-cell CFs, where $k\ge 2$, depending on the technology used, the accuracy of the testing, and the costs involved, two classes of fault models have been defined to cover the most common memory errors, namely, (a) the classical model class in which it is considered that a memory fault can be sensitized only by a transition write operation, and (b) an extended class of models in which it is admitted that memory faults can be sensitized by transition write operations, as well as by non-transition writes or read operations—extended CF (ECF) models [9,12,13,14]. With the increase in density and the decrease in supply voltage, the range of memory defects has diversified, and, as a result, for high testing accuracy, ECF models are increasingly used. The authors appreciate, however, that a memory test covering the classical CF model can be adapted relatively easily to cover the corresponding ECF model [12]. This is also highlighted in this work.

For three-cell or four-cell classical CF models, reference tests are reported in [10,11,21,22,23,24]. For three-cell or four-cell ECF models, near-optimal tests are presented in [14].

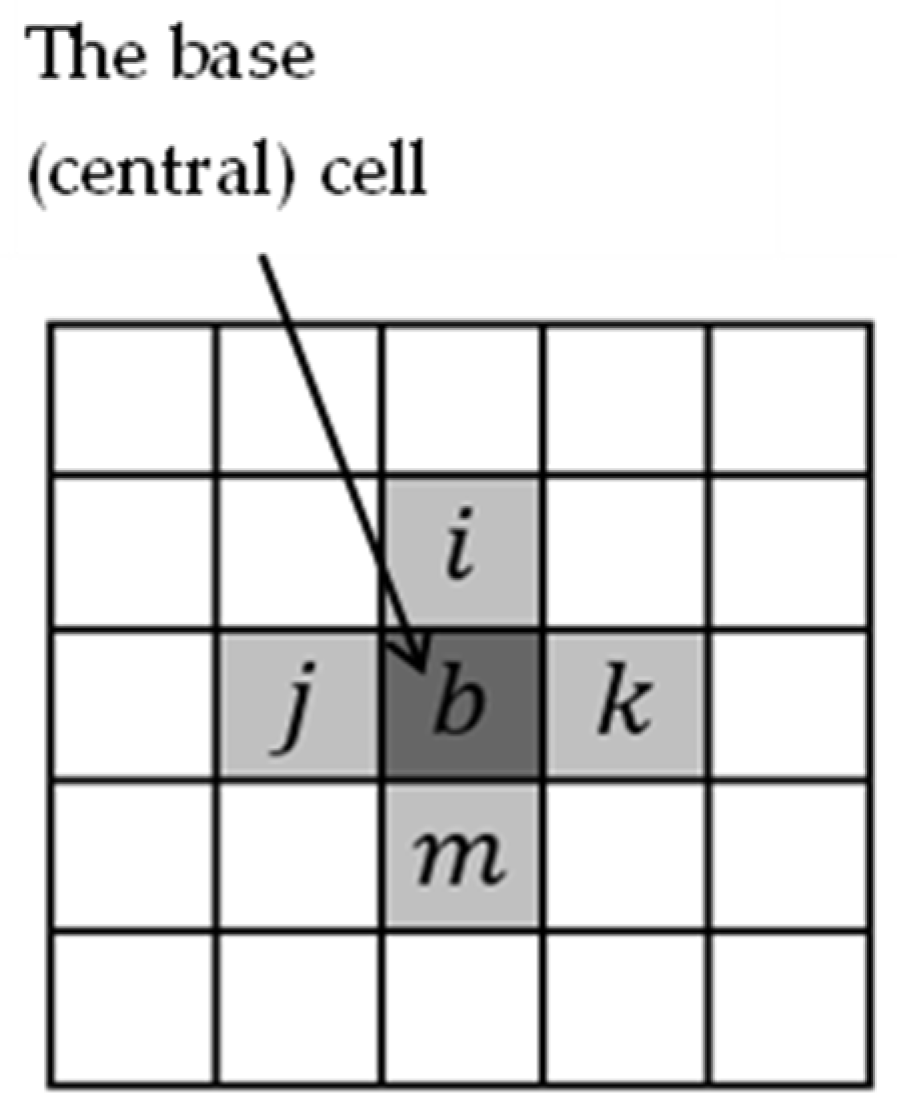
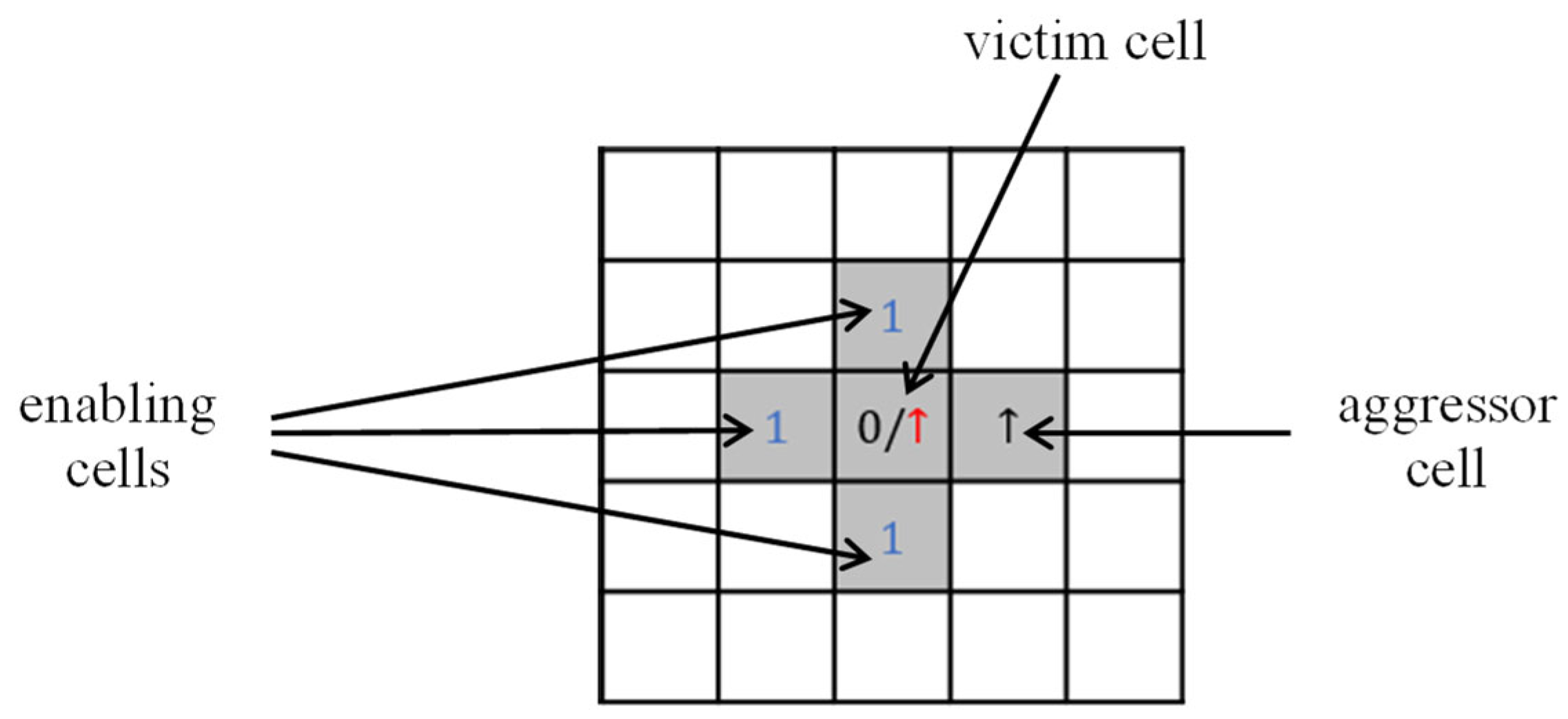
In this paper, we focus exclusively on the NPSF model, which is a subclass of $k$-cell CFs, where $k=5$. The NPSF model involves five physically adjacent memory cells arranged in a configuration like the one shown in Figure 1. Note that this five-cell configuration also covers the six configurations of three-cell CF model involving neighboring memory cells arranged in a corner or on a row or column, as considered in [5,13,14], for example, but does not completely cover the configuration of four-cell CF model in which neighboring memory cells are arranged in a square [14].

This fault model, which reflects the influence of neighboring cells on the central memory cell, has been defined since the 1970s [25]. Specifically, we refer here to the classical NPSF model in which a fault sensitization involves a transition write operation in a cell in the group, and the other four cells are in a certain state that favors the occurrence of the memory error affecting the central cell. The scientific community has continuously studied the NPSF model because of its importance and complexity. Memory testing for NPSF models is covered extensively in books, like [2,3,4,26], or in review papers, such as [16,17,19].

For the NPSF model, some memory tests have been proposed since the 1980s that were quite effective for the memory sizes of that period [27,28]. For example, the memory test given by Suk and Reddy [28], which completely covers this model, is based on an algorithm for dividing the set of memory cells into two halves, based on row and column addresses, and is $165N$ long. A reduction in testing time was possible by applying march-type tests on different memory initialization patterns (data backgrounds). This idea was first proposed by Cockborn [23]. This technique, called “multirun march memory testing”, was then used to identify efficient memory tests for this complex NPSF model [29,30,31,32]. For example, in [31], to reduce the length of the test, Buslowska and Yarmolik propose a multirun technique with a random background variation. However, in that case, the NPSF model is only partially covered. A first near-optimal deterministic memory test for the NPSF model was proposed by Cheng, Tsai, and Wu in 2002 [32]. This memory test called CM-79N is ${79}^{1/3}N$ long and uses 16 memory initialization patterns of the size 3 × 3. Ten years later, Huzum and Cașcaval [33] improved this result with another near-optimal memory test (called March-76N) that was slightly shorter, of length $76N.$Compared to CM-79N, the March-76N memory test applies a different testing technique, but also uses 3 × 3 data background patterns. CM-79N and March-76N are the shortest deterministic memory tests that completely cover this complex fault model. Their authors consider these memory tests to be near-optimal and not optimal, as additional write operations are required for multiple memory initializations. Although near-optimal, these tests are not exactly suitable for BIST implementation due to the complexity of the address-based data generation logic. More on this issue can be found in the works [34,35,36,37,38,39], but an in-depth analysis is also presented in this paper. For this reason, Cheng, Tsai and Wu also proposed in the same article [32] another memory test (March-100N), which, although it is longer (and obviously non-optimal), is easier to implement in BIST-RAM architectures due to its 4 × 4 memory initialization patterns. A modified version of the March-100N memory test for the diagnosis of SRAM is given by Julie, Sidek, and Wan Zuha [36].

In this work, a new near-optimal test (MT_NPSF_81N) able to completely cover the classical NPSF model is proposed. This new test is of length $81N$ and uses 16 data backgrounds with patterns of 4 × 4 in size, making it suitable for implementation in BIST-RAM architectures. Compared to the March-100N test, this new memory test is significantly shorter and has a simpler structure. The synthesis of the address-based data generation logic for this memory test, considering a possible BIST implementation, is also discussed. This work also highlights the simplicity of address-based data generation logic in the case of 4 × 4 data backgrounds compared to 3 × 3 data backgrounds. For the extended NPSF model (ENPSF), a near-optimal test of length $177N$ is proposed.

The remainder of this paper is organized as follows: Section 2 includes assumptions, notations, a short description of the NPSF model, and some considerations related to multirun memory tests, or to the necessary and sufficient conditions for detecting coupling faults. Section 3 describes new near-optimal memory tests for the classical NPSF model and the extended NPSF model that use 4 × 4 data background patterns. Section 4 presents a synthesis of address-based data generation logic for memory operations for a possible BIST implementation of the proposed memory tests. To emphasize the advantage of the proposed tests, compared to other known memory tests that use 3 × 3 background patterns, where modulo 3 residues are required for row and column addresses, Section 5 presents a synthesis of address-based data generation logic for the March-76N memory test. A discussion related to the proposed new memory tests, covering several different aspects, is included in Section 6. Some experimental results that complete the comparative analysis between the proposed tests and other known tests are presented in Section 7. Some conclusions regarding this work, presented in Section 8, complete this paper.

2. Assumptions, Notations, and Preliminaries

2.1. Assumptions

As in other works dedicated to NPSF models, it is assumed that the memory structure is fully known, so that based on the physical address information, a multirun march test can be applied using different data backgrounds. Of course, in the memory, there can be one or more groups of coupled cells. As in other similar works, such as [4,26,30,31,32,33,34,35], it is assumed that the coupled cell groups are disjoint.

2.2. Notations

The notations used to describe memory operations or certain memory errors are shown in

Table 1. Notations used to describe memory operations or certain memory errors.

Notation	Meaning of the Notation
$r$	Operation of reading a memory cell and checking the value read by comparing it with the expected value.
$w_0\left(w_1\right)$	Operation of writing the logical value 0 (1) to the addressed cell.
$0w1\left(1w0\right)$	Write operation to change the state of the addressed cell from 0 to 1 (from 1 to 0).
$w_t$	$\mathrm{Transition}\mathrm{write}\mathrm{operation},0w1$ $\mathrm{or}1w0$.
$w_{nt}$	Write operation without changing the state of the addressed cell (non-transition write operation).
$r^i,{w_{nt}^i,w}_t^i$$,w_0^i,w_1^i$	$\mathrm{Memory}\mathrm{operations}\mathrm{with}\mathrm{cell}i$.
$\uparrow$ $(\downarrow$)	$\mathrm{A}\mathrm{change}\mathrm{of}\mathrm{logical}\mathrm{state}\mathrm{in}\mathrm{a}\mathrm{memory}\mathrm{cell}\mathrm{from}0$ $\mathrm{to}1(1$ to 0) by sensitizing a memory fault (i.e., a memory error).
$A_r\left(A_c\right)$	Row (column) address in a memory operation.
$v_i$	$\mathrm{The}\mathrm{logical}\mathrm{value}\mathrm{of}\mathrm{memory}\mathrm{cell}i$.

.

2.3. The NPSF Model and Preliminary Considerations for Multirun Memory Testing

Generally, for a $k$-cell CF model, the affected cell (the cell where the memory error occurs) is considered $victimcell$ ($v-cell$) and the other $k-1$ cells in the group are considered $aggressorcells$ ($a-cells$) [7]. In order to describe more clearly how a memory fault is sensitized, sometimes the cell where the fault-sensitizing operation is performed is considered the $aggressorcell$, and the other $k-2$ cells in the group which, based on the state they are in, allow the appearance of the memory error, are called $enablingcells$ ($e-cells$) [6,7]. These aspects are illustrated in Figure 2 and Figure 3. Since neighboring cells can exert a passive or active influence on the central cell, the NPSF model includes two types of faults, passive NPSF and active NPSF, as shown in Figure 2 and Figure 3, respectively [27,28].

Specifically, in the case of a passive NPSF, a configuration of neighboring bits (a data pattern) prevents a certain transition in the central cell, from zero to one or from one to zero, as appropriate. Hence, this characteristic of this fault model is “pattern-sensitive”. In the case of an active NPSF, making a transition in one of the neighboring cells ($a-cell$) in a certain state of the other cells that facilitate the occurrence of the error ($e-cells$) can cause the state to change in the central cell as well (↑ or ↓, as appropriate). Example of primitive faults for the classical NPSF model are presented in

Table 2. Example of primitive faults for the NPSF model: 1–32 active faults and 129–160 passive faults.

Fault Number	Fault Sensitization (Transition Write Operation) and the Initial State of the Other Cells in the Group					$\mathbf{Effect}\mathbf{of}\mathbf{Fault}\mathbf{Sensitization}\mathbf{on}\mathbf{the}\mathbf{Victim}\mathbf{Cell}\mathit{b}$ (Memory Error)
	$\mathbf{Cell}\mathit{i}$	$\mathbf{Cell}\mathit{j}$	$\mathbf{Cell}\mathit{k}$	$\mathbf{Cell}\mathit{m}$	$\mathbf{Cell}\mathit{b}$
1	$0w1$	0	0	0	0	↑
2	$1w0$	0	0	0	0	↑
3	$0w1$	0	0	0	1	↓
4	$1w0$	0	0	0	1	↓
5	$0w1$	0	0	1	0	↑
6	$1w0$	0	0	1	0	↑
7	$0w1$	0	0	1	1	↓
8	$1w0$	0	0	1	1	↓
⋅	⋅	⋅	⋅	⋅	⋅	⋅
29	$0w1$	1	1	1	0	↑
30	$1w0$	1	1	1	0	↑
31	$0w1$	1	1	1	1	↓
32	$1w0$	1	1	1	1	↓
⋅	⋅	⋅	⋅	⋅	⋅	⋅
129	0	0	0	0	$0w1$	$0$
130	0	0	0	0	$1w0$	$1$
131	0	0	0	1	$0w1$	$0$
132	0	0	0	1	$1w0$	$1$
133	0	0	1	0	$0w1$	0
134	0	0	1	0	$1w0$	$1$
135	0	0	1	1	$0w1$	$0$
136	0	0	1	1	$1w0$	$1$
⋅	⋅	⋅	⋅	⋅	⋅	⋅
159	1	1	1	1	$0w1$	$0$
160	1	1	1	1	$1w0$	$1$

.

For all active faults shown in Table 2 (rows 1–32), cell $i$ plays the role of the aggressor cell, while cells $j$, $k$, and $m$ are considered enabling cells. For the passive faults in this table (rows 129–160), cells $i$, $j$, $k$, and $m$ are considered aggressor cells. The classical NPSF model comprises $2^5$ passive primitive faults and $4\times 2^5$ active primitive faults [28].

To detect a memory error, the test must sensitize the fault with a suitable transition write operation and then read the victim cell to observe the error. For the classical NPSF model, in terms of satisfying the sensitization condition of any fault, a memory test must entirely cover the state transition graph for any group of five cells in the known configuration.

Let $g=\{i,j,b,k,m\}$ be a group of five cells as shown in Figure 1, where $i<j<b<k<m$, which means that when memory addresses are traversed in ascending order (⇑), the cells are accessed in this order, and when memory addresses are traversed in descending order (⇓), the cells are accessed in the reverse order. Given this aspect, it can be said that a memory test is optimal if, for any group $g$ of cells, any transition write operation in the state graph is performed once and only once (i.e., for any group $g$ of cells, the state graph is Eulerian).

Considering the two types of NPSFs (passive and active faults), as also mentioned in other works, e.g., Refs. [2,4,9,10], in order to detect any error resulting from memory fault sensitization, two necessary and sufficient observability conditions must be met:

(${OC}_1$) A memory cell must be read after performing a fault-sensitizing operation prior to a new write to verify that this operation was performed correctly.

(${OC}_2$) Before writing to a cell, it must first be read to verify that a state change has not occurred as a result of an operation previously performed in another possibly aggressor cell.

For RAM testing, the most commonly used tests are march-type tests. These memory tests are distinguished by their simplicity of implementation and the fact that they belong to the $O\left(N\right)$ complexity class. Therefore, the length of the testing algorithms and, implicitly, the duration of the memory testing process are reduced.

A march memory test consists of a set of march items, each of them describing a sequence of operations that must be performed successively on all memory locations (moving to the next cell is performed only after performing all operations on the current cell). The first symbol of a march element specifies the order in which memory locations are accessed. Given a sequential enumeration of memory addresses, the symbol ⇑ indicates that these addresses are traversed in ascending order, while the symbol ⇓ indicates that they are traversed in reverse order.

In general, to cover $k$-cell CF models, where $k\ge 3$, a multi-stage testing technique with different memory initializations is applied. This technique is called “multirun memory testing”.

In the case of multirun march memory testing, a given march test is applied repeatedly on different data backgrounds. A data background is obtained by multiplying a data pattern in memory both horizontally and vertically. Data backgrounds with row stripe, column stripe, or checkerboard patterns are commonly used in multirun memory testing [12,13]. For these data backgrounds, the initialization patterns are of the size 2 × 2. But the NPSF model we consider requires more complicated initialization patterns, concretely of the size 3 × 3 or 4 × 4, as shown in [32,33], and as presented extensively in this work. Specifically, a data background pattern must completely cover the five-cell configuration shown in Figure 1 and, for this reason, the pattern must be at least 3 × 3 in size.

3. Near-Optimal March Tests for the NPSF Model

To cover the classical NPSF model, where a fault sensitization involves a transition write operation in a cell of the coupled cell group with the configuration shown in Figure 1, a new memory test is proposed, called MT_NPSF_81N. In this test, two march elements are applied sixteen times on different data backgrounds (i.e., a multirun technique). 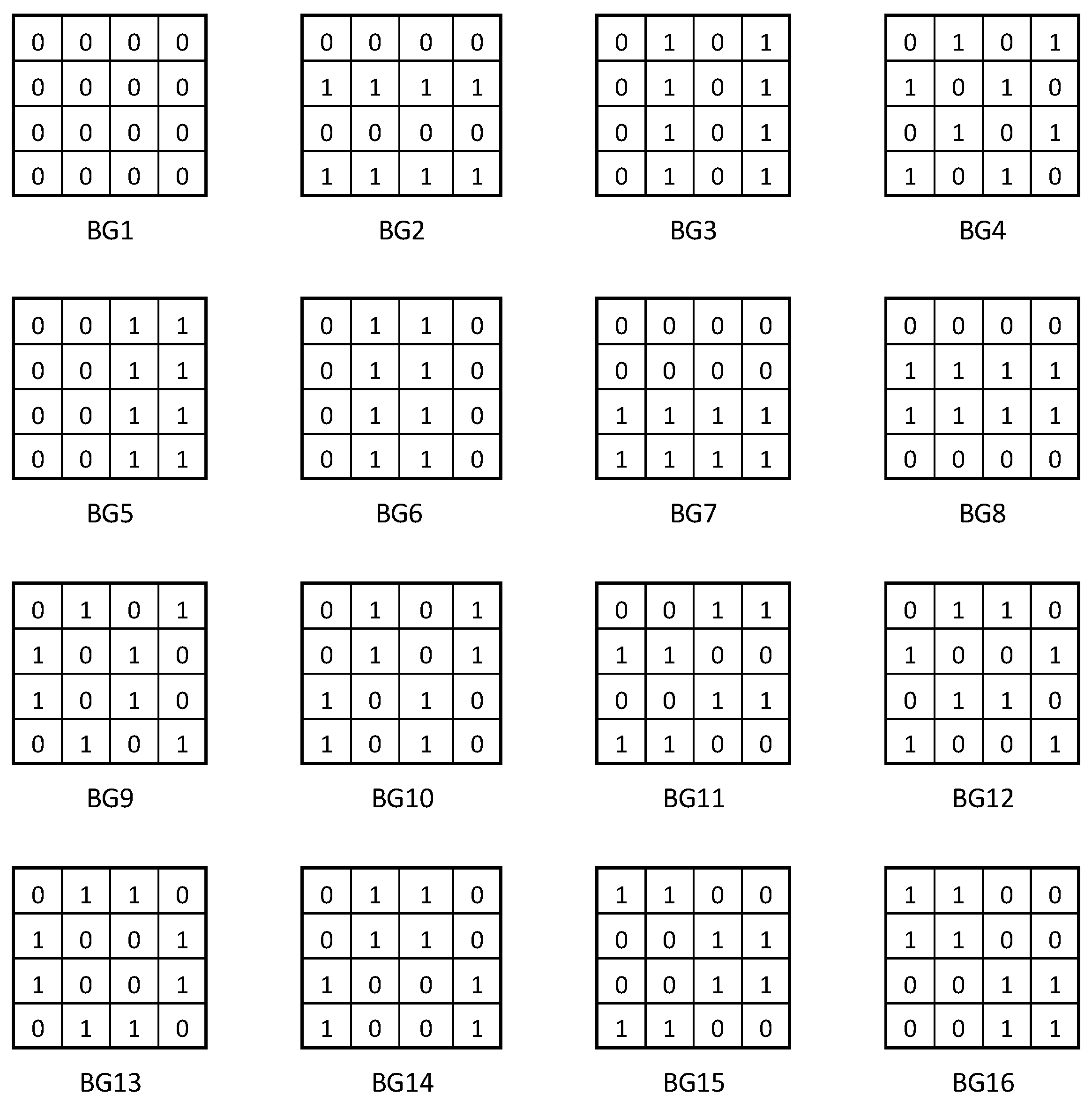The description of this new march multirun memory test is given in Figure 4, and the sixteen patterns used for memory initialization are shown in Figure 5.

In this description, ${BGC}_1$ indicates the primary memory initialization sequence while ${BGC}_i$, $i\in \left\{2,3,\dots ,16\right\}$, represent test sequences with background changes, according to the patterns shown in Figure 5. Note that, any change in the data background involves a status update only for half of the memory cells. On the other hand, in order to satisfy the ${OC}_2$ observability condition, any write operation to change the state of a memory cell is preceded by a read operation. Thus, the initialization sequence ${BGC}_1$ of the form $\Uparrow \left(w_0\right)$ involves $N$ write operations, while a test sequence with a background change, ${BGC}_i$, $i\in \left\{2,3,\dots ,16\right\}$, requires $N/2$ read operations and $N/2$ write operations (so, the same number $N$ of memory operations). Thus, the length of the memory test is

$$\mathcal{L}=16\times \left(1+4\right)N+N=81N.$$

(1)

The ability of the MT_NPSF_81N memory test to fully cover the classical NPSF model is discussed in the following.

Theorem 1.

The $MT\text{\_}NPSF\text{\_}81N$ test algorithm is able to detect all unlinked static faults of this classical NPSF model.

Proof. 

Let $g=\{i,j,b,k,m\}$ be an arbitrary group of five neighboring memory cells corresponding to the well-known NPSF configuration shown in Figure 1. The ability of the MT_NPSF_81N test algorithm to sensitize and observe any fault that may affect a cell in the g-group of cells is demonstrated in the following.

• MT_NPSF_81N is able to sensitize any fault in a $g$-group of coupled cells

To prove this statement, it is shown that during memory testing, MT_NPSF_81N performs all possible operations in this g-group of cells. In other words, MT_NPSF_81N completely covers the graph of states describing the normal operation of cells in this group.

But the $g$-group of cells can be anywhere in memory. The operations performed during memory testing differ from one group of cells to another because the initializations of the cells in a group depend on their position in memory (a position fully specified by the base cell address). But how can we monitor the operations performed within a group of cells under these circumstances when the number of distinct cases is so large? The following analysis aims to answer this question or, at least, to provide a solution to master the complexity of this problem.

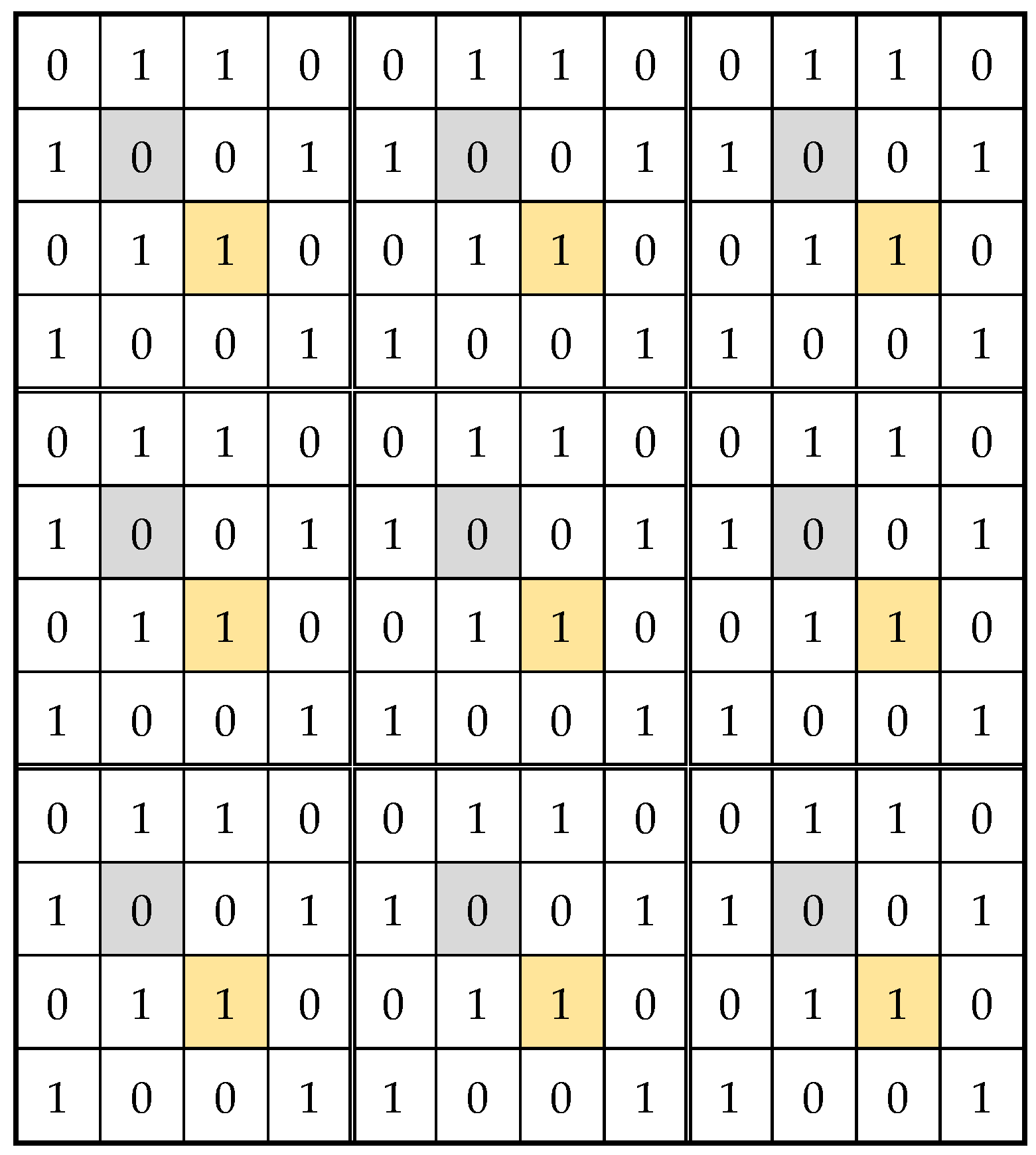
As it is known, a data background is obtained by multiplying a data pattern in memory both horizontally and vertically. Given that this test algorithm uses 4 × 4 memory initialization patterns, it follows that the cells selected 4 by 4 per row or column are brought to the same initial state. This aspect is illustrated in Figure 6, where the BG12 pattern is applied. For easier understanding, two groups of cells identically initialized are highlighted in this figure: a group of cells marked in gray, initialized with zero, and another group of cells marked in yellow, initialized with one.

Note that for cells initialized with the same value, the same memory operations will be performed when a march element is applied. Starting from this observation, the memory cells are divided into 16 classes (subsets), denoted by $C_1,C_2,\dots ,C_{16},$ depending on the residues of the row address modulo 4 ($A_r\mathrm{m}\mathrm{o}\mathrm{d}4$) and the column address modulo 4 ($A_c\mathrm{m}\mathrm{o}\mathrm{d}4$), as shown in

Table 3. Dividing the cells into sixteen classes by row and column addresses.

		${\mathit{A}}_{\mathit{c}}$mod 4
		0	1	2	3
${\mathit{A}}_{\mathit{r}}$ mod 4	0	${\mathcal{C}}_1$	${\mathcal{C}}_2$	${\mathcal{C}}_3$	${\mathcal{C}}_4$
	1	${\mathcal{C}}_5$	${\mathcal{C}}_6$	${\mathcal{C}}_7$	${\mathcal{C}}_8$
	2	${\mathcal{C}}_9$	${\mathcal{C}}_{10}$	${\mathcal{C}}_{11}$	${\mathcal{C}}_{12}$
	3	${\mathcal{C}}_{13}$	${\mathcal{C}}_{14}$	${\mathcal{C}}_{15}$	${\mathcal{C}}_{16}$

. For example, the cells highlighted in gray in Figure 6 belong to class ${\mathcal{C}}_6$ because for any of these cells, $A_r\mathrm{m}\mathrm{o}\mathrm{d}4=1$ and $A_c\mathrm{m}\mathrm{o}\mathrm{d}4=1$, while the cells highlighted in yellow belong to class ${\mathcal{C}}_{11}$, for which $A_r\mathrm{m}\mathrm{o}\mathrm{d}4=2$ and $A_c\mathrm{m}\mathrm{o}\mathrm{d}4=2$. This division of the memory cell set into 16 classes according to row and column addresses is illustrated in Figure 7.

Let $G_i$ now be the class (subset) of all $g$-groups of five cells in the known configuration for which the base cell ${b\in C}_i,i\in \left\{1,2,\dots ,16\right\}$. This class division of the $g$-groups of five cells is also illustrated in Figure 7 in different colors. This figure shows that the cells in the neighborhood of the base cells also belong to the same classes. For example, for the groups of cells in the subset $G_6$, the cells identified with $i$ belong to $C_2$, those identified with $j$ belong to $C_5$, and so on. As a result, for all groups within the same class, exactly the same operations will be performed during the testing process, and therefore the same state transitions will result. Given this, the study of monitoring state transitions in a group of cells $g$ is limited to 16 distinct groups, one for each class $G_i,i\in \left\{1,2,\dots ,16\right\}$. This idea is the basis for understanding this proof.

Given this simplification, in the following, let us analyze the initial state for a $g$-group of five memory cells in the known configuration, depending on the data background $\left(\mathrm{B}\mathrm{G}1-\mathrm{B}\mathrm{G}16\right)$ and the class of groups it belongs to $\left(G_1-G_{16}\right)$.

The status code for a $g$-group of cells is a five-bit word corresponding to the component cells in the form $v_i{v}_j{v}_b{v}_k{v}_m$. It is worth noting that a group $g$ of cells in the state $S=v_i{v}_j{v}_b{v}_k{v}_m$ will reach the complementary state $S^{\prime }=\overline{v_i}\overline{v_j}\overline{v_b}\overline{v_k}\overline{v_m}$ when the march element $\Uparrow \left(r{w}_t\right)$ is applied. We say that $S$ and $S^{\prime }$ are complementary states taking into account the following property:

$$S+S^{\prime }={11111}_{\mathrm{B}}={1\mathrm{F}}_{\mathrm{H}}.$$

(2)

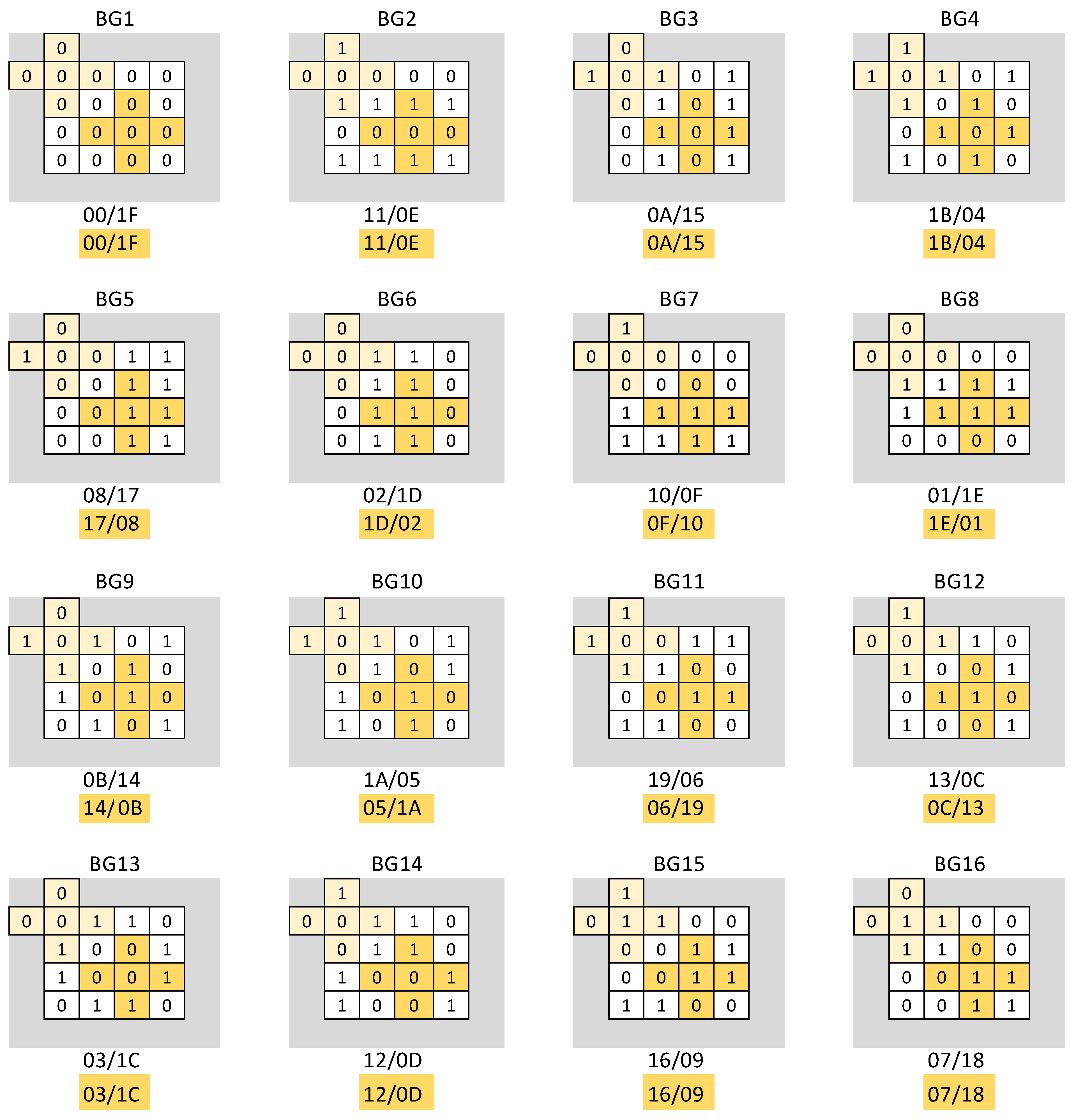
Figure 8 illustrates the initial and complementary states, $I_x$ and $I_x^{\prime }$, for two groups of cells $G_1$ and $G_{11}$, depending on the data background, BG$x,x\in \left\{1,2,\dots ,16\right\}$. For the other 14 cell groups, the values of $I_x$ and $I_x^{\prime }$ are obtained in the same way.

Table 4. Initial and complementary states $\left(\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{d}\mathrm{a}\mathrm{s}{\displaystyle \frac{I_x}{I_x^{\prime }}}\right)$ for a $g$-group of cells depending on the data background and the class to which the group belongs.

	${\mathit{G}}_1$	${\mathit{G}}_2$	${\mathit{G}}_3$	${\mathit{G}}_4$	${\mathit{G}}_5$	${\mathit{G}}_6$	${\mathit{G}}_7$	${\mathit{G}}_8$	${\mathit{G}}_9$	${\mathit{G}}_{10}$	${\mathit{G}}_{11}$	${\mathit{G}}_{12}$	${\mathit{G}}_{13}$	${\mathit{G}}_{14}$	${\mathit{G}}_{15}$	${\mathit{G}}_{16}$
BG1	00	00	00	00	00	00	00	00	00	00	00	00	00	00	00	00
	1F	1F	1F	1F	1F	1F	1F	1F	1F	1F	1F	1F	1F	1F	1F	1F
BG2	11	11	11	11	0E	0E	0E	0E	11	11	11	0E	0E	11	0E	0E
	0E	0E	0E	0E	11	11	11	11	0E	0E	0E	11	11	0E	11	11
BG3	0A	15	0A	15	0A	15	0A	15	0A	0A	0A	15	0A	15	0A	15
	15	0A	15	0A	15	0A	15	0A	15	15	15	0A	15	0A	15	0A
BG4	1B	04	1B	04	04	1B	04	1B	1B	04	1B	04	04	1B	04	1B
	04	1B	04	1B	1B	04	1B	04	04	1B	04	1B	1B	04	1B	04
BG5	08	02	07	1D	08	02	17	1D	08	02	17	1D	08	02	17	1D
	17	1D	08	02	17	1D	08	02	17	1D	08	02	17	1D	08	02
BG6	02	17	1D	08	02	17	1D	08	02	17	1D	08	02	17	1D	08
	1D	08	02	17	1D	08	02	17	1D	08	02	17	1D	08	02	17
BG7	10	10	10	10	01	01	01	01	0F	0F	0F	0F	1E	1E	1E	1E
	0F	0F	0F	0F	1E	1E	1E	1E	10	10	10	10	01	01	01	01
BG8	01	01	01	01	0F	0F	0F	0F	1E	1E	01	1E	10	10	10	10
	1E	1E	1E	1E	10	10	10	10	01	01	1E	01	0F	0F	0F	0F
BG9	0B	14	0B	14	05	1A	05	1A	14	0B	14	0B	1A	05	1A	05
	14	0B	14	0B	1A	05	1A	05	0B	14	0B	14	05	1A	05	1A
BG10	1A	05	1A	05	0B	14	0B	14	05	1A	05	1A	14	0B	14	0B
	05	1A	05	1A	14	0B	14	0B	1A	05	1A	05	0B	14	0B	14
BG11	19	13	06	0C	06	0C	19	13	19	13	06	0C	06	0C	19	13
	06	0C	19	13	19	13	06	0C	06	0C	19	13	19	13	06	0C
BG12	13	06	0C	19	0C	19	13	06	13	06	0C	19	0C	19	13	06
	0C	19	13	06	13	06	0C	19	0C	19	13	06	13	06	0C	19
BG13	03	16	1C	09	0D	18	12	07	1C	09	03	16	12	07	0D	18
	1C	09	03	16	12	07	0D	18	03	16	1C	09	0D	18	12	07
BG14	12	07	0D	18	03	16	1C	09	0D	18	12	07	1C	09	03	16
	0D	18	12	07	1C	09	03	16	12	07	0D	18	03	16	1C	09
BG15	16	1C	09	03	18	12	07	0D	09	03	16	1C	07	0D	18	12
	09	03	16	1C	07	0D	18	12	16	1C	09	03	18	12	07	0D
BG16	07	0D	18	12	16	1C	09	03	18	12	07	0D	09	03	16	1C
	18	12	07	0D	09	03	16	1C	07	0D	18	12	16	1C	09	03
Fulfillment Equation (5)	$\surd$	$\surd$	$\surd$	$\surd$	$\surd$	$\surd$	$\surd$	$\surd$	$\surd$	$\surd$	$\surd$	$\surd$	$\surd$	$\surd$	$\surd$	$\surd$

lists the initial and complementary states for any group of cells in the known configuration, depending on the initialization pattern $\left(\mathrm{B}\mathrm{G}1,\mathrm{B}\mathrm{G}2,\dots .,\mathrm{B}\mathrm{G}16\right)$ and the class to which the group belongs $\left(G_1,G_2,...,G_{16}\right)$.

The hexadecimal values in Figure 8 are listed in Table 4 in columns $G_1$and $G_{11}$. In this table, it can be verified that for any group $g$ of five neighboring cells in the known configuration, regardless of the class to which the group belongs (i.e., any column), the 16 background changes result in 16 distinct initial states, such that

$$I_x\ne I_y,\forall x,y\in \left\{1,2,\dots ,16\right\},x\ne y.$$

(3)

Furthermore, for any column in Table 3, the following equation is valid:

$$I_x\ne I_y^{\prime },\forall x,y\in \left\{1,2,\dots ,16\right\}.$$

(4)

If $\mathcal{S}$ represents the set of all $2^5=32$ states (as in the truth table), based on Equations (3) and (4) we can write the following equation:

$$\bigcup _{x=1}^{16}\left(I_x\cup I_x^{\prime }\right)=\mathcal{S}.$$

(5)

Note that the states in any of the 16 columns of Table 4 satisfy Equation (5), which means that all initial complementary states are different from each other and all together form the set $\mathcal{S}$.

As a remark, identifying those initialization models for which this property is fulfilled has involved a considerable research effort.

It is also important to note that, starting from an initial state $I_x,x\in \left\{1,2,\dots ,16\right\}$, upon the execution of the first march element (of the form $\Uparrow \left(r{w}_t\right)$), a $g$-group of cells is brought to the complementary state $I_x^{\prime }$, and after the next march element (identical to the first), that group of cells is returned to the initial state $I_x$.

Based on all these aspects, we can conclude that any $g$-group of cells in the known configuration is brought into each of the 32 possible states, and then a test sequence of the form $\Uparrow \left(r{w}_t\right)$ is applied. In a full memory scan with the march element $\Uparrow \left(r{w}_t\right)$, five different transitions are performed in any group of five cells. On the whole, in a group of five cells, $32\times 5=160$ transitions are performed.

Figure 9 shows the transitions performed in a $g$-group of cells of class $G_1$ in the first six of the sixteen stages of the memory test. The initial states after the six background changes are highlighted in bold. For easier identification, the transitions performed at each iteration are shown in different colors, and for the first transition within an iteration, an identification number is written on the edge.

For example, the 10 blue arcs that appear on the outer edge of the graph reflect the transitions made in a $g$-group of cells in the first stage of the test, when the memory is initialized with zero everywhere (BG1-0 solid data background) and then the full memory is scanned twice in ascending order by applying the test sequence of the following form: $\Uparrow \left(r{w}_t\right);\Uparrow \left(r{w}_t\right)$. The cells in group $g$ are accessed in the order $i\to j\to b\to k\to m$. During the first scan of the memory, as these cells are accessed, the state evolution for group $g$ is as follows: 00000, 10000, 11000, 11100, 11110, and 11111. Then, during the second scan, the group of cells successively reaches the following states: 01111, 00111, 00011, 00001, and finally 00000. So, the group of cells is returned to the initial state from which it started. In the same way, the transitions in the graph can be tracked for the other iterations of the memory test. Isolated nodes in the graph, without incident edges, reflect states that have not yet been reached in the first six iterations of the memory test. It should be noted that a complete graph with 160 edges would be difficult to draw and track.

Next, it is shown that all 160 transitions performed in a group $g$ of cells are different transitions and therefore the state transition graph is completely covered. Figure 10 shows the state evolution for a $g$-group of cells starting from two different initial states, $I_{x_0}$ $\ne$ $I_{y_0}$, when the march element $\Uparrow \left(r{w}_t\right)$ is applied.

The intermediate states that appear in the figure, $I_{x_u}$ and $I_{y_u}$, $u=1,2,3,4,$ are detailed in

Table 5. The intermediate states illustrated in Figure 10.

$\mathbf{Evolution}\mathbf{from}{\mathit{I}}_{{\mathit{x}}_0}$	$\mathbf{Evolution}\mathbf{from}{\mathit{I}}_{{\mathit{y}}_0}$
$I_{x_1}=I_{x_0}\oplus {10}_{\mathrm{H}}$	$I_{y_1}=I_{y_0}\oplus {10}_{\mathrm{H}}$
$I_{x_2}=I_{x_0}\oplus {18}_{\mathrm{H}}$	$I_{y_2}=I_{y_0}\oplus {18}_{\mathrm{H}}$
$I_{x_3}=I_{x_0}\oplus {1\mathrm{C}}_{\mathrm{H}}$	$I_{y_3}=I_{y_0}\oplus {1\mathrm{C}}_{\mathrm{H}}$
$I_{x_4}=I_{x_0}\oplus {1\mathrm{E}}_{\mathrm{H}}$	$I_{y_4}=I_{y_0}\oplus {1\mathrm{E}}_{\mathrm{H}}$

.

From Table 5 it follows that, since $I_{x_0}\ne I_{y_0}$ and $I_{x_u}\ne I_{y_u},u\in \left\{1,2,3,4\right\}.$ Note that although often $I_{x_u}=I_{y_v}$, $u\ne v,$ in the two cases, the write operations are performed on different memory cells and therefore the respective transitions are also different. Several such cases are found in Figure 9, such as the transitions made in the states 10000, 10100, 10010, or 01001.

In conclusion, by applying the MT_NPSF_81N memory test, $16\times 2\times 5=160$ different transitions are performed in the $g$-group of cells, completely covering the state transition graph. Moreover, each of these transitions is performed only once. As a result, the sensitization condition for all coupling faults specific to this classical NPSF model is met.

II.

MT_NPSF_81N detects any sensitized fault in a group g of coupled cell

Proving this property involves verifying the fulfillment of the two observability conditions, ${OC}_1$ and ${OC}_2$, presented in Section 2. For an easier and more direct verification of the fulfillment of the observability conditions, Figure 11 shows all the operations performed in a group of cells $g=\left\{i,j,b,k,m\right\}$ during the execution of the MT_NPSF_81N memory test. In the sequence of operations performed on cells in group $g$, write operations for initialization or background change are written in normal font, and those with the role of memory fault sensitization are highlighted in blue. Read operations that have the role of detecting possible errors resulting from fault sensitization are written in red.

Analyzing the sequence of operations shown in Figure 11, it can be seen that when a cell is accessed, it is first read, thus checking whether a state change has occurred in the cell as a result of an influence from another aggressor cell. This check is required by condition ${OC}_2$. Also, by analyzing the sequence of operations illustrated in this figure, it can be seen that after performing a write operation on a cell, it is then read (immediately or later) to verify that the operation was performed correctly. Thus, condition ${OC}_1$ is also met.

With the verification of both conditions regarding the sensitization of all considered memory faults and the ability to detect any resulting errors, the proof of the theorem is complete. □

Remark 1.

For any group of cells that corresponds to the considered NPSF model, the state transition graph is completely covered, and furthermore, each transition is performed only once. That means that the graph of states is Eulerian. The only redundant operations are used for background changes. With this argument, it can be said that this memory test is near-optimal.

The proposed memory test can be adapted to cover the extended NPSF model (ENPSF), in which memory faults can be sensitized by transition write operations but also by read or non-transition write operations [12,14]. To this end, the two march elements of form $\Uparrow \left({r,w}_t\right)$ are extended to the form $\Uparrow \left({r,w_{nt},r,r,w}_t\right)$. This extension leads to a near-optimal memory test for the ENPSF model, called MT_ENPSF, of length $177N$, as shown in Figure 12.

Note that in this case, when a certain state is reached, the $w_{nt}$ and $r$ operations are first executed and checked, and then the state is changed by a $w_t$ operation.

Remark 2.

The ability of each of the two memory tests to cover the considered NPSF model was also verified by simulation.

Verifying by simulation the ability of a memory test to detect faults within the considered fault model is not a difficult problem. The following clarifications are made regarding this experiment:

(1)

The memory is simulated by a binary matrix of appropriate size (in our case, a matrix of 16 × 16 was sufficient). The operations described in the test algorithm are performed on this matrix.

(2)

Within the matrix, a group of five cells is chosen for each of the sixteen classes, $G_1,G_2,...,G_{16}$, which are then studied and monitored in turn.

(3)

The faults considered (see Table 1) are simulated/injected within the current $g$-group of cells and verified one by one. For each simulated fault, the test program is run to verify whether the fault is detected or not.

(4)

For the classical NPSF model, simulating a fault requires permanent evidence of the state of the five cells in group $g$: $i$, $j$, $b$, $k$, and $m$. Monitoring all write operations in group $g$ allows any change in state of a cell in the group to be captured. Based on the state of the other cells, it is checked whether the sensitizing condition of the current fault is met. When this condition is met, the simulation of the memory error is performed by changing the value in the binary matrix at the location corresponding to the victim cell (cell $b$ in this model).

(5)

To simulate a memory error, it is more advantageous to use the facility provided by the TRAP interrupt. In some microcontroller-based systems (as be STM32 Nucleo-64 development board with STM32F103RB MCU), this facility is available to users. Thus, the operations for simulating a fault are implemented in the TRAP interrupt handling routine and, in this way, the test program remains unchanged.

(6)

For the extended NPSF model, the simulation experiment is more complex but does not pose any particular problems for an experienced programmer. The facility provided by the TRAP interrupt is no longer useful in this case.

4. Considerations for BIST Implementation of the Proposed Memory Tests

In this section, the issue of a possible BIST implementation of the proposed memory tests is addressed. Considering the number of memory areas tested in parallel and the number of bits that form the memory words (the number of bits accessed simultaneously), there are four memory BIST architectures, namely [8,17,18,19,20], SASB (Single-Array Single-Bit), SAMB (Single-Array Multiple-Bit), MASB (Multiple-Array Single-Bit), and MAMB (Multiple-Array Multiple-Bit).

Since SASB is the basic architecture, in the following section, we will limit ourselves to this architecture only. As mentioned in [19], adaptation for other architectures does not pose particular problems.

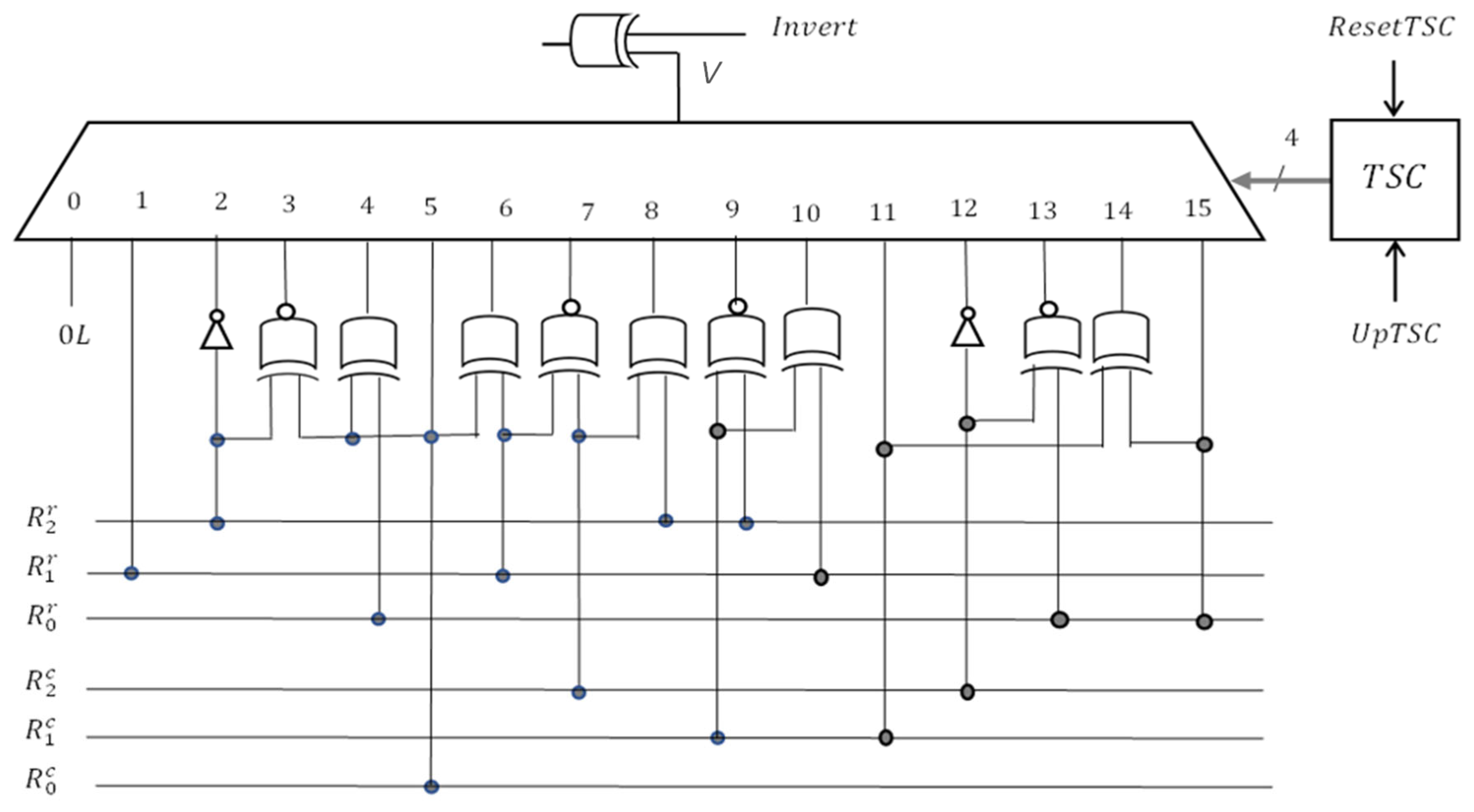
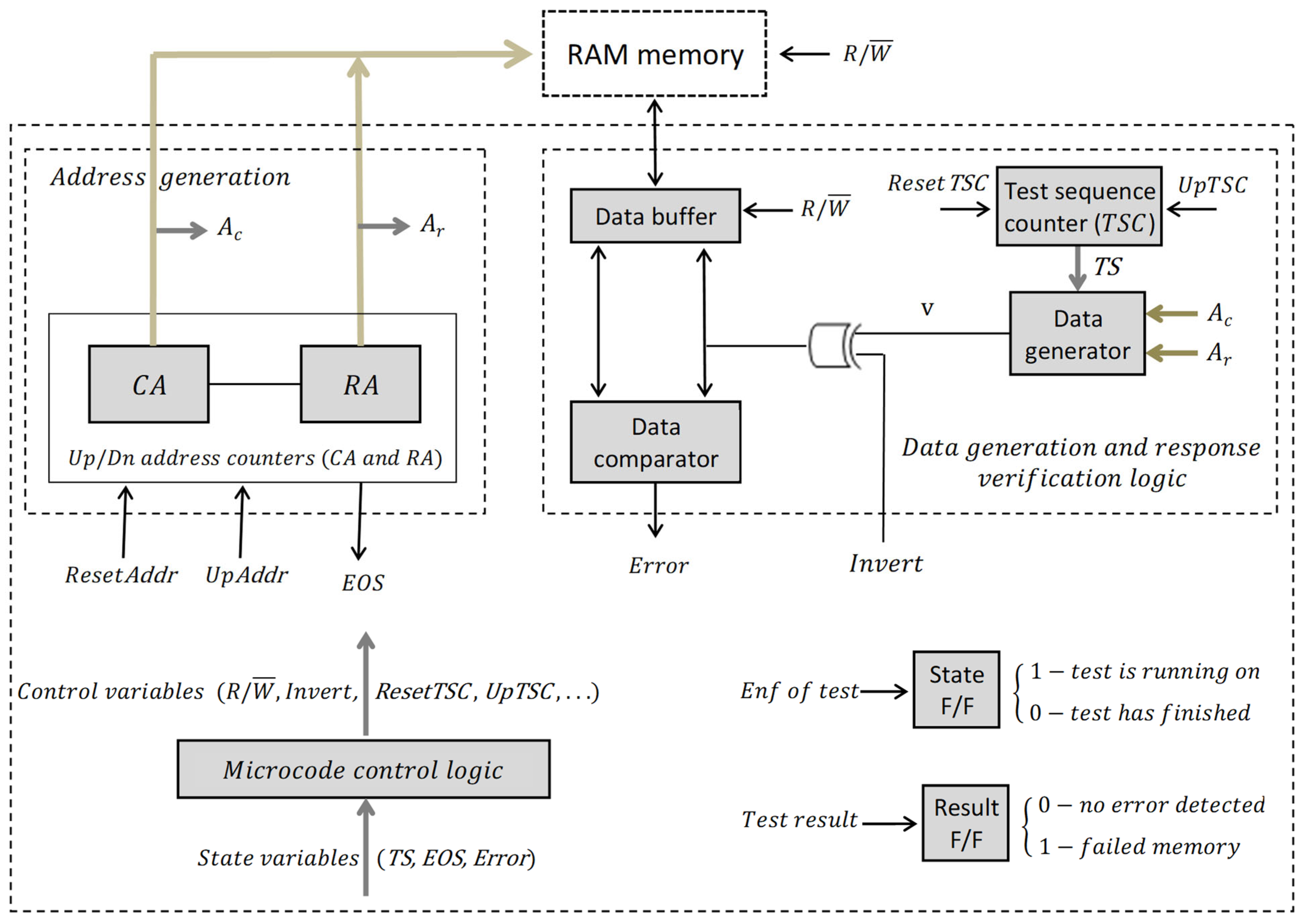
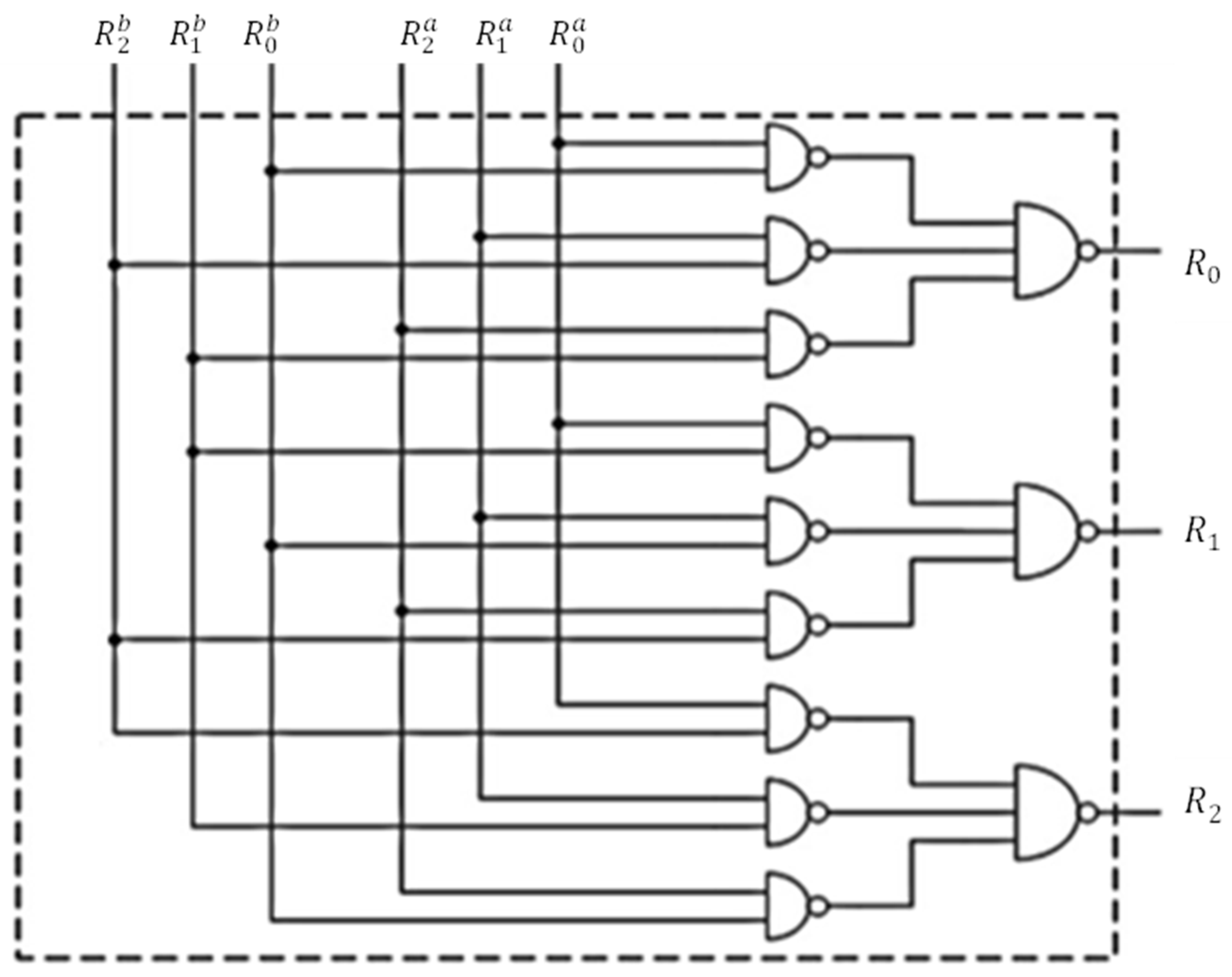
A block diagram of the self-test logic considered for implementing the proposed memory tests is shown in Figure 13. This self-test test logic has three parts: microcode control logic, address generation logic, and data generation and response verification logic. The other two flip-flops reflect the status of the test process and the test result.

The address generation logic is essentially composed of two counters, one for the row address denoted by $RA$ and the other for the column address denoted by $CA$. If during the testing process the memory is scanned only in ascending order, the counters are simple, and if the memory is scanned in both directions, the counters must be reversible. In our case, the counters are simple. The commands in the address generation logic are for resetting the address ($ResetAddr$) or for incrementing the address ($UpAddr$). When the upper limit of the tested memory area is reached, the $EOS$status signal is generated.

Remember that the tests proposed in this paper are multirun-type march memory tests. Specific to such a multirun test is the dependency between the value of a memory cell and its address. The proposed tests are distinguished from other known memory tests dedicated to the NPSF model, especially by the data patterns used for memory initializations. For this reason, this analysis focuses mainly on the synthesis of the address-based data generation logic (data generator, in brief).

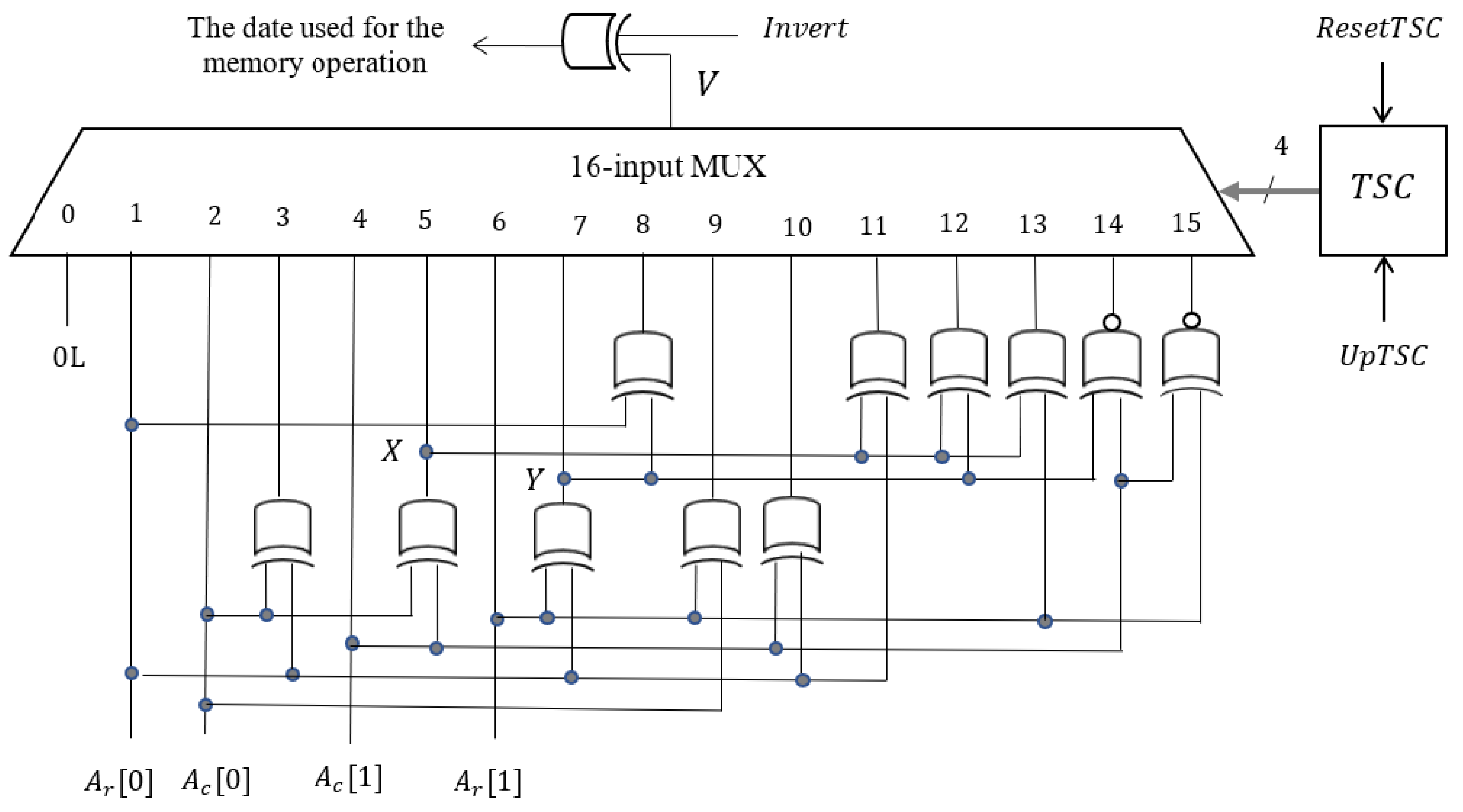
The dependency between the date and address differs from one test step to another (from one iteration to another) because a different memory initialization pattern is used each time. To adapt the date generation logic to the current data background, a test sequence counter ($TSC$) of length four is used. The commands for this counter are reset ($ResetTSC$) and increment ($UpTSC$). Next, we will show that the 4 × 4 background patterns used by the proposed memory tests lead to the synthesis of a simple data generation logic, which is incomparably simpler than that implied by the 3 × 3 background patterns. This is due to the fact that the logical value for the current cell is generated based on the two least significant bits of the row address $\left(A_r\right)$ and/or the column address $\left(A_c\right).$

Let us denote by $A_r\left[1\right]$ and $A_r\left[0\right]$ the two least significant bits of the row address and by $A_c\left[1\right]$ and $A_c\left[0\right]$ the two least significant bits of the column address. Depending on the background pattern, the calculation relationship of the initialization value of a memory cell according to the address, denoted by $V$, is shown in

Table 6. The initialization value of a cell depending on the address in the MT_NPSF_81N memory test.

Background Pattern					$\mathbf{The}\mathbf{Value}\mathbf{of}\mathbf{a}\mathbf{Cell}(\mathit{V}$) According to the Address
$\mathrm{B}\mathrm{G}1$	0	0	0	0	$V=0$
	0	0	0	0
	0	0	0	0
	0	0	0	0
$\mathrm{B}\mathrm{G}2$	0	0	0	0	$V=A_r\left[0\right]$
	1	1	1	1
	0	0	0	0
	1	1	1	1
$\mathrm{B}\mathrm{G}3$	0	1	0	1	$V=A_c\left[0\right]$
	0	1	0	1
	0	1	0	1
	0	1	0	1
$\mathrm{B}\mathrm{G}4$	0	1	0	1	$V=A_r\left[0\right]\oplus A_c\left[0\right]$
	1	0	1	0
	0	1	0	1
	1	0	1	0
$\mathrm{B}\mathrm{G}5$	0	0	1	1	$V=A_c\left[1\right]$
	0	0	1	1
	0	0	1	1
	0	0	1	1
$\mathrm{B}\mathrm{G}6$	0	1	1	0	$V=A_c\left[0\right]\oplus A_c\left[1\right]=X$
	0	1	1	0
	0	1	1	0
	0	1	1	0
$\mathrm{B}\mathrm{G}7$	0	0	0	0	$V=A_r\left[1\right]$
	0	0	0	0
	1	1	1	1
	1	1	1	1
$\mathrm{B}\mathrm{G}8$	0	0	0	0	$V=A_r\left[0\right]\oplus A_r\left[1\right]=Y$
	1	1	1	1
	1	1	1	1
	0	0	0	0
$\mathrm{B}\mathrm{G}9$	0	1	0	1	$V=\overline{A_r\left[0\right]\oplus A_r\left[1\right]}$ $A_c\left[0\right]+\left(A_r\left[0\right]\oplus A_r\left[1\right]\right)\overline{A_c\left[0\right]}$ ${=A}_r\left[0\right]\oplus A_r\left[1\right]\oplus A_c\left[0\right]=Y\oplus A_c\left[0\right]$
	1	0	1	0
	1	0	1	0
	0	1	0	1
$\mathrm{B}\mathrm{G}10$	0	1	0	1	$V={\overline{A_r\left[1\right]}A}_c\left[0\right]+A_r\left[1\right]\overline{A_c\left[0\right]}=A_c\left[0\right]\oplus A_r\left[1\right]$
	0	1	0	1
	1	0	1	0
	1	0	1	0
$\mathrm{B}\mathrm{G}11$	0	0	1	1	$V=A_r\left[0\right]\overline{A_c\left[1\right]}+\overline{A_r\left[0\right]}{A}_c\left[1\right]=A_r\left[0\right]\oplus A_c\left[1\right]$
	1	1	0	0
	0	0	1	1
	1	1	0	0
$\mathrm{B}\mathrm{G}12$	0	1	1	0	$V=\overline{A_r\left[0\right]}\left(A_c\left[0\right]\oplus A_c\left[1\right]\right)+A_r\left[0\right]\overline{A_c\left[0\right]\oplus A_c\left[1\right]}$ ${=A}_r\left[0\right]\oplus A_c\left[0\right]\oplus A_c\left[1\right]{=X\oplus A}_r\left[0\right]$
	1	0	0	1
	0	1	1	0
	1	0	0	1
$\mathrm{B}\mathrm{G}13$	0	1	1	0	$V=\overline{A_r\left[0\right]\oplus A_r\left[1\right]}\left(A_c\left[0\right]\oplus A_c\left[1\right]\right)+\left(A_r\left[0\right]\oplus A_r\left[1\right]\right)\overline{A_c\left[0\right]\oplus A_c\left[1\right]}$ $=A_r\left[0\right]\oplus A_r\left[1\right]\oplus A_c\left[0\right]\oplus A_c\left[1\right]=X\oplus Y.$
	1	0	0	1
	1	0	0	1
	0	1	1	0
$\mathrm{B}\mathrm{G}14$	0	1	1	0	$V=$ $\overline{A_r\left[1\right]}\left(A_c\left[0\right]\oplus A_c\left[1\right]\right)+A_r\left[1\right]\overline{A_c\left[0\right]\oplus A_c\left[1\right]}$ ${=A}_r\left[1\right]\oplus A_c\left[0\right]\oplus A_c\left[1\right]{=X\oplus A}_r\left[1\right]$
	0	1	1	0
	1	0	0	1
	1	0	0	1
$\mathrm{B}\mathrm{G}15$	1	1	0	0	$V=\overline{A_r\left[0\right]\oplus A_r\left[1\right]}\overline{A_c\left[1\right]}$ + $\left(A_r\left[0\right]\oplus A_r\left[1\right]\right)A_c\left[1\right]$ $=\overline{A_r\left[0\right]\oplus A_r\left[1\right]\oplus A_c\left[1\right]}=\overline{{Y\oplus A}_c\left[1\right]}$
	0	0	1	1
	0	0	1	1
	1	1	0	0
$\mathrm{B}\mathrm{G}16$	1	1	0	0	$V=\overline{A_r\left[1\right]}\overline{A_c\left[1\right]}+A_r\left[1\right]A_c\left[1\right]=\overline{A_r\left[1\right]\oplus A_c\left[1\right]}$
	1	1	0	0
	0	0	1	1
	0	0	1	1

. The background patterns are shown in the table for easier verification.

The MT_NPSF_81N memory test repeats two march elements 16 times, on different data backgrounds. Consequently, in order to adapt the logical value of the accessed cell to the data background, a 16-input multiplexer is required. The 4-bit code provided by the test sequence counter, denoted by $TS$, is applied to the selection inputs. Considering the relationships between date and address depending on the data background, as presented in Table 6, a possible solution for the data generation logic is shown in Figure 14.

The $Invert$ command that appears in the data generation logic and provided by the control logic is required to perform transition write operations in the first memory scan and read operations in the second scan, as highlighted in green in this test sequence: $\Uparrow \left(r{w}_t\right);\Uparrow \left(r{w}_t\right)$.

This synthesis shows that the MT_NPSF_81N memory test, despite using a large number of initialization patterns with some irregular structures, can be implemented quite easily in BIST-RAM architectures. For comparison, the following section presents aspects regarding to the synthesis of address-based data generation logic for a test that uses 3 × 3 memory initialization patterns, such as March-76N, the shortest near-optimal test currently known [34].

5. Considerations for Address-Based Data Generation in the Case of 3 × 3 Background Patterns

In memory tests using 3 × 3 background patterns, address-based data generation requires the modulo 3 residues of the row and column addresses. In the following, we remind how the modulo 3 residues can be generated, stressing that this is a difficult problem.

5.1. Hardware Generation of Modulo 3 Residues

For a word $W$ of length $n$ (a non-negative integer), let $R_3\left(W\right)=W\mathrm{m}\mathrm{o}\mathrm{d}3$ be the residue (remainder) of dividing $W$ by $three$. As $W$ is of the form

$$W=\sum _{i=0}^{n-1}{c}_i{2}^i$$

(6)

then $R_3\left(W\right)$can be calculated starting from the well-known equation [40] (pp. 37–59) as follows:

$$R_3\left(W\right)=R_3\left(\sum _{i=0}^{n-1}{c}_i{2}^i\right)=\left(\sum _{i=0}^{n-1}{c}_i{R}_3\left(2^i\right)\right)\mathrm{m}\mathrm{o}\mathrm{d}3.$$

(7)

But, for numbers expressed by $2^i$, the values of $R_3\left(2^i\right)$ are shown in

Table 7. Values for $R_3\left(2^i\right).$

$i$	0	1	2	3	4	5	6	$\dots$
$2^i$	1	2	4	8	16	32	64	$\dots$
$R_3\left(2^i\right)$	1	2	1	2	1	2	1	$\dots$

.

Based on Equation (7) and the values in Table 7, the following equation results:

$$R_3\left(W\right)=\left(c_0+2c_1+c_2+2c_3+c_4+2c_5+\dots \right)\mathrm{mod}3.$$

(8)

Equation (8) highlights the fact that the values of the coefficients for even positions and those of the coefficients for odd positions have equal weights in calculating the $R_3\left(W\right)$value. Therefore, the evaluation of Equation (7) starts from calculating the residue modulo 3 for the sum of two consecutive terms, one in the even position and the other in the immediate next odd position $\left(c_{2i}+2c_{2i+1},i=0,1,2,\dots \right)$.

Let us consider the value $R_3\left(W\right)$ expressed in redundant form as follows:

$$R_3\left(W\right)=\left(R_2,R_1,R_0\right)=\left\{\begin{array}{c}\left(1,0,0\right)\mathrm{i}\mathrm{f}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{u}\mathrm{l}\mathrm{t}\mathrm{i}\mathrm{s}2\\ \left(0,1,0\right)\mathrm{i}\mathrm{f}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{u}\mathrm{l}\mathrm{t}\mathrm{i}\mathrm{s}1\\ \left(0,0,1\right)\mathrm{i}\mathrm{f}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{u}\mathrm{l}\mathrm{t}\mathrm{i}\mathrm{s}0\end{array}\right.$$

(9)

For the sum of two consecutive terms $\left(c_{2i}+2c_{2i+1},i=0,1,2,\dots \right)$, the logical values $R_0,R_1,R_2$are determined based on the truth table presented in

Table 8. Truth table for logical variables $R_0,R_1,R_2.$

${\mathit{c}}_{2\mathit{i}}$	${\mathit{c}}_{2\mathit{i}+1}$	${\mathit{R}}_0$	${\mathit{R}}_1$	${\mathit{R}}_2$
0	0	1	0	0
0	1	0	0	1
1	0	0	1	0
1	1	1	0	0

.

From this truth table, for the output variables $R_0,R_1,R_2,$the following equations result:

$$\left\{\begin{array}{c}{R}_0=\overline{c_{2i}{\oplus c}_{2i+1}}\\ R_1=c_{2i}\overline{c_{2i+1}}\\ R_2=\overline{c_{2i}}{c}_{2i+1}\end{array}\right.$$

(10)

Let us denote by CLC1 the network of logic gates that performs these operations. The structure of this combinational logic circuit is given in Figure 15.

For two pairs of coefficients of this type, identified as $a$ and $b$, the outputs are denoted by $\left(R_2^a,R_1^a,R_0^a\right)$ and $\left(R_2^b,R_1^b,R_0^b\right)$, respectively. These intermediate results are then processed by another combinational logic, called CLC2, which generates the residue of the sum divided by three in the form $\left(R_2,R_1,R_0\right)$, as shown in the Figure 16.

The logical values $R_0,R_1,R_2$are obtained based on the following equations:

$$\left\{\begin{array}{c}{R}_0=R_0^a{R}_0^b+R_1^a{R}_2^b+R_2^a{R}_1^b\\ R_1=R_0^a{R}_1^b+{R_1^{a}R}_0^b+R_2^a{R}_2^b\\ R_2=R_0^a{R}_2^b+R_1^a{R}_1^b+R_2^a{R}_0^b\end{array}\right.$$

(11)

The network of logic gates that performs these operations is given in Figure 17.

For a word $W$=$2^n$, calculating the value of $R_3\left(W\right)$ requires $2^{n-1}$ CLC1 cells on the first level and a number of other CLC2 cells on the following levels. This results in a series–parallel logical structure. Operations on the same level are performed in parallel, and those on different levels are performed in series. Such a series–parallel structure for $n=16$ is shown in Figure 18.

For a quantitative analysis, let us follow a classical approach, taking as reference a primary two-input logic gate, for which the complexity is considered to be 1 eqg (equivalent logic gate). For the combinational logics CLC1 and CLC2, the complexity is given in

Table 9. Complexity of the CLC1 and CLC2 logics.

Combinational Logic	Complexity (eqg)
CLC1	$C_1=5.5$
CLC2	$C_2=13.5$

.

The series–parallel structure (SPS) in Figure 18 comprises eight CLC1 logics and seven CLC2 logics. The complexity for SPS is given by the following equations:

$$C_{SPS}=8C_1+7C_2=8\times 5.5+7\times 13.5=138.5\mathrm{eqg}.$$

(12)

Figure 18 and Equation (12) highlight the difficulty of determining the modulo 3 residues.

With these basic elements, let us return to the synthesis of address-based data generation logic for the March_76N memory test.

5.2. Address-Based Data Generation for the March_76N Memory Test

The March_76N memory test has the same structure as the MT_NPSF_81N test in the sense that it uses the same test sequence, $\Uparrow \left(r{w}_t\right);\Uparrow \left(r{w}_t\right)$, applied 16 times, but on other data backgrounds. Specifically, for memory initialization, the March_76N test uses the 3 × 3 size of data patterns, as presented in Table 9. Applying these 3 × 3 data models requires generating modulo 3 residues for the row and column addresses $A_r$ and $A_c$. For the two addresses, the values of the modulo 3 residues are expressed in the following form:

$${R_3\left(A_r\right)=(R}_2^r,R_1^r,R_0^r),R_3\left(A_c\right)={(R}_2^c,R_1^c,R_0^c).$$

(13)

For the calculation of these sets of logical values, ${(R}_2^r,R_1^r,R_0^r)$ and ${(R}_2^c,R_1^c,R_0^c)$, two series–parallel structures, such as the one presented in Figure 18, are required. These additional logics, denoted by SPSr and SPSc, are illustrated in Figure 19.

Table 10. Determining the value of a cell ($V$) based on the address in the March_76N memory test.

Background Pattern				$\mathbf{The}\mathbf{Value}\mathbf{of}\mathbf{a}\mathbf{Cell}(\mathit{V}$) According to the Address
$\mathrm{B}\mathrm{G}1$	0	0	0	$V=0$
	0	0	0
	0	0	0
$\mathrm{B}\mathrm{G}2$	0	0	0	$V=R_1^r$
	1	1	1
	0	0	0
$\mathrm{B}\mathrm{G}3$	1	1	1	$V=\overline{R_2^r}$
	1	1	1
	0	0	0
$\mathrm{B}\mathrm{G}4$	0	1	1	$V=\overline{R_2^r}\overline{R_0^c}+R_2^r{R}_0^c=\overline{R_2^r\oplus R_0^c}$
	0	1	1
	1	0	0
$\mathrm{B}\mathrm{G}5$	0	1	1	$V=R_0^r\overline{R_0^c}+\overline{R_0^r}{R}_0^c=R_0^r\oplus R_0^c$
	1	0	0
	1	0	0
$\mathrm{B}\mathrm{G}6$	1	0	0	$V=R_0^c$
	1	0	0
	1	0	0
$\mathrm{B}\mathrm{G}7$	1	0	0	$V=R_1^r\overline{R_0^c}+\overline{R_1^r}{R}_0^c=R_1^r\oplus R_0^c$
	0	1	1
	1	0	0
$\mathrm{B}\mathrm{G}8$	1	1	0	$V=R_1^r{R}_2^c+\overline{R_1^r}\overline{R_2^c}=\overline{R_1^r\oplus R_2^c}$
	0	0	1
	1	1	0
$\mathrm{B}\mathrm{G}9$	0	0	1	$V=R_2^r\overline{R_2^c}+\overline{R_2^r}{R}_2^c=R_2^r\oplus R_2^c$
	0	0	1
	1	1	0
$\mathrm{B}\mathrm{G}10$	1	0	1	$V=R_2^r{R}_1^c+\overline{R_2^r}\overline{R_1^c}=\overline{R_2^r\oplus R_1^c}$
	1	0	1
	0	1	0
$\mathrm{B}\mathrm{G}11$	0	1	0	$V=R_1^r\overline{R_1^c}+\overline{R_1^r}{R}_1^c=R_1^r\oplus R_1^c$
	1	0	1
	0	1	0
$\mathrm{B}\mathrm{G}12$	0	1	0	$V=R_1^c$
	0	1	0
	0	1	0
$\mathrm{B}\mathrm{G}13$	1	1	0	$V=\overline{R_2^c}$
	1	1	0
	1	1	0
$\mathrm{B}\mathrm{G}14$	0	0	1	$V=R_0^r{R}_2^c+\overline{R_0^r}\overline{R_2^c}=\overline{R_0^r\oplus R_2^c}$
	1	1	0
	1	1	0
$\mathrm{B}\mathrm{G}15$	1	0	1	$V=R_0^r\overline{R_1^c}+\overline{R_0^r}{R}_1^c=R_0^r\oplus R_1^c$
	0	1	0
	0	1	0
$\mathrm{B}\mathrm{G}16$	1	1	1	$V=R_0^r$
	0	0	0
	0	0	0

also presents the relationships for data calculation according to the address for the 16 background patterns used in the March_76N memory test.

Considering the relationships between the date and address depending on the data background, as presented in Table 10, a solution for the data generation logic is shown in Figure 20.

Figure 19. Additional SPS logics for address modulo 3 residue generation.

Figure 19. Additional SPS logics for address modulo 3 residue generation.

Figure 20. Data generation logic for the March_76N memory test.

Figure 20. Data generation logic for the March_76N memory test.

Comparing the two address-based data generation logics, according to the background models, for the memory tests MT_NPSF_81N and March_76N, the following conclusions can be drawn:

(1)

Because the two memory tests use the same testing technique, the self-test logics that implement these tests are similar in structure.

(2)

The main difference is that when implementing the March_76N memory test, two additional logics are required to generate modulo 3 residues for the row and column addresses.

(3)

These two additional logics have high complexity and increase the propagation time through the combinational logic, which can affect the test time. For example, for two structures of the form shown in Figure 18, which correspond to 4 Gbit of memory, the additional logic complexity is $2\times 138.5=277$ eqg. Regarding the influence of propagation time through additional logic on the memory test running speed, a quantitative assessment must be made with caution because the memory access time with the control logic microcode must also be taken into account (see Figure 13).

(4)

In the March_76N memory test, because the initialization patterns are smaller in size, the network of logic gates that feed the multiplexer is simpler. Specifically, comparing Figure 14 and Figure 20, it results that in the MT_NPSF_81N test, eleven two-input XOR or XNOR gates are used, while in the March_76N test, only nine XOR or XNOR gates and two inverters are used. Since the complexity of a two-input XOR or XNOR gate is 2.5 eqg and that of an inverter is 0.5 eqg, it results that the network of gates in the March_76N test is somewhat simpler, with a complexity reduced by 4 eqg. However, compared to the complexity of the additional logic for calculating modulo 3 residues at row and column addresses of 277 eqg, this reduction is insignificant.

This comparative analysis highlights the major advantage of the proposed tests compared to other near-optimal tests that use 3 × 3 memory initialization patterns. For this reason, the authors argue that the new MT_NPSF_81N memory test, although slightly longer, is more suitable for implementation in self-testing RAM structures compared to the other two known near-optimal memory tests, CM-79N and March-76N.

6. Discussion

In relation to the new tests proposed in this paper, additional considerations covering several different aspects are made in this section.

In this research paper, only the optimal memory tests in terms of the ability to detect faults of the NPSF model were considered. Specifically, all three memory tests dedicated to the classical NPSF model, CM-79N, March-76N, and MT_NPSF_81N, fully cover this model with a minimum number of test operations. Additional write operations are used only for background changes. For this reason, the paper does not refer to “fault coverage” as the main performance indicator of memory tests. The other performance indicator regarding the number of memory operations or the length of the test is found in the name of the memory test itself. This paper targeted another aspect regarding memory tests, namely, the ease of implementation in self-testing structures of the BIST-RAM type, and the proposed memory tests, MT_NPSF_81N and MT_ENPSF, were designed specifically for this purpose.

The difference in length at the three near-optimal tests comes from the different share of memory cells that update to a background change, which is 33.3% for March_76N, 44.4% for CM_79N, and 50% for MT_NPSF_81N. This difference is reflected in the duration of the memory testing. However, in [32], it is pointed out that selectively updating memory cells for background changes raises some implementation difficulties without a significant time gain. Therefore, designers often prefer to scan the entire memory on a background change. In these situations, the small disadvantage of the proposed test in terms of length disappears, and the advantage of simplicity of implementation in BIST-RAM type structures becomes even more important.

The main disadvantage of memory tests using 3 × 3 data background patterns comes from the fact that additional logic is required to generate modulo 3 residues for row and column addresses. Related to this, it should also be noted that if the word length of the row or column address is not a power of two (and most often this condition is not met), an asymmetry appears in the expression for calculating the modulo 3 residues, which further complicates the synthesis of additional logic.

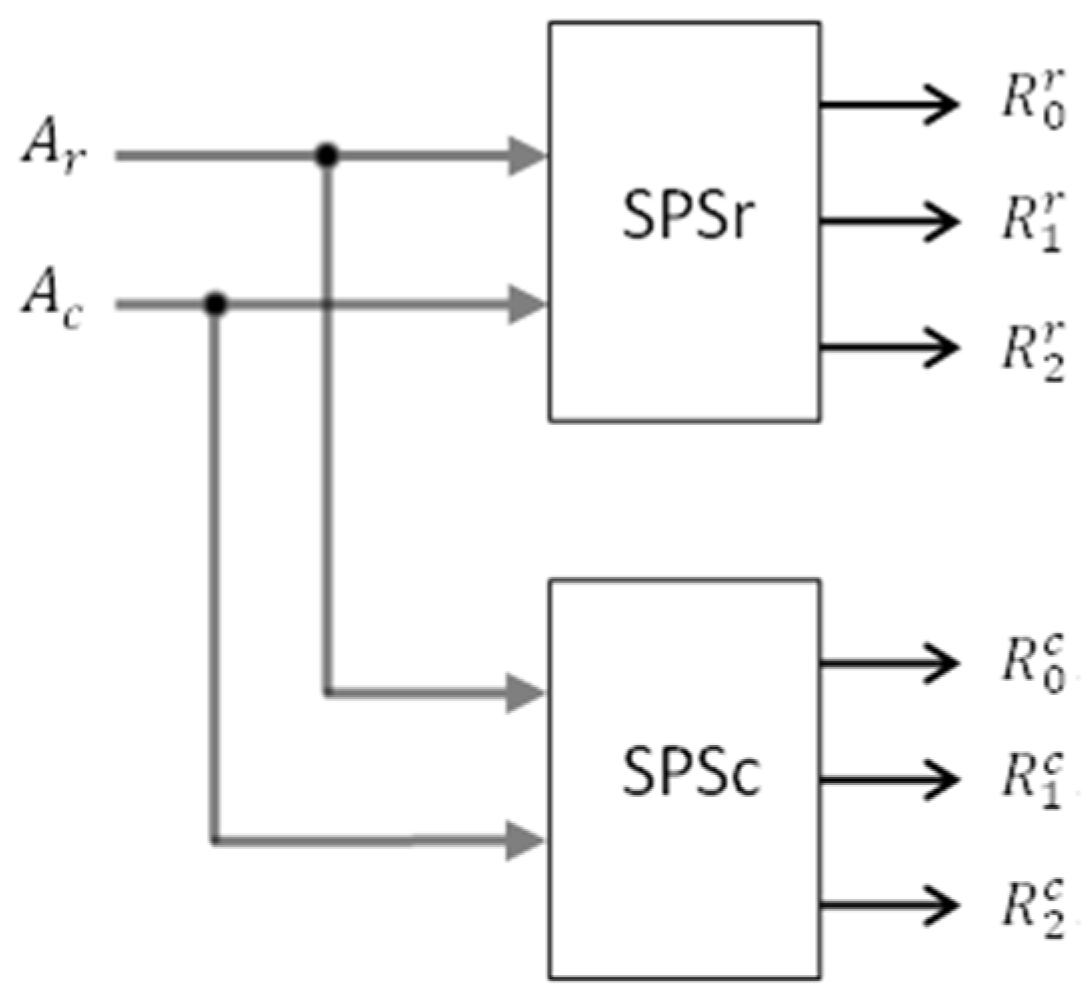
In the case of tests using 2 × 2 or 4 × 4 background patterns, the address-based data generation logic does not depend on the size of the memory being tested. The same can be said about the control logic. Only the address counters must be sized according to the geometry of the memory area. However, in the case of tests using 3 × 3 background patterns, the two additional logics for calculating the modulo 3 residues of the row and column addresses (SPSr and SPSc) differ depending on the length of the address words and therefore differ from one memory to another. The propagation time through these additional logics is also variable. And this is a major disadvantage of the March_76N and CM_79N tests compared to the proposed test, MT_NPSF_81N.

BIST structures are implemented especially in SRAM memories, which have a short response time (on the order of nanoseconds) and, as a result, can operate at high frequencies. To detect faults that manifest at high frequencies, the memory must be tested in its normal operating mode. For memories with self-test facilities, an important limitation on the speed of operation in memory test mode is related to how the control logic is implemented. If the frequency at which the memory needs to be tested is critical, then the control logic can be implemented hardwired, rather than microprogrammed, as is usually performed. In such a situation, the propagation time through the additional logic for generating the modulo 3 residues of the row and column addresses has a greater influence on the speed at which the memory test is performed. However, a quantitative assessment of this influence requires detailed knowledge of the structure of the control unit.

In BIST-RAMs, the share of additional self-test logic in the entire structure, also reflected in terms of area overhead or additional power consumption, depends largely on the size of the memory being tested. This is because, as previously mentioned, the complexity of the additional logic that provides self-test facilities is almost the same, regardless of the size of the memory being tested.

As mentioned in the previous section, more complex architectures are commonly found in memory circuits, such as the MAMB architecture in 3D memories. From a testing perspective, these architectures do not present any different problems, since their structure is designed so that multiple areas can be tested in parallel. Therefore, the basis of any testing experiment is the fault models and tests designed for SASB architectures.

The proposed tests also cover the three-cell coupling model involving neighboring memory cells arranged in a corner or on a row or column [5,10,11,12,13,14] in the classical and extended version, respectively, since the three-cell configurations are included in the five-cell configuration (see Figure 1).

The background models used when approaching the NPSF model of the size 3 × 3 or 4 × 4 also influence to some extent the ability of memory tests to cover other simpler coupling fault models, such as two-cell coupling, three-cell coupling, or four-cell coupling. To highlight this point, the following section presents the experimental results obtained through a simulation of the ability of the March_76N and MT_NPSF_81N memory tests to cover these simpler fault models. Note that the two tests apply the same testing technique but use different background patterns of the size 3 × 3 and 4 × 4, respectively.

7. Simulation Results

To evaluate the ability of a memory test to cover a specific fault model, the simulation technique briefly described in Section 3 was used. The following fault models were considered in this study: (1) two-cell coupling, where the cells in a group can be any memory cells; (2) three-cell coupling; (3) four-cell coupling; and (4) the classical NPSF model. As presented in the Introduction, for the three-cell and four-cell coupling models, the evaluation is limited to cases where the cells in a group are physically adjacent.

Depending on the fault model considered and the memory test evaluated, a large number of cell groups were selected for monitoring to cover all write operations performed during memory testing that may sensitize faults within the studied model.

For this purpose, when evaluating the MT_NPSF_81N test, which uses 4 × 4 background patterns, the set of memory cells is divided into sixteen classes ($C_1,C_2,\dots ,C_{16}$), as known from Section 3, while when evaluating the March_76N test, which uses 3 × 3 background patterns, the set of memory cells is divided into nine classes (${\mathcal{C}}_1^{\prime },{\mathcal{C}}_2^{\prime },\dots ,{\mathcal{C}}_9^{\prime }$), depending on the modulo 3 residues of the row and column addresses, as shown in

Table 11. Dividing cells into nine classes by row and column addresses.

			${\mathit{A}}_{\mathit{c}}$mod 3
		0	1	2
${\mathit{A}}_{\mathit{r}}$ mod $\mathbf{3}$	0	${\mathcal{C}}_1^{\prime }$	${\mathcal{C}}_2^{\prime }$	${\mathcal{C}}_3^{\prime }$
	1	${\mathcal{C}}_4^{\prime }$	${\mathcal{C}}_5^{\prime }$	${\mathcal{C}}_6^{\prime }$
	2	${\mathcal{C}}_7^{\prime }$	${\mathcal{C}}_8^{\prime }$	${\mathcal{C}}_9^{\prime }$

.

Next, the fault models considered and how the cell groups for monitoring and fault injection were selected are briefly described.

(1)

Two-cell coupling

Considering that when applying the studied tests to two cells of the same class, identical operations are performed, in order to evaluate the ability of the tests to detect faults that may affect pairs of memory cells in the binary matrix that simulates the tested memory, in the simulation experiment, pairs of cells ($i,j$) were chosen, such that

$$i,j\in \left\{{\mathcal{C}}_1^{\prime },{\mathcal{C}}_2^{\prime },\dots ,{\mathcal{C}}_9^{\prime }\right\}\mathrm{for}\mathrm{the}\mathrm{March}\text{\_}76\mathrm{N}\mathrm{memory}\mathrm{test},$$

(14)

and

$$i,j\in \left\{C_1,C_2,\dots ,C_{16}\right\}\mathrm{for}\mathrm{the}\mathrm{MT}\text{\_}\mathrm{NPSF}\text{\_}81\mathrm{N}\mathrm{memory}\mathrm{test}.$$

(15)

Specifically, in the simulation experiment, for the March_76N memory test, 9 × 9 pairs of cells were checked, monitoring 9 × 9 × 8 = 648 different transitions, while in the case of the MT_NPSF_81N memory test, 16 × 16 pairs of cells were checked, monitoring 16 × 16 × 8 = 2048 different transitions. For verification, 10 different experiments were performed, each time obtaining the same result.

(2)

Three-cell coupling

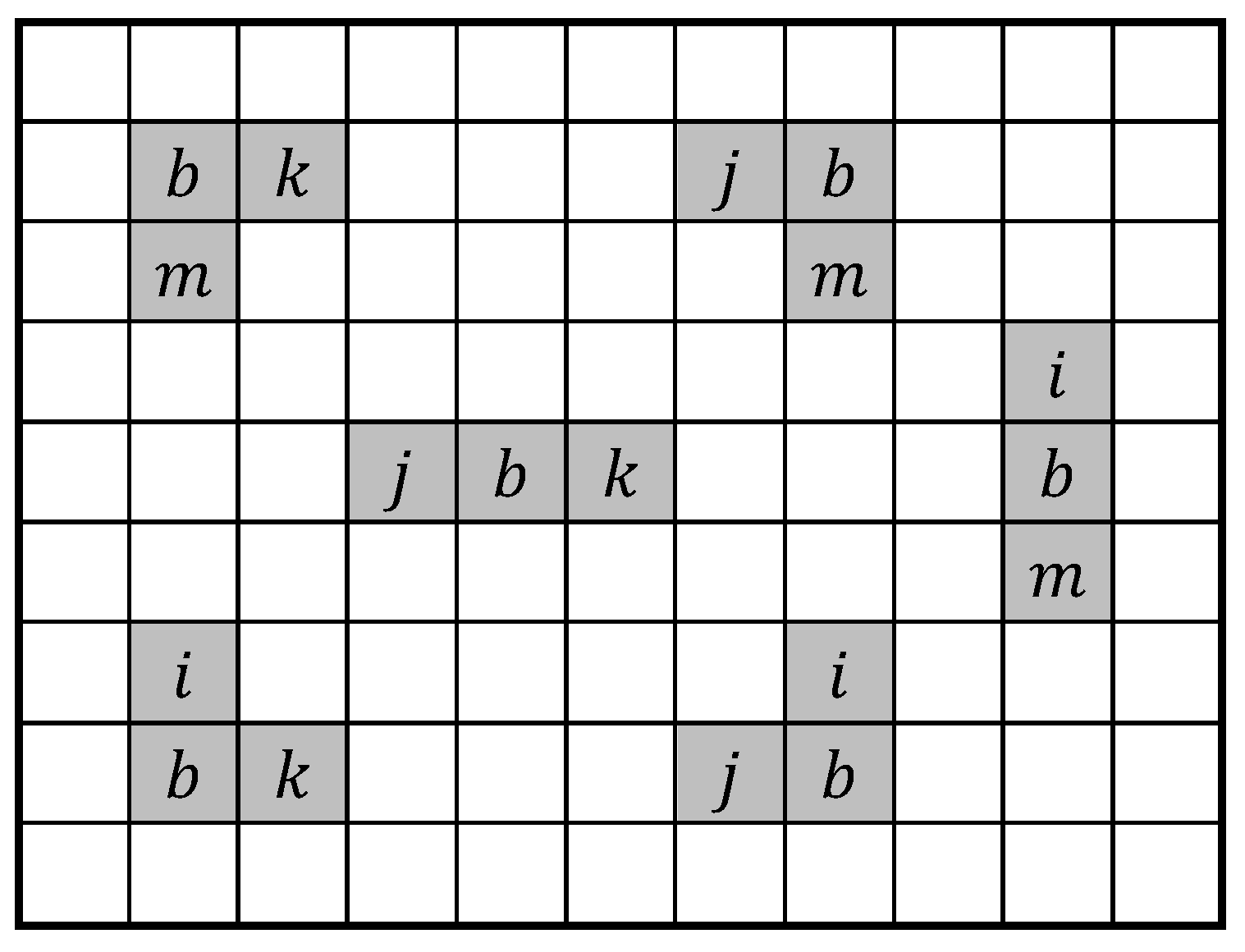
For this coupling fault model, the following six configurations of three physically neighboring cells are usually considered, as shown in Figure 21. All these six neighboring cell configurations are part of the more complex NPSF model (see Figure 1). However, in this model, any of the three cells in the group can be a victim cell, not just the central cell, as is the case in the five-cell NPSF model.

To select groups of cells for simulation, the address of the central cell, denoted by $b$, is indicated, around which all six configurations are formed in turn. In a group of three cells, $3\times 2^3=24$ transitions are possible. In the case of the memory test March_76N, a cell address is selected in the binary matrix for each of the nine classes $\left(b\in \left\{{\mathcal{C}}_1^{\prime },{\mathcal{C}}_2^{\prime },\dots ,{\mathcal{C}}_9^{\prime }\right\}\right)$, around which the six configurations are formed in turn. Thus, in the simulation experiment, $9\times 6\times 24=1296$ distinct transitions are monitored.

In the case of the memory test MT_NPSF_81N, a cell address is selected for each of the sixteen classes $\left(b\in \left\{C_1,C_2,\dots ,C_{16}\right\}\right)$, so that in a simulation experiment, $16\times 6\times 24=2304$ distinct transitions are monitored. For verification, 10 different experiments were performed, each time obtaining the same result.

(3)

Four-cell coupling

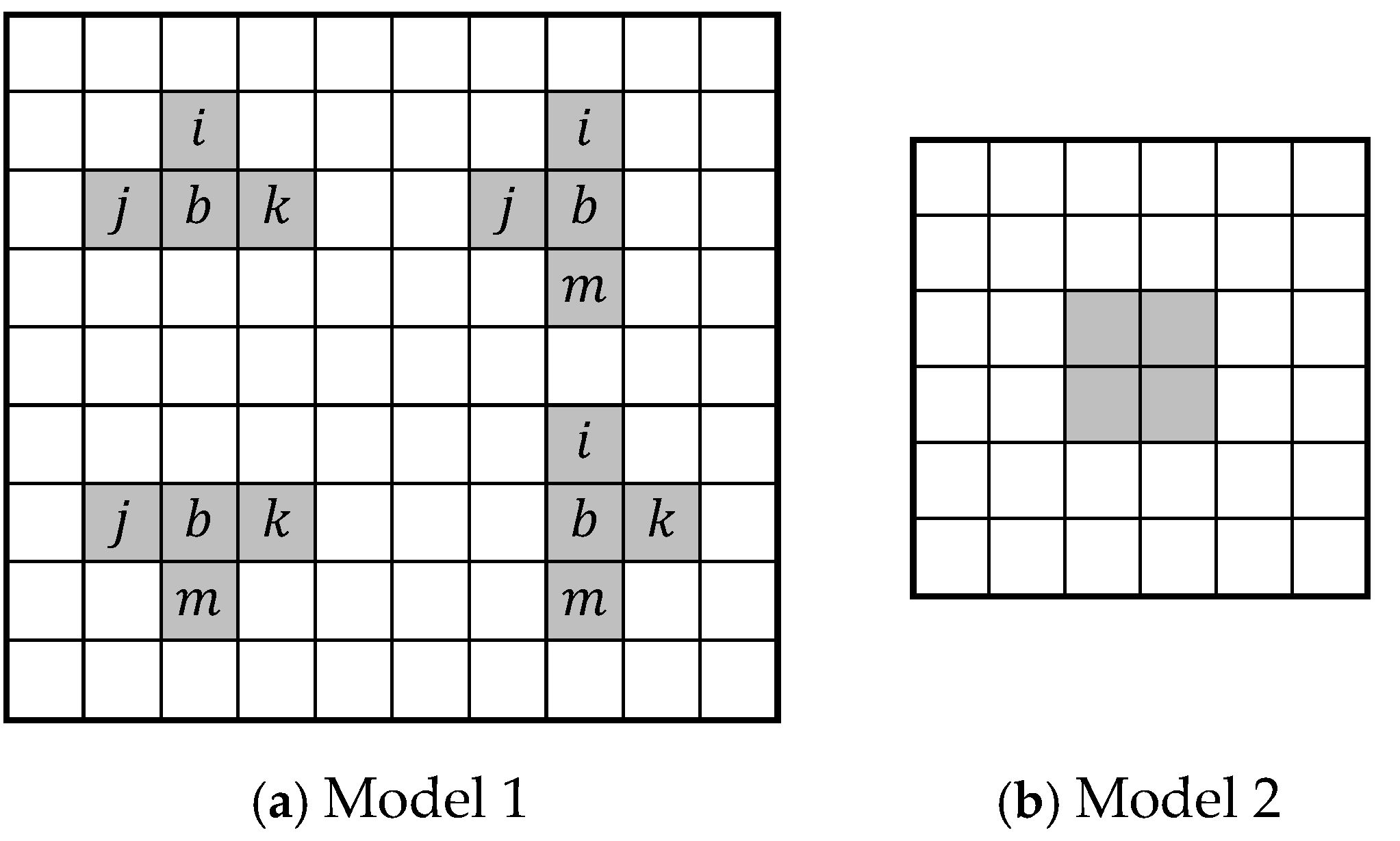
Two distinct cases were studied for this complex fault model, as shown in Figure 22. The first model (Model 1) includes four configurations derived from the five-cell configuration of the NPSF model. The other model (Model 2) considers the configuration of four cells arranged in a square. In both cases, any cell in the group can play the role of victim, aggressor, or enabling cell.

In a group of four cells, $4\times 2^4=64$ transitions are possible. In this case too, when forming the groups of cells to be monitored, only the address of the central cell is indicated in Model 1 (cell $b$) and of the cell in the upper left corner in Model 2. The group of cells is formed around this base cell in the desired configuration.

As for the previous model, one base cell from each class is chosen in the binary matrix. Thus, for the first model, in the simulation experiment, $9\times 4\times 64=2304$ transitions are monitored when evaluating the March_76N memory test, and $16\times 4\times 64=4096$ transitions are monitored when evaluating the MT_NPSF_81N memory test. For the second model, the number of monitored transitions is four times smaller.

For all these fault models, the simulation results regarding fault coverage by the two memory tests are presented in

Table 12. Simulation results: fault coverage (expressed as %).

Memory Test	Memory Fault Model
	Two-Cell Coupling	Three-Cell Coupling	Four-Cell Coupling Model 1	Four-Cell Coupling Model 2	NPSF
March_76N (3 × 3 patterns)	94.44	100	100	75.69	100
MT_NPSF_81N (4 × 4 patterns)	96.88	100	100	78.03	100

. The fault coverage is expressed as the ratio between the number of detected faults and the total number of simulated faults. For verification, the simulation program also calculates the ratio between the number of transitions performed in all considered cell groups and the total number of monitored transitions. Both calculation relationships led to the same result.

The simulation results confirm that the two dedicated memory tests fully cover the NPSF model. As a verification, both memory tests also fully cover the fault models including simpler three-cell and four-cell models derived from the five-cell configuration of the NPSF model.

However, the two memory tests only partially cover the four-cell coupling fault model with the cells arranged in a square (Model 2), as these tests were not designed for this purpose. Most surprising, however, is the fact that neither of the two tests completely covers the two-cell coupling fault model, the most often used model in practice. But this is a characteristic of all tests dedicated to the NPSF model. For example, the test proposed Suk and Reddy [28] of the length $165N$ covers the two-cell coupling model by 76.04%, and the four-cell coupling, Model 2, by only 54.3%.

To detect all coupling faults between any two memory cells, these dedicated tests should be supplemented with other test sequences. For example, for both the $March\text{\_}76N$ and MT_NPSF_81N memory tests, a new initialization with one everywhere (one-solid data background) followed by a simple memory scan using the march element $\Uparrow \left({rw}_t\right)$ before the final check is sufficient to cover this class of faults as well.

Comparing the two memory tests, March_76N and MT_NPSF_81N$,$ it results that the new test proposed in this paper offers slightly better performance in terms of covering other fault models. Since the two memory tests apply the same testing technique, this difference in fault coverage is explained exclusively by the contribution of the 4 × 4 background patterns.

8. Conclusions

The paper proposes two near-optimal memory tests dedicated to the complex NPSF model, both in the classic version in which it is accepted that a fault is only sensitized by a transition write operation, and in the extended version in which faults sensitized by a non-transition write or a read operation are also taken into account. The proposed tests, MT_NPSF_81N and MT_ENPSF are multirun march memory tests that use 4 × 4 data background patterns and are specifically designed to be easy to implement in self-testing RAM architectures. These are the first near-optimal memory tests dedicated to the NPSF model using 4 × 4 data initialization patterns reported to date.

Due to the difficulty of generating modulo 3 residues for row and column addresses, the authors state that memory tests using 3 × 3 memory initialization patterns (as are the other two known near-optimal tests for the classical NPSF model, CM-79N and March-76N) are not exactly suitable for implementation in self-testing RAM structures.

The evaluation of the optimality of the proposed tests is based on the fact that for any group of cells corresponding to the NPSF model, the state graph is completely covered, and each arc is traversed only once, which means that the graph is Eulerian. Some additional memory write operations are only required for background changes. All these aspects were also verified through simulation.

The memory initialization patterns were designed so that any group of five cells in the known configuration would be brought into each of the 32 possible states only once. A great deal of research effort was required to fulfill this condition. The authors identified this optimal solution intuitively, but in future research, they will try to identify other solutions through search methods specific to artificial intelligence.