Further Results on Bijective Product k-Cordial Labeling
Abstract
1. Introduction
2. Preliminaries
- There is a bijective labeling such that , and .
- There is a bijective labeling such that , and .
- ;
- g is a k-to-1 labeling; that is, for ;
- for and .
- (a)
- Suppose , where . We label by for and by for . Since , , , and , the induced label for the edge or is , for . This is the required labeling.
- (b)
- Suppose , where . Similar to the above case, we label by and by for . This is the required labeling.
- for and ;
- for .
| Vertex labeling | Induced edge labeling | |
| (3, 0, 4, 1, 5, 2, 0, 3, 1, 4, 2, 5, 3, 0, 4, 1, 5, 2) | (3, 4, 5, 0, 1, 2, 3, 4, 5, 0, 1, 2, 3, 4, 5, 0, 1) | |
| (0, 3, 1, 4, 2, 5, 3, 0, 4, 1, 5, 2) | (3, 4, 5, 0, 1, 2, 3, 4, 5, 0, 1) |
| Vertex labeling | Induced edge labeling | |
| (3, 0, 4, 1, 5, 2, 0, 3, 1, 4, 2, 5, 3, 0, 4, 1, 5, 2, 0) | (3, 4, 5, 0, 1, 2, 3, 4, 5, 0, 1, 2, 3, 4, 5, 0, 1, 2) | |
| (0, 3, 1, 4, 2, 5, 3, 0, 4, 1, 5, 2, 0) | (3, 4, 5, 0, 1, 2, 3, 4, 5, 0, 1, 2) |
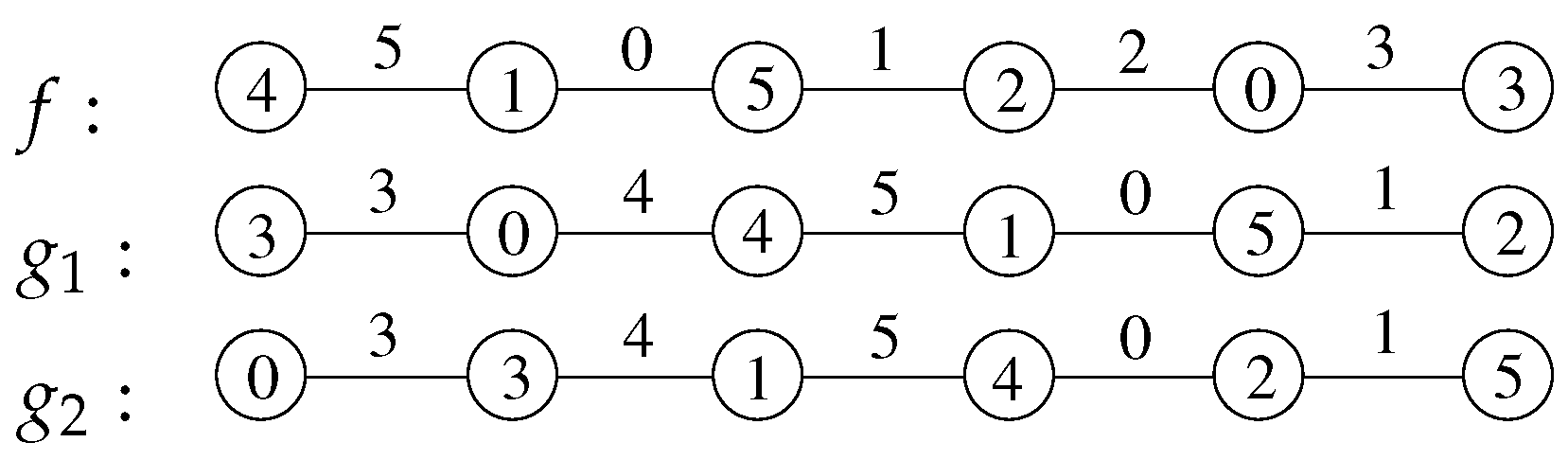
3. Bijective Product Prime-Cordial Labelings for Paths
- (a)
- Suppose . Let and . Let g be the labeling for R defined in Corollary 2 by letting .Similar to Theorem 5, we define a labeling . In this case, and . Then for and , and for . The previous two sentences mean that for . Thus, is a -product cordial labeling for , which satisfies condition (1). From Theorem 4, is bijective product -cordial.
- (b)
- Let be the -product cordial labeling of defined in Case (a). We extend to by labeling the last vertex of by 2. We still denote the -product cordial labeling of as . Then for ; and for ; and . Thus, is a -product cordial labeling for , which satisfies condition (1). From Theorem 4, is bijective product -cordial.
- (c)
- Let be the -product cordial labeling for defined in Theorem 5, where . Now, we delete the first vertex of , which is labeled by 0. We still denote the -product cordial labeling of as . Namely, and for , and for , and , where a is a primitive root of .
4. Bijective Product -Cordial Labeling of Path and Cycle, Where
- (a)
- is bijective product π-cordial for .
- (b)
- Suppose and . is bijective product π-cordial.
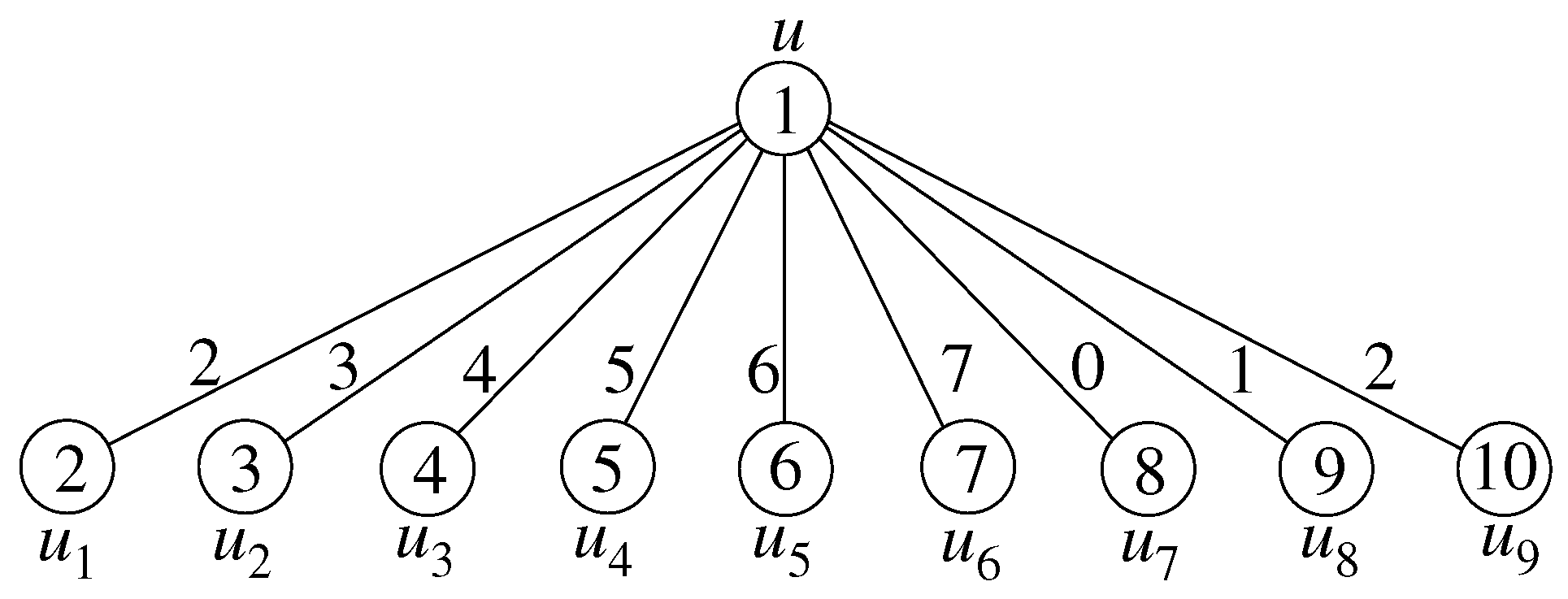
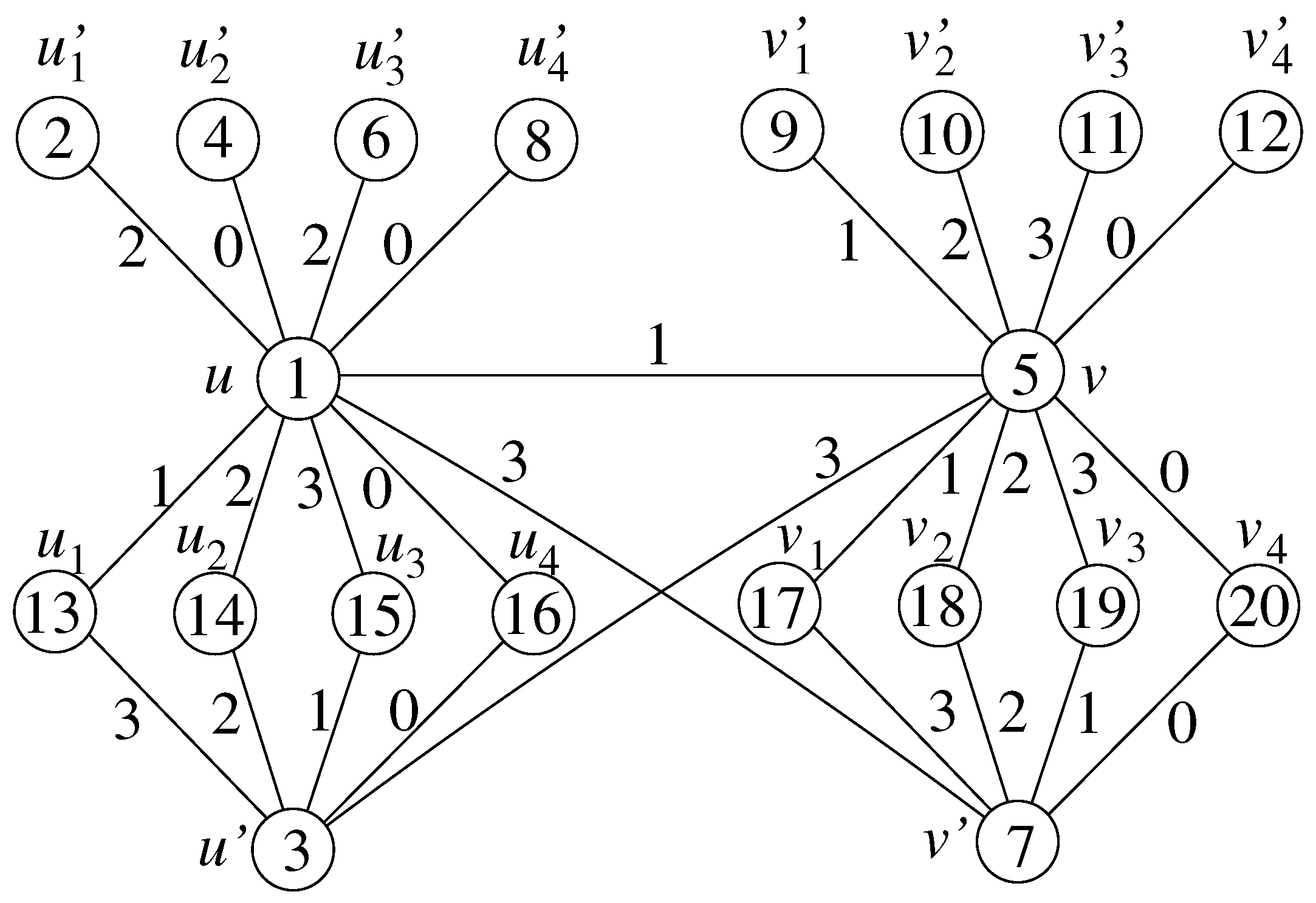
5. Bijective Product -Cordial Labeling of Star and Symmetric Bistar
- Case 1:
- For , define , , and .
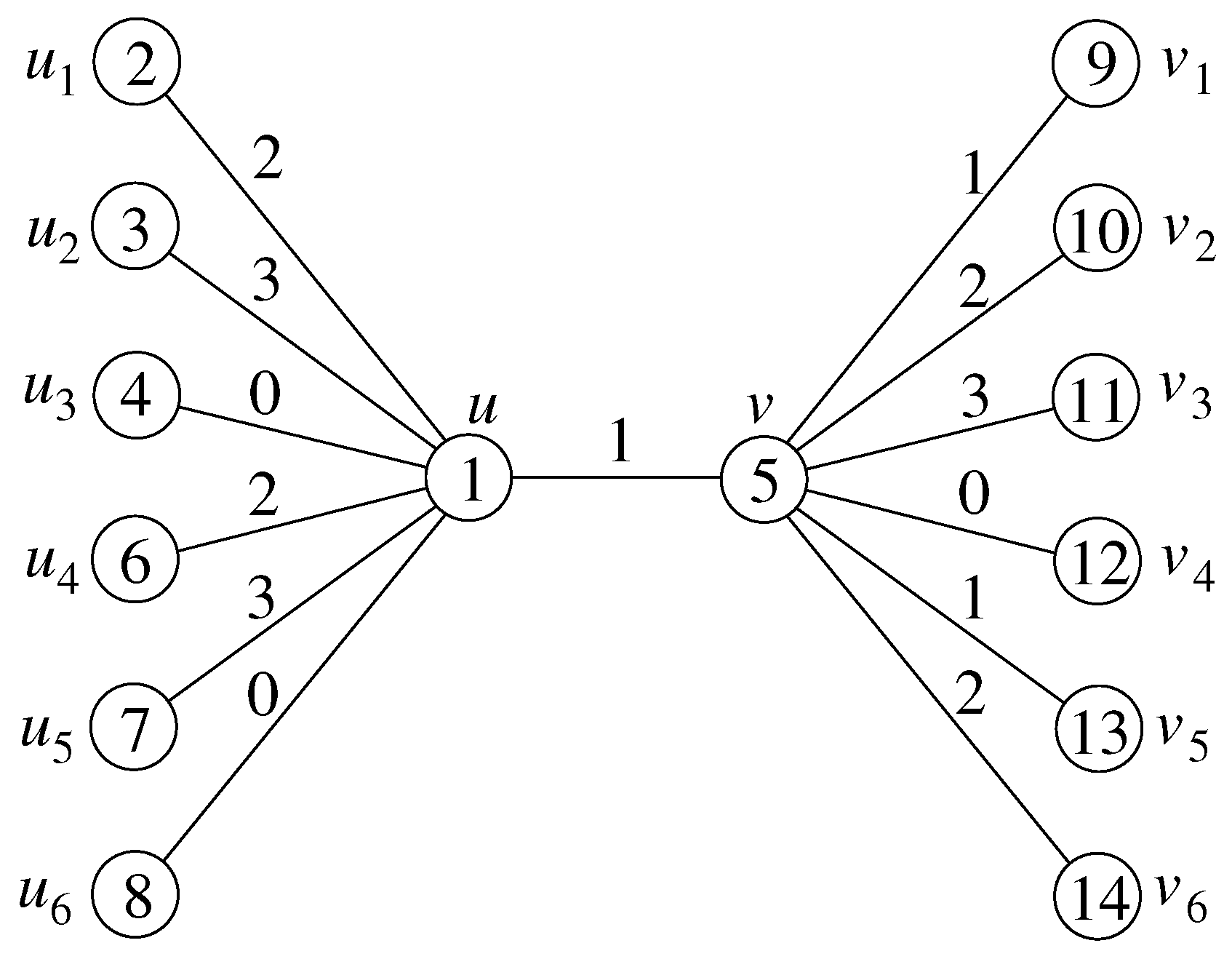
- Case 2:
- For , define , , , , and .
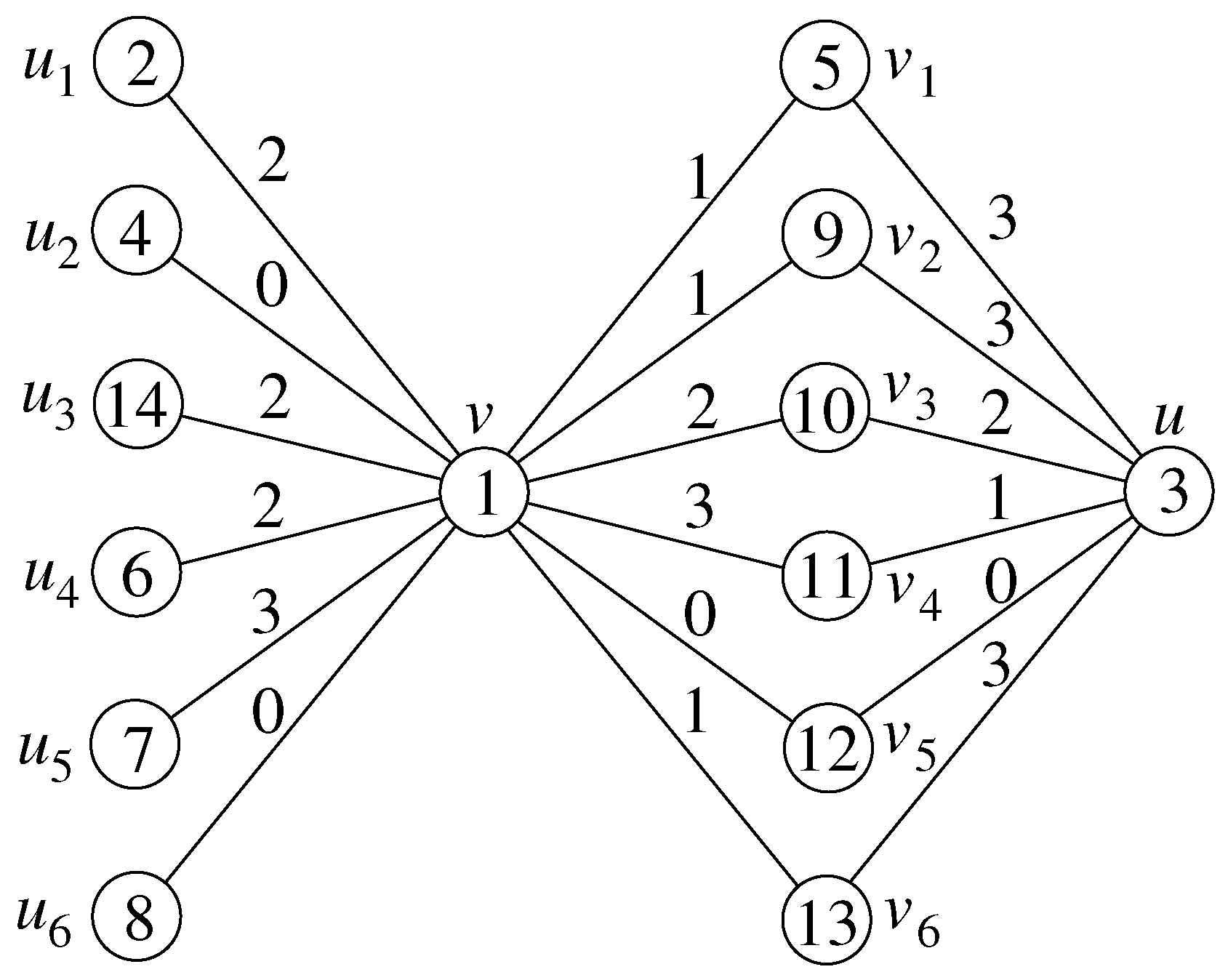
- Case 3:
- For , define , , , , , for if , , and for .Before taking modulo 4, the sets and .Since ,Now . Hence f is a bijective product 4-cordial labeling for .
- For , define , , , , , , and . Then the set (multiset) of edge labels is .
- For , define , , , , , , , , , , and . Then the set of edge labels is .
- For , define , , , , , , , and if , .for , for andfor .
- Firstly, we have , , , , and .When , the set .Thus for .
- The set .
- Since , the set and the set .
- Since , .
- Since , .
Now the set of all induced edge labels is congruent to modulo 4.Suppose , . Then , where means m copies of .Suppose , . Then .
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bondy, J.A.; Murty, U.S.R. Graph Theory with Applications; American Elsevier: New York, NY, USA, 1976. [Google Scholar]
- Rosa, A. On certain valuations of the vertices of a graph. In Theory of Graphs (International Symposium, Rome, July 1966); Dunod Gordon & Breach Science Publishers, Inc.: Paris, France, 1967; pp. 349–355. [Google Scholar]
- Gallian, J.A. A dynamic survey of graph labeling. Electron. J. Combin. 2024, 1, DS6. [Google Scholar] [CrossRef] [PubMed]
- Cahit, I. Cordial graphs: A weaker version of graceful and harmonious graphs. Ars Combin. 1987, 23, 201–207. [Google Scholar]
- Sundaram, M.; Ponraj, R.; Somasundaram, S. Product cordial labeling of graphs. Bull. Pure Appl. Sci. 2004, 23E, 155–163. [Google Scholar]
- Ponraj, R.; Sivakumar, M.; Sundaram, M. k-Product cordial labeling of graphs. Int. J. Contemp. Math. Sci. 2012, 7, 733–742. [Google Scholar]
- Shiu, W.C.; Santrin Sabibha, R.; Jeyanthi, P.; Jeya Daisy, K.; Lau, G.C. Bijective product and product square k-cordial labeling of graphs. Jordan J. Math. Stat. 2024, 17, 391–400. [Google Scholar]
| r | f for or | for | for | |
|---|---|---|---|---|
| 7 | 4 | 1, 2, 3, 4 | 2, 6, 5 | 2, 6, 5, 4 |
| 5 | 1, 2, 5, 3, 4 | 2, 3, 1, 5 | 2, 3, 1, 5, 4 | |
| 11 | 4 | 1, 2, 3, 4 | 2, 6, 1 | 2, 6, 1, 4 |
| 5 | 1, 2, 3, 4, 5 | 2, 6, 1, 9 | 2, 6, 1, 9, 5 | |
| 6 | 1, 2, 3, 6, 5, 4 | 2, 6, 7, 8, 9 | 2, 6, 7, 8, 9, 4 | |
| 7 | 1, 7, 2, 3, 4, 6, 5 | 7, 3, 6, 1, 2, 8 | 7, 3, 6, 1, 2, 8, 5 | |
| 8 | 1, 8, 7, 2, 3, 6, 4, 5 | 8, 1, 3, 6, 7, 2, 9 | 8, 1, 3, 6, 7, 2, 9, 5 | |
| 9 | 1, 2, 7, 9, 3, 4, 5, 8, 6 | 2, 3, 8, 5, 1, 9, 7, 4 | 2, 3, 8, 5, 1, 9, 7, 4, 6 | |
| 13 | 5 | 1, 2, 3, 4, 5 | 2, 6, 12, 7 | 2, 6, 12, 7, 5 |
| 6 | 1, 2, 4, 5, 6, 3 | 2, 8, 7, 4, 5 | 2, 8, 7, 6, 4, 3 | |
| 7 | 1, 2, 4, 3, 6, 5, 7 | 2, 8, 12, 5, 4, 9 | 2, 8, 12, 5, 4, 9, 7 | |
| 8 | 1, 2, 8, 4, 3, 6, 5, 7 | 2, 3, 6, 12, 5, 4, 9 | 2, 3, 6, 12, 5, 4, 9, 7 | |
| 9 | 1, 4, 2, 8, 3, 6, 9, 5, 7 | 4, 8, 3, 11, 5, 2, 6, 9 | 4, 8, 3, 11, 5, 2, 6, 9, 7 | |
| 10 | 1, 7, 10, 9, 4, 6, 5, 3, 2, 8 | 7, 5, 12, 10, 11, 4, 2, 6, 3 | 7, 5, 12, 10, 11, 4, 2, 6, 3, 8 | |
| 11 | 1, 5, 7, 6, 9, 3, 10, 2, 4, 8, 11 | 5, 9, 3, 2, 1, 4, 7, 8, 6, 10 | 5, 9, 3, 2, 1, 4, 7, 8, 6, 10, 11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bashammakh, S.A.; Shiu, W.C.; Sabibha, R.S.; Jeyanthi, P.; Abdel-Aal, M.E. Further Results on Bijective Product k-Cordial Labeling. Mathematics 2025, 13, 2451. https://doi.org/10.3390/math13152451
Bashammakh SA, Shiu WC, Sabibha RS, Jeyanthi P, Abdel-Aal ME. Further Results on Bijective Product k-Cordial Labeling. Mathematics. 2025; 13(15):2451. https://doi.org/10.3390/math13152451
Chicago/Turabian StyleBashammakh, Sabah A., Wai Chee Shiu, Robinson Santrin Sabibha, Pon Jeyanthi, and Mohamed Elsayed Abdel-Aal. 2025. "Further Results on Bijective Product k-Cordial Labeling" Mathematics 13, no. 15: 2451. https://doi.org/10.3390/math13152451
APA StyleBashammakh, S. A., Shiu, W. C., Sabibha, R. S., Jeyanthi, P., & Abdel-Aal, M. E. (2025). Further Results on Bijective Product k-Cordial Labeling. Mathematics, 13(15), 2451. https://doi.org/10.3390/math13152451







