Optimization Method for Reliability–Redundancy Allocation Problem in Large Hybrid Binary Systems

Abstract

This paper addresses a well-known research topic in the design of complex systems, specifically within the class of reliability optimization problems (ROPs). It focuses on optimal reliability–redundancy allocation problems (RRAPs) for large binary systems with hybrid structures. Two main objectives are considered: (1) to maximize system reliability under cost and volume constraints, and (2) to achieve the required reliability at minimal cost under a volume constraint. The system reliability model includes components with only two states: normal operating or failed. High reliability can result from directly improving component reliability, allocating redundancy, or using both approaches together. Several redundancy strategies are covered: active, passive, hybrid standby with hot, warm, or cold spares, static redundancy such as TMR and 5MR, TMR structures with control logic and spares, and reconfigurable TMR/Simplex structures. The proposed method uses a zero–one integer programming formulation that applies log-transformed reliability functions and binary decision variables to represent subsystem configurations. The experimental results validate the approach and confirm its efficiency.

1. Introduction

Reliability optimization problems (ROPs) encountered in the design of complex systems are some of the most well-known operational research topics, to which researchers are still paying special attention today [1,2,3,4,5]. These optimization problems aim to improve system reliability and other indicators, such as volume or weight, and reduce costs as much as possible.

In the design of complex systems with a hybrid structure, when formulating an optimization problem of the ROP-type, several aspects must be taken into account, namely, (1) the type of subsystems (binary or multi-state); (2) the type of redundancy for each subsystem, technically appropriate, which can be static (e.g., TMR or 5MR), dynamic/switchable (with active or standby components), or hybrid (e.g., a reconfigurable redundant TMR/Simplex structure, also provided with cold-maintained spare components [6]); and (3) the reliability improvement way for each subsystem, namely by directly increasing reliability and/or by providing a higher level of fault tolerance based on redundancy, etc.

Depending on the way in which reliability is increased, ROPs are divided into three categories [7]:

• $Reliability Allocation Problems$ where the solution directly or indirectly reflects component reliability for each subsystem;
• $Redundancy Allocation Problems$ ($\mathrm{R}\mathrm{A}\mathrm{P}\mathrm{s}$) where the solution concerns the number of components for each subsystem;
• $Reliability-Redundancy Allocation Problems \left(\mathrm{R}\mathrm{R}\mathrm{A}\mathrm{P}\mathrm{s}\right)$ where the decision variables reflect both component reliability and the level of redundancy for each subsystem.

Research has shown that the most difficult optimization problems are the RAP and especially RRAP types. This paper addresses RRAP-type optimization problems. RRAPs involve NP-hard search algorithms with high complexity, as the solution space is extremely large.

This topic is extensively covered in the literature. For comprehensive overviews, the authors recommend the studies [1,2,7,8,9,10], which present the reliability models considered, the optimization problems involved in the design of redundant systems, and the methods for addressing these complex problems.

Among the elements that greatly influence the difficulty of RAP optimization problems, and especially RRAP ones, the following should be mentioned first:

• The number of subsystems ($n$) as a measure of system complexity;
• The reliability model structure: homogeneous or heterogeneous (i.e., hybrid structure [4,6]; mixed redundancy strategy [11,12,13]; robust design/robust redundancy allocation problem [14,15]);
• The type of components at the subsystem level: with identical or different components (i.e., heterogeneous components [16,17,18]; component mixing [11,13]).
• The type of optimization problem: single-objective [6,19] (the usual case), or multi-objective [3,20,21,22].
• The type of subsystems: binary state (the usual case) [6,7], or multi-state [23].

To master the complexity of these optimization problems, various techniques can be applied, namely, intuitive methods [24,25,26,27]; analytical methods based on Lagrange multipliers and branch-and-bound techniques, especially for systems with active redundancy [28,29,30]; dynamic programming, especially for low complexity systems [26,31,32]; heuristic methods [25,26,33,34,35,36]; evolutionary algorithms [4,19,37,38,39,40,41,42]; and linear programming methods [2,6,43,44].

In the case of large systems, the difficulty of ROPs grows fast, and intensive research efforts are currently being made to master the complexity of these issues [2]. Furthermore, reliability models are increasingly complex to cover a wide range of reliability improvement techniques encountered in practice, for which these issues are even more complex [2,4,6,16,17,18]. Such an extended reliability model which considers complex systems with hybrid structure is considered in this work.

In some previously cited studies, ROPs are formulated considering redundant systems with hybrid redundancy strategies and/or reliability models with heterogeneous components, which means that each component of a subsystem may have its own failure rate. In this work, we consider only the case where subsystems include homogeneous components, but we extend ROPs to cover several redundancy strategies, including static redundancy, dynamic redundancy or reconfigurable structures such as TMR/Simplex with cold-maintained spare components. Our limitation simplifies the reliability assessment but does not significantly reduce the complexity of the optimization problems. Based on previous results on some RAP optimization problems [6], where the zero–one integer programming method was found to be the most efficient, the authors use it again to solve the RRAPs considered in this paper. However, in this case, this approach requires more elaborate mathematical modeling.

This study addresses the reliability–redundancy allocation problem in large hybrid binary systems by developing a formal optimization approach that jointly considers both redundancy strategies and direct reliability improvement of components. The objective is twofold: first, to maximize system reliability under given cost and volume constraints, and second, to minimize the total cost while ensuring a required reliability threshold. To achieve this, the RRAP is modeled using a 01IP formulation that encodes subsystem configurations as binary decision variables. This formulation enables efficient resolution of the complex trade-offs inherent in reliability optimization for large-scale, constrained systems.

The two optimization problems both fall within the broader context of reliability engineering and systems optimization, particularly as applied in safety-critical or resource-constrained domains. The first problem, i.e., maximizing reliability under cost and volume constraints, can be relevant in fields such as aerospace, defense, or medical devices, where system failure is unacceptable but resources are limited. The second problem, i.e., minimizing cost while meeting a reliability threshold, can apply to areas such as telecommunications or industrial automation, where budget constraints dominate but reliability cannot fall below regulatory or operational standards.

The work is organized as follows: Section 2 presents the problem description of the issue addressed. The types of redundancy considered in this work and the models or equations used for reliability assessment are given in Section 3. Related works are presented in Section 4. The proposed method for these optimization problems, also illustrated by a concrete example, is described in Section 5. The experimental results are presented in Section 6. This paper concludes with Section 7, where final remarks and some ideas regarding future work are presented.

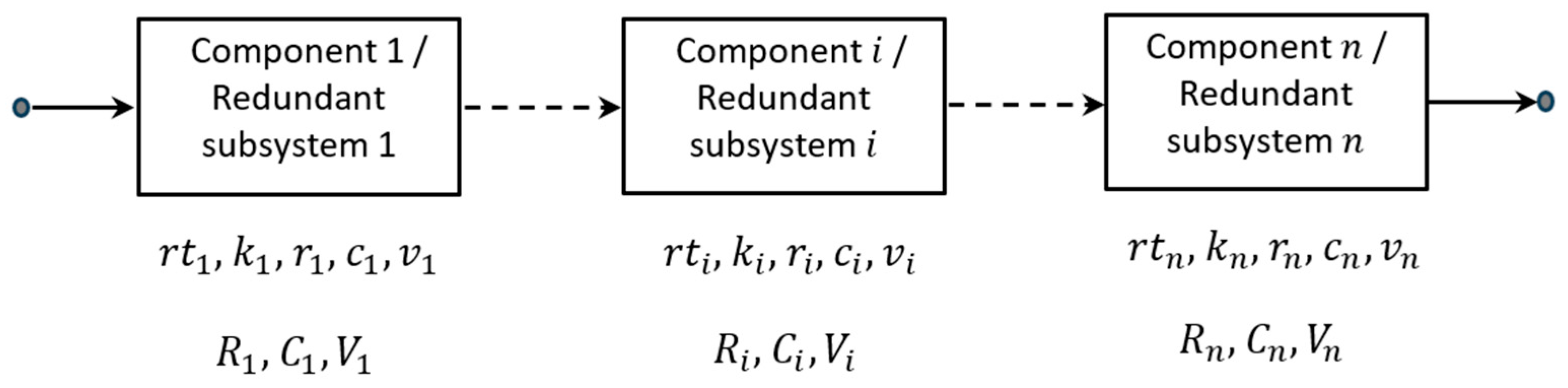
2. Problem Description

For non-redundant systems with many components, reliability is generally low, and to achieve a certain reliability imposed by the design specifications, reliability improvements are required at least for the components with lower reliability. To this end, one can consider a direct increase in reliability by purchasing components with increased reliability, ensuring a certain level of fault tolerance based on redundancy, or a solution that combines both approaches to improve reliability. Under these conditions, the system reliability model consists of a chain of components and/or redundant subsystems, as shown in Figure 1.

The type of redundancy for each subsystem depends on the technical characteristics and the designer’s choice and can be static, dynamic or hybrid, as presented in the next section.

Typically, in ROPs, the criteria may be reliability, cost, weight and/or volume. One or more criteria are used to define the objective function, while the others can be considered constraints [26]. In this paper, the criteria considered are reliability, cost and volume. Under these conditions, when designing complex systems, the following two optimization problems often appear in practice:

(a)

Maximizing system reliability under cost and volume constraints;

(b)

Achieving the required reliability at the lowest possible cost and possibly under volume constraints.

In the first problem, one needs to maximize the reliability function:

$$R_{rs}\left(R_1,R_2,\cdots ,R_n\right)=\prod _{i=1}^n{R}_i$$

(1)

subject to the cost constraint:

$$C_{rs}\left(C_1,C_2,\cdots ,C_n\right)=\sum _{i=1}^n{C}_i\le C_{max}$$

(2)

and the volume constraint:

$$V_{rs}\left(V_1,V_2,\cdots ,V_n\right)=\sum _{i=1}^n{V}_i\le V_{max}.$$

(3)

In the second optimization problem, one needs to minimize the cost function:

$$C_{rs}\left(C_1,C_2,\cdots ,C_n\right)=\sum _{i=1}^n{C}_i$$

(4)

subject to the reliability constraint:

$$R_{rs}\left(R_1,R_2,\cdots ,R_n\right)=\prod _{i=1}^n{R}_i\ge R_{req},$$

(5)

and possibly the volume constraint (3).

For example, if the same type of redundancy is adopted for all subsystems, where the primary component and spare components operate in parallel under the same conditions (i.e., active redundancy), a series-parallel reliability model is appropriate. In this case, the reliability function, the cost function and the volume function are expressed by the following equations:

$$R_{rs}\left(k_1,r_1,k_2,r_2,\dots ,k_n,r_n\right)=1-\prod _{i=1}^n{(1-r_i)}^{k_i}$$

(6)

$$C_{rs}\left(k_1,c_1,k_2,c_2,\dots ,k_n,c_n\right)=\sum _{i=1}^n{c}_i{k}_i$$

(7)

$$V_{rs}\left(k_1,v_1,k_2,v_2,\dots ,k_n,v_n\right)=\sum _{i=1}^n{v}_i{k}_i$$

(8)

One needs to determine the values $k_1$, $k_2$, …, $k_n$ that maximize the reliability function (6) respecting the cost constraint (2) and the volume constraint (3), or minimize the cost function (7) while ensuring the reliability condition (5) and respecting the volume constraint (3), as appropriate.

Regarding the possibility of directly increasing the reliability of a component, this study assumes that each step of improvement halves the probability of failure. Thus, through an appropriate number of reliability growth steps, the reliability of a component can reach the desired level, as illustrated by an example in Figure 2.

Consequently, after a number of direct reliability allocation steps (${sir}_i$), the current reliability for a component of type $i$ is calculated as presented in Algorithm 1.

Algorithm 1: The computation of the reliability of a subsystem with direct reliability allocation steps.

$r_i={\_r}_i$ for $s=1:{sir}_i$ do ∟ $r_i=r_i+(1-r_i)/2$

Regarding the component cost increase after a series of direct reliability allocation steps, the scenarios are countless, but regarding the actual optimization problem, differences appear only related to the calculation of this cost. In our study, the following scenario was considered.

Let us consider the component $i, i\in \left\{1, \dots , n\right\},$ for which the initial cost (${\_c}_i$) and the cost increase factor for any step of reliability allocation (${\rho }_i$) are given. The additional cost for a step of direct reliability improvement (${\Delta c}_i$) can be expressed as a function of the initial cost of the component or as a function of the current cost ($c_i$).

In the first case (alternative 1), after a number of reliability allocation steps (${sir}_i)$, the cost for a component of type $i$ is calculated as follows:

$${\Delta c}_i={\_c}_i·{\rho }_i;$$

(9)

$$c_i={\_c}_i+{sir}_i·{\Delta c}_i={\_c}_i\left(1+{sir}_i·{\rho }_i\right)$$

(10)

In the second case (alternative 2), the method of determining the cost is presented in the form of a pseudocode, as presented in Algorithm 2.

Algorithm 2: The computation of the cost of a subsystem with direct reliability allocation steps (alternative 2).

$c_i={\_c}_i$ for $s=1:{sir}_i$ do ∟ $c_i=c_i+{\rho }_i{\ast c}_i$

Both alternatives are considered in our study.

3. Types of Redundancy

As in the RAP-type problems presented in [6], in order to cover most of the cases encountered in practice, the following types of redundancy are considered in this RRAP optimization problem, namely:

• Active redundancy $\left(rt=\mathrm{A}\right)$;
• Passive redundancy (or cold standby redundancy) $\left(rt=\mathrm{B}\right)$;
• Hybrid standby redundancy with a hot spare $\left(rt=\mathrm{C}\right)$ or a warm one;
• $\left(rt=\mathrm{D}\right)$ and possibly other CSCs;
• Hybrid redundancy consisting of a TMR structure with control facilities and possibly other CSCs $\left(rt=\mathrm{E}\right);$
• Static redundancy structure implementing an $n$ out of $2n-1$ majority logic: TMR or 5MR $\left(rt=\mathrm{F}\right);$
• Reconfigurable TMR/Simplex structure with possibly other CSCs $\left(rt=\mathrm{G}\right)$.

This section presents reliability models and equations used to assess reliability for each type of redundancy. First, according to assumption A2, we consider that the time to failure has a negative-exponential distribution; so, the following equations hold:

$$r(\lambda ,T)=e^{-\lambda T}$$

(11)

and

$$\lambda T=-\ln r.$$

(12)

3.1. Active Redundancy ($\mathit{t}\mathit{r}=A$)

In this case, when all components work in parallel under the same working conditions, the reliability model is a parallel one; so, the well-known equation applies:

$$R(k,r)=1-{(1-r)}^k,k=2,3,\cdots$$

(13)

3.2. Passive Redundancy ($\mathit{t}\mathit{r}=B$)

In the case of passive redundancy, only one component is in operation, while all other $k - 1$ spare components are on standby. This means that a spare component does not fail until it is brought into service. The following equation holds for this model:

$$R\left(k,\lambda ,T\right)=\sum _{j=0}^{k-1}{\displaystyle \frac{{\left(\lambda T\right)}^j}{j!}}{e}^{-\lambda T},\hspace{1em}k\ge 2.$$

(14)

It should be noted that, in this case, the reliability function includes the first $k$ terms of the Poisson distribution of the parameter $\lambda T$ [26]. Considering Equations (11) and (12), the reliability function becomes:

$$R\left(k,r\right)=r\sum _{j=0}^{k-1}{\displaystyle \frac{{\left(-\ln r\right)}^j}{j!}},\hspace{1em}k\ge 2.$$

(15)

3.3. Hybrid Standby Redundancy with a Hot ($\mathit{t}\mathit{r}=\mathit{C}) or a Warm (\mathit{t}\mathit{r}=\mathit{D}$) Spare and Possibly Other CSCs

In this type of standby redundancy, one component is operational, a spare component is active or kept in warm conditions, and possibly other spare components are kept in a passive state (CSCs). A hot or warm component may fail before it is put into operation. Compared to the failure rate of the component in operation, its failure rate is of the form $\alpha \lambda , 0<\alpha \le 1$. To obtain a reliability function for such a redundant structure, a Markov model can be used. The complexity of the model depends on the total number of components, $k$, or more specifically, on the number of CSCs. A detailed presentation of these models can be found in [6]. The relations for calculating the reliability of the subsystem according to $k$ are given below.

Case 1. $k=2$

$$R\left(r,\alpha \right)=r+{\displaystyle \frac{1}{\alpha }}r\left(1-r^{\alpha }\right),\hspace{1em}0<\alpha \le 1.$$

(16)

Case 2. $k=3$

$$R\left(r,\alpha \right)={\displaystyle \frac{{\left(1+\alpha \right)}^2}{{\alpha }^2}}r-\left({\displaystyle \frac{1+2\alpha }{{\alpha }^2}}-{\displaystyle \frac{1+\alpha }{\alpha }}\ln r\right)r^{1+\alpha }, 0<\alpha \le 1.$$

(17)

Case 3. $k=4$

$$R\left(r,\alpha \right)={\displaystyle \frac{{\left(1+\alpha \right)}^3}{{\alpha }^3}}r-\left({\displaystyle \frac{1+3\alpha +3{\alpha }^2}{{\alpha }^3}}-{\displaystyle \frac{1+3\alpha +2{\alpha }^2}{{\alpha }^2}}\ln r+{\displaystyle \frac{{\left(1+\alpha \right)}^2}{2\alpha }}{\left(\ln r\right)}^2\right)r^{1+\alpha },\hspace{1em}0<\alpha \le 1.$$

(18)

3.4. TMR Structure with Control Facilities and Optionally Other CSCs ($\mathit{t}\mathit{r}=E$)

Another type of hybrid redundancy is considered in this case. More specifically, a TMR structure with control facilities constitutes the basic structure (i.e., static redundancy). Optionally, spare components maintained in a passive state can be provided (standby redundancy). This type of hybrid redundancy is illustrated in Figure 3.

The decision logic known as “voter” (and denoted by V in Figure 3) operates on the principle of 2 out of 3 majority logic. If one of the three operational components fails, the system continues to operate successfully, but fault tolerance is lost. The faulty component is indicated by the corresponding error signal. If this failed component is replaced with a spare, the fault tolerance from the beginning is restored. In this way, this hybrid redundant subsystem can tolerate one or more failed components, as the case may be.

The failure rate for the additional decision and control block, denoted by ${\lambda }_{dc}$, expressed based on the failure rate of the basic components, is of the form:

$${\lambda }_{dc}\left(\lambda ,\beta \right)={\displaystyle \frac{\lambda }{\beta }},\hspace{1em}\beta >0.$$

(19)

Consequently, for this decision and control block, the reliability function denoted by $r_{dc}$ can be calculated as follows:

$$r_{dc}\left({\lambda }_{dc},T\right)=e^{-{\lambda }_{dc}T},$$

(20)

or based on (19),

$$r_{dc}\left(\lambda ,\beta ,T\right)=e^{-{\displaystyle \frac{\lambda }{\beta }} T}={\left(e^{-\lambda T}\right)}^{{\beta }^{-1}},$$

(21)

or finally, based on (11),

$$r_{dc}\left(r,\beta \right)=r^{{\beta }^{-1}},\hspace{1em}\beta >0.$$

(22)

Regarding the reliability assessment of this redundant structure, when spare components are provided, this study is based on Markov models. More details about these models can be found in [6]. The reliability functions of the subsystem, depending on the level of redundancy (the number of CSCs) expressed by the variable $k$, are shown below.

• Case 1. TMR structure without standby redundancy

If the TMR structure is not provided with spare components (i.e., $k=3$), the redundant subsystem tolerates only one failed component. Under these conditions, the reliability function of the TMR structure has the following well-known expression:

$$R\left(r,r_{dc}\right)=\left(3r^2-2r^3\right)r_{dc},$$

(23)

or based on (22):

$$R\left(r,\beta \right)=\left(3r^2-2r^3\right)r^{{\beta }^{-1}},\hspace{1em}\beta >0.$$

(24)

• Case 2. TMR structure and one CSC

A subsystem with hybrid redundancy composed of a TMR structure and one CSC (i.e., $k=4$) tolerates two faulty components. In this case, the subsystem reliability as a function of $r$ and $\beta$ obtained based on a Markov chain model is given by the following equation:

$$R\left(r,\beta \right)=\left(9r^2-r^3\left(8-6\ln r\right)\right)r^{{\beta }^{-1}},\hspace{1em}\beta >0.$$

(25)

• Case 3. TMR structure and two CSCs

A redundant subsystem with hybrid redundancy composed of a TMR structure and two CSCs (i.e., $k=5$) tolerates three defective components. The reliability of the subsystem as a function of $r$ and $\beta$ is of the following form:

$$R\left(r,\beta \right)=\left(27r^2-r^3\left(26-24\ln r+9{\left(\ln r\right)}^2\right)\right)r^{{\beta }^{-1}},\hspace{1em}\beta >0.$$

(26)

3.5. Static Redundancy: TMR or 5MR ($\mathit{t}\mathit{r}=F$)

This type of static redundancy refers to the subsystems that operate on the principle of $n$ out of $2n-1$ majority logic. Depending on the level of reliability to be achieved, a TMR or 5MR structure is adopted. Consequently, in the optimization algorithm, for variable $k$, 1, 3 or 5 are the only valid values.

• Case 1. TMR structure

$Case 1$, for which $k=3,$ has already been treated in Section 3.4, The reliability function is given by Equation (24).

• Case 2. 5MR structure

A 5MR structure can tolerate up to two failed/down components; so, taking into account the three success variants, the reliability of this redundant structure as a function of $r$ can be expressed as follows:

$$R\left(r\right)=r^5+5r^4(1-r)+10r^3{(1-r)}^2.$$

(27)

In this case, the decision and control logic are more complex than that used for the TMR structure. Consequently, the failure rate, denoted by ${\lambda }_{dc}^{\prime }$, expressed based on the failure rate of the basic components, is considered as follows:

$${\lambda }_{dc}^{\prime }\left(\lambda ,\gamma \right)={\displaystyle \frac{\lambda }{\gamma }},\gamma >0,$$

(28)

where the reduction factor $\gamma$ is smaller than the $\beta$ factor used for the TMR structure.

Also, taking into account the possibility of failure of the decision and control logic, for which the reliability function is denoted by $r_{dc}^{\prime }$, the reliability of the entire 5MR structure as a function of $r$ and $r_{dc}^{\prime }$ has the following form:

$$R\left(r,r_{dc}^{\prime }\right)=\left(r^5+5r^4(1-r)+10r^3{(1-r)}^2\right)r_{dc}^{\prime }.$$

(29)

After an algebraic simplification of expression (29) and taking into account Equations (11) and (28), for the reliability function of the 5MR structure, the following equation finally results in the following:

$$R\left(r,\gamma \right)=\left(10r^3-15r^4+6r^5\right)r^{{\gamma }^{-1}},\hspace{1em}\gamma >0.$$

(30)

3.6. TMR/Simplex and Optionally Other CSCs ($\mathit{t}\mathit{r}=G$)

This hybrid redundant structure comprises a TMR configuration with control and reconfiguration facilities to which passive standby components (CSCs) can be added. Based on redundancy, the subsystem works successfully even if one of the components fails. In this case, the control logic generates an error signal that indicates the failed component. If the failed component is replaced with a spare one, the initial fault tolerance is restored.

Let us assume that this replacement is carried out quickly enough for the system to tolerate this short interruption. To improve reliability, when only two components operate normally, it is preferable for a single component to work, not both. This reconfigurable redundant structure is known as TMR/Simplex [45], p. 233, or TMR 3-2-1 [26], p. 152.

As with the other redundant structures, for the logic block of decision, control and reconfiguration, the failure rate denoted by ${\lambda }_{dcr}$ is expressed based on the failure rate of the basic components. Thus:

$${\lambda }_{dcr}\left(\lambda ,\delta \right)={\displaystyle \frac{\lambda }{\delta }}, \delta >0,$$

(31)

where $\delta <\beta$ (factor used for the classical TMR structure).

For the decision, control and reconfiguration logic, the reliability function denoted by $r_{dcr}$ is expressed as follows:

$$r_{dcr}\left({\lambda }_{dcr},T\right)=e^{-{\lambda }_{dcr}T},$$

(32)

or based on (31):

$$r_{dcr}\left(\lambda ,\delta ,T\right)=e^{-{\displaystyle \frac{\lambda }{\delta }}T}={\left(e^{-\lambda T}\right)}^{{\delta }^{-1}},\hspace{1em}\delta >0,$$

(33)

and finally, based on (11):

$$r_{dcr}\left(r,\delta \right)=r^{{\delta }^{-1}},\hspace{1em}\delta >0.$$

(34)

For a subsystem with a hybrid structure of this type, the reliability function depends on the degree of redundancy, or more precisely, on the number of spare components maintained in a passive state (CSCs), as shown below.

• Case 1. TMR/Simplex without standby redundancy

In the simplest version of the reconfigurable TMR/Simplex structure, where no spare components are provided (i.e., $k=3$), the reliability function is given by the well-known equation [45], p. 233:

$$R\left(r,r_{dcr}\right)=\left(1.5r-0.5r^3\right)r_{dcr}.$$

(35)

Based on (34), the equation becomes:

$$R\left(r,\delta \right)=\left(1.5r-0.5r^3\right)r^{{\delta }^{-1}},\hspace{1em}\delta >0.$$

(36)

• Case 2. TMR/Simplex with one CSC

For this case of hybrid redundancy, a Markov chain for reliability assessment can be found in [6]. The reliability of the redundant subsystem as a whole, which reflects the possibility of failure of both the basic components and the decision, control and reconfiguration logic, has the following expression:

$$R\left(r,r_{dcr}\right)=\left(2.25r-r^3(1.25-1.5\ln r)\right)r_{dcr}.$$

(37)

Based on (34), we can finally write:

$$R\left(r,\delta \right)=\left(2.25r-r^3(1.25-1.5\ln r\right))r^{{\delta }^{-1}},\hspace{1em}\delta >0.$$

(38)

• Case 3. TMR/Simplex with two CSCs

A reconfigurable redundant hybrid structure composed of a TMR/Simplex and two CSCs (i.e., $k=5$) tolerates three down components. The reliability of the entire subsystem as a function of $r$ and $\delta$ has the following form:

$$R\left(r,\delta \right)=\left(3.375r-0.125\left(19-30\mathit{ln}r+18{\left(\mathit{ln}r\right)}^2\right)r^3\right)r^{{\delta }^{-1}},\hspace{1em}\delta >0.$$

(39)

Remark 1.

As the level of redundancy is higher (i.e., the number of CSCs increases), the reliability function becomes strongly nonlinear (see, for example, (26), (30), (39)), which is likely to complicate the solution of the RRAP optimization problem addressed in this paper.

Remark 2.

The type of redundancy is most often adopted depending on the particularities of the component under consideration. For example, in the case of monitors, a spare component is obviously kept in a passive state. The problem is completely different in the case of a magnetic disk, where the most important requirement is the security of the stored data. In this case, an active redundancy reflected in a disk-mirroring architecture is required. Or, if we refer to a microcontroller integrated in a control system with high safety requirements, a static redundancy structure (TMR, for example) or a reconfigurable TMR/Simplex structure could be the right technical solution.

4. Related Work

Optimization problems involving the maximization of system reliability under constraints such as cost and/or volume, or conversely, the minimization of cost while meeting reliability and/or volume requirements, can be approached through several techniques. One analytical approach employs Lagrange multipliers, where reliability is reformulated into a different mathematical representation [19,28]. Solving the resulting algebraic system is feasible, but it depends on certain approximations that may reduce the precision of the solution. Additionally, since the method yields continuous (real-number) solutions, a subsequent conversion to discrete (integer) values is necessary, which can further compromise accuracy. As a result, heuristic methods are often more suitable for practical implementation. In the context of RAPs, Shooman [26] proposed a greedy algorithm that incrementally enhances system reliability. The process begins with the most basic system configuration and iteratively adds a component to the subsystem with the lowest reliability, provided the cost constraint is not violated.

Another heuristic, introduced by Misra [25], aims to quicken the allocation process using the observation that subsystems with higher reliability requirements should be assigned fewer components, whereas those with lower reliability should receive more. This method begins with an initial system configuration and progressively adds a component to each subsystem while satisfying the cost constraint. For the subsystem with the highest reliability, the allocation is final. The procedure continues with the remaining subsystems until further additions are no longer feasible within the imposed constraints. In the case of RRAP-type optimization problems, even heuristic approaches are much more complicated.

Several recent studies have introduced improved algorithms and formulations for reliability–redundancy optimization. The Enhanced Zebra Optimization Algorithm was developed to avoid premature convergence and improve exploration through strategies such as Levy flight and opposition-based learning [46].

Time-dependent failure behavior has also been addressed. One study proposed a genetic algorithm for redundancy allocation when component failure rates follow an Erlang distribution with time-varying parameters [47]. The results showed that optimal configurations can differ significantly when time dependence is taken into account.

In structural reliability optimization, an algebraic approach demonstrated that symmetric configurations in parallel systems and asymmetric ones in series–parallel systems consistently improve reliability without requiring knowledge of individual component reliabilities [48]. This insight is based on a new inequality that governs redundancy arrangements.

Other studies have focused on mission-specific systems. One approach proposed a redundancy optimization model for a command post phased-mission system divided into four operational stages [49]. The authors identified critical nodes using a multitasking node index and selected hot backup structures to maximize mission success.

Beyond redundancy optimization, techniques from artificial intelligence have been applied to uncertain environments. A fuzzy neural architecture search method was developed for defect recognition problems where data noise and uncertainty are significant [50]. The evolutionary search and fuzzy encoding strategy used there highlight how similar techniques might be adapted for uncertain reliability modeling.

In the field of real-time decision systems, researchers have proposed task allocation frameworks that combine reinforcement learning and predictive modeling in vehicular networks [51]. Although applied to edge computing, the hybrid algorithmic structure and focus on constrained resource optimization can provide relevant intuitions for system design with a focus on reliability.

In previous studies, the authors of the present paper compared different optimization methods for the two reciprocal problems: maximizing reliability under cost and/or volume constraints and minimizing cost under reliability and/or volume constraints. These methods include a standard evolutionary algorithm [19], and an enhanced variant of hill climbing known as “pairwise hill climbing” (PHC), which incorporates swapping operations of unit components between subsystems [28].

An original evolutionary algorithm called “cross-generational evolutionary algorithm with local improvements” (RELIVE) was also proposed, which combines local and global search, relies on various mutation types and has a population of varying size, where individuals survive and self-improve over several generations [6].

Additionally, the formulation of the problem as a quadratic unconstrained binary optimization (QUBO) was explored [43], which can be executed on the D-Wave quantum computer [52].

Furthermore, the formulation of the problem as linear programming, more precisely as a zero–one integer programming (01IP) problem, was assessed. Zero–one integer programming is a mathematical optimization technique in which decision variables are restricted to binary values, either 0 or 1. These variables usually represent inclusion or exclusion decisions, such as selecting components or assigning resources. The objective function and constraints are typically linear, and the solution must satisfy all constraints while optimizing the objective. 01IP is a special case of integer linear programming (ILP), an optimization method that seeks to maximize or minimize a linear objective function subject to linear constraints, where some or all variables must take integer values. This proved to be the best choice in terms of both time efficiency and solution quality, particularly for large instance problems, such as those involving 100 subsystems.

That is why the authors use 01IP again to solve the RRAPs considered in this paper. However, in this case, this approach requires more elaborate mathematical modeling. A formulation is created for the new problem, and the lpsolve v5.5.2 software [53] is employed to obtain the actual solutions. lpsolve is an open-source mixed-integer linear programming solver based on the revised simplex method and the branch-and-bound technique. It supports a variety of linear and integer programming formulations and is widely used in academic and industrial optimization applications due to its efficiency and reliability for large-scale combinatorial models. This approach can find the optimal solutions with high confidence, as proved by its ability to solve the converse optimization problem: maximizing reliability within a cost and/or volume constraints and then using that value to solve the reciprocal problem of minimizing cost with the imposed reliability found from the initial problem. When the solutions for both problems are identical, one can assert with high confidence that they represent the optimal solutions.

5. The Optimization Approach

As explained in Section 3, the maximization of the reliability with cost and volume constraints can be expressed as follows (repeated here for convenience):

$$\begin{array}{cc}\mathrm{Maximize}:\hfill & \\ & {\displaystyle \prod _{i=1}^n}{R}_i\\ \mathrm{Subject} \mathrm{to}\text{:}\hfill & \\ & \left\{\begin{array}{l}{\displaystyle \sum _{i=1}^n}{C}_i\le C_{max}\\ {\displaystyle \sum _{i=1}^n}{V}_i\le V_{max}\end{array}\right.\end{array}$$

(40)

The 01IP formulation expands on the idea proposed by the authors in [43]. To derive it from the nonlinear formulation in Equation (40), we apply two steps: a logarithmic transformation and discretization using binary decision variables.

Since the natural logarithm is a strictly increasing function, maximizing the product is equivalent to maximizing the sum of the logarithms: $\mathit{max}:\sum \mathit{log}{R}_i$. This transformation converts the nonlinear multiplicative objective into an additive form that is easier to handle in optimization models.

Next, for each subsystem $i$, we enumerate a finite set of feasible configuration pairs that contain the number of components allocated to the subsystem and the number of reliability improvement steps applied through direct allocation. For each pair, we introduce a binary decision variable 0$x_{iks},$ which equals 1 if subsystem $i$ uses a certain configuration, and 0 otherwise.

More specifically, $x_{ijk}\in \left\{0, 1\right\}$, $\forall i\in \left\{1,\hspace{0.33em}\dots ,\hspace{0.33em}n\right\}$, $\forall j\in \left\{1,\hspace{0.33em}\dots ,\hspace{0.33em}{k}_{max}\right\}$, $\forall k\in \left\{1,\hspace{0.33em}\dots ,\hspace{0.33em}{s}_{max}\right\}$ are binary variables that show that for a subsystem $i$, $j$ components and $k$ steps of direct reliability allocation are needed to maximize reliability. Let $R_i(j, k)$ denote the reliability of subsystem $i$when it contains $j$ components for which $k$ direct reliability improvement steps were first applied. For a subsystem $i$, only one solution is possible, i.e., its binary indicator must be 1, and the rest must be 0. Accordingly, Equation (40) is transformed into:

$$\begin{array}{cc}\mathrm{Maximize}\text{:}\hfill & \\ & {\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^{k_{max}}}{\displaystyle \sum _{k=1}^{s_{max}}}{x}_{ijk}·\mathit{log}{R}_i(j,k)\\ \mathrm{Subject} \mathrm{to}\text{:}\hfill & \\ & \left\{\begin{array}{l}{\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^{k_{max}}}{\displaystyle \sum _{k=1}^{s_{max}}}{x}_{ijk}·C_i(j,k)\le C_{max}\\ {\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^{k_{max}}}{\displaystyle \sum _{k=1}^{s_{max}}}{x}_{ijk}·V_i\left(j\right)\le V_{max}\\ {\displaystyle \sum _{j=1}^{k_{max}}}{\displaystyle \sum _{k=1}^{s_{max}}}{x}_{ijk}=1,\forall i\in \left\{1, \dots , n\right\}\end{array}\right.\end{array}$$

(41)

Conversely, the minimization of the cost of the redundant system with a required reliability and volume bound can be expressed as follows:

$$\begin{array}{cc}\mathrm{Minimize}\text{:}\hfill & \\ & {\displaystyle \sum _{i=1}^n}{C}_i\\ \mathrm{Subject} \mathrm{to}\text{:}\hfill & \\ & \left\{\begin{array}{l}{\displaystyle \prod _{i=1}^n}{R}_i\ge R_{max}\\ {\displaystyle \sum _{i=1}^n}{V}_i\le V_{max}\end{array}\right.\end{array}$$

(42)

Its corresponding 01IP formulation is as follows:

$$\begin{array}{cc}\mathrm{Minimize}\text{:}\hfill & \\ & {\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^{k_{max}}}{\displaystyle \sum _{k=1}^{s_{max}}}{x}_{ijk}·C_i(j,k)\\ \mathrm{Subject} \mathrm{to}\text{:}\hfill & \\ & \left\{\begin{array}{l}{\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^{k_{max}}}{\displaystyle \sum _{k=1}^{s_{max}}}{x}_{ijk}·\mathit{log}{R}_i(j,k)\ge \mathit{log}{R}_{req}\\ {\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^{k_{max}}}{\displaystyle \sum _{k=1}^{s_{max}}}{x}_{ijk}·V_i\left(j\right)\le V_{max}\\ {\displaystyle \sum _{j=1}^{k_{max}}}{\displaystyle \sum _{k=1}^{s_{max}}}{x}_{ijk}=1,\forall i\in \left\{1, \dots , n\right\}\end{array}\right.\end{array}$$

(43)

The meaning of the variables is the same as in Equation (41). Equation (43) is derived by reversing the objective of Equation (41). Instead of maximizing system reliability under cost and volume constraints, we now minimize total system cost while enforcing a reliability and a volume constraint. The structure of the model remains the same: each subsystem must adopt exactly one configuration from a finite set of feasible pairs, where the binary variables x_ijk indicate which configuration is selected in the optimal solution.

To summarize the proposed optimization procedure, Figure 4 presents a flowchart that outlines the sequence of steps used to solve the RRAP using the zero–one integer programming method. It depicts the process from initialization and configuration generation to specific problem construction, solution computation, and final output.

Examples

Because the formulations are somewhat abstract, in this subsection, we will present a few concrete examples of simple problems to illustrate how the equations above capture the ideas of objective functions and constraints.

We will consider only three subsystems with active redundancy. Their reliability is computed using Equation (13) and Algorithm 1, and their cost is computed using Equations (7) and (10).

The characteristics of the system are as follows: $\mathbf{r} = [0.8, 0.95, 0.99]$, $\mathbf{c}=[5, 5, 5]$. At first, we will not consider the possibility of direct reliability allocation nor the volume constraint. The objective function and the constraints include terms that correspond to all subsystems. We will represent these terms with colors: red for the first subsystem, green for the second, and blue for the third.

The objective function is as follows:

$$\begin{array}{cc}\max \text{:}& -2.23·{10}^{-1}·x_1-4.08·{10}^{-2}·x_2-8.03·{10}^{-3}·x_3\\ & -5.13·{10}^{-2}·x_4-2.50·{10}^{-3}·x_5-1.25·{10}^{-4}·x_6\\ & -1.01·{10}^{-2}·x_7-1.00·{10}^{-4}·x_8-1.00·{10}^{-6}·x_9\end{array}$$

(44)

The coefficients are the ones computed in

Table 1. The computation of the reliability terms of the subsystems and their natural logarithm.

0.800, 0.000, 0.000	−2.23144 · 10−1 · x1
0.960, 0.000, 0.000	−4.08220 · 10−2 · x2
0.992, 0.000, 0.000	−8.03217 · 10−3 · x3
0.000, 0.950, 0.000	−5.12933 · 10−2 · x4
0.000, 0.998, 0.000	−2.50313 · 10−3 · x5
0.000, 1.000, 0.000	−1.25008 · 10−4 · x6
0.000, 0.000, 0.990	−1.00503 · 10−2 · x7
0.000, 0.000, 1.000	−1.00005 · 10−4 · x8
0.000, 0.000, 1.000	−1.00000 · 10−6 · x9

.

Each row corresponds to one coefficient. The first row suggests that the first subsystem has no redundant components. Its reliability is the initial one, equal to 0.8. The second row corresponds to one redundant component for the first subsystem, whose reliability becomes: $R_1=1-{\left(1-r_1\right)}^2=1-{\left(1-0.8\right)}^2 =0.96$. Similarly, the third row reflects the reliability with two redundant components: $R_1=1-{\left(1-r_1\right)}^3=1-{\left(1-0.8\right)}^3 =0.992$. The right column includes the natural logarithm of the reliability and the binary variable x_a that corresponds to that term.

If we impose a $C_{max}=30$ limit, the cost constraint is as follows:

4 · x₁ + 10 · x₂ + 15 · x₃ + 5 · x₄ + 10 · x₅ + 15 · x₆
+ 5 · x₇ + 10 · x₈ + 15 · x₉ ≤ 30

(45)

Finally, only one variant out of three (no redundant component, one redundant component, two redundant components) is feasible for each subsystem. Therefore, we have three additional constraints:

x₁ + x₂ + x₃ = 1
x₄ + x₅ + x₆ = 1
x₇ + x₈ + x₉ = 1

(46)

Also, the x_a variables need to be binary, hence the zero–one integer programming approach.

The solution to this problem is an allocation of $\mathbf{k}=[3, 2, 1]$, with a cost of 30 and a reliability of 0.979625.

Now, let us assume that the basic components have the following volumes: $\mathbf{v} = [1, 1, 1]$, and we impose a volume limit of $V_{max}=5$. In the previous problem, the total volume would have been 6. This leads to the introduction of a new constraint:

1 · x₁ + 2 · x₂ + 3 · x₃ + 1 · x₄ + 2 · x₅ + 3 · x₆ + 1 · x₇ + 2 · x₈ + 3 · x₉ ≤ 5

(47)

The solution to this problem is now an allocation of $\mathbf{k}=[2, 2, 1]$, with a cost of 25, a volume of 5, and a reliability of 0.948024.

We now introduce the possibility of direct reliability allocation with a maximum of one step, with coefficients $\mathbf{\rho }=[0.5, 0.5, 0.5]$.

The expression of the objective function changes; in fact, the number of terms doubles because we duplicate the terms in Equation (44) for each direct allocation step. The terms corresponding to one direct reliability allocation step ($sir=1$) are underlined:

$$\begin{array}{cc}\mathrm{Max}\text{:}& -2.23·{10}^{-1}·x_1-4.08·{10}^{-2}·x_2-8.03·{10}^{-3}·x_3\\ & \underset{-}{-1.05·{10}^{-1}·x_4-2.02·{10}^{-2}·x_5-4.01·{10}^{-3}·x_6}\\ & -5.13·{10}^{-2}·x_7-2.50·{10}^{-3}·x_8-1.25·{10}^{-4}·x_9\\ & \underset{-}{-2.53·{10}^{-2}·x_{10}-1.25·{10}^{-3}·x_{11}-6.25·{10}^{-5}·x_{12}}\\ & -1.01·{10}^{-2}·x_{13}-1.00·{10}^{-4}·x_{14}-1.00·{10}^{-6}·x_{15}\\ & \underset{-}{-5.01·{10}^{-3}·x_{16}-5.00·{10}^{-5}·x_{17}-5.00·{10}^{-7}·x_{18}}\end{array}$$

(48)

The constraints for the cost and volume, respectively, are the following:

5 · x₁ + 10 · x₂ + 15 · x₃ + 8 · x₄ + 15 · x₅ + 23 · x₆
+ 5 · x₇ + 10 · x₈ + 15 · x₉ + 8 · x₁₀ + 15 · x₁₁ + 23 · x₁₂
+ 5 · x₁₃ + 10 · x₁₄ + 15 · x₁₅ + 8 · x₁₆ + 15 · x₁₇ + 23 · x₁₈ ≤ 30

(49)

1 · x₁ + 2 · x₂ + 3 · x₃ + 1 · x₄ + 2 · x₅ + 3 · x₆
+ 1 · x₇ + 2 · x₈ + 3 · x₉ + 1 · x₁₀ + 3 · x₁₁ + 3 · x₁₂
+ 1 · x₁₃ + 2 · x₁₄ + 3 · x₁₅ + 1 · x₁₆ + 2 · x₁₇ + 3 · x₁₈ ≤ 5

(50)

Finally, the constraints for the binary variables that impose the mutual exclusivity of terms are as follows:

x₁ + x₂ + x₃ + x₄ + x₅ + x₆ = 1
x₇ + x₈ + x₉ + x₁₀ + x₁₁ + x₁₂ = 1
x₁₃ + x₁₄ + x₁₅ + x₁₆ + x₁₇ + x₁₈ = 1

(51)

The solution to this problem is an allocation of ($\mathbf{k},\mathbf{s}\mathbf{i}\mathbf{r}$) = [(2, 1), (2, 0), (1, 0)], with a cost of 30, a volume of 5, and a reliability of 0.967775.

6. Experimental Results

To evaluate the performance of the proposed method, a large number of RRAP-type optimization problems were analyzed. For each problem studied, all seven types of redundancy presented in Section 3 were considered. For each subsystem, the type of redundancy was randomly generated, based on predetermined weights shown in

Table 2. Weights for types of redundancy considered in experimental studies.

Type of redundancy	A, B, C, D, E, G	F
Weight	$15\%$	$10\%$

.

Reliability, cost and volume values for each component of the studied system were randomly generated. Regarding reliability, the range of initial values differs depending on the type of redundancy, as shown in

Table 3. Value ranges for initial component reliability by type of redundancy.

Type of redundancy	A, B, C, D	E, F, G
Value ranges	$[0.8, 1)$	$[0.9, 1)$

.

For cost, the values are in the range of [1,50] cost units, and for volume, the values are in the range of [1,20] volume units for all $n$ subsystems.

Regarding the reduction coefficient $\alpha$ and the factors $\beta$ and $\delta$ used, the values considered were also randomly generated, taking into account the following ranges of values:

$$0<\alpha <1,\hspace{1em}50\le \beta \le 100,\hspace{1em}40\le \delta \le 80$$

(52)

In the case of type F of redundancy subsystems, the value of the reduction factor $\gamma$ is taken as half of the value for $\beta \left(\gamma ={\displaystyle \frac{\beta }{2}}\right)$.

As for the cost increase factor for a reliability improvement step ($\rho$), the values were randomly generated in the range of [0.25, 0.75].

For a given reliability model, reliability optimization studies were performed as follows.

First, a RRAP-type problem is considered to maximize system reliability within the limit of cost $C_{max}=4\times C_{ns}$ and within the limit of volume $V_{max}=1.5\times V_{ns}$. Let $R_{max}$ be the maximum reliability of the system obtained in this way.

Then, another RRAP-type problem is solved to obtain the required reliability $R_{req}=R_{max}$ at a minimum cost, under the volume constraint $V_{max}=1.5\times V_{ns}$. In this way, either the solution from the first optimization problem is validated, or an improved solution is obtained. This is the final allocation that we consider, reflected by the pair of vectors ($\mathbf{k},\mathbf{s}\mathbf{i}\mathbf{r}$) and for which the reliability, cost and volume are $R_{rs}$, $C_{rs}$, and $V_{rs}$, respectively.

For any solution, the efficiency is then calculated as follows:

$$Ef={\displaystyle \frac{1-R_{sn}}{1-R_{rs}}}.$$

(53)

Efficiency is a more intuitive indicator that expresses how many times the risk of failure of the redundant system decreases compared to the non-redundant one. To illustrate this approach, numerical results of some experimental studies for a given reliability model are presented below.

6.1. Example of an RRAP Optimization Problem

To illustrate an RRAP optimization problem with its proposed variants and their solutions, a reliability model for a system with 50 subsystems $(n=50$) is considered. All the details of this model are presented in

Table 4. Reliability model for $n=50$ subsystems.

Structural details: tuples of $(i: {rt}_i,\_r_i {,\_c_i,v_i,\rho }_i$) extended with parameters ${\alpha }_i$, ${\beta }_i$, ${\gamma }_i$or ${\delta }_i$ as appropriate, $i=1:n.$

(1: B, 0.921, 4, 16; 0.358), (2: A, 0.800, 47, 15; 0.347), (3: B, 0.861, 6, 14; 0.568), (4: B, 0.924, 2, 4; 0.637), (5: D, 0.838, 17, 9, 0.420; α = 0.183), (6: G, 0.931, 37, 17, 0.704; δ = 47), (7: A, 0.880, 33, 4, 0.327), (8: A, 0.889, 6, 7, 0.718), (9: D, 0.810, 15, 8, 0.734; α = 0.481), (10: G, 0.904, 18, 5, 0.563; δ = 42), (11: C, 0.849, 9, 0.412), (12: D, 0.894, 15, 8, 0.346, α = 0.625), (13: D, 0.807, 40, 6, 0.424; α = 0.611), (14: G, 0.920, 41, 18, 0.433; δ = 72), (15: D, 0.812, 12, 17, 0.365; α = 0.397), (16: A, 0.826, 47, 2, 0.649), (17: F, 0.918, 13, 5, 0.485; β = 69, γ = 34), (18: G, 0.940, 36, 3, 0.367; δ = 46), (19: G, 0.947, 44, 15, 0.519; δ = 50), (20: E, 0.969, 30, 15, 0.383; β = 90), (21: F, 0.974, 48, 13, 0.327; β = 97, γ = 48), (22: G, 0.965, 11, 7, 0.484; δ = 54), (23: D, 0.960, 38, 9, 0.519; α = 0.139), (24: F, 0.934, 38, 4, 0.508; β = 83, γ = 41), (25: A, 0.930, 31, 13, 0.489), (26: D, 0.909, 6, 6, 0.745; α = 0.881), (27: E, 0.902, 35, 6, ρ = 0.617; β = 85), (28: D, 0.843, 13, 13, 0.674; α = 0.499), (29: G, 0.910, 41, 4, 0.319; δ = 62), (30: C, 0.930, 19, 6, 0.317), (31: F, 0.974, 25, 17, 0.450; β = 52, γ = 26), (32: C, 0.887, 6, 15, 0.439), (33: C, 0.805, 5, 4, 0.716), (34: A, 0.953, 34, 2, 0.562), (35: C, 0.929, 3, 11, 0.484), (36: E, 0.971, 23, 15, 0.563; β = 52), (37: C, 0.986, 14, 8, 0.662), (38: A, 0.940, 45, 18, 0.375), (39: A, 0.973, 15, 5, 0.483), (40: D, 0.801, 36, 4, 0.638; α = 0.958), (41: A, 0.854, 48, 6, 0.572), (42: B, 0.958, 35, 18, 0.272), (43: G, 0.989, 47, 10, 0.634; δ = 73), (44: C, 0.989, 6, 2, 0.392), (45: E, 0.922, 30, 13, 0.592; β = 88), (46: C, 0.905, 17, 11, 0.298), (47: E, 0.915, 13, 8, 0.494; β = 81), (48: B, 0.922, 46, 1, 0.564), (49: D, 0.856, 3, 6, 0.632; α = 0.410), (50: B, 0.893, 37, 11, 0.474).

$C_{ns}=1240$, $C_{max}=4\times C_{ns}=4960, V_{ns}=455$, $V_{max}=1.5\times V_{ns}=682$

. This number of subsystems was chosen based on out previous studies [6,19], where instances with 50 and 100 subsystems were considered. A system with 50 subsystems is sufficiently large to capture the complexity of the RRAP and to illustrate the scalability of the optimization method. While solving a problem with 100 subsystems is also feasible, it requires more computational time and its details are harder to follow by the reader. For this experimental demonstration, we selected 50 subsystems to have a balance between complexity and clarity.

For this model, it is required to maximize the reliability within the limits of the maximum cost $C_{max}=4960,$ and the maximum volume $V_{max}=682$.

We will first consider only the cost constraint.

In a first step, we try to improve the reliability of the system only based on redundancy allocation (i.e., an RAP-type optimization problem). The solution obtained with $lpsolve$ is presented in

Table 5. Best solution obtained only on the basis of redundancy (maximizing reliability under cost constraint: $n=50, C_{max}=4960$).

Optimal allocation: $k_1$, $k_2$, …, $k_n$	$C_{rs}$	$V_{rs}$	$R_{rs}$	$Ef$
4, 5, 5, 5, 4, 5, 4, 5, 4, 5, 5, 4, 4, 5, 4, 5, 3, 5, 4, 4, 3, 5, 3, 3, 4, 4, 5, 4, 5, 4, 3, 5, 5, 3, 5, 4, 3, 3, 3, 4, 5, 3, 3, 3, 5, 4, 5, 3, 4, 3	4960	1857	0.976633	42.51

.

In the second stage, we try to maximize the reliability of system only by directly increasing the reliability of the components, without using redundant, fault-tolerant structures (i.e., a reliability allocation problem). The cost calculation of a subsystem with direct reliability allocation steps is carried out by applying Equation (10) (alternative 1).

The best solution achieved by directly increasing the component reliability is presented in

Table 6. Best solution obtained only by reliability allocation (maximizing reliability under cost constraint: $n=50, C_{max}=4960$).

Steps of increasing reliability: ${sir}_1$, ${sir}_2$, …, ${sir}_n$	$C_{rs}$	$V_{rs}$	$R_{rs}$	$Ef$
10, 8, 9, 10, 8, 5, 7, 9, 8, 7, 9, 8, 7, 6, 9, 6, 8, 6, 5, 5, 5, 6, 5, 6, 6, 8, 6, 8, 7, 7, 5, 9, 10, 5, 9, 5, 5, 6, 6, 7, 6, 6, 3, 6, 6, 8, 8, 6, 10, 7	4959.91	455	0.959565	24.57

.

Next, we try to maximize the reliability of the system, within the limit of the maximum cost $C_{max}$, by applying both reliability improvement techniques (i.e., an RRAP optimization problem). The solution provided by $lpsolve$is presented in

Table 7. Best solution obtained by reliability–redundancy allocation (maximizing reliability under cost constraint: $n=50, C_{max}=4960$).

Value pairs: (${k_1, sir}_1)$, (${k_2, sir}_2)$, …, (${k_n, sir}_n)$	$C_{rs}$	$V_{rs}$	$R_{rs}$	$Ef$
(4, 0), (1, 9), (4, 0), (4, 0), (4, 0), (1, 7), (4, 0), (5, 0), (4, 0), (1, 9), (5, 0), (4, 0), (4, 0), (1, 8), (4, 0), (5, 0), (1, 9), (1, 8), (1, 7), (1, 7), (3, 0), (1, 8), (3, 0), (1, 8), (3, 0), (4, 0), (1, 8), (4, 0), (1, 9), (3, 0), (3, 0), (4, 0), (5, 0), (3, 0), (4, 0), (1, 7), (3, 0), (3, 0), (3, 0), (4, 0), (4, 0), (3, 0), (3, 0), (3, 0), (1, 8), (4, 0), (1, 9), (3, 0), (4, 0), (3, 0)	4959.09	1251	0.990937	109.61

.

The reliability obtained in this way is clearly superior to that of previous tests. The importance of applying both solutions to improve reliability at the subsystem level is clearly highlighted.

Having highlighted this particularly important aspect in the design of complex systems, let us return to the original problem to be solved also considering the volume constraint.

The solution given by $lpsolve$ to the reliability optimization problem with cost and volume constraints shown in Table 3 is presented in

Table 8. The solution for maximizing system reliability under cost and volume constraints (${n=50, C}_{max}=4960, V_{max}=682$).

Value pairs: (${k_1, sir}_1)$, (${k_2, sir}_2)$, …, (${k_n, sir}_n)$	$C_{rs}$	$V_{rs}$	$R_{rs}$	$Ef$
(1, 10), (1, 9), (1, 10), (1, 10), (1, 10), (1, 7), (1, 9), (1, 10),(4, 0), (1, 9), (4, 0), (1, 10), (4, 0), (1, 7), (1, 10), (4, 0), (1, 9), (1, 7), (1, 7), (1, 7), (1, 6), (1, 8), (3, 0), (1, 7), (3, 0), (4, 0), (1, 7), (1, 9), (1, 8), (1, 9), (1, 6), (1, 10), (5, 0), (3, 0), (1, 10), (1, 6), (2, 0), (1, 7), (3, 0), (4, 0), (4, 0), (1, 7), (3, 0), (2, 0), (1, 7), (1, 9), (1, 9), (3, 0), (1, 10), (3, 0).	4959.79	682	0.986308	72.55

.

Compared to the previous solution, by introducing the volume restriction, a somewhat lower reliability is obtained for the studied system.

The complete solution of the system reliability maximization problem also involves a cost minimization study while ensuring a required level of reliability where $R_{req}$ is the previously obtained $R_{sr}$ value. Obviously, the volume constraint is maintained. In other words, the reliability found by maximization is set as the threshold for the minimization problem. The goal is to find systems with a lower total cost for the same reliability. During maximization, if there are more candidates with the same reliability but different costs, the choice between them is indifferent from the point of view of the objective function. Therefore, a solution with a higher cost but still lower than or equal to the cost threshold can be selected. The second optimization can identify better solutions from both points of view.

The final solution to this optimization problem is presented in

Table 9. Solution to the system cost minimization problem with a required reliability level and volume constraint (${n=50, R}_{req}=0.986308, V_{max}=682$).

Value pairs: (${k_1, sir}_1)$, (${k_2, sir}_2)$, …, (${k_n, sir}_n)$	$C_{rs}$	$V_{rs}$	$R_{rs}$	$Ef$
(1, 10), (1, 9), (1, 10), (1, 10), (1, 10), (1, 7), (1, 9), (1, 10), (4, 0), (1, 9), (4, 0), (1, 10), (4, 0), (1, 7), (1, 10), (4, 0), (1, 9), (1, 7), (1, 7), (1, 7), (1, 6), (1, 8), (3, 0), (1, 7), (3, 0), (4, 0), (1, 7), (1, 9), (1, 8), (1, 9), (1, 6), (1, 10), (5, 0), (3, 0), (1, 10), (1, 6), (2, 0), (1, 7), (3, 0), (4, 0), (4, 0), (1, 7), (3, 0), (2, 0), (1, 7), (1, 9), (1, 9), (3, 0), (1, 10), (3, 0).	4959.79	682	0.986308	72.55

.

Note that the solution obtained confirms the result from the previous maximization problem. The values from Table 9 (the same as those in Table 8) are adopted as the final solution to the studied optimization problem.

To verify and evaluate the efficiency of the proposed RRAP optimization method based on zero–one integer programming, hundreds of problems of this type were analyzed in this way.

6.2. Discussion

The experimental results highlight the importance of combining redundancy and direct reliability allocation when designing complex systems. When only one of these strategies is used, either adding spare components or improving component reliability, the improvement is limited. In contrast, when both mechanisms are applied together, the system achieves a significantly lower failure probability under the same cost constraint.

Introducing a volume constraint naturally limits the number of spares that can be added. In response, the optimizer shifts toward improving component reliability rather than relying on redundancy. This confirms a practical principle: when space is abundant, redundancy is preferred because it adds fault tolerance at a relatively low cost. When space is limited, enhancing the reliability of individual components becomes the more viable option, even though it may be more expensive.

The optimal solutions tend to follow two distinct patterns, depending on the characteristics of each subsystem. In the first pattern, the optimizer assigns several spare components and no reliability improvement steps. This occurs when components are small and inexpensive, which makes redundancy both affordable and effective. Adding spares in such cases greatly increases subsystem reliability without significantly impacting cost or volume.

In the second pattern, the solution includes only one or no spare component, with several reliability improvement steps applied instead. This typically happens when components already occupy substantial volume or when the system is constrained by tight space limits. Since adding spares would exceed the volume constraint, the optimizer improves reliability by upgrading the existing components.

These patterns suggest that the optimizer implicitly evaluates the trade-off between cost, volume, and fault tolerance for each subsystem. It selects the most suitable improvement strategy according to the characteristics of the subsystem and the global constraints. From a design perspective, this behavior reflects what experienced engineers often do: when space is tight, they harden components; when the cost is high but space is available, they add redundancy.

The experimental results reinforce the value of addressing redundancy and direct reliability allocation as a unified optimization problem. The proposed 01IP formulation automatically balances cost and volume across the system and adjusts the allocation strategy to the needs of each subsystem. This leads to high-quality solutions and provides a practical framework for reliability engineering in large, complex systems.

7. Conclusions

This study examined the reliability–redundancy allocation problem (RRAP) for large binary systems with hybrid structures, with a focus on two optimization objectives: maximizing system reliability under cost and volume constraints, and minimizing cost while meeting a required reliability threshold. The analysis considered both direct reliability enhancement of components and redundancy allocation as complementary strategies. One contribution was the development of a zero–one integer programming (01IP) formulation that models subsystem configurations using log-transformed reliability functions and binary decision variables. This formulation enables efficient handling of the combinatorial complexity of the problem.

The approach accommodates various redundancy types and integrates constraints related to cost and volume. The method can be easily extended to take into account other constraints, such as a constraint on the weight of the system, which commonly arises in the design of complex systems.

Beyond the theoretical contribution, the proposed model has practical relevance for industries where system reliability under strict resource constraints is critical. For example, in telecommunication networks, ensuring uninterrupted service often requires allocating redundant paths or nodes while meeting cost and equipment limitations. In aerospace and avionics systems, fault tolerance is essential, but both weight and volume are severely constrained, which makes the trade-offs addressed by this model directly applicable. Similarly, energy distribution networks, particularly in remote or mission-critical environments, can benefit from optimized redundancy planning to maintain service continuity with limited infrastructure. In these domains, the ability to evaluate and balance cost, volume, and reliability in a unified framework can support more effective system-level design decisions.

A possible direction for future research is to develop an RRAP-type optimization method for complex systems with a hybrid structure that also considers the possibility of repairing defective components within the specified time interval (during the mission). If the system is repairable, a further challenge appears in evaluating reliability at the subsystem level.

Another area of investigation is to explore recent optimization algorithms that could offer a faster or better performance than that of the current approach. One such method is LB-RELAX [54], which uses LP relaxations to accelerate local branching in large neighborhood search. A related approach is BALANS [55], which applies online decision-making models to adaptively guide large neighborhood search. Another one is Feasibility Jump [56], a primal heuristic for 0-1 integer programs that can escape local minima through feasibility-directed perturbations. Such algorithms may enhance scalability or reduce computation time for RRAP formulations.

8. Assumptions

A1. In any redundant system, the spare components are considered identical to the basic ones; with this assumption, the assessment of subsystem reliability is simplified, but the optimization problem remains as complex.

A2. For the components in operating mode and for the spares kept in warm conditions, the random variable expressing the time to failure has a negative-exponential distribution law—a widely accepted assumption in the study of the reliability of electronic systems and necessary for the use of Markov chains in the assessment of the reliability of reconfigurable redundant structures.

A3. Faults occurring in the system are independent events, not correlated in any way with one another.

A4. When increasing the reliability of a component by direct allocation, the volume does not change.