Solving Fredholm Integral Equations of the First Kind Using a Gaussian Process Model Based on Sequential Design

Abstract

In this study, a Gaussian process model is utilized to study the Fredholm integral equations of the first kind (FIEFKs). Based on the H–$H_k$ formulation, two cases of FIEFKs are under consideration with respect to the right-hand term: discrete data and analytical expressions. In the former case, explicit approximate solutions with minimum norm are obtained via a Gaussian process model. In the latter case, the exact solutions with minimum norm in operator forms are given, which can also be numerically solved via Gaussian process interpolation. The interpolation points are selected sequentially by minimizing the posterior variance of the right-hand term, i.e., minimizing the maximum uncertainty. Compared with uniform interpolation points, the approximate solutions converge faster at sequential points. In particular, for solvable degenerate kernel equations, the exact solutions with minimum norm can be easily obtained using our proposed sequential method. Finally, the efficacy and feasibility of the proposed method are demonstrated through illustrative examples provided in this paper.

1. Introduction

In recent years, mathematical models have been extensively employed to solve complex systems. Many inverse problems in these systems can be reduced to solving specific FIEFKs, such as image restoration [1,2], the backward heat conduction problem [3,4,5], nuclear magnetic resonance [6], and so forth. Additionally, some mathematical inverse problems—such as numerical differentiation, the numerical inversion of integral transformations, and numerical solutions of differential equations—can be translated into FIEFKs.

The solvability and construction of FIEFKs have been considered in [7,8]. However, this type of equation has a significant property, referred to as ill-posedness, which is relative to well-posedness as defined by Jacques Hadamard [9] in the 1920s. Due to the difficulty in obtaining exact solutions for such equations, researchers often resort to numerical methods. Currently, ill-posedness has been manifested as a relatively large condition number of the coefficient matrix in a linear system. It is well known that this condition number can be effectively dominated through regularization, which has subsequently given rise to various regularization methods [10,11,12,13,14,15,16,17]. Herein, finite-dimensional regularized approximate methods [15,16,17] are proposed within specific subspaces. These subspaces are typically obtained in two ways, either by selecting basis functions to perform an orthogonal decomposition of the space or meshing the definition domain. In addition, other finite rank approximate projection methods [18,19] have been developed based on these subspaces, yielding least squares solutions with minimum norm through operator inversion. In recent years, some machine learning methods, such as support vector regression [20,21], have also been used to study Fredholm integral equations.

In addition to regularization methods, wavelet techniques are also used to solve FIEFKs. S. Yousefi and A. Banifatemi [22] proposed a method for estimating the coefficients of numerical solutions by means of the orthogonal properties of CAS wavelets. The wavelet–Galerkin method proposed by K. Maleknejad et al. [23] can transform FIEFKs into linear algebraic equations that possess sparse coefficient matrixes. F. Fattahzadeh [24] propounded a numerical direct method to research two-dimensional linear and nonlinear FIEFKs via the Haar wavelet; however, this method did not involve numerical integration. In addition, block-pulse functions are popular. For example, Z. Masouri et al. [17,25] proposed a regularization–direct method to overcome the ill-posedness of integral equations based on vector forms of block-pulse functions without employing any projection techniques. K. Maleknejad and E. Saeedipoor [26] enhanced block-pulse functions and proposed a numerical direct method based on orthogonal hybrid block-pulse functions and Legendre polynomials. Furthermore, numerous other methods have been developed for solving integral equations. For example, iteration methods [2], Taylor expansion methods [27], maximum entropy regularization [28], and additional methods can be found in [29].

In practice, the majority of methods are devoted to numerical solutions by transforming integral equations into linear algebraic equations. For FIEFKs, the condition number is dominated by certain regularization parameters as follows:

$${\int }_{E}h(x,t)f\left(t\right)dt=g\left(x\right),x\in D.$$

(1)

For convenience, the above equation can be rewritten as

$$Lf=g,$$

(2)

whereby the linear operator L is herein referred to as

$$\left(Lf\right)\left(x\right):={⟨f,h_x⟩}_H={\int }_{E}h(x,t)f\left(t\right)dt,$$

(3)

and its adjoint operator is defined as

$$\left(L^{*}g\right)\left(t\right):={⟨g,h_t^{*}⟩}_{L^2\left(D\right)}={\int }_{D}h(x,t)g\left(x\right)dx.$$

(4)

Here, $h(x,t)$ is an explicit continuous function on $D\times E$, and the objective function $f\left(t\right)$ is pending in H, which is either a square-integrable space $L^2\left(E\right)$ or a reproducing kernel Hilbert space (RKHS) $H_Q$.

It is common for the right-hand term $g\left(x\right)$ to be unknown, yet discrete data with respect to it are typically given, such as

$$y_i=g\left(x_i\right)+{\epsilon }_i,1\le i\le n.$$

Assume that ${\epsilon }_i$ is bounded, i.e.,

$${\displaystyle \frac{1}{n}}\sum _{i=1}^n{\epsilon }_i^2\le \delta ,$$

where $\delta$ is a noise level. According to this assumption,

$$\underset{f\in H}{min}\left\{{\displaystyle \frac{1}{n}\sum _{i=1}^n{\left[L\left(f\right)\left(x_i\right)-y_i\right]}^2+\lambda {\parallel f\parallel }_H^2}\right\},$$

which has been widely studied in [10,11,12], and the norm ${\parallel ·\parallel }_H$ is considered in the solution space H ($L^2\left(E\right)$ or RKHS $H_Q$). This problem has a unique solution:

$$f_{n,\lambda }\left(t\right)=\left({\eta }_{x_1}\left(t\right),\cdots ,{\eta }_{x_n}\left(t\right)\right){(K_{XX}+n\lambda I_n)}^{-1}Y,$$

(5)

where $X={\left(x_1,\cdots ,x_n\right)}^T$, $Y={\left(y_1,\cdots ,y_n\right)}^T$, and

$${\eta }_x\left(t\right)=\left\{\begin{array}{cc}{h}_x\left(t\right),\hfill & H=L^2\left(E\right)\hfill \\ {\int }_E{h}_x\left(s\right)Q(t,s)ds,\hfill & H=H_Q\hfill \end{array}\right.,$$

(6)

and its $ij$-th entry $k(x_i,x_j)$ of matrix $K_{XX}$ is referred to as

$$k(x,x^{\prime })=\left\{\begin{array}{cc}{\int }_E{\int }_E{h}_x\left(t\right)h_{x^{\prime }}\left(s\right)Q(s,t)dsdt,\hfill & H=H_Q\hfill \\ {\int }_E{h}_x\left(t\right)h_{x^{\prime }}\left(t\right)dt,\hfill & H=L^2\left(E\right)\hfill \end{array}\right..$$

However, in terms of practical problems, it may be difficult to determine the noise level $\delta$. Thus, it was assumed that ${\epsilon }_i\sim N\left(0,{\sigma }^2\right)$ was i.i.d. In this instance, they also presented the following solution based on Gaussian process regression (GPR) [30,31,32]:

$${\overline{f}}_n^{†}\left(t\right)=\left({\eta }_{x_1}\left(t\right),\cdots ,{\eta }_{x_n}\left(t\right)\right){(K_{XX}+{\sigma }^2{I}_n)}^{-1}Y.$$

(7)

Notice that Equations (5) and (7) are based on the H–$H_k$ formulation, which was suggested by Qian [33], and this formulation was used to study Equation (1) by R. Qiu et al. [34,35,36]. More specifically, this formulation can transform the range space $R\left(L\right)$ (the non-closed subspace in $L^2\left(D\right)$) of L into an RKHS, which is a closed space with its topology; that is, it transforms ill-posed problems into well-posed problems in the mathematical sense. Based on this formulation, the results in [34,35] can be extended in this paper using GPR. Moreover, an adaptive RKHS regularization with additive Gaussian noise was proposed in [37], which was also associated with the H–$H_k$ formulation.

Beyond this, we are more concerned with the essential question of Equation (1): when there are explicit analytical expressions for $h(x,t)$ and $g\left(x\right)$, can the exact solution be obtained accordingly? Exact solutions with minimum norm are rarely found, except in [10], where the analytical solution in operator form has been presented. Based on the H–$H_k$ formulation, we also present exact solutions in $L^2\left(D\right)$ for all the operator forms regardless of $H=H_Q$ or $L^2\left(E\right)$ in Theorems 1 and 2. We further analyze the potential challenges in the computation of these solutions. For this reason, we provide an approximate solution with the minimum norm based on Gaussian process interpolation as

$${\overline{f}}_n^{†}\left(t\right)=\left({\eta }_{x_1}\left(t\right),\cdots ,{\eta }_{x_n}\left(t\right)\right)K_{XX}^{†}Y.$$

(8)

Herein, $K_{XX}^{†}$ is the Moore–Penrose pseudoinverse of $K_{XX}$, and its minimum positive eigenvalue acts as a regularization parameter (see [38,39]). Our proposed method can sequentially select interpolation points by minimizing the posterior variance $V\left[\overline{g}\left(x\right)\right]$ of $g\left(x\right)$, defined as Equation (27); that is, each point is generated at the maximum uncertainty of $\overline{g}\left(x\right)$, which is the Gaussian process interpolation of $g\left(x\right)$ in Equation (1). Compared with uniform points, the solution in Equation (8) generally has a better approximation at sequential points. For convenience, we refer to this method as the sequential Gaussian process interpolation (SGPI).

The remainder of this paper is structured as follows. We introduce the H–$H_k$ formulation and present the exact solutions in operator form for a given $g\left(x\right)$ in Section 2. In Section 3, we utilize a Gaussian process model to solve FIEFKs and present our strategy of selecting the sequential points for the interpolation model. In Section 4, we demonstrate that the exact solutions of degenerate kernel equations can be found using the SGPI method for any initial point. Several examples illustrate the efficacy and feasibility of the SGPI method in Section 5. Finally, we present a brief conclusion of this paper in Section 6.

2. Minimal-Norm Solution

2.1. Moore–Penrose Pseudoinverse

Let $N\left(L\right)$ and $R\left(L\right)$ be denoted as the null space and range space, respectively. It can be demonstrated that $N\left(L\right)$ is a closed linear space in H and $R\left(L\right)$ is a non-closed subspace in $L^2\left(D\right)$ unless $R\left(L\right)$ is a finite-dimensional space.

Definition 1.

For $g\left(x\right)\in L^2\left(D\right)$, a function $f\in H$ is named an ordinary least squares (OLS) solution of Equation (2) if

$${\parallel Lf-g\parallel }_{L^2\left(D\right)}=inf\left\{{\parallel Lv-g\parallel }_{L^2\left(D\right)}:v\in H\right\}.$$

A function $u\in H$ is called the minimal-norm solution (or the best approximate solution), denoted by $f^{†}$, if ${\parallel u\parallel }_H=\underset{f\in S}{inf}{\parallel f\parallel }_H$. Here, S denotes all OLS solutions. Additionally, $L^{†}$ is called the Moore–Penrose pseudoinverse of L, defined as Equation (3), if $L^{†}g=f^{†}$.

In general, $L^{†}$ is a closed operator on $D\left(L^{†}\right):=R\left(L\right)\oplus R{\left(L\right)}^{\perp }\subseteq L^2\left(D\right)$. The focal point that warrants our attention is that $D\left(L^{†}\right)=L^2\left(D\right)$ if and only if subspace $R\left(L\right)$ is closed [19] in $L^2\left(D\right)$. Moreover, there exists another orthogonal decomposition $H=N\left(L\right)\oplus N{\left(L\right)}^{\perp }$ on E; thus,

$$f^{†}\in N{\left(L\right)}^{\perp },S=f^{†}+N\left(L\right).$$

The null space of a special integral equation has been studied in [40], and the uniqueness of solutions is considered in [41,42]. In fact, the solution $f^{†}$ is also unique in the sense of the Moore–Penrose pseudoinverse (see [10,38,43,44,45]).

2.2. H–$H_k$ Formulation

For a linear integral operator L, defined as Equation (3), it is known that L is a compact linear operator from H to $L^2\left(D\right)$ and $R\left(L\right)$ is a non-clsoed subspace in $L^2\left(D\right)$. This means that Equation (1) is ill-posed. Nevertheless, $R\left(L\right)$ can be transformed into an RKHS $H_k$, for which its norm is endowed with a reproducing kernel topology through the H–$H_k$ formulation. Henceforth, $R\left(L\right)$ is denoted as $H_k$. Based on this formulation, Equation (1) has been transformed mathematically into a well-posed equation.

For any positive definite kernel k, via the Moore–Aronszajn theorem [46], a unique RKHS $H_k$ exists such that its reproducing kernel equals k. This means that there is a one-to-one correspondence between an RKHS and a certain positive definite kernel. More properties and their applications about RKHS have been summarized in [1].

For any $g_1=L\left(f_1\right)$ and $g_2=L\left(f_2\right)$ in $H_k$, its inner product

$${⟨g_1,g_2⟩}_{H_k}:={⟨P_{N{\left(L\right)}^{\perp }}{f}_1,P_{N{\left(L\right)}^{\perp }}{f}_2⟩}_H,$$

(9)

and

$$k(x,x^{\prime }):={⟨h_x,h_{x^{\prime }}⟩}_H,$$

(10)

where $P_{N{\left(L\right)}^{\perp }}$ represents an orthogonal projection operator.

Hereafter, Equations (9) and (10), which contain the following isometric isomorphism relationship, are referred to as the H–$H_k$ formulation according to [33], and $H_k$ represents the canonical range space. Based on Equations (9) and (10), we obtain the following lemma.

Lemma 1

(Lemma 1 and Proposition 2 in [35]). Let L be defined as Equation (3); then,

(1)

If $H=L^2\left(E\right)$, then $N\left(L\right)=span{\left\{h_x\mid x\in D\right\}}^{\perp }$;

(2)

If $H=H_Q$, then $N\left(L\right)=span{\left\{{\eta }_x\mid x\in D\right\}}^{\perp }$; ${\eta }_x\left(t\right)$ is defined as Equation (6);

(3)

$R\left(L\right)$ is an RKHS.

Apart from this, there exist some isometric isomorphisms between $N{\left(L\right)}^{\perp }$ and $H_k$, which yield the following correspondence:

$$N{\left(L\right)}^{\perp }\sim H_k,$$

(11)

$$h_{x^{\prime }}\left(t\right),{\eta }_{x^{\prime }}\left(t\right)\sim k_{x^{\prime }}\left(x\right),$$

(12)

$$P_{N{\left(L\right)}^{\perp }}f\left(t\right)\sim g\left(x\right),$$

(13)

$$P_{N{\left(L\right)}^{\perp }}{Q}_{t^{\prime }}\left(t\right)\sim {\eta }_{t^{\prime }}^{*}\left(x\right),$$

(14)

where $a\sim b$ means $La=b$ and $a\in N{\left(L\right)}^{\perp }$. The definitions of ${\eta }_{t^{\prime }}^{*}$ and ${\eta }_x$ can be found in Equations (4) and (6); herein, $f\left(t\right)$ and $g\left(x\right)$ satisfy Equation (1).

2.3. Minimal-Norm Solution in $H_Q$

Let H be an RKHS $H_Q$, and, given the continuous function $g\left(x\right)\in H_k$, Equation (1) is solvable. In this case, the conclusion has been obtained by the authors of [10].

Theorem 1

(Theorem 4.1 in [10]). Let L satisfy Equation (14) and the continuous function $g\left(x\right)\in H_k$; then,

$$f^{†}\left(t\right)={⟨{\eta }_t^{*},g⟩}_{H_k},t\in E.$$

(15)

2.4. Minimal-Norm Solution in $L^2\left(E\right)$

In this subsection, we assume that $H=L^2\left(E\right)$. Generally speaking, it can be noted that $L^{†}$ is an unbounded operator from $R\left(L\right)$ (topology in $L^2\left(D\right)$) to $L^2\left(E\right)$, unless $h(x,t)$ of Equation (1) is a degenerate integral kernel. However, based on the H–$H_k$ formulation, we can make the following conclusion.

Lemma 2.

Let $H=L^2\left(E\right)$ and $R\left(L\right)=H_k$; then, $L^{†}$ is bounded.

Proof. 

Let $g\in R\left(L\right)(g\ne 0)$ and $Lf=g$; then,

$$\parallel L^{†}\parallel =\underset{g\ne 0}{sup}{\displaystyle \frac{\parallel L^{†}{g\parallel }_{L^2\left(E\right)}}{{\parallel g\parallel }_{H_k}}}=\underset{g\ne 0}{sup}{\displaystyle \frac{\parallel P_{N{\left(L\right)}^{\perp }}{f\parallel }_{L^2\left(E\right)}}{{\parallel g\parallel }_{H_k}}}=\underset{g\ne 0}{sup}{\displaystyle \frac{\parallel P_{N{\left(L\right)}^{\perp }}{f\parallel }_{L^2\left(E\right)}}{\parallel P_{N{\left(L\right)}^{\perp }}{f\parallel }_{L^2\left(E\right)}}}=1.$$

Hence, $L^{†}$ is bounded. □

Remark 1.

Based on the H–$H_k$ formulation, whether the integral kernel of Equation (1) is degenerate or not, $R\left(L\right)$ with $H_k$-topology is always closed. Hence, solving Equation (1) is a well-conditioned problem mathematically.

Theorem 2.

Let $H=L^2\left(E\right)$ and $g\left(x\right),h_t^{*}\in R\left(L\right)$ for fixed $t\in E$; then,

$$f^{†}\left(t\right)={⟨g,h_t^{*}⟩}_{H_k}.$$

(16)

Proof. 

Based on Equation (10),

$$g\left(x\right)={⟨g\left(y\right),K_x\left(y\right)⟩}_{H_k}={⟨g\left(y\right),{⟨h_x,h_y⟩}_H⟩}_{H_k}={⟨h_x,{⟨g\left(y\right),h_y⟩}_{H_k}⟩}_H.$$

By Equation (3), show that ${⟨g\left(y\right),h_y⟩}_{H_k}$ is a solution of Equation (2). Since

$$h_t^{*}\left(y\right)=h_y\left(t\right),{⟨g,h_t^{*}⟩}_{H_k}\in N{\left(L\right)}^{\perp },$$

then Equation (16) has been proven. □

In this section, we present expressions of two operator forms of $f^{†}$, that is, solutions in Equations (15) and (16), regardless of whether $g\left(x\right)$ is in $R\left(L\right)$. Among them, Equation (15) also depends on RKHS $H_Q$, which can usually be selected as some absolutely continuous function spaces, for example $W_2^1[a,b]$ in [4] and W in [38]. In addition, these solutions in operator forms may be calculated analytically. However, it is possible that some of these solutions can only be computed numerically, which are implemented through the Gaussian process model mentioned below in this paper.

3. Gaussian Process Model

For a Gaussian process (GP), one positive definite kernel is often called the covariance kernel, which is used to represent the covariance function of some random variables. Therefore, every RKHS has a covariance function (its reproducing kernel).

Definition 2.

Let $m:D\to \mathbb{R}$ be a real-valued function and $k:D\times D\to \mathbb{R}$ be a positive definite kernel; then, $g:D\to \mathbb{R}$ is called a Gaussian process such that $g_X={(g\left(x_1\right),g\left(x_2\right)\cdots ,g\left(x_n\right))}^T$ is a joint Gaussian distribution for any $X={\left(x_1,\cdots ,x_n\right)}^T$; herein, $x_i\in D$, $1\le i\le n$, and $\forall n\in \mathbb{N}$.

Usually, a Gaussian process is written as

$$g\sim GP(m,k),$$

(17)

where $m\left(x\right)=E\left[g\right(x\left)\right]$ and $k(x,x^{\prime })=E\left[(g\left(x\right)-m\left(x\right))(g\left(x^{\prime }\right)-m\left(x^{\prime }\right))\right]$.

The above definition was derived from Ref. [31], whose authors refer to many applications of the Gaussian process in machine learning. Furthermore, it should be mentioned that connections and equivalences between Gaussian processes and kernel methods are established in [32]; for example, the estimator of kernel ridge regression (KRR) is consistent with the posterior mean of GPR. Inspired by this equivalence, we can employ the Gaussian process model (regression and interpolation) to study the numerical approximation of $g\left(x\right)$ of Equation (1) in $R\left(L\right)$ and then obtain numerical forms for solutions in Equations (15) and (16).

3.1. Gaussian Process Regression

To distinguish the vector $X={\left(x_1,\cdots ,x_n\right)}^T$, customarily, $X_n:=\left\{x_1,\cdots ,x_n\right\}$ is referred to as an experimental design on D. We assume that the observed values $y_i$ and the function values $g\left(x_i\right)$ satisfy

$$y_i=g\left(x_i\right)+{\epsilon }_i,x_i\in X_n,$$

(18)

where ${\epsilon }_i\sim N\left(0,{\sigma }^2\right)$ are independent and identically distributed normal distributions. In the Gaussian process of Equation (17), without loss of generality, let the mean function $m\left(x\right)\equiv 0$ in this paper, i.e., $g\sim GP\left(0,k\right)$. Based on the H–$H_k$ formulation, $k\left(x,x^{\prime }\right)={⟨h_{x^{\prime }},h_x⟩}_H$, and then the posterior mean and variance at x are

$${\overline{g}}_n\left(x\right):=E[g\left(x\right)\mid X,Y]=K_{xX}^T{(K_{XX}+{\sigma }^2{I}_n)}^{-1}Y,$$

(19)

$$V\left[{\overline{g}}_n\left(x\right)\right]:=V[g\left(x\right)\mid X,Y]=k(x,x)-K_{xX}^T{(K_{XX}+{\sigma }^2{I}_n)}^{-1}{K}_{xX},$$

(20)

where $Y={\left(y_1,\cdots ,y_n\right)}^T$, $K_{xX}={\left(k\left(x_1,x\right),\cdots ,k\left(x_n,x\right)\right)}^T$, $K_{XX}=\left(K_{x_{1}X},\cdots ,K_{x_{n}X}\right)$ is known as the covariance matrix, and ${\overline{g}}_n\left(x\right)$ is the Gaussian process regression of $g\left(x\right)$.

For certain complex reproducing kernels, deriving analytical expressions for the solutions in Equations (15) and (16) may be impractical, in which case they can be approximated separately by the minimal-norm solution of the following equation:

$$Uf=\overline{w},$$

(21)

where $U=L^{*}L$, $\overline{w}=L^{*}{\overline{g}}_n$, and ${\overline{g}}_n$ is defined as Equation (19) when $H=L^2\left(E\right)$ or $H=H_Q$. Likewise, let ${\overline{f}}_{D,n}^{†}:=U^{†}\overline{w}$. Its analytical expression is provided in Proposition 1, which has extended the results found in [35].

Proposition 1.

Let $z_i=w\left(t_i\right)+{\epsilon }_i,t_i\in E,{\epsilon }_i\sim N\left(0,{\sigma }^2\right),i=1,\cdots ,n$.

If $H=H_Q$ and $g\in D\left(L^{†}\right)$, then

$${\overline{f}}_{D,n}^{†}\left(t\right)=\left(\left(U{Q}_{t_1}\right)\left(t\right),\cdots ,\left(U{Q}_{t_n}\right)\left(t\right)\right){(P+{\sigma }^2{I}_n)}^{-1}Z.$$

(22)

If $H=L^2\left(E\right)$ and $g\in D\left(L^{†}\right)$, then

$${\overline{f}}_{D,n}^{†}\left(t\right)=\left(\left(L^{*}{h}_{t_1}^{*}\right)\left(t\right),\cdots ,\left(L^{*}{h}_{t_n}^{*}\right)\left(t\right)\right){(K+{\sigma }^2{I}_n)}^{-1}Z,$$

(23)

where

$$Z={\left(z_1,\cdots ,z_n\right)}^T,P(i,j)={⟨U{Q}_{t_i},U{Q}_{t_j}⟩}_{H_Q},K(i,j)={⟨L^{*}{h}_{t_i}^{*},L^{*}{h}_{t_j}^{*}⟩}_{L^2\left(D\right)}.$$

Furthermore, with probability 1, we have

$$\underset{n\to \infty }{lim}\underset{\sigma \to 0}{lim}{∥{\overline{f}}_{D,n}^{†}-f^{†}∥}_H=0.$$

(24)

Proof. 

This is the repetition of Theorems 1 and 2 in [35] when L is replaced by U, g by w, and k by $k_U$. □

Meanwhile, it is important to emphasize the role of ${\sigma }^2$, which functions as a double-edged sword. On the one hand, the ill-posedness of $K_{XX}$ worsens as n increases. The variance ${\sigma }^2$ is added to the diagonal of $K_{XX}$, which can effectively improve its stability. In this case, ${\sigma }^2$ is referred to as “nugget”, which is a regularization parameter. On the other hand, if the problem at hand is itself an interpolation model—for example, given certain points on $g\left(x\right)$ of Equation (1) to determine its optimal interpolation function—${\sigma }^2$ can make this problem a non-interpolation model. Therefore, it is necessary to discuss the interpolation model separately. At that point, the minimum positive eigenvalue of $K_{XX}$ acts as a regularization parameter, as seen in methods such as truncated eigendecomposition (TEIG), discussed in [38], and kriging with pseudoinverse (PI kriging) regularization, proposed in [39].

3.2. Gaussian Process Interpolation

In this subsection, we focus on the noise-free scenario (interpolation). Suppose that there are interpolated points ${\left\{x_i,y_i\right\}}_{i=1}^n$ that satisfy

$$y_i=g\left(x_i\right),x_i\in X_n.$$

(25)

With the help of the Moore–Penrose pseudoinverse, the regression model in Equation (18) can be transformed into the interpolation model in Equation (25), as shown in the following Lemma 3, which can be found in [47,48].

Lemma 3

(Theorem 3.4 in [48]). Let $g\sim GP\left(0,k\right)$ satisfy Equation (25); then,

$${\overline{g}}_n\left(x\right)=K_{xX}^T{K}_{XX}^{†}Y,$$

(26)

$$V\left[{\overline{g}}_n\left(x\right)\right]=k(x,x)-K_{xX}^T{K}_{XX}^{†}{K}_{xX}.$$

(27)

Firstly, let $g\left(x\right)\in R\left(L\right)$, and let ${\overline{f}}_n^{†}$ be the posterior mean of $f^{†}$. Then, ${\overline{f}}_n^{†}=L^{†}{\overline{g}}_n$; i.e., it is also the minimal-norm solution of the following equation:

$$Lf={\overline{g}}_n.$$

(28)

In order to describe the approximation error between ${\overline{f}}_n^{†}$ and $f^{†}$, we also need to introduce the fill distance, defined as

$$h_{X_n}:=\underset{x\in D}{sup}\underset{x_i\in X_n}{inf}{\parallel x-x_i\parallel }_2,$$

(29)

for a given $X_n=\left\{x_1,\cdots ,x_n\right\}$. Obviously, if $\underset{n\to \infty }{lim}{h}_{X_n}=0$, then $X_n$ is dense in D.

Theorem 3.

Let $g\sim GP\left(0,k\right)$ and $g\left(x\right)\in H_k$ satisfy Equation (25).

If $H=L^2\left(E\right)$, then

$${\overline{f}}_n^{†}\left(t\right)=H_{tX}^T{K}_{XX}^{†}Y,$$

(30)

$$V\left[{\overline{f}}_n^{†}\left(t\right)\right]={⟨h_t^{*},h_t^{*}⟩}_{H_k}-H_{tX}^T{K}_{XX}^{†}{H}_{tX},$$

(31)

where $H_{tX}^T=(h_{x_1}\left(t\right),\cdots ,h_{x_n}\left(t\right))$.

If $H=H_Q$, then

$${\overline{f}}_n^{†}\left(t\right)={\eta }_{tX}^T{K}_{XX}^{†}Y,$$

(32)

$$V\left[{\overline{f}}_n^{†}\left(t\right)\right]={⟨{\eta }_t^{*},{\eta }_t^{*}⟩}_{H_k}-{\eta }_{tX}^T{K}_{XX}^{†}{\eta }_{tX},$$

(33)

where ${\eta }_{tX}^T=({\eta }_{x_1}\left(t\right),\cdots ,{\eta }_{x_n}\left(t\right))$ and ${\eta }_t^{*}\left(x\right)=\eta (x,t)={\eta }_x\left(t\right)$.

If $\underset{h_{X_n}\to 0}{lim}V\left[{\overline{g}}_n\left(x\right)\right]=0$, then

$$\underset{h_{X_n}\to 0}{lim}{\parallel {\overline{f}}_n^{†}-f^{†}\parallel }_H=0.$$

(34)

Proof. 

We only need to prove Equations (30) and (31), and similar methods can prove Equations (32) and (33). Based on Equation (12), we have

$$L{h}_x=k_x, L{H}_{tX}^T=K_{xX}^T.$$

Therefore, in view of Equation (26) in Lemma 3, we have

$${\overline{f}}_n^{†}\left(t\right)=L^{†}{\overline{g}}_n\left(x\right)=H_{tX}^T{K}_{XX}^{†}Y.$$

Since $g\sim GP\left(0,k\right)$, then

$$E\left[g{g}^T\right]=k.$$

In accordance with Lemma 2, we can obtain $E\left[f^{†}\right]=E\left[L^{†}g\right]=L^{†}E\left[g\right]=0$. Moreover,

$$E\left[\left[\left(L^{†}g\right)\left(t\right)\right]{\left[L^{†}g\left(t^{\prime }\right)\right]}^T\right]=L_x^{†}k\left(x,x^{\prime }\right){\left(L_{x^{\prime }}^{†}\right)}^T,$$

$$f^{†}\left(t\right)\sim GP\left(0,L_x^{†}k\left(x,x^{\prime }\right){\left(L_{x^{\prime }}^{†}\right)}^T\right).$$

Based on $E\left[Y{\left(L^{†}g\right)}^T\right]=E\left[Y{g}^T\right]{\left(L_x^{†}\right)}^T=K_{xX}{\left(L_x^{†}\right)}^T$,

$${\left.\left[\begin{array}{c}Y\\ \left(L^{†}g\right)\left(t\right)\end{array}\right]\sim N\left(\left[\begin{array}{c}0\hfill \\ 0\hfill \end{array}\right],\left[\begin{array}{cc}{K}_{XX}& K_{x^{\prime }X}{\left(L_{x^{\prime }}^{†}\right)}^T\\ L_x^{†}{K}_{xX}^T& L_x^{†}k\left(x,x^{\prime }\right){\left(L_{x^{\prime }}^{†}\right)}^T\end{array}\right]\right)\right|}_{x^{\prime }=x},$$

and, therefore,

$$V\left[{\overline{f}}_n^{†}\left(t\right)\right]={\left.\left[L_x^{†}k\left(x,x^{\prime }\right){\left(L_{x^{\prime }}^{†}\right)}^T-L_x^{†}{K}_{xX}^T{K}_{XX}^{†}{K}_{x^{\prime }X}{\left(L_{x^{\prime }}^{†}\right)}^T\right]\right|}_{x^{\prime }=x}.$$

On account of $k\left(x,x^{\prime }\right)={⟨k_x,k_{x^{\prime }}⟩}_{H_k}$ and Lemma 2, we have

$$L_x^{†}k\left(x,x^{\prime }\right){\left(L_{x^{\prime }}^{†}\right)}^T={⟨L_x^{†}{k}_x,k_{x^{\prime }}{\left(L_{x^{\prime }}^{†}\right)}^T⟩}_{H_k}={⟨h_t^{*},h_{t^{\prime }}^{*}⟩}_{H_k},$$

$$L_x^{†}{K}_{xX}^T{K}_{XX}^{†}{K}_{x^{\prime }X}{\left(L_{x^{\prime }}^{†}\right)}^T=H_{tX}^T{K}_{XX}^{†}{H}_{t^{\prime }X}.$$

Consequently,

$$V\left[{\overline{f}}_n^{†}\left(t\right)\right]={⟨h_t^{*},h_t^{*}⟩}_{H_k}-H_{tX}^T{K}_{XX}^{†}{H}_{tX}.$$

Next, we will show Equation (34).

Based on the H–$H_k$ formulation, we get

$$\parallel {\overline{f}}_n^{†}-f^{†}{\parallel }_H={\parallel K_{xX}^T{K}_{XX}^{†}Y-g\parallel }_{H_k},$$

and then we can simply show that

$$\underset{h_{X_n}\to 0}{lim}{\parallel K_{xX}^T{K}_{XX}^{†}Y-g\parallel }_{H_k}=0.$$

(35)

For any $c_1,\cdots ,c_n$, we have

$$\underset{{\parallel m\parallel }_{H_k}\le 1}{sup}\sum _{i=1}^n{c}_{i}m\left(x_i\right)=\underset{{\parallel m\parallel }_{H_k}\le 1}{sup}{⟨\sum _{i=1}^n{c}_{i}k(·,x_i),m⟩}_{H_k}.$$

According to the Cauchy–Schwartz inequality, we get

$$\underset{{\parallel m\parallel }_{H_k}\le 1}{sup}{⟨\sum _{i=1}^n{c}_{i}k(·,x_i),m⟩}_{H_k}\le \underset{{\parallel m\parallel }_{H_k}\le 1}{sup}\parallel \sum _{i=1}^n{c}_{i}k(·,x_i){\parallel }_{H_k}{\parallel m\parallel }_{H_k}={\parallel \sum _{i=1}^n{c}_{i}k(·,x_i)\parallel }_{H_k}.$$

Let $u\left(x\right):={\displaystyle \sum _{i=1}^n}{c}_{i}k(·,x_i)/{\parallel {\displaystyle \sum _{i=1}^n}{c}_{i}k(·,x_i)\parallel }_{H_k}$; then, ${\parallel u\parallel }_{H_k}=1$, and, further,

$$\underset{{\parallel m\parallel }_{H_k}\le 1}{sup}{⟨\sum _{i=1}^n{c}_{i}k(·,x_i),m⟩}_{H_k}\ge {⟨\sum _{i=1}^n{c}_{i}k(·,x_i),u⟩}_{H_k}={\parallel \sum _{i=1}^n{c}_{i}k(·,x_i)\parallel }_{H_k}.$$

That is,

$$\underset{{\parallel m\parallel }_{H_k}\le 1}{sup}\sum _{i=1}^n{c}_{i}m\left(x_i\right)={\parallel \sum _{i=1}^n{c}_{i}k(·,x_i)\parallel }_{H_k}.$$

We set $c_i={\left(K_{xX}^T{K}_{XX}^{†}\right)}_i$ and $m=g$ based on the above equality, yielding

$$\underset{{\parallel m\parallel }_{H_k}\le 1}{sup}(g(x)-\sum _{i=1}^n{c}_{i}g\left(x_i\right))={\parallel k(·,x)-\sum _{i=1}^n{c}_{i}k(·,x_i)\parallel }_{H_k},$$

$$\begin{array}{cc}& \parallel k(·,x)-\sum _{i=1}^n{c}_{i}k\left(·,x_i\right){\parallel }_{H_k}^2\hfill \\ \hfill =& k(x,x)-2\sum _{i=1}^n{c}_{i}k\left(x,x_i\right)+\sum _{i=1}^n\sum _{i=j}^n{c}_i{c}_{j}k\left(x_i,x_j\right)\hfill \\ \hfill =& k(x,x)-2K_{xX}^T{K}_{XX}^{†}{K}_{xX}+K_{xX}^T{K}_{XX}^{†}{K}_{XX}{K}_{XX}^{†}{K}_{xX}\hfill \\ \hfill =& k(x,x)-2K_{xX}^T{K}_{XX}^{†}{K}_{xX}+K_{xX}^T{K}_{XX}^{†}{K}_{xX}\hfill \\ \hfill =& k(x,x)-K_{xX}^T{K}_{XX}^{†}{K}_{xX}\hfill \\ \hfill =& V\left[{\overline{g}}_n\left(x\right)\right].\hfill \end{array}$$

As a result of $g\left(x\right)-{\displaystyle \sum _{i=1}^n}{c}_{i}g\left(x_i\right)=g\left(x\right)-K_{xX}^T{K}_{XX}^{†}Y$, we have

$${(g\left(x\right)-K_{xX}^T{K}_{XX}^{†}Y)}^2\le V\left[{\overline{g}}_n\left(x\right)\right].$$

(36)

Since $\underset{h_{X_n}\to 0}{lim}V\left[{\overline{g}}_n\left(x\right)\right]=0$, then

$$\underset{h_{X_n}\to 0}{lim}{K}_{xX}^T{K}_{XX}^{†}Y=g\left(x\right).$$

Thus, this proves Equation (35); that is, we have completed the proof of Equation (34).

□

Theorem 4.

Suppose that $g\left(x\right)\notin \overline{R\left(L\right)}/R\left(L\right)$ satisfies Equation (25); then,

$$\underset{h_{X_n}\to 0}{lim}{\parallel {\overline{f}}_n^{†}\parallel }_H=+\infty .$$

(37)

Proof. 

In fact, we can simply show that, if $\underset{h_{X_n}\to 0}{lim}{\parallel {\overline{f}}_n^{†}\parallel }_H<+\infty$, then $g\left(x\right)\in R\left(L\right)$. Let $H_n$ be the set of all functions in $R\left(L\right)$ satisfying Equation (25); that is,

$$H_n:=\left\{m\left(x\right)\in R\left(L\right)|m\left(x_i\right)=g\left(x_i\right)=y_i,x_i\in X_D,1\le i\le n\right\},$$

and then $H_1\supseteq \cdots \supseteq H_n\supseteq \cdots \supseteq H_{\infty }=\left\{g\left(x\right)\right\}$. Because $L{\overline{f}}_n^{†}\left(t\right)=K_{xX}^T{K}_{XX}^{†}Y\in H_n$, we get

$$\parallel K_{xX}^T{K}_{XX}^{†}{Y\parallel }_{H_k}={\parallel {\overline{f}}_n^{†}\left(t\right)\parallel }_H.$$

As a result of $\underset{h_{X_n}\to 0}{lim}{\parallel {\overline{f}}_n^{†}\parallel }_H<+\infty$, we know that ${\left\{K_{xX}^T{K}_{XX}^{†}Y\right\}}_{n=1}^{\infty }$ is a Cauchy sequence in $R\left(L\right)(=H_k)$. Therefore,

$$\underset{h_{X_n}\to 0}{lim}{K}_{xX}^T{K}_{XX}^{†}Y=g\left(x\right).$$

Based on $K_{xX}^T{K}_{XX}^{†}Y\in H_n\subseteq R\left(L\right)$, $g\left(x\right)\in R\left(L\right)$. This conflicts with $g\left(x\right)\notin \overline{R\left(L\right)}/R\left(L\right)$, resulting in

$$\underset{h_{X_n}\to 0}{lim}{\parallel {\overline{f}}_n^{†}\parallel }_H=+\infty .$$

Theorem 4 has thus been proven. □

Secondly, we consider the case where $g\left(x\right)\in D\left(L^{†}\right)$ via the following remark.

Remark 2.

Let $g\in D\left(L^{†}\right)$; then, $w=L^{*}g\in H_{k_U}$. Hence, we can assume that $w\sim GP(0,k_U)$, where $k_U(t,t^{\prime })={⟨L^{*}{h}_t^{*},L^{*}{h}_{t^{\prime }}^{*}⟩}_{L^2\left(D\right)}$ if $H=L^2\left(E\right)$ and $k_U(t,t^{\prime })={⟨U{Q}_t,U{Q}_{t^{\prime }}⟩}_{H_Q}$ if $H=H_Q$. With a derivation process similar to that in Lemma 3 and Theorem 3, similar conclusions of Theorems 3 and 4 can also be obtained.

3.3. Sequential Design

It is common knowledge that the regularization parameter ${\sigma }^2$ in Equations (22) and (23) can be estimated using maximum likelihood or cross-validation methods. Additionally, calculating the pseudoinverse $K_{XX}^{†}$ involves a parameter, i.e., the positive threshold $\eta$ below, in which an eigenvalue is considered as zero. One suggestion is given in [39] whereby $\eta$ is equal to ${\lambda }_1/{\kappa }_{max}$, where ${\lambda }_1$ is the maximum eigenvalue of $K_{XX}$ and ${\kappa }_{max}$ is a reasonable condition number, such as ${\kappa }_{max}={10}^8$. In addition to these methods, this paper considers the regularization problem from another perspective, that is, by selecting as few points in Equation (25) as possible to ensure that ${\overline{f}}_n^{†}\left(t\right)$ converges faster under an acceptable condition number of $K_{XX}$.

In practice, the selection of an experimental design $X_n=\left\{x_1,\cdots ,x_n\right\}$ has also been widely studied. For example, Wahba proposed the collocation–projection method based on certain asymptotically optimal sequences in a specific RKHS to solve FIEFKs on [0,1] [49]. However, validating such optimal sequences in this RKHS may be inconvenient. The optimal design of discrete points is determined by maximizing the singular value (smallest) of the semi-discrete or the fully discrete matrix in [50], which facilitates the control of the condition number. Bardow proposed a method to minimize the expected total error between an exact solution and estimated solution, which is useful in addressing the bias–variance trade-off that is crucial for ill-posed problems [51]. Furthermore, the concept of a redundant point set was proposed by Mohammadi et al. to obtain linear-dependent information that makes $K_{XX}$ non-invertible [39]. However, despite the above examples, there remains no systematic strategy for an optimal experimental design for FIEFKs.

In this paper, an optimal experimental design is determined via the posterior variance $V\left[{\overline{g}}_n\left(x\right)\right]$ of $g\left(x\right)$. Based on the H–$H_k$ formulation and Equation (36), we have

$$\parallel {\overline{f}}_n^{†}-f^{†}{\parallel }_H={\parallel K_{xX}^T{K}_{XX}^{†}Y-g\parallel }_{H_k},$$

(38)

and

$$|g\left(x\right)-K_{xX}^T{K}_{XX}^{†}Y|\le \sqrt{V\left[{\overline{g}}_n\left(x\right)\right]}.$$

(39)

Therefore, we simply need to minimize $V\left[{\overline{g}}_n\left(x\right)\right]$ at each step to obtain the next point, which is a greedy algorithm. We notice that Equation (39) becomes an equality at each point; that is, $\sqrt{V\left[{\overline{g}}_n\left(x\right)\right]}$ is a precise supremum.

For a given design ($X_n=\left\{x_1,\cdots ,x_n\right\}$), new points ($\left\{x_{n+1}^{\left(1\right)},\cdots ,x_{n+1}^{\left(l\right)}\right\}$) have been obtained by minimizing $V\left[{\overline{g}}_n\left(x\right)\right]$, denoted as $D_{n+1}$. In this case, the next point ($x_{n+1}$) is incorporated into the design $X_n$ through the following:

$$\underset{x_{n+1}^{\left(j\right)}\in D_{n+1}}{max}\underset{x_i\in X_n}{min}{\parallel x_{n+1}^{\left(j\right)}-x_i\parallel }_2,$$

(40)

where ${\parallel ·\parallel }_2$ denotes the Euclidean distance. It should be noted that there may be more than one point to satisfy Equation (40), from which only one needs to be selected. In this paper, the initial point in design $X_n$ is usually selected as the center of D. More selections can be found in [52].

4. Degenerate Kernel Equation

It should be emphasized that there is a special integral kernel that warrants a separate discussion, i.e., the degenerate kernel:

$$h(x,t)=\sum _{i=1}^m{a}_i\left(x\right)b_i\left(t\right).$$

(41)

In this case, if Equation (1) with the integral kernel represented as Equation (41) is solvable, i.e., $g\left(x\right)\in R\left(L\right)$, then we can obtain the following corollary.

Corollary 1.

Let Equation (1) be solvable with integral kernel $h(x,t)$ as Equation (41) and satisfy Equation (25). We then have

$${\overline{f}}_n^{†}\left(t\right)=B_m^T\left(t\right)A^{†}A{B}^{-1}{A}^{†}Y,$$

(42)

$${\overline{g}}_n\left(x\right)=A_m^T\left(x\right)B{A}^{†}A{B}^{-1}{A}^{†}Y,$$

(43)

$$V\left[{\overline{f}}_n^{†}\left(t\right)\right]=L^{†}L{B}_m^T\left(t\right)B^{-1}{L}^{†}L{B}_m\left(t\right)-{\left(A^{†}A{B}_m\left(t\right)\right)}^T{B}^{-1}{A}^{†}A{B}_m\left(t\right),$$

(44)

$$V\left[{\overline{g}}_n\left(x\right)\right]=A_m^T\left(x\right)B[B^{-1}-A^{†}A{B}^{-1}{A}^{†}A]B{A}_m\left(x\right),$$

(45)

where $B_m\left(t\right)={\left(b_1\left(t\right),\cdots ,b_m\left(t\right)\right)}^T$, $A_m\left(x\right)={\left(a_1\left(x\right),\cdots ,a_m\left(x\right)\right)}^T$, $b_{ij}={\int }_E{b}_i\left(t\right)b_j\left(t\right)dt$, $B={\left\{b_{ij}\right\}}_{1\le i,j\le m}$, $A^T$ is the conjugate transpose of $A={\left(A_m\left(x_1\right),\cdots ,A_m\left(x_n\right)\right)}^T$.

Proof. 

According to Equation (10), we have $k(x,x^{\prime })=A_m^T\left(x\right)B{A}_m\left(x^{\prime }\right),$ so $K_{XX}=AB{A}^T$. Because ${\left\{b_i\left(t\right)\right\}}_{i=1}^m$ is linearly independent, B is obtained as a positive definite matrix. Thus, we can claim that

$$K_{XX}^{†}={\left(A^T\right)}^{†}{B}^{-1}{A}^{†}.$$

(46)

According to Corollary 3.2 in [53], we can prove that

$$rank\left(\begin{array}{ccc}B& C& {\left(AB\right)}^T{K}_{XX}\\ A& 0& 0\\ K_{XX}{\left(B{A}^T\right)}^T& 0& 0\end{array}\right)=rank\left(K_{XX}\right)+rank\left(B\right),$$

where $rank\left(K_{XX}\right)$ represents the rank of matrix $K_{XX}$. Evidently, through direct calculation, $rank\left(K_{XX}\right)\le rank\left(B\right)$ and

$$rank\left(\begin{array}{ccc}B& C& {\left(AB\right)}^T{K}_{XX}\\ A& 0& 0\\ K_{XX}{\left(B{A}^T\right)}^T& 0& 0\end{array}\right)=rank\left(\begin{array}{ccc}B& 0& 0\\ 0& A{B}^{-1}A& A{A}^{\top }{K}_{XX}\\ 0& K_{XX}A{A}^{\top }& K_{XX}^3\end{array}\right).$$

At this point, we simply need to prove that

$$rank\left(\begin{array}{cc}A{B}^{-1}A& A{A}^{\top }{K}_{XX}\\ K_{XX}A{A}^{\top }& K_{XX}^3\end{array}\right)=rank\left(K_{XX}\right).$$

We notice that

$$\left(\begin{array}{cc}A{B}^{-1}A& A{A}^{\top }{K}_{XX}\\ K_{XX}A{A}^{\top }& K_{XX}^3\end{array}\right)=\left(\begin{array}{c}A{B}^{-1/2}\\ K_{XX}A{B}^{1/2}\end{array}\right){\left(\begin{array}{c}A{B}^{-1/2}\\ K_{XX}A{B}^{1/2}\end{array}\right)}^T.$$

Therefore, we simply need to show that

$$rank\left(\begin{array}{c}A{B}^{-1/2}\\ K_{XX}A{B}^{1/2}\end{array}\right)=rank\left(K_{XX}\right).$$

(47)

Based on $rank\left(K_{XX}\right)=rank\left(A\right)$ and

$$rank\left(\begin{array}{c}A{B}^{-1/2}\\ K_{XX}A{B}^{1/2}\end{array}\right)=rank\left(\begin{array}{c}A\\ K_{XX}AB\end{array}\right)=rank\left(\begin{array}{c}A\\ AB{A}^{T}AB\end{array}\right)=rank\left(A\right),$$

this completes the proof of Equation (47); that is, Equation (46) is correct. According to Theorem 1.1.2 in [54] and Equation (46), we have

$$K_{XX}^{†}={\left(A^{†}\right)}^T{B}^{-1}{A}^{†}.$$

Since $h(x,t)=B_m^T\left(t\right)A_m\left(x\right)$, we obtain $K_{xX}^T=L{H}_{tX}^T=A_m^T\left(x\right)B{A}^T$. Thus,

$$L^{†}{K}_{xX}^T=H_{tX}^T=B_m^T\left(t\right)A^T,$$

$$L^{†}{A}_m^T\left(x\right)=L^{†}L{B}_m^T\left(t\right)B^{-1}.$$

Therefore, based on Equations (30) and (31), we have

$${\overline{f}}_n^{†}\left(t\right)=B_m^T\left(t\right)A^{†}A{B}^{-1}{A}^{†}Y,$$

$$V\left[{\overline{f}}_n^{†}\left(t\right)\right]=L^{†}L{B}_m^T\left(t\right)B^{-1}{L}^{†}L{B}_m\left(t\right)-{\left(A^{†}A{B}_m\left(t\right)\right)}^T{B}^{-1}{A}^{†}A{B}_m\left(t\right).$$

Similarly, based on Lemma 3 and Equation (46), we obtain

$${\overline{g}}_n\left(x\right)=A_m^T\left(x\right)B{A}^{†}A{B}^{-1}{A}^{†}Y,$$

$$V\left[{\overline{g}}_n\left(x\right)\right]=A_m^T\left(x\right)[B-B{A}^{†}A{B}^{-1}{A}^{†}AB]A_m\left(x\right).$$

□

Let us analyze the minimal-norm solution in Equation (42) from another point of view. Under the assumption of Equation (25), we expect that one solution $f\left(t\right)=B_m^T\left(t\right)C$ can simultaneously minimize

$$\sum _{i=1}^n{\left({\int }_{E}h\left(x_i,t\right)f\left(t\right)dt-y_i\right)}^2+{\parallel C\parallel }_2^2,$$

(48)

where $h\left(x_i,t\right)$ is defined as Equation (41) and C is to be determined. Obviously, by minimizing the first part of Equation (48), we obtain $C=B^{-1}{A}^{†}Y.$ In conjunction with the second part, C is unique and acquired as

$$C=A^{†}A{B}^{-1}{A}^{†}Y.$$

Namely, the solution $B_m^T\left(t\right)C$, obtained by optimizing Equation (48), is the minimal-norm.

Corollary 2.

Let Equation (1) be solvable with the integral kernel $h(x,t)$ as defined in Equation (41). Suppose that there are m distinct points ${\left\{x_i,y_i\right\}}_{i=1}^m$ such that $|K_{XX}|\ne 0$. Then,

$${\overline{f}}_m^{†}=B_m^T{B}^{-1}{A}^{-1}{g}_X,$$

$${\overline{g}}_m=g=A_m^T{A}^{-1}Y,$$

$$V\left[{\overline{f}}_m^{†}\right]=V\left[{\overline{g}}_m\right]=0,$$

where $|K_{XX}|$ is the determinant of $K_{XX}$.

Proof. 

According to $K_{XX}^{†}={\left(A^T\right)}^{†}{B}^{-1}{A}^{†}$ and $det\left(K_{XX}\right)\ne 0$, we know that A is an invertible matrix; that is, $A^{†}=A^{-1}$. In this case, $L^{†}L=I$ and $A^{†}A=I_m$. Here, I and $I_m$ denote the identity operator and identity matrix with order m, respectively. With this notation, the conclusions to be proven immediately follow.

□

Remark 3.

Corollary 1 has two improvements compared with Corollary 2. On the one hand, we do not require $|K_{XX}|\ne 0$, which is difficult to guarantee in practical problems. The exact solution can be obtained by simply taking the points sequentially such that $rank\left(K_{XX}\right)=m$. On the other hand, we present an analytical representation of the minimum-norm solution regardless of whether n and m are equal. That is to say, the conclusions in Corollary 1 are valid for any solvable degenerate kernel equation.

5. Illustrative Examples

Example 1.

Let us consider the classical FIEFKs below [29]:

$${\int }_0^1{\mathrm{e}}^{xt}f\left(t\right)dt=g\left(x\right),$$

where $g\left(x\right)={\displaystyle \frac{{\mathrm{e}}^{x+1}-1}{x+1}}$, which has the exact solution of $f^{†}\left(t\right)={\mathrm{e}}^t$.

Let $h_x\left(t\right)={\mathrm{e}}^{xt}$ and $H=L^2\left([0,1]\right)$ according to Equation (10). Then,

$$K(x,x^{\prime })={\displaystyle \frac{{\mathrm{e}}^{x+x^{\prime }}-1}{x+x^{\prime }}},g\left(x\right)=K(x,1).$$

According to Equation (16), then

$$f^{†}\left(t\right)={⟨g,h_t^{*}⟩}_{H_K}=h_t^{*}\left(1\right)=h_1\left(t\right)={\mathrm{e}}^t.$$

Example 2.

Let us consider

$${\int }_0^{1}h(x,t)f\left(t\right)dt=g\left(x\right),$$

(49)

with integral kernel

$$h(x,t)=\left\{\begin{array}{cc}x(1-t),\hfill & 0⩽x⩽t⩽1\hfill \\ t(1-x),\hfill & 0⩽t<x⩽1\hfill \end{array}\right..$$

Similarly to [55], assume that $g\left(x\right)$ of Equation (49) is chosen as

$$g\left(x\right)={\displaystyle \frac{25}{1008}}x(x-1)\left(-17-17x+11x^2+11x^3-3x^4-3x^5+x^6\right),$$

and then

$$f^{†}\left(t\right)=-{\displaystyle \frac{25}{18}}t(t-1)\left(3+3t-2t^2-2t^3+t^4\right),$$

is the minimal-norm solution of Equation (1).

Our aim is to obtain an optimally approximate solution with as few points as sequentially possible. According to Equation (10), if $x\le x^{\prime }$, we get

$$k(x,x^{\prime })={\displaystyle \frac{x^3}{3}}(1-x)\left(1-x^{\prime }\right)+x{x}^{\prime }{\displaystyle \frac{{\left(1-x^{\prime }\right)}^3}{3}}+\left(1-x^{\prime }\right)x[{\displaystyle \frac{{\left(x^{\prime }\right)}^2-x^2}{2}}-{\displaystyle \frac{{\left(x^{\prime }\right)}^3-x^3}{3}}].$$

If $x^{\prime }<x$, $x^{\prime }$, and x is interchangeable in the above equality. At this point, we can apply Equations (27) and (30) to discuss this example.

In comparison with uniform points, the new point can be obtained by sequentially minimizing $V\left[{\overline{g}}_n\left(x\right)\right]$ when we choose the initial point as 0.5 in this numerical experiment, as shown in Figure 1. This is because it is the midpoint of the interval [0,1]. Therefore, under the same number of points, the approximate solution obtained via sequential sampling yields a lower absolute error compared to uniform sampling. When the points reach a certain amount, their approximate effect is consistent, as shown in Figure 2.

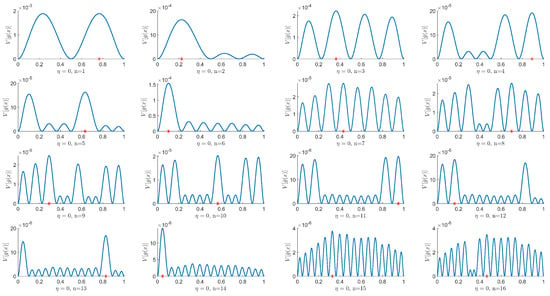
Figure 1. Minimizing the posterior variance $V\left[{\overline{g}}_n\left(x\right)\right]$ of $g\left(x\right)$ also minimizes the maximum uncertainty of ${\overline{g}}_n\left(x\right)$. The subfigure on the right was obtained by minimizing the left subfigure. It can be seen that the generated points (red stars) are not uniformly distributed on [0,1].

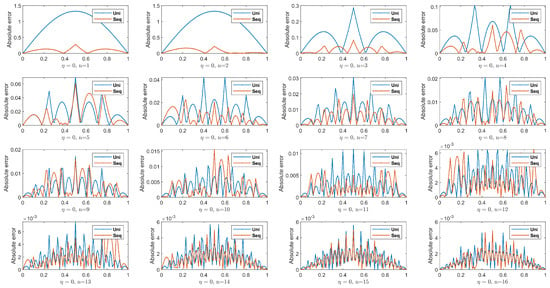
Figure 2. The absolute error was plotted under the uniform and sequential points, which are denoted as Uni and Seq in this figure, respectively. In most cases, the approximate solutions under sequential points have smaller absolute error than uniform points. When $h_{X_n}$ is less than a certain value, that is, when n is greater than a positive integer, the two have almost the same absolute error.

It is emphasized that the covariance matrix $K_{XX}$ is always invertible, and the maximum condition number is $2.0193\times {10}^4$ during sequential sampling.

Example 3

(Phillips Equation [56]). Let us consider the following FIEFKs:

$${\int }_{-6}^{6}h(x,t)f\left(t\right)dt=g\left(x\right),-6\le x\le 6,$$

(50)

where $f\left(t\right)$, $h(x,t)$, and $g\left(x\right)$ are presented by

$$h(x,t)=f(x-t), f\left(t\right)=\left\{\begin{array}{cc}1+cos{\displaystyle \frac{\pi t}{3}},\hfill & \left|t\right|<3\hfill \\ 0,\hfill & \left|t\right|\ge 3\hfill \end{array}\right.,$$

$$g\left(x\right)=(6-|x\left|\right)\left(1+{\displaystyle \frac{1}{2}}cos{\displaystyle \frac{\pi x}{3}}\right)+{\displaystyle \frac{9}{2\pi }}sin{\displaystyle \frac{\pi \left|x\right|}{3}}.$$

This integral equation has also been studied in Refs. [57,58], in which the right-hand term $g\left(x\right)$ is assumed to be unknown, so the observations are considered to be noisy. However, our starting point is to make full use of the $g\left(x\right)$ information and use as few points as possible to approximate the exact solution so as to save the observation cost. In this example, we cannot assume that the initial point equals the midpoint 0 of $[-6,6]$; otherwise, the exact solution would be obtained directly based on Equation (30), i.e.,

$${\overline{f}}_1^{†}\left(t\right)=h(0,t)k{(0,0)}^{-1}g\left(0\right)=1+cos{\displaystyle \frac{\pi t}{3}}.$$

(51)

Strategically choosing $\pm 1$ as the initial point can take advantage of the symmetry of the domain and may not necessarily take the midpoint of the interval. As Figure 3 demonstrates, sequential point generation via posterior variance minimization $V\left[{\overline{g}}_n\left(x\right)\right]$ dynamically responds to regularization threshold $\eta$. This parameter fundamentally transforms the solution paradigm: when $\eta >0$, the Gaussian process transitions from exact interpolation to approximate smoothing—a deliberate regularization mechanism in ill-posed problems. Crucially, $\eta$ balances dual objectives: (1) numerical stability through condition number control of $K_{XX}$ and (2) approximation fidelity via error minimization. Experimental validation in Figure 4 reveals that $\eta ={10}^{-4}$ emerges as a better configuration: it maintains solution stability (preventing exponential error growth observed at $\eta <{10}^{-6}$) while achieving the accuracy required for the lower threshold configuration, as shown in Figure 4. At this threshold, sequential design achieves comparable absolute error to uniform discretization. It was also determined that the threshold $\eta$ and the number of interpolation points n are closely related, and that a precise mathematical relationship is not yet available. The sensitivity analysis confirms the role of $\eta$ as a bias–variance trade-off controller: higher values (higher bias at $\eta ={10}^{-2}$, as shown in Figure 4) make the solution too smooth, while lower values ($\eta >{10}^{-6}$) lead to instability. This identifies $\eta ={10}^{-4}$ as being close to the stability–accuracy threshold for the problem.

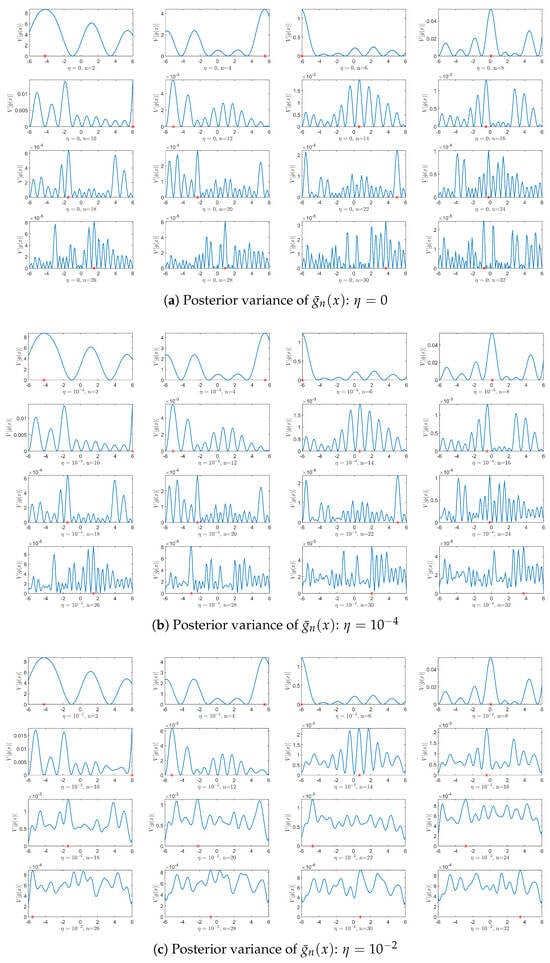
Figure 3. The new point obtained by sequentially minimizing $V\left[{\overline{g}}_n\left(x\right)\right]$ for different $\eta$. In this case, the Gaussian process interpolation model has turned into a non-interpolated model.

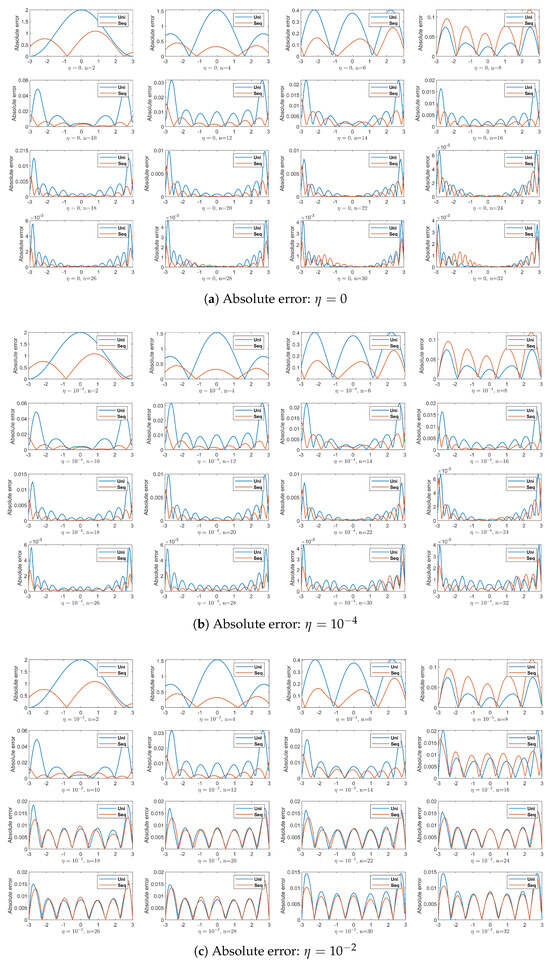
Figure 4. The absolute error between the exact solution and the approximate solution is plotted under uniform and sequential points for different $\eta$.

Remark 4.

The core computational workflow employs a greedy algorithm to sequentially determine the next interpolation point by minimizing the posterior variance

$$V\left[{\overline{g}}_n\left(x\right)\right]=k(x,x)-K_{xX}^T{K}_{XX}^{†}{K}_{xX}.$$

This process generates multiple candidate points at each step. Crucially, the final selection among these candidates follows the maximin criterion: prioritizing points that maximize the minimum distance to existing nodes. This dual-stage approach ensures optimal spatial distribution. Furthermore, as defined by the mathematical expression of $V\left[{\overline{g}}_n\left(x\right)\right]$, the point generation mechanism operates independently of the specific form of $g\left(x\right)$—the right-hand term of Equation (1). This intrinsic independence from $g\left(x\right)$ fundamentally distinguishes the method from uniform discretization methods, where adaptation is not possible and more information about $g\left(x\right)$ needs to be known, limiting the scope of application.

6. Conclusions

This paper sought to address the most fundamental question in integral equations: if the right-hand term possessed an analytical expression, could an analytical expression of the solution likewise be derived? It was concluded that various analytical solutions could be presented in operator forms. Given the computational complexity associated with the inner product of the complex reproducing kernel, numerical solutions were investigated. Utilizing the H–$H_k$ formulation, a novel point selection strategy was proposed by minimizing the posterior variance $V\left[{\overline{g}}_n\left(x\right)\right]$ of the integral equation’s right-hand term. This greedy algorithm for point selection yielded enhanced approximation accuracy for the solutions. Specifically, it achieved comparable absolute error to the other regularization methods while requiring fewer discretization points. Consequently, the condition number of $K_{XX}$ was effectively maintained within acceptable bounds, thereby ensuring solution stability. Furthermore, increasing the threshold $\eta$ could be implemented as a supplementary measure. Future research will investigate methodologies for the precise selection of $\eta$ to solve FIEFKs.