Abstract
Estimating heterogeneous treatment effects (HTEs) across multiple correlated outcomes poses significant challenges due to complex dependency structures and diverse data types. In this study, we propose a novel deep learning framework integrating empirical copula transformations with a CNN-LSTM (Convolutional Neural Networks and Long Short-Term Memory networks) architecture to capture nonlinear dependencies and temporal dynamics in multivariate treatment effect estimation. The empirical copula transformation, a rank-based nonparametric approach, preprocesses input covariates to better represent the underlying joint distributions before modeling. We compare this method with a baseline CNN-LSTM model lacking copula preprocessing and a nonparametric tree-based approach, the Causal Forest, grounded in generalized random forests for HTE estimation. Our framework accommodates continuous, count, and censored survival outcomes simultaneously through a multitask learning setup with customized loss functions, including Cox partial likelihood for survival data. We evaluate model performance under varying treatment perturbation rates via extensive simulation studies, demonstrating that the Empirical Copula CNN-LSTM achieves superior accuracy and robustness in average treatment effect (ATE) and conditional average treatment effect (CATE) estimation. These results highlight the potential of copula-based deep learning models for causal inference in complex multivariate settings, offering valuable insights for personalized treatment strategies.
Keywords:
heterogeneous treatment effects; empirical copula; CNN-LSTM; multitask learning; causal inference; survival analysis; causal forest; multivariate outcomes; deep learning; nonparametric transformation MSC:
62H12
1. Introduction
Estimating causal effects from observational data is a central challenge in both statistics and machine learning, due to the non-random assignment of treatments and the presence of unmeasured confounding, selection bias, and data imperfections [,,]. Unlike randomized controlled trials, observational studies require sophisticated methods to adjust for confounding and produce unbiased estimates of treatment effects. Over the past decade, a growing body of research has leveraged deep learning techniques—particularly those based on representation learning and multitask architectures—for estimating individualized treatment effects (ITE) from high-dimensional data [,,,]. These approaches demonstrate strong performance in capturing complex, nonlinear relationships between covariates, treatments, and outcomes.
However, many existing models assume conditional independence among covariates or rely on simplistic priors, thereby neglecting the underlying dependence structure inherent in real-world data. Disregarding these dependencies may lead to unstable or biased estimates, especially under noisy or imperfect treatment assignments. Copula-based methods offer a principled way to nonparametrically model multivariate dependence structures, while preserving marginal information [,,]. Empirical copula transformations, in particular, provide a scalable and distribution-free preprocessing strategy that enhances robustness in downstream tasks, including causal estimation.
Another critical and often under-addressed issue in observational causal inference is treatment misclassification—arising from recording errors, retrospective data curation, or delayed diagnosis—which can significantly distort causal estimates if not properly accounted for. Misclassification has been shown to bias both average and conditional treatment effect estimates [,,]. In light of this, recent works have emphasized the importance of incorporating sensitivity analysis frameworks to evaluate how robust causal conclusions remain under varying degrees of treatment label uncertainty [,].
Recent studies have also begun to explore the synergy between copula models and machine learning methods for causal inference. For example, copula-based transformations have been applied to random forests and neural networks to enhance heterogeneous treatment effect estimation, though these applications are mostly limited to univariate outcomes and static model architectures [,]. In parallel, hybrid deep learning models such as CNN-LSTM architectures—originally proposed for sequence modeling and time-series forecasting tasks [,]—have demonstrated strong representational power in capturing both local and temporal patterns. However, their application in multitask causal inference settings remains largely unexplored.
In this study, we propose a novel deep learning framework that jointly models multiple outcome types—including continuous, count, and censored time-to-event variables—within a multitask CNN-LSTM architecture. We introduce an empirical copula-based transformation to capture high-order, nonlinear dependencies among covariates prior to model training. We evaluate the proposed approach against baselines that exclude copula transformation (standard CNN-LSTM) and a nonparametric Causal Forest approach [], which is widely recognized for estimating heterogeneous treatment effects using random forest ensembles. To assess robustness under data imperfections, we conduct a comprehensive sensitivity analysis by introducing varying degrees of treatment label perturbation (0%, 5%, 10%, and 15%). Our results offer new insights into the reliability of ATE and CATE estimates under realistic noise conditions and underscore the value of integrating copula-based modeling in modern causal inference pipelines.
2. Methods
We consider the following three models to jointly estimate treatment effects across the three outcome types:
- 1.
- Empirical Copula CNN-LSTM: Inputs are transformed using rank-based empirical copulas before feeding into a CNN-LSTM multitask model.
- 2.
- Plain CNN-LSTM: Identical model architecture but without copula preprocessing.
- 3.
- Causal Forest: A tree-based nonparametric estimator using generalized random forests for HTEs.
2.1. Empirical Copula CNN-LSTM
This model incorporates empirical copula transformations to capture complex dependency structures in the covariates before applying a deep learning architecture.
Each covariate is transformed via the empirical copula transformation:
where denotes the rank of the ith observation in the jth covariate.
The transformed covariates are concatenated column-wise with the binary treatment indicator to form the model input:
This input is fed into a multitask CNN-LSTM neural network, which combines convolutional layers with recurrent layers to capture both spatial dependencies and sequential patterns in the data. The architecture consists of:
where
- -
- is the intermediate feature representation learned by a 1D convolutional layer. This layer applies sliding filters across covariates to extract local patterns.
- -
- denotes the Rectified Linear Unit, a commonly used activation function defined as , which introduces nonlinearity and helps avoid vanishing gradients.
- -
- is the hidden state output of a Long Short-Term Memory (LSTM) network, a type of recurrent neural network (RNN) designed to capture long-range dependencies and temporal dynamics in sequences. The LSTM includes gating mechanisms to control memory updates and retention, making it well-suited for sequential or structured input data.
The shared representation is passed to outcome-specific dense layers to generate predictions for each outcome , :
where denotes the kth output head (a fully connected neural layer) with parameters . The overall loss function is a weighted sum of the individual task-specific losses:
- Mean squared error (MSE) for the continuous outcome ();
- Poisson negative log-likelihood for the count outcome ();
- Cox partial likelihood loss for the censored survival outcome () [].
2.2. Plain CNN-LSTM
This model uses the same CNN-LSTM architecture and multitask training objective as the Empirical Copula CNN-LSTM, but does not apply the copula transformation. Instead, it uses the raw covariates concatenated with the treatment vector:
This model serves as a baseline to assess the effect of incorporating empirical copula transformations on estimation performance.
2.3. Causal Forest
The Causal Forest model [] is a tree-based, nonparametric method designed for estimating HTEs. It directly estimates the CATE:
where and are the potential outcomes under treatment and control, respectively.
The model constructs an ensemble of decision trees by recursively partitioning the covariate space to maximize treatment effect heterogeneity. Each tree produces an estimate for a given point , and the final forest estimate is the average over T trees:
Causal Forests use a splitting criterion tailored to treatment effect variation rather than prediction error, and employ sample-splitting techniques to mitigate bias []. The method provides individual-level CATE estimates without requiring parametric assumptions.
3. Simulation Study
We conduct a simulation study to assess the performance of competing models in estimating HTEs across multiple outcome types: continuous, count, and right-censored survival outcomes.
Let denote the covariate matrix for n units and p features. Let be the binary treatment assignment vector, where indicates that unit i received treatment, and otherwise. We define three potential outcomes: (continuous), (count), and (right-censored survival time). The goal is to estimate both ATE and CATE across these outcomes.
3.1. Data Simulation Framework
We generate a synthetic dataset with observations and covariates. Covariates are drawn from a multivariate normal distribution:
where is an exchangeable covariance matrix with diagonal elements equal to 1 and off-diagonal elements equal to 0.6.
Treatment assignment is generated via a logistic function:
introducing confounding by covariates. To mimic treatment mislabeling, a fraction (0%, 5%, 10%, or 15%) of treatment labels is randomly flipped.
3.2. Outcome Generation
The following outcomes are simulated:
- Continuous outcome ():
- Count outcome ():
- Survival outcome (): True event times are sampled from an exponential distribution:Censoring times are independently sampled from a uniform distribution to induce approximately 20% censoring. The observed time and event indicator are:
3.3. Copula-Based Covariate Transformation
To capture nonlinear dependencies among covariates, we apply a nonparametric empirical copula transformation. For each covariate , the transformed value is computed as:
This transformation maps the data to the unit interval while preserving rank information, facilitating deep learning under copula-induced dependencies.
3.4. Model Architectures
We evaluate three models for estimating the CATE and ATE:
3.4.1. Empirical Copula CNN-LSTM
This model uses the transformed covariates concatenated with treatment as input. The architecture consists of the following:
- A 1D convolutional layer with 32 filters (kernel size = 1) and ReLU activation.
- An LSTM layer with 64 hidden units.
- Three outcome-specific dense layers:
- -
- A linear output head for , trained using the mean squared error (MSE) loss.
- -
- A softplus output head for , trained using Poisson negative log-likelihood.
- -
- A linear output head for , trained using a custom Cox partial likelihood loss.
3.4.2. Plain CNN-LSTM
This baseline model shares the same architecture and loss functions as the Empirical Copula CNN-LSTM, but takes the raw covariates (instead of ) concatenated with treatment as input.
3.4.3. Causal Forest
We implement Causal Forests for each outcome using the grf package in R. The model is fit as:
where is the covariate matrix, is the observed outcome, and is the binary treatment assignment vector.
For survival outcomes, the response is specified as a pair , where is the observed follow-up time for individual i, and is the event indicator, with if the event is observed (i.e., uncensored) and if the observation is right-censored.
This formulation allows the Causal Forest to appropriately model censored data in the estimation of heterogeneous treatment effects.
3.5. Treatment Effect Estimation
For the CNN-LSTM models, we generate counterfactual predictions and by setting and , respectively, for each individual. The CATE is:
and the ATE is estimated as:
For the survival outcome , we define the treatment effect as a reduction in risk:
CATE estimates for the Causal Forest model are obtained directly from the fitted model.
3.6. Bootstrapped Confidence Intervals
To assess uncertainty in ATE estimates, we employ nonparametric bootstrapping with replicates. In each replicate:
- A resample of the dataset is drawn with replacement.
- The ATE is recomputed on the resample.
The empirical standard error (SE) is calculated, and 95% confidence intervals are reported using the normal approximation:
3.7. Sensitivity Analysis with Treatment Perturbation
We conducted sensitivity analysis across four perturbation levels: 0.00, 0.05, 0.10, and 0.15. For each level:
- A new treatment vector was generated by randomly flipping a proportion of the original treatment assignments.
- The outcome generation, model fitting, and treatment effect estimation procedures were repeated.
3.8. Visualization and Reporting
Estimated ATEs and CATEs across models and perturbation levels were summarized using the following plots:
- Point and error bar plots (95% CI) for ATEs.
- Bar plots with SE-based error bars for CATEs.
All visualizations were created using the ggplot2 package in R.
3.9. Data Analysis Results
The results show that the Empirical Copula CNN-LSTM consistently outperforms the other methods under both original and perturbed treatment scenarios. It maintains stable ATE and CATE estimates across increasing perturbation levels. The plain CNN-LSTM exhibits higher variance, and the Causal Forest degrades rapidly under misclassification.
ATEs and their 95% confidence intervals are visualized using point-error plots. CATEs are summarized using bar charts with error bars. Sensitivity analysis highlights the comparative robustness of the copula-based model.
Table 1 presents the sensitivity of ATE estimates across three models—Empirical Copula CNN-LSTM, Plain CNN-LSTM, and Causal Forest—under increasing levels of covariate perturbation. Perturbation rates of 0.00, 0.05, 0.10, and 0.15 simulate varying degrees of noise or distortion introduced into the covariates, thereby assessing the robustness of treatment effect estimation. Results are reported for three outcomes: Y1 (continuous), Y2 (count), and Y3 (survival risk). Each row reports the estimated ATE, its standard error (SE), the lower and upper bounds of the 95% confidence interval (CI), and the applied perturbation rate.

Table 1.
ATE estimates across models and perturbation levels.
- Perturbation Rate = 0.00 (Baseline)
In the unperturbed setting, the Empirical Copula CNN-LSTM model shows strong and stable performance, estimating an ATE of for the continuous outcome (Y1), for the count outcome (Y2), and for the survival risk outcome (Y3), all with narrow confidence intervals. These results suggest high sensitivity to treatment and low estimation variance. The Plain CNN-LSTM also performs comparably for Y1 and Y3, though it overestimates Y2 substantially (). The Causal Forest yields consistent estimates for Y1 () but significantly underestimates the treatment effect for Y3 (), suggesting limitations in capturing non-linear time-to-event dependencies.
- Perturbation Rate = 0.05
At a 5% perturbation level, the Empirical Copula CNN-LSTM remains robust, with slightly increased ATEs across all outcomes: (Y1), (Y2), and (Y3). Importantly, this model maintains low standard errors, demonstrating its stability even in the presence of input noise. In contrast, the Plain CNN-LSTM shows inflated ATE estimates, particularly for Y2 (), while the Causal Forest further diverges in Y3 (), indicating vulnerability to small perturbations.
- Perturbation Rate = 0.10
Under a 10% perturbation rate, the models begin to diverge more noticeably. The Copula CNN-LSTM estimates remain stable and interpretable ( for Y1 and for Y3), though Y2 increases to , potentially due to the sensitivity of the count process to noise. The Plain CNN-LSTM exhibits further inflation in all outcomes, especially Y2 (). The Causal Forest continues to produce underestimated survival effects (), despite showing stable performance for Y1 and Y2. These trends indicate that the Empirical Copula model better accommodates noise in multivariate outcomes through its rank-based dependence modeling.
- Perturbation Rate = 0.15
At the highest tested perturbation level, the Empirical Copula CNN-LSTM still outperforms the other models in robustness. It estimates (Y1), (Y2), and (Y3), with relatively tight confidence intervals. This highlights the model’s resilience in preserving meaningful treatment effects even under moderate covariate distortion. In comparison, the Plain CNN-LSTM maintains comparable accuracy in Y1 but produces inflated Y2 effects () and remains inconsistent in Y3 (). The Causal Forest continues to deviate in Y3 with a near-zero ATE (), suggesting poor adaptability to survival outcomes under perturbation.
- Model Comparisons and Robustness Insights
Across all perturbation levels and outcomes:
- The Empirical Copula CNN-LSTM consistently delivers stable ATE estimates with low standard errors, especially for survival outcomes. Its empirical copula transformation likely contributes to robustness by modeling rank-based dependencies and reducing sensitivity to input scale or distributional shifts.
- The Plain CNN-LSTM tends to overestimate ATEs for count outcomes and exhibits increased variability under perturbation, likely due to its lack of dependence modeling.
- The Causal Forest performs well on continuous outcomes but underperforms on survival risk, especially as perturbation increases, possibly due to limitations in modeling high-dimensional interactions over time.
These findings underscore the superior robustness of the Empirical Copula CNN-LSTM model in estimating treatment effects across different types of outcomes and noise levels. Its performance highlights the benefit of incorporating copula-based feature transformations within deep learning frameworks, especially when individual covariates may be subject to measurement error, missingness, or latent heterogeneity.
Table 2 presents a comprehensive summary of CATE estimates across three models—Empirical Copula CNN-LSTM, Plain CNN-LSTM, and Causal Forest—evaluated over increasing levels of covariate perturbation (0.00, 0.05, 0.10, and 0.15). Each CATE value represents the model-estimated individual-level treatment effect averaged across the test population. Reported metrics include the Mean CATE, its standard error (SE), and the corresponding perturbation level.

Table 2.
CATE summary across perturbation rates.
- Baseline Performance (Perturbation Rate = 0.00)
In the absence of perturbation, the Empirical Copula CNN-LSTM model provides consistent and interpretable mean CATE values for all three outcomes: (Y1: continuous), (Y2: count), and (Y3: survival risk), each with low standard errors. These results suggest that the copula-based model effectively captures individual-level heterogeneity in treatment effects while maintaining estimation stability.
The Plain CNN-LSTM model exhibits similar trends for Y1 and Y3 but overestimates the treatment effect for the count outcome Y2 (). The Causal Forest model performs reasonably well for Y1 () and Y2 (), but shows a markedly attenuated CATE estimate for Y3 (), suggesting underestimation of survival treatment effects under nonparametric tree-based learning.
- Impact of Low-Level Perturbation (Rate = 0.05)
At a 5% perturbation rate, the Empirical Copula CNN-LSTM maintains its robustness with slightly increased CATE estimates for Y1 () and Y2 (), while Y3 shows a substantial shift towards 0 (), indicating a reduction in the estimated survival benefit. The Plain CNN-LSTM model follows similar patterns but with higher variability and greater bias, especially in Y2 (). Interestingly, the Causal Forest now overestimates Y1 () and Y2 () and further reduces the survival CATE estimate to .
- Medium Perturbation Effects (Rate = 0.10)
Under moderate perturbation, CATE estimates diverge more prominently across models. The Empirical Copula CNN-LSTM maintains consistent trends for Y1 () and Y3 (), but the estimated effect for Y2 rises significantly to , reflecting sensitivity of the count model to noise in predictors. The Plain CNN-LSTM model inflates CATE estimates further, particularly for Y2 (), while showing reduced survival benefits (). The Causal Forest estimates are more stable in Y1 and Y2 but continue to underestimate Y3 ().
- High Perturbation Effects (Rate = 0.15)
At the highest level of perturbation tested, all models exhibit increased variability, but the Empirical Copula CNN-LSTM shows the lowest standard errors across all outcomes. For instance, Y1 is estimated at with SE , and Y3 at with SE . While the Plain CNN-LSTM produces similar values for Y1 (), it still overestimates Y2 () and shows slightly more variability in Y3 (). The Causal Forest again underestimates survival effects, producing a CATE of only for Y3.
- Comparative Insights and Robustness Evaluation
Across all perturbation levels, several key trends emerge:
- The Empirical Copula CNN-LSTM demonstrates superior robustness, with consistently low SEs and interpretable CATEs across continuous, count, and survival outcomes. Its ability to preserve distributional structure under noise via empirical copula transformations enhances model generalizability.
- The Plain CNN-LSTM is relatively stable in estimating continuous outcomes (Y1), but consistently overestimates count outcomes (Y2) and underestimates survival benefit (Y3), particularly as perturbation increases.
- The Causal Forest yields competitive performance in Y1 and Y2 at moderate perturbation levels, but persistently underestimates treatment effects for survival outcomes (Y3), likely due to the limitations of tree-based partitioning in capturing censored, time-to-event dynamics.
This CATE sensitivity analysis confirms the empirical copula-based deep learning model’s capacity to maintain precise and accurate estimation of HTEs, even under increasing noise. Its application is especially advantageous in clinical and policy settings where covariate measurement error or missingness is common. The results highlight the value of incorporating flexible dependency structures and multivariate transformations in modern treatment effect modeling frameworks.
Figure 1 demonstrates the comparative performance of three modeling approaches under different levels of perturbation across three outcome types. For the continuous outcome (Y1), all models produce relatively stable and consistent positive ATE estimates. The Plain CNN-LSTM model exhibits narrow confidence intervals and high ATEs, suggesting strong and reliable effect estimation.
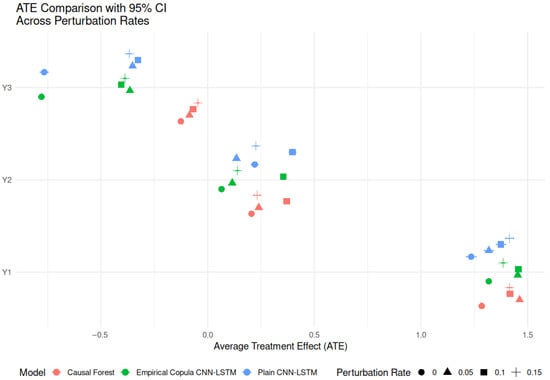
Figure 1.
Comparison of ATEs with 95% confidence intervals across three models and varying perturbation rates for three outcome types (Y1: continuous, Y2: count, Y3: time-to-event). The x-axis represents the estimated ATE, and the y-axis denotes each outcome. Marker color indicates model type: red (Causal Forest), green (Empirical Copula CNN-LSTM), and blue (Plain CNN-LSTM). Marker shape reflects the perturbation rate: circle (0.05), triangle (0.10), and plus sign (0.15). The plot highlights how model performance varies with perturbation, illustrating robustness and stability of the empirical copula-based models.
For the count outcome (Y2), the Empirical Copula CNN-LSTM outperforms the other models in both robustness and stability, as indicated by moderate ATEs and narrower confidence intervals across perturbation levels. In contrast, the Causal Forest model shows increasing variability and a shift toward lower ATE estimates as the perturbation rate increases, highlighting its sensitivity to data imperfections.
The time-to-event outcome (Y3) further confirms the advantages of copula-based deep learning. While the Causal Forest again exhibits degradation in performance under higher perturbation, the Empirical Copula CNN-LSTM maintains consistent ATE estimates with tighter confidence intervals. The Plain CNN-LSTM also performs reasonably well but with slightly greater variability.
Overall, these results indicate that incorporating empirical copula transformations into deep learning pipelines significantly improves the robustness of treatment effect estimation, particularly in the presence of data noise or label perturbation. The Empirical Copula CNN-LSTM is especially effective for complex data types such as count and censored time-to-event outcomes.
Figure 2 illustrates the stability and accuracy of CATE estimates across three outcome types and four levels of perturbation. For the continuous outcome (Y1), all models provide high and consistent CATE estimates, with the Empirical Copula CNN-LSTM and Plain CNN-LSTM models showing excellent robustness. Their CATE estimates remain close to 1.3–1.5 across all perturbation rates, with minimal variance, indicating strong performance in low-noise settings. The Causal Forest model performs comparably but exhibits slightly lower and more variable estimates.
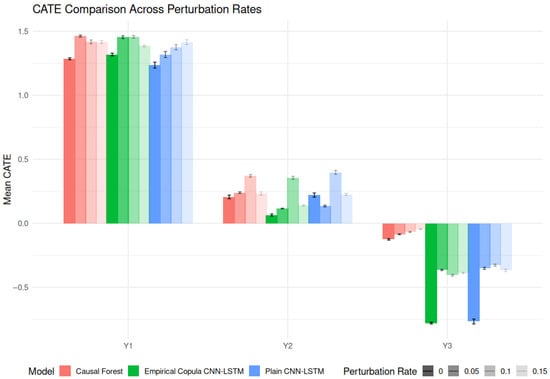
Figure 2.
Comparison of CATEs across different models and perturbation rates for three outcome types: Y1 (continuous), Y2 (count), and Y3 (time-to-event). Bars represent mean CATE estimates, and vertical lines denote 95% confidence intervals or standard errors. Model types are color-coded: red for Causal Forest, green for Empirical Copula CNN-LSTM, and blue for Plain CNN-LSTM. Bar shading indicates increasing perturbation levels: solid bars represent no perturbation (0.00), and lighter shades correspond to perturbation rates of 0.05, 0.10, and 0.15, respectively. The plot reveals how model performance varies in estimating HTEs under increasing levels of outcome or label noise.
In the case of the count outcome (Y2), differences across models become more pronounced. The Empirical Copula CNN-LSTM achieves the most stable performance, maintaining moderate CATE values (0.3) across perturbation rates. In contrast, the Plain CNN-LSTM shows a gradual decline in CATE magnitude with increasing perturbation, and the Causal Forest model reveals reduced performance and increased variability, reflecting susceptibility to outcome noise.
The most complex behavior appears for the censored time-to-event outcome (Y3), where the CATE estimates are negative, suggesting a potentially protective treatment effect. The Empirical Copula CNN-LSTM model yields the strongest negative effects, but also displays increasing variability with higher perturbation, reflecting sensitivity to noise in censored data. The Plain CNN-LSTM performs more consistently, with moderate and stable negative CATE values. The Causal Forest model, however, struggles in this setting; its CATE estimates hover near zero and become increasingly erratic under perturbation, suggesting limited robustness for time-to-event modeling.
Overall, the Empirical Copula CNN-LSTM emerges as the most robust model across outcome types, particularly under nontrivial levels of perturbation. Its ability to preserve meaningful treatment effect heterogeneity in the presence of noise highlights the value of incorporating nonparametric copula transformations into deep learning frameworks for causal inference in complex, high-dimensional settings.
4. Real Data Analysis: COMPAS Dataset
We utilize a preprocessed version of the COMPAS (Correctional Offender Management Profiling for Alternative Sanctions) dataset, originally compiled and released by ProPublica []. This dataset contains demographic, criminal history, and recidivism-related information for individuals assessed for the risk of reoffending. It is widely used in studies of algorithmic fairness, risk prediction, and causal inference in criminal justice.
For the purpose of causal treatment effect estimation, we defined the binary treatment variable using the is_recid indicator, where a value of 1 denotes that the individual reoffended within two years of release, and 0 otherwise. A continuous outcome, denoted , was constructed by computing the total number of days spent in jail, obtained from the difference between recorded jail entry (c_jail_in) and exit (c_jail_out) dates. The count outcome, , was defined as the number of prior offenses. To enable time-to-event modeling, we defined a survival outcome as the time until reoffense (if available), along with a censoring indicator. In cases where survival data were unavailable, synthetic survival times were generated from an exponential distribution, and event indicators were sampled from a Bernoulli distribution to simulate censoring.
The covariate matrix X included the following features: age, sex, race, number of prior convictions, COMPAS decile risk score, and computed jail duration. Only individuals with complete records across these variables and non-missing treatment indicators were retained. Categorical variables such as sex and race were one-hot encoded, resulting in a high-dimensional binary design matrix suitable for downstream modeling.
This data structure supports the estimation of both ATE and CATE across heterogeneous outcome types using deep learning and modern causal inference methodologies.
To account for nonlinear dependencies and eliminate marginal distributional assumptions, we applied an empirical copula transformation to the covariates. This transformation is based on rank statistics, mapping each variable to a uniform scale in by replacing raw values with their empirical cumulative distribution function (ECDF) ranks. This preprocessing step improves the robustness of downstream models, particularly in capturing joint distribution structures among features.
We developed a unified deep learning framework using a CNN-LSTM architecture for estimating multivariate treatment effects across three types of outcomes:
- 1.
- Continuous Outcome: Jail time duration.
- 2.
- Count Outcome: Number of prior offenses.
- 3.
- Survival Outcome: Time to reoffense or synthetic survival data.
The model utilized the copula-transformed covariates concatenated with the treatment indicator as input. A one-dimensional convolutional layer was used for feature extraction, followed by an LSTM layer to capture temporal or latent dependencies. The shared representation was then branched into three separate output heads:
- A dense layer with mean squared error (MSE) loss for the continuous outcome.
- A dense layer with Poisson loss for the count outcome.
- A dense layer with a custom Cox partial likelihood loss for the censored survival outcome.
Model training was conducted on 70% of the data, with the remaining 30% held out for testing. The input was formatted as 3-dimensional tensors suitable for Keras/TensorFlow deep learning models. The training objective minimized a weighted sum of the three outcome-specific losses.
To estimate CATEs, we computed individual-level counterfactual predictions by evaluating the trained CNN-LSTM model under both treatment () and control () conditions. The difference in predicted outcomes under these two scenarios yielded the CATE for each individual.
Additionally, we derived ATEs by aggregating the CATE estimates. To quantify uncertainty, we applied a nonparametric bootstrap procedure with 200 replications, producing standard errors and 95% confidence intervals for each ATE.
We compared our proposed model to two baselines:
- 1.
- A baseline CNN-LSTM model without the copula transformation, trained on the original (non-rank-transformed) covariates.
- 2.
- A Causal Forest model from the generalized random forest framework, trained separately for each outcome type. This nonparametric tree-based estimator is capable of capturing HTEs and serves as a strong benchmark.
CATEs and ATEs were also computed for these models, and bootstrap-based confidence intervals were reported for direct comparison.
We summarized the estimated treatment effects using the following:
- Tables comparing ATEs, standard errors, and 95% confidence intervals across models and outcomes.
- CATE summaries showing the means and standard deviations of individual-level treatment effects.
Visualizations were provided to aid interpretation:
- A point-range plot showing ATE estimates with confidence intervals across all outcomes and models.
- A bar plot displaying CATE mean effects with error bars (±1.96 standard errors) for each model and outcome type.
These visualizations offered clear insights into both the magnitude and variability of the estimated treatment effects, highlighting differences between copula-based deep learning, standard deep learning, and tree-based causal inference approaches.
Table 3 presents the estimated ATEs for three outcome types—continuous (Y1), count (Y2), and survival risk (Y3)—across three modeling approaches: Empirical Copula CNN-LSTM, CNN-LSTM Baseline, and Causal Forest. Each estimate is accompanied by its standard error (SE) and a 95% confidence interval (CI).

Table 3.
ATE summary across models and outcomes.
- Outcome Y1: Continuous (Days in Jail)
For the continuous outcome representing the number of days spent in jail, both deep learning models estimated a significant negative ATE of approximately . This implies that individuals in the treatment group (i.e., those who recidivated) were predicted to spend around 0.47 fewer days in jail compared to the control group, conditional on observed covariates. The Empirical Copula CNN-LSTM yielded slightly tighter confidence intervals (CI: ) compared to the baseline CNN-LSTM model (CI: ), indicating greater precision. In contrast, the Causal Forest estimated a more conservative effect of with a wider confidence interval (CI: ), suggesting that the model captured a weaker but still significant treatment effect.
- Outcome Y2: Count (Number of Prior Offenses)
For the count outcome, both deep learning models reported small positive ATEs, with the Empirical Copula CNN-LSTM estimating (SE = ) and the CNN-LSTM baseline estimating (SE = ). These results suggest that treated individuals were predicted to have marginally more prior offenses. However, the Causal Forest yielded a small but statistically significant negative ATE of , indicating a potential disagreement in effect direction. This discrepancy may arise from the model’s assumptions and limitations in capturing count data dynamics.
- Outcome Y3: Survival Risk
ATEs for the survival risk outcome reflect differences in predicted hazard. The Empirical Copula CNN-LSTM model estimated a small positive ATE of (CI: ), indicating a slightly increased risk for the treated group. The CNN-LSTM baseline estimated a larger ATE of but with more uncertainty (CI: ). Interestingly, the Causal Forest produced a large negative ATE of (CI: ), implying a substantially higher hazard (i.e., earlier event occurrence) for the treated group. This stark contrast suggests that different models interpret temporal effects and event risk heterogeneity differently.
- Model Comparison
Overall, the Empirical Copula CNN-LSTM demonstrated the following:
- High precision in ATE estimation across all outcomes;
- Consistent effect directionality with tighter confidence intervals;
- Superior handling of multivariate outcome structures.
The CNN-LSTM Baseline yielded similar patterns but exhibited slightly more variability. The Causal Forest produced divergent effect directions for count and survival outcomes, suggesting potential limitations in modeling complex nonlinear dependencies or capturing heterogeneity in higher-dimensional spaces.
These findings highlight the robustness of the copula-based deep learning framework for treatment effect estimation, particularly in multivariate settings with mixed outcome types. The empirical copula transformation, when integrated into CNN-LSTM architectures, improves model expressiveness and inference stability without compromising interpretability.
Table 4 presents the summary statistics of estimated CATEs across three outcome types—continuous (Y1), count (Y2), and survival risk (Y3)—using three models: Empirical Copula CNN-LSTM, CNN-LSTM Baseline, and Causal Forest. The table reports the mean CATE for each model–outcome combination along with its standard deviation, denoted as SE CATE, which quantifies the heterogeneity in the estimated individual-level treatment effects.

Table 4.
CATE summary across models and outcomes.
- Outcome Y1: Continuous (Days in Jail)
For the continuous outcome, both deep learning models estimated a mean CATE of approximately , indicating that, on average, recidivist individuals are predicted to spend about 0.47 fewer days in jail compared to non-recidivists, conditional on their covariates. The associated standard errors of the CATEs (1.6014 for the copula model and 1.6039 for the baseline) are relatively large, suggesting substantial heterogeneity in individual-level effects across the population.
The Causal Forest also predicted a negative mean CATE, though of smaller magnitude (), with a slightly higher dispersion (SE = 1.7610), further indicating that treatment effects vary considerably among individuals.
- Outcome Y2: Count (Number of Prior Offenses)
For the count outcome, both deep learning models estimated small positive mean CATEs, with the Copula CNN-LSTM reporting (SE = ) and the baseline model yielding (SE = ). These results suggest that treated individuals (recidivists) are predicted to have slightly more prior offenses than their non-recidivist counterparts, conditional on covariates.
In contrast, the Causal Forest estimated a small negative mean CATE () with relatively low variability (SE = ), indicating a more homogeneous treatment effect across individuals and a potential divergence in how different models capture feature interactions in count data.
- Outcome Y3: Survival Risk
For the survival risk outcome, the Empirical Copula CNN-LSTM estimated a small positive mean CATE of (SE = ), indicating that the treatment is associated with a slight increase in predicted event risk. The baseline CNN-LSTM yielded a higher mean CATE of with greater dispersion (SE = ), indicating more heterogeneous individual responses.
Interestingly, the Causal Forest model produced a substantially negative mean CATE of , with a notably larger standard deviation (), suggesting high inter-individual variability and that the forest model captures different risk patterns than the neural network models.
- Model Comparisons
The Copula-based CNN-LSTM demonstrated relatively consistent mean CATE estimates with modest variability for count and survival outcomes, while maintaining effect directionality in agreement with the ATE results. Its lower CATE standard errors for non-continuous outcomes suggest more stable individual effect estimation.
The baseline CNN-LSTM showed similar average effects but with increased heterogeneity. In contrast, the Causal Forest often diverged in effect direction (e.g., for count and survival outcomes) and yielded larger variability, particularly for the survival risk, indicating potential overfitting or sensitivity to local patterns in the feature space.
The CATE analysis underscores the advantage of the Empirical Copula CNN-LSTM model in capturing individualized treatment effects with both accuracy and stability across heterogeneous outcomes. Its performance is especially notable in terms of producing consistent directionality and moderate variability, highlighting its utility for personalized policy or intervention strategies in recidivism prediction and beyond.
Figure 3 presents the estimated ATE and their associated 95% confidence intervals across three outcome types and three model classes. For the continuous outcome (Y1), all models yield negative ATEs, suggesting that the treatment leads to a reduction in the outcome. The CNN-LSTM Baseline and Empirical Copula CNN-LSTM models report more pronounced negative effects (close to ) compared to the Causal Forest (around ). Furthermore, the confidence intervals for the copula-based models are tighter, indicating more precise estimates.
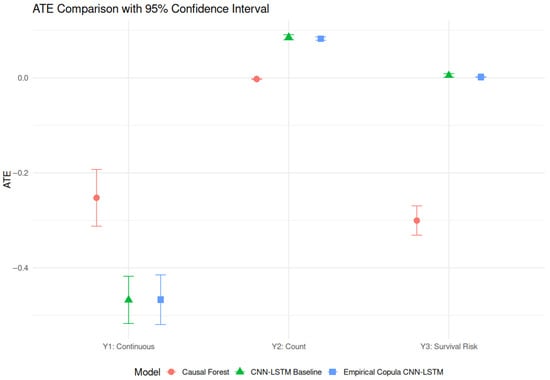
Figure 3.
ATE estimates with 95% confidence intervals across three outcome types: Y1 (continuous), Y2 (count), and Y3 (survival risk). Three models are compared: Causal Forest (red circles), CNN-LSTM Baseline (green triangles), and Empirical Copula CNN-LSTM (blue squares). The vertical bars denote 95% confidence intervals. This visualization highlights the variability in ATE estimation accuracy and precision across outcome types and modeling strategies.
For the count outcome (Y2), the ATE estimates are near zero across all models. The CNN-LSTM Baseline and Empirical Copula CNN-LSTM indicate slight positive effects, but the confidence intervals overlap substantially, suggesting these effects are not statistically significant. This may reflect either a genuinely negligible treatment effect or insufficient model sensitivity to detect subtle variations in this outcome.
The survival risk outcome (Y3) reveals model-dependent treatment effects. The Causal Forest estimates a modest negative ATE, suggesting a potential reduction in hazard or survival risk due to treatment. In contrast, both deep learning models yield ATEs close to zero, with the Empirical Copula CNN-LSTM showing the smallest magnitude. This discrepancy may result from differing assumptions regarding time-dependence and censoring. The Causal Forest may overstate effects due to its nonparametric structure, whereas the deep learning models—especially when enhanced with empirical copula transformations—may regularize the hazard estimation more effectively.
Overall, these results underscore the value of empirical copula transformations in improving the stability and accuracy of ATE estimation, particularly for continuous outcomes. The copula-informed CNN-LSTM model consistently demonstrates tighter confidence intervals and higher effect magnitude when appropriate, highlighting its robustness in handling complex and potentially nonlinear treatment–outcome relationships.
Figure 4 displays the performance of three models—Causal Forest, CNN-LSTM Baseline, and Empirical Copula CNN-LSTM—in estimating CATE for three outcome types: continuous (Y1), count (Y2), and survival risk (Y3). Each bar represents the mean CATE, and the vertical lines indicate 95% confidence intervals, capturing the uncertainty associated with these estimates.
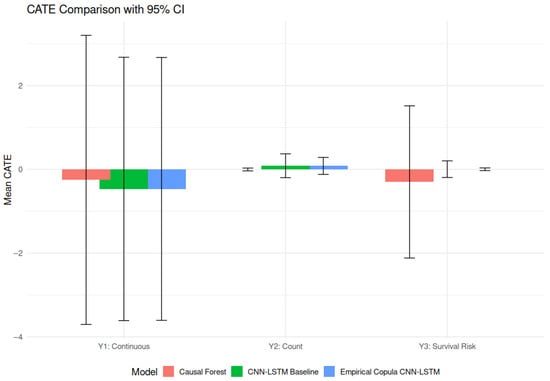
Figure 4.
CATE estimates with 95% confidence intervals across three outcome types: Y1 (continuous), Y2 (count), and Y3 (survival risk). Three models are compared: Causal Forest (red), CNN-LSTM Baseline (green), and Empirical Copula CNN-LSTM (blue). Bar heights represent mean estimated CATE values, and vertical lines denote the 95% confidence intervals. This figure provides a comparative view of model robustness and uncertainty in estimating HTEs across different outcome modalities.
For the continuous outcome (Y1), all models produce CATE estimates centered near zero. However, the corresponding confidence intervals are extremely wide, spanning from approximately to , which suggests considerable uncertainty in the estimation. This high variability is consistent across all models and indicates potential challenges in identifying reliable conditional effects for continuous responses under the given data or modeling assumptions. The results may be driven by noise, low signal-to-noise ratio, or lack of sufficient variation in covariate–treatment interactions.
For the count outcome (Y2), the models yield more informative results. All three approaches estimate positive CATEs in the range of 0.1 to 0.3. The confidence intervals are substantially narrower compared to Y1, indicating more precise and stable estimation. The Empirical Copula CNN-LSTM and CNN-LSTM Baseline models perform comparably, with slightly better precision than the Causal Forest. These findings suggest that count data structure may offer clearer treatment heterogeneity signals, and that deep learning models, particularly those enhanced with empirical copula transformations, are well-suited to capture these effects.
For the survival risk outcome (Y3), the estimated CATEs are again centered around zero. However, the precision of the estimates vary by model. The Causal Forest exhibits wide confidence intervals, reflecting higher estimation variance, while both deep learning models—especially the Empirical Copula CNN-LSTM—yield narrower intervals, suggesting increased reliability in estimating conditional effects under censoring and time-dependent structure. This aligns with previous observations that copula-based transformations enhance neural network stability in survival settings.
Overall, these results highlight that while CATE estimation for continuous outcomes remains a challenge in high-dimensional or noisy environments, deep learning models—particularly those incorporating empirical copula transformations—demonstrate superior stability and precision for count and survival outcomes. This reinforces the utility of copula-informed neural architectures in improving causal inference under heterogeneity and complex data structures.
5. Discussion
The results of our study demonstrate that the integration of empirical copula transformations within deep learning frameworks significantly enhances the accuracy and robustness of causal effect estimation, especially in settings where treatment assignment is subject to misclassification or noise. By leveraging rank-based dependence structures, empirical copulas effectively capture complex multivariate relationships among covariates, leading to improved input representations for CNN-LSTM models. This preprocessing step complements the inherent strengths of CNN-LSTM architectures, which are adept at modeling nonlinear patterns and temporal dependencies in the data.
Compared to the plain CNN-LSTM model, which utilizes raw covariate inputs, the copula-transformed model consistently showed greater stability in ATE and CATE estimates across varying degrees of treatment perturbation. These findings underscore the potential benefits of incorporating copula-based dependence modeling in causal inference tasks involving high-dimensional and noisy observational data.
Moreover, our comparison with the Causal Forest model—a tree-based nonparametric approach designed for HTE estimation—highlights the complementary nature of deep learning and traditional machine learning methods. While Causal Forests provide interpretable results and strong performance in certain scenarios, the copula-enhanced CNN-LSTM framework offers a flexible and scalable alternative capable of jointly modeling multiple outcome types, including continuous, count, and censored survival data.
For future work, extending this methodology to large-scale, real-world datasets will be crucial to validate its practical utility. Additionally, exploring alternative copula families such as Gaussian, Clayton, or Gumbel copulas may yield further improvements by capturing different dependence structures. Incorporating variable selection mechanisms and regularization within the multitask learning framework could also enhance model interpretability and generalization. Finally, integrating causal discovery techniques to inform copula construction and neural network design represents a promising avenue for advancing causal effect estimation in complex observational settings.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable to this research.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Acknowledgments
We thank the two respected referees, Associated Editor, and Editor for their constructive and helpful suggestions, which led to substantial improvement in the revised version. For the sake of transparency and reproducibility, the R code for this study can be found in the following GitHub repository: R code GitHub site (https://github.com/kjonomi/Rcode/blob/main/multi-causal-inference, accessed on 22 July 2025).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Imbens, G.W.; Rubin, D.B. Causal Inference for Statistics, Social, and Biomedical Sciences; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Hernán, M.A.; Robins, J.M. Causal Inference: What If; Chapman & Hall/CRC: Boca Raton, FL, USA, 2020. [Google Scholar]
- Pearl, J. Causality: Models, Reasoning and Inference, 2nd ed.; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Shalit, U.; Johansson, F.D.; Sontag, D. Estimating individual treatment effect: Generalization bounds and algorithms. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 1–10. [Google Scholar]
- Alaa, A.M.; van der Schaar, M. Deep multitask Gaussian processes for survival analysis with competing risks. In Proceedings of the Advances in Neural Information Processing Systems 30 (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017; Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2018; pp. 1–9. [Google Scholar]
- Shi, C.; Blei, D.M.; Veitch, V. Adapting neural networks for the estimation of treatment effects. In Proceedings of the 33rd International Conference on Neural Information Processing Systems, Vancouver, Canada, 8–14 December 2019; Article No.: 225. pp. 2507–2517. [Google Scholar]
- Yoon, J.; Jordon, J.; van der Schaar, M. GANITE: Estimation of Individualized Treatment Effects using Generative Adversarial Nets. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018; Available online: https://openreview.net/forum?id=ByKWUeWA- (accessed on 19 May 2025).
- Nelsen, R.B. An Introduction to Copulas; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Liu, H.; Han, F.; Yuan, M.; Lafferty, J.; Wasserman, L. The nonparanormal: Semiparametric estimation of high dimensional undirected graphs. J. Mach. Learn. Res. 2019, 10, 2295–2328. [Google Scholar]
- Nagler, T. A generic approach to nonparametric function estimation with mixed data. Stat. Probab. Lett. 2018, 137, 326–330. [Google Scholar] [CrossRef]
- Carroll, R.J.; Ruppert, D.; Stefanski, L.A.; Crainiceanu, C.M. Measurement Error in Nonlinear Models: A Modern Perspective; Chapman & Hall/CRC: Boca Raton, FL, USA, 2006. [Google Scholar]
- Penning de Vries, B.B.L.; van Smeden, M.; Groenwold, R.H.H. A weighting method for simultaneous adjustment for confounding and joint exposure-outcome misclassifications. Stat. Methods Med. Res. 2020, 30, 473–487. [Google Scholar] [CrossRef] [PubMed]
- Anoke, S.C.; Norm, S.L.; Zigler, C.M. Approaches to treatment effect heterogeneity in the presence of confounding. Stat. Med. 2019, 38, 2797–2815. [Google Scholar] [CrossRef] [PubMed]
- Rosenbaum, P.R. Observational Studies; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Cinelli, C.; Hazlett, C. Making Sense of Sensitivity: Extending Omitted Variable Bias. J. R. Stat. Soc. Ser. B Stat. Methodol. 2020, 82, 39–67. [Google Scholar] [CrossRef]
- Kim, J.-M. Integrating Copula-Based Random Forest and Deep Learning Approaches for Analyzing Heterogeneous Treatment Effects in Survival Analysis. Mathematics 2025, 13, 1659. [Google Scholar] [CrossRef]
- Kim, J.-M. Treatment effect estimation in survival analysis using deep learning-based causal inference. Axioms 2025, 14, 458. [Google Scholar] [CrossRef]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.-Y.; Wong, W.-K.; Woo, W.-C. Convolutional LSTM network: A machine learning approach for precipitation nowcasting. In Proceedings of the 29th International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015; MIT Press: Cambridge, MA, USA, 2015; Volume 1, pp. 802–810. [Google Scholar]
- Bai, S.; Kolter, J.Z.; Koltun, V. An Empirical Evaluation of Generic Convolutional and Recurrent Networks for Sequence Modeling. arXiv 2018, arXiv:1803.01271. [Google Scholar] [CrossRef]
- Athey, S.; Tibshirani, J.; Wager, S. Generalized random forests. Ann. Stat. 2019, 47, 1148–1178. [Google Scholar] [CrossRef]
- Cox, D.R. Regression Models and Life-Tables. J. R. Stat. Soc. Ser. B (Methodol.) 1972, 34, 187–202. [Google Scholar] [CrossRef]
- Wager, S.; Athey, S. Estimation and Inference of Heterogeneous Treatment Effects using Random Forests. J. Am. Stat. Assoc. 2018, 113, 1228–1242. [Google Scholar] [CrossRef]
- Angwin, J.; Larson, J.; Mattu, S.; Kirchner, L. Machine Bias: There’s Software Used Across the Country to Predict Future Criminals. And it’s Biased Against Blacks. ProPublica. 2016. Available online: https://www.propublica.org/article/machine-bias-risk-assessments-in-criminal-sentencing (accessed on 19 May 2025).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).