On the Mathematical Background of Sliding Mode-Based Friction Compensation of a Micro-Telemanipulation System

Abstract

Modeling of various phenomena in engineering work is always a kind of simplification of real processes, aiming at a model where a certain level of mathematical theory and computational procedures is sufficient. If the complexity of the required theory corresponds to the general mathematical competence of engineers, then technical problems can be treated separately in engineering (or physical) models without regard to the mathematical background. However, in some advanced engineering fields, the harmonized development of engineering and mathematical models and toolboxes is necessary to find efficient solutions. For example, modeling variable structure systems in ideal sliding mode requires a mathematical toolbox that goes far beyond general engineering competence through the theory of discontinuous right-hand-side differential equations. Although sliding mode control is popular in practice and the concept of sliding mode allows a significant reduction of model complexity, its exact mathematical description is rarely encountered. The problem of friction compensation of a micro-telemanipulator using sliding mode control demonstrates a harmonized application of the mathematical and engineering approaches. Based on Filippov’s theory, the ideal sliding mode can be discussed. Although an ideal system cannot be implemented in reality, the real systems can be kept close enough to it; therefore, the discussion of the solution of the ideal model is important for practical applications. Although several elements of the topic are available in the literature, in this paper a unique complex approach is given for users of sliding mode control with experimental considerations, different engineering models, and codes. The paper concludes that sliding mode control is a case where engineering and mathematical modeling are inseparable and requires the competence of both fields.

1. Introduction

Micro-telemanipulation is an area where the use of sophisticated control methods is necessary. A central issue is friction compensation, which causes difficulties due to its nonlinearity. Several methods have been developed for the control of telemanipulation systems; one of these efficient and robust methods is the sliding mode control method.

1.1. The Concept of Telemanipulation

The definition of telemanipulation is when a human operator controls a remote environment as the movement of the slave device in the remote environment is controlled by a master device, while receiving certain types of information from the remote environment (see Figure 1). The main parts of telemanipulation systems are as follows:

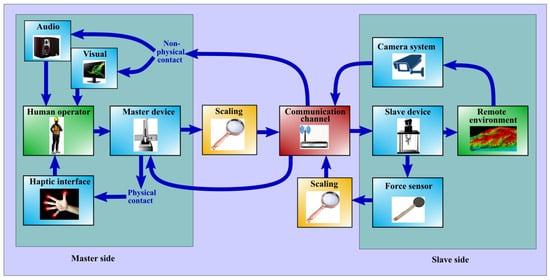
Figure 1. Block diagram of information and energy flow in an telemanipulation environment.

• master device;
• slave device;
• communication channel to transfer sufficient information;
• force and motion sensors (if force and torque are necessary information for the specified task);
• audio-visual displays (direct or 3D created visual information); 
• actuators conveying force and tactile information to the operator (haptic devices).

A specific and focused type of telemanipulation is micro-telemanipulation, where both force and position scaling are required to ensure efficient operation. The motion and force information sent from the master side needs to be downscaled (reduced), and the information coming in the slave/remote direction from the micro side needs to be upscaled (increased) (Figure 1). The scaling can be linear, piecewise linear, or nonlinear, depending on the nature of the application. Of course, if force and torque feedback is required, then the telemanipulation process is to enforce Newton’s third law (action–reaction forces) between the local and remote devices. In addition, due to the human–robot collaboration nature of the master device, certain safety functions (rate of change, absolute magnitude) should be considered in practice to prevent damage on both sides.

1.2. The History of Telemanipulation and the State of the Art

The first teleoperated devices were built in 1890 by Nicola Tesla [1]. In the mid-1940s, Goertz built the first mechanical master–slave teleoperator machine [2], mainly to avoid working in a dangerous environment.

Until the mid-1960s, telemanipulator systems had a very small working distance range, so the time delay problem did not arise. In 1965, a move-and-wait strategy was shown to cope with the delay [3]. The goals of space exploration made it necessary to extend the range of telemanipulation so that the problems of time delay were compensated by the controller for the human operator. [4] It also made it necessary to place the telemanipulator’s slave device on a vehicle that can deliver the device to its target area [5]. The role of the human factor in telemanipulation systems has also become the subject of study in both the design and operational parts [6].

In the mid-1980s and early 1990s, there was a lot of progress in time delay. In [7], a design framework for teleoperators with kinesthetic feedback and bilateral impedance control was introduced. And [8] informs us that the first true telerobot was operated in space. With the development of MEMS technology, the first micro-telemanipulation systems appeared.

In [9], a 6 DOF micromanipulator with PZT actuators was designed and tested. In [10], force and vision feedback were combined for a sensor-based microassembly task.

In the 2000s, micromanipulation was widespread. In [11], a microrobot-based micro-assembly station was presented. In [12], an electrostatic MEMS microrobot was presented that is one to two orders of magnitude smaller than previous microrobot systems and can be controlled by teleoperation. In [13], a haptic rendering technique for a telemanipulation system for micro and macro applications was presented. In [14], the design and integration of a telerobotic system for surgical purposes was presented. In [15], the precision control of a piezo-actuated micro-telemanipulation system was demonstrated. In [16], a novel control strategy for a nonlinear bilateral macro–micro teleoperation system with time delay was designed. In [17], a new evaluation and training system for micro-telemanipulation for middle ear surgery purposes was presented.

Over the past five years, research in micromanipulation has produced the following results. In [18], an origami-inspired micromanipulator for remote microsurgery was presented. In [19], an intuitive and comprehensive platform for force-assisted micromanipulation applications was presented. In [20], a combined control for a piezoelectric actuator using a feedforward neural network and feedback integral fast terminal sliding mode control was designed. In [21], a review of magnetic microrobots for micro- and nanomanipulation was presented. In [22], acoustic actuators for micro- and nanorobot manipulation were presented. In [23], the design and evaluation of an adjustable compliant constant force microgripper was shown and in [24] a microgripper robot with end electropermanent magnet collaborative actuation was presented.

1.3. About Sliding Mode Control

The theory of variable structure systems and related sliding mode control was first developed in the Soviet Union in the 1950s and 1960s, mostly published in Russian. The spread of the theory in English is mainly due to Vadim I. Utkin [25]. Its first application in the Soviet Union was in aeronautics and rocketry, and it became increasingly widespread in the English-language literature in the fields of robot control [26] and servo drives [27]. In the early 1980s, the sliding mode appeared in the control of induction motor drives [28]. Early applications highlighted some very advantageous properties of sliding mode control. Power electronic devices contain switching elements and therefore belong to the class of variable structure systems. Sliding mode control can be easily implemented on these devices. Starting in the 1980s onwards, sliding mode control became a popular tool for power electronics applications [29], and is still widely used in this field today. An exact mathematical description of the ideal sliding mode requires the theory of differential equations with discontinuous right-hand side [30,31]. In [32], a sliding mode controller composed of a PID-type sliding mode surface with an inverse tangent hyperbolic function and a variable-gain hyperbolic tracking law is proposed for trajectory tracking under uncertainty. In [33], a sensorless control system based on a continuous terminal sliding mode controller (CT-SMC) and fuzzy super-twisted sliding mode observer (F-ST-SMO) was designed. In [34], a model-based, chatter-free sliding mode control (CFSMC) algorithm is developed to maintain a desired heating value trajectory of the syngas mixture of an underground coal gasification (UCG) process. Nowadays, most control algorithms are implemented digitally [35]. The authors in [36] propose a combination of a data-driven algorithm represented by continuous-time active disturbance rejection control (ADRC) and a sliding mode control (SMC) algorithm. The MATLAB code is presented in Appendix A.

1.4. Structure of the Article

In Section 2, we describe our telemanipulation system. Section 2.1 and Section 2.2 describe the problem to be solved from an engineering point of view and the essence of applied sliding mode control, respectively. Finally, in Section 2.3 we formulate the mathematical problem, the solution of which is one of the main contributions of the article.

In Section 3, we first present the mathematical background of the theory of differential equations with discontinuous right-hand side (Section 3.1), and then apply the theory to the solution of a relay system (Section 3.2).

In Section 4, we first write the equations of the experimental system, then we solve the equations by following the steps in Section 3.2 (see Section 4.1). Finally, we address the challenges of computer implementation (see Section 4.2).

The simulation and experimental results are presented in Section 5 and Section 6. Section 7 concludes the article. Appendix A presents the details of MATLAB simulation.

2. Problem Statement

The aim of this article is to demonstrate that sliding mode control requires advanced mathematical and engineering modeling tools, so a complex approach is required for planning. Therefore, we refer to the referenced literature for deeper considerations related to engineering technology.

2.1. The Experimental Setup (Engineering Approach of the Problem Statement)

A 6 DOF telemanipulation system is given with specific devices and mechanisms on the master and slave sides (see Figure 1). On the master side, a joystick is held, can be moved, and rotated manually by the operator. The workspace is 800 mm × 800 mm × 800 mm for translational motion, and the maximum rotation is $\pm 60°$ for each axis. The operation is based on force feedback in response to manipulations in all types of motion (all degrees of freedom). The simplified structure belonging to a translational motion is shown in Figure 2.

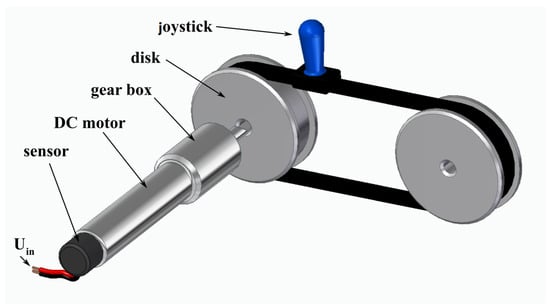
Figure 2. Simplified model of one translational DOF.

In the experimental device, due to the frictional forces (e.g., in the chatter-free planetary gear) and the inertia of the mechanical elements, a relatively large force (of about 10 N) is required to move the joystick, even in unloaded operation (see Table 1). In other words, an additional force of about 10 N must be applied by the operator when manipulating the device. In the case of a micromanipulation task, this amount of force is too large compared to the reaction force acting on the part on the slave side, and prevents a sufficiently smooth operation. The higher the additional force compensated by the operator, the more uncertain (less reliable and accurate) the operation.

Table 1. Summary of maximum sensed forces.

Controller/Axes	X	Y	Z
no controller $\left[\mathrm{N}\right]$	10	32	14
PD without compensation $\left[\mathrm{N}\right]$	1.2	1.9	2.8
PD with SM compensation $\left[\mathrm{N}\right]$	0.07	0.14	0.09

In telemanipulation, a bilateral control problem, as shown in Figure 3, must be solved. Figure 3 does not indicate that in the case of micromanipulation, the workspace of the remote environment and the forces arising in the remote environment must be rescaled to the workspace of the master device and the perception range of the operator. In many cases, it is not enough to simply multiply and divide the signals, but due to the dynamic differences, time must also be rescaled, which causes additional difficulties. In contrast, the main point of this article is how we can virtually change the unknown dynamics of the telemanipulation system.

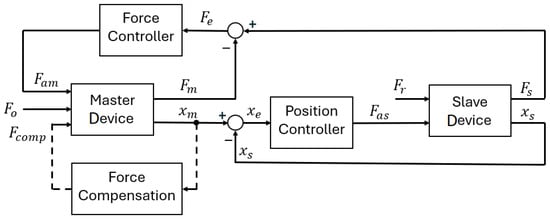
Figure 3. Schematic diagram of the bilateral control of a telemanipulation system.

$F_o$ and $F_r$ are the two external forces acting on the master and slave sides. The former is the operator’s force on the master device, and the latter is the reaction force exerted by the remote environment on the slave side. Ideally, these are identical, i.e., the operator can feel how much force the remote environment is exerting on the slave device. $F_{am}$ and $F_{as}$ are the two internal (Newtonian) acceleration forces on the master and slave sides. According to the bilateral control, $F_{am}$ is generated by a force controller and $F_{as}$ is generated by a position controller. On both sides, the total force $F_m$ and the force $F_s$ are measured. On the master side, the goal is that the force error $F_e$ and the position error $x_e$ on the slave side should be zero or as small as possible. $x_m$ and $x_s$ are the displacements of the master and slave devices. Similar block diagrams are associated with each degree of freedom. In the case of rotary joints, torque and angular displacement should be written instead of force and displacement.

Although in the ideal case $F_{am}=F_{as}$ and $F_m=F_s$, and therefore $F_o=F_r$, in many cases in practice $F_{am}\ne F_{as}$, i.e., the real value of the force $F_r$ cannot be felt by the operator due to internal and external disturbances, so the disturbing effects must be compensated. In our experimental device, this means that the movement of the master device is mainly performed by servomotors with additional torque control.

The role of the force controller (see Figure 3) is to balance the total forces $F_m$ and $F_s$, for which traditional PID controllers are commonly used. In certain applications, such as micromanipulation control tasks, a PID controller may not be able to properly compensate for the force difference, and it is necessary to add another type of force compensation. The goal of the compensation is to create a mode of operation where the operator can mainly feel the reaction force $F_r$ (feedback) and comfortably move the master device (joystick) when controlling the remote device.

In our study, tests were conducted to determine the physical parameters of joystick motion that would give the operator a sense of ease of operation, resulting in a linearized reference model discussed below. For simplicity, all mass, inertia, and friction values in the model are converted to equivalent mass, inertia, and friction forces acting on the joystick.

In the control task discussed, the goal is twofold: to feed back the reaction force generated in the remote environment to the operator and to compensate for the forces required to move the master-side mechanism. In practice, a perfect compensation is impossible due to time delays and frequency bandwidth limitations of the master and slave devices. Instead, we force the system to follow a virtual dynamic characteristic, namely a reference dynamic model with much less moving mass and friction effect than the master device actually has. In the case of free motion (no force feedback from the remote environment), the operator feels that the joystick (master device) is easy to move because the motors are operating the mechanism instead of the operator. This is the model reference adaptive approach.

Based on the reference dynamic model, we determine the ideal state of the motion trajectory belonging to the control task, and force the system to return to it if the actual state of the system is not on the ideal trajectory using a so-called bang–bang control, where force is the input and velocity is the output of the master system.

In our experimental setup, due to the special force compensation, the “artificial friction force” is only $0.1$ N at a constant speed of $2.5$ m/s. We assume that the operator applies force pulses of alternating sign to the master device along the x axis. The magnitudes of the force pulses are $0.1$ N and $0.01$ N, respectively. To ensure smooth motion of the master device, the compensation force was generated by a compensation toolset (model reference adaptive control loop) instead of the operator. In the steady state of the master device, this force results in a velocity of $0.25$ m/s and $0.025$ m/s in the case of the reference model (see Section 6).

The master device transfer function belonging to the translational movement in a given direction (let us say x) was experimentally determined as

$$V_x\left(s\right)={\displaystyle \frac{20}{s+8}}{F}_o\left(s\right),$$

(1)

where $V_x\left(s\right)$ is the Laplace transform of the velocity-time function of the master device joystick’s movement in the x direction and $F_o\left(s\right)$ is the Laplace transform of the force exerted by the operator.

2.2. The Application of the Sliding Mode (A Control Tool for the Solution of the Engineering Problem)

To illustrate the benefits of sliding mode control, consider a system modeled by the following system of first-order differential equations:

$$\begin{array}{c}{\displaystyle {\dot{x}}_1\left(t\right)=x_2\left(t\right),}\\ {\dot{x}}_2\left(t\right)=f_{op}\left(x_1\left(t\right),x_2\left(t\right)\right)+g_{op}\left(x_1\left(t\right),x_2\left(t\right)\right)u\left(t\right)+d\left(t\right),\\ y\left(t\right)=x_1\left(t\right),\end{array}$$

(2)

where $u\left(t\right)$, $y\left(t\right)$, and $d\left(t\right)$ are the input, the output, and the disturbance signals, respectively, and $f_{op}$, $g_{op}$, u, and d are given bounded functions. This system represents a second-order nonlinear differential equation for the function $x_1\left(t\right)$.

Suppose that we start from an arbitrary initial state, and the goal of the control is to make the output signal $y\left(t\right)$ go to zero. Since, due to the laws of physics, the state variables can only change continuously (they cannot “jump” in time), it makes sense to design a smooth trajectory in the two-dimensional phase plane ending at the origin and force the system to follow it. In the practical implementation of the sliding mode, the control signal is different on the two sides of the trajectory and, to keep the state in the small neighborhood of the ideal trajectory, we have to “switch” it according to the current state. In this process, breakpoints of the function $x_2\left(t\right)$ induced by the control signal $u\left(t\right)$ through the jumps of ${\dot{x}}_2\left(t\right)$ play an important role. In higher dimensional phase spaces, a hyper-surface, the so-called sliding surface, is defined (designed in applications) and the switching takes place when the trajectory passes through a point of the sliding surface. Therefore, it can also be called a switching surface.

In our example, consider a switching curve given by $s(x_1,x_2)=0$, where s is a smooth scalar-valued function with a different sign on each side of the curve in the two-dimensional $x_1-x_2$ phase plane (Figure 4). When the real trajectory crosses the switching curve, the control signal is changed to force it back to the ideal trajectory. Since switching in real systems is time-delayed, the real trajectory cannot “turn back” at the switching curve, but must move away from it a little. This phenomenon (called chattering) is inevitable in real systems. There are several studies dealing with chatter reduction methods [37]. Ideally, in the so-called sliding mode, the state never leaves the switching curve (sliding curve) but moves along it toward the target state.

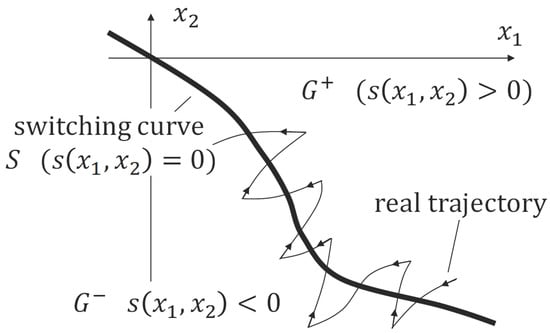
Figure 4. Illustration of the mutual position of a real trajectory and a switching curve in 2D phase space.

Let s be a linear combination of the state variables $x_1$ and $x_2$ (typical in applications). Then the sliding curve is a straight line that can be given as

$$s(x_1,x_2)=x_1+\tau x_2=0.$$

(3)

If we assume that the system does not leave this line in the phase plane during operation, then Equation (2) has the simple form

$$\dot{y}\left(t\right)=-{\displaystyle \frac{1}{\tau }}y\left(t\right),$$

(4)

which is a first-order homogeneous differential equation for the output signal $y\left(t\right)$, whose solution is

$$y\left(t\right)=Y_0·e^{-{\displaystyle \frac{t}{\tau }}},t>0,$$

(5)

where $Y_0=y\left(0\right)$ is the initial value of the output signal and $\tau$ is the time constant of the system. We can conclude that operating a dynamic system in sliding mode provides an opportunity to significantly reduce the complexity of the model (the order of the differential equation).

2.3. The Mathematical Challenge

The key idea in sliding mode control is that if we can somehow ensure that the trajectory stays on the sliding surface in phase space, then the control becomes independent of the system parameters and the system equations can be overwritten by the sliding surface equation (by a given relationship between the state variables). Filippov’s theory shows under which conditions this can be performed in the mathematical model. If the conditions are met, then the “motion” in phase space is limited to the sliding surface, so we can apply the above method of reduction.

In a real system, the state trajectory is kept in a small neighborhood of the sliding surface by switching between two appropriate control signals at appropriate times. This procedure results in a trajectory that alternates around the sliding surface. In the mathematical model of the ideal case, it is assumed that the reversal effect is activated “immediately” when the state leaves the sliding surface, i.e., the time between switches is zero (infinitesimal). In the differential equation of the system, the two different control actions are represented by two different functions on the right-hand side, defined on both sides of the sliding surface. That is, the right-hand side of the differential equation is discontinuous at the points of the sliding surface.

In the example above where the system was originally described by a second-order differential equation (Equation (2)), we could obtain a first-order differential equation (Equation (4)) that provides the solution (Equation (5)) under special circumstances.

With the theory of differential equations with discontinuous right-hand side, which now has been extensively studied in the literature, Filippov established the theoretical background of the control task related to switching mode. In his work, the engineering (physical) and mathematical models were developed together, resulting in an approach that can be used in practical control design.

3. The Mathematical Model

3.1. Some Basic Definitions in the Theory of Differential Equations with Discontinuous Right-Hand Side

Several important technical problems lead to differential equations with discontinuous right-hand side. Well-known examples are mechanical systems where friction appears or electrical systems where relays are used. Two basic types are the following.

Let $G\subset {\mathbb{R}}^n$ be an open domain and $M\subset G$ be a set of Lebesgue measure zero. Let us introduce two equations (systems of differential equations) as follows. First consider the following equation:

$${\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}\mathbf{x}\left(t\right)=\mathbf{f}\left(\mathbf{x}\left(t\right)\right),$$

(6)

where $\mathbf{f}:G\to {\mathbb{R}}^n$ is continuous on $G\setminus M$ and discontinuous on M.

Since in control theory problems the external control signal (excitation) $u\left(\mathbf{x}\left(t\right)\right)$ is generally discontinuous, it is advisable to represent it explicitly on the right-hand side and to write

$${\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}\mathbf{x}\left(t\right)={\mathbf{f}}_1\left(\mathbf{x}\left(t\right),u\left(\mathbf{x}\left(t\right)\right)\right),$$

(7)

where ${\mathbf{f}}_1$ is continuous, while $u:G\to \mathbb{R}$ is continuous on $G\setminus M$ and discontinuous on M.

In [30,31], a connection is established between these differential equations and the so-called differential inclusions

$${\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}\mathbf{x}\left(t\right)\in \mathbf{F}\left(\mathbf{x}\left(t\right)\right)\mathrm{and}{\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}\mathbf{x}\left(t\right)\in {\mathbf{F}}_1\left(\mathbf{x}\left(t\right),U\left(\mathbf{x}\left(t\right)\right)\right),$$

(8)

respectively, where $\mathbf{F}$, ${\mathbf{F}}_1$, and U are suitable set-valued functions. Solutions of (8) are considered as solutions of Equations (6) and (7), respectively. Under certain circumstances ${\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}\mathbf{x}\left(t\right)$ can be uniquely defined using values at points of continuity. It is an important special case in practice when M is a smooth hyper-surface in G.

In the case of Equation (6), $\mathbf{F}\left(\mathbf{x}\right)=\mathbf{f}\left(\mathbf{x}\right)$ if $\mathbf{x}\in G\setminus M$ while $\mathbf{F}\left(\mathbf{x}\right)$ is the closure of the convex hull of limits $\underset{x^{*}\notin M,{\mathbf{x}}^{*}\to \mathbf{x}}{lim}\mathbf{f}\left({\mathbf{x}}^{*}\right)$ if $\mathbf{x}\in M$. The illustrative meaning of this is that the derivative (the right-hand side of the differential equation) at the discontinuity points is determined by the derivatives valid at the nearby continuity points, which differs on the two sides of the surface. To clarify this idea we introduce the following concepts.

Let $\mathbf{f}$ be discontinuous on a smooth surface $S\subset G$ given as $s\left(\mathbf{x}\right)=0$, $s:G\to \mathbb{R}$ and continuous on $G\setminus S$. The two “sides” of S are defined as

$$G^{+}=\{\mathbf{x}:s\left(\mathbf{x}\right)>0\}\mathrm{and}{G}^{-}=\{\mathbf{x}:s\left(\mathbf{x}\right)<0\};$$

(9)

furthermore, functions

$$\begin{array}{c}\hfill {\mathbf{f}}^{+}\left(\mathbf{x}\right)=\mathbf{f}\left(\mathbf{x}\right)\mathbf{x}\in G^{+}\mathrm{and}{\mathbf{f}}^{-}\left(\mathbf{x}\right)=\mathbf{f}\left(\mathbf{x}\right),\mathbf{x}\in G^{-}\end{array}$$

(10)

and limits

$$\begin{array}{c}\hfill L_{{\mathbf{f}}^{+}}\left(\mathbf{x}\right)=\underset{x^{*}\in G^{+},{\mathbf{x}}^{*}\to \mathbf{x}}{lim}\mathbf{f}\left({\mathbf{x}}^{*}\right)\mathrm{and}{L}_{{\mathbf{f}}^{-}}\left(\mathbf{x}\right)=\underset{x^{*}\in G^{-},{\mathbf{x}}^{*}\to \mathbf{x}}{lim}\mathbf{f}\left({\mathbf{x}}^{*}\right),\mathbf{x}\in S\end{array}$$

(11)

are introduced. Then set $\mathbf{F}\left(\mathbf{x}\right)$ can be defined as a segment joining ${\mathbf{f}}^{+}\left(\mathbf{x}\right)$ and ${\mathbf{f}}^{-}\left(\mathbf{x}\right)$. If this segment intersects the tangent plane P of S belonging to point $\mathbf{x}$, then denote the intersection of the tangent plane and the segment by ${\mathbf{f}}^{eq}\left(\mathbf{x}\right)$. A solution $\mathbf{x}$ of

$${\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}\mathbf{x}\left(t\right)={\mathbf{f}}^{eq}\left(\mathbf{x}\left(t\right)\right)$$

(12)

is assumed to be a solution of Equation (6). If ${\mathbf{f}}^{+}\left(\mathbf{x}\right)\ne {\mathbf{f}}^{eq}\left(\mathbf{x}\right)\ne {\mathbf{f}}^{-}\left(\mathbf{x}\right)$, then such a solution is called sliding mode.

A continuous function $\mathbf{x}\left(t\right)$ which for a part of the time interval lies in $G^{+}$ (or in $G^{-}$) and satisfies Equation (6) there, while for the rest of the time interval lies on surface S and satisfies Equation (12), is assumed to be a solution of Equation (6).

Note that a trajectory provided by this method consists of states for which the original differential equation is not defined. This is what the theory of the differential equations with discontinuous right-hand side contributes to the system modeling when studying certain special engineering systems.

To describe the mutual position of the gradient of surface S and the directions ${\mathbf{f}}^{+}$ and ${\mathbf{f}}^{-}$, we introduce notations

$$L_{{\mathbf{f}}^{+}}s\left(\mathbf{x}\right)={\displaystyle \frac{\nabla s\left(\mathbf{x}\right)}{|\nabla s(\mathbf{x}\left)\right|}}·{\mathbf{f}}^{+}\left(\mathbf{x}\right)\mathrm{and}{L}_{{\mathbf{f}}^{-}}s\left(\mathbf{x}\right)={\displaystyle \frac{\nabla s\left(\mathbf{x}\right)}{|\nabla s(\mathbf{x}\left)\right|}}·{\mathbf{f}}^{-}\left(\mathbf{x}\right),$$

(13)

where · is the inner product operator. If

$$L_{{\mathbf{f}}^{+}}s\left(\mathbf{x}\right)<0\mathrm{and}{L}_{{\mathbf{f}}^{-}}s\left(\mathbf{x}\right)>0,\mathbf{x}\in S,$$

(14)

then near the surface S all solutions approach S from both sides (as time increases) and none of them leaves S after reaching it (a solution which passes through a point of S will therefore remain on S). Equation (14) is a sufficient condition of the sliding mode. ${\mathbf{f}}^{eq}$ can be written as a convex combination

$${\mathbf{f}}^{eq}=\zeta {\mathbf{f}}^{+}+(1-\zeta ){\mathbf{f}}^{-},$$

(15)

where

$$\zeta ={\displaystyle \frac{L_{{\mathbf{f}}^{-}}s\left(\mathbf{x}\right)}{L_{{\mathbf{f}}^{-}}s\left(\mathbf{x}\right)-L_{{\mathbf{f}}^{+}}s\left(\mathbf{x}\right)}}$$

(16)

(see [31] and Figure 5).

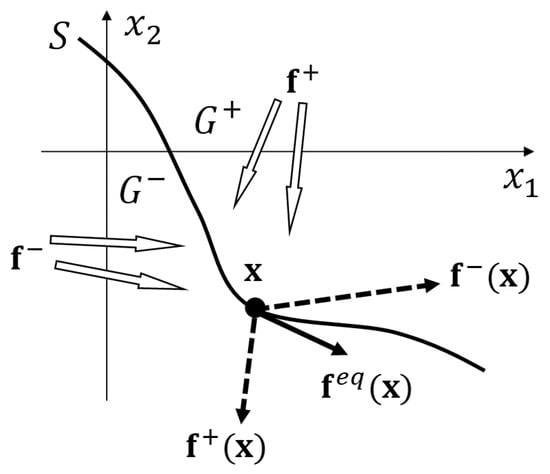
Figure 5. Illustration of ${\mathbf{f}}^{eq}$ in 2D.

In the case of Equation (7), we define function U as follows: $U\left(\mathbf{x}\right)=u\left(\mathbf{x}\right)$ if $\mathbf{x}\in G\setminus M$ while $U\left(\mathbf{x}\right)$ is the closure of the convex hull of limits $\underset{x^{*}\notin M,{\mathbf{x}}^{*}\to \mathbf{x}}{lim}u\left({\mathbf{x}}^{*}\right)$ if $x\in M$. Then ${\mathbf{F}}_1\left(\mathbf{x}\right)={\mathbf{f}}_1\left(\mathbf{x}\right)$ if $\mathbf{x}\in G\setminus M$ and ${\mathbf{F}}_1\left(\mathbf{x}\right)$ is the closure of the convex hull of set ${\mathbf{f}}_1\left(\mathbf{x},U\left(\mathbf{x}\right)\right)$ if $\mathbf{x}\in M$.

A particular case is the following. At points of S we assume

$${\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}\mathbf{x}\left(t\right)={\mathbf{f}}_1\left(\mathbf{x},u^{eq}\left(\mathbf{x}\right)\right),$$

(17)

where so-called equivalent control $u^{eq}$ is defined so that g is tangent to S and $u^{eq}\left(\mathbf{x}\right)$ is contained in closed interval with endpoints $u^{+}\left(\mathbf{x}\right)$ and $u^{-}\left(\mathbf{x}\right)$, where $u^{+}$ and $u^{-}$ are limiting values of u on both sides of S. Function $u^{eq}\left(\mathbf{x}\right)$ can be determined from equality

$$\nabla s\left(\mathbf{x}\right)·{\mathbf{f}}_1\left(\mathbf{x},u^{eq}\left(\mathbf{x}\right)\right)=0.$$

(18)

The solution is an absolutely continuous function which satisfies Equation (6) outside S and satisfies Equation (8) on S. The endpoint of vector ${\mathbf{f}}_1(\mathbf{x},u^{eq}\left(\mathbf{x}\right))$ lies on the intersection of the plane tangent to S at $\mathbf{x}$ and the arc spanned by the endpoints of ${\mathbf{f}}_1(\mathbf{x},u\left(\mathbf{x}\right))$ when u varies from $u^{+}\left(\mathbf{x}\right)$ to $u^{-}\left(\mathbf{x}\right)$.

In the following, we prefer writing the formula $\mathbf{f}\left(\mathbf{x}\right)$ rather than ${\mathbf{f}}_1(\mathbf{x},u\left(\mathbf{x}\right))$ in the general explanations. Of course, the control signal u appears in the calculations.

3.2. Using Filippov’s Approach in Modeling

Let S be a smooth surface, and let sets $G^{+}$ and $G^{-}$ and continuous functions $f^{+}$ and $f^{-}$ be defined according to Section 3.1. Consider a system modeled by autonomous differential equation

$${\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}\mathbf{x}\left(t\right)=\left\{\begin{array}{c}{\mathbf{f}}^{+}\left(\mathbf{x}\left(t\right)\right),\mathrm{if}\mathbf{x}\in G^{+}\hfill \\ {\mathbf{f}}^{-}\left(\mathbf{x}\left(t\right)\right),\mathrm{if}\mathbf{x}\in G^{-}\hfill \end{array}\right..$$

(19)

Note that Equation (19) is not interpreted on S, and ${\mathbf{f}}^{+}$ and ${\mathbf{f}}^{-}$ do not coincide on the two sides of S. The graphical interpretation of this system is given in Figure 6.

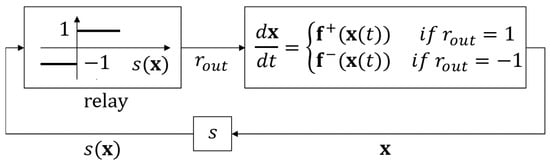
Figure 6. Closed loop relay controller.

The state of the relay depends on the sign of s (on which side of the sliding surface S the current state is) and switches the right-hand side of the equation between ${\mathbf{f}}^{+}$ and ${\mathbf{f}}^{-}$. The purpose of the control is to force the state trajectory onto S, in other words, to implement sliding mode control. This problem was studied by Filippov (see [30,31]). He searched for the solution $\mathbf{x}$ of Equation (19) at the points of S by considering how the differential equation (the derivative of $\mathbf{x})$ behaves in the neighborhood of that point. He allowed the behavior of the derivative on a set of Lebesgue measure zero to be different from its environment. In this paper, we deal with autonomous differential equations, although Filippov’s original definition is also valid for non-autonomous equations.

He assumed that $\mathbf{f}$ is a measurable and locally bounded function defined and continuous almost everywhere in an open domain in ${\mathbb{R}}^n$. For points of discontinuity $\mathbf{x}$ he defined the set

$$K_{conv}\left(\mathbf{x}\right)=\bigcap _{\delta >0}\bigcap _{\mu \left(N\right)=0}\mathrm{conv}\mathbf{f}\left(Q(\mathbf{x},\delta )\setminus N\right),$$

(20)

where $Q(\mathbf{x},\delta )$ is a neighborhood of $\mathbf{x}$ with radius $\delta$, $\mu$ is the Lebesgue measure, and “conv” is the closure of the convex hull of a set.

For the solutions of the equation

$${\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}\mathbf{x}\left(t\right)=\mathbf{f}\left(\mathbf{x}\left(t\right)\right),$$

(21)

Filippov introduced the following definition.

 Definition 1. 

An absolute continuous function $\mathbf{x}:[T_0,T_2]\to G\subset {\mathbb{R}}^n$ is a solution to the differential Equation (21) if

$${\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}\mathbf{x}\left(t\right)\in K_{conv}\left(\mathbf{x}\right)$$

(22)

holds almost everywhere in $[T_0,T_2]$

Note that if $\mathbf{f}$ is continuous at $\mathbf{x}$, then $K_{conv}\left(\mathbf{x}\right)$ has only one element, namely $\mathbf{f}\left(\mathbf{x}\right)$, that by Filippov’s definition is consistent with the solution of the differential equations with continuous right-hand side.

4. Experimental Application of Sliding Mode Model-Following Control

Instead of Equation (6), we use the quasi-Linear Parameter-Varying (qLPV) state-space model common in control engineering and supported by MATLAB [38]. It has the following general form:

$$\left[\begin{array}{c}\dot{\mathbf{x}}\\ \mathbf{y}\end{array}\right]=\left[\begin{array}{c}{\mathbf{S}}_{LPV}\left(\mathbf{p}\right)\end{array}\right]\left[\begin{array}{c}\mathbf{x}\\ \mathbf{u}\end{array}\right],$$

(23)

where ${\mathbf{x}}^a$, ${\mathbf{y}}^c$, and ${\mathbf{u}}^b$ are the state, output, and input vectors, respectively, and $\mathbf{p}$ is the vector of parameters in the qLPV. ${\left[\begin{array}{c}\mathbf{S}\left(\mathbf{p}\right)\end{array}\right]}^{(a+c)\times (a+b)}$ is a parameter-dependent system matrix which can be written in the form

$$\left[\begin{array}{c}{\mathbf{S}}_{LPV}\left(\mathbf{p}\right)\end{array}\right]=\left[\begin{array}{cc}\mathbf{A}\left(\mathbf{p}\right)& \mathbf{B}\left(\mathbf{p}\right)\\ \mathbf{C}\left(\mathbf{p}\right)& \mathbf{D}\left(\mathbf{p}\right)\end{array}\right].$$

(24)

4.1. Writing and Solving the State-Space Equations for Sliding Mode Friction Compensation

Our equations are based on Newton’s well-known second law (the law of motion). For the master device we have

$$F_a=m_{eq}a=m_{eq}{\displaystyle \frac{dv}{dt}},F_a=F_{in}-F_{fric},$$

(25)

where $F_a$ is the force accelerating the system, and $F_{in}$ and $F_{fric}$ are the input and the friction force.

Note that this section focuses on sliding mode friction compensation and does not deal with how the $F_{in}$ force is generated by the external bilateral control system (hence the notation $F_{in}$). In other words, $F_{in}$ is the input force signal of the friction compensation subsystem, and it is the input of the reference model. $F_{sys}$ is the input of the mechanical system ($F_{in}$) plus the compensation (see Figure 7).

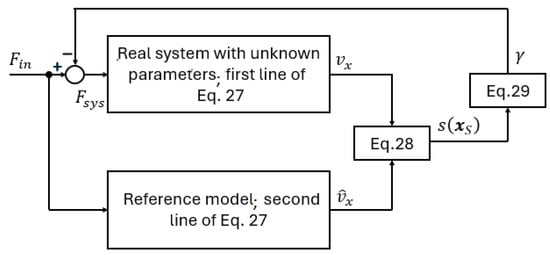
Figure 7. Sliding mode-based model referencing position control.

To study sliding mode control of the master device, choose

$${\mathbf{x}}_S=\left[\begin{array}{c}{v}_x\\ {\widehat{v}}_x\end{array}\right]\mathrm{and}{\mathbf{u}}_S=\left[\begin{array}{c}{F}_{sys}\\ F_{in}\end{array}\right]$$

(26)

as state variables and control inputs, where $v_x$ and ${\widehat{v}}_x$ are the velocity in the real system and in the reference model, respectively, and $F_{sys}$ and $F_{in}$ are the input forces of the mechanical system of the master and the reference model. In this paper, “hat” is used to denote variables and constants related to the reference model.

Since all state variables are also considered as outputs ($\mathbf{x}\equiv \mathbf{y}$), there is no need to write a separate equation for the output $\mathbf{y}$ in the systems of equations. To study sliding mode control of the master device, consider the following state-space equations:

$$\begin{array}{c}\hfill {\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}\left[\begin{array}{c}{\mathbf{x}}_S\end{array}\right]=\left[\begin{array}{c}{\mathbf{S}}_{LPV}\left(\mathbf{p}\right)\end{array}\right]\left[\begin{array}{c}{\mathbf{x}}_S\\ {\mathbf{u}}_S\end{array}\right]=\left[\begin{array}{cc}\mathbf{A}\left(\mathbf{p}\right)& \mathbf{B}\left(\mathbf{p}\right)\end{array}\right]\left[\begin{array}{c}{v}_x\\ {\widehat{v}}_x\\ F_{sys}\\ F_{in}\end{array}\right],\\ \hfill {\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}\left[\begin{array}{c}{v}_x\\ {\widehat{v}}_x\end{array}\right]=\left[\begin{array}{cc}0& -a_{21}\left(p_{a_{21}}\right)\\ 0& -{\widehat{a}}_{22}\end{array}\right]\left[\begin{array}{c}{v}_x\\ {\widehat{v}}_x\end{array}\right]+\left[\begin{array}{cc}{b}_1\left(p_{b_1}\right)& 0\\ 0& {\widehat{b}}_2\end{array}\right]\left[\begin{array}{c}{F}_{sys}\\ F_{in}\end{array}\right]\\ \hfill a_{21}\left(p_{a_{21}}\right)={\widehat{a}}_{22}+\Delta a_{21}={\displaystyle \frac{{\widehat{\nu }}_{eq}+\Delta {\nu }_{eq}}{{\widehat{m}}_{eq}+\Delta m_{eq}}},\\ \hfill b_1\left(p_{b_1}\right)={\widehat{b}}_2+\Delta b_1+{\displaystyle \frac{F_{n{l}_f}\left(v_x\right)}{F_{sys}}}={\displaystyle \frac{{\widehat{G}}_{eq}+\Delta G_{eq}}{{\widehat{m}}_{eq}+\Delta m_{eq}}}+{\displaystyle \frac{F_{n{l}_f}\left(v_x\right)}{F_{sys}}},\end{array},$$

(27)

where m and G are the mass and the gain of the system, and $\nu$ is the parameter of the linear viscous friction. $F_{n{l}_f}\left(v_x\right)$ represents the nonlinear component of friction (it can also be considered as the external disturbance $d\left(t\right)$ in Equation (2)). In this paper, the subscript “$eq$” is used to denote the so-called equivalent value of quantities of different types in the system equations, e.g., a single $m_{eq}$ is used in calculations where the mass appears rather than the mass of all elements in the mechanism separately.

The ultimate purpose of the compensation is to force the system to follow the dynamics of the reference model with parameters ${\widehat{a}}_{22}$ and ${\widehat{b}}_2$ instead of the original (natural) dynamics of the system. The equation of the reference model contains two parameters that we choose (${\widehat{a}}_{22}$ and ${\widehat{b}}_2$). Let the sliding surface be given as

$$s\left({\mathbf{x}}_S\right)=\left[\begin{array}{cc}1& -1\end{array}\right]\left[\begin{array}{c}{v}_x\\ {\widehat{v}}_x\end{array}\right]=0$$

(28)

and

$$\gamma =\left\{\begin{array}{c}\mathrm{\Gamma },\mathrm{if}s\left(\mathbf{x}\right)>0\hfill \\ -\mathrm{\Gamma },\mathrm{if}s\left(\mathbf{x}\right)<0\hfill \end{array}\right.,$$

(29)

where $\mathrm{\Gamma }$ is a constant which plays the role of $F_{comp}$ in Figure 3. Let the input signal of the system (mechanism of the master device) be

$$F_{sys}=F_{in}-\gamma .$$

(30)

Then Equation (27) can be written in the form of Equation (19) with

$${\mathbf{f}}^{+}\left({\mathbf{x}}_S\right)=\left[\begin{array}{c}-({\widehat{a}}_{22}+\Delta a_{21})v_x+({\widehat{b}}_2+\Delta b_1)(F_{in}-\mathrm{\Gamma })+F_{n{l}_f}\left(v_x\right)\\ -{\widehat{a}}_{22}{\widehat{v}}_x+{\widehat{b}}_2{F}_{in}\end{array}\right],$$

(31)

$${\mathbf{f}}^{-}\left({\mathbf{x}}_S\right)=\left[\begin{array}{c}-({\widehat{a}}_{22}+\Delta a_{21})v_x+({\widehat{b}}_2+\Delta b_1)(F_{in}+\mathrm{\Gamma })+F_{n{l}_f}\left(v_x\right)\\ -{\widehat{a}}_{22}{\widehat{v}}_x+{\widehat{b}}_2{F}_{in}\end{array}\right].$$

(32)

At the points ${\mathbf{x}}_S$ of the sliding surface S, the directional derivative of s in direction $\mathbf{f}\left({\mathbf{x}}_S\right)$ on both sides of S are

$$L_{f^{+}}s\left({\mathbf{x}}_S\right)=-({\widehat{a}}_{22}+\Delta a_{21})v_x+{\widehat{a}}_{22}{\widehat{v}}_x+\Delta b_1{F}_{in}+F_{n{l}_f}\left(v_x\right)-({\widehat{b}}_2+\Delta b_1)\mathrm{\Gamma }$$

(33)

and

$$L_{f^{-}}s\left({\mathbf{x}}_S\right)=-({\widehat{a}}_{22}+\Delta a_{21})v_x+{\widehat{a}}_{22}{\widehat{v}}_x+\Delta b_1{F}_{in}+F_{n{l}_f}\left(v_x\right)+({\widehat{b}}_2+\Delta b_1)\mathrm{\Gamma },$$

(34)

respectively. Conditions

$$\begin{array}{c}\hfill L_{f^{+}}s\left({\mathbf{x}}_S\right)<0,\mathrm{if}s\left({\mathbf{x}}_S\right)>0,L_{f^{-}}s\left({\mathbf{x}}_S\right)>0,\mathrm{if}s\left({\mathbf{x}}_S\right)<0\end{array}$$

(35)

need to be checked for the establishment of the sliding mode. Comparison of Equations (33)–(35) shows that the sliding mode is established by

$$|-({\widehat{a}}_{22}+\Delta a_{21})v_x+{\widehat{a}}_{22}{\widehat{v}}_x+\Delta b_1{F}_{in}+F_{n{l}_f}\left(v_x\right)|<|({\widehat{b}}_2+\Delta b_1)\mathrm{\Gamma }|.$$

(36)

If Equation (36) is satisfied, then the equivalent vector

$${\mathbf{f}}^{eq}\left({\mathbf{x}}_S\right)=\zeta {\mathbf{f}}^{+}\left({\mathbf{x}}_S\right)+(1-\zeta ){\mathbf{f}}^{-}\left({\mathbf{x}}_S\right)$$

(37)

describes the change in trajectory at ${\mathbf{x}}_S$, where

$$\zeta ={\displaystyle \frac{-\Delta a_{21}{v}_{x_s}+\Delta b_1{F}_{in}+F_{n{l}_f}\left(v_x\right)+({\widehat{b}}_2+\Delta b_1)\mathrm{\Gamma }}{2({\widehat{b}}_2+\Delta b_1)\mathrm{\Gamma }}}.$$

(38)

Substituting Equations (38), (31), and (32) into Equation (37), we obtain

$${\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}\left[\begin{array}{c}{v}_{x_s}\\ {\widehat{v}}_{x_s}\end{array}\right]={\mathbf{f}}^{eq}\left(\left[\begin{array}{c}{v}_{x_s}\\ {\widehat{v}}_{x_s}\end{array}\right]\right)=\left[\begin{array}{c}-{\widehat{a}}_{22}{v}_{x_s}+{\widehat{b}}_2{F}_{in}\\ -{\widehat{a}}_{22}{v}_{x_s}+{\widehat{b}}_2{F}_{in}\end{array}\right],$$

(39)

which means that the change of $v_{x_s}$ and ${\widehat{v}}_{x_s}$ is described by the same differential equation. Based on Equation (39), starting from the same initial state, $v_x$ and ${\widehat{v}}_{x_s}$ will be equal. Since the systems start from an energy-free state (i.e., the initial value of all state variables is zero), the initial values are the same. The above is summarized in the block diagram shown in Figure 7.

4.2. The Discrete-Time Model

To prepare the computer program for the implementation of the bilateral control, a discrete-time version of Equation (27) is required. Figure 8 is the discrete-time version of Figure 7.

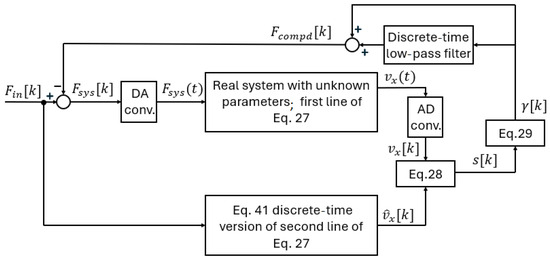
Figure 8. Discrete-time sliding mode compensation.

In the experiment, $F_r=0$, and the goal is to ensure that the operator can move the system with as little operator force ($F_o$) as possible. Ideally, the force controller should follow the time-varying reference signal, and in this particular operating condition, $F_o=0$, while $v_x\ne 0$. Since a suitably low level of error $F_e=0$ cannot be ensured with a PID-type controller, there is a need for force $F_{comp}=\gamma$, which can be considered as a feedforward component for motion information.

In this session, the input signal $F_{in}$ is not generated by the external bilateral controller, nor the force exerted by the operator (because the operator cannot exert a constant force very accurately), but $F_{in}$ is a square force signal with software generated with a very small amplitude. In this phase, the research question was whether the response of the high-amplification reference model to a small-amplitude $F_{in}$ reference square signal can be tracked in reality despite amplification an order of magnitude lower with the help of compensation.

In real systems, the limited switching frequency causes several kinds of problems; to reduce these effects, it is advisable to reduce the magnitude of the discontinuous term $\mathrm{\Gamma }$ in Equation (30). This can be performed up to an order of magnitude by filtering as shown in Figure 8 or by generating an estimated equivalent compensating term ${\widehat{\gamma }}_{eq}$ according to [39]. When low-pass filtering is used, it is sufficient to force the trajectory back to the sliding surface if the magnitude of $\mathrm{\Gamma }$ is greater than the change in the equivalent control signal between two switches, which is much smaller than the magnitude of the signal.

The velocity signal is calculated from the incremental position sensor signal by numerical differentiation, which is known to increase the noise. Therefore, in the real system, the velocity signal must be filtered with a low-pass filter. Similarly, the low-pass filter can help to reduce the value of $\mathrm{\Gamma }$ (see [39]). In both cases, three series-connected low-pass filters of the first type were used (see Appendix A) characterized by the Laplace transform

$$signa{l}_{filtered}={\displaystyle \frac{1}{T_{c}s+1}}signa{l}_{measured},$$

(40)

where $T_c$ is the time constant of the filter. ($T_c=T_{f_{v_x}}$ in the case of the velocity filter and $T_c=T_{f_{relay}}$ in the case of the relay filter; see Table 2) Instead of Equation (40), its z-transform is used (see Appendix A).

Table 2. Summary of parameters.

State-Space Model	Reference Model	Identified
${\widehat{a}}_{22}$	8	2.8896
${\widehat{b}}_2$	20	1.1317
Other parameters	Reference Model	Identified
$m_{eq}$	0.0500	0.8836
${\nu }_{eq}$	8	2.8896
$F_{of{f}_{eq}}$	0	0.03
$F_{C_{eq}}$	0	0.3593
$F_{{Str}_{eq}}$	0	1.3250
$v_s$	-	0.0026
$T_{f_{v_x}}$	-	0.0001
$T_{f_{relay}}$	-	0.0010
$\gamma$	-	0.7000

Friction compensation uses only the velocity signal, but position is also important when testing the master device. In the subsystem “master device x axis” (Figure 9), a position signal is added to the equations, but the reference model still refers only to velocity. The controller is implemented with operational amplifiers that have a small offset error, i.e., a constant value is added to the measurement signals passing through the operational amplifiers. As a result, the positive and negative half periods of the measurement signals are not properly symmetric. This deviation is simulated by adding the equivalent value $F_{of{f}_{eq}}$ (see Figure 9 and MATLAB code in Appendix A). In the reference model, instead of Equation (1), its z-transform

$$v_x\left[z\right]={\displaystyle \frac{0.007987}{z+0.9968}}{F}_{in}\left[z\right]$$

(41)

is used (see Appendix A).

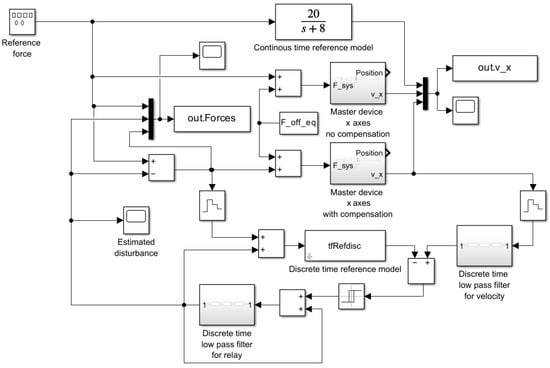
Figure 9. MATLAB Simulink whole simulation model.

5. Simulation Results

An advantage of sliding mode control is that it can be applied without the detailed knowledge of the controlled plant. The parameters of the system were identified by a machine learning program in order to create the simulation. These identified system parameters do not appear in the controller algorithm. The sliding mode-based friction compensation works even without knowledge of the system parameters.

Some of our measurement results were published earlier [40], but the equivalent parameters of the telemanipulation system were not known at that time. Since then, using machine learning algorithms and higher capacity computers, we have identified the parameters of the Equation (27) simulation model on the basis of the measurement results. (A separate article will report on machine learning identification.) Thus, it is possible to compare the simulation and measurements now.

Many different friction models are available in the literature. We used the following simple model for the nonlinear components in the simulation:

$$F_{n{l}_f}\left(v_x\right)=-\mathrm{sign}\left(v_x\right)F_{C_{eq}}-\mathrm{sign}\left(v_x\right){\displaystyle \frac{F_{{Str}_{eq}}}{1+{(v_x/v_S)}^2}},$$

(42)

where $F_{C_{eq}}$ and $F_{{Str}_{eq}}$ are the Coulomb and Stribeck friction parameters, respectively. The MATLAB code of Equation (42) and more details can be found in Appendix A.

The sampling time is $T_s=0.0004$ s (2.5 kHz) [41]. The parameters of the reference and identified model are summarized in Table 2.

The measured and simulated velocities and forces are compared in Figure 10 and Figure 11 for the $0.1$ N reference force. The comparison of responses for the $0.01$ N reference force are shown in Figure 12 and Figure 13. If the amplitude of the reference pulses is reduced, we reach the limit of operation (see Figure 14 and Figure 15).

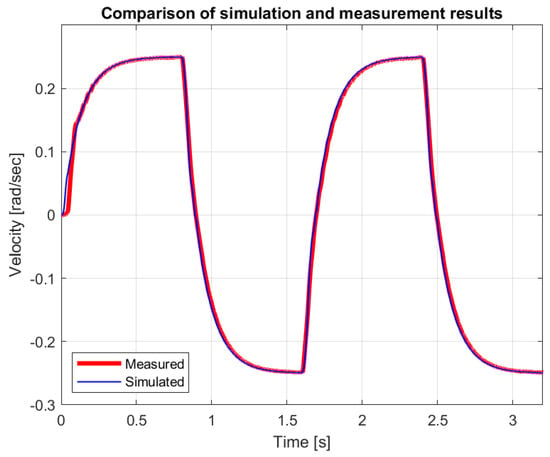
Figure 10. Measured and simulated velocity with $F_{in}$ alternating 0.1 N force impulses.

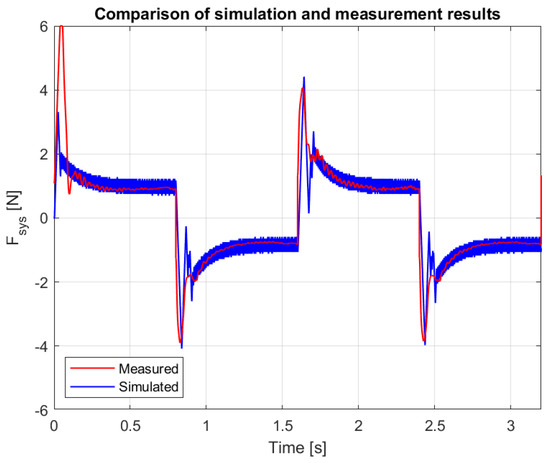
Figure 11. Measured and simulated $F_{sys}$ force with alternating 0.1 N reference force impulses.

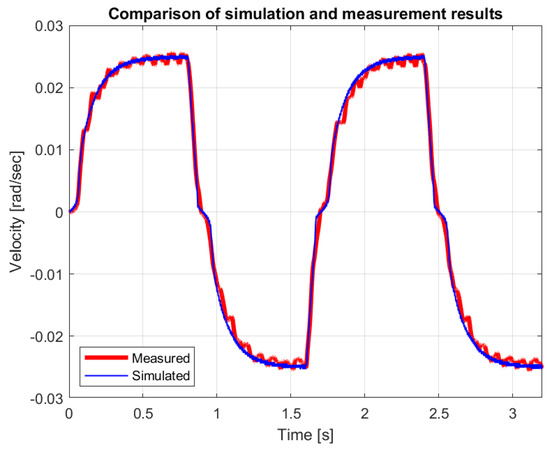
Figure 12. Measured and simulated velocity with $F_{in}$ alternating 0.01 N force impulses.

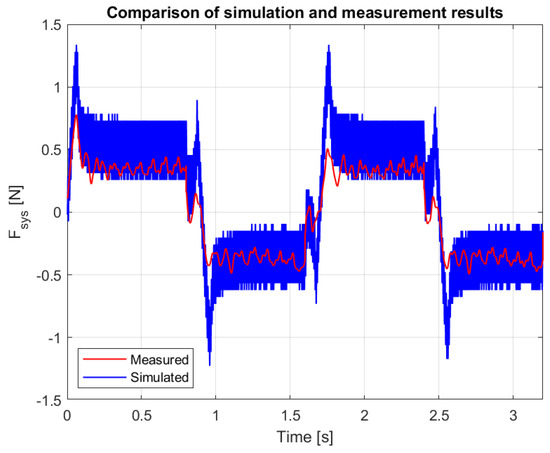
Figure 13. Measured and simulated $F_{sys}$ force with alternating 0.01 N reference force impulses.

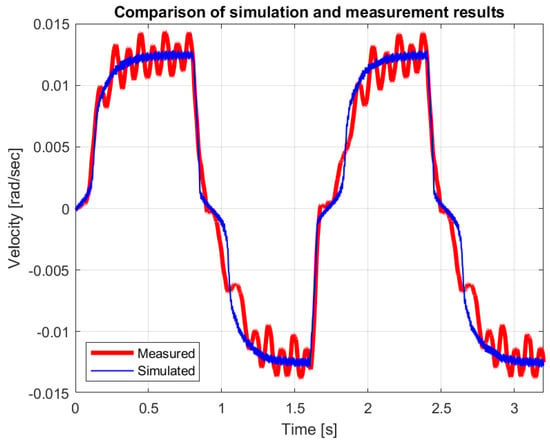
Figure 14. Measured and simulated velocity with $F_{in}$ alternating 0.005 N force impulses.

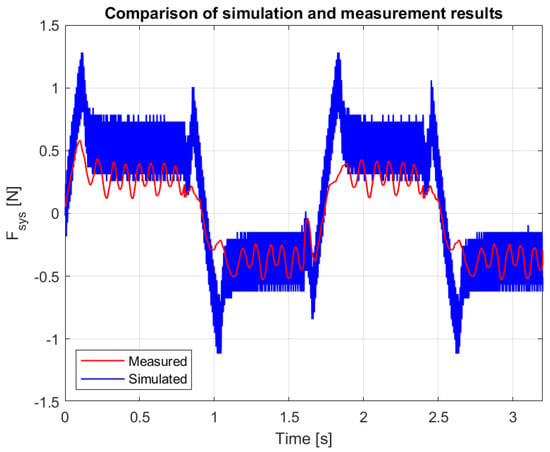
Figure 15. Measured and simulated $F_{sys}$ force with alternating 0.005 N reference force impulses.

A real system always contains so-called unmodeled dynamics, which prevent the sudden changes in the real system that are experienced in the simulated signal. Small-amplitude oscillations are visible in the measured signals (see Figure 12 and Figure 13). There is a theoretical possibility that the system can become unstable due to resonance of the unmodeled dynamics. Fortunately, we have not experienced this during long-term use of the telemanipulation system. Note that we have previously published how to reduce the unstable resonance caused by unmodeled dynamics [42], but this was not necessary in our measurements.

6. Experimental Results

During the experiment, we assumed that the remote environment does not affect the slave device ($F_r=0$), and that the operator interacts with the system with a force signal consisting of square pulses of different sizes, but in order to achieve a comparable smooth operation, we replaced the operator with an additional force controller.

The real system follows the velocity of the reference model well. If we further increase the magnitude of the force pulses, the movement of the joystick can follow the reference model with sufficient accuracy for the telemanipulation task. We experienced problems with smaller values. Figure 16 and Figure 17 can be considered as borderline cases.

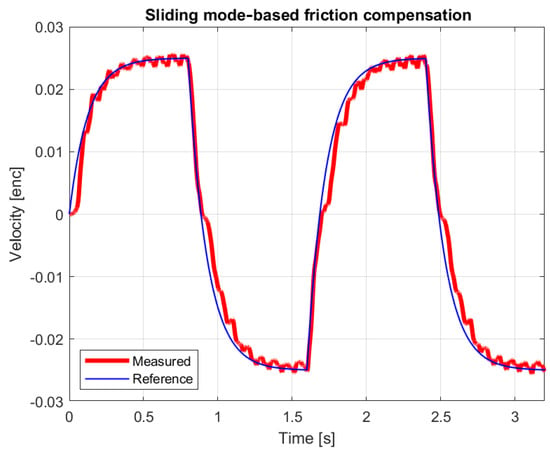
Figure 16. Reference and measured velocity $F_{in}$ with alternating 0.01 N force impulses.

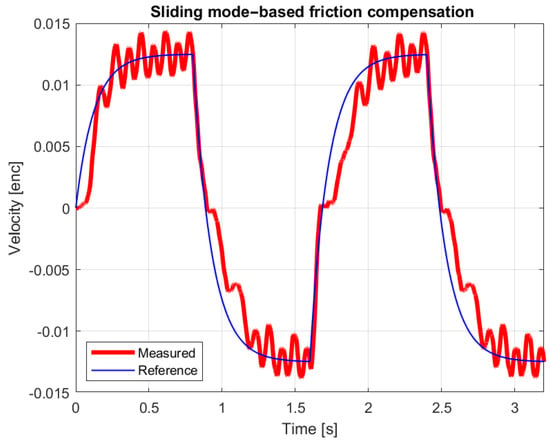
Figure 17. Reference and measured velocity with $F_{in}$ alternating 0.005 N force impulses.

If the force is further reduced, we reach the limit of the practical applicability of the method (see Figure 18). This is due to the upper limit of the sampling frequency. This is no longer important because a force of 0.001 N is outside the operator’s sensing range.

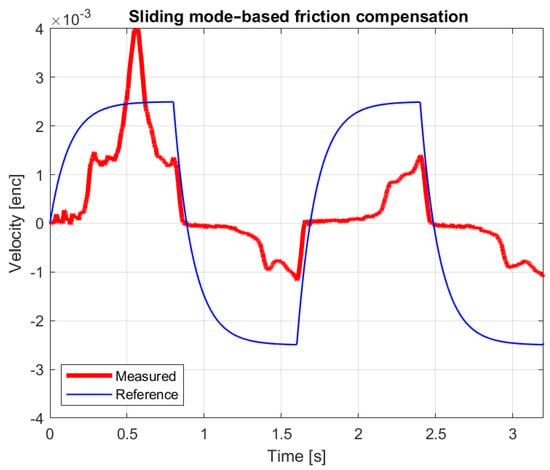
Figure 18. Reference and measured velocity with $F_{in}$ 0.001 N force impulses.

In order for the master device to achieve the desired movement with such a small amount of effort from the operator, the movement of the mechanism is mainly performed by the motors. It can be clearly seen in Figure 19 that the master device cannot move until then. The force $F_{in}$ is smaller than the adhesion friction force, so the system cannot move by $F_{in}$ alone, i.e., the force $F_{comp}$ is needed, which, due to the discrete-time low-pass filter, can only reach the required size after a ramp-up time. The joystick starts to move when the following condition is satisfied:

$$\mathrm{abs}(F_{comp}+F_{in})>\mathrm{abs}(F_{C_{eq}}+F_{{Str}_{eq}}).$$

(43)

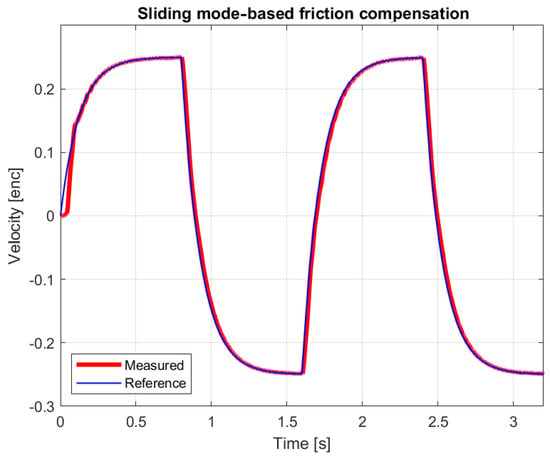
Figure 19. Reference and measured velocity with $F_{in}$ alternating 0.1 N force impulses.

The forces exerted by the operator $F_{in}$ and the $F_{sys}$ required to move the mechanism are compared in Figure 20, Figure 21, Figure 22 and Figure 23. In the figures, the force $F_{sys}$ is shown as a continuous curve for better visibility, but in reality it is a discontinuous signal. It can be seen that moving the mechanism requires a force almost two orders of magnitude greater than that exerted by the operator.

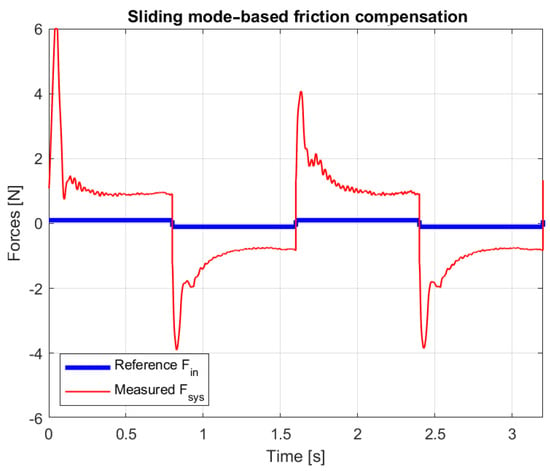
Figure 20. Measured $F_{sys}$ force and reference with alternating 0.1 N force impulses.

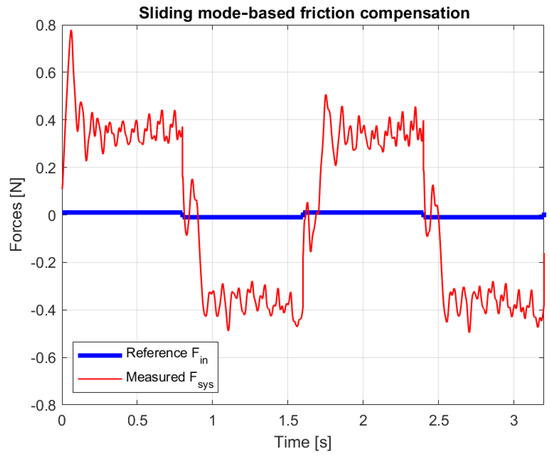
Figure 21. Measured $F_{sys}$ force and reference $F_{in}$ with alternating 0.01 N force impulses.

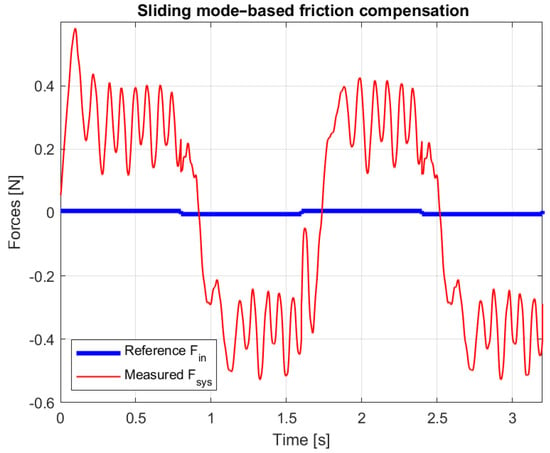
Figure 22. Measured $F_{sys}$ force and reference $F_{in}$ with alternating 0.005 N force impulses.

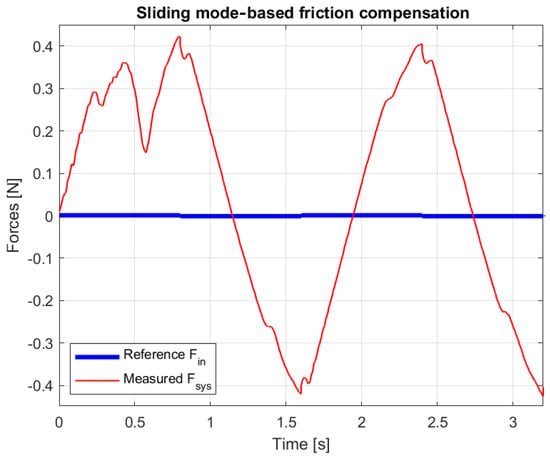
Figure 23. Measured $F_{sys}$ force and reference $F_{in}$ with alternating 0.001 N force impulses.

The operator moved the master device on a spatial spiral trajectory with force control off, with simple PD control (without SM compensation), and with PD and the SM compensation presented in the article. Obviously, these motions were not exactly identical (an illustrative example is shown in Figure 24), so the time function of the forces felt by the operator in the different cases cannot be compared; instead, the maximum forces felt by the operator during spiral operation are summarized in Table 1.

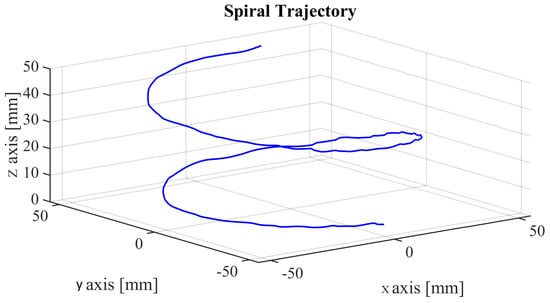
Figure 24. Three-dimensional trajectory of operator’s freehand movement.

We can roughly say that with the force control shown in Figure 3, the operator can move the master device with approximately one order of magnitude less force than without control, and the SM compensation proposed in the article can reduce the force to be exerted by the operator by another order of magnitude. A force of about 1 N is definitely perceived by the operator. A force of less than $0.01$ N is already so small that it is hardly perceived by the operator.

When following the spiral trajectory, the force perceived by the operator in different directions can be seen in Figure 25. It can be seen that in this particular experiment the force does not exceed $0.1$ N in either direction.

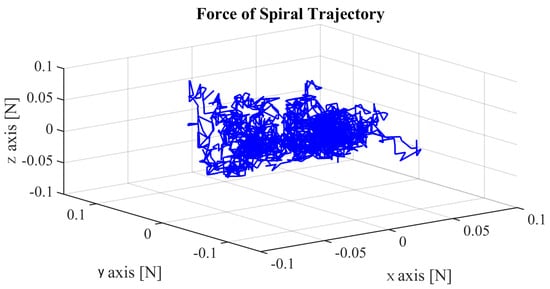
Figure 25. Three-dimensional trajectory of operator’s force during freehand movement.

7. Conclusions

This paper deals with force compensation from both mathematical and engineering approaches when the sliding mode control method is used. In this method, the challenge is to force the trajectory on a surface in the phase plane that represents an ideal operation. Mathematically, this means that the required ideal trajectory in the phase plane consists of states where the original autonomous differential equation is not defined. The theory of differential equations with discontinuous right-hand side provides a set of tools for handling this type of problem. In telemanipulation, from a practical point of view, the dynamic properties of the master device must be changed so that when the operators move it they feel smaller reaction forces or torques (a “virtual” system with smaller mass and inertia) than the real ones, and feel only a small part of the friction force, which can be relatively quite large. Essentially, force compensation is applied to change the characteristics of a dynamic system. In terms of the mathematical model, a sufficient condition of the sliding mode is presented through the theory of the differential equation with discontinuous right-hand side. The suitability of the mathematically discussed method for practical applications is shown by measurements with an experimental device and with a simulation elaborated in the current research.

To explain the effectiveness of sliding mode control, we can roughly say that with a conventional PID-type force controller, the operator can move the master device with about an order of magnitude less force than without the controller, and the sliding mode-based force compensation can reduce the operator’s force by another order of magnitude. According to our experiments, the limit of applicability was not reached in the operator’s perception range.

Sliding mode control is a method that does not require prior knowledge of the phenomenon (e.g., friction) that causes the nonlinearity of the system, but it can still provide very accurate compensation. We have described the mathematical background necessary for the application of the method in depth, according to the nature of the technical problem under investigation, which was not available in the scientific literature in such a complex approach.