Moran’s I for Multivariate Spatial Data

Abstract

Moran’s I is a spatial autocorrelation measure of univariate spatial data. Therefore, even if p spatial data exist, we can only obtain p values for Moran’s I. In other words, Moran’s I cannot measure the degree of spatial autocorrelation of multivariate spatial data as a single value. This paper addresses this issue. That is, we extend Moran’s I so that it can measure the degree of spatial autocorrelation of multivariate spatial data as a single value. In addition, since the local version of Moran’s I has the same problem, we extend it as well. Then, we establish their properties, which are fundamental for applied work. Numerical illustrations of the theoretical results obtained in the paper are also provided.

1. Introduction

Spatial autocorrelation is a notion that describes the similarities/discrepancies between data at different vertices/spatial units. It is fundamental to spatial science, which includes spatial statistics, spatial econometrics, geographical analysis, and so on. Many measures of it have been proposed. For a historical overview of spatial autocorrelation, see, e.g., Getis [1]. Among them, Moran’s I is the most prominent spatial autocorrelation measure and was developed by Moran [2] and Cliff and Ord [3,4,5,6]. Roughly speaking, like Pearson’s sample correlation coefficient, a positive (respectively, negative) Moran’s I indicates the presence of positive (respectively, negative) spatial autocorrelation. (However, unlike Pearson’s sample correlation coefficient, its range is not necessarily $[-1,1]$. As will be shown later, it depends on the spatial weight matrix. See also de Jong et al. [7] and Maruyama [8].) Later, Anselin [9] developed a local version of Moran’s I: local Moran’s I. To distinguish them, Moran’s I is sometimes referred to as global Moran’s I.

Moran’s I is designed to measure the spatial autocorrelation of univariate spatial data. Therefore, even if p spatial data exist, we can only obtain p values of Moran’s I. In other words, Moran’s I cannot measure the degree of spatial autocorrelation of multivariate spatial data as a single value. In this paper: (i) We address this issue. That is, we extend Moran’s I so that it can measure the degree of spatial autocorrelation of multivariate spatial data as a single value. (ii) In addition, since the local version of Moran’s I has the same problem, we extend it as well. (iii) Subsequently, we establish their properties, which are fundamental for applied work. (iv) Numerical illustrations of the theoretical results are also provided.

Here, we discuss existing research related to this study. In addition to the papers listed above, the following papers are closely related to this paper: Wartenberg [10], Anselin [11], Lin [12], and Yamada [13,14]. First, Yamada [13] presented several results on univariate global Moran’s I. This paper depends on them. Second, Yamada [14] dealt with the multivariate extension of Geary’s c, which was developed by Geary [15] and modified by Cliff and Ord [3,4,5,6]. Thus, the present paper can be seen as a companion paper to it. It should be noted that the multivariate local Geary’s c was developed by Anselin [11]. Third, the relevance of Wartenberg [10] as well as Lin [12] to this paper is discussed in the second section from the end. This is mainly because we want to use our notations as following to describe their studies.

The paper is organized as follows. In Section 2, we sketch how Moran’s I is extended in this paper. In Section 3, we provide some preliminaries. More specifically, after stating the multivariate spatial data that will be considered in the paper, we review global and local Moran’s I for univariate spatial data. In Section 4, we define two new measures, i.e., multivariate global and local Moran’s I, and establish their properties. Section 5 provides numerical illustrations of the theoretical results obtained in Section 4. Section 6 clarifies the relationship between our multivariate global Moran’s I and Wartenberg’s [10] spatial correlation matrix. Section 7 concludes the paper.

2. A Sketch of How Moran’s I is Extended

In this section, we sketch how Moran’s I is extended in this paper.

Let $y_i$ denote a realization of a single variable y at the vertex/spatial unit $v_i$ for $i=1,\dots ,n$. Moran’s I uses the product given by

$$\begin{array}{c}\hfill \left({\displaystyle \frac{y_i-\overline{y}}{s}}\right)\left({\displaystyle \frac{y_j-\overline{y}}{s}}\right),\end{array}$$

(1)

for $i,j=1,\dots ,n$, where $\overline{y}={\displaystyle \frac{1}{n}}{\sum }_{i=1}^n{y}_i$, and s is the positive square root of ${\displaystyle \frac{1}{n}}{\sum }_{i=1}^n{(y_i-\overline{y})}^2$. Roughly speaking, like the sample correlation coefficient, a positive (respectively, negative) global Moran’s I indicates the presence of positive (respectively, negative) spatial autocorrelation.

Let ${\mathit{y}}_i={[y_{\left(1\right),i},\dots ,y_{\left(p\right),i}]}^{\top }$ denote a realization of a multivariate vector $\mathit{y}={[y_{\left(1\right)},\dots ,y_{\left(p\right)}]}^{\top }$ at the vertex/spatial unit $v_i$ for $i=1,\dots ,n$. We ask how we can measure the similarity/discrepancy between ${\mathit{y}}_i$ and ${\mathit{y}}_j$, which are both p-dimensional column vectors. A natural approach is to extend (1). That is, it can be measured with the inner product given by

$$\begin{array}{c}\hfill {({\mathit{y}}_i-\overline{\mathit{y}})}^{\top }{\mathit{S}}^{-1}({\mathit{y}}_j-\overline{\mathit{y}}),\end{array}$$

(2)

for $i,j=1,\dots ,n$, where $\overline{\mathit{y}}={[{\overline{y}}_{\left(1\right)},\dots ,{\overline{y}}_{\left(p\right)}]}^{\top }$, and ${\mathit{S}}^{-{\displaystyle \frac{1}{2}}}=\mathrm{diag}(s_{\left(1\right)}^{-1},\dots ,s_{\left(p\right)}^{-1})$. Here, ${\overline{y}}_{\left(h\right)}={\displaystyle \frac{1}{n}}{\sum }_{i=1}^n{y}_{\left(h\right),i}$, and $s_{\left(h\right)}$ is the positive square root of ${\displaystyle \frac{1}{n}}{\sum }_{i=1}^n{(y_{\left(h\right),i}-{\overline{y}}_{\left(h\right)})}^2$ for $h=1,\dots ,p$. We develop a spatial autocorrelation measure that uses (2).

3. Preliminaries

In this section, after clarifying the multivariate spatial data that will be considered in the paper, we review global and local Moran’s I for univariate spatial data.

Before we do this, we introduce some notation. Let ${\mathit{I}}_n$ be the identity matrix of order n, and let ${\mathit{e}}_i$ be the i-th column of ${\mathit{I}}_n$. Let $\mathit{\iota }$ be the n-dimensional vector of ones, and let ${\mathit{Q}}_{\iota }={\mathit{I}}_n-\mathit{\iota }{\left({\mathit{\iota }}^{\top }\mathit{\iota }\right)}^{-1}{\mathit{\iota }}^{\top }$. Note that ${\mathit{Q}}_{\iota }$ is a symmetric and idempotent matrix, i.e., ${\mathit{Q}}_{\iota }^{\top }={\mathit{Q}}_{\iota }$ and ${\mathit{Q}}_{\iota }^2={\mathit{Q}}_{\iota }$.

3.1. Multivariate Spatial Data

Following de Jong et al. [7], we treat the problem of spatial autocorrelation in terms of a graph. Let $G=(V,E)$ denote a directed/undirected graph with n vertices. In addition, denote its vertex set by $V=\{v_1,\dots ,v_n\}$, where $n\ge 2$. For $i,j=1,\dots ,n$, let

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{w}_{i,j}>0\hfill & \mathrm{if}(v_i,v_j)\in E,\hfill \\ w_{i,j}=0\hfill & \mathrm{otherwise},\hfill \end{array}\right.\end{array}$$

and $\mathit{W}=\left[w_{i,j}\right]\in {\mathbb{R}}^{n\times n}$. We assume that $w_{i,i}=0$ for $i=1,\dots ,n$, and accordingly, $\mathit{W}$ is a hollow matrix by assumption. In addition, we assume that ${\sum }_{i=1}^n{\sum }_{j=1}^n{w}_{i,j}>0$. Then $\mathit{W}$ is a nonzero matrix. For example, when $V=\{v_1,v_2,v_3,v_4\}$ and $E=\{(v_1,v_2),(v_1,v_4),$$(v_2,v_1),(v_2,v_3),(v_3,v_4),(v_4,v_2)\}$, its binary weight matrix (adjacency matrix) is

$$\begin{array}{c}\hfill \mathit{W}=\left[\begin{array}{cccc}0& 1& 0& 1\\ 1& 0& 1& 0\\ 0& 0& 0& 1\\ 0& 1& 0& 0\end{array}\right].\end{array}$$

(Note that the corresponding graph is shown in Figure 1. The edge between $v_1$ and $v_2$ is undirected because both $(v_1,v_2)$ and $(v_2,v_1)$ belong to E.)

Figure 1. A graph consists of 4 vertices.

As illustrated above, $\mathit{W}$ is not necessarily symmetric. However, for any $\mathit{x}\in {\mathbb{R}}^n$, given that ${\mathit{x}}^{\top }\mathit{W}\mathit{x}={\left({\mathit{x}}^{\top }\mathit{W}\mathit{x}\right)}^{\top }={\mathit{x}}^{\top }{\mathit{W}}^{\top }\mathit{x}$, it follows that ${\mathit{x}}^{\top }\mathit{W}\mathit{x}={\mathit{x}}^{\top }\mathcal{W}\mathit{x}$, where $\mathcal{W}={\displaystyle \frac{\mathit{W}+{\mathit{W}}^{\top }}{2}}$. Note that $\mathcal{W}$ is symmetric even though $\mathit{W}$ is not symmetric. (If $G=(V,E)$ is an undirected graph, then $\mathcal{W}$ is identical to $\mathit{W}$. We provide such a $\mathit{W}$ in Section 5.2) Accordingly, given that ${\mathit{\iota }}^{\top }\mathit{W}\mathit{\iota }={\sum }_{i=1}^n{\sum }_{j=1}^n{w}_{i,j}$, it follows that ${\mathit{\iota }}^{\top }\mathcal{W}\mathit{\iota }={\sum }_{i=1}^n{\sum }_{j=1}^n{w}_{i,j}$. Moreover, as $w_{i,i}=0$ for $i=1,\dots ,n$ by assumption, $\mathrm{tr}\left(\mathcal{W}\right)={\displaystyle \frac{\mathrm{tr}\left(\mathit{W}\right)+\mathrm{tr}\left({\mathit{W}}^{\top }\right)}{2}}=\mathrm{tr}\left(\mathit{W}\right)=0$.

Let

$$\begin{array}{c}\hfill \mathit{Y}=\left[\begin{array}{ccc}{y}_{\left(1\right),1}& \cdots & y_{\left(p\right),1}\\ ⋮& & ⋮\\ y_{\left(1\right),n}& \cdots & y_{\left(p\right),n}\end{array}\right]=\left[\begin{array}{c}{\mathit{y}}_1^{\top }\\ ⋮\\ {\mathit{y}}_n^{\top }\end{array}\right]=[{\mathit{y}}_{\left(1\right)},\dots ,{\mathit{y}}_{\left(p\right)}]\in {\mathbb{R}}^{n\times p}.\end{array}$$

(3)

Recall that ${\mathit{y}}_i^{\top }=[y_{\left(1\right),i},\dots ,y_{\left(p\right),i}]$ in (3) denotes a realization of a multivariate vector ${\mathit{y}}^{\top }=[y_{\left(1\right)},\dots ,y_{\left(p\right)}]$ at the vertex/spatial unit $v_i$ for $i=1,\dots ,n$.

Let

$$\begin{array}{c}\hfill \mathit{Z}=\left[\begin{array}{ccc}{z}_{\left(1\right),1}& \cdots & z_{\left(p\right),1}\\ ⋮& & ⋮\\ z_{\left(1\right),n}& \cdots & z_{\left(p\right),n}\end{array}\right]=\left[\begin{array}{c}{\mathit{z}}_1^{\top }\\ ⋮\\ {\mathit{z}}_n^{\top }\end{array}\right]=[{\mathit{z}}_{\left(1\right)},\dots ,{\mathit{z}}_{\left(p\right)}]\in {\mathbb{R}}^{n\times p},\end{array}$$

(4)

where

$$\begin{array}{c}\hfill z_{\left(h\right),i}={\displaystyle \frac{y_{\left(h\right),i}-{\overline{y}}_{\left(h\right)}}{s_{\left(h\right)}}},i=1,\dots ,n,h=1,\dots ,p.\end{array}$$

(5)

Then, by construction, ${\mathit{z}}_i$ is related to ${\mathit{y}}_i$ as

$$\begin{array}{c}\hfill {\mathit{z}}_i=\left[\begin{array}{c}{z}_{\left(1\right),i}\\ ⋮\\ z_{\left(p\right),i}\end{array}\right]=\left[\begin{array}{c}{\displaystyle \frac{y_{\left(1\right),i}-{\overline{y}}_{\left(1\right)}}{s_{\left(1\right)}}}\\ ⋮\\ {\displaystyle \frac{y_{\left(p\right),i}-{\overline{y}}_{\left(p\right)}}{s_{\left(p\right)}}}\end{array}\right]={\mathit{S}}^{-{\displaystyle \frac{1}{2}}}({\mathit{y}}_i-\overline{\mathit{y}}),i=1,\dots ,n,\end{array}$$

(6)

which appears in (2). Accordingly, it follows that

$$\begin{array}{c}\hfill {\mathit{z}}_i^{\top }{\mathit{z}}_j={({\mathit{y}}_i-\overline{\mathit{y}})}^{\top }{\mathit{S}}^{-1}({\mathit{y}}_j-\overline{\mathit{y}}).\end{array}$$

(7)

In addition, ${\mathit{z}}_{\left(h\right)}$ is related to ${\mathit{y}}_{\left(h\right)}$ as

$$\begin{array}{c}\hfill {\mathit{z}}_{\left(h\right)}=\left[\begin{array}{c}{z}_{\left(h\right),1}\\ ⋮\\ z_{\left(h\right),n}\end{array}\right]=\left[\begin{array}{c}{\displaystyle \frac{y_{\left(h\right),1}-{\overline{y}}_{\left(h\right)}}{s_{\left(h\right)}}}\\ ⋮\\ {\displaystyle \frac{y_{\left(h\right),n}-{\overline{y}}_{\left(h\right)}}{s_{\left(h\right)}}}\end{array}\right]={\displaystyle \frac{1}{s_{\left(h\right)}}}({\mathit{y}}_{\left(h\right)}-{\overline{y}}_{\left(h\right)}\mathit{\iota })={\displaystyle \frac{1}{s_{\left(h\right)}}}{\mathit{Q}}_{\iota }{\mathit{y}}_{\left(h\right)},h=1,\dots ,p.\end{array}$$

(8)

3.2. Global Moran’s I for Univariate Spatial Data

Denote the global Moran’s I for a univariate spatial data, ${\mathit{y}}_{\left(h\right)}={[y_{\left(h\right),1},\dots ,y_{\left(h\right),n}]}^{\top }$, by $I_{\left(h\right)}$:

$$\begin{array}{c}\hfill I_{\left(h\right)}={\displaystyle \frac{n}{q}}{\displaystyle \frac{{\sum }_{i=1}^n{\sum }_{j=1}^n{w}_{i,j}(y_{\left(h\right),i}-{\overline{y}}_{\left(h\right)})(y_{\left(h\right),j}-{\overline{y}}_{\left(h\right)})}{{\sum }_{k=1}^n{(y_{\left(h\right),k}-{\overline{y}}_{\left(h\right)})}^2}},h=1,\dots ,p,\end{array}$$

(9)

where $q={\sum }_{i=1}^n{\sum }_{j=1}^n{w}_{i,j}$.

Then, as shown in, e.g., de Jong et al. [7], Dray [16], Maruyama [8], Murakami and Griffith [17], and Nishi et al. [18], $I_{\left(h\right)}$ can be expressed in matrix notation as

$$\begin{array}{c}\hfill I_{\left(h\right)}={\displaystyle \frac{n}{q}}{\displaystyle \frac{{\mathit{y}}_{\left(h\right)}^{\top }{\mathit{Q}}_{\iota }^{\top }\mathit{W}{\mathit{Q}}_{\iota }{\mathit{y}}_{\left(h\right)}}{{\mathit{y}}_{\left(h\right)}^{\top }{\mathit{Q}}_{\iota }^{\top }{\mathit{Q}}_{\iota }{\mathit{y}}_{\left(h\right)}}}={\displaystyle \frac{n}{q}}{\displaystyle \frac{{\mathit{y}}_{\left(h\right)}^{\top }{\mathit{Q}}_{\iota }^{\top }\mathcal{W}{\mathit{Q}}_{\iota }{\mathit{y}}_{\left(h\right)}}{{\mathit{y}}_{\left(h\right)}^{\top }{\mathit{Q}}_{\iota }^{\top }{\mathit{Q}}_{\iota }{\mathit{y}}_{\left(h\right)}}},h=1,\dots ,p.\end{array}$$

(10)

$I_{\left(h\right)}$ in (9) can also be represented by using $z_{\left(h\right),1},\dots ,z_{\left(h\right),n}$ as

$$\begin{array}{cc}\hfill I_{\left(h\right)}& ={\displaystyle \frac{1}{q}}\sum _{i=1}^n\sum _{j=1}^n{w}_{i,j}\left({\displaystyle \frac{y_{\left(h\right),i}-{\overline{y}}_{\left(h\right)}}{s_{\left(h\right)}}}\right)\left({\displaystyle \frac{y_{\left(h\right),j}-{\overline{y}}_{\left(h\right)}}{s_{\left(h\right)}}}\right)\hfill \\ \hfill & ={\displaystyle \frac{1}{q}}\sum _{i=1}^n\sum _{j=1}^n{w}_{i,j}{z}_{\left(h\right),i}{z}_{\left(h\right),j},h=1,\dots ,p.\hfill \end{array}$$

(11)

Accordingly, given that ${\sum }_{i=1}^n{\sum }_{j=1}^n{w}_{i,j}{z}_{\left(h\right),i}{z}_{\left(h\right),j}={\mathit{z}}_{\left(h\right)}^{\top }\mathit{W}{\mathit{z}}_{\left(h\right)}={\mathit{z}}_{\left(h\right)}^{\top }\mathcal{W}{\mathit{z}}_{\left(h\right)}$, $I_{\left(h\right)}$ in (11) can be expressed in matrix notation as follows.

$$\begin{array}{c}\hfill I_{\left(h\right)}={\displaystyle \frac{1}{q}}{\mathit{z}}_{\left(h\right)}^{\top }\mathit{W}{\mathit{z}}_{\left(h\right)}={\displaystyle \frac{1}{q}}{\mathit{z}}_{\left(h\right)}^{\top }\mathcal{W}{\mathit{z}}_{\left(h\right)},h=1,\dots ,p.\end{array}$$

(12)

Incidentally, given that $s_{\left(h\right)}^2={\displaystyle \frac{1}{n}}{\mathit{y}}_{\left(h\right)}^{\top }{\mathit{Q}}_{\iota }^{\top }{\mathit{Q}}_{\iota }{\mathit{y}}_{\left(h\right)}$ and ${\mathit{z}}_{\left(h\right)}={\displaystyle \frac{{\mathit{Q}}_{\iota }{\mathit{y}}_{\left(h\right)}}{s_{\left(h\right)}}}$, (12) can be obtained directly from (10).

Denote a spectral decomposition of a real symmetric matrix ${\mathit{Q}}_{\iota }^{\top }\mathcal{W}{\mathit{Q}}_{\iota }$ by

$$\begin{array}{c}\hfill {\mathit{Q}}_{\iota }^{\top }\mathcal{W}{\mathit{Q}}_{\iota }=\mathit{U}\mathsf{\Lambda }{\mathit{U}}^{\top },\end{array}$$

(13)

where $\mathit{U}=[{\mathit{u}}_1,\dots ,{\mathit{u}}_n]$, and $\mathsf{\Lambda }=\mathrm{diag}({\lambda }_1,\dots ,{\lambda }_n)$. Then, given that ${\mathit{Q}}_{\iota }^{\top }\mathcal{W}{\mathit{Q}}_{\iota }\mathit{\iota }=\mathbf{0}$, we can let $({\lambda }_n,{\mathit{u}}_n)=\left(0,{\displaystyle \frac{1}{\sqrt{n}}}\mathit{\iota }\right)$. With respect to the other eigenvalues, let ${\lambda }_1,\dots ,{\lambda }_{n-1}$ be in ascending order.

We document two known results with respect to $I_{\left(h\right)}$.

Proposition 1.

(Equation (19) of de Jong et al. [7], Theorem 2.1 of Maruyama [8]). It follows that $I_{\left(h\right)}\in \left[{\displaystyle \frac{n}{q}}{\lambda }_1,{\displaystyle \frac{n}{q}}{\lambda }_{n-1}\right]$. $I_{\left(h\right)}={\displaystyle \frac{n}{q}}{\lambda }_1$ when ${\mathit{y}}_{\left(h\right)}=\mu \mathit{\iota }+{\gamma }_{\left(h\right)}{\mathit{u}}_1$ such that ${\gamma }_{\left(h\right)}\ne 0$. Likewise, $I_{\left(h\right)}={\displaystyle \frac{n}{q}}{\lambda }_{n-1}$ when ${\mathit{y}}_{\left(h\right)}=\mu \mathit{\iota }+{\gamma }_{\left(h\right)}{\mathit{u}}_{n-1}$ such that ${\gamma }_{\left(h\right)}\ne 0$.

Proof. 

Omitted. □

Remark 1.

(i) Although the range of Pearson’s sample correlation coefficient is $[-1,1]$, that of Moran’s I is $[{\displaystyle \frac{n}{q}}{\lambda }_1,{\displaystyle \frac{n}{q}}{\lambda }_{n-1}]$, which depends on $\mathcal{W}={\displaystyle \frac{\mathit{W}+{\mathit{W}}^{\top }}{2}}$. (ii) From Poincaré’s separation theorem Rao [19] (p. 64), Scott and Styan [20] (Theorem 1), Abadir and Magnus [21] (p. 347), Seber [22] (p. 113), it follows that

$$\begin{array}{c}\hfill {\zeta }_1\le {\lambda }_1\le {\zeta }_2,{\zeta }_{n-1}\le {\lambda }_{n-1}\le {\zeta }_n,\end{array}$$

(14)

where ${\zeta }_1,\dots ,{\zeta }_n$ are the eigenvalues of $\mathcal{W}$ in ascending order. Accordingly, it follows that

$$\begin{array}{c}\hfill I_{\left(h\right)}\in \left[{\displaystyle \frac{n}{q}}{\lambda }_1,{\displaystyle \frac{n}{q}}{\lambda }_{n-1}\right]\subseteq \left[{\displaystyle \frac{n}{q}}{\zeta }_1,{\displaystyle \frac{n}{q}}{\zeta }_n\right],h=1,\dots ,p.\end{array}$$

(15)

Incidentally, if $G=(V,E)$ is an undirected bipartite graph whose weight matrix is binary, then ${\zeta }_n=-{\zeta }_1$. See, e.g., Bapat [23] (Lemma 3.13) and Estrada and Knight [24] (p. 68).

Denote $I_{\left(h\right)}$ in (10) by $I\left({\mathit{y}}_{\left(h\right)}\right)$. Then, from Yamada [13] (Proposition 1(b)), it follows that

$$\begin{array}{c}\hfill I\left({\mathit{u}}_1\right)\le \cdots \le I\left({\mathit{u}}_{n-1}\right).\end{array}$$

(16)

In addition, let ${\psi }_{\left(h\right),i}={\displaystyle \frac{a_{\left(h\right),i}^2}{{\sum }_{j=1}^{n-1}{a}_{\left(h\right),j}^2}}$, where $a_{\left(h\right),i}={\mathit{u}}_i^{\top }{\mathit{y}}_{\left(h\right)}$ for $i=1,\dots ,n-1$. Then, ${\psi }_{\left(h\right),i}\ge 0$ for $i=1,\dots ,n-1$ and ${\sum }_{i=1}^{n-1}{\psi }_{\left(h\right),i}=1$.

Proposition 2.

(Proposition 1(a) of Yamada [13]). $I_{\left(h\right)}$ in (9) is a weighted average of $I\left({\mathit{u}}_1\right),\dots ,I\left({\mathit{u}}_{n-1}\right)$ as follows.

$$\begin{array}{c}\hfill I_{\left(h\right)}=\sum _{i=1}^{n-1}{\psi }_{\left(h\right),i}I\left({\mathit{u}}_i\right).\end{array}$$

(17)

Proof. 

Omitted. □

3.3. Local Moran’s I for Univariate Spatial Data

Denote the local Moran’s I of a univariate spatial data ${\mathit{y}}_{\left(h\right)}={[y_{\left(h\right),1},\dots ,y_{\left(h\right),n}]}^{\top }$ by $I_{\left(h\right),i}$:

$$\begin{array}{c}\hfill I_{\left(h\right),i}={\displaystyle \frac{n}{q}}{\displaystyle \frac{(y_{\left(h\right),i}-{\overline{y}}_{\left(h\right)}){\sum }_{j=1}^n{w}_{i,j}(y_{\left(h\right),j}-{\overline{y}}_{\left(h\right)})}{{\sum }_{k=1}^n{(y_{\left(h\right),k}-{\overline{y}}_{\left(h\right)})}^2}},i=1,\dots ,n.\end{array}$$

(18)

Then, $I_{\left(h\right),i}$ in (18) can also be represented using $z_{\left(h\right),1},\dots ,z_{\left(h\right),n}$ as

$$\begin{array}{c}\hfill I_{\left(h\right),i}={\displaystyle \frac{1}{q}}{z}_{\left(h\right),i}\sum _{j=1}^n{w}_{i,j}{z}_{\left(h\right),j},i=1,\dots ,n.\end{array}$$

(19)

Note that $I_{\left(h\right),i}$ is constructed so that

$$\begin{array}{c}\hfill I_{\left(h\right)}=\sum _{i=1}^n{I}_{\left(h\right),i}.\end{array}$$

(20)

We can confirm (20) as follows.

$$\begin{array}{c}\hfill \sum _{i=1}^n{I}_{\left(h\right),i}=\sum _{i=1}^n{\displaystyle \frac{1}{q}}{z}_{\left(h\right),i}\sum _{j=1}^n{w}_{i,j}{z}_{\left(h\right),j}={\displaystyle \frac{1}{q}}\sum _{i=1}^n\sum _{j=1}^n{w}_{i,j}{z}_{\left(h\right),i}{z}_{\left(h\right),j}=I_{\left(h\right)}.\end{array}$$

Given that $z_{\left(h\right),i}={\mathit{z}}_{\left(h\right)}^{\top }{\mathit{e}}_i$ and ${\sum }_{j=1}^n{w}_{i,j}{z}_{\left(h\right),j}=w_{i,1}{z}_{\left(h\right),1}+\cdots +w_{i,n}{z}_{\left(h\right),n}={\mathit{e}}_i^{\top }\mathit{W}{\mathit{z}}_{\left(h\right)}$, $I_{\left(h\right),i}$ in (19) can be represented in matrix notation as

$$\begin{array}{c}\hfill I_{\left(h\right),i}={\displaystyle \frac{1}{q}}{z}_{\left(h\right),i}\sum _{j=1}^n{w}_{i,j}{z}_{\left(h\right),j}={\displaystyle \frac{1}{q}}{\mathit{e}}_i^{\top }\mathit{W}{\mathit{z}}_{\left(h\right)}{\mathit{z}}_{\left(h\right)}^{\top }{\mathit{e}}_i={\mathit{e}}_i^{\top }\left({\displaystyle \frac{1}{q}}\mathit{W}{\mathit{z}}_{\left(h\right)}{\mathit{z}}_{\left(h\right)}^{\top }\right){\mathit{e}}_i,i=1,\dots ,n.\end{array}$$

(21)

Incidentally, we can give another proof of $I_{\left(h\right)}={\sum }_{i=1}^n{I}_{\left(h\right),i}$ based on (21) as follows. From (21), since $I_{\left(h\right),i}$ is the $(i,i)$-entry of ${\displaystyle \frac{1}{q}}\mathit{W}{\mathit{z}}_{\left(h\right)}{\mathit{z}}_{\left(h\right)}^{\top }$, it follows that

$$\begin{array}{c}\hfill \sum _{i=1}^n{I}_{\left(h\right),i}=\mathrm{tr}\left({\displaystyle \frac{1}{q}}\mathit{W}{\mathit{z}}_{\left(h\right)}{\mathit{z}}_{\left(h\right)}^{\top }\right)={\displaystyle \frac{1}{q}}\mathrm{tr}\left({\mathit{z}}_{\left(h\right)}^{\top }\mathit{W}{\mathit{z}}_{\left(h\right)}\right)={\displaystyle \frac{1}{q}}{\mathit{z}}_{\left(h\right)}^{\top }\mathit{W}{\mathit{z}}_{\left(h\right)}=I_{\left(h\right)}.\end{array}$$

(22)

4. Moran’s I’s for Multivariate Spatial Data

In this section, we newly introduce multivariate global and local Moran’s I and establish their properties.

4.1. Global Moran’s I for Multivariate Spatial Data

We define the following measure as the global Moran’s I for multivariate spatial data ${\mathit{y}}_1,\dots ,{\mathit{y}}_n$, which are p-dimensional column vectors:

$$\begin{array}{cc}\hfill I& ={\displaystyle \frac{1}{pq}}\sum _{i=1}^n\sum _{j=1}^n{w}_{i,j}{({\mathit{y}}_i-\overline{\mathit{y}})}^{\top }{\mathit{S}}^{-1}({\mathit{y}}_j-\overline{\mathit{y}})\hfill \\ \hfill & ={\displaystyle \frac{1}{pq}}\sum _{i=1}^n\sum _{j=1}^n{w}_{i,j}{\mathit{z}}_i^{\top }{\mathit{z}}_j,\hfill \end{array}$$

(23)

which we refer to as “multivariate global Moran’s I” or simply “multivariate Moran’s I”. Note that the second equality in (23) follows from (7). When $p=1$, given that ${\mathit{z}}_i^{\top }$ reduces to $z_{\left(1\right),i}$ for $i=1,\dots ,n$, it follows that $I={\displaystyle \frac{1}{q}}{\sum }_{i=1}^n{\sum }_{j=1}^n{w}_{i,j}{z}_{\left(1\right),i}{z}_{\left(1\right),j}=I_{\left(1\right)}$. See (11). Thus, the multivariate Moran’s I given by (23) is a generalization of the conventional Moran’s I for univariate spatial data.

Let $\overline{I}={\displaystyle \frac{1}{p}}{\sum }_{h=1}^p{I}_{\left(h\right)}$, which is the simple average of the univariate global Moran’s I’s, $I_{\left(1\right)},\dots ,I_{\left(p\right)}$. Then, I has the following property:

Proposition 3.

I in (23) is equal to $\overline{I}$.

Proof. 

Given that ${\mathit{z}}_i^{\top }=[z_{\left(1\right),i},\dots ,z_{\left(p\right),i}]$ for $i=1,\dots ,n$, ${\mathit{z}}_i^{\top }{\mathit{z}}_j={\sum }_{h=1}^p{z}_{\left(h\right),i}{z}_{\left(h\right),j}$. Accordingly, it follows that

$$\begin{array}{cc}\hfill I& ={\displaystyle \frac{1}{pq}}\sum _{i=1}^n\sum _{j=1}^n{w}_{i,j}{\mathit{z}}_i^{\top }{\mathit{z}}_j={\displaystyle \frac{1}{pq}}\sum _{i=1}^n\sum _{j=1}^n{w}_{i,j}\sum _{h=1}^p{z}_{\left(h\right),i}{z}_{\left(h\right),j}\hfill \\ \hfill & ={\displaystyle \frac{1}{p}}\sum _{h=1}^p\left({\displaystyle \frac{1}{q}}\sum _{i=1}^n\sum _{j=1}^n{w}_{i,j}{z}_{\left(h\right),i}{z}_{\left(h\right),j}\right)={\displaystyle \frac{1}{p}}\sum _{h=1}^p{I}_{\left(h\right)}=\overline{I}.\hfill \end{array}$$

□

For any $\mathit{A}=[{\mathit{a}}_1,\dots ,{\mathit{a}}_p]\in {\mathbb{R}}^{n\times p}$, given that ${\mathit{a}}_k^{\top }\mathit{W}{\mathit{a}}_k={\mathit{a}}_k^{\top }\mathcal{W}{\mathit{a}}_k$, it follows that

$$\begin{array}{cc}\hfill \mathrm{tr}\left({\mathit{A}}^{\top }\mathit{W}\mathit{A}\right)& =\mathrm{vec}{\left(\mathit{A}\right)}^{\top }({\mathit{I}}_p\otimes \mathit{W})\mathrm{vec}\left(\mathit{A}\right)=\sum _{k=1}^p{\mathit{a}}_k^{\top }\mathit{W}{\mathit{a}}_k=\sum _{k=1}^p{\mathit{a}}_k^{\top }\mathcal{W}{\mathit{a}}_k\hfill \\ =\mathrm{vec}{\left(\mathit{A}\right)}^{\top }({\mathit{I}}_p\otimes \mathcal{W})\mathrm{vec}\left(\mathit{A}\right)=\mathrm{tr}\left({\mathit{A}}^{\top }\mathcal{W}\mathit{A}\right).\hfill \end{array}$$

(24)

We use (24) to derive the following results.

Proposition 4.

I in (23) can be represented compactly in matrix form as

$$\begin{array}{c}\hfill I={\displaystyle \frac{1}{pq}}\mathrm{tr}\left({\mathit{Z}}^{\top }\mathit{W}\mathit{Z}\right)={\displaystyle \frac{1}{pq}}\mathrm{tr}\left({\mathit{Z}}^{\top }\mathcal{W}\mathit{Z}\right).\end{array}$$

(25)

Proof. 

Given that ${\mathit{z}}_j^{\top }$ is the j-th row of $\mathit{Z}$, ${\mathit{z}}_j^{\top }$ can be represented as ${\mathit{e}}_j^{\top }\mathit{Z}$. Accordingly, it follows that ${\mathit{z}}_i^{\top }{\mathit{z}}_j={\mathit{z}}_j^{\top }{\mathit{z}}_i=\mathrm{tr}\left({\mathit{z}}_j^{\top }{\mathit{z}}_i\right)=\mathrm{tr}\left({\mathit{z}}_i{\mathit{z}}_j^{\top }\right)=\mathrm{tr}\left({\mathit{Z}}^{\top }{\mathit{e}}_i{\mathit{e}}_j^{\top }\mathit{Z}\right)$, from which we have

$$\begin{array}{cc}\hfill \sum _{i=1}^n\sum _{j=1}^n{w}_{i,j}{\mathit{z}}_i^{\top }{\mathit{z}}_j& =\sum _{i=1}^n\sum _{j=1}^n{w}_{i,j}\mathrm{tr}\left({\mathit{Z}}^{\top }{\mathit{e}}_i{\mathit{e}}_j^{\top }\mathit{Z}\right)=\mathrm{tr}\left\{{\mathit{Z}}^{\top }\left(\sum _{i=1}^n\sum _{j=1}^n{w}_{i,j}{\mathit{e}}_i{\mathit{e}}_j^{\top }\right)\mathit{Z}\right\}\hfill \\ & =\mathrm{tr}\left({\mathit{Z}}^{\top }\mathit{W}\mathit{Z}\right).\hfill \end{array}$$

Thus, substituting this result into (23), we have $I={\displaystyle \frac{1}{pq}}\mathrm{tr}\left({\mathit{Z}}^{\top }\mathit{W}\mathit{Z}\right)$. Finally, the second equality in (25) follows from (24). □

Remark 2.

Regarding Proposition 4, we make three remarks: (i) (25) is useful to calculate I. (ii) Given (24), it immediately follows that

$$\begin{array}{c}\hfill I={\displaystyle \frac{1}{pq}}\mathrm{vec}{\left(\mathit{Z}\right)}^{\top }({\mathit{I}}_p\otimes \mathit{W})\mathrm{vec}\left(\mathit{Z}\right)={\displaystyle \frac{1}{pq}}\mathrm{vec}{\left(\mathit{Z}\right)}^{\top }({\mathit{I}}_p\otimes \mathcal{W})\mathrm{vec}\left(\mathit{Z}\right),\end{array}$$

(26)

which are representations corresponding to those in (12). Using (26), we can give another proof of Proposition 3 as follows.

$$\begin{array}{c}\hfill I={\displaystyle \frac{1}{pq}}\mathrm{vec}{\left(\mathit{Z}\right)}^{\top }({\mathit{I}}_p\otimes \mathcal{W})\mathrm{vec}\left(\mathit{Z}\right)={\displaystyle \frac{1}{p}}\sum _{h=1}^p\left({\displaystyle \frac{1}{q}}{\mathit{z}}_{\left(h\right)}^{\top }\mathcal{W}{\mathit{z}}_{\left(h\right)}\right)={\displaystyle \frac{1}{p}}\sum _{h=1}^p{I}_{\left(h\right)}=\overline{I}.\end{array}$$

(27)

(iii) A MATLAB/GNU Octave user-defined function for calculating I in (25) is as follows:

• function I = calc_I(Y,W)
•      p = size(Y,2); Z = zscore(Y,1); q = sum(sum(W));
•      I = trace(Z′ ∗ W ∗ Z)/(p ∗ q);
• end

Note that as $I_{\left(1\right)}$ is a special case of I, the function can also be used for obtaining $I_{\left(1\right)}$.

The following result shows the bounds of I.

Proposition 5.

It follows that $I\in \left[{\displaystyle \frac{n}{q}}{\lambda }_1,{\displaystyle \frac{n}{q}}{\lambda }_{n-1}\right]$. $I={\displaystyle \frac{n}{q}}{\lambda }_1$ when ${\mathit{y}}_{\left(h\right)}=\mu \mathit{\iota }+{\gamma }_{\left(h\right)}{\mathit{u}}_1$ such that ${\gamma }_{\left(h\right)}\ne 0$. Likewise, $I={\displaystyle \frac{n}{q}}{\lambda }_{n-1}$ when ${\mathit{y}}_{\left(h\right)}=\mu \mathit{\iota }+{\gamma }_{\left(h\right)}{\mathit{u}}_{n-1}$ such that ${\gamma }_{\left(h\right)}\ne 0$.

Proof. 

The proposition immediately follows from Propositions 1 and 3. □

Remark 3.

Regarding Proposition 5, we make two remarks: (i) As in the case of global Moran’s I for univariate spatial data, the bounds of global Moran’s I for multivariate spatial data also depend only on the structure of the graph represented by $\mathit{W}$. (ii) From Proposition 5 and Equation (15), it follows that

$$\begin{array}{c}\hfill I\in \left[{\displaystyle \frac{n}{q}}{\lambda }_1,{\displaystyle \frac{n}{q}}{\lambda }_{n-1}\right]\subseteq \left[{\displaystyle \frac{n}{q}}{\zeta }_1,{\displaystyle \frac{n}{q}}{\zeta }_n\right].\end{array}$$

(28)

Proposition 6.

I in (23) is a weighted average of $I\left({\mathit{u}}_1\right),\dots ,I\left({\mathit{u}}_{n-1}\right)$ as follows.

$$\begin{array}{c}\hfill I=\sum _{i=1}^{n-1}{\overline{\psi }}_{i}I\left({\mathit{u}}_i\right),\end{array}$$

(29)

where ${\overline{\psi }}_i={\displaystyle \frac{1}{p}}{\sum }_{h=1}^p{\psi }_{\left(h\right),i}$ for $i=1,\dots ,n-1$.

Proof. 

From Propositions 2 and 3, it follows that

$$\begin{array}{c}\hfill I={\displaystyle \frac{1}{p}}\sum _{h=1}^p{I}_{\left(h\right)}={\displaystyle \frac{1}{p}}\sum _{h=1}^p\sum _{i=1}^{n-1}{\psi }_{\left(h\right),i}I\left({\mathit{u}}_i\right)=\sum _{i=1}^{n-1}\left({\displaystyle \frac{1}{p}}\sum _{h=1}^p{\psi }_{\left(h\right),i}\right)I\left({\mathit{u}}_i\right),=\sum _{i=1}^{n-1}{\overline{\psi }}_{i}I\left({\mathit{u}}_i\right).\end{array}$$

Here, ${\overline{\psi }}_i\ge 0$ because ${\psi }_{\left(h\right),i}\ge 0$ for $h=1,\dots ,p$. In addition, since ${\sum }_{i=1}^{n-1}{\psi }_{\left(h\right),i}=1$, it follows that

$$\begin{array}{c}\hfill \sum _{i=1}^{n-1}{\overline{\psi }}_i=\sum _{i=1}^{n-1}{\displaystyle \frac{1}{p}}\sum _{h=1}^p{\psi }_{\left(h\right),i}={\displaystyle \frac{1}{p}}\sum _{h=1}^p\sum _{i=1}^{n-1}{\psi }_{\left(h\right),i}=1.\end{array}$$

□

Remark 4.

Regarding Proposition 6, we make two remarks. (i) Proposition 6 is a generalization of Yamada [13] (Proposition 1(a)). (ii) Given (16), the distribution of ${\overline{\psi }}_1,\dots ,{\overline{\psi }}_{n-1}$ represents the spatial autocorrelation structure of the multivariate spatial data ${\mathit{y}}_1,\dots ,{\mathit{y}}_n$.

4.2. Local Moran’s I for Multivariate Spatial Data

Then, as we defined I from $I_{\left(h\right)}$, we define the multivariate local Moran’s I from $I_{\left(h\right),i}$ as follows.

$$\begin{array}{c}\hfill I_i={\displaystyle \frac{1}{pq}}{\mathit{z}}_i^{\top }\sum _{j=1}^n{w}_{i,j}{\mathit{z}}_j,i=1,\dots ,n,\end{array}$$

(30)

which we refer to as the “multivariate local Moran’s I”. When $p=1$, given that ${\mathit{z}}_i=z_{\left(1\right),i}$ for $i=1,\dots ,n$, it follows that

$$\begin{array}{c}\hfill I_i={\displaystyle \frac{1}{pq}}{\mathit{z}}_i^{\top }\sum _{j=1}^n{w}_{i,j}{\mathit{z}}_j={\displaystyle \frac{1}{q}}{z}_{\left(1\right),i}\sum _{j=1}^n{w}_{i,j}{z}_{\left(1\right),j}=I_{\left(1\right),i},i=1,\dots ,n.\end{array}$$

(31)

Thus, the multivariate local Moran’s I given by (30) is a generalization of the local Moran’s I for univariate spatial data. In addition, it follows that

$$\begin{array}{c}\hfill \sum _{i=1}^n{I}_i=\sum _{i=1}^n\left({\displaystyle \frac{1}{pq}}{\mathit{z}}_i^{\top }\sum _{j=1}^n{w}_{i,j}{\mathit{z}}_j\right)={\displaystyle \frac{1}{pq}}\sum _{i=1}^n\sum _{j=1}^n{w}_{i,j}{\mathit{z}}_i^{\top }{\mathit{z}}_j=I.\end{array}$$

(32)

Let ${\overline{I}}_i={\displaystyle \frac{1}{p}}{\sum }_{h=1}^p{I}_{\left(h\right),i}$, which is the average of the univariate local Moran’s I’s, $I_{\left(1\right),i},\dots ,I_{\left(p\right),i}$. Then, we have the following results.

Proposition 7.

$I_i$ in (31) is equal to ${\overline{I}}_i$ for $i=1,\dots ,n$.

Proof. 

Given ${\mathit{z}}_i^{\top }=[z_{\left(1\right),i},\dots ,z_{\left(p\right),i}]$, it follows that

$$\begin{array}{cc}\hfill I_i& ={\displaystyle \frac{1}{pq}}{\mathit{z}}_i^{\top }\sum _{j=1}^n{w}_{i,j}{\mathit{z}}_j={\displaystyle \frac{1}{pq}}\sum _{j=1}^n{w}_{i,j}{\mathit{z}}_i^{\top }{\mathit{z}}_j={\displaystyle \frac{1}{pq}}\sum _{j=1}^n{w}_{i,j}\sum _{h=1}^p{z}_{\left(h\right),i}{z}_{\left(h\right),j}\hfill \\ \hfill & ={\displaystyle \frac{1}{p}}\sum _{h=1}^p\left({\displaystyle \frac{1}{q}}{z}_{\left(h\right),i}\sum _{j=1}^n{w}_{i,j}{z}_{\left(h\right),j}\right)={\displaystyle \frac{1}{p}}\sum _{h=1}^p{I}_{\left(h\right),i}={\overline{I}}_i,i=1,\dots ,n.\hfill \end{array}$$

□

The following result is useful to calculate $I_i$.

Proposition 8.

$I_i$ in (31) can be represented compactly in matrix form as

$$\begin{array}{c}\hfill I_i={\mathit{e}}_i^{\top }\left({\displaystyle \frac{1}{pq}}\mathit{W}\mathit{Z}{\mathit{Z}}^{\top }\right){\mathit{e}}_i,i=1,\dots ,n.\end{array}$$

(33)

Proof. 

From Proposition 7, Equation (21), and ${\sum }_{h=1}^p{\mathit{z}}_{\left(h\right)}{\mathit{z}}_{\left(h\right)}^{\top }=\mathit{Z}{\mathit{Z}}^{\top }$, it follows that

$$\begin{array}{cc}\hfill I_i& ={\displaystyle \frac{1}{p}}\sum _{h=1}^p{I}_{\left(h\right),i}={\displaystyle \frac{1}{p}}\sum _{h=1}^p{\displaystyle \frac{1}{q}}{\mathit{e}}_i^{\top }\mathit{W}{\mathit{z}}_{\left(h\right)}{\mathit{z}}_{\left(h\right)}^{\top }{\mathit{e}}_i={\displaystyle \frac{1}{pq}}{\mathit{e}}_i^{\top }\mathit{W}\left(\sum _{h=1}^p{\mathit{z}}_{\left(h\right)}{\mathit{z}}_{\left(h\right)}^{\top }\right){\mathit{e}}_i\hfill \\ & ={\displaystyle \frac{1}{pq}}{\mathit{e}}_i^{\top }\mathit{W}\mathit{Z}{\mathit{Z}}^{\top }{\mathit{e}}_i={\mathit{e}}_i^{\top }\left({\displaystyle \frac{1}{pq}}\mathit{W}\mathit{Z}{\mathit{Z}}^{\top }\right){\mathit{e}}_i,i=1,\dots ,n.\hfill \end{array}$$

□

Remark 5.

Regarding Proposition 8, we make two remarks: (i) We can give another proof of ${\sum }_{i=1}^n{I}_i=I$ based on (33) as follows. From (33), since $I_i$ is the $(i,i)$-entry of ${\displaystyle \frac{1}{pq}}\mathit{W}\mathit{Z}{\mathit{Z}}^{\top }$, it follows that

$$\begin{array}{c}\hfill \sum _{i=1}^n{I}_i=\mathrm{tr}\left({\displaystyle \frac{1}{pq}}\mathit{W}\mathit{Z}{\mathit{Z}}^{\top }\right)={\displaystyle \frac{1}{pq}}\mathrm{tr}\left({\mathit{Z}}^{\top }\mathit{W}\mathit{Z}\right)=I.\end{array}$$

(34)

(ii) A MATLAB/GNU Octave user-defined function for calculating $I_i$ in (33) is as follows:

• function Ii = calc_Ii(Y,W,i)
•      p = size(Y,2); Z = zscore(Y,1); q = sum(sum(W));
•      Ii = (W(i,:) * Z * Z(i,:)’)/(p * q);
• end

Note that as $I_{\left(1\right),i}$ is a special case of $I_i$, the function can also be used for obtaining $I_{\left(1\right),i}$.

5. Numerical Illustrations

In this section, we provide numerical illustrations of the theoretical results obtained in the previous section. Before showing these, we introduce a table of Moran’s I’s.

5.1. Table of Moran’s I’s

Table 1 tabulates Moran’s I’s. In the next subsection, we make a table from two sets of generated multivariate spatial data. $I_1,\dots ,I_n$ and I in the table are the measures that are newly defined in the paper. Recall that $I_i$ is the multivariate local Moran’s I at vertex $v_i$ and I is the multivariate global Moran’s I. They are located in the last column of the table. In this sense, the contribution of this paper can be expressed as the addition of a final column to this table. Again, recall that $I_{\left(h\right),i}$ denotes the local Moran’s I for variable h at vertex $v_i$ and $I_{\left(h\right)}$ denotes the Moran’s I for variable h for $h=1,\dots ,p$ and $i=1,\dots ,n$. As shown, among the measures, there are the following relations:

$$\begin{array}{cc}\hfill \mathrm{Proposition} 7:& I_i={\displaystyle \frac{1}{p}}(I_{\left(1\right),i}+\cdots +I_{\left(p\right),i}),i=1,\dots ,n,\hfill \end{array}$$

(35)

$$\begin{array}{cc}\hfill \mathrm{Proposition} 3:& I={\displaystyle \frac{1}{p}}(I_{\left(1\right)}+\cdots +I_{\left(p\right)}),\hfill \end{array}$$

(36)

$$\begin{array}{cc}\hfill \mathrm{Equation} \left(20\right):& I_{\left(h\right)}=I_{\left(h\right),1}+\cdots +I_{\left(h\right),n},h=1,\dots ,p,\hfill \end{array}$$

(37)

$$\begin{array}{cc}\hfill \mathrm{Equation} \left(32\right):& I=I_1+\cdots +I_n.\hfill \end{array}$$

(38)

Table 1. Table of Moran’s I’s.

	$h=1$	$h=2$	⋯	$h=p$
$v_1$	$I_{\left(1\right),1}$	$I_{\left(2\right),1}$	⋯	$I_{\left(p\right),1}$	$I_1$
$v_2$	$I_{\left(1\right),2}$	$I_{\left(2\right),2}$	⋯	$I_{\left(p\right),2}$	$I_2$
⋮	⋮	⋮		⋮	⋮
$v_n$	$I_{\left(1\right),n}$	$I_{\left(2\right),n}$	⋯	$I_{\left(p\right),n}$	$I_n$
	$I_{\left(1\right)}$	$I_{\left(2\right)}$	⋯	$I_{\left(p\right)}$	I

Note: Among the values in this table, the relations in (35)–(38) hold.

5.2. Numerical Illustrations

For numerical illustrations of the theoretical results obtained in Section 4, consider the undirected graph shown in Figure 2. It is a two-dimensional square lattice graph, which is a Cartesian product of two path graphs. We suppose that it has a binary weight matrix, and accordingly, its $\mathit{W}$ is given by

$$\begin{array}{c}\hfill \mathit{W}=\left[\begin{array}{ccccccccc}0& 1& 0& 1& 0& 0& 0& 0& 0\\ 1& 0& 1& 0& 1& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 1& 0& 0& 0\\ 1& 0& 0& 0& 1& 0& 1& 0& 0\\ 0& 1& 0& 1& 0& 1& 0& 1& 0\\ 0& 0& 1& 0& 1& 0& 0& 0& 1\\ 0& 0& 0& 1& 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 1& 0& 1& 0& 1\\ 0& 0& 0& 0& 0& 1& 0& 1& 0\end{array}\right]\in {\mathbb{R}}^{9\times 9}.\end{array}$$

(39)

In this case, $q={\sum }_{i=1}^n{\sum }_{j=1}^n{w}_{i,j}$ is equal to 24. Note that since $\mathit{W}$ in (39) is symmetric, it is identical to $\mathcal{W}={\displaystyle \frac{\mathit{W}+{\mathit{W}}^{\top }}{2}}$. Incidentally, Moran’s [2] $r_{11}$ is a univariate global Moran’s I for a two-dimensional square lattice graph. For details, see Yamada [25].

Figure 2. A two-dimensional square lattice graph.

We generate $\mathit{Y}=[{\mathit{y}}_{\left(1\right)},\dots ,{\mathit{y}}_{\left(p\right)}]\in {\mathbb{R}}^{n\times p}$ by

$$\begin{array}{c}{\mathit{y}}_{\left(h\right)}=\mu \mathit{\iota }+{\gamma }_{\left(h\right)}\mathit{x}+\mathit{\epsilon },h=1,\dots ,p,\end{array}$$

(40)

$$\begin{array}{c}\mathit{x}={\mathit{u}}_{n-1},{\mathit{u}}_1,\mathit{\epsilon }\sim \mathrm{i}.\mathrm{i}.\mathrm{d}.\mathrm{N}(\mathbf{0},{\sigma }^2{\mathit{I}}_n),\end{array}$$

(41)

where $n=9$, $p=4$, $\mu =0$, $\sigma =0.1$, and $[{\gamma }_{\left(1\right)},{\gamma }_{\left(2\right)},{\gamma }_{\left(3\right)},{\gamma }_{\left(4\right)}]=[0.5,1,2,4]$. Recall that ${\mathit{u}}_{n-1}$ and ${\mathit{u}}_1$ are eigenvectors of ${\mathit{Q}}_{\iota }^{\top }\mathcal{W}{\mathit{Q}}_{\iota }$. Note that when $\mathcal{W}$ is given by (39), both $I_{\left(h\right)}$ for $h=1,\dots ,p$ and I belong to $[-1.0590,0.5303]$. In addition, given that ${\mathit{Q}}_{\iota }\mathit{\iota }=\mathbf{0}$, $\mu$ in (40) does not affect Moran’s I’s even though it does affect ${\mathit{y}}_{\left(h\right)}$.

Figure 3 (respectively, Figure 4) depicts the heatmaps of ${\mathit{y}}_{\left(h\right)}$ for $h=1,\dots ,4$, which are generated by (40) and (41) when $\mathit{x}={\mathit{u}}_{n-1}$ (respectively, $\mathit{x}={\mathit{u}}_1$). In both figures, Panel A plots ${\mathit{y}}_{\left(1\right)}$. Likewise, Panels B, C, and D respectively plot ${\mathit{y}}_{\left(2\right)}$, ${\mathit{y}}_{\left(3\right)}$, and ${\mathit{y}}_{\left(4\right)}$. As expected, in both cases, the spatial autocorrelation structure of ${\mathit{y}}_{\left(4\right)}$ (respectively, ${\mathit{y}}_{\left(1\right)}$) is (respectively, not) the clearest.

Figure 3. Heatmaps of ${\mathit{y}}_{\left(h\right)}$ generated by (40) and (41) for $h=1,\dots ,4$ when $\mathit{x}={\mathit{u}}_{n-1}$. Panel A plots ${\mathit{y}}_{\left(1\right)}$. Likewise, Panels B, C, and D respectively plot ${\mathit{y}}_{\left(2\right)}$, ${\mathit{y}}_{\left(3\right)}$, and ${\mathit{y}}_{\left(4\right)}$.

Figure 4. Heatmaps of ${\mathit{y}}_{\left(h\right)}$ generated by (40)–(41) for $h=1,\dots ,4$ when $\mathit{x}={\mathit{u}}_1$. Panel A plots ${\mathit{y}}_{\left(1\right)}$. Likewise, Panels B, C, and D respectively plot ${\mathit{y}}_{\left(2\right)}$, ${\mathit{y}}_{\left(3\right)}$, and ${\mathit{y}}_{\left(4\right)}$.

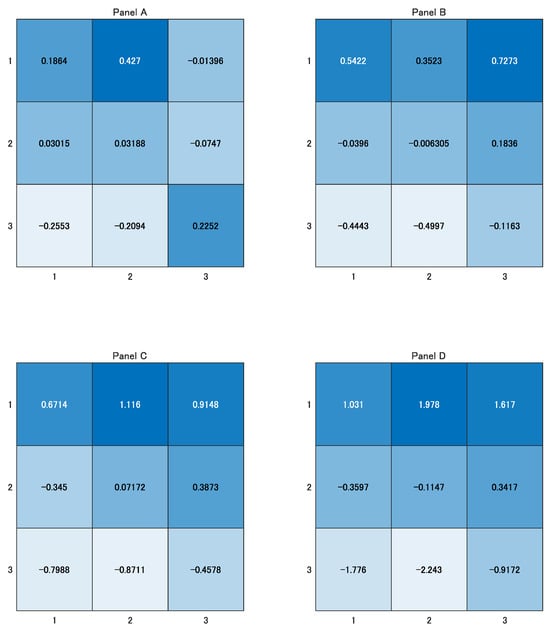
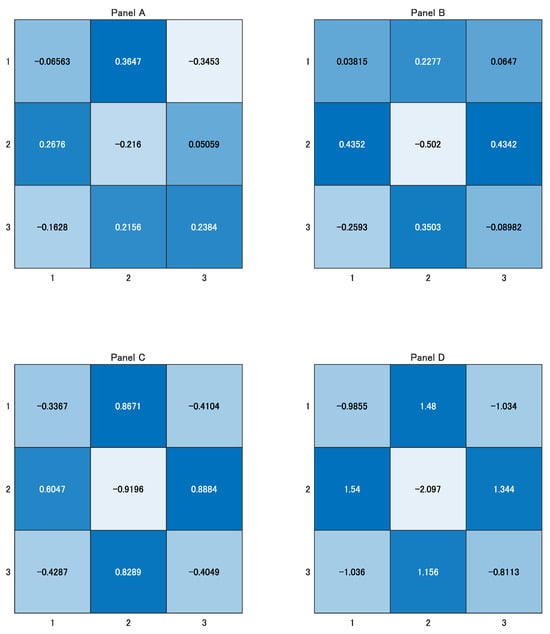
Table 2 (respectively, Table 3) is the table of Moran’s I’s corresponding to the data depicted in Figure 3 (respectively, Figure 4). From these tables, we can confirm that the relations in (35)–(38) hold. For example, in Table 2, $I_1=0.0373$ is the average of $I_{\left(1\right),1}=0.0568$, $I_{\left(2\right),1}=0.0197$, $I_{\left(3\right),1}=0.0316$, and $I_{\left(4\right),1}=0.0413$, and $I=0.3948$ is the average of $I_{\left(1\right)}=0.1001$, $I_{\left(2\right)}=0.4324$, $I_{\left(3\right)}=0.5225$, and $I_{\left(4\right)}=0.5241$. In addition, from the tables, it is observable that $I_{\left(h\right)}$ for $h=1,\dots ,4$ and I certainly belong to $[-1.0590,0.5303]$.

Table 2. Table of Moran’s I’s: $\mathit{x}={\mathit{u}}_{n-1}$ in (40) and (41).

	$h=1$	$h=2$	$h=3$	$h=4$
$v_1$	$0.0568$	$0.0197$	$0.0316$	$0.0413$	$0.0373$
$v_2$	$0.0347$	$0.0764$	$0.1277$	$0.1209$	$0.0899$
$v_3$	$-0.0146$	$0.0668$	$0.0973$	$0.0896$	$0.0598$
$v_4$	$0.0013$	$0.0045$	$0.0103$	$0.0049$	$0.0053$
$v_5$	$-0.0001$	$0.0071$	$0.0000$	$0.0001$	$0.0018$
$v_6$	$-0.0146$	$0.0106$	$0.0080$	$0.0064$	$0.0026$
$v_7$	$0.0761$	$0.0979$	$0.1030$	$0.0962$	$0.0933$
$v_8$	$0.0286$	$0.1247$	$0.1152$	$0.1298$	$0.0996$
$v_9$	$-0.0681$	$0.0247$	$0.0293$	$0.0348$	$0.0052$
	$0.1001$	$0.4324$	$0.5225$	$0.5241$	$0.3948$

Note: See Table 1 for what is tabulated in this table.

Table 3. Table of Moran’s I’s: $\mathit{x}={\mathit{u}}_1$ in (40) and (41).

	$h=1$	$h=2$	$h=3$	$h=4$
$v_1$	$-0.0439$	$-0.0091$	$-0.0509$	$-0.0691$	$-0.0432$
$v_2$	$-0.1839$	$-0.0428$	$-0.1400$	$-0.1436$	$-0.1276$
$v_3$	$-0.0986$	$-0.0030$	$-0.0729$	$-0.0681$	$-0.0606$
$v_4$	$-0.0974$	$-0.1543$	$-0.0944$	$-0.1492$	$-0.1238$
$v_5$	$-0.1439$	$-0.2973$	$-0.2681$	$-0.2770$	$-0.2466$
$v_6$	$-0.0040$	$-0.1223$	$-0.1489$	$-0.1251$	$-0.1001$
$v_7$	$-0.0621$	$-0.0958$	$-0.0604$	$-0.0652$	$-0.0709$
$v_8$	$-0.0344$	$-0.1334$	$-0.1393$	$-0.1083$	$-0.1038$
$v_9$	$0.0287$	$-0.0475$	$-0.0703$	$-0.0468$	$-0.0340$
	$-0.6395$	$-0.9054$	$-1.0452$	$-1.0523$	$-0.9106$

Note: See Table 1 for what is tabulated in this table.

Finally, we make a remark. From Propositions 1 and 5, $I_{\left(h\right)}$ for $h=1,\dots ,4$ and I of ${\gamma }_{\left(h\right)}{\mathit{u}}_{n-1}$ (respectively, ${\gamma }_{\left(h\right)}{\mathit{u}}_1$) equal $0.5303$ (respectively, $-1.0590$), which is the upper (respectively, lower) bound, regardless of ${\gamma }_{\left(h\right)}$ if ${\gamma }_{\left(h\right)}\ne 0$. Nevertheless, the values corresponding to ${\mathit{y}}_{\left(1\right)}$ are far from these values, whereas those of ${\mathit{y}}_{\left(4\right)}$ are close to these values. This is due to the fact that ${\mathit{y}}_{\left(1\right)}$ is more highly contaminated by noise than ${\mathit{y}}_{\left(4\right)}$ is.

6. Discussion

In this section, we clarify the relationship between our multivariate global Moran’s I in (23) and Wartenberg’s [10] spatial correlation matrix $\mathit{M}$. Wartenberg [10] defined the following $p\times p$ matrix in our notation:

$$\begin{array}{c}\hfill \mathit{M}={\displaystyle \frac{1}{q}}{\mathit{Z}}^{\top }\mathit{W}\mathit{Z}\end{array}$$

(42)

and the analysis based on its spectral decomposition is called Moran component analysis (MCA) (Lin [12]). When $p=1$, given that $\mathit{Z}={\mathit{z}}_{\left(1\right)}$, $\mathit{M}$ reduces to $I_{\left(1\right)}$ in (12) as

$$\begin{array}{c}\hfill \mathit{M}={\displaystyle \frac{1}{q}}{\mathit{Z}}^{\top }\mathit{W}\mathit{Z}={\displaystyle \frac{1}{q}}{\mathit{z}}_{\left(1\right)}^{\top }\mathit{W}{\mathit{z}}_{\left(1\right)}=I_{\left(1\right)}.\end{array}$$

From Proposition 4, our multivariate global Moran’s I in (23) is related to the eigenvalues of $\mathit{M}$ as follows:

$$\begin{array}{c}\hfill I={\displaystyle \frac{1}{pq}}\mathrm{tr}\left({\mathit{Z}}^{\top }\mathit{W}\mathit{Z}\right)={\displaystyle \frac{1}{p}}\mathrm{tr}\left(\mathit{M}\right)={\displaystyle \frac{1}{p}}\sum _{k=1}^p{\theta }_k,\end{array}$$

(43)

where ${\theta }_k$ for $k=1,\dots ,p$ are the eigenvalues of $\mathit{M}$. Hence, I is identical to the average of the eigenvalues of $\mathit{M}$. In this sense, our multivariate global Moran’s I can be regarded as a value obtained from the spatial correlation matrix, $\mathit{M}$. Nevertheless, it should be emphasized that $\mathit{M}$ is a matrix and not a single measure of spatial autocorrelation of multivariate spatial data.

7. Concluding Remarks

Conventional Moran’s I cannot measure the degree of spatial autocorrelation of multivariate spatial data as a single value. To address this issue, we developed Moran’s I for multivariate spatial data. It can describe the similarity/discrepancy between vectors of data at different vertices/spatial units. In addition, since the local version of Moran’s I has the same problem, we extended it as well. Subsequently, we established their properties, which are fundamental for applied work. They are summarized in Propositions 3–8. We have also illustrated them numerically.

Finally, we make a remark. In this paper, we developed Moran’s I’s for multivariate spatial data ${\mathit{y}}_1,\dots ,{\mathit{y}}_n$. Although we did not impose a stochastic model on ${\mathit{y}}_1,\dots ,{\mathit{y}}_n$, it is of course an interesting research topic to investigate the distribution of multivariate Moran’s I’s when such an assumption is made. Such investigations could be done using Imhof’s [26] method. However, this is beyond the scope of this paper.