Robust and Adaptive Stabilization Controllers of State-Constrained Nonholonomic Chained Systems: A Discontinuous Approach

Abstract

In this paper, two systematic control design strategies are proposed for strict-feedback nonholonomic systems with full-state constraints to solve stabilization and adaptive stabilization problems. The stabilization schemes involve the introduction of state scaling, the barrier Lyapunov function (BLF), the integrator backstepping method, and the tuning function approach. In addition, a discontinuous switching control strategy is proposed to achieve the control goal if the first system state’s initial state is confined to zero. In both stabilization and adaptive stabilization control, the system states can be regulated at the origin, and meanwhile, the full-state constraints are realized. Finally, it is shown that the simulation results are consistent with the theory analysis results, which further demonstrates the effectiveness of the proposed control schemes.

1. Introduction

Generally, a nonintegrable speed constraint can be formulated for a motion system running on a smooth horizontal plane since there is no sideslip. Nonholonomic systems refer to these motion systems which suffer from nonintegrable speed or acceleration constraints [1], such as rear-driven mobile robots and knife edge motion [2]. Various nonholonomic systems arise from practical engineering applications, especially with the high complexity of robot systems, the large number of applications of unmanned aerial vehicles, unmanned vehicles, and the wide adoption of large, flexible intelligent manufacturing systems.

In the literature, Brockett’s second example is described as

$$\left\{\begin{array}{c}\dot{x}=u_1,\hfill \\ \dot{y}=u_2,\hfill \\ \dot{z}=y{u}_1.\hfill \end{array}\right.$$

Although the originally proposed nonholonomic systems are seemingly driftless nonlinear systems, both their stabilization and tracking control problems have brought about many tough and thorny issues that cannot be directly solved by the traditional nonlinear control approaches. Brockett pointed out in [3] that there were no smooth, even continuous time-invariant stabilizing controllers for nonholonomic systems, although these systems could be formed into chained forms [1]. Therefore, discontinuous time-invariant, smooth time-varying, and hybrid control methods have become the most effective weapons to address the related stabilization control designs [4,5,6] even for stochastic nonholonomic systems [7,8].

Tracking control is mainly investigated for driftless nonholonomic systems including multiple-system cases, while stabilization is commonly addressed for uncertain nonholonomic systems. The control problems associated with stabilization further involve fast control containing finite-time or fixed-time control [9,10], input-saturated control [11], anti-disturbance control [12], and model predictive control [13]. In recent years, safe control, which can be classified into information security and physical security, has grasped extensive attention in control community. State-constrained control belongs to physical security and has been widely studied for nonlinear systems. When reviewing the existing results, it can be claimed that the BLF-based methods are the most commonly utilized tools to address state-constrained problems of nonlinear systems, such as those in [14,15,16,17,18]. The rapid development of control technologies facilitates the combination of state-constrained control and other control problems, such as neural network control [19], fuzzy control [20], finite-time control [21], and anti-disturbance control [22]. It should be mentioned that the fully actuated system approach has also been applied to solve the stabilization issues associated with nonholonomic systems in recent years, such as in [23,24,25,26].

In the literature, some works have been reported on nonholonomic systems with full-state or output-state constraints. The authors of [27] studied the tracking controller design for an uncertain nonholonomic system under time-varying disturbances and full-state constraints. The authors of [28] proposed the the fixed-time trajectory-tracking switching control for a full-state constrained nonholonomic system. The authors of [29,30] focused on the tracking controllers for two classes of state-constrained nonholonomic systems. The authors of [31] investigated the adaptive neural control for stochastic nonholonomic systems suffered from unknown covariance noise and full-state constraints. The authors of [32] elaborated upon the MPC-based cooperative controller design for nonholonomic system mobile agents with constraints and disturbances. The authors of [33] provided an anti-disturbance stabilization controller for a class of full-state constrained nonholonomic systems. The authors of [34] studied the fixed-time stabilization issue for uncertain nonholonomic systems under time-varying state constraints. The authors of [35] considered the cooperative tracking controller of multiple state-constrained nonholonomic wheeled mobile robots. The existing works studied either the output-state constrained problem or full-state constrained problem with bounded stability. This in turn implies that it is meaningful to address a full-state constrained controller with asymptotical convergence for nonholonomic systems. However, to achieve this control intention, the encountered difficulty focuses on how to construct a new non-constant input to drive the system state and maintain the desired state constraint in the second control stage.

This work studies both the stabilization and adaptive stabilization control problems of nonholonomic systems in strict feedback form subjected to full-state constraints. The summarized main contributions of this submitted work are as follows:

(1)

The state-constrained stabilization control issue is addressed roundly for a strict feedback nonholonomic system with drift nonlinearities and parameter uncertainties by imposing the linear growth restriction on the drift nonlinearities.

(2)

The constraint adaptive stabilization controller is also developed with no restrictions on the drift nonlinearities. It is shown that both the robust and adaptive stabilization controllers can simultaneously accomplish the asymptotic regulation and full-state constraint tasks.

(3)

When $x_0\left(t_0\right)=0$, nonzero constant action is the most commonly used method to drive the $x_0$ state away from zero [8,36]. Different from this, in this paper, we provide a new non-constant discontinuous switching approach to realize simultaneously both the stabilization control aims and the desired state constraints.

2. Robust Stabilization of Uncertain Nonholonomic Systems

In this section, we consider the following complicated version of uncertain nonholonomic systems:

$$\begin{array}{ccc}\hfill {\dot{x}}_0& =& {\lambda }_0\left(t\right)u_0+{\varphi }_0(t,x_0)\hfill \\ \hfill {\dot{x}}_1& =& {\lambda }_1\left(t\right)x_2{u}_0+{\varphi }_1(t,x_0,x,u_0)\hfill \\ & \cdots & \hfill \\ \hfill {\dot{x}}_{n-1}& =& {\lambda }_{n-1}\left(t\right)x_n{u}_0+{\varphi }_{n-1}(t,x_0,x,u_0)\hfill \\ \hfill {\dot{x}}_n& =& {\lambda }_n\left(t\right)u_1+{\varphi }_n(t,x_0,x,u_0)\hfill \end{array}$$

(1)

where ${(x_0,x^T)}^T={(x_0,x_1,\dots ,x_n)}^T$ represents the system state vector, ${\varphi }_i$’s $(i=0,1,\dots ,n)$ stands for the uncertain nonlinear functions, including the neglected dynamics and the possible modeling errors, ${\lambda }_i$’s represents the disturbed virtual control directions, and $u_0$ and $u_1$ are control inputs. In the sequel, for the state $x_i$, ${\overline{x}}_i={(x_1,\dots ,x_i)}^T$. For ${\varphi }_0(t,x_0)$, we first assume that ${\varphi }_0(t,x_0)$ is uniformly Lipschitz in $x_0$.

Now, the control attention focuses on designing robust stabilization control laws $u_i$ $(i=0,1)$ such that the system in Equation (1) is asymptotically stable, while the full-state constraints $|x_i|\le k_{ci}$ $(0\le i\le n)$ are not violated, where $k_{ci}$ represents positive constants. In order to accomplish this control objective, the following assumptions are orderly and are given as

Assumption 1.

For each virtual control direction ${\lambda }_i\left(t\right)$ $(0\le i\le n)$, we assume that two positive known constants ${\beta }_{i1}$ and ${\beta }_{i2}$ can be found in such a way that

$$\begin{array}{c}\hfill {\beta }_{i1}\le {\lambda }_i\left(t\right)\le {\beta }_{i2}.\end{array}$$

(2)

Assumption 2.

For uncertain functions ${\varphi }_i$ $(0\le i\le n)$, suppose that there are known nonnegative $C^1$ functions ${\vartheta }_i(x_0,{\overline{x}}_i,u_0)$ $(1\le i\le n)$ such that

$$\begin{array}{c}|{\varphi }_0(t,x_0)|\le c_0\left|x_0\right|,c_0>0\\ |{\varphi }_i(t,x_0,x,u_0)|\le (|x_1|+|x_2|+\cdots +|x_i\left|\right){\vartheta }_i(x_1,{\overline{x}}_i,u_0).\end{array}$$

(3)

Remark 1.

Assumption 1 has been commonly used in the stabilization control of nonholonomic systems, such as in [4,7,10].

Two frequently used lemmas in control design are as follows:

Lemma 1 

([19]). If $b\in {\mathbb{R}}^n$ is a constant vector, then for any $x\in {\mathbb{R}}^n$ complying with $\left|x\right|<\left|b\right|$, the following inequality holds readily:

$$\begin{array}{c}\hfill ln\frac{b^{T}b}{b^{T}b-x^{T}x}\le \frac{x^{T}x}{b^{T}b-x^{T}x}.\end{array}$$

(4)

Lemma 2

([37]). Assume that ${\zeta }_1$ and ${\zeta }_2$ are positive constants. Then, for $x,y\in \mathbb{R}$ and a real-valued function $\epsilon (x,y)>0$, the following holds:

$$\begin{array}{c}\hfill {\left|x\right|}^{{\zeta }_1}{\left|y\right|}^{{\zeta }_2}\le \frac{{\zeta }_1\epsilon {\left|x\right|}^{{\zeta }_1+{\zeta }_2}}{{\zeta }_1+{\zeta }_2}+\frac{{\zeta }_2{\epsilon }^{-{\zeta }_1/{\zeta }_2}{\left|y\right|}^{{\zeta }_1+{\zeta }_2}}{{\zeta }_1+{\zeta }_2}.\end{array}$$

(5)

2.1. State Scaling

The overall controller development is presented in two separate stages due to the inherently triangular structure of the system in Equation (1). For the $x_0$ subsystem, we first consider the following asymmetric BLF:

$$\begin{array}{c}\hfill V_0=\frac{1}{2}ln\frac{b_1^2}{b_1^2-x_0^2},b_1>0\end{array}$$

(6)

whose time derivative complies with

$$\begin{array}{c}\hfill {\dot{V}}_0=\frac{x_0{\dot{x}}_0}{b_1^2-x_0^2}=\frac{x_0({\lambda }_0\left(t\right)u_0+{\varphi }_0)}{b_1^2-x_0^2}.\end{array}$$

(7)

The control signal $u_0$ is selected such that

$$\begin{array}{c}\hfill u_0=-k_0{x}_0,k_0>c_0/{\beta }_{01},\end{array}$$

(8)

which leads to the following result:

$$\begin{array}{c}\hfill {\dot{V}}_0\le \frac{-(k_0{\beta }_{01}-c_0)x_0^2}{b_1^2-x_0^2}\le -2(k_0{\beta }_{01}-c_0)V_0\le 0\end{array}$$

(9)

where $V_0\le x_0^2/\left[2(b_1^2-x_0^2)\right]$, obtained by using Lemma 1, is considered in Equation (9). With Equation (9) in mind, we can find the following proposition:

Proposition 1.

For the $x_0$ subsystem with the control input in Equation (8), one has ${lim}_{t\to \infty }{x}_0\left(t\right)=0$ and $|x_0\left(t\right)|<k_{c0}$ for any t as long as $|x_0\left(0\right)|<b_1$ and $b_1<k_{c0}$.

Proof. 

By recalling LaSalle’s invariant theorem [38], in light of Equation (9), the results in Proposition 1 can be proven easily.

Subsequently, following the application of Gronwall–Bellman inequality [38], one has

$$\begin{array}{c}\hfill V_0\left(0\right)e^{-2(k_0{\beta }_{02}+c_0)(t-t_0)}\le V_0\left(t\right)\\ \hfill \le V_0\left(0\right)e^{-2(k_0{\beta }_{01}-c_0)(t-t_0)}.\end{array}$$

(10)

□

Remark 2.

It follows from Equation (10) that the following set $\{(x_0,x)\in \mathbb{R}\times {\mathbb{R}}^n|\left|x_0\right|<b_1\}$ stands for a positive invariant set for the system in Equation (1) with the control input $u_0$ defined by Equation (8) and any controller $u_1$.

Based on the results in Proposition 1, it is given that the $x_0$ state in Equation (1) can be easily exponentially regulated to zero via $u_0$, defined by Equation (8). However, the x system becomes uncontrollable in the limit, namely where $u_0=0$. In order to treat this difficulty, the following discontinuous state transformations are given:

$$\begin{array}{c}\hfill z_i=x_i/x_0^{n-i},1\le i\le n.\end{array}$$

(11)

Remark 3.

The main property of the presented discontinuous state transformations in Equation (11) is reminiscent of the notion of the σ process generated in the dynamical systems theory [39], and it has been commonly used in nonholonomic control systems, such as in [4].

Next, by applying a state transformation (Equation (11)), the x subsystem in Equation (1) is converted into

$$\begin{array}{ccc}\hfill {\dot{z}}_i& =& -k_0{\lambda }_i\left(t\right)z_{i+1}+{\overline{\varphi }}_i(t,x_0,x),1\le i\le n-1\hfill \\ \hfill {\dot{z}}_n& =& u_1{\lambda }_n\left(t\right)+{\overline{\varphi }}_n(t,x_0,x)\hfill \end{array}$$

(12)

where the nonlinear functions ${\overline{\varphi }}_i$ $(1\le i\le n)$ are given as

$$\begin{array}{ccc}\hfill {\overline{\varphi }}_i& =& \frac{{\varphi }_i(t,x_0,x,-k_0{x}_0)}{x_0^{n-i}}\hfill \\ & & -z_i\frac{(n-i)(-k_0{\lambda }_0\left(t\right)x_0+{\varphi }_0(t,x_0))}{x_0}\hfill \end{array}$$

(13)

Remark 4.

Since the transformed system in Equation (12) is in strict feedback form, backstepping control design is applicable now.

Lemma 3. 

For each nonlinear function ${\overline{\varphi }}_i$ $(1\le i\le n)$, there is a nonnegative smooth function ${\overline{\vartheta }}_i(x_0,{\overline{z}}_i)$ such that

$$\begin{array}{c}\hfill |{\overline{\varphi }}_i(t,x_0,x)|\le (|z_1|+|z_2|+\cdots +|z_i\left|\right){\overline{\vartheta }}_i(x_0,{\overline{z}}_i).\end{array}$$

(14)

Proof. 

Under Assumptions 1 and 2, the following holds:

$$\begin{array}{ccc}\hfill |{\overline{\varphi }}_i|& \le & \frac{|x_1|+|x_2|+\cdots +|x_i|}{|x_0{|}^{n-i}}{\vartheta }_i(x_0,{\overline{x}}_i,-k_0{x}_0)\hfill \\ & & +({\beta }_{02}{k}_0+c_0)(n-i)\left|z_i\right|\hfill \\ & \le & \left(\right|z_1{x}_0^{i-1}|+|z_2{x}_0^{i-2}|+\cdots +|z_i\left|\right)\hfill \\ & & \times {\vartheta }_i(x_0,z_1{x}_0^{n-1},\dots ,z_i{x}_0^{n-i},-k_0{x}_0)\hfill \\ & & +({\beta }_{02}{k}_0+c_0)(n-i)\left|z_i\right|.\hfill \end{array}$$

(15)

Therefore, Lemma 3 follows readily. □

2.2. Robust Stabilization Control Backstepping Design

Subsequently, the backstepping control design will be presented step by step to develop a control input $u_1$ under $x_0\left(0\right)\ne 0$. In addition, the case of $x_0\left(0\right)=0$ will be handled and discussed in the next subsection. The backstepping recursive procedure is given in detail below.

Step 1: When taking $z_2$ as the virtual control input, we first study the $z_1$ subsystem of Equation (12). We construct the first BLF candidate $V_1\left(z_1\right)=1/2ln[k_1^2/(k_1^2-z_1^2)]$ with $k_1>0$, whose time derivative satisfies

$$\begin{array}{c}\hfill {\dot{V}}_1\le \frac{-k_0{\lambda }_1{z}_1(z_2-z_2^{*})}{k_1^2-z_1^2}+\frac{z_1^2{\overline{\vartheta }}_1(x_0,z_1)}{k_1^2-z_1^2}-\frac{k_0{\lambda }_1{z}_1{z}_2^{*}}{k_1^2-z_1^2}.\end{array}$$

(16)

By choosing the first continuous virtual controller $z_2^{*}(x_0,z_1)$ for $z_2$ to be

$$\begin{array}{c}\hfill z_2^{*}=\frac{1}{k_0{\beta }_{11}}{z}_1(n(k_1^2-z_1^2)+{\overline{\vartheta }}_1(x_0,z_1))\triangleq z_1{\chi }_1(x_0,z_1),\end{array}$$

(17)

it arrives at

$$\begin{array}{c}\hfill {\dot{V}}_1\le -n{z}_1^2-\frac{k_0{\lambda }_1\left(t\right)z_1(z_2-z_2^{*})}{k_1^2-z_1^2}.\end{array}$$

(18)

Step i $(2\le i<n)$: At this step, we suppose that there exists a BLF

$$\begin{array}{c}\hfill V_{i-1}=\frac{1}{2}\sum _{j=1}^{i-1}ln\frac{k_j^2}{k_j^2-{\xi }_j^2},k_j>0\end{array}$$

(19)

and a set of virtual controllers $z_1^{*},z_2^{*},\cdots ,z_i^{*}$ defined by

$$\begin{array}{cccccc}{z}_1^{*}\hfill & =\hfill & 0,\hfill & {\xi }_1\hfill & =\hfill & z_1-z_1^{*}\hfill \\ z_2^{*}\hfill & =\hfill & {\chi }_1(x_0,z_1){\xi }_1,\hfill & {\xi }_2\hfill & =\hfill & z_2-z_2^{*}\hfill \\ \hfill & ⋮\hfill & \hfill & & ⋮\hfill & \\ z_i^{*}\hfill & =\hfill & {\chi }_{i-1}(x_0,{\overline{z}}_{i-1}){\xi }_{i-1},\hfill & {\xi }_i\hfill & =\hfill & z_i-z_i^{*}\hfill \end{array}$$

(20)

with ${\chi }_1(·)>0,\dots ,{\chi }_{i-1}(·)>0$ being $C^1$ functions such that time derivative of $V_{i-1}$ is as follows:

$$\begin{array}{c}\hfill {\dot{V}}_{i-1}=-\frac{k_0{\lambda }_{i-1}\left(t\right){\xi }_{i-1}(z_i-z_i^{*})}{k_{i-1}^2-{\xi }_{i-1}^2}-(n-i+2)\sum _{j=1}^{i-1}{\xi }_j^2\end{array}$$

(21)

where $k_j>0$, $1\le j\le i$. Next, we will develop a similar analysis result. To achieve this attention, the candidate BLF is constructed as follows:

$$\begin{array}{c}\hfill V_i=\frac{1}{2}\sum _{j=1}^{i}ln\frac{k_j^2}{k_j^2-{\xi }_j^2}.\end{array}$$

(22)

It is easy to show that the time derivative of $V_i$ along the solutions to Equation (12) satisfies

$$\begin{array}{ccc}\hfill {\dot{V}}_i& \le & -\frac{k_0{\lambda }_{i-1}\left(t\right){\xi }_{i-1}(z_i-z_i^{*})}{k_{i-1}^2-{\xi }_{i-1}^2}-(n-i+2)\sum _{j=1}^{i-1}{\xi }_j^2\hfill \\ & & -\frac{k_0{\lambda }_i\left(t\right){\xi }_i(z_{i+1}-z_{i+1}^{*})}{k_i^2-{\xi }_i^2}+\frac{{\xi }_i{\overline{\varphi }}_i}{k_i^2-{\xi }_i^2}\hfill \\ & & -\frac{k_0{\lambda }_i\left(t\right){\xi }_i{z}_{i+1}^{*}}{k_i^2-{\xi }_i^2}-\frac{{\xi }_i{\dot{z}}_i^{*}}{k_i^2-{\xi }_i^2}.\hfill \end{array}$$

(23)

In light of Lemmas 2 and 3, one has

$$\begin{array}{c}\hfill \left|\frac{k_0{\lambda }_{i-1}{\xi }_{i-1}{\xi }_i}{k_{i-1}^2-{\xi }_{i-1}^2}\right|\le \frac{1}{3}{\xi }_{i-1}^2+{\xi }_i^2{\omega }_{i1}(z_1,\dots ,z_{i-1})\end{array}$$

(24)

where ${\omega }_{i1}$ is a $C^1$ function. Recall that $|z_j|=|{\xi }_j+z_j^{*}|\le |{\xi }_j|+|{\xi }_{i-1}|{\chi }_{j-1}$. For the nonlinear function ${\overline{\varphi }}_i$, one has

$$\begin{array}{ccc}\hfill |{\overline{\varphi }}_i|& \le & \left(|{\xi }_1|+\sum _{j=2}^i\left(\right|{\xi }_j|+|{\xi }_{j-1}\left|{\chi }_{j-1}\right)\right){\overline{\vartheta }}_i\hfill \\ & \le & \left(\right|{\xi }_1|+|{\xi }_2|+\cdots +|{\xi }_i\left|\right){\widehat{\vartheta }}_i(x_0,{\overline{z}}_i).\hfill \end{array}$$

(25)

Under the results in Equation (25), we have

$$\begin{array}{ccc}\hfill \left|\frac{{\xi }_i{\overline{\varphi }}_i}{k_i^2-{\xi }_i^2}\right|& \le & \left|\frac{{\xi }_i}{k_i^2-{\xi }_i^2}\right|\left(\sum _{j=1}^i\left|{\xi }_j\right|\right){\widehat{\vartheta }}_i(x_0,{\overline{z}}_i)\hfill \\ & \le & \frac{1}{3}\left(\sum _{j=1}^{i-1}{\xi }_j^2\right)+{\xi }_i^2{\omega }_{i2}(x_0,{\overline{z}}_i).\hfill \end{array}$$

(26)

where ${\omega }_{i2}$ is a $C^1$ function.

For the coming development, the following result is presented.

Proposition 2. 

There exists a $C^1$ function ${\varpi }_i(x_0,{\overline{z}}_i)\ge 0$ such that

$$\begin{array}{c}\hfill \left|\frac{d{z}_i^{*}}{dt}\right|\le \left(\right|{\xi }_1|+|{\xi }_2|+\cdots +|{\xi }_i\left|\right){\varpi }_i(x_0,{\overline{z}}_i).\end{array}$$

(27)

Proof. 

The proof of Proposition 2 is included in Appendix A.

As a further result of Proposition 2, it readily follows that

$$\begin{array}{ccc}\hfill \left|\frac{{\xi }_i{\dot{z}}_i^{*}}{k_i^2-{\xi }_i^2}\right|& \le & \left|\frac{{\xi }_i}{k_i^2-{\xi }_i^2}\right|\left(\sum _{j=1}^i\left|{\xi }_j\right|\right){\varpi }_i(x_0,{\overline{z}}_i)\hfill \\ & \le & \frac{1}{3}\left(\sum _{j=1}^{i-1}{\xi }_j^2\right)+{\xi }_i^2{\omega }_{i3}(x_0,{\overline{z}}_i)\hfill \end{array}$$

(28)

where ${\omega }_{i3}$ is a continuous function. Substituting Equations (24), (26), and (28) back into Equation (23) yields that

$$\begin{array}{ccc}\hfill {\dot{V}}_i& \le & -(n-i+1)\sum _{j=1}^{i-1}{\xi }_j^2-\frac{k_0{\lambda }_i{\xi }_i(z_{i+1}-z_{i+1}^{*})}{k_i^2-{\xi }_i^2}\hfill \\ & & -\frac{k_0{\lambda }_i{\xi }_i{z}_{i+1}^{*}}{k_i^2-{\xi }_i^2}+{\xi }_i^2({\omega }_{i1}+{\omega }_{i2}+{\omega }_{i3}).\hfill \end{array}$$

(29)

According to the obtained results in Equation (29), the virtual control $z_{i+1}^{*}(x_0,{\overline{z}}_i)$ is specified as

$$\begin{array}{ccc}\hfill z_{i+1}^{*}& =& \frac{1}{k_0{\beta }_{i1}}{\xi }_i(n-i+1+{\omega }_{i1}+{\omega }_{i2}+{\omega }_{i3})(k_i^2-{\xi }_i^2)\hfill \\ & \triangleq & {\xi }_i{\chi }_i(x_0,{\overline{z}}_i),\hfill \end{array}$$

(30)

which, together with Equation (29), implies that

$$\begin{array}{c}\hfill {\dot{V}}_i\le -(n-i+1)\sum _{j=1}^i{\xi }_j^2-\frac{k_0{\lambda }_i\left(t\right){\xi }_i(z_{i+1}-z_{i+1}^{*})}{k_i^2-{\xi }_i^2}.\end{array}$$

(31)

By applying a similar control design process in the final step (Step n), we can conclude that there exist $C^1$ functions ${\chi }_1(x_0,z_1)>0$, …, ${\chi }_{n-1}(x_0,z_1,\dots ,z_{n-1})>0$, and ${\omega }_{nj}(z_1,\dots ,z_n)\ge 0$, $j=1,2,3$ such that

$$\begin{array}{c}\hfill {\dot{V}}_i\le -\sum _{j=1}^{n-1}{\xi }_j^2+\frac{{\lambda }_n\left(t\right){\xi }_n{u}_1}{k_n^2-{\xi }_n^2}+{\xi }_n^2({\omega }_{n1}+{\omega }_{n2}+{\omega }_{n3})\end{array}$$

(32)

where the last BLF is defined as

$$\begin{array}{c}\hfill V_n=\frac{1}{2}\sum _{j=1}^{n}ln\frac{k_j^2}{k_j^2-{\xi }_j^2},k_n>0,{\xi }_n=z_n-z_n^{*}.\end{array}$$

(33)

Then, based on the structure of Equation (32), the actual control input $u_1$ can be proposed to be

$$\begin{array}{c}\hfill u_1=-\frac{1}{{\beta }_{n1}}{\xi }_n(1+{\omega }_{n1}+{\omega }_{n2}+{\omega }_{n3})(k_n^2-{\xi }_n^2),\end{array}$$

(34)

which leads to

$$\begin{array}{c}\hfill {\dot{V}}_n\le -\sum _{j=1}^n{\xi }_j^2.\end{array}$$

(35)

□

2.3. Switching Control and Main Results

In the preceding section, the controller has been elaborated provided that $x_0\left(0\right)\ne 0$. Now, we will show how to design controllers $u_0$ and $u_1$ in the case of $x_0\left(0\right)=0$. If $x_0\left(0\right)=0$, like in [33], then we propose controller $u_0$ to be

$$\begin{array}{c}\hfill u_0=-k_0{x}_0+u_{0c}\sqrt{b_1^2-x_0^2}\end{array}$$

(36)

where $u_{0c}>0$ is a constant. Considering the same BLF as in Equation (6), one has

$$\begin{array}{c}\hfill {\dot{V}}_0\le -\left(k_0{\beta }_{01}-c_0-\frac{1}{2}\right)\frac{x_0^2}{b_1^2-x_0^2}+\frac{{\beta }_{02}^2{u}_{0c}^2}{2}\end{array}$$

(37)

where positive constants $k_0$ and $u_{0c}$ are chosen to satisfy ${\beta }_{02}{u}_{0c}/\sqrt{2k_0{\beta }_{01}-2c_0-1}<1$ and $k_0{\beta }_{01}-c_0-1/2>0$. Returning to Equation (37), it can be seen that ${\dot{V}}_0$ is negative once $|x_0\left(t\right)|\ge \left(u_{0c}{b}_1{\beta }_{02}\right)/\sqrt{2k_0{\beta }_{01}-2c_0-1}$. Therefore, $x_0\left(t\right)$ is bounded provided that $|x_0\left(0\right)|<b_1$. In addition, $|x_0\left(t\right)|<b_1$ for any $t\ge 0$. Under the controller in Equation (36), the resulting obtained closed-loop $x_0$ subsystem is said to be

$$\begin{array}{c}\hfill {\dot{x}}_0=({\varphi }_0(t,x_0)-{\lambda }_0\left(t\right)k_0{x}_0)+{\lambda }_0\left(t\right)u_{0c}\sqrt{b_1^2-x_0^2}.\end{array}$$

(38)

In light of Equation (38), we can claim that the state $x_0\left(t\right)$ is increasing at the beginning since $x\left(0\right)=0$ and ${\dot{x}}_0\left(0\right)>0$. In the following, we need to consider two cases that can happen: (1) state $x_0\left(t\right)$ keeps growing as shown in the left subgraph of Figure 1, and (2) state $x_0\left(t\right)$ first increases and then goes down, but it will increase if $x_0\left(t\right)\to 0$. Please note that the second term on the right-hand side of Equation (38) is quite large while the first term is rather small. This phenomenon can be roughly illustrated by the right subgraph in Figure 1.

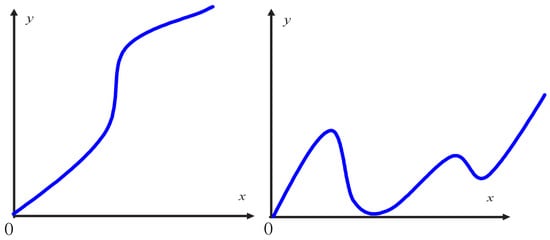
Figure 1. The possible responses of the solution $x_0\left(t\right)$.

Therefore, it can be claimed that the state $x_0\left(t\right)$ remains positive and does not escape within any given finite time $t_f$. Since the state $x_0\left(t\right)$ will not blow up on the time interval $[0,t_f]$, by specifying controller $u_0$ with Equation (36), we can utilize a backstepping control design to produce a controller $u_1=u_1^{★}(x_0,x)$ for the original x system in Equation (1). Then, from a result like that in Equation (35), we can conclude that the state x will not blow up on the time interval $[0,t_f]$. Since $x_0\left(t_f\right)\ne 0$, the system controllers $u_0$ and $u_1$ can be switched into Equations (8) and (34) at time $t=t_f$, respectively.

Now, in this moment, we are ready to summarize the main result of this section in the following theorem:

Theorem 1. 

Suppose that Assumptions 1 and 2 hold. If the control scheme is actuated to the system in Equation (1) in such a way that (1) when $x_0\left(0\right)\ne 0$, $u_0=\left(8\right)$ and $u_1=\left(34\right)$ and (2) when $x_0\left(0\right)=0$, $u_0=\left(36\right)\to u_0={\left(8\right)}_{t=t_f}$ and $u_1=u_1^{★}(x_0,x)\to u_1={\left(34\right)}_{t=t_f}$, then the uncertain system in Equation (1) is asymptotically stable, while the full-state constraints are not violated by choosing appropriate parameters.

Proof. 

By choosing the entire BLF $V=V_0+\frac{1}{2}{\sum }_{j=1}^{n}ln{k}_j^2/(k_j^2-{\xi }_j^2)$, one has $\dot{V}\le -(k_0{\beta }_{01}-c_0)x_0^2/(b_1^2-x_0^2)-{\displaystyle \sum _{j=1}^n}{\xi }_j^2$. Since $|x_0|<b_1$ and $|{\xi }_j\left(0\right)|<k_j$, by using the proof process of Proposition 1, it can be proven that $x_0\left(t\right)$ and ${\xi }_j\left(t\right)$ are bounded, and meanwhile, $|x_0\left(t\right)|<b_1$ and $|{\xi }_j\left(t\right)|<k_j$ $(1\le j\le n)$. By applying the well-known LaSalle’s invariant theorem, it follows that $(x_0\left(t\right),{\xi }_j\left(t\right))$ tends toward the largest invariant set $\Omega$ contained in the set where $\dot{V}=0$. This fact in turn implies that $x_0\left(t\right)\to 0$ and ${\xi }_j\left(t\right)\to 0$ as $t\to \infty$. Note that all the virtual control variables $z_j^{*}\to 0$ once ${\xi }_{j-1}\to 0$. The above stability analysis results further indicate that $x_0\left(t\right)\to 0$ and $z_j\left(t\right)\to 0$ as $t\to \infty$. Accordingly, one can show that $x_0\left(t\right)\to 0$ and $x_j\left(t\right)\to 0$ as $t\to \infty$. Now, we will demonstrate how the desired full-state constraints are guaranteed. From Proposition 1, it holds readily that $|x_0\left(t\right)|<k_{c0}$ can be obtained directly by choosing $b_1<k_{c0}$. Since $|z_1\left(t\right)|<k_1$, in light of Equation (10), we have $|x_1\left(t\right)|<|z_1\left(t\right)\left|\right|x_0{\left(t\right)|}^{n-1}<k_1{b}_1^{n-1}$. Hence, by choosing $k_1{b}_1^{n-1}<k_{c1}$, one has $|x_1\left(t\right)|<k_{c1}$. By using a similar proof process, we can prove in an orderly manner that $|x_i|\le k_{ci}$, $i=0,1,\dots ,n$. □

3. Adaptive Stabilization of Nonholonomic Uncertain Systems

In this section, we investigate a classical kind of uncertain nonholonomic system whose model is expressed as

$$\begin{array}{ccc}\hfill {\dot{x}}_0& =& u_0+{\psi }_0^T\left(x_0\right)\theta \hfill \\ \hfill {\dot{x}}_1& =& x_2{u}_0+{\psi }_1^T(x_0,x,u_0)\theta \hfill \\ & \cdots & \hfill \\ \hfill {\dot{x}}_{n-1}& =& x_n{u}_0+{\psi }_{n-1}^T(x_0,x,u_0)\theta \hfill \\ \hfill {\dot{x}}_n& =& u_1+{\psi }_n^T(x_0,x,u_0)\theta \hfill \end{array}$$

(39)

where ${(x_0,x^T)}^T={(x_0,x_1,\dots ,x_n)}^T$ represents the system state vector, ${\psi }_i$’s $(i=0,1,\dots ,n)$ denote the smooth nonlinear function vectors, $\theta$ stands for an unknown bounded constant parameter vector, and $u_0$ and $u_1$ are the system control inputs.

The control objective of this part is to design the adaptive stabilization control laws $u_0$ and $u_1$ of the form $u_0=u_0(x_0,\widehat{\theta })$, $u_1=u_1(z,\widehat{\theta })$, and $\dot{\widehat{\theta }}=v(z,\widehat{\theta })$ such that all states of the system in Equation (39) converge to zero asymptotically while the aforementioned full-state constraints are not violated. To achieve this aim, the assumption imposed on the system in Equation (39) is expressed as follows:

Assumption 3. 

We assume that there is a smooth known function vector ${\phi }_0$ such that

$$\begin{array}{c}\hfill {\psi }_0\left(x_0\right)=x_0{\phi }_0.\end{array}$$

(40)

For each $1\le i\le n$, there exists a smooth known function vector ${\phi }_j$ $(1\le j\le i)$ such that

$$\begin{array}{c}\hfill {\psi }_i(x_0,x,u_0)=\sum _{j=1}^i{x}_j{\phi }_j(u_0,x_0,{\overline{x}}_i).\end{array}$$

(41)

3.1. State Transformations

Assumption 3 implies that the system in Equation (39) possesses a triangularity structure. To clearly grasp the essence of the control design, the case where $x_0\left(0\right)\ne 0$ is studied first. Then, the case of $x_0\left(0\right)=0$ will be discussed in Section 3.3.

For the $x_0$ subsystem, we consider the following BLF:

$$\begin{array}{c}\hfill V_0=\frac{1}{2}ln\frac{b_1^2}{b_1^2-x_0^2}+\frac{1}{2}{\tilde{\theta }}_0^T{{\rm Y}}^{-1}{\tilde{\theta }}_0,b_1>0.\end{array}$$

(42)

where ${\rm Y}$ denotes a positive definite matrix, ${\tilde{\theta }}_0=\theta -{\widehat{\theta }}_0$, and ${\widehat{\theta }}_0$ represents the first on-line estimation of $\theta$. Therefore, the control input $u_0(x_0,{\theta }_0)$ is designed such that

$$\begin{array}{ccc}\hfill u_0& =& -x_0{\phi }_0^T\left(x_0\right){\widehat{\theta }}_0-x_0\sqrt{k_0^2+{\left({\phi }_0^T\left(x_0\right){\widehat{\theta }}_0\right)}^2}\hfill \\ & =& x_0{d}_0(x_0,{\widehat{\theta }}_0)\hfill \end{array}$$

(43)

and the adaptive law is defined as

$$\begin{array}{c}\hfill {\dot{\widehat{\theta }}}_0=\frac{{\rm Y}{x}_0{\phi }_0\left(x_0\right)}{b_1^2-x_0^2}\end{array}$$

(44)

with $k_0>0$. Under Equations (43) and (44), the time derivative of $V_0$ is computed as follows:

$$\begin{array}{c}\hfill {\dot{V}}_0\le -\frac{k_0{x}_0^2}{b_1^2-x_0^2}.\end{array}$$

(45)

From Equation (45), we know that $x_0\left(t\right)$ and ${\tilde{\theta }}_0\left(t\right)$ are bounded, and $|x_0\left(t\right)|<b_1$, $x_0\left(t\right)\to 0$ as $t\to \infty$, provided that $|x_0\left(0\right)|<b_1$. With the designed control law in Equation (43), the resulting closed-loop $x_0$ subsystem can be formulated as follows:

$$\begin{array}{c}\hfill {\dot{x}}_0=-x_0\left(\sqrt{k_0^2+{\left({\phi }_0^T{\widehat{\theta }}_0\right)}^2}-{\phi }_0^T{\tilde{\theta }}_0\right).\end{array}$$

(46)

We denote $\sigma \left(s\right)=\sqrt{k_0^2+{\left({\phi }_0^T{\widehat{\theta }}_0\left(s\right)\right)}^2}-{\phi }_0^T{\tilde{\theta }}_0\left(s\right)$. Since both $x_0\left(t\right)$ and ${\tilde{\theta }}_0\left(t\right)$ are bounded, the solution for the system in Equation (46) is expressed as $x_0\left(t\right)=x_0\left(t_0\right)e^{-{\int }_0^t\sigma \left(s\right)ds}$. Hence, $x_0\left(t\right)=0$ happens for two possible cases: (1) $x_0\left(0\right)=0$ and (2) $t\to \infty$. Note that $x_0\left(0\right)\ne 0$ has been assumed, and as a result, $u_0$, defined by Equation (43), can guarantee that the state $x_0\left(t\right)$ will not cross zero for any time t.

We apply the control law in Equation (43) for the control input $u_0$ and state scaling (Equation (11)) to convert the x subsystem of Equation (39) into

$$\begin{array}{ccc}\hfill {\dot{z}}_i& =& d_0(x_0,{\widehat{\theta }}_0)z_{i+1}+g_i(x_0,z_i,{\widehat{\theta }}_0)+{\overline{\psi }}_i^T(x_0,{\overline{z}}_i,{\widehat{\theta }}_0)\theta \hfill \\ \hfill {\dot{z}}_n& =& u_1+{\overline{\psi }}_n(u_0,x_0,x)\theta \hfill \end{array}$$

(47)

where

$$\begin{array}{ccc}\hfill {\overline{\psi }}_i(x_0,{\overline{z}}_i,{\widehat{\theta }}_0)& =& \frac{{\psi }_i(u_0,x_0,{\overline{x}}_i)}{x_0^{n-i}}-\frac{(n-i)z_i{\psi }_0\left(x_0\right)}{x_0}\hfill \\ \hfill g_i(x_0,z_i,{\widehat{\theta }}_0)& =& -(n-i)d_0(x_0,{\widehat{\theta }}_0)z_i.\hfill \end{array}$$

(48)

3.2. Tuning Function Design

To design the adaptive control law $u_1$, the tuning function is presented step by step as follows. As usual, the recursive design begins with a simple subsystem and then goes on to a higher-order system, and it ultimately stops once the actual input $u_1$ occurs.

Step 1: We introduce ${\xi }_1=z_1$ and ${\xi }_2=z_2-z_2^{*}$, where $z_2^{*}$ is referred to as the first virtual control which is used to stabilize the $z_1$ subsystem. Now, we choose the first BLF to be

$$\begin{array}{c}\hfill V_1=\frac{1}{2}ln\frac{k_1^2}{k_1^2-{\xi }_1^2}+\frac{1}{2}{\tilde{\theta }}^T{\Gamma }^{-1}\tilde{\theta }\end{array}$$

(49)

where $k_i$ $(1\le i\le n)$ are positive constants and $\Gamma$ denotes a positive definite matrix. In this step, it is easy to determine the virtual control $z_2^{*}(x_0,z_1,{\widehat{\theta }}_0,\widehat{\theta })$ and tuning function ${\tau }_1(x_0,z_1,{\widehat{\theta }}_0)$ to be

$$\begin{array}{ccc}\hfill z_2^{*}& =& \frac{1}{d(x_0,{\widehat{\theta }}_0)}[-{\beta }_1(k_1^2-{\xi }_1^2)-g_1(x_0,z_1,{\widehat{\theta }}_0)\hfill \\ & & -{\overline{\psi }}_1^T(x_0,z_1,{\widehat{\theta }}_0)\widehat{\theta }]\hfill \\ \hfill {\tau }_1& =& \frac{\Gamma {\xi }_1{\overline{\psi }}_1(x_0,z_1,{\widehat{\theta }}_0)}{k_1^2-{\xi }_1^2}.\hfill \end{array}$$

(50)

Then, we can find that

$$\begin{array}{c}\hfill {\dot{V}}_1\le -{\beta }_1{\xi }_1^2+\frac{d_0{\xi }_1{\xi }_2}{k_1^2-{\xi }_1^2}-{\tilde{\theta }}^T{\Gamma }^{-1}\left(\dot{\widehat{\theta }}-{\tau }_1\right).\end{array}$$

(51)

Step i $(3\le i<n)$: We consider the BLF to be $V_i=V_{i-1}+1/2ln[k_i^2/(k_i^2-{\xi }_i^2)]$ with ${\xi }_i=z_i-z_i^{*}$ and define ${\Pi }_1(x_0,z_1,{\widehat{\theta }}_0,\widehat{\theta })=0$ and

$$\begin{array}{c}\hfill w_i(x_0,{\overline{z}}_i,{\widehat{\theta }}_0,\widehat{\theta })={\overline{\psi }}_i(x_0,{\overline{z}}_i,{\widehat{\theta }}_0)-\frac{\partial z_i^{*}(x_0,{\overline{z}}_{i-1},{\widehat{\theta }}_0,\widehat{\theta })}{\partial x_0}\\ \hfill \times {\psi }_0\left(x_0\right)-\cdots -\frac{\partial z_i^{*}}{\partial z_{i-1}}{\overline{\psi }}_{i-1}(x_0,{\overline{z}}_{i-1},{\widehat{\theta }}_0)\end{array}$$

(52)

$$\begin{array}{c}\hfill {\eta }_i(x_0,{\overline{z}}_i,{\widehat{\theta }}_0,\widehat{\theta })=\frac{\partial z_i^{*}(x_0,{\overline{z}}_{i-1},{\widehat{\theta }}_0,\widehat{\theta })}{\partial \widehat{\theta }}\end{array}$$

(53)

$$\begin{array}{ccc}\hfill {\Pi }_i(x_0,{\overline{z}}_i,{\widehat{\theta }}_0,\widehat{\theta })& =& {\Pi }_{i-1}(x_0,{\overline{z}}_{i-1},{\widehat{\theta }}_0,\widehat{\theta })\hfill \\ & & +\frac{{\xi }_i}{k_i^2-{\xi }_i^2}{\eta }_i(x_0,{\overline{z}}_i,{\widehat{\theta }}_0,\widehat{\theta }).\hfill \end{array}$$

(54)

In this step, the virtual control $z_{i+1}^{*}(x_0,{\overline{z}}_i,{\widehat{\theta }}_0,\widehat{\theta })$ and tuning function ${\tau }_i(x_0,{\overline{z}}_i,{\widehat{\theta }}_0,\widehat{\theta })$ are designed as follows:

$$\begin{array}{ccc}\hfill & & z_{i+1}^{*}=\frac{1}{d_0(x_0,{\widehat{\theta }}_0)}[-d_0(x_0,{\widehat{\theta }}_0)\frac{{\xi }_{i-1}(k_i^2-{\xi }_i^2)}{k_{i-1}^2-{\xi }_{i-1}^2}\hfill \\ & & -{\beta }_i{\xi }_i(k_i^2-{\xi }_i^2)-g_i(x_0,z_i,{\widehat{\theta }}_0)-w_i^T(x_0,{\overline{z}}_i,{\widehat{\theta }}_0,\widehat{\theta })\widehat{\theta }\hfill \\ & & +\frac{\partial z_i^{*}}{\partial x_0}{u}_0(x_0,{\widehat{\theta }}_0)+\frac{\partial z_i^{*}(x_0,{\overline{z}}_{i-1},{\widehat{\theta }}_0,\widehat{\theta })}{\partial {\widehat{\theta }}_0}{\tau }_0\left(x_0\right)\hfill \\ & & +\frac{\partial z_i^{*}}{\partial z_1}(d_0(x_0,{\widehat{\theta }}_0)z_2+g_1(x_0,z_1,{\widehat{\theta }}_0))+\cdots \hfill \\ & & +\frac{\partial z_i^{*}}{\partial z_{i-1}}(d_0(x_0,{\widehat{\theta }}_0)z_i+g_{i-1}(x_0,z_{i-1},{\widehat{\theta }}_0))\hfill \\ & & +{\Pi }_{i-1}(x_0,{\overline{z}}_{i-1},{\widehat{\theta }}_0,\widehat{\theta })\Gamma w_i(x_0,{\overline{z}}_i,{\widehat{\theta }}_0,\widehat{\theta })\hfill \\ & & +{\eta }_i(x_0,{\overline{z}}_i,{\widehat{\theta }}_0,\widehat{\theta }){\tau }_i(x_0,{\overline{z}}_i,{\widehat{\theta }}_0,\widehat{\theta })]\hfill \end{array}$$

(55)

where

$$\begin{array}{ccc}\hfill {\tau }_i(x_0,{\overline{z}}_i,{\widehat{\theta }}_0,\widehat{\theta })& =& {\tau }_{i-1}(x_0,{\overline{z}}_{i-1},{\widehat{\theta }}_0,\widehat{\theta })\hfill \\ & & +\frac{\Gamma {\xi }_i{w}_i(x_0,{\overline{z}}_i,{\widehat{\theta }}_0,\widehat{\theta })}{k_i^2-{\xi }_i^2},\hfill \end{array}$$

(56)

which generates the following results:

$$\begin{array}{ccc}\hfill {\dot{V}}_i& \le & -\sum _{j=1}^i{\beta }_j{\xi }_j^2+\frac{d_0{\xi }_i{\xi }_{i+1}}{k_i^2-{\xi }_i^2}-{\tilde{\theta }}^T{\Gamma }^{-1}(\dot{\widehat{\theta }}-{\tau }_i)\hfill \\ & & +\frac{{\xi }_i}{k_i^2-{\xi }_i^2}\frac{\partial z_i^{*}}{\partial \widehat{\theta }}({\tau }_i(x_0,{\overline{z}}_i,{\widehat{\theta }}_0,\widehat{\theta })-\dot{\widehat{\theta }}).\hfill \end{array}$$

(57)

At the last step, the actual control law $u_1$ and adaptive law $\dot{\widehat{\theta }}$ are specified as follows:

$$\begin{array}{ccc}\hfill & & u_1=-{\beta }_n{\xi }_n(k_n^2-{\xi }_n^2)-d_0(x_0,{\widehat{\theta }}_0)\frac{{\xi }_{n-1}(k_n^2-{\xi }_n^2)}{k_{n-1}^2-{\xi }_{n-1}^2}\hfill \\ & & -w_n^T(x_0,z,{\widehat{\theta }}_0,\widehat{\theta })\widehat{\theta }+\frac{\partial z_n^{*}(x_0,{\overline{z}}_{n-1},{\widehat{\theta }}_0,\widehat{\theta })}{\partial {\widehat{\theta }}_0}{\tau }_0\left(x_0\right)\hfill \\ & & +\frac{\partial z_n^{*}(x_0,{\overline{z}}_{n-1},{\widehat{\theta }}_0,\widehat{\theta })}{\partial x_0}{u}_0(x_0,{\widehat{\theta }}_0)\hfill \\ & & +\frac{\partial z_n^{*}}{\partial z_1}(d_0(x_0,{\widehat{\theta }}_0)z_2+g_1(x_0,z_1,{\widehat{\theta }}_0))+\cdots \hfill \\ & & +\frac{\partial z_n^{*}}{\partial z_{n-1}}(d_0(x_0,{\widehat{\theta }}_0)z_n+g_{n-1}(x_0,z_{n-1},{\widehat{\theta }}_0))\hfill \\ & & +{\Pi }_{n-1}(x_0,{\overline{z}}_{n-1},{\widehat{\theta }}_0,\widehat{\theta })\Gamma w_n(x_0,z,{\widehat{\theta }}_0,\widehat{\theta })\hfill \\ & & +{\eta }_n(x_0,z,{\widehat{\theta }}_0,\widehat{\theta }){\tau }_n(x_0,z,{\widehat{\theta }}_0,\widehat{\theta })\hfill \end{array}$$

(58)

and

$$\begin{array}{c}\hfill \dot{\widehat{\theta }}={\tau }_n(x_0,z,{\widehat{\theta }}_0,\widehat{\theta }).\end{array}$$

(59)

Under Equations (58) and (59), one has

$$\begin{array}{c}\hfill {\dot{V}}_n\le -\sum _{j=1}^n{\beta }_j{\xi }_j^2.\end{array}$$

(60)

3.3. Adaptive Switching and the Main Results

In the aforementioned discussion, we completed the control development when $x_0\left(0\right)\ne 0$. Next, we will present the control design procedure for $u_0$ and $u_1$ in the case where $x_0\left(0\right)=0$. When $x_0\left(0\right)=0$, like in [33], we design $u_0$ as follows:

$$\begin{array}{c}\hfill u_0=x_0{d}_0+u_{0c}\sqrt{b_1^2-x_0^2}\end{array}$$

(61)

where $d_0$ is defined by Equation (43). Considering the same BLF (Equation (42)) and adaptive law (Equation (44)), we can have

$$\begin{array}{c}\hfill {\dot{V}}_0\le -\left(k_0-\frac{1}{2}\right)\frac{x_0^2}{b_1^2-x_0^2}+\frac{u_{0c}^2}{2}\end{array}$$

(62)

where positive constants $k_0$ and $u_{0c}$ are chosen to satisfy $k_0>1/2$ and $u_{0c}/\sqrt{2k_0-1}<1$. Returning to Equation (62), it can be seen that ${\dot{V}}_0$ is negative once $|x_0\left(t\right)|\ge \left(u_{0c}{b}_1\right)/\sqrt{2k_0-1}$. Hence, as long as $|x_0\left(0\right)|<b_1$, $x_0\left(t\right)$ and ${\tilde{\theta }}_0\left(t\right)$ are bounded, moreover, $|x_0\left(t\right)|<b_1$ for any $t\ge 0$. Under Equation (61), the closed-loop $x_0$ subsystem is described as follows:

$$\begin{array}{c}\hfill {\dot{x}}_0=-x_0\left(\sqrt{k_0^2+{\left({\phi }_0^T{\widehat{\theta }}_0\right)}^2}-{\phi }_0^T{\tilde{\theta }}_0\right)+u_{0c}\sqrt{b_1^2-x_0^2}.\end{array}$$

(63)

Under Equation (63), by using the same arguments as in Section 2.3, we can conclude that for any given finite time $t_f$, state $x_0\left(t\right)$ remains positive and does not escape. Once $x_0\left(t_f\right)\ne 0$ when $t=t_f$, the control input $u_0$ is switched from Equation (61) into Equation (43). Consequently, the state scaling can be carried out for the upcoming control development.

On the time interval $[0,t_f]$, under $u_0$ (defined by Equation (61)), using backstepping-based state feedback, $u_1=u_1^{★}(x_0,x,\widehat{\theta })$ and an another adaptive law $\dot{\widehat{\theta }}={\dot{\widehat{\theta }}}^{★}(x_0,x,\widehat{\theta })$ can be designed by a similar control procedure (presented in Section 3.2) to the original x system in (39). Then, it can be claimed that state x will not blow up during the time period $[0,t_f]$. Note that $x_0\left(t_f\right)\ne 0$ when $t=t_f$, and the control inputs $u_0$ and $u_1$ are switched into Equations (43) and (58), respectively.

Now, the main result of this section is included in the following theorem:

Theorem 2. 

Suppose that Assumption 3 holds for the system in Equation (39). If the control input in Equation (43) and the state feedback control input in Equation (58) are applied to the system in Equation (39) with the adaptive laws in Equations (44) and (59) along with the aforementioned adaptive switching strategy, then the uncertain system in Equation (39) is globally asymptotically stable while the full-state constraints are not violated.

Proof. 

The proof of Theorem 2 is similar to that of Theorem 1. Therefore, it was omitted here to avoid duplication. □

Remark 5. 

In adaptive stabilization control, the viscous friction term can be considered since it is linearly dependent on the physical parameters. For example, let us consider the model of viscous friction to be $F_r=f_{r0}tanh(\dot{x}/\xi )-f_{r1}\left|\dot{x}\right|\dot{x}$. Then, this friction can be rewritten into a compact form ${\psi }^T\theta$ with $\psi =[tanh(\dot{x}/\xi ),|\dot{x}{\left|\dot{x}\right]}^T$ and $\theta ={[f_{r0},f_{r1}]}^T$, which can be treated with the proposed adaptive stabilization control approach.

4. Simulation Results

In this part, we will demonstrate the effectiveness of the systematic stabilization control law design methods proposed above through two examples.

Example 1. 

The first considered example is the tricycle-type mobile robot with parametric uncertainty [4]:

$$\begin{array}{ccc}\hfill {\dot{x}}_c& =& p_1^{★}vcos\left(\theta \right)\hfill \\ \hfill {\dot{y}}_c& =& p_1^{★}vsin\left(\theta \right)\hfill \\ \hfill \dot{\theta }& =& p_2^{★}\omega \hfill \end{array}$$

(64)

where $(x_c,y_c)$ represents the coordinate of the mass center, θ represents the heading angle, v and ω stand for the forward linear velocity and the angular velocity, respectively, and the parameters $p_i^{★}$ $(i=1,2)$ take values in a known interval $[p_{\min },p_{\max }]$ with $0<p_{\min }<p_{\max }<\infty$.

Next, we will show that the system in Equation (64) can be transformed into an equivalent system characterized by Equation (1), subject to Assumptions 1 and 2. Now, under the following state and input transformations

$$\begin{array}{ccc}\hfill x_0& =& \theta \hfill \\ \hfill x_1& =& x_{c}sin\left(\theta \right)-y_{c}cos\left(\theta \right)\hfill \\ \hfill x_2& =& x_{c}cos\left(\theta \right)+y_{c}sin\left(\theta \right)\hfill \\ \hfill u_0& =& \omega \hfill \\ \hfill u_1& =& v,\hfill \end{array}$$

(65)

the system in Equation (64) is reformulated as

$$\begin{array}{ccc}\hfill {\dot{x}}_0& =& p_2^{★}{u}_0\hfill \\ \hfill {\dot{x}}_1& =& p_2^{★}{x}_2{u}_0\hfill \\ \hfill {\dot{x}}_2& =& p_1^{★}{u}_1-p_2^{★}{x}_1{u}_0,\hfill \end{array}$$

(66)

which belongs to the type from Equation (1). Assume that $x_0\left(0\right)\ne 0$. By applying the controller design in Section 2.1 and Section 2.2, we have

$$\begin{array}{ccc}\hfill u_0& =& -k_0{x}_0\hfill \\ \hfill u_1& =& -\frac{1}{p_{\min }}{\xi }_2(1+{\omega }_{21}+{\omega }_{22}+{\omega }_{23})(k_2^2-{\xi }_2^2)\hfill \end{array}$$

(67)

where $z_1=x_1/x_0$, $z_2=x_2$, ${\xi }_1=z_1$, ${\xi }_2=z_2-z_1{\chi }_1$, ${\chi }_1=2(k_1^2-z_1^2)/\left(k_0{p}_{\min }\right)$, $f_1=({\chi }_1+(1+z_1^2)(1+16z_1^2/\left(k_0^2{p}_{\min }^2\right)))k_0{p}_{\max }$, $f_2=({\chi }_1+(1+z_1^2)(1+16z_1^2/\left(k_0^2{p}_{\min }^2\right)))k_0{p}_{\max }{\chi }_1$, ${\omega }_{21}=3k_0^2{p}_{\max }^2/\left(4{(k_1^2-z_1^2)}^2\right)$, ${\omega }_{22}=3k_0^2{p}_{\max }^2{x}_0^4/\left(4{(k_2^2-{\xi }_2^2)}^2\right)$, and ${\omega }_{23}=f_1/(k_2^2-{\xi }_2^2)+3f_2^2/\left(4{(k_2^2-{\xi }_2^2)}^2\right)$.

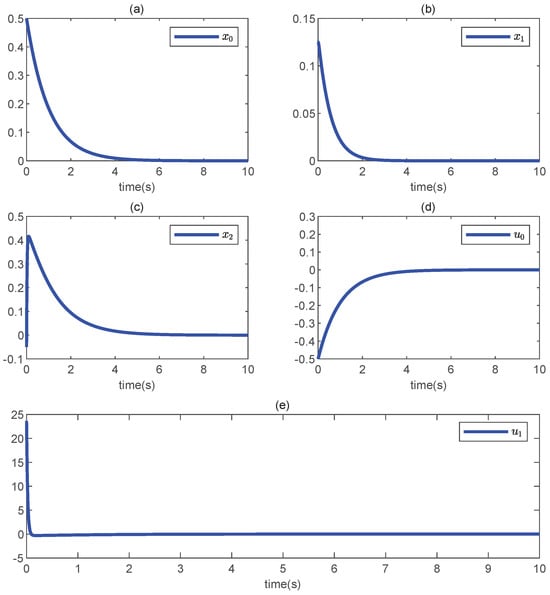
To proceed with the simulation, the system parameters were chosen to be $p_1^{★}=1$, $p_2^{★}=1$, $p_{\min }=1.5$, and $p_{\max }=2$. The control design parameters were configured to be $k_0=1$, $b_1=1$ $k_1=1$, and $k_2=2$. The initial conditions were designed to be $x_0\left(0\right)=0.5$, $x_1\left(0\right)=0.125$, and $x_2\left(0\right)=-0.05$. The simulation results are provided in Figure 2. After a careful look at all the subgraphs in Figure 2, all the closed-loop system signals converged to zero as the time approached infinity. Obviously, the desired state constraints were not violated since all system states decayed to zero with no fluctuation. The simulation results are consistent with the theoretical analysis.

Figure 2. The responses of the closed-loop system (66). (a) $x_0\left(0\right)=0.5$, (b) $x_1\left(0\right)=0.125$, (c) $x_2\left(0\right)=-0.05$, (d) $u_0$ is the system control inputs, (e) $u_1$ is the system control inputs.

Example 2. 

To illustrate the validity of the adaptive stabilization control law, we consider the following numerical example:

$$\begin{array}{ccc}\hfill {\dot{x}}_0& =& u_0+x_0\theta \hfill \\ \hfill {\dot{x}}_1& =& x_2{u}_0+x_1\theta \hfill \\ \hfill {\dot{x}}_2& =& u_1\hfill \end{array}$$

(68)

where ${(x_0,x_1,x_2)}^T$ is the system state vector, θ denotes the unknown parameter, and $u_0$ and $u_1$ are the system control inputs. By applying the controller design in Section 3.1 and Section 3.2, one has

$$\begin{array}{ccc}\hfill u_0& =& -x_0{\widehat{\theta }}_0-x_0\sqrt{k_0^2+{\widehat{\theta }}_0^2}=x_0{d}_0\left({\widehat{\theta }}_0\right)\hfill \\ \hfill {\dot{\widehat{\theta }}}_0& =& \frac{{\rm Y}{x}_0}{b_1^2-x_0^2}\hfill \\ \hfill {\omega }_2& =& -\frac{z_1(-{\beta }_1{k}_1^2+3{\beta }_1{z}_1^2+d_0+\widehat{\theta })}{d_0\left({\widehat{\theta }}_0\right)}\hfill \\ \hfill {\tau }_1& =& -\frac{\Gamma {\xi }_1{z}_1}{k_1^2-{\xi }_1^2}\hfill \\ \hfill {\tau }_2& =& {\tau }_1+\frac{\Gamma {\xi }_2{\omega }_2}{k_2^2-{\xi }_2^2}\hfill \end{array}$$

$$\begin{array}{ccc}\hfill u_1& =& -{\beta }_2{\xi }_2(k_2^2-{\xi }_2^2)-d_0\left({\widehat{\theta }}_0\right)\frac{{\xi }_1(k_2^2-{\xi }_2^2)}{k_1^2-{\xi }_1^2}-{\omega }_2\widehat{\theta }\hfill \\ & & -\frac{{\beta }_1{\xi }_1(k_1^2-z_1^2)}{{\left({\widehat{\theta }}_0+\sqrt{k_0^2+{\widehat{\theta }}_0^2}\right)}^2}\left(1+\frac{{\widehat{\theta }}_0}{\sqrt{k_0^2+{\widehat{\theta }}_0^2}}\right)\frac{{\rm Y}{x}_0}{b_1^2-x_0^2}\hfill \\ & & +(d_0\left({\widehat{\theta }}_0\right)+\widehat{\theta }+3{\beta }_1{z}_1^2-{\beta }_1{k}_1^2)(z_2-z_1)+\frac{z_1{\tau }_2}{d_0\left({\widehat{\theta }}_0\right)}\hfill \\ \hfill \dot{\widehat{\theta }}& =& {\tau }_2\hfill \end{array}$$

(69)

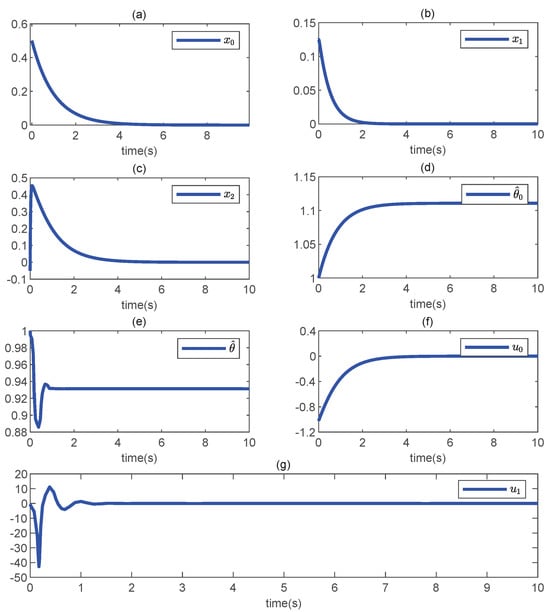
where $z_1=x_1/x_0$, $z_2=x_2$, ${\xi }_1=z_1$, ${\xi }_2=z_2-z_2^{*}$, and $z_2^{*}=(-{\beta }_1(k_1^2-{\xi }_1^2)+d_0\left({\widehat{\theta }}_0\right)z_1+z_1\widehat{\theta })/d_0\left({\widehat{\theta }}_0\right)$. For the simulation, we chose $k_0=0.3$, $k_1=0.4$, $k_2=2$, $b_1=2$, ${\beta }_1=0.1$, ${\beta }_2=2$, ${\rm Y}=1$, $\Gamma =1$, and $\theta =1$. The initial system conditions were designed to be $x_0\left(0\right)=0.5$, $x_1\left(0\right)=0.125$, $x_2\left(0\right)=-0.05$, ${\widehat{\theta }}_0\left(0\right)=1$, and $\widehat{\theta }\left(0\right)=1$. The simulation results are shown in Figure 3. From Figure 3, it can be easily seen that the closed-loop system signals tended toward zero as $t\to \infty$. Meanwhile, the adaptive law converged to its own steady state. In addition, the desired state constraints were also not violated, since all system states decayed to zero with no fluctuation. The simulation results are satisfactory in terms of work efficiency.

Figure 3. The responses of the closed-loop system (68). (a) $x_0\left(0\right)=0.5$, (b) $x_1\left(0\right)=0.125$, (c) $x_2\left(0\right)=-0.05$, (d) ${\widehat{\theta }}_0\left(0\right)=1$, (e) $\widehat{\theta }\left(0\right)=1$, (f) $u_0$ is the system control inputs, (g) $u_1$ is the system control inputs.

5. Conclusions

Two recursive BLF techniques have been developed for the stabilization control for a strict-feedback nonholonomic system. It is crucial to mention that the designed stabilization control techniques are analytically simple and guarantee that the system states can be regulated to zero asymptotically while the full-state constraints are not violated. The validity of the stabilization control strategies is illustrated through two examples of chained-form nonholonomic systems, namely the tricycle-type mobile robot with parametric uncertainty and a numerical example.