Abstract
In this study, confined slot nano-jet impingement cooling of a hot moving surface is investigated under the combined utilization multiple rotating cylinders and magnetic field. Both convective heat transfer and entropy generation analysis are conducted using a finite element method. Parametric variation of the rotational Reynolds number (Rew between −500 and 500), velocity ratio (VR between 0 and 0.25), Hartmann number (Ha between 0 and 20) and the horizontal location of cylinders (Mx between −8 and 8) are considered. Rotation of the cylinders generally resulted in the degradation of cooling performance while increasing the wall velocity, and the horizontal location of the cylinder was found to positively contribute to this. Heat transfer rate reductions of 20% and 12.5% are obtained using rotations at the highest Rew for the case of stationary (VR = 0) and moving wall (VR = 0.25). When magnetic field at the highest strength is imposed in the rotating cylinder case, the cooling performance is increased by about 18.6%, while it is reduced by about 28% for the non-rotating cylinder case. The hot wall movement contributes, by about 14%, to the overall cooling performance enhancement. Away from the inlet location of the rotating cylinders, thermal performance improvement of 12% is obtained. The entropy generation rises with higher hot wall velocity and higher horizontal distances of the rotating cylinders, while it is reduced with a higher magnetic field for non-rotating cylinders. The best configurations in terms of cooling performance provide 8.7% and 34.2% enhancements for non-rotating and rotating cylinders compared with the reference case of (Rew, VR, Ha, Mx) = (0, 0, 0, 0), while entropy generation becomes 1% and 15% higher.
Keywords:
magnetic field; slot jet impingement; finite element method; multiple rotating cylinders; entropy generation; moving wall MSC:
76D25; 76D55; 80M10; 80M50; 76S05
1. Introduction
The use of impinging jets has been considered for effective cooling in many thermal applications, including solar power, drying, electronic cooling and materials processing such as glass annealing, among others [1,2,3]. Higher localized heat and mass transfer coefficients can be obtained by using impinging jets. The flow features and basic heat transfer (HT) mechanism by using impinging jets have been provided with important design and operating parameters [4,5,6]. Due to the complicated nature of the flow field and its interaction with the thermal field, complex geometry and pressure gradients, theoretical treatment of the convective HT with impinging jets is challenging. Magnetic field (MGF) in jet impingement has been considered in several studies. The applications in jet flow with MGF may be relevant in electromagnetic braking. The utilization of MGF in convective HT has been considered in many studies as HT and flow control method. An external MGF, which may be active, partial, non-uniform or time dependent, can be imposed for thermal system and several studies used MGF in slot jet impingement (SJ-I) HT applications. The performance of the SJ-I cooling can be improved by using nanofluids (NFs). This technology of NFs has already been implemented in diverse engineering systems, including energy storage, refrigeration, renewable energy and many more [7,8,9]. For electrically conducting fluids, nanoparticles can be used in base fluid to alter the thermophysical properties, including thermal and electrical conductivity, while application of MGF will be more efficient. Sheikholeslami and Rokni [10] performed a review for application of NFs in the existence of MGF effects by analyzing many numerical and analytical studies. They also considered the Brownian motion and thermophoresis effects of NFs. Improvements in the thermal performance were reported with NFs while discrepancies between single and two-phase models were noted. M’hamed et al. [11] performed an extensive review of the application of MGF considering NFs. They noted successful application of the flow control with MGF, while some challenges were also mentioned, such as the stability and cost of using NFs. In jet impingement, NFs have been used. In their review work, [12] analyzed the existing studies for NF applications in impinging jet HT. Many aspects of the NF were covered, including non-Newtonian fluid behavior and single- and two-phase modeling approaches. They noted that single-phase non-Newtonian models required higher pumping power even if they had higher HT rates. They recommended considering the application of hybrid NFs, multiphase model and erosion impacts of NFs in jet impingement applications. Even though diverse studies have been considered for the application of NF in jet impingement HT [13,14,15], there are few works that have considered the MGF and NF impacts with jets together [16,17,18].
Many different methods of HT enhancement have been considered in J-I cooling. MGF and NF applications have been discussed above. The utilization of rotating circular cylinders (CCs) in HT has been considered before in many studies. The size, rotational speed, conductivity ratio and location of the CCs are some of the most influencing factors for the overall thermal performance [19,20,21]. In J-I systems, cooling of rotating hot surfaces has been considered in several studies [22,23,24], but rotating CCs as a control method for cooling performance of SJ-I onto a hot flat surface has only been considered in [25].
Entropy generation analysis (EG-A) can be used in thermal system for performance evaluations and design optimizations. The basics and some applications of EG minimization can be found in several sources [26,27,28]. The HT and fluid friction irreversibility analysis can be performed by using EG studies in convective HT. EG-A have been considered in NF studies [29,30,31]. A review of EG in NF systems has been performed by Mahian et al. [32]. They considered different NF and various geometry with different boundary conditions. They noted that the EG can be reduced by using NF depending upon the geometry and flow regime while in viscous dominated micro-channels, and using NFs resulted in increased EG. In another review, Huminic and Huminic [33] presented an overview of the NF and hybrid NF applications for EG of different thermal systems. Micro-channel flow and cavities were considered while both experimental and numerical studies were covered. The potential of using NFs in EG minimization was explored. In MGF with NF, EG-A has been been performed in many different studies [34,35,36].
In this study, slot J-I (SJ-I) cooling of moving hot surface under the combined effects of using MGF and multiple rotating CCs are considered. The combined method can be considered either as a novel HT enhancement technique for SJ-I or rotating CCs or MGF can be present in the thermal system. In the literature, utilization of MGF and NF together has been considered in several studies, while only one study exists for a single rotating CC in SJ-I cooling. As novel contributions to the exiting literate, multiple rotating CCs are used, and movement of the hot surface to be cooled is considered along with the MGF and NF. The study also includes EG analysis for the evaluation of system performance. Figure 1 shows the schematic view of the available HT enhancement methods that can be used for J-I cooling system with the jet and wall features considered in this study. The coupled impacts of moving wall, rotation of multiple CCs and MGF will be explored for cooling of an isothermal hot surface by using confined SJ-I. Performance of the system for varying parameters of interest is indicated in terms of EG, which results in higher possibility to assess the system performance. The outcomes of the current work are useful in initial design and optimization studies for development of cooling systems with SJ-I. The applications can be encountered in microfluidic devices, photovoltaic (PV) /thermal systems, material processing, drying and diverse HT equipment.
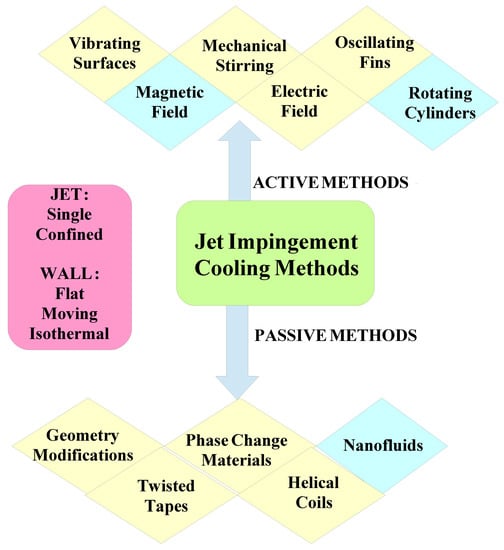
Figure 1.
Different available methods that can be used for flow control and thermal performance improvement of jet impingement cooling.
2. Numerical Model
We consider SJ-I cooling of a hot moving wall under the combined utilization of three identical rotating CCs and inclined MGF effects. A schematic view is given in Figure 2. Cold fluid enters with velocity of uc and temperature of Tc, while a hot wall is moving with velocity uw and is kept at a temperature of Th. Velocity ratio (VR) is defined as VR = uw/uc. The slot size is wj, and the hot plate length is L = 150wj and the vertical distance between them is H = 7wj. The rotating CCs are identical and have radius of r = 0.1H and are rotating with same speed of . Their center locations are (xc1, yc1) = (0.5L + Mx, 0.35H), (xc2, yc2) = (0.5L + Mx + 0.6H, 0.35H) and (xc3, yc3) = (0.5L + Mx + 0.3H, 0.65H). An external uniform MGF is imposed with inclination of with horizontal. The hybrid NF, which contains Ag–MgO nanoparticles in water, is utilized while the solid volume fraction of is considered. The Pr of the base fluid is 6.9. The flow is 2D and laminar. The MGF is uniform, and induced MGF effects along with the electric currents are not taken into account. The impacts of natural convection, radiation and viscous dissipation are ignored.
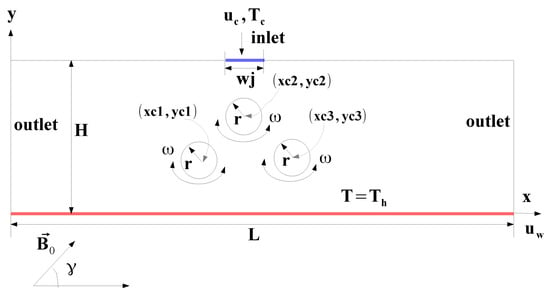
Figure 2.
Schematic description of the SJ-I cooling system for a moving hot wall under combined effects of MGF and multiple rotating CCs.
The conservation equations under the above assumptions are:
The related non-dimensional parameters and numbers are:
where is the characteristic length.
In the above representation, , and .
In dimensional form, the boundary conditions are given as:
- Jet inlet,
- Outlet:
- At the target plate:
- Upper plate walls:
- At the rotating cylinder walls:
Local and average Nusselt numbers (Nu) are used for thermal performance evaluations, which are given as:
The EG equation is stated as in the following:
where impacts of HT, viscous dissipation and MGF effects are represented by various terms in the above equation.
The Galerkin weighted (GW) residual finite element method (R-FEM) is employed as the solution method. The application of FEM and basic steps in modeling for HT and flow problems can be found in many sources [37,38]. The FEM-based solution of convective HT problems including SJ-I cooling has been considered in many studies [39,40,41]. In the method, the field variables (f) are approximated by using different ordered Lagrange finite elements as in the following:
where denotes the shape function and F is the nodal value. The weighted average of the resulting residual (R) is set to be zero as:
SUPG method is used to handle the numerical instability while BICGStab is considered for the flow and HT modules of the code. The convergence of the solution is assumed when the relative error for each of the variables satisfy convergence criteria of .
Grid independence test results are shown in Figure 3a considering average Nu variations with different grid sizes at two different rotations of CCs (Rew = 0 and Rew = −500). A grid with 470,870 number of triangular elements is selected, and its variation in the domain near the CCs is given in Figure 3b. Near-wall refinement is performed.
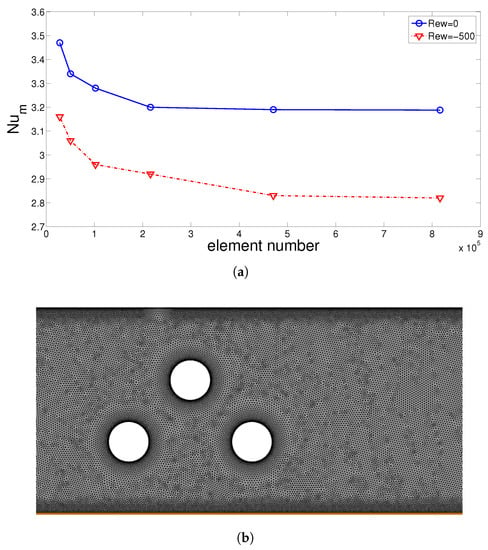
Figure 3.
Test results for grid independence: Average Nu for different grid sizes considering rotating and non-rotating CCs (a) (Ha = 5, Mx = −1) and grid distribution near the CCs (b).
Validation of the code is performed by using different available studies. In the first work, convection in a differentially cavity under MGF effects is analyzed. Comparison results of average Nu at three different MGF strength are shown in Figure 4a by using the available results in [42]. The value of the Grashof number is fixed to while Ha values of 0, 50 and 100 are taken. The highest difference is seen at Ha = 0, and it is below 5%. For SJ-I cooling, the results available in [43,44] are used. An isothermal plate is considered while Re values of 100 and 300 are taken. The maximum difference between the available results is below 4% (Figure 4b). The MGF effects in convection and SJ-I cooling effects are accurately captured by using the current solver.
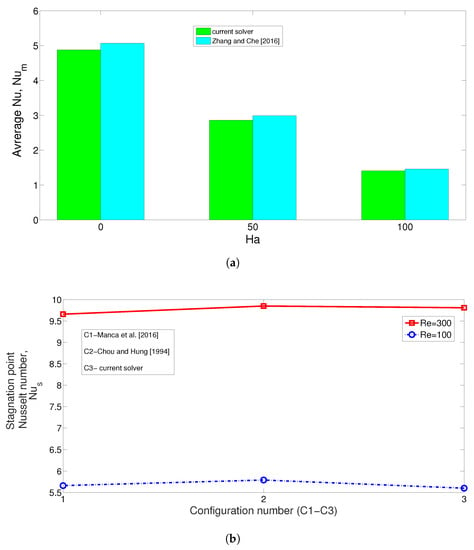
Figure 4.
Code validation 1: Average Nu comparisons at three different Ha considering the convection in a differentially heated enclosure. Results in [42] are used, and Grashof number is fixed to Gr = (a). Code validation 2: Stagnation point Nu comparison for SJ-I cooling of an isothermal surface by using the reference results in [43,44] at Reynolds number 100 and 300 (b).
3. Results and Discussion
Convective HT and EG analysis for confined SJ-I cooling of a moving hot surface under the combined effects of using MGF and triple rotating CCs is conducted. The CCs are identical and rotating at the same speed, while the hot wall is moving with constant speed. The numerical study is conducted for various values of rotational speed of the CCs (Rew between −500 and 500), velocity ratio (VR between 0 and 0.25), MGF strength (Ha between 0 and 20) and horizontal distance of the rotating CCs to the jet entrance (Mx between −8 and 8). EG-A is also conducted for the varying parameters of interest. Hybrid nanoparticles volume fraction is considered as .
Figure 5 shows the impacts of rotational speeds of the CCs on the streamline variation at two different velocity of the hot wall. In the case of non-moving wall and without the activation of the CCs, vortices form near the inlet due to confinement and entrainment, while the right vortex is smaller in size due to the existence of the CC. A large elongated vortex near the right CC is formed, which extends toward the upper plate. When the CCs start to rotate with higher speeds, the sizes of the inlet region vortices are reduced, while vortices near the left and right CC on the bottom wall are established, and their sizes increase with higher speeds. When the hot bottom wall moves in +x direction without rotation of the CCs, a large vortex on the left bottom wall is formed. When the value of Rew is increased, this vortex zone expands in vertical direction while suppression of the inlet vortices with rotations of the CCs is obtained with higher Rew. Due to the wall movement, no vortex is formed on the right part of the inlet near the bottom wall which exists at VR = 0.
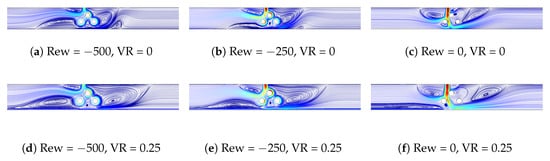
Figure 5.
Effects of Rew on streamline variations considering two different velocities of hot wall (Ha = 5, Mx = −1).
Impacts of hot bottom wall velocity on the flow pattern distribution are shown in Figure 6 for two cases of CCs. In the case of non-rotating CCs, on the left part of the bottom wall, a large elongated vortex is formed with higher values of VR. This is attributed to the higher velocity of the hot wall, which induces drag force on the fluid while the flow field is distorted. A vortex is also formed below the left CC, and this region becomes larger with higher VR. When rotations become active, the existence of this elongated vortex on the left part is also seen due to the hot wall movement. Some slight modifications of the vortices near the upper CCs are observed. At highest speed wall velocity (VR = 0.25), rotation of the cylinders results in formation of the large vortices near the right CC adjacent to top wall, while the vortex near the left CC extends in size. The inlet vortex on the left part elongates toward the left due to the rotations of the CCs. Characteristics of the HT are seen in Figure 7 considering the variation of average Nu with respect to changes in Rew and VR. The rotation of the CCs results in reduction of HT performance for CW rotations of the CCs for both stationary (VR = 0) or moving wall (VR = 0.25) cases. In the case of VR = 0, the reduction amount becomes 20%, while it is 12.5% at VR = 0.25 when configurations with rotations CCs at Rew = −500 are compared with the case of non-rotating CCs. The impact of rotation on the HT reduction becomes lower with movement of the hot wall due to the increased HT. When CCW rotations are considered, there is 10% reduction at VR = 0.25, while it becomes 2% increment at VR = 0 when configuration of non-rotating (Rew = 0) and rotating CCs at Rew = 500 are compared. The wall velocity is small compared with the jet velocity, whereas the shear-driven impacts due to wall movement are not significant when the rotations of the CCs are the determining factors. When VR is increased, the average Nu becomes higher for the case of rotating or non-rotating CCs. In both cases, the movement of the wall at the highest velocity contributes 14% increment in the average Nu compared with the stationary wall configuration.
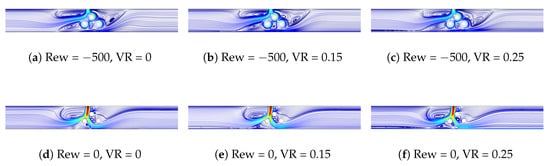
Figure 6.
Effects of hot wall velocity on streamline variations for rotating and non-rotating CC cases (Ha = 5, Mx = −1).
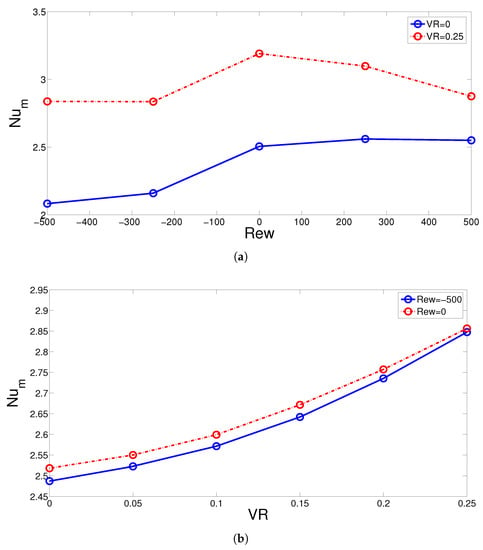
Figure 7.
Average Nu versus Rew (a) and versus VR (b) (Ha = 5, Mx = −1).
The impacts of MGF strength on streamline variations are shown in Figure 8a–h considering both rotating and non-rotating CC cases. When CCs are not rotating (Rew = 0) at Ha = 0, large vortices near the bottom wall (left part), near the right CC on the top wall and near the inlet are established. When MGF strength is increased to Ha = 5, the top and bottom wall vortices are significantly suppressed while at the highest MGF strength (Ha = 20), and most have disappeared. Similar observations can be made with higher MGF strength when the rotations of the CCs become active. In the case of no MGF, two large elongated vortices are formed in the left and right part of the bottom wall that result from the combined utilization of rotation and movement of the hot wall. As the Ha value is increased, the extent of this vortex is largely suppressed. The suppression of vortices due to the complex interaction of the SJ-I, shear effects due to the wall movement and rotation of the CCs are seen by imposing the MGF and increasing its strength. The HT behavior shows different characteristics when imposing the MGF effects depending upon if the rotations are active or not. When the rotations of the CCs are not considered, reduction of the HT is seen until Ha = 10, and after this Ha, it is slightly varying. The amount of HT reduction becomes 28% until Ha = 10 at Rew = 0 (Figure 8i). However, when rotations become active at Rew = −200, the average Nu rises by about 18.6% by increasing the MGF strength at Ha = 5. Further increment of MF strength has little influence on the variation of average Nu. As the rotations of the CCs are activated, the average Nu values are higher until Ha = 10 compared with the non-rotating cylinder case and then become almost identical after this value until Ha = 20. This is attributed to the rotations of the cylinders, which deflect the fluid flow toward the upper wall in the left region of the inlet while effective impinging to the hot wall is hindered. When MGF is used for rotating case, the amount of deflection of this fluid flow toward the upper wall becomes reduced.
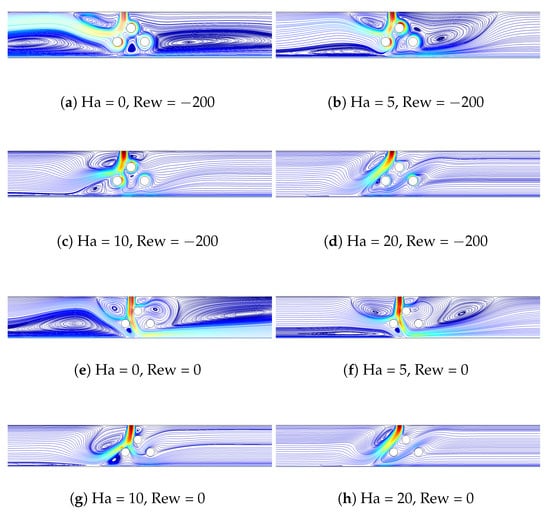
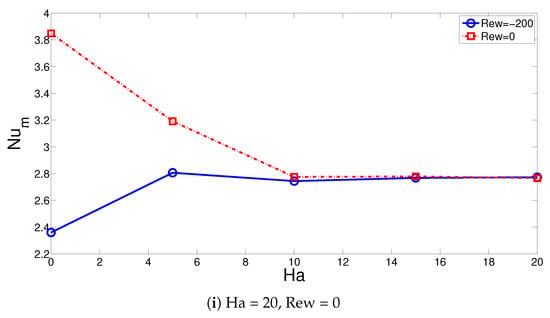
Figure 8.
Impacts of MGF strength on the streamline distributions considering rotating (a–d), non-rotating CC cases (e–h) and on the average Nu variations (i) (VR = 0.25, Mx = −1).
The horizontal location of the multiple rotating CCs influence on the flow patterns, as shown in Figure 9a–f considering rotating and non-rotating CCs. When the rotating CCs are away from the inlet jet, large recirculations are formed near the inlet while effective impinging of the jet onto the hot moving plate is obtained. When the rotating CCs are near the inlet jet, due to the rotations of the CCs, inlet vortices are damped out and mechanism of the HT is mainly due to the rotating effects of CCs in contrast to jet impingement HT. When rotations are not used at location Mx = 0, the deflection of the impinging jet on the hot surface is seen due to the presence of stationary bottom cylinder, while below it, a small vortex is established. Average Nu versus location (Mx) of the CCs is shown in Figure 9g. The horizontal location closer to the inlet results in lower HT rates when rotations are active at Rew = −500. Higher Nu values are obtained when the rotating CCs become way from the inlet in horizontal direction. Compared with the case of Mx = 0, average Nu enhancements of 12% and 7.5% are obtained for cases with locations of Mx = −8 and 8. For both rotating and non-rotating CC case, the location of Mx = −2 provides the lowest value of average Nu, where the upper CC is just located below the inlet jet and horizontal distance between the cylinder center and jet center becomes 0. A sudden increment in average Nu is seen when the rotations are not active if Mx is increased from Mx = −2 to Mx = 0, which is not the case with rotations of the CCs due to the rotational effects that hinder the effective impingement of cold fluid onto the hot surface.
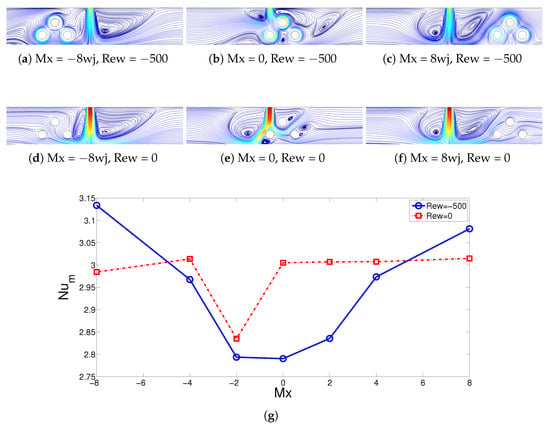
Figure 9.
Variations of streamlines with changes in the horizontal location of the multiple CCs considering rotational (a–c) and stationary (d–f) cases of CCs and impacts of horizontal location of CCs on the variation of average Nu considering rotating and non-rotating CC cases (g) (Ha = 5, Mx = −1).
EG-A is also considered for the SJ-I problem under combined effects of rotational CCs and MGF. Variations of normalized EG with respect to changes rotational speed of the CCs (Rew) and hot wall velocity (VR) are given in Figure 10. As the velocity of the hot wall is not significant, the shear-driven effects due to wall movement are not profound. The SG values show the dominance of HT irreversibility, while EG generation achieves the minimum value when non-rotating CC case is considered. Higher velocities of the moving wall result in higher entropy production due to the higher HT and viscous irreversibility. At the highest VR, the discrepancy between the rotating and non-rotating increases. The EG rises by about 6.25%/ for non-rotating/rotating cases when comparing the moving wall case (VR = 0.25) with the stationary wall case (VR = 0). The reductions of the EG by activation of rotations in CW direction of the CCs at the highest speed become 18.5% and 16.5% for cases of VR = 0 and VR = 0.25. Depending upon whether the rotations are active or not, the EG shows different behavior with higher MGF strength. For stationary CCs, EG is reduced by about 23% at the highest MGF strength, while it is increased by about 66% for non-stationary CCs at Rew = −200. The behavior shows similar trends as in the average Nu variations due to the higher irreversibility in the HT, as the wall velocity is not significant. The location of the rotating CCs closer to the inlet position in horizontal direction produces less entropy, while for both cases the EG rises with higher Mx (Figure 11).
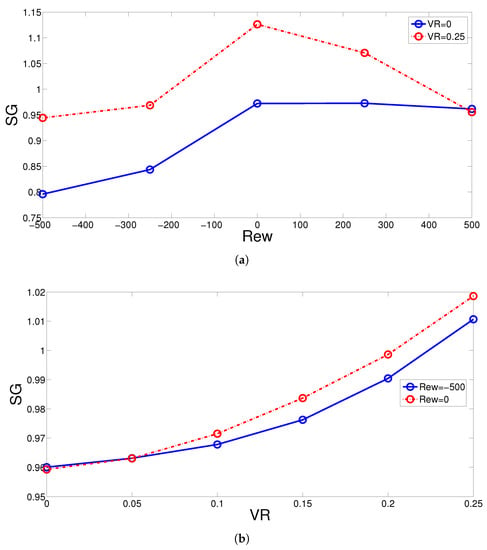
Figure 10.
Impacts of rotational Re on the variation of EG for stationary (VR = 0) and moving wall (VR = 0.25) cases (a) and impacts of VR on EG for rotating (Rew = −500) and non-rotating CC cases (Rew = 0) CC cases (b) (Ha = 5, Mx = −1).
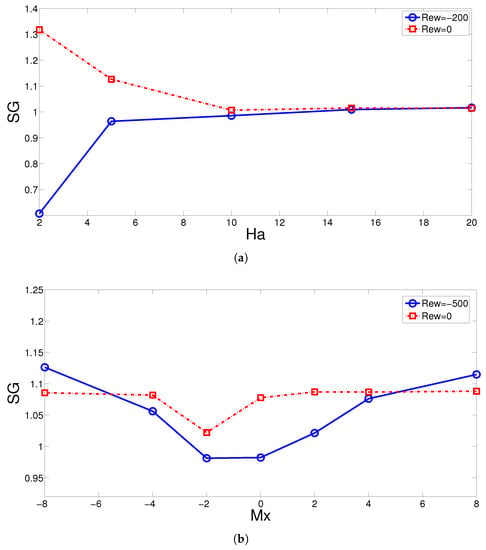
Figure 11.
Effects of MGF strength (a) horizontal location of the CCs (b) on the variation of EG considering rotating and non-rotating CC cases (VR = 0.25, Mx = −1).
A summary of different cases in terms of thermal performance and production of entropy is shown in Figure 12. Case 1 (C1) shows the reference configuration for the set of parameters (Rew = 0, VR = 0, Ha = 0, Mx = 0) where non-rotating CCs with stationary hot wall is considered without MGF effects. When rotations are active at Rew = −500, the best case is obtained for (Ha, VR, Mx) = (0, 0.25, −4wj), while thermal performance improvement becomes 8.7%, and without rotation, improvement of up to 34.2% is obtained at (Ha, VR, Mx) = (20, 0.25, −8wj). When no cylinders are installed in the SJ-I system, thermal performance improvements of 14.2% and 5.9% are obtained compared with the reference case at Ha = 0 and Ha = 20. When EG performances are compared, the highest EG is obtained for case 3, which is 15% higher than the reference case. Case 2 has only 1% higher EG than the reference case. When movement of the wall is not considered, even without installation of CCs, the EG becomes higher either with (Ha = 20) or without MGF effects (Ha = 0).
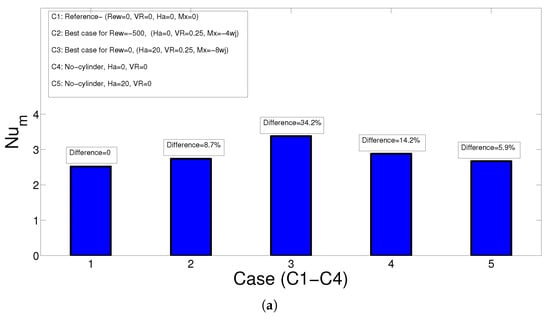
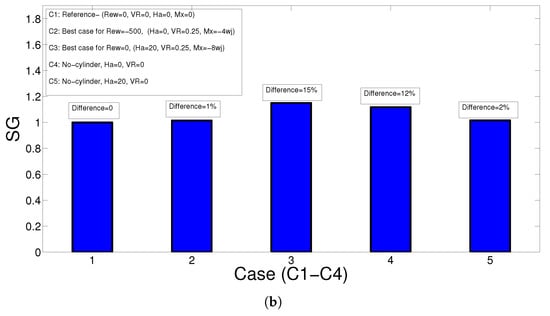
Figure 12.
Comparison of best cases in terms of thermal performance (a) and EG (b) considering both rotating and non-rotating CC case.
4. Conclusions
Convective HT and EG analysis of a SJ-I cooling system for a moving hot wall was conducted under the combined utilization of MGF effects and multiple rotating CCs. Some of the important outcomes can be listed as:
- Rotations of the CCs near the jet inlet have negative impacts of the HT enhancement for both stationary and moving hot wall cases. Reductions in the average Nu of up to 20% and 12.5% are obtained by using rotations at Rew = −500 for stationary (V = 0) and moving wall (VR = 0.25) cases.
- The wall movement contributes positively to the cooling performance while HT enhancements up to 14% are achieved by wall velocity at the highest speed (VR = 0.25).
- Depending upon the activation of cylinder rotations, the impacts of MGF strength on the HT characteristics are different. For non-rotating CCs, cooling performance is reduced by about 28% until Ha = 10, while by using rotations at Rew = −200, it is increased by about 18.6%.
- For the rotating CC case, average Nu variations up to 12% can be achieved by varying the horizontal location of the CCs while away from the inlet, higher cooling performances are obtained.
- When the hot wall starts to move at VR = 0.25, the EG increments up to 6.25% and are obtained for non-rotating and rotating CC cases compared with the stationary wall (VR = 0) configuration.
- The MGF acts to reduce the EG by about 23% for non-rotating cylinders while increment of EG by about 66% is obtained for rotating cylinders at Rew = 200. Away from the jet inlet, the EG rises.
- The best configuration for the case of non-rotating CCs is achieved at (Ha, VR, Mx) = (0, 0.25, −4), and HT increment becomes 8.7% compared with the reference case of (Rew = 0, VR = 0, Ha = 0, Mx = 0). For the non-rotating CC case, the optimum set of parameters is achieved at (Ha, VR, Mx) = (20, 0.25, −8) with HT enhancement of 34.2% compared with the reference.
- The maximum EG is obtained for configuration with (Ha, VR, Mx) = (20, 0.25, −8) with non-rotating CCs, while the value is 15% higher than the reference case. When rotations are active at Rew = −500, the case (Ha, VR, Mx) = (0, 0.25, −4) has only 1% higher EG when compared to reference.
Author Contributions
Methodology, F.S. and K.G.; Software, L.K.; Validation, F.S., S.L., H.A. and B.M.A.; Formal analysis, F.S., K.G. and B.M.A.; Investigation, L.K., S.L. and T.L.; Writing—original draft, F.S.; Writing—review & editing, L.K., F.S., K.G. and H.A.; Visualization, T.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research project was funded by the Deanship of Scientific Research, Princess Nourah bint Abdulrahman University, through the Program of Research Project Funding After Publication, grant No (44- PRFA-P-16).
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| B | Magnetic field strength |
| Ha | Hartmann number |
| H | separating distance |
| h | heat transfer coefficient |
| k | thermal conductivity |
| L | plate length |
| n | unit normal vector |
| Nu | local Nusselt number |
| Nu | average Nusselt number |
| p | pressure |
| Pr | Prandtl number |
| r | cylinder radius |
| Re | Reynolds number |
| Rew | rotational Reynolds number |
| T | temperature |
| u, v | x-y velocity components |
| uc | jet velocity |
| uw | wall velocity |
| VR | velocity ratio |
| wj | slot width |
| x, y | Cartesian coordinates |
| Greek Characters | |
| thermal diffusivity | |
| magnetic field inclination | |
| non-dimensional temperature | |
| kinematic viscosity | |
| density of the fluid | |
| electrical conductivity | |
| solid volume fraction | |
| rotational speed | |
| Subscripts | |
| c | cold |
| h | hot |
| m | average |
| nf | nanofluid |
| w | wall |
References
- Javidan, M.; Moghadam, A.J. Experimental investigation on thermal management of a photovoltaic module using water-jet impingement cooling. Energy Convers. Manag. 2021, 228, 113686. [Google Scholar] [CrossRef]
- Bahaidarah, H.M. Experimental performance evaluation and modeling of jet impingement cooling for thermal management of photovoltaics. Sol. Energy 2016, 135, 605–617. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Coban, S.O.; Öztop, H.F. Comparative study and hybrid modeling approach with POD for convective drying performance of porous moist object with multi-impinging jet and channel flow configurations. Int. Commun. Heat Mass Transf. 2022, 132, 105897. [Google Scholar] [CrossRef]
- Jambunathan, K.; Lai, E.; Moss, M.; Button, B. A review of heat transfer data for single circular jet impingement. Int. J. Heat Fluid Flow 1992, 13, 106–115. [Google Scholar] [CrossRef]
- Webb, B.; Ma, C. Single-Phase Liquid Jet Impingement Heat Transfer. Adv. Heat Transf. 1995, 26, 105–217. [Google Scholar]
- Tyagi, P.K.; Kumar, R.; Mondal, P.K. A review of the state-of-the-art nanofluid spray and jet impingement cooling. Phys. Fluids 2020, 32, 121301. [Google Scholar] [CrossRef]
- Kakaç, S.; Pramuanjaroenkij, A. Single-phase and two-phase treatments of convective heat transfer enhancement with nanofluids–A state-of-the-art review. Int. J. Therm. Sci. 2016, 100, 75–97. [Google Scholar] [CrossRef]
- Pordanjani, A.H.; Aghakhani, S.; Afrand, M.; Mahmoudi, B.; Mahian, O.; Wongwises, S. An updated review on application of nanofluids in heat exchangers for saving energy. Energy Convers. Manag. 2019, 198, 111886. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Molana, M.; Rahnama, A.; Ghadami, F. On the nanofluids applications in microchannels: A comprehensive review. Powder Technol. 2018, 332, 287–322. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Rokni, H.B. Simulation of nanofluid heat transfer in presence of magnetic field: A review. Int. J. Heat Mass Transf. 2017, 115, 1203–1233. [Google Scholar] [CrossRef]
- M’hamed, B.; Sidik, N.A.C.; Yazid, M.N.A.W.M.; Mamat, R.; Najafi, G.; Kefayati, G. A review on why researchers apply external magnetic field on nanofluids. Int. Commun. Heat Mass Transf. 2016, 78, 60–67. [Google Scholar] [CrossRef]
- Mohammadpour, J.; Lee, A. Investigation of nanoparticle effects on jet impingement heat transfer: A review. J. Mol. Liq. 2020, 316, 113819. [Google Scholar] [CrossRef]
- Li, P.; Guo, D.; Liu, R. Mechanism analysis of heat transfer and flow structure of periodic pulsating nanofluids slot-jet impingement with different waveforms. Appl. Therm. Eng. 2019, 152, 937–945. [Google Scholar] [CrossRef]
- Manca, O.; Mesolella, P.; Nardini, S.; Ricci, D. Numerical study of a confined slot impinging jet with nanofluids. Nanoscale Res. Lett. 2011, 6, 188. [Google Scholar] [CrossRef] [PubMed]
- Yousefi-Lafouraki, B.; Ramiar, A.; Mohsenian, S. Entropy generation analysis of a confined slot impinging jet in a converging channel for a shear thinning nanofluid. Appl. Therm. Eng. 2016, 105, 675–685. [Google Scholar] [CrossRef]
- Nakharintr, L.; Naphon, P. Magnetic field effect on the enhancement of nanofluids heat transfer of a confined jet impingement in mini-channel heat sink. Int. J. Heat Mass Transf. 2017, 110, 753–759. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Öztop, H.F. Hybrid nano-jet impingement cooling of a curved elastic hot surface under the combined effects of non-uniform magnetic field and upper plate inclination. J. Magn. Magn. Mater. 2022, 561, 169684. [Google Scholar] [CrossRef]
- Hashemi-Tilehnoee, M.; del Barrio, E.P. Magneto laminar mixed convection and entropy generation analyses of an impinging slot jet of Al2O3-water and Novec-649. Therm. Sci. Eng. Prog. 2022, 36, 101524. [Google Scholar] [CrossRef]
- Roslan, R.; Saleh, H.; Hashim, I. Effect of rotating cylinder on heat transfer in a square enclosure filled with nanofluids. Int. J. Heat Mass Transf. 2012, 55, 7247–7256. [Google Scholar] [CrossRef]
- Costa, V.A.F.; Raimundo, A.M. Steady mixed convection in a differentially heated square enclosure with an active rotating circular cylinder. Int. J. Heat Mass Transf. 2010, 53, 1208–1219. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Öztop, H.F. Mixed convection in a PCM filled cavity under the influence of a rotating cylinder. Sol. Energy 2020, 200, 61–75. [Google Scholar] [CrossRef]
- Jiang, L.; Lyu, Y.; Zhu, P.; Gao, W.; Liu, Z. Numerical investigation of conjugate heat transfer on a rotating disk under round liquid jet impingement. Int. J. Therm. Sci. 2021, 170, 107097. [Google Scholar] [CrossRef]
- Lallave, J.C.; Rahman, M.M.; Kumar, A. Numerical analysis of heat transfer on a rotating disk surface under confined liquid jet impingement. Int. J. Heat Fluid Flow 2007, 28, 720–734. [Google Scholar] [CrossRef]
- Iacovides, H.; Kounadis, D.; Launder, B.E.; Li, J.; Xu, Z. Experimental study of the flow and thermal development of a row of cooling jets impinging on a rotating concave surface. J. Turbomach. 2005, 127, 222–229. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Öztop, H.F. Analysis and predictive modeling of nanofluid-jet impingement cooling of an isothermal surface under the influence of a rotating cylinder. Int. J. Heat Mass Transf. 2018, 121, 233–245. [Google Scholar] [CrossRef]
- Bejan, A. Fundamentals of exergy analysis, entropy generation minimization, and the generation of flow architecture. Int. J. Energy Res. 2002, 26. [Google Scholar] [CrossRef]
- Bejan, A. Entropy Generation Minimization: The Method of Thermodynamic Optimization of Finite-Size Systems and Finite-Time Processes; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Narayan, G.P.; Lienhard V, J.H.; Zubair, S.M. Entropy generation minimization of combined heat and mass transfer devices. Int. J. Therm. Sci. 2010, 49, 2057–2066. [Google Scholar] [CrossRef]
- Tayebi, T.; Dogonchi, A.S.; Karimi, N.; Ge-JiLe, H.; Chamkha, A.J.; Elmasry, Y. Thermo-economic and entropy generation analyses of magnetic natural convective flow in a nanofluid-filled annular enclosure fitted with fins. Sustain. Energy Technol. Assess. 2021, 46, 101274. [Google Scholar] [CrossRef]
- Ellahi, R.; Sait, S.M.; Shehzad, N.; Ayaz, Z. A hybrid investigation on numerical and analytical solutions of electro-magnetohydrodynamics flow of nanofluid through porous media with entropy generation. Int. J. Numer. Methods Heat Fluid Flow 2020, 30, 834–854. [Google Scholar] [CrossRef]
- Li, J.; Kleinstreuer, C. Entropy generation analysis for nanofluid flow in microchannels. J. Heat Transf. 2010, 132, 122401. [Google Scholar] [CrossRef]
- Mahian, O.; Kianifar, A.; Kleinstreuer, C.; Mohd A, A.N.; Pop, I.; Sahin, A.Z.; Wongwises, S. A review of entropy generation in nanofluid flow. Int. J. Heat Mass Transf. 2013, 65, 514–532. [Google Scholar] [CrossRef]
- Huminic, G.; Huminic, A. Entropy generation of nanofluid and hybrid nanofluid flow in thermal systems: A review. J. Mol. Liq. 2020, 302, 112533. [Google Scholar] [CrossRef]
- Aghakhani, S.; Pordanjani, A.H.; Afrand, M.; Sharifpur, M.; Meyer, J.P. Natural convective heat transfer and entropy generation of alumina/water nanofluid in a tilted enclosure with an elliptic constant temperature: Applying magnetic field and radiation effects. Int. J. Mech. Sci. 2020, 174, 105470. [Google Scholar] [CrossRef]
- Barnoon, P.; Toghraie, D.; Eslami, F.; Mehmandoust, B. Entropy generation analysis of different nanofluid flows in the space between two concentric horizontal pipes in the presence of magnetic field: Single-phase and two-phase approaches. Comput. Math. Appl. 2019, 77, 662–692. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Öztop, H.F.; Chamkha, A.J. MHD mixed convection and entropy generation of nanofluid filled lid driven cavity under the influence of inclined magnetic fields imposed to its upper and lower diagonal triangular domains. J. Magn. Magn. Mater. 2016, 406, 266–281. [Google Scholar] [CrossRef]
- Reddy, J.N.; Gartling, D.K. The Finite Element Method in Heat Transfer and Fluid Dynamics; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Lewis, R.W.; Nithiarasu, P.; Seetharamu, K.N. Fundamentals of the Finite Element Method for Heat and Fluid Flow; John Wiley & Sons: West Sussex, UK, 2004. [Google Scholar]
- Das, S.; Biswas, A.; Das, B. Numerical analysis of a solar air heater with jet impingement?comparison of performance between jet designs. J. Sol. Energy Eng. 2022, 144, 011001. [Google Scholar] [CrossRef]
- Froissart, M.; Ziółkowski, P.; Dudda, W.; Badur, J. Heat exchange enhancement of jet impingement cooling with the novel humped-cone heat sink. Case Stud. Therm. Eng. 2021, 28, 101445. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Kolsi, L.; Ayadi, B.; Aich, W.; Alresheedi, F.; Borjini, M.N. Jet impingement cooling using shear thinning nanofluid under the combined effects of inclined separated partition at the inlet and magnetic field. Eur. Phys. J. Spec. Top. 2022, 231, 2491–2508. [Google Scholar] [CrossRef]
- Zhang, T.; Che, D. Double MRT thermal lattice Boltzmann simulation for MHD natural convection of nanofluids in an inclined cavity with four square heat sources. Int. J. Heat Mass Transf. 2016, 94, 87–100. [Google Scholar] [CrossRef]
- Manca, O.; Ricci, D.; Nardini, S.; Di Lorenzo, G. Thermal and fluid dynamic behaviors of confined laminar impinging slot jets with nanofluids. Int. Commun. Heat Mass Transf. 2016, 70, 15–26. [Google Scholar] [CrossRef]
- Chou, Y.; Hung, Y. Impingement cooling of an isothermally heated surface with a confined slot jet. ASME Trans. J. Heat Transf. 1994, 116, 479–482. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).