Minimization of the Compliance under a Nonlocal p-Laplacian Constraint

Abstract

This work is an extension of the paper by Cea and Malanowski to the nonlocal and nonlinear framework. The addressed topic is the study of an optimal control problem driven by a nonlocal p-Laplacian equation that includes a coefficient playing the role of control in the optimization problem. The cost functional is the compliance, and the constraint on the states are of the Dirichlet homogeneous type. The goal of the present work is a numerical scheme for the nonlocal optimal control problem and its use to approximate solutions in the local setting. The main contributions of the paper are a maximum principle and a uniqueness result. These findings and the monotonicity properties of the p-Laplacian operator have been crucial to building an effective numerical scheme, which, at the same time, has provided the existence of optimal designs. Several numerical simulations complete the work.

1. Introduction

In recent decades, nonlocal modelization has been employed to solve a wide variety of problems in applied mathematics, and nowadays it is a very appealing alternative to classical methods. In the development of this type of modelling, it has been fundamental to dispose of a nonlocal vector calculus that has made it possible to obtain nonlocal representations of operators such as the gradient or the divergence (see [1,2]). Of particular interest is the application of nonlocal models to the study of certain phenomena in the field of mechanics, a fact that is evident in a large number of works (see for instance [3,4,5,6]). This type of formulation has been employed to model and solve classical differential equations where the aim is the approximation of solutions through the solutions of nonlocal models. Several papers have studied stationary configurations for a local classical problem by exploring the asymptotic behavior of the corresponding nonlocal or fractional equation. The reader may consult, among others, the pioneering works [1,7,8,9].

Another aspect to be taken into account is the way in which solutions to nonlocal problems are approximated. It has commonly been seen in the literature how, through numerical examples of problems such as the nonlocal fractional Laplacian problem (${\left(-\mathsf{\Delta }\right)}^s$ with $s\in \left(0,1\right)$), the usage of finite elements has provided meaningful results of existence and convergence. Moreover, it has been shown that by solving the nonlocal problem it is possible to obtain accurate approximations of the local problem. References of interest in this sense are [10,11,12,13,14,15]. Noteworthy is the work [16] in which, besides analyzing the fractional diffusion model involving the fractional Laplacian, the authors make an extensive discussion about different numerical methods that can be applied in the approximation of solutions of the nonlocal fractional diffusion model. In addition to the finite element method, they discuss the finite difference method and spectral methods. Concerning significant examples, in the reference [17], a large part of the most recent mathematical and computational developments applied to the analysis of nonlocal peridynamic models are collected.

A more specific issue is the nonlocal optimal design and its application to the numerical approximation of the underlying local optimal design problem. Searching for an approximate solution to a classical optimal design problem is a rather arduous task. This is mainly due to the requirements imposed on the formulation of the state equation and the set of admissibility. A broad overview of this issue can be found in the classical books [18,19,20,21]. The nonlocal framework can be proposed as an alternative to overcome some of these difficulties. One of the first works with this approach is [22]. This paper focuses on an optimal control problem in which the state equation is a nonlocal diffusion equation, the control is the source and a finite elements scheme is the tool employed to solve the heat transfer problem in a rod with a discontinuous conduction coefficient.

In the present paper, we deal with a problem of optimal distribution of conductivities in a nonlocal diffusion framework. We study a system governed by a nonlocal p-Laplacian equation containing a diffusion coefficient that plays the role of control in the optimization problem. The aim of our analysis is the numerical approximation of solutions for this nonlocal optimal control problem. The original source of this problem in the local classical context dates back to the work of Cea and Malanowski ([23]). In that problem, the goal was to minimize the compliance functional under a system governed by a linear elliptic equation ($p=2$), with the control in the diffusion coefficient and constrained by homogeneous Dirichlet conditions on the boundary. More concretely, they addressed the minimization of the compliance functional constrained to the problem

$$\left\{\begin{array}{c}-{div}_x\left(h\left(x\right)\nabla u\left(x\right)\right)=f\left(x\right)\mathrm{in}\mathsf{\Omega }\hfill \\ u\in H_0^1\left(\mathsf{\Omega }\right)\hfill \end{array}\right.$$

(1)

This is a problem of optimal design where h is the control. It is used for the description of the distribution of a conducting material in a fixed domain $\mathsf{\Omega }.$ Here, h is the conductivity (or diffusion); the compliance functional, which measures the energy dissipated in $\mathsf{\Omega }\subset {\mathbb{R}}^N,$ is defined as

$$J_{loc}\left(h,u\right)={\int }_{\mathsf{\Omega }}f\left(x\right)u\left(x\right)\mathrm{d}x,$$

(2)

and u is the potential (or temperature) satisfying (1). To complete the formulation, the source f is assumed to be in $L^2$, and the set of controls participating in the optimization is

$$\mathcal{H}=\left\{h:h\left(x\right)\in \left[h_{min},h_{max}\right]\mathrm{a}.\mathrm{e}.x\in \mathsf{\Omega }\mathrm{and}{\int }_{\mathsf{\Omega }}h\left(x\right)\mathrm{d}x=V_0\right\}$$

where $0<h_{min}<h_{max}$ and $h_{min}\left|\mathsf{\Omega }\right|<V_0<h_{max}\left|\mathsf{\Omega }\right|.$

In the sequel, when we talk about the nonlinear classical problem ($p>1$), we will be referring to the optimal control problem

$$\underset{\left(h,u\right)\in {\mathcal{A}}_{loc}}{min}{J}_{loc}\left(h,u\right)$$

(3)

where $f\in L^{p^{\prime }}\left(\mathsf{\Omega }\right),$ with $\frac{1}{p}+\frac{1}{p^{\prime }}=1$,

$${\mathcal{A}}_{loc}=\left\{(h,u)\in \mathcal{H}\times W_0^{1,p}\left(\mathsf{\Omega }\right):u\mathrm{is}\mathrm{the}\mathrm{unique}\mathrm{solution}\mathrm{to}(5)\right\}$$

(4)

and the state equation is

$$\left\{\begin{array}{c}-{div}_x\left(h\left(x\right){\left|\nabla u\left(x\right)\right|}^{p-2}\nabla u\left(x\right)\right)=f\left(x\right)\mathrm{in}\mathsf{\Omega }\hfill \\ u\in W_0^{1,p}\left(\mathsf{\Omega }\right)\hfill \end{array}\right.$$

(5)

Problem (5) is the p-Laplacian equation. It has been employed for the modelization of meaningful phenomena in diffusion or in conductivity theory where, for some purposes, the compliance functional (2) has been considered as the objective to optimize. See [18,19,20] for $p=2$. In addition, a remarkable field where the optimization of the compliance functional plays an important role is the design of material with a maximum global stiffness (see [24,25]). There are also a large number of outstanding papers dealing with different fractional Laplacian equations modelling diffusion (see [26,27] and references therein).

The problem we pose now is the nonlocal counterpart of (5). The explicit formulation needs to introduce the following definitions: the state equation is

$$\left(P_{\delta }\right)\equiv \left\{\begin{array}{c}{L}_{\delta }\left(u\right)=f\left(x\right),\mathrm{in}\mathsf{\Omega }\hfill \\ u=0\mathrm{in}\partial {\mathsf{\Omega }}^{nl}:={\mathsf{\Omega }}_{\delta }\backslash \mathsf{\Omega }\hfill \end{array}\right.$$

(6)

where ${\mathsf{\Omega }}_{\delta }:=\mathsf{\Omega }\cup \left\{{\cup }_{p\in \partial \mathsf{\Omega }}B\left(p,\delta \right)\right\},$

$$L_{\delta }\left(u\right)=-2{\int }_{B\left(x,\delta \right)}H\frac{k_{\delta }\left(\left|x^{\prime }-x\right|\right)}{{\left|x^{\prime }-x\right|}^p}{\left|u\left(x^{\prime }\right)-u\left(x\right)\right|}^{p-2}\left(u\left(x^{\prime }\right)-u\left(x\right)\right)\mathrm{d}{x}^{\prime },x\in \mathsf{\Omega }$$

and

(1)

$\mathsf{\Omega }$ is a smooth bounded domain in ${\mathbb{R}}^N$, and $B\left(x,r\right)$ is the notation for an open ball centered at $x\in {\mathbb{R}}^N$ and radius $r>0.$

(2)

$f\in L^{p^{\prime }}\left(\mathsf{\Omega }\right)$, and the design function H is given by $H\left(x^{\prime },x\right):=\frac{h\left(x\right)+h\left(x^{\prime }\right)}{2}$ with h in the space

$${\mathcal{H}}_{\delta }=\left\{h:h\left(x\right)\in [h_{min},h_{max}]\mathrm{a}.\mathrm{e}.x\in \mathsf{\Omega },h=0\mathrm{in}{\mathsf{\Omega }}_{\delta }\backslash \mathsf{\Omega }\mathrm{and}{\int }_{\mathsf{\Omega }}h\left(x\right)\mathrm{d}x=V_0\right\}$$

and the constants $0<h_{min}<h_{max}$ are assumed to satisfy the volume constraints $h_{min}\left|\mathsf{\Omega }\right|<V_0<h_{max}\left|\mathsf{\Omega }\right|$. These inequalities are usually assumed to avoid trivial solutions for the optimal design problem.

(3)

The index $\delta ,$ the horizon parameter, is fixed, and it is assumed to be small. Here, ${\left(k_{\delta }\right)}_{\delta }$ is a non-negative radial function such that:

(a)

$$\frac{1}{N}{\int }_{{\mathbb{R}}^N}{k}_{\delta }\left(\left|z\right|\right)\mathrm{d}z=1,$$

(7)

(b)

for every $\delta \le {\delta }_0$ (${\delta }_0$ is small and has been previously fixed) the following inclusion holds

$$supp{k}_{\delta }\subset B\left(0,\delta \right),$$

(c)

there is a positive constant $C_0$, $s\in \left(0,1\right)$ and such that

$$k_{\delta }\left(\left|z\right|\right)\ge \frac{C_0}{{\left|z\right|}^{N+2s-2}}\forall z\in supp{k}_{\delta }\backslash \left\{0\right\}.$$

(8)

Problem (6) must be understood in a weak sense. To be precise, we are going to specify the functional spaces we will deal with. Throughout the paper, $L_0^p\left({\mathsf{\Omega }}_{\delta }\right)$ is

$$L_0^p\left({\mathsf{\Omega }}_{\delta }\right)=\left\{u:{\mathsf{\Omega }}_{\delta }\to \mathbb{R}:u\in L^p\left(\mathsf{\Omega }\right),u=0\mathrm{in}{\mathsf{\Omega }}_{\delta }\backslash \mathsf{\Omega }\right\},$$

and the space $X$ is defined as

$$X=\left\{u\in L_0^p\left({\mathsf{\Omega }}_{\delta }\right):B_h\left(u,u\right)<\infty \right\},$$

(9)

where

$$B_h\left(u,v\right)={\int }_{{\mathsf{\Omega }}_{\delta }}{\int }_{{\mathsf{\Omega }}_{\delta }}H\frac{k_{\delta }\left(\left|x^{\prime }-x\right|\right)}{{\left|x^{\prime }-x\right|}^p}{\left|u\left(x^{\prime }\right)-u\left(x\right)\right|}^{p-2}\left(u\left(x^{\prime }\right)-u\left(x\right)\right)\left(v\left(x^{\prime }\right)-v\left(x\right)\right)\mathrm{d}{x}^{\prime }\mathrm{d}x.$$

(10)

We also define the space $X_0$ as

$$X_0=\overline{C_{co}^{\infty }\left({\mathsf{\Omega }}_{\delta }\right)},$$

where

$$C_{co}^{\infty }\left({\mathsf{\Omega }}_{\delta }\right)=\left\{v:{\mathsf{\Omega }}_{\delta }\to \mathbb{R}:v\in C_c^{\infty }\left(\mathsf{\Omega }\right)\mathrm{and}v=0\mathrm{in}{\mathsf{\Omega }}_{\delta }\backslash \mathsf{\Omega }\right\}\subset X,$$

$C_c^{\infty }\left(\mathsf{\Omega }\right)$ is the set consisting of all infinitely differentiable functions with compact support, and $\overline{C_c^{\infty }\left({\mathsf{\Omega }}_{\delta }\right)}$ is its closure with respect to the norm $∥·∥$ given in X trough the quadratic form $B_h\left(·,·\right),$ that is

$$X_0=\left\{v\in X:\mathrm{there}\mathrm{is}{\left(v_j\right)}_j\subset C_c^{\infty }\left({\mathsf{\Omega }}_{\delta }\right)\mathrm{such}\mathrm{that}\underset{j\to \infty }{lim}{B}_h\left(v_j-v,v_j-v\right)=0\right\}.$$

Definition 1.

It is said that $u\in X_0$ is a solution for the problem $\left(P_{\delta }\right)$ described in (6) if the equality

$$B_h\left(u,v\right)={\displaystyle {\int }_{\mathsf{\Omega }}}f\left(x\right)v\left(x\right)\mathrm{d}x$$

(11)

holds for any $v\in X_0.$

In summary, the nonlocal problem is defined as

$$\underset{\left(h,u\right)\in {\mathcal{A}}_{\delta }}{min}{J}_{\delta }\left(h,u\right),$$

(12)

where the cost functional is

$$J_{\delta }\left(h,u\right):={\displaystyle {\int }_{\mathsf{\Omega }}}f\left(x\right)u\left(x\right)\mathrm{d}x,$$

(13)

and the set of admissibility is given by

$${\mathcal{A}}_{\delta }=\left\{(h,u)\in \mathcal{H}\times X_0:u\mathrm{is}\mathrm{the}\mathrm{unique}\mathrm{solution}\mathrm{to}\left(6\right)\right\}.$$

(14)

The analysis of problems such as (12)–(14) has been accurately studied in previous works. Reference [28] proposes nonlocal models and employs a refined analysis of the nonlocal vector calculus to show the existence of solutions and to take the first steps in their approximation. References [29,30] provide the well-posedness of the weak formulation of nonlocal boundary value problems for general kernel functions that are practical in the peridynamics setting. References [22,31] formulate the first nonlocal optimal control problems and perform the first numerical approximations. The first paper considers the source of the steady equation as control, and the second one faces a distributed optimal problem. Both cases analyze the noncal Laplacian. Some interesting papers dealing with nonlocal control problems with the p-Laplacian equation are: [32], where different formulation of the obstacle problem are analyzed; References [33,34], where different approaches to the optimal control of the coefficient under the assumption of bounded variation are treated; and also [35], where the control is the source, and the study is performed by means of a descent method.

A key point for the study of the above optimization problem is the asymptotic analysis, the $\mathsf{\Gamma }$-convergence or the G-convergence, applied both to the steady equation and to the control problem. References [1,8,31,36,37,38,39,40,41,42,43,44,45,46,47] are papers where the reader can obtain a fairly detailed idea of this issue when the state equation is of a p-Laplacian type.

To understand the intimate relationship between the above two problems, and therefore the purpose of this manuscript, we must point out that an essential part of the design of the nonlocal model lies in the degree of nonlocality that we consider for the interconnection between two points that may be far apart. This issue is reflected in the model by a parameter $\delta >0$ known as the horizon. Due to the analysis carried out in previous works it is now well-known that the nonlocal problem does have a solution and that when the horizon tends to zero, it strongly converges to the classical solution (see Theorem 3 and the references from above concerning $\mathsf{\Gamma }$-convergence or G-convergence). This fact is undoubtedly essential because it offers the possibility of approximating the solution of the local problem at “a lower cost”. This is an aspect that we will try to highlight in the present paper. In this regard, it will be worth comparing the numerical approximations obtained here with the results reported in the bibliography. While [20,23,48] deal with the minimization of the compliance, [49,50] are papers focusing on the maximization of that functional.

Organization and Contributions

The purpose of Section 2 is to recall the basic tools for the setting of the problem. Concerning the state equation, the following issues are examined: existence and uniqueness of solution (Theorem 1) and the G-convergence result with respect to the control (Theorem 2). Regarding the optimal design problems (12)–(14), the existence of a solution is proved, and its convergence to the corresponding solution of the local optimal design problems (2)–(4) are recalled (see Theorem 3).

After these preliminaries, the article will be devoted to presenting a series of contributions, which are organized as follows.

(1)

The obtainment of a maximum principle as a tool to characterize optimal controls: Section 3 contains all the details on which our numerical algorithm is based. The main foundation is a maximum principle on the control (Theorem 4).

(2)

Uniqueness of the state: Section 3 provides a uniqueness result for the states (see Theorem 5 and Corollary 1) and a characterization of the optimal designs (Corollary 2).

(3)

Numerical algorithm: based on the maximum principle and on the properties of the p-Laplacian operator the development of a descent method is obtained (see Section 4).

(4)

True convergence of the numerical procedure towards an optimal control: see Theorems 6 and 7 in Section 4.

(5)

Explicit numerical approximations, both for the nonlocal and local problem (with $\delta$ small enough): Section 5 shows the result of some numerical simulations for the case $p=2.$

Section 6 concludes the work by emphasizing again all the previous points.

2. Preliminary Results

Our goal now is to clarify some of the definitions and formulations given in Section 1. The first issue to analyze is the existence and uniqueness of the solution of (6). Next, we study the convergence of the sequence of solutions ${\left(u_j\right)}_j$ that corresponds to the sequence of Problem (6) when we put $h=h_j.$ This convergence for each $\delta >0$ will serve to ensure existence of nonlocal optimal control. Finally, we approximate the solution of the local problem by the one attained for the nonlocal problem when $\delta$ is small enough.

2.1. A Dirichlet Principle

The first step in our approach is to solve the state equation. This issue has already been thoroughly analyzed. It was proved that the solution of this nonlocal boundary problem is characterized as the unique minimizer on $X_0$ of the functional $E\left(w\right):=\frac{1}{p}{B}_h\left(w,w\right)-{\int }_{\mathsf{\Omega }}f\left(x\right)w\left(x\right)\mathrm{d}x:$

Theorem 1.

For each $h\in$$\mathcal{H}$, there exists a unique function $u\in X_0$ that solves in a weak sense the state equation

$$\left(P_{\delta }\right)\equiv \left\{\begin{array}{c}{B}_h\left(u,w\right)={\displaystyle {\int }_{\mathsf{\Omega }}}f\left(x\right)w\left(x\right)\mathrm{d}x,\mathit{for}\mathit{any}w\in X_0\hfill \\ u=0\mathrm{in}\partial {\mathsf{\Omega }}^{nl}:={\mathsf{\Omega }}_{\delta }\backslash \mathsf{\Omega }.\hfill \end{array}\right.$$

(15)

This solution is unique, and it is characterized as the solution of the problem

$$\underset{w\in X_0}{min}\left\{\frac{1}{p}{B}_h\left(w,w\right)-{\displaystyle {\int }_{\mathsf{\Omega }}}f\left(x\right)w\left(x\right)\mathrm{d}x\right\}$$

and the minimum value is $\left(1-\frac{1}{p}\right){\displaystyle {\int }_{\mathsf{\Omega }}}f\left(x\right)u\left(x\right)\mathrm{d}x.$

(For the proof, see for instance [51] Theorem 1.2) In the sequel, if given $h\in \mathcal{H},$ the function $u\in X_0$ is the solution of (15). Then, $\left(h,u\right)\in {\mathcal{A}}_{\delta }$ will be called an admissible pair for that problem.

We also recall that the same characterization is true for the local problem: $\left(h,u\right)\in {\mathcal{A}}_{loc}$ if and only if

$$u=\underset{w\in X_0}{argmin}\left\{\frac{1}{p}{b}_h\left(w,w\right)-{\displaystyle {\int }_{\mathsf{\Omega }}}f\left(x\right)w\left(x\right)\mathrm{d}x\right\},$$

where

$$b_h\left(v,w\right)={\int }_{\mathsf{\Omega }}h\left(x\right){\left|\nabla v\left(x\right)\right|}^{p-2}\nabla v\left(x\right)\nabla w\left(x\right)\mathrm{d}x.$$

2.2. G-Convergence and Existence of Optimal Control

The pass to the limit in (15) when we are considering a sequence of controls, say ${\left(h_j\right)}_j$, is a crucial step in our study (see [36]).

Theorem 2.

If ${\left(u_j\right)}_j$ is the sequence of solution of the problem

$$\underset{w\in X_0}{min}\left\{\frac{1}{p}{B}_{h_j}\left(w,w\right)-{\int }_{\mathsf{\Omega }}f\left(x\right)w\left(x\right)\mathrm{d}x\right\}$$

and $h_j\rightharpoonup h$ weak-∗ in $L^{\infty }\left(\mathsf{\Omega }\right)$, then we can extract a subsequence from ${\left(u_j\right)}_j$ (which is denoted again by ${\left(u_j\right)}_j)$, and there exists $u\in X_0$ such that

$$u_j\to u\mathit{strongly}\mathit{in}{L}^p\left(\mathsf{\Omega }\right)\mathit{and}{B}_{h_j}\left(u_j-u,u_j-u\right)\to 0\mathit{as}j\to \infty .$$

Moreover, u is the solution of ${min}_{w\in X_0}\left\{\frac{1}{p}{B}_h\left(w,w\right)-{\int }_{\mathsf{\Omega }}f\left(x\right)w\left(x\right)\mathrm{d}x\right\}.$

By using the above convergence, the existence of optimal controls for (12)–(14) is automatic. Factually, this existence result can be extended to a wider class of cost functionals (see [36] Theorem 7). Thus, throughout the paper and for each $\delta ,$ we assume the existence of a pair $\left(h_{\delta },u_{\delta }\right)$ that solves (12)–(14). Moreover, the solution is unique with respect to the state. As we shall point out later, that means that if $\left(h_{\delta },u_{\delta }\right)$ and $\left(g_{\delta },v_{\delta }\right)$ are two solutions of (12)–(14), then $u_{\delta }=v_{\delta }.$

2.3. Approximation

The path we take to solve Problems (3) and (4) is marked by

Theorem 3.

Let ${\left(h_{\delta },u_{\delta }\right)}_{\delta }$ be a sequence of minimizers for Problems (12)–(14). Then, there is a subsequence of index δ, and there is a pair $\left(h,u\right)\in \mathcal{H}\times W_0^{1,p}\left(\mathsf{\Omega }\right)$ for which

$$\begin{array}{cc}{h}_{\delta }\hfill & \rightharpoonup h\mathit{weakly}-\ast \mathit{in}{L}^{\infty }\left(\mathsf{\Omega }\right),\hfill \\ u_{\delta }\hfill & \to u\mathit{strongly}\mathit{in}{L}^p\left(\mathsf{\Omega }\right)\hfill \end{array}$$

and

$$\underset{\delta \to 0}{lim}{B}_{h_{\delta }}\left(u_{\delta }-u,u_{\delta }-u\right)=0.$$

Furthermore,

$$\underset{\delta \to 0}{lim}\underset{w\in X_0}{min}\left\{\frac{1}{p}{B}_{h_{\delta }}\left(w,w\right)-{\displaystyle {\int }_{\mathsf{\Omega }}}f\left(x\right)w\left(x\right)\mathrm{d}x\right\}=\underset{w\in X_0}{min}\left\{\frac{1}{p}{b}_h\left(w,w\right)-{\displaystyle {\int }_{\mathsf{\Omega }}}f\left(x\right)w\left(x\right)\mathrm{d}x\right\}$$

and $\left(h,u\right)$ is a solution to the classical Problems (3) and (4).

See [36] Theorem 8 for the details.

Remark 1.

As we shall see in the nonlocal case, if $\left(h,u\right)$ and $\left(g,v\right)$ are two solutions of Problems (3) and (4), then $u=v.$

3. Maximum Principle and Numerical Algorithm

We are now concerned with computing a numerical approximation of the problem

$$\left\{\begin{array}{c}\underset{\left(h,u\right)\in \mathcal{H}\times X_0.}{min}{\displaystyle {\int }_{\mathsf{\Omega }}}fu\mathrm{d}x\\ \mathrm{subject}\mathrm{to}{B}_h\left(u,v\right)={\displaystyle {\int }_{\mathsf{\Omega }}}f\left(x\right)v\left(x\right)\mathrm{d}x\mathrm{for}\mathrm{any}v\in X_0\\ u=0\mathrm{in}\partial {\mathsf{\Omega }}^{nl}.\end{array}\right.$$

(16)

We shall build a descent method, and we shall show its convergence to the optima. In this procedure, we shall prove a maximum principle for the controls that will determine the direction of descent. This maximum principle is the key part of the construction of the algorithm, and from it we shall deduce a uniqueness theorem for the states.

3.1. Maximum Principle

Theorem 4.

Let $\left(h,u\right)$ be a solution to Problem (16), then $\left(h,u\right)$ satisfies the next maximum principle:

$$B_h\left(u,u\right)\ge B_g\left(u,u\right)\mathit{for}\mathit{every}g\in \mathcal{H}.$$

(17)

Proof. 

Take $g\in \mathcal{H}$ and any $\rho$ such that $0\le \rho \le 1$ and $h+\rho \left(g-h\right)\in \mathcal{H}.$ If $u+\mathsf{\Delta }u$ is the state associated to the control $h+\rho \left(g-h\right)$, then

$$B_{h+\rho \left(g-h\right)}\left(u+\mathsf{\Delta }u,v\right)=\int fv\mathrm{d}x\mathrm{for}\mathrm{any}v\in X_0.$$

For clarity, in most subsequent discussions we will delete the domain of integration $\mathsf{\Omega }$ and omit the dependence on x. For instance, we shall write $\int fv\mathrm{d}x$ instead of ${\int }_{\mathsf{\Omega }}f\left(x\right)v\left(x\right)\mathrm{d}x$.

By linearity with respect to the control, this is equivalent to write

$$B_h\left(u+\mathsf{\Delta }u,v\right)+\rho B_{g-h}\left(u+\mathsf{\Delta }u,v\right)={\int }_{\mathsf{\Omega }}fv\mathrm{d}x.$$

Since $\left(h,u\right)$ is a solution to the state equation, we have $B_h\left(u,v\right)={\int }_{\mathsf{\Omega }}fv\mathrm{d}x,$ and thus

$$B_h\left(u+\mathsf{\Delta }u,v\right)+\rho B_{g-h}\left(u+\mathsf{\Delta }u,v\right)-B_h\left(u,v\right)=0\mathrm{for}\mathrm{any}v\in X_0.$$

(18)

Since $u+\mathsf{\Delta }u\in X_0$, the above formula gives

$$B_h\left(u+\mathsf{\Delta }u,u+\mathsf{\Delta }u\right)+\rho B_{g-h}\left(u+\mathsf{\Delta }u,u+\mathsf{\Delta }u\right)-B_h\left(u,u+\mathsf{\Delta }u\right)=0.$$

(19)

We compute the cost for the admissible pair $(h+\rho \left(g-h\right),u+\mathsf{\Delta }u)\in$${\mathcal{A}}_{\delta }$, and we note

$$J_{\delta }\left(h+\rho \left(g-h\right),u+\mathsf{\Delta }u\right)={\int }_{\mathsf{\Omega }}f\left(u+\mathsf{\Delta }u\right)\mathrm{d}x=J_{\delta }\left(h,u\right)+B_h\left(u,\mathsf{\Delta }u\right),$$

(20)

From (20) and the minimality of the pair $\left(h,u\right)$ in (16), we obtain

$$\int f\mathsf{\Delta }u\mathrm{d}x\ge 0.$$

(21)

Again, the fact that $\left(h,u\right)\in {\mathcal{A}}_{\delta }$ implies

$$\frac{1}{p}{B}_h\left(u,u\right)-\int fudx\le \frac{1}{p}{B}_h\left(u+\mathsf{\Delta }u,u+\mathsf{\Delta }u\right)-\int f\left(u+\mathsf{\Delta }u\right)\mathrm{d}x$$

i.e.,

$$\frac{1}{p}{B}_h\left(u,u\right)\le \frac{1}{p}{B}_h\left(u+\mathsf{\Delta }u,u+\mathsf{\Delta }u\right)-\int f\mathsf{\Delta }u\mathrm{d}x$$

By using (21), we obtain

$$B_h\left(u,u\right)+\int f\mathsf{\Delta }u\mathrm{d}x\le B_h\left(u+\mathsf{\Delta }u,u+\mathsf{\Delta }u\right)$$

or equivalently

$$B_h\left(u,u+\mathsf{\Delta }u\right)\le B_h\left(u+\mathsf{\Delta }u,u+\mathsf{\Delta }u\right).$$

This inequality and (19) ensure

$$B_{g-h}\left(u+\mathsf{\Delta }u,u+\mathsf{\Delta }u\right)\le 0$$

and therefore

$$B_g\left(u+\mathsf{\Delta }u,u+\mathsf{\Delta }u\right)\le B_h\left(u+\mathsf{\Delta }u,u+\mathsf{\Delta }u\right).$$

We take limits (if it is necessary for a subsequence) and have in mind that $u+\mathsf{\Delta }u\to u$ strongly in $L^p,$ if $\rho \to 0,$ and we use Theorem 2 to realize that

$$\begin{array}{cc}\hfill & \underset{\rho \to 0}{lim}{B}_h\left(u+\mathsf{\Delta }u,u+\mathsf{\Delta }u\right)\hfill \\ \hfill & =\underset{\rho \to 0}{lim}{B}_{h+\rho \left(g-h\right)}\left(u+\mathsf{\Delta }u,u+\mathsf{\Delta }u\right)-\underset{\rho \to 0}{lim}{B}_{\rho \left(g-h\right)}\left(u+\mathsf{\Delta }u,u+\mathsf{\Delta }u\right)\hfill \\ \hfill & =B_h\left(u,u\right)-\underset{\rho \to 0}{lim}\rho B_{g-h}\left(u+\mathsf{\Delta }u,u+\mathsf{\Delta }u\right)\hfill \end{array}$$

In addition, it is clear that there exists a constant $C>0$ such that

$$\begin{array}{cc}\left|B_{g-h}\left(u+\mathsf{\Delta }u,u+\mathsf{\Delta }u\right)\right|\hfill & \le \left|B_{\frac{g-h}{h+\rho \left(g-h\right)}h+\rho \left(g-h\right)}\left(u+\mathsf{\Delta }u,u+\mathsf{\Delta }u\right)\right|\hfill \\ \hfill & \le \frac{2h_{max}}{h_{min}}{∥f∥}_{L^{p^{\prime }}}{∥u+\mathsf{\Delta }u∥}_{L^p}<C\hfill \end{array}$$

for any $\rho .$ Consequently, ${lim}_{\rho \to 0}\rho B_{\left(g-h\right)}\left(u+\mathsf{\Delta }u,u+\mathsf{\Delta }u\right)=0$ and hence

$$\underset{\rho \to 0}{lim}{B}_g\left(u+\mathsf{\Delta }u,u+\mathsf{\Delta }u\right)\le B_h\left(u,u\right).$$

Theorem 2 and the above inequality ensure

$$B_g\left(u,u\right)\le B_h\left(u,u\right)\mathrm{for}\mathrm{any}g\in \mathcal{H}$$

which is what we pursued. □

3.2. Uniqueness

Theorem 5.

If $\left(h,u\right)$ is a solution of (16) and $\left(g,w\right)$ is an admissible pair that satisfies the maximum Principle (17), then $u=w.$

Proof. 

The maximum principle on $\left(h,u\right)$ ensures

$$B_H\left(u,u\right)\le B_h\left(u,u\right)\mathrm{for}\mathrm{any}H\in \mathcal{H}$$

In addition, we know

$$B_G\left(w,w\right)\le B_g\left(w,w\right)\mathrm{for}\mathrm{any}G\in \mathcal{H}$$

By using these inequalities, we derive

$$\begin{array}{cc}\hfill & \left(1-\frac{1}{p}\right)\int fw\mathrm{d}x=\underset{v}{min}\left\{\frac{1}{p}{B}_g\left(v,v\right)-\int fv\mathrm{d}x\right\}\hfill \\ \hfill & \le \frac{1}{p}{B}_g\left(u,u\right)-\int fu\mathrm{d}x\le \frac{1}{p}{B}_h\left(u,u\right)-\int fu\mathrm{d}x\hfill \\ \hfill & =\underset{v}{min}\left\{\frac{1}{p}{B}_h\left(v,v\right)-\int fv\mathrm{d}x\right\}\hfill \\ \hfill & \le \frac{1}{p}{B}_h\left(w,w\right)-\int fw\mathrm{d}x\le \frac{1}{p}{B}_g\left(w,w\right)-\int fw\mathrm{d}x\hfill \\ \hfill & =\underset{v}{min}\left\{\frac{1}{p}{B}_g\left(v,v\right)-\int fv\mathrm{d}x\right\}=\left(1-\frac{1}{p}\right)\int fw\mathrm{d}x\hfill \end{array}$$

and hence $B_h\left(u,u\right)=B_g\left(u,u\right)$ and $B_h\left(w,w\right)=B_g\left(w,w\right).$ Moreover,

$$\int fu\mathrm{d}x=\int fw\mathrm{d}x,$$

That means $\left(g,w\right)$ is a solution of (16). Since, in particular,

$$\frac{1}{p}{B}_h\left(w,w\right)-\int fw\mathrm{d}x=\underset{v}{min}\left\{\frac{1}{p}{B}_h\left(v,v\right)-\int fv\mathrm{d}x\right\},$$

then, by the uniqueness, it implies that $w=u.$ □

Corollary 1.

If $\left(h,u\right)$ and $\left(g,w\right)$ are two solutions of (16), then $u=w.$

Corollary 2.

Any admissible pair that satisfies the maximum principle is a solution of (16).

Proof. 

If $\left(h,u\right)$ satisfies the maximum principle (17) and $\left(g,w\right)$ is any other admissible pair, then

$$\begin{array}{cc}\left(1-\frac{1}{p}\right)B_h\left(u,u\right)\hfill & =\frac{1}{p}{B}_h\left(u,u\right)-\int fu\mathrm{d}x\hfill \\ \hfill & \ge \frac{1}{p}{B}_g\left(u,u\right)-\int fu\mathrm{d}x\hfill \\ \hfill & \ge \underset{v}{inf}\left\{\frac{1}{p}{B}_g\left(v,v\right)-\int fv\mathrm{d}x\right\}\hfill \\ \hfill & =\frac{1}{p}{B}_g\left(w,w\right)-\int fw\mathrm{d}x\hfill \\ \hfill & =\left(1-\frac{1}{p}\right)B_g\left(w,w\right),\hfill \end{array}$$

which is equivalent to claiming that $\left(h,u\right)$ is a solution of (16). □

4. The Algorithm Construction

Here, we detail the descent mechanism that ensures convergence towards the optimum. To do that, we follow the ideas of [23] which for clarity are reproduced here in the nonlocal context and for the nonlinear case $p>1$. The final goal is to search a sequence of admissible pairs ${\left\{\left(h_r,u_r\right)\right\}}_r$ such that

$$\underset{r\to \infty }{lim}{J}_{\delta }\left(h_r,u_r\right)=\underset{\left(h,u\right)\in \mathcal{H}\times X_0}{min}{\displaystyle {\int }_{\mathsf{\Omega }}}f\left(x\right)u\left(x\right)\mathrm{d}x$$

From an initial pair $(h_0,u_0)\in {\mathcal{A}}_{\delta }$, we assume we have built until $(h_r,u_r)\in {\mathcal{A}}_{\delta }$ and $J_{\delta }\left(h_j,u_j\right)\le J_{\delta }\left(h_{j-1},u_{j-1}\right)$ for all $j\in \left\{0,1,...,r\right\}.$ Now, we search a pair $(h_{r+1},u_{r+1})\in {\mathcal{A}}_{\delta }$ such that $J_{\delta }\left(h_{r+1},u_{r+1}\right)\le J_{\delta }\left(h_j,u_j\right)$. To do that, we select $\rho >0$, $g\in \mathcal{H}$, and we define $h_{r+1}=h_r+\rho \left(g-h_r\right)\in \mathcal{H}.$ Let $u_{r+1}=u_r+\mathsf{\Delta }{u}_r$ be the underlying state, which clearly depends on $\rho .$ The corresponding costs to the pairs $(h_r,u_r)$ and $(h_{r+1},u_{r+1})$ are, respectively,

$$J_{\delta }\left(h_r,u_r\right)=B_{h_r}\left(u_r,u_r\right)=\int f{u}_r\mathrm{d}x$$

and

$$J_{\delta }\left(h_{r+1},u_{r+1}\right)=B_{h_{r+1}}\left(u_r+\mathsf{\Delta }{u}_r,u_r+\mathsf{\Delta }{u}_r\right)=\int f\left(u_r+\mathsf{\Delta }{u}_r\right)\mathrm{d}x.$$

We also consider the increment of the cost:

$$E_r:=J_{\delta }\left(h_r,u_r\right)-J_{\delta }\left(h_{r+1},u_{r+1}\right).$$

It is immediate to check

$$E_r=\int f{u}_r\mathrm{d}x-\int f\left(u_r+\mathsf{\Delta }{u}_r\right)\mathrm{d}x=-\int f\mathsf{\Delta }{u}_r\mathrm{d}x$$

(22)

This section is devoted to choosing g and $\rho .$ We divide the study into four subsections:

4.1. Direction

We look for the optimal $g.$ Since the pair $\left(h_r,u_r\right)$ is optimal, we have

$$\begin{array}{cc}\frac{1}{p}{B}_{h_r}\left(u_r,u_r\right)-\int f{u}_r\mathrm{d}x\hfill & \le \frac{1}{p}{B}_{h_r}\left(u_r+\mathsf{\Delta }{u}_r,u_r+\mathsf{\Delta }{u}_r\right)-\int f\left(u_r+\mathsf{\Delta }{u}_r\right)\mathrm{d}x\hfill \\ \hfill & =\frac{1}{p}{B}_{h_{r+1}}\left(u_r+\mathsf{\Delta }{u}_r,u_r+\mathsf{\Delta }{u}_r\right)-\int f\left(u_r+\mathsf{\Delta }{u}_r\right)\mathrm{d}x\hfill \\ \hfill & -\frac{1}{p}{B}_{\rho \left(g-h_r\right)}\left(u_r+\mathsf{\Delta }{u}_r,u_r+\mathsf{\Delta }{u}_r\right)\hfill \end{array}$$

However, this estimate can be read as

$$\left(\frac{1}{p}-1\right)\left[B_{h_r}\left(u_r,u_r\right)-B_{h_{r+1}}\left(u_r+\mathsf{\Delta }{u}_r,u_r+\mathsf{\Delta }{u}_r\right)\right]\le -\frac{1}{p}{B}_{\rho \left(g-h_r\right)}\left(u_r+\mathsf{\Delta }{u}_r,u_r+\mathsf{\Delta }{u}_r\right)$$

from where we have the inequality

$$E_r\ge \frac{\rho }{p-1}{B}_{g-h_r}\left(u_r+\mathsf{\Delta }{u}_r,u_r+\mathsf{\Delta }{u}_r\right).$$

(23)

Note that the same procedure when we take into account that $\left(h_{r+1},u_{r+1}\right)$ is optimal gives the inequality $\frac{\rho }{p-1}{B}_{g-h_r}\left(u_r,u_r\right)\ge E_r.$

By (23), it is clear that we need $B_{g-h_r}\left(u_r+\mathsf{\Delta }{u}_r,u_r+\mathsf{\Delta }{u}_r\right)>0$ in order to ensure $E_r>0.$ Therefore, to attain the inequality $E_r>0,$ for $\rho$ small enough, we impose $B_{g-h_r}\left(u_r,u_r\right)>0.$ However, this is to say g has to be selected so that

$$B_g\left(u_r,u_r\right)>B_{h_r}\left(u_r,u_r\right).$$

(24)

In practice, the above analysis indicates that g should be chosen as the solution of

$$\underset{g\in \mathcal{H}}{max}{B}_g\left(u_r,u_r\right),$$

namely,

$$g=g_r:=\underset{G\in \mathcal{H}}{argmax}{B}_G\left(u_r,u_r\right).$$

(25)

4.2. Size of the Step $\rho$

We now study how to select ${\rho }_r$ such that $E_r>0.$ We have already taken $g_r={argmax}_{G\in \mathcal{H}}{B}_G\left(u_r,u_r\right)$, and we have proved that

$$E_r\ge \frac{\rho }{p-1}\left\{B_{g_r-h_r}\left(u_r+\mathsf{\Delta }{u}_r,u_r+\mathsf{\Delta }{u}_r\right)-B_{g_r-h_r}\left(u_r,u_r\right)\right\}+\frac{\rho }{p-1}{B}_{g_r-h_r}\left(u_r,u_r\right)$$

Concerning the first term, the inequality $\left|{\lambda }^p-{\mu }^p\right|\le p\left|\lambda -\mu \right|\left({\lambda }^{p-1}-{\mu }^{p-1}\right)$ if $p\ge 1$ and $\lambda ,$$\mu \ge 0,$ allows us to write

$$\begin{array}{cc}F\hfill & :=\left|B_{g_r-h_r}\left(u_r+\mathsf{\Delta }{u}_r,u_r+\mathsf{\Delta }{u}_r\right)-B_{g_r-h_r}\left(u_r,u_r\right)\right|\hfill \\ \hfill & =\left|{\int }_{{\mathsf{\Omega }}_{\delta }}{\int }_{{\mathsf{\Omega }}_{\delta }}\left(G_r-H_r\right)\frac{k_{\delta }\left(\left|x^{\prime }-x\right|\right)}{{\left|x^{\prime }-x\right|}^p}\left({\left|\left(u_r+\mathsf{\Delta }{u}_r\right)-{\left(u_r+\mathsf{\Delta }{u}_r\right)}^{\prime }\right|}^p-{\left|\left(u_r\right)-{\left(u_r\right)}^{\prime }\right|}^p\right)\mathrm{d}{x}^{\prime }\mathrm{d}x\right|\hfill \\ \hfill & \le \left(h_{max}-h_{min}\right){\int }_{{\mathsf{\Omega }}_{\delta }}{\int }_{{\mathsf{\Omega }}_{\delta }}\frac{k_{\delta }\left(\left|x^{\prime }-x\right|\right)}{{\left|x^{\prime }-x\right|}^p}p\left|\mathsf{\Delta }{u}_r-\mathsf{\Delta }{u}_r^{\prime }\right|{\left|\left(u_r+\mathsf{\Delta }{u}_r\right)-{\left(u_r+\mathsf{\Delta }{u}_r\right)}^{\prime }\right|}^{p-1}\mathrm{d}{x}^{\prime }\mathrm{d}x\hfill \\ \hfill & +\left(h_{max}-h_{min}\right){\int }_{{\mathsf{\Omega }}_{\delta }}{\int }_{{\mathsf{\Omega }}_{\delta }}\frac{k_{\delta }\left(\left|x^{\prime }-x\right|\right)}{{\left|x^{\prime }-x\right|}^p}p\left|\mathsf{\Delta }{u}_r-\mathsf{\Delta }{u}_r^{\prime }\right|{\left|\left(u_r\right)-{\left(u_r\right)}^{\prime }\right|}^{p-1}\mathrm{d}{x}^{\prime }\mathrm{d}x\hfill \end{array}$$

If we use the Hölder inequality, we obtain

$$F\le \left(h_{max}-h_{min}\right)p{∥\mathsf{\Delta }{u}_r∥}_{X_0}\left\{{∥u_r+\mathsf{\Delta }{u}_r∥}_{X_0}^{p-1}+{∥u_r∥}_{X_0}^{p-1}\right\}$$

where ${∥w∥}_{X_0}^p:=B\left(w,w\right).$ Now, by using the inequalities

$${∥u_r+\mathsf{\Delta }{u}_r∥}_{X_0}^{p-1}\le {\left({∥u_r∥}_{X_0}+{∥\mathsf{\Delta }{u}_r∥}_{X_0}\right)}^{p-1}\le 2^{p-2}\left({∥u_r∥}_{X_0}^{p-1}+{∥\mathsf{\Delta }{u}_r∥}_{X_0}^{p-1}\right),$$

we obtaint

$$\begin{array}{cc}F\hfill & \le \left(h_{max}-h_{min}\right)p{∥\mathsf{\Delta }{u}_r∥}_{X_0}\left\{2^{p-2}\left({∥u_r∥}_{X_0}^{p-1}+{∥\mathsf{\Delta }{u}_r∥}_{X_0}^{p-1}\right)+{∥u_r∥}_{X_0}^{p-1}\right\}\hfill \\ \hfill & =\left(h_{max}-h_{min}\right)p\left(2^{p-2}{∥\mathsf{\Delta }{u}_r∥}_{X_0}^p+\left(2^{p-2}+1\right){∥\mathsf{\Delta }{u}_r∥}_{X_0}{∥u_r∥}_{X_0}^{p-1}\right).\hfill \end{array}$$

To complete the estimate, we use the monotonicity property of the p-Laplacian operator. Indeed, since for any $\lambda \ge 0$ and $\mu \ge 0,$

$$C_1{\left|\lambda -\mu \right|}^p\le \left({\left|\lambda \right|}^{p-2}\lambda -{\left|\mu \right|}^{p-2}\mu \right)\left(\lambda -\mu \right)$$

where $C_1=arg{min}_{z\in {\mathbb{R}}^{+}}\frac{1-z^{p-1}}{{\left(1+z\right)}^{p-2}\left(1-z\right)}=\left(p-1\right)e^{-\left(p-2\right)\left(log2\right)}$ (see [52] Proposition 17.3 and Theorem 17.1), then

$$C_1{B}_{h_{r+1}}\left(\mathsf{\Delta }{u}_r,\mathsf{\Delta }{u}_r\right)\le B_{h_{r+1}}\left(u_r+\mathsf{\Delta }{u}_r,\mathsf{\Delta }{u}_r\right)-B_{h_{r+1}}\left(u_r,\mathsf{\Delta }{u}_r\right).$$

Thanks to the linearity with respect to the control, the above inequality can be expressed as

$$\begin{array}{cc}{C}_1{B}_{h_{r+1}}\left(\mathsf{\Delta }{u}_r,\mathsf{\Delta }{u}_r\right)\hfill & \le B_{h_r}\left(u_r,\mathsf{\Delta }{u}_r\right)-B_{h_r}\left(u_r,\mathsf{\Delta }{u}_r\right)-\rho B_{g_r-h_r}\left(u_r,\mathsf{\Delta }{u}_r\right)\hfill \\ \hfill & =-\rho B_{g_r-h_r}\left(u_r,\mathsf{\Delta }{u}_r\right).\hfill \end{array}$$

In addition, the Hölder inequality provides

$$\left|B_{g_r-h_r}\left(u_r,\mathsf{\Delta }{u}_r\right)\right|\le \left(h_{max}-h_{min}\right){∥u_r∥}_{X_0}^{p-1}{∥\mathsf{\Delta }{u}_r∥}_{X_0}$$

and consequently, since $h_{min}{∥\mathsf{\Delta }{u}_r∥}_{X_0}^p\le B_{h_{r+1}}\left(\mathsf{\Delta }{u}_r,\mathsf{\Delta }{u}_r\right),$ we derive

$$C_1{h}_{min}{∥\mathsf{\Delta }{u}_r∥}_{X_0}^p\le \rho \left(h_{max}-h_{min}\right){∥u_r∥}_{X_0}^{p-1}{∥\mathsf{\Delta }{u}_r∥}_{X_0},$$

and hence the estimate

$${∥\mathsf{\Delta }{u}_r∥}_{X_0}\le {\left[\frac{\rho \left(h_{max}-h_{min}\right)}{C_1{h}_{min}}\right]}^{1/\left(p-1\right)}{∥u_r∥}_{X_0}.$$

We gather all the previous estimates by writing

$$F\le A{\rho }^{p^{\prime }}{∥u_r∥}_{X_0}^p+B{\rho }^{1/\left(p-1\right)}{∥u_r∥}_{X_0}^p,$$

where

$$\begin{array}{cc}A\hfill & =\left(h_{max}-h_{min}\right)p{2}^{p-2}{\left[\frac{h_{max}-h_{min}}{C_1{h}_{min}}\right]}^{p/\left(p-1\right)},\hfill \\ B\hfill & =\left(h_{max}-h_{min}\right)p\left(2^{p-2}+1\right){\left[\frac{\left(h_{max}-h_{min}\right)}{C_1{h}_{min}}\right]}^{1/\left(p-1\right)}.\hfill \end{array}$$

We conclude

$$\begin{array}{cc}{E}_r\hfill & \ge \frac{\rho }{p-1}{B}_{g_r-h_r}\left(u_r,u_r\right)-\frac{\rho }{p-1}\left(A{\rho }^{p^{\prime }}{∥u_r∥}_{X_0}^p+B{\rho }^{1/\left(p-1\right)}{∥u_r∥}_{X_0}^p\right)\hfill \\ \hfill & =\frac{\rho }{p-1}{B}_{g_r-h_r}\left(u_r,u_r\right)-\frac{{∥u_r∥}_{X_0}^p}{p-1}\left(A{\rho }^{p^{\prime }+1}+B{\rho }^{p^{\prime }}\right)\hfill \\ \hfill & \ge \frac{\rho }{p-1}{B}_{g_r-h_r}\left(u_r,u_r\right)-\frac{{\rho }^{p^{\prime }}{∥u_r∥}_{X_0}^p}{p-1}\left(A+B\right)\hfill \end{array}$$

Proposition 1.

By denoting $\alpha =\frac{B_{g_r-h_r}\left(u_r,u_r\right)}{p-1}$ and $\beta =\frac{{∥u_r∥}_{X_0}^p}{p-1}\left(A+B\right)$

$$E_r\ge \alpha \rho -\beta {\rho }^{p^{\prime }}.$$

Notice the derivative of the function $\psi \left(\rho \right):=\alpha \rho -\beta {\rho }^{p^{\prime }}$ with respect to $\rho$ is ${\psi }^{\prime }\left(\rho \right)=\alpha -\beta p^{\prime }{\rho }^{p^{\prime }-1}$ and the only critical point is

$${\rho }_0={\left(\frac{\alpha }{\beta p^{\prime }}\right)}^{p-1}={\left(\frac{B_{g_r-h_r}\left(u_r,u_r\right)}{p^{\prime }{∥u_r∥}_{X_0}^p\left(A+B\right)}\right)}^{p-1}.$$

The function $\psi \left(\rho \right)=\alpha \rho -\beta {\rho }^{p^{\prime }}$ attains the absolute maximum at this point, and this maximum value is

$$\psi \left({\rho }_0\right)={\left[\frac{\left(p-1\right)\alpha }{p\beta }\right]}^{p-1}\frac{\alpha }{p}.$$

(26)

Our choice of the step of the size is

$${\rho }_r=min\left\{{\rho }_0,1\right\}.$$

(27)

The above discussion leads us to choose $g=g_r$ and $\rho ={\rho }_r$ in order to majorize $E_r.$ In either case, with these selections we have $E_r\ge 0.$

4.3. An Essential Remark

A crucial term for the development of our descent method is the analysis of the sequence $b_r:=B_{g_r-h_r}\left(u_r,u_r\right).$ We know

$$\underset{r}{lim}{b}_r=B_{g-h}\left(u,u\right)$$

where g and h are the weak-∗ limits in $L^{\infty }$ of the sequences ${\left(g_r\right)}_r$ and ${\left(h_r\right)}_r$ respectively, at least for a subsequence of $r^{\prime }$s. In addition, u is the strong limit in $X_0$ of ${\left(u_r\right)}_r$ so that $\left(h,u\right)$ is an admissible pair. Now, we look at the following fact:

Theorem 6.

${lim}_r{b}_r=0,$ that is, $B_{g-h}\left(u,u\right)=0.$

Proof. 

It is clear that

$$0=\underset{r}{lim}{E}_r$$

(28)

and

$$\begin{array}{cc}{E}_r\hfill & \ge \frac{{\rho }_r}{p-1}{B}_{g_r-h_r}\left(u_r,u_r\right)-\frac{{\rho }_r^{p^{\prime }}{∥u_r∥}_{X_0}^p}{p-1}\left(A+B\right)\hfill \\ \hfill & =\left\{\begin{array}{cc}\frac{1}{p-1}{B}_{g_r-h_r}\left(u_r,u_r\right)-\frac{{∥u_r∥}_{X_0}^p}{p-1}\left(A+B\right)& \mathrm{if}{\rho }_r=1\\ \frac{{\rho }_r}{p-1}{B}_{g_r-h_r}\left(u_r,u_r\right)-\frac{{\rho }_r^{p^{\prime }}{∥u_r∥}_{X_0}^p}{p-1}\left(A+B\right)& \mathrm{if}{\rho }_r={\rho }_0.\end{array}\right.\hfill \end{array}$$

Because of the choice (27) ${\rho }_r=1$ occurs if and only if ${\left(\frac{B_{g_r-h_r}\left(u_r,u_r\right)}{p^{\prime }{∥u_r∥}_{X_0}^p\left(A+B\right)}\right)}^{p-1}>1$ and $E_r>\psi \left({\rho }_0\right)$ if ${\rho }_r={\rho }_0$ (see (26)), therefore

$$\begin{array}{cc}{E}_r\hfill & \ge \left\{\begin{array}{cc}{B}_{g_r-h_r}\left(u_r,u_r\right)\left(\frac{1}{p-1}-\frac{1}{p}\right)& \mathrm{if}{\rho }_r=1\\ {\left[\frac{\left(p-1\right)\alpha }{p\beta }\right]}^{p-1}\frac{\alpha }{p}& \mathrm{if}{\rho }_r={\rho }_0.\end{array}\right.\hfill \\ \hfill & =\left\{\begin{array}{cc}{B}_{g_r-h_r}\left(u_r,u_r\right)\left(\frac{1}{p-1}-\frac{1}{p}\right)& \mathrm{if}{\rho }_r=1\\ {\left(B_{g_r-h_r}\left(u_r,u_r\right)\right)}^p{\left[\frac{1}{p^{\prime }{∥u_r∥}_{X_0}^p\left(A+B\right)}\right]}^{p-1}\frac{1}{\left(p-1\right)p}& \mathrm{if}{\rho }_r={\rho }_0.\end{array}\right.\hfill \end{array}$$

The above estimate and (28) provide the result. □

4.4. Convergence toward the Optima

The steps described in the previous subsections have served to construct a sequence of admissible pairs ${\left(h_r,u_r\right)}_r$. We know the sequence ${\left(h_r\right)}_r$ is uniformly bounded in $L^{\infty }\left({\mathsf{\Omega }}_{\delta }\right)$, and therefore, for a subsequence of index $r,$$h_r\rightharpoonup h$ weakly ∗ in $L^{\infty }\left({\mathsf{\Omega }}_{\delta }\right)$ for some $h\in \mathcal{H}.$ Under the circumstances that convergence guarantees the existence of a function $u\in X_0,$ and subsequence of ${\left(u_r\right)}_r,$ which will be denoted again ${\left(u_r\right)}_r,$ such that $u_r\to u$ strongly in $X_0$ (also in $L^p)$ in the sense that

$$\underset{r\to \infty }{lim}{B}_{h_r}\left(u_r-u,u_r-u\right)=0$$

and $\left(h,u\right)$ is an admissible pair, that is

$$B_h\left(u,v\right)={\int }_{\mathsf{\Omega }}f\left(x\right)v\left(x\right)\mathrm{d}x\mathrm{for}\mathrm{any}v\in X_0.$$

It remains to show $\left(h,u\right)$ is an optimal pair for the problem (16), or in other words, it is still to be shown whether $\left(h,u\right)$ satisfies the maximum principle (17). For this purpose, we recall that the choice of $g_r$ had been made so that the following inequality would be satisfied

$$B_{g_r}\left(u_r,u_r\right)\ge B_G\left(u_r,u_r\right)\mathrm{for}\mathrm{any}G\in \mathcal{H}.$$

Then, by adding and subtracting the term $B_{h_r}\left(u_r,u_r\right)$ in the left part of the above inequality we have

$$B_{h_r}\left(u_r,u_r\right)+B_{g_r-h_r}\left(u_r,u_r\right)\ge B_G\left(u_r,u_r\right)\mathrm{for}\mathrm{any}G\in \mathcal{H},$$

which amounts to

$${\int }_{\mathsf{\Omega }}f\left(x\right)u_r\left(x\right)\mathrm{d}x+B_{g_r-h_r}\left(u_r,u_r\right)\ge B_G\left(u_r,u_r\right)\mathrm{for}\mathrm{any}G\in \mathcal{H}.$$

(29)

Since ${\left(u_r\right)}_r$ strongly converges to u in $L^p\left({\mathsf{\Omega }}_{\delta }\right)$ and ${lim}_{r\to \infty }{B}_{g_r-h_r}\left(u_r,u_r\right)=0,$ as we have just proved above, the inequality (29), in the limit as $r\to \infty$, gives

$${\int }_{\mathsf{\Omega }}f\left(x\right)u\left(x\right)\mathrm{d}x\ge \underset{r\to \infty }{lim}{B}_G\left(u_r,u_r\right)\mathrm{for}\mathrm{any}G\in \mathcal{H}.$$

(30)

However, if we pay attention to the lower semicontinuity of the operator $B_G\left(·,·\right),$ (30) establishes

$$B_h\left(u,u\right)={\int }_{\mathsf{\Omega }}f\left(x\right)u\left(x\right)\mathrm{d}x\ge \underset{r\to \infty }{lim}{B}_G\left(u_r,u_r\right)\ge B_G\left(u,u\right)\mathrm{for}\mathrm{any}G\in \mathcal{H}.$$

or equivalently, $\left(h,u\right)$ satisfies the maximum principle. This assertion and Corollary 2 allow us to claim that $\left(h,u\right)$ is a solution to the control problem, and we have proved the iterative method converges to a solution. Furthermore, thanks to Corollary 1, the state u is unique, and therefore, it is straightforward to show the whole sequence of states $\left(u_r\right)$ is strongly convergent to $u.$

We have proved

Theorem 7 (Convergence).

The sequence of admissible pairs ${\left(h_r,u_r\right)}_r$ converges to an optimal pair $\left(h,u\right).$

5. Numerical Simulations

Before proceeding further, these three considerations are of interest.

(1)

Here, we sketch the plots of the optimal pairs for different examples. We performed serial computing on a 3.6 GHz Intel Core i9 with a RAM of 128, and we simplified the computational task by limiting it to the case $p=2$. Despite the fact that our fundamental purpose has not been the development of a high-efficiency algorithm, the convergence is accomplished and is very fast. To guarantee the convergence of the numerical algorithm towards the optimal pair, the criterion we have chosen is the zero decay of both sequences $h_j-h_{j-1}$ and $u_j-u_{j-1}$ in the $L^p$ norm.

(2)

The dimension is $N=2$, and the type of kernel we have chosen is not the only one that is possible, more specifically: for any sequence of non-negative radial functions ${\left(k_{\delta }\right)}_{\delta }$ such that $\frac{1}{N}{\int }_{B\left(0,\delta \right)}{k}_{\delta }\left(\left|s\right|\right)\mathrm{d}s=1,$$supp{k}_{\delta }\subset B\left(0,\delta \right)$, $K_r\left(z\right):=\frac{k_{\delta }\left(\left|z\right|\right)}{\left|z\right|}\in L^1\left(B\left(0,\delta \right)\right),$ and $K_s\left(z\right)=\frac{k_{\delta }\left(\left|z\right|\right)}{{\left|z\right|}^2}$$\left(z\ne 0\right)$ is singular near the origin, in the sense that ${lim}_{\theta \to 0^{+}}{\int }_{B\left(0,\delta \right)-B\left(0,\theta \right)}{K}_s\left(z\right)dz=+\infty ,$ all the results we have previously considered are still valid. The details can be checked in [51].

(3)

The specific kernel we have used in all the examples is $k_{\delta }\left(\left|s\right|\right)=C_{\delta }exp\left(-\left|z\right|\right)$ (where $C_{\delta }$ is a positive regularizing constant ensuring the constraint (7)). In addition, as is done in many other papers, we can use the Riesz kernel $k_{\delta }\left(r\right)=C_{\delta }\frac{1}{{\left|z\right|}^{2s}}$ (where $s\in \left(0,1\right))$, and in such a case, the results and convergence of the method do not essentially change.

5.1. Delfour and Zolésio Example

We face the minimization of the compliance when the source is the function $f\left(x,y\right)=56{\left(1-\left|x\right|-\left|y\right|\right)}^6$ defined on the diamond $D=\left\{\left(x,y\right)\in {\mathbb{R}}^2:\left|x\right|+\left|y\right|\le 1\right\}.$ After a $\frac{\pi }{4}$rotation, the approximated solution obtained for the local problem can be seen at [20,48]. The computations are given for $h_{min}=1$ and $h_{max}=2.$

The results provided by the numerical simulations seem to reflect an accurate approximation of the local setting by the nonlocal model we have proposed (see [20,48]). It is enough to have a look at the Figure 1, Figure 2 and Figure 3 below to be convinced of that statement:

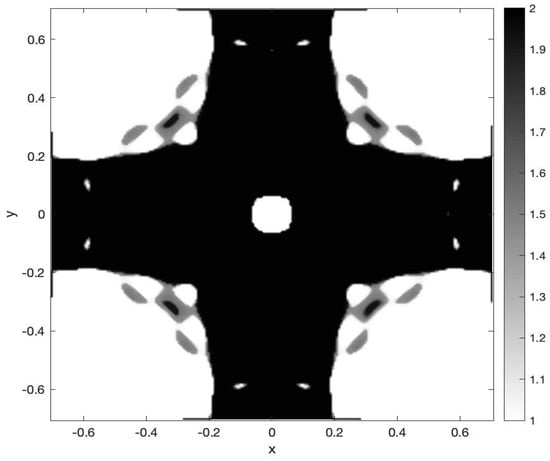
Figure 1. Approximated optimal control.

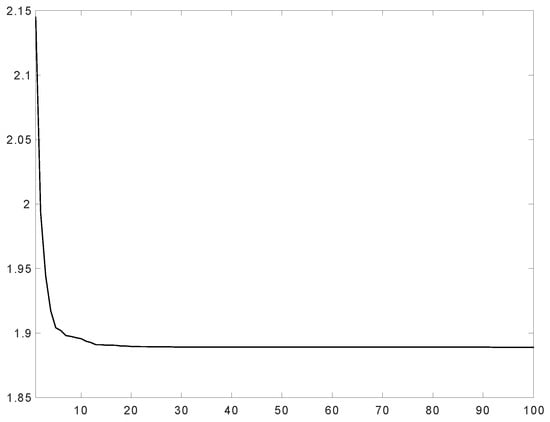
Figure 2. Compliancealong the iteration process.

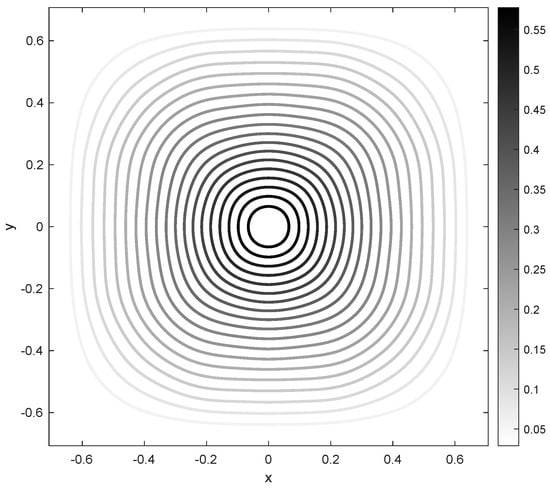
Figure 3. Approximationof the optimal estate.

Additional numerical information is contained in the adjoint table, where $\delta$ is the horizon, n the number of points used to discretized $\mathsf{\Omega }$, N is the number of iterations and $V_0$ the volume.

$\mathbf{\delta }$	$\mathit{n}$	$\mathit{N}$	${\mathit{V}}_{\mathbf{0}}$	Minimum Compliance
$0.01$	$44,521$	100	$1.5$	$1.886$

5.2. Example 2: The Allaire Minimization Problem

Instead of the local maximization principle analyzed in [18], we consider the minimization problem. The numerical procedure applied to the source $f\left(x,y\right)=1$ defined on the $\left[0,1\right]\times \left[0,1\right],$ with $h_{min}=1$ and $h_{max}=2,$ have given rise to the next optimal configuration, where again it is an approximation both of the nonlocal and local problem. The results are plotted in Figure 4, Figure 5 and Figure 6.

$\mathbf{\delta }$	$\mathit{n}$	$\mathit{N}$	${\mathit{V}}_{\mathbf{0}}$	Minimum Compliance
$0.01$	22,201	100	$1.5$	$0.021$

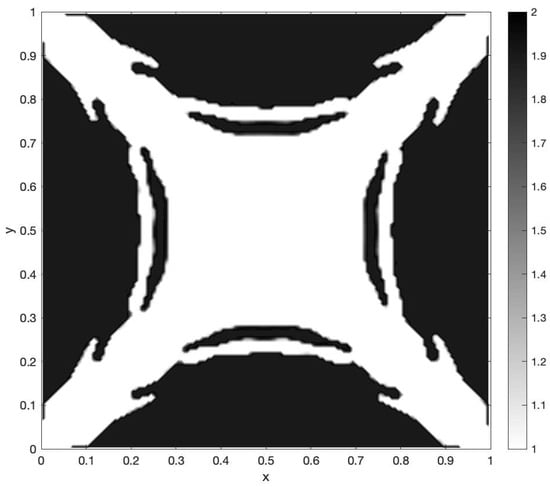
Figure 4. Approximated optimal control.

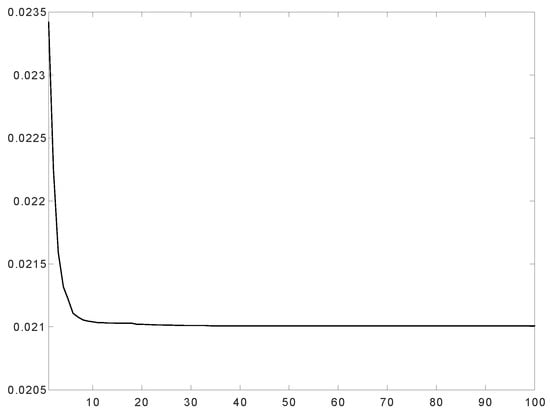
Figure 5. Compliance along the iteration process.

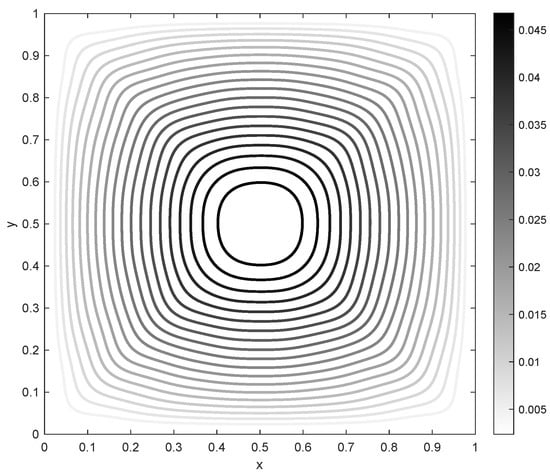
Figure 6. Approximation of the optimal estate.

5.3. Example 3

The speed of convergence is greatly influenced by the limits of variation given for the control. For some values of $h_{min}$ and $h_{max},$ the size of $\rho$ can be too small. This fact makes it necessary to perform a specific strategy to choose the size of the step. The example we now analyze is the same as in the previous case, only that the variation limits are $h\in [{10}^{-3},1].$ The following Figure 7, Figure 8 and Figure 9 contain the graphs of the obtained results:

$\mathbf{\delta }$	$\mathit{n}$	$\mathit{N}$	${\mathit{V}}_{\mathbf{0}}$	Minimum Compliance
$0.01$	22,201	100	$0.5005$	$0.0558$

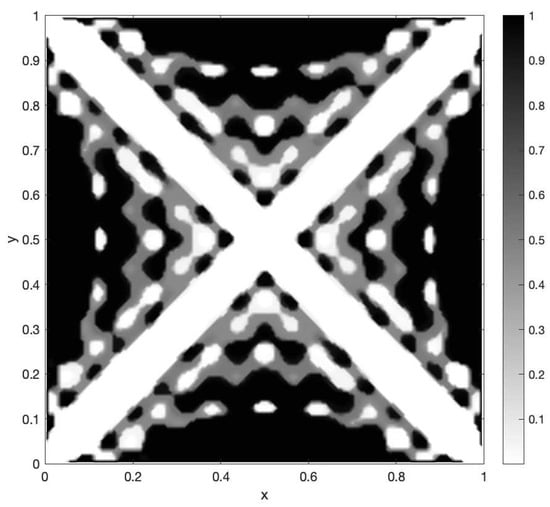
Figure 7. Approximated optimal control.

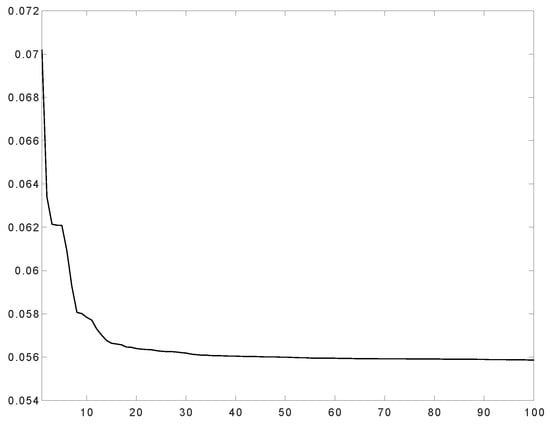
Figure 8. Compliance along the iteration process.

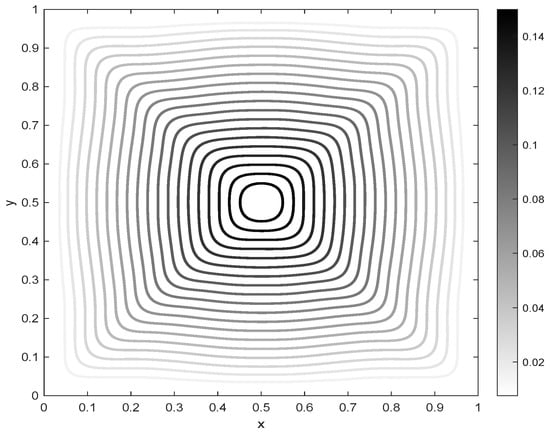
Figure 9. Approximation of the optimal estate.

6. Conclusions

The methodology, the proposed numerical algorithm, applied to the cases studied above provides confidence that the optimum will be fully achieved in all situations. Moreover, the scheme by itself demonstrates the existence of an optimum. Apart from this, from the exposed methodology, we can infer a way to find minimizing sequences whose associated states can belong to a broader set beyond the classical functional framework in which strict regularity conditions are assumed. We understand that this is an aspect that broadens the possibilities in the modelling of a phenomenon.

Concerning the numerics and the convergence, we must remark that the paper does not pursue any significant improvement compared to other algorithms. Nevertheless, as we have mentioned, all the examined examples ran at a very acceptable speed compared to the results obtained in previous works ([18,20,48] or [40] for a nonlocal formulation). It is worth noting that numerical analysis is necessary if we wish to effectively control the error of all the iterative processes. This aspect is particularly critical in a nonlocal model. Although some elementary procedures have been implemented to ensure accuracy, the problem is of some magnitude and requires further study. It must be noted that the replacement of derivatives by double integrals is a clear advantage in some aspects (provides richer modelling and allows a good first approximation with a few iterations), but, in contrast, the numerical complication derived from the double quadrature makes the problem very demanding.

The conclusion is that in this manuscript we have obtained a numerical method for compliance minimization, under the p-Laplacian constraint that proves the existence of an optimum, that converges to such an optimum and that does so with a low computational cost.

Future steps to complete the study would focus on refining the numerical techniques and verifying their use in problems with different constraints on the boundary or with other geometries for the domain $\mathsf{\Omega }$. The possibility of extending the proposal to models given by monotonic maximal operators has been the motivation of a work that is already in progress and that could give rise to interesting models in continuous media.