Abstract
Electric vehicles are anticipated to be essential components of future energy systems, as they possess the capability to assimilate surplus energy generated by renewable sources. With the increasing popularity of plug-in hybrid electric vehicles (PHEVs), conventional internal combustion engine (ICE)-based vehicles are expected to be gradually phased out, thereby decreasing greenhouse gases and reliance on foreign oil. Intensive research and development efforts across the globe are currently concentrated on developing effective PHEV charging solutions that can efficiently cater to the charging needs of PHEVs, while simultaneously minimizing their detrimental effects on the power infrastructure. Efficient PHEV charging strategies and technologies are necessary to overcome the obstacles presented. Forecasting PHEV charging loads provides a solution by enabling energy delivery to power systems based on anticipated future loads. We have developed a novel approach, utilizing machine learning methods, for accurately forecasting PHEV charging loads at charging stations across three phases of powering (smart, non-cooperative, and cooperative). The proposed Q-learning method outperforms conventional AI techniques, such as recurrent neural and artificial neural networks, in accurately forecasting PHEV loads for various charging scenarios. The findings indicate that the Q-learning method effectively predicts PHEV loads in three scenarios: smart, non-cooperative, and cooperative. Compared to the ANN and RNN models, the forecast precision of the QL model is higher by 31.2% and 40.7%, respectively. The Keras open-source set was utilized to simulate three different approaches and evaluate the efficacy and worth of the suggested Q-learning technique.
Keywords:
Q-learning; electric vehicles; artificial neural network; plug-in hybrid electric vehicles MSC:
68T07
1. Introduction
Electric vehicles (EVs) have been mainly integrated into power grids because of their significant benefit over traditional combustion engine vehicles, which includes bolstered energy self-sufficiency and diminished levels of carbon emissions [1]. There have been numerous creative works on EV recharge infrastructure [2,3]. The surging demand for EVs is introducing intricacy to the energy grid system, leading to difficulties in efficient management. One of the significant apprehensions for executives in this world is accurately projecting the charging capacity of automobiles, to determine their energy consumption requirements [4,5]. Recently, plug-in hybrid electric vehicle (PHEV) energy control methods have used reinforcement learning (RL) [6]. The incorporation of forecasting methods was also used in [7] to explore the merging of PHEVs into microgrids. Furthermore, Ref. [8] considered blockchain technology for trading energy. Additionally, Ref. [9] proposed PHEV energy management with data-driven techniques to estimate battery discharge depth.
The forecasting of EV charging station load has drawn a lot of interest in the literature. For instance, in [10], the load demand for Ev was predicted using online ride-hailing services. To model the load demands of PHEVs and EVs, the authors examined the stochastic load demand of EVs [11]. A statistical utilization strategy has been examined to forecast the PHEVs load profile. The energy shift at midday and night has been predicted using the inverse load flow and a localized charging time-shift procedure [12]. For example, Refs. [13,14] used charging stations with battery storage systems to supplement energy or capacity or to delay demand. Intelligent PHEV charging demand forecasting in [15] aims to keep a constant daily network load profile while ensuring that each PHEVs load requirement is fulfilled in [16]. Ensemble learning predicts load consumption of cooperative PHEVs using innovative data mining to forecast charging sites [17].
1.1. Literature Survey
The battery charging of PHEVs is primarily done at night because everyday vehicle travel considerably lowers the charging time. Due to the high number of these vehicles, early night charging of vehicles damages power infrastructure traits like overloading and fast ramping of energy sources. Increased EV adoption may also lead to more severe grid features like feeder overcrowding, unfavourable peak demand, increased power loss, decreased load factor, harmonic distortion, phase unbalance, etc. The charging of PHEVs during high demand has these negative impacts [18]. Smart recharge for electric vehicles is the remedy to the problems mentioned above [19]. EVSC can effectively handle EV charging, particularly at night, to satisfy the network’s technical restrictions. According to data, vehicles are typically only driven 4 to 5 percent of the time, with the remainder of the day being spent in parking lots or basements [20]. The extra storage space provided by the batteries of electric vehicles can be used to create a large-scale energy storage system [21].
PHEV owners have expressed high satisfaction with the cooperative charging of EVs, and grid characteristics are considered when deciding the number of EVs to be charged per time interval [22]. In addition to considering the use of renewable energy production in a power network, the EVSC process should also consider PHEV owners and technological limitations on renewable-based power [23]. PHEVs have the potential to contribute significantly to helping keep or enhance the normal functioning of a power grid. PHEV charging via EVSC can also provide extra services like frequency regulation [24]. The schematic diagram of EVSC is shown in Figure 1. Both centralized and decentralized types of charging—in which electric vehicles are refuelled in intelligent houses, at home or by fleet operators, as well as parking lots occupied by EVs parked overnight—can be used to refill the batteries of electric cars. EVSCs flexible charging and auxiliary services can reduce the energy cost of plug-in cars by as much as 60% when compared to conventional vehicles [25].
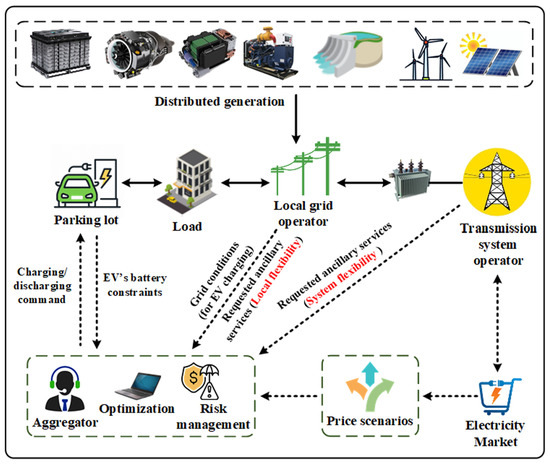
Figure 1.
A diagrammatic representation illustrating the charging process of plug-in hybrid electric vehicles within power distribution networks.
A company that operates a fleet of electric vehicles must be able to forecast its load in order to optimize the number of EVs, their charging rates and available charging sites. Additionally, more energy-efficient use of existing resources can be enabled by predicting the future capacity needs [26,27,28]. The load profile of EVs in particular geographic region results from the habits people have while driving and contributes to the overall demand for electricity [29,30]. A method has been developed to forecast electric vehicle travel patterns and arrival/departure times. In addition, an ensemble learning-based forecasting method can predict the number of charging stations required in any given area [31,32]. The proposed method was developed by combining three different types of learning algorithms: Linear regression (to find the weighting for each primary learner), recurrent neural networks, and long short-term memory. The ability of three neural network models to predict the load profile in an EVS has been examined in other research [33]. The Radial Basis Function technique has produced better results in load forecasting than the traditional method, but it also had a higher error rate and processing cost. In [34], six distinct deep-learning techniques have been examined from the EV usage prediction perspective. The methods included canonical LSTM, ANN, RNN, gated recurrent units, bi-directional LSTM forecasting algorithms, and stacked auto-encoders.
1.2. Motivation and Problem Statement
Deep learning (DL) techniques are increasingly being used to improve the prediction performance of highly nonlinear systems to reduce the computational burden on a design and allow the real-time application of complex controllers [34]. The literature achieves the aforementioned goals by utilizing a variety of machine learning (ML) methods [35]. Artificial neural networks (ANN) were mainly used in [36] for datasets with no time dependency between the accessible datasets. Time-varying data sets are commonly processed using recurrent neural networks (RNNs).RNNs and CNNs are two popular AI techniques used to gather data for text and media applications, respectively [12]. SARSA and Q-learning are two additional reinforcement learning techniques that facilitate real-time learning of intricate problems. The action-reward system underlies these techniques [32,33,34,35,36,37]. Consequently, the RL technique may impose a different reward for each activity that moves an agent from one condition to another. This paper foresees PHEV loads using one of the RL techniques, the Q-learning (QL) approach. Out of all possible actions and states, the QL method can identify the best ones. As a result, by using the outputs of other ML techniques, like ANN, LSTM, RNN, GRU, and CNN, as initial inputs, the efficacy of the QL technique can be improved [38].
Despite the variety of methods used to predict PHEV load demand [11,12,13], more research still needs to be focussed on an overarching tactic that encompasses all PHEV load demand scenarios, including smart, cooperative, and non-cooperative situations. In this study, the authors have explored the potential of an RL-based QL approach in forecasting PHEV load under diverse scenarios. This research evaluated three commonly used artificial intelligence techniques–RNN, ANN, and QL–to determine their efficacy in prediction. The investigation indicates that implementation of the QL technique, which leverages the initial outcomes of the ANN and RNN methodologies, yields enhanced predictive precision.
1.3. Real Contribution
The leading contributions and innovations of this article are as follows:
- A comprehensive investigation of load forecasting challenges for PHEV charging remains imperative through implementing RL, a potent tool for combining multiple ML models [6]. To address this matter, a new approach based on QL for forecasting load at EV charging stations has been introduced in this publication. QL has been frequently employed in problems with distinct states and actions. Our proposed QL model is suitable for the control task that demands ongoing response to the prevailing circumstances. The system comprises neural networks and deduces the differential for the state evolution of unknown epistemic uncertainty. This solution presents an opportunity to enhance the operational efficiency of PHEV charging, while also serving as a mechanism of reinforcement for energy dispatching within power grids.
- The recommended RL methodology for determining the optimal framework for PHEV load forecasting encompasses smart, cooperative, and non-cooperative scenarios. The developed QL approach exhibits superior efficiency, precision, and flexibility in PHEV load estimation when compared to traditional ANN and RNN models. Furthermore, incorporating modifications such as adjusting the epoch, hidden layer, and node quantities can significantly augment the accuracy of PHEV charging load predictions, as evidenced by empirical analyses.
1.4. Paper Organization
This article is organized as follows. Section 2 presents the technical background for the three models utilized in this paper. Section 3 describes the charging behaviour of the PHEVS. Section 4 presents the proposed framework for the PHEVs load forecasting. Section 5 and Section 6 show the evaluation criteria and QL-model forecasting performance with different network depths. The implementation of ANN, RNN and the proposed model and simulation results considering the test cases are described in Section 7. Sensitivity analysis, validation of the proposed model, QL in terms of speed, flexibility and accuracy, and discussion are presented in Section 8, Section 9, Section 10 and Section 11, respectively. Finally, Section 12 concludes the article.
2. Technical Background
The three models—ANN, RNN, and QL—used in this paper are briefly introduced in this part.
2.1. ANN
Figure 2a shows the schematic unit of ANN [23]. The Artificial Neural Network (ANN) comprises three distinctive layers i.e., input layer (X), hidden layer (H), and output layer (Y) that operate using multiple nodes. As shown in Figure 2a, a weight () is used in every line of the ANN technique in between each pair of successive layers (ith previous layer, and jth present layer). The Equation (1) can be used to determine each output node:
In the context of neural networks, the jth output of the pth layer is represented by , whereas represents the jth output of the th layer. Similarly, and respectively refer to the bias and activation function of the jth node in the pth layer. Furthermore, denotes the number of nodes in the th layer.
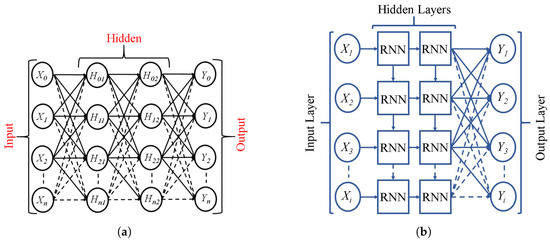
Figure 2.
ANN and RNN Blocks Techniques. (a) ANN Block. (b) RNN Block.
2.2. RNN
The RNN technique’s block layout is depicted in Figure 2b. The time-series data set’s future is predicted using RNNs [24]. It can be applied to various chores, including predicting weather patterns, green energy trends, stock market trends, and other activities. The line the RNN method uses between each hidden layer’s node is the primary distinction between it and the ANN technique. The output of the RNN unit is shown in Equation (2):
At time t, the state of the hidden layers is denoted by , while at time , it is indicated by . Similarly, the input and output of the RNN unit at time t are represented by and , correspondingly. K, W and U are the weight matrices of , , and respectively. Both f and g are the activation functions (softmax, tanh, etc.) of memory and output of the RNN unit, while b and d are the biases.
2.3. QL
The QL method, which uses the Markov decision process to select the most appropriate action from all possible options, is one of the model-free RL techniques [25,26]. QL falls under the category of off-policy methods. When choosing the best future action, the QL technique selects the initial state, reward, current state, and accessible activities in a very similar way to the SARSA. The primary equation, which is used by the QL technique to choose, presented in (3):
where and are the current states and current actions of the QL technique. is the Q-value updated Q-value of and can be denoted as . The QL method has a learning rate that satisfies the condition , while the discount factor is between 0 and 1 (). The optimal future value estimation is given by . The proposed QL reward for the future action and state is . The initial conditions for the Q-value in this proposed technique are zero. The optimal solution for PHEV loads is found using the QL method. The proposed QL technique updates the Q-value depending on and after each iteration. The best course of action for the subsequent steps is determined using Equation (4):
3. Charging Behavior of PHEVs
The charging strategy, charging time, amount of charged PHEVs, battery capacity, battery state of charge (), and start time are all unknown variables that affect PHEV load behaviour. The three charging cases for PHEVs—smart, cooperative, and non-cooperative—are explored in this article.
3.1. Non-Cooperative PHEV Charging
The simplest charging approach for PHEVs is the non-cooperative strategy, which involves plugging them into charging stations. PHEVs are believed to commute daily from their homes in the morning to their homes in the evening. In this instance, around 5:30 p.m., when most people get home, most PHEVs are hooked up and begin charging. As a result, this strategy considers a limited range uniformly distributed probability density function (PDF) with a charging start time of 5:30 p.m. Such a PDFs mathematical form is provided in Equation (5) [25]:
where u and v are constant values, is the charging start time of PHEV.
3.2. Cooperative PHEV Charging
Stockholders in the cooperative charging plan typically link their cars to chargers during off-peak hours to prevent confrontation with the sunset peak hours, when power costs are higher. Consequently, to save money on their electricity prices, people defer charging until after 9:30 p.m. The cooperative charging strategy presented in Equation (6) is then modelled using the provided pdf:
3.3. Smart PHEV Charging
A smart charging plan schedules charging when energy is most reasonably priced, demand is at its lowest point, or excess capacity exists. All smart charging techniques adhere to the fundamental principle that a vehicle should only be charged when doing so benefits both the owner and the utility. A typical pdf, as shown in Equation (7), illustrates the difficulty of choosing the charging start time using various smart charging options [24]:
where is the mean of values and is the covariance.
Once the PHEV is connected to the home charger, the battery begins to charge. The battery’s leftover is calculated using the vehicle’s daily mileage. The ratio of available energy to maximal stored energy is known as a battery’s . The daily mileage of a car is said to follow a log-normal PDF presented in Equation (8):
The at the time of plug-in is then calculated using the vehicle’s driven mile and all-electric range () as follows in Equation (9):
A multitude of PHEVs exist, including the PHEV-20, PHEV-30, PHEV-40, and PHEV-60, each characterized by a unique denoted by a numerical subscript. The PHEV-20 has been selected as a primary example in the investigation of market potential over time [29], but consideration may be extended to additional PHEV models given the unrestricted nature of the methodology. Equation (10) is used to determine the charging time of a PHEV [29].
where , , and T and the PHEV battery capacity (in kWh), depth of discharge of PHEV battery, charging efficiency, and PHEV charger rate (kW), respectively. The charging types for PHEVs are outlined in the Table 1, and are contingent on the charging levels provided by the charger [20]. Ethics dictate that the first two charging stages are suitable for PHEVs that are charged domestically. As the charging stations with the third stage are specifically constructed for public transportation, this write-up excludes their inclusion. As per Table 2, PHEVs are segregated into four groups, with each group possessing characteristic market and share traits. In this study, the market share of PHEVs can be represented with a discrete distribution. Each PHEV group is arbitrarily selected from the market shares shown in Equations (11) and (12) using a normal distribution.
The proposed QL approach can compile training data to forecast PHEV charging demand using three simulated charging methods: Smart, non-cooperative, and cooperative, based on the (5) to (12). Min and Max represent the minimum and maximum values, respectively.

Table 1.
Various Charger Types for PHEVs.

Table 2.
Various Classes for PHEVs.
4. Proposed QL-Based PHEV Charging Load Forecasting Framework
In this article, using the results of RNN and ANN, we developed a novel RL-based model that optimally forecasts the load demands of smart, cooperative, and non-cooperative PHEVs.The proposed model has two major parts: (1) Data Preprocessing Phase, (2) QL-based forecasting considering the optimal results of ANN and RNN as initial inputs. Figure 3 shows the structure of the proposed reinforcement learning-based forecasting model.
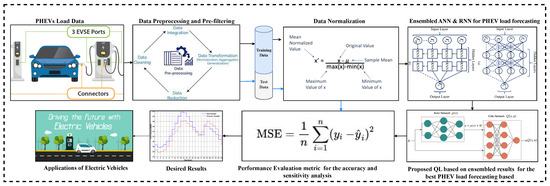
Figure 3.
Proposed QL based PHEVs load forecasting Model.
4.1. Data Source
Caltech has made the ACN-Data [39] available to academics for research purposes; this dataset comprises EV charging events from various workplaces. More than 30,000 charging events are organized in the dataset from two Californian workplace charging locations, the Jet Propulsion Laboratory, and the Caltech campus. For this article, our test data consists of charging information collected from the charging station on the Caltech campus. The ACN (Adaptive Charging Network) is open to the public and equipped with a 50 kW DC rapid charger, frequently used by non-drivers. The dataset covers details of all transactions made within the architecture of ACN, with 54 EV supply equipment. The dataset’s related data categories are described in Table 3. The exactitude of load forecasting depends on data pre-processing because the initial data will contain anomalies and missing numbers.

Table 3.
Data fields in ACN-Data.
4.2. Preprocessing Module
The EV charging stack data were initially analyzed and refined for inquiry. To enable real-time charging control based on energy usage during charging periods, it is imperative to establish the average hourly charging capacity of the stations, taking into account the variability of data encountered due to its random nature. To achieve this, the dataset was pre-processed, whereby inaccurate data points were replaced with the average charging load observed during a given time slot across different days. This step was essential to ensure accurate forecasting without being impacted by erroneous data.
For practical reasons, the data pertaining to the charging load operation were bifurcated into training and test sets using a proportion of 0.7/0.3. The model was suitably trained with the training instances, while the final function evaluation utilized the test collection. Multiple neural networks were employed to learn from the charging load data; however, the efficiency of these networks was significantly influenced by the size of the data. As a resolution, the input data of the forecast model were altered through min-max normalisation, which constrained the information within a specific limit (0–1), as illustrated in Equation (13):
4.3. QL-Based Forecasting Module
The three primary learners, ANN, RNN, and QL, were trained using the training set by the training technique. Following the last training session, predictions were made using the training data and prepared elementary learners. Forecasts from the training data and the proper labels were then set as the features. During the testing process, predictions were generated using the trained base of learners on test data. The forecasts made by the primary learners were then used to test the learned weighted averaging model. After reversing normalization, the outcomes were obtained, and the test labels and marks used to calculate the prediction accuracy.
- When using the ANN technique to forecast the load on PHEVs, the input and output ANN units should be chosen appropriately. Due to the time series nature of PHEVS load data, the ANN unit utilized prior PHEV load data. The baseline 24-h PHEVs load data were helpful for more accurate one-hour-ahead load forecasting. The deployment of ANN and RNN for predicting one hour ahead is shown in Figure 4.
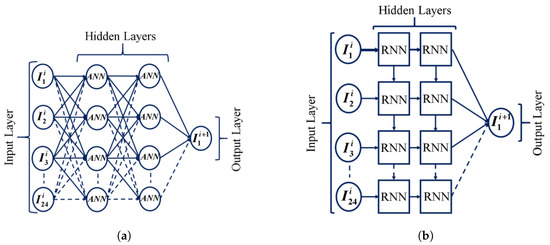 Figure 4. Employing artificial neural network (ANN) and recurrent neural network (RNN) methodologies to forecast plug-in hybrid electric vehicle (PHEV) demand. (a) The PHEV load forecasting by ANN method. (b) The PHEV load forecasting by RNN method.
Figure 4. Employing artificial neural network (ANN) and recurrent neural network (RNN) methodologies to forecast plug-in hybrid electric vehicle (PHEV) demand. (a) The PHEV load forecasting by ANN method. (b) The PHEV load forecasting by RNN method. - The proposed QL method for the PHEVs load forecasting used the previous days’ ANN and RNN forecasting results. In hopes of identifying the best day-ahead PHEV load forecasting, the proposed QL approach chose the best course of action based on the output of ANN and RNN. The proposed QL model’s reward function is shown in Equation (14):where is the random number of the jth action. The proposed approach chose one of two possible courses of action for each time horizon ( for ANN and for RNN). The power forecast for the ANN or RNN method was . Additionally, contains the PHEV data for the tth period. The ANN and RNN predicted results were used in the devised method to predict the PHEV future load and compare it with actual data. Thus, 24 optimal actions were chosen in the proposed QL approach for the day ahead horizon. Therefore t can be any integer between 1 and 24 for the day ahead horizon. , , and were the optimal, ANN, and RNN PHEV load of the tth day, respectively. The values between 0 and 2 were used to improve the ability of the QL technique to find the best search locations. When the action was 1, the RNN technique chose the reward function. Alternatively, the reward function was determined from the results of the ANN method.
QL is a learning system that is built on values. Value-based algorithms update the value function based on a calculation (particularly Bellman equation). The other policy-based version calculates the value function using the most recent policy improvement’s greedy policy. QL is an ad hoc student. This implies that it learns the value of the best strategy independent of the agent’s behaviours. On the other hand, an on-policy learner learns the value of the policy being carried out by the agent, including the exploration stages, and it will find an optimum strategy that considers the exploration implicit in the approach.
5. Evaluation Criteria
The predicting performance of the analyzed techniques was evaluated using the mean square error (MSE), a standard evaluation criterion. Considering and are the actual and expected loads of the EV charging station at time step t, respectively. The MSE measured the errors between the real and the forecasting values, which can be formulated in Equation (15) as below:
6. QL-Model Forecasting Performance with Different Network Depths
We evaluated the predicting effectiveness in comparison to various network levels. The results of the Mean Squared Error (MSE) and Mean Absolute Error (MAE) that were found when the layers were changed from two to six when using the prepared dataset are shown in Figure 5. The proposed QL model worked best with five layers. As the network depth increased from two to five, the MSE and MAE values became smaller, and the prediction performance improved. Properly boosting network depth and settings significantly enhanced the predicting performance. Due to increased parameter redundancy and reduced data variety, as a network’s depth grows, it may overfit and suffer from performance loss. The training period needed for each layer of QL is listed in Table 4. As layers increased, factors for training optimization increased, causing a longer required time. More layers were needed to improve forecast accuracy, resulting in time consumption.
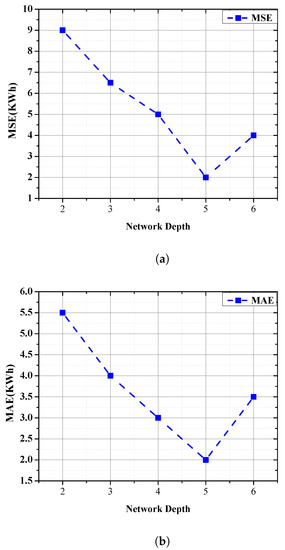
Figure 5.
The metrics (a) MSE and (b) MAE for the QL model, adjusted for alterations in network depth. (a) MSE versus different network layers. (b) MAE versus different network layers.

Table 4.
Training time for different layers of QL.
Convergence of the QL
In Figure 6, the state marks the convergence of the QL model. The optimal value function is approached as converges. The synchronized parallel Q-learning procedure involves offline learning of the QL model, in which batch updates of all state-action pairs (Q-functions) occur at each training instance. The step sizes utilized in this process are inversely proportional to the number of visits (updates) to each combination of state and action.
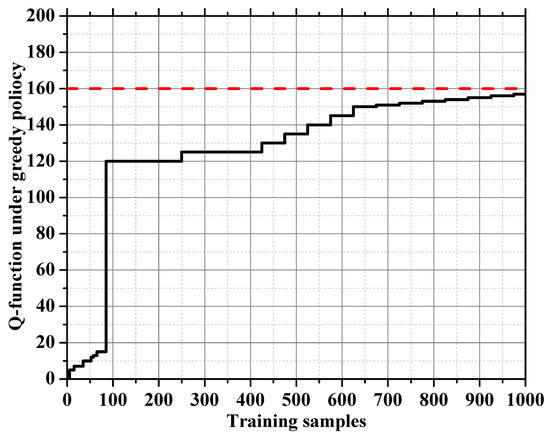
Figure 6.
The convergence of the QL at state (c, m) = (0, 50). The red dotted line signifies the ideal value, while the black dotted line denotes the point at which convergence occurs.
7. Test Cases Simulations and Results
This section compares three techniques (RNN, ANN, and QL) in various scenarios to show the benefits and efficacy of the proposed ML techniques. The number of hidden layers used for RNN and ANN is shown in Table 5. The number 24 is the input for the ML methods. (For example, the charging load for the following hour is forecast using the most current 24-h data). This analysis estimated the devised PHEV load forecasting approach using the free and open-source Keras software [26]. Additionally, MATLAB was utilized to build the original PHEV data for various charging techniques.

Table 5.
Examining and projecting the charging demand of PHEVs utilizing ANN, RNN, and QL approaches (MSE, MAPE and Epoch) across various penetrations (30%, 60% and 90%).
7.1. Load Forecasting of Non-Cooperative PHEVs Charging
This article predicts non-cooperative PHEV load demands using ML approaches such as RNN, ANN, and the proposed QL techniques. A predicted load with a 30% PHEV adoption is shown in Figure 7a. The necessary information is given in Table 5, along with the epoch numbers and means square errors (MSEs) used for the different ML techniques in this work during the training phase. ANN and QL methods have lower MSEs but higher accuracies than the RNN strategy. The more significant epoch number used during training was the primary factor that makes the ANN technique perform better in terms of accuracy than the RNN method. The non-cooperative PHEV hourly load forecasting with 60% penetration is shown in Figure 7b. The charging of the PHEV load started at 5:30 p.m. and ended at 5:30 a.m. depicted in Figure 7. Additionally, the AI technique had a 60% penetration of PHEV load and an insignificant MSE (significant accuracy). Table 5 shows that the RNN method had a more significant mean squared error (MSE) and smaller epoch number than other techniques. The devised QL method predicted PHEV load using ANN or RNN outcomes with lower MSEs than the other two methods, which makes this approach more accurate. This illustration shows how the QL approach was more valuable than ANN and RNN for predicting PHEV loads.
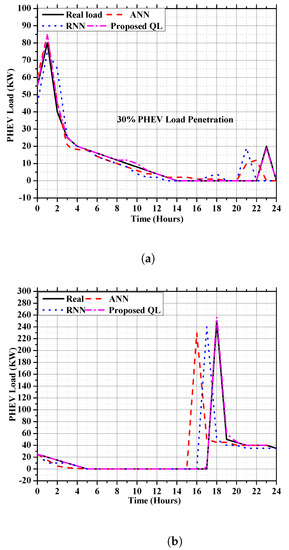
Figure 7.
Non-cooperative charging PHEV load forecasting with a 30% and 60% penetrations. (a) Non-cooperative charging PHEV load forecasting with a 30% penetration. (b) Non-cooperative charging PHEV load forecasting with a 60% penetration.
7.2. Load Forecasting of Cooperative PHEVs Charging
The predicted load consumption for cooperative PHEVs is given in this subsection. When PHEV penetration is 30%, Figure 8a shows the cooperative PHEVs hourly load forecasting with 30% penetration using ANN, RNN, and QL algorithms. Training iterations (1000 (ANN), 3000 (RNN), and 10,000 (QL)) were used. The cooperative PHEV charging strategy lasted from 7:00 p.m. to 11:00 a.m. as shown in Figure 8. As shown in Table 5, the QL method predicted the cooperative PHEVs hourly charging load more precisely (with a reduced MSE) than the ANN and RNN approaches. Additionally, the output of the QL method in Figure 8 demonstrates less deviation from the actual data.
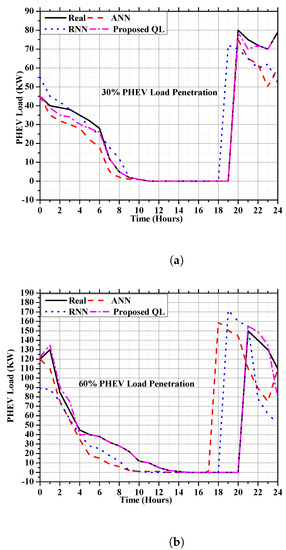
Figure 8.
Cooperative charging PHEV load forecasting with a 30% and 60% penetrations. (a) Cooperative charging PHEV load forecasting with a 30% penetration. (b) Cooperative charging PHEV load forecasting with a 60% penetration.
7.3. Load Forecasting of Smart PHEVs Charging
The 60% and 30% penetration levels of the smart PHEVs charging hourly load are forecasted in this subsection. The training iterations (1000 (ANN), 3000 (RNN), and 10,000 (QL)) are used. Figure 9 shows that all techniques were capable of forecasting PHEV loads with accuracy. However, because the RNN method employed fewer iterations than the ANN and QL techniques, its error in calculating the PHEV load was more important. The proposed QL approach has a reduced MSE (a better precision) than the ANN and RNN methods because it chose the optimal policy from the potential actions for each state (each hour). The proposed strategy’s accuracy can be improved by applying the QL method to more extensive and diverse data sets.
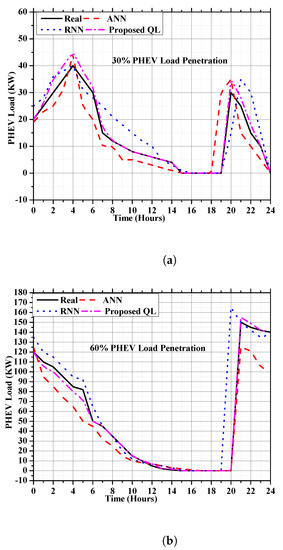
Figure 9.
Smart charging PHEV load forecasting with a 30% and 60% penetrations. (a) Smart charging PHEV load forecasting with a 30% penetration. (b) Smart charging PHEV load forecasting with a 60% penetration.
8. Sensitivity Analysis of Three Charging Techniques
Figure 10 shows the sensitivity evaluations of three PHEV charging load strategies implemented with different hidden layers, node numbers, and several neurons in the proposed QL. Figure 10a shows how the proposed QL method’s forecasting accuracy varied with different epoch spans when increased from three to four hidden layers, each having 200–400 nodes. Table 5 shows that when more nodes and hidden layers were used in the ML model, it accurately predicted PHEV loads for the cooperative charging method. Table 5 shows that the quality of a forecast was improved by increasing the number of nodes in each hidden layer. It can be seen from the Figure 10b that the QL technique for the non-cooperative PHEV load forecasting was unable to model the PHEV load filling consistently. The more layers and nodes a QL has, the better it can handle large datasets. Figure 10c shows the sensitivity analysis of the QL method for smart PHEV load forecasting with various nodes and hidden layers when penetration was 30%. Therefore, it can accurately predict PHEV load if the proposed QL method employed more nodes and hidden layers than other techniques—such as ANNs or RNNs.
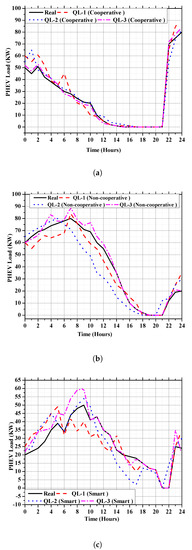
Figure 10.
QL sensitivity analysis for the three PHEV charging (Cooperative, Non-cooperative and Smart) (kW). (a) QL sensitivity analysis for cooperative PHEV charging (kW). (b) QL sensitivity analysis for non-cooperative PHEV charging (kW). (c) QL sensitivity analysis for smart PHEV charging (kW).
9. Validation of Proposed QL
To produce accurate forecasting results for comparison, the parameters and hyperparameters of the QL approach should be developed appropriately. The validation test selected these values through trial and error. For instance, the MAPE evaluated QL efficiency, as seen in Figure 11. The QL with five hidden layers among ten guaranteed the best MAPE and the QL selected 41 hidden neurons among fifty to achieve the smallest MAPE.
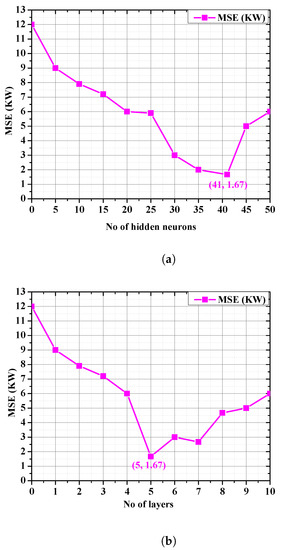
Figure 11.
Demonstration of QLs validity with a various number of hidden neurons and layers. (a) Demonstration of QLs validity with various numbers of hidden neurons. (b) Demonstration of QLs validity with various numbers of hidden layers.
10. QL in Terms of Speed, Flexibility and Accuracy
The flexibility, speed, and accuracy of the three DL methods are discussed with their ability to predict PHEV charging loads.
10.1. Faster Speed
In this paper, we integrate two ML methods—ANN and RNN—to enhance the QL method’s real-time ability to forecast PHEV load. Our three ML methods focus on training times but vary substantially across applications. When ANN and RNN have trained accurately with PHEV data, their networks can efficiently predict the input data to implement the QL technique in real-time. Therefore, utilizing ANN and RNN techniques to their full potential can significantly improve the QL technique’s capability to carry out this process quickly.
10.2. Improved Accuracy
It is essential to examine all DL techniques currently being used; after evaluating the three ML techniques described in this article, the most efficient QL for forecasting PHEV charging loads was chosen. From the results of the simulations, predictions from ML techniques may be inaccurate if there are substantial variations from the initial charging points. Therefore, the QL approach, which gets its data from ANN and RNN, may precisely forecast optimal PHEV charging. As Table 5 demonstrates, increasing the epoch number can reduce forecasting errors.
10.3. Flexibility
The simulation results show that ML techniques can be used to model PHEVs by training charge methodologies. Any complex load-charging scenario can be variably predicted by increasing the training iterations for ML techniques. The estimate for PHEV charging potential was correct as a consequence. Forecasting PHEV loads for cooperative, non-cooperative, and smart charging can be elevated by combining nodes and hidden layers of ANN and RNN techniques. Moreover, the QL technique’s capacity to choose the best course of action out of numerous choices can be improved by having more precise estimates of PHEV load charging.
11. Discussion
A significant study is being done to increase the accuracy of load forecasting for PHEV charging sites, which can both guide the efficient dispatch of the power system and advance the growth of EVs. This study proposes a QL method for forecasting the demand at electric car charging sites. The data preprocessing unit handles the original dataset, builds time series data, and adds characteristics to prediction data in our technique. We use the QL forecasting technique and approximate the posterior distribution using variational inference. Results show the success of this method in predicting PHEV charging station demand. Comparing the devised method to some forecast methods further indicates its better performance. The designed model is around 38.2%, 41.5% lower in MSE and MAE, and 17.9% higher than the standard techniques, according to the findings of point forecasting. The devised strategy can be used to forecast load for PHEV charging stations in the real world, as evidenced by its outstanding performance on various datasets.
12. Conclusions
This manuscript presents a novel QL approach for PHEV load forecasting employing ANN and RNN techniques. Various PHEV models, such as smart, cooperative, and non-cooperative, are analyzed in this study. Our results indicate that the proposed QL method achieved accurate predictions of PHEV load charging by leveraging data from the ANN and RNN techniques. Importantly, our findings suggest that the QL method outperformed the ANN and RNN techniques in predicting PHEV loads accurately, as substantiated by the simulation outcomes. Table 5 shows that in the worst-case scenario for PHEV charging (smart charging), the QL method exhibited superior performance compared to traditional ANN and RNN techniques, surpassing them by over 60%. Furthermore, increasing the number of iterations demonstrated that the ANN technique delivers more precise predictions of PHEV loads (MSE) than the RNN approach. The QL methodology under consideration demonstrates superior tracking capabilities for PHEV loads when compared to ANN and RNN techniques, exhibiting greater precision and adaptability in the process. Further enhancements in the form of adjustments to the hidden layer, epoch, and node numbers have been shown to significantly enhance the accuracy of PHEV charging load forecasts, as corroborated by the case studies.The forecasting methodology developed here demonstrates the potential for future implementation in expansive power networks that contain complex PHEV loads. The performance of this probabilistic forecasting technique can be improved through ongoing optimization efforts. Reliable load projections derived from PHEV charging facilities will facilitate a structured approach to electric vehicle charging, and effectively reduce energy usage variations while optimizing distribution network resource allocation. We are committed to further forecasting the load from various charging stations, including those with AC, DC, and higher power capabilities. We plan to extend our suggested model to more PHEV charging data sets. Additionally, we intend to utilize this methodology in additional applications, including dispersed grid capacity forecasting and wind power forecasting, to expand its potential impact.
Author Contributions
Conceptualization, M.Z.; Methodology, M.B.R.; Software, M.Z.; Validation, M.Z., N.F.A. and M.B.R.; Investigation, M.B.R.; Writing—original draft, M.Z. and M.B.R.; Writing—review & editing, M.B.R.; Visualization, N.F.A.; Project administration, N.F.A.; Funding acquisition, N.F.A. All authors have read and agreed to the published version of the manuscript.
Funding
The authors extend their appreciation to the Deputyship for Research and Innovation, Ministry of Education in Saudi Arabia for funding this research work through project number 223202.
Data Availability Statement
The dataset utilized in our publication can be accessed at the following link: https://ev.caltech.edu/dataset, accessed on 2 March 2023.
Conflicts of Interest
The authors affirm that there are no conflict of interest.
References
- Taherzadeh, E.; Javadi, S.; Dabbaghjamanesh, M. New optimal power management strategy for series plug-in hybrid electric vehicles. Int. J. Auto. Technol. 2018, 19, 1061–1069. [Google Scholar] [CrossRef]
- Moeini, A.; Zhao, H.; Wang, S. A current-reference-based selective harmonic current mitigation PWM technique to improve the performance of cascaded H-bridge multilevel active rectifiers. IEEE Trans. Ind. Electron. 2018, 65, 727–737. [Google Scholar] [CrossRef]
- Moeini, A.; Wang, S. The state of charge balancing techniques for electrical vehicle charging stations with cascaded H-bridge multilevel converters. In Proceedings of the 2018 IEEE Applied Power Electronics Conference and Exposition (APEC), San Antonio, TX, USA, 4–8 March 2018; pp. 637–644. [Google Scholar]
- Liu, Z.; Wen, F.; Ledwich, G. Optimal planning of electric-vehicle charging stations in distribution systems. IEEE Trans. Power Deliv. 2012, 28, 102–110. [Google Scholar] [CrossRef]
- Zheng, Y.; Dong, Z.Y.; Xu, Y.; Meng, K.; Zhao, J.H.; Qiu, J. Electric vehicle battery charging/swap stations in distribution systems: Comparison study and optimal planning. IEEE Trans. Power Syst. 2013, 29, 221–229. [Google Scholar] [CrossRef]
- Liu, T.; Hu, X.; Hu, W.; Zou, Y. A heuristic planning reinforcement learning-based energy management for power-split plug-in hybrid electric vehicles. IEEE Trans. Ind. Informat. 2019, 15, 6436–6445. [Google Scholar] [CrossRef]
- Chen, C.; Duan, S. Optimal integration of plug-in hybrid electric vehicles in microgrids. IEEE Trans. Ind. Informat. 2014, 10, 1917–1926. [Google Scholar] [CrossRef]
- Kang, J.; Yu, R.; Huang, X.; Maharjan, S.; Zhang, Y.; Hossain, E. Enabling localized peer-to-peer electricity trading among plug-in hybrid electric vehicles using consortium blockchains. IEEE Trans. Ind. Informat. 2017, 13, 3154–3164. [Google Scholar] [CrossRef]
- Xie, S.; Qi, S.; Lang, K. A data-driven power management strategy for plug-in hybrid electric vehicles including optimal battery depth of discharging. IEEE Trans. Ind. Informat. 2019, 16, 3387–3396. [Google Scholar] [CrossRef]
- Xing, Q.; Chen, Z.; Zhang, Z.; Huang, X.; Leng, Z.; Sun, K.; Chen, Y.; Wang, H. Charging demand forecasting model for electric vehicles based on online ride-hailing trip data. IEEE Access 2019, 7, 137390–137409. [Google Scholar] [CrossRef]
- Alizadeh, M.; Scaglione, A.; Davies, J.; Kurani, K.S. A scalable stochastic model for the electricity demand of electric and plug-in hybrid vehicles. IEEE Trans. Smart Grid. 2014, 5, 848–860. [Google Scholar] [CrossRef]
- Koyanagi, F.; Uriu, Y. A strategy of load leveling by charging and discharging time control of electric vehicles. IEEE Trans. Power Syst. 1998, 13, 1179–1184. [Google Scholar] [CrossRef]
- Ortega-Vazquez, M.A.; Bouffard, F.; Silva, V. Electric vehicle aggregator/system operator coordination for charging scheduling and services procurement. IEEE Trans. Power Syst. 2013, 28, 1806–1815. [Google Scholar] [CrossRef]
- Dai, Q.; Cai, T.; Duan, S.; Zhao, F. Stochastic modeling and forecasting of load demand for electric bus battery-swap station. IEEE Trans. Power Deliv. 2014, 29, 1909–1917. [Google Scholar] [CrossRef]
- Kisacikoglu, M.C.; Erden, F.; Erdogan, N. Distributed control of PEV charging based on energy demand forecast. IEEE Trans. Ind. Inform. 2018, 14, 332–341. [Google Scholar] [CrossRef]
- Gomez-Quiles, C.; Asencio-Cortes, G.; Gastalver-Rubio, A.; Martinez-Alvarez, F.; Troncoso, A.; Manresa, J.; Riquelme, J.C.; Riquelme-Santos, J.M. A novel ensemble method for electric vehicle power consumption forecasting: Application to the Spanish system. IEEE Access 2019, 7, 120840–120856. [Google Scholar] [CrossRef]
- Xydas, E.S.; Marmaras, C.E.; Cipcigan, L.M.; Hassan, A.S.; Jenkins, N. Electric vehicle load forecasting using data mining methods. In Proceedings of the IET Hybrid and Electric Vehicles Conference 2013 (HEVC 2013), London, UK, 6–7 November 2013; pp. 1–6. [Google Scholar]
- Nguyen, V.L.; Tran-Quoc, T.; Bacha, S.; Nguyen, B. Charging strategies to minimize the peak load for an electric vehicle fleet. In Proceedings of the IECON 2014-40th Annual Conference of the IEEE Industrial Electronics Society, Dallas, TX, USA, 29 October–1 November 2014; pp. 3522–3528. [Google Scholar] [CrossRef]
- Mal, S.; Chattopadhyay, A.; Yang, A.; Gadh, R. Electric vehicle smart charging and vehicle-to-grid operation. Int. J. Parallel Emergent Distrib. Syst. 2013, 28, 249–265. [Google Scholar] [CrossRef]
- Yilmaz, M.; Krein, P.T. Review of benefits and challenges of vehicle-to-grid technology. In Proceedings of the 2012 IEEE Energy Conversion Congress and Exposition (ECCE), Raleigh, NC, USA, 15–20 September 2012; pp. 3082–3089. [Google Scholar] [CrossRef]
- Oshnoei, A.; Kheradmandi, M.; Muyeen, S.M. Robust control scheme for distributed battery energy storage systems in load frequency control. IEEE Trans. Power Syst. 2020, 35, 4781–4791. [Google Scholar] [CrossRef]
- Ahmadi, A.; Tavakoli, A.; Jamborsalamati, P.; Rezaei, N.; Miveh, M.R.; Gandoman, F.H.; Heidari, A.; Nezhad, A.E. Power quality improvement in smart grids using electric vehicles: A review. IET Electr. Syst. Transp. 2019, 9, 53–64. [Google Scholar] [CrossRef]
- Weis, A.; Jaramillo, P.; Michalek, J. Estimating the potential of controlled plug-in hybrid electric vehicle charging to reduce operational and capacity expansion costs for electric power systems with high wind penetration. Appl. Energy 2014, 115, 190–204. [Google Scholar] [CrossRef]
- Zhang, J.; Yan, J.; Liu, Y.; Zhang, H.; Lv, G. Daily electric vehicle charging load profiles considering demographics of vehicle users. Appl. Energy 2020, 274, 115063. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Z.; Liu, P.; Zhang, Z. Energy consumption analysis and prediction of electric vehicles based on real-world driving data. Appl. Energy 2020, 275, 115408. [Google Scholar] [CrossRef]
- Mackenzie, J.; Roddick, J.F.; Zito, R. An evaluation of HTM and LSTM for short-term arterial traffic flow prediction. IEEE Trans. Intell. Transp. Syst. 2019, 20, 1847–1857. [Google Scholar] [CrossRef]
- Alquthami, T.; Zulfiqar, M.; Kamran, M.; Milyani, A.H.; Rasheed, M.B. A performance comparison of machine learning algorithms for load forecasting in smart grid. IEEE Access 2022, 10, 48419–48433. [Google Scholar] [CrossRef]
- Zulfiqar, M.; Kamran, M.; Rasheed, M.B.; Alquthami, T.; Milyani, A.H. A hybrid framework for short term load forecasting with a navel feature engineering and adaptive grasshopper optimization in smart grid. Appl. Energy 2023, 338, 120829. [Google Scholar] [CrossRef]
- Li, Q.; Wang, F.; Wang, J.; Li, W. LSTM-based SQL injection detection method for intelligent transportation system. IEEE Trans. Veh. Technol. 2019, 68, 4182–4191. [Google Scholar] [CrossRef]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef]
- Rostami, M.-A.; Kavousi-Fard, A.; Niknam, T. Expected cost minimization of smart grids with plug-in hybrid electric vehicles using optimal distribution feeder reconfiguration. IEEE Trans. Ind. Informat. 2015, 11, 388–397. [Google Scholar] [CrossRef]
- Qian, K.; Zhou, C.; Allan, M.; Yuan, Y. Modeling of load demand due to EV battery charging in distribution systems. IEEE Trans. Power Syst. 2010, 26, 802–810. [Google Scholar] [CrossRef]
- Li, G.; Zhang, X.-P. Modeling of plug-in hybrid electric vehicle charging demand in probabilistic power flow calculations. IEEE Trans. Smart Grid 2012, 3, 492–499. [Google Scholar] [CrossRef]
- Zurada, J.M. Introduction to Artificial Neural Systems; West Publishing Company: St. Paul, MN, USA, 1992; Volume 8. [Google Scholar]
- Hecht-Nielsen, R. Theory of the backpropagation neural network. In Neural Networks for Perception; Elsevier: Amsterdam, The Netherlands, 1992; pp. 65–93. [Google Scholar]
- Rummery, G.A.; Niranjan, M. On-Line Q-Learning Using Connectionist Systems; Department of Engineering, University of Cambridge: Cambridge, UK, 1994; Volume 37. [Google Scholar]
- Chollet, F. Keras. 2015. Available online: https://keras.io (accessed on 22 February 2023).
- Liu, D.; Zeng, P.; Cui, S.; Song, C. Deep Reinforcement Learning for Charging Scheduling of Electric Vehicles Considering Distribution Network Voltage Stability. Sensors 2023, 23, 1618. [Google Scholar] [CrossRef]
- Lee, Z.J.; Li, T.X.; Low, S.; Assoc Comp, M. ACN-Data: Analysis and Applications of an Open EV Charging Dataset. In Proceedings of the E-Energy’19: Proceedings of the 10th ACM International Conference on Future Energy Systems, Phoenix, AZ, USA, 25–28 June 2019; pp. 139–149. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).