Abstract
The capital asset pricing model (CAPM) is often based on the Gaussianity or normality assumption. However, such an assumption is frequently violated in practical situations. In this paper, we introduce the symmetric CAPM considering distributions with lighter or heavier tails than the normal distribution. These distributions are symmetric and belong to the family of elliptical distributions. We pay special attention to the family members related to the normal, power-exponential, and Student-t cases, with the power-exponential distribution being particularly considered, as it has not been explored widely. Based on these cases, the expectation-maximization algorithm can be used to facilitate the estimation of model parameters utilizing the maximum likelihood method. In addition, we derive the leverage and local influence methods to carry out diagnostics in the symmetric CAPM. We conduct a detailed case study to apply the obtained results estimating the systematic risk of the financial assets of a Chilean company with real data. We employ the Akaike information criterion to conclude that the studied models provide better results than the CAPM under Gaussianity.
Keywords:
CAPM; expectation-maximization algorithm; financial asset valuation; generalized leverage; local influence diagnostics; symmetric or univariate elliptical distributions; systematic risk MSC:
62J20
1. Introduction
In portfolio theory [], the capital asset pricing model (CAPM) [] is widely employed []. This model is based on a simple linear regression used for portfolio analysis []. In the CAPM, each financial asset’s systematic risk or market risk is estimated through a beta coefficient, allowing us to configure a set of optimal asset investments within a given financial market, considering the profitability and, in turn, the systematic risk of each asset.
The existence of risk implies that the gain or return on the investment will rarely coincide with its expected value. In [] (p. 181), it is mentioned that “the expected value measures the central tendency of the payoff or value that we would expect on average”. In addition, the expected return is defined in [] as the rate of return that an investor expects to obtain by holding an asset or bond during a given period and determines what an investor is willing to pay for a share.
There are alternative models to the CAPM, such as beta consumption versus beta market, developed in []; the arbitrage pricing theory proposed in [] and later in []; and the three-factor model designed in []. Several studies deal with the CAPM, predominantly those elaborated in [,,,,,], which have developed and exposed the model and, in some cases, contrasted cross-sectionally the alternative models and the CAPM.
In [], the existence of empirical studies carried out in [,,] is evidenced, where the stock returns have distributions with heavier tails than the normal distribution.
The Student-t model is employed instead of the normal model in []. The Student-t model also is utilized in [], considering the maximum likelihood method to estimate its parameters. In [], it was concluded that the asset valuation using the CAPM and the discounted dividend model in emerging economies should be studied.
The family of symmetric or univariate elliptical distributions, also called elliptically contoured models in the multivariate case [,,,], has been investigated since the 1970s, starting with the studies presented in [,,,,]. In the current century, the works described in [,,,,,] can be mentioned. Table 1 summarizes the state-of-the-art research on the CAPM, starting in 1964 with the work by Sharpe [], and on symmetric/elliptical distributions. In the following, we refer to this type of distribution as symmetric or elliptical.

Table 1.
Research on CAPM and symmetric/elliptical distributions (ED).
After considering the elliptical CAPM and estimating its parameters, one can use the Akaike information criterion (AIC) [,], which provides a simple method for selecting the most appropriate model to characterize a set of data. In [], it was concluded that AIC is helpful when working with large samples and is specifically suitable for selecting predictive models. Once the best model is selected, one can conduct a diagnostic analysis. The local influence technique was proposed to evaluate the change produced in the maximum likelihood estimates by performing small perturbations in the response (if it is continuous), explanatory variables, or by introducing case weighting. The purpose of the local influence method is to check, by using some appropriate measure, the effect of small alterations in the model or the data on the main results of the fit. If there are disproportionate effects in some results, these may indicate that the model is poorly fitted or that there are deviations in its assumptions. Scale perturbations can also be performed.
The concept of leverage employed in statistical modeling must be differentiated from financial leverage. In [], financial leverage was defined as the use of debt financing to increase investment returns, analyze the company’s financial structure, and indicate the amount of debt utilized to support resources and operations. In [], it was pointed out that operating leverage refers to the fixed operating costs that accentuate the profit variations. This is the proportion between fixed and variable costs. A production plant with a high proportion of fixed over variable costs has high operating leverage. Total leverage is the potential use of fixed costs (operational and financial) to increase the effects of changes in sales on the company’s profits. Nevertheless, in statistics, the idea of generalized leverage is to assess the influence of the response variable on its own predicted values []. A generalized version of leverage is developed in [], when the parameter has no restrictions. Furthermore, there are also versions for the case where the parameter is restricted to linear inequalities [,,].
The objectives of the present investigation are (i) to introduce the symmetric CAPM, paying special attention to the normal, power-exponential (PE), and Student-t cases, with the PE distribution being particularly considered, as it has not been explored widely in methodological and practical applications; (ii) to use the expectation-maximization (EM) algorithm to calculate the maximum likelihood estimates of the model parameters, whose algorithm is facilitated when considering the mentioned elliptical cases; (iii) to derive leverage and local influence analyses for the symmetric CAPM; and (iv) to conduct a detailed case study with real data from a Chilean company.
This paper is structured as follows. In Section 2, concepts and calculations of systematic risk and return are presented, ending with the CAPM. In this section, we also introduce definitions and properties of elliptical distributions. In Section 3, we discuss the EM algorithm and carry out local influence and generalized leverage diagnostic analyses. In Section 4, we apply the CAPM under elliptical distributions and its diagnostic analysis on real data. Section 5 presents a description and economic justification of the diagnostic analysis results. Section 6 includes conclusions and future lines of research. The acronyms used in the present article are defined in Table A1 of Appendix A.
2. Background
2.1. The Capital Asset Pricing Model
Next, we present concepts of risk and return. All financial assets traded on the stock market are subject to risk; of course, different types of assets will have different types of risk. However, the effect of the risk, whatever its kind, is always the same: the returns obtained today will be different from those expected by the investor at the time that he acquired the asset. The yield of security i during a period t is defined by
where is the price of asset i at the end of period t; is the price of the asset at the beginning of period t; is title return i in period t; is the dividend received during period t. Once the probability distribution of the possible returns of a given security is available, its expected value is calculated using the mathematical expectation or average stated as If we consider the expression given in (1), it is possible to break down the return or yield linked exclusively to variations in the closing price of a share, whether in days, weeks, months, or years. The calculation of price returns is carried out as , where is the price return in period t; is the price of the asset in period t; and the price of the asset in the previous period. The financial asset pricing model indicates that the expected risk premium of each investment is proportional to its beta coefficient. This suggests that each investment should lie on the sloping line of the stock market that connects treasury bills to the market portfolio. Figure 1 represents the expected returns for the treasury bills and the market portfolio.
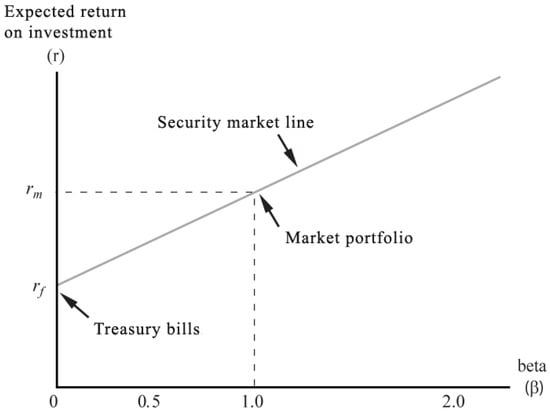
Figure 1.
Plot of the expected return treasury bills and the market portfolio. Source: [].
Note that the treasury bills have a beta coefficient and risk premium of 0. The case of the market portfolio has a beta coefficient of 1.0 and a risk premium of . This gives us two benchmarks for the expected risk premium.
The following question emerges: What is the expected risk premium when the beta coefficient is neither 0 nor 1? The CAPM provides the answer, which attempts to calculate the expected risk premium when the beta coefficient is neither 0 nor 1 to calculate the risk premium for any investment. To do this, the model states that the risk premium fluctuates directly with the beta coefficient as long as it is a competitive market. Graphically, all investments must lie on the stock market line. The model is formulated as expected risk premium = beta coefficient × market risk premium, that is, . From this expression, it is possible to deduce that the expected yield is . We consider the CAPM stated as
where is the return of assets in the period t; is the risk-free rate return for the period t; is the independent return on the share; is the systematic risk; is the market return in period t; is the market risk premium for period t; is the expected return in period t; and are the normal random errors, with .
Systematic risk is the risk that each asset can provide to the market portfolio—that is, the risk that cannot be diversified and is obtained by calculating the beta coefficient. The systematic risk of a stock is , where is the beta coefficient of asset i, and represents the relationship between changes in market profitability () and the return on asset i (); is the covariance between the profitability of asset i and the market profitability; and is the variance of the market return. The beta coefficient indicates how a stock’s price responds to market forces. This means that as the stock’s price is more sensitive to market changes, the beta coefficient of that stock will higher. The beta coefficient is obtained by relating the historical returns of a stock to the market return. Then, the market return is the average return of all the stocks or an indicator that groups a considerable number of stocks, such as the selective stock price index (IPSA of Chile, due to its acronym in Spanish). The CAPM uses the beta coefficient to calculate the expected return. The interpretation of the beta coefficient is simple. It is assumed that the market beta is a value, whereas the other betas are compared with this value. If a stock’s beta is positive, it indicates that it is moving in the same direction as the market. In addition, if the beta is negative, it indicates that it is moving in the opposite direction to the market. Most stocks have positive betas, and their values fluctuate between 0.5 and 1.75. When a stock has a beta coefficient of 0.5, it suggests that it is half as sensitive as the market, and for every 1% change in the market portfolio (or indicator), the stock changes by 0.5%. A stock with a beta ratio equal to two indicates that it will change 2% for every 1% change in the market portfolio; that is, it is twice as sensitive as the market. A beta coefficient equal to one indicates that the stock is equally as sensitive as the market. The helpfulness of the beta coefficient lies in the fact that it allows us to evaluate market risk and also to understand its effects on a given stock.
2.2. Elliptical Distributions
Definition 1.
Let , for , follow an elliptical distribution with characteristic function (CF) given by , where is a location parameter, is the scale matrix (symmetric and positive semidefinite), corresponds a function that generates CFs, with , , and is the exponential function. If X follows an elliptical distribution with CF as above defined, then we write or [].
Definition 2.
If , the density of X is , for , where the function g satisfies and . This function is traditionally named the density generating function, where . If X follows an elliptical distribution, with the above density, we denote it by or simply . Next, four examples of elliptical distributions are discussed assuming that [].
Example 1.
The normal distribution is denoted by , with , , and its density is expressed as , for , where and .
Example 2.
The Student-t distribution is denoted by , with , , (degrees of freedom), and its density is stated as
where , for . If , we obtain the Cauchy distribution [].
Example 3.
The contaminated normal distribution is denoted by and its density is , with , , indicating the contamination proportion, and being a scale factor []. Note that , for
Example 4.
The PE distribution is denoted by , with , , , and its density is given by
where for . This subfamily of distributions has both types of tails: lighter than a normal distribution when and heavier when . It also includes the normal distribution as a particular case if [].
Next, we present some properties of the elliptical distributions.
Property 1.
Suppose that with . When the vector of means and covariance matrix of X exist, then and , with , and ϕ corresponding to the generating function of CFs. In the univariate elliptical (symmetric) case, , that is, the variance of X.
Property 2.
Let with . Then, where “” indicates equality in distribution. The density of is expressed as , for . Note that can be written in terms of as , and that is integrable, with which the k-th moment of X exists.
Example 5.
Consider that:
- (a)
- If , we have that and therefore . Then, . , and the function that generates the CF is , for .
- (b)
- If , then . Thus, , , and , for . For the Student-t distribution, the CF is given in [].
- (c)
- If , we have , , , and , for
- (d)
- If , then For (integer), we obtain and . The CF of the PE distribution is given in [].
The following property provides a procedure to find the moments of R, derived from the CF of an elliptical distribution.
Property 3.
Let , with . Then, the -th moment of R is given by with and being an integer number. The above result is presented in [], and it is helpful to find an expression for in those elliptical densities that are more complex to be treated.
Example 6.
The use of Property 3, and considering and , allows us to find the CFs for the Student-t and PE distributions, which are complex to deal with. Thus:
- (a)
- Let . Then, we have that , for , and , for . Therefore, we have , for , and , for .
- (b)
- Let . Then, we get , The above implies that and Note that when , the normal case is recovered, that is, and .
The following property indicates that the elliptical distributions are closed under linear operations.
Property 4.
Let , with , and consider that , and A is a matrix of rank q. Then, we obtain Thus, we can observe that any marginal distribution of is also an elliptical distribution.
A subclass of elliptical distributions called scale-mixture of normals (SMN) is discussed below; see details in [].
Definition 3 (SMN distribution).
Let , Ω be a positive definitive matrix, H be a distribution function, and k be a strictly positive function. Then, the density f is defined as . If X has this density, then it has an SMN distribution, which is denoted by []. A random vector is admissible if , where , and is a random variable with distribution function H, independent of Z. Hence, from the above expression, we find that the distribution of X conditional on is . In the SMN distributions, the computation of the conditional moments, defined by , are helpful in the application of the EM algorithm to calculate the maximum likelihood estimates [].
3. Estimation and Diagnostics in the Elliptical CAPM
3.1. EM Algorithm
To implement this algorithm, augmented or complete data are used, which are formed from the observed data and the missing data. Thus, we have that , where the vector represents the complete data, the observed data, and the missing (or unobserved) data. In the EM algorithm, two important steps must be followed, expectation and maximization, which form each iteration to obtain the maximum likelihood estimates. To develop this algorithm, we consider the function , where the logarithm of the likelihood of the complete data is labeled by and represents the parameter of interest. For the r-th iteration, the EM algorithm is defined as follows:
- First step (E): Calculate previously defined for , that is, .
- Second step (M): Choose that maximizes such that
Steps E and M must be alternated until convergence is reached. Each iteration of the EM algorithm increments the logarithm of the observed likelihood function [].
3.2. Local Influence Analysis
The local influence technique is applied to data to detect potentially influential cases. Let be the log-likelihood function of the model and a vector of perturbations varying in an open region . The perturbations are applied to the log-likelihood function, obtaining . Representing the nonperturbation vector by (null vector), it is possible to assess the influence of the perturbations on the estimates and of the original and perturbed log-likelihood functions, respectively. To compare and while fluctuates in the perturbation space, we use the log-likelihood displacement that is the difference between and given by where , for . The graphical plot of versus gives important information regarding the influence of a case based on perturbation scheme. For example, suppose that the values of when varies are similar. In this case, the fitted model is stable concerning the perturbation scheme. The surface that we are interested in is formed by a vector of the values of and , when varies over a determined space.
The graph of the function can be represented by a geometric surface given by the values of , when fluctuates in . The surface described is known in statistics as a local influence graph. Because it is helpful in some situations, we can analyze how the surface deviates from its tangent plane at . As reaches its minimum value at , is parallel to . Each vector h in with norm equal to one, that is, , establishes a plane containing h, orthogonal to . The intersection (normal section) is named the “lifted line”, which is represented by the graph versus . The normal curvature of the raised line, represented by , is defined as the curvature of the plane at .
Note that is named the normal curvature of the surface at , in the direction h. When large values of are obtained, they suggest a sensitivity to the perturbation scheme on h. Therefore, is named the local influence on the estimate of the perturbation scheme in the direction h. Thus, we display the normal curvature in the direction h defined by
where is a perturbation matrix with elements . The matrix is given by . Hence, we have that . This indicates how to perturb the suggested model to obtain the largest local shifts in .
Let and be the eigenvectors corresponding to the first and second largest eigenvalues in absolute value of , where is known as the direction of maximal normal curvature, denoted by . If we observe that the i-th element of is large, it indicates that perturbations of the weight can lead to considerable changes in the analysis results. Thus, the largest element in the first direction of the vector requires our full attention if we consider that the paired elements give us with information on potentially influential cases. Then, the plot versus is relevant to observe.
Another important element to consider is , that is, the i-th element of the identity matrix, to perturb the i-th case. Thus, the normal curvature is defined by , where is the i-th component of the diagonal of B, with . If we consider the plot versus , for , we obtain an index plot of . Also, versus i is an important component of the local influence diagnostic technique. It is proposed as a cutoff point that exceeds , where .
If we partition , and are interested in the subset , the normal curvature for this subset is defined by where
with being obtained from corresponding to the splitting of . Then, the eigenvector of is of interest.
It is possible to perturb the elliptical CAPM using schemes for adequately interpreting the results. For our research, perturbations of scale and cases are stated. When we assume a scale perturbation, a heteroscedastic CAPM is considered and given by , where , with , and is the weight of observation i, for . If we obtain that , the heteroscedastic model given above reduces to , such as in the CAPM stated in (2). In the case that the scale parameter is perturbed by changing to for observation i, the matrix is given by
where , with , for ; ; and , with . In the case-weight perturbation, the log-likelihood function for is expressed by , with . In this perturbation, the matrix takes the form stated as
where ; , with ; and , with , for .
3.3. Generalized Leverage
When considering leverage under normality, the importance of analyzing data with high leverage is that a given observation can strongly influence the prediction and the fit of the chosen model. We recall that and Given the above, it is possible to identify a matrix that, in statistics, we call hat, which is also known as the projection matrix, and given by . It is possible to deduce from the above matrix that .
Close attention must be paid to the components of the diagonal of the hat matrix, , namely. The so-called leverage [] is defined as where is the leverage for observation i. In addition, we have that where p corresponds to the number of model parameters and is the rank of the matrix H. Note that high values of indicate that observation i has a strong influence, especially if is greater than twice (or three times) the mean of the leverage, that is, it holds that
In the case of generalized leverage, if is the log-ikelihood function of , and is the estimate that maximizes , the leverage matrix is . Then, the generalized leverage is given by
where , , and . Note that the formulation stated in (3) generalizes the definition of leverage points given in [].
Considering that in our case , and as , where , with , and , it is possible to use the formulation stated in (3) to generalize the matrix of leverage points for the symmetric CAPM. Thus, this matrix takes the form with and , where , with and , with ; , with and , with , , , with ; and is the identity matrix.
4. Empirical Application
4.1. Descriptive Analysis
The data set comprises the historical daily opening, high, low, close, and volume prices of the stock corresponding to Compañía Manufacturera de Papeles de Chile (CMPC) and the IPSA indicator. The period from 30 December 2008 to 30 December 2019 is considered. The data set was extracted from Yahoo Finance (CMPC), Investing (IPSA), and the Central Bank of Chile. Although the opening, maximum, minimum, closing, and volume values were used to prepare the descriptive financial charts, only the monthly return (monthly yield), based on the CMPC adjusted by closing prices and IPSA closing price, was used for the CAPM. The monthly yields of 10-year Central Bank of Chile bonds, extracted from the Central Bank of Chile database, were utilized for the risk-free rate of gain. All values are expressed in Chilean pesos.
The IPSA indicator considers the 30 stocks with the most significant stock market presence, selected annually. Its purpose is to reflect the price variations of the most active securities in the market. For this reason, the IPSA has been chosen as the market indicator for the CAPM. As of August 2016, the S&P Dow Jones and Santiago Stock Exchange indices signed an operating agreement, and the IPSA was renamed S&P CLX IPSA. Currently, the securities considered for the IPSA are related to the following organizations: Aguas Andinas, Aesgener, Banco de Chile, Banco Santander, BCI, CAP, CCU, Cencosud, Cencosud shopping, CMPC, Colbun, Concha & Toro, Copec, ENELAM, ECL, Embotelladora Andina, Enel Chile, ENTEL, Falabella, IAM, ILC, Itaú-Corpbanca, Mall Plaza, Parque Arauco, Ripley, Security, SMU, Sonda, SQMB, and Vapores.
4.2. Descriptive Measures of Monthly Returns
Table 2 summarizes the descriptive measures of the monthly returns of the CMPC and IPSA, such as the minimum and maximum values, first and third quartile, mean (average), median, standard deviation, variance, range, and the coefficients of variation, skewness, and kurtosis. It can be deduced from Table 2 that the monthly return of IPSA has the lowest range of 0.26 and the highest coefficient of variation (7.19). The coefficient of variation for the CMPC share is 6.99.

Table 2.
Descriptive measures for CMPC and IPSA monthly returns 2009–2019.
In the monthly return of CMPC and IPSA, the median is less than the mean, which indicates certain asymmetry, with a slight skewness to the right (positive) and long tails to the right in the histograms. However, the values are still close. The asymmetry shows a positive value of for CMPC, close to 1. It is considered a slight asymmetry to the right. The coefficient of asymmetry for the IPSA indicator is , which reports a slight asymmetry to the right as well. The coefficient of kurtosis is greater than zero in both cases, being for CMPC and for IPSA.
The descriptive analysis indicates that the monthly returns of CMPC and IPSA have a skewness close to 1, which is still considered acceptable to assume symmetry and normality in the data distribution. The kurtosis does not exceed the value of 1, which is also acceptable. Note that it is not possible to assume normality or symmetry in the data considering the analysis of descriptive measures exclusively. It is necessary to conduct normality tests. For the present research, the Lilliefors test [], a normality test based on the Kolmogorov–Smirnov test, is performed.
4.3. Descriptive Graphs for Monthly Returns of CMPC
Histograms, box plots, and density plots are obtained for the monthly returns of the CMPC financial asset (adjusted closing prices). A scatter plot is also displayed using the monthly returns of the CMPC and IPSA index.
Figure 2 displays the histogram and box plot of the monthly returns of the CMPC share. This figure shows good symmetry, with a slight positive skewness and a long tail to the right. Based on the box plot located at the bottom of the figure, outliers are identified on the third quartile, the upper whisker of the box plot is more elongated, and the median is closer to the first quartile and farther away from the third quartile. Unimodal behavior is also detected in the frequency of the data.
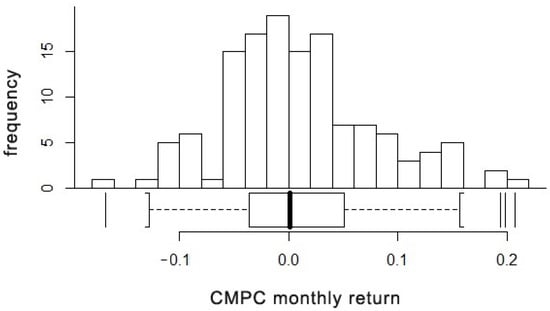
Figure 2.
Histogram and box plot of CMPC monthly returns.
Figure 3 shows good symmetry in the distribution of the data (monthly returns), with a slight positive skewness already detected in the descriptive measures and the histogram, as well as unimodal behavior of the empirical density.
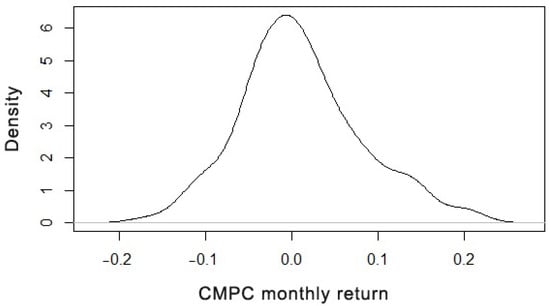
Figure 3.
Plot of density estimation of CMPC monthly returns.
Figure 4 sketches a scatter plot, which shows the positive correlation between the monthly return of CMPC shares and the monthly return of the IPSA indicator. The green line represents the linear regression. There is a positive correlation between the closing prices of CMPC and IPSA. If we observe when the returns are close to zero, they are grouped around the regression line. However, there are some outliers, which we have already observed in the box plot analysis. Table 3 summarizes the result of the Lilliefors test.
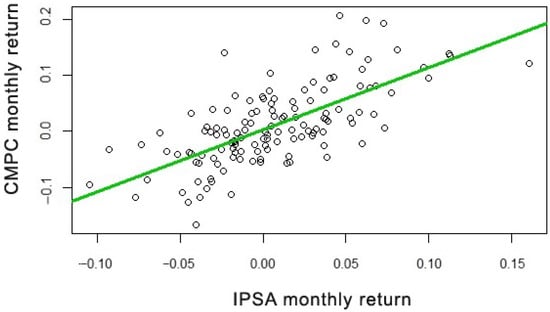
Figure 4.
Scatter plot of the CMPC and IPSA monthly returns.

Table 3.
Lilliefors normality statistic and its p-value for CMPC monthly returns.
As with the Kolmogorov–Smirnov test, the Lilliefors test contrasts the normality hypothesis. Then, we are looking not to reject the null hypothesis at a 5% of significance, that is, to find a p-value . For the month-to-month returns of CMPC, the p-value is 0.05, whose value is at the bound of the significance. Therefore, we cannot reject the hypothesis of normality, and then it is possible to assume that the data have a normal distribution. With the normality test, we finish the descriptive analysis. Next, the graphical plots corresponding to the technical, financial analysis are detailed, before elaborating on the financial asset valuation.
Figure 5 covers the historical closing prices from 30 December 2008 to 30 December 2019 for the CMPC and IPSA. As observed in this figure, the return of the highest variation corresponds to the CMPC. However, potentially influential values exist, and a considerable increase in closing prices between 2011 and 2018 is registered. The CMPC starts with a closing price expressed in Chilean pesos of and ends the period with a closing value of . The curve corresponding to the CMPC closing price can behave very similarly to the IPSA. The closing price corresponding to the IPSA has a greater value than the CMPC. The IPSA starts the period with a closing price of , ending with a closing value of . Note that the IPSA closing price behavior resembles that of the CMPC, but in a greater magnitude in 2011 and 2018, registering a solid increase in its closing value. Based on the closing price graph, we can summarize that the CMPC share has low variability over time and is sensitive to market variations (IPSA). Based on Figure 5, we detect the high sensitivity of the CMPC shares to market variations, with the calculation of in the CAPM corroborating or refuting this observation.
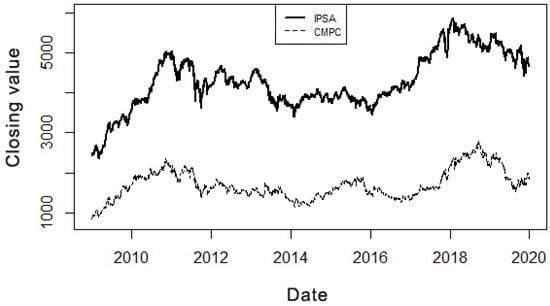
Figure 5.
Plots of the CMPC and IPSA daily closing prices for December 2008 to December 2019.
4.4. CAPM under Normality Assumption
The CAPM assumes the normality of monthly return distribution for the financial asset (CMPC), and market (IPSA). To configure the CAPM, it is necessary to extract different data which are: (a) the monthly returns established on the daily closing price of the CMPC share; (b) the monthly returns of the IPSA indicator established on the daily closing prices; and (c) the risk-free rate, which, for this research, we consider as the monthly returns of the bonds issued by the Central Bank of Chile for ten years. The following is a detailed description of the development of the CAPM. Recall that we seek to measure the responsiveness of a stock’s return (CMPC) to variations in the market (IPSA).
We consider the structure given in (2) for practical purposes. In this case, it is better to consider the CAPM in the form of excess return and estimate both and using an ordinary least squares regression. For the month-to-month returns of the risk-free rate, in [], it is warned that when transforming the monthly gain of the risk-free rate using “to.monthly”, the returns of each month are annualized, which is why the code “rf.monthly” must be applied before creating the data frame. The summary of the regression measures of the CAPM under normality is detailed in Table 4, including the corresponding p-values of the t-tests. This table indicates that the intercept is estimated at , and at , with being non-significant statistically at 5%. Then, the expected return of CMPC, according to the CAPM regression performed, is given by

Table 4.
Linear regression for the CAPM under normality with data of CMPC monthly returns.
The importance of is that it indicates a stock’s price sensitivity to market or portfolio changes. The CAPM, developed for the monthly returns of the CMPC share, gives an estimate of . As it is positive, this indicates that the CMPC share moves similarly to the market. Note that is very close to 1 (market value), which suggests that the CMPC share is slightly more sensitive than the market. For every change in the market, the value of the CMPC share changes by .
Figure 6 corresponds to a scatter plot of the monthly returns of the CMPC and the monthly returns of the IPSA. The green line corresponds to the CAPM line, whose positive slope is . A positive correlation is detected between the CMPC and IPSA monthly returns. As observed in the box plot of the CMPC closing price, there are some outliers, which persist for the CMPC monthly returns in the scatter plot. The scatter plot and the CAPM line in Figure 6 complete the application of the CAPM under normality in the data distribution. The following section analyzes the results corresponding to the CAPM under the Student-t distribution.
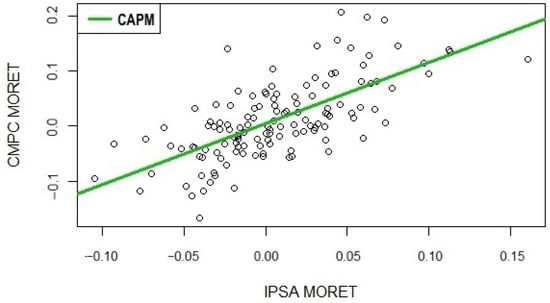
Figure 6.
Scatter plot of monthly returns for the IPSA and CMPC with fitted CAPM line.
4.5. CAPM under Elliptical Distributions
Next, we assume a Student-t distribution for the CAPM, calculating the beta coefficient values according to different degrees of freedom (). To compare both models (normal and Student-t), we use the AIC, which is established as
where is the log-likelihood function, and K represents the number of parameters of the model. The value of the AIC is not interpretable by itself. The AIC values have a meaning when comparing candidate models using the same data. Moreover, the AIC estimates the distance between the proposed model and the mechanism (model) that generated the observed data. If two or more candidate models are proposed, the AIC formulates the selection problem as the search for the model that gives the smallest value of AIC. This condition indicates that the model with a lower AIC is superior and fits the data better.
Table 5 summarizes the estimates for the intercept , the slope , the parameter , and the AIC value. The Student-t distribution with 4 degrees of freedom yields the largest AIC value of 400.08, with an estimated intercept value of , an estimated beta coefficient of , and an estimated of . The smallest AIC value of is obtained with the Student-t distribution with 13 degrees of freedom; and the estimated intercept being , with an estimated beta coefficient of and an estimated of . The estimated intercept and beta coefficient are less than the corresponding values under normality. Focusing on the beta coefficient, the difference is . The interpretation of this difference indicates that, under the normal model, the sensitivity of the CMPC share to market variations is overestimated, so it is assigned a higher risk and then a higher expected return value as well. The consequence of having a higher systematic risk value is that the stock is disregarded in the configuration of a portfolio with greater risk aversion. Otherwise, if the stock is included in a higher-risk portfolio, since it has a lower risk, it will not generate the returns expected by the investor.

Table 5.
CAPM fit under the Student-t distribution with data of monthly returns.
Figure 7 shows the differences in the slopes of the linear regression lines for the CAPM with different values of the parameter of the Student-t distribution, specifically for 4, 13, 50, and 100 degrees of freedom. As increases, the slope increases, and it is closer to the slope of the CAPM line under a normal distribution, represented by the dashed line. The flatter line matches the CAPM, whereas the black line represents the CAPM, whose AIC is the smallest of all the CAPM cases under the Student-t distribution.
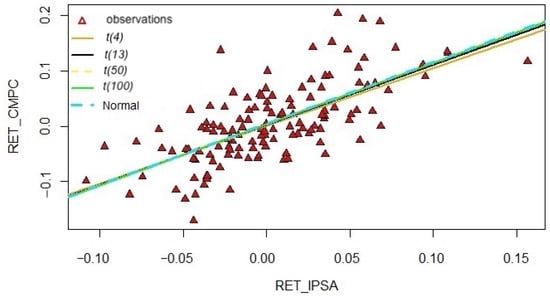
Figure 7.
Scatter plot of monthly returns for the IPSA and CMPC with fitted CAPM lines under the Student-t and normal distributions.
Next, we apply a PE distribution to the CAPM, calculating the intercept and beta coefficient values according to different values of . Table 6 reports the estimates of the CAPM parameters under a PE distribution for different values of . The PE distribution with gives the same values as a normal distribution. The PE model with yields the smallest AIC value (), an estimated intercept of , an estimated beta coefficient of , and . The PE model with yields the largest AIC value (), along with a positive estimated intercept , , and . The CAPM estimated under a PE distribution, with , indicates that the sensitivity to market changes of the CMPC stock is greater than 1, which has more sensitivity than under normality. As with the Student-t distribution, the estimate of the systematic risk of the CMPC stock, in a CAPM under the PE distribution with , is less than the corresponding estimate under a normal distribution. Figure 8 summarizes some of the generated lines with the values of the CAPM under the PE distribution with equal to , , , and 1, in addition to the line of the normal model. The less steep line corresponds to the PE distribution with (green color). The black straight line matches the PE distribution with , which corresponds to the model that obtained the smallest AIC value. Figure 9 summarizes the lines corresponding to the CAPM under the normal, , and PE(0.1) distributions.

Table 6.
CAPM fit under the PE distribution with data of monthly returns.
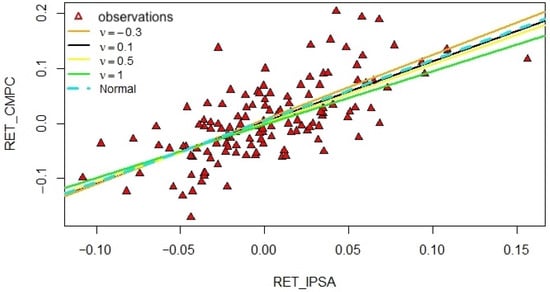
Figure 8.
Scatter plot of monthly returns for the IPSA and CMPC with fitted CAPM line under the PE distribution.
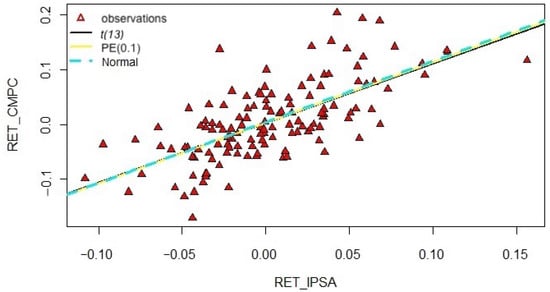
Figure 9.
Scatter plot of monthly returns for the IPSA and CMPC with fitted CAPM lines under the normal, Student-t, and PE distributions.
The summary of the regression measures of the CAPM under the distributions selected with the AIC is detailed in Table 7, including the corresponding p-values of the t-tests. This table indicates that the intercept is estimated at and , whereas is estimated at and , for the and PE(0.1) distributions, respectively, with being non-significant statistically at 5% in both cases. Then, the expected returns of the CMPC, according to both CAPM performed, are given by

Table 7.
Linear regression for the CAPM under the indicated distribution with monthly returns.
Now, we perform the diagnostic analysis in the following section for the selected models.
4.6. Diagnostic Analysis of Selected Models
Next, the diagnostic analysis results, carried out on the models already selected, are presented. The normal, , and PE(0.1) models are considered. First, we provide graphical plots for generalized leverage, case-weight perturbation, and scale perturbation. The second part presents the economic causes that explain the observations (months) detected as potentially influential by the diagnostic analysis. For this purpose, we use the statistical synthesis bulletins of the Santiago Stock Exchange, the monthly business confidence index (IMCE), and the press releases of the Central Bank of Chile.
Figure 10 compares the three models and describes the generalized leverage analysis, that is, the influence of on its prediction. The left graph corresponds to the normal model, the center graph to the Student-t model with , and the right graph corresponds to the PE model with .
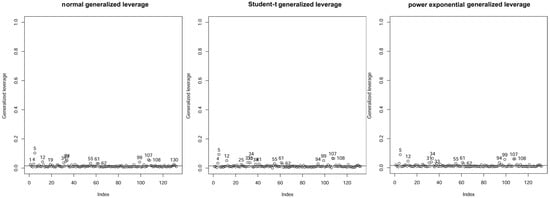
Figure 10.
Plots of generalized leverage for the indicated models with data of monthly returns.
Table 8 reports the influential values for the three models, taking the order of values according to the normal model as a reference. Month #5, corresponding to May 2009, stands out as the most influential month (observation) for the three models, followed by Month #107, corresponding to December 2017, the second most influential month for the normal and Student-t models. The second most influential month for the PE model corresponds to month #34 (October 2011). Month #34 is the third most influential value for the normal and Student-t models. Month #108, corresponding to December 2017, is the third most influential value for the PE model and the fourth most influential for the normal and Student-t models. The economic explanation of these values are provided in the next section.

Table 8.
Generalized leverage influencing values in the indicated model with data of monthly returns.
Figure 11 compares the results of the local influence analysis, applying the case-weight perturbation, to the selected models. The left plot corresponds to the normal model, the central plot corresponds to the Student-t model with , and the right plot corresponds to the PE model with .
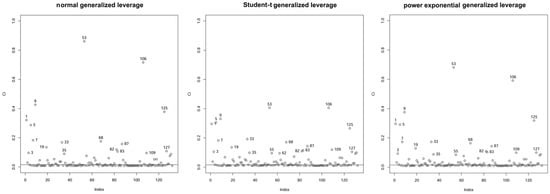
Figure 11.
Plots of total local influence under case-weight perturbations in the indicated model with data of monthly returns.
Figure 11 shows that the model better fits case-weight perturbations. Based on the normal model, the influential observations are ordered in the model estimates in the presence of a case-weight perturbation. Months #53 and #106 are the most influential. The normal model provides the highest value for month #53 (), which corresponds to May 2019. If we observe the Student-t model, it registers a lower value of influence () for month #53. The PE model records a value of . Table 9 reports the values for the influential observations. Under the perturbation of cases, the order is based on the results for the normal model. When observing Table 9, the only month in which the model results in a higher influence value than the other two models is month #5, corresponding to May 2009, which will be analyzed with special attention in the economic analysis of the next section.

Table 9.
Total local influence under case-weight perturbations influencing values in the indicated model with data of monthly returns.
Figure 12 compares the results of the local influence analysis, applying the scale perturbation, to the selected models. The left plot corresponds to the normal model, the middle plot corresponds to the Student-t model with , and the right plot corresponds to the PE model with .
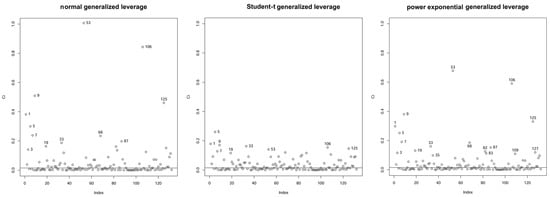
Figure 12.
Plots of total local influence under the scale perturbations in the indicated model with data of monthly returns.
Figure 12 displays that the model fits better to a scale perturbation when comparing its values with the other two models. Again, the highest influence value in the three models is month #53, which corresponds to May 2019. The Student-t model records a low influence value (). The same occurs in month #106, that is, October 2017, and the third value is month #9 (September 2009). Next, Table 10 presents the influential values for the scale perturbation, with the order being stated according to the values of the normal model.

Table 10.
Values of total local influence under scale perturbations in the indicated model with data of monthly returns.
5. Economic Rationale for the Results of the Diagnostic Analysis
5.1. Context
The diagnostic analysis, along with exposing the goodness of fit against perturbations and the influence of the response variable against its prediction, gives information about specific observations (months, in our case). These observations, when perturbed, can have a strong influence on the predictions of the model. The values of the most significant influence for generalized leverage are detailed in the following subsections indicated per date and with its economic explanation about the obtained values.
5.2. January 2009
January 2009 registered the lowest opening price for the CMPC of and the second lowest closing price of the year (). The IPSA in January 2009 showed a positive variation of compared to the previous month. The monthly business confidence indicator reached points, increasing by one point compared to the previous month, but falling by points compared to the same month of the previous year. The monetary policy rate, established by the Central Bank of Chile, is reduced by 100 points, reaching per year. International commodity prices remain low. At the national level, inflation was negative in December, and the government announced a fiscal stimulus program.
5.3. May 2009
For May 2009, although 2009 was a year of economic contraction, the Santiago Stock Exchange reported a positive variation in the IPSA of . Unfortunately, the indicator continued showing negative numbers. Compared to the same month of the previous year, the variation of May 2009 is the highest for the IPSA. The CMPC’s annual report shows that from April 2009, the sale price of its products increased. In April 2009, the acquisition of the company Melhoramentos Papéis became effective, which added 75 thousand tons of tissue paper production capacity. This explains the interest in the CMPC share, with May 2009 being the month with a positive variation of , closing the price at . As for the monthly business confidence indicator, it reached a level of points for May 2009, registering an increase of concerning the previous month. For May 2009, the Central Bank of Chile reduced the monetary policy interest rate by 50 points, reaching per year, projecting an annual inflation rate of close to . Internationally, uncertainty persists, but growth prospects are stabilizing. There is a rebound in the international stock markets, and commodity prices are rising, especially for copper and oil. The low interest rate incentivizes investors to invest in shares in search of higher profitability.
5.4. September 2009
For September 2009, the CMPC share registered a positive variation of and the highest monthly closing price of the year (). The IPSA indicator showed a positive variation of . The IMCE for September reached , up points compared to the previous month and up the same month last year. The monetary policy interest rate remained at per year. In the international scenario, global growth prospects stabilized, and commodity prices remained stable. On the domestic front, the demand was expanding, and the increase in unemployment was moderated.
5.5. December 2009
For December 2009, the CMPC share registered a negative variation of −2.72%. The IPSA indicator reached a positive variation of . The IMCE for December recorded , up from the previous month, and up points concerning the previous year. The Central Bank’s monetary policy rate remained at per year. In the international arena, there was the progressive stabilization of the financial markets. Reductions and low annual inflation records were expected at the national level.
5.6. October 2011
The CMPC share recorded the best positive variation of the year, , concerning the closing price of the previous month. The IPSA indicator attained a positive variation of , the highest of 2011. The IMCE reached , dropping points compared to the previous month. The monetary policy rate, set by the Central Bank, remained at per year. Domestically, activity and demand figures were moderate and inflation remained at around . In the international arena, indicators showed slow growth in the United States and Europe. Financial volatility was high, raw material prices experienced reductions, and the central banks of the major economies adopted additional measures to add expansiveness to their monetary policy.
5.7. May 2013
The CMPC share registered a variation of . The IPSA indicator reported a variation of . The IMCE reached , points below the previous month. The Central Bank’s monetary policy rate remained at per year. Internationally, the dollar rose in international markets, the eurozone continued in recession and in a fragile fiscal and financial situation, and the price of copper fell. Locally, activity and domestic demand slowed down, the peso depreciated, and inflation was around .
5.8. October 2017
The closing price of the CMPC share recorded a positive variation of in October 2017, compared to the previous month, reaching the second highest closing price of the year, . The IPSA indicator recorded a positive variation of compared to the previous month. The ICME reached , points above last month. The Central Bank’s monetary policy rate remained at per year. On the domestic front, the negative consumer’s price index for September brings the annual consumer’s price index to per year. The international environment is marked by the stability of global activity and a slight increase in raw materials such as copper and oil prices.
5.9. November 2017
The closing price of the CMPC share registered a negative variation of regarding the previous month. The IPSA indicator presented the most considerable negative variation of the year at . The IMCE reached , less than the previous month. The Central Bank’s monetary policy rate remained at per year. Internationally, oil prices increased, and the price of copper fell slightly. Domestically, October inflation was , bringing the consumer’s price index to per year. Weak investment movement was noted.
5.10. December 2017
The closing price of the CMPC share reached , attaining a positive variation of . The IPSA indicator registered a positive variation of , the highest of the year. The IMCE reached 44 points, less than the previous month. The Central Bank’s monetary policy rate remained at per year. On the domestic front, with greater dynamism in employment, the consumer’s price index for November increased by , and annual inflation remained at . In the international arena, financial activity did not register relevant changes but there was a slight decrease in the price of copper.
5.11. May 2019
The closing price of the CMPC share registered a negative variation of , compared to the previous month. The IPSA indicator also showed a negative variation of . The IMCE for May 2019 reached , points less than the previous month. The Central Bank’s monetary policy rate remained at per year. In the international arena, the increase in trade friction between the United States and China increased global risk aversion and increased volatility. Also, increased riskier assets were reversed, and the price of raw materials was reduced. According to preliminary data for the first half of the year, there was a drop in the stock market and depreciation of the Chilean peso at the national level, and the Central Bank reported low gross domestic product growth due to the drop in mining activity.
5.12. Lessons for Dummies
We would like to emphasize the importance of having a more accurate model when estimating the cost of capital rate of a company. We recall that the cost of capital rate represents the opportunity cost of money. Thus, this is helpful to determine whether the company’s projects should be financed with equity or debt. From an investors’ point of view, our model allows them to make a better decision when analyzing the possibility of leaving their profits within the company (reinvestment) or if it is more convenient to invest in other businesses that are more profitable. What investors should value most is that, with the use of statistical models different from the normal structure for calculating the beta coefficient in each financial asset, the result of the valuation is more in line with reality and the historical data. This more general modeling allows a better configuration of forms for the investment portfolio, since the beta coefficients of the assets are not overestimated.
6. Conclusions
In this article, we introduced the symmetric CAPM and concluded that it is feasible to reckon the systematic risk of a financial asset using the Student-t and power-exponential CAPM. The Student- CAPM obtained the smallest AIC value, above the power-exponential model with and the normal model. The Student-t model () was less affected by scale and case-weight perturbations. In generalized leverage, the Student-t model with presented less leverage than the normal model in month #5. However, the power-exponential model with was less affected than the normal and Student-t models in terms of leverage. The normal CAPM estimated a higher systematic risk () and so a higher expected return on the CMPC asset. The Student- CAPM estimated the risk of the CMPC asset at , with less than the normal model. The CMPC asset behaved similarly to the market, with a positive estimated beta coefficient close to one. The difference between the estimation of the beta coefficient of the CMPC asset under the normal model versus the Student-t model with was , which was significant and supported the proposal to extend the CAPM to elliptical distributions. Adequate estimation of the beta coefficient allows us to determine the systematic risk of a stock and its response to changes in the market. Consequently, it permit us to adjust the expected return associated with the stock, configuring an optimal investment portfolio, since the stock combinations are based on accurate information on the systematic risk of each stock. The CAPM enables us to measure the cost of equity capital. Estimating the beta coefficient associated with a company allows us to establish the minimum expected profitability for an investment project financed with the company’s resources. The result of measuring a beta coefficient lower than the CAPM under normality implies a lower risk associated with the company and a lower minimum expected return. Thus, an investment project previously discarded can generate a minimum expected return and to be executed.
The influential observations (months) detected in the diagnostic analysis showed the sensitivity of the CAPM to extreme variations in the price of an asset or the market. The month of May 2009 (observation #5) showed a positive variation in the IPSA of and the monthly return of the CMPC share of . This can explain the generalized leverage detected in the three models. The local influence diagnostic analysis allowed the detection of the adverse fluctuations of the IPSA and CMPC. The months of October, November, and December 2017 showed the volatility of the market, with the IPSA showing variations of , , and . For May 2013 and 2019, whose influential observations were months #53 and #125, and the IPSA registered a variation in its return of and , respectively. The CMPC asset showed variations of , respectively. The CMPC asset indicated variations of , , and . The economic factors analyzed can help to explain the fluctuations in monthly returns. At the national level, the monthly IMCE is directly linked to the fluctuations of the financial market because when the IMCE rises, certain financial assets and the IPSA respond with positive variations in closing prices. When it decreases, the monetary policy rate, set by the Central Bank of Chile, encourages investment in the financial market. In the international arena, the year 2009 was the beginning of the recovery from the subprime crisis. The year 2017 was uncertain and volatile in the international economic markets. The year 2019 shows the consequences of the trade war between the United States and China, among which we can highlight the drop in the prices of raw materials (oil and copper), the devaluation of the Chilean peso, and uncertainty in the growth expectations of the European Union. The last 12 years, in the national and international financial environment, have been of great uncertainty. For this reason, a CAPM is proposed assuming a distribution with heavier tails to be protected against this uncertainty. We could call it the “CAPM of uncertainty”, which is capable of estimating the beta coefficient of each stock with an adequate adjustment to the data. Regarding the empirical value of the present investigation, with our diagnostic analysis, it was evident how outliers disturb the calculation of the beta coefficient in a financial asset under a CAPM with normal distribution. The overestimation of this coefficient impairs the configuration of an investment portfolio and distorts the profitability of a financial asset.
For future lines of research, we state the following. Several financial stock returns present an asymmetric statistical distribution, which allows us to explore the possibility of working with this type of distributions under the current proposal. In addition, there are no alternative methods to calculate the expected return of the market, and it is possible to study some aspects along these lines. In particular, in [], it was presented a stochastic model for the IPSA, which could be used with the CAPM model as well. Another future line of research is considering financial asset valuation models, as alternatives to the CAPM (for example, the three-factor model). Furthermore, it is possible to analyze the CAPM considering the historical data of Chilean financial assets that are not part of the IPSA but of another indicator called the general stock price index, which is more volatile. one can study the joint effect that the explanatory variables can have on several parameters in regression formulations. Moreover, we can analyze statistical structures generated from the current research under settings related to censored data, mixture distributions, mixed models, multivariate, partial least squares, quantile regression, spatial, and temporal frameworks [,,,,,,,,].
We are planning to conduct studies on these issues in the future and also use data from more companies on the Chilean Stock Exchange. Since we are dealing with the calculation of the cost of capital rate, and the volatility of the companies is different, having a generic model presents problems when facing the particularity of each company, and this is precisely what we seek to propose in the current study. A new model that refers to systematic risk might be tested on a sample of several companies to provide some first global evidence. For example, one could extend the present analysis to a sample of 30 stocks, preferably of large companies. By using a sample of 30 firms during a period of 10 years, for example, one may find evidence that can be relevant and set the pace for devising a new model. Expanding the analysis to more financial assets, especially to more volatile financial assets, which are the ones that register atypical values historically, would be interesting, and we might carry out a comparative investigation of the asset beta calculations of financial institutions from developed and emerging economies, using the CAPM under elliptical distributions. This issue poses a challenge to us for future study.
Author Contributions
Conceptualization, R.J., M.R., D.L. and V.L. Data curation, R.J. Formal analysis, M.R., D.L. and V.L. Investigation, R.J., M.R., D.L. and V.L. Methodology, R.J., M.R. and D.L. Writing—original draft, Writing—review and editing, V.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially supported by FONDECYT, grant number 1200525 (V.L.), from the National Agency for Research and Development (ANID) of the Chilean government under the Ministry of Science and Technology, Knowledge, and Innovation.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data and computational codes are available upon request.
Acknowledgments
The authors thank four reviewers for their comments, which helped to improve the presentation of this article.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Acronyms
The acronyms used in the present article are defined in Table A1.

Table A1.
Acronyms used in the present article.
Table A1.
Acronyms used in the present article.
| Acronyms | Meaning |
|---|---|
| AIC | Akaike information criterion |
| BCI | Credit and Investment Bank of Chile |
| CAPM | Capital asset pricing model |
| CCU | The United Breweries Company of Chile |
| CMPC | Chilean Paper Manufacturing Company |
| ECL | Engie Energia Chile SA |
| ED | Elliptical distribution |
| EM | Expectation-maximization |
| ENELAM | ENEL Americas SA Company |
| ENTEL | Chilean telecommunications company |
| IAM | Investments Metropolitan Waters |
| IBOVESPA | Brazilian stock market index |
| IMCE | Monthly Indicator of Business Confidence |
| IPSA | Selective stock price index, Chilean market |
| PE | Power-exponential |
| SMN | Scale mixture of normals |
| SMU | Supermarket retail company in Chile |
| SQMB | Chemical and Mining Society of Chile |
References
- Markowitz, H. Portfolio selection. J. Financ. 1952, 7, 77–91. [Google Scholar]
- Sharpe, W.F. Capital asset prices: A theory of market equilibrium under conditions of risk. J. Financ. 1964, 19, 425–442. [Google Scholar]
- Peng, C.L.; Chen, W.K.; Wei, A.P. Teaching CAPM for a pre-finance graduate program at the STEM undergraduate level: Linear algebra perspective. Mathematics 2021, 9, 668. [Google Scholar] [CrossRef]
- Zheng, D.; Ding, S.; Cui, T.; Jin, H. Real economy effects on consumption-based CAPM. Mathematics 2022, 10, 360. [Google Scholar] [CrossRef]
- Pindyck, R.S.; Rubinfeld, D.L. Microeconomics; Pearson: London, UK, 2018. [Google Scholar]
- Gitman, L.; Smart, S.; Joehnk, M. Fundamentals of Investing; Pearson: London, UK, 2017. [Google Scholar]
- Breeden, D.T. An intertemporal asset pricing model with stochastic consumption and investment opportunities. J. Financ. Econ. 1979, 7, 265–296. [Google Scholar] [CrossRef]
- Ross, S.A. The arbitrage theory of capital asset pricing. J. Econ. Theory 1976, 13, 341–360. [Google Scholar] [CrossRef]
- Roll, R.; Ross, S.A. An empirical investigation of the arbitrage pricing theory. J. Financ. 1980, 35, 1073–1103. [Google Scholar] [CrossRef]
- Fama, E.F.; French, K.R. Common risk factors in the returns on stocks and bonds. J. Financ. Econ. 1993, 33, 3–56. [Google Scholar] [CrossRef]
- Chen, J.; Wu, Y.; Xu, Y. Research and analysis of asset pricing model based on the empirical test of stock price. In Proceedings of the Third International Conference on Economic Management and Cultural Industry, Guangzhou, China, 22–24 October 2021; pp. 1288–1293. [Google Scholar]
- Hung, D.C.H.; Shackleton, M.; Xu, X. CAPM, higher co-moment and factor models of UK stock returns. J. Bus. Financ. Account. 2004, 31, 87–112. [Google Scholar] [CrossRef]
- Ang, C. Analyzing Financial Data and Implementing Financial Models Using R; Springer: New York, NY, USA, 2015. [Google Scholar]
- Ruppert, D.; Matteson, D.S. Statistics and Data Analysis for Financial Engineering; Springer: New York, NY, USA, 2015. [Google Scholar]
- Brealey, R.; Myers, S.; Allen, F. Principles of Corporate Finance; McGraw-Hill: New York, NY, USA, 2017. [Google Scholar]
- Zhang, L. The investment CAPM. Eur. Financ. Manag. 2017, 23, 545–603. [Google Scholar] [CrossRef]
- Cademartori, D.; Romo, C.; CAPMos, R.; Galea, M. Robust estimation of systematic risk using the t distribution in the chilean stock markets. Appl. Econ. Lett. 2003, 10, 447–453. [Google Scholar] [CrossRef]
- Fama, E.F. The behavior of stock-market prices. J. Bus. 1965, 38, 34–105. [Google Scholar] [CrossRef]
- Blattberg, R.C.; Gonedes, N.J. A comparison of the stable and student distributions as statistical models for stock prices. J. Bus. 1974, 47, 244–280. [Google Scholar] [CrossRef]
- Zhou, G. Asset-pricing tests under alternative distributions. J. Financ. 1993, 48, 1927–1942. [Google Scholar] [CrossRef]
- Lange, K.L.; Little, R.J.; Taylor, J.M. Robust statistical modeling using the t distribution. J. Am. Stat. Assoc. 1989, 84, 881–896. [Google Scholar] [CrossRef]
- Díaz-García, J.A.; Galea, M.; Leiva, V. Influence diagnostics for multivariate elliptical regression linear models. Commun. Stat. 2003, 32, 625–641. [Google Scholar] [CrossRef]
- Díaz-García, J.A.; Leiva, V. Doubly non-central t and F distribution obtained under singular and non-singular elliptical distributions. Commun. Stat. 2003, 32, 11–32. [Google Scholar] [CrossRef]
- Díaz-García, J.A.; Leiva, V.; Galea, M. Singular elliptical distribution: Density and applications. Commun. Stat. 2002, 31, 665–681. [Google Scholar] [CrossRef]
- Galea, M.; Cademartori, D.; Curci, R.; Molina, A. Robust inference in the capital asset pricing model using the multivariate t-distribution. J. Risk Financ. Manag. 2020, 13, 123. [Google Scholar] [CrossRef]
- Kelker, D. Distribution theory of spherical distributions and a location-scale parameter generalization. Sankhyā 1970, 32, 419–430. [Google Scholar]
- Kariya, T.; Eaton, M.L. Robust tests for spherical symmetry. Ann. Stat. 1977, 5, 206–215. [Google Scholar] [CrossRef]
- Muirhead, R.J. The effects of elliptical distributions on some standard procedures involving correlation coefficients: A review. In Multivariate Statistical Analysis; Gupta, R.P., Ed.; North-Holland: Amsterdam, The Netherlands, 1980; pp. 143–159. [Google Scholar]
- Hayakana, T.; Puri, M.L. Asymptotic distributions of likelihood ratio criteria for testing latent roots and latent vectors of a covariance matrix under an elliptical population. Biometrika 1985, 72, 331–338. [Google Scholar] [CrossRef]
- Fang, K.; Zhang, Y. Generalized Multivariate Analysis; Springer: Berlin, Germany, 1990. [Google Scholar]
- Galea, M.; Paula, G.A.; Uribe-Opazo, M. On influence diagnostic in univariate elliptical linear regression model. Stat. Pap. 2003, 44, 23–45. [Google Scholar] [CrossRef]
- Riquelme, M.; Leiva, V.; Galea, M.; Sanhueza, A. Influence diagnostics on the coefficient of variation of elliptically contoured distributions. J. Appl. Stat. 2011, 38, 513–532. [Google Scholar] [CrossRef]
- Riquelme, M.; Bolfarine, H.; Galea, M. Robust linear functional mixed models. J. Multivar. Anal. 2015, 134, 82–98. [Google Scholar] [CrossRef]
- Arashi, M.; Nadarajah, S. Generalized elliptical distributions. Commun. Stat. 2017, 46, 6412–6432. [Google Scholar] [CrossRef]
- Ventura, M.; Saulo, H.; Leiva, V.; Monsueto, S. Log-symmetric regression models: Information criteria and application to movie business and industry data with economic implications. Appl. Stoch. Model. Bus. Ind. 2019, 35, 963–977. [Google Scholar] [CrossRef]
- Lesniewska-Choquet, C.; Mauris, G.; Atto, A.M.; Mercier, G. On elliptical possibility distributions. IEEE Trans. Fuzzy Syst. 2020, 28, 1631–1639. [Google Scholar] [CrossRef]
- Hodgson, D.J.; Linton, O.; Vorkink, K. Testing the capital asset pricing model efficiently under elliptical symmetry: A semiparametric approach. J. Appl. Econom. 2002, 17, 617–639. [Google Scholar] [CrossRef]
- Galea, M.; Díaz-García, J.A.; Vilca, F. Influence diagnostics in the capital asset pricing model under elliptical distributions. J. Appl. Stat. 2008, 35, 179–192. [Google Scholar] [CrossRef]
- Xu, X.S.; Hou, C.Q. Capital asset pricing model with generalized elliptical distribution. Syst. Eng. 2008, 28, 17–23. [Google Scholar] [CrossRef]
- Hamada, M.; Valdez, E.A. CAPM and option pricing with elliptically contoured distributions. J. Risk Insur. 2008, 75, 387–409. [Google Scholar] [CrossRef]
- Castro, F.H.F.D.; Silveira, H.P.D. Modelagem das distribuições das taxas de retorno dos índices IBOVESPA e S&P500. Rev. Adm. Mackenzie 2009, 10, 114–133. [Google Scholar]
- Paula, G.A.; Cysneiros, F.J.A. Systematic risk estimation in symmetric models. Appl. Econ. Lett. 2009, 16, 217–221. [Google Scholar] [CrossRef]
- Tzang, S.W.; Wang, C.W.; Yu, M.T. Systematic risk and volatility skew. Int. Rev. Econ. Financ. 2016, 43, 72–87. [Google Scholar] [CrossRef]
- Galea, M.; Giménez, P. Local influence diagnostics for the test of mean–variance efficiency and systematic risks in the capital asset pricing model. Stat. Pap. 2019, 60, 293–312. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control. 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Cavanaugh, J.E.; Neath, A.A. The Akaike information criterion: Background, derivation, properties, application, interpretation, and refinements. Comput. Stat. 2019, 11, e1460. [Google Scholar] [CrossRef]
- St Laurent, R.T.; Cook, R.D. Leverage and superleverage in nonlinear regression. J. Am. Stat. Assoc. 1992, 87, 985–990. [Google Scholar] [CrossRef]
- Paula, G.A. Assessing local influence in restricted regression models. Comput. Stat. Data Anal. 1993, 16, 63–79. [Google Scholar] [CrossRef]
- Paula, G.A. Influence and residuals in restricted generalized linear models. J. Stat. Comput. Simul. 1995, 51, 315–331. [Google Scholar]
- Paula, G.A. Leverage in inequality-constrained regression models. J. R. Stat. Soc. D 1999, 48, 529–538. [Google Scholar] [CrossRef]
- Sutradhar, B.C. On the characteristic function of multivariate student t-distribution. Can. J. Stat. 1986, 14, 329–337. [Google Scholar] [CrossRef]
- Gómez, E.; Gomez-Villegas, M.A.; Marín, J.M. A multivariate generalization of the power exponential family of distributions. Commun. Stat. 1998, 27, 589–600. [Google Scholar] [CrossRef]
- Andrews, D.; Mallows, C. Scale mixtures of normal distributions. J. R. Stat. Soc. B 1974, 36, 99–102. [Google Scholar] [CrossRef]
- Dalpiaz, D. Applied Statistics with R; University Illinois: Urbana, IL, USA, 2020. [Google Scholar]
- Lilliefors, H.W. On the Kolmogorov-Smirnov test for normality with mean and variance unknown. J. Am. Stat. Assoc. 1967, 62, 399–402. [Google Scholar] [CrossRef]
- Stehlik, M.; Leal, D.; Kiseak, J.; Leers, J.; Strelec, J.; Fuders, F. Stochastic approach to heterogeneity in short-time announcement effects on the Chilean stock market indexes within 2016–2019. Stoch. Anal. Appl. 2023. [Google Scholar] [CrossRef]
- Huerta, M.; Leiva, V.; Liu, S.; Rodriguez, M.; Villegas, D. On a partial least squares regression model for asymmetric data with a chemical application in mining. Chemom. Intell. Lab. Syst. 2019, 190, 55–68. [Google Scholar] [CrossRef]
- Leiva, V.; Saulo, H.; Leao, J.; Marchant, C. A family of autoregressive conditional duration models applied to financial data. Comput. Stat. Data Anal. 2014, 79, 175–191. [Google Scholar] [CrossRef]
- Marchant, C.; Leiva, V.; Cysneiros, F.J.A. A multivariate log-linear model for an asymmetric distribution. IEEE Trans. Reliab. 2016, 65, 816–827. [Google Scholar] [CrossRef]
- Martinez, S.; Giraldo, R.; Leiva, V. Functional regression models for spatial data. Stoch. Environ. Res. Risk Assess. 2019, 33, 1765–1780. [Google Scholar] [CrossRef]
- Saulo, H.; Leao, J.; Leiva, V.; Aykroyd, R.G. Autoregressive conditional duration models applied to high-frequency financial data. Stat. Pap. 2019, 60, 1605–1629. [Google Scholar] [CrossRef]
- Sanchez, L.; Leiva, V.; Galea, M.; Saulo, H. Quantile regression models with application to spatial data. Mathematics 2020, 8, 1000. [Google Scholar] [CrossRef]
- Leao, J.; Leiva, V.; Saulo, H.; Tomazella, V. Incorporation of frailties into a cure rate regression model and its diagnostics and application to melanoma data. Stat. Med. 2018, 37, 4421–4440. [Google Scholar] [CrossRef]
- Kotz, S.; Leiva, V.; Sanhueza, A. Two new mixture models related to the inverse Gaussian distribution. Methodol. Comput. Appl. Probab. 2010, 12, 199–212. [Google Scholar] [CrossRef]
- Giampaoli, V.; Tamura, K.A.; Caro, N.P.; de Araujo, L.J.S. Prediction of a financial crisis in Latin American companies using the mixed logistic regression model. Chil. J. Stat. 2016, 7, 31–41. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).