Abstract
A lot of work has been completed in efforts to extend the notions of soft set and fuzzy soft set and their applications to other domains. However, neither of the two concepts has been examined in the study of functional equations in b-metric spaces. Given this background information, this paper proposes the idea of b-hybrid fuzzy soft contraction in b-metric space and investigates new criteria for the existence of fixed points for such mappings. The significance of the obtained principal result lies in the fact that the contractive inequalities can be specialized in various ways, depending on the choice of the parameters, thereby making it possible to unify, deduce, and refine several corresponding results. To motivate further studies in the directions studied herein, two applications regarding decision-making problems and an existence theorem of integral inclusion are considered, using fuzzy soft set-valued maps.
Keywords:
b-metric space; soft set; fuzzy soft set; fuzzy soft set-valued map; hybrid contraction; integral inclusion MSC:
46S40; 47H10; 54H25; 34A12; 46J10
1. Introduction
The study of new spaces and their applications has been an area of interesting research in mathematical realms. On this development, the idea of b-metric spaces (BMS) is presently receiving enormous attractions. The idea of BMS started with the work of Czerwik [1], who presented a hypothesis which is more relaxed than the conventional triangle inequality. For some recent results of BMS, one can consult [2,3,4,5,6]. On related advancements, one of the agile areas of invariant point theory that is equally attracting the attention of mathematicians is the notion of hybrid contractions. This concept has been viewed in two ways, namely, hybrid contraction which is concerned with contractions involving both single-valued and set-valued mappings and the second combines linear and non-linear contractions. Recently, Karapinar and Fulga [7] presented the concept of b-hybrid contraction in the setting of BMS and examined the existence and uniqueness of invariant points for such operators.
The real world is filled with uncertainty, vagueness, and imprecision. The notions we meet in everyday life are vague rather than precise. In recent time, researchers have shown keen interest in modelling vagueness due to the fact that many practical problems within fields such as biology, economics, engineering, environmental sciences, and medical sciences involve data containing various forms of uncertainties. To handle the complexity of vagueness, one cannot successfully employ classical mathematical methods due to the presence of different kinds of incomplete knowledge. Earlier in the literature, there were four known theories for dealing with imperfect knowledge. The three most applied of these theories were: Probability theory, Fuzzy set theory, and Rough set theory. All the aforementioned tools require pre-assignment of some parameters. Such pre-specifications, viewed in the backdrop of incomplete knowledge, give rise to every day problems. With this concern, Molodstov [8] initiated the concept of soft set theory with the aim of handling phenomena and notions of ambiguous, undefined and imprecise environments. A soft set does not need the pre-specifications of parameters, rather, it accommodates approximate descriptions of objects. Molodstov [8] emphasized that the models by fuzzy sets and soft sets are interrelated. Yang et al. [9] observed that soft set theory needed to be expanded in different directions to stem its applications to other fields. Currently, the concept of soft sets has been refined by several researchers. By combining the ideas of soft sets and fuzzy sets, Maji et al. [10] initiated the notion of fuzzy soft sets and discussed its various properties. For related developments in fuzzy soft sets, the reader can check out [11] and some citations therein. Not long ago, Mohammed and Azam [12,13] studied the concept of soft set-valued maps and introduced the notions of e-soft fixed points and E-soft fixed points of maps whose range set is a family of soft sets. It was shown in [12] that every fuzzy mapping is a particular kind of soft set-valued map. Since every fuzzy mapping has its corresponding multifunction analogue (see [14] [Theorem 2.2]), hence, the idea of e-soft invariant point theorems is a generalization of the concept of fuzzy fixed points and fixed points of crisp set-valued maps.
Decision making is an intellectual action to make right choice on the subject of trouble-free management process. Each assessment needs vigilant analysis. An extremely efficient as well as methodical approach that can assist us in winning the true decisions is introduced by mathematical investigators as applications of soft sets and fuzzy set theory. In real life dilemma, a large variety of objects do not contain well-defined criteria. This phenomenon creates disorder about inclusion or exclusion of items in the class. As a result, we must face uncertainty in decision making problems. These types of tribulations can be resolved by existing theories such as theory of fuzzy sets and soft sets, etc. Moreover, this type of situation can be handled by a more efficient way if we involve both concepts in a decision-making problem. Therefore, the launching of idea of fuzzy soft sets and hence the concept of fuzzy soft set-valued mappings is become reasonable. This has been performed in this article.
In a group decision-making process, the role of fuzzy soft set-valued mappings becomes more significant. This can be seen in the given example of selection of cricket players. For a fastest and clearest decision, each decision-maker of the concern committee is asked to provide his or her independent opinions. Then each decision-maker becomes a fuzzy soft set-valued mapping during the conversion of given descriptive information into mathematical formulation. Therefore, by comparing the roles of fuzzy soft set-valued maps with other maps in decision-making problems, it is worthwhile to say that involvement of required parameters and their weight regarding vagueness is possible if a selector or decision-maker has all properties of fuzzy soft set-valued mappings. Differential and integral equations have significant applications in both educational and real life problems. If we solve these equations by involving fuzzy soft set-valued mappings, then it will be possible to handle uncertain phenomena via parameters of fuzzy soft sets. Therefore, for solution of Fredholm integral inclusion, a fuzzy soft set-valued mapping have been used here.
Following the existing findings, we note that solutions of functional equations in the set up of hybrid invariant point results, using fuzzy soft sets has not been developed. Therefore, this paper proposes the notion of b-hybrid fuzzy soft contraction in BMS and examines criteria for the existence of fixed points for such contraction. To attract further researches in the proposed direction, a non-trivial example is provided to support the abstractions of our theorems. Thereafter, a few significant particular cases are deduced which include some recently announced results in the literature. As an application, one of our results is utilized to examine new conditions for the realization of solutions to an integral inclusion of Fredholm type. Within the realms of differential equations and invariant point theory of both crisp and non-classical sets, it is observed that the notions put forward in this work unify and extend a significant number of developments in the related literature.
2. Preliminaries
In what follows, we gather specific basis of BMS. Throughout this manuscript, we take .
Definition 1
([1]). Let Υ be a non-empty set and be a constant. Suppose that the mapping satisfies the following conditions for all :
- (i)
- if and only if ;
- (ii)
- ;
- (iii)
- .
Then, the tripled is called a BMS.
It is pertinent to note that every metric is a b-metric with the parameter . Additionally, in general, a b-metric is not a continuous functional. Whence, the class of b-metrics is larger than the class of classical metrics.
Definition 2
([15]). Let be a BMS. A sequence is said to be:
- (i)
- Convergent if, and only if, we can find for which as , and we write this as .
- (ii)
- Cauchy if, and only if, as .
- (iii)
- The b-metric Υ is said to be complete if every Cauchy sequence in Υ is convergent.
Definition 3
([15]). Let be a BMS. Then, a subset A of Υ is called:
- (i)
- Compact if, and only if, for every sequence of elements of A, we can find a subsequence that converges to an element of A.
- (ii)
- Closed if, and only if, for every sequence of elements of A that converges to an element γ, we have .
Definition 4
([16]). A non-empty subset A of Υ is called proximal if, for each , we can find for which .
Definition 5
([7,17]). A non-decreasing function is called:
- (i)
- A c-comparison function if as for every ;
- (ii)
- A b-comparison function if we can find , and a convergent non-negative series for which , for and any , where denotes the iterate of Δ.
Depict by , the family of functions satisfying the following conditions:
- (i)
- is a b-comparison function;
- (ii)
- if, and only if, ;
- (iii)
- is continuous.
Remark 1
([7]). A b-comparison function is a c-comparison function when . Moreover, it can be shown that a c-comparison function is a comparison function, but the converse is not always true.
Lemma 1
([17]). For a b-comparison function , the following properties hold:
- (i)
- Each iterate is also a b-comparison function;
- (ii)
- for all .
Lemma 2
([17]). Let be a b-comparison function. Then, the series converges for every .
Remark 2
([7]). In Lemma 2, every b-comparison function is a comparison function and thus, in Lemma 1, every b-comparison function satisfies .
Followed herewith, specific basis of soft sets and fuzzy soft sets are collated. Accordingly, let be the universe of discourse, E be the parameter set and represents the power set of .
Definition 6
([8]). The pair is called a soft set over Υ under E, where and F is a mapping given by .
We denote the set of all soft sets over under E by .
Definition 7
([12]). The mapping is called a soft set-valued map. A point is called an e-soft invariant point of T if , for a few . This is also written as , for short. If and for all , then γ is said to be an E-soft invariant point of T.
Throughout this manuscript, and, by , we mean the family of fuzzy sets in .
Definition 8
([10]). The pair is a fuzzy soft set over Υ, where and is a mapping.
For each , we represent the set of all proximal and bounded proximal subsets of under E by and , respectively. As an extension of soft set-valued map (see [12]), Mohammed [18] put forward the concept of fuzzy soft set-valued map and studied the existence of fuzzy soft fixed points for such mappings in metric space. Let denotes the family of fuzzy soft sets over under E. By , we mean the mapping .
Definition 9
([18]). The mapping is called fuzzy soft set-valued map.
Definition 10.
Let be a fuzzy soft set-valued map, and . Then, the α-level set of T is given as
Note that for , , that is, . This means that . This implies that , and hence . So that for , is well-given.
Definition 11.
A point u is called fuzzy soft invariant point of , if we can find for which . The point u is said to be a common fuzzy soft invariant point of if .
3. Decision Making Using Fuzzy Soft Set-Valued Maps
It is a familiar information that decision making is considered as the intellectual procedure used to solve the problems we face in our daily lives. It is one of the most prominent efforts, which aim to find a perfect or at least adequate solution by categorizing and choosing substitutes. In the present circumstances, fuzzy soft set theory is playing an appropriate role for dealing with uncertainty. In the following, an uncomplicated example is furnished to explain these trends.
Example 1.


Suppose that a Cricket Association conducts trials across the country to unearth talent at the grassroot level. The trials have been conducted by three respected first-class and Test cricketers, who are also best coaches of this game. At a stage, 15 player have been selected and it is decided that a training camp should be organized to select best 11 players for finalization of the cricket team. Firstly, a training session has been organised by these three coaches. Then final trials are held and these instructors/coaches are requested to provide their independent opinions as selectors. After the selection of the team, each player is also asked to give his judgement about training and assortment by indicating best coach of his choice. Let us see this phenomenon mathematically with the help of fuzzy soft set theory as follows:
and be given by , where and stand for batting, bowling, and fielding, respectively. The independent opinion from the three coaches: is given by the following fuzzy soft sets.
(
(
(.
Assume that weights for batting, bowling, and fielding is decided, respectively, as 5:4:3. In this way, the following formulation is used to final score of a player.
This information is given in Table 1.

Table 1.
Opinion polls of the coaches.
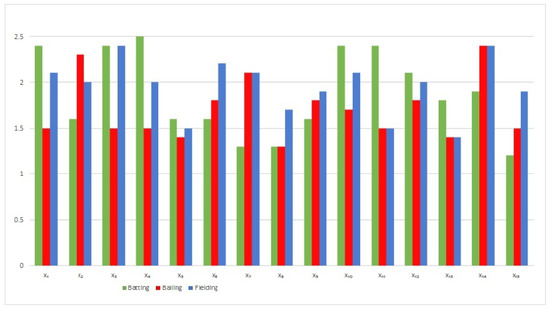
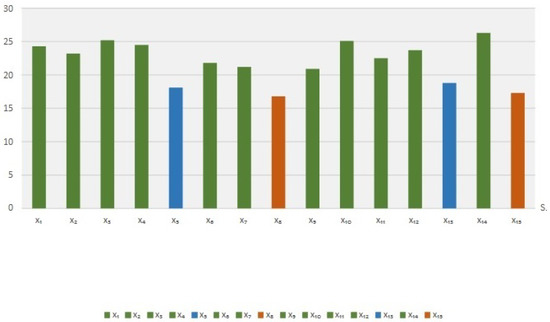
A portion of this information can be seen in the following graphs. A short view of these graphs tells us that are the best five batsman; are the best five bowlers; and are best fielders.
According to the adopted secure function, Figure 1 and Figure 2 have been constructed which finalize the team of 11 players

Figure 1.
Individual score.

Figure 2.
Final score.
Next, the opinions of the players regarding the best coach of their choices is assumed in Table 2.

Table 2.
Opinions of the players.
According to Table 2, coach has the highest opinion polls of the players and hence is considered as the best coach for the national cricket team.
Now, consider a fuzzy soft set-valued mapping T as follows:
Note that . That is, the best player is a fuzzy soft invariant point of T.
The fuzzy soft set-valued maps in Example 1 can be visualized as in Figure 3. We present in Figure 4, further schematic diagram to show the preeminence of applying fuzzy soft sets in decision-making mechanisms. As a matter of extension, the role of fuzzy soft sets, as depicted hereunder, is also inherited by fuzzy soft set-valued mappings.
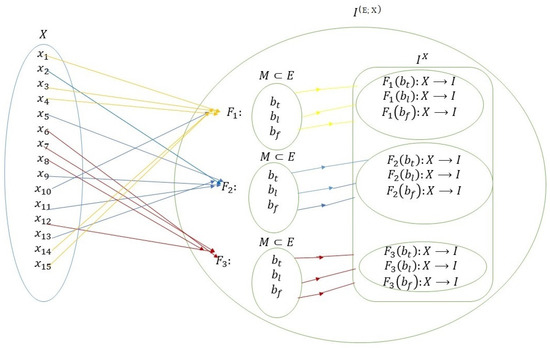
Figure 3.
Pictorial representation of fuzzy soft set-valued maps in Example 1.
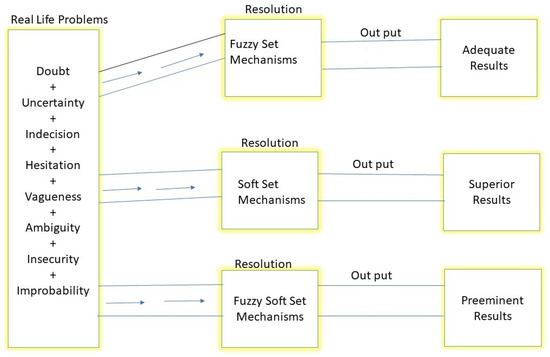
Figure 4.
Decision-making mechanisms.
4. Hybrid Invariant Point Theorems of Fuzzy Soft Set-Valued Maps
We now study hybrid invariant point results involving fuzzy soft set-valued maps. The following auxiliary results are needed in the sequel. Let be a BMS. For each , consider two fuzzy soft sets and . Assume that . Then, we define
where
and .
Motivated by [7] ([Definition 1]), we propose the following concept of b-hybrid fuzzy soft contraction and examine conditions for the existence of fuzzy soft fixed points for such contractions.
Definition 12.
Let be a BMS and be fuzzy soft set-valued maps. Then, forms a b-hybrid fuzzy soft contraction, if for all and , there exist , such that
where
and , , , with .
Our principal result is discussed hereunder.
Theorem 1.
Let be a complete BMS and be fuzzy soft set-valued maps. For , suppose that for each , we can find , such that and are in . If is a b-hybrid fuzzy soft contraction, then S and T have a common fuzzy soft invariant point in Υ.
Proof.
Consider , then, by assumptions, we can find , such that . As e is made fixed, we may write instead of . Choose , such that . Similarly, we can find , such that . So, we can find , such that . Continuing in this fashion, we can find a sequence of elements of such that
and
By the above relations and the proximality of and , we have
Suppose that , for some and . Then,
Hence, using the continuity of and the proximality of and , we obtain
an impossibility. It follows that . Therefore,
So, turns out to be the common fuzzy soft invariant point of S and T.
Again, for and , for some , we obtain . Therefore, by characterization of , one obtains , from which, on similar arguments as above, the same conclusion follows that . For this purpose, hereafter, we presume that for all ,
- Case 1:
- . Suppose that , then from (5), we have
Since is a b-comparison function, therefore, (7) implies that
which is not a possibility. Therefore, it follows that that . Whence, from (7), we realize
Setting in (8), we have
From (9), applying Lemma 2 and the triangle inequality regarding to , for all , we have
Therefore, is a Cauchy sequence of points of . The completeness of this space implies that we can find such that
Now, we show that u is the expected common fuzzy soft invariant point of S and T. First, assume that for all . Then, by the proximality of the level sets of S and T, and considering the case in the contractive inequality (1), we have
Letting in (11), and using the fact that , gives
and as ,
yields an impossibility. Therefore, . On similar steps, by assuming that u is not a fuzzy soft invariant point of T, and considering
one can show that . Whence, for , u is a common fuzzy soft invariant point of S and T.
- Case 2:
- . Employing (1) on account of b-comparison of , we have
Notice that (14) is equivalent to (9). So, we deduce that the iterative sequence is Cauchy in . Whence, the completeness of this space guarantees that as , for some . To see that u is a common fuzzy soft invariant point of T and S, we apply the inequality (1) as follows:
where
We see that . Therefore, under this limiting case, (15) becomes
By condition of , (16) implies that . Therefore, . On similar steps, we can show that . Therefore, u is the common fuzzy soft invariant point of S and T. □
Corollary 1.
Let be a complete BMS and be a fuzzy soft set-valued map. Suppose that for each , we can find for which . If
for all , where and
Then, we can find for which .
Proof.
Take , , and in Theorem 1. □
Corollary 2.
Let be a complete BMS and be fuzzy soft set-valued maps. Assume that for each , we can find and for which
where are bounded proximal subsets of Υ. Then S and T have a common fuzzy soft invariant point in Υ.
Proof.
Take , and in Theorem 1. □
Corollary 3.
Let be a complete BMS and be a fuzzy soft set-valued map. Suppose that for each , we can find for which are bounded proximal subset of Υ, and
Then, we can find for which .
Proof.
Put , , and in Theorem 1. □
Corollary 4.
Let be a complete metric space and be fuzzy soft set-valued maps. Assume that for each , we can find for which and are bounded proximal subsets of Υ, and
where , , , with and
where
. Then, S and T have a common fuzzy soft invariant point in Υ.
Proof.
Take in Theorem 1. □
5. Solvability of Fredholm-Type Integral Inclusions via Fuzzy Soft Set-Valued Maps
In this subsection, we apply one of the results in the previous section to study sufficient conditions for the existence of solutions of a Fredholm Integral inclusion. For some related problems of integral inclusions, the reader can consult [16] and the references therein. Consider the following integral inclusion of Fredholm type:
for , where is an unknown function, is a given real-valued function and is a given set-valued map, where we denote the family of non-empty compact and convex subsets of by . The set of all real-valued continuous functions on is represented by . Now, we study the existence of solutions of (17) under the following assumptions:
Theorem 2.
Suppose that:
- For every , the map is lower semi-continuous;
- ;
- we can find a b-comparison function for which for all ,for each and , where and .Then, the integral inclusion (17) possesses solutions in .
Proof.
Let and be given by
Then, is a complete BMS with the parameter . Note that endowed with this metric is not a classical metric space. Let and consider a fuzzy soft set-valued map , given as follows:
Then, for each , we can find for which
Obviously, the set of solutions of (17) coincides with the set of fuzzy soft fixed points of S. Therefore, we have to show that under the given suppositions, S has at least one fuzzy soft invariant point in . For this, we shall verify that all the hypotheses of Corollary 1 are satisfied.
Take be arbitrary. For the set-valued map , it comes up from Michael’s selection theorem ([19] [Theorem 1]) that we can find a continuous map for which , for each . Therefore, . So, is non-empty. One can note that is a closed subset of . Further, since and is continuous on , their range sets are compact. Therefore, is also compact for each .
Take ; then we can find for which and are non-empty compact subsets of . Let be arbitrary for which
This means for each , we can find for which
Since, from ,
for each and . So, we can find for which
for all .
Now, examine the set-valued map given by
Taking into account the fact that from , is lower semi-continuous, therefore, we can find a continuous map for which , for all . Then,
Hence, , and
Hence, , that is,
therefore, for and ,
Therefore, all the conditions of Corollary 1 are satisfied. So, the conclusion of Theorem 2 holds consequently. □
6. Conclusions
This article introduced the concept of b-hybrid fuzzy soft contraction in BMS and investigated conditions for the existence of fuzzy soft fixed points for such mappings. The pre-eminence of the new contractive inequalities and the associated invariant point results is that several existing results can easily be deduced as consequences. An illustrative example is provided to indicate one of the roles of fuzzy soft set-valued maps in decision-making problems. As a further application, an existence result for a Fredholm-type integral inclusion is provided via the notion of fuzzy soft set-valued maps. Within the realms of differential equations and invariant point theory of both crisp and non-classical sets, it is observed that the notions put forward in this work unify and extend a significant number of developments in the related literature [20,21,22].
Author Contributions
Conceptualization: M.S.S., methodology: M.N. and A.A., formal analysis, A.A. and M.S.S., review and editing, A.A. and M.N., funding acquisition, M.N., writing, review, and editing, M.S.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research work was funded by Institutional Fund Projects under grant no. (IFPIP: 314-247-1443). The authors gratefully acknowledge the technical and financial support provided by the Ministry of Education and King Abdulaziz University, DSR, Jeddah, Saudi Arabia.
Data Availability Statement
Not applicable.
Acknowledgments
The authors gratefully acknowledge the technical and financial support provided by the Ministry of Education and King Abdulaziz University, DSR, Jeddah, Saudi Arabia.
Conflicts of Interest
The authors declare that they have no competing interests.
References
- Czerwik, S. Contraction mappings in b-metric spaces. Acta Math. Inform. Univ. Ostrav. 1993, 1, 5–11. [Google Scholar]
- Hussain, N.; Mitrović, Z.D. On multi-valued weak quasi-contractions in b-metric spaces. J. Nonlinear Sci. Appl. 2017, 10, 3815–3823. [Google Scholar] [CrossRef]
- Kutbi, M.A.; Karapınar, E.; Ahmad, J.; Azam, A. Some fixed point results for multi-valued mappings in b-metric spaces. J. Inequal. Appl. 2014, 2014, 126. [Google Scholar] [CrossRef]
- Monairah, A.; Shehu, S.M.; Akbar, A.; Nawab, H. On multivalued hybrid contractions with applications. J. Funct. Spaces 2020, 2020, 8401403. [Google Scholar] [CrossRef]
- Rao, K.P.R.; Swamy, P.R.; Prasad, J.R. A common fixed point theorem in complex valued b-metric spaces. Bull. Math. Stat. Res. 2013, 1, 1–8. [Google Scholar]
- Tomonari, S. Basic inequality on a b-metric space and its applications. J. Inequal. Appl. 2017, 2017, 256. [Google Scholar]
- Karapinar, E.; Fulga, A. New hybrid contractions on b-metric spaces. Mathematics 2019, 7, 578. [Google Scholar] [CrossRef]
- Molodtsov, D. Soft set theory—First results. Comput. Math. Appl. 1999, 37, 19. [Google Scholar] [CrossRef]
- Yang, X.; Yu, D.; Yang, J.; Wu, C. Generalization of soft set theory: From crisp to fuzzy case. Fuzzy Inf. Eng. 2007, 345–354. [Google Scholar] [CrossRef]
- Maji, P.K.; Biswas, P.; Roy, A.R. Fuzzy soft sets. J. Fuzzy Math. 2001, 589–602. [Google Scholar] [CrossRef]
- Mohammed, S.S.; Azam, A. An algorithm for fuzzy soft set based decision making approach. Yugosl. J. Oper. Res. 2020, 30, 59–70. [Google Scholar] [CrossRef]
- Mohammed, S.S.; Azam, A. Fixed points of soft-set valued and fuzzy set-valued maps with applications. J. Intell. Fuzzy Syst. 2019, 37, 3865–3877. [Google Scholar] [CrossRef]
- Mohammed, S.S.; Azam, A. Integral type contractions of soft set-valued maps with application to neutral differential equation. AIMS Math. 2019, 5, 342–358. [Google Scholar]
- Frigon, M.; O’Regan, D. Fuzzy contractive maps and fuzzy fixed points. Fuzzy Sets Syst. 2002, 129, 39–45. [Google Scholar] [CrossRef]
- Boriceanu, M. Fixed point theory for multivalued generalized contraction on a set with two b-metrics. Mathematica 2009, 4, 126–132. [Google Scholar]
- Kannan, R.; O’Regan, D. A note on the solutions of integral inclusions. J. Integr. Equ. Appl. 2000, 12, 85–94. [Google Scholar] [CrossRef]
- Rus, I.A. Generalized Contractions and Applications; Cluj University Press: Cluj-Napoca, Romania, 2001; Volume 2, pp. 60–71. [Google Scholar]
- Mohammed, S.S. On fuzzy soft set-valued maps with application. J. Niger. Soc. Phys. Sci. 2020, 2, 26–35. [Google Scholar] [CrossRef]
- Michael, E. A selection theorem. Proc. Am. Math. Soc. 1966, 17, 1404–1406. [Google Scholar] [CrossRef]
- Aleksić, S.; Mitrovic, Z.; Radenovic, S. Picard sequences in b-metric spaces. Fixed Point Theory 2020, 21, 35–46. [Google Scholar] [CrossRef]
- Berinde, V. Generalized contractions in quasimetric spaces. In Seminar on Fixed Point Theory; Babes-Bolyai University: Cluj-Napoca, Romania, 1993; pp. 3–9. [Google Scholar]
- Debnath, P.; Konwar, N.; Radenovic, S. Metric Fixed Point Theory: Applications in Science, Engineering and Behavioural Sciences; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).