Modified DTS Iteration Methods for Spatial Fractional Diffusion Equations

Abstract

For the discretized linear systems of the spatial fractional diffusion equations, we construct a class of a modified DTS iteration method and give its asymptotic convergence conditions. Then, we design a fast modified DTS preconditioner by replacing Toeplitz matrix $T$ with the $\tau$ matrix to accelerate the convergence rates of GMRES method. Theoretically, we show that the spectrum of fast modified DTS preconditioned matrix is clustered around one. Numerical experiments verify the validity of the constructed fast modified DTS preconditioner for GMRES method.

1. Introduction

We consider the following spatial fractional diffusion equations

$$\left\{\begin{array}{l}d\left(x,t\right)\frac{\partial u\left(x,t\right)}{\partial t}-\frac{{\partial }^{\beta }u\left(x,t\right)}{{\partial }_{+}{x}^{\beta }}-\frac{{\partial }^{\beta }u\left(x,t\right)}{{\partial }_{-}{x}^{\beta }}=f\left(x,t\right),\\ u\left(x_L,t\right)=u\left(x_R,t\right)=0,\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\left(x,t\right)\in \left(x_L,x_R\right)\times \left(0,T\right],\\ u\left(x,0\right)=u_0\left(x\right),\end{array}\right.$$

(1)

where $d\left(x,t\right)$ is a prescribed nonnegative function. $\frac{{\partial }^{\beta }u\left(x,t\right)}{{\partial }_{+}{x}^{\beta }}$ and $\frac{{\partial }^{\beta }u\left(x,t\right)}{{\partial }_{-}{x}^{\beta }}$ are the left and right Riemann–Liouville fractional derivatives [1,2], respectively, with the order being $\beta \in \left(1,2\right)$, that is,

$$\begin{array}{c}\frac{{\partial }^{\beta }u\left(x,t\right)}{{\partial }_{+}{x}^{\beta }}=\frac{1}{\Gamma \left(2-\beta \right)}\frac{d^2}{d{x}^2}{\displaystyle {\int }_{x_L}^x{\left(x-\xi \right)}^{1-\beta }u\left(\xi ,t\right)d\xi ,}\\ \frac{{\partial }^{\beta }u\left(x,t\right)}{{\partial }_{-}{x}^{\beta }}=\frac{1}{\Gamma \left(2-\beta \right)}\frac{d^2}{d{x}^2}{\displaystyle {\int }_x^{x_R}{\left(\xi -x\right)}^{1-\beta }u\left(\xi ,t\right)d\xi ,}\end{array}$$

where $\Gamma \left(·\right)$ is the Gamma function. $f\left(x,t\right)$ is a given source term.

Compared with the traditional integer order differential equations, the fractional diffusion equations can provide an adequate and accurate description for abnormal diffusion phenomenon, which is applied in many fields such as biology [3], physics [4,5,6], finance [7], etc. Since the closed-form analytical solutions of the spatial fractional diffusion Equation (1) are usually not available, numerical methods are proposed to get the numerical solutions.

A proper finite difference discretization of Equation (1) leads to a system of linear equations of the coefficient matrix $D+T\in {ℝ}^{n\times n}$ at every temporal step, where $D\in {ℝ}^{n\times n}$ is a non-negative diagonal matrix and $T\in {ℝ}^{n\times n}$ is a Hermitian positive definite Toeplitz matrix, with $n$ being the number of grid point number. In order to solve this kind of linear system and reduce computation, the Krylov subspace method, such as GMRES, CG, etc., becomes a good choice [8]. Hence, it is important to find an appropriate preconditioner to accelerate the convergence speeds of the Krylov subspace methods. An approximate inverse circulant plus diagonal (AICD) preconditioner was constructed by Ng and Pan [9], but with certain requirements for the elements of matrices $D$ and $T$. To overcome the shortcomings of the AICD preconditioners, Bai, Lu and Pan [10] propose the diagonal and Toeplitz splitting (DTS) iteration method and build the diagonal and circulant splitting (DCS) preconditioner by replace the Toeplitz matrix $T$ with a circulant matrix. For the ill-conditioned Toeplitz matrices, sine-transform-based preconditioners as $\tau$ matrix are superior to circulant preconditioners [11,12]. Based on the DTS iteration method, Xin, Fang and Sun [13] replace the Toeplitz matrix $T$ by $\tau$ matrix and obtained the sine-transform-based splitting preconditioner.

In this paper, based on the DTS iteration method, we designed a modified DTS (MDTS) iteration method, and analyzed its convergence. Then, we developed the $\tau$ matrix to replace the Toeplitz matrix $T$ as a fast MDTS (FMDTS) preconditioner, and discuss the aggregation of eigenvalues of the preconditioned matrix theoretically.

The outline of this paper is as follows. In Section 2, we obtain the linear system by discretize the spatial fractional diffusion Equation (1). In Section 3, we construct MDTS iteration method and analyze its convergence. In Section 4, FMDTS preconditioner is proposed and analyzed. In Section 5, numerical results are shown. In Section 6, we draw conclusions to end the paper.

2. The Discrete Linear System

We denote ${\left(·\right)}^{\ast }$ being the transpose of a matrix or vector in real space or the conjugate transpose of complex space. Without loss of generality, we make that $x_L=0$ and $x_R=1$. Let the spatial grids $x_i=ih\left(i=0,1,\dots ,n+1\right)$ with isometric step size $h=1/\left(n+1\right)$ and the temporal grids $t_j=j\Delta t\left(j=0,1,\dots ,m\right)$ with the isometric step size $\Delta t=T/m$.

Discretizing Equation (1) by using the shifted finite-difference formula of the Grünwald–Letnikov type [2,14]

$$\begin{array}{c}\frac{{\partial }^{\beta }u\left(x,t\right)}{{\partial }_{+}{x}^{\beta }}=\underset{h\to 0}{\lim }\frac{1}{h^{\beta }}{\displaystyle \sum _{k=0}^{⌊x/h⌋}{g}_k^{\left(\beta \right)}u\left(x-\left(k-1\right)h,t\right)},\\ \frac{{\partial }^{\beta }u\left(x,t\right)}{{\partial }_{-}{x}^{\beta }}=\underset{h\to 0}{\lim }\frac{1}{h^{\beta }}{\displaystyle \sum _{k=0}^{⌊\left(1-x\right)/h⌋}{g}_k^{\left(\beta \right)}u\left(x+\left(k-1\right)h,t\right)},\end{array}$$

where $⌊·⌋$ represents the floor of the corresponding real number which is the largest integer not larger than that real number, $g_k^{\left(\beta \right)}={\left(-1\right)}^k\left(\begin{array}{l}\beta \\ k\end{array}\right)$, $\left(\begin{array}{l}\beta \\ k\end{array}\right)$ is the fractional binomial coefficient, which is

$$\left(\begin{array}{l}\beta \\ k\end{array}\right)=\frac{\beta \left(\beta -1\right)\cdots \left(\beta -k+1\right)}{k!}.$$

By denoting $u_i^j\approx u\left(x_i,t_j\right)$, $d_i^j=d\left(x_i,t_j\right)$, $f_i^j=f\left(x_i,t_j\right)$, as discretized in [10], we can get the linear system as the following form:

$$A^{j+1}{u}^{j+1}:=\left(D^{j+1}+T\right)u^{j+1}=\Delta t{f}^{j+1}+D^{j+1}{u}^j:=b^{j+1},\hspace{1em}j=0,1,\dots ,m-1,$$

(2)

where $u^j={\left[u_1^j,u_2^j,\dots ,u_n^j\right]}^{\ast }$, $f^j={\left[f_1^j,f_2^j,\dots f_n^j\right]}^{\ast }$, $D^{j+1}=diag\left(d_1^{j+1},d_2^{j+1},\dots ,d_n^{j+1}\right)$ is a nonnegative diagonal matrix,

$$T=\frac{\Delta t}{h^{\beta }}\left(T_{\beta }+T_{\beta }^{\ast }\right)$$

(3)

is a Toeplitz matrix, where

$$T_{\beta }=-\left(\begin{array}{cccccc}{g}_1^{\left(\beta \right)}& g_0^{\left(\beta \right)}& 0& \cdots & 0& 0\\ g_2^{\left(\beta \right)}& g_1^{\left(\beta \right)}& g_0^{\left(\beta \right)}& \ddots & \ddots & 0\\ ⋮& g_2^{\left(\beta \right)}& g_1^{\left(\beta \right)}& \ddots & \ddots & ⋮\\ ⋮& \ddots & \ddots & \ddots & \ddots & 0\\ g_{n-1}^{\left(\beta \right)}& \ddots & \ddots & \ddots & g_1^{\left(\beta \right)}& g_0^{\left(\beta \right)}\\ g_n^{\left(\beta \right)}& g_{n-1}^{\left(\beta \right)}& \cdots & \cdots & g_2^{\left(\beta \right)}& g_1^{\left(\beta \right)}\end{array}\right)$$

is the Toeplitz matrix of lower Hessenberg form.

3. The MDTS Iteration Methods

For convenience, we abbreviate (2) as

$$Au:=\left(D+T\right)u=b$$

(4)

We split the coefficient matrix $A$ as follows:

$$\begin{array}{ll}\hfill A& =D-\left(-T\right)\hfill \\ \hfill & =\left(\alpha I+T\right)-\left(\alpha I-D\right).\hfill \end{array}$$

On this basis, we construct the modified DTS (MDTS) iteration method, which is described as follows.

The MDTS iteration method. Given an initial guess $u^{\left(0\right)}\in {ℝ}^n$, for $k=0,1,2,\dots ,$ until the iteration sequence $\left\{u^{\left(k\right)}\right\}\subset {ℝ}^n$ converges, compute the next iterate $u^{\left(k+1\right)}\in {ℝ}^n$ according to the following procedure:

$$\left\{\begin{array}{l}D{u}^{\left(k+\frac{1}{2}\right)}=-T{u}^{\left(k\right)}+b,\\ \left(\alpha I+T\right)u^{\left(k+1\right)}=\left(\alpha I-D\right)u^{\left(k+\frac{1}{2}\right)}+b,\end{array}\right.$$

(5)

where $\alpha$ is a prescribed positive constant.

The MDTS iteration (5) can be written in the following standard form:

$$P\left(\alpha \right)u^{\left(k+1\right)}=Q\left(\alpha \right)u^{\left(k\right)}+b,$$

where

$$P\left(\alpha \right)=\frac{1}{\alpha }D\left(\alpha I+T\right)$$

(6)

and

$$Q\left(\alpha \right)=-\frac{1}{\alpha }\left(\alpha I-D\right)T.$$

(7)

The iteration matrix of the MDTS iteration method is

$$L\left(\alpha \right)=P{\left(\alpha \right)}^{-1}Q\left(\alpha \right)=-{\left(\alpha I+T\right)}^{-1}{D}^{-1}\left(\alpha I-D\right)T.$$

(8)

The MDTS iteration method is convergent if and only if the spectral radius $\rho \left(L\left(\alpha \right)\right)$ of its iteration matrix $L\left(\alpha \right)$ defined by (8) is less than 1.

Let $‖·‖$ denote the Euclidean norm of the vector or the matrix, $\lambda \left(·\right)$ and $sp\left(·\right)$ denote the eigenvalue and the spectral radius of the matrix, respectively.

Theorem 1.

Let $d_{\min }$ and $d_{\max }$ be the minimal and maximal elements of $D$, respectively. ${\lambda }_{\min }$ and ${\lambda }_{\max }$ represent the minimal and maximal eigenvalues of the Toeplitz matrix $T$, respectively. For any initial vector $u^{\left(0\right)}\in {ℝ}^n$, the MDTS iteration method (5) sequence $\left\{u^{\left(k\right)}\right\}\subset {ℝ}^n$ converges to the unique solution of the linear system (4) when the parameter $\alpha$ meets one of the following two conditions:

(a) If ${\lambda }_{\max }\le d_{\min }$, then $\alpha$ can be any positive number;

(b) If ${\lambda }_{\max }>d_{\min }$, then $0<\alpha <\frac{2d_{\min }{\lambda }_{\max }}{{\lambda }_{\max }-d_{\min }}$.

Proof. 

The iteration matrix $L\left(\alpha \right)$ in (8) is similar to

$$\widehat{L}\left(\alpha \right)=-D^{-1}\left(\alpha I-D\right)T{\left(\alpha I+T\right)}^{-1},$$

then, it is clearly

$$\begin{array}{cc}\hfill \rho \left(L\left(\alpha \right)\right)& =\rho \left(\widehat{L}\left(\alpha \right)\right)\hfill \\ \hfill & \le ‖-D^{-1}\left(\alpha I-D\right)T{\left(\alpha I+T\right)}^{-1}‖\hfill \\ \hfill & \le ‖D^{-1}\left(\alpha I-D\right)‖‖T{\left(\alpha I+T\right)}^{-1}‖\hfill \\ \hfill & =\underset{d\in sp\left(D\right)}{\max }\left\{\frac{\left|\alpha -d\right|}{d}\right\}\underset{\lambda \in sp\left(T\right)}{\max }\left\{\frac{\lambda }{\alpha +\lambda }\right\}\hfill \\ \hfill & \le \underset{d_{\min }\le d\le d_{\max }}{\max }\left\{\frac{\left|\alpha -d\right|}{d}\right\}\underset{{\lambda }_{\min }\le \lambda \le {\lambda }_{\max }}{\max }\left\{\frac{\lambda }{\alpha +\lambda }\right\}\hfill \\ \hfill & =\sigma \left(\alpha \right).\hfill \end{array}$$

By straightforward computations, we have

$$\underset{d_{\min }\le d\le d_{\max }}{\max }\left\{\frac{\left|\alpha -d\right|}{d}\right\}=\left\{\begin{array}{l}\frac{d_{\max }-\alpha }{d_{\max }},\hspace{1em}\alpha <\frac{2d_{\min }{d}_{\max }}{d_{\min }+d_{\max }}\\ \frac{\alpha -d_{\min }}{d_{\min }},\hspace{1em}\alpha \ge \frac{2d_{\min }{d}_{\max }}{d_{\min }+d_{\max }}\end{array}\right.$$

and

$$\underset{{\lambda }_{\min }\le \lambda \le {\lambda }_{\max }}{\max }\left\{\frac{\lambda }{\alpha +\lambda }\right\}=\frac{{\lambda }_{\max }}{\alpha +{\lambda }_{\max }}.$$

It follows that when $\alpha <\frac{2d_{\min }{d}_{\max }}{d_{\min }+d_{\max }}$, to make

$$\rho \left(L\left(\alpha \right)\right)\le \frac{d_{\max }-\alpha }{d_{\max }}\cdot \frac{{\lambda }_{\max }}{\alpha +{\lambda }_{\max }}<1,$$

which clearly established.

When $\alpha \ge \frac{2d_{\min }{d}_{\max }}{d_{\min }+d_{\max }}$, to make

$$\rho \left(L\left(\alpha \right)\right)\le \frac{\alpha -d_{\min }}{d_{\min }}\cdot \frac{{\lambda }_{\max }}{\alpha +{\lambda }_{\max }}<1.$$

Through straightforward computations, it can be obtained that parameter $\alpha$ should meet the following conditions

$$\alpha \left({\lambda }_{\max }-d_{\min }\right)<2d_{\min }{\lambda }_{\max }.$$

If ${\lambda }_{\max }\le d_{\min }$, then the above formula obviously holds.

If ${\lambda }_{\max }>d_{\min }$, then $\alpha <\frac{2d_{\min }{\lambda }_{\max }}{{\lambda }_{\max }-d_{\min }}$.

The proof is completed. □

4. The MDTS Preconditioner

The MDTS iteration method naturally leads to a preconditioner. We use the matrix $P\left(\alpha \right)$ as the preconditioning matrix to accelerate the rate of convergence of Krylov subspace method. For convenience, we denote $\vartheta =\Delta t/h^{\beta }$. $P\left(\alpha \right)$ is defined as (6). However, since the inverse of matrix $\alpha I+T$ is hard to calculate in the operation of $P\left(\alpha \right)$ inverse, Toeplitz matrix $T$ is replaced by $\tau$ matrix in order to reduce the amount of calculation and storage and speed up the rate of convergence, then, the FMDTS preconditioner is obtained as follows

$$P_{\tau }\left(\alpha \right)=\frac{1}{\alpha }D\left(\alpha I+\tau \left(T\right)\right),$$

(9)

where

$$\tau \left(T\right)=T-H\left(T\right),$$

(10)

where $H\left(T\right)$ is the Hankel matrix [15] whose antidiagonals are constant and equal to

$$-\vartheta {\left(g_3^{\left(\beta \right)},g_4^{\left(\beta \right)},\dots ,g_n^{\left(\beta \right)},0,0,0,g_n^{\left(\beta \right)},\dots ,g_4^{\left(\beta \right)},g_3^{\left(\beta \right)}\right)}^{\ast },$$

and the $\tau$ matrix can be diagonalized as follows

$$\begin{array}{c}\tau \left(T\right)=W^{\ast }\Lambda W,\\ {\left[W\right]}_{i,j}=\sqrt{\frac{2}{n+1}}\sin \left(\frac{\pi ij}{n+1}\right),\hspace{1em}1\le i,j\le n,\\ \Lambda =diag\left({\sigma }_1,\dots ,{\sigma }_n\right),\end{array}$$

clearly, $W$ is symmetric and orthogonal matrix, ${\sigma }_i$ are the eigenvalues of $\tau \left(T\right)$, which are determined by its first column and can be depicted as

$${\sigma }_i=\frac{{\displaystyle {\sum }_{l=1}^n{t}_l\sin \left(l\pi i/\left(n+1\right)\right)}}{\sin \left(\pi i/\left(n+1\right)\right)},\hspace{0.33em}i=1,2,\dots n,$$

${\left(t_1,t_2,\dots ,t_n\right)}^{\ast }$ is the first column of $\tau \left(T\right)$.

Lemma 1.

(see [13], Theorem 5) The matrix $\tau \left(T\right)$ is defined in (10). Then, for any $\mu >0$, there exists $N$ and $M>0$ such that for all $n>N$,

$$T-\tau \left(T\right)=Y_n+Z_n,$$

where $rank\left(Y_n\right)\le M$, and $‖Z_n‖<\mu$.

Lemma 2.

(see [13], Lemma 8) The Toeplitz matrix $T$ and matrix $\tau \left(T\right)$ are defined in (3) and (10), respectively. Denote

$$\chi :=\frac{e^{\beta +1}{\left(4-\beta \right)}^{9/2}}{e^{13/12}{5}^{9/2}{2}^{\beta }\beta \Gamma \left(-\beta \right)}$$

Then, for $n\ge 3$, we can get

$$2\chi \Delta t<\lambda \left(T\right)\le 4\beta \vartheta ,$$

and

$$2\chi \Delta t<\lambda \left(\tau \left(T\right)\right)<\vartheta g_3^{\left(\beta \right)}+4\beta \vartheta -2\chi \Delta t.$$

Theorem 2.

Let $A=D+T\in {ℂ}^{n\times n}$, where $D\in {ℂ}^{n\times n}$ is a non-negative diagonal matrix and $T\in {ℂ}^{n\times n}$ is a Hermitian positive definite Toeplitz matrix. Suppose that the conditions in Theorem 1 hold, the matrices $P\left(\alpha \right)$ and $P_{\tau }\left(\alpha \right)$are defined in Equations (6) and (9), respectively. Then, for any$\mu >0$, there exists $N$ and $M>0$ such that for all $n>N$,

$$P_{\tau }{\left(\alpha \right)}^{-1}A=P{\left(\alpha \right)}^{-1}A+E_n+F_n,$$

where rank $\left(E_n\right)\le M$, and $‖F_n‖\le \mu$.

Proof. 

According to Lemma 1, for any $\mu >0$, there exists $N$ and $M>0$ such that for all $n>N$,

$$T-\tau \left(T\right)=Y_n+Z_n$$

where $rank\left(Y_n\right)\le M$, and $‖Z_n‖<\frac{{\left(\alpha +2\chi \Delta t\right)}^2\mu }{2\left(\alpha +4\beta \vartheta \right)}$.

We consider the following form

$$P_{\tau }{\left(\alpha \right)}^{-1}A=P_{\tau }{\left(\alpha \right)}^{-1}P\left(\alpha \right)\cdot P{\left(\alpha \right)}^{-1}A.$$

We analyze $P_{\tau }{\left(\alpha \right)}^{-1}P\left(\alpha \right)$ firstly. Based on Equations (6) and (9), we have

$$\begin{array}{cc}\hfill P_{\tau }{\left(\alpha \right)}^{-1}P\left(\alpha \right)-I& ={\left(\alpha I+\tau \left(T\right)\right)}^{-1}\left(\alpha I+T\right)-I\hfill \\ \hfill & ={\left(\alpha I+\tau \left(T\right)\right)}^{-1}\left(T-\tau \left(T\right)\right)\hfill \\ \hfill & ={\left(\alpha I+\tau \left(T\right)\right)}^{-1}\left(Y_n+Z_n\right)\hfill \\ \hfill & ={\left(\alpha I+\tau \left(T\right)\right)}^{-1}{Y}_n+{\left(\alpha I+\tau \left(T\right)\right)}^{-1}{Z}_n.\hfill \end{array}$$

Consequently,

$$\begin{array}{cc}\hfill P_{\tau }{\left(\alpha \right)}^{-1}A& =\left[I+{\left(\alpha I+\tau \left(T\right)\right)}^{-1}{Y}_n+{\left(\alpha I+\tau \left(T\right)\right)}^{-1}{Z}_n\right]\cdot P{\left(\alpha \right)}^{-1}A\hfill \\ \hfill & =P{\left(\alpha \right)}^{-1}A+E_n+F_n,\hfill \end{array}$$

where $E_n={\left(\alpha I+\tau \left(T\right)\right)}^{-1}{Y}_{n}P{\left(\alpha \right)}^{-1}A$ and $F_n={\left(\alpha I+\tau \left(T\right)\right)}^{-1}{Z}_{n}P{\left(\alpha \right)}^{-1}A$.

Next we analyze the range of $‖P{\left(\alpha \right)}^{-1}A‖$. The matrix $Q\left(\alpha \right)$ as defined by (7), we know that the coefficient matrix $A$ can be written as $A=P\left(\alpha \right)-Q\left(\alpha \right)$, so we have

$$\begin{array}{l}P{\left(\alpha \right)}^{-1}A=I-P{\left(\alpha \right)}^{-1}Q\left(\alpha \right)\\ \hspace{1em}\hspace{1em}=I+{\left(\alpha I+T\right)}^{-1}{D}^{-1}\left(\alpha I-D\right)T\\ \hspace{1em}\hspace{1em}={\left(\alpha I+T\right)}^{-1}\left(I-\widehat{L}\left(\alpha \right)\right)\left(\alpha I+T\right),\end{array}$$

By using Lemma 2, there are

$$‖{\left(\alpha I+T\right)}^{-1}‖‖\left(\alpha I+T\right)‖\le \frac{\alpha +4\beta \vartheta }{\alpha +2\chi \Delta t}$$

When the conditions in Theorem 1 hold, by some calculations, we get

$$‖P{\left(\alpha \right)}^{-1}A‖\le \frac{2\left(\alpha +4\beta \vartheta \right)}{\alpha +2\chi \Delta t}$$

It can be seen from Lemma 2 that

$$2\chi \Delta t<\lambda \left(\tau \left(T\right)\right)<\vartheta g_3^{\left(\beta \right)}+4\beta \vartheta -2\chi \Delta t,$$

hence, for any $\mu >0$, there exists $N$ and $M>0$ such that for all $n>N$, it holds

$$rank\left(E_n\right)=rank\left({\left(\alpha I+\tau \left(T\right)\right)}^{-1}{Y}_{n}P{\left(\alpha \right)}^{-1}A\right)=rank\left(Y_n\right)\le M$$

and

$$\begin{array}{cc}\hfill ‖F_n‖& =‖{\left(\alpha I+\tau \left(T\right)\right)}^{-1}{Z}_{n}P{\left(\alpha \right)}^{-1}A‖\hfill \\ \hfill & \le ‖{\left(\alpha I+\tau \left(T\right)\right)}^{-1}‖\cdot ‖Z_n‖\cdot ‖P{\left(\alpha \right)}^{-1}A‖\hfill \\ \hfill & \hspace{1em}\hspace{1em}\le \frac{2\left(\alpha +4\beta \vartheta \right)‖Z_n‖}{{\left(\alpha +2\chi \Delta t\right)}^2}<\mu .\hfill \end{array}$$

Theorem 2 is proved. □

According to Theorem 2, the eigenvalues of the FMDTS preconditioned matrix $P_{\tau }{\left(\alpha \right)}^{-1}A$ gather near the eigenvalues of matrix $P{\left(\alpha \right)}^{-1}A$. Further, according to Theorem 1, under the condition of MDTS iteration method convergence, the eigenvalues of the matrix $P_{\tau }{\left(\alpha \right)}^{-1}A$ are clustered on the complex disk with 1 as the center and $\sigma \left(\alpha \right)$ as the radius.

5. Numerical Results

In this section, we give two numerical examples to verify the effectiveness of the FMDTS preconditioner. We denote “DCS-GMRES” as the GMRES method with DCS preconditioner [10], “$DT{S}_{\tau }$-GMRES” as the GMRES method with sine-transform-based splitting preconditioner [13], and “FMDTS-GMRES” as GMRES method with FMDTS preconditioner. As comparisons, we use the three methods mentioned above to solve the discrete linear system (4), respectively.

In the table, $n$ is the number of grid points, and we take $\Delta t=h$. The IT represents the average number of iteration steps over all time layers, CPU represents the sum of iteration time in seconds over all time layers. We set the fractional order as $\beta =1.2$ and $\beta =1.8$, respectively. At each time layer, $u^{\left(0\right)}=0$ is the initial guess, the criterion for iteration termination is that the residual error satisfies the condition $‖b-A{u}^{\left(k\right)}‖\le {10}^{-6}‖b‖$. The parameters in the experiment are the experimentally computed optimal values.

The numerical examples are run on MATLAB (version R2016a) on machine with 16.00 GB memory, windows 10 system and central processing unit with 2.50 GHz (Intel(R) Core (TM) i5-10300H CPU).

Example 1.

We consider Equation (1) with $\left(x_L,x_R\right)=\left(0,1\right)$, and $T=1$, in which $u_0\left(x\right)=x^2\left(1-x\right)$,

$$d\left(x,t\right)=\frac{1}{x^2{\left(1-x\right)}^2},$$

and the source term is

$$f\left(x,t\right)=tx\left(1-x\right)-x^{1-\beta }-2x^{2-\beta }.$$

This kind of equations can be applied to the particle diffusion phenomenon in physics [4].

In Table 1, the IT and CPU of the DCS-GMRES, $DT{S}_{\tau }$-GMRES and FMDTS-GMRES methods are presented. It can be seen that compared with the DCS-GMRES and $DT{S}_{\tau }$-GMRES methods, both IT and CPU of the FMDTS-GMRES method are significantly reduced. When $\beta =1.2$, with the increase of $n$, the number of iteration steps of FMDTS-GMRES remains in a very stable state. When $\beta =1.8$, with the increase of $n$, the IT of DCS-GMRES decreases slowly, while the IT of FMDTS-GMRES is significantly reduced. The IT and CPU of FMDTS-GMRES are reduced to nearly half of that of DCS-GMRES and $DT{S}_{\tau }$-GMRES, which also proves the effectiveness of new method.

Table 1. Numerical results for solving Example 1.

$\mathit{\beta }$	$\mathit{n}$	DCS-GMRES		$\mathit{D}\mathit{T}{\mathit{S}}_{\mathit{\tau }}$-GMRES		FMDTS-GMRES
		IT	CPU	IT	CPU	IT	CPU
1.2	$2^9$	7	0.1807	4	0.1083	2	0.0682
	$2^{10}$	6.0283	2.0189	4	1.5477	2	1.0941
	$2^{11}$	5.0146	23.3152	3	15.5859	2	11.7321
	$2^{12}$	4.0232	194.9779	3	130.2591	2	98.1337
1.8	$2^9$	7.4113	0.1806	8.1423	0.1974	6.2300	0.1493
	$2^{10}$	7.2478	2.2419	7.2098	2.2455	4.5893	1.6439
	$2^{11}$	7.1581	31.2854	6.4388	28.7044	3.1615	16.1050
	$2^{12}$	7.1228	270.1647	5.5355	217.7170	2.6522	119.1842

Figure 1 plot the distribution of the eigenvalues of the matrix $A$, DCS preconditioned matrix, $DT{S}_{\tau }$ preconditioned matrix and FMDTS preconditioned matrix of example 1 at $\beta =1.2$ and $n=2^{10}$. In Figure 1, we can see that the spectral radius of the FMDTS preconditioned matrix has dropped significantly by nearly 20,000 times, eigenvalues of the matrix $A$ are clustered within 30,000, and the eigenvalues of the FMDTS preconditioned matrix are clustered within 1.5. The spectral radius of the FMDTS preconditioned matrix is more clustered than that of the DCS preconditioned matrix and $DT{S}_{\tau }$ preconditioned matrix, which exhibit good clustering characteristics around 1.

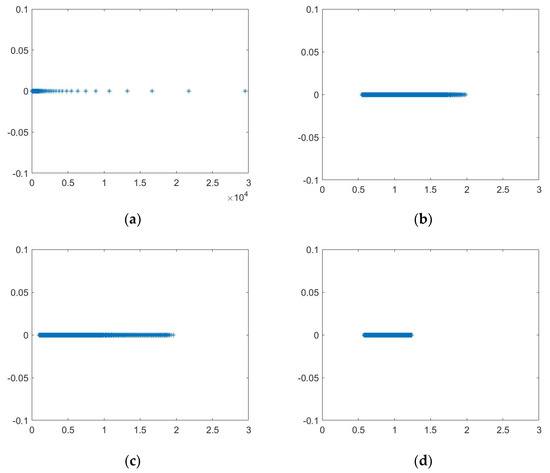
Figure 1. The eigenvalues of the matrix $A$ (a), DCS preconditioned matrix (b), $DT{S}_{\tau }$ preconditioned matrix (c) and FMDTS preconditioned matrix (d) of Example 1.

Example 2.

Considering Equation (1) on $\left(0,1\right)\times \left(0,\infty \right)$, the coefficient function is $d\left(x,t\right)=e^{2x^2}$, the initial condition is $u_0\left(x\right)=x^2{\left(1-x\right)}^2$ and the source term $f\left(x,t\right)=0$.

In Table 2, we give the results of the DCS-GMRES, $DT{S}_{\tau }$-GMRES and FMDTS-GMRES methods. It can be seen that compared with the first two methods, the FMDTS-GMRES method has significantly improvement of the number of iteration steps and the time of iteration. When $\beta =1.2$, the number of iteration steps and the time of iteration of FMDTS-GMRES are half of those of DCS-GMRES and $DT{S}_{\tau }$-GMRES. When $\beta =1.8$, with the increase of $n$, the number of iteration steps of DCS-GMRES and $DT{S}_{\tau }$-GMRES are kept at a stable value, while the iteration steps of FMDTS-GMRES gradually decrease. The results of the example prove that the FMDTS preconditioner is numerically more effective than the DCS preconditioner and $DT{S}_{\tau }$ preconditioner.

Table 2. Numerical results for solving Example 2.

$\mathit{\beta }$	$\mathit{n}$	DCS-GMRES		$\mathit{D}\mathit{T}{\mathit{S}}_{\mathit{\tau }}$-GMRES		FMDTS-GMRES
		IT	CPU	IT	CPU	IT	CPU
1.2	$2^{10}$	8	0.0035	6	0.0047	3	0.0016
	$2^{11}$	7	0.0154	6	0.0175	3	0.0077
	$2^{12}$	6	0.0544	5	0.0471	2	0.0236
	$2^{13}$	5	0.2550	4	0.1572	2	0.0922
1.8	$2^{10}$	8	0.0038	7	0.0035	7	0.0031
	$2^{11}$	8	0.0180	7	0.0155	6	0.0134
	$2^{12}$	8	0.0709	7	0.0622	6	0.0560
	$2^{13}$	8	0.2840	7	0.2537	5	0.1885

Figure 2 plot the distribution of the eigenvalues of the matrix $A$, DCS preconditioned matrix, $DT{S}_{\tau }$ preconditioned matrix and FMDTS preconditioned matrix of Example 2 at order $\beta =1.2$ and $n=2^{10}$. In Figure 2, we can see that the spectral radius of the FMDTS preconditioned matrix has dropped significantly by nearly 20 times, eigenvalues of the matrix $A$ are clustered within 30, and the eigenvalues of the FMDTS preconditioned matrix are clustered within 1.5. The spectral radius of the FMDTS preconditioned matrix is more clustered than that of the DCS preconditioned matrix and $DT{S}_{\tau }$ preconditioned matrix.

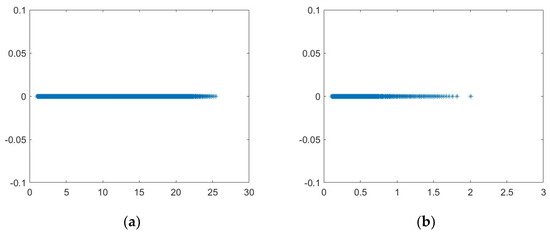
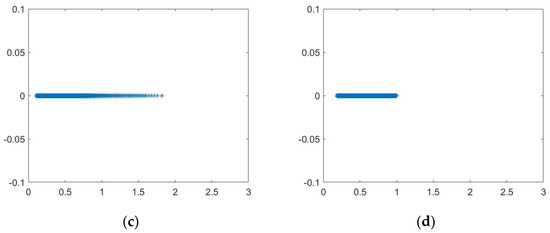
Figure 2. The eigenvalues of the matrix $A$ (a), DCS preconditioned matrix (b), $DT{S}_{\tau }$ preconditioned matrix (c) and FMDTS preconditioned matrix (d) of Example 2.

6. Conclusions

We construct the MDTS iteration method to solve the discretized linear system of spatial fractional diffusion equations and analyze its convergence. Then, the Toeplitz matrix is replaced by the $\tau$ matrix, and the FMDTS preconditioner is proposed. We theoretically analyze the effect of preconditioned matrix, and the effectiveness of our method is verified by numerical experiments. Finding an effective method to calculate the optimal value of the parameters for the preconditioned GMRES method is worth our further study.