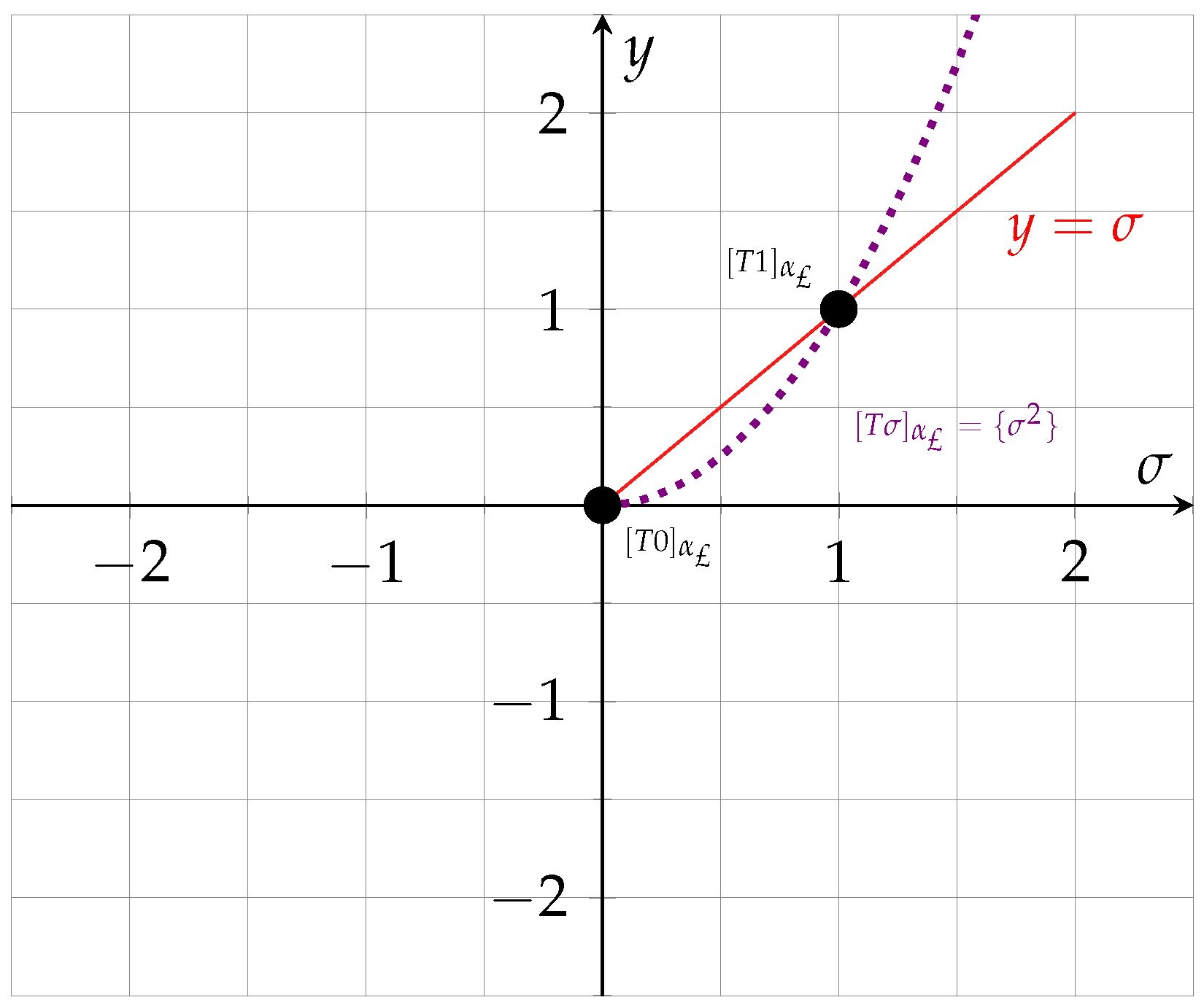A Comprehensive Study on Advancement in Hybrid Contraction and Graphical Analysis of £-Fuzzy Fixed Points with Application

Abstract

Hybrid contractions serve as a flexible and versatile framework for establishing fixed-point Theorems and analyzing the convergence of iterative algorithms. This paper demonstrates the adapted form of the admissible hybrid fuzzy $\mathfrak{Z}$-contraction in the perspective of £-fuzzy set-valued maps for extended ♭-metric spaces. Sufficient criteria for obtaining £-fuzzy fixed points for this contraction have been established. In addition, the hypotheses of its main result are endorsed by some nontrivial supportive examples featuring graphical illustrations. Consequently, the concept of graphical extended ♭-metric spaces is introduced and a £-fuzzy fixed point result in the context of newly defined space is derived. Illustrative examples, incorporating relevant graphs, are provided with the support of a computer simulation to validate the established results, enhancing the understanding of the underlying notions and investigations. The concepts presented here not only considerably improve, enrich, and extend a number of well-known pre-existing fixed-point results but also assemble and merge several ones in the corresponding domain.

1. Introduction

Metric fixed-point theory has its roots traced back to the Banach contraction principle (BCP, in short), which is considered as its foundational concept and is a crucial technique for determining the existence and solutions of multiple problems, together with differential and integral equations. A number of articles have since been published on the expansion and advancement of Banach’s Theorem for mappings, both single and set valued. This has been achieved through modifications to the contraction conditions or by expanding the metric space (MS)’s structural definition, see [1]. This exceptional Theorem has been explored and generalized to increase its applicability in numerous other ambient spaces (see, for instance, refs. [2,3] and the references therein). In this setting, through their respective contributions, Czerwik [4] and Bakhtin [5] developed the idea of a ♭-MS by relaxing the triangle inequality of an MS. Following that, a number of articles covered fixed-point (FP, in short) Theorems for single-valued and set-valued mappings by considering ♭-MS, which is a generalized form of MS, see [6,7,8,9]. Later, Fagin [10] used this type of relaxed triangular inequality to combine with pattern matching. A similar approach was implemented to measure ice floes and trade measures. In this context, Kamran et al. [11], in 2017, proposed the concept of extended ♭-MS by generalizing the structure of ♭-MS. He weakened the ♭-metric’s triangular inequality and developed FP Theorems for a class of contractions. It is helpful to extend the Banach contraction principle from MSs to ♭-MSs, and subsequently to extended ♭-MSs, in order to demonstrate the existence and uniqueness of Theorems for various integral and differential equation types.

Since Zadeh’s [12] discovery of fuzzy set (FS) theory in 1965, real-world problems have been solved more easily and effectively because it makes the description of ambiguity and inaccuracy more precise and understandable. When dealing with the uncertainties and imprecision in given data, FS theory is regarded as a crucial tool to handle a variety of challenges. The system is now extensively utilized to comprehend confusions arising from various materialistic circumstances. FS theory has made notable advancement in recent years. Not only does FS theory have applications in physical and applied sciences, but it also has applications in mathematical evaluation, decision making, clustering, data mining, and soft sciences, which can easily be found in [13,14] and the references therein. Afterward, Heilpern [15] presented the theory of fuzzy mapping (FM) by utilizing the idea of FSs and furnished an FP Theorem for fuzzy contraction maps which is considered as a fuzzy version of Nadler’s [16] and Banach’s [17] FP Theorems. After that, a wide number of researchers worked for the existence of FPs for FMs, see, for example, [18,19]. Later, in 1967, the concept of £-FSs was furnished by Goguen [20], which is an intriguing generalization of FSs because it replaced the interval $[0,1]$ by a complete distributive lattice. So, it makes £-FSs superior to FSs.

On the other hand, Samet et al. [21] introduced the notion of $\beta$-admissibility for single-valued mappings and applied it to illustrate the validity of FP Theorems. After that, Asl et al. [22] expanded this idea to $\alpha -\psi$-multi-valued mappings. Later, Mohammadi et al. [23] inaugurated the above-mentioned concept for multi-valued mappings in the sense it was different from the one given in [22].

Recently, Phiangsungneon et al. [24] used Mohammadi’s concept of $\beta$-admissibility [23] and demonstrated some FFP Theorems. Then, Rashid et al. [25], in 2014, launched its generalized version for a pair of £-FS-valued maps and named it ${\beta }_{F_{\pounds }}$-admissible. By using this idea, they evinced the existence of a common £-FFP result. In the same year, for £-FSs, Rashid et al. [26] initiated the theories of Hausdorff distances for $\alpha$-cuts and the ${\delta }_{\pounds }^{\infty }$-metric. The authors investigated a few coincidence and FP Theorems for £-FMs and a crisp mapping along with a sequence of £-FMs, respectively. Equivalently, coincidence Theorems for fuzzy and multi-valued mappings have been yielded as the consequence of the main result. In 2016, Azam et al. [27] examined some £-FFP results by using local and global contractions. Later, in 2017, Rashid et al. [28] presented some £-FFP results by involving £-fuzzy contractive mappings. Then, in 2018, Rawashdeh et al. [29] applied the idea of an integral $\beta$-admissible to derive a few coincidence and common FP Theorems for a pair of £-FMs and to also generalize an integral contraction. In 2019, Kanwal and Azam [30] established common coincidence points for £-FMs under a generalized contractive condition and obtained many beneficial results as corollaries of the main result. For more results in this regard, see [31,32].

The present article inaugurates the modified form of an admissible hybrid fuzzy $\mathfrak{Z}$-contraction in the bodywork of £-FS-valued maps for extended ♭-MSs and furnished the sufficient criteria for £-FFP results. Some special cases of the main result are also discussed in the form of corollaries. The application lies in the £-FFP result in the framework of an extended ♭-MS equipped with a graph. All the results in this paper are followed by nontrivial examples to validate the hypotheses of the results. As far as we are aware, FP Theorems within the framework of £-FSs using simulation functions have not been covered yet. Consequently, the concepts presented here are novel and specifically complement the main results provided in [4,15,16,21,33,34,35,36,37,38] and a lot more in the corresponding domain.

2. Preliminaries

Within this particular section, we provide a brief summary of key definitions, outcomes, and instances from the existing literature that are vital for a proper understanding of the subject matter. Throughout this article, ${\mathbb{R}}_{+},\mathbb{R}$, and $\mathbb{N}$ represent the sets of non-negative real, real, and natural numbers, respectively.

2.1. Basic Framework

Definition 1

([4,5]). Let Ξ be a non-empty set and $♭\ge 1$ be a predetermined real number. If all the listed below criteria are fulfilled for all $\sigma ,\nu ,\omega \in \mathrm{\Xi }$, then the real-valued function $\delta :\mathrm{\Xi }\times \mathrm{\Xi }⟶{\mathbb{R}}_{+}$ is referred to as a ♭-metric on Ξ.

(δ1)

$\delta (\sigma ,\nu )=0$ if and only if $\sigma =\nu$;

(δ2)

$\delta (\sigma ,\nu )=\delta (\nu ,\sigma )$;

(δ3)

$\delta (\sigma ,\nu )\le ♭\left[\delta \right(\sigma ,\omega )+\delta (\omega ,\nu \left)\right]$.

The triple $(\mathrm{\Xi },\delta ,♭)$ is known as a ♭-MS.

Remark 1.

The concept of a ♭-MS coincides with the concept of an MS in the case of $♭=1$.

Example 1.

Let $\mathrm{\Xi }=[0,1]$ be a non-empty set and $\delta :\mathrm{\Xi }\times \mathrm{\Xi }⟶{\mathbb{R}}_{+}$ is defined as $\delta (\sigma ,\nu )={|\sigma -\nu |}^2$ for all $\sigma ,\nu \in \mathrm{\Xi }$. Then, $(\mathrm{\Xi },\delta ,♭=2)$ is a ♭-MS.

For more details on ♭-MSs, the readers are referred to [39,40]. Kamran et al. [11] defined the notion of an extended ♭-MS by weakening the triangle inequality of a ♭-MS.

Definition 2

([11]). Let Ξ be a non-empty set and $e:\mathrm{\Xi }\times \mathrm{\Xi }⟶[1,\infty )$ be a function. Then, an extended ♭-metric is a function ${\delta }_e:\mathrm{\Xi }\times \mathrm{\Xi }⟶{\mathbb{R}}_{+}$ that fulfills the following conditions for every $\sigma ,\nu ,\omega \in \mathrm{\Xi }$:

(δ_e1)

${\delta }_e(\sigma ,\nu )=0$ if and only if $\sigma =\nu$;

(δ_e2)

${\delta }_e(\sigma ,\nu )={\delta }_e(\nu ,\sigma )$;

(δ_e3)

${\delta }_e(\sigma ,\nu )\le e(\sigma ,\nu )[{\delta }_e(\sigma ,\omega )+{\delta }_e(\omega ,\nu )]$.

The pair $(\mathrm{\Xi },{\delta }_e)$ is referred to as an extended ♭-MS.

Remark 2.

The definition of extended ♭-MS reduces to that of ♭-MS if $e(\sigma ,\nu )=♭$ for $♭\ge 1$.

Example 2.

Taking $\mathrm{\Xi }=\{3,4,5\}$, we define the functions $e:\mathrm{\Xi }\times \mathrm{\Xi }⟶[1,\infty )$ and ${\delta }_e:\mathrm{\Xi }\times \mathrm{\Xi }⟶{\mathbb{R}}_{+}$ as:

$$\begin{array}{c}\hfill e(\sigma ,\nu )=\sigma +\nu +1\mathit{and}\end{array}$$

$$\begin{array}{c}\hfill {\delta }_e(3,4)={\delta }_e(4,3)=40,{\delta }_e(3,5)={\delta }_e(5,3)=300,{\delta }_e(4,5)={\delta }_e(5,4)=3000.\end{array}$$

Of course, ${\delta }_e(\sigma ,\sigma )=0$, for all $\sigma \in \mathrm{\Xi }$. Then, $(\mathrm{\Xi },{\delta }_e)$ is an extended ♭-MS.

Definition 3

([11]). Let $(\mathrm{\Xi },{\delta }_e)$ be an extended ♭-MS. Then, the sequence ${\left\{{\sigma }_n\right\}}_{n\in \mathbb{N}}\subset \mathrm{\Xi }$ is said to be as follows:

(i) 

Convergent to $x\in X$ if for every $\epsilon >0$, there exists a natural number (depending on ε) N such that ${\delta }_e({\sigma }_n,\sigma )<\epsilon$ for all $n\ge N$.

(ii) 

A Cauchy sequence if for every $\epsilon >0$, there exists a natural number (depending on ε) N such that ${\delta }_e({\sigma }_n,{\sigma }_m)<\epsilon$ for all $n,m\ge N$.

If every Cauchy sequence converges in Ξ, then the extended ♭-MS $(\mathrm{\Xi },{\delta }_e)$ is said to be complete.

Definition 4

([41]). A subset U of an extended ♭-MS $(\mathrm{\Xi },{\delta }_e)$ is termed as compact if, for any sequence $\left({\sigma }_n\right)$ in U, there exists a subsequence $({\sigma }_{n_k})$ and a point $\sigma \in U$ such that ${lim}_{k\to \infty }{\sigma }_{n_k}=\sigma$.

Definition 5.

Let ∇ be a non-empty subset of an extended ♭-MS $(\mathrm{\Xi },{\delta }_e)$. If for any $\sigma \in \mathrm{\Xi }$ there exists an element $b\in \nabla$ such that ${\delta }_e(\sigma ,\nabla )={\delta }_e(\sigma ,b)$, then ∇ is considered to be proximal (prox).

Let $\mathbb{k}\left(\mathrm{\Xi }\right)$ and $P\left(\mathrm{\Xi }\right)$ denote, respectively, the set of all non-empty compact and prox subsets of $\mathrm{\Xi }$.

Definition 6

([41]). Let $(\mathrm{\Xi },{\delta }_e)$ be an extended ♭-MS. For $\mathrm{\Gamma },\mathrm{\Pi }\in \mathbb{k}\left(\mathrm{\Xi }\right)$, the real-valued function H on $\mathbb{k}\left(\mathrm{\Xi }\right)\times \mathbb{k}\left(\mathrm{\Xi }\right)$, described by

$$\begin{array}{c}\hfill H(\mathrm{\Gamma },\mathrm{\Pi })=max\{\underset{\sigma \in \mathrm{\Gamma }}{sup}{\delta }_e(\sigma ,\mathrm{\Pi }),\underset{\sigma \in \mathrm{\Pi }}{sup}{\delta }_e(\sigma ,\mathrm{\Gamma })\},\end{array}$$

is called the Pompeiu–Hausdorff metric induced by ${\delta }_e$, where ${\delta }_e(\sigma ,\mathrm{\Gamma })=inf\{{\delta }_e(\sigma ,\nu ):\nu \in \mathrm{\Gamma }\}$.

Khojasteh et al. [36] recently proposed a family of auxiliary functions known as simulation functions (SF) in an effort to standardize various contraction types.

Definition 7

([36]). An SF is a mapping $\rho :{\mathbb{R}}_{+}\times {\mathbb{R}}_{+}⟶\mathbb{R}$ that satisfies the properties listed below:

(S1)

$\rho (0,0)=0$;

(S2)

$\rho (\tau ,\kappa )<\kappa -\tau$ for all $\tau ,\kappa >0$;

(S3)

If ${\left\{{\tau }_n\right\}}_{n\in \mathbb{N}}$ and ${\left\{{\kappa }_n\right\}}_{n\in \mathbb{N}}$ are two sequences with terms in the interval $(0,\infty )$ in such a way that ${lim}_{n⟶\infty }{\tau }_n={lim}_{n⟶\infty }{\kappa }_n>0$, then

$$\begin{array}{c}\hfill \underset{n⟶\infty }{lim\; sup}\rho ({\tau }_n,{\kappa }_n)<0.\end{array}$$

The set comprising all SFs can be represented by $\mathfrak{Z}$.

Example 3

([42]). Take a function $g:{\mathbb{R}}_{+}\times {\mathbb{R}}_{+}⟶\mathbb{R}$ with $g(\tau ,\kappa )<1$ for every $\tau ,\kappa >0$ and for any two sequences $\left\{{\tau }_n\right\}$ and $\left\{{\kappa }_n\right\}$ in $(0,\infty )$ such that ${lim}_{n⟶\infty }{\tau }_n={lim}_{n⟶\infty }{\kappa }_n>0$, and we have ${lim\; sup}_{n⟶\infty }g({\tau }_n,{\kappa }_n)<1$. Then, a function $\rho :{\mathbb{R}}_{+}\times {\mathbb{R}}_{+}⟶\mathbb{R}$ given by:

$$\begin{array}{c}\hfill \rho (\tau ,\kappa )=\kappa g(\tau ,\kappa )-\tau \mathit{for} \mathit{each}\tau ,\kappa \in {\mathbb{R}}_{+},\end{array}$$

is an example of an SF.

Example 4

([42]). Define a function $\rho :{\mathbb{R}}_{+}\times {\mathbb{R}}_{+}⟶\mathbb{R}$ by

$$\begin{array}{c}\hfill \rho (\tau ,\kappa )=⋌\kappa -\tau \mathit{for} \mathit{each}\tau ,\kappa \in {\mathbb{R}}_{+},\end{array}$$

where $⋌\in [0,1)$. Then, ρ is an SF.

We refer the readers to [36,43,44,45] for further and more interesting examples of SFs. In 2015, Khojasteh [36] introduced the notion of a $\mathfrak{Z}$-contraction, which serves as a generalized version of the Banach contraction along with its corresponding FP Theorem.

Definition 8

([36]). Let $(\mathrm{\Xi },\delta )$ be an MS. If the mapping $T:\mathrm{\Xi }⟶\mathrm{\Xi }$ satisfies:

$$\begin{array}{c}\hfill \rho \left(\delta \right(T\sigma ,T\nu ),\delta (\sigma ,\nu \left)\right)\ge 0\mathit{for} \mathit{all}\sigma ,\nu \in \mathrm{\Xi },\end{array}$$

then it is identified as a $\mathfrak{Z}$-contraction with respect to $\rho \in \mathfrak{Z}$.

Theorem 1

([36]). Let Ξ be a complete MS on which the self-map $T:\mathrm{\Xi }⟶\mathrm{\Xi }$ is a $\mathfrak{Z}$-contraction, and then T admits a unique FP in Ξ.

2.2. Fundamental Concepts from Fuzzy Set Theory

Definition 9

([12]). An FS on a set Ξ is a kind of generalized characteristic function on Ξ, whose degrees of membership may be more general than yes or no. Formally, it can be stated as follows: An FS on Ξ is a function from a non-empty set Ξ to I where $I=[0,1]$. If Γ is an FS and $\sigma \in \mathrm{\Xi }$, then the function value $\mathrm{\Gamma }\left(\sigma \right)$ is known as the degree of membership of σ in Γ. The α-cut set of an FS Γ, denoted by ${\left[\mathrm{\Gamma }\right]}_{\alpha }$, is defined by

$$\begin{array}{c}\hfill {\left[\mathrm{\Gamma }\right]}_{\alpha }=\{\sigma \in \mathrm{\Xi }:\mathrm{\Gamma }\left(\sigma \right)\ge \alpha \},\end{array}$$

where $\alpha \in (0,1]$.

The family of all the fuzzy subsets of $\mathrm{\Xi }$ is represented by $I^{\mathrm{\Xi }}$ or $F\left(\mathrm{\Xi }\right)$.

Definition 10

([15]). For a non-empty set Ξ and an MS ∇, a function $T:\mathrm{\Xi }⟶F(\nabla )$ is called an FS-valued map.

Definition 11

([15]). An element ${\sigma }^{*}\in \mathrm{\Xi }$ is said to be the FP of an FM $T:\mathrm{\Xi }⟶F\left(\mathrm{\Xi }\right)$ if ${\sigma }^{*}\in {\left[T{\sigma }^{*}\right]}_{\alpha }$ where $\alpha \in (0,1]$.

Definition 12

([20]). Let $(\pounds ,⪯)$ be a non-empty partially ordered set.

(£1)

If $\tau \vee \kappa \in \pounds$ and $\tau \wedge \kappa \in \pounds$ for all $\tau ,\kappa \in \pounds$, then £ is known as a lattice.

(£2)

If $\vee \mathrm{\Gamma }\in \pounds$ and $\wedge \mathrm{\Gamma }\in \pounds$ for all $\mathrm{\Gamma }\subseteq \pounds$, then £ is termed as a complete lattice.

(£3)

If $\tau \vee (\kappa \wedge \iota )=(\tau \vee \kappa )\wedge (\tau \vee \iota )$, $\tau \wedge (\kappa \vee \iota )=(\tau \wedge \kappa )\vee (\tau \wedge \iota )$ for all $\tau ,\kappa ,\iota \in \pounds$, then £ is said to be a distributive lattice.

(£4)

If $\tau \vee \left({\wedge }_i{\kappa }_i\right)={\wedge }_i(\tau \vee {\kappa }_i)$, $\tau \wedge \left({\vee }_i{\kappa }_i\right)={\vee }_i(\tau \wedge {\kappa }_i)$ for all $\tau ,{\kappa }_i\in \pounds$, then £ is a complete distributive lattice (or simply CDL).

(£5)

If in addition to a lattice, £ satisfies $0_{\pounds }{⪯}_{\pounds }\tau {⪯}_{\pounds }{1}_{\pounds }$, for each $\tau \in \pounds$, where $1_{\pounds }$ and $0_{\pounds }$ are, respectively, the top and bottom elements of lattice £, then £ is referred to as a bounded lattice.

Example 5.

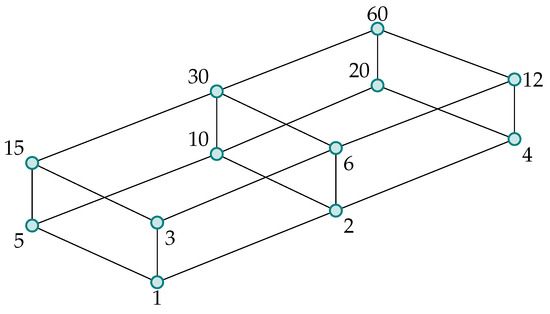
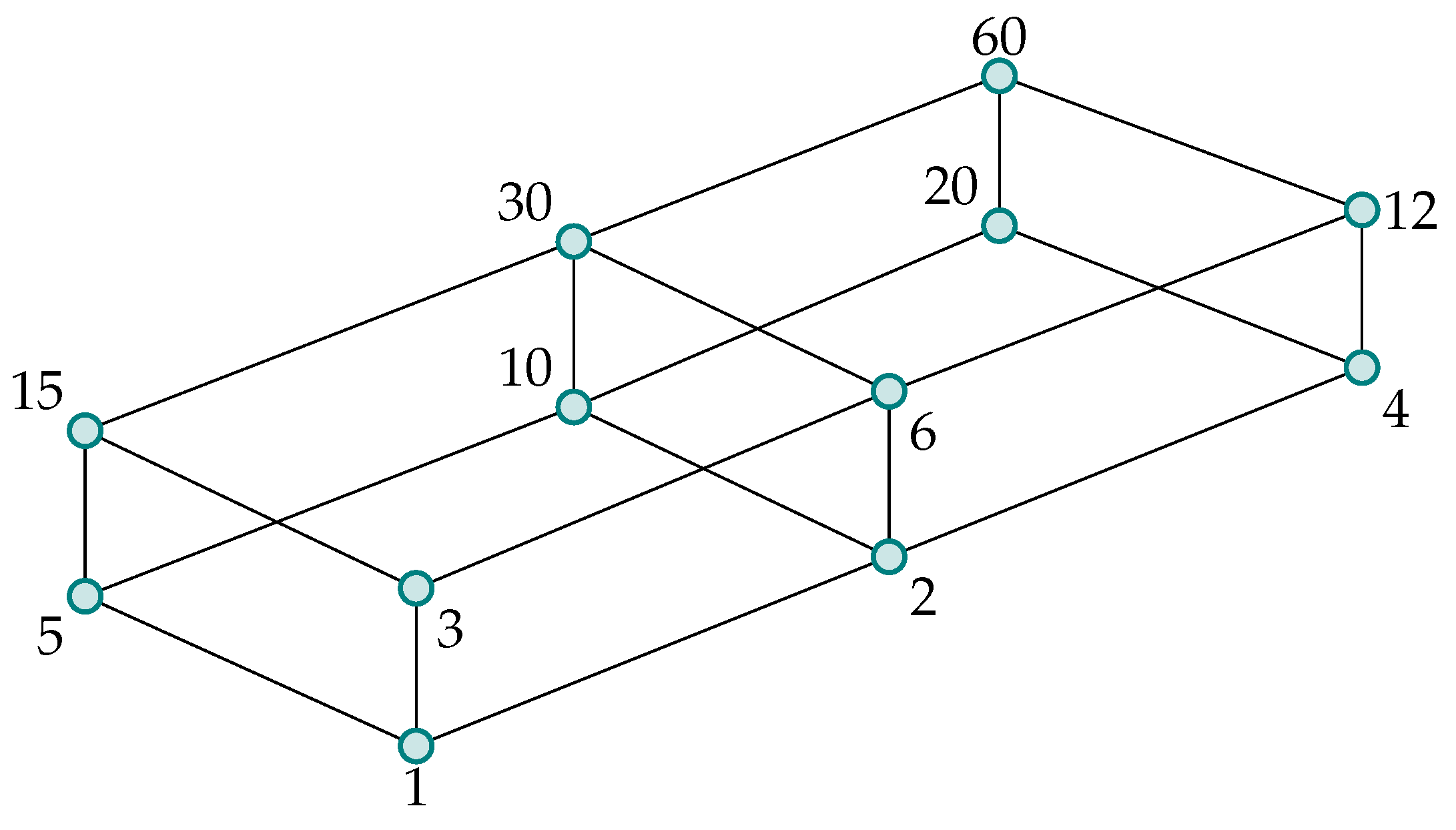
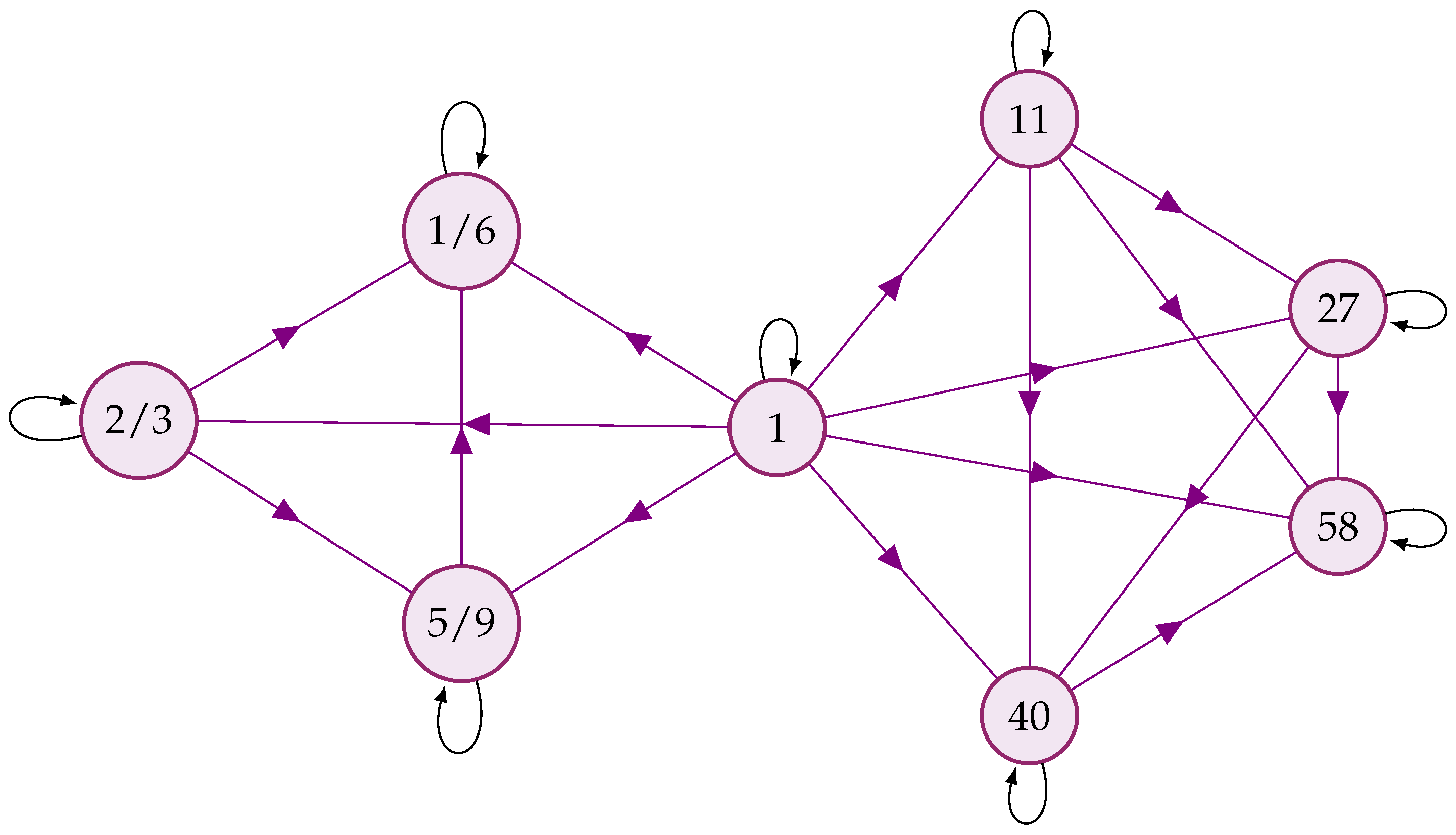
Consider the set $({\mathbb{N}}_0,⪯)$ of non-negative integers, partially ordered by division, that is, $\tau ⪯\kappa$ if τ divides κ. Let the join and meet for any $\tau ,\kappa \in {\mathbb{N}}_0$, be defined as:

$$\begin{array}{c}\hfill \tau \vee \kappa =\{\tau ,\kappa \}\mathit{and}\tau \wedge \kappa =gcd\{\tau ,\kappa \}.\end{array}$$

Then, $({\mathbb{N}}_0,⪯)$ is a lattice. Moreover, this is a CDL with 0 and 1 as the top and bottom elements, respectively. Figure 1 depicts a finite sublattice having integer divisors of 60.

Figure 1. Lattice of integer divisors of 60, ordered by “divides”.

Definition 13

([20]). Consider a non-empty set Ξ and a CDL L having $1_{\pounds }$ and $0_{\pounds }$. Then, the function $\mathrm{\Gamma }:\mathrm{\Xi }⟶\pounds$ is said to be a £-FS on Ξ.

The set of all the £-fuzzy subsets of $\mathrm{\Xi }$ is indicated by $F_{\pounds }\left(\mathrm{\Xi }\right)$.

Remark 3.

The family of £-FSs is bigger than that of FSs as a £-FS becomes an FS by considering $\pounds =[0,1]$.

The ${\alpha }_{\pounds }$-cut set of a £-FS $\mathrm{\Gamma }$, symbolized by ${\mathrm{\Gamma }}_{{\alpha }_{\pounds }}$, is characterized as:

$$\begin{array}{c}\hfill {\left[\mathrm{\Gamma }\right]}_{{\alpha }_{\pounds }}=\left\{\begin{array}{cc}\{\sigma \in \mathrm{\Xi }:{\alpha }_{\pounds }{⪯}_{\pounds }\mathrm{\Gamma }\left(\sigma \right)\},\hfill & \mathrm{if}{\alpha }_{\pounds }\in \pounds \setminus \left\{0_{\pounds }\right\};\hfill \\ \mathrm{cl}\left(\{\sigma \in \mathrm{\Xi }:0_{\pounds }{⪯}_{\pounds }\mathrm{\Gamma }\left(\sigma \right)\}\right),\hfill & \mathrm{if}{\alpha }_{\pounds }=0_{\pounds },\hfill \end{array}\right.\end{array}$$

where cl$\left(\mathrm{\Gamma }\right)$ indicates the closure of set $\mathrm{\Gamma }$.

The characteristic function ${\chi }_{{\pounds }_{\mathrm{\Gamma }}}$ of a £-FS $\mathrm{\Gamma }$ is defined as:

$$\begin{array}{c}\hfill {\chi }_{{\pounds }_{\mathrm{\Gamma }}}=\left\{\begin{array}{cc}{0}_{\pounds },\hfill & \mathrm{if}\sigma \notin \mathrm{\Gamma },\hfill \\ 1_{\pounds },\hfill & \mathrm{if}\sigma \in \mathrm{\Gamma }.\hfill \end{array}\right.\end{array}$$

Definition 14

([26]). In a metric linear space Λ, a £-FS Γ is considered an approximate quantity if and only if two conditions are met: First, ${\left[\mathrm{\Gamma }\right]}_{\alpha \pounds }$ must be both compact and convex in Λ, and second, ${sup}_{\sigma \in \mathsf{\Lambda }}\mathrm{\Gamma }\left(\sigma \right)=1_{\pounds }$. The set comprising all the approximate quantities in Λ is represented by $W_{\pounds }\left(\mathsf{\Lambda }\right)$. For ${\alpha }_{\pounds }\in \pounds \setminus \left\{0_{\pounds }\right\}$ such that ${\left[\mathrm{\Gamma }\right]}_{{\alpha }_{\pounds }},{\left[\mathrm{\Pi }\right]}_{{\beta }_{\pounds }}\in P\left(\mathrm{\Xi }\right)$, define

$$\begin{array}{ccc}\hfill D_{{\alpha }_{\pounds }}(\mathrm{\Gamma },\mathrm{\Pi })& =& H({\left[\mathrm{\Gamma }\right]}_{{\alpha }_{\pounds }},{\left[\mathrm{\Pi }\right]}_{{\beta }_{\pounds }})\hfill \\ \hfill {\delta }_{\pounds }^{\infty }(\mathrm{\Gamma },\mathrm{\Pi })& =& \underset{{\alpha }_{\pounds }}{sup}{D}_{{\alpha }_L}(\mathrm{\Gamma },\mathrm{\Pi }).\hfill \end{array}$$

Definition 15

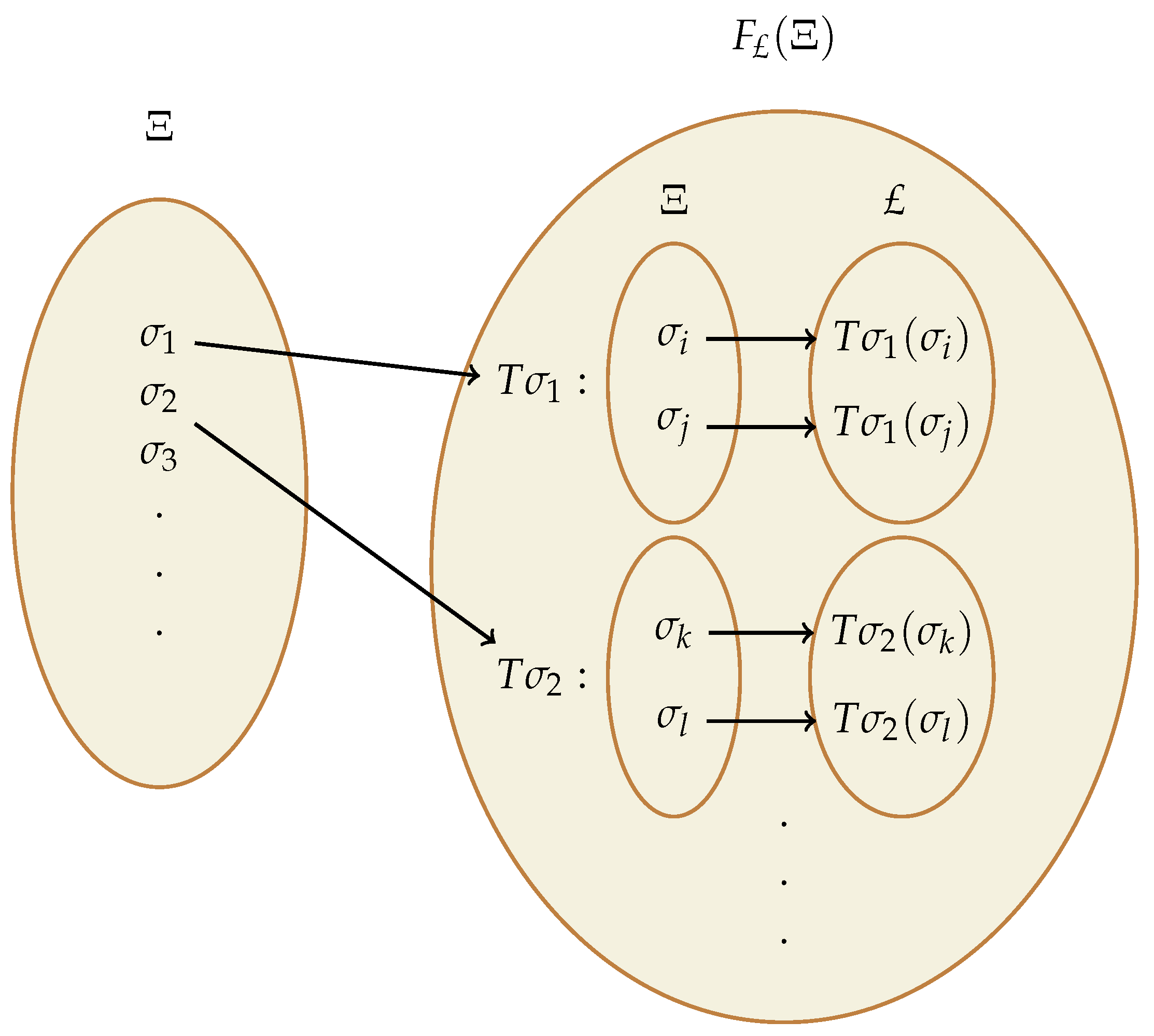
([25]). Consider an arbitrary set Ξ and any MS ∇. A mapping T is called a £-FM if T is a mapping from Ξ into $F_{\pounds }(\nabla )$. A £-FM T is a £-fuzzy subset of $\mathrm{\Xi }\times \nabla$ with a membership function $T\left(\sigma \right)\left(\nu \right)$. The function value $T\left(\sigma \right)\left(\nu \right)$ is called the degree of membership of ν in $T\left(\sigma \right)$.

The concept is better understood through Figure 2.

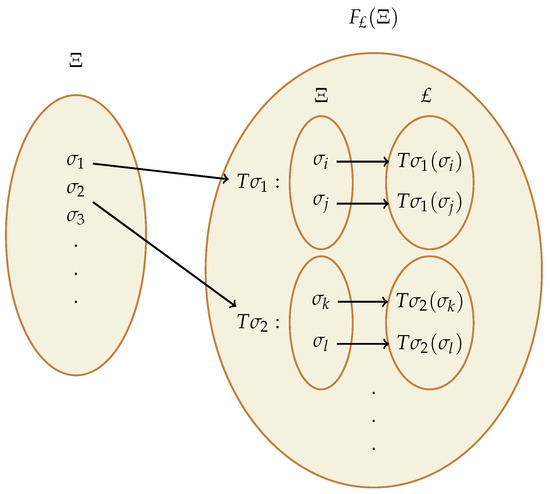
Figure 2. An illustration of L-FM.

Definition 16

([25]). Consider an MS Ξ and a £-FM $T:\mathrm{\Xi }⟶F_{\pounds }\left(\mathrm{\Xi }\right)$, and then a point $u\in \mathrm{\Xi }$ is referred to as a £-FFP of T if there exists an ${\alpha }_{\pounds }\in \pounds \setminus \left\{0_{\pounds }\right\}$ such that $u\in {\left[Tu\right]}_{\alpha \pounds }$.

In an effort to extend the range of contraction-type mappings, Rus [46] first proposed the notion of a comparison function, which has since been thoroughly explored by several authors.

Definition 17

([46]). A nondecreasing function $\vartheta :{\mathbb{R}}_{+}⟶{\mathbb{R}}_{+}$ is said to be a comparison function (CF) if the condition ${lim}_{n⟶\infty }{\vartheta }^n\left(t\right)=0$ is fulfilled for all $t\in {\mathbb{R}}_{+}$.

Example 6.

For all $t\ge 0$, consider the below-defined functions as examples of CFs.

(i) 

$\vartheta \left(t\right)=\eta t$, where $\eta \in (0,1)$.

(ii) 

$\vartheta \left(t\right)=\frac{t}{t+1}$.

Definition 18

([35]). A function $\vartheta :{\mathbb{R}}_{+}⟶{\mathbb{R}}_{+}$ is called a c-CF if it is nondecreasing and satisfies the requirement ${\sum }_{n=0}^{\infty }{\vartheta }^n\left(t\right)<\infty$ for each $t>0$.

Definition 19

([47]). Consider a real number $♭\ge 1$ and a CF ϑ for which there exists a convergent series of positive terms ${\sum }_{n=0}^{\infty }{v}_n$ and a real number α, with $0<\alpha <1$ such that

$$\begin{array}{c}\hfill {♭}^{i+1}{\vartheta }^{i+1}\left(t\right)\le \alpha {♭}^i{\vartheta }^i\left(t\right)+v_i,\mathit{for} \mathit{each} t\in {\mathbb{R}}_{+} \mathit{and} \mathit{each} i\ge N\left(\mathit{fixed}\right),\end{array}$$

and then ϑ is called a ♭-CF.

Lemma 1

([47]). A function $\vartheta :{\mathbb{R}}_{+}⟶{\mathbb{R}}_{+}$ is called a ♭-CF if it is nondecreasing and the series ${\sum }_{i=0}^{\infty }{♭}^i{\vartheta }^i\left(t\right)$ converges for each $t>0$.

Definition 20

([48]). Let $(\mathrm{\Xi },{\delta }_e)$ be an extended ♭-MS and $S\subset \mathrm{\Xi }$, and then a nondecreasing function $\vartheta :{\mathbb{R}}_{+}⟶{\mathbb{R}}_{+}$ is said to be an extended ♭-CF if there exists a mapping $h:S⟶\mathrm{\Xi }$ such that for some ${\sigma }_0\in S,\mathrm{O}\left({\sigma }_0\right)\subset S$, and the series ${\sum }_{k=0}^{\infty }{\vartheta }^k\left(t\right){\prod }_{j=1}^{k}e({\sigma }_j,{\sigma }_s)$ converges for every $s\in \mathbb{N}$ and for all $t\in {\mathbb{R}}_{+}$. Here, ${\sigma }_k=h^k{\sigma }_0$ for $k=1,2,\dots$, and ϑ is an extended ♭-CF for h at ${\sigma }_0$.

Remark 4

([48]). By taking $e(p,q)=♭\ge 1$ for any $p,q\in \mathrm{\Xi }$, the notion of an extended ♭-CF coincides with that of a ♭-CF for any arbitrary self-map h on Ξ.

Example 7

([48]). Let $(X,d_e)$ be an extended ♭-metric space and h a self-map on X, and assume that for $x_0\in X,{lim}_{n,m⟶\infty }e(x_n,x_m)$ exist. Define $\phi :{\mathbb{R}}_{+}⟶{\mathbb{R}}_{+}$ as

$$\begin{array}{c}\hfill \phi \left(t\right)=\eta t,\mathit{such}\mathit{that}\underset{n,m⟶\infty }{lim}e(x_n,x_m)<\frac{1}{\eta }.\end{array}$$

(1)

Then, by using the ratio test, one can easily see that the series ${\sum }_{n=0}^{\infty }{\phi }^n\left(t\right){\prod }_{i=1}^{n}e(x_i,x_m)$ converges.

Let ${\mathsf{\Omega }}_{e♭}$ denote the collection of all the continuous extended ♭-CFs $\vartheta :{\mathbb{R}}_{+}⟶{\mathbb{R}}_{+}$ fulfilling

$$\begin{array}{c}\hfill \vartheta \left(t\right)=0\mathrm{if}\mathrm{and}\mathrm{only}\mathrm{if}t=0;\end{array}$$

Lemma 2

([46]). For a CF $\vartheta :{\mathbb{R}}_{+}⟶{\mathbb{R}}_{+}$, every iteration ${\vartheta }^k,k\in \mathbb{N}$ also serves as a CF. Additionally, $\vartheta \left(t\right)<t$ for all $t>0$.

Lemma 3

([49]). For an extended ♭-MS $(\mathrm{\Xi },{\delta }_e)$ and $\mathrm{\Gamma },\mathrm{\Pi },\mathrm{\Sigma }\in \mathbb{k}\left(\mathrm{\Xi }\right)$, the below-listed properties always hold for all $\sigma ,\nu \in \mathrm{\Xi }$.

(i) 

${\delta }_e(\sigma ,\mathrm{\Pi })\le H(\mathrm{\Gamma },\mathrm{\Pi })$, for each $\sigma \in \mathrm{\Gamma }$.

(ii) 

${\delta }_e(\sigma ,\mathrm{\Pi })\le {\delta }_e(\sigma ,\nu )$, for any $\nu \in \mathrm{\Pi }$.

(iii) 

${\delta }_e(\sigma ,\mathrm{\Gamma })=0$ if and only if $\sigma \in \mathrm{\Gamma }$.

(iv) 

$H(\mathrm{\Gamma },\mathrm{\Pi })=0$ if and only if $\mathrm{\Gamma }=\mathrm{\Pi }$.

(v) 

$H(\mathrm{\Gamma },\mathrm{\Pi })=H(\mathrm{\Pi },\mathrm{\Gamma })$.

(vi) 

$H(\mathrm{\Gamma },\mathrm{\Pi })\le e(\mathrm{\Gamma },\mathrm{\Pi })\left[H\right(\mathrm{\Gamma },\mathrm{\Sigma })+H(\mathrm{\Sigma },\mathrm{\Pi }\left)\right]$.

where $e:\mathbb{k}\left(\mathrm{\Xi }\right)\times \mathbb{k}\left(\mathrm{\Xi }\right)⟶[1,\infty )$ is defined as

$$\begin{array}{c}\hfill e(\mathrm{\Gamma },\mathrm{\Pi })=sup\left\{e\right(\sigma ,\nu ):\sigma \in \mathrm{\Gamma },\nu \in \mathrm{\Pi }\},\end{array}$$

with $e(\mathrm{\Gamma },\mathrm{\Pi })=e(\mathrm{\Pi },\mathrm{\Gamma })$.

Definition 21

([32]). Let Ξ be a non-empty set and $T:\mathrm{\Xi }⟶F_{\pounds }\left(\mathrm{\Xi }\right)$ be a £-FM. Then, T is called β-admissible with respect to a real-valued function $\beta :\mathrm{\Xi }\times \mathrm{\Xi }⟶{\mathbb{R}}_{+}$, if there exists an ${\alpha }_{\pounds }\in \pounds \setminus \left\{0_{\pounds }\right\}$ such that for each $\sigma \in \mathrm{\Xi }$ and $\nu \in {\left[T\sigma \right]}_{{\alpha }_{\pounds }}$ with $\beta (\sigma ,\nu )\ge 1$ we have $\beta (\nu ,\omega )\ge 1$ for all $\omega \in {\left[T\nu \right]}_{{\alpha }_{\pounds }}$.

3. Main Results

Within this section, we introduce the concept of modified admissible hybrid £-fuzzy $\mathfrak{Z}$-contractions, along with the necessary definitions needed to establish the results.

Definition 22.

Let $(\mathrm{\Xi },{\delta }_e)$ be an extended ♭-MS and $T:\mathrm{\Xi }⟶F_{\pounds }\left(\mathrm{\Xi }\right)$ be a £-FS-valued map. Then, T is termed as a modified admissible hybrid £-fuzzy $\mathfrak{Z}$-contraction with respect to $\rho \in \mathfrak{Z}$, if there exists ${\alpha }_{\pounds }\in \pounds \setminus \left\{0_{\pounds }\right\}$, a function $\beta :\mathrm{\Xi }\times \mathrm{\Xi }⟶{\mathbb{R}}_{+}$, and an extended ♭-CF $\vartheta :{\mathbb{R}}_{+}⟶{\mathbb{R}}_{+}$ such that it satisfies the following inequality:

$$\begin{array}{c}\hfill \rho (\beta (\sigma ,\nu )H({\left[T\sigma \right]}_{{\alpha }_{\pounds }},{\left[T\nu \right]}_{{\alpha }_{\pounds }}),\vartheta (M_T^r(\sigma ,\nu )))\ge 0,\end{array}$$

(2)

for each $\sigma ,\nu \in \mathrm{\Xi }$, where

$$\begin{array}{c}\hfill M_T^r(\sigma ,\nu )=\left\{\begin{array}{cc}{\left[\mathrm{\Gamma }(\sigma ,\nu )\right]}^{\frac{1}{r}},\hfill & \mathit{for}r>0,\sigma ,\nu \in \mathrm{\Xi }\hfill \\ \mathrm{\Pi }(\sigma ,\nu ),\hfill & \mathit{for}r=0,\sigma ,\nu \in \mathrm{\Xi },\hfill \end{array}\right.\end{array}$$

$$\begin{array}{ccc}\hfill \mathrm{\Gamma }(\sigma ,\nu )& =& max\left\{\begin{array}{c}{\left({\delta }_e(\sigma ,\nu )\right)}^r,{({\delta }_e(\sigma ,{\left[T\sigma \right]}_{{\alpha }_{\pounds }}))}^r,{({\delta }_e(\nu ,{\left[T\nu \right]}_{{\alpha }_{\pounds }}))}^r,\\ {\left(\frac{{\delta }_e(\nu ,{\left[T\nu \right]}_{{\alpha }_{\pounds }})(1+{\delta }_e(\sigma ,{\left[T\sigma \right]}_{{\alpha }_{\pounds }}))}{1+{\delta }_e(\sigma ,\nu )}\right)}^r,\\ {\left(\frac{{\delta }_e(\nu ,{\left[T\sigma \right]}_{{\alpha }_{\pounds }})(1+{\delta }_e(\sigma ,{\left[T\nu \right]}_{{\alpha }_{\pounds }}))}{1+{\delta }_e(\sigma ,\nu )}\right)}^r,\\ {\left(\frac{{\delta }_e(\nu ,{\left[T\sigma \right]}_{{\alpha }_{\pounds }}).{\delta }_e(\sigma ,{\left[T\nu \right]}_{{\alpha }_{\pounds }})}{1+{\delta }_e(\sigma ,\nu )}\right)}^r\end{array}\right\},\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill \mathrm{\Pi }(\sigma ,\nu )& =& min\left\{\begin{array}{c}{\delta }_e(\sigma ,\nu ),{\delta }_e(\sigma ,{\left[T\sigma \right]}_{{\alpha }_{\pounds }}),{\delta }_e(\nu ,{\left[T\nu \right]}_{{\alpha }_{\pounds }}),\\ \frac{{\delta }_e(\nu ,{\left[T\nu \right]}_{{\alpha }_{\pounds }})(1+{\delta }_e(\sigma ,{\left[T\sigma \right]}_{{\alpha }_{\pounds }}))}{1+{\delta }_e(\sigma ,\nu )},\\ \frac{{\delta }_e(\nu ,{\left[T\sigma \right]}_{{\alpha }_{\pounds }})(1+{\delta }_e(\sigma ,{\left[T\nu \right]}_{{\alpha }_{\pounds }}))}{1+{\delta }_e(\sigma ,\nu )},\\ \frac{{\delta }_e(\sigma ,{\left[T\nu \right]}_{{\alpha }_{\pounds }})+{\delta }_e(\nu ,{\left[T\sigma \right]}_{{\alpha }_{\pounds }})}{2e(\sigma ,[T\nu \left]\right)}\end{array}\right\},\hfill \end{array}$$

with $r\ge 0$.

Remark 5.

(i) 

In the above definition, if $\beta (\sigma ,\nu )=1$, then T is a modified hybrid £-fuzzy $\mathfrak{Z}$-contraction with respect to $\rho \in \mathfrak{Z}$.

(ii) 

If T is a modified admissible hybrid £-fuzzy $\mathfrak{Z}$-contraction with respect to $\rho \in \mathfrak{Z}$, then by using the second axiom of Definition 7, we can easily formulate:

$$\begin{array}{c}\hfill \beta (\sigma ,\nu )H({\left[T\sigma \right]}_{{\alpha }_{\pounds }},{\left[T\nu \right]}_{{\alpha }_{\pounds }})<\vartheta (M_T^r(\sigma ,\nu )),\end{array}$$

for all $\sigma ,\nu \in \mathrm{\Xi }$.

The customary definition of continuity for a set-valued mapping typically relies on the concepts of lower and upper semicontinuity, employing the notion of the Hausdorff separation. Within the framework of extended ♭-MSs, we introduce a complementary approach to this concept as follows.

Definition 23.

Let $(\mathrm{\Xi },{\delta }_e)$ be an extended ♭-MS and $T:\mathrm{\Xi }⟶F_{\pounds }\left(\mathrm{\Xi }\right)$ is a £-FS-valued map. Then, T is referred to as Hausdorff-continuous (H-continuous) at $\varsigma \in \mathrm{\Xi }$, if for any sequence ${\left\{{\sigma }_n\right\}}_{n\in \mathbb{N}}$ in Ξ,

$$\begin{array}{c}\hfill \underset{n⟶\infty }{lim}{\delta }_e({\sigma }_n,\varsigma )=0\mathit{implies}\underset{n⟶\infty }{lim}H({\left[T{\sigma }_n\right]}_{{\alpha }_{\pounds }},{\left[T\varsigma \right]}_{{\alpha }_{\pounds }})=0,\end{array}$$

where ${\alpha }_{\pounds }\in \pounds \setminus \left\{0_{\pounds }\right\}$. A function T is considered to be H-continuous if it exhibits continuity at every single point within the set Ξ.

The above definition can be rewritten as follows: $T:\mathrm{\Xi }⟶F_{\pounds }\left(\mathrm{\Xi }\right)$ is known as H-continuous at a point $\varsigma$ if for every $\epsilon >0$, there exists a $\mathit{\partial }>0$ and an ${\alpha }_{\pounds }\in \pounds \setminus \left\{0_{\pounds }\right\}$ such that

$$\begin{array}{c}\hfill {\delta }_e({\sigma }_n,\varsigma )<\mathit{\partial }\Rightarrow H({\left[T{\sigma }_n\right]}_{{\alpha }_{\pounds }},{\left[T\varsigma \right]}_{{\alpha }_{\pounds }})<\epsilon .\end{array}$$

Let us consider an example to aid our comprehension of the definition.

Example 8.

Let $\mathrm{\Xi }=[0,\infty )$ be a non-void set. For each $\sigma ,\nu \in \mathrm{\Xi }$, define ${\delta }_e:\mathrm{\Xi }\times \mathrm{\Xi }⟶{\mathbb{R}}_{+}$ as ${\delta }_e(\sigma ,\nu )={(\sigma -\nu )}^2$ and $e:\mathrm{\Xi }\times \mathrm{\Xi }⟶[1,\infty )$ as $e(\sigma ,\nu )=\sigma +\nu +2$. Then, $(\mathrm{\Xi },{\delta }_e)$ is an extended ♭-MS. Moreover, let $\pounds =\{\xi ,\varpi ,\pi ,\gamma \}$ with $\xi {⪯}_{\pounds }\varpi {⪯}_{\pounds }\gamma$ and $\xi {⪯}_{\pounds }\pi {⪯}_{\pounds }\gamma$, where $\varpi ,\pi$ are not comparable. Then, $(\pounds ,{⪯}_{\pounds })$ is a CDL. For each $\sigma \in \mathrm{\Xi }$, define a £-FS, $T\sigma :\mathrm{\Xi }⟶\pounds$ as:

$$\begin{array}{c}\hfill \left(T\sigma \right)\left(a\right)=\left\{\begin{array}{cc}\pi ,\hfill & \mathit{if}0\le a\le \sigma /6;\hfill \\ \gamma ,\hfill & \mathit{if}\sigma /6<a\le \sigma /2;\hfill \\ \xi ,\hfill & \mathit{if}\sigma /2<a\le 2\sigma +3{\sigma }^2;\hfill \\ \varpi ,\hfill & \mathit{if}2\sigma +3{\sigma }^2<a<\infty .\hfill \end{array}\right.\end{array}$$

Let ${\alpha }_{\pounds }=\pi$, and then

$$\begin{array}{c}\hfill {\left[T\sigma \right]}_{{\alpha }_{\pounds }}=[0,\sigma /2].\end{array}$$

Suppose ${\delta }_e(\sigma ,\nu )<\mathit{\partial }$ for $\mathit{\partial }>0$ and for all $\sigma ,\nu \in \mathrm{\Xi }$. Then, we have

$$\begin{array}{ccc}\hfill H({\left[T\sigma \right]}_{\pi },{\left[T\nu \right]}_{\pi })& =& H\left(\right[0,\sigma /2],[0,\nu /2\left]\right)\hfill \\ & =& \frac{1}{4}{(\sigma -\nu )}^2\hfill \\ & <& {(\sigma -\nu )}^2<\mathit{\partial }.\hfill \end{array}$$

Let $\mathit{\partial }=\frac{\epsilon }{3}$, and then ${\delta }_e(\sigma ,\nu )<\mathit{\partial }$ implies $H({\left[T\sigma \right]}_{\pi },{\left[T\nu \right]}_{\pi })<\epsilon$. Thus, T is H-continuous.

Let $F_{{\pounds }_S}\left(\mathrm{\Xi }\right)$ be a subset of $F_{\pounds }\left(\mathrm{\Xi }\right)$ defined by

$$\begin{array}{c}\hfill F_{{\pounds }_S}\left(\mathrm{\Xi }\right)=\{\mathrm{\Gamma }\in F_{\pounds }\left(\mathrm{\Xi }\right):{\left[\mathrm{\Gamma }\right]}_{{\alpha }_{\pounds }}\in \mathbb{k}\left(\mathrm{\Xi }\right),\mathrm{where}{\alpha }_{\pounds }\in \pounds \setminus \left\{0_{\pounds }\right\}\}.\end{array}$$

Theorem 2.

Let $(\mathrm{\Xi },{\delta }_e)$ be a complete extended ♭-MS and $T:\mathrm{\Xi }⟶F_{{\pounds }_S}\left(\mathrm{\Xi }\right)$ be an admissible hybrid £-fuzzy $\mathfrak{Z}$-contraction with respect to $\rho \in \mathfrak{Z}$. Also, consider the following:

(i) 

T is β-admissible;

(ii) 

There exists ${\sigma }_0\in \mathrm{\Xi }$ and ${\sigma }_1\in {\left[T{\sigma }_0\right]}_{{\alpha }_{\pounds }}$ such that $\beta ({\sigma }_0,{\sigma }_1)\ge 1$, where ${\alpha }_{\pounds }\in \pounds \setminus \left\{0_{\pounds }\right\}$;

(iii) 

T is H-continuous;

(iv) 

The set ${\left[T\sigma \right]}_{{\alpha }_{\pounds }}$ is prox for each $\sigma \in \mathrm{\Xi }$.

Then, T has at least one £-FFP in Ξ.

Proof. 

Using $\left(ii\right)$, we have ${\alpha }_{\pounds }\in \pounds \setminus \left\{0_{\pounds }\right\},{\sigma }_0\in \mathrm{\Xi }$, and ${\sigma }_1\in {\left[T{\sigma }_0\right]}_{{\alpha }_{\pounds }}$ such that $\beta ({\sigma }_0,{\sigma }_1)\ge 1$. If ${\sigma }_0={\sigma }_1$, then from (2) we obtain

$$\begin{array}{ccc}\hfill 0& \le & \rho (\beta ({\sigma }_0,{\sigma }_1)H({\left[T{\sigma }_0\right]}_{{\alpha }_{\pounds }},{\left[T{\sigma }_1\right]}_{{\alpha }_{\pounds }}),\vartheta (M_T^r({\sigma }_0,{\sigma }_1)))\hfill \\ & <& \vartheta (M_T^r({\sigma }_0,{\sigma }_1))-\beta ({\sigma }_0,{\sigma }_1)H({\left[T{\sigma }_0\right]}_{{\alpha }_{\pounds }},{\left[T{\sigma }_1\right]}_{{\alpha }_{\pounds }}),\hfill \end{array}$$

which is equivalent to

$$\begin{array}{c}\hfill \beta ({\sigma }_0,{\sigma }_1)H({\left[T{\sigma }_0\right]}_{{\alpha }_{\pounds }},{\left[T{\sigma }_1\right]}_{{\alpha }_{\pounds }})\le \vartheta (M_T^r({\sigma }_0,{\sigma }_1)).\end{array}$$

(3)

Then, by using the proximality of T for $r>0$, we have that

$$\begin{array}{ccc}\hfill M_T^r({\sigma }_0,{\sigma }_1)& =& {\left[\mathrm{\Gamma }({\sigma }_0,{\sigma }_1)\right]}^{\frac{1}{r}}\hfill \\ & =& {\left[max\left\{\begin{array}{c}{\left({\delta }_e({\sigma }_0,{\sigma }_1)\right)}^r,{({\delta }_e({\sigma }_0,{\left[T{\sigma }_0\right]}_{{\alpha }_{\pounds }}))}^r,{({\delta }_e({\sigma }_1,{\left[T{\sigma }_1\right]}_{{\alpha }_{\pounds }}))}^r,\\ {\left(\frac{{\delta }_e({\sigma }_1,{\left[T{\sigma }_1\right]}_{{\alpha }_{\pounds }})(1+{\delta }_e({\sigma }_0,{\left[T{\sigma }_0\right]}_{{\alpha }_{\pounds }}))}{1+{\delta }_e({\sigma }_0,{\sigma }_1)}\right)}^r,\\ {\left(\frac{{\delta }_e({\sigma }_1,{\left[T{\sigma }_0\right]}_{{\alpha }_{\pounds }})(1+{\delta }_e({\sigma }_0,{\left[T{\sigma }_1\right]}_{{\alpha }_{\pounds }}))}{1+{\delta }_e({\sigma }_o,{\sigma }_1)}\right)}^r,\\ {\left(\frac{{\delta }_e({\sigma }_1,{\left[T{\sigma }_0\right]}_{{\alpha }_{\pounds }}).{\delta }_e({\sigma }_0,{\left[T{\sigma }_1\right]}_{{\alpha }_{\pounds }})}{1+{\delta }_e({\sigma }_o,{\sigma }_1)}\right)}^r\end{array}\right\}\right]}^{\frac{1}{r}}\hfill \\ & =& {\left[max\left\{\begin{array}{c}{\left({\delta }_e({\sigma }_0,{\sigma }_1)\right)}^r,{\left({\delta }_e({\sigma }_0,{\sigma }_1)\right)}^r,{({\delta }_e({\sigma }_1,{\left[T{\sigma }_1\right]}_{{\alpha }_{\pounds }}))}^r,\\ {\left(\frac{{\delta }_e({\sigma }_1,{\left[T{\sigma }_1\right]}_{{\alpha }_{\pounds }})(1+{\delta }_e({\sigma }_0,{\sigma }_1))}{1+{\delta }_e({\sigma }_0,{\sigma }_1)}\right)}^r,\\ {\left(\frac{{\delta }_e({\sigma }_1,{\sigma }_1)(1+{\delta }_e({\sigma }_0,{\left[T{\sigma }_1\right]}_{{\alpha }_{\pounds }}))}{1+{\delta }_e({\sigma }_0,{\sigma }_1)}\right)}^r,\\ {\left(\frac{{\delta }_e({\sigma }_1,{\sigma }_1).{\delta }_e({\sigma }_0,{\left[T{\sigma }_1\right]}_{{\alpha }_{\pounds }})}{1+{\delta }_e({\sigma }_0,{\sigma }_1)}\right)}^r\end{array}\right\}\right]}^{\frac{1}{r}}\hfill \\ & =& {[max\{{\left({\delta }_e({\sigma }_0,{\sigma }_1)\right)}^r,{({\delta }_e({\sigma }_1,{\left[T{\sigma }_1\right]}_{{\alpha }_{\pounds }}))}^r\}]}^{\frac{1}{r}}\hfill \\ & =& {[max\{{\left({\delta }_e({\sigma }_1,{\sigma }_1)\right)}^r,{({\delta }_e({\sigma }_1,{\left[T{\sigma }_0\right]}_{{\alpha }_{\pounds }}))}^r\}]}^{\frac{1}{r}}(\because {\sigma }_0={\sigma }_1)\hfill \\ & =& 0.\hfill \end{array}$$

Similarly, $\mathrm{\Pi }({\sigma }_0,{\sigma }_1)=0$. Hence, (3) becomes $\beta ({\sigma }_0,{\sigma }_1)H({\left[T{\sigma }_0\right]}_{{\alpha }_{\pounds }},{\left[T{\sigma }_1\right]}_{{\alpha }_{\pounds }})\le \vartheta \left(0\right)=0$. This implies that ${\left[T{\sigma }_0\right]}_{{\alpha }_{\pounds }}={\left[T{\sigma }_1\right]}_{{\alpha }_{\pounds }}$, which means ${\sigma }_1\in {\left[T{\sigma }_0\right]}_{{\alpha }_{\pounds }}={\left[T{\sigma }_1\right]}_{{\alpha }_{\pounds }}$, that is, ${\sigma }_1$ is a £-FFP of T. Hence, hereafter we presume that ${\sigma }_0\ne {\sigma }_1$ and ${\sigma }_1\notin {\left[T{\sigma }_1\right]}_{{\alpha }_{\pounds }}$; therefore, ${\delta }_e({\sigma }_1,{\left[T{\sigma }_1\right]}_{{\alpha }_{\pounds }})>0$. Because ${\left[T{\sigma }_1\right]}_{{\alpha }_{\pounds }}\in \mathbb{k}\left(\mathrm{\Xi }\right)$ and ${\sigma }_1\in {\left[T{\sigma }_0\right]}_{{\alpha }_{\pounds }}$, there exists ${\sigma }_2\in {\left[T{\sigma }_1\right]}_{{\alpha }_{\pounds }}$ with ${\sigma }_1\ne {\sigma }_2$ such that

$$\begin{array}{c}\hfill {\delta }_e({\sigma }_1,{\sigma }_2)\le H({\left[T{\sigma }_0\right]}_{{\alpha }_{\pounds }},{\left[T{\sigma }_1\right]}_{{\alpha }_{\pounds }})\le \beta ({\sigma }_0,{\sigma }_1)H({\left[T{\sigma }_0\right]}_{{\alpha }_{\pounds }},{\left[T{\sigma }_1\right]}_{{\alpha }_{\pounds }}).\end{array}$$

(4)

From (2), we have

$$\begin{array}{c}\hfill \beta ({\sigma }_0,{\sigma }_1)H({\left[T{\sigma }_0\right]}_{{\alpha }_{\pounds }},{\left[T{\sigma }_1\right]}_{{\alpha }_{\pounds }})\le \vartheta (M_T^r({\sigma }_0,{\sigma }_1)).\end{array}$$

(5)

Combining (4) and (5) generates

$$\begin{array}{c}\hfill {\delta }_e({\sigma }_1,{\sigma }_2)\le \vartheta (M_T^r({\sigma }_0,{\sigma }_1)).\end{array}$$

Given that T is $\beta$-admissible and ${\sigma }_2\in {\left[T{\sigma }_1\right]}_{{\alpha }_{\pounds }}$, we have $\beta ({\sigma }_1,{\sigma }_2)\ge 1$. If ${\sigma }_2\in {\left[T{\sigma }_2\right]}_{{\alpha }_{\pounds }}$, then taking ${\sigma }_1={\sigma }_2$, as we have proved earlier, we directly find out that ${\sigma }_2$ is a £-FFP of T. Therefore, assume that ${\sigma }_2\notin {\left[T{\sigma }_2\right]}_{{\alpha }_{\pounds }}$ so ${\delta }_e({\sigma }_2,{\left[T{\sigma }_2\right]}_{{\alpha }_{\pounds }})>0$. Because ${\left[T{\sigma }_1\right]}_{{\alpha }_{\pounds }},{\left[T{\sigma }_2\right]}_{{\alpha }_{\pounds }}\in \mathbb{k}\left(\mathrm{\Xi }\right)$ and ${\sigma }_2\in {\left[T{\sigma }_1\right]}_{{\alpha }_{\pounds }}$, there exists a point ${\sigma }_3\in {\left[T{\sigma }_2\right]}_{{\alpha }_{\pounds }}$ with ${\sigma }_2\ne {\sigma }_3$ such that

$$\begin{array}{c}\hfill {\delta }_e({\sigma }_2,{\sigma }_3)\le H({\left[T{\sigma }_1\right]}_{{\alpha }_{\pounds }},{\left[T{\sigma }_2\right]}_{{\alpha }_{\pounds }})\le \beta ({\sigma }_1,{\sigma }_2)H({\left[T{\sigma }_1\right]}_{{\alpha }_{\pounds }},{\left[T{\sigma }_2\right]}_{{\alpha }_{\pounds }}).\end{array}$$

(6)

Putting $\sigma ={\sigma }_1$ and $\nu ={\sigma }_2$ in (2), we obtain

$$\begin{array}{ccc}\hfill 0& \le & \rho (\beta ({\sigma }_1,{\sigma }_2)H({\left[T{\sigma }_1\right]}_{{\alpha }_{\pounds }},{\left[T{\sigma }_2\right]}_{{\alpha }_{\pounds }}),\vartheta (M_T^r({\sigma }_1,{\sigma }_2)))\hfill \\ & <& \vartheta (M_T^r({\sigma }_1,{\sigma }_2))-\beta ({\sigma }_1,{\sigma }_2)H({\left[T{\sigma }_1\right]}_{{\alpha }_{\pounds }},{\left[T{\sigma }_2\right]}_{{\alpha }_{\pounds }}),\hfill \end{array}$$

which is equivalent to

$$\begin{array}{c}\hfill \beta ({\sigma }_1,{\sigma }_2)H({\left[T{\sigma }_1\right]}_{{\alpha }_{\pounds }},{\left[T{\sigma }_2\right]}_{{\alpha }_{\pounds }})\le \vartheta (M_T^r({\sigma }_1,{\sigma }_2)).\end{array}$$

(7)

Combining (6) and (7), we obtain

$$\begin{array}{c}\hfill {\delta }_e({\sigma }_2,{\sigma }_3)\le \vartheta (M_T^r({\sigma }_1,{\sigma }_2)).\end{array}$$

In this way, a sequence ${\left\{{\sigma }_n\right\}}_{n\in \mathbb{N}}$ can be generated in $\mathrm{\Xi }$ with ${\sigma }_n\in {\left[T{\sigma }_{n-1}\right]}_{{\alpha }_{\pounds }},{\sigma }_{n+1}\in {\left[T{\sigma }_n\right]}_{{\alpha }_{\pounds }}$ and $\beta ({\sigma }_n,{\sigma }_{n+1})\ge 1$ such that

$$\begin{array}{c}\hfill {\delta }_e({\sigma }_n,{\sigma }_{n+1})\le \vartheta (M_T^r({\sigma }_{n-1},{\sigma }_n)).\end{array}$$

(8)

Now, we examine (8) under the below-mentioned scenarios:

Case 1: Taking $r>0$ and utilizing the proximality of T, one obtains from (2) that

$$\begin{array}{ccc}\hfill M_T^r({\sigma }_{n-1},{\sigma }_n)& =& {\left[\mathrm{\Gamma }({\sigma }_{n-1},{\sigma }_n)\right]}^{\frac{1}{r}}\hfill \\ & =& {\left[max\left\{\begin{array}{c}{\left({\delta }_e({\sigma }_{n-1},{\sigma }_n)\right)}^r,{({\delta }_e({\sigma }_{n-1},{\left[T{\sigma }_{n-1}\right]}_{{\alpha }_{\pounds }}))}^r,{({\delta }_e({\sigma }_n,{\left[T{\sigma }_n\right]}_{{\alpha }_{\pounds }}))}^r,\\ {\left(\frac{{\delta }_e({\sigma }_n,{\left[T{\sigma }_n\right]}_{{\alpha }_{\pounds }})(1+{\delta }_e({\sigma }_{n-1},{\left[T{\sigma }_{n-1}\right]}_{{\alpha }_{\pounds }}))}{1+{\delta }_e({\sigma }_{n-1},{\sigma }_n)}\right)}^r,\\ {\left(\frac{{\delta }_e({\sigma }_n,{\left[T{\sigma }_{n-1}\right]}_{{\alpha }_{\pounds }})(1+{\delta }_e({\sigma }_{n-1},{\left[T{\sigma }_n\right]}_{{\alpha }_{\pounds }}))}{1+{\delta }_e({\sigma }_{n-1},{\sigma }_n)}\right)}^r,\\ {\left(\frac{{\delta }_e({\sigma }_n,{\left[T{\sigma }_{n-1}\right]}_{{\alpha }_{\pounds }}).{\delta }_e({\sigma }_{n-1},{\left[T{\sigma }_n\right]}_{{\alpha }_{\pounds }})}{1+{\delta }_e({\sigma }_{n-1},{\sigma }_n)}\right)}^r\end{array}\right\}\right]}^{\frac{1}{r}}\hfill \\ & =& {\left[max\left\{\begin{array}{c}{\left({\delta }_e({\sigma }_{n-1},{\sigma }_n)\right)}^r,{\left({\delta }_e({\sigma }_{n-1},{\sigma }_n)\right)}^r,{\left({\delta }_e({\sigma }_n,{\sigma }_{n+1})\right)}^r,\\ {\left(\frac{{\delta }_e({\sigma }_n,{\sigma }_{n+1})(1+{\delta }_e({\sigma }_{n-1},{\sigma }_n))}{1+{\delta }_e({\sigma }_{n-1},{\sigma }_n)}\right)}^r,\\ {\left(\frac{{\delta }_e({\sigma }_n,{\sigma }_n)(1+{\delta }_e({\sigma }_{n-1},{\sigma }_{n+1}))}{1+{\delta }_e({\sigma }_{n-1},{\sigma }_n)}\right)}^r,\\ {\left(\frac{{\delta }_e({\sigma }_n,{\sigma }_n).{\delta }_e({\sigma }_{n-1},{\sigma }_{n+1})}{1+{\delta }_e({\sigma }_{n-1},{\sigma }_n)}\right)}^r\end{array}\right\}\right]}^{\frac{1}{r}}\hfill \\ & =& {[max\{{\left({\delta }_e({\sigma }_{n-1},{\sigma }_n)\right)}^r,{\left({\delta }_e({\sigma }_n,{\sigma }_{n+1})\right)}^r\}]}^{\frac{1}{r}}.\hfill \end{array}$$

(9)

From (8) and (9), we have

$$\begin{array}{c}\hfill {\delta }_e({\sigma }_n,{\sigma }_{n+1})\le \vartheta ({[max\{{\left({\delta }_e({\sigma }_{n-1},{\sigma }_n)\right)}^r,{\left({\delta }_e({\sigma }_n,{\sigma }_{n+1})\right)}^r\}]}^{\frac{1}{r}}).\end{array}$$

(10)

Assume that ${\delta }_e({\sigma }_{n-1},{\sigma }_n)\le {\delta }_e({\sigma }_n,{\sigma }_{n+1})$. Because $\vartheta$ is nondecreasing, from (10), we have

$$\begin{array}{ccc}\hfill {\delta }_e({\sigma }_n,{\sigma }_{n+1})& \le & \vartheta ({\left[{\left({\delta }_e({\sigma }_n,{\sigma }_{n+1})\right)}^r\right]}^{\frac{1}{r}})\hfill \\ & =& \vartheta \left({\delta }_e({\sigma }_n,{\sigma }_{n+1})\right)<{\delta }_e({\sigma }_n,{\sigma }_{n+1}),\hfill \end{array}$$

which is a contradiction. Therefore, (10) becomes

$$\begin{array}{ccc}\hfill {\delta }_e({\sigma }_n,{\sigma }_{n+1})& \le & \vartheta \left({\delta }_e({\sigma }_{n-1},{\sigma }_n)\right)\hfill \\ & \le & {\vartheta }^2\left({\delta }_e({\sigma }_{n-2},{\sigma }_{n-1})\right)\hfill \\ & ⋮& \hfill \\ & \le & {\vartheta }^n\left({\delta }_e({\sigma }_0,{\sigma }_1)\right).\hfill \end{array}$$

(11)

Let $m,n\in \mathbb{N}$ with $m>n$, and then

$$\begin{array}{ccc}\hfill {\delta }_e({\sigma }_n,{\sigma }_m)& \le & e({\sigma }_n,{\sigma }_m)[{\delta }_e({\sigma }_n,{\sigma }_{n+1})+{\delta }_e({\sigma }_{n+1},{\sigma }_m)]\hfill \\ & \le & e({\sigma }_n,{\sigma }_m){\delta }_e({\sigma }_n,{\sigma }_{n+1})+e({\sigma }_n,{\sigma }_m)e({\sigma }_{n+1},{\sigma }_m){\delta }_e({\sigma }_{n+1},{\sigma }_{n+2})\hfill \\ & & +\cdots +e({\sigma }_n,{\sigma }_m)e({\sigma }_{n+1},{\sigma }_m)e({\sigma }_{n+2},{\sigma }_m)\cdots e({\sigma }_{m-1},{\sigma }_m){\delta }_e({\sigma }_{m-1},{\sigma }_m).\hfill \end{array}$$

Using (11), we obtain

$$\begin{array}{ccc}\hfill {\delta }_e({\sigma }_n,{\sigma }_m)& \le & e({\sigma }_n,{\sigma }_m){\vartheta }^n\left({\delta }_e({\sigma }_0,{\sigma }_1)\right)+e({\sigma }_n,{\sigma }_m)e({\sigma }_{n+1},{\sigma }_m){\vartheta }^{n+1}\left({\delta }_e({\sigma }_0,{\sigma }_1)\right)\hfill \\ & & +\cdots +e({\sigma }_n,{\sigma }_m)e({\sigma }_{n+1},{\sigma }_m)\cdots e({\sigma }_{m-1},{\sigma }_m){\vartheta }^{m-1}\left({\delta }_e({\sigma }_0,{\sigma }_1)\right)\hfill \\ & \le & \sum _{i=n}^{m-1}\left(\prod _{j=n}^{i}e({\sigma }_j,{\sigma }_m)\right){\vartheta }^i\left({\delta }_e({\sigma }_0,{\sigma }_1)\right)\hfill \\ & \le & \sum _{i=1}^{\infty }\left(\prod _{j=1}^{i}e({\sigma }_j,{\sigma }_m)\right){\vartheta }^i\left({\delta }_e({\sigma }_0,{\sigma }_1)\right).\hfill \end{array}$$

(12)

Because $\vartheta$ is an extended ♭-CF, the series ${\sum }_{i=1}^{\infty }\left({\prod }_{j=1}^{i}e({\sigma }_j,{\sigma }_m)\right)$.

${\vartheta }^i\left({\delta }_e({\sigma }_0,{\sigma }_1)\right)$ is therefore convergent. Setting $S={\sum }_{i=1}^{\infty }\left({\prod }_{j=1}^i({\sigma }_j,{\sigma }_m)\right){\vartheta }^i\left({\delta }_e({\sigma }_0,{\sigma }_1)\right)$ and $S_k={\sum }_{i=1}^k\left({\prod }_{j=1}^{i}e({\sigma }_j,{\sigma }_m)\right)({\vartheta }^i\left({\delta }_e({\sigma }_0,{\sigma }_1)\right)$. Thus, (12) can be written as

$$\begin{array}{c}\hfill {\delta }_e({\sigma }_n,{\sigma }_m)\le (S_{m-1},S_{n-1}).\end{array}$$

Applying ${lim}_{n,m\to \infty }$ on both sides of the above inequality, we obtain ${\delta }_e({\sigma }_n,{\sigma }_m)⟶0$ indicating that ${\left\{{\sigma }_n\right\}}_{n\in \mathbb{N}}$ is a Cauchy sequence in $\mathrm{\Xi }$. Seeing that $\mathrm{\Xi }$ is a complete extended ♭-MS, there exists an element $u\in \mathrm{\Xi }$ such that

$$\begin{array}{c}\hfill \underset{n⟶\infty }{lim}{\delta }_e({\sigma }_n,u)=0.\end{array}$$

Now, by using the triangle inequality in $\mathrm{\Xi }$, we obtain

$$\begin{array}{ccc}\hfill {\delta }_e(u,{\left[Tu\right]}_{{\alpha }_{\pounds }})& \le & e(u,{\left[Tu\right]}_{{\alpha }_{\pounds }})[{\delta }_e(u,{\sigma }_n)+{\delta }_e({\sigma }_n,{\left[Tu\right]}_{{\alpha }_{\pounds }})]\hfill \\ & \le & e(u,{\left[Tu\right]}_{{\alpha }_{\pounds }}){\delta }_e(u,{\sigma }_n)+e(u,{\left[Tu\right]}_{{\alpha }_{\pounds }})H({\left[T{\sigma }_{n-1}\right]}_{{\alpha }_{\pounds }},{\left[Tu\right]}_{{\alpha }_{\pounds }}).\hfill \end{array}$$

(13)

Because T is H-continuous, by applying lim as $n⟶\infty$ in (13), we obtain ${\delta }_e(u,{\left[Tu\right]}_{{\alpha }_{\pounds }})=0$, which implies $u\in {\left[Tu\right]}_{{\alpha }_{\pounds }}$.

Case 2: $r=0$. In this case, take $\sigma ={\sigma }_{n-1}$ and $\nu ={\sigma }_n$ in (2), and then by the proximality of T,

$$\begin{array}{ccc}\hfill M_T^r({\sigma }_{n-1},{\sigma }_n)& =& \mathrm{\Pi }({\sigma }_{n-1},{\sigma }_n)\hfill \\ & =& min\left\{\begin{array}{c}{\delta }_e({\sigma }_{n-1},{\sigma }_n),{\delta }_e({\sigma }_{n-1},{\left[T{\sigma }_{n-1}\right]}_{{\alpha }_{\pounds }}),{\delta }_e({\sigma }_n,{\left[T{\sigma }_n\right]}_{{\alpha }_{\pounds }}),\\ \frac{{\delta }_e({\sigma }_n,{\left[T{\sigma }_n\right]}_{{\alpha }_{\pounds }})(1+{\delta }_e({\sigma }_{n-1},{\left[T{\sigma }_{n-1}\right]}_{{\alpha }_{\pounds }}))}{1+{\delta }_e({\sigma }_{n-1},{\sigma }_n)},\\ \frac{{\delta }_e({\sigma }_n,{\left[T{\sigma }_{n-1}\right]}_{{\alpha }_{\pounds }})(1+{\delta }_e({\sigma }_{n-1},{\left[T{\sigma }_n\right]}_{{\alpha }_{\pounds }}))}{1+{\delta }_e({\sigma }_{n-1},{\sigma }_n)},\\ \frac{{\delta }_e({\sigma }_{n-1},{\left[T{\sigma }_n\right]}_{{\alpha }_{\pounds }})+{\delta }_e({\sigma }_n,{\left[T{\sigma }_{n-1}\right]}_{{\alpha }_{\pounds }})}{2e({\sigma }_{n-1},\left[T{\sigma }_n\right])}\end{array}\right\}\hfill \\ & =& min\left\{\begin{array}{c}{\delta }_e({\sigma }_{n-1},{\sigma }_n),{\delta }_e({\sigma }_{n-1},{\sigma }_n),{\delta }_e({\sigma }_n,{\sigma }_{n+1}),\\ \frac{{\delta }_e({\sigma }_n,{\sigma }_{n+1})(1+{\delta }_e({\sigma }_{n-1},{\sigma }_n))}{1+{\delta }_e({\sigma }_{n-1},{\sigma }_n)},\frac{{\delta }_e({\sigma }_{n-1},{\sigma }_{n+1})+{\delta }_e({\sigma }_n,{\sigma }_n)}{2e({\sigma }_{n-1},{\sigma }_{n+1})}\end{array}\right\}\hfill \\ & \le & min\left\{{\delta }_e({\sigma }_{n-1},{\sigma }_n),{\delta }_e({\sigma }_n,{\sigma }_{n+1}),\frac{{\delta }_e({\sigma }_{n-1},{\sigma }_n)+{\delta }_e({\sigma }_n,{\sigma }_{n+1})}{2}\right\}.\hfill \end{array}$$

(14)

Using (14) in (8) and noting that $\vartheta$ is nondecreasing, we obtain

$$\begin{array}{c}\hfill {\delta }_e({\sigma }_n,{\sigma }_{n+1})\le \vartheta \left[min\left\{{\delta }_e({\sigma }_{n-1},{\sigma }_n),{\delta }_e({\sigma }_n,{\sigma }_{n+1}),\frac{{\delta }_e({\sigma }_{n-1},{\sigma }_n)+{\delta }_e({\sigma }_n,{\sigma }_{n+1})}{2}\right\}\right].\end{array}$$

(15)

We will take into consideration the following scenarios to clarify the inequality above:

(i)

If $min\left\{{\delta }_e({\sigma }_{n-1},{\sigma }_n),{\delta }_e({\sigma }_n,{\sigma }_{n+1}),\frac{{\delta }_e({\sigma }_{n-1},{\sigma }_n)+{\delta }_e({\sigma }_n,{\sigma }_{n+1})}{2}\right\}={\delta }_e({\sigma }_n,{\sigma }_{n+1})$, then from (15),

$$\begin{array}{c}\hfill {\delta }_e({\sigma }_n,{\sigma }_{n+1})\le \vartheta \left({\delta }_e({\sigma }_n,{\sigma }_{n+1})\right)<{\delta }_e({\sigma }_n,{\sigma }_{n+1}),\end{array}$$

a contradiction.

(ii)

If $min\left\{{\delta }_e({\sigma }_{n-1},{\sigma }_n),{\delta }_e({\sigma }_n,{\sigma }_{n+1}),\frac{{\delta }_e({\sigma }_{n-1},{\sigma }_n)+{\delta }_e({\sigma }_n,{\sigma }_{n+1})}{2}\right\}=\frac{{\delta }_e({\sigma }_{n-1},{\sigma }_n)+{\delta }_e({\sigma }_n,{\sigma }_{n+1})}{2}$. Then, (15) implies,

$$\begin{array}{c}\hfill min\{{\delta }_e({\sigma }_{n-1},{\sigma }_n),{\delta }_e({\sigma }_n,{\sigma }_{n+1})\}\ge \frac{{\delta }_e({\sigma }_{n-1},{\sigma }_n)+{\delta }_e({\sigma }_n,{\sigma }_{n+1})}{2}.\end{array}$$

(16)

Two subcases arise:

(a)

Assume that $min\{{\delta }_e({\sigma }_{n-1},{\sigma }_n),{\delta }_e({\sigma }_n,{\sigma }_{n+1})\}={\delta }_e({\sigma }_{n-1},{\sigma }_n)$, and then

$$\begin{array}{c}\hfill {\delta }_e({\sigma }_{n-1},{\sigma }_n)<{\delta }_e({\sigma }_n,{\sigma }_{n+1}).\end{array}$$

(17)

On the other hand, from (16), we have

$$\begin{array}{ccc}\hfill {\delta }_e({\sigma }_{n-1},{\sigma }_n)& \ge & \frac{{\delta }_e({\sigma }_{n-1},{\sigma }_n)+{\delta }_e({\sigma }_n,{\sigma }_{n+1})}{2}.\hfill \end{array}$$

From the inequality mentioned above, we can easily calculate that

$$\begin{array}{ccc}\hfill {\delta }_e({\sigma }_{n-1},{\sigma }_n)& \ge & {\delta }_e({\sigma }_n,{\sigma }_{n+1}),\hfill \end{array}$$

which deviates from the assumption (17).

(b)

Suppose that $min\{{\delta }_e({\sigma }_{n-1},{\sigma }_n),{\delta }_e({\sigma }_n,{\sigma }_{n+1})\}={\delta }_e({\sigma }_n,{\sigma }_{n+1})$, then

$$\begin{array}{c}\hfill {\delta }_e({\sigma }_n,{\sigma }_{n+1})<{\delta }_e({\sigma }_{n-1},{\sigma }_n).\end{array}$$

(18)

Additionally, we see from (16) that

$$\begin{array}{ccc}\hfill {\delta }_e({\sigma }_n,{\sigma }_{n+1})& \ge & \frac{{\delta }_e({\sigma }_{n-1},{\sigma }_n)+{\delta }_e({\sigma }_n,{\sigma }_{n+1})}{2}.\hfill \end{array}$$

The above inequality leads to the simple evaluation that

$$\begin{array}{c}\hfill {\delta }_e({\sigma }_n,{\sigma }_{n+1})\ge {\delta }_e({\sigma }_{n-1},{\sigma }_n),\end{array}$$

which contradicts the assumption (18).

(iii)

If $min\left\{{\delta }_e({\sigma }_{n-1},{\sigma }_n),{\delta }_e({\sigma }_n,{\sigma }_{n+1}),\frac{{\delta }_e({\sigma }_{n-1},{\sigma }_n)+{\delta }_e({\sigma }_n,{\sigma }_{n+1})}{2}\right\}={\delta }_e({\sigma }_{n-1},{\sigma }_n)$, then (15) gives

$$\begin{array}{c}\hfill {\delta }_e({\sigma }_n,{\sigma }_{n+1})\le \vartheta \left({\delta }_e({\sigma }_{n-1},{\sigma }_n)\right).\end{array}$$

Therefore, (15) becomes

$$\begin{array}{ccc}\hfill {\delta }_e({\sigma }_n,{\sigma }_{n+1})& \le & \vartheta \left({\delta }_e({\sigma }_{n-1},{\sigma }_n)\right)\hfill \\ & \le & {\vartheta }^2\left({\delta }_e({\sigma }_{n-2},{\sigma }_{n-1})\right)\hfill \\ & ⋮& \hfill \\ & \le & {\vartheta }^n\left({\delta }_e({\sigma }_0,{\sigma }_1)\right).\hfill \end{array}$$

(19)

Repeating the process similar to Case $r>0$, it can be deduced from (19) that ${\left\{{\sigma }_n\right\}}_{n\ge 1}$ is a Cauchy sequence in $\mathrm{\Xi }$. As $\mathrm{\Xi }$ is complete, there exists an element $u\in \mathrm{\Xi }$ such that

$$\begin{array}{c}\hfill \underset{n⟶\infty }{lim}{\delta }_e({\sigma }_n,u)=0.\end{array}$$

Next, we demonstrate that $u\in {\left[Tu\right]}_{{\alpha }_{\pounds }}$.

$$\begin{array}{ccc}\hfill {\delta }_e(u,{\left[Tu\right]}_{{\alpha }_{\pounds }})& \le & e(u,{\left[Tu\right]}_{{\alpha }_{\pounds }})\{{\delta }_e(u,{\sigma }_n)+{\delta }_e({\sigma }_n,{\left[Tu\right]}_{{\alpha }_{\pounds }})\}\hfill \\ & \le & e(u,{\left[Tu\right]}_{{\alpha }_{\pounds }})\{{\delta }_e(u,{\sigma }_n)+H({\left[T{\sigma }_{n-1}\right]}_{{\alpha }_{\pounds }},{\left[Tu\right]}_{{\alpha }_{\pounds }})\}.\hfill \end{array}$$

Applying ${lim}_{n⟶\infty }$ in the above inequality and using the H-continuity of T, one can easily see that ${\delta }_e(u,{\left[Tu\right]}_{{\alpha }_{\pounds }})=0$, which implies $u\in {\left[Tu\right]}_{{\alpha }_{\pounds }}$. □

The following result is established from Case 1 in the proof of Theorem 2.

Theorem 3.

Let $(\mathrm{\Xi },{\delta }_e)$ be a complete extended ♭-MS and $T:\mathrm{\Xi }⟶F_{{\pounds }_S}\left(\mathrm{\Xi }\right)$ be a £-FS-valued map satisfying the following:

(i) 

T is β-admissible;

(ii) 

There exists ${\sigma }_0\in \mathrm{\Xi }$ and ${\sigma }_1\in {\left[T{\sigma }_0\right]}_{{\alpha }_{\pounds }}$ such that $\beta ({\sigma }_0,{\sigma }_1)\ge 1$, where ${\alpha }_{\pounds }\in \pounds \setminus \left\{0_{\pounds }\right\};$

(iii) 

T is H-continuous;

(iv) 

${\left[T\sigma \right]}_{{\alpha }_{\pounds }}$ is a prox set for every $\sigma \in \mathrm{\Xi }$.

Furthermore, suppose that there exists $\rho \in \mathfrak{Z}$, $\vartheta \in {\mathsf{\Omega }}_{e♭}$ and $\beta :\mathrm{\Xi }\times \mathrm{\Xi }⟶{\mathbb{R}}_{+}$ such that for each $\sigma ,\nu \in \mathrm{\Xi }$,

$$\begin{array}{c}\hfill \rho \left(\beta (\sigma ,\nu )H({\left[T\sigma \right]}_{{\alpha }_{\pounds }},{\left[T\nu \right]}_{{\alpha }_{\pounds }}),\vartheta ({\left[\mathrm{\Gamma }(\sigma ,\nu )\right]}^{\frac{1}{r}})\right)\ge 0.\end{array}$$

(20)

where $\mathrm{\Gamma }(\sigma ,\nu )$ is defined earlier. Then, T has at least one £-FFP in Ξ.

Example 9.

Let $\mathrm{\Xi }=[0,\infty )$. Define ${\delta }_e:\mathrm{\Xi }\times \mathrm{\Xi }⟶{\mathbb{R}}_{+}$ and $e:\mathrm{\Xi }\times \mathrm{\Xi }⟶[1,\infty )$ as ${\delta }_e(\sigma ,\nu )={(\sigma -\nu )}^2$ and $e(\sigma ,\nu )=\sigma +\nu +2$, for each $\sigma ,\nu \in \mathrm{\Xi }$. Then, $(\mathrm{\Xi },{\delta }_e)$ is a complete extended ♭-MS, which is not an MS, as by taking $\sigma =3,\nu =6$, and $\omega =5$, we have

$$\begin{array}{c}\hfill {\delta }_e(3,6)=9\nleqq 5={\delta }_e(3,5)+{\delta }_e(5,6).\end{array}$$

Furthermore, it is worth noting that $(\mathrm{\Xi },{\delta }_e)$ is not a b-MS due to the fact that $e(\sigma ,\nu )$ is not equal to any constant term as it depends on σ and ν. Moreover, let $\pounds =\{\xi ,\varpi ,\pi ,\gamma \}$ with $\xi {⪯}_{\pounds }\varpi {⪯}_{\pounds }\gamma$ and $\xi {⪯}_{\pounds }\pi {⪯}_{\pounds }\gamma$, where $\varpi ,\pi$ are non-comparable. Then, $(\pounds ,{⪯}_{\pounds })$ is a CDL. For each $\sigma \in \mathrm{\Xi }$, consider a £-FS $T\sigma :\mathrm{\Xi }⟶\pounds$, which we define as:

If $\sigma =1$

$$\begin{array}{c}\hfill \left(T\sigma \right)\left(a\right)=\left\{\begin{array}{cc}\gamma ,\hfill & \mathit{if}a=1;\hfill \\ \varpi ,\hfill & \mathit{if}a\ne 1.\hfill \end{array}\right.\end{array}$$

If $\sigma \ne 1$

$$\begin{array}{c}\hfill \left(T\sigma \right)\left(a\right)=\left\{\begin{array}{cc}\gamma ,\hfill & \mathit{if}0\le a\le {\sigma }^2;\hfill \\ \xi ,\hfill & \mathit{if}{\sigma }^2<a\le {\sigma }^2+2;\hfill \\ \varpi ,\hfill & \mathit{if}{\sigma }^2+2<a\le 4{\sigma }^2+9;\hfill \\ \pi ,\hfill & \mathit{if}4{\sigma }^2+9<a<\infty .\hfill \end{array}\right.\end{array}$$

Let ${\alpha }_{\pounds }=\gamma$, and then

$$\begin{array}{c}\hfill {\left[T\sigma \right]}_{{\alpha }_{\pounds }}=\left\{\begin{array}{cc}\left\{1\right\},& if\sigma =1;\\ \left[0,{\sigma }^2\right],& if\sigma \ne 1.\end{array}\right.\end{array}$$

(21)

Clearly, $T\sigma \in F_{{\pounds }_S}\left(\mathrm{\Xi }\right)$ for each $\sigma \in \mathrm{\Xi }$. Define the functions $\beta :\mathrm{\Xi }\times \mathrm{\Xi }⟶{\mathbb{R}}_{+}$ and $\vartheta :{\mathbb{R}}_{+}⟶{\mathbb{R}}_{+}$ by

$$\begin{array}{c}\hfill \beta (\sigma ,\nu )=\left\{\begin{array}{cc}3,\hfill & \mathit{if}\sigma =\nu =1;\hfill \\ \frac{1}{290},\hfill & \mathit{if}\sigma ,\nu \in \{2,3\}\mathit{and}\sigma \ne \nu ;\hfill \\ 0,\hfill & \mathit{elsewhere}.\hfill \end{array}\right.\end{array}$$

and $\vartheta \left(t\right)=\frac{t}{4}$, for every $t>0$. Let $\rho (\tau ,\kappa )=\frac{2}{5}\kappa -\tau$ for every $\tau ,\kappa \in {\mathbb{R}}_{+}$. Obviously, $\rho \in \mathfrak{Z}$ and $\vartheta \in {\mathsf{\Omega }}_{e♭}$. Next, we proceed to verify (20) in the subsequent cases:

Case 1: If $\sigma =\nu =1$, then ${\left[T\sigma \right]}_{{\alpha }_{\pounds }}={\left[T\nu \right]}_{{\alpha }_{\pounds }}=\left\{1\right\}$, and so, $H({\left[T\sigma \right]}_{{\alpha }_{\pounds }},{\left[T\nu \right]}_{{\alpha }_{\pounds }})=0$ for all $\sigma ,\nu \in \mathrm{\Xi }$. Therefore,

$$\begin{array}{ccc}\hfill \rho \left(\beta (\sigma ,\nu )H({\left[T\sigma \right]}_{{\alpha }_{\pounds }},{\left[T\nu \right]}_{{\alpha }_{\pounds }}),\vartheta ({\left[\mathrm{\Gamma }(\sigma ,\nu )\right]}^{\frac{1}{r}})\right)& =& \rho \left(0,\vartheta ({\left[\mathrm{\Gamma }(\sigma ,\nu )\right]}^{\frac{1}{r}})\right)\hfill \\ & =& \frac{2}{5}\vartheta ({\left[\mathrm{\Gamma }(\sigma ,\nu )\right]}^{\frac{1}{r}})\ge 0\hfill \end{array}$$

Case 2: If $\sigma ,\nu \in \{2,3\}$ with $\sigma \ne \nu$, then let $\sigma =2$ and $\nu =3$ so ${\left[T\sigma \right]}_{{\alpha }_{\pounds }}=[0,4]$, ${\left[T\nu \right]}_{{\alpha }_{\pounds }}=[0,9]$, $\beta (\sigma ,\nu )=\frac{1}{290}$, and $H\left({\left[T\sigma \right]}_{{\alpha }_{\pounds }},{\left[T\nu \right]}_{{\alpha }_{\pounds }}\right)=H\left([0,4],[0,9]\right)=25$.

$$\begin{array}{ccc}\hfill {\left[\mathrm{\Gamma }(2,3)\right]}^{\frac{1}{r}}& =& {\left[max\left\{\begin{array}{c}{\left({\delta }_e(2,3)\right)}^r,{({\delta }_e(2,{\left[T2\right]}_{{\alpha }_{\pounds }}))}^r,{({\delta }_e(3,{\left[T3\right]}_{{\alpha }_{\pounds }}))}^r,\\ {\left(\frac{{\delta }_e(3,{\left[T3\right]}_{{\alpha }_{\pounds }})(1+{\delta }_e(2,{\left[T2\right]}_{{\alpha }_{\pounds }}))}{1+{\delta }_e(2,3)}\right)}^r,\\ {\left(\frac{{\delta }_e(3,{\left[T2\right]}_{{\alpha }_{\pounds }})(1+{\delta }_e(2,{\left[T3\right]}_{{\alpha }_{\pounds }}))}{1+{\delta }_e(2,3)}\right)}^r,\\ {\left(\frac{{\delta }_e(3,{\left[T2\right]}_{{\alpha }_{\pounds }}).{\delta }_e(2,{\left[T3\right]}_{{\alpha }_{\pounds }})}{1+{\delta }_e(2,3)}\right)}^r\end{array}\right\}\right]}^{\frac{1}{r}}\hfill \\ & =& 1.\hfill \end{array}$$

Thus, (20) becomes

$$\begin{array}{ccc}\hfill \rho \left(\beta (2,3)H({\left[T2\right]}_{{\alpha }_{\pounds }},{\left[T3\right]}_{{\alpha }_{\pounds }}),\vartheta ({\left[\mathrm{\Gamma }(2,3)\right]}^{\frac{1}{r}})\right)& =& \rho \left(\frac{1}{290}\left(25\right),\vartheta \left(1\right)\right)\hfill \\ & =& \frac{2}{5}\vartheta \left(1\right)-\frac{25}{290}\hfill \\ & =& \frac{2}{5}\left(\frac{1}{4}\right)-\frac{5}{58}\ge 0.\hfill \end{array}$$

Case 3: If $\sigma ,\nu \in \mathrm{\Xi }\setminus \{1,2,3\}$, then $\beta (\sigma ,\nu )=0$, and therefore

$$\begin{array}{c}\hfill \rho \left(0,\vartheta ({\left[\mathrm{\Gamma }(\sigma ,\nu )\right]}^{\frac{1}{r}})\right)=\frac{2}{5}\vartheta ({\left[\mathrm{\Gamma }(\sigma ,\nu )\right]}^{\frac{1}{r}})\ge 0.\end{array}$$

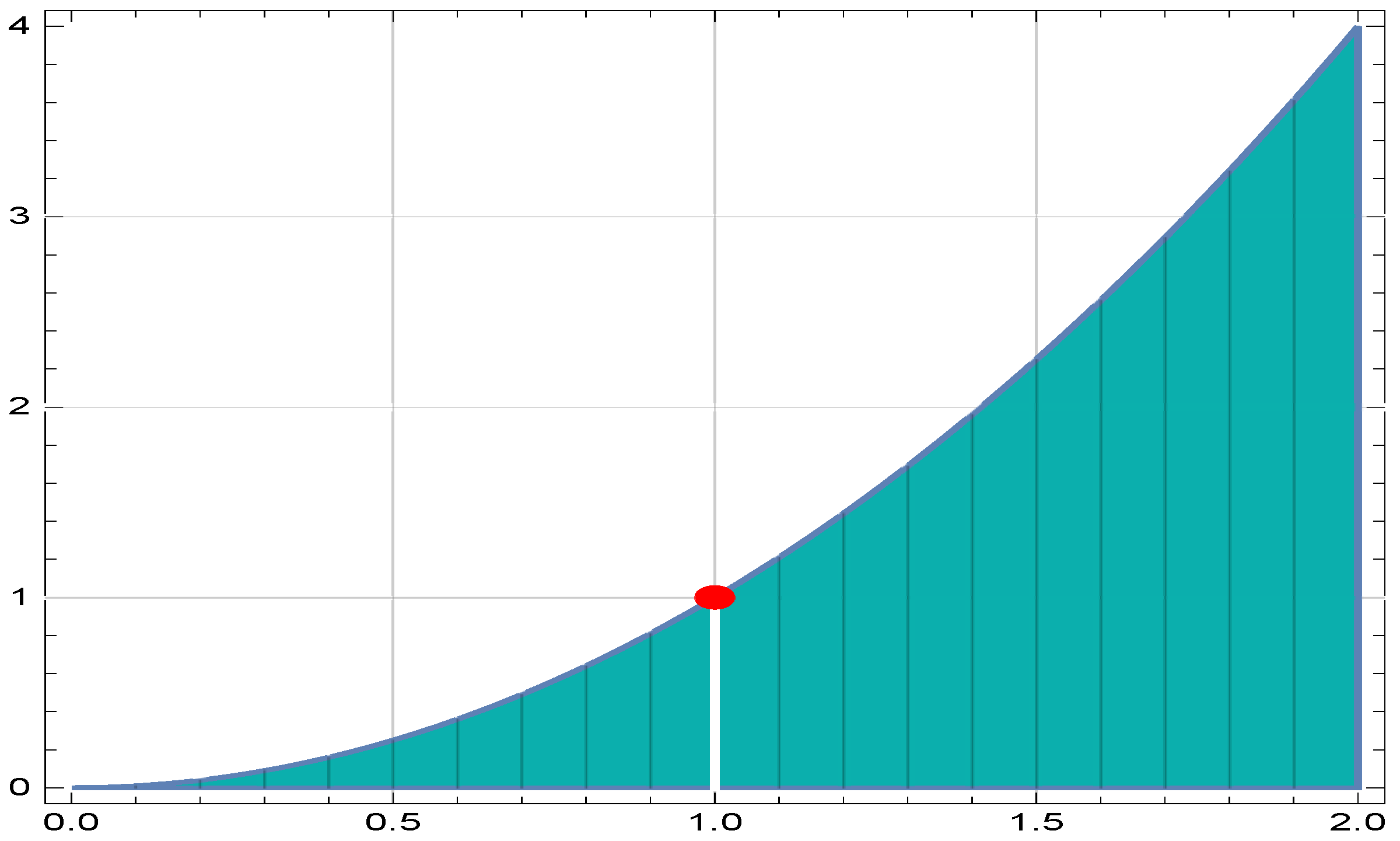
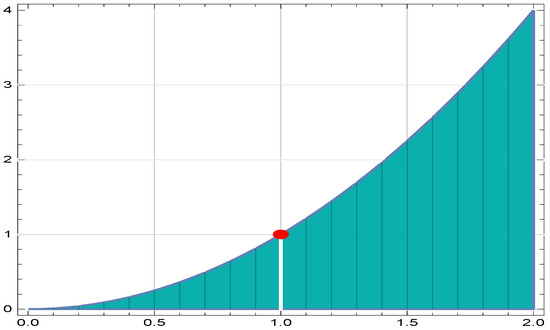
Additionally, it is clear that the £-FS-valued map T is β-admissible and H-continuous. It can also be shown that ${\left[T\sigma \right]}_{{\alpha }_{\pounds }}$ is prox for each $\sigma \in \mathrm{\Xi }$. Because Theorem 3 meets all its assumptions, T possesses numerous £-FFPs within Ξ. It can also be observed by the Figure 3, where the red dot represents the point ${\left[T\sigma \right]}_{{\alpha }_{\pounds }}=\left\{1\right\}$ and the teal-colored region corresponds to ${\left[T\sigma \right]}_{{\alpha }_{\pounds }}=[0,{\sigma }^2]$.

Figure 3. Graphical illustration of (21) representing infinitely many fixed points.

Now, we provide another example supporting our results.

Example 10.

Let $\mathrm{\Xi }=\{1,2,3,\dots \}$. Define $e:\mathrm{\Xi }\times \mathrm{\Xi }⟶[1,\infty )$ and ${\delta }_e:\mathrm{\Xi }\times \mathrm{\Xi }⟶{\mathbb{R}}_{+}$ by

$$e(\sigma ,\nu )=\left\{\begin{array}{cc}{|\sigma -\nu |}^3,\hfill & \mathit{if}\sigma \ne \nu ;\hfill \\ 1,\hfill & \mathit{if}\sigma =\nu .\hfill \end{array}\right.$$

and ${\delta }_e(\sigma ,\nu )={(\sigma -\nu )}^4$, respectively, for each $\sigma ,\nu \in \mathrm{\Xi }$. Then, $(\mathrm{\Xi },{\delta }_e)$ is a complete extended ♭-MS. Additionally, let $\pounds =\{\xi ,\varpi ,\pi ,\gamma \}$ with $\xi {⪯}_{\pounds }\varpi {⪯}_{\pounds }\gamma$ and $\xi {⪯}_{\pounds }\pi {⪯}_{\pounds }\gamma$, where $\varpi ,\pi$ are non-comparable. Then, $(\pounds ,{⪯}_{\pounds })$ is a CDL. For each $\sigma \in \mathrm{\Xi }$, consider a £-FS $T\sigma :\mathrm{\Xi }⟶\pounds$, which is defined as:

$$\begin{array}{c}\hfill \left(T\sigma \right)\left(a\right)=\left\{\begin{array}{cc}\pi ,\hfill & \mathit{if}a=\sigma ;\hfill \\ \gamma ,\hfill & \mathit{if}4\sigma -3;\hfill \\ \varpi ,\hfill & \mathit{if}a={\sigma }^2;\hfill \\ \xi ,\hfill & \mathit{otherwise}.\hfill \end{array}\right.\end{array}$$

Then, for ${\alpha }_{\pounds }=\pi$, we obtain

$$\begin{array}{c}\hfill {\left[T\sigma \right]}_{{\alpha }_{\pounds }}=\{\sigma ,4\sigma -3\}.\end{array}$$

Clearly, $T\sigma \in F_{{\pounds }_S}\left(\mathrm{\Xi }\right)$ for each $\sigma \in \mathrm{\Xi }$. Define the functions $\beta :\mathrm{\Xi }\times \mathrm{\Xi }⟶{\mathbb{R}}_{+}$ and $\vartheta :{\mathbb{R}}_{+}⟶{\mathbb{R}}_{+}$ by

$$\begin{array}{c}\hfill \beta (\sigma ,\nu )=\left\{\begin{array}{cc}1,\hfill & \mathit{if}\sigma =\nu =1;\hfill \\ \frac{1}{1650},\hfill & \mathit{if}\sigma ,\nu \in \{3,4\}\mathit{and}\sigma \ne \nu ;\hfill \\ 0,\hfill & \mathit{elsewhere}.\hfill \end{array}\right.\end{array}$$

and $\vartheta \left(t\right)=\frac{9t}{10}$, for every $t>0$. Let $\rho (\tau ,\kappa )=\frac{9}{10}\kappa -\tau$ for every $\tau ,\kappa \in {\mathbb{R}}_{+}$. Then, $\rho \in \mathfrak{Z}$ and $\vartheta \in {\mathsf{\Omega }}_{e♭}$. By following the pattern described in the example above, it becomes evident that T possesses £-FFPs within Ξ.

4. Consequences

In this section, we demonstrate how our main Theorem can be used to derive a number of intriguing FP results existing in the literature, especially when using different forms of SFs. That is, SFs are very beneficial to express different kinds of contractivity conditions.

Corollary 1.

Let $(\mathrm{\Xi },{\delta }_e)$ be a complete extended ♭-MS and $T:\mathrm{\Xi }⟶F_{{\pounds }_S}\left(\mathrm{\Xi }\right)$ be a £-FS-valued map satisfying the condition:

$$\begin{array}{c}\hfill \beta (\sigma ,\nu )H({\left[T\sigma \right]}_{{\alpha }_{\pounds }},{\left[T\nu \right]}_{{\alpha }_{\pounds }})\le \vartheta (M_T^r(\sigma ,\nu )),\end{array}$$

(22)

for all $\sigma ,\nu \in \mathrm{\Xi }$, where $\vartheta \in {\mathsf{\Omega }}_{e♭}$ and $\beta :\mathrm{\Xi }\times \mathrm{\Xi }⟶{\mathbb{R}}_{+}$ is a function. Also, assume the following:

(i) 

T is a β-admissible £-FS-valued map;

(ii) 

There exists ${\sigma }_0\in \mathrm{\Xi }$ and ${\sigma }_1\in {\left[T{\sigma }_0\right]}_{{\alpha }_{\pounds }}$ such that $\beta ({\sigma }_0,{\sigma }_1)\ge 1$, where ${\alpha }_{\pounds }\in \pounds \setminus \left\{0_{\pounds }\right\}$;

(iii) 

T is H-continuous;

(iv) 

${\left[T\sigma \right]}_{{\alpha }_{\pounds }}$ is prox for each $\sigma \in \mathrm{\Xi }$.

Then, T has at least one £-FFP in Ξ.

Proof. 

Set $\rho (\tau ,\kappa )=\vartheta \left(\kappa \right)-\tau$ for all $\tau ,\kappa \in {\mathbb{R}}_{+}$ in Theorem 2. Then, (22) follows easily. Note that $\vartheta \left(\kappa \right)-\tau \in \mathfrak{Z}$. Consequently, Theorem 2 can be applied to find $u\in \mathrm{\Xi }$ such that $u\in {\left[Tu\right]}_{{\alpha }_{\pounds }}$. □

The below-mentioned corollary is the proper extension and fuzzification of the result of Rhoades [38].

Corollary 2.

Consider a complete extended ♭-MS $(\mathrm{\Xi },{\delta }_e)$ and let $T:\mathrm{\Xi }⟶F_{{\pounds }_S}\left(\mathrm{\Xi }\right)$ be a £-FS-valued map such that there exists a lower semicontinuous function $\vartheta :{\mathbb{R}}_{+}⟶{\mathbb{R}}_{+}$ verifying ${\vartheta }^{-1}\left(0\right)=\left\{0\right\}$ and satisfying the following condition:

$$\begin{array}{c}\hfill H({\left[T\sigma \right]}_{{\alpha }_{\pounds }},{\left[T\nu \right]}_{{\alpha }_{\pounds }})\le \vartheta (M_T^r(\sigma ,\nu ))-{\vartheta }^2(M_T^r(\sigma ,\nu )),\end{array}$$

for all $\sigma ,\nu \in \mathrm{\Xi }$. Further, assume the following:

(i) 

T is H-continuous;

(ii) 

${\left[T\sigma \right]}_{{\alpha }_{\pounds }}$ is prox for each $\sigma \in \mathrm{\Xi }$.

Then, there exists $u\in \mathrm{\Xi }$ such that $u\in {\left[Tu\right]}_{{\alpha }_{\pounds }}$.

Proof. 

This result follows by taking $\rho ={\rho }_{\mathrm{\Gamma }}$ in Theorem 2 where the function ${\rho }_{\mathrm{\Gamma }}:{\mathbb{R}}_{+}\times {\mathbb{R}}_{+}⟶\mathbb{R}$ is defined by ${\rho }_{\mathrm{\Gamma }}(\tau ,\kappa )=\kappa -\vartheta \left(\kappa \right)-\tau$ for all $\tau ,\kappa \in {\mathbb{R}}_{+}$. Clearly, ${\rho }_{\mathrm{\Gamma }}\in \mathfrak{Z}$. □

The following corollary is the improvement in the first metric FP Theorem under multi-valued contractions due to Nadler [16] by considering ${\alpha }_{\pounds }=1_{\pounds }$ and defining a crisp set-valued map $H:\mathrm{\Xi }⟶\mathbb{k}\left(\mathrm{\Xi }\right)$ as $H\sigma ={\left[T\sigma \right]}_{1_{\pounds }}$ for all $\sigma \in \mathrm{\Xi }$.

Corollary 3.

Consider a complete extended ♭-MS $(\mathrm{\Xi },{\delta }_e)$ and suppose $T:\mathrm{\Xi }⟶F_{{\pounds }_S}\left(\mathrm{\Xi }\right)$ is a £-FS-valued map that satisfies:

$$\begin{array}{c}\hfill H({\left[T\sigma \right]}_{{\alpha }_{\pounds }},{\left[T\nu \right]}_{{\alpha }_{\pounds }})\le ⋌{\delta }_e(\sigma ,\nu ),\end{array}$$

for all $\sigma ,\nu \in \mathrm{\Xi }$, where $⋌\in (0,1)$. Moreover, assume the following:

(i) 

T is H-continuous;

(ii) 

${\left[T\sigma \right]}_{{\alpha }_{\pounds }}$ is prox for each $\sigma \in \mathrm{\Xi }$.

Then, T has a £-FFP in Ξ.

Proof. 

It is the special case of Theorem 2 that is derived by using the SF $\rho (\tau ,\kappa )=⋌\kappa -\tau$ for all $\tau ,\kappa \in {\mathbb{R}}_{+}$, $\beta (\sigma ,\nu )=1$, $\vartheta \left(t\right)=⋌t$ for all $t\ge 0$ with $⋌\in (0,1)$ along with $M_T^r(\sigma ,\nu )={\delta }_e(\sigma ,\nu )$ (taking $r=1$). □

Given below is the definition of a single-valued $\beta$-admissible map raised by Samet in [21].

Definition 24

([21]). Let $\mathsf{ϝ}:\mathrm{\Xi }⟶\mathrm{\Xi }$ and $\beta :\mathrm{\Xi }\times \mathrm{\Xi }⟶{\mathbb{R}}_{+}$ be mappings. Then, ϝ is known as β-admissible if for all $\sigma ,\nu \in \mathrm{\Xi }$,

$$\begin{array}{c}\hfill \beta (\sigma ,\nu )\ge 1\mathit{implies}\beta (\mathsf{ϝ}\sigma ,\mathsf{ϝ}\nu )\ge 1.\end{array}$$

The main finding of Chifu and Karapinar [33] (Theorem 2) without involving the triangular $\beta$-admissibility of $\mathsf{ϝ}$ is stated as follows:

Corollary 4.

Consider a complete extended ♭-MS $(\mathrm{\Xi },{\delta }_e)$ and let $\mathsf{ϝ}:\mathrm{\Xi }⟶\mathrm{\Xi }$ be a β-admissible single-valued map satisfying:

$$\begin{array}{c}\hfill \rho (\beta (\sigma ,\nu )H(\mathsf{ϝ}\sigma ,\mathsf{ϝ}\nu ),\vartheta (M_{\mathsf{ϝ}}^r(\sigma ,\nu )))\ge 0,\end{array}$$

for all $\sigma ,\nu \in \mathrm{\Xi }$, where $\vartheta \in {\mathsf{\Omega }}_{e♭}$,

$$\begin{array}{c}\hfill M_{\mathsf{ϝ}}^r(\sigma ,\nu )=\left\{\begin{array}{cc}{\left[\mathrm{\Sigma }(\sigma ,\nu )\right]}^{\frac{1}{r}},\hfill & \mathit{for}r>0,\sigma ,\nu \in \mathrm{\Xi }\hfill \\ \mathsf{\Omega }(\sigma ,\nu ),\hfill & \mathit{for}r=0,\sigma ,\nu \in \mathrm{\Xi },\hfill \end{array}\right.\end{array}$$

$$\begin{array}{ccc}\hfill \mathrm{\Sigma }(\sigma ,\nu )& =& max\left\{\begin{array}{c}{\left({\delta }_e(\sigma ,\nu )\right)}^r,{\left({\delta }_e(\sigma ,\mathsf{ϝ}\sigma )\right)}^r,{\left({\delta }_e(\nu ,\mathsf{ϝ}\nu )\right)}^r,\\ {\left(\frac{{\delta }_e(\nu ,\mathsf{ϝ}\nu )(1+{\delta }_e(\sigma ,\mathsf{ϝ}\sigma ))}{1+{\delta }_e(\sigma ,\nu )}\right)}^r,\\ {\left(\frac{{\delta }_e(\nu ,\mathsf{ϝ}\sigma )(1+{\delta }_e(\sigma ,\mathsf{ϝ}\nu ))}{1+{\delta }_e(\sigma ,\nu )}\right)}^r,\\ {\left(\frac{{\delta }_e(\nu ,\mathsf{ϝ}\sigma ).{\delta }_e(\sigma ,\mathsf{ϝ}\nu )}{1+{\delta }_e(\sigma ,\nu )}\right)}^r,\end{array}\right\},\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill \mathsf{\Omega }(\sigma ,\nu )& =& min\left\{\begin{array}{c}{\delta }_e(\sigma ,\nu ),{\delta }_e(\sigma ,\mathsf{ϝ}\sigma ),{\delta }_e(\nu ,\mathsf{ϝ}\nu ),\\ \frac{{\delta }_e(\nu ,\mathsf{ϝ}\nu )(1+{\delta }_e(\sigma ,\mathsf{ϝ}\sigma ))}{1+{\delta }_e(\sigma ,\nu )},\\ \frac{{\delta }_e(\nu ,\mathsf{ϝ}\sigma )(1+{\delta }_e(\sigma ,\mathsf{ϝ}\nu ))}{1+{\delta }_e(\sigma ,\nu )},\\ \frac{{\delta }_e(\sigma ,\mathsf{ϝ}\nu )+{\delta }_e(\nu ,\mathsf{ϝ}\sigma )}{2e(\sigma ,\mathsf{ϝ}\nu )}\end{array}\right\},\hfill \end{array}$$

with $r\ge 0$. Then, there exists $u\in \mathrm{\Xi }$ such that $\mathsf{ϝ}u=u$.

Proof. 

Let ${\alpha }_{\pounds }\in \pounds \setminus \left\{0_{\pounds }\right\}$ and consider a £-FS-valued map $T\sigma :\mathrm{\Xi }⟶\pounds$ for each $\sigma \in \mathrm{\Xi }$, defined by

$$\begin{array}{c}\hfill T\left(\sigma \right)\left(t\right)=\left\{\begin{array}{cc}{\alpha }_{\pounds },\hfill & \mathrm{if}t=\mathsf{ϝ}\sigma \hfill \\ 0_{\pounds },\hfill & \mathrm{if}t\ne \mathsf{ϝ}\sigma .\hfill \end{array}\right.\end{array}$$

Then,

$$\begin{array}{c}\hfill {\left[T\sigma \right]}_{{\alpha }_{\pounds }}=\left\{\mathsf{ϝ}\sigma \right\}.\end{array}$$

Clearly, $\left\{\mathsf{ϝ}\sigma \right\}\in \mathbb{k}\left(\mathrm{\Xi }\right)$. In the present case, $H({\left[T\sigma \right]}_{{\alpha }_{\pounds }},{\left[T\nu \right]}_{{\alpha }_{\pounds }})={\delta }_e(\mathsf{ϝ}\sigma ,\mathsf{ϝ}\nu )$. Hence, Theorem 2 can be used to obtain $u\in \mathrm{\Xi }$ such that $u\in {\left[Tu\right]}_{{\alpha }_{\pounds }}=\left\{\mathsf{ϝ}u\right\}$, which implies that $u=\mathsf{ϝ}u$. □

Corollary 5.

The main result of Shagari in [37] can be expressed as a consequence of our main result by taking $\pounds =[0,1]$ in Theorem 2.

5. Application in Graphic Contraction

In this section, the main focus centers on the application of the £-FFP result in a graphic contraction. The exploration is supplemented with examples that feature intriguing 2D and 3D graphs and captivating computer simulations. We begin by recalling some definitions from graph theory.

5.1. Exploring the Basics from Graph Theory

Jachymski, in [34], generalizes the BCP by proposing the conception of contraction mapping and FPs for an MS equipped with a directed graph. In this subsection, we consider an extended ♭-MS which is equipped with a graph and derive an FP result. In the light of [34], let $(\mathrm{\Xi },{\delta }_e)$ be an extended ♭-MS and the diagonal of the Cartesian product $\mathrm{\Xi }\times \mathrm{\Xi }$ is represented by $\mathbb{D}$. Let $\mathbb{G}=\left(\mathbb{V}\right(\mathbb{G}),\mathbb{E}(\mathbb{G}\left)\right)$ be a directed graph with no parallel edges, where $\mathbb{V}\left(\mathbb{G}\right)$ represents the set of vertices, while $\mathbb{E}\left(\mathbb{G}\right)$ manifests the set of edges in $\mathbb{G}$. Then, $\mathrm{\Xi }$ is said to be equipped with $\mathbb{G}$ if $\mathbb{V}\left(\mathbb{G}\right)=\mathrm{\Xi }$ and $\mathbb{E}\left(\mathbb{G}\right)$ involves all loops $\left\{\right(u,u):u\in \mathrm{\Xi }\}$, that is, $\mathbb{D}\subseteq \mathbb{E}\left(\mathbb{G}\right)$. Additionally, the graph $\mathbb{G}$ is considered to be a weighted graph by allotting to every edge the distance between its vertices. In a graph $\mathbb{G}$, a walk comprises a sequence of edges and is a way of getting from one vertex to another of the form ${\sigma }_0{\sigma }_1,{\sigma }_1{\sigma }_2,\cdots ,{\sigma }_{m-1}{\sigma }_m$, in which any two edges are adjacent. A sequence of vertices ${\sigma }_0,{\sigma }_1,\dots ,{\sigma }_m$ can be determined by this type of walk. A walk in which no vertex appears more than once is called a path. Formally, for $\sigma ,\nu \in \mathbb{V}\left(\mathbb{G}\right)$, a path from $\sigma$ to $\nu$ of length l (the number of edges in a walk is called its length) is a sequence ${\left\{{\sigma }_n\right\}}_{n=0}^l$ of $l+1$ vertices such that ${\sigma }_0=\sigma ,{\sigma }_l=\nu$ and $({\sigma }_{n-1},{\sigma }_n)\in \mathbb{E}\left(\mathbb{G}\right)$ for $n=1,2,\dots ,l$. Furthermore, a graph is defined as connected if, whenever its set of vertices is divided into two non-empty sets $\mathrm{\Xi }$ and ∇, there exists an edge that connects a vertex from $\mathrm{\Xi }$ to a vertex from ∇, that is, for each pair of vertices there always exists a path between them.

Example 11.

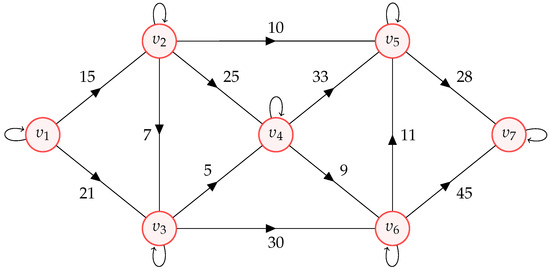
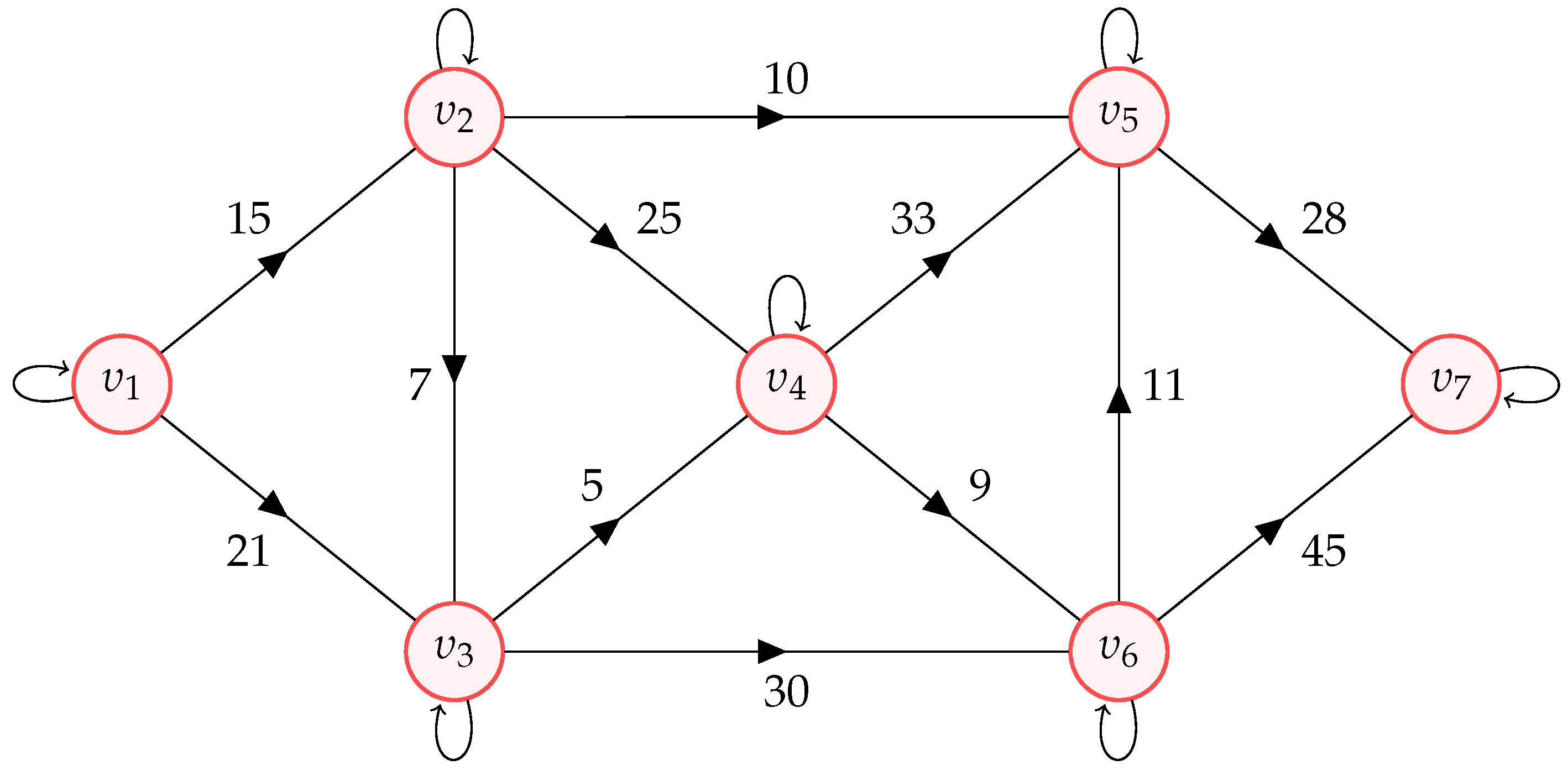
Let $\mathbb{G}=\left(\mathbb{V}\right(\mathbb{G}),\mathbb{E}(\mathbb{G}\left)\right)$ be a directed graph with $\mathbb{V}\left(\mathbb{G}\right)=\{{\upsilon }_1,{\upsilon }_2,{\upsilon }_3,{\upsilon }_4,{\upsilon }_5,{\upsilon }_6,{\upsilon }_7\}$ as a set of vertices and $\mathbb{E}\left(\mathbb{G}\right)=\{{\upsilon }_1{\upsilon }_1,{\upsilon }_1{\upsilon }_2,{\upsilon }_1{\upsilon }_3,{\upsilon }_2{\upsilon }_2,{\upsilon }_2{\upsilon }_3,{\upsilon }_2{\upsilon }_4,{\upsilon }_2{\upsilon }_5,{\upsilon }_3{\upsilon }_3,{\upsilon }_3{\upsilon }_4,{\upsilon }_3{\upsilon }_6,{\upsilon }_4{\upsilon }_4,{\upsilon }_4{\upsilon }_5,{\upsilon }_4{\upsilon }_6,{\upsilon }_5{\upsilon }_5,{\upsilon }_5{\upsilon }_7,{\upsilon }_6{\upsilon }_6,{\upsilon }_6{\upsilon }_5,{\upsilon }_6{\upsilon }_7,{\upsilon }_7{\upsilon }_7\}$ as a set of edges. It can be observed that $\mathbb{D}\subseteq \mathbb{E}\left(\mathbb{G}\right)$, and the graph $\mathbb{G}$ does not have any parallel edge. Additionally, each edge of $\mathbb{G}$ is assigned a numerical value, known as its edge-weight. Hence, $\mathbb{G}$ can be classified as a weighted graph. The visual representation of $\mathbb{G}$ is depicted by Figure 4.

Figure 4. Visual representation of weighted graph $\mathbb{G}$.

5.2. £-Fuzzy Fixed Points in Graphical Extended b-MSs

Keeping in mind Jachymski’s definition of $\mathbb{G}$-continuity for a single-valued map in [34], we define it for a £-FS-valued map.

Definition 25.

Let $(\mathrm{\Xi },{\delta }_e,\mathbb{G})$ be an extended ♭-MS equipped with a graph $\mathbb{G}$. A £-FS-valued map $T:\mathrm{\Xi }⟶F_{\pounds }\left(\mathrm{\Xi }\right)$ is known as $\mathbb{G}$-continuous at a point $u\in \mathrm{\Xi }$, if the following condition holds: for any sequence ${\left\{{\sigma }_n\right\}}_{n\in \mathbb{N}}$ in Ξ with ${\delta }_e({\sigma }_n,u)⟶0$ as $n⟶\infty$ and $({\sigma }_n,{\sigma }_{n+1})\in \mathbb{E}\left(\mathbb{G}\right)$ for all $n\in \mathbb{N}$, we have $H({\left[T{\sigma }_n\right]}_{{\alpha }_{\pounds }},{\left[Tu\right]}_{{\alpha }_{\pounds }})⟶0$ as $n⟶\infty$. To be classified as $\mathbb{G}$-continuous, a function T must show continuity at every point in the set Ξ.

Some other concepts needed for our result are also established.

Definition 26.

Let $(\mathrm{\Xi },\mathbb{G})$ be a non-empty set. A £-FS-valued map $T:\mathrm{\Xi }⟶F_{\pounds }\left(\mathrm{\Xi }\right)$ is edge-preserving if for all $\sigma ,\nu \in \mathrm{\Xi },(\sigma ,\nu )\in \mathbb{E}\left(\mathbb{G}\right)$, there exists an ${\alpha }_{\pounds }\in \pounds \setminus \left\{0_{\pounds }\right\}$ such that $({\left[T\sigma \right]}_{{\alpha }_{\pounds }},{\left[T\nu \right]}_{{\alpha }_{\pounds }})\subseteq \mathbb{E}\left(\mathbb{G}\right)$.

Definition 27.

Let $(\mathrm{\Xi },{\delta }_e,\mathbb{G})$ be an extended ♭-MS equipped with a graph $\mathbb{G}$. A subset Γ of Ξ is termed as prox if for every point $\sigma \in \mathrm{\Xi }$, there exists an element $k\in \mathrm{\Gamma }$ with an edge $(\sigma ,k)\in \mathbb{E}\left(\mathbb{G}\right)$ such that ${\delta }_e(\sigma ,\mathrm{\Gamma })={\delta }_e(\sigma ,k)$.

Theorem 4.

Let $(\mathrm{\Xi },{\delta }_e,\mathbb{G})$ be a complete extended ♭-MS with a graph $\mathbb{G}$ and $T:\mathrm{\Xi }⟶F_{{\pounds }_S}\left(\mathrm{\Xi }\right)$ be a £-FS-valued map. Suppose there exists $\beta :\mathrm{\Xi }\times \mathrm{\Xi }⟶{\mathbb{R}}_{+},\rho \in \mathfrak{Z}$ and $\vartheta \in {\mathsf{\Omega }}_{e♭}$ such that it satisfies:

$$\begin{array}{c}\hfill \rho (\beta (\sigma ,\nu )H({\left[T\sigma \right]}_{{\alpha }_{\pounds }},{\left[T\nu \right]}_{{\alpha }_{\pounds }}),\vartheta (M_T^r(\sigma ,\nu )))\ge 0,\end{array}$$

(23)

for all $\sigma ,\nu \in \mathrm{\Xi }$. Additionally, suppose the following:

(i) 

$(\sigma ,\nu )\in \mathbb{E}\left(\mathbb{G}\right)$ implies $({\left[T\sigma \right]}_{{\alpha }_{\pounds }},{\left[T\nu \right]}_{{\alpha }_{\pounds }})\subseteq \mathbb{E}\left(\mathbb{G}\right)$ for all $\sigma ,\nu \in \mathrm{\Xi }$;

(ii) 

There exists ${\sigma }_0\in \mathrm{\Xi }$ and ${\sigma }_1\in {\left[T{\sigma }_0\right]}_{{\alpha }_{\pounds }}$ with $({\sigma }_0,{\sigma }_1)\in \mathbb{E}\left(\mathbb{G}\right)$, where ${\alpha }_{\pounds }\in \pounds \setminus \left\{0_{\pounds }\right\}$;

(iii) 

For each $\sigma \in \mathrm{\Xi }$ and $\nu \in {\left[T\sigma \right]}_{{\alpha }_{\pounds }}$ with $({\left[T\sigma \right]}_{{\alpha }_{\pounds }},{\left[T\nu \right]}_{{\alpha }_{\pounds }})\subseteq \mathbb{E}\left(\mathbb{G}\right)$, we have $({\left[T\nu \right]}_{{\alpha }_{\pounds }},{\left[T\omega \right]}_{{\alpha }_{\pounds }})\subseteq \mathbb{E}\left(\mathbb{G}\right)$ for all $\omega \in {\left[T\nu \right]}_{{\alpha }_{\pounds }}$;

(iv) 

T is $\mathbb{G}$-continuous;

(v) 

${\left[T\sigma \right]}_{{\alpha }_{\pounds }}$ is prox for every element σ in Ξ.

Then, T has at least a £-FFP in Ξ.

Proof. 

Define $\beta :\mathrm{\Xi }\times \mathrm{\Xi }⟶{\mathbb{R}}_{+}$ by

$$\begin{array}{c}\hfill \beta (\sigma ,\nu )=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}(\sigma ,\nu )\in \mathbb{E}\left(\mathbb{G}\right),\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.\end{array}$$

(24)

To show that T is $\beta$-admissible, we consider $\sigma \in \mathrm{\Xi }$ and $\nu \in {\left[T\sigma \right]}_{{\alpha }_{\pounds }}$ with $\beta (\sigma ,\nu )\ge 1$. Then, from (24), we have $(\sigma ,\nu )\in \mathbb{E}\left(\mathbb{G}\right)$ that, by condition $\left(i\right)$, implies that $({\left[T\sigma \right]}_{{\alpha }_{\pounds }},{\left[T\nu \right]}_{{\alpha }_{\pounds }})\subseteq \mathbb{E}\left(\mathbb{G}\right)$. Therefore, by $\left(iii\right)$, we obtain $({\left[T\nu \right]}_{{\alpha }_{\pounds }},{\left[T\omega \right]}_{{\alpha }_{\pounds }})\subseteq \mathbb{E}\left(\mathbb{G}\right)$ for all $\omega \in {\left[T\nu \right]}_{{\alpha }_{\pounds }}$, which further implies $(\nu ,\omega )\in \mathbb{E}\left(\mathbb{G}\right)$. So, $\beta (\nu ,\omega )\ge 1$. We see that condition $\left(i\right)$ of Theorem 2 is satisfied. Furthermore, it is clear that the axioms $\left(ii\right),\left(iv\right)$, and $\left(v\right)$ stated in Theorem 4 imply, respectively, the assertions $\left(ii\right),\left(iii\right)$, and $\left(iv\right)$ of Theorem 2. As a result, all the claims of Theorem 2 are satisfied. Hence, T has a £-FFP in $\mathrm{\Xi }$. □

Example 12.

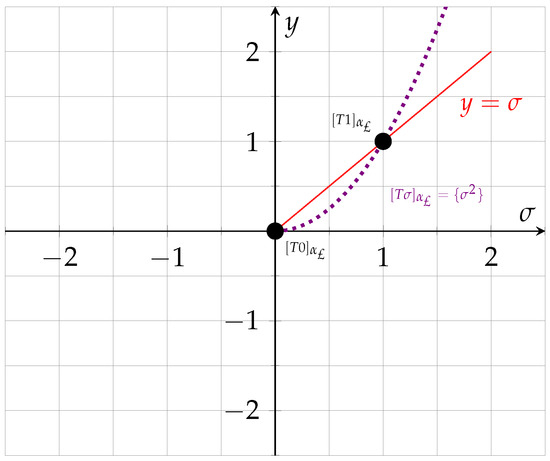
Let $\mathrm{\Xi }=[0,\infty )$ and define ${\delta }_e:\mathrm{\Xi }\times \mathrm{\Xi }⟶{\mathbb{R}}_{+}$ by ${\delta }_e(\sigma ,\nu )={(\sigma -\nu )}^2$ with $e:\mathrm{\Xi }\times \mathrm{\Xi }⟶[1,\infty )$ by $e(\sigma ,\nu )=\sigma +\nu +2$ for every $\sigma ,\nu \in \mathrm{\Xi }$. Let $\mathbb{G}=\left(\mathbb{V}\right(\mathbb{G}),\mathbb{E}(\mathbb{G}\left)\right)$ be a directed graph where $\mathbb{V}\left(\mathbb{G}\right)=\mathrm{\Xi }$ and $\mathbb{E}\left(\mathbb{G}\right)=\left\{\right(\sigma ,\sigma ):\sigma \in \mathrm{\Xi }\}\cup \left\{\right(\sigma ,\nu ):\sigma \ge \nu \mathit{for}\mathit{all}\sigma ,\nu \in [0,1\left]\right\}\cup \left\{\right(\sigma ,\nu ):\sigma \le \nu \mathit{for}\mathit{all}\sigma ,\nu \in [1,\infty \left)\right\}$. Then, $(\mathrm{\Xi },{\delta }_e,\mathbb{G})$ is a complete extended ♭-MS equipped with a graph $\mathbb{G}$. Let $\pounds =\{\xi ,\varpi ,\pi ,\gamma \}$ with $\xi {⪯}_{\pounds }\varpi {⪯}_{\pounds }\gamma$ and $\xi {⪯}_{\pounds }\pi {⪯}_{\pounds }\gamma$, where $\varpi ,\pi$ are not comparable. Then, $(\pounds ,{⪯}_{\pounds })$ is a CDL. For each $\sigma \in \mathrm{\Xi }$, consider a £-FS, $T\sigma :\mathrm{\Xi }⟶\pounds$, which is defined as:

$$\begin{array}{c}\hfill \left(T\sigma \right)\left(a\right)=\left\{\begin{array}{cc}\xi ,\hfill & \mathit{if}0\le a<{\sigma }^2;\hfill \\ \gamma ,\hfill & \mathit{if}a={\sigma }^2;\hfill \\ \pi ,\hfill & \mathit{if}{\sigma }^2<a<\infty .\hfill \end{array}\right.\end{array}$$

Then, for ${\alpha }_{\pounds }=\varpi$, we can obtain

$$\begin{array}{c}\hfill {\left[T\sigma \right]}_{{\alpha }_{\pounds }}=\left\{{\sigma }^2\right\}.\end{array}$$

(25)

We can easily see that $T\left(\sigma \right)\in F_{{\pounds }_S}\left(\mathrm{\Xi }\right)$ for each $\sigma \in \mathrm{\Xi }$. Now, defining $\beta :\mathrm{\Xi }\times \mathrm{\Xi }⟶{\mathbb{R}}_{+}$ by

$$\begin{array}{c}\hfill \beta (\sigma ,\nu )=\left\{\begin{array}{cc}4,\hfill & \mathit{if}\sigma =\nu =1;\hfill \\ \frac{1}{7},\hfill & \mathit{if}\sigma ,\nu \in \{2,3\}\mathit{and}\sigma \ne \nu ;\hfill \\ 0,\hfill & \mathit{elsewhere}.\hfill \end{array}\right.\end{array}$$

and $\vartheta :{\mathbb{R}}_{+}⟶{\mathbb{R}}_{+}$ by $\vartheta \left(t\right)=\frac{t}{2}$, for all $t>0$. Let $\rho (\tau ,\kappa )=\frac{2}{3}\kappa -\tau$ for all $\tau ,\kappa \in {\mathbb{R}}_{+}$. Then, $\rho \in \mathfrak{Z}$ and $\vartheta \in {\mathsf{\Omega }}_{e♭}$. Following the pattern discussed in Example 9, we can also verify (23) under the above-mentioned cases. Also, it is not difficult to show that T is edge-preserving and $\mathbb{G}$-continuous, and the subset ${\left[T\sigma \right]}_{{\alpha }_{\pounds }}$ of Ξ is prox for each $\sigma \in \mathrm{\Xi }$, and the conditions $\left(ii\right)$ and $\left(iii\right)$ of Theorem 4 are also met. Because all the hypotheses of Theorem 4 are fulfilled, it can be concluded that T has £-FFPs in Ξ.

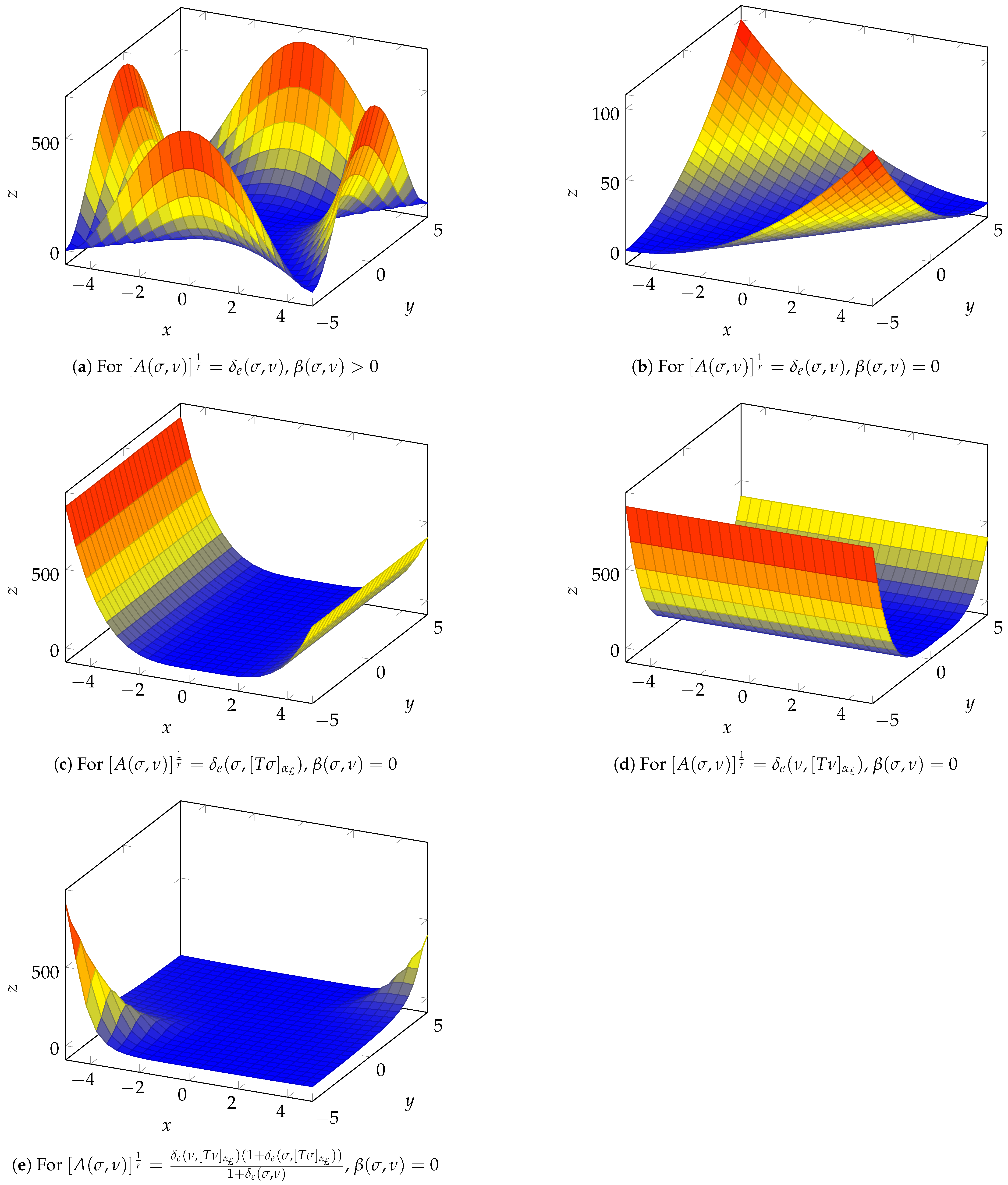
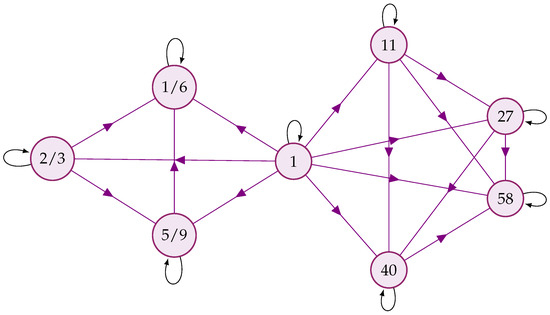
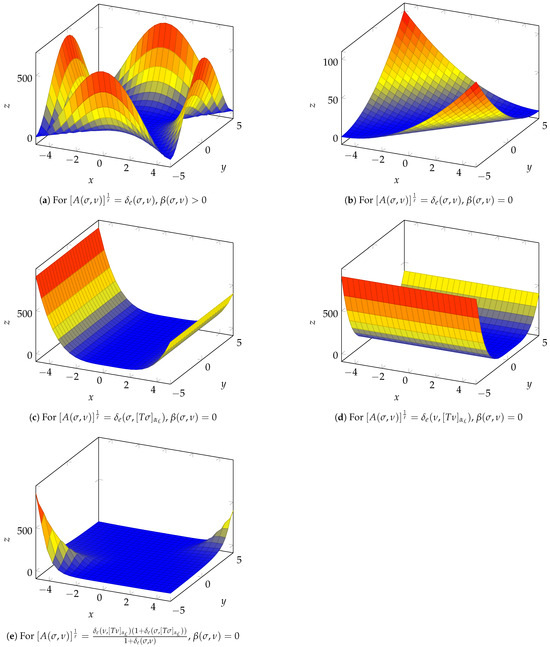
Figure 5 illustrates the weighted graph for $\mathbb{W}\left(\mathbb{G}\right)=\{\frac{1}{6},\frac{5}{9},\frac{2}{3},1,11,27,40,58\}\subseteq \mathbb{V}\left(\mathbb{G}\right)$ where the weight of edge $(\sigma ,\nu )$ is given by ${\delta }_e(\sigma ,\nu )$, Figure 6 displays the FPs of ${\left[T\sigma \right]}_{{\alpha }_{\pounds }}$, and Figure 7 justifies the inequality (23) under various cases of ${\left[A(\sigma ,\nu )\right]}^{\frac{1}{r}}$ and function β (a detailed explanation can be found in the Appendix A at the end of this paper).

Figure 5. Weighted graph for $\mathbb{W}\left(\mathbb{G}\right)\subseteq \mathbb{V}\left(\mathbb{G}\right)$ having edge-weight ${\delta }_e(\sigma ,\nu )$ for each edge $(\sigma ,\nu )$.

Figure 6. Graph indicating that $\sigma =0,1$ are the fixed points of mapping defined in (25).

Figure 7. Validation of inequality (23) under different cases of ${\left[A(\sigma ,\nu )\right]}^{\frac{1}{r}}$ and $\beta$.

6. Conclusions

In this paper, a number of existing FP results in the literature have been fused and rectified by proposing the term modified admissible hybrid £-fuzzy $\mathfrak{Z}$-contraction in the framework of extended ♭-MSs. The concepts of $\beta$-admissible mappings, SFs, and hybrid contractions have been implemented to consolidate several published results. Consequently, the above-mentioned results are accurate in the setup of complete ♭-MSs by considering $e(\sigma ,\nu )=♭$, for some $♭\ge 1$, and also in the bodywork of complete MSs by letting $♭=1$. In addition, the proved Theorems are also valid for FSs by taking $\pounds =[0,1]$. It is essential to note that by using various forms of SFs, one can obtain a number of new implications of the existing findings.

Open Problems:

• While this article extensively addresses the existence criteria for fixed points, what criteria can be formulated to determine the uniqueness of fixed points within the context of the discussed problems?
• Is it possible to extend the results obtained for L-fuzzy mappings to the domain of L-q-rung orthopair fuzzy mappings? What are the specific challenges and considerations that need to be addressed in order to achieve this extension?