Research on the Factors Influencing Tourism Revenue of Shandong Province in China Based on Uncertain Regression Analysis

Abstract

According to the analysis of historical tourism data, it was found that tourism revenue is influenced by multiple factors, and there exists a linear relationship between these factors and tourism revenue. Therefore, this paper employs a linear regression model to investigate the factors influencing tourism revenue. However, research on tourism data has found that the disturbance term of the linear regression model is not frequency-stable. This indicates that the disturbance term should be an uncertain variable rather than a random variable. Therefore, this paper adopts an uncertain linear regression analysis model and employs the tourism data of Shandong Province in China from 2011 to 2020 as the sample to investigate the factors influencing tourism revenue. The study provides parameter estimation and residual analysis of the model, as well as predictions and confidence intervals of tourism revenue. Additionally, through an uncertain hypothesis test, it was verified that the adopted model fitted the relevant tourism data well. The results show that factors such as the number of travel agencies, railway length, domestic tourist numbers, and per capita disposable income of urban residents have a significant impact on tourism revenue. Based on the study, recommendations and measures for improving tourism revenue of Shandong Province are proposed.

1. Introduction

Tourism revenue refers to all monetary income earned by tourism and sightseeing organizations through the sale of tourism-related goods during a certain period [1]. In order to analyze various factors influencing tourism revenue, many scholars have conducted meaningful research in this field. Deng H [2] show that since tourism revenue is an important indicator to reflect and measure the level of tourism development of a country or region, it is necessary to conduct in-depth research on factors influencing tourism revenue. Through the analysis of multiple linear regression model, it is concluded that the improvement in the ticket market economy, the expansion of urban green spaces, and the construction of tourism infrastructure are the main factors affecting tourism revenue. Li J [1] pointed out that China’s tourism industry has entered a period of explosive growth, and the domestic tourism revenue has also increased rapidly. Through a multiple linear regression model and econometric analysis, it is found that the main factors affecting the domestic tourism revenue include the number of domestic tourists and the number of travel agencies, and it is concluded that when other factors remain unchanged, the tourism income will increase by about CNY 1.2 billion with an increase of 1 million tourists, and every increase of one travel agency, tourism revenue will decrease by about CNY 50 million on average. Zhou X [3] firstly applied principal component analysis to extract two main factors, namely transportation and reception factor, as well as resource quality factor, through dimensionality reduction. They then conducted a horizontal comparison of 16 cities of Anhui Province in China based on the comprehensive ranking of these factors in 2017. Secondly, through the horizontal comparison of multiple linear regression models, the analysis shows that the green coverage area, the total number of tourists received, the annual average air quality index, the railway transportation volume, highway mileage, etc., all have important effects on the tourism revenue. Ren F [4] used the improved multiple linear regression method and step-up regression method to analyze the influencing factors of tourism revenue in Yan‘an city, and concluded that the number of tourists and tourist turnover had the most significant impact on tourism revenue, followed by residents’ disposable income and private car ownership. Lin X et al. [5] adopted R language software to establish multiple linear regression model, analyzed and studied the main factors affecting Shanghai’s tourism revenue, and concluded that the number of inbound tourists, railway mileage, and per capita disposable income of urban residents had the greatest impact on Shanghai’s tourism revenue. Pan J [6] used principal component analysis to extract several principal components and build a linear regression model. The analysis found that economic development level, urban and rural residents’ income, and consumer prices were the main reasons affecting tourism income, and the regression model established on this basis also had good prediction results. Jiang R [7] applied the grey correlation analysis method in the grey system theory and took grey comprehensive correlation as the metric index to analyze relevant factors affecting domestic tourism income, and concluded that the disposable income of urban residents, the average annual salary of employees and the per capita GDP were the leading factors affecting domestic tourism revenue. He Z [8] selected nine factors that have an impact on tourism economic income, made a quantitative analysis by using the grey comprehensive correlation degree analysis method of grey system theory, and concluded that the development of social economy and the continuous improvement in infrastructure have a greater promoting effect on tourism revenue.

According to the literature mentioned above, some studies have employed traditional quantitative analysis methods such as multiple linear regression analysis [1,2,3,4,5,9] and principal component analysis [6,10] to investigate the influencing factors of tourism revenue. These traditional methods typically assume the accuracy of the obtained sample data and the stability of disturbance term frequencies. On the other hand, other studies have utilized grey correlation analysis, a method derived from grey system theory, to study the influencing factors of tourism revenue [7,8,11]. Although grey correlation analysis does not require the stability of disturbance term frequencies, it assumes the accuracy of the obtained data. However, numerous examples have shown that disturbance term frequencies in sample data are often unstable and significantly deviate from the true frequencies. Moreover, it is difficult to ensure the accuracy of data during the collection process. Therefore, the aforementioned methods are ineffective in such cases. In contrast, uncertainty theory does not require the sample data to be accurate or assume the stability and closeness of disturbance term frequencies to the true frequencies when dealing with data. Hence, this paper employs uncertainty theory for the first time to study the influencing factors of tourism revenue. Through the research on the relationship between tourism revenue and its influencing factors, a linear relationship is found. Consequently, this paper adopts the method of uncertain linear regression analysis to study the influencing factors of tourism revenue and proposes an uncertain linear regression model.

The rest of the paper is organized as follows. The uncertain linear regression model is introduced in Section 2, and is applied in data collection and model assumptions in Section 3. Then, results and analysis are given in Section 4. Finally, conclusions are made in Section 5.

2. Uncertain Linear Regression Model

Uncertainty theory is a branch of mathematics that focuses on the study of reliability, including uncertain measures, uncertain variables, uncertain statistics, and uncertain programming. Among them, uncertain regression analysis is a primary research topic in uncertain statistics.

As a major research area in uncertain statistics, uncertain regression analysis utilizes uncertainty theory to study the relationship between the dependent and independent variables. Furthermore, it provides estimates of regression model parameters and residual analysis, as well as predictions and confidence intervals.

2.1. Uncertain Linear Regression Model

Let $x=(x_1,x_2,\cdots ,x_k)$ be a vector of explanatory variables, and $y$ be a response variable. Yao-Liu [12] suggested the functional relationship between $x$ and $y$ is expressed by an uncertain regression model:

$$y=f(x_1,x_2,\cdots ,x_k|\beta )+\epsilon ,$$

(1)

where $\beta ={({\beta }_0,{\beta }_1,{\beta }_2,\cdots ,{\beta }_k)}^T$ is a vector of parameters, and $\epsilon$ is an uncertain disturbance term (uncertain variable).

When there is a linear relationship between $x$ and $y$, an uncertain linear regression model is obtained [13]:

$$y={\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2+\cdots +{\beta }_k{x}_k+\epsilon .$$

(2)

2.2. Parameter Estimation

Assume we have a set of observed data $(x_{i1},x_{i2},\cdots ,x_{ik},y_i),i=1,2,\cdots ,n.$ Based on the observed data, the least squares estimate of $\beta$ in the uncertain linear regression model [12]:

$$y={\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2+\cdots +{\beta }_k{x}_k+\epsilon$$

is

$$\widehat{\beta }={(X^{T}X)}^{-1}{X}^{T}Y,$$

(3)

provided that $X^{T}X$ is a non-singular matrix, where

$$\widehat{\beta }=\left(\begin{array}{c}{\widehat{\beta }}_0\\ {\widehat{\beta }}_1\\ {\widehat{\beta }}_2\\ ⋮\\ {\widehat{\beta }}_k\end{array}\right),X=\left(\begin{array}{ccccc}1& x_{11}& x_{12}& \cdots & x_{1k}\\ 1& x_{21}& x_{22}& \cdots & x_{2k}\\ ⋮& ⋮& ⋮& ⋮& ⋮\\ 1& x_{n1}& x_{n2}& \cdots & x_{nk}\end{array}\right),Y=\left(\begin{array}{c}{y}_1\\ y_2\\ ⋮\\ y_n\end{array}\right).$$

(4)

2.3. Residual Analysis

Let $(x_{i1},x_{i2},\cdots ,x_{ik},y_i),i=1,2,\cdots ,n$ be a set of observed data, and let the fitted regression model be [14]:

$$\widehat{y}={\widehat{\beta }}_0+{\displaystyle \sum _{i=1}^k{\widehat{\beta }}_i{x}_i}$$

(5)

Then for each $i (i=1,2,\cdots ,n)$, the term

$${\epsilon }_i=y_i-{\widehat{\beta }}_0-{\displaystyle \sum _{i=1}^k{\widehat{\beta }}_i{x}_i}$$

(6)

is called the i-th residual.

The residuals ${\epsilon }_1,{\epsilon }_2,\cdots ,{\epsilon }_n$ will be regarded as the samples of the uncertain disturbance term $\epsilon$ in the uncertain regression model:

$$y={\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2+\cdots +{\beta }_k{x}_k+\epsilon .$$

Thus, the expected value of the uncertain disturbance term $\epsilon$ can be estimated as the average of residuals, i.e.,

$$\widehat{e}=\frac{1}{n}{\displaystyle \sum _{i=1}^n{\epsilon }_i}$$

(7)

and the variance can be estimated as

$${\widehat{\sigma }}^2=\frac{1}{n}{\displaystyle \sum _{i=1}^n{({\epsilon }_i-\widehat{e})}^2}.$$

(8)

Therefore, the estimated disturbance term $\widehat{\epsilon }$ is an uncertain variable with expected value $\widehat{e}$ and variance ${\widehat{\sigma }}^2.$

2.4. Forecast Value

Assume the forecast uncertain variable of response variable $y$ with respect to $(x_1,x_2,\cdots ,x_k)$ is determined by

$$\tilde{y}=f(x_1,x_2,\cdots ,x_k|\widehat{\beta })+\widehat{\epsilon },\widehat{\epsilon }\sim N(\widehat{e},\widehat{\sigma }).$$

(9)

Lio and Liu [14] suggested that the forecast value is defined as the expected value of the forecast uncertain variable $\widehat{u}$, i.e.,

$$\widehat{\mu }=f(x_1,x_2,\cdots ,x_k|\widehat{\beta })+\widehat{e}.$$

(10)

2.5. Confidence Interval

Assume the forecast uncertain variable of response variable $y$ with respect to a new explanatory vector $(x_1,x_2,\cdots ,x_k)$ is

$$\tilde{y}=f(x_1,x_2,\cdots ,x_k|\widehat{\beta })+\widehat{\epsilon },\widehat{\epsilon }\sim N(\widehat{e},\widehat{\sigma }),$$

and the forecast value of response variable $y$ is

$$\widehat{\mu }=f(x_1,x_2,\cdots ,x_k|\widehat{\beta })+\widehat{e}.$$

It follows from the operational law that $\tilde{y}$ has a normal uncertainty distribution $N(\widehat{u},\widehat{\sigma }),$ i.e.,

$$\widehat{\Psi }(z)={\left(1+\exp \left(\frac{\pi \left(\widehat{u}-z\right)}{\sqrt{3}\widehat{\sigma }}\right)\right)}^{-1}.$$

(11)

Taking $\alpha$ as the confidence level (e.g., 95%), it is easy to verify that

$$\widehat{b}=\frac{\sqrt{3}\widehat{\sigma }}{\pi }\ln \frac{1+\alpha }{1-\alpha }$$

(12)

is the minimum value b so that

$$\widehat{\Psi }(\widehat{\mu }+b)-\widehat{\Psi }(\widehat{\mu }-b)\ge \alpha .$$

(13)

Since $m\{\widehat{\mu }-\widehat{b}\le \widehat{y}\le \widehat{\mu }+\widehat{b}\}\ge \widehat{\Psi }(\widehat{\mu }+\widehat{b})-\widehat{\Psi }(\widehat{\mu }-\widehat{b})=\alpha ,$ Lio and Liu [14] suggested that the $\alpha$ confidence interval of response variable $y$ is

$$\widehat{\mu }\pm \frac{\sqrt{3}\widehat{\sigma }}{\pi }\ln \frac{1+\alpha }{1-\alpha }.$$

(14)

2.6. Uncertain Hypothesis Test

In order to test whether the estimated disturbance term $\widehat{\epsilon }$ is appropriate, we consider the following hypotheses [15]:

$$H_0:e=\widehat{e} \mathrm{and} \sigma =\widehat{\sigma } \mathrm{versus} H_1:e\ne \widehat{e} \mathrm{or} \sigma \ne \widehat{\sigma }.$$

(15)

Given a level of significance $\alpha$ (e.g., 5%), it follows from Corollary 1 that the test for the hypotheses (14) is

$$W=\{\left(z_1,z_2,\cdots ,z_n\right),$$

There are at least two of indexes i’s with $1\le i\le n$, so that

$$z_i<{\Phi }^{-1}\left(\frac{\alpha }{2}\right)\mathrm{or} z_i>{\Phi }^{-1}\left(1-\frac{\alpha }{2}\right)\},$$

(16)

where

$${\Phi }^{-1}\left(\alpha \right)=\widehat{e}+\frac{\widehat{\sigma }\sqrt{3}}{\pi }\ln \frac{\alpha }{1-\alpha }.$$

(17)

For each $i(i=1,2,\cdots ,n)$, if

$${\epsilon }_i<{\Phi }^{-1}\left(\frac{\alpha }{2}\right) \mathrm{or} {\epsilon }_i>{\Phi }^{-1}\left(1-\frac{\alpha }{2}\right),$$

(18)

then $(x_{i1},x_{i2},\cdots ,x_{ik},y_i)$ is regarded as an outlier. If the number of outlier is at least $\alpha n$, i.e.,

$$({\epsilon }_1,{\epsilon }_2,\cdots ,{\epsilon }_n)\in W,$$

(19)

Then either the estimated disturbance term $N(\widehat{e},\widehat{\sigma })$ or the fitted regression model (1) is inappropriate. Otherwise, both the estimated disturbance term $N(\widehat{e},\widehat{\sigma })$ and the fitted regression model (1) are appropriate.

With the continuous development of uncertain regression analysis theory, an increasing number of scholars have made significant contributions in the field of uncertain regression analysis and have further advanced and improved the theory. These research achievements include studies on the uncertain regression analysis theory itself [16,17,18,19,20,21], as well as research applying uncertain regression analysis to practical problems [22]. Although the application research is relatively in its early stages, the application domain of uncertain regression analysis is quite extensive.

3. Data Collection and Model Assumptions

This paper analyzes tourism-related data from 2011 to 2020 in Shandong Province, with specific data and statistical information provided in Table 1. The main sources of data are the Statistical Yearbook of Shandong Province and the Statistical Bulletin on National Economy and Social Development of Shandong Province from 2011 to 2020.

Table 1. Tourism-related data of Shandong Province from 2011 to 2020.

Particular Year	Domestic Tourism Revenue (CNY 100 Million)	Number of Domestic Tourists (10,000 Person Times)	Per Capita Disposable Income of Urban Residents (CNY)	Per Capita Disposable Income of Rural Residents (CNY)	Highway Length (km)	Railway Length (km)	Number of Travel Agencies (Nos.)
2011	3573.70	41,696	21,678	8395	233,189	4177	1865
2012	4335.03	48,739	24,496	9506	244,586	4306	1951
2013	5014.74	54,262	26,882	10,687	252,785	4397	2001
2014	5711.20	59,577	29,222	11,882	259,514	4546	2024
2015	6505.11	65,045	31,545	12,930	263,447	4863	2109
2016	7399.61	70,716	34,012	13,954	265,720	4882	2116
2017	8491.46	77,966	36,789	15,118	270,590	5115	2216
2018	9661.50	85,899	39,549	16,297	275,642	5676	2303
2019	10,851.33	93,288	42,329	17,775	280,325	5972	2630
2020	6005.32	57,670	43,726	18,753	286,814	6881	2685

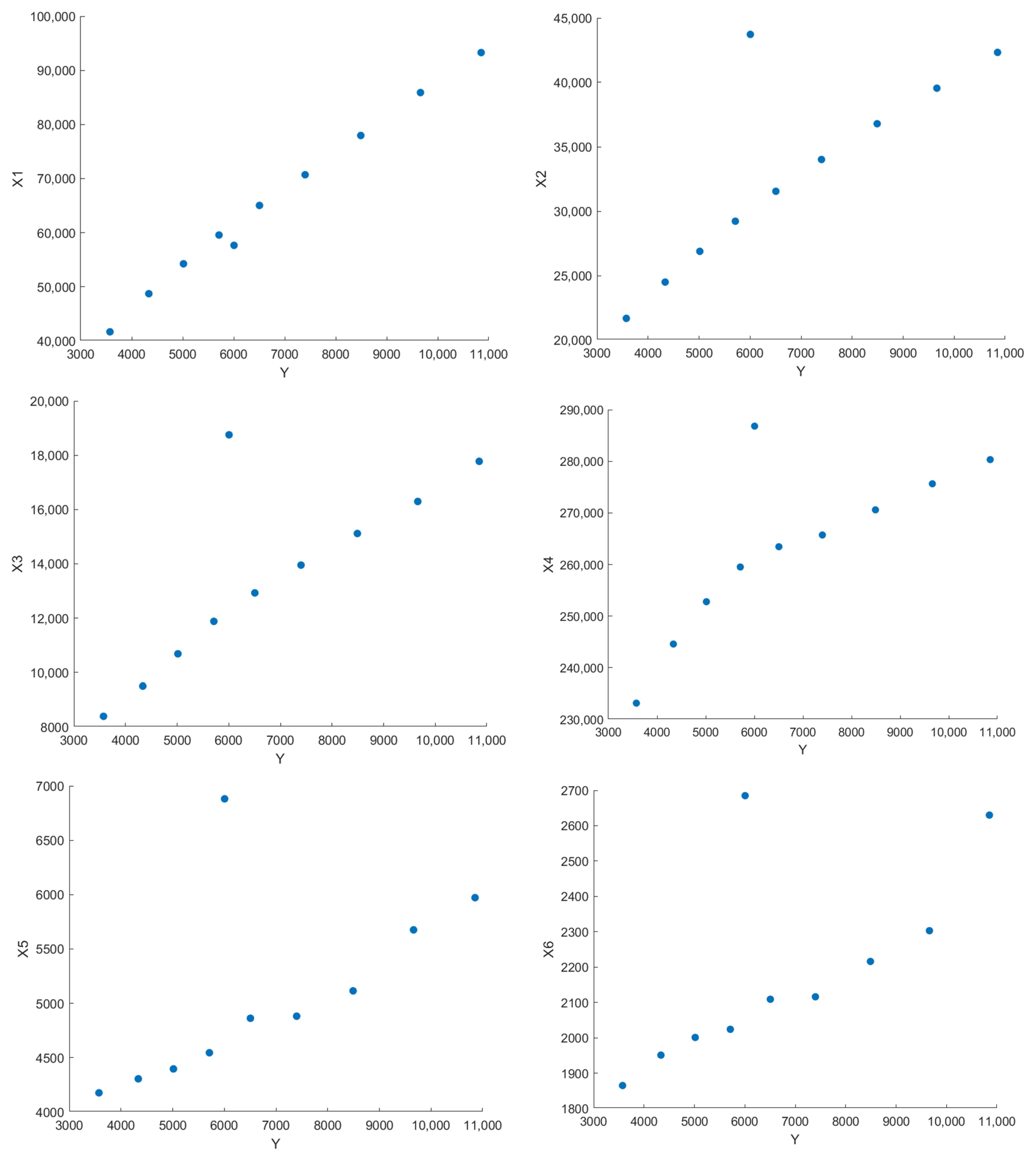
According to the relevant tourism data in Table 1, a scatter plot of the sample data in Figure 1 was plotted. The horizontal axis represents tourism revenue, while the vertical axes represent domestic tourist numbers, per capita disposable income of urban residents, per capita disposable income of rural residents, road length, railway length, and the number of travel agencies, respectively.

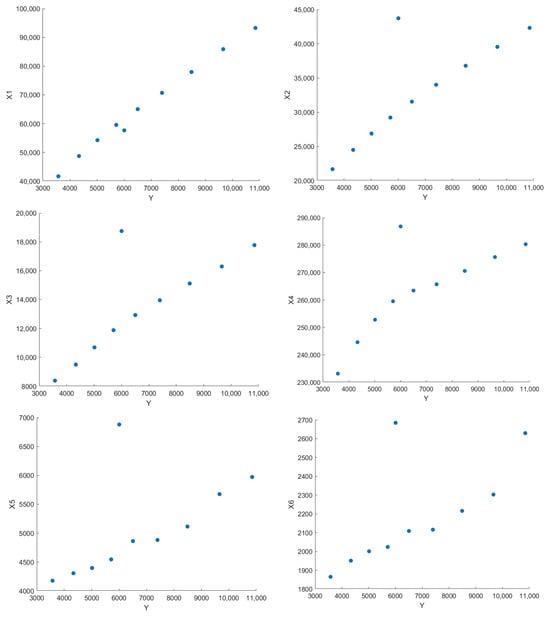
Figure 1. Scatter plots of sample data.

From Figure 1, it is evident that the sample data points for $(y_i,x_i)$ roughly fall near their respective straight lines. This indicates that there is a strong linear relationship between variables Y and $X_1,X_2,X_3,X_4,X_5,X_6$, and the uncertain linear regression model can be used to describe their relationship. Therefore, an uncertain linear regression model is established:

$$Y={\beta }_0+{\beta }_1{X}_1+{\beta }_2{X}_2+{\beta }_3{X}_3+{\beta }_4{X}_4+{\beta }_5{X}_5+{\beta }_6{X}_6+\epsilon ,$$

(20)

where Y is the tourism revenue, $X_1$ is the number of domestic tourists, $X_2$ is the per capita disposable income of urban residents, $X_3$ is the per capita disposable income of rural residents, $X_4$ is the highway length, $X_5$ is the railway length, $X_6$ is the number of travel agencies, and $\epsilon$ is the uncertain disturbance term.

4. Results and Analysis

4.1. Parameter Estimation

According to the above uncertain linear regression model and the data provided in Table 1, and according to the following formula in the literature [13]:

$$\beta ={(X^{T}X)}^{-1}{X}^{T}Y,$$

(21)

where

$$\begin{gathered} Y=\left(\begin{array}{c}3573.70\\ 4335.03\\ 5014.74\\ 5711.20\\ 6505.11\\ 7399.61\\ 8491.46\\ 9661.50\\ 10851.33\\ 6005.32\end{array}\right), \\ X=\left(\begin{array}{ccccccc}1& 41696& 21678& 8395& 233189& 4177& 1865\\ 1& 48739& 24496& 9506& 244586& 4306& 1951\\ 1& 54262& 26882& 10687& 252785& 4397& 2001\\ 1& 59577& 29222& 11882& 259514& 4546& 2024\\ 1& 65045& 31545& 12930& 263447& 4863& 2109\\ 1& 70716& 34012& 13954& 265720& 4882& 2116\\ 1& 77966& 36789& 15118& 270590& 5115& 2216\\ 1& 85899& 39549& 16297& 275642& 5676& 2303\\ 1& 93288& 42329& 17775& 280325& 5972& 2630\\ 1& 57670& 43726& 18753& 286814& 6881& 2685\end{array}\right), \end{gathered}$$

and $X^{T}X$ is a full-rank matrix. Therefore, the parameter estimates for the uncertain linear regression model are as follows:

$$\widehat{\beta }={(X^{T}X)}^{-1}{X}^{T}Y={\left(0.0000,0.1377,0.1190,-0.2143,-0.0213,0.2337,0.5171\right)}^T.$$

4.2. Residual Analysis

According to the above uncertain linear regression model, the formula for calculating the residuals of a linear regression model is

$${\epsilon }_i=y_i-\widehat{{\beta }_0}-{\displaystyle \sum _{j=1}^6\widehat{{\beta }_j}}{x}_{ij},$$

and then

$$\begin{array}{c}{\epsilon }_1=77.8966,{\epsilon }_2=-59.7110,{\epsilon }_3=-43.8468,{\epsilon }_4=-5.0207,{\epsilon }_5=-50.1684,{\epsilon }_6=29.6600,{\epsilon }_7=39.7361,\hfill \\ {\epsilon }_8=-26.8641,{\epsilon }_9=-7.1030,{\epsilon }_{10}=-7.8301,\hfill \end{array}$$

and the estimated mean and variance of the residual are, respectively,

$$\widehat{e}=\frac{1}{10}{\displaystyle \sum _{i=1}^{10}{\epsilon }_i}=\frac{1}{10}{\displaystyle \sum _{i=1}^{10}\left(y_i-\widehat{{\beta }_0}-{\displaystyle \sum _{j=1}^6\widehat{{\beta }_j}}{x}_{ij}\right)}=-5.3251,$$

$$\widehat{{\sigma }^2}=\frac{1}{10}{\displaystyle \sum _{i=1}^{10}{({\epsilon }_i-\widehat{e})}^2}=\frac{1}{10}{{\displaystyle \sum _{i=1}^{10}\left(y_i-\widehat{{\beta }_0}-{\displaystyle \sum _{j=1}^6\widehat{{\beta }_j}}{x}_{ij}-\widehat{e}\right)}}^2=1710.6.$$

4.3. Forecast Tourism Revenue

According to the above uncertain linear regression model, the predicted value of tourism revenue for the year 2020 is

$$\widehat{\mu }=\widehat{{\beta }_0}+{\displaystyle \sum _{i=1}^6\widehat{{\beta }_i}{x}_i}+\widehat{e}=6007.8.$$

4.4. Confidence Interval

According to the above uncertain linear regression model, the uncertain distribution function of tourism revenue is

$$\widehat{\Psi }(z)={\left(1+\exp \left(\frac{\pi \left(\widehat{\mu }-z\right)}{\sqrt{3}\widehat{\sigma }}\right)\right)}^{-1}={\left(1+\exp \left(\frac{\pi \left(10854-z\right)}{41.3943\sqrt{3}}\right)\right)}^{-1}.$$

Assume that the confidence level is $\alpha =95\%$, and then the confidence interval of the above uncertain linear regression model is

$$\left(6007.8-\frac{41.3594\sqrt{3}}{\pi }\ln \frac{1+0.95}{1-0.95},6007.8+\frac{41.3594\sqrt{3}}{\pi }\ln \frac{1+0.95}{1-0.95}\right),$$

that is $\left(5924.3,6091.3\right).$

4.5. Uncertain Hypothesis Test

To test whether $N(-5.3251,41.3594)$ is appropriate, we consider the following hypotheses:

$$H_0:e=-5.3251 \mathrm{and} \sigma =41.3594 \mathrm{versus} H_1:e\ne -5.3251 \mathrm{or} \sigma \ne 41.3594.$$

(22)

Given a significance level $\alpha =5\%$, we obtain

$${\Phi }^{-1}\left(0.025\right)=-88.8639,{\Phi }^{-1}\left(0.975\right)=78.2137,$$

where ${\Phi }^{-1}$ is the inverse uncertainty distribution of $N(-5.3251,41.3594)$, i.e.,

$${\Phi }^{-1}\left(\alpha \right)=-5.3251+\frac{41.3594\sqrt{3}}{\pi }\ln \frac{\alpha }{1-\alpha }.$$

Since $\alpha \times 10=0.5,$ it follows from (16) that the test for the hypotheses (22) is $W=\{\left(z_1,z_2,\cdots ,z_{10}\right)$: there is at least one of index i’s with $1\le i\le 10$, such that

$$z_i<-88.8639\mathrm{or} z_i>78.2137\}.$$

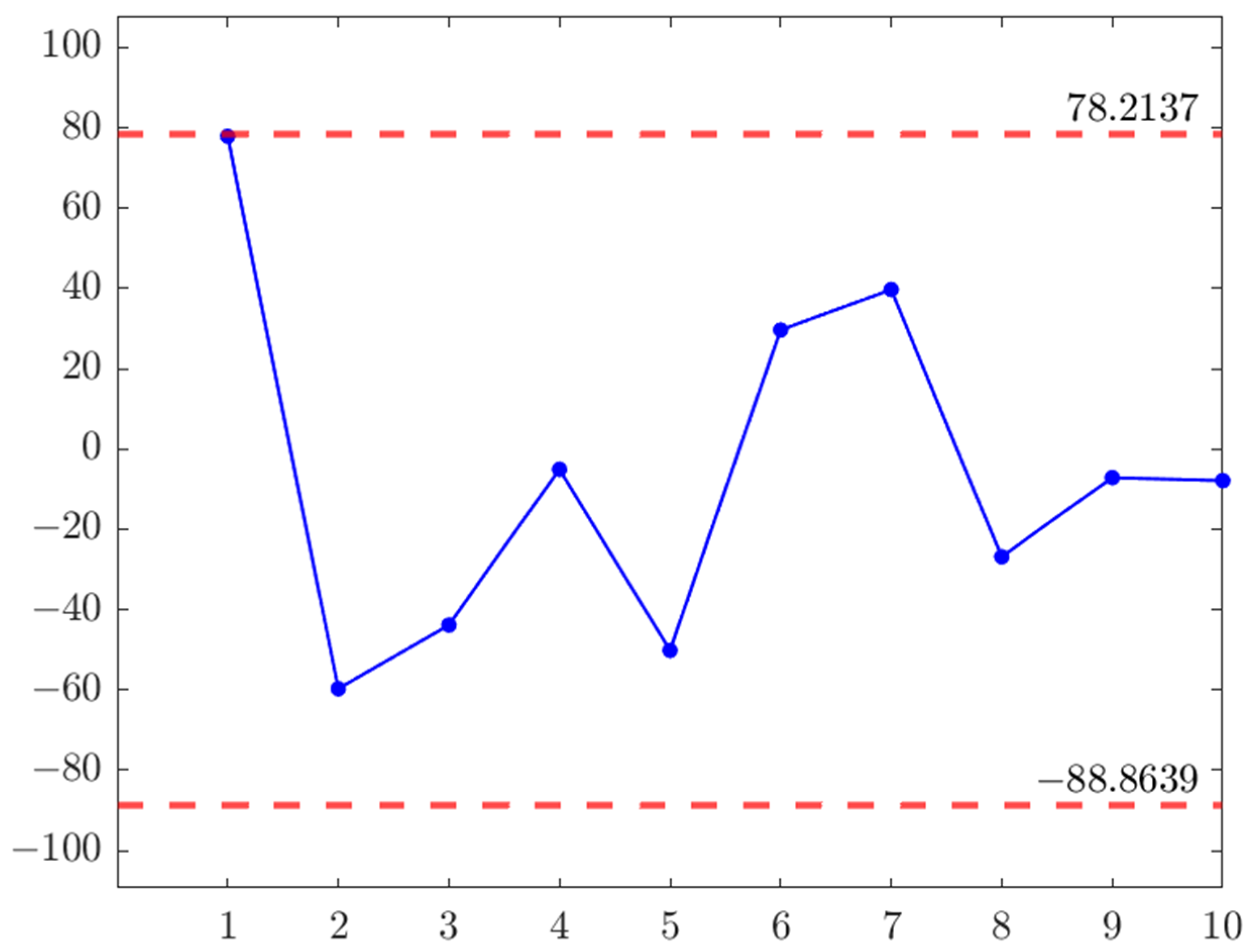
As shown in Figure 2, we can see that none of ${\epsilon }_i\notin [-88.8639,78.2137].$ Thus, $({\epsilon }_1,{\epsilon }_2,\cdots ,{\epsilon }_{10})\notin W$. Therefore, we think the estimated disturbance term $N(-5.3251,41.3594)$ and the fitted linear regression model (20) are appropriate.

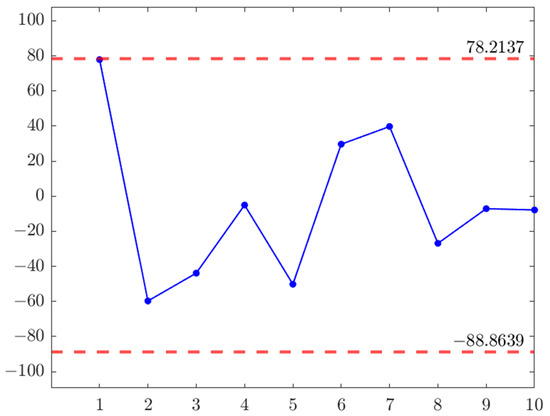
Figure 2. Sample residual plot.

4.6. Result Analysis

By observing the obtained residuals and their residual plot (Figure 2) of the aforementioned uncertain linear regression model, it was found that the frequency of the disturbance term is indeed unstable, which aligns with our previous assumption. Additionally, through the analysis of tourism data, a linear relationship between tourism revenue and the selected influencing factors was discovered. Therefore, it is reasonable for this paper to choose uncertain linear regression analysis to study the influencing factors of tourism revenue.

To better validate the rationality of the obtained uncertain linear regression model in the study, an uncertain hypothesis test was conducted. The final test results confirm that the uncertain linear regression model fits the tourism data well. This indicates that the established uncertain linear regression model in this paper is reasonable and can effectively study the relationship between tourism revenue and the selected influencing factors.

After observing the uncertain linear regression model, it was found that the parameter estimates for $X_3$ and $X_4$ were negative, which contradicted the actual situation. Therefore, in order to achieve a more accurate model, $X_3$ and $X_4$ were removed from the regression equation. The final result is an optimized uncertain linear regression model, which is

$$Y=0.1377X_1+0.1190X_2+0.2337X_5+0.5171X_6+N(-5.3251,41.3594).$$

In the context of other factors remaining constant, the impact on tourism revenue, from largest to smallest, is as follows: the number of travel agencies, railway length, domestic tourist numbers, and per capita disposable income of urban residents. For every additional 100 million domestic tourist numbers, tourism revenue increases by CNY 0.1386 billion. For every increase of CNY 1 in per capita disposable income of urban residents, tourism revenue increases by CNY 0.0961 billion. For every additional 1 km of railway length, tourism revenue increases by CNY 0.2145 billion, and for every additional travel agency, tourism revenue increases by CNY 0.6123 billion.

5. Conclusions

When studying the factors affecting tourism revenue, compared to traditional methods such as multiple linear regression analysis, principal component analysis, and grey relational analysis, uncertain linear regression analysis does not require data accuracy and does not assume the frequency stability of the disturbance term in the regression model, making it more aligned with real-world situations. Additionally, through the uncertain hypothesis test, it has been verified that the uncertain linear regression model fits the related tourism data well. Based on these reasons, this paper utilizes uncertain linear regression analysis for the first time to investigate the influencing factors of tourism revenue and proposes a corresponding uncertain linear regression model. However, considering that there may be other factors affecting tourism revenue, various uncertain linear regression models can be proposed based on uncertain linear regression analysis.

Based on the tourism data from 2011 to 2020 in Shandong Province, the obtained uncertain linear regression model reveals that factors such as the number of travel agencies, railway mileage, domestic tourist arrivals, and per capita disposable income of urban residents have significant impacts on tourism revenue. In order to better promote the growth of tourism revenue and the development of the tourism industry in Shandong Province, the following recommendations are proposed.

5.1. Enriching the Types of Tourism Products and Expanding the Domestic Tourism Market

The tourism industry in Shandong Province has mainly relied on sightseeing-oriented tourism products, resulting in a relatively simple market structure and limited variety of tourism products. Visitors often have brief sightseeing experiences and are unable to deeply immerse themselves in the local culture, leading to short stays and an inability to fully unleash their consumption potential. As a result, the growth in tourism revenue in Shandong Province has been slow, impacting the economic and social development of cities heavily reliant on tourism revenue. Therefore, to increase tourism revenue, efforts should be made to innovate tourism products and continuously attract domestic tourists for consumption.

On one hand, based on the unique resource advantages of each city in Shandong Province, it is advisable to draw inspiration from popular tourism projects in other provinces and cities. While meeting the diverse, personalized, and innovative demands of current tourists, emphasis should be placed on incorporating local cultural elements and enhancing visitor engagement to create immersive tourism products.

On the other hand, Shandong Province can actively promote the “tourism+” model according to the resource advantages of each city. This involves developing related tourism projects such as “tourism + agriculture”, “tourism + industry”, “tourism + marine”, etc., to create tourism products with distinctive regional characteristics, thereby attracting more domestic tourists.

5.2. Improving Transportation Infrastructure and Reducing Travel Costs for Tourism

Research analysis indicates that a convenient, fast, and low-cost transportation system plays a crucial role in promoting the development of tourism economy. Therefore, Shandong Province should continuously improve its comprehensive transportation system, including roads, railways, and aviation, to enhance the accessibility of tourist attractions in different cities. Additionally, Shandong Province should leverage its policy advantages to coordinate the development and planning of transportation departments in various cities, aiming to establish an interconnected and unified transportation system that prioritizes safety, comfort, speed, and convenience. By integrating tourism routes to meet the diverse needs of tourists, the overall service level of tourism transportation can be improved, thereby reducing the travel costs for visitors.

5.3. Increasing the per Capita Disposable Income of Residents to Promote the Development of Tourism Economy

Generally speaking, urban residents have relatively higher and stable sources of per capita disposable income. To enhance the tourism consumption level of urban residents, it is necessary to eliminate their negative expectations about future employment while ensuring employment stability and a high level of disposable income. Therefore, measures such as gradually raising the minimum wage standard and continuously improving the social security system can be implemented to alleviate their concerns about a potential decline in future living standards caused by tourism consumption. This will fully unleash the tourism consumption potential of urban residents and increase the total tourism revenue of Shandong Province.

However, rural residents have relatively lower levels of disposable income, and they often reduce their travel expenses in order to ensure a certain frequency of tourism. Therefore, to enhance the tourism consumption level of rural residents, it is necessary to vigorously develop the agricultural economy and continuously increase the disposable income of rural residents, thereby increasing their demand for tourism consumption.

In the future, when dealing with uncertain statistical data, it is necessary to consider not only uncertain linear regression models but also further study other types of uncertain regression models, such as exponential growth models, logarithmic growth models, and logistic growth models.