On a Symmetric Image Cryptosystem Based on a Novel One-Dimensional Chaotic System and Banyan Network

Abstract

In this paper, a Banyan network with high parallelism and nonlinearity is used for the first time in image encryption to ensure high complexity and randomness in a cipher image. To begin, we propose a new 1-D chaotic system (1-DSCM) which improves the chaotic behavior and control parameters’ structure of the sin map. Then, based on 1-DSCM, a Banyan network, and SHA-256 hash function, a novel image encryption algorithm is conducted. Firstly, a parameter is calculated using SHA-256 hash function and then employed to preprocess the plaintext image to guarantee high plaintext sensitivity. Secondly, a row–column permutation operation is performed to gain the scrambled image. Finally, based on the characteristic of DNA encoding, a novel DNA mapping is constructed using an $N=4$ Banyan network and is used to diffuse the scrambled image. Simulation results show that the 1-DSCM has excellent performance in chaotic behavior and that our encryption algorithm exhibits strong robustness against various attacks and is suitable for use in modern cryptosystems.

1. Introduction

A chaotic system, characterized by its nonlinear dynamical nature with a positive Lyapunov exponent and global boundedness, produces pseudo-random numbers with randomness, complexity, and sensitivity to initial conditions. These qualities render chaotic systems highly suitable for application in image encryption [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18]. For example, some novel hyperchaotic systems were introduced based on the Hopfield chaotic neural network [1] or cellular neural network (CNN) [2] and employed for image encryption because of their large key spaces. Compared to high-dimensional chaotic systems, 1-D chaotic maps possess simpler architectures and faster iteration speeds, rendering them highly suitable for fast image encryption. Thus, Wang et al. developed a one-dimensional discrete chaotic system (1-DFCS) which is used to design a fast image encryption system with high sensitivity of key and a strong ability to withstand differential attacks [3]. In other work [4], a novel one-dimensional cosine polynomial (1-DCP) chaotic map was proposed and employed to develop a fast encryption system based on parallel permutation substitution. Leveraging chaotic systems, researchers have proposed various image encryption algorithms in conjunction with diverse techniques, including bit-level operations [6,7,8,9,10], semitensor product approaches [11,12], quantum walks [13], and multiple image encryption methods [14,15].

In the past few years, encryption algorithms based on DNA coding and nonlinear mapping have been widely studied. DNA encoding concepts from genetic engineering were used in their development. By leveraging the advantages of biological computers, such as high parallelism and extensive storage capacity, scientists have devised many image encryption methods based on DNA encoding [19,20,21,22,23]. For example, in [20], K.N. Singh et al. introduced an innovative image encryption framework, which utilizes deoxyribonucleic acid (DNA) encoding in conjunction with recursive cellular automata (RCA) to change the pixel values to obtain a lower correlation coefficient. In [22], two scrambling sequences were generated through Feistel Network and employed in a permutation stage to achieve a highly complex scrambled image. In recent years, many nonlinear mappings have been used in diffusion operation [24,25,26,27,28,29]. In [24], random numbers were generated using elliptic curves (ECs) which are isomorphic to a fixed public EC and perform the pixel scrambling and diffusion to achieve high security of the encrypted image. Based on the features of natural image, a dynamic S-box was conducted to affect the pixel values in the diffusion stage. In [28], by using the discrete wavelet transform and dynamic S-box, the natural images were selectively encrypted, which can reduce the computational complexity of the algorithm. Moreover, the Banyan network holds significant application in designing various switching circuits [30,31], facilitating the eventual hardware implementation of our algorithm. Furthermore, the Banyan network possesses the characteristics of nonlinearity and parallelism. Therefore, in this paper, combined with DNA encoding and a Banyan network, we propose a novel image encryption scheme with high security and efficiency.

The contributions of the proposed encryption algorithm can be summarized as follows:

1.

We developed a novel discrete chaotic system (1-DSCM) that enhances the parameters’ structure and nonlinearity of the sin map.

2.

Taking advantage of its high parallelism and nonlinearity, the Banyan network is the first to be used in an encryption algorithm.

3.

Comprehensive testing was conducted for both the cryptosystem and chaotic system.

The remainder of this paper is structured as follows. Section 2 discusses the shuffle-exchange network and DNA encoding. Section 3 displays the 1-DSCM and comprehensive tests of the proposed chaotic system. Section 4 proposes a novel Banyan network DNA mapping which can be used in diffusion. Section 5 details the encryption framework based on 1-DSCM, shuffle-exchange network, and DNA encoding. The comparison analysis of similar algorithms is carried out in Section 6, and the conclusion of the paper is given in Section 7.

2. Related Work

2.1. Shuffle-Exchange Network

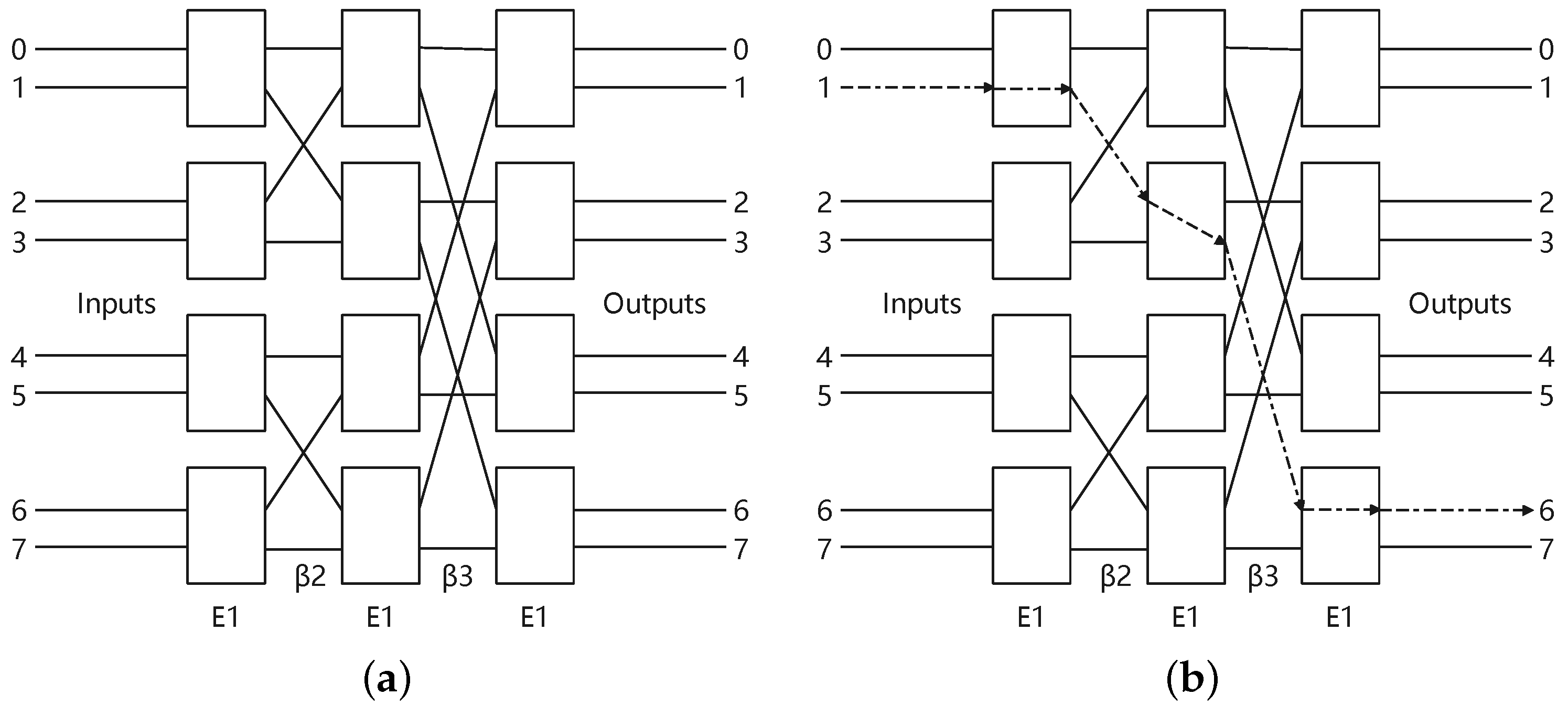
The shuffle-exchange network, like the Banyan network, Omega network, and indirect binary n-cube network, is a network that uses full shuffling functions and switching functions to realize interconnection between nodes. A topology diagram of the Banyan network with $N=8$ is shown in Figure 1a.

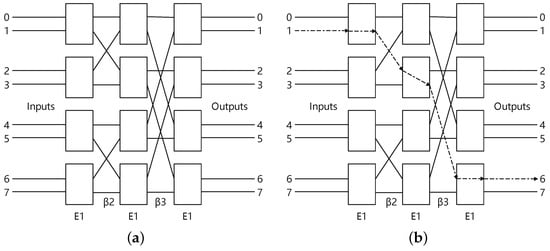
Figure 1. The Banyan network. (a) The $N=8$ Banyan network. (b) The diffusion example in $N=8$ Banyan network.

2.1.1. Exchange Unit

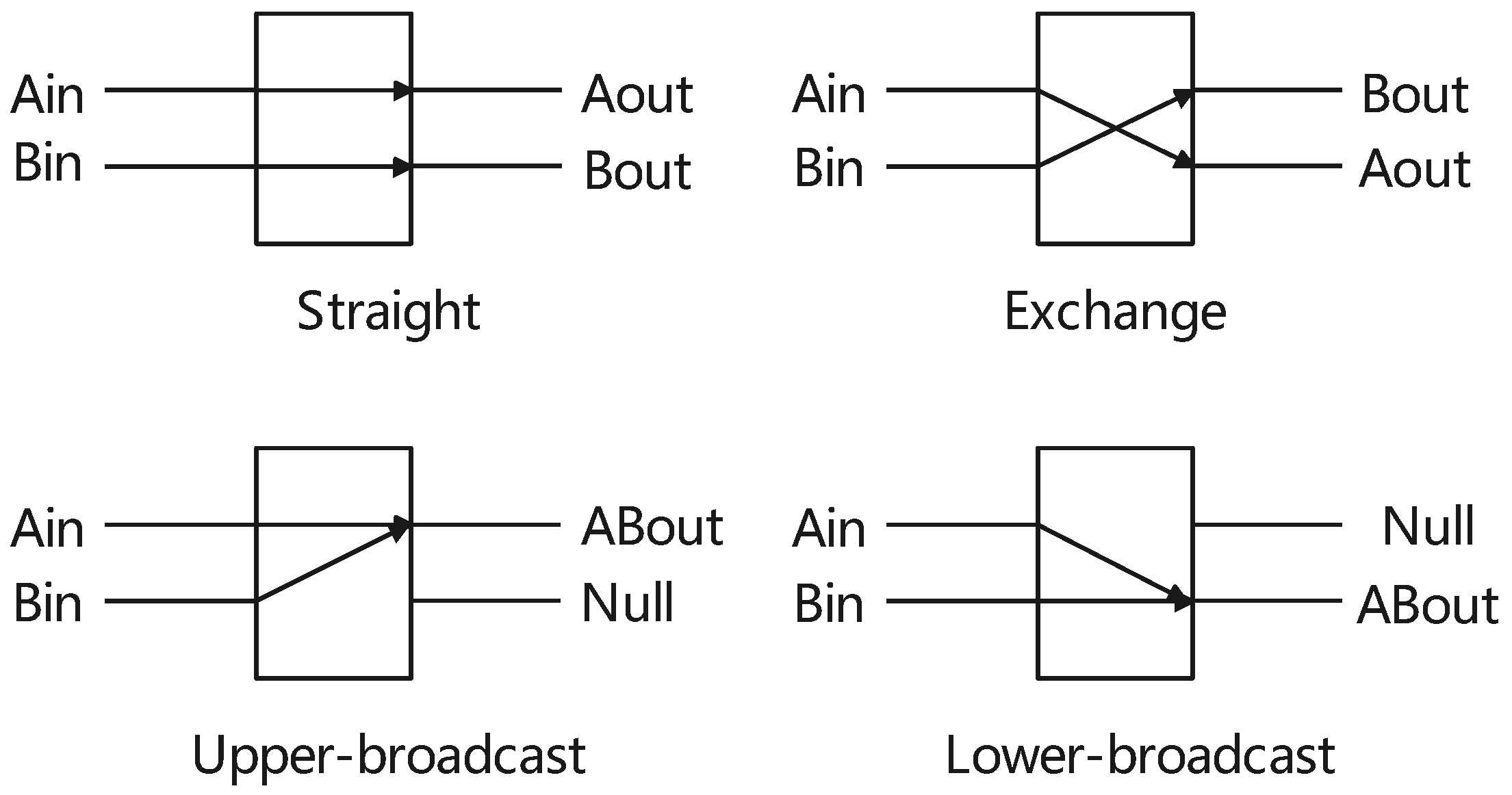
The exchange unit has two inputs and two outputs, serving as the fundamental component in various shuffle-exchange networks. Different multilevel interconnection networks employ distinct types of exchange units, topologies, and control methods. In general, there are four distinct switching states or connection modes, as illustrated in Figure 2: straight, exchange, upper-broadcast, and lower-broadcast. In our algorithm, we utilize straight and exchange switching units.

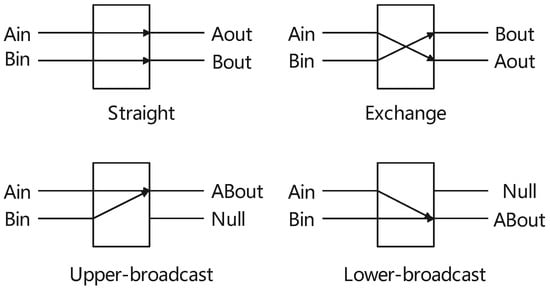
Figure 2. The exchange unit.

2.1.2. Banyan Network

The Banyan network is a type of interconnection network, and its composite routing function $Y_n$ is shown in Equation (1):

$$Y_n=E_1{\beta }_2{E}_1{\beta }_3\dots {\beta }_n{E}_1$$

(1)

where $E_1$ represents the exchange unit and ${\beta }_i$ represents the ith replacement stage. For each control switch, we configure the exchange units in the straight state when $E_1=0$ and the exchange state when $E_1=1$. As an example depicted in Figure 1b, when the input is 1 and the control signal $E_1$ is 010, the output is 6.

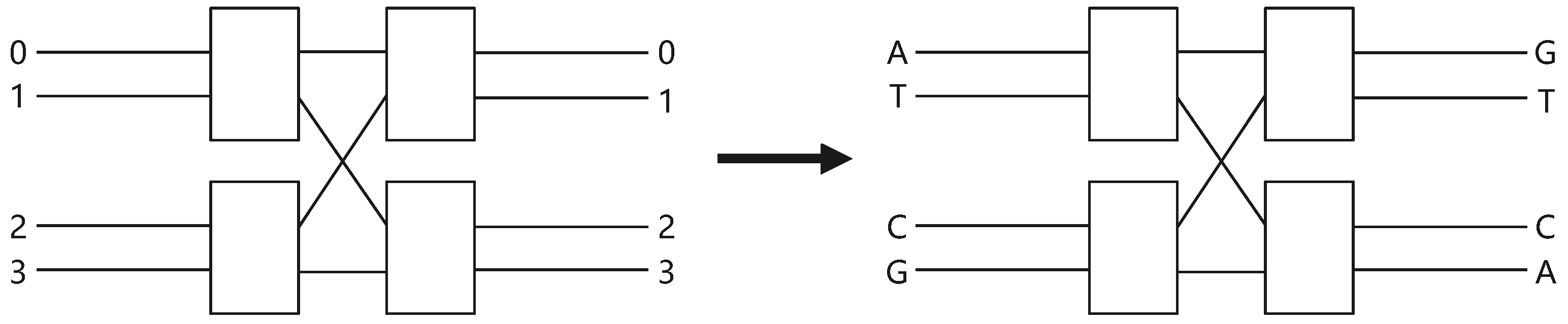
2.2. DNA Encoding

To use biocomputers in the future, the information processing techniques based on DNA coding have been studied. First of all, the information being processed will be encoded to four distinct nucleic acids, namely, A (adenine), T (thymine), C (cytosine), and G (guanine). According to the base pairing principle, A pairs with T and C pairs with G. Coincidentally, 0 and 1 are complementary in the binary system; therefore, 00 and 01 are regarded as complementary with 11 and 10. For example, when using encoding rules $A=00$, $T=11$, $C=10$, and $G=01$, $36={\left(00111001\right)}_2$ can be encoded as $ACGA$ and $CGTC$ can be decoded as ${\left(10011110\right)}_2=158$.

3. Proposed Chaotic System

The mathematical representation of the sin map is given by Equation (2):

$$\begin{array}{c}{x}_{n+1}=\frac{\gamma }{4}sin\left(\pi x_n\right)\end{array}$$

(2)

where $\gamma$ is the control parameter. As shown in Figure 3b, the sin map has some nonchaotic ranges when $\gamma \in [0,10]$. Among the characteristics of chaotic systems, the positive Lyap exponent and orbital global bounding are widely used as evidence for judging chaos. According to the theory of the Chen-Lai algorithm [32], a high-gain feedback controller is constructed to obtain the positive Lyap exponent of the dynamic system. Furthermore, a modular operation to make the system globally bounded is designed. Drawing inspiration from the sin map and Chen-Lai algorithm, we construct a 1-DSCM, which is depicted in Equation (3).

$$\begin{array}{c}{x}_{n+1}=sin\left(\pi x_n\right)+2x_n+rx{e}^{x_n}mod1\end{array}$$

(3)

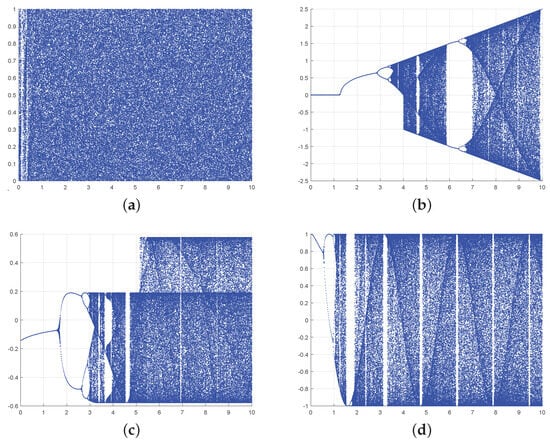
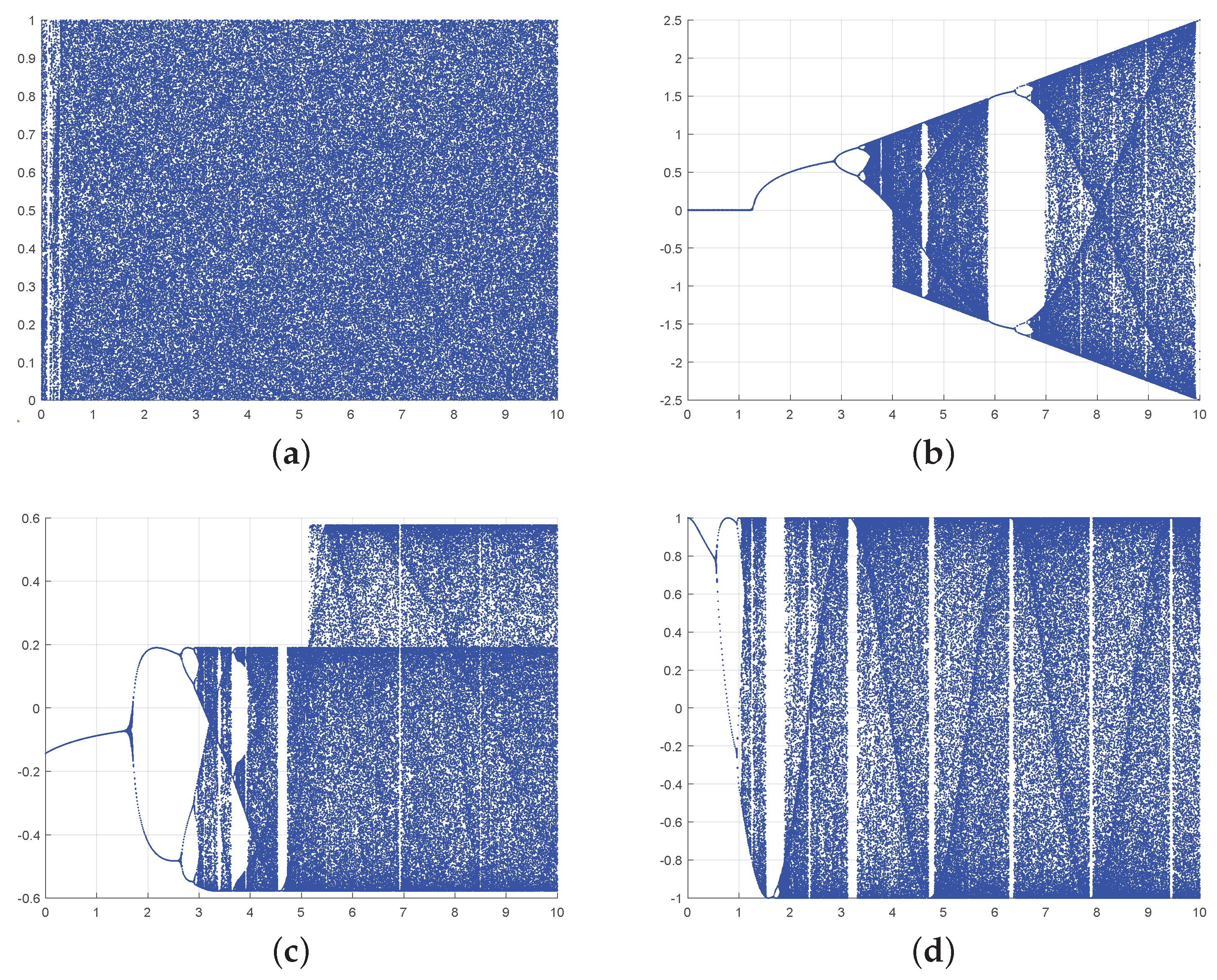
Figure 3. The bifurcation diagram of 1-DSCM, 1-DFCS, and 1-DCP. (a) The bifurcation diagram of 1-DSCM with $r\in (0,10)$. (b) The bifurcation diagram of sin map with $r\in (0,10)$. (c) The bifurcation diagram of 1-DFCS with $r\in (0,10)$. (d) The bifurcation diagram of 1-DCP with $r\in (0,10)$.

Here, r is the control parameter of the 1-DSCM. To evaluate the performance of the 1-DSCM, various tests, including Lyapunov exponent test, bifurcation analysis, sample entropy, 0-1 test, and NIST test, are performed in the following subsections.

3.1. Lyapunov Exponent Test

The Lyapunov exponent (LE), which signifies the rate of separation between neighboring trajectories, serves as a pivotal criterion in assessing the chaotic nature of a dynamic system $x_{n+1}=f\left(x_n\right)$. The definition of the Lyapunov exponent is presented in Equation (4).

$$\begin{array}{c}\lambda =\underset{k\to \infty }{lim}\frac{1}{k}ln|\frac{f^k(x_0+\Delta x)-f^k\left(x_0\right)}{\Delta x}|=\underset{k\to \infty }{lim}\frac{1}{k}{\displaystyle \sum _{i=0}^{k-1}}ln{\left|\frac{\partial f\left(x\right)}{\partial x}\right|}_{x=x_i}\end{array}$$

(4)

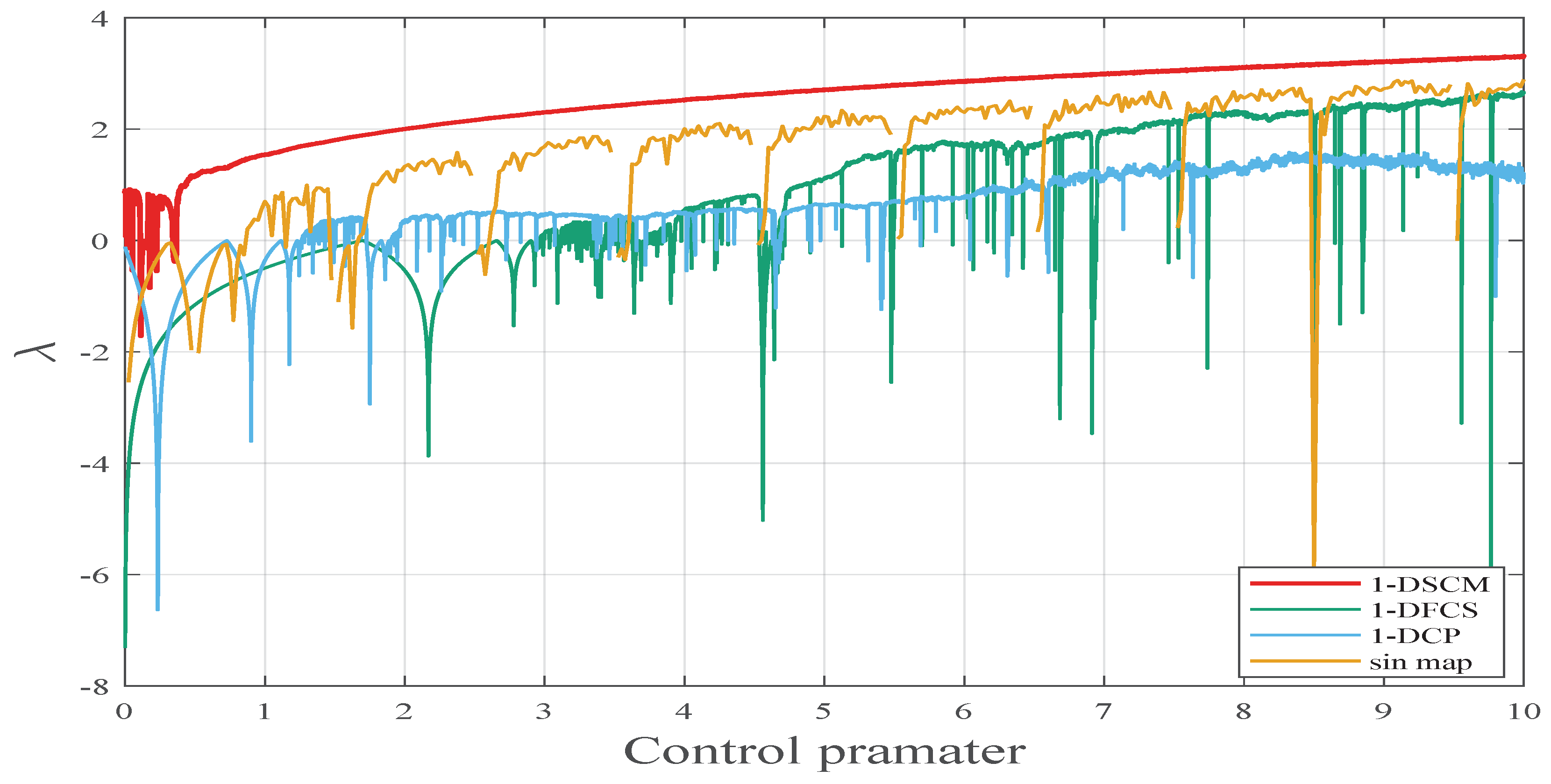
where n represents the dimension of the generated time series $f\left(x_n\right)$. A positive Lyapunov exponent (LE) means the high sensitivity to the initial value. Moreover, the larger the LE value is, the better the chaotic behavior of the system is. The LE values of the sin map 1-DFCS [3], 1-DCP [4], and 1-DSCM are provided in Figure 4. As illustrated in Figure 4, compared to other recently proposed chaotic systems, 1-DSCM exhibits higher Lyapunov exponent (LE) value across a broader parameter range.

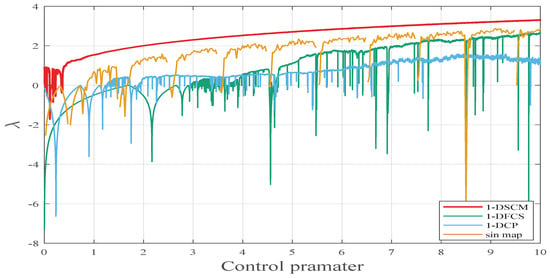
Figure 4. The Lyapunov exponent of 1-DSCM, 1-DFCS, 1-DCP, and sin map with $r\in (0,10)$.

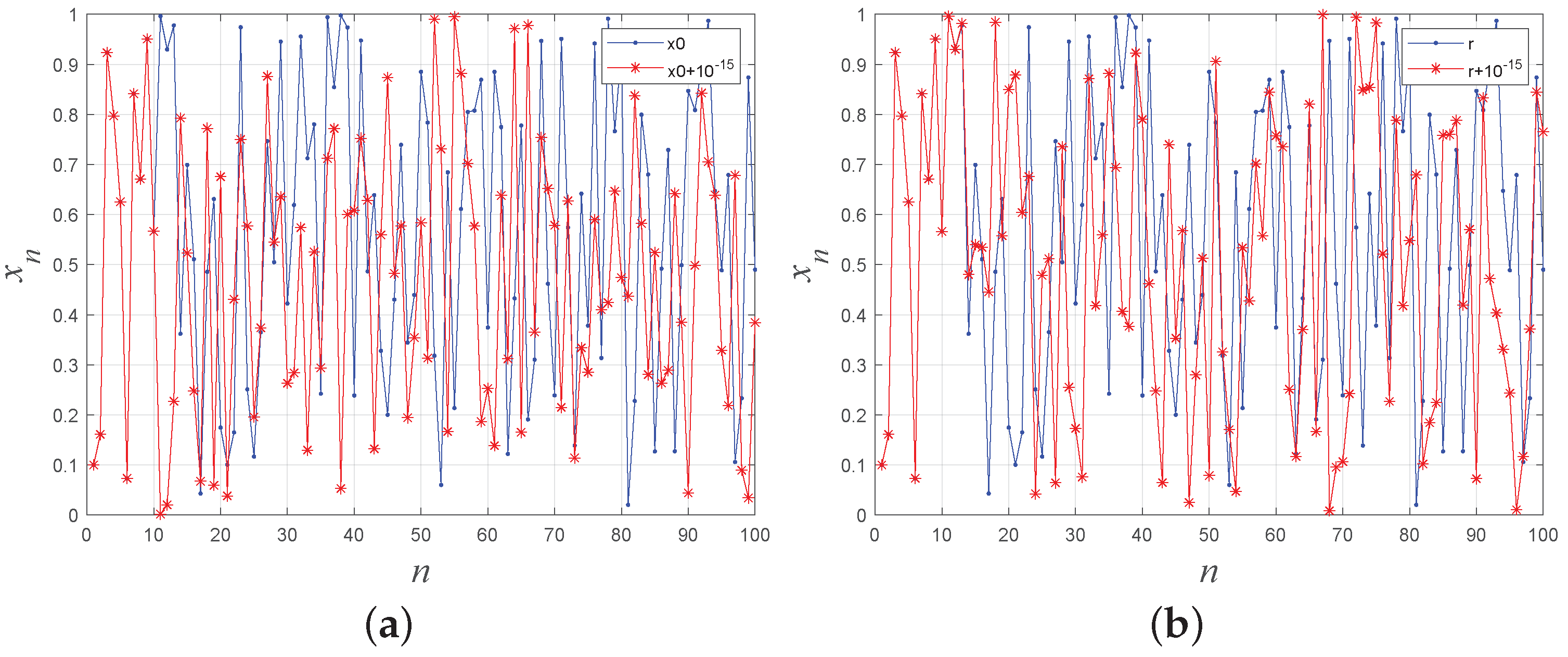
For a visual assessment of the proposed system’s sensitivity to initial values and control parameters, the generated chaotic sequences with a slight variation in initial values or control parameters are plotted in Figure 5, providing evidence of 1-DSCM’s high sensitivity to initial values and control parameters.

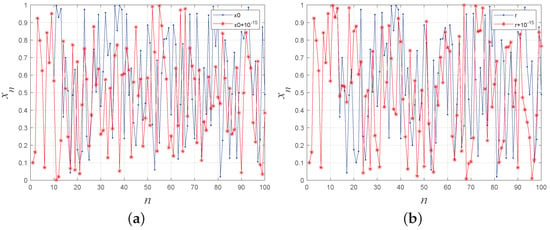
Figure 5. (a) The sensitivity of the initial value. (b) The sensitivity of the control parameter.

3.2. Bifurcation Analysis

The dynamics of a system can be effectively depicted through the diagram of bifurcation. In Figure 3, we present the bifurcation diagrams for the 1-DSCM, 1-DFCS, and 1-DCP. In comparison to other chaotic systems, 1-DSCM displays a more extensive chaotic region and without the emergence of periodic phases.

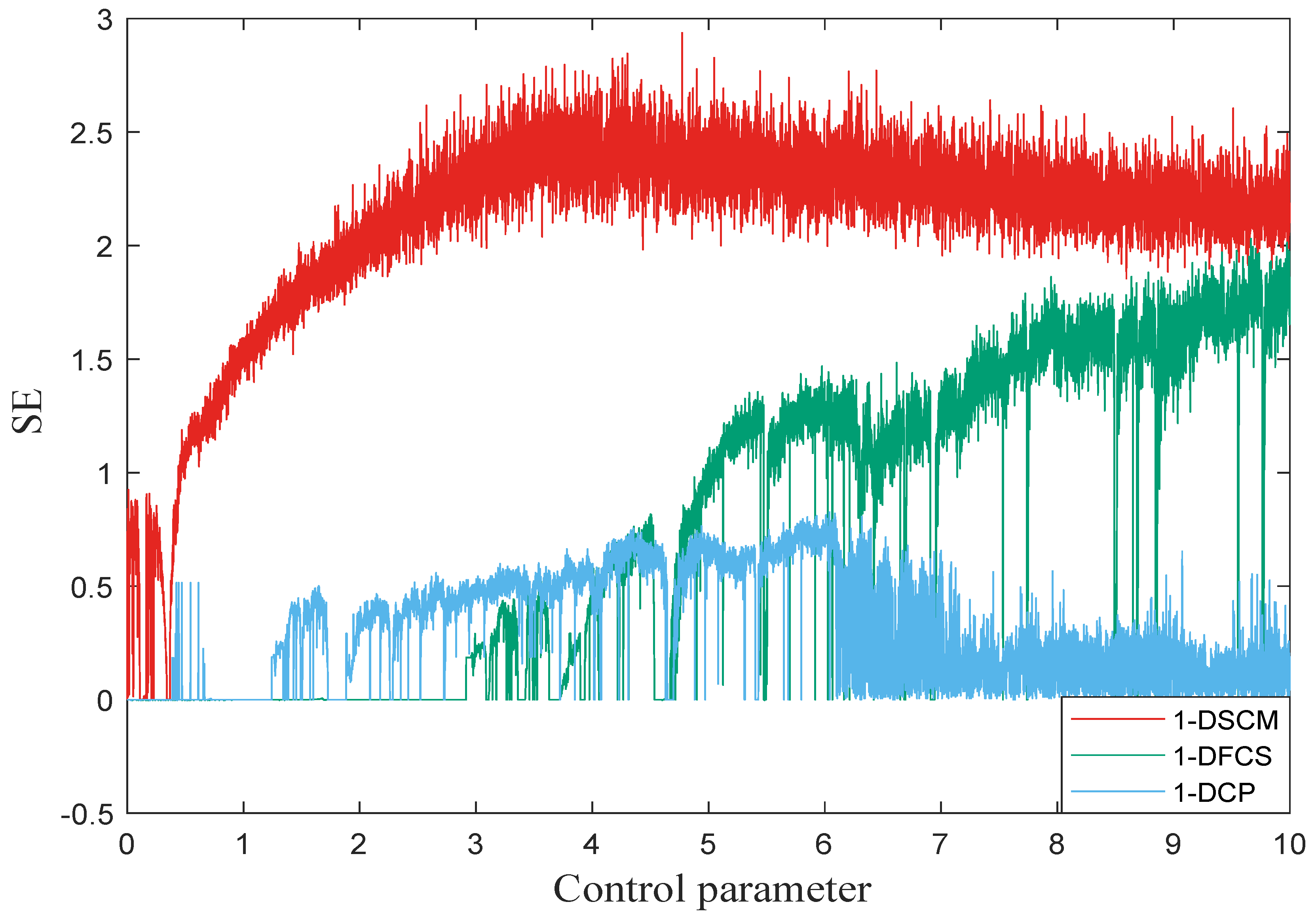
3.3. Sample Entropy

The time series’ self-similarity of chaotic systems can be quantified through sample entropy (SE) [33]. A larger SE value indicates higher complexity in the dynamic behavior and lower regularity in the time series. The SE value for the time series X can be modeled by Equations (5)–(7):

$$\begin{array}{c}{D}_m\left(i\right)=[X\left(i\right),X(i+1),\dots ,X(i+m-1)]\end{array}$$

(5)

$$\begin{array}{c}A=\frac{1}{N-m}{\displaystyle \sum _{i=1}^{N-m}}\frac{1}{N-m-1}{A}_i\\ B=\frac{1}{N-m}{\displaystyle \sum _{i=1}^{N-m}}\frac{1}{N-m-1}{B}_i\end{array}$$

(6)

$$\begin{array}{c}SE(m,r,N)=-ln\frac{A}{B}\end{array}$$

(7)

where $d[X_m\left(i\right),X_m\left(j\right)]$ is the Chebyshev distance between $X\left(i\right)$ to $X(i+m-1)$, r is the specified distance, $D_m\left(i\right)$ represents the template vector, and $A_i$ and $B_i$ are the counts of vectors that satisfy the conditions $d[X_{m+1}\left(i\right),X_{m+1}\left(j\right)]<r$ and $d[X_m\left(i\right),X_m\left(j\right)]<r$, respectively. We set $m=2,r=0.2\times std$ in our simulation, and the comparative analysis results of 1-DSCM with other chaotic systems are provided in Figure 6. This analysis proves that 1-DSCM exhibits superior performance in SE analysis to other chaotic systems.

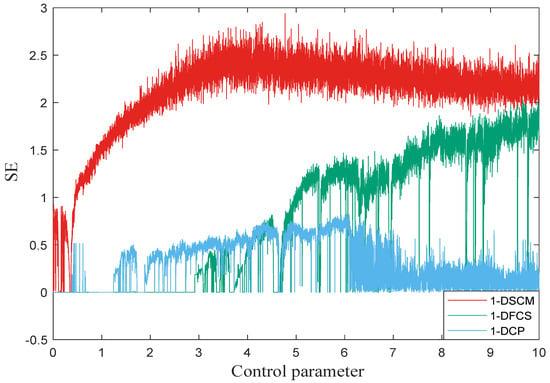
Figure 6. The sample entropy of 1-DSCM, 1-DFCS, and 1-DCP with $r\in (0,10)$.

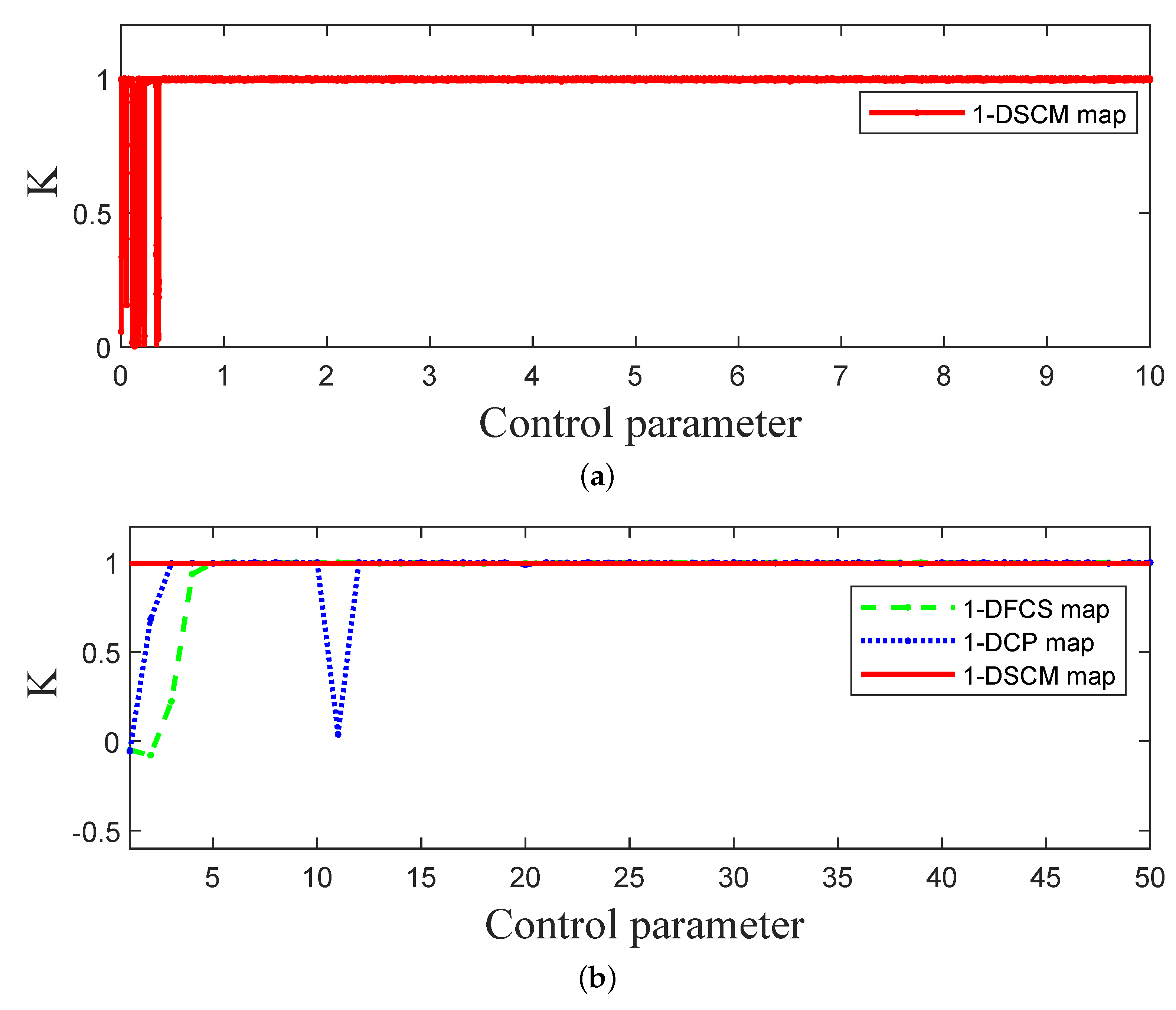
3.4. 0-1 Test

In this subsection, we utilize 0-1 test to judge the chaotic status of 1-DSCM, 1-DFCS, and 1-DCP. The K value can be calculated using Equations (8)–(11):

$$\begin{array}{c}s\left(n\right)={\displaystyle \sum _{i=1}^n}X\left(i\right)sin\left(ir\right)\end{array}$$

(8)

$$\begin{array}{c}p\left(n\right)={\displaystyle \sum _{i=1}^n}X\left(i\right)cos\left(ir\right)\end{array}$$

(9)

$$\begin{array}{c}M\left(n\right)=\underset{N\to \infty }{lim}\frac{1}{N}{\displaystyle \sum _{i=1}^n}{[p(i+n)-p\left(i\right)]}^2+{[s(i+n)-s\left(i\right)]}^2\end{array}$$

(10)

$$\begin{array}{c}K=\frac{logM\left(n\right)}{logn}\end{array}$$

(11)

where X represents the sequence of size N generated by the 1-DSCM. Here, we set $r=2$, and the value of K close to 1 indicates that the dynamic system is in a chaotic state. Figure 7 depicts the outcomes of the 0-1 test for 1-DSCM, 1-DFCS, and 1-DCP. The results demonstrate that the K scores of 1-DSCM are close to 1.

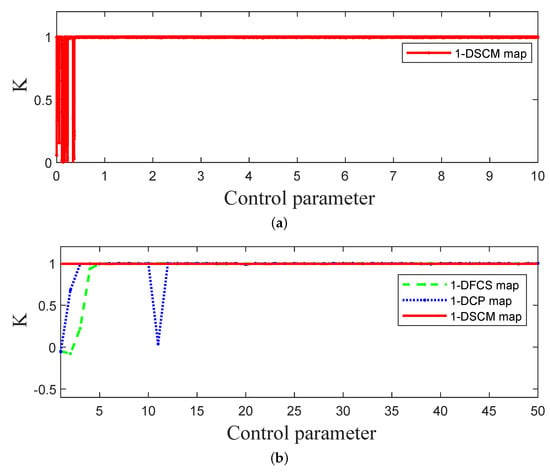
Figure 7. The 0-1 test of 1-DSCM, 1-DFCS, and 1-DCP. (a) The 0-1 test of 1-DSCM with $r\in (0,10)$. (b) The 0-1 test of 1-DSCM, 1-DCP, and 1-DFCS with $r\in (0,50)$.

3.5. NIST SP 800-22 Test

We utilize the National Institute of Standards and Technology (NIST) SP 800-22 test suite to further validate the randomness of the sequences generated by the 1-DSCM. Firstly, a time series with 12,500,000 values, which is denoted as $seq$, is generated by the 1-DSCM. Then, the values of $seq$ are mapped into the interval 0 to 255 using Equation (12):

$$\begin{array}{c}se{q}_{amplified}=mod(seq\times {10}^{10},256)\end{array}$$

(12)

Finally, the integer part of each value in $se{q}_{amplified}$ is transformed to 8 bits. The test results are presented in Table 1, where all p-values fall within the range $(0.001,1)$. This affirms that the sequence produced by the 1-DSCM processes high randomness and it is suitable for image encryption.

Table 1. NIST test results of 1-DSCM.

Test Index	p-Value	Result
Frequency	0.574903	PASS
BlockFrequency	0.114550	PASS
CumulativeSums	0.455937	PASS
Runs	0.275709	PASS
LongestRun	0.494392	PASS
Rank	0.739918	PASS
FFT	0.390936	PASS
NonOverlappingTemplate	0.719747	PASS
OverlappingTemplate	0.494392	PASS
Universal	0.867692	PASS
ApproximateEntropy	0.657933	PASS
RandomExcursions	0.634308	PASS
RandomExcursionsVariant	0.514124	PASS
Serial	0.262249	PASS
LinearComplexity	0.595549	PASS

4. Banyan Network-DNA Mapping

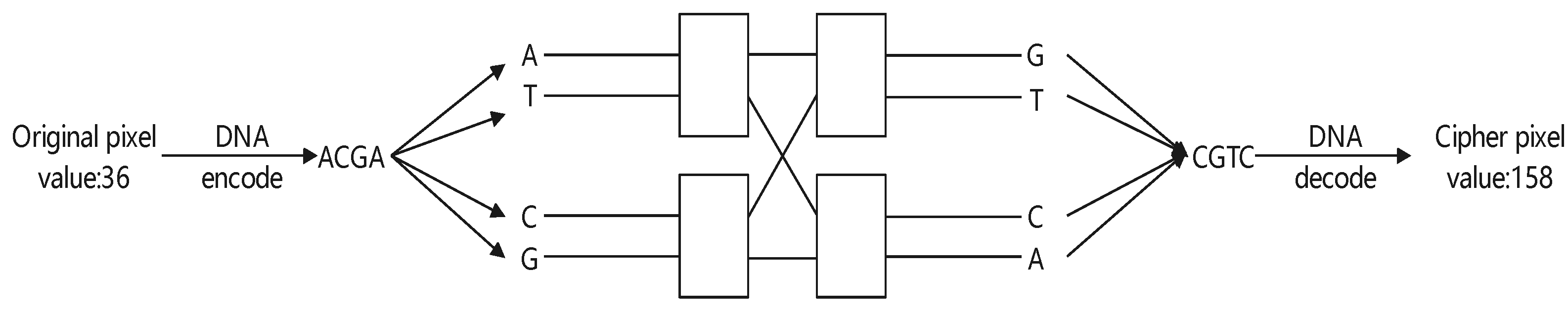
In this section, based on the characteristic of DNA encoding, we constructed a novel DNA mapping using an $N=4$ Banyan network. The topological graph of the $N=4$ Banyan network is demonstrated on the left of Figure 8. Here, we set input ports 0–3 that correspond to ATCG, respectively, and output ports 0–3 that correspond to GTCA, respectively, which is illustrated on the right of Figure 8. The Banyan network-DNA mapping rule is given in Table 2.

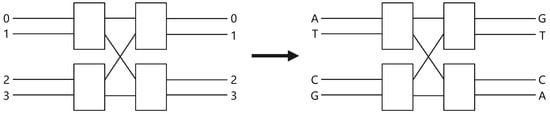
Figure 8. The Banyan network-DNA mapping.

Table 2. Banyan network-DNA mapping rules.

E1	A	T	C	G
A	11	01	10	00
T	01	11	00	10
C	10	00	11	01
G	00	10	01	11

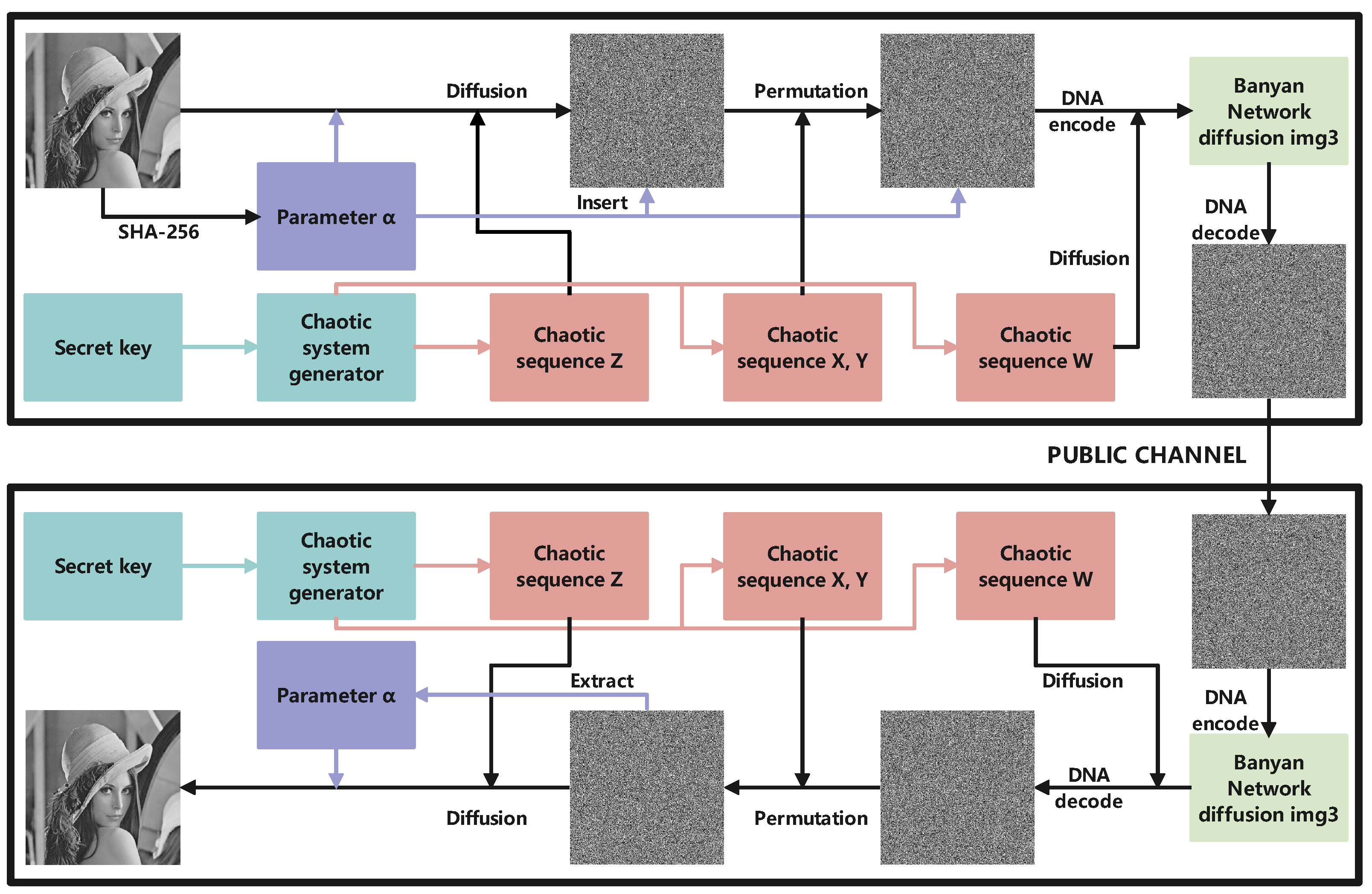
5. Encryption Framework

In this paper, we present a novel image encryption framework using the technology of the Banyan network to obtain a better diffusion effect. The flow chart of our algorithm is shown in Figure 9.

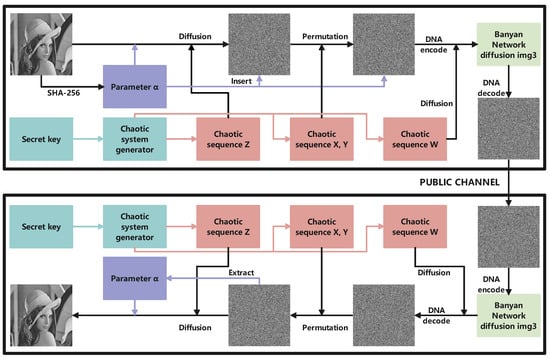
Figure 9. The flow chart of our algorithm.

Step 1: A natural image P($M\times N$) is first input into the SHA-256 hash function to yield a 256-bit hash value h.

Step 2: Subsequently, the h is further divided into eight discrete segments to obtain $\alpha$ using Equation (13).

$$\left\{\begin{array}{c}tmp=h(1:32)\oplus h(33:64)\oplus \dots \oplus h(225:256)\hfill \\ \alpha =mod(fix\left(\frac{tmp}{2^{20}}\right),256)\hfill \end{array}\right.$$

(13)

where $tmp$ is a temporary variable.

Step 3: Four sequences, $x_n,y_n,z_n,w_n$, shown in Equation (14) with the size of $M,N,M\times N,4\times M\times N$, respectively, are generated by 1-DSCM using the key $\{x_0,y_0,z_0,w_0\}$, and the first $N_0$ iteration values are discarded.

$$\left\{\begin{array}{c}{x}_n=\{x_1,x_2,x_3,\dots x_M\}\hfill \\ y_n=\{y_1,y_2,y_3,\dots y_N\}\hfill \\ z_n=\{z_1,z_2,z_3,\dots z_{M\times N}\}\hfill \\ w_n=\{w_1,w_2,w_3,\dots w_{4\times M\times N}\}\hfill \end{array}\right.$$

(14)

According to Equation (15), these sequences are processed to obtain $\{X,Y,Z,W\}$ to be used in the continued stages.

$$\left\{\begin{array}{c}X=mod(fix(x_n\times {10}^{15}),M)\hfill \\ Y=mod(fix(y_n\times {10}^{15}),N)\hfill \\ Z=mod(fix(z_n\times {10}^{15}),256)\hfill \\ W=mod(fix(w_n\times {10}^{15}),4)\hfill \end{array}\right.$$

(15)

Step 4: We use Equation (16) to perform the first diffusion operation on P to obtain $im{g}_1$.

$$\begin{array}{c}im{g}_1=mod(P+Z+\alpha \times 10,256)\end{array}$$

(16)

Step 5: We insert the parameter $\alpha$ into $im{g}_1$. Firstly, we generate a null vector $\overrightarrow{v}$ and add it to the last row of the image $im{g}_1$. Secondly, the value of the $pos$-th element in $\overrightarrow{v}$ is changed to $\alpha$. The position $pos$ can be calculated by Equation (17). It is worth noting that the size of $im{g}_1$ now becomes $(M+1)\times N$.

$$\begin{array}{c}pos=fix\left(mod(x_1\times y_1\times z_1\times w_1\times {10}^{15},N)\right)+1\end{array}$$

(17)

Step 6: We perform a row permutation operation using X and a column permutation operation using Y. The details of the scrambling procedure are displayed in Algorithm 1.

Step 7: We perform the Banyan network diffusion operation. Each pixel of $im{g}_2$ is encoded into four nucleic acids which are input into the Banyan network-DNA mapping shown in Figure 8. Using the W as the control signal, the output of the Banyan network-DNA mapping is obtained and then decoded to obtain the corresponding cipher pixel. The final encrypted image is denoted as $img$. For example, as per the example detailed in Section 2.2, 36 can be encoded as $ACGA$. When the control signal of the $N=4$ Banyan network is 10, the output is $CGTC$, which can be decoded into a cipher pixel value of 158. A visualization of the example is shown in Figure 10.

Algorithm 1 Encryption algorithm.

Input: The original image P, parameter $\alpha$ and four chaotic sequences X, Y, Z, W. Output: Encrypted image $img$. 1: for$i=1:M\times N$do 2:     $im{g}_1\left(i\right)=mod(P\left(i\right)+Z\left(i\right)+\alpha \times 10,256)$ 3: end for 4: $im{g}_1\leftarrow$ Insert $\alpha$. 5: for$i=1:M+1$do 6:     $temp=im{g}_1(i,:)$ 7:     $im{g}_1(i,:)=im{g}_1(mod(X\left(i\right),M+1)+1,:)$ 8:     $im{g}_1(mod(X\left(i\right),M+1)+1,:)=temp$ 9: end for 10: for$j=1: N$do 11:     $temp=im{g}_1(:,j)$ 12:     $im{g}_1(:,j)=im{g}_1(:,mod(Y\left(j\right),N)+1)$ 13:     $im{g}_1(:,mod(Y\left(j\right),N)+1)=temp$ 14: end for 15: $im{g}_2\leftarrow im{g}_1$ DNA encode 16: $im{g}_3\leftarrow im{g}_2$ Banyan Network diffusion using W. 17: $img\leftarrow im{g}_3$ DNA decode

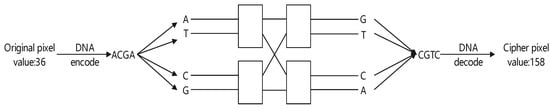
Figure 10. Example of Banyan network diffusion operation.

Decryption is the converse methodology to encryption, elucidated in Algorithm 2.

Algorithm 2 Decryption algorithm.

Input: The encrypted image $img$ and four sequences X, Y, Z and W. Output: The original image P. 1: $im{g}_3\leftarrow img$ DNA encode 2: $im{g}_2\leftarrow im{g}_3$ Banyan Network inverse diffusion using W. 3: $im{g}_1\leftarrow im{g}_2$ DNA decode 4: for$j= N:-1:1$do 5:     $temp=im{g}_1(:,j)$ 6:     $im{g}_1(:,j)=im{g}_1(:,mod(Y\left(j\right),N)+1)$ 7:     $im{g}_1(:,mod(Y\left(j\right),N)+1)=temp$ 8: end for 9: for$i=M+1:-1:1$do 10:     $temp=im{g}_1(i,:)$ 11:     $im{g}_1(i,:)=im{g}_1(mod(X\left(i\right),M+1)+1,:)$ 12:     $im{g}_1(mod(X\left(i\right),M+1)+1,:)=temp$ 13: end for 14: Extract $\alpha$ from $im{g}_1$. 15: for$i=1:M\times N$do 16:     $P\left(i\right)=mod(im{g}_1\left(i\right)-Z\left(i\right)-\alpha \times 10,256)$ 17: end for

6. Simulation Results

In this section, the evaluation of the proposed cryptosystem through distinct experimental analyses is given. Experiments were performed on a personal computer with Matlab R2021a software in Windows 11 operating system. The natural and encrypted images are visually presented in Figure 11.

Figure 11. The original and cipher images. (a) Lena gray image. (b) Encrypted image of gray Lena. (c) Lena color image. (d) Encrypted image of color Lena. (e) Baboon gray image. (f) Encrypted image of gray baboon. (g) Baboon color image. (h) Encrypted image of color baboon. (i) Sailboat gray image. (j) Encrypted image of gray sailboat. (k) Sailboat color image. (l) Encrypted image of color sailboat.

6.1. Plaintext Sensitivity

A cryptosystem with high security should be sensitive to a small change in plaintext to resist differential power attacks (DPAs). The number of pixels changing rate (NPCR) and the unified averaged changed intensity (UACI) can be used to assess the ability of encryption algorithms against DPA [34]. NPCR and UACI are calculated as follows:

$$\left\{\begin{array}{c}NPCR={\displaystyle \sum _{i=0}^M}\sum _{j=0}^{N}D(i,j)\times 100\%\hfill \\ UACI=\frac{1}{M\times N}{\displaystyle \sum _{i=0}^M}{\displaystyle \sum _{j=0}^N}\frac{\left|c_1(i,j)-c_2(i,j)\right|}{255}\times 100\%\hfill \end{array}\right.$$

(18)

where $c_1$ and $c_2$ are two cipher images corresponding to two natural images differing by a single pixel and $D(i,j)=\left\{\begin{array}{c}0,if{c}_1(i,j)=c_2(i,j)\hfill \\ 1,if{c}_1(i,j)\ne c_2(i,j)\hfill \end{array}\right.$. The vertical and horizontal dimensions of the images are denoted as M and N, respectively. As shown in Table 3, our system exhibits strong robustness against differential attacks.

Table 3. NPCR and UACI analysis for plaintext sensitivity of different algorithms.

Algorithm	Image	NPCR	UACI	Result
	Size $256\times 256$	$N_{0.05}^{*}\ge 99.5693$	$U_{0.05}^{*-}\ge 33.2824$
Ours	Lena256	100	34.5079	PASS
	Baboon256	100	33.4653	PASS
	Airfield256	100	34.2185	PASS
Ref. [10]	Cameraman256	99.6414	33.5156	PASS
	Pepper256	99.5926	33.4412	PASS
	fabio256	99.6158	33.3941	PASS
Ref. [12]	Lena256	99.6170	33.4828	PASS
Ref. [23]	Lena256	99.6063	33.2830	PASS
	Baboon256	99.5865	33.3835	PASS
	Camera256	99.5987	33.4316	PASS
Ref. [27]	Lena256	99.6166	33.4476	PASS
Ref. [28]	Lena256	99.0017	32.1443	FAIL
	Size $512\times 512$	$N_{0.05}^{*}\ge 99.5893$	$U_{0.05}^{*-}\ge 33.3730$
Ours	Lena	100	33.6941	PASS
	Baboon	100	33.8055	PASS
	Airfield	100	34.7584	PASS
	Black	100	33.9145	PASS
Ref. [10]	Lena	99.5922	33.4408	FAIL
	Boat	99.6117	33.5061	PASS
	Baboon	99.6002	33.4628	PASS
Ref. [12]	Lena	99.6170	33.4828	PASS
Ref. [23]	Lena	99.6178	33.4412	PASS
	Baboon	99.6004	33.4522	PASS
	Peppers	99.6197	33.4957	PASS
Ref. [27]	Lena	99.6099	33.4511	PASS
Ref. [28]	Lena	99.0631	33.4859	FAIL

6.2. Exhaustive Attack Analysis

6.2.1. Security Key Space

According to [35], the key space of an encryption algorithm should not be less than $2^{100}$ to protect against brute-force attacks. Our encryption framework incorporates an ensemble of secret keys, denoted as $x_0\in (-10,10),y_0\in (-10,10),z_0\in (-10,10),w_0\in (-10,10)$, $r=100$, and $N_0\in (200,2000)$. It is assumed that the computational precision of the system is ${10}^{15}$ and the key space can be described as $keyspace={(20\times {10}^{15})}^4\times 1800\approx 2^{227}\gg 2^{100}$. This provides evidence for the inherent strength of our encryption algorithm to withstand brute-force attacks.

6.2.2. Secret Key Sensitivity

A strong cryptosystem should have high sensitivity to the key. From Figure 12, a slight change in the key will make the decrypted image distort completely. Furthermore, the NPCR and UACI test results are displayed in Table 4. This demonstrates that the proposed algorithm is highly dependent on the key.

Figure 12. The original, encrypted, and decrypted images. (a) The plain image. (b) The encrypted image. (c) The decrypted image with correct key. (d) The decrypted image with $x_0+{10}^{-15}$.

Table 4. Key sensitivity analysis.

Key	${\mathit{x}}_0$	${\mathit{y}}_0$	${\mathit{z}}_0$	${\mathit{w}}_0$	${\mathit{N}}_0$
NPCR	99.6085	99.6047	99.6151	99.6170	99.6155
UACI	33.4735	33.4683	33.5749	33.4580	33.4684

6.3. Statistical Attack Analysis

6.3.1. Correlation Coefficient Test

In natural images, neighboring pixels consistently display a notable correlation. To counteract statistical attacks, the correlation among neighboring pixels is expected to be disrupted after encryption. The correlation coefficient of a gray image is described by Equation (19):

$$\left\{\begin{array}{c}E\left(x\right)=\frac{1}{N}{\displaystyle \sum _{i=0}^N}{x}_i,E\left(y\right)=\frac{1}{N}{\displaystyle \sum _{i=0}^N}{y}_i\hfill \\ D\left(x\right)=\frac{1}{N}{\displaystyle \sum _{i=0}^N}{(x_i-E\left(x\right))}^2,D\left(y\right)=\frac{1}{N}{\displaystyle \sum _{i=0}^N}{(y_i-E\left(y\right))}^2\hfill \\ cov(x,y)=\frac{1}{N}{\displaystyle \sum _{i=0}^N}(x_i-E\left(x\right))(y_i-E\left(y\right))\hfill \\ r_{xy}=\frac{\mathrm{cov}(x,y)}{\sqrt{D\left(x\right)}\times \sqrt{D\left(y\right)}}\hfill \end{array}\right.$$

(19)

where two variables, x and y, denote adjacent pixel values derived from four orientations.

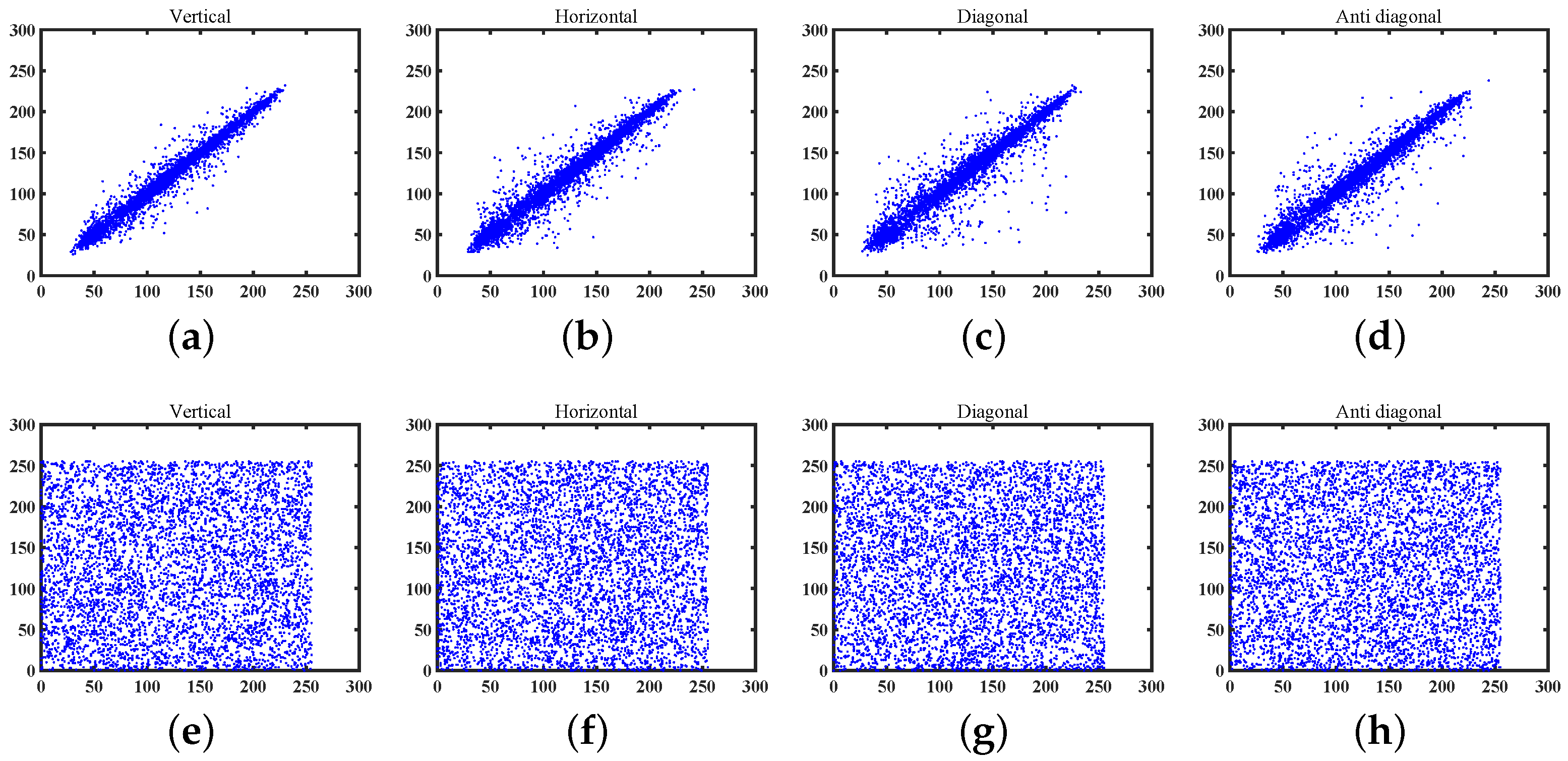
We chose 5000 pixel pairs from both the original and encrypted Lena images in four directions to calculate the correlation coefficient, and the results are outlined in Table 5. In addition, the corresponding correlation distributions of these images are graphically presented in Figure 13. It can be observed that our encryption algorithm possesses excellent performance in eliminating the inherent correlations of neighbor pixels in natural images.

Table 5. Correlation analysis of original images and encrypted images.

Algorithm	Image	Horizontal		Vertical		Diagonal
		Original	Ciphered	Original	Ciphered	Original	Ciphered
Ours	Lena	0.9851	0.0010	0.9722	−0.0053	0.9622	0.0069
	Baboon	0.7398	−0.0060	0.8764	−0.0062	0.7185	0.0068
	Airfield	0.9423	−0.0029	0.9014	−0.0028	0.9103	−0.0077
Ref. [10]	Lena	0.9851	0.0020	0.9722	0.0003	0.9622	0.0005
	Baboon	0.7398	0.0024	0.8764	−0.0005	0.7185	−0.0039
	Boat	0.9383	7.0253 × 10${}^{-4}$	0.9713	−7.5260 × 10${}^{-4}$	0.9223	−0.0016
Ref. [12]	HeadCT	0.9809	−0.0212	0.9530	−0.0111	0.9402	−0.0075
Ref. [23]	Lena	0.9851	0.0019	0.9722	0.0007	0.9622	0.0038
Ref. [27]	Lena	0.9851	−0.0018	0.9722	0.0038	0.9622	−0.0006
Ref. [28]	Lena	0.9851	0.0031	0.9722	−0.0034	0.9622	−0.0326

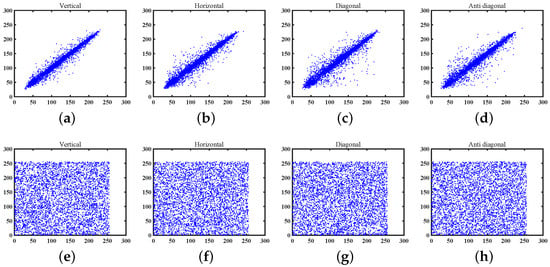
Figure 13. The correlation coefficient of Lena. (a) Vertical correlation. (b) Horizontal correlation. (c) Diagonal correlation. (d) Antidiagonal correlation. (e) Vertical correlation of encrypted image. (f) Horizontal correlation of encrypted image. (g) Diagonal correlation of encrypted image. (h) Antidiagonal correlation of encrypted image.

6.3.2. Histogram Analysis

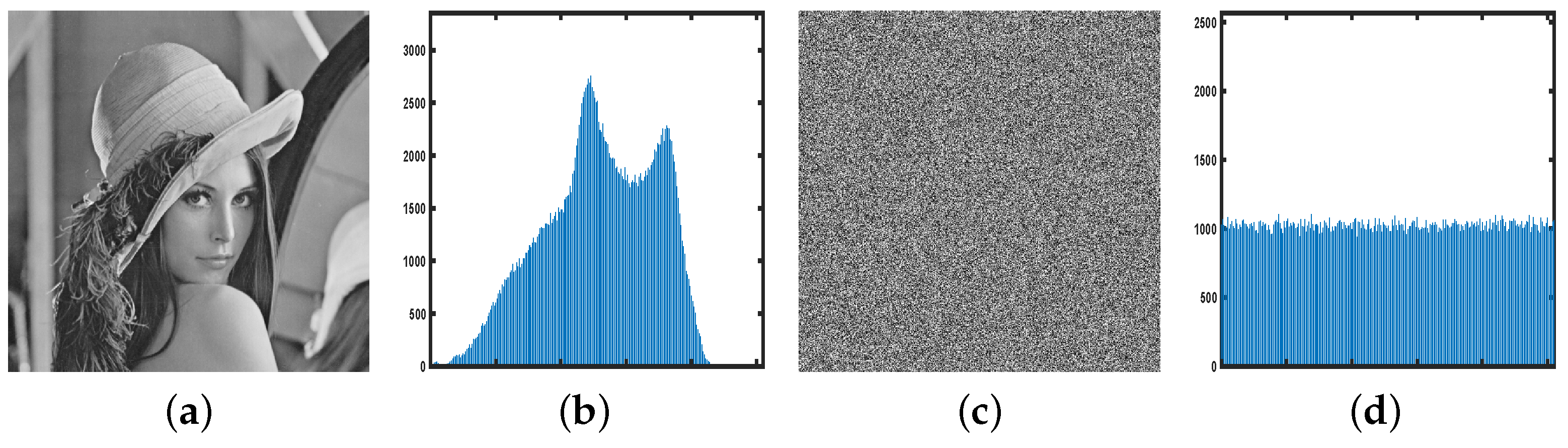
To resist statistical attacks, histogram of the encrypted image should be flat. Figure 14 displays the histograms of both the original and encrypted images, illustrating that all pixel values appear almost equally frequently. Therefore, it is impossible for attackers to acquire relevant statistics that could enable the inference of original image information.

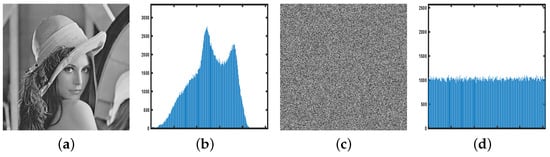
Figure 14. The histogram analysis. (a) The natural image. (b) Histogram of the natural image. (c) The cipher image. (d) Histogram of the cipher image.

Furthermore, the flatness of the histogram can be tested through the ${\chi }^2$ test, which can be calculated by Equation (20):

$$\begin{array}{c}{\chi }^2={\displaystyle \sum _{i=0}^{255}}\frac{{(f_i-f)}^2}{f}\end{array}$$

(20)

where i denotes the gray level and $f_i$ represents the frequency of the gray level i within the image. When the significance level $\alpha =0.05$ and the outcome of the ${\chi }^2$ test falls below $293.24783$, the test passes. Table 6 implies that all cipher images achieve a satisfactory level of histogram flatness.

Table 6. ${\chi }^2$ test result of gray images $(\alpha =0.05)$.

Image	${\mathit{\chi }}^2$	Result $({\mathit{\chi }}^2\le 293.2478)$	Image	${\mathit{\chi }}^2$	Result $({\mathit{\chi }}^2\le 293.2478)$
Baboon	234.4807	PASS	Lena	210.1808	PASS
Airfield	250.4073	PASS	Flower	284.6099	PASS
Fruits	255.3760	PASS	Pepper	250.3575	PASS
Sailboat	255.3752	PASS	Black	170.4671	PASS

6.3.3. Information Entropy Analysis

Information entropy $H\left(m\right)$ is often used to quantify the uncertainty of information. The theoretical value of the 256-level information source is 8. The formula of information entropy $H\left(m\right)$ is given by Equation (21):

$$H\left(m\right)=-{\displaystyle \sum _{i=1}^n}p(x_i){log}_{2}p\left(x_i\right)$$

(21)

where $x_i$ represents the value of each level. It can be observed from Table 7 that the $H\left(m\right)$ of the cipher image is close to 8, proving that the images encrypted by our algorithm exhibit a high level of randomness.

Table 7. The information entropy of gray images.

Image	Airfield	Baboon	Lena	Flower	Fruits	Pepper	Sailboat
Original	7.1206	7.3585	7.4455	7.6900	7.3644	7.3063	7.2673
Cipher	7.9992	7.9993	7.9994	7.9993	7.9992	7.9993	7.9993

6.4. Encrypted Time Analysis

When a cryptosystem is utilized on a resource-limited platform or scenario that requires real-time encryption, low time complexity is crucial. Assuming that the size of the original image is $M\times N$, the time complexity of the first diffusion operation and row–column permutation stage are both $O\left(MN\right)$. The time complexity of the Banyan network diffusion stage is $O\left(9MN\right)$. Therefore, the time complexity of the whole algorithm is $O\left(11MN\right)$. Furthermore, encrypted time analysis is given in this subsection. The overall encryption time comprises several components: iteration of the chaotic sequence, the first diffusion, row–column permutation, and Banyan network diffusion. Table 8 displays the results of the comparable encryption time analysis with other similar algorithms [10,12,23,27,28], indicating that our cryptosystem is highly efficient in encryption and has the potential for real-time encryption.

Table 8. Time required for encryption (in seconds) of each gray image.

Image Size	Ours	Ref. [10]	Ref. [12]	Ref. [23]	Ref. [27]	Ref. [28]
$512\times 512$	0.5043	1.4765	0.7449	2.5089	0.9256	4.5621
$256\times 256$	0.1295	0.1824	0.4480	0.6495	0.2764	2.1100

6.5. Chosen-Plaintext Attack Analysis

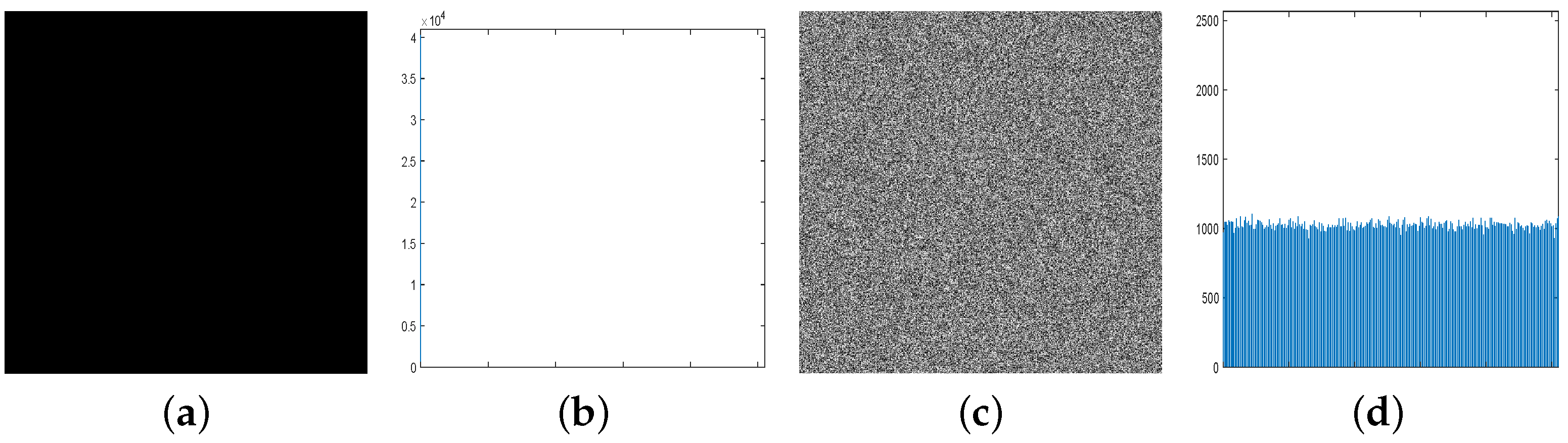
Attackers often employ the chosen/known-plaintext attacks to deduce the secret keys or reveal the underlying correlation between plaintexts and ciphertexts. For instance, attackers may deliberately select or generate a specific plaintext, such as an all-black or an all-white image, to obtain the corresponding ciphertext. As illustrated in Figure 15, the encrypted image exhibits noise-like characteristics, preventing attackers from deriving any meaningful information from it.

Figure 15. Chosen-plaintext attack analysis. (a) All-black image. (b) Histogram of all-black image. (c) The cipher image. (d) Histogram of cipher image.

6.6. PSNR Analysis

The peak signal-to-noise ratio is a metric used to assess image quality and can be used to judge the dissimilarities between the ciphertext image and the plaintext image. Its formulation is delineated in Equation (22).

$$\left\{\begin{array}{c}MSE=\frac{1}{H\times W}{\displaystyle \sum _{i=1}^H}{\displaystyle \sum _{j=1}^W}{(c_1(i,j)-c_2(i,j))}^2\hfill \\ PSNR=10lg\left(\frac{255\times 255}{MSE}\right)\hfill \end{array}\right.$$

(22)

where H and W are the dimensions of images $c_1$ and $c_2$. A lower PSNR value between the original image and the encrypted image means a higher level of randomness of the cipher image. As shown in Table 9, our algorithm has a high quality of encryption.

Table 9. PSNR value of cipher image.

Algorithm	Image	PSNR
Ours	Lena	9.2517
	Baboon	9.2073
	Airfield	8.4064
	Flower	8.3428
	Fruits	8.7510
	Pepper	8.4398
	Sailboat	8.4687
Ref. [10]	Lena	9.2878
	Baboon	9.4006
Ref. [12]	Lena	10.4370
Ref. [23]	Lena	9.6028
Ref. [27]	Lena	9.5399
	Sailboat	9.2962
Ref. [28]	Cameraman	10.6250
	Plain white	10.4563

6.7. Noise Attack and Cropping Attack Analysis

When transmitting encrypted data over public channels, they may suffer from noise effect or data loss. From Figure 16 and Figure 17 and Table 10, our algorithm has a strong robustness against the noise attack and the cropping attack, which means that the main information of the original image can be recovered when the cipher image suffers from the noise effect or data loss.

Figure 16. The Salt and pepper noise attack of Lena. (a) 0.1 Salt and pepper. (b) 0.2 Salt and pepper. (c) 0.3 Salt and pepper. (d) Decryption image of (a). (e) Decryption image of (b). (f) Decryption image of (c). (g) 0.4 Salt and pepper. (h) 0.5 Salt and pepper. (i) 0.6 Salt and pepper. (j) Decryption image of (g). (k) Decryption image of (h). (l) Decryption image of (i).

Figure 17. The cropping attack of Lena. (a) Cropping attack ($10\%$). (b) Cropping attack ($20\%$). (c) Cropping attack ($30\%$). (d) Decryption image of (a). (e) Decryption image of (b). (f) Decryption image of (c). (g) Cropping attack ($25\%$). (h) Cropping attack (≈$20\%$). (i) Cropping attack (≈$50\%$). (j) Decryption image of (g). (k) Decryption image of (h). (l) Decryption image of (i).

Table 10. PSNR value of noise attack.

Type of Attack	PSNR
Salt & pepper noise (0.1)	19.5317
Salt & pepper noise (0.2)	16.1517
Salt & pepper noise (0.3)	14.9478
Salt & pepper noise (0.4)	13.5630
Salt & pepper noise (0.5)	12.4120
Salt & pepper noise (0.6)	11.3858
Gaussian noise (0.01)	14.4505
Figure 17a cropping attack ($10\%$)	19.2930
Figure 17b cropping attack ($20\%$)	16.7923
Figure 17c cropping attack ($30\%$)	14.4860
Figure 17g cropping attack ($25\%$)	15.5209
Figure 17h cropping attack (≈$20\%$)	16.5307
Figure 17i cropping attack (≈$50\%$)	12.4853

7. Conclusions

This paper introduces a novel 1-D chaotic system 1-DSCM, and several tests, such as 0-1 test and NIST test, were performed to prove its better performance in chaotic behavior and parameters’ structure than the sin map. In addition, a new image encryption algorithm was conducted using 1-DSCM, SHA-256 hash function, and Banyan network. Taking advantage of the 1-DSCM, which can generate pseudorandom sequences quickly, and the Banyan network, which can offer parallel operation and nonlinearity, the proposed encryption algorithm processes high security and efficiency. Complete experiments show that our system has excellent performance in security and encryption speed, and it is more suitable for the scenarios requiring real-time encryption or with limited resources. In the future, we will implement the proposed encryption algorithm on an FPGA to verify the effectiveness of the network’s parallel operation in image encryption and the feasibility of the encryption system in video encryption.