Peakons and Persistence Properties of Solution for the Interacting System of Popowicz

Abstract

This paper focuses on a two-component interacting system introduced by Popowicz, which has the coupling form of the Camassa–Holm and Degasperis–Procesi equations. Using distribution theory, single peakon solutions and several double peakon solutions of the system are described in an explicit expression. Moreover, dynamic behaviors of several types of double peakon solutions are illustrated through figures. In addition, the persistence properties of the solutions to the Popowicz system in weighted $L^p$ spaces is considered via a large class of moderate weights.

1. Introduction

In this work, the following two-component interacting system [1]

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{m}_t=-3m(2u_x+v_x)-m_x(2u+v),t>0,x\in \mathbb{R},\hfill \\ n_t=-2n(2u_x+v_x)-n_x(2u+v),t>0,x\in \mathbb{R},\hfill \\ m=u-u_{xx},n=v-v_{xx},\hfill \end{array}\right.\end{array}$$

(1)

which is first derived by Popowicz via generalization of the second Hamiltonian operator of the Degasperis–Procesi equation to the two-dimensional matrix operator is systematically investigated. The system can be regarded as a coupling between the Camassa–Holm (CH) and Degasperis–Procesi (DP) equations, which indicates the case of $u=0$ or $v=0$ of Equation (1), where it is reduced to the original CH equation [2] and DP equation [3], respectively. Moreover, their various properties are extensively studied here, including the local well-posedness [4,5], persistence properties of solutions [6,7,8,9], blow-up phenomenon and global strong solutions [10], and peakon solutions [11,12,13,14,15].

It has very recently become known that N-soliton solutions can be systematically studied by the Hirota bilinear method [16], by Riemann–Hilbert problems, particularly for higher-order integrable equations [17,18,19], and for reduced nonlocal integrable equations [20,21]. All this will help to understand nonlinear complex wave models, including nonlinear nonlocal integrable models. It should be noted that the peaked solitary wave solution $u(x,t)=c{e}^{-|x-ct|}$ was first obtained in the CH equation by Camassa and Holm [2], where c is the wave speed. They showed that it has peaked solitary wave solutions which have discontinuous first derivative at the wave peak, in contrast to the smoothness of most previously known species of solitary wave solutions; thus, these are called “peakons”. Subsequently, many researchers have found that peakons are a common physical phenomenon occurring in most nonlinear wave equations, and the idea has attracted wide attention; see [11,22,23] and related references.

Currently, the majority of reported works in the literature have dealt with the interaction system of the Popowicz Equation (1). At first, Popowicz speculated that it should be integrable. However, the authors of [24] provided strong evidence of the non-integrability of the system by performing a combination of a reciprocal transformation together with Painlevé analysis. On top of that, Fu, Qu, and Ma [25] considered the well-posedness and blow-up phenomena for the system when $(u_0,v_0)\in H^s\times H^s$ with $s>5/2$. At the same time, Wang and Qin [26] obtained blow-up results for the system as well. Using the transport equations theory and the classical Friedrichs regularization method, Zhou [27] established the local well-posedness of the solutions for this system in nonhomogeneous Besov spaces $B_{p,r}^s\times B_{p,r}^s$ with $1\le p, r\le +\infty ,$ $s>max\{2+\frac{1}{p},\frac{5}{2}\}$, which further improved upon the work in reference [25].

Although there are many works in the literature concerning the CH and DP equations, the N-peakon solutions and the persistence properties of the solutions for the Popowicz system in Equation (1) have been scarcely examined. Along these lines, the main purpose of this work is to precisely describe the dynamic behaviors of single peakon and double peakon solutions by providing figures for the system in Equation (1) and exploring a different perspective on the the CH and DP equations. Furthermore, the generalized persistence properties of the solutions were thoroughly studied in weighted $L^p$ spaces via a large class of moderate weights which extends the results of Brandolese [9] on the CH equation to the Popowicz system in Equation (1).

The outline of this work is as follows. In Section 2, single peakon and double peakon solutions of the system in Equation (1) are investigated. In Section 3, the persistence properties of the solutions for the system in Equation (1) in weighted $L^p$ spaces are derived. Finally, in Section 4, the main conclusions are drawn.

2. Peakon Solution

2.1. Single Peakon Solution

First, it was assumed that the single peakon solutions of Equation (1) are of the following form:

$$\begin{array}{cc}\hfill & u=p_1{e}^{-|x-q_1|},v=r_1{e}^{-|x-q_1|},\hfill \end{array}$$

(2)

where $p_1,r_1$, and $q_1$ represent the functions of t to be determined later. The first-order derivatives of Equation (2) do not exist at point $x=q_1$; thus, Equation (2) cannot satisfy the system of Equation (1) in the classical sense. However, using distribution theory, the expressions of $u_x, u_{xx}, v_x, v_{xx}$ and $m, n, m_x, n_x, m_t, n_t$ in the weak sense can be written as follows:

$$\begin{array}{cc}\hfill & u_x=-p_{1}sgn(x-q_1)e^{-|x-q_1|},v_{{}_x}=-r_{1}sgn(x-q_1)e^{-|x-q_1|},\hfill \\ \hfill & u_{xx}=p_1{e}^{-|x-q_1|}-2p_1\delta (x-q_1),v_{xx}=r_1{e}^{-|x-q_1|}-2r_1\delta (x-q_1),\hfill \\ \hfill & m=2p_1\delta (x-q_1),n=2r_1\delta (x-q_1),\hfill \\ \hfill & m_x=2p_1{\delta }^{\prime }(x-q_1),n_x=2r_1{\delta }^{\prime }(x-q_1),\hfill \\ \hfill & m_t=2p_{1t}\delta (x-q_1)-2p_1{q}_{1t}{\delta }^{\prime }(x-q_1),\hfill \\ \hfill & n_t=2r_{1t}\delta (x-q_1)-2r_1{q}_{1t}{\delta }^{\prime }(x-q_1).\hfill \end{array}$$

(3)

Substituting Equations (2) and (3) into Equation (1) and integrating through test functions yields

$$\begin{array}{c}\hfill p_{1t}=0,r_{1t}=0,q_{1t}=(2p_1+r_1).\end{array}$$

(4)

Solving the system of Equation (4), the following expression can be derived:

$$\begin{array}{c}\hfill p_1=c_1,r_1=c_2,q_1=(2c_1+c_2)t,\end{array}$$

(5)

where $c_1,c_2$ are two arbitrary constants. Putting Equation (5) into Equation (2), the single peakon solution has the following form:

$$\begin{array}{cc}\hfill & u=c_1{e}^{-|x-(2c_1+c_2\left)t\right|},v=c_2{e}^{-|x-(2c_1+c_2\left)t\right|}.\hfill \end{array}$$

(6)

The single peakon solution Equation (6) is depicted in Figure 1. In the meantime, it can be seen that the amplitudes of $u,v$ are determined by the wave speed $c_1,c_2$; see Figure 1c,f.

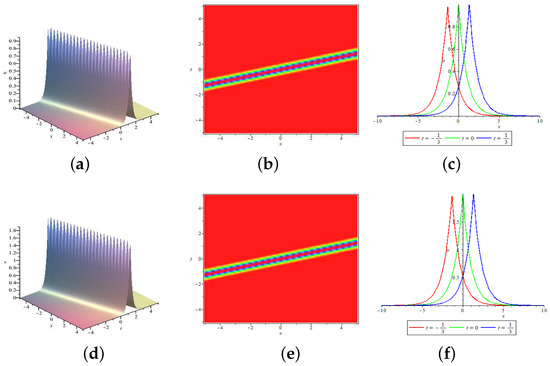
Figure 1. (Color–Online) The single peakon Equation (6) for parameters $c_1=1$ and $c_2=2$: (a,d) the 3D-polt of the solution with $u,v$; (b,e) the overhead view of the solution corresponding to (a,d) at different times shown in red, green and blue; (c,f) the wave propagation pattern of the solution along the axis $(t=-\frac{1}{3},0,\frac{1}{3})$ corresponding to (a,d) shown in red, green and blue.

2.2. Double Peakons Solutions

Next, it was assumed that the double peakons solutions of the system (1) are of the following form

$$\begin{array}{cc}\hfill & u=p_1{e}^{-|x-q_1|}+p_2{e}^{-|x-q_2|},v=r_1{e}^{-|x-q_1|}+r_2{e}^{-|x-q_2|},\hfill \end{array}$$

(7)

where $p_i,r_i$, and $q_i(i=1,2)$ are functions of t to be determined later. In addition, $u_x, v_x, m, n$ and $m_t, n_t$ have the following forms in the weak sense:

$$\begin{array}{cc}\hfill & u_x=-p_{1}sgn(x-q_1)e^{-|x-q_1|}-p_{2}sgn(x-q_2)e^{-|x-q_2|},\hfill \\ \hfill & v_x=-r_{1}sgn(x-q_1)e^{-|x-q_1|}-r_{2}sgn(x-q_2)e^{-|x-q_2|},\hfill \\ \hfill & m=2p_1\delta (x-q_1)+2p_2\delta (x-q_2),\hfill \\ \hfill & n=2r_1\delta (x-q_1)+2r_2\delta (x-q_2),\hfill \\ \hfill & m_t=2p_{1t}\delta (x-q_1)-2p_1{q}_{1t}{\delta }^{\prime }(x-q_1)+2p_{2t}\delta (x-q_2)-2p_2{q}_{2t}{\delta }^{\prime }(x-q_2),\hfill \\ \hfill & n_t=2r_{1t}\delta (x-q_1)-2r_1{q}_{1t}{\delta }^{\prime }(x-q_1)+2r_{2t}\delta (x-q_2)-2r_2{q}_{2t}{\delta }^{\prime }(x-q_2).\hfill \end{array}$$

(8)

Substituting Equations (7) and (8) into Equation (1) and integrating through test functions yields the following dynamic systems:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{p}_{1t}=2p_1(2p_2+r_2)sgn(q_1-q_2)e^{-|q_1-q_2|},\hfill \\ p_{2t}=2p_2(2p_1+r_1)sgn(q_2-q_1)e^{-|q_1-q_2|},\hfill \\ q_{1t}=2(2p_1+r_1)+2(2p_2+r_2)e^{-|q_1-q_2|},\hfill \\ q_{2t}=2(2p_2+r_2)+2(2p_1+r_1)e^{-|q_1-q_2|},\hfill \end{array}\right.\end{array}$$

(9)

and

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{r}_{1t}=2r_1(2p_2+r_2)sgn(q_1-q_2)e^{-|q_1-q_2|},\hfill \\ r_{2t}=2r_2(2p_1+r_1)sgn(q_2-q_1)e^{-|q_1-q_2|},\hfill \\ q_{1t}=2(2p_1+r_1)+2(2p_2+r_2)e^{-|q_1-q_2|},\hfill \\ q_{2t}=2(2p_2+r_2)+2(2p_1+r_1)e^{-|q_1-q_2|}.\hfill \end{array}\right.\end{array}$$

(10)

According to Equations (9) and (10), we have

$$\begin{array}{c}\hfill \frac{p_{1t}}{r_{1t}}=\frac{p_1}{r_1},\frac{p_{2t}}{r_{2t}}=\frac{p_2}{r_2},\frac{p_{1t}}{p_{2t}}=-\frac{p_1(2p_2+r_2)}{p_2(2p_1+r_1)},\frac{r_{1t}}{r_{2t}}=-\frac{r_1(2p_2+r_2)}{r_2(2p_1+r_1)}.\end{array}$$

(11)

Thus, it can be derived that

$$\begin{array}{c}\hfill p_1=-p_2+c,r_1=-r_2+c,p_2=r_2.\end{array}$$

(12)

Assuming $Q=q_1-q_2>0$ and combining the third and the fourth parts of Equation (10), the following expression applies:

$$\begin{array}{c}\hfill Q_t=6(c-2r_2)(1-e^{-Q}).\end{array}$$

(13)

According to the second Equation of (10), we can obtain the following expression:

$$\begin{array}{c}\hfill Q=ln\frac{6r_2(r_2-c)}{r_{2t}}.\end{array}$$

(14)

Substituting the above Equation (14) into Equation (13), we obtain

$$\begin{array}{c}\hfill r_{2t}=6r_2(r_2-c)+d,\end{array}$$

(15)

where d is an integral constant.

To analyze the structure of the solution of the above ordinary differential equation, the following three cases are provided for discussion.

(i)

When $2d>3c^2$, assuming $d-\frac{3c^2}{2}={\mathrm{\Delta }}^2$, according to Equation (15) we obtain

$$\begin{array}{cc}\hfill & p_1=r_1=\frac{c}{2}-\frac{\sqrt{6}}{6}\mathrm{\Delta }tan\left(\sqrt{6}\mathrm{\Delta }t\right),\hfill \\ \hfill & p_2=r_2=\frac{c}{2}+\frac{\sqrt{6}}{6}\mathrm{\Delta }tan\left(\sqrt{6}\mathrm{\Delta }t\right),\hfill \\ \hfill & Q=ln[{sin}^2\left(\sqrt{6}\mathrm{\Delta }t\right)-\frac{3c^2}{2{\mathrm{\Delta }}^2}{cos}^2\left(\sqrt{6}\mathrm{\Delta }t\right)],\hfill \\ \hfill & q_1=-q_2=\frac{1}{2}ln[{sin}^2\left(\sqrt{6}\mathrm{\Delta }t\right)-\frac{3c^2}{2{\mathrm{\Delta }}^2}{cos}^2\left(\sqrt{6}\mathrm{\Delta }t\right)].\hfill \end{array}$$

(16)

Thus the first form of the double peakon solution Equation (7) is found.

$$\begin{array}{cc}\hfill u=v=& [\frac{c}{2}-\frac{\sqrt{6}}{6}\mathrm{\Delta }tan\left(\sqrt{6}\mathrm{\Delta }t\right)]e^{-\mid x-\frac{1}{2}ln[{sin}^2\left(\sqrt{6}\mathrm{\Delta }t\right)-\frac{3c^2}{2{\mathrm{\Delta }}^2}{cos}^2\left(\sqrt{6}\mathrm{\Delta }t\right)]\mid }\hfill \\ \hfill & +[\frac{c}{2}+\frac{\sqrt{6}}{6}\mathrm{\Delta }tan\left(\sqrt{6}\mathrm{\Delta }t\right)]e^{-\mid x+\frac{1}{2}ln[{sin}^2\left(\sqrt{6}\mathrm{\Delta }t\right)-\frac{3c^2}{2{\mathrm{\Delta }}^2}{cos}^2\left(\sqrt{6}\mathrm{\Delta }t\right)]\mid }.\hfill \end{array}$$

(17)

Figure 2 shows the first form of Equation (17) for the double peakon solution Equation (7).

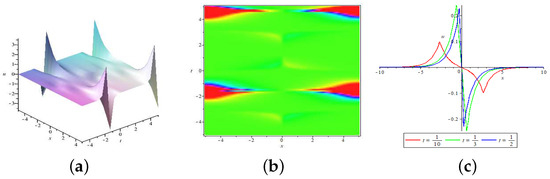Figure 2. (Color–Online) The double peakon Equation (17) for parameters $c=0$ and $\mathrm{\Delta }=\frac{1}{\sqrt{6}}$: (a) the 3D plot of the solution with u; (b) the overhead view of the solution corresponding to (a) at different times shown in red, green and blue; (c) the wave propagation pattern of the solution along the axis $(t=\frac{1}{10},\frac{1}{3},\frac{1}{2})$ corresponding to (a) shown in red, green and blue.

(ii)

When $2d<3c^2$, assuming $d-\frac{3c^2}{2}=-{\mathrm{\Theta }}^2$, according Equation (15) we obtain

$$\begin{array}{cc}\hfill & p_1=r_1=\frac{c}{2}+\frac{\sqrt{6}}{6}\mathrm{\Theta }coth\left(\sqrt{6}\mathrm{\Theta }t\right),\hfill \\ \hfill & p_2=r_2=\frac{c}{2}-\frac{\sqrt{6}}{6}\mathrm{\Theta }coth\left(\sqrt{6}\mathrm{\Theta }t\right),\hfill \\ \hfill & Q=ln\frac{{tan}^2\left(\sqrt{6}\mathrm{\Theta }t\right)-\frac{3c^2}{2{\mathrm{\Theta }}^2}}{{tan}^2\left(\sqrt{6}\mathrm{\Theta }t\right)-1},\hfill \\ \hfill & q_1=-q_2=\frac{1}{2}ln\frac{{tan}^2\left(\sqrt{6}\mathrm{\Theta }t\right)-\frac{3c^2}{2{\mathrm{\Theta }}^2}}{{tan}^2\left(\sqrt{6}\mathrm{\Theta }t\right)-1}.\hfill \end{array}$$

(18)

Therefore, the second form of the double peakon solution Equation (7) can be found.

$$\begin{array}{cc}\hfill u=v=& [\frac{c}{2}+\frac{\sqrt{6}}{6}\mathrm{\Theta }coth\left(\sqrt{6}\mathrm{\Theta }t\right)]e^{-\mid x-\frac{1}{2}ln\frac{{tan}^2\left(\sqrt{6}\mathrm{\Theta }t\right)-\frac{3c^2}{2{\mathrm{\Theta }}^2}}{{tan}^2\left(\sqrt{6}\mathrm{\Theta }t\right)-1}\mid }\hfill \\ \hfill & +[\frac{c}{2}-\frac{\sqrt{6}}{6}\mathrm{\Theta }coth\left(\sqrt{6}\mathrm{\Delta }t\right)]e^{-\mid x+\frac{1}{2}ln\frac{{tan}^2\left(\sqrt{6}\mathrm{\Theta }t\right)-\frac{3c^2}{2{\mathrm{\Theta }}^2}}{{tan}^2\left(\sqrt{6}\mathrm{\Theta }t\right)-1}|}.\hfill \end{array}$$

(19)

Figure 3 displays the second form of Equation (19) for the double peakon solution Equation (7).

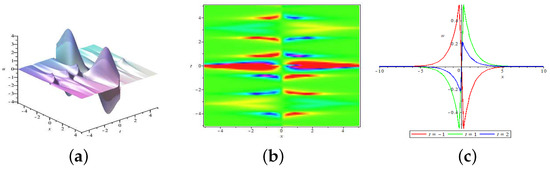Figure 3. (Color–Online) The double peakon Equation (19) for parameters $c=0$ and $\mathrm{\Theta }=\frac{1}{\sqrt{6}}$: (a) the 3D plot of the solution with u; (b) the overhead view of the solution corresponding to (a) at different times shown in red, green and blue; (c) the wave propagation pattern of the solution along the axis $(t=-1,1,2)$ corresponding to (a) shown in red, green and blue.

(iii)

When $d-\frac{3c^2}{2}=0$, according Equation (15), we have

$$\begin{array}{cc}\hfill & p_1=r_1=\frac{c}{2}+\frac{1}{6t},\hfill \\ \hfill & p_2=r_2=\frac{c}{2}-\frac{1}{6t},\hfill \\ \hfill & Q=ln(1-9c^2{t}^2),\hfill \\ \hfill & q_1=-q_2=\frac{1}{2}ln(1-9c^2{t}^2).\hfill \end{array}$$

(20)

Hence, the third form of the double peakon solution Equation (7) can be found.

$$\begin{array}{c}\hfill u=v=[\frac{c}{2}+\frac{1}{6t}]e^{-\mid x-\frac{1}{2}ln(1-9c^2{t}^2)\mid }+[\frac{c}{2}-\frac{1}{6t}]e^{-\mid x+\frac{1}{2}ln(1-9c^2{t}^2)\mid }.\end{array}$$

(21)

The profile of the third double peakon solution Equation (21) is demonstrated in Figure 4.

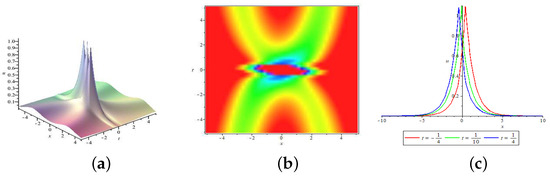Figure 4. (Color–Online) The double peakon Equation (21) for parameters $c=1$; (a) the 3D plot of the solution with u; (b) the overhead view of the solution corresponding to (a) at different times shown in red, green and blue; (c) the wave propagation pattern of the solution along the axis $(t=-\frac{1}{4},\frac{1}{10},\frac{1}{4})$ corresponding to (a) shown in red, green and blue.

2.3. N-Peakon Solutions

Finally, it was assumed that the N-peakon solutions of the system Equation (1) are of the following form:

$$\begin{array}{c}\hfill u=\sum _{i=1}^n{p}_i{e}^{-|x-q_i|},v=\sum _{i=1}^n{r}_i{e}^{-|x-q_i|}.\end{array}$$

(22)

Substituting them into Equation (1), the dynamic system can be derived as follows:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{p}_{it}=2p_i\sum _{j=1}^n(2p_j+r_j)sgn(q_i-q_j)e^{-|q_i-q_j|},\hfill \\ r_{it}=2r_i\sum _{j=1}^n(2p_j+r_j)sgn(q_i-q_j)e^{-|q_i-q_j|},\hfill \\ q_{it}=2(2p_i+r_i)+2\sum _{j=1}^n(2p_j+r_j)e^{-|q_i-q_j|}.\hfill \end{array}\right.\end{array}$$

(23)

Therefore, N-peakon solutions of Equation (1) can be established in the weak sense.

3. Persistence Property

In this section, the Cauchy problem of the interacting system in Equation (1) is considered

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{m}_t=-3m(2u_x+v_x)-m_x(2u+v),t>0,x\in \mathbb{R},\hfill \\ n_t=-2n(2u_x+v_x)-n_x(2u+v),t>0,x\in \mathbb{R},\hfill \\ m=u-u_{xx},n=v-v_{xx},t>0,x\in \mathbb{R},\hfill \\ u(0,x)=u_0\left(x\right),v(0,x)=v_0\left(x\right),x\in \mathbb{R},\hfill \\ m(0,x)=m_0\left(x\right)=u_0-u_{0xx},n(0,x)=n_0\left(x\right)=v_0-v_{0xx},x\in \mathbb{R}.\hfill \end{array}\right.\end{array}$$

(24)

Note that if $G\left(x\right)=\frac{1}{2}{e}^{-\left|x\right|},x\in \mathbb{R}$, then ${(1-{\partial }_x^2)}^{-1}f=G\ast f$ for all $f\in L^2\left(\mathbb{R}\right)$ and $G\ast m=u$. Thus, we can rewrite Equation (24) as

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{u}_t=-(2u+v)u_x-G\ast F_1-{\partial }_{x}G\ast F_2,t>0,x\in \mathbb{R},\hfill \\ v_t=-(2u+v)v_x-G\ast H_1,t>0,x\in \mathbb{R},\hfill \\ u(0,x)=u_0\left(x\right),v(0,x)=v_0\left(x\right),x\in \mathbb{R},\hfill \end{array}\right.\end{array}$$

(25)

where

$$F_1=3u(2u_x+v_x)+2u_x{(2u_x+v_x)}_x,F_2=-u_x(2u_x+v_x),$$

$$H_1=2v(2u_x+v_x)+v_x{(2u_x+v_x)}_x.$$

3.1. Weight Function

For convenience, standard definitions and lemmas concerning the weight function [9] are introduced below.

Definition 1. 

A non-negative function $\omega :{\mathbb{R}}^n\to \mathbb{R}$ is called sub-multiplicative if $\omega (x+y)\le \omega \left(x\right)w\left(y\right)$ for all $x,y\in {\mathbb{R}}^n$. A positive function φ is called ω-moderate if there exists a constant $C_0>0$ such that $\phi (x+y)\le C_0\omega \left(x\right)\phi \left(y\right)$ holds for all $x,y\in {\mathbb{R}}^n$, where ω is a given sub-multiplicative function.

Lemma 1 

(See Proposition 3.2 in [9]). φ is a ω-moderate weight function with constant $C_0$ if and only if the weighted Young estimate

$$\parallel (f_1\ast f_2){\phi \parallel }_{L^p}\le C_0\parallel f_1{\omega \parallel }_{L^1}{\parallel f_2\phi \parallel }_{L^p}$$

holds for any two measurable functions $f_1,f_2$ and $1\le p\le \infty$, where $f_1\ast f_2$ denotes the convolution $f_1\ast f_2\left(x\right)={\int }_{\mathbb{R}}{f}_1(x-y)f_2\left(y\right)dy$.

Definition 2. 

A positive function is called an admissible weighted function for the system of Equation (24) if it is a locally absolutely continuous function satisfying $|{\phi }^{\prime }\left(x\right)|\le R|\phi \left(x\right)|$ for some $R>0$ and if $a.e.x\in \mathbb{R}$, φ is ω-moderate with a sub-multiplicative weight function ω satisfying

$$\underset{x\in \mathbb{R}}{inf}\omega \left(x\right)>0,and{\int }_{\mathbb{R}}\omega \left(x\right)e^{-\left|x\right|}dx<\infty .$$

3.2. Persistence Property of the Interacting System

In the next moment, the persistence property in weighted spaces is extended to the interacting system of Equation (24) with the help of the admissible weighted function.

Theorem 1. 

Let $(u_0,v_0)\in H^s\left(\mathbb{R}\right)\times H^s\left(\mathbb{R}\right)$ with $s\ge \frac{5}{2}, 2\le p\le \infty$ and let $(u,v)\in C([0,T);H^s\left(\mathbb{R}\right)\times H^s\left(\mathbb{R}\right))\cap C([0,T);H^{s-1}\left(\mathbb{R}\right)\times H^{s-1}\left(\mathbb{R}\right))$ be the strong solution to the system of Equation (24) starting from $(u_0,v_0)$ such that $u_0\phi , u_{0x}\phi , u_{0xx}\phi , v_0\phi , v_{0x}\phi , v_{0xx}\phi \in L^p\left(\mathbb{R}\right)$, where φ is an admissible weight function for the system of Equation (24). Then, the following estimate satisfies

$$\begin{array}{cc}& {||u\left(t\right)\phi ||}_{L^p}+||u_x{\left(t\right)\phi ||}_{L^p}+||u_{xx}{\left(t\right)\phi ||}_{L^p}+{||v\left(t\right)\phi ||}_{L^p}+||v_x{\left(t\right)\phi ||}_{L^p}+||v_{xx}\left(t\right)\phi {||}_{L^p}\\ \hfill \le & e^{CMt}\left(||u_0{\phi ||}_{L^p}+||u_{0x}{\phi ||}_{L^p}+||u_{0xx}{\phi ||}_{L^p}+||v_0{\phi ||}_p+||v_{0x}{\phi ||}_p+||v_{0xx}\phi {||}_p\right),\end{array}$$

for all $t\in [0,T)$, where the constant $C>0$ depends on $R, p, C^{\prime }$, the weight functions ω and φ, and

$$M\equiv \underset{t\in [0,T)}{sup}\left({\left|\right|u\left|\right|}_{H^s}+{\left|\right|v\left|\right|}_{H^s}\right).$$

Remark 1. 

The standard class examples of the application for admissible weighted functions can be found by taking the weight function

$$\phi ={\phi }_{a,b,c,d}\left(x\right)=e^{{a\left|x\right|}^b}{(1+x)}^c(log(e+{\left|x\right|\left)\right)}^d$$

satisfying the conditions $a\ge 0, 0\le b\le 1, ab<1, c, d\in \mathbb{R}.$ The original work introducing the persistence property of the CH equation can be found in [6] (exponential), [8] (algebraical), and [9] (weighted space).

Remark 2. 

Let $M\equiv \underset{t\in [0,T)}{sup}\left({\left|\right|u\left|\right|}_{H^s}+{\left|\right|v\left|\right|}_{H^s}\right), s>\frac{3}{2}$. Per Sobloev’s embedding theorem, we have

$${\left|\right|u(·,t)\left|\right|}_{L^{\infty }}+\left|\right|u_x{(·,t)\left|\right|}_{L^{\infty }}+\left|\right|u_{xx}(·,t){\left|\right|}_{L^{\infty }}\le C^{\prime }M,$$

$${\left|\right|v(·,t)\left|\right|}_{L^{\infty }}+\left|\right|v_x{(·,t)\left|\right|}_{L^{\infty }}+\left|\right|v_{xx}(·,t){\left|\right|}_{L^{\infty }}\le C^{\prime }M,$$

where $C^{\prime }$ is a positive constant.

Proof of Theorem 1. 

$N\in \mathbb{N}\setminus \left\{0\right\}$, consider the following $N$–truncation: $f\left(x\right)=f_N\left(x\right)=min\{\phi ,N\}.$ Then, it is obvious that $f\left(x\right):\mathbb{R}\to \mathbb{R}$ is a locally absolutely continuous function satisfying ${\left|\right|f\left|\right|}_{L^{\infty }}\le N, |f^{\prime }\left(x\right)|\le R|f\left(x\right)|,a.ex\in \mathbb{R}.$ Multiplying the first equation in Equation (25) by $f\left(x\right){\left(uf\left(x\right)\right)}^{p-1}$ and integrating over $\mathbb{R}$, we have

$$\begin{array}{ccc}\hfill & & {\displaystyle \frac{1}{p}\frac{d}{dt}{\left|\right|uf\left(x\right)\left|\right|}_{L^p}^p}\hfill \\ \hfill & =& {\displaystyle -{\int }_{\mathbb{R}}[(2u+v)u_{x}f\left(x\right){\left(uf\left(x\right)\right)}^{p-1}+G\ast F_1{\left(uf\left(x\right)\right)}^{p-1}f\left(x\right)}\hfill \\ & & +{\partial }_{x}G\ast F_2{\left(uf\left(x\right)\right)}^{p-1}f\left(x\right)]dx\hfill \\ \hfill & =& {\displaystyle -{\int }_{\mathbb{R}}\{(2u+v)[{\left(uf\left(x\right)\right)}_x-u{f}^{\prime }\left(x\right)]{\left(uf\left(x\right)\right)}^{p-1}+(G\ast F_1){\left(uf\left(x\right)\right)}^{p-1}f\left(x\right)}\hfill \\ & & +({\partial }_{x}G\ast F_2){\left(uf\left(x\right)\right)}^{p-1}f\left(x\right)\}dx\hfill \\ \hfill & \le & {\displaystyle \left|\frac{1}{p}{\int }_{\mathbb{R}}{(2u+v)}_x{\left(uf\left(x\right)\right)}^{p}dx\right|+\left|{\int }_{\mathbb{R}}(2u+v)\left(u{f}^{\prime }\left(x\right)\right){\left(uf\left(x\right)\right)}^{p-1}dx\right|}\hfill \\ & & +\left|\right|f\left(x\right)·G\ast F_1{\left|\right|}_{L^p}{\left|\right|\left(uf\left(x\right)\right)\left|\right|}_{L^p}^{p-1}+\left|\right|f\left(x\right)·{\partial }_{x}G\ast F_2{\left|\right|}_{L^p}{\left|\right|\left(uf\left(x\right)\right)\left|\right|}_{L^p}^{p-1}\hfill \\ \hfill & \le & C_1{M\left|\right|uf\left(x\right)\left|\right|}_{L^p}^p+\left|\right|f\left(x\right)·G\ast F_1{\left|\right|}_{L^p}{\left|\right|\left(uf\left(x\right)\right)\left|\right|}_{L^p}^{p-1}\hfill \\ \hfill & & +\left|\right|f\left(x\right)·{\partial }_{x}G\ast F_2{\left|\right|}_{L^p}{\left|\right|\left(uf\left(x\right)\right)\left|\right|}_{L^p}^{p-1},\hfill \end{array}$$

(26)

where $C_1$ depends only on $R, p$, and $C^{\prime }$. It follows that

$$\begin{array}{c}\hfill {\displaystyle \frac{d}{dt}{\left|\right|uf\left(x\right)\left|\right|}_{L^p}\le C_1{M\left|\right|uf\left(x\right)\left|\right|}_{L^p}+\left|\right|f\left(x\right)·G\ast F_1{\left|\right|}_{L^p}+\left|\right|f\left(x\right)·{\partial }_{x}G\ast F_2{\left|\right|}_{L^p}.}\end{array}$$

(27)

Now, we can to find a similar estimate on $u_{x}f$. Differentiating by x the first Equation in (25), we have

$$u_{tx}=-{(2u+v)}_x{u}_x-(2u+v)u_{xx}-{\partial }_{x}G\ast F_1-{\partial }_x^{2}G\ast F_2.$$

(28)

Multiplying Equation (28) by $f\left(x\right){\left(u_{x}f\left(x\right)\right)}^{p-1}$ and integrating over $\mathbb{R}$, we now have

$$\begin{array}{ccc}\hfill & & {\displaystyle \frac{1}{p}\frac{d}{dt}\left|\right|u_{x}f\left(x\right){\left|\right|}_{L^p}^p}\hfill \\ \hfill & =& {\displaystyle -{\int }_{\mathbb{R}}[{(2u+v)}_x{u}_{x}f\left(x\right){\left(u_{x}f\left(x\right)\right)}^{p-1}+(2u+v)u_{xx}f\left(x\right){\left(u_{x}f\left(x\right)\right)}^{p-1}}\hfill \\ & & +{\partial }_{x}G\ast F_1{\left(u_{x}f\left(x\right)\right)}^{p-1}f\left(x\right)+{\partial }_x^{2}G\ast F_2{\left(u_{x}f\left(x\right)\right)}^{p-1}f\left(x\right)]dx\hfill \\ \hfill & =& {\displaystyle -{\int }_{\mathbb{R}}\{{(2u+v)}_x{\left(u_{x}f\left(x\right)\right)}^p+(2u+v)[{\left(u_{x}f\left(x\right)\right)}_x-u_x{f}^{\prime }\left(x\right)]{\left(u_{x}f\left(x\right)\right)}^{p-1}}\hfill \\ & & +{\partial }_{x}G\ast F_1{\left(u_{x}f\left(x\right)\right)}^{p-1}f\left(x\right)+{\partial }_x^{2}G\ast F_2{\left(u_{x}f\left(x\right)\right)}^{p-1}f\left(x\right)\}dx\hfill \\ \hfill & \le & C_{2}M\left|\right|u_x{f\left(x\right)\left|\right|}_{L^p}^p+\left|\right|f\left(x\right)·{\partial }_{x}G\ast F_1{\left|\right|}_{L^p}\left|\right|\left(u_{x}f\left(x\right)\right){\left|\right|}_{L^p}^{p-1}\hfill \\ \hfill & & +\left|\right|f\left(x\right)·{\partial }_x^{2}G\ast F_2{\left|\right|}_{L^p}\left|\right|\left(u_{x}f\left(x\right)\right){\left|\right|}_{L^p}^{p-1},\hfill \end{array}$$

(29)

where $C_2$ depends only on $C^{\prime }$ and R. It follows that

$$\begin{array}{c}\hfill {\displaystyle \frac{d}{dt}\left|\right|u_x{f\left(x\right)\left|\right|}_{L^p}\le C_{2}M\left|\right|u_x{f\left(x\right)\left|\right|}_{L^p}+\left|\right|f\left(x\right)·{\partial }_{x}G\ast F_1{\left|\right|}_{L^p}+\left|\right|f\left(x\right)·{\partial }_x^{2}G\ast F_2{\left|\right|}_{L^p}.}\end{array}$$

(30)

Now, we can find a similar estimate on $u_{xx}f$. Differentiating Equation (28) by x, we have

$$u_{txx}=-{(2u+v)}_{xx}{u}_x-2{(2u+v)}_x{u}_{xx}-(2u+v)u_{xxx}-{\partial }_x^{2}G\ast F_1-{\partial }_x^{3}G\ast F_2.$$

(31)

Multiplying Equation (31) by $f\left(x\right){\left(u_{xx}f\left(x\right)\right)}^{p-1}$ and integrating over $\mathbb{R}$, we have

$$\begin{array}{ccc}\hfill & & {\displaystyle \frac{1}{p}\frac{d}{dt}\left|\right|u_{xx}f\left(x\right){\left|\right|}_{L^p}^p}\hfill \\ \hfill {\displaystyle }& =& {\displaystyle -{\int }_{\mathbb{R}}[{(2u+v)}_x{u}_{x}f\left(x\right){\left(u_{xx}f\left(x\right)\right)}^{p-1}+2{(2u+v)}_x{u}_{xx}f\left(x\right){\left(u_{xx}f\left(x\right)\right)}^{p-1}}\hfill \\ & & +(2u+v)u_{xxx}f\left(x\right){\left(u_{xx}f\left(x\right)\right)}^{p-1}+{\partial }_x^{2}G\ast F_1{\left(u_{xx}f\left(x\right)\right)}^{p-1}f\left(x\right)\hfill \\ \hfill & & +{\partial }_x^{3}G\ast F_2{\left(u_{xx}f\left(x\right)\right)}^{p-1}f\left(x\right)]dx\hfill \\ \hfill & \le & C_{3}M\left|\right|u_{xx}{f\left(x\right)\left|\right|}_{L^p}^{p-1}\left|\right|u_x{f\left(x\right)\left|\right|}_{L^p}+CM\left|\right|u_{xx}f\left(x\right){\left|\right|}_{L^p}^p\hfill \\ & & +CM\left|\right|u_{xx}{f\left(x\right)\left|\right|}_{L^p}^p+\left|\right|f\left(x\right)·{\partial }_x^{2}G\ast F_1{\left|\right|}_{L^p}\left|\right|\left(u_{xx}f\left(x\right)\right){\left|\right|}_{L^p}^{p-1}\hfill \\ \hfill & & +\left|\right|f\left(x\right)·{\partial }_x^{3}G\ast F_2{\left|\right|}_{L^p}\left|\right|\left(u_{xx}f\left(x\right)\right){\left|\right|}_{L^p}^{p-1}.\hfill \end{array}$$

(32)

It follows that

$$\begin{array}{ccc}\hfill {\displaystyle \frac{d}{dt}\left|\right|u_{xx}f\left(x\right){\left|\right|}_{L^p}}& \le & C_{3}M\left(\right||u_x{f\left(x\right)\left|\right|}_{L^p}+\left|\right|u_{xx}{f\left(x\right)\left|\right|}_{L^p})+||f\left(x\right)·{\partial }_x^{2}G\ast F_1{\left|\right|}_{L^p}\hfill \\ \hfill & & +\left|\right|f\left(x\right)·{\partial }_x^{3}G\ast F_2{\left|\right|}_{L^p},\hfill \end{array}$$

(33)

where $C_3$ depends only on $C^{\prime }$ and R. Combining this with Equations (27), (29), and (33),

$$\begin{array}{ccc}\hfill & & {\displaystyle \frac{d}{dt}{(|\left|uf\left(x\right)\right||}_{L^p}+\left|\right|u_x{f\left(x\right)\left|\right|}_{L^p}+\left|\right|u_{xx}{f\left(x\right)\left|\right|}_{L^p})}\hfill \\ \hfill & \le & C_4{M\left(\right|\left|uf\left(x\right)\right||}_{L^p}+\left|\right|u_x{f\left(x\right)\left|\right|}_{L^p}+\left|\right|u_{xx}{f\left(x\right)\left|\right|}_{L^p})\hfill \\ \hfill & & +\left|\right|f\left(x\right)·G\ast F_1{\left|\right|}_{L^p}+\left|\right|f\left(x\right)·{\partial }_{x}G\ast F_2{\left|\right|}_{L^p}\hfill \\ \hfill & & +\left|\right|f\left(x\right)·{\partial }_{x}G\ast F_1{\left|\right|}_{L^p}+\left|\right|f\left(x\right)·{\partial }_x^{2}G\ast F_2{\left|\right|}_{L^p}\hfill \\ \hfill & & +\left|\right|f\left(x\right)·{\partial }_x^{2}G\ast F_1{\left|\right|}_{L^p}+\left|\right|f\left(x\right)·{\partial }_x^{3}G\ast F_2{\left|\right|}_{L^p},\hfill \end{array}$$

(34)

where $C_4$ depends only on $C^{\prime }, R$, and p. Note that f is $\omega$–moderate; thus, per Lemma 1, we arrive at

$$\begin{array}{ccc}\hfill \left|\right|(G\ast F_1)f\left(x\right){\left|\right|}_{L^p}& \le & C_0{\left|\right|G\omega \left|\right|}_{L^1}\left|\right|F_1{f\left(x\right)\left|\right|}_{L^p}\le C_5\left|\right|F_{1}f\left(x\right){\left|\right|}_{L^p}\hfill \\ \hfill & \le & C_5{M\left(\right|\left|uf\left(x\right)\right||}_{L^p}+\left|\right|u_x{f\left(x\right)\left|\right|}_{L^p}+\left|\right|u_{xx}{f\left(x\right)\left|\right|}_{L^p}).\hfill \end{array}$$

(35)

Checking that ${\partial }_{x}G=sgn\left(x\right)G$ in the weak sense, we obtai

$$\begin{array}{ccc}\hfill \left|\right|({\partial }_{x}G\ast F_2)f\left(x\right){\left|\right|}_{L^p}& \le & C_0\left|\right|{\partial }_x{G\omega \left|\right|}_{L^1}\left|\right|F_2{f\left(x\right)\left|\right|}_{L^p}\le C_6\left|\right|F_{2}f\left(x\right){\left|\right|}_{L^p}\hfill \\ \hfill & \le & C_{6}M\left|\right|u_{x}f\left(x\right){\left|\right|}_{L^p},\hfill \end{array}$$

(36)

$$\begin{array}{ccc}\hfill \left|\right|({\partial }_{x}G\ast F_1)f\left(x\right){\left|\right|}_{L^p}& \le & C_0\left|\right|{\partial }_x{G\omega \left|\right|}_{L^1}\left|\right|F_1{f\left(x\right)\left|\right|}_{L^p}\le C_7\left|\right|F_{1}f\left(x\right){\left|\right|}_{L^p}\hfill \\ \hfill & \le & C_7{M\left(\right|\left|uf\left(x\right)\right||}_{L^p}+\left|\right|u_x{f\left(x\right)\left|\right|}_{L^p}+\left|\right|u_{xx}{f\left(x\right)\left|\right|}_{L^p}).\hfill \end{array}$$

(37)

Due to ${\partial }_x^{2}G\ast f=G-\delta$, we can estimate some term as follows:

$$\begin{array}{ccc}\hfill \left|\right|({\partial }_x^{2}G\ast F_2)f\left(x\right){\left|\right|}_{L^p}& \le & C_0\left|\right|{\partial }_x^2{G\omega \left|\right|}_{L^1}\left|\right|F_2{f\left(x\right)\left|\right|}_{L^p}\le C_8\left|\right|F_{2}f\left(x\right){\left|\right|}_{L^p}\hfill \\ \hfill & \le & C_{8}M\left|\right|u_{x}f\left(x\right){\left|\right|}_{L^p},\hfill \end{array}$$

(38)

$$\begin{array}{ccc}\hfill \left|\right|({\partial }_x^{2}G\ast F_1)f\left(x\right){\left|\right|}_{L^p}& \le & C_0\left|\right|{\partial }_x^2{G\omega \left|\right|}_{L^1}\left|\right|F_1{f\left(x\right)\left|\right|}_{L^p}\le C_9\left|\right|F_{1}f\left(x\right){\left|\right|}_{L^p}\hfill \\ \hfill & \le & C_9{M\left(\right|\left|uf\left(x\right)\right||}_{L^p}+\left|\right|u_x{f\left(x\right)\left|\right|}_{L^p}+\left|\right|u_{xx}{f\left(x\right)\left|\right|}_{L^p}),\hfill \end{array}$$

(39)

$$\begin{array}{ccc}\hfill \left|\right|({\partial }_x^{3}G\ast F_2)f\left(x\right){\left|\right|}_{L^p}& =& \left|\right|({\partial }_x^{2}G\ast {\partial }_x{F}_2)f\left(x\right){\left|\right|}_{L^p}\le C_{10}M\left(\right||u_{x}f\left(x\right){\left|\right|}_{L^p}+\left|\right|u_{xx}f\left(x\right){\left|\right|}_{L^p}).\hfill \end{array}$$

(40)

Here $C_5, C_6, C_7, C_8, C_9, C_{10}$ depend on $C^{\prime }$ and the weight functions $\phi , \omega$. Substituting Equations (35)–(40) into Equation (34), we obtain

$$\begin{array}{c}\hfill {\displaystyle \frac{d}{dt}{\left(\right|\left|uf\left(x\right)\right||}_{L^p}+\left|\right|u_x{f\left(x\right)\left|\right|}_{L^p}+\left|\right|u_{xx}{f\left(x\right)\left|\right|}_{L^p}{)\le CM(\left|\right|uf\left(x\right)\left|\right|}_{L^p}+\left|\right|u_x{f\left(x\right)\left|\right|}_{L^p}+\left|\right|u_{xx}{f\left(x\right)\left|\right|}_{L^p}),}\end{array}$$

(41)

where C depends on $R, p, C^{\prime }$, and the weight functions $\phi , \omega$. Per Gronwall’s inequality, we arrive at

$$\begin{array}{c}\hfill {\displaystyle {\left|\right|uf\left(x\right)\left|\right|}_{L^p}+\left|\right|u_x{f\left(x\right)\left|\right|}_{L^p}+\left|\right|u_{xx}{f\left(x\right)\left|\right|}_{L^p}\le e^{CMt}\left(\right||u_0{f\left(x\right)\left|\right|}_{L^p}+\left|\right|u_{0x}{f\left(x\right)\left|\right|}_{L^p}+\left|\right|u_{0xx}{f\left(x\right)\left|\right|}_{L^p}).}\end{array}$$

(42)

Using a similar method for the second equation in Equation (25), we have

$$\begin{array}{c}\hfill {\displaystyle {\left|\right|vf\left(x\right)\left|\right|}_{L^p}+\left|\right|v_x{f\left(x\right)\left|\right|}_{L^p}+\left|\right|v_{xx}{f\left(x\right)\left|\right|}_{L^p}\le e^{CMt}\left(\right||v_0{f\left(x\right)\left|\right|}_{L^p}+\left|\right|v_{0x}{f\left(x\right)\left|\right|}_{L^p}+\left|\right|v_{0xx}{f\left(x\right)\left|\right|}_{L^p}).}\end{array}$$

(43)

Due to $f\left(x\right)\to \phi \left(x\right)$, as $N\to \infty$ for a.e $x\in \mathbb{R}$, per the assumed conditions $u_0\phi \left(x\right), u_{0x}\phi \left(x\right), u_{0xx}\phi \left(x\right), v_0\phi \left(x\right), v_{0x}\phi , v_{0xx}\phi \left(x\right)\in L^p\left(\mathbb{R}\right)$, for $2\le p<\infty , 0\le t<T$ we obtain

$$\begin{array}{ccc}\hfill {\displaystyle }& & {\left|\right|u\phi \left(x\right)\left)\right||}_{L^p}+\left|\right|u_x{\phi \left(x\right)\left|\right|}_{L^p}+\left|\right|u_{xx}\phi \left(x\right){\left|\right|}_{L^p}\hfill \\ & & +{\left|\right|v\phi \left(x\right)\left|\right|}_{L^p}+\left|\right|v_x{\phi \left(x\right)\left)\right||}_{L^p}+\left|\right|v_{xx}\phi \left(x\right){\left|\right|}_{L^p}\hfill \\ \hfill & \le & e^{CMt}\left(\right||u_0{\phi \left(x\right)\left|\right|}_{L^p}+\left|\right|u_{0x}{\phi \left(x\right)\left|\right|}_{L^p}+\left|\right|u_{0xx}\phi \left(x\right){\left|\right|}_{L^p}\hfill \\ & & +\left|\right|v_0{\phi \left(x\right)\left|\right|}_{L^p}+\left|\right|v_{0x}{\phi \left(x\right)\left|\right|}_{L^p}+\left|\right|v_{0xx}{\phi \left(x\right)\left|\right|}_{L^p}).\hfill \end{array}$$

(44)

Letting $p\to \infty$, due to the term $e^{CMt}$ being independent on p, the implication is that

$$\begin{array}{ccc}\hfill {\displaystyle }& & {\left|\right|u\phi \left(x\right)\left)\right||}_{L^{\infty }}+\left|\right|u_x{\phi \left(x\right)\left|\right|}_{L^{\infty }}+\left|\right|u_{xx}\phi \left(x\right){\left|\right|}_{L^{\infty }}\hfill \\ & & +{\left|\right|v\phi \left(x\right)\left|\right|}_{L^{\infty }}+\left|\right|v_x{\phi \left(x\right)\left)\right||}_{L^{\infty }}+\left|\right|v_{xx}\phi \left(x\right){\left|\right|}_{L^{\infty }}\hfill \\ \hfill & \le & e^{CMt}\left(\right||u_0{\phi \left(x\right)\left|\right|}_{L^{\infty }}+\left|\right|u_{0x}{\phi \left(x\right)\left|\right|}_{L^{\infty }}+\left|\right|u_{0xx}\phi \left(x\right){\left|\right|}_{L^{\infty }}\hfill \\ & & +\left|\right|v_0{\phi \left(x\right)\left|\right|}_{L^{\infty }}+\left|\right|v_{0x}{\phi \left(x\right)\left|\right|}_{L^{\infty }}+\left|\right|v_{0xx}{\phi \left(x\right)\left|\right|}_{L^{\infty }}).\hfill \end{array}$$

(45)

This completes the proof of Theorem 1. □

Corollary 1. 

In Theorem 1, when taking $\phi =e^{a\left|x\right|}, 0<a<1$ and leaving all other conditions the same, the following estimate satisfies

$$\begin{array}{ll}& \left|\right|u\left(t\right)e^{a\left|x\right|}{\left|\right|}_{L^p}+\left|\right|u_x\left(t\right)e^{a\left|x\right|}{\left|\right|}_{L^p}+\left|\right|u_{xx}\left(t\right)e^{a\left|x\right|}{\left|\right|}_{L^p}+\left|\right|v\left(t\right)e^{a\left|x\right|}{\left|\right|}_{L^p}+\left|\right|v_x\left(t\right)e^{a\left|x\right|}{\left|\right|}_{L^p}+\left|\right|v_{xx}\left(t\right)e^{a\left|x\right|}{\left|\right|}_{L^p}\\ & \le e^{CMt}\left(\left|\right|u_0{e}^{a\left|x\right|}{\left|\right|}_{L^p}+\left|\right|u_{0x}{e}^{a\left|x\right|}{\left|\right|}_{L^p}+\left|\right|u_{0xx}{e}^{a\left|x\right|}{\left|\right|}_{L^p}+\left|\right|v_0{e}^{a\left|x\right|}{\left|\right|}_{L^p}+\left|\right|v_{0x}{e}^{a\left|x\right|}{\left|\right|}_{L^p}+\left|\right|v_{0xx}{e}^{a\left|x\right|}{\left|\right|}_{L^p}\right),\end{array}$$

for all $t\in [0,T)$.

Corollary 2. 

In Theorem 1, taking $\phi ={(1+x)}^{\gamma }$ and leaving all other conditions the same, the following estimate satisfies

$$\begin{array}{cc}& {\left|\right|u\left(t\right)(1+x)}^{\gamma }{\left|\right|}_{L^p}+\left|\right|u_x\left(t\right){(1+x)}^{\gamma }{\left|\right|}_{L^p}+\left|\right|u_{xx}\left(t\right){(1+x)}^{\gamma }{\left|\right|}_{L^p}\\ & +{\left|\right|v\left(t\right)(1+x)}^{\gamma }{\left|\right|}_{L^p}+\left|\right|v_x\left(t\right){(1+x)}^{\gamma }{\left|\right|}_{L^p}+\left|\right|v_{xx}\left(t\right){(1+x)}^{\gamma }{\left|\right|}_{L^p}\\ & \le e^{CMt}\left(\right||u_0{(1+x)}^{\gamma }{\left|\right|}_{L^p}+\left|\right|u_{0x}{(1+x)}^{\gamma }{\left|\right|}_{L^p}+\left|\right|u_{0xx}{(1+x)}^{\gamma }{\left|\right|}_{L^p}\\ & +\left|\right|v_0{(1+x)}^{\gamma }{\left|\right|}_{L^p}+\left|\right|v_{0x}{(1+x)}^{\gamma }{\left|\right|}_{L^p}+\left|\right|v_{0xx}{(1+x)}^{\gamma }{\left|\right|}_{L^p}),\end{array}$$

for all $t\in [0,T)$.

4. Conclusions

In this work, distribution theory was developed to investigate a two-component interacting system as introduced by Popowicz, whereby the cases of single peakon solutions, double peakon solutions, and multi-peakon solutions for the system were provided. It is worth noting that along with the various peakon solutions of the Popowicz system being derived, in this paper the persistence properties of the solutions in weighted $L^p$ spaces via a large class of moderate weights have been considered. The Popowicz system can additionally be considered as a coupling between the CH and DP equations. Therefore, further properties of this system should be investigated in future works, for example, the stability of peakons solutions.