Coarse Sheaf Cohomology

Abstract

A certain Grothendieck topology assigned to a metric space gives rise to a sheaf cohomology theory which sees the coarse structure of the space. Already constant coefficients produce interesting cohomology groups. In degree 0, they see the number of ends of the space. In this paper, a resolution of the constant sheaf via cochains is developed. It serves to be a valuable tool for computing cohomology. In addition, coarse homotopy invariance of coarse cohomology with constant coefficients is established. This property can be used to compute cohomology of Riemannian manifolds. The Higson corona of a proper metric space is shown to reflect sheaves and sheaf cohomology. Thus, we can use topological tools on compact Hausdorff spaces in our computations. In particular, if the asymptotic dimension of a proper metric space is finite, then higher cohomology groups vanish. We compute a few examples. As it turns out, finite abelian groups are best suited as coefficients on finitely generated groups.

1. Introduction

The sheaf-theoretic approach to coarse metric spaces has been applied in many different contexts [1,2,3]. Sheaf-theoretic methods play an important role in our paper. We also present three other computational tools. Cochain complexes assigned to a filtration of Vietoris–Rips complexes have not just been used in the coarse setting [4]. Many well-known coarse (co-)homology theories are coarse homotopy invariant [5,6,7]. The cohomology of the Higson corona is of course as a composition of functors a coarse invariant which has been studied before [8]. Even in combination with other computational methods [9], coarse invariants are hard to compute for the spaces one is most interested in, which include Riemannian manifolds and finitely generated groups.

Coarse sheaf cohomology has been designed by the author in her thesis. Aside from an agenda to present new computational methods which may be suitable for a large number of spaces, there are two immediate results:

Theorem 1. 

If M is a non-positively curved closed Riemannian n-manifold and A a finite abelian group, then

$${\check{H}}_{ct}^q(M,A)=H_{sing}^q(S^{n-1};A)$$

the left side denotes coarse sheaf cohomology with values in the constant sheaf A and the right side denotes singular cohomology with values in the group A.

This result can be immediately applied to define a coarse version of mapping degree associated to a coarse map between manifolds.

Theorem 2. 

If T is a simplicial tree with infinitely many ends and A is a finite abelian group, then

$${\check{H}}_{ct}^q(T;A)=\left\{\begin{array}{cc}\underset{\mathbb{N}}{⨁}A\hfill & q=0\hfill \\ 0\hfill & otherwise.\hfill \end{array}\right.$$

(1)

There are many interesting cohomology theories on coarse metric spaces. The most prominent examples are Roe’s coarse cohomology [10,11,12] and controlled operator K-theory [13,14,15,16]. If two metric spaces $X,Y$ have the same coarse type, then specifying a coarse equivalence $X\to Y$ is a proof. If on the other hand $X,Y$ do not have the same coarse type, then a coarse invariant which does not have the same values on X and Y gives a proof. In general, a well-designed cohomology theory delivers a rich source of invariants which are easy to compute. To this date, cohomology of finitely generated free abelian groups has been calculated for Roe’s coarse cohomology and also controlled operator K-theory. There is still a gap in knowledge about cohomology of other finitely generated groups. Riemannian manifolds on the other hand do not show interesting cohomology groups since every Riemannian n-manifold with nonpositive sectional curvature is coarsely homotopic to ${\mathbb{R}}^n$ and most coarse cohomology theories are coarse homotopy invariant [10].

Our coarse cohomology theory ${\check{H}}_{ct}^q(·;·)$ is a sheaf cohomology theory on a Grothendieck topology $X_{ct}$ assigned to a metric space X [17]. If A is an abelian group, then for the constant sheaf A on X we obtain in dimension 0 a copy of A for every end of X or an infinite direct sum of copies of A if X does not have finitely many ends [17].

In this paper, we design a cochain complex ${\left(C{Y}_b^q(X;A)\right)}_q$ assigned to a metric space X and abelian group A. The functor $U\subseteq X\mapsto C{Y}_b^q(U,A)$ forms a flabby sheaf on $X_{ct}$. The sequence of sheaves

$$0\to A_X\to C{Y}_b^0(·,A)\to C{Y}_b^1(·,A)\to C{Y}_b^2(·,A)\to \cdots$$

is exact. Thus, cohomology of

$$0\to C{Y}_b^0(X,A)\to C{Y}_b^1(X,A)\to C{Y}_b^2(X,A)\to \cdots$$

computes coarse sheaf cohomology of X with values in $A_X$.

Theorem 3. 

If X is a metric space, then there is a flabby resolution $C{Y}_b^q(·;A)$ of the constant sheaf $A_X$ on $X_{ct}$. We can compute sheaf cohomology with values in the constant sheaf using cochain complexes:

$${\check{H}}_{ct}^q(X;A_X)=H{Y}_b^q(X,A).$$

For $q\ge 1$, there is a comparison map $H{Y}_b^q(X;A)\to H{X}^{q+1}(X;A)$ with Roe coarse cohomology. This map is neither injective nor surjective though. The main difference is that our cochains are defined as maps that need to be “blocky” while coarse cochains do not have this restriction. Thus, general statements on cohomology are easier to prove for Roe coarse cohomology, while we hope that combinatorical computations are easier realized using blocky cochains.

There are several notions of homotopy on the coarse category which are all equivalent in some way. The homotopy theory we are going to employ uses the asymptotic product as coarse substitute for a product and the first quadrant in ${\mathbb{R}}^2$ equipped with the Manhattan metric as a coarse substitute for an interval [18]. In effect, this homotopy theory and the other coarse homotopy theories are only of use if one wants to compute cohomology of ${\mathbb{R}}^n$ and maybe Riemannian manifolds. Nonetheless, we prove that coarse sheaf cohomology is a coarse homotopy invariant using the resolution via cochains.

Theorem 4. 

If two coarse maps $\alpha ,\beta :X\to Y$ between metric spaces are coarsely homotopic, then they induce the same map

$${\alpha }^{\ast },{\beta }^{\ast }:{\check{H}}_{ct}^q(Y;A)\to {\check{H}}_{ct}^q(X;A)$$

in cohomology with values in a constant sheaf A.

A coarse map $\alpha :X\to Y$ between metric spaces induces a cochain map ${\alpha }^{\ast }:C{Y}_b^q(Y;A)\to C{Y}_b^q(X;A)$ which in turn induces a homomorphism ${\alpha }^{\ast }:H{Y}_b^q(Y;A)\to H{Y}_b^q(X;A)$. Conversely, the inverse image functor maps the constant sheaf $A_Y$ on $Y_{ct}$ to the constant sheaf $A_X$ on $X_{ct}$. Thus, there is an induced homomorphism ${\alpha }^{\ast }$ in cohomology. One may wonder if both homomorphisms ${\alpha }^{\ast },{\alpha }^{\ast }$ coincide, and indeed they do.

To a proper metric space X we can assign a compact Hausdorff topological space $\nu \left(X\right)$, the Higson corona of X. This version of boundary reflects sheaf cohomology in the following way: There is a functor ${·}^{\nu }$ which maps a sheaf $\mathcal{F}$ on $X_{ct}$ to a sheaf ${\mathcal{F}}^{\nu }$ on $\nu \left(X\right)$. Conversely, the functor $\widehat{·}$ maps a sheaf $\mathcal{G}$ on $\nu \left(X\right)$ to a sheaf $\hat{\mathcal{G}}$ on $X_{ct}$, Together, they provide an equivalence of categories between “reflective” sheaves on $X_{ct}$ and sheaves on $\nu \left(X\right)$. In particular, the constant sheaf $A_X$ on $X_{ct}$ is reflective and mapped to the constant sheaf $A_{\nu \left(X\right)}$ on $\nu \left(X\right)$. We can compute cohomology with constant coefficients either way:

Theorem 5. 

If X is a proper metric space and A an abelian group, then

$${\check{H}}_{ct}^q(X;A_X)=\check{H}(\nu \left(X\right);A_{\nu \left(X\right)})$$

the qth cohomology of X with values in the constant sheaf A on $X_{ct}$ is isomorphic to the qth sheaf cohomology of the Higson corona $\nu \left(X\right)$ of X with values in the constant sheaf $A_{\nu \left(X\right)}$.

Moreover, if asdim$\left(X\right)\le n$ then ${\check{H}}_{ct}^q(X,A_X)=0$ for $q>n$.

This paper provides enough computational methods to compute metric cohomology of finitely generated groups. Vanishing of ${\check{H}}_{ct}^1(\mathbb{Z},A)=0$ for finite A can be computed directly using cochains. Then, our result on the Higson corona implies that $\mathbb{Z}$ is acyclic for finite coefficients. The same method can be employed to show that trees are acyclic for finite coefficients. Thus, we computed metric cohomology of the free group $F_n$ with $n<\infty$ generators. Computing cohomology of the free abelian groups ${\mathbb{Z}}^n$ with $n<\infty$ is more challenging. A coarse homotopy equivalence ${\mathbb{Z}}^{n-1}\times {\mathbb{Z}}_{\ge 0}\to {\mathbb{Z}}_{\ge 0}$ provides a Leray cover of ${\mathbb{Z}}^n$ which has the same combinatorical information as the nerve of a Leray cover of the topological space $S^{n-1}$. Thus, cohomology with finite coefficients can be derived.

Theorem 6. 

If A is a finite abelian group, then

$${\check{H}}_{ct}^q({\mathbb{Z}}^n;A)=\left\{\begin{array}{cc}A\oplus A\hfill & n=1,q=0\hfill \\ A\hfill & n\ne 1,q=0\vee q=n-1\hfill \\ 0\hfill & otherwise.\hfill \end{array}\right.$$

There is a more general notion of coarse space which includes the class of coarse metric spaces. Most of our concepts work in more generality. We restrict our attention to metric spaces only since a wider audience (than coarse geometers) is interested in this class of coarse spaces only. The coarse sheaf cohomology theory is defined on coarse spaces with connected coarse structure. The resolution via cochains also works for this class of spaces. The homotopy theory is only defined for metric spaces and the results on the Higson corona work for proper metric spaces and coarse structures generated by a compactification of a paracompact, locally compact Hausdorff space.

This article is organized in 10 sections. Some can be read independently but there are also a few dependencies as depicted in the following diagram.

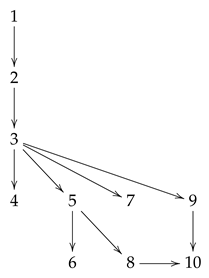
The final section uses every aspect so far discussed. Sheaf-theoretic methods, the resolution via cochains, coarse homotopy and the Higson corona are employed in the computation of metric cohomology of ${\mathbb{Z}}^n$.

2. Coarse Cohomology by Roe and the Higson Corona

This chapter introduces terminology and concepts which are well known to coarse geometers.

If X is a metric space, then a subset $E\subseteq X\times X$ is called an entourage if

$$\underset{(x,y)\in E}{sup}d(x,y)<\infty$$

The set of entourages forms the coarse structure of X. If $R\ge 0$, then the set

$${\Delta }_R:=\{(x,y)\in X\times X|d(x,y)\le R\}$$

is an entourage. If $E\subseteq X\times X,B\subseteq X$ are two subsets, then

$$E\left[B\right]:=\{x\in X\mid (x,y)\in E,y\in B\}$$

A subset $B\subseteq X$ is called bounded if there exists $x_0\in X$ and $R\ge 0$ such that ${\Delta }_R\left[x_0\right]\supseteq B$.

A map $\alpha :X\to Y$ between metric spaces is called coarsely uniform if for every $R\ge 0$ there exists $S\ge 0$ such that $d(x,y)\le R$ in X implies $d\left(\alpha \right(x),\alpha (y\left)\right)\le S$ in Y. The map $\alpha$ is called coarsely proper if for every bounded set $B\subseteq Y$ the set ${\alpha }^{-1}\left(B\right)$ is bounded in X. The map $\alpha$ is called coarse if $\alpha$ is both coarsely uniform and coarsely proper. Two maps $\alpha ,\beta :X\to Y$ between metric spaces are called close if the set $\alpha \times \beta \left({\Delta }_0\right)$ is an entourage in Y. The coarse category consists of metric spaces as objects and coarse maps modulo close as morphisms. Isomorphisms in this category are called coarse equivalences.

This paper presents a resolution of the constant sheaf which consists of cochains which closely resemble coarse cochains of Roe’s coarse cohomology. For this purpose, we give a quick introduction to coarse cohomology by Roe which was invented by Roe in [10,11].

If X is a metric space, then the set of q-simplices of the R-Vietoris–Rips complex of X is defined as

$${\Delta }_R^q:=\{(x_0,\dots ,x_q)\mid d(x_i,x_j)\le R\forall i,j\}.$$

A subset $B\subseteq X^{q+1}$ is called bounded if the projection to every factor is bounded. Then, a subset $C\subseteq X^{q+1}$ is called cocontrolled if for every $R\ge 0$ the set $C\cap {\Delta }_R^q$ is bounded.

Definition 1. 

If X is a metric space and A an abelian group, then the coarse cochains $C{X}^q(X;A)$ is the set of functions $X^{q+1}\to A$ with cocontrolled support. It is a group by pointwise addition. The coboundary map ${\partial }_q:C{X}^q(X;A)\to C{X}^{q+1}(X;A)$ is defined by

$$\left({\partial }_q\phi \right)(x_0,\dots ,x_{q+1})=\sum _{i=0}^{q+1}{(-1)}^i\phi (x_0,\dots ,{\widehat{x}}_i,\dots ,x_{q+1}).$$

This makes $(C{X}^q(X;A),{\partial }_q)$ a cochain complex. Its homology is called coarse cohomology by Roe and denoted by $H{X}^{\ast }(X;A)$.

If $\alpha :X\to Y$ is a coarse map, then it induces a cochain map

$$\begin{array}{cc}\hfill {\alpha }^q:C{X}^q(Y,A)& \to C{X}^q(X,A)\hfill \\ \hfill \phi & \mapsto \phi \circ {\alpha }^{\times (q+1)}\hfill \end{array}$$

Two coarse maps which are close induce the same map in cohomology. If $A=\mathbb{R}$ and $X={\mathbb{R}}^n$, then

$$H{X}^q({\mathbb{R}}^n,\mathbb{R})=\left\{\begin{array}{cc}\mathbb{R}\hfill & q=n\hfill \\ 0\hfill & otherwise.\hfill \end{array}\right.$$

A section in this paper transfers sheaves on a proper metric space to sheaves on its Higson corona. For this purpose, we give a definition of the Higson corona which is equivalent to the usual one [19].

Let X be a metric space. Two subsets $A,B\subseteq X$ are called close (or not coarsely disjoint) if there exists an unbounded sequence ${(a_i,b_i)}_i\subseteq A\times B$ and some $R\ge 0$ such that $d(a_i,b_i)\le R$ for every i. We write $A⋏B$ in this case.

A metric space is called locally finite if every bounded set is finite. Every proper metric space is coarsely equivalent to a locally finite metric space.

Definition 2. 

Let X be a proper metric space and $S\subseteq X$ a locally finite subset where the inclusion is coarsely surjective. Denote by $\widehat{S}$ the set of nonprincipal ultrafilters on S. If $A\subseteq S$ is a subset, define

$$\mathsf{cl}\left(A\right):=\{\mathcal{F}\in \widehat{S}:A\in \mathcal{F}\}.$$

Then, define a relation ⋏ on subsets of $\widehat{S}$: ${\pi }_1⋏{\pi }_2$ if for every $A,B\subseteq S$ the relations ${\pi }_1\subseteq \mathsf{cl}\left(A\right),{\pi }_2\subseteq \mathsf{cl}\left(B\right)$ imply $A⋏B$.

The relation ⋏ on subsets of $\widehat{S}$ determines a Kuratowski closure operator

$$\overline{\pi }=\{\mathcal{F}\in \widehat{S}:\left\{\mathcal{F}\right\}⋏\pi \}.$$

Now, define a relation λ on $\widehat{S}$: $\mathcal{F}\lambda \mathcal{G}$ if $A\in \mathcal{F},B\in \mathcal{G}$ implies $A⋏B$.

Now, the Higson corona $\nu \left(X\right)$ of X is defined $\nu \left(X\right)=\widehat{S}/\lambda$ as the quotient by λ.

If $A\subseteq X$ is a subset of a metric space, then $\mathsf{cl}\left(A\right)=\overline{A}\cap \nu \left(X\right)$ where the closure is taken in the Higson compactification. We call ${\left(\mathsf{cl}{\left(A\right)}^c\right)}_{A\subseteq X}$ the basic open sets and ${\left(\mathsf{cl}\left(A\right)\right)}_{A\subseteq X}$ the basic closed sets. There are two observations: If $A,B\subseteq X$ are two subsets, then

• $\mathsf{cl}\left(A\right)\cap \mathsf{cl}\left(B\right)=Ø$ if and only if $A /⋏B$ are not close
• $\mathsf{cl}\left(A\right)\cup \mathsf{cl}\left(B\right)=\mathsf{cl}\left(A\cup B\right)$.

3. Coarse Sheaf Cohomology, a Survey

This chapter gives a survey on coarse sheaf cohomology or coarse cohomology with twisted coefficients as we call it [17]. There are several facts on sheaf cohomology on topological spaces which hold in more generality for sheaf cohomology defined on a Grothendieck topology. Since the literature does not provide every aspect, we are going to prove these facts by hand.

Let $U\subseteq X$ be a subset of a metric space. A finite family of subsets $U_1,\dots ,U_n\subseteq U$ forms a coarse cover of U if for every entourage $E\subseteq U\times U$ the set

$$E\left[U_1^c\right]\cap \cdots \cap E\left[U_n^c\right]$$

is bounded. This is equivalent to saying that the set

$$(U\times U)\cap {(\bigcup _i{U}_i\times U_i)}^c$$

is a cocontrolled subset of $X^2$.

To a metric space X we associate a Grothendieck topology $X_{ct}$ in the following way. The underlying category $Cat\left(X_{ct}\right)$ is the poset of subsets of X. Subsets ${\left(U_i\right)}_i$ form a covering of $U\subseteq X$ if they coarsely cover U.

A contravariant functor $\mathcal{F}$ on subsets of X is a sheaf on $X_{ct}$ if for every coarse cover $U_1,\dots ,U_n\subseteq U$ of a subset of X the following diagram is an equalizer

$$\mathcal{F}\left(U\right)\to \prod _i\mathcal{F}\left(U_i\right)\rightrightarrows \prod _{i,j}\mathcal{F}(U_i\cap U_j).$$

If $\mathcal{F}$ is a sheaf on $X_{ct}$ then the right derived functor of the global sections functor is called coarse sheaf cohomology, written ${\check{H}}_{ct}^{\ast }(X;\mathcal{F})$.

If

$$0\to \mathcal{F}\to \mathcal{G}\to \mathcal{H}\to 0$$

is a short exact sequence of sheaves on $X_{ct}$ then there is a long exact sequence in cohomology

$$\begin{array}{cc}\hfill 0& \to {\check{H}}_{ct}^0(X,\mathcal{F})\to {\check{H}}_{ct}^0(X,\mathcal{G})\to {\check{H}}_{ct}^0(X,\mathcal{H})\hfill \\ \hfill & \to {\check{H}}_{ct}^1(X,\mathcal{F})\to \cdots \hfill \\ \hfill \cdots & \to {\check{H}}_{ct}^q(X,\mathcal{F})\to {\check{H}}_{ct}^q(X,\mathcal{G})\to {\check{H}}_{ct}^q(X,\mathcal{H})\hfill \\ \hfill & \to {\check{H}}_{ct}^{q+1}(X,\mathcal{F})\to \cdots \hfill \end{array}$$

If A is an abelian group, the sheafification of the constant presheaf A on $X_{ct}$ is called the constant sheaf $A_X$ on X. In this paper, we are interested in the computation of ${\check{H}}_{ct}^q(X;A_X)$ in higher dimension. The zeroth cohomology group is related to the number of ends $e\left(X\right)$ of the metric space X:

$${\check{H}}_{ct}^0(X;A_X)=A_X\left(X\right)=\left\{\begin{array}{cc}{A}^{e\left(X\right)}\hfill & e\left(X\right)<\infty \hfill \\ \underset{\mathbb{N}}{⨁}A\hfill & e\left(X\right)=\infty .\hfill \end{array}\right.$$

A sheaf $\mathcal{F}$ on $X_{ct}$ is called acyclic if ${\check{H}}_{ct}^q(X,\mathcal{F})=0$ for $q>0$. A sequence of sheaves

$$\cdots \to {\mathcal{F}}_i\stackrel{{\phi }_i}{\to }{\mathcal{F}}_{i+1}\stackrel{{\phi }_{i+1}}{\to }{\mathcal{F}}_{i+2}\to \cdots$$

is exact if $im{\phi }_i=ker{\phi }_{i+1}$. Here, $im\phi$ is the sheafification of the image presheaf $U\mapsto im\left(\phi \right(U\left)\right)$.

Lemma 1. 

If

$$0\to \mathcal{F}\to {\mathcal{F}}_0\to {\mathcal{F}}_1\to \cdots$$

is an acyclic resolution of sheaves on $X_{ct}$ then

$${\check{H}}_{ct}^q(X,\mathcal{F})=H^q(0\to {\mathcal{F}}_0\left(X\right)\to {\mathcal{F}}_1\left(X\right)\to \cdots ),$$

cohomology of $\mathcal{F}$ can be computed by taking homology of the cocomplex

$$0\to {\mathcal{F}}_0\left(X\right)\to {\mathcal{F}}_1\left(X\right)\to \cdots .$$

Proof. 

Suppose

$$0\to \mathcal{F}\stackrel{i}{\to }{\mathcal{F}}_0\stackrel{d_0}{\to }{\mathcal{F}}_1\stackrel{d_1}{\to }{\mathcal{F}}_2\stackrel{d_2}{\to }\cdots$$

is an exact sequence with ${\mathcal{F}}_i$ acyclic for every i.

For every $i=1,2,\dots$ define ${\epsilon }_i=ker{d}_i$. The exact sequence

$$0\to \mathcal{F}\to {\mathcal{F}}_0\to {\epsilon }_1\to 0$$

gives rise to a long exact sequence

$$\begin{array}{ccc}\hfill 0& \to {\check{H}}_{ct}^0(X,\mathcal{F})\to {\check{H}}_{ct}^0(X,{\mathcal{F}}_0)\hfill & \hfill \to {\check{H}}_{ct}^0(X,{\epsilon }_1)\\ & \to {\check{H}}_{ct}^1(X,\mathcal{F})\to 0\hfill & \hfill \to \cdots \\ & & \hfill 0\to {\check{H}}_{ct}^q(X,{\epsilon }_1)\\ & \to {\check{H}}_{ct}^{q+1}(X,\mathcal{F})\to 0\hfill \end{array}$$

Thus, ${\check{H}}_{ct}^{q+1}(X,\mathcal{F})={\check{H}}^q(X,{\epsilon }_1)$ for $q\ge 1$ and

$$\begin{array}{cc}\hfill {\check{H}}_{ct}^1(X,\mathcal{F})& ={\epsilon }_1\left(X\right)/im\left(d_0\left(X\right)\right)\hfill \\ \hfill & =(ker d_1)\left(X\right)/im\left(d_0\left(X\right)\right)\hfill \\ \hfill & =H^1(0\to {\mathcal{F}}_0\left(X\right)\to {\mathcal{F}}_1\left(X\right)\to \cdots )\hfill \end{array}$$

The inclusion ${\epsilon }_i\to {\mathcal{F}}_i$ and the corestriction of $d_i$ to $im{d}_i={\epsilon }_{i+1}$ combine to an exact sequence

$$0\to {\epsilon }_i\to {\mathcal{F}}_i\to {\epsilon }_{i+1}\to 0.$$

This sequence gives rise to a long exact sequence

$$\begin{array}{ccc}\hfill 0& \to {\check{H}}_{ct}^0(X,{\epsilon }_i)\to {\check{H}}_{ct}^0(X,{\mathcal{F}}_i)\hfill & \to {\check{H}}_{ct}^0(X,{\epsilon }_{i+1})\hfill \\ & \to {\check{H}}_{ct}^1(X,{\epsilon }_i)\to \cdots \hfill & \\ & & \hfill 0\to {\check{H}}_{ct}^q(X,{\epsilon }_{i+1})\\ & \to {\check{H}}_{ct}^{q+1}(X,{\epsilon }_i)\to 0\hfill \end{array}$$

which reads ${\check{H}}_{ct}^{q+1}(X,{\epsilon }_i)={\check{H}}_{ct}^q(X,{\epsilon }_{i+1})$ for $q\ge 1$. If $q\ge 2$, then we obtain inductively

$$\begin{array}{cc}\hfill {\check{H}}_{ct}^q(X,\mathcal{F})& ={\check{H}}_{ct}^{q-1}(X,{\epsilon }_1)=\cdots ={\check{H}}_{ct}^1(X,{\epsilon }_{q-1})\hfill \\ \hfill & =H^1(0\to {\mathcal{F}}_{q-1}\left(X\right)\to {\mathcal{F}}_q\left(X\right)\to \cdots )=H^q(0\to {\mathcal{F}}_0\left(X\right)\to {\mathcal{F}}_1\left(X\right)\to \cdots ).\hfill \end{array}$$

□

Lemma 2. 

If X is a metric space, every injective sheaf on $X_{ct}$ is flabby.

Proof. 

Let $\mathcal{I}$ be an injective sheaf on $X_{ct}$ and let $V\subseteq U$ be an inclusion of subsets. We define a presheaf ${\mathbb{Z}}_{U,X}$ on $X_{ct}$ by

$$W\mapsto \left\{\begin{array}{cc}\mathbb{Z}\hfill & W\subseteq U\hfill \\ 0\hfill & otherwise\hfill \end{array}\right.$$

Denote by ${\mathbb{Z}}_{U,X}^{\#}$ the sheafification. In a similar way, we define ${\mathbb{Z}}_{V,X}$ and ${\mathbb{Z}}_{V,X}^{\#}$. Then, ${\mathbb{Z}}_{V,X}^{\#}\le {\mathbb{Z}}_{U,X}^{\#}$ is a subsheaf in a canonical way. Thus, we have an exact sequence

$$0\to {\mathbb{Z}}_{V,X}^{\#}\to {\mathbb{Z}}_{U,X}^{\#}$$

Since $\mathcal{I}$ is an injective object the sequence

$$Ho{m}_{Sh}({\mathbb{Z}}_{U,X}^{\#},\mathcal{I})\to Ho{m}_{Sh}({\mathbb{Z}}_{V,X}^{\#},\mathcal{I})\to 0$$

is exact. Now

$$Ho{m}_{Sh}({\mathbb{Z}}_{U,X}^{\#},\mathcal{I})=Ho{m}_{PSh}({\mathbb{Z}}_{U,X},\mathcal{I})=\mathcal{I}\left(U\right)$$

and

$$Ho{m}_{Sh}({\mathbb{Z}}_{V,X}^{\#},\mathcal{I})=Ho{m}_{PSh}({\mathbb{Z}}_{V,X},\mathcal{I})=\mathcal{I}\left(V\right)$$

which proves the claim. □

Lemma 3. 

If X is a metric space, then flabby sheaves on $X_{ct}$ are acyclic.

Proof. 

We mimic the proof of ([20], Proposition 2.5).

If $\mathcal{F}$ is a flabby sheaf, then it can be embedded in an injective sheaf $\mathcal{I}$. The quotient of this inclusion is denoted $\mathcal{G}$. Then, we have an exact sequence

$$\begin{array}{c}\hfill 0\to \mathcal{F}\to \mathcal{I}\to \mathcal{G}\to 0\end{array}$$

(2)

with $\mathcal{F}$ flabby, $\mathcal{I}$ flabby by Lemma 2 and $\mathcal{G}$ is flabby by a standard argument. General theory on flabby sheaves also implies that the sequence

$$\begin{array}{c}\hfill 0\to \mathcal{F}\left(X\right)\to \mathcal{I}\left(X\right)\to \mathcal{G}\left(X\right)\to 0\end{array}$$

(3)

is exact. Then, the long exact sequence in cohomology to the short exact sequence (2), the exactness of (3) and ${\check{H}}_{ct}^q(X,I)=0$ for $q\ge 1$ implies ${\check{H}}_{ct}^1(X,\mathcal{F})=0$ and

$$\begin{array}{c}\hfill {\check{H}}_{ct}^q(X,\mathcal{F})={\check{H}}_{ct}^{q-1}(X,\mathcal{G})\end{array}$$

(4)

for $q\ge 2$. Since $\mathcal{G}$ satisfies the requirements for this Lemma, we obtain the result for $q\ge 2$ using inductively $\mathcal{G}$ and the isomorphism (4). □

4. Standard Resolution

This chapter proves Theorem 3.

Let A be an abelian group. If $A_1\bigsqcup \cdots \bigsqcup A_n=U$ is a disjoint union of a subset $U\subseteq X$ of a metric space, then

$$C_{A_1,\dots ,A_n}^q(U,A)=\{\phi :U^{q+1}\to A|\phi {|}_{A_{i_0}\times \cdots \times A_{i_q}}\mathrm{constant}\forall i_0,\dots ,i_q\in \{1,\dots ,q\}\}$$

Then, we define

$$C^q(U,A)=\underset{A_1\bigsqcup \cdots \bigsqcup A_n=U}{\underrightarrow{lim}}{C}_{A_1,\dots ,A_n}^q(U,A)$$

where the indexing category consists of pairwise disjoint subsets $A_1,\dots ,A_n\subseteq U$ with $A_1\cup \cdots \cup A_n=U$. There is an arrow $A_1\bigsqcup \cdots \bigsqcup A_n\to C_1\bigsqcup \cdots \bigsqcup C_l$ if ${\left(C_i\right)}_i$ is a refinement of ${\left(A_i\right)}_i$. Then $\phi \in C_{A_1,\dots ,A_n}^q(U,A)$ is equivalent to $\psi \in C_{B_1,\dots ,B_m}^q(U,A)$ if

$${\phi |}_{A_{i_0}\cap B_{j_0}\times \cdots \times A_{i_q}\cap B_{j_q}}{=\psi |}_{A_{i_0}\cap B_{j_0}\times \cdots \times A_{i_q}\cap B_{j_q}}$$

for every $i_0,\dots i_q\in \{1,\dots ,n\},j_0,\dots ,j_q\in \{1,\dots ,m\}$. We equip $C^q(U;A)$ with a group operation by pointwise addition. The elements of $C^q(U;A)$ are called blocky functions with blocks $A_1,\dots ,A_n$. They can be compared with the group of all functions $U^{q+1}\to A$.

A differential on $C^q(U,A)$ is defined by

$$\begin{array}{cc}\hfill d_q:C^q(U,A)& \to {\mathcal{C}}^{q+1}(U,A)\hfill \\ \hfill \phi & \mapsto (x_0,\dots ,x_{q+1})\mapsto \sum _{i=0}^{q+1}{(-1)}^i\phi (x_0,\dots ,{\widehat{x}}_i,\dots ,x_{q+1}).\hfill \end{array}$$

Now, $C{X}_b^q(U,A)$ defines the subcomplex of functions in $C^q(U,A)$ with cocontrolled support. Then, we define $C{Y}_b^q(U,A):=C^q(U,A)/C{X}_b^q(U,A)$.

Definition 3. 

If X is a metric space, A an abelian group and $q\ge 0$ then coarse cohomology $H{Y}_b^q(X,A)$ is defined to be the qth homology of the coarse cochain complex ${(C{Y}_b^q(X,A),d_q)}_{q\ge 0}$.

Subsets $U_1,\dots ,U_n$ of a subset $U\subseteq X$ of a metric space form a coarse disjoint union of U if they coarsely cover U and every two elements are disjoint.

Lemma 4. 

If $U\subseteq X$ is a subset of a metric space and A an abelian group, then

$$H{Y}_b^0(U,A)=ker{d}_0=A\left(U\right)$$

Proof. 

We compute $H{Y}_b^0(U,A)$. Let $\phi \in ker{d}_0$ be a cocycle. Then, $x\sim y$ if $d_0\phi (x,y)=0$ defines an equivalence relation on X with equivalence classes ${\left({\phi }^{-1}\left(k\right)\right)}_{k\in A}$. The ${\phi }^{-1}\left(k\right)$ form a coarse disjoint union since $d_0\phi$ has cocontrolled support. We can assume all ${\phi }^{-1}\left(k\right)$ are not bounded otherwise we subtract a cochain with bounded (cocontrolled) support. Thus, $\phi$ is an element of $A\left(U\right)$.

If we are given a coarse disjoint union $U_1,\dots ,U_n$ of U and ${\left(a_i\right)}_{U_i}\in A\left(U\right)$ then we can assume the $U_i$ are disjoint and not bounded. Then,

$$\begin{array}{cc}\hfill \phi :U& \to A\hfill \\ \hfill x& \mapsto a_i,x\in U_i\hfill \end{array}$$

defines a cocycle in $C{Y}_b^0(U,A)$. □

If $\alpha :X\to Y$ is a coarse map between metric spaces and $\phi \in C^q(Y,A)$ a cochain, then ${\alpha }^{\ast }\left(\phi \right):=\phi \circ {\alpha }^{\times q+1}$ defines a cochain in $C^q(X,A)$, specifically $C_{A_1,\dots ,A_n}^q(Y,A)$ is mapped to $C_{{\alpha }^{-1}\left(A_1\right),\dots ,{\alpha }^{-1}\left(A_n\right)}^q(X,A)$. If $\phi$ has cocontrolled support, so does ${\alpha }^{\ast }\phi$. Thus, there is a well-defined cochain map ${\alpha }^{\ast }:C{Y}_b^q(Y,A)\to C{Y}_b^q(X,A)$.

In particular, an inclusion $U\subseteq V$ of subsets induces a restriction map $i^{\ast }:C{Y}_b^q(V,A)\to C{Y}_b^q(U,A)$. Thus, $C{Y}_b^q(·,A)$ forms a presheaf on $X_{ct}$.

Lemma 5. 

If X is a metric space, the presheaf $C{Y}_b^q(·,A)$ is sheaf on $X_{ct}$.

Proof. 

Let $U_1,\dots ,U_n$ be a coarse cover of a subset $U\subseteq X$. We show the identity axiom. Let $\phi \in C{Y}_b^q(U,A)$ be a section with ${\phi }_R{|}_{U_i}=0$ for every i. By Lemma 6, the set $V:={(U_1^{q+1}\cup \cdots \cup U_n^{q+1})}^c$ is cocontrolled. Then

$${\phi =\phi |}_{U_1}+\cdots +\phi {{|}_{U_n}+\phi |}_V$$

as a finite sum of functions with cocontrolled support has cocontrolled support.

We show the gluing axiom. Suppose ${\phi }_i\in C{Y}_b^q(U_i,A)$ are functions with ${\phi }_i{{|}_{U_j}={\phi }_j|}_{U_i}$ for every $i,j$. Define a function

$$\begin{array}{cc}\hfill \phi :U^{q+1}& \to A\hfill \\ \hfill (x_0,\dots ,x_q)& \mapsto \left\{\begin{array}{cc}{\phi }_1(x_0,\dots ,x_q)\hfill & (x_0,\dots ,x_q)\in U_1^{q+1}\hfill \\ {\phi }_2(x_0,\dots ,x_q)\hfill & (x_0,\dots ,x_q)\in U_2^{q+1}\backslash U_1^{q+1}\hfill \\ ⋮\hfill & ⋮\hfill \\ {\phi }_n(x_0,\dots ,x_q)\hfill & (x_0,\dots ,x_q)\in U_n^{q+1}\cap {(U_1^{q+1}\cup \cdots \cup U_{n-1}^{q+1})}^c\hfill \\ 0\hfill & otherwise.\hfill \end{array}\right.\hfill \end{array}$$

If ${\phi }_i\in C_{A_{i1},\dots ,A_{i{n}_1}}(U_i,A)$ then $\phi \in C_{A_{11},\dots ,A_{1n_1},A_{21}\backslash U_1,\dots ,A_{n,n_n}\backslash (U_1\cup \cdots U_{n-1}),{(U_1\cup \cdots \cup U_n)}^c}(U,A)$. As can easily be seen, the cochain $\phi$ restricts to ${\phi }_i$ for every i. □

Lemma 6. 

If $R\ge 0$ and $U_1,\dots ,U_n$ are a coarse cover of a subset $U\subseteq X$ of a metric space then

$${(U_1^{q+1}\cup \cdots \cup U_n^{q+1})}^c\cap {\Delta }_R^q$$

is bounded.

Proof. 

If $f:\{1,\dots ,n\}\to \{0,\dots ,q\}$ is a function, then denote

$$A_f:=\bigcap _{i\in f^{-1}\left(0\right)}{U}_i^c\times \cdots \times \bigcap _{i\in f^{-1}\left(q\right)}{U}_i^c.$$

Here, the empty intersection denotes U. Then,

$$\begin{array}{cc}{(U_1^{q+1}\cup \cdots \cup U_n^{q+1})}^c\cap U^{q+1}\hfill & =\{(x_0,\dots ,x_q)\in U^{q+1}:\forall i\in \{1,\dots ,n\}\exists j\in \{0,\dots ,q\}{x}_j\notin U_i\}\hfill \\ \hfill & =\bigcup _{f:\{1,\dots ,n\}\to \{0,\dots ,q\}}{A}_f.\hfill \end{array}$$

Now, the projection to the ith factor of $A_f\cap {\Delta }_R^q$ is

$$\begin{array}{cc}\hfill {(A_f\cap {\Delta }_R^q)}_i& \subseteq \{x\in U:d(x,\bigcap _{i\in f^{-1}\left(0\right)}{U}_i^c)\le R,\dots ,d(x,\bigcap _{i\in f^{-1}\left(q\right)}{U}_i^c)\le R\}\hfill \\ \hfill & ={\Delta }_R\left[\bigcap _{i\in f^{-1}\left(0\right)}{U}_i^c\right]\cap \cdots \cap {\Delta }_R\left[\bigcap _{i\in f^{-1}\left(q\right)}{U}_i^c\right]\hfill \\ \hfill & \subseteq \bigcap _{i=1}^n{\Delta }_R\left[U_i^c\right]\hfill \end{array}$$

bounded. Since ${(U_1^{q+1}\cup \cdots \cup U_n^{q+1})}^c\cap U^{q+1}$ is a finite union of the $A_f$ this proves the claim. □

Lemma 7. 

The sheaf $C{Y}_b^q(·,A)$ on $X_{ct}$ is flabby.

Proof. 

If $U\subseteq V$ is an inclusion of subsets and $\phi \in C^q(U,A)$ then there is a disjoint union $A_1\bigsqcup \cdots \bigsqcup A_n=U$ with $\phi \in C_{A_1,\dots ,A_n}(U,A)$. Define

$$\begin{array}{cc}\hfill \tilde{\phi }:V^{q+1}& \to A\hfill \\ \hfill (x_0,\dots ,x_q)& \mapsto \left\{\begin{array}{cc}0\hfill & \exists i\in \{0,\dots ,q\}:x_i\notin U\hfill \\ \phi (x_0,\dots ,x_q)\hfill & otherwise.\hfill \end{array}\right.\hfill \end{array}$$

Then, $\tilde{\phi }\in C_{A_1,\dots ,A_n,U^c}(V,A)$ restricts to $\phi$ on U. □

Lemma 8. 

The homology of $C^q(X,A)$ is concentrated in degree zero.

Proof. 

We compute $H^q\left(C^{\ast }(X,A)\right)=\left\{\begin{array}{cc}A\hfill & q=0\hfill \\ 0\hfill & otherwise\hfill \end{array}\right.$. If $q=0$ then

$$\begin{array}{cc}\hfill ker{d}_0& =\{\phi :X\to A:d_0\phi =0\}\hfill \\ \hfill & =\{\phi :X\to A:\phi \left(x_1\right)-\phi \left(x_0\right)=0\forall x_1,x_0\in X\}\hfill \\ \hfill & =\{\phi :X\to A \mathrm{constant}\}\hfill \\ \hfill & =A\hfill \end{array}$$

If $q\ge 1$ and $\phi \in ker{d}_q$ then define the cochain

$$\begin{array}{cc}\hfill \tilde{\phi }:X^q& \to Z\hfill \\ \hfill (x_0,\dots ,x_{q-1})& \mapsto \phi (0,x_0,\dots ,x_{q-1}).\hfill \end{array}$$

Here, $0\in X$ is a fixed point. If $\phi \in C_{A_1,\dots ,A_n}^q(X,A)$ then $\tilde{\phi }\in C_{A_1,\dots ,A_n}^{q-1}(X,A)$. Then

$$\begin{array}{cc}\hfill d_{q-1}\tilde{\phi }(x_0,\dots ,x_q)& =\sum _{i=0}^q{(-1)}^i\phi (0,x_0,\dots ,{\widehat{x}}_i,\dots ,x_q)\hfill \\ \hfill & =\sum _{i=1}^{q+1}{(-1)}^{i+1}\phi (0,x_0,\dots ,{\widehat{x}}_{i-1},\dots ,x_q)+d_q\phi (0,x_0,\dots ,x_q)\hfill \\ \hfill & =\phi (x_0,\dots ,x_q)\hfill \end{array}$$

Thus, higher homology of $C^q(X,Z)$ vanishes. □

We note an exact sequence of cochain complexes:

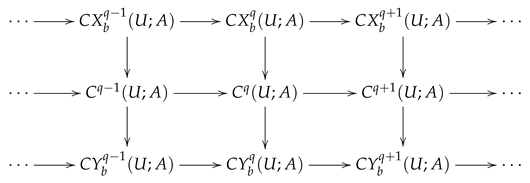
Lemma 9. 

If $q\ge 1$ and for every subset $U\subseteq X$ and $\psi \in kerd{X}_{q+1}^b$ there exists a coarse cover $U_i$ of U and ${\psi }_i\in C{X}_b^q(U_i;A)$ with $d_q\left({\psi }_i\right){=\psi |}_{U_i}$ then $C{Y}_b^{\ast }(·;A)$ is exact at q.

Proof. 

Let $\phi \in kerd{Y}_q^b\subseteq C{Y}_b^q(U;A)$ be an element. Then, $\psi :=d_q\phi$ has cocontrolled support; thus, it is an element of $C{X}_b^{q+1}(U;A)$. Since $d_{q+1}\psi =d_{q+1}{d}_q\phi =0$ the element $\psi$ is even a cocycle in $C{X}_b^{q+1}(X;A)$. Then, there exists a coarse cover ${\left(U_i\right)}_i$ and elements ${\psi }_i\in C{X}_b^q(U_i;A)$ with $d_q\left({\psi }_i\right)=\left(d_q\phi \right){|}_{U_i}$. Then, ${\phi |}_{U_i}-{\psi }_i$ is a cocycle in $C^q(U_i;A)$ for every i. Thus, there exists ${\phi }_i\in C^{q-1}(U_i;A)$ with $d_{q-1}{\phi }_i{=\phi |}_{U_i}-{\psi }_i$. Thus, ${\phi |}_{U_i}$ represents a coboundary. □

Lemma 10. 

If $q\ge 1$ and ${(U_1^{q+1}\cup \cdots \cup U_n^{q+1})}^c$ is cocontrolled in $U^{q+1}$ then $U_1,\dots ,U_n$ is a coarse cover of U.

Proof. 

Let $R\ge 0$ be a number. If $(x,y)\in {\left({\bigcup }_i{U}^2\right)}^c\cap {\Delta }_R$ then $(x,y,\dots ,y)\in {\left({\bigcup }_i{U}_i^{q+1}\right)}^c\cap {\Delta }_R^q$. Since this set is bounded, $(x,y)$ must be contained in a bounded set too. □

Lemma 11. 

If $\psi \in C{X}_b^q(U,A)$ is a cocycle, then there exists a coarse cover $U_1,\dots ,U_n$ of U with ${\psi |}_{U_i}=0$ for every $i=1,\dots ,n$.

Proof. 

Suppose $\psi \in C_{A_1,\dots ,A_n}(U,A)$ and fix $a_i\in A_i$ for every i. Then $A_i$ is bounded if $\psi (a_i,\dots ,a_i)\ne 0$. We add i to a list $\mathcal{C}$. Likewise, $A_i\times A_j$ is cocontrolled if there exists a map $f:\{0,\dots ,q\}\to \{i,j\}$ with $\psi (a_{f\left(0\right)},\dots ,a_{f\left(q\right)})\ne 0$. We add the set $\{i,j\}$ to the list $\mathcal{C}$. We proceed likewise with $A_i\times \cdots \times A_j$ of up to $q+1$ factors. We then define

$$\mathcal{U}=\{A_{i_1}\cup \cdots \cup A_{i_m}\mid S\notin \mathcal{C}\forall S\subseteq \{i_1,\dots ,i_m\}\}$$

We show $\mathcal{U}$ is the desired coarse cover.

If $V\in \mathcal{U}$ then it is of the form $V=A_{i_1}\cup \cdots \cup A_{i_m}$. Let $f:\{0,\dots ,q\}\to \{i_1,\dots ,i_m\}$ be a function. Since $\{f\left(0\right),\dots ,f\left(q\right)\}\subseteq \{i_1,\dots ,i_m\}$ we have $\left\{f\right(0),\dots ,f(q\left)\right\}\notin \mathcal{C}$. Thus $\psi (a_{f\left(0\right)},\dots ,a_{f\left(q\right)})=0$. Since f was arbitrary this implies ${\psi |}_V=0$.

If $(a_{i_0},\dots ,a_{i_q})\in {\left({\bigcup }_{V\in \mathcal{U}}{V}^{q+1}\right)}^c$ then $A_{i_0}\cup \cdots \cup A_{i_q}\notin \mathcal{U}$. Thus there exists a subset $S\subseteq \{i_0,\dots ,i_q\}$ with $S\in \mathcal{C}$. Which implies that $A_{i_0}\times \cdots \times A_{i_q}$ is cocontrolled. This way we showed that ${\left({\bigcup }_{V\in \mathcal{U}}{V}^{q+1}\right)}^c$ is cocontrolled in $U^{q+1}$. By Lemma 10 we can conclude that $\mathcal{U}$ is a coarse cover. □

Theorem 7. 

If X is a metric space and A an abelian group then the $C{Y}_b^q(X,A)$ are a flabby resolution of the constant sheaf A on $X_{ct}$. We can compute

$${\check{H}}^q(X,A)=H{Y}_b^q(X,A).$$

for every $q\ge 0$.

Proof. 

We prove that

$$0\to A\to C{Y}_b^0(X,A)\to C{Y}_b^1(X,A)\to \cdots$$

is a flabby resolution of A. By Lemma 5, the $C{Y}_b^q(X,A)$ are sheaves. They are flabby by Lemma 7. By Lemma 4, the sequence is exact at 0. If we combine Lemmas 9 and 11, then we see that it is exact for $q\ge 1$. □

5. Functoriality, Graded Ring Structure and Mayer–Vietoris

This chapter presents a few immediate applications of Theorem 3.

Lemma 12. 

If two coarse maps $\alpha ,\beta :X\to Y$ are close then they induce the same map in cohomology.

Proof. 

The chain homotopy for coarse cohomology presented in ([11], Proposition 5.12) can be costumized for our setting. Define a map $h:C{Y}_b^q(Y,A)\to C{Y}_b^{q-1}(X,A)$ by

$$\left(h\phi \right)(x_0,\dots ,x_{q-1})=\sum _{i=0}^{q-1}{(-1)}^i\phi (\alpha \left(x_0\right),\dots ,\alpha \left(x_i\right),\beta \left(x_i\right),\dots ,\beta \left(x_{q-1}\right)).$$

If $\phi \in C_{A_1,\dots ,A_n}^q(Y,A)$ then $h\phi \in C_{{\alpha }^{-1}\left(A_i\right)\cap {\beta }^{-1}\left(A_j\right)}^{q-1}(X,A)$. Since $\alpha ,\beta$ are close, cocontrolled support of $\phi$ implies cocontrolled support of $h\phi$. Thus, h is well-defined.

The combinatorical calculation presented in the proof of ([11], Proposition 5.12) shows that

$$d_{q-1}\left(h\phi \right)+h\left(d_q\phi \right)={\beta }^{\ast }\phi -{\alpha }^{\ast }\phi .$$

Thus ${\alpha }^{\ast },{\beta }^{\ast }$ are cochain homotopic. □

Throughout this section, X denotes a metric space and R a commutative ring.

We define a map on cochains

$$\begin{array}{cc}\hfill C{Y}_b^p(X,R)\times C{Y}_b^q(X,R)& \to C{Y}_b^{p+q}(X,R)\hfill \\ \hfill (\varphi ,\psi )& \mapsto \varphi \vee \psi \hfill \end{array}$$

with

$$(\varphi \vee \psi )(x_0,\dots ,x_{p+q})=\varphi (x_0,\dots ,x_p)\psi (x_p,\dots ,x_{p+q}).$$

Lemma 13. 

This product ∨ is well-defined.

Proof. 

We show $\varphi \vee \psi$ has cocontrolled support if one of $\varphi ,\psi$ does.

Suppose $\varphi$ has cocontrolled support. Then, $supp\varphi \cap {\Delta }_R^p$ is bounded for every $R\ge 0$. This implies the 0th factor $B:={(supp\varphi \cap {\Delta }_R^p)}_0$ is bounded. If $p\le i\le p+q$, then the ith factor

$${(supp (\varphi \vee \psi )\cap {\Delta }_R^{p+q})}_i\subseteq \{x\in X:d(x,B)\le R\}$$

is bounded. This proves the claim. □

The formula

$$d_{p+q}(\varphi \vee \psi )=d_p\varphi \vee \psi +{(-1)}^p\varphi \vee d_q\psi$$

is easy to check. From that, we deduce that the ∨-product of two cocycles is a cocycle and the product of a cocycle with a coboundary is a coboundary. Thus, ∨ gives rise to a cup-product ∪ on $H{Y}_b^{\ast }(X,R)$. Associativity and the distributive law can be checked on cochain level. This makes $(H{Y}_b^{\ast }(X;R),+,\cup )$ a graded ring.

Theorem 8. 

(Mayer–Vietoris) If $U_1,U_2$ is a coarse cover of a metric space X, then there is a long exact sequence in cohomology

$$\begin{array}{cc}\hfill 0& \to {\check{H}}_{ct}^0(X;A)\to {\check{H}}_{ct}^0(U_1;A)\oplus {\check{H}}_{ct}^0(U_2;A)\to {\check{H}}_{ct}^0(U_1\cap U_2;A)\hfill \\ \hfill & \to {\check{H}}_{ct}^1(X;A)\to \cdots \hfill \\ \hfill & \to {\check{H}}_{ct}^q(X;A)\to {\check{H}}_{ct}^q(U_1;A)\oplus {\check{H}}_{ct}^q(U_2;A)\to {\check{H}}_{ct}^0(U_1\cap U_2;A)\hfill \\ \hfill & \to {\check{H}}_{ct}^{q+1}(X;A)\to \cdots \hfill \end{array}$$

Proof. 

We examine a sequence of cocomplexes

$$\begin{array}{c}\hfill 0\to C{Y}_b^q(X;A)\stackrel{\alpha }{\to }C{Y}_b^q(U_1;A)\oplus C{Y}_b^q(U_2;A)\stackrel{\beta }{\to }C{Y}_b^q(U_1\cap U_2;A)\to 0.\end{array}$$

Here, $\alpha$ is defined by $\phi \mapsto (\phi {|}_{U_1},\phi {|}_{U_2})$ and $\beta$ by $({\phi }_1,{\phi }_2)\mapsto {\phi }_2{{|}_{U_1}-{\phi }_1|}_{U_2}$. This sequence is exact at $C{Y}_b^q(X;A)$ and $C{Y}_b^q(U_1;A)\oplus C{Y}_b^q(U_2;A)$ since $C{Y}_b^q(·;A)$ is a sheaf on $X_{ct}$ and $U_1,U_2$ are a coarse cover of X. It is exact at $C{Y}_b^q(U_1\cap U_2)$ since $C{Y}_b^q(·;A)$ is a flabby sheaf.

The result is obtained by taking the long exact sequence in cohomology of the exact sequence of cochain complexes. □

We denote by $H{X}_b^q(X;A)$ the qth homology group of the cochain complex $C{X}_b^q(X;A)$ given a metric space X and an abelian group A.

Proposition 1. 

Let X be a metric space and A an abelian group. Then,

$$H{X}_b^0(X,A)=\left\{\begin{array}{cc}A\hfill & e\left(X\right)=0\hfill \\ 0\hfill & e\left(X\right)>0;\hfill \end{array}\right.$$

$$H{X}_b^1(X,A)=\left\{\begin{array}{cc}0\hfill & e\left(X\right)=0\hfill \\ A^{e\left(X\right)-1}\hfill & 0<e\left(X\right)<\infty \hfill \\ \underset{\mathbb{N}}{⨁}A\hfill & e\left(X\right)=\infty \hfill \end{array}\right.$$

and

$$H{X}_b^{q+1}(X,A)=H{Y}_b^q(X,A)$$

for every $q\ge 1$.

Proof. 

Suppose $q=0$. An element of $ker{d}_0$ is a constant function. If X is bounded, every constant function represents an element of $H{X}_b^0(X,A)=A$. If X is not bounded, then every constant function with bounded (cocontrolled) support must be zero.

If $q>0$, we use the short exact sequence of cochain complexes

$$0\to C{X}_b^q(X,A)\to C^q(X,A)\to C{Y}_b^q(X,A)\to 0.$$

This splits since every element of $C{Y}_b^q(X,A)$ is represented by a blocky map $\phi :X^{q+1}\to A$.

Now we produce the long exact sequence in cohomology. The first few terms are

$$0\to H{X}_b^0(X,A)\to H^0(X,A)\to H{Y}_b^0(X,A)\to H{X}^1(X,A)\to 0.$$

If X is bounded then, this reads

$$0\to A\stackrel{id}{\to }A\stackrel{0}{\to }0\to H{X}^1(X,A)\to 0.$$

Thus, $H{X}_b^1(X,A)=0$. If X is not bounded, then the first few terms of the long exact sequence in cohomology read

$$0\to 0\to A\to A\left(X\right)\to H{X}_b^1(X,A)\to 0$$

Then

$$H{X}_b^1(X,A)={\mathcal{C}}_f(X,A)/A=\left\{\begin{array}{cc}{A}^{e\left(X\right)-1}\hfill & e\left(X\right)<\infty \hfill \\ \underset{\mathbb{N}}{⨁}A\hfill & e\left(X\right)=\infty \hfill \end{array}\right.$$

In the middle term, we mod out the constant functions.

For $q\ge 1$, the long exact in cohomology reads

$$0\to H{Y}_b^q(X,Z)\to H{X}_b^{q+1}(X,Z)\to 0.$$

Thus we proved the claimed results. □

6. Computations

Theorem 3 can also be applied to compute cohomology groups in a combinatorical manner.

Lemma 14. 

If A is a finite abelian group, then ${\check{H}}_{ct}^1({\mathbb{Z}}_{\ge 0},A)=0$.

Proof. 

If $\phi \in kerd{Y}_1^b$ then $d_1\phi$ has cocontrolled support. This means for every $n\in \mathbb{N}$ the set $supp\left(d_1\phi \right)\cap {\Delta }_n^1$ is bounded. This amounts to saying that the function

$${\phi }_n:x\mapsto \phi (x,x+n)-\phi (x,x+1)-\cdots -\phi (x+n-1,x+n)$$

has finite support $x_1,\dots ,x_{r_n}\in {\mathbb{Z}}_{\ge 0}$. Then define

$$\begin{array}{cc}\hfill \tilde{\phi }:{\mathbb{Z}}_{\ge 0}& \to A\hfill \\ \hfill x& \mapsto \sum _{i=0}^{x-1}\phi (i,i+1).\hfill \end{array}$$

This function is blocky since $\tilde{\phi }$ assumes only finitely many values. Here, we use that A is finite. Moreover, we have

$$\begin{array}{cc}\hfill d_0\tilde{\phi }(x,x+n)& =\sum _{i=0}^{x+n-1}\phi (i,i+1)-\sum _{i=0}^{x-1}\phi (i,i+1)\hfill \\ \hfill & =\sum _{i=x}^{x+n-1}\phi (i,i+1)\hfill \\ \hfill & =\left\{\begin{array}{cc}\phi (x,x+n)-{\phi }_n\left(x\right)\hfill & x=x_1,\dots ,x_{r_n}\hfill \\ \phi (x,x+n)\hfill & otherwise.\hfill \end{array}\right.\hfill \end{array}$$

This shows that $\phi -d_0\tilde{\phi }$ has cocontrolled support. Thus $\phi$ is a coboundary in $C{Y}_b^1({\mathbb{Z}}_{\ge 0},A)$. □

Theorem 9. 

If T is a tree and A is a finite abelian group then

$${\check{H}}_{ct}^1(T;A)=0.$$

Proof. 

Designate an element $t_0\in T$ as the root of the tree and define

$$S=\{t\in T\mid d(t_0,t)\in {\mathbb{N}}_0\}.$$

Let $\phi \in C{Y}_b^1(S,A)$ be a cocycle. Then for every $s\in S$, there is a unique 1-path $a_0=t_0,\dots ,a_n=s$ joining $t_0$ to s. Define

$$\begin{array}{cc}\hfill \tilde{\phi }:S& \to A\hfill \\ \hfill s& \mapsto \sum _{i=0}^{n-1}\phi (a_i,a_{i+1})\hfill \end{array}$$

Let $n\ge 0$ be a number. If $s,t\in S$ and $d(s,t)=n$ then there exist paths $a_0,\dots ,a_k,c_0,\dots ,c_m$ joining $t_0$ to t and $a_0,\dots ,a_k,b_0,\dots ,b_l$ joining $t_0$ to s with $n=m+l+2$ or $n=m+l$ depending on whether $c_m,c_{m-1},\dots ,c_0,a_k,b_0,b_1,\dots ,b_l$ or $c_m,c_{m-1},\dots ,c_0,b_0,\dots ,b_l$ is a 1-path joining t to s. Then

$$d_0\tilde{\phi }(s,t)-\phi (s,t)=\phi (a_k,c_0)+\sum _{i=0}^{m-1}\phi (c_i,c_{i+1})-\phi (a_k,b_0)-\sum _{i=0}^{l-1}\phi (b_i,b_{i+1})-\phi (s,t)$$

is a would-be cocycle in ${\Delta }_{n+2}^1$; thus, it has bounded support. Thus, we showed $\phi$ is a coboundary.

Since the inclusion $S\subseteq T$ is coarsely surjective, we can conclude ${\check{H}}_{ct}^1(T,A)={\check{H}}_{ct}^1(S,A)=0$. □

We will compute the following example later in more detail. This version of the proof is more combinatorical though.

Lemma 15. 

If $\mathbb{Z}$ is the free abelian group on two generators, then ${\check{H}}_{ct}^1({\mathbb{Z}}^2,\mathbb{Z}/3\mathbb{Z})\ne 0$; indeed, the first cohomology group contains a copy of $\mathbb{Z}/3\mathbb{Z}$.

Proof. 

We divide ${\mathbb{Z}}^2$ into 4 quadrants: $A_0={\mathbb{Z}}_{\ge 0}\times {\mathbb{Z}}_{\ge 0},A_1={\mathbb{Z}}_{\ge 0}\times {\mathbb{Z}}_{<0},A_2={\mathbb{Z}}_{<0}\times {\mathbb{Z}}_{<0},A_3={\mathbb{Z}}_{<0}\times {\mathbb{Z}}_{\ge 0}$. Fix points $0\in A_0,\dots ,3\in A_3$. We define a cocycle $\phi \in C{Y}_b^1({\mathbb{Z}}^2,\mathbb{Z}/3\mathbb{Z})$ by

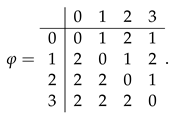Among other equations, we obtain $d_1\phi (0,2,0)=2-0+2=1$ and $d_1\phi (1,3,1)=2-0+2=1$. Thus, $A_0\times A_2\times A_0$ and $A_1\times A_3\times A_1$ lie in the support of $d_1\phi$. Since $A_0\times A_2$ and $A_1\times A_3$ are cocontrolled, this is okay. Checking the other finitely many equations, we obtain that $d_1\phi$ does indeed have cocontrolled support. Thus, $\phi$ is indeed a cocycle. We show that $\phi$ is not a coboundary. Suppose for contradiction that $\phi =d_0\psi +\tilde{\phi }$ with $\psi \in C{Y}_b^0({\mathbb{Z}}^2,\mathbb{Z}/3\mathbb{Z})$ and $\tilde{\phi }\in C{X}_b^1({\mathbb{Z}}^2,\mathbb{Z}/2\mathbb{Z})$. First we show $\psi \in C_{A_0,\dots ,A_3}({\mathbb{Z}}^2,\mathbb{Z}/3\mathbb{Z})$. Suppose for contradiction $A_0=A_{01}\bigsqcup A_{02}$ and ${\psi |}_{A_{01}}\equiv k$ while ${\psi |}_{A_{02}}$ does not take the value k. Then, $A_{01}\times A_{02}\subseteq supp{d}_0\psi =supp(\phi -\tilde{\phi })$. Since ${\phi |}_{A_0\times A_0}\equiv 0$ this implies $A_{01}\times A_{02}$ is contained in the support of $\tilde{\phi }$ and therefore is cocontrolled. Since $A_0$ is one-ended, this is a contradiction. Now, we construct $\psi$. Suppose $\psi \left(0\right)=k\in \mathbb{Z}/3\mathbb{Z}$. Since $A_0\times A_1$ is not cocontrolled, we obtain $\psi \left(1\right)=\psi \left(1\right)-\psi \left(0\right)+\psi \left(0\right)=\phi (0,1)+\psi \left(0\right)=2+k$ and similarly $\psi \left(3\right)=2+k$. Since $A_1\times A_2$ is not cocontrolled, we obtain $\psi \left(2\right)=\psi \left(2\right)-\psi \left(1\right)+\psi \left(1\right)=\phi (1,2)+\psi \left(1\right)=1+k$. Then

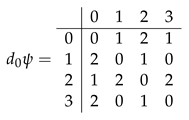If we compare the tables, we see that $d_0\psi -\phi$ does not have cocontrolled support. Thus, $\phi$ is a proper cocycle. □

7. Infinite Coefficients

The computations in Section 6 only work for finite coefficients. This chapter shows that the coefficient $\mathbb{Z}$ does not produce interesting cohomology groups.

If X is a proper metric space and A a metric space denoted by ${\mathcal{C}}_h(X,A)$ the abelian group of Higson functions $\phi :X\to A$ modulo functions with bounded support. Namely, a bounded function $\phi :X\to A$ is called Higson if for every entourage $E\subseteq X\times X$ and every $\epsilon >0$ there exists a compact subset $K\subseteq X$ such that $(x,y)\in E\backslash (K\times K)$ implies $d\left(\phi \right(x),\phi (y\left)\right)<\epsilon$.

Lemma 16. 

If X is a proper R-discrete for some $R>0$ metric space and A a metric space then $U\mapsto {\mathcal{C}}_h(U,A)$ for $U\subseteq X$ with the obvious restriction maps is a sheaf on $X_{ct}$.

Proof. 

Let $U_1,\dots ,U_n$ be a coarse cover of a subspace $U\subseteq X$.

We prove the base identity axiom. Let $\phi \in {\mathcal{C}}_h(U,A)$ be an element. If ${\phi |}_{U_1}{,\dots ,\phi |}_{U_n}$ have bounded support $B_1,\dots ,B_n$ then $\phi$ has support contained in the set

$$B_1\cup \cdots \cup B_n\cup {(U_1\cup \cdots \cup U_n)}^c$$

which is a finite union of bounded sets and therefore itself bounded. Thus, $\phi$ has bounded support.

Now, we prove the gluing axiom. Suppose there are functions ${\phi }_1\in {\mathcal{C}}_h(U_1,A),\dots ,{\phi }_n\in {\mathcal{C}}_h(U_n,A)$ with ${\phi }_i{{|}_{U_j}={\phi }_j|}_{U_i}$ for every $i,j\in \{1,\dots ,n\}$. Then, define a function

$$\begin{array}{cc}\hfill \phi :U& \to A\hfill \\ \hfill x& \mapsto \left\{\begin{array}{cc}{\phi }_1\left(x\right)\hfill & x\in U_1\hfill \\ {\phi }_2\left(x\right)\hfill & x\in U_2\backslash U_1\hfill \\ ⋮\hfill & ⋮\hfill \\ {\phi }_n\left(x\right)\hfill & x\in U_n\cap U_1^c\cap \cdots \cap U_{n-1}^c\hfill \\ 0\hfill & x\in U_1^c\cap \cdots \cap U_n^c\hfill \end{array}\right.\hfill \end{array}$$

which restricts to ${\phi }_i$ on each $U_i$. Here, $0\in A$ is any choice of point. Now $\phi$ is continuous since U is R-discrete. The image of $\phi$

$$im\phi =im{\phi }_1\cup \cdots \cup im{\phi }_n\cup \left\{0\right\}$$

is bounded. Now, we check the Higson property. If $E\subseteq U^2$ is an entourage, then

$${E=E|}_{U_1^2}\cup \cdots \cup E{{|}_{U_n^2}\cup E|}_{B^2}$$

where $B\subseteq U$ is bounded. Let $\epsilon >0$ be a number. Then for each i, there exists a bounded subset $K_i\subseteq U_i$ with $|{\phi }_i\left(x\right)-{\phi }_i\left(y\right)|<\epsilon$ for each ${(x,y)\in E|}_{U_i^2}\backslash K_i^2$. Now define $K=K_1\cup \cdots \cup K_n\cup B$. Then $\left|\phi \right(x)-\phi (y\left)\right|<\epsilon$ for each $(x,y)\in E\backslash K^2$. Thus, $\phi$ satisfies the Higson property. □

Denote by ${\mathcal{C}}_f(X,A)$ the abelian group of Freudenthal functions $\phi :X\to A$ modulo functions with bounded support. Namely, a bounded function $\phi :X\to A$ is called Freudenthal if for every entourage $E\subseteq X\times X$, there exists a compact subset $K\subseteq X$ such that $(x,y)\in E\backslash (K\times K)$ implies $\phi \left(x\right)=\phi \left(y\right)$.

Lemma 17. 

If X is a proper metric space and A is a countable abelian group, then the constant sheaf A on $X_{ct}$ is isomorphic to ${\mathcal{C}}_h(·,A)$ which is isomorphic to ${\mathcal{C}}_f(·,A)$.

Proof. 

For each $U\subseteq X$ we show that the inclusion ${\mathcal{C}}_f(U,A)\to {\mathcal{C}}_h(U,A)$ is bijective. Let $\phi \in {\mathcal{C}}_h(U,A)$ be an element. We show that $\phi$ is Freudenthal. Let $E\subseteq U^2$ be an entourage and choose $\epsilon =1/2$. Then, there exists a bounded set $K_{\epsilon }\subseteq U$ with $d\left(\phi \right(x),\phi (y\left)\right)<1/2$ for each $(x,y)\in E\backslash K^2$. Since A is 1-discrete, this implies $\phi \left(x\right)=\phi \left(y\right)$ for each $(x,y)\in E\backslash K^2$. Thus $\phi$ is Freudenthal.

Now, we show the constant sheaf A is isomorphic to ${\mathcal{C}}_f(·,A)$. We define a homomorphism $\Phi :A\left(U\right)\to {\mathcal{C}}_f(U,A)$. If $a\in A\left(U\right)$ then it can be written $a=a_1\oplus \cdots \oplus a_n$ corresponding to a coarse disjoint union $U_1\bigsqcup \cdots \bigsqcup U_n$. Then, we define

$$\begin{array}{cc}\hfill {\phi }_i:U_i& \to A\hfill \\ \hfill x& \mapsto a_i\hfill \end{array}$$

The ${\phi }_i$ are Higson and glue to a Higson function $\Phi \left(a\right):U\to A$. If $b\in A\left(U\right)$ is another element represented by $b_1\oplus \cdots \oplus b_m$ corresponding to $V_1\bigsqcup \cdots \bigsqcup V_m$ then $a+b$ is represented by ${⨁}_{ij}(a_i+b_j)$ corresponding to ${(U_i\cap V_j)}_{ij}$. Without loss of generality, the $U_i$ are pairwise disjoint and cover U and likewise, the $V_j$ are pairwise disjoint and cover U. Then,

$$(\Phi \left(a\right)+\Phi \left(b\right))\left(x\right)=\left\{\begin{array}{cc}{a}_1\hfill & x\in U_1\hfill \\ ⋮\hfill & ⋮\hfill \\ a_n\hfill & x\in U_n\hfill \end{array}\right.+\left\{\begin{array}{cc}{b}_1\hfill & x\in V_1\hfill \\ ⋮\hfill & ⋮\hfill \\ b_m\hfill & x\in V_m\hfill \end{array}\right.=\left\{\begin{array}{cc}{a}_1+b_1\hfill & x\in U_1\cap V_1\hfill \\ ⋮\hfill & ⋮\hfill \\ a_n+b_m\hfill & x\in U_n\cap V_m\hfill \end{array}\right.=\Phi (a+b)$$

Thus, $\Phi$ is a homomorphism. We show that $\Phi$ is well defined. Suppose $c\in A\left(U\right)$ is represented by 0 on $B^c$ where B is finite. Then $\Phi \left(c\right)$ has bounded support. Thus, $\Phi$ is well defined.

Now, we construct the inverse $\Psi :{\mathcal{C}}_f(U,A)\to A\left(U\right)$. If $\phi \in {\mathcal{C}}_f(U,A)$ is Freudenthal, then in particular its image $im\phi =\{a_1,\dots ,a_n\}$ is finite. Since $\phi$ is Higson, the ${\phi }^{-1}\left(a_1\right),\dots ,{\phi }^{-1}\left(a_n\right)$ are a pairwise coarsely disjoint union of U. Then, define $\Psi \left(\phi \right)$ to be the element represented by $a_1\oplus \cdots \oplus a_n$ corresponding to ${\phi }^{-1}\left(a_1\right),\dots ,{\phi }^{-1}\left(a_n\right)$. It is mapped by $\Phi$ to $\phi$. Thus, $\Phi$ is surjective. Now, we show $\Phi$ is injective: If $\phi$ has bounded support B then $\Psi \left(\phi \right)$ is represented by 0 on ${\phi }^{-1}\left(B^c\right)$. □

Proposition 2. 

If X is a proper metric space, the following sequence of sheaves on $X_{ct}$ is exact:

$$0\to {\mathcal{C}}_f(·,\mathbb{Z})\to {\mathcal{C}}_h(·,\mathbb{R})\to {\mathcal{C}}_h(·,S^1)\to 0$$

Proof. 

Let $U\subseteq X$ be a subset.

The map ${\mathcal{C}}_f(U,\mathbb{Z})\to {\mathcal{C}}_h(U,\mathbb{R})$ is induced by the inclusion $\mathbb{Z}\to \mathbb{R}$. This map is well defined since every Freudenthal function is Higson. It is injective. Thus exactness at ${\mathcal{C}}_f(·,\mathbb{Z})$ is guaranteed.

The map ${\mathcal{C}}_h(U,\mathbb{R})\to {\mathcal{C}}_h(U,S^1)$ is induced by the quotient map $\mathbb{R}\to \mathbb{R}/\mathbb{Z}$. A Higson function is in the kernel of this map exactly when its image is contained in $\mathbb{Z}$. Thus, exactness at ${\mathcal{C}}_h(·,\mathbb{R})$ is ensured.

Now we show exactness at ${\mathcal{C}}_h(·,S^1)$. Let $\phi \in {\mathcal{C}}_h(·,S^1)$ be a function. Its image $\mathbb{R}/\mathbb{Z}$ is covered by $V_1:=[0.25,1]+\mathbb{Z},V_2:=[0.75,1.5]+\mathbb{Z}$. Since

$$\overline{V_1^c}\cap \overline{V_2^c}=([0,0.25]+\mathbb{Z})\cap ([0.5,0.75]+\mathbb{Z})=Ø$$

we obtain that ${\phi }^{-1}\left(V_1^c\right)/⋏{\phi }^{-1}\left(V_2^c\right)$ are coarsely disjoint. Thus, $U_1:={\phi }^{-1}\left(V_1\right),U_2:={\phi }^{-1}\left(V_2\right)$ are a coarse cover of U. Now we describe a lift ${\phi }_1:U_1\to \mathbb{R}$ of ${\phi |}_{U_1}$: If $x\in U_1$ then ${\phi }_1\left(x\right)$ is defined to be the representative of $\phi \left(x\right)$ in the interval $[0.25,1]$. A lift ${\phi }_2:U_2\to \mathbb{R}$ of ${\phi |}_{U_2}$ is obtained by defining ${\phi }_2\left(x\right)$ to be the representative of $\phi \left(x\right)$ in the interval $[0.75,1.5]$. Thus, the right morphism in the diagram is surjective. □

Lemma 18. 

If X is a proper metric space, the sheaf ${\mathcal{C}}_h(·,\mathbb{R})$ is flabby.

Proof. 

Let $A\subseteq X$ be a subset. Since $A\subseteq hX$ is a subset, the closure of A in $hX$ is a compactification $\overline{A}$ generated by $C_h{\left(X\right)|}_A:=\{\phi {|}_A:\phi \in C_h\left(X\right)\}$. Now, $\overline{A}$ is equivalent (as a compactification) to $hA$ and thus also generated by $C_h\left(A\right)$. Since both $C_h{\left(X\right)|}_A$ and $C_h\left(A\right)$ separate points from closed sets, they are both contained in $C_h$, the algebra of bounded functions on A which extend to $hA$ ([21], Proposition 2). The ([21], Proposition 2) also states that $C_h\subseteq C^{\ast }\left(A\right)$ is the smallest unital, closed $C^{\ast }$-algebra with this property. Since both $C_h{\left(X\right)|}_A$ and $C_h\left(A\right)$ are unital, closed the equality

$$C_h{\left(X\right)|}_A=C_h=C_h\left(A\right)$$

holds.

We provide another proof using the Tietze extension theorem. If an element in ${\mathcal{C}}_h(U,\mathbb{R})$ is represented by $\phi \in {\mathcal{C}}_h\left(U\right)$ then it extends to $\overline{\phi }$ on $hU$. By the Tietze extension theorem, we can extend $\overline{\phi }$ to a bounded function $\widehat{\phi }$ on $hX$. Then, $\widehat{\phi }{|}_X$ represents an element in ${\mathcal{C}}_h(X,\mathbb{R})$ that restricts to $\phi$. □

Example 1. 

We show ${\mathcal{C}}_h(·,\mathbb{R})$ is flabby on the specific example $\mathbb{Z}$ constructing a concrete global lift of a Higson function $\phi :U\to \mathbb{R}$ on a subspace of $\mathbb{Z}$. If $z\in U^c$ then there are $z_{-},z_{+}\in U$ with $z_{-}$ the largest number in U with $z_{-}<z$ and $z_{+}$ the smallest number in U with $z<z_{+}$. Define

$$\overline{\phi }\left(z\right)=\frac{\phi \left(z_{-}\right)(z_{+}-z)+\phi \left(z_{+}\right)(z-z_{-})}{z_{+}-z_{-}}.$$

This function $\overline{\phi }$ is Higson: If $\epsilon >0$ then there exists an $N\in \mathbb{N}$ with $|\phi \left(y\right)-\phi \left(y^{\prime }\right)|<\epsilon$ for every $y,y^{\prime }\in U$ with $|y-y^{\prime }|<2|\phi |/\epsilon$ and $y,y^{\prime }>N$. If $z,z^{\prime }\in U^c$ with $|z-z^{\prime }|=1$ then

$$\begin{array}{cc}\hfill |\overline{\phi }\left(z\right)-\overline{\phi }\left(z^{\prime }\right)|& =\left|\frac{\phi \left(z_{-}\right)(z_{+}-z)+\phi \left(z_{+}\right)(z-z_{-})}{z_{+}-z_{-}}-\frac{\phi \left(z_{-}\right)(z_{+}-z^{\prime })+\phi \left(z_{+}\right)(z^{\prime }-z_{-})}{z_{+}-z_{-}}\right|\hfill \\ \hfill & =\left|\frac{\phi \left(z_{-}\right)(z^{\prime }-z)+\phi \left(z_{+}\right)(z-z^{\prime })}{z_{+}-z_{-}}\right|\hfill \\ \hfill & =\left|\frac{\phi \left(z_{+}\right)-\phi \left(z_{-}\right)}{z_{+}-z_{-}}\right|\hfill \\ \hfill & <\left\{\begin{array}{cc}\frac{2\left|\phi \right|}{2\left|\phi \right|/\epsilon }\hfill & z_{+}-z_{-}>2\left|\phi \right|/\epsilon \hfill \\ \frac{\epsilon }{z_{+}-z_{-}}\hfill & z_{+}-z_{-}\le 2\left|\phi \right|/\epsilon \hfill \end{array}\right.\hfill \\ \hfill & \le \epsilon \hfill \end{array}$$

provided $z,z^{\prime }>N$.

Remark 1. 

By the long exact sequence in cohomology, we obtain

$${\check{H}}_{ct}^1(X;A)=\frac{{\mathcal{C}}_h(X,S^1)}{{\mathcal{C}}_h(X,\mathbb{R})}.$$

If $X=\mathbb{Z}$ we can define

$$\begin{array}{cc}\hfill \phi :\mathbb{Z}& \to \mathbb{R}\hfill \\ \hfill z& \mapsto \sum _{n=1}^{\left|z\right|}\frac{1}{n}.\hfill \end{array}$$

This function satisfies the Higson condition but is not bounded. Post-composition with the projection $\mathbb{R}\to S^1$ gives a Higson function $\tilde{\phi }:\mathbb{Z}\to S^1$ which does not have a lift. Compare this result with [8].

Remark 2. 

It would be great if we could find an algorithm that computes coarse cohomology with constant coefficients of a finitely presented group. This does not work even in degree 0. If we could decide whether ${\check{H}}_{ct}^0(G;A)$ vanishes, then we can decide whether G is finite. This is in general not decidable.

8. The Inverse Image Functor

In this section, we fix a coarse map $\alpha :X\to Y$ between metric spaces.

If $\mathcal{G}$ is a sheaf on $Y_{ct}$ then the inverse image (or pullback sheaf) ${\alpha }^{\ast }\mathcal{G}$ is the sheafification of the presheaf on $X_{ct}$ which assigns $U\subseteq X$ with $\mathcal{G}\left(\alpha \right(U\left)\right)$.

Conversely, if $\mathcal{F}$ is a sheaf on $X_{ct}$ then the direct image ${\alpha }_{\ast }\mathcal{F}$ is the sheaf on $Y_{ct}$ which assigns $\mathcal{F}\left({\alpha }^{-1}\left(V\right)\right)$ to $V\subseteq Y$.

Lemma 19. 

The functor ${\alpha }^{\ast }$ is left adjoint to ${\alpha }_{\ast }$. The functor ${\alpha }_{\ast }$ is left exact and the functor ${\alpha }^{\ast }$ is exact. The functor ${\alpha }_{\ast }$ maps injectives to injectives.

Proof. 

The functor

$$\begin{array}{cc}\hfill {\alpha }^{-1}:Cat\left(Y_{ct}\right)& \to Cat\left(X_{ct}\right)\hfill \\ \hfill V& \mapsto {\alpha }^{-1}\left(V\right)\hfill \end{array}$$

is a morphism of Grothendieck topologies and therefore gives rise to functors ${\left({\alpha }^{-1}\right)}^p,{\left({\alpha }^{-1}\right)}_p$ between categories of presheaves ([22], Chapter I,2.3). The functor ${\left({\alpha }^{-1}\right)}^p$ maps a presheaf $\mathcal{F}$ on $X_{ct}$ to the presheaf $V\mapsto \mathcal{F}\left({\alpha }^{-1}\left(V\right)\right)$ on $Y_{ct}$. ${\left({\alpha }^{-1}\right)}_p$ is defined in ([22], Theorem I,2.3.1). If $\mathcal{G}$ is a presheaf on $Y_{ct}$ and $U\subseteq X$ we define ${\left({\alpha }^{-1}\right)}_p\mathcal{G}\left(U\right)$: Consider all $V\in Cat\left(Y_{ct}\right)$ with $U\subseteq {\alpha }^{-1}\left(V\right)$. They form a category ${\mathcal{I}}_U$. Then,

$${\left({\alpha }^{-1}\right)}_p\mathcal{G}\left(U\right)=\underset{V\in {\mathcal{I}}_U^{op}}{\underrightarrow{lim}}\mathcal{G}\left(V\right)=\mathcal{G}\left(\alpha \left(U\right)\right)$$

since $\alpha \left(U\right)$ is the initial object in ${\mathcal{I}}_U$.

Then ([22], Chapter I,3.6) discusses functors ${\left({\alpha }^{-1}\right)}^s$ and ${\left({\alpha }^{-1}\right)}_s$ between categories of sheaves. We obtain the direct image functor ${\alpha }_{\ast }={\left({\alpha }^{-1}\right)}^s$ and the inverse image functor ${\alpha }^{\ast }={\left({\alpha }^{-1}\right)}_s$. Then ([22], Proposition I,3.6.2) implies that ${\alpha }^{\ast }$ is left adjoint to ${\alpha }_{\ast }$, the functor ${\alpha }_{\ast }$ is left exact and if ${\alpha }^{\ast }$ is actually exact then the functor ${\alpha }_{\ast }$ maps injectives to injectives. It remains to show that ${\alpha }^{\ast }$ is exact. By ([22], Proposition I,3.6.7) the functor ${\alpha }^{\ast }$ is exact if ${\alpha }^{-1}$ preserves finite fibre products and final objects. Indeed, the inverse image of an intersection is an intersection of inverse images and the inverse image of the whole space is the whole space. □

There are of course non-metrizable coarse spaces. Usually, we are only interested in metric spaces except in the following case. Note that coarse cohomology with twisted coefficients has been defined on all coarse spaces.

Proposition 3. 

If we equip $\mathbb{N}$ with the topological coarse structure associated to the one-point compactification ${\mathbb{N}}^{+}$ of $\mathbb{N}$, we obtain a coarse space called ∗. This space ∗ is not metrizable but a final object for metric spaces. The constant sheaf on ∗ is flabby.

Proof. 

A set $C\subseteq {\mathbb{N}}^{+}$ is closed if it is finite or contains +. Thus, a subset $E\subseteq \mathbb{N}\times \mathbb{N}$ is an entourage if for every subset $E^{\prime }\subseteq E$ the projection of $E^{\prime }$ to the first factor is finite exactly when the projection of $E^{\prime }$ to the second factor is finite.

Let X be a metric space and $x_0\in X$ a basepoint. We define a map

$$\begin{array}{cc}\hfill \rho :X& \to \ast \hfill \\ \hfill x& \mapsto \lfloor d(x,x_0)\rfloor .\hfill \end{array}$$

We show that this map is coarsely uniform: If $R\ge 0$ and $F\subseteq {\rho }^{\times 2}\left({\Delta }_R\right)$ a subset such that the projection to the first factor is finite then choose arbitrary $(x,y)\in {\Delta }_R$ with $\left(\rho \right(x),\rho (y\left)\right)\in F$. Since the first factor of F is finite, there is some $S\ge 0$ with $\lfloor d(x,x_0)\rfloor \le S$. Then,

$$\begin{array}{cc}\hfill \lfloor d(y,x_0)\rfloor & \le d(y,x)+d(x,x_0)+1\hfill \\ \hfill & \le R+S+2.\hfill \end{array}$$

Thus, the projection of F to the second factor is finite. This implies that $\rho$ is coarsely uniform. If $B\subseteq \ast$ is bounded, then there exists some $S\ge 0$ such that $b\in B$ implies $b\le S-1$. Then, ${\rho }^{-1}\left(B\right)$ is contained in a ball of diameter S around $x_0$. Thus, $\rho$ is coarsely proper. This way, we showed that $\rho$ is a coarse map. Suppose $\phi :X\to \ast$ is another coarse map. Let $H^{\prime }\subseteq (\rho \times \phi )\left({\Delta }_0\right)$ be a subset such that the projection of $H^{\prime }$ to the first factor is finite. We have that $H^{\prime }$ is of the form

$$H^{\prime }=\{(\rho \left(x\right),\phi \left(x\right))\mid x\in A\}$$

for some subset $A\subseteq X$. Then, the projection of $H^{\prime }$ to the first factor is $\rho \left(A\right)$. Since $\rho$ is coarsely proper, the set $A\subseteq {\rho }^{-1}\circ \rho \left(A\right)$ is bounded. This implies that $\phi \left(A\right)$ is bounded which is the projection of $H^{\prime }$ to the second factor. Since we only used that $\rho ,\phi$ are coarse maps, we can use the same argument with the factors reversed. Thus, we showed that $(\rho \times \phi )\left({\Delta }_0\right)$ is an entourage in ∗. This implies that $\rho ,\phi$ are close; they represent the same coarse map. This way we showed that ∗ is a final object for metric spaces.

If $A,B\subseteq \ast$ are infinite subspaces, then there exists a bijection $\phi :A\to B$. The set $E:=\left\{\right(a,\phi \left(a\right))\mid a\in A\}$ is an entourage and $(A\times B)\cap E=E$ is not bounded. Thus, $A\times B$ is not cocontrolled. We conclude that a coarse cover of a subset $U\subseteq \ast$ contains an element which is cofinite in U. Let A be an abelian group. Then,

$$A_{\ast }\left(U\right)=\left\{\begin{array}{cc}A\hfill & U \mathrm{infinite}\hfill \\ 0\hfill & U \mathrm{finite}\hfill \end{array}\right.$$

This shows that $A_{\ast }$ is flabby. □

Lemma 20. 

If A is an abelian group, then $A_X={\alpha }^{\ast }{A}_Y$. The unit of ${\alpha }^{\ast },{\alpha }_{\ast }$ at $A_Y$ is given by

$$\begin{array}{cc}\hfill {\eta }_{A_Y}\left(V\right):A_Y\left(V\right)& \to A_X\left({\alpha }^{-1}\left(V\right)\right)\hfill \\ \hfill (\phi :V\to A)& \mapsto (\phi \circ \alpha :{\alpha }^{-1}\left(V\right)\to A).\hfill \end{array}$$

Proof. 

If Z is a metric space and ${\rho }_Z:Z\to \ast$ the unique coarse map we prove $A_Z={\rho }_Z^{\ast }{A}_{\ast }$. This proves the claim since

$${\alpha }^{\ast }{A}_Y={\alpha }^{\ast }\circ {\rho }_Y^{\ast }{A}_{\ast }={({\rho }_Y\circ \alpha )}^{\ast }{A}_{\ast }={\rho }_X^{\ast }{A}_{\ast }=A_X.$$

The sheaf ${\rho }_Z^{\ast }{A}_{\ast }$ is the sheafification of the following presheaf

$$U\mapsto A_{\ast }\left(\rho \left(U\right)\right)=\left\{\begin{array}{cc}A\hfill & U \mathrm{not} \mathrm{bounded}\hfill \\ 0\hfill & U \mathrm{bounded}\hfill \end{array}\right..$$

Now, this is just the constant sheaf on Z.

Now, we compute the unit of the adjunction ${\alpha }^{\ast },{\alpha }_{\ast }$. We denote by ${\alpha }^{-1}$ the presheaf inverse image functor. Then, the unit of the adjunction ${\alpha }^{-1},{\alpha }_{\ast }$ at $A_Y$ is given by

$$\begin{array}{cc}\hfill {\eta }_{A_Y}^1\left(V\right):A_Y\left(V\right)& \to {\alpha }_{\ast }{\alpha }^{-1}{A}_Y\left(V\right)=A_Y(\alpha \circ {\alpha }^{-1}\left(V\right))\hfill \\ \hfill \phi & {\mapsto \phi |}_{\alpha \circ {\alpha }^{-1}\left(W\right)}\hfill \end{array}$$

The unit of the adjunction sheafification # and inclusion $\iota$ of presheaves in sheaves at ${\alpha }^{-1}{A}_Y$ is given by

$$\begin{array}{cc}\hfill {\eta }_{{\alpha }^{-1}{A}_Y}^2\left(U\right):{\alpha }^{-1}{A}_Y\left(U\right)=A_Y\left(\alpha \left(U\right)\right)& \to {\alpha }^{\ast }{A}_Y\left(U\right)=A_X\left(U\right)\hfill \\ \hfill (\phi :\alpha (U)\to A)& \mapsto (\phi \circ \alpha :U\to A)\hfill \end{array}$$

This makes sense since $\phi$ assigns a value $a_{V_i}$ to $V_i\subseteq \alpha \left(U\right)$ where ${\left(V_i\right)}_i$ is a coarse disjoint union of $\alpha \left(U\right)$. Since $\alpha$ is a coarse map, the ${\alpha }^{-1}\left(V_i\right)$ form a coarse disjoint union of U. Then, ${\left(a_{V_i}\right)}_{{\alpha }^{-1}\left(V_i\right)}$ represents $\phi$ on U which in cocycle notation is ${\phi \circ \alpha |}_U$. Now, we compose the units:

$$A_Y\stackrel{{\eta }_{A_Y}^1}{\to }{\alpha }_{\ast }{\alpha }^{-1}{A}_Y\stackrel{{\alpha }_{\ast }\left({\eta }_{{\alpha }^{-1}{A}_Y}^2\right)}{\to }{\alpha }_{\ast }{\alpha }^{\ast }{A}_Y$$

and obtain the desired result. □

Theorem 10. 

The map induced by the inverse image functor

$${\alpha }^{\ast }:{\check{H}}_{ct}^q(Y,A_Y)\to {\check{H}}_{ct}^q(X,A_X)$$

coincides with the canonical map

$${\alpha }^{\ast }:H{Y}_b^q(Y,A)\to H{Y}_b^q(X,A).$$

Proof. 

We apply ([23], Scolium II.5.2). We checked that the proof of this result also works for sheaves on a Grothendieck topology. We choose $f=\alpha$, $G=A_Y$ and $T^q=C{Y}^q(·,A)$ a resolution on Y. Then, ${\alpha }^{\ast }G=A_X$ has a resolution $C{Y}^q(·,A)$ on X. The morphism of complexes is given by

$$\begin{array}{cc}\hfill {\psi }^q:C{Y}_b^q(V,A)& \to C{Y}_b^q({\alpha }^{-1}\left(V\right),A)\hfill \\ \hfill (\phi :V^{q+1}\to A)& \mapsto (\phi \circ {\alpha }^{\times (q+1)}:{\left({\alpha }^{-1}\left(U\right)\right)}^{q+1}\to A)\hfill \end{array}$$

which makes the diagram

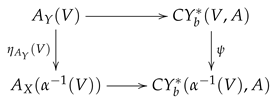commute. □

9. Sheaves on the Higson Corona

This chapter proves Theorem 5.

Lemma 21. 

Let X be a metric space. If $U_1,\dots ,U_n$ is a coarse cover of X then there exists a coarse cover $V_1,\dots ,V_n$ of X with $V_i /⋏U_i^c$ for every $i=1,\dots ,n$.

Proof. 

By ([24], Lemma 15) there exists a cover $W_1,\cdots ,W_n$ of X as a set such that $W_i /⋏U_i^c$ for every i. For every i there exists an in-between set $C_i$ with $W_i /⋏C_i^c$ and $C_i /⋏U_i^c$. Then for every i, the sets $A_i^1:=W_i^c,A_i^2:=C_i$ are a coarse cover. Taking the intersection over those coarse covers provides a coarse cover

$$\mathcal{B}:=\{A_1^{{\epsilon }_1}\cap \cdots \cap A_n^{{\epsilon }_n}:{ϵ}_i=1,2\}.$$

Now, let $B:=A_1^{{\epsilon }_1}\cap \cdots \cap A_n^{{\epsilon }_n}\in \mathcal{B}$ be an element. If there is some i with ${\epsilon }_i=2$ then

$$B\subseteq C_i /⋏U_i^c$$

and in the other case ${\epsilon }_i=1$ for every i. Thus,

$$B=W_1^c\cap \cdots \cap W_n^c={\left(\bigcup _i{W}_i\right)}^c=Ø.$$

Now, we join appropriate elements of $\mathcal{B}$ and obtain the desired coarse cover:

$$V_i:=\bigcup _{({\epsilon }_1,\dots ,{\epsilon }_n)\in {\{1,2\}}^n,{\epsilon }_i=2}{A}_1^{{\epsilon }_1}\cap \cdots \cap A_n^{{\epsilon }_n}.$$

□

Given a sheaf F on $X_{ct}$ we define a sheaf $F^{\nu }$ on $\nu \left(X\right)$: If both $A /⋏U^c,B /⋏U^c$ then $A\cup B /⋏U^c$. Thus, ${\left(A\right)}_{A /⋏U^c}$ is a directed poset by inclusion. Now we define a sheaf $F^{\nu }$ on basic open subsets of $\nu \left(X\right)$. If $U\subseteq X$ is a subset, then

$$F^{\nu }\left(\mathsf{cl}{\left(U^c\right)}^c\right):=\underset{A /⋏U^c}{\underleftarrow{lim}}F\left(A\right).$$

If $V\subseteq U$ is an inclusion of subspaces then $A /⋏V^c$ implies $A /⋏U^c$. Thus, there is a well-defined restriction map $F^{\nu }\left(\mathsf{cl}{\left(U^c\right)}^c\right)\to F^{\nu }\left(\mathsf{cl}{\left(V^c\right)}^c\right)$ which maps ${\left({\phi }_A\right)}_{A /⋏U^c}$ to ${\left({\phi }_A\right)}_{A /⋏V^c}$. This makes $F^{\nu }$ a presheaf.

Proposition 4. 

If X is a proper metric space and F a sheaf on $X_{ct}$ then $F^{\nu }$ is a sheaf on $\nu \left(X\right)$.

Proof. 

Let $\mathsf{cl}{\left(U^c\right)}^c={\bigcup }_i\mathsf{cl}{\left(U_i^c\right)}^c$ be a cover of a basic open set by basic open sets.

Let $A\subseteq X$ be a subset with $A /⋏U^c$. Then,

$$\mathsf{cl}\left(A\right)\cap \bigcap _i\mathsf{cl}\left(U_i^c\right)=\mathsf{cl}\left(A\right)\cap \mathsf{cl}\left(U^c\right)=Ø$$

Thus, ${\left(\mathsf{cl}{\left(U_i^c\right)}^c\right)}_i,\mathsf{cl}{\left(A\right)}^c$ is an open cover of $\nu \left(X\right)$. Since $\nu \left(X\right)$ is compact, there exists a finite subcover $\mathsf{cl}{\left(U_1^c\right)}^c\cup \cdots \cup \mathsf{cl}{\left(U_n^c\right)}^c\cup \mathsf{cl}{\left(A\right)}^c$. By ([25], Lemma 32) the subsets $U_1,\dots ,U_n,A^c$ are a coarse cover of X. By Lemma 21 there exists a finite coarse cover $V_1,\dots ,V_n,B$ of X such that $V_i /⋏U_i^c$ for every i and $B /⋏A$. Then $V_1,\dots ,V_n$ are a coarse cover of A.

We show the base identity axiom: Let $\varphi ,\psi \in F^{\nu }\left(\mathsf{cl}{\left(U^c\right)}^c\right)$ be elements with ${\varphi |}_{\mathsf{cl}{\left(U_i^c\right)}^c}{=\psi |}_{\mathsf{cl}{\left(U_i^c\right)}^c}$ for every i. Since ${\varphi }_{V_i}={\psi }_{V_i}$ for every i the identity axiom on coarse covers implies ${\varphi }_A={\psi }_A$.

Now we show the base gluablity axiom. Let ${\varphi }_i\in F^{\nu }\left(\mathsf{cl}{\left(U_i^c\right)}^c\right)$ be a section for every i such that ${\varphi }_i{{|}_{\mathsf{cl}{\left({(U_i\cap U_j)}^c\right)}^c}={\varphi }_j|}_{\mathsf{cl}{\left({(U_i\cap U_j)}^c\right)}^c}$ for every $i,j$. Then the ${\left({\varphi }_i\right)}_{V_i}$ glue to a section ${\varphi }_A$ on A by the gluablity axiom on coarse covers. □

If $\alpha :F\to F^{\prime }$ is a morphism of sheaves on $X_{ct}$ then we define for every basic open $\mathsf{cl}{\left(U^c\right)}^c$:

$$\begin{array}{cc}\hfill {\alpha }^{\nu }\left(\mathsf{cl}{\left(U^c\right)}^c\right):F^{\nu }\left(\mathsf{cl}{\left(U^c\right)}^c\right)& \to F^{\prime \nu }\left(\mathsf{cl}{\left(U^c\right)}^c\right)\hfill \\ \hfill {\left({\phi }_A\right)}_{A /⋏U^c}& \mapsto {\left(\alpha \left(A\right)\left({\phi }_A\right)\right)}_{A /⋏U^c}.\hfill \end{array}$$

This definition makes sense since $B\subseteq A$ implies that $\left(\alpha \left(A\right)\left({\phi }_A\right)\right){|}_B=\alpha \left(B\right)\left({\phi }_A{|}_B\right)$. Thus, ${\left(\alpha \left(A\right)\left({\phi }_A\right)\right)}_{A /⋏U^c}$ is an element in ${\underleftarrow{lim}}_{A /⋏U^c}{F}^{\prime }\left(A\right)$. By gluing along basic open covers, we obtain for every open $\pi \subseteq \nu \left(X\right)$ a map ${\alpha }^{\nu }\left(\pi \right):F^{\nu }\left(\pi \right)\to F^{\prime \nu }\left(\pi \right)$. We show that ${\alpha }^{\nu }:F^{\nu }\to F^{\prime \nu }$ is a morphism of sheaves: If $V\subseteq U$ is an inclusion of subsets and ${\left({\phi }_A\right)}_{A /⋏U^c}\in F^{\nu }\left(\mathsf{cl}{\left(U^c\right)}^c\right)$ an element, then

$$\begin{array}{cc}\hfill {\alpha }^{\nu }\left(\mathsf{cl}{\left(V^c\right)}^c\right){\circ ·|}_{\mathsf{cl}{\left(V^c\right)}^c}\left({\left({\phi }_A\right)}_{A /⋏U^c}\right)& ={\alpha }^{\nu }\left(\mathsf{cl}{\left(V^c\right)}^c\right)\left({\left({\phi }_A\right)}_{A /⋏V^c}\right)\hfill \\ \hfill & ={\left(\alpha \left(A\right)\left({\phi }_A\right)\right)}_{A /⋏V^c})\hfill \\ \hfill & {=·|}_{\mathsf{cl}{\left(V^c\right)}^c}\left({\left(\alpha \left(A\right)\left({\phi }_A\right)\right)}_{A /⋏U^c}\right))\hfill \\ \hfill & {=·|}_{\mathsf{cl}{\left(V^c\right)}^c}\circ {\alpha }^{\nu }\left(\mathsf{cl}{\left(U^c\right)}^c\right)\left({\left({\phi }_A\right)}_{A /⋏U^c}\right).\hfill \end{array}$$

Moreover, $i{d}_F^{\nu }=i{d}_{F^{\nu }}$ and ${(\alpha \circ \beta )}^{\nu }={\alpha }^{\nu }\circ {\beta }^{\nu }$. Thus, we have proved that ${·}^{\nu }$ is a functor. Namely, if $\mathtt{Sheaf}\left(X_{ct}\right)$ denotes the category of sheaves on $X_{ct}$ and $\mathtt{Sheaf}\left(\nu \right(X\left)\right)$ denotes the category of sheaves on $\nu \left(X\right)$, then

$${·}^{\nu }:\mathtt{Sheaf}\left(X_{ct}\right)\to \mathtt{Sheaf}\left(\nu \left(X\right)\right)$$

is a functor between categories of sheaves.

Lemma 22. 

Let X be a proper metric space. If $U_1^c,\dots ,U_n^c,A\subseteq X$ are subsets with $\mathsf{cl}\left(U_1^c\right)\cap \cdots \cap \mathsf{cl}\left(U_n^c\right)\cap \mathsf{cl}\left(A\right)=Ø$ then there exists a subset $U^c\subseteq X$ with

$$\mathsf{cl}{\left({(U_1\cap U)}^c\right)}^c\cup \cdots \cup \mathsf{cl}{\left({(U_n\cap U)}^c\right)}^c=\mathsf{cl}{\left(U^c\right)}^c$$

an open cover and $U^c/ ⋏A$.

Proof. 

Since $\nu \left(X\right)$ is compact there only exists one proximity relation on $\nu \left(X\right)$ which induces the topology on $\nu \left(X\right)$. Thus, the relation $\delta$ defined by ${\pi }_1\delta {\pi }_2$ if $\overline{{\pi }_1}\cap \overline{{\pi }_2}\ne Ø$ and the relation induced by ⋏ on the quotient coincide. Since both $\pi :=\mathsf{cl}\left(U_1^c\right)\cap \cdots \cap \mathsf{cl}\left(U_n^c\right)$ and $\mathsf{cl}\left(A\right)$ are closed sets, we obtain

$$\overline{\pi }\cap \overline{\mathsf{cl}\left(A\right)}=\pi \cap \mathsf{cl}\left(A\right)=Ø.$$

Thus, $\pi /⋏\mathsf{cl}\left(A\right)$. Then, there exist $U^c,B\subseteq X$ with $\pi \subseteq \mathsf{cl}\left(U^c\right),\mathsf{cl}\left(A\right)\subseteq \mathsf{cl}\left(B\right)$ and $U^c /⋏B$. This in particular implies that $U^c /⋏A$. Then,

$$\begin{array}{cc}\hfill \mathsf{cl}\left({(U_1\cap U)}^c\right)\cup \cdots \cup \mathsf{cl}\left({(U_n\cap U)}^c\right)& =\bigcup _i\mathsf{cl}{\left(U_1^c\cup U^c\right)}^c\hfill \\ \hfill & ={\left(\bigcap _i\left(\mathsf{cl}\left(U_i^c\right)\cup \mathsf{cl}\left(U^c\right)\right)\right)}^c\hfill \\ \hfill & =\bigcup _i\mathsf{cl}{\left(U_i^c\right)}^c\cap \mathsf{cl}{\left(U^c\right)}^c\hfill \\ \hfill & ={\pi }^c\cap \mathsf{cl}{\left(U^c\right)}^c\hfill \\ \hfill & =\mathsf{cl}{\left(U^c\right)}^c.\hfill \end{array}$$

□

Given a subset $A\subseteq X$ of a proper metric the relations $U^c /⋏A$ and $V^c /⋏A$ imply $U^c\cup V^c /⋏A$. Thus, ${\left(U^c\right)}_{U^c /⋏A}$ is a directed poset. If G is a sheaf on $\nu \left(X\right)$ we define

$$\widehat{G}\left(A\right):=\underset{A /⋏U^c}{\underrightarrow{lim}}G\left(\mathsf{cl}{\left(U^c\right)}^c\right)$$

If $A\subseteq B$ then $U^c /⋏B$ implies $U^c /⋏A$. Thus, we can define a well-defined restriction map $\widehat{G}\left(B\right)\to \widehat{G}\left(A\right)$ which maps $\left[{\phi }_{U^c}\right]$ to $\left[{\phi }_{U^c}\right]$. This makes $\widehat{G}$ a presheaf on $X_{ct}$.

A sheaf F on $X_{ct}$ is called reflective if for every subset $A\subseteq X$ the canonical map

$$\underset{A /⋏U^c}{\underrightarrow{lim}}F\left(U\right)\to F\left(A\right)$$

is an isomorphism.

Proposition 5. 

Let X be a proper metric space. If G is a sheaf on $\nu \left(X\right)$, then $\widehat{G}$ is a reflective sheaf on $X_{ct}$.

Proof. 

Let $A_1,\dots ,A_n$ be a coarse cover of $A\subseteq X$.

We prove the identity axiom. Let $s\in \widehat{G}\left(A\right)$ be a section with ${s|}_{A_i}=0$ for every i. Then there exists $U_i^c /⋏A_i$ with $s_{U_i^c}=t_{U_i^c}$ in $G\left(\mathsf{cl}{\left(U_i^c\right)}^c\right)$. Since $\mathsf{cl}\left(A_i\right)\cap \mathsf{cl}\left(U_i^c\right)=Ø$ we obtain

$$\begin{array}{cc}\hfill \mathsf{cl}\left(U_1^c\right)\cap \cdots \cap \mathsf{cl}\left(U_n^c\right)\cap \mathsf{cl}\left(A\right)& \subseteq \mathsf{cl}{\left(A_1\right)}^c\cap \cdots \cap \mathsf{cl}{\left(A_n\right)}^c\cap \mathsf{cl}\left(\right)A\hfill \\ \hfill & ={(\mathsf{cl}\left(A_1\right)\cup \cdots \cup \mathsf{cl}\left(A_n\right))}^c\cap \mathsf{cl}\left(\right)A\hfill \\ \hfill & =Ø.\hfill \end{array}$$

By Lemma 22 there is some $U\subseteq X$ with $\mathsf{cl}{\left({(U_1\cap U)}^c\right)}^c\cup \cdots \cup \mathsf{cl}{\left({(U_n\cap U)}^c\right)}^c=\mathsf{cl}{\left(U^c\right)}^c$ an open cover and $U^c /⋏A$. Thus, the identity axiom for open covers implies $s_{U^c}=0$. This proves $s=0$ in $\widehat{G}\left(A\right)$.

Now, we prove the gluablity axiom. Let $s_i\in \widehat{G}\left(A_i\right)$ be a section for every i with $s_i{{|}_{A_j}=s_j|}_{A_i}$ for every $i,j$. Suppose $s_i$ are represented by ${\left(s_i\right)}_{U_i^c}\in G\left(\mathsf{cl}{\left(U_i^c\right)}^c\right)$ with $U_i^c /⋏A_i$. As in the first part of this proof, there is some subset $U^c\subseteq X$ with

$$\mathsf{cl}{\left({(U_1\cap U)}^c\right)}^c\cup \cdots \cup \mathsf{cl}{\left({(U_n\cap U)}^c\right)}^c=\mathsf{cl}{\left(U^c\right)}^c$$

and $U^c /⋏A$. By the gluablity axiom on open covers the ${\left(s_i\right)}_{U_i^c}$ glue to a section $s_{U^c}\in G\left(\mathsf{cl}{\left(U^c\right)}^c\right)$ which represents a section $s\in \widehat{G}\left(A\right)$.

Now, we show that $\widehat{G}$ is reflective. For every $A,U\subseteq X$ with $A /⋏U^c$ there exists $T\subseteq X$ with $A /⋏T^c$ and $T /⋏U^c$. Thus,

$$\underset{A /⋏T^c}{\underrightarrow{lim}}\widehat{G}\left(T\right)=\underset{A /⋏T^c}{\underrightarrow{lim}}\underset{T /⋏U^c}{\underrightarrow{lim}}G\left(\mathsf{cl}{\left(U^c\right)}^c\right)\to \underset{A /⋏U^c}{\underrightarrow{lim}}G\left(\mathsf{cl}{\left(U^c\right)}^c\right)$$

is an isomorphism. □

If $\beta :G\to G^{\prime }$ is a morphism of sheaves on $\nu \left(X\right)$ and $A\subseteq X$ a subset then

$$\begin{array}{cc}\hfill \widehat{\beta }\left(A\right):\widehat{G}\left(A\right)& \to {\widehat{G}}^{\prime }\left(A\right)\hfill \\ \hfill [{\phi }_{U^c}]& \mapsto \left[\beta \left(\mathsf{cl}{\left(U^c\right)}^c\right)\left({\phi }_{U^c}\right)\right]\hfill \end{array}$$

is well defined since $V^c\subseteq U^c$ implies

$$\beta \left(\mathsf{cl}{\left(U^c\right)}^c\right)\left({\phi }_{V^c}{|}_{\mathsf{cl}{\left(U^c\right)}^c}\right)=\left(\beta \left(\mathsf{cl}{\left(V^c\right)}^c\right)\right)\left({\phi }_{V^c}\right){\left)\right|}_{\mathsf{cl}{\left(U^c\right)}^c}.$$

We show ${\left(\widehat{\beta }\left(A\right)\right)}_{A\subseteq X}$ defines a morphism of sheaves on $X_{ct}$. If $B\subseteq A$ then

$$\begin{array}{cc}\hfill {\beta \left(B\right)\circ ·|}_B{\left[{\phi }_{U^c}\right]}_A& ={\left[\beta \left(\mathsf{cl}{\left(U^c\right)}^c\right)\left({\phi }_{U^c}\right)\right]}_B\hfill \\ \hfill & {=·|}_B\circ \beta \left(A\right){\left[{\phi }_{U^c}\right]}_A.\hfill \end{array}$$

Moreover, $\widehat{i{d}_G}=i{d}_{\widehat{G}}$ and $\widehat{\alpha \circ \beta }=\widehat{\alpha }\circ \widehat{\beta }$. Thus, we showed that $\widehat{·}$ is a functor between categories of sheaves:

$$\widehat{·}:\mathtt{Sheaf}\left(\nu \left(X\right)\right)\to \mathtt{Sheaf}\left(X_{ct}\right).$$

In fact, its image is contained in the full subcategory of reflective sheaves.

Theorem 11. 

If X is a proper metric space, the category of reflective sheaves $\mathtt{S}\mathtt{h}\mathtt{e}\mathtt{a}\mathtt{f}\left(X_{ct}\right)$ on X is equivalent to the category of sheaves $\mathtt{S}\mathtt{h}\mathtt{e}\mathtt{a}\mathtt{f}\left(\nu \right(X\left)\right)$ on $\nu \left(X\right)$ via ${·}^{\nu },\widehat{·}$.

Proof. 

Let G be a sheaf on $\nu \left(X\right)$. Then, for every $U\subseteq X$ there is a morphism

$$\begin{array}{cc}\hfill {\eta }_G\left(\mathsf{cl}{\left(U^c\right)}^c\right):G\left(\mathsf{cl}{\left(U^c\right)}^c\right)& \to {\left(\widehat{G}\right)}^{\nu }\left(\mathsf{cl}{\left(U^c\right)}^c\right)\hfill \\ \hfill s& \mapsto {\left({\left[s\right]}_U\right)}_{A /⋏U^c}\hfill \end{array}$$

which naturally defines a morphism of sheaves ${\eta }_G$. We show this map is bijective. Suppose $s\in G\left(\mathsf{cl}{\left(U^c\right)}^c\right)$ is mapped by ${\eta }_G\left(\mathsf{cl}{\left(U^c\right)}^c\right)$ to 0. Then for every $A /⋏U^c$ there exists $U_A^c /⋏A$ with ${s|}_{U_A}=0$. Then,

$$\begin{array}{cc}\hfill \bigcap _{A /⋏U^c}\mathsf{cl}\left(U_A^c\right)\cap \mathsf{cl}{\left(U^c\right)}^c& \subseteq \bigcap _{A /⋏U^c}\mathsf{cl}{\left(A\right)}^c\cap \mathsf{cl}{\left(U^c\right)}^c\hfill \\ \hfill & ={\left(\bigcup _{A /⋏U^c}\mathsf{cl}\left(A\right)\cup \mathsf{cl}\left(U^c\right)\right)}^c\hfill \\ \hfill & ={\left(\nu \left(X\right)\right)}^c\hfill \\ \hfill & =Ø.\hfill \end{array}$$

Thus, ${\left(\mathsf{cl}{\left(U_A^c\right)}^c\right)}_{A /⋏U^c}$ is an open cover of $\mathsf{cl}{\left(U^c\right)}^c$. The global axiom on open covers of $\nu \left(X\right)$ shows that $s=0$ on $\mathsf{cl}{\left(U^c\right)}^c$. Suppose ${\left({\left[t_A\right]}_{U_A}\right)}_{A /⋏U^c}$ is an element in ${\left(\widehat{G}\right)}^{\nu }\left(\mathsf{cl}{\left(U^c\right)}^c\right)$. Then, as before, ${\left(\mathsf{cl}{\left(U_A^c\right)}^c\right)}_{A /⋏U^c}$ is an open cover of $\mathsf{cl}{\left(U^c\right)}^c$. Then ${\left(t_A\right)}_{A /⋏U^c}\in {\prod }_{A /⋏U^c}G\left(\mathsf{cl}{\left(U_A^c\right)}^c\right)$ is an element with

$$\begin{array}{cc}\hfill {\eta }_G\left(\mathsf{cl}{\left(U_A^c\right)}^c\right)\left(t_A\right)& ={\left({\left[t_A\right]}_{U_A}\right)}_{A^{\prime } /⋏U_A^c}\hfill \\ \hfill & {=·|}_{\mathsf{cl}{\left(U_A^c\right)}^c}{\left({\left[t_{A^{\prime }}\right]}_{U_{A^{\prime }}}\right)}_{A^{\prime } /⋏U^c}\hfill \end{array}$$

Thus, ${\eta }_G$ is surjective. It is easy to see that $\eta :G\mapsto {\eta }_G$ defines a natural transformation. This way, we showed that $\eta$ is a natural isomorphism between $i{d}_{\mathtt{Sheaf}\left(\nu \right(X\left)\right)}$ and ${·}^{\nu }\circ \widehat{·}$.

Now, let F be a sheaf on $X_{ct}$. Then, for every $A\subseteq X$, there is a map

$$\begin{array}{cc}\hfill {ϵ}_F\left(A\right):\widehat{\left(F^{\nu }\right)}\left(A\right)& \to F\left(A\right)\hfill \\ \hfill \left[\right(s_{A^{\prime }}{{)}_{A^{\prime } /⋏U^c}]}_U& \mapsto s_A.\hfill \end{array}$$

This map is well defined since $\left[{\left(s_{A^{\prime }}\right)}_{A^{\prime } /⋏U^c}\right]=0$ implies there is some $U^c /⋏A$ such that for every $A^{\prime } /⋏U^c$ the section $s_{A^{\prime }}=0$ vanishes. This in particular implies that $s_A=0$. Now, we show ${ϵ}_F\left(A\right)$ is injective. If ${\left[{\left(s_{A^{\prime }}\right)}_{A^{\prime } /⋏U}\right]}_U$ maps to 0 by ${\epsilon }_F\left(A\right)$ then the support $supp\left({\left(s_{A^{\prime }}\right)}_{A^{\prime } /⋏U^c}\right)$ is closed in $\nu \left(X\right)$. Thus there exists an open $\mathsf{cl}{\left(V^c\right)}^c\supseteq \mathsf{cl}\left(A\right)$ on which ${\left(s_{A^{\prime }}\right)}_{A^{\prime } /⋏V^c}$ vanishes. Thus ${\left(s_{A^{\prime }}\right)}_{A^{\prime } /⋏U^c}$ represents the 0 element. Now we show ${ϵ}_F\left(A\right)$ is surjective if F is reflective. If $s_A\in F\left(A\right)$, then there exists some $A /⋏U^c$ and $s\in F\left(U\right)$ such that ${s|}_A=s_A$. Then, ${\left[{\left(s{|}_{A^{\prime }}\right)}_{A^{\prime } /⋏U^c}\right]}_U$ maps by ${ϵ}_F\left(A\right)$ to $s_A$. □

Theorem 12. 

If F is a reflective sheaf on $X_{ct}$ then ${\check{H}}_{ct}^q(X,F)={\check{H}}^q(\nu \left(X\right),F^{\nu })$. The right side denotes sheaf cohomology on $\nu \left(X\right)$.

Proof. 

We first show if G is a flabby sheaf on $\nu \left(X\right)$ then $\widehat{G}$ is a flabby sheaf on $X_{ct}$. For every $U\subseteq X$, the restriction $G\left(\nu \left(X\right)\right)\to G\left(\mathsf{cl}{\left(U^c\right)}^c\right)$ is surjective. If ${\left[s_U\right]}_U\in {\underrightarrow{lim}}_{A /⋏U^c}G\left(\mathsf{cl}{\left(U^c\right)}^c\right)$ then there exists some $s_X\in G\left(\nu \left(X\right)\right)=\widehat{G}\left(X\right)$ with $s_X{|}_U=s_U$.

Now we show $\widehat{·}$ is an exact functor. Let

$$G_1\stackrel{\alpha }{\to }{G}_2\stackrel{\beta }{\to }{G}_3$$

be an exact sequence of sheaves on $\nu \left(X\right)$. If $\left[s_U\right]\in ker\widehat{\beta }\left(A\right)$ then there exists $A /⋏V^c$ with $\beta (\mathsf{cl}{\left(V^c\right)}^c\left(s_U\right){|}_{\mathsf{cl}{\left(V^c\right)}^c}=0$. Since $ker\beta \subseteq im\alpha$ there is a cover $\bigcup \mathsf{cl}{\left(U_i^c\right)}^c=\mathsf{cl}{\left(V^c\right)}^c$ and $s_{U_i}\in G_1\left(\mathsf{cl}{\left(U_i^c\right)}^c\right)$ with $\alpha \left(\mathsf{cl}{\left(U_i^c\right)}^c\right)\left(s_{U_i}\right)=s_V{|}_{\mathsf{cl}{\left(U_i^c\right)}^c}$. Then ${\left(\mathsf{cl}{\left(U_i^c\right)}^c\right)}_i$ cover $\mathsf{cl}\left(A\right)$. Since $\mathsf{cl}\left(A\right)$ is compact a finite subcover $\mathsf{cl}{\left(U_1^c\right)}^c,\cdots ,\mathsf{cl}{\left(U_n^c\right)}^c$ will do. Then $U_1,\cdots ,U_n$ form a coarse cover of A. By Lemma 21, there exists a coarse cover $V_1,\cdots ,V_n$ of A with $V_i /⋏U_i^c$. Then, $\left[s_{U_i}\right]\in \prod {\widehat{G}}_1\left(V_i\right)$ maps to $\left[s_U\right]$ by $\widehat{\alpha }$. Thus, we have proved $ker\widehat{\beta }\subseteq im\widehat{\alpha }$. If conversely, ${\left[\alpha \left(\mathsf{cl}{\left(U_i^c\right)}^c\right)\left(s_{U_i}\right)\right]}_i\in \prod {\widehat{G}}_2\left(A_i\right)$ with $A_i$ a coarse cover of A and $A_i /⋏U_i^c$ represents an element in $im\widehat{\alpha }\left(A\right)$, then in particular $(\mathsf{cl}{\left(U_i^c\right)}^c$ is an open cover containing $\mathsf{cl}\left(A\right)$. By Lemma 22, there exists $A /⋏U^c$ with $\mathsf{cl}{\left(U^c\right)}^c$ covered by $\mathsf{cl}{\left(U_i^c\right)}^c$. Since $ker\beta \supseteq im\alpha$ there exists $s_U\in ker\beta (\mathsf{cl}{\left(U^c\right)}^{)}$ with $s_U{|}_{\mathsf{cl}{\left(U_i^c\right)}^c}=s_{U_i}$. Then, ${\left[s_U\right]}_U\in ker\widehat{\beta }\left(A\right)$ has the property that ${\left[s_U\right]}_U{|}_{A_i}=\widehat{\alpha }\left(A_i\right)\left({\left[s_{U_i}\right]}_{U_i}\right)$. Thus, $ker\widehat{\beta }\supseteq im\widehat{\alpha }$. This way we proved $ker\widehat{\beta }=im\widehat{\alpha }$, the sequence ${\widehat{G}}_1\to {\widehat{G}}_2\to {\widehat{G}}_3$ is exact at ${\widehat{G}}_2$.

If F is a reflective sheaf on $X_{ct}$, then there exists a flabby resolution

$$0\to F^{\nu }\to G_0\to G_1\to \cdots$$

of sheaves on $\nu \left(X\right)$. Since $\widehat{·}$ is an exact functor, we obtain an exact resolution of flabby sheaves

$$0\to \widehat{F^{\nu }}\to {\widehat{G}}_0\to {\widehat{G}}_1\to \cdots$$

with an isomorphism $\widehat{F^{\nu }}\to F$. The global section functor on the reduced sequences gives the same result. □

Proposition 6. 

If A is an abelian group and X a proper metric space, then $A_X{}^{\nu }=A_{\nu \left(X\right)}$ on $\nu \left(X\right)$ and ${\widehat{A}}_{\nu \left(X\right)}=A_X$ on $X_{ct}$ are isomorpic. In particular, $A_X$ is a reflective sheaf.

Proof. 

If $B\subseteq X$ is a subset and $i:B\to X$ denotes the inclusion then $\nu \left(i\right):\nu \left(B\right)\to \nu \left(X\right)$ is an inclusion of a closed subset. We have ${\widehat{A}}_{\nu \left(X\right)}\left(B\right)={\underrightarrow{lim}}_{B /⋏U^c}{A}_{\nu \left(X\right)}\left(\mathsf{cl}{\left(U^c\right)}^c\right)=\nu {\left(i\right)}^{-1}{A}_{\nu \left(X\right)}\left(\mathsf{cl}\left(B\right)\right)=A_{\nu \left(B\right)}\left(\nu \left(B\right)\right)$. There is a bijective map $A_X\left(B\right)\to A_{\nu \left(B\right)}\left(\nu \left(B\right)\right)$ defined as follows: A section in $A_X\left(B\right)$ is represented by a Higson function $\phi :B\to A$ where A is equipped with the word length metric. This function can be extended to the boundary $\nu \left(B\right)$ since it is Higson. Then this function is a continuous map $\nu \left(B\right)\to A$ where A is equipped with the discrete topology. Since a coarse disjoint union of B is 1:1 with disjoint unions of $\nu \left(B\right)$ by clopen sets we obtain a bijection. This tells us that $A_X={\widehat{A}}_{\nu \left(X\right)}$. Applying the ${·}^{\nu }$ functor we obtain a bijection $A_X^{\nu }={\widehat{A}}_{\nu \left(X\right)}^{\nu }=A_{\nu \left(X\right)}$. □

Theorem 13. 

If X is a proper metric space with $asdim\left(X\right)=n$ then ${\check{H}}_{ct}^q(X,\mathcal{F})=0$ for every reflective sheaf $\mathcal{F}$ and $q>n$.

Proof. 

The space $\nu \left(X\right)$ is paracompact since it is compact. By ([26], Chapitre II.5.12) it is sufficient to show that the covering dimension of $\nu \left(X\right)$ does not exceed n. By ([27], Theorem 1.1) we obtain $dim\left(\nu X\right)\le asdim\left(X\right)$. Thus the result follows. □

This result can be used to finalize our computations in Section 6.

Theorem 14. 

If A is a finite abelian group, then

$${\check{H}}_{ct}^q({\mathbb{Z}}_{\ge 0};A)=\left\{\begin{array}{cc}A\hfill & q=0\hfill \\ 0\hfill & otherwise.\hfill \end{array}\right.$$

If $F_n$ denotes the free group with $n<\infty$ generators and A is finite again, then

$${\check{H}}_{ct}^q(F_n;A)=\left\{\begin{array}{cc}\underset{\mathbb{N}}{⨁}A\hfill & q=0\hfill \\ 0\hfill & otherwise.\hfill \end{array}\right.$$

Proof. 

The cohomology in degree 0 is clear since ${\mathbb{Z}}_{\ge 0}$ has one end and $F_n$ has infinitely many ends. In degree 1, cohomology with finite coefficients vanishes by Lemmas 14 and 9, respectively. Now, both ${\mathbb{Z}}_{\ge 0}$ and trees have asymptotic dimension 1 [28]. Then, Theorem 13 implies that the higher cohomology groups vanish. □

10. Coarse Homotopy Invariance

This chapter proves Theorem 4.

Lemma 23. 

If ${\alpha }_0,\dots ,{\alpha }_q:X\to Y$ are coarse maps which are close to each other and $\phi \in C{X}_b^q(Y,A)$ is a cochain, then

1 

$\phi \circ ({\alpha }_0\times \cdots \times {\alpha }_q)$ is a cochain;

2 

the composition of $(y_0,\dots ,y_{q-1})\mapsto (y_0,\dots ,y_i,y_i,\dots ,y_{q-1})$ with the map φ is a cochain in $C{X}_b^{q-1}(Y,A)$;

3 

the composition of $(y_0,\dots ,y_{q-2})\mapsto (y_0,\dots ,y_i,y_i,\dots ,y_j,y_j,\dots ,y_{q-2})$ with φ is a cochain in $C{X}_b^{q-2}(Y,A)$.

Proof. 

We prove 1. first. Suppose $D\subseteq Y^{q+1}$ is cocontrolled. We show ${({\alpha }_0\times \cdots \times {\alpha }_q)}^{-1}\left(D\right)$ is cocontrolled. If $R\ge 0$, then $({\alpha }_0\times \cdots \times {\alpha }_q)\left({\Delta }_R\right)$ is cocontrolled since ${\alpha }_0,\dots ,{\alpha }_q$ are coarse and close to each other. Thus, there exists some $0\in Y$ and $S\ge 0$ with

$$D\cap ({\alpha }_0\times \cdots \times {\alpha }_q)\left({\Delta }_R\right)\subseteq {\left({\Delta }_S\left[0\right]\right)}^{q+1}$$

Then,

$$\begin{array}{cc}\hfill {({\alpha }_0\times \cdots \times {\alpha }_q)}^{-1}\left(D\right)\cap {\Delta }_R& \subseteq {({\alpha }_0\times \cdots \times {\alpha }_q)}^{-1}\left(D\right)\cap {({\alpha }_0\times \cdots \times {\alpha }_q)}^{-1}\circ ({\alpha }_0\times \cdots \times {\alpha }_q)\left({\Delta }_R\right)\hfill \\ \hfill & \subseteq {({\alpha }_0\times \cdots \times {\alpha }_q)}^{-1}\left({\Delta }_S{\left[0\right]}^{q+1}\right)\hfill \end{array}$$

is bounded. Thus, ${({\alpha }_0\times \cdots \times {\alpha }_q)}^{-1}\left(D\right)$ is cocontrolled. Now, $supp\phi$ is cocontrolled. Then,

$$\begin{array}{cc}\hfill supp(\phi \circ ({\alpha }_0\times \cdots \times {\alpha }_q))& ={({\alpha }_0\times \cdots \times {\alpha }_q)}^{-1}(supp\phi {|}_{im({\alpha }_0\times \cdots \times {\alpha }_q)})\hfill \\ \hfill & ={({\alpha }_0\times \cdots \times {\alpha }_q)}^{-1}(supp\phi )\hfill \end{array}$$

is cocontrolled. If $\phi \in C_{A_1,\dots ,A_n}(Y,A)$ then $\phi \circ ({\alpha }_0\times \cdots \times {\alpha }_q)\in C_{{\alpha }_0^{-1}\left(A_{i_0}\right)\cap \cdots \cap {\alpha }_q^{-1}\left(A_{i_q}\right)}(X,A)$. Thus, $\phi \circ ({\alpha }_0\times \cdots \times {\alpha }_q)$ is blocky. This way we showed that $\phi \circ ({\alpha }_0\times \cdots \times {\alpha }_q)$ is a cochain.

Now, we prove 2. Name the map $(y_0,\dots ,y_{q-1})\mapsto (y_0,\dots ,y_i,y_i,\dots ,y_{q-1})$ by ${\delta }_i$. If $R\ge 0$, then there exist $0\in Y,S\ge 0$ such that ${supp\phi |}_{{\Delta }_R}\subseteq {\left({\Delta }_S\left[0\right]\right)}^{q+1}$. Now ${\delta }_i\left({\Delta }_R^{q-1}\right)\subseteq {\Delta }_R^q$ and ${\delta }_i^{-1}\left({\left({\Delta }_S\left[0\right]\right)}^{q+1}\right)\subseteq {\left({\Delta }_S\left[0\right]\right)}^q$. We use this to prove

$$\begin{array}{cc}\hfill supp(\phi \circ {\delta }_i){|}_{{\Delta }_R^{q-1}}& ={\delta }_i^{-1}(supp\phi {|}_{{\delta }_i\left({\Delta }_R^{q-1}\right)})\hfill \\ \hfill & \subseteq {\delta }_i^{-1}(supp\phi {|}_{{\Delta }_R^q})\hfill \\ \hfill & \subseteq {\delta }_i^{-1}\left({\left({\Delta }_S\left[0\right]\right)}^{q+1}\right)\hfill \\ \hfill & \subseteq {\left({\Delta }_S\left[0\right]\right)}^q.\hfill \end{array}$$

Thus, $\phi \circ {\delta }_i$ has cocontrolled support. Moreover, if $\phi \in C_{A_1,\dots ,A_n}^q(Y,A)$, then we have $\phi \circ {\delta }_i\in C_{A_1,\dots ,A_n}^{q-1}(Y,A)$. Thus, $\phi \circ {\delta }_i$ is blocky. This way, we showed that $\phi \circ {\delta }_i$ defines a cochain.

The proof of 3. is similar to the proof of 2. and left to the reader. □

Lemma 24. 

If I is a metric space, $h_0,h_1,h_2:I\to I$ coarse maps which are close to each other and $\phi \in C{X}_b^q(I,A)$ is a cocycle then

$$\begin{array}{cc}\hfill \sum _{i=0}^{q-1}{(-1)}^i(& \phi (h_0\left(z_0\right),\dots ,h_0\left(z_i\right),h_1\left(z_i\right),\dots ,h_1\left(z_{q-1}\right))+\phi (h_1\left(z_0\right),\dots ,h_1\left(z_i\right),h_2\left(z_i\right),\dots ,h_2\left(z_{q-1}\right))\hfill \\ \hfill & -\phi (h_0\left(z_0\right),\dots ,h_0\left(z_i\right),h_2\left(z_i\right),\dots ,h_2\left(z_{q-1}\right)))\hfill \end{array}$$

is a coboundary in $C{X}_b^{q-1}(I,A)$.

Proof. 

First, we define for $0\le i\le j\le q-2$ a map

$$\begin{array}{cc}\hfill {\chi }_{ij}:I^{q-1}& \to A\hfill \\ \hfill (x_0,\dots ,x_{q-2})& \mapsto \phi (h_0\left(x_0\right),\dots ,h_0\left(x_i\right),h_1\left(x_i\right),\dots ,h_1\left(x_j\right),h_2\left(x_j\right),\dots ,h_2\left(x_{q-2}\right))\hfill \end{array}$$

This map defines a cochain by Lemma 23.

If $(z_0,\dots ,z_{k-1})\in I^q$ then $\left({\widehat{z}}_k\right)$ is short for $(z_0,\dots ,{\widehat{z}}_k,\dots ,z_{k-1})\in I^{q-1}$. We compute

$$\begin{array}{cc}\hfill 0& =\sum _{0\le i\le j\le q-1}{(-1)}^{i+j}{d}_q\phi (h_0\left(z_0\right),\dots ,h_0\left(z_i\right),h_1\left(z_i\right),\dots ,h_1\left(z_j\right),h_2\left(z_j\right),\dots ,h_2\left(z_{q-1}\right))\hfill \\ \hfill & =\sum _{0\le i\le j\le q-1}\hfill \\ \hfill & (\sum _{k=0}^i{(-1)}^{i+j+k}\phi (h_0\left(z_0\right),\dots ,\widehat{h_0\left(z_k\right)},\dots ,h_0\left(z_i\right),h_1\left(z_i\right),\dots ,h_1\left(z_j\right),h_2\left(z_j\right),\dots ,h_2\left(z_{q-1}\right))\hfill \\ \hfill & +\sum _{k=i}^j{(-1)}^{i+j+k+1}\phi (h_0\left(z_0\right),\dots ,h_0\left(z_i\right),h_1\left(z_i\right),\dots ,\widehat{h_1\left(z_k\right)},\dots ,h_1\left(z_j\right),h_2\left(z_j\right),\dots ,h_2\left(z_{q-1}\right))\hfill \\ \hfill & +\sum _{k=j}^{q-1}{(-1)}^{i+j}\phi (h_0\left(z_0\right),\dots ,h_0\left(z_i\right),h_1\left(z_i\right),\dots ,h_1\left(z_j\right),h_2\left(z_j\right),\dots ,\widehat{h_2\left(z_k\right)},\dots ,h_2\left(z_{q-1}\right)))\hfill \\ \hfill & =\sum _{0\le i\le j\le q-1}\hfill \\ \hfill & (\sum _{k=0}^{i-1}{(-1)}^{i+j+k}{\chi }_{i-1,j-1}\left({\widehat{z}}_k\right)\hfill \\ \hfill & +{(-1)}^{i+j+i}\phi {(h_0\left(z_0\right),\dots ,h_0\left(z_{i-1}\right),h_1\left(z_i\right),\dots ,h_1\left(z_j\right),h_2\left(z_j\right),\dots ,h_2\left(z_{q-1}\right))}^{\begin{array}{|c|}\hline 1\\ \hline\end{array}}\hfill \\ \hfill & +{(-1)}^{i+j+i+1}\phi {(h_0\left(z_0\right),\dots ,h_0\left(z_i\right),h_1\left(z_{i+1}\right),\dots ,h_1\left(z_j\right),h_2\left(z_j\right),\dots ,h_2\left(z_{q-1}\right))}^{\begin{array}{|c|}\hline 2\\ \hline\end{array}}\hfill \\ \hfill & +\sum _{k=i+1}^{j-1}{(-1)}^{i+j+k+1}{\chi }_{i,j-1}\left({\widehat{z}}_k\right)\hfill \\ \hfill & +{(-1)}^{i+j+j+1}\phi {(h_0\left(z_0\right),\dots ,h_0\left(z_i\right),h_1\left(z_i\right)\dots ,h_1\left(z_{j-1}\right),h_2\left(z_j\right),\dots ,h_2\left(z_{q-1}\right))}^{\begin{array}{|c|}\hline 3\\ \hline\end{array}}\hfill \\ \hfill & +{(-1)}^{i+j+j}\phi {(h_0\left(z_0\right),\dots ,h_0\left(z_i\right),h_1\left(z_i\right),\dots ,h_1\left(z_j\right),h_2\left(z_{j+1}\right),\dots ,h_2\left(z_{q-1}\right))}^{\begin{array}{|c|}\hline 4\\ \hline\end{array}}\hfill \\ \hfill & +\sum _{k=j+1}^{q-1}{(-1)}^{i+j+k}{\chi }_{ij}\left({\widehat{z}}_k\right))\hfill \end{array}$$

We arrived at a sum where the terms marked with $\begin{array}{|c|}\hline 1\\ \hline\end{array},\begin{array}{|c|}\hline 2\\ \hline\end{array},\begin{array}{|c|}\hline 3\\ \hline\end{array},\begin{array}{|c|}\hline 4\\ \hline\end{array}$ either contribute the desired terms or cancel each other out. The terms with ${\chi }_{ij}$ add to a coboundary.

We first look at the terms $\begin{array}{|c|}\hline 1\\ \hline\end{array},\begin{array}{|c|}\hline 2\\ \hline\end{array},\begin{array}{|c|}\hline 3\\ \hline\end{array},\begin{array}{|c|}\hline 4\\ \hline\end{array}$. If $0\le i<j\le q-1$ the term $\begin{array}{|c|}\hline 1\\ \hline\end{array}$ for $i+1,j$ cancels with the term $\begin{array}{|c|}\hline 2\\ \hline\end{array}$ for $i,j$. If $0\le i<j\le q-1$ the term $\begin{array}{|c|}\hline 3\\ \hline\end{array}$ for $i,j$ cancels with the term $\begin{array}{|c|}\hline 4\\ \hline\end{array}$ for $i,j-1$. We did not yet count the terms $\begin{array}{|c|}\hline 1\\ \hline\end{array}$ for $i=0,0\le j\le q-1$ which give ${(-1)}^j\phi (h_1\left(z_0\right),\dots ,h_1\left(z_j\right),h_2\left(z_j\right),\dots ,h_2\left(z_{q-1}\right))$. The terms $\begin{array}{|c|}\hline 4\\ \hline\end{array}$ for $j=q-1,0\le i\le q-1$ contribute ${(-1)}^i\phi (h_0\left(z_0\right),\dots ,h_0\left(z_i\right),h_1\left(z_i\right),\dots ,h_1\left(z_{q-1}\right))$. Finally if $0\le i=j\le q-1$ then $\begin{array}{|c|}\hline 2\\ \hline\end{array}=\begin{array}{|c|}\hline 3\\ \hline\end{array}$ is counted only once and contributes ${(-1)}^{i+i+i+1}\phi (h_0\left(z_0\right),\dots ,h_0\left(z_i\right),h_2\left(z_i\right),\dots ,h_2\left(z_{q-1}\right))$.

It remains to show that the other terms contribute a coboundary:

$$\begin{array}{cc}\hfill \cdots & =\sum _{0\le i\le j\le q-1}(\sum _{k=0}^{i-1}{(-1)}^{i+j+k}{\chi }_{i-1,j-1}\left({\widehat{z}}_k\right)+\sum _{k=i+1}^{j-1}{(-1)}^{i+j+k+1}{\chi }_{i,j-1}\left({\widehat{z}}_k\right)\hfill \\ \hfill & +\sum _{k=j+1}^{q-1}{(-1)}^{i+j+k}{\chi }_{ij}\left({\widehat{z}}_k\right))\hfill \\ \hfill & =\sum _{0\le i\le j\le q-2}(\sum _{k=0}^i{(-1)}^{i+j+k}{\chi }_{i,j}\left({\widehat{z}}_k\right)+\sum _{k=i+1}^j{(-1)}^{i+j+k}{\chi }_{i,j}\left({\widehat{z}}_k\right)\hfill \\ \hfill & +\sum _{k=j+1}^{q-1}{(-1)}^{i+j+k}{\chi }_{ij}\left({\widehat{z}}_k\right))\hfill \\ \hfill & =d_{q-2}\left(\sum _{0\le i\le j\le q-2}{(-1)}^{i+j}{\chi }_{ij}\right)(z_0,\dots ,z_{q-1}).\hfill \end{array}$$

□

Lemma 25. 

If I is a metric space, $\phi \in C{X}_b^q(I,A)$ a cochain and ${\left(h_t\right)}_t$ a family of coarse maps $I\to I$ with the properties

1.

$d(z_0,z_1)\ge d(h_t\left(z_0\right),h_t\left(z_1\right))$ for every $z_0,z_1\in I,t$;

2.

$d(z_0,0)=d(h_t\left(z_0\right),0)$ for every $z_0\in I,t$ and some $0\in I$;

then for every $R\ge 0$, there exists $S\ge 0$ such that

$$supp\phi (h_{t_0}(·),\dots ,h_{t_q}(·)){|}_{{\Delta }_R^q}\subseteq {\left({\Delta }_S\left[0\right]\right)}^{q+1}.$$

independent of $t_0,\dots ,t_q$.

Proof. 

If $R\ge 0$ then ${supp\phi |}_{{\Delta }_R}$ is bounded, namely, contained in ${\left({\Delta }_S\left[0\right]\right)}^{q+1}$ for some $S\ge 0$.

$$\begin{array}{cc}\hfill supp(\phi \circ (h_{t_0}\times \cdots \times h_{t_q})){|}_{{\Delta }_R^q}& ={(h_{t_0}\times \cdots \times h_{t_q})}^{-1}(supp\phi {|}_{(h_{t_0}\times \cdots \times h_{t_q})\left({\Delta }_R^q\right)})\hfill \\ \hfill & \subseteq {(h_{t_0}\times \cdots \times h_{t_q})}^{-1}(supp\phi {|}_{{\Delta }_R^q})\hfill \\ \hfill & \subseteq {(h_{t_0}\times \cdots \times h_{t_q})}^{-1}\left({\left({\Delta }_S\left[0\right]\right)}^{q+1}\right)\hfill \\ \hfill & ={\left({\Delta }_S\left[0\right]\right)}^{q+1}.\hfill \end{array}$$

□

The proof of Theorem 15 can be illustrated by an example. Proposition 7 carries out the essential step of the proof for $X={\mathbb{Z}}_{\ge 0}$.

Proposition 7. 

If $I_0:={\mathbb{Z}}_{\ge 0}\times {\mathbb{Z}}_{\ge 0}\subseteq {\mathbb{Z}}^2$ the projection

$$\begin{array}{cc}\hfill \pi :I_0& \to {\mathbb{Z}}_{\ge 0}\hfill \\ \hfill (x,y)& \mapsto x+y\hfill \end{array}$$

induces an isomorphism in cohomology ${\pi }^{\ast }$ inverse to the induced map ${\iota }^{\ast }$ associated to the inclusion $\iota :x\mapsto (x,0)$.

Proof. 

In the following proof, $z_i$ is short for $\left(\begin{array}{c}{x}_i\\ y_i\end{array}\right)$ and $\overline{z}$ abbreviates $\left(\left(\begin{array}{c}{x}_0\\ y_0\end{array}\right),\dots ,\left(\begin{array}{c}{x}_q\\ y_q\end{array}\right)\right)$ or $\left(\left(\begin{array}{c}{x}_0\\ y_0\end{array}\right),\dots ,\left(\begin{array}{c}{x}_{q-1}\\ y_{q-1}\end{array}\right)\right)$.

We show that the map

$$\begin{array}{cc}\hfill p:=\iota \circ \pi :I_0& \to I_0\hfill \\ \hfill (x,y)& \mapsto (x+y,0)\hfill \end{array}$$

induces the same map $p^{\ast }$ in cohomology as the identity on $I_0$.

For $t\in {\mathbb{N}}_0$ we define an auxilary map

$$\begin{array}{cc}\hfill h_t:I_0& \to I_0\hfill \\ \hfill (x,y)& \mapsto \left\{\begin{array}{cc}(x+t,y-t)\hfill & t<y\hfill \\ (x+y,0)\hfill & t\ge y.\hfill \end{array}\right.\hfill \end{array}$$

We obtain $p(x,y)=h_y(x,y)$. The ${\left(h_t\right)}_t$ satisfy the conditions of Lemmas 24 and 25.

Suppose $q\ge 2$. Let $\phi \in C{X}_b^q(I_0,A)$ be a cocyle. Then, $(h_t^{\ast }-i{d}_{I_0}^{\ast })\phi \in im{d}_{q-1}$ since $h_t,i{d}_{I_0}$ are close. Thus, there is some ${\psi }_t\in C{X}_b^{q-1}(I_0,A)$ with $d_{q-1}{\psi }_t=h_t^{\ast }\phi -\phi$. Namely,

$${\psi }_t(z_0,\dots ,z_{q-1})=\sum _{i=0}^{q-1}{(-1)}^i\phi (z_0,\dots ,z_i,h_t\left(z_i\right),\dots ,h_t\left(z_{q-1}\right)).$$

Then, define the map

$$\tilde{\psi }\left(\left(\begin{array}{c}{x}_0\\ y_0\end{array}\right),\dots ,\left(\begin{array}{c}{x}_{q-1}\\ y_{q-1}\end{array}\right)\right)=\sum _{t=0}^{max\left(y_j\right)-1}\left(h_t^{\ast }{\psi }_1\right)\left(\left(\begin{array}{c}{x}_0\\ y_0\end{array}\right),\dots ,\left(\begin{array}{c}{x}_{q-1}\\ y_{q-1}\end{array}\right)\right).$$

This map is well defined, since for each fixed point in $I_0^q$, only finitely many terms in the above sum are defined. If $R\ge 0$, then Lemma 25 implies that there exists some $S\ge 0$ such that each summand of ${\psi |}_{{\Delta }_R^{q-1}}$ has support contained in ${\left({\Delta }_S\left[0\right]\right)}^q$. This implies that $supp\left(\tilde{\psi }{|}_{{\Delta }_R^{q-1}}\right)\subseteq {\left({\Delta }_S\left[0\right]\right)}^q$. Thus, $\tilde{\psi }$ has cocontrolled support. Now, $\tilde{\psi }$ may or may not be blocky. We have to go the extra step to produce a map with cocontrolled support which is also blocky. To obtain such a map, we are going to add a coboundary.

By Lemma 24 we obtain

$$\begin{array}{cc}\hfill h_0^{\ast }{\psi }_1\left(\overline{z}\right)+h_1^{\ast }{\psi }_1\left(\overline{z}\right)& =\sum _{i=0}^{q-1}{(-1)}^i\phi (h_0\left(z_0\right),\dots ,h_0\left(z_i\right),h_1\left(z_i\right),\dots ,h_1\left(z_{q-1}\right))\hfill \\ \hfill & +\sum _{i=0}^{q-1}{(-1)}^i\phi (h_1\left(z_0\right),\dots ,h_1\left(z_i\right),h_2\left(z_i\right),\dots ,h_2\left(z_{q-1}\right))\hfill \\ \hfill & =\sum _{i=0}^{q-1}{(-1)}^i\phi (h_0\left(z_0\right),\dots ,h_0\left(z_i\right),h_2\left(z_i\right),\dots ,h_2\left(z_{q-1}\right))+d_{q-2}{\chi }_1\left(\overline{z}\right)\hfill \\ \hfill & ={\psi }_2\left(\overline{z}\right)+d_{q-2}{\chi }_1\left(\overline{z}\right).\hfill \end{array}$$

in the next step, we obtain

$$\begin{array}{cc}\hfill {\psi }_2\left(\overline{z}\right)+h_2^{\ast }{\psi }_1\left(\overline{z}\right)& =\sum _{i=0}^{q-1}{(-1)}^i\phi (h_0\left(z_0\right),\dots ,h_0\left(z_i\right),h_2\left(z_i\right),\dots ,h_2\left(z_{q-1}\right))\hfill \\ \hfill & +\sum _{i=0}^{q-1}{(-1)}^i\phi (h_2\left(z_0\right),\dots ,h_2\left(z_i\right),h_3\left(z_i\right),\dots ,h_3\left(z_{q-1}\right))\hfill \\ \hfill & =\sum _{i=0}^{q-1}{(-1)}^i\phi (h_0\left(z_0\right),\dots ,h_0\left(z_i\right),h_3\left(z_i\right),\dots ,h_3\left(z_{q-1}\right))+d_{q-2}{\chi }_2\left(\overline{z}\right)\hfill \\ \hfill & ={\psi }_3\left(\overline{z}\right)+d_{q-2}{\chi }_2\left(\overline{z}\right).\hfill \end{array}$$

Successively, we obtain

$$\tilde{\psi }\left(\overline{z}\right)={\psi }_{max\left(y_j\right)}\left(\left(\begin{array}{c}{x}_0\\ y_0\end{array}\right),\dots ,\left(\begin{array}{c}{x}_{q-1}\\ y_{q-1}\end{array}\right)\right)+\sum _{t=1}^{max\left(y_j\right)-1}{d}_{q-2}{\chi }_t\left(\left(\begin{array}{c}{x}_0\\ y_0\end{array}\right),\dots ,\left(\begin{array}{c}{x}_{q-1}\\ y_{q-1}\end{array}\right)\right)$$

By the proof of Lemma 24 the map $d_{q-2}{\chi }_t$ satisfies the conditions of Lemma 25. Thus, the sum ${\sum }_{t=1}^{max\left(y_j\right)-1}{d}_{q-2}{\chi }_t$ has cocontrolled support. This implies that the map

$$\psi \left(\left(\begin{array}{c}{x}_0\\ y_0\end{array}\right),\dots ,\left(\begin{array}{c}{x}_{q-1}\\ y_{q-1}\end{array}\right)\right):={\psi }_{max\left(y_i\right)}\left(\left(\begin{array}{c}{x}_0\\ y_0\end{array}\right),\dots ,\left(\begin{array}{c}{x}_{q-1}\\ y_{q-1}\end{array}\right)\right)$$

has cocontrolled support. We have

$$\psi (z_0,\dots ,z_{q-1})=\sum _{i=0}^{q-1}{(-1)}^i\phi (z_0,\dots ,z_i,p\left(z_i\right),\dots ,p\left(z_{q-1}\right)).$$

Thus, $\psi$ is blocky, namely, if $\phi \in C_{A_1,\dots ,A_n}^q(I_0,A)$ then $\psi \in C_{p^{-1}{A}_i\cap A_j}^{q-1}(I_0,A)$. This way we have proved that $\psi$ is a cochain.

Lastly, we have

$$\begin{array}{cc}\hfill \left(d_{q-1}\psi \right)\left(\overline{z}\right)& =\psi \left(\left(\begin{array}{c}{x}_1\\ y_1\end{array}\right),\dots ,\left(\begin{array}{c}{x}_q\\ y_q\end{array}\right)\right)-\cdots \pm \psi \left(\left(\begin{array}{c}{x}_0\\ y_0\end{array}\right),\dots ,\left(\begin{array}{c}{x}_{q-1}\\ y_{q-1}\end{array}\right)\right)\hfill \\ \hfill & ={\psi }_{{max}_i{y}_i}\left(\left(\begin{array}{c}{x}_1\\ y_1\end{array}\right),\dots ,\left(\begin{array}{c}{x}_q\\ y_q\end{array}\right)\right)-\cdots \pm {\psi }_{{max}_i{y}_i}\left(\left(\begin{array}{c}{x}_0\\ y_0\end{array}\right),\dots ,\left(\begin{array}{c}{x}_{q-1}\\ y_{q-1}\end{array}\right)\right)\hfill \\ \hfill & =\left(d_{q-1}{\psi }_{{max}_i{y}_i}\right)\left(\overline{z}\right)\hfill \\ \hfill & =h_{{max}_i{y}_i}^{\ast }\phi \left(\overline{z}\right)-\phi \left(\overline{z}\right)\hfill \\ \hfill & =(p^{\ast }\phi -\phi )\left(\overline{z}\right)\hfill \end{array}$$

Thus, $p^{\ast }\phi -\phi$ defines a coboundary. This way, we showed $p^{\ast }$ induces the identity on ${\check{H}}_{ct}^q(I_0,A)$ for $q\ge 1$. It remains to show the statement for $q=0$.

Since $I_0$ is one-ended a cocycle, $\phi \in C{Y}^0(I_0,A)$ is represented by a constant $a\in A$ function on $I_0$ except on a bounded set. Then, $p^{\ast }\phi$ is constant $a\in A$ except on a bounded set. Thus, $p^{\ast }$ is the same map as the identity on $H{Y}^0(I_0,A)$. □

Now, denote $I:={\mathbb{R}}_{\ge 0}\times {\mathbb{R}}_{\ge 0}$ and equip this space with the Manhattan metric. Namely, if $(s_1,t_1),(s_2,t_2)\in I$ then,

$$d((s_1,t_1),(s_2,t_2))=|s_2-s_1|+|t_2-t_1|.$$

If X is a metric space and $x_0\in X$ a point, then the asymptotic product of X and I is defined to be

$$X\ast I=\{(x,i)\in X\times I\mid d(x,x_0)=d(i,(0,0))\}$$

The paper [18] shows that $X\ast I$ is the pullback of $d(·,x_0)$ and $d(·,(0,0\left)\right)$. Moreover, we can define a well-defined homotopy theory: If X is a metric space, define maps

$$\begin{array}{cc}\hfill \begin{array}{cc}\hfill {\iota }_0:X& \to X\ast I\hfill \\ \hfill x& \mapsto (x,(d(x,x_0),0))\hfill \end{array}& \begin{array}{cc}\hfill {\iota }_1:X& \to X\ast I\hfill \\ \hfill x& \mapsto (x,(0,d(x,x_0)))\hfill \end{array}\hfill \end{array}$$

Definition 4. 

If $\alpha ,\beta :X\to Y$ are two coarse maps, they are coarsely homotopic if there exists a coarse map $h:X\ast I\to Y$ with $h\circ {\iota }_0=\alpha$ and $h\circ {\iota }_1=\beta$.

The paper [18] shows that coarse homotopy is an equivalence relation and compares this theory with other homotopy theories on the coarse category.

Lemma 26. 

If X is a metric space, then $e(X\ast I)=e\left(X\right)$.

Proof. 

Denote by $\pi$ the projection of $X\ast I$ to the first factor. Since $\pi$ is a surjective coarse map, the inequality $e(X\ast I)\ge e\left(X\right)$ follows easily.

Now, suppose $X\ast I=A\bigsqcup B$ is a coarse disjoint union. This means that $A,B$ are disjoint and form a coarse cover of X. Namely, the set ${\Delta }_R\left[A\right]\cap {\Delta }_R\left[B\right]$ is bounded for every $R\ge 0$. Then, the set $\{x\in X\mid \exists i,j\in I:(x,i)\in A,(x,j)\in B\}$ is bounded. Without loss of generality, we assume it is empty. Thus, for fixed $x\in X$ either $(x,i)\in A$ for every $i\in I$ or $(x,i)\in B$ for every $i\in I$.

Now, we show $\pi \left(A\right),\pi \left(B\right)$ form a coarse disjoint union. They are disjoint by the assumption. Let $R\ge 0$ be a number and let $x\in \pi \left(A\right),y\in \pi \left(B\right)$ be two points with $d(x,y)\le R$. Then, $(x,0)\in A,(y,0)\in B$ with $d\left(\right(x,0),(y,0\left)\right)\le R$. Then, the set $\left(\right(x,0),(y,0\left)\right)$ is bounded, which implies that $(x,y)$ is bounded. □

Theorem 15. 

If two maps $\alpha ,\beta :X\to Y$ are coarsely homotopic, then they induce the same map in cohomology.

Proof. 

We just need to show that the projection $\pi :X\ast I\to X$ which sends an element $(x,i)$ to x induces an isomorphism in cohomology. Indeed, since $\pi \circ {\iota }_0=i{d}_X=\pi \circ {\iota }_1$ the maps ${\iota }_0^{\ast },{\iota }_1^{\ast }$ are both the unique inverse to ${\pi }^{\ast }$. Then, $\alpha =h\circ {\iota }_0$ and $\beta =h\circ {\iota }_1$ induce the same map in cohomology.

Now, Proposition 7 already showed ${\pi }^{\ast }$ is an isomorphism with ${\mathbb{Z}}_{\ge 0}$ in place of X and $I_0$ in place of I. The same proof can be transferred to this situation where we use Lemma 26 for the step in degree 0.

Namely, we proceed as follows. In the following proof, $z_i$ is short for $(x_i,(s_i,t_i))$ and $\overline{z}$ abbreviates $(z_0,\dots ,z_q)$ or $(z_0,\dots ,z_{q-1})$.

We show that the map

$$\begin{array}{cc}\hfill p:={\iota }_0\circ \pi :X\ast I& \to X\ast I\hfill \\ \hfill (x,(s,t\left)\right)& \mapsto (x,(s+t,0\left)\right)\hfill \end{array}$$

induces the same map $p^{\ast }$ in cohomology as the identity on $X\ast I$.

For $n\in {\mathbb{N}}_0$, we define an auxilary map

$$\begin{array}{cc}\hfill h_n:X\ast I& \to X\ast I\hfill \\ \hfill (x,(s,t\left)\right)& \mapsto \left\{\begin{array}{cc}(x,(s+n,t-n\left)\right)\hfill & n<t\hfill \\ (x,(s+t,0\left)\right)\hfill & n\ge t.\hfill \end{array}\right.\hfill \end{array}$$

We obtain $p(x,(s,t))=(x,(s+t,0))=h_{\lfloor t\rfloor +1}(x,(s,t))$. The ${\left(h_n\right)}_n$ satisfy the conditions of Lemmas 24 and 25.

Suppose $q\ge 2$. Let $\phi \in C{X}_b^q(X\ast I,A)$ be a cocyle. Then, $(h_n^{\ast }-i{d}_{X\ast I}^{\ast })\phi \in im{d}_{q-1}$ since $h_n,i{d}_{X\ast I}$ are close. Thus, there is some ${\psi }_n\in C{X}_b^{q-1}(X\ast I,A)$ with $d_{q-1}{\psi }_n=h_n^{\ast }\phi -\phi$. Namely,

$${\psi }_n(z_0,\dots ,z_{q-1})=\sum _{i=0}^{q-1}{(-1)}^i\phi (z_0,\dots ,z_i,h_n\left(z_i\right),\dots ,h_n\left(z_{q-1}\right)).$$

Then, define the map

$$\tilde{\psi }((x_0,(s_0,t_0)),\dots ,(x_{q-1},(s_{q-1},t_{q-1})))=\sum _{n=0}^{\lfloor max\left(t_j\right)\rfloor }\left(h_n^{\ast }{\psi }_1\right)((x_0,(s_0,t_0)),\dots ,(x_{q-1},(s_{q-1},t_{q-1}))).$$

This map is well defined since for each fixed point in ${(X\ast I)}^q$, only finitely many terms in the above sum are defined. If $R\ge 0$, then Lemma 25 implies that there exists some $S\ge 0$ such that each summand of ${\psi |}_{{\Delta }_R^{q-1}}$ has support contained in ${\left({\Delta }_S\left[0\right]\right)}^q$. This implies that $supp\left(\tilde{\psi }{|}_{{\Delta }_R^{q-1}}\right)\subseteq {\left({\Delta }_S\left[0\right]\right)}^q$. Thus, $\tilde{\psi }$ has cocontrolled support. Now, $\tilde{\psi }$ may or may not be blocky. We have to go the extra step to produce a map with cocontrolled support which is also blocky. To obtain such a map, we are going to add a coboundary.

By Lemma 24, we obtain

$$\begin{array}{cc}\hfill h_0^{\ast }{\psi }_1\left(\overline{z}\right)+h_1^{\ast }{\psi }_1\left(\overline{z}\right)& =\sum _{i=0}^{q-1}{(-1)}^i\phi (h_0\left(z_0\right),\dots ,h_0\left(z_i\right),h_1\left(z_i\right),\dots ,h_1\left(z_{q-1}\right))\hfill \\ \hfill & +\sum _{i=0}^{q-1}{(-1)}^i\phi (h_1\left(z_0\right),\dots ,h_1\left(z_i\right),h_2\left(z_i\right),\dots ,h_2\left(z_{q-1}\right))\hfill \\ \hfill & =\sum _{i=0}^{q-1}{(-1)}^i\phi (h_0\left(z_0\right),\dots ,h_0\left(z_i\right),h_2\left(z_i\right),\dots ,h_2\left(z_{q-1}\right))+d_{q-2}{\chi }_1\left(\overline{z}\right)\hfill \\ \hfill & ={\psi }_2\left(\overline{z}\right)+d_{q-2}{\chi }_1\left(\overline{z}\right).\hfill \end{array}$$

In the next step, we obtain

$$\begin{array}{cc}\hfill {\psi }_2\left(\overline{z}\right)+h_2^{\ast }{\psi }_1\left(\overline{z}\right)& =\sum _{i=0}^{q-1}{(-1)}^i\phi (h_0\left(z_0\right),\dots ,h_0\left(z_i\right),h_2\left(z_i\right),\dots ,h_2\left(z_{q-1}\right))\hfill \\ \hfill & +\sum _{i=0}^{q-1}{(-1)}^i\phi (h_2\left(z_0\right),\dots ,h_2\left(z_i\right),h_3\left(z_i\right),\dots ,h_3\left(z_{q-1}\right))\hfill \\ \hfill & =\sum _{i=0}^{q-1}{(-1)}^i\phi (h_0\left(z_0\right),\dots ,h_0\left(z_i\right),h_3\left(z_i\right),\dots ,h_3\left(z_{q-1}\right))+d_{q-2}{\chi }_2\left(\overline{z}\right)\hfill \\ \hfill & ={\psi }_3\left(\overline{z}\right)+d_{q-2}{\chi }_2\left(\overline{z}\right).\hfill \end{array}$$

Successively, we obtain

$$\begin{array}{cc}\hfill \tilde{\psi }\left(\overline{z}\right)& ={\psi }_{\lfloor max\left(t_j\right)\rfloor +1}((x_0,(s_0,t_0)),\dots ,(x_{q-1},(s_{q-1},t_{q-1})))\hfill \\ \hfill & +\sum _{n=1}^{\lfloor max\left(t_j\right)\rfloor }{d}_{q-2}{\chi }_n((x_0,(s_0,t_0)),\dots ,(x_{q-1},(s_{q-1},t_{q-1}))\hfill \end{array}$$

By the proof of Lemma 24, the map $d_{q-2}{\chi }_t$ satisfies the conditions of Lemma 25. Thus, the sum ${\sum }_{t=1}^{max\left(y_j\right)-1}{d}_{q-2}{\chi }_t$ has cocontrolled support. This implies that the map

$$\psi ((x_0,(s_0,t_0)),\dots ,(x_{q-1},(s_{q-1},t_{q-1}))):={\psi }_{\lfloor max\left(t_j\right)\rfloor +1}((x_0,(s_0,t_0)),\dots ,(x_{q-1},(s_{q-1},t_{q-1})))$$

has cocontrolled support. We have

$$\psi (z_0,\dots ,z_{q-1})=\sum _{i=0}^{q-1}{(-1)}^i\phi (z_0,\dots ,z_i,p\left(z_i\right),\dots ,p\left(z_{q-1}\right)).$$

Thus, $\psi$ is blocky; namely, if $\phi \in C_{A_1,\dots ,A_n}^q(X\ast I,A)$ then $\psi \in C_{p^{-1}{A}_i\cap A_j}^{q-1}(X\ast I,A)$. This way, we have proved that $\psi$ is a cochain.

Lastly, we have

$$\begin{array}{cc}\hfill \left(d_{q-1}\psi \right)\left(\overline{z}\right)& =\psi ((x_1,(s_1,t_1)),\dots ,(x_q,(s_q,t_q)))-\cdots \pm \psi ((x_0,(s_0,t_0)),\dots ,(x_{q-1},(s_{q-1},t_{q-1})))\hfill \\ \hfill & ={\psi }_{\lfloor max\left(t_j\right)\rfloor +1}((x_1,(s_1,t_1)),\dots ,(x_q,(s_q,t_q)))-\cdots \hfill \\ \hfill & \pm {\psi }_{\lfloor max\left(t_j\right)\rfloor +1}((x_0,(s_0,t_0)),\dots ,(x_{q-1},(s_{q-1},t_{q-1})))\hfill \\ \hfill & =\left(d_{q-1}{\psi }_{\lfloor max\left(t_j\right)\rfloor +1}\right)\left(\overline{z}\right)\hfill \\ \hfill & =h_{\lfloor max\left(t_j\right)\rfloor +1}^{\ast }\phi \left(\overline{z}\right)-\phi \left(\overline{z}\right)\hfill \\ \hfill & =(p^{\ast }\phi -\phi )\left(\overline{z}\right)\hfill \end{array}$$

Thus, $p^{\ast }\phi -\phi$ defines a coboundary. This way, we showed $p^{\ast }$ induces the identity on ${\check{H}}_{ct}^q(X\ast I,A)$ for $q\ge 1$. It remains to show the statement for $q=0$.

The proof of Lemma 26 shows that $p^{\ast }$ induces the identity on $H{Y}_b^0(X\ast I,A)$. Namely, if $\phi \in kerd{Y}_0^b$ then there are only boundedly many $x\in X$ such that $\phi$ has mixed values on $\left\{x\right\}\ast I$. Thus $\phi$ is the same map as $(x,(s,t\left)\right)\mapsto \phi (x,(s+t,0\left)\right)$ up to bounded error. □

A metric space X is called coarsely contractible if the map $d(x_0,·)$ is a coarse homotopy equivalence.

Lemma 27. 

If X is a coarsely contractible metric space, then ${\check{H}}_{ct}^q(X,A)=0$ for every $q>0$ and finite abelian group A.

Proof. 

By definition, the map $d(x_0,·)$ is a coarse homotopy equivalence. Therefore, it induces an isomorphism in cohomology by Theorem 15. Since ${\mathbb{Z}}_{\ge 0}$ is acyclic, so is X by Theorem 14. □

11. Cohomology of Free Abelian Groups

This chapter proves Theorem 6.

If X is a uniquely geodesic metric space and $a,b,c\in X$ then a geodesic triangle $\Delta (a,b,c)$ with vertices $a,b,c$ is the union of the geodesics joining a to b, b to c and c to a. There is a comparison map $f:\Delta (a,b,c)\to \Delta (f\left(a\right),f\left(b\right),f\left(c\right))\subseteq {\mathbb{R}}^2$ which is an isometry on each of the edges. Then, X is called CAT(0) if $d(x,y)\le \parallel f\left(x\right)-f\left(y\right)\parallel$ for every $x,y\in \Delta (a,b,c)$ for every $a,b,c\in X$.

Lemma 28. 

If X is a CAT(0) space then $X\times {\mathbb{R}}_{\ge 0}$ is coarsely contractible.

Proof. 

We define two maps

$$\begin{array}{cc}\hfill \begin{array}{cc}\hfill \pi :X\times {\mathbb{R}}_{\ge 0}& \to {\mathbb{R}}_{\ge 0}\hfill \\ \hfill (x,i)& \mapsto d(x,x_0)+i\hfill \end{array}& \begin{array}{cc}\hfill \iota :{\mathbb{R}}_{\ge 0}& \to X\times {\mathbb{R}}_{\ge 0}\hfill \\ \hfill i& \mapsto (x_0,i)\hfill \end{array}\hfill \end{array}$$

and show that they are coarse homotopy inverses.

Since X is CAT(0), there exists for every $x\in X$ a geodesic ${\gamma }_x:[0,1]\to X$ joining $x_0$ to x. The inequality $d({\gamma }_x\left(t\right),{\gamma }_y\left(t\right))\le d(x,y)$ holds for every $t\in [0,1]$ by the curvature condition.

We define

$$\begin{array}{cc}\hfill h:(X\times {\mathbb{R}}_{\ge 0})\ast I& \to X\times {\mathbb{R}}_{\ge 0}\hfill \\ \hfill \left(\right(x,i),(s,t\left)\right)& \mapsto ({\gamma }_x\left(\widehat{t}\right),i+\widehat{s}d(x,x_0)).\hfill \end{array}$$

Here $\widehat{s}=\frac{s}{s+t}$ and $\widehat{t}=\frac{t}{s+t}$. The map h joins $\iota \circ \pi$ to $i{d}_{X\times {\mathbb{Z}}_{\ge 0}}$. It remains to show that h is coarse. If $R\ge 0$ and $d(((x_1,i_1),(s_1,t_1)),((x_2,i_2),(s_2,t_2))\le R$, then

$$\begin{array}{cc}\hfill d({\gamma }_{x_1}\left({\widehat{t}}_1\right),{\gamma }_{x_2}\left({\widehat{t}}_2\right))& \le d({\gamma }_{x_1}\left({\widehat{t}}_1\right),{\gamma }_{x_1}\left({\widehat{t}}_2\right))+d({\gamma }_{x_1}\left({\widehat{t}}_2\right),{\gamma }_{x_2}\left({\widehat{t}}_2\right))\hfill \\ \hfill & \le |{\widehat{t}}_1-{\widehat{t}}_2|d(x_0,x_1)+d(x_1,x_2)\hfill \\ \hfill & =\left|\frac{t_1}{s_1+t_1}-\frac{t_2}{s_2+t_2}\right|d(x_0,x_1)+d(x_1,x_2)\hfill \\ \hfill & \le \left|\frac{t_1}{d(x_0,x_1)}-\frac{t_2}{d(x_0,x_1)-R}\right|d(x_0,x_1)+R\hfill \\ \hfill & =\left|\frac{(d(x_0,x_1)-R)t_1-d(x_0,x_1)t_2}{d(x_0,x_1)-R}\right|+R\hfill \\ \hfill & \le \frac{2R}{1-\frac{R}{d(x_0,x_1)}}+R\hfill \\ \hfill & \le 4R+R\hfill \end{array}$$

for $d(x_0,x_1)$ large compared to R. Then,

$$\begin{array}{cc}& |i_1+{\widehat{s}}_{1}d(x_1,x_0)-(i_2+{\widehat{s}}_{2}d(x_2,x_0))|\hfill \\ \hfill & \le |i_1-i_2|+|{\widehat{s}}_{1}d(x_1,x_0)-{\widehat{s}}_{1}d(x_2,x_0)|+|{\widehat{s}}_{1}d(x_2,x_0)-{\widehat{s}}_{2}d(x_2,x_0)|\hfill \\ \hfill & \le R+{\widehat{s}}_{1}d(x_1,x_2)+4R\hfill \\ \hfill & \le 6R\hfill \end{array}$$

for $d(x_0,x_2)$ large compared to R. Thus, h is coarsely uniform.

If $S\ge 0$ and $((x,i),(s,t))\in h^{-1}\left({\Delta }_S\left[(x_0,0)\right]\right)$ then,

$$\begin{array}{c}\hfill \widehat{t}d(x,x_0)=\widehat{t}d({\gamma }_x\left(1\right),{\gamma }_x\left(0\right))=d({\gamma }_x\left(\widehat{t}\right),{\gamma }_x\left(0\right))\le S\end{array}$$

(5)

and

$$\begin{array}{c}\hfill \widehat{s}d(x,x_0)\le S.\end{array}$$

(6)

The inequalities (5) and (6) add to an inequality $d(x,x_0)\le S$. This inequality and $\left|i\right|\le S$ show that h is coarsely proper. This way, we have showed that h is a coarse map. □

Lemma 28 in particular implies that ${\mathbb{R}}_{\ge 0}\times {\mathbb{R}}^{n-1}$ is a coarsely contractible subspace of ${\mathbb{R}}^n$. In fact, ${\mathbb{R}}^i\times {\mathbb{R}}_{\ge 0}\times {\mathbb{R}}^{n-1-i}$ and ${\mathbb{R}}^i\times {\mathbb{R}}_{<0}\times {\mathbb{R}}^{n-1-i}$ are coarsely contractible subspaces of ${\mathbb{R}}^n$ and so is every finite intersection of them.

Lemma 29. 

If $\mathcal{F}$ is a sheaf on a metric space X and ${\left(U_i\right)}_i$ a Leray cover of X, namely, a coarse cover such that every finite intersection $U_{i_0}\cap \cdots \cap U_{i_q}$ is $\mathcal{F}$-acyclic, then

$${\check{H}}_{ct}^q(X,\mathcal{F})={\check{H}}^q({\left(U_i\right)}_i,\mathcal{F}).$$

The right side denotes Čech-cohomology of the cover ${\left(U_i\right)}_i$.

Proof. 

For sheaves on a topological space, there exist a number of proofs for this result. We mimic the proof of ([20], Theorem III.4.5).

Embed $\mathcal{F}$ in a flabby sheaf $\mathcal{G}$ and take the quotient ${\mathcal{F}}_1$. Then, there is a short exact sequence of sheaves

$$\begin{array}{c}\hfill 0\to \mathcal{F}\to \mathcal{G}\to {\mathcal{F}}_1\to 0.\end{array}$$

(7)

Since ${\check{H}}^1(U_{i_0}\cap \cdots \cap U_{i_q},\mathcal{F})=0$ there is a short exact sequence of abelian groups

$$0\to \mathcal{F}(U_{i_0}\cap \cdots \cap U_{i_q})\to \mathcal{G}(U_{i_0}\cap \cdots \cap U_{i_q})\to {\mathcal{F}}_1(U_{i_0}\cap \cdots \cap U_{i_q})\to 0.$$

Taking products, we obtain an exact sequence of Čech-cocomplexes

$$0\to {\check{C}}^{\ast }({\left(U_i\right)}_i,\mathcal{F})\to {\check{C}}^{\ast }({\left(U_i\right)}_i,\mathcal{G})\to {\check{C}}^{\ast }({\left(U_i\right)}_i,{\mathcal{F}}_1)\to 0.$$

This results in a long exact sequence of Čech cohomology. Since $\mathcal{G}$ is flabby, its Čech cohomology vanishes for $q>0$. This way, we get an exact sequence

$$\begin{array}{c}\hfill 0\to {\check{H}}^0({\left(U_i\right)}_i,\mathcal{F})\to {\check{H}}^0({\left(U_i\right)}_i,\mathcal{G})\to {\check{H}}^0({\left(U_i\right)}_i,{\mathcal{F}}_1)\to {\check{H}}^1({\left(U_i\right)}_i,\mathcal{F})\to 0.\end{array}$$

(8)

and isomorphisms

$$\begin{array}{c}\hfill {\check{H}}^q({\left(U_i\right)}_i,{\mathcal{F}}_1)={\check{H}}^{q+1}({\left(U_i\right)}_i,\mathcal{F})\end{array}$$

(9)

for each $q\ge 1$. Associated to the exact sequence of sheaves (7) there is an exact sequence

$$\begin{array}{c}\hfill 0\to {\check{H}}_{ct}^0(X,\mathcal{F})\to {\check{H}}_{ct}^0(X,\mathcal{G})\to {\check{H}}_{ct}^0(X,{\mathcal{F}}_1)\to {\check{H}}_{ct}^1(X,\mathcal{F})\to 0.\end{array}$$

(10)

Since ${\check{H}}^0({\left(U_i\right)}_i,\mathcal{H})={\check{H}}_{ct}^0(X,\mathcal{H})$ for any sheaf $\mathcal{H}$ we can compare the exact sequences (8) and (10) and obtain

$${\check{H}}^1({\left(U_i\right)}_i,\mathcal{F})={\check{H}}_{ct}^1(X,\mathcal{F}).$$

Now, the long exact sequence in cohomology for (7) and $U_{i_0}\cap \cdots \cap U_{i_q}$ being $\mathcal{F}$-acyclic implies that $U_{i_0}\cap \cdots \cap U_{i_q}$ is ${\mathcal{F}}_1$-acyclic. Thus, ${\mathcal{F}}_1$ satisfies the conditions of this Lemma. This way, we use induction and isomorphisms (9) to obtain the result for $q>1$. □

Theorem 16. 

We can compute cohomology:

$${\check{H}}_{ct}^q({\mathbb{Z}}^n;A)=\left\{\begin{array}{cc}A\oplus A\hfill & n=1,q=0\hfill \\ A\hfill & n\ne 1,q=0\vee q=n-1\hfill \\ 0\hfill & otherwise.\hfill \end{array}\right.$$

if A is a finite abelian group.

Proof. 

If $n=1$, this result is already Theorem 14.

Suppose $n\ge 2$. We compute cohomology of ${\mathbb{R}}^n$. The result for ${\mathbb{Z}}^n$ follows since the spaces ${\mathbb{Z}}^n$ and ${\mathbb{R}}^n$ are coarsely equivalent. For $i=1,\dots ,n$ define $U_i^{+}:={\mathbb{R}}^{i-1}\times {\mathbb{R}}_{\ge 0}\times {\mathbb{R}}^{n-i}$ and $U_i^{-}:={\mathbb{R}}^{i-1}\times {\mathbb{R}}_{<0}\times {\mathbb{R}}^{n-i}$. A finite intersection of those halfspaces is coarsely contractible by Lemma 28. We show the ${(U_i^{+},U_i^{-})}_i$ form a coarse cover. Let $\overline{x}:=(x_1,\dots ,x_n)\in {\bigcap }_{i=1}^n({\Delta }_R\left[{\left(U_i^{+}\right)}^c\right]\cap {\Delta }_R\left[{\left(U_i^{-}\right)}^c\right])$ be a point. We show $d(\overline{x},(0,\dots ,0))\le nR$. If $i=1,\dots ,n$ then $\overline{x}\in {\Delta }_R\left[{\left(U_i^{-}\right)}^c\right]$ implies $x_i\ge -R$. Additionally, $\overline{x}\in {\Delta }_R\left[{\left(U_i^{+}\right)}^c\right]$ implies $x_i\le R$. Together they imply $d(x_i,0)\le R$ and in all together the result. Thus, $\mathcal{U}:={(U_i^{+},U_i^{-})}_i$ forms a Leray cover.

By Lemma 29, the metric cohomology of ${\mathbb{R}}^n$ is the Čech cohomology of $\mathcal{U}$. In the topological world the sphere $S^{n-1}$ admits a Leray cover by $V_i^{+}:=\{(x_1,\dots ,x_n)\in S^{n-1}|x_i>0\}$ and $V_i^{-}:=\{(x_1,\dots ,x_n)\in S^{n-1}|x_i<0\}$. The combinatorical information of this cover is the same as that of $\mathcal{U}$. Thus, both covers have the same nerve. Since the nerve contains all the cohomological information, we just proved that ${\mathbb{R}}^n$ (as a metric space) has the same cohomology as $S^{n-1}$ (as a topological space). This proves the claim. □

There is another method we can use to compute the cohomology of ${\mathbb{R}}^n$. If X is a CAT(0) metric space, then the coarse cone over X is given by $X\times {\mathbb{R}}_{\ge 0}$. Lemma 28 tells us that the coarse cone is coarsely contractible. Now, the coarse suspension of a CAT(0) metric space X is given by $X\times \mathbb{R}$.

Lemma 30. 

If X is a CAT(0) metric space, then the coarse suspension shifts coarse sheaf cohomology by one degree, namely, ${\check{H}}_{ct}^q(X,A)\cong {\check{H}}_{ct}^{q+1}(X\times \mathbb{R},A)$ for $q\ge 1$.

Proof. 

We cover $X\times \mathbb{R}$ by two sets $U_1=\left\{(x,t)\right|t\le d(x_0,x)\}$ and $U_2=\left\{(x,t)\right|t\ge -d(x,x_0)\}$. They form a coarse cover: if $(y,s)\in U_1^c,(x,t)\in U_2^c$ with $d\left(\right(y,s),(x,t\left)\right)\le R$ then $|s-t|\le R$, $s>d(x_0,y)$ and $t<-d(x_0,x)$. Since s is positive and t is negative, we obtain $\left|s\right|,\left|t\right|\le R$. Furthermore, $d(x_0,y)<s\le R$ and $d(x_0,x)\le \left|t\right|\le R$. Thus, $U_1,U_2$ coarsely cover X.

There are coarse homotopy equivalences $U_1,U_2\simeq X\times {\mathbb{R}}_{\ge 0}$ and $U_1\cap U_2\simeq X$. Namely, the inclusion $i_1:X\times {\mathbb{R}}_{\ge 0}\to U_2$ has a coarse homotopy inverse

$$\begin{array}{cc}\hfill p_1:U_2& \to X\times {\mathbb{R}}_{\ge 0}\hfill \\ \hfill (x,t)& \mapsto \left\{\begin{array}{cc}(x,t)\hfill & t\ge 0\hfill \\ (x,0)\hfill & t<0\hfill \end{array}\right.\hfill \end{array}$$

The coarse homotopy connecting $i_1\circ p_1$ with $i{d}_{U_2}$ is given by

$$\begin{array}{cc}\hfill h_1:U_2\ast I& \to U_2\hfill \\ \hfill \left(\right(x,t),(i,j\left)\right)& \mapsto \left\{\begin{array}{cc}(x,\widehat{i}t)\hfill & t<0\hfill \\ (x,t)\hfill & t\ge 0.\hfill \end{array}\right.\hfill \end{array}$$

Here $\widehat{i}:=\frac{i}{i+j}$. We show h is coarse: If $d\left(\right((x,t),(i,j)),((y,s),(n,m)\left)\right)\le R$ then in particular $d(x,y)\le R$ and

$$d(\widehat{i}t,\widehat{n}s)\le d(\widehat{i}t,\widehat{i}s)+d(\widehat{i}s,\widehat{n}s)\le 2R.$$

Thus, $h_1$ is coarsely uniform. If $d((x,\widehat{i}t),(x_0,0))\le S$ then $d(x,x_0)\le S$ and if $t<0$ then $\left|t\right|\le d(x,x_0)\le S$ or if $t\ge 0$ then $d(t,0)\le S$. Thus, $h_1$ is coarsely proper.

The coarse homotopy equivalence connecting X with $U_1\cap U_2$ is given by $i_2:x\mapsto (x,0)$ and its inverse is

$$\begin{array}{cc}\hfill p_2:U_1\cap U_2& \to X\hfill \\ \hfill (x,t)& \mapsto x.\hfill \end{array}$$

The coarse homotopy joining $i_2\circ p_2$ to $i{d}_{U_1\cap U_2}$ is given by

$$\begin{array}{cc}\hfill h_2:(U_1\cap U_2)\ast I& \to U_1\cap U_2\hfill \\ \hfill \left(\right(x,t),(i,j\left)\right)& \mapsto (x,\widehat{i}t).\hfill \end{array}$$

We prove that $h_2$ is coarsely proper; the property coarsely uniform can be shown similarly as for $h_1$. If $d((x,\widehat{i}t),(x_0,0))\le S$ then $d(x,x_0)\le S$ and $\left|t\right|\le d(x,x_0)\le S$.

Then, the long exact sequence of Theorem 8 gives us

$${\check{H}}_{ct}^q(X,A)\cong {\check{H}}_{ct}^q(U_1\cap U_2,A)\cong {\check{H}}_{ct}^{q+1}(U_1\cup U_2,A)={\check{H}}_{ct}^{q+1}(X\times \mathbb{R},A)$$

in degree $q\ge 1$. □

Remark 3. 

The suspension functor has a right adjoint, the loop space. If X is a metric space, then the loop space of X, $\Omega X$ consists of coarse maps $\mathbb{R}\to X$. A subset $E\subseteq \Omega X\times \Omega X$ is an entourage if for every $R\ge 0$ the set $\{(\phi \left(r\right),\psi \left(r^{\prime }\right))\mid (\phi ,\psi )\in E,|r-r^{\prime }|\le R\}$ is an entourage in Y. Note that $\Omega Y$ defined this way does not have a connected coarse structure. Then, there exists a natural isomorphism

$$Hom(X\times \mathbb{R},Y)=Hom(X,\Omega Y).$$

Suppose coarse maps ${\mathbb{R}}^n\to Y$ denote the $n-1$th coarse homotopy group of Y. If we insert ${\mathbb{R}}^n$ for X in the adjoint relation, then we can see that the loop space shifts coarse homotopy groups down a dimension.