Finite-Time Stability Analysis of Linear Differential Systems with Pure Delay

Abstract

Nonhomogeneous systems governed by second-order linear differential equations with pure delay are considered. As an application, the exact solutions of these systems and their delayed matrix functions are used to obtain the finite-time stability results. Our results extend and improve some previous results by removing some restrictive conditions. Finally, an example is provided to illustrate our theoretical results.

1. Introduction

Numerous processes in mechanical and technological systems were described using delay differential equations. These systems are frequently utilized in the modeling of phenomena in technological and scientific problems. These models have applications in diffusion processes, forced oscillations, signal analysis, control theory, viscoelastic systems, modeling disease, biology, computer engineering, finance, and population dynamics. Time-delays are frequently associated with the economy, electric networks, physico-chemical processes, heredity in population growth, hydraulic networks, and other relevant industries. Generally, these mathematical models have a peculiarity, which is that the rate of change of these processes is determined by their history. On the other hand, in 2003, Khusainov and Shuklin [1] represented the solutions of linear delay differentiaL equations by constructing a new concept of a delayed exponential matrix function. In 2008, Khusainov et al. [2] adopted this approach to represent the solutions of an oscillating system with pure delay by establishing a delayed matrix sine and a delayed matrix cosine. This pioneering research yielded plenty of novel results on the exact solutions that were used in the stability analysis and control problems of time-delay systems; see for example [3,4,5,6,7,8,9,10,11,12,13] and the references therein.

Finite-time stability is a novel definition that involves a fixed finite-time interval and a prescribed constraint for the system, as opposed to the exponential/asymptotic stability definition, which is exposed to an infinite-time interval. In the literature, there has been a considerable interest in finite-time stability analysis of differential or fractional delay systems, and several methods for studying finite-time stability of differential or fractional delay systems have been developed; for example, fundamental matrix and the largest singular value of matrix coefficients [14], Lyapunov-like approach with Jensen’s and Coppel’s inequality [15], Grownwall’s approach [16], method of steps [17], Hölder inequality [18], delayed Mittag–Leffler matrix function [19], Gronwall inequality [20], linear matrix inequality [21], the delayed matrix exponential and Jensen and Coppel inequalities [22], the delayed matrix exponential function and Gronwall integral inequalities [23], the delayed matrix cosine and sine [24], the explicit solution of the system [25], and conformable delayed matrix functions [26].

However, to the best of our knowledge, no study exists dealing with finite-time stability analysis of a system of second-order linear differential equations with pure delay of the form

$$\begin{array}{c}{y}^{″}\left(x\right)=-By\left(x-h\right)+f\left(x\right),\mathrm{for}h>0,x\in W:=\left[0,L\right],\\ y\left(x\right)\equiv \psi \left(x\right),y^{\prime }\left(x\right)\equiv {\psi }^{\prime }\left(x\right)\mathrm{for}-h\le x\le 0,\end{array}$$

(1)

where h is a delay, L is a pre-fixed positive number, $y\left(x\right)\in {\mathbb{R}}^n$, $\psi \in C^2\left(\left[-h,0\right],{\mathbb{R}}^n\right)$, B$\in {\mathbb{R}}^{n\times n}$ is a constant nonzero matrix and $f\in C\left(\left[0,\infty \right),{\mathbb{R}}^n\right)$ is a given function.

Very recently, Elshenhab and Wang [8] gave a new representation of solutions of (1) as follows:

$$\begin{array}{cc}\hfill y\left(x\right)& ={\mathcal{H}}_h\left(B\left(x-h\right)\right)\psi \left(0\right)+{\mathcal{M}}_h\left(B\left(x-h\right)\right){\psi }^{\prime }\left(0\right)\hfill \\ \hfill & -B{\int }_{-h}^0{\mathcal{M}}_h\left(B\left(x-2h-\varrho \right)\right)\psi \left(\varrho \right)d\varrho \hfill \\ \hfill & +{\int }_0^x{\mathcal{M}}_h\left(B\left(x-h-\varrho \right)\right)f\left(\varrho \right)d\varrho ,\hfill \end{array}$$

(2)

and they also derived alternative formulas of solutions of (1) as follows:

$$\begin{array}{cc}\hfill y\left(x\right)& ={\mathcal{H}}_h\left(Bx\right)\psi \left(-h\right)+{\mathcal{M}}_h\left(Bx\right){\psi }^{\prime }\left(-h\right)\hfill \\ \hfill & +{\int }_{-h}^0{\mathcal{M}}_h\left(B\left(x-h-\varrho \right)\right){\psi }^{″}\left(\varrho \right)d\varrho \hfill \\ \hfill & +{\int }_0^x{\mathcal{M}}_h\left(B\left(x-h-\varrho \right)\right)f\left(\varrho \right)d\varrho ,\hfill \end{array}$$

(3)

or

$$\begin{array}{cc}\hfill y\left(x\right)& ={\mathcal{H}}_h\left(Bx\right)\psi \left(-h\right)+{\mathcal{M}}_h\left(B\left(x-h\right)\right){\psi }^{\prime }\left(0\right)\hfill \\ \hfill & +{\int }_{-h}^0{\mathcal{H}}_h\left(B\left(x-h-\varrho \right)\right){\psi }^{\prime }\left(\varrho \right)d\varrho \hfill \\ \hfill & +{\int }_0^x{\mathcal{M}}_h\left(B\left(x-h-\varrho \right)\right)f\left(\varrho \right)d\varrho ,\hfill \end{array}$$

(4)

where ${\mathcal{H}}_h\left(Bx\right)$ and ${\mathcal{M}}_h\left(Bx\right)$ are called the delayed matrix functions formulated by

$${\mathcal{H}}_h\left(Bx\right):=\left\{\begin{array}{c}\Theta ,-\infty <x<-h,\\ I,-h\le x<0,\\ I-B\frac{x^2}{2!},0\le x<h,\\ ⋮⋮\\ I-B\frac{x^2}{2!}+B^2\frac{{\left(x-h\right)}^4}{4!}\\ +\cdots +{(-1)}^m{B}^m\frac{{\left(x-\left(m-1\right)h\right)}^{2m}}{\left(2m\right)!},\left(m-1\right)h\le x<mh,\end{array}\right.$$

(5)

$${\mathcal{M}}_h\left(Bx\right):=\left\{\begin{array}{c}\Theta ,-\infty <x<-h,\\ I\left(x+h\right),-h\le x<0,\\ I\left(x+h\right)-B\frac{x^3}{3!},0\le x<h,\\ ⋮⋮\\ I\left(x+h\right)-B\frac{x^3}{3!}+B^2\frac{{\left(x-h\right)}^5}{5!}\\ +\cdots +{(-1)}^m{B}^m\frac{{\left(x-\left(m-1\right)h\right)}^{2m+1}}{\left(2m+1\right)!},\left(m-1\right)h\le x<mh,\end{array}\right.$$

(6)

respectively, where $m=0,1,2,\cdots$, the notation I is the $n\times n$ identity matrix and $\Theta$ is the $n\times n$ null matrix.

Motivated by [8,24], as an application, the explicit formulas of solutions of the system (1) and the delayed matrix functions are used to obtain finite-time stability results on $W=\left[0,L\right]$.

The rest of this paper is arranged as follows: In Section 2, we present some basic definitions and estimations of norms for the delayed matrix functions, which are used while discussing finite-time stability. In Section 3, as an application, the representation of the solutions of (1) are used to obtain finite-time stability results. Finally, we give an example to illustrate the main results.

2. Preliminaries

Throughout the paper, we denote the vector norm as $∥y∥={\sum }_{i=1}^n\left|y_i\right|$ and the matrix norm as $∥B∥={max}_{1\le j\le n}{\sum }_{i=1}^n\left|a_{ij}\right|$; $y_i$ and $a_{ij}$ are the elements of the vector y and the matrix B, respectively. Denote $C\left(W,{\mathbb{R}}^n\right)$ the Banach space of vector-valued continuous function from $W\to {\mathbb{R}}^n$ endowed with the norm ${∥y∥}_C={max}_{x\in W}∥y\left(x\right)∥$ for a norm $∥·∥$ on ${\mathbb{R}}^n$. We introduce a space $C^1\left(W,{\mathbb{R}}^n\right)=\left\{y\in C\left(W,{\mathbb{R}}^n\right):y^{\prime }\in C\left(W,{\mathbb{R}}^n\right)\right\}$. Furthermore, we see ${∥\psi ∥}_C={max}_{\varrho \in \left[-h,0\right]}∥\psi \left(\varrho \right)∥$.

We recall some basic definitions used further in this paper.

Definition 1

([27]). The two-parameter Mittag–Leffler function is given by

$${\mathbb{E}}_{\alpha ,\gamma }\left(z\right)=\sum _{k=0}^{\infty }\frac{z^k}{\Gamma \left(\alpha k+\gamma \right)},\alpha ,\gamma >0,z\in \mathbb{C}.$$

Especially, if $\gamma =1$, then

$${\mathbb{E}}_{\alpha ,1}\left(z\right)={\mathbb{E}}_{\alpha }\left(z\right)=\sum _{k=0}^{\infty }\frac{z^k}{\Gamma \left(\alpha k+1\right)},\alpha >0.$$

Definition 2

([16]). The system (1) is finite-time stable with respect to $\left\{0,W,h,\delta ,\rho \right\}$, $\delta <\rho$ if and only if $\varrho <\delta$ implies $∥y\left(x\right)∥<\rho$ for all $x\in W$, where $\varrho =max\left\{{∥\psi ∥}_C,{∥{\psi }^{\prime }∥}_C,{∥{\psi }^{″}∥}_C\right\}$ and δ, ρ are real positive numbers.

To conclude this section, we provide estimations of norms for the delayed matrix functions, which are used in discussing finite-time stability.

Lemma 1.

For any $x\in \left[\left(m-1\right)h,mh\right]$, $m=1,2,\dots$, we have

$$∥{\mathcal{H}}_h\left(Bx\right)∥\le {\mathbb{E}}_2\left(∥B∥x^2\right).$$

Proof. 

Using (5), we get

$$\begin{array}{cc}\hfill ∥{\mathcal{H}}_h\left(Bx\right)∥& \le 1+∥B∥\frac{x^2}{2!}+{∥B∥}^2\frac{{\left(x-h\right)}^4}{4!}\hfill \\ \hfill & +\cdots +{∥B∥}^m\frac{{\left(x-\left(m-1\right)h\right)}^{2m}}{\left(2m\right)!}\hfill \\ \hfill & \le 1+∥B∥\frac{x^2}{2!}+{∥B∥}^2\frac{x^4}{4!}+\cdots +{∥B∥}^m\frac{x^{2m}}{\left(2m\right)!}\hfill \\ \hfill & \le \sum _{k=0}^{\infty }\frac{{\left(∥B∥x^2\right)}^k}{\left(2k\right)!}={\mathbb{E}}_2\left(∥B∥x^2\right).\hfill \end{array}$$

This completes the proof.  □

Lemma 2.

For any $x\in \left[\left(m-1\right)h,mh\right]$, $m=1,2,\dots$, we have

$$∥{\mathcal{M}}_h\left(Bx\right)∥\le \left(x+h\right){\mathbb{E}}_{2,2}\left(∥B∥{\left(x+h\right)}^2\right).$$

Proof. 

Using (6), we get

$$\begin{array}{cc}\hfill ∥{\mathcal{M}}_h\left(Bx\right)∥& \le \left(x+h\right)+∥B∥\frac{x^3}{3!}+{∥B∥}^2\frac{{\left(x-h\right)}^5}{5!}\hfill \\ \hfill & +\cdots +{∥B∥}^m\frac{{\left(x-\left(m-1\right)h\right)}^{2m+1}}{\left(2m+1\right)!}\hfill \\ \hfill & \le \left(x+h\right)+∥B∥\frac{{\left(x+h\right)}^3}{3!}+{∥B∥}^2\frac{{\left(x+h\right)}^5}{5!}\hfill \\ \hfill & +\cdots +{∥B∥}^m\frac{{\left(x+h\right)}^{2m+1}}{\left(2m+1\right)!}\hfill \\ \hfill & \le \sum _{k=0}^{\infty }\frac{{\left[∥B∥{\left(x+h\right)}^2\right]}^k\left(x+h\right)}{\left(2k+1\right)!}=\left(x+h\right){\mathbb{E}}_{2,2}\left(∥B∥{\left(x+h\right)}^2\right).\hfill \end{array}$$

This completes the proof.  □

3. Main Results

In this section, we derived finite-time stability results of (1) by making use of the three possible formulas of solutions (2), (3) and (4), respectively.

Theorem 1.

The system (1) is finite-time stable with respect to $\left\{0,W,h,\delta ,\rho \right\}$, if

$${\mathbb{E}}_2\left(∥B∥{\left(L-h\right)}^2\right)<\frac{\rho -\left(\delta L+\frac{L^2}{2}\left(\delta ∥B∥+{∥f∥}_C\right)\right){\mathbb{E}}_{2,2}\left(∥B∥L^2\right)}{\delta }.$$

(7)

Proof. 

By using Definition 2 and (2), we have $\varrho <\delta$ and

$$\begin{array}{cc}\hfill ∥y\left(x\right)∥& \le ∥{\mathcal{H}}_h\left(B\left(x-h\right)\right)∥∥\psi \left(0\right)∥+∥{\mathcal{M}}_h\left(B\left(x-h\right)\right)∥∥{\psi }^{\prime }\left(0\right)∥\hfill \\ \hfill & +∥B∥∥{\int }_{-h}^0{\mathcal{M}}_h\left(B\left(x-2h-\varrho \right)\right)\psi \left(\varrho \right)d\varrho ∥\hfill \\ \hfill & +∥{\int }_0^x{\mathcal{M}}_h\left(B\left(x-h-\varrho \right)\right)f\left(\varrho \right)d\varrho ∥\hfill \\ \hfill & \le ∥{\mathcal{H}}_{h,\alpha }\left(B\left(x-h\right)\right)∥∥\psi \left(0\right)∥+∥{\mathcal{M}}_h\left(B\left(x-h\right)\right)∥∥{\psi }^{\prime }\left(0\right)∥\hfill \\ \hfill & +∥B∥{\int }_{-h}^0∥{\mathcal{M}}_h\left(B\left(x-2h-\varrho \right)\right)∥∥\psi \left(\varrho \right)∥d\varrho \hfill \\ \hfill & +{\int }_0^x∥{\mathcal{M}}_h\left(B\left(x-h-\varrho \right)\right)∥∥f\left(\varrho \right)∥d\varrho \hfill \\ \hfill & \le \delta ∥{\mathcal{H}}_{h,\alpha }\left(B{\left(x-h\right)}^{\alpha }\right)∥+\delta ∥{\mathcal{M}}_{h,\alpha }\left(B{\left(x-h\right)}^{\alpha }\right)∥\hfill \\ \hfill & +\delta ∥B∥{\int }_{-h}^0∥{\mathcal{M}}_h\left(B\left(x-2h-\varrho \right)\right)∥d\varrho \hfill \\ \hfill & +{∥f∥}_C{\int }_0^x∥{\mathcal{M}}_h\left(B\left(x-h-\varrho \right)\right)∥d\varrho .\hfill \end{array}$$

(8)

From Lemma 2, we have

$$\begin{array}{cc}\hfill ∥{\mathcal{M}}_h\left(B\left(x-2h-\varrho \right)\right)∥& \le \left(x-h-\varrho \right){\mathbb{E}}_{2,2}\left(∥B∥{\left(x-h-\varrho \right)}^2\right)\hfill \\ \hfill & \le \left(x-h-\varrho \right){\mathbb{E}}_{2,2}\left(∥B∥x^2\right),\hfill \end{array}$$

(9)

for $-h\le \varrho \le 0$, $x\in W$, and since ${\mathbb{E}}_{2,2}\left(∥B∥x^2\right)$ is increasing function when $x\ge 0$. From (9), we get

$${\int }_{-h}^0∥{\mathcal{M}}_h\left(B{\left(x-2h-\varrho \right)}^{\alpha }\right)∥d\varrho \le \frac{x^2}{2}{\mathbb{E}}_{2,2}\left(∥B∥x^2\right),$$

(10)

and

$$\begin{array}{cc}\hfill {\int }_0^x∥{\mathcal{M}}_h\left(B{\left(x-h-\varrho \right)}^{\alpha }\right)∥d\varrho & \le {\mathbb{E}}_{2,2}\left(∥B∥x^2\right){\int }_0^x\left(x-\varrho \right)d\varrho \hfill \\ \hfill & =\frac{x^2}{2}{\mathbb{E}}_{2,2}\left(∥B∥x^2\right).\hfill \end{array}$$

(11)

From (8), (10) and (11), we have

$$\begin{array}{cc}\hfill ∥y\left(x\right)∥& \le \delta {\mathbb{E}}_2\left(∥B∥{\left(x-h\right)}^2\right)+\delta x{\mathbb{E}}_{2,2}\left(∥B∥x^2\right)\hfill \\ \hfill & +\frac{x^2}{2}\left(\delta ∥B∥+{∥f∥}_C\right){\mathbb{E}}_{2,2}\left(∥B∥x^2\right),\hfill \end{array}$$

(12)

for all $x\in W$. Combining (7) with (12), we get $∥y\left(x\right)∥<\rho$ for all $x\in W$. This ends the proof.  □

Theorem 2.

The system (1) is finite-time stable with respect to $\left\{0,W,h,\delta ,\rho \right\}$, if

$${\mathbb{E}}_2\left(∥B∥L^2\right)<\frac{\rho -\frac{\delta \left(L+h\right)\left(L+h+2\right)}{2}{\mathbb{E}}_{2,2}\left(∥B∥{\left(L+h\right)}^2\right)-\frac{L^2{∥f∥}_C}{2}{\mathbb{E}}_{2,2}\left(∥B∥L^2\right)}{\delta }.$$

(13)

Proof. 

By using Definition 2 and (3), we have $\varrho <\delta$ and

$$\begin{array}{cc}\hfill ∥y\left(x\right)∥& \le ∥{\mathcal{H}}_h\left(Bx\right)∥∥\psi \left(-h\right)∥+∥{\mathcal{M}}_h\left(Bx\right)∥∥{\psi }^{\prime }\left(-h\right)∥\hfill \\ \hfill & +∥{\int }_{-h}^0{\mathcal{M}}_h\left(B\left(x-h-\varrho \right)\right){\psi }^{″}\left(\varrho \right)d\varrho ∥\hfill \\ \hfill & +∥{\int }_0^x{\mathcal{M}}_h\left(B\left(x-h-\varrho \right)\right)f\left(\varrho \right)d\varrho ∥\hfill \\ \hfill & \le \delta ∥{\mathcal{H}}_h\left(Bx\right)∥+\delta ∥{\mathcal{M}}_h\left(Bx\right)∥+\delta {\int }_{-h}^0∥{\mathcal{M}}_h\left(B\left(x-h-\varrho \right)\right)∥d\varrho \hfill \\ \hfill & +{∥f∥}_C{\int }_0^x∥{\mathcal{M}}_h\left(B\left(x-h-\varrho \right)\right)∥d\varrho .\hfill \end{array}$$

(14)

From Lemma 2, we have

$$\begin{array}{cc}\hfill {\int }_{-h}^0∥{\mathcal{M}}_h\left(B\left(x-h-\varrho \right)\right)∥d\varrho & \le {\mathbb{E}}_{2,2}\left(∥B∥{\left(x+h\right)}^2\right){\int }_{-h}^0\left(x-\varrho \right)d\varrho \hfill \\ \hfill & \le \frac{{\left(x+h\right)}^2}{2}{\mathbb{E}}_{2,2}\left(∥B∥{\left(x+h\right)}^2\right).\hfill \end{array}$$

(15)

From (11), (14) and (15), we get

$$\begin{array}{cc}\hfill ∥y\left(x\right)∥& \le \delta {\mathbb{E}}_2\left(∥B∥x^2\right)+\delta \left(x+h\right){\mathbb{E}}_{2,2}\left(∥B∥{\left(x+h\right)}^2\right)\hfill \\ \hfill & +\frac{\delta {\left(x+h\right)}^2}{2}{\mathbb{E}}_{2,2}\left(∥B∥{\left(x+h\right)}^2\right)+\frac{{∥f∥}_C}{2}{x}^2{\mathbb{E}}_{2,2}\left(∥B∥x^2\right)\hfill \end{array}$$

(16)

for all $x\in W$. Combining (13) with (16), we have $∥y\left(x\right)∥<\rho$ for all $x\in W$. This ends the proof.  □

Theorem 3.

The system (1) is finite-time stable with respect to $\left\{0,W,h,\delta ,\rho \right\}$, if

$${\mathbb{E}}_2\left(∥B∥L^2\right)<\frac{\rho -L\left(\delta +\frac{{∥f∥}_C}{2}L\right){\mathbb{E}}_{2,2}\left(∥B∥L^2\right)}{\delta \left(1+h\right)}.$$

(17)

Proof. 

By using Definition 2 and (4), we have $\eta <\delta$ and

$$\begin{array}{cc}\hfill ∥y\left(x\right)∥& \le ∥{\mathcal{H}}_h\left(Bx\right)∥∥\psi \left(-h\right)∥+∥{\mathcal{M}}_h\left(B\left(x-h\right)\right)∥∥{\psi }^{\prime }\left(0\right)∥\hfill \\ \hfill & +∥{\int }_{-h}^0{\mathcal{H}}_h\left(B\left(x-h-\varrho \right)\right){\psi }^{\prime }\left(\varrho \right)d\varrho ∥\hfill \\ \hfill & +∥{\int }_0^x{\mathcal{M}}_h\left(B\left(x-h-\varrho \right)\right)f\left(\varrho \right)d\varrho ∥\hfill \\ \hfill & \le \delta ∥{\mathcal{H}}_h\left(Bx\right)∥+\delta ∥{\mathcal{M}}_h\left(B\left(x-h\right)\right)∥\hfill \\ \hfill & +\delta {\int }_{-h}^0∥{\mathcal{H}}_h\left(B\left(x-h-\varrho \right)\right)∥d\varrho \hfill \\ \hfill & +{∥f∥}_C{\int }_0^x∥{\mathcal{M}}_h\left(B\left(x-h-\varrho \right)\right)∥d\varrho .\hfill \end{array}$$

(18)

From Lemma 1, we have

$${\int }_{-h}^0∥{\mathcal{H}}_h\left(B\left(x-h-\varrho \right)\right)∥d\varrho \le h{\mathbb{E}}_2\left(∥B∥x^2\right).$$

(19)

From (11), (18) and (19), we get

$$\begin{array}{cc}\hfill ∥y\left(x\right)∥& \le \delta {\mathbb{E}}_2\left(∥B∥x^2\right)+\delta x{\mathbb{E}}_{2,2}\left(∥B∥x^2\right)\hfill \\ \hfill & +\delta h{\mathbb{E}}_2\left(∥B∥x^2\right)+\frac{{∥f∥}_C}{2}{x}^2{\mathbb{E}}_{2,2}\left(∥B∥x^2\right).\hfill \end{array}$$

(20)

for all $x\in W$. Combining (17) with (20), we have $∥y\left(x\right)∥<\rho$ for all $x\in W$. This ends the proof.  □

Remark 1.

We see that by dropping the nonsingularity criterion on a matrix coefficient B and making the matrix B an arbitrary, not necessarily squared matrix $B^2$, our results in Theorems 1–3 improve and extend the corresponding results in Theorems 3.1–3.3 in [24].

4. An Example

Consider the delay differential equations

$$\begin{array}{c}{y}^{″}\left(x\right)=-By\left(x-0.5\right)+f\left(x\right),x\in \left[0,1\right],\\ \psi \left(x\right)={\left(0.1x^2,0.2x\right)}^T,{\psi }^{\prime }\left(x\right)={\left(0.2x,0.2\right)}^T,{\psi }^{″}\left(x\right)={\left(0.2,0\right)}^T,-0.5\le x\le 0,\end{array}$$

(21)

where

$$h=0.5,B=\left(\begin{array}{cc}2& 0\\ 0& 0\end{array}\right),f\left(x\right)=\left(\begin{array}{c}1\\ 2\end{array}\right).$$

From (3), for all $0\le x\le 1$, and through a basic calculation, we can obtain

$$\begin{array}{cc}\hfill y\left(x\right)& =\left(\begin{array}{c}0.025{\mathcal{H}}_{0.5}\left(2x\right)\\ -0.1\end{array}\right)+\left(\begin{array}{c}-0.1{\mathcal{M}}_{0.5}\left(2x\right)\\ 0.2\left(x+0.5\right)\end{array}\right)\hfill \\ \hfill & +\left(\begin{array}{c}0.2{\int }_{-0.5}^0{\mathcal{M}}_{0.5}\left(2\left(x-0.5-\varrho \right)\right)d\varrho \\ 0\end{array}\right)\hfill \\ \hfill & +\left(\begin{array}{c}{\int }_0^x{\mathcal{M}}_{0.5}\left(2\left(x-0.5-\varrho \right)\right)d\varrho \\ 2{\int }_0^x\left(x-\varrho \right)d\varrho \end{array}\right)=\left(\begin{array}{c}{y}_1\left(x\right)\\ y_2\left(x\right)\end{array}\right),\hfill \end{array}$$

which implies that

$$\begin{array}{cc}\hfill y_1\left(x\right)& =0.025{\mathcal{H}}_{0.5}\left(2x\right)-0.1{\mathcal{M}}_{0.5}\left(2x\right)\hfill \\ \hfill & +0.2{\int }_{-0.5}^0{\mathcal{M}}_{0.5}\left(2\left(x-0.5-\varrho \right)\right)d\varrho \hfill \\ \hfill & +{\int }_0^x{\mathcal{M}}_{0.5}\left(2\left(x-0.5-\varrho \right)\right)d\varrho ,\hfill \end{array}$$

and

$$y_2\left(x\right)=x^2+\frac{1}{5}x,$$

where

$${\mathcal{H}}_{0.5}\left(2x\right)=\left\{\begin{array}{c}1,-0.5\le x<0,\\ 1-x^2,0\le x<0.5,\\ 1-x^2+\frac{1}{6}{\left(x-0.5\right)}^4,0.5\le x<1,\end{array}\right.$$

and

$${\mathcal{M}}_{0.5}\left(2x\right)=\left\{\begin{array}{c}\left(x+0.5\right),-0.5\le x<0,\\ \left(x+0.5\right)-\frac{1}{3}{x}^3,0\le x<0.5,\\ \left(x+0.5\right)-\frac{1}{3}{x}^3+\frac{1}{30}{\left(x-0.5\right)}^5,0.5\le x<1.\end{array}\right.$$

Thus, the explicit solutions of (21) are

$$\begin{array}{cc}\hfill y_1\left(x\right)& =0.025{\mathcal{H}}_{0.5}\left(2x\right)-0.1{\mathcal{M}}_{0.5}\left(2x\right)\hfill \\ \hfill & +0.2{\int }_{-0.5}^{x-0.5}{\mathcal{M}}_{0.5}\left(2\left(x-0.5-\varrho \right)\right)d\varrho \hfill \\ \hfill & +0.2{\int }_{x-0.5}^0{\mathcal{M}}_{0.5}\left(2\left(x-0.5-\varrho \right)\right)d\varrho \hfill \\ \hfill & +{\int }_0^x{\mathcal{M}}_{0.5}\left(2\left(x-0.5-\varrho \right)\right)d\varrho ,\hfill \end{array}$$

$$y_2\left(x\right)=x^2+\frac{1}{5}x,$$

where $0\le x\le 0.5$, which implies that

$$y_1\left(x\right)=-\frac{1}{60}{x}^4+\frac{1}{30}{x}^3+\frac{19}{40}{x}^2,$$

$$y_2\left(x\right)=x^2+\frac{1}{5}x,$$

and

$$\begin{array}{cc}\hfill y_1\left(x\right)& =0.025{\mathcal{H}}_{0.5}\left(2x\right)-0.1{\mathcal{M}}_{0.5}\left(2x\right)\hfill \\ \hfill & +0.2{\int }_{-0.5}^{x-1}{\mathcal{M}}_{0.5}\left(2\left(x-0.5-\varrho \right)\right)d\varrho \hfill \\ \hfill & +0.2{\int }_{x-1}^0{\mathcal{M}}_{0.5}\left(2\left(x-0.5-\varrho \right)\right)d\varrho \hfill \\ \hfill & +{\int }_0^{x-0.5}{\mathcal{M}}_{0.5}\left(2\left(x-0.5-\varrho \right)\right)d\varrho \hfill \\ \hfill & +{\int }_{x-0.5}^x{\mathcal{M}}_{0.5}\left(2\left(x-0.5-\varrho \right)\right)d\varrho ,\hfill \end{array}$$

$$y_2\left(x\right)=x^2+\frac{1}{5}x,$$

where $0.5\le x\le 1$, which implies that

$$\begin{array}{cc}\hfill y_1\left(x\right)& =\frac{1}{900}{\left(x-0.5\right)}^6-\frac{1}{300}{\left(x-0.5\right)}^5-\frac{1}{16}{\left(x-0.5\right)}^4\hfill \\ \hfill & +\frac{19}{40}{x}^2+\frac{1}{30}{x}^3-\frac{1}{60}{x}^4,\hfill \end{array}$$

$$y_2\left(x\right)=x^2+\frac{1}{5}x.$$

By calculating we get $\eta =max\left\{{∥\psi ∥}_C,{∥{\psi }^{\prime }∥}_C,{∥{\psi }^{″}∥}_C\right\}=0.3$, $∥B∥=2$, ${∥f∥}_C=3$, ${\mathbb{E}}_2\left(2L^2\right)=2.1782$, ${\mathbb{E}}_{2,2}\left(2{\left(L+0.5\right)}^2\right)=1.938$, ${\mathbb{E}}_{2,2}\left(2L^2\right)=1.3683$, then we choose $\delta =0.31>0.3=\eta$. Figure 1 shows the state $y\left(x\right)$ and the norm $∥y\left(x\right)∥$ of (21). Now, Theorems 1–3 imply that $∥y\left(x\right)∥\le 3.29158$, $∥y\left(x\right)∥\le 4.3047395$ and $∥y\left(x\right)∥\le 3.489486$, respectively, we simply take $\rho =3.3$, $4.31$, $3.49$, respectively. Table 1 shows the data.

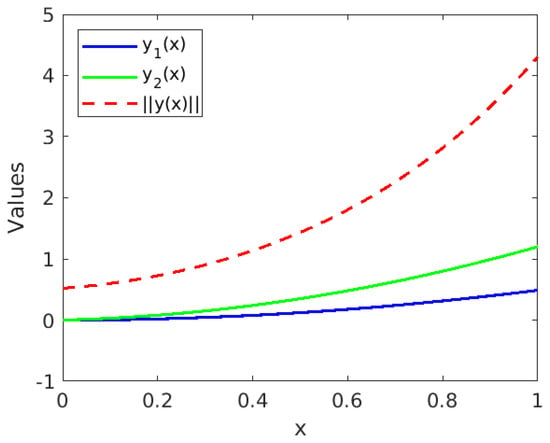
Figure 1. The state $y\left(x\right)$ and $\left|\right|y\left(x\right)\left|\right|$ of (21).

Table 1. Finite-time stability results of (21) and fixed the time L = 1.

Theorem	L	$∥\mathit{B}∥$	$\mathit{\delta }$	$∥\mathit{y}\left(\mathit{x}\right)∥$	$\mathit{\rho }$	h	Finite-Time Stability
1	1	2	$0.31$	≤3.29158	$3.3$ (optimal)	$0.5$	Yes
2	1	2	$0.31$	≤4.30474	$4.31$	$0.5$	Yes
3	1	2	$0.31$	≤3.48949	$3.49$	$0.5$	Yes

We can see $∥y\left(x\right)∥<\rho$ for all $x\in W$ and (21) is finite-time stable under Theorems 1–3. Concerning the definition of finite-time stable, we need to determine a specific threshold $\rho$. By checking the value of $\rho$ in Theorems 1–3, we find that in this example the result of Theorem 1 is the optimal.

Remark 2.

We note that Theorems 3.1–3.3 in [24] cannot be applied to (21) because the matrix B is singular, and an arbitrary, not necessarily squared matrix $B^2$.

5. Conclusions

In this work, by making use of three possible formulas of solutions of nonhomogeneous systems governed by second-order linear delay differential equations, and estimations of norms for the delayed matrix functions, we derived finite-time stability results of these systems. Finally, we provided an example to demonstrate the effectiveness of the obtained results. The results are applicable to all singular, non-singular and arbitrary matrices, not necessarily squared. Consequently, our results improve and extend upon the existing results in [24].

One possible direction in which to extend the results of this paper is toward that of fractional differential and conformable fractional differential systems of order $\alpha \in \left(1,2\right]$.