Abstract
This paper presents research work in which an innovative didactic proposal was designed for the study of 3D metric geometry in the second year of A-level courses (secondary education) in the specialty of the sciences. The designed didactic proposal has the format of a workshop of geometry practices and is framed in the Didactic Situations Theory and in the Anthropological Theory of the Didactic. Although the mentioned theories, which the French school has developed since the seventies, are widely known and studied by secondary school mathematics teachers during their training in pedagogy, especially in Spanish- and French-speaking countries, their innovative approach has not been fully implemented in the field of algebraic geometry. Mathematics textbooks follow the traditional approach in which the teacher simply provides the contents and instructs the student, who captures these concepts and reproduces them as they have been supplied. In the presented didactic proposal, the approach proposed by Brousseau is followed, in which three fundamental elements take part: student, teacher, and the didactic environment. The teacher is the one who facilitates the environment in which the student builds his knowledge. In the proposal the didactic contract is stablished, the didactic situations are designed, and the means and didactic variables for the study of 3D metric geometry are chosen. The methodology followed in this study consisted of identifying educational problems; describing the theoretical framework; developing the didactic proposal; and analysis, reflection, and criticism of this training product. The contextualization of the geometry workshop in the field of the construction of structures and the use of deductive reasoning techniques that are applied in synthetic geometry and also in the building information modeling (BIM) methodology may be a way of showing the use of analytical geometry in the industries of engineering and architecture; they also serve as an opportunity for students to better understand this mathematical work.
Keywords:
teaching mathematics; 3D metric geometry; synthetic geometry and analytic geometry; BIM digital geometric models; didactic situations; geometry practice workshop MSC:
97G70
1. Introduction
The work presented here aimed to design a didactic proposal through a geometry practice workshop for students in their second year of A-level courses in the specialty of the sciences to study the mathematical work of 3D metric geometry. In the geometry practice workshop mentioned, students perform a series of activities or tasks following a didactic dynamic that could be framed in the Theory of Didactic Situations of Brousseau [1,2]. According to this theory, in the teaching–learning process of mathematics we talk about the Didactic Situation that refers to the set of interrelations between three subjects: teacher–student–didactic environment. The teacher is the one who facilitates the environment in which the student builds his knowledge. Within this dynamic we have another dimension: the a-didactic situation, which is the process in which the teacher poses to the student a problem that resembles real-life situations that he will be able to address through his previous knowledge and that will allow him to also generate hypotheses and conjectures that resemble the work that is done in a scientific community. In other words, the student will be seen in a scientific micro-community solving situations without the direct intervention of the teacher with the purpose of participating later in the institutionalization of the acquired knowledge, that is, in establishing conclusions from what the student has learned.
On the other hand, it will be ensured that the geometry practices workshop has in a certain way the sense of a “Mathematical Practice Workshop”, which Ancholea [3] describes, quoting Bosch and Gascón [4], as:
a didactic device where the student can learn to do the type of work necessary to deepen the study of a problems field. Thus, the starting set is a type of problems that progressively expands as the study process progresses thanks to the development of mathematical techniques and the emergence of new technological-theoretical needs.
Under this conception of a practice workshop, framed within the Anthropological Theory of the Didactic (ATD) [5], it will be observed whether the student makes an interpretation and a justification of the different techniques used to solve the proposed tasks. The model currently proposed by the ATD describes mathematical knowledge in terms of organizations or mathematical praxeologies whose main components are types of tasks, techniques, technologies, and theories. Mathematical organizations are composed of a practical block or “know-how” formed by the types of tasks and techniques and by a theoretical block or “knowledge” formed by the technological–theoretical discourse that describes, explains, and justifies teaching practice.
The mentioned theories of didactic of mathematics, which have been developed by the French school of Brousseau and Chevallard since the seventies, are widely known and studied by secondary school mathematics teachers during their training in pedagogy, especially in Spanish- and French-speaking countries. In the scientific literature we can find in Spanish, French and English many research works on the design of training activities to implement these theories [6,7,8,9,10]. Nevertheless, their innovative approach has not been fully implemented in the field of algebraic geometry. Mathematics textbooks follow the traditional approach in which the teacher simply provides the contents and instructs the student, who captures these concepts and reproduces them as they have been supplied. In the proposal of this work the didactic contract is stablished, the didactic situations are designed, and the means and didactic variables for the study of 3D metric geometry are given.
The didactic proposal is set in geometric models of simple building structures. In addition, students will be told in this geometry workshop about one of the applications of 3D metric geometry and its techniques in the field of construction engineering and architecture: the BIM methodology.
The issues or problems that affect the students and the target of the didactic proposal are topics already known and explored by several authors in the scientific literature of mathematics didactics. These problems include the following:
- Disconnection between the scarce synthetic geometry (construction of figures with ruler and compass) of the curriculum of secondary education and the analytical geometry that is taught in A-level courses in countries such as Spain [3,10].
- High school students fail to engage with many of the mathematical works of the curriculum. In other words, students fail to comprehend the essence, usefulness, and meaning of mathematical works. So that students are able to understand a mathematic work, four aspects of the mathematical discipline should be addressed, which are: “not to forget the questions to which the work responds; combine “deductive reasoning” with “conjectural thinking”; identify and respect the laws governing the development of techniques; and produce appropriate technology to increase the efficiency and intelligibility of techniques” [11] (p. 133).
- The study of mathematics in the second year of A-level courses is becoming the training to prepare for the university entrance exam. This fact is evidenced by the numerous existing publications of resolved exercises to this exam and by the collections of exercise types solved in the A-level course textbooks [12,13].
- Algorithmizing the techniques used to solve problematic issues or tasks. An algorithm is understood as a mathematical technique whose application is totally determined [3].
If students just reproduce a technique or an algorithm, they do not build knowledge. The teaching–learning process, then, does not work, because students do not need to understand the meaning of the mathematical work to simply reproduce an algorithm. In this way, their learning is limited to being able to solve mathematical problems in which the algorithm works. However, they cannot apply properties to deduce others with deductive reasoning or to solve other problems.
Obviously, the didactic proposal that is designed and presented in this work will not solve the mentioned problems. However, it is intended to improve the current situation of students to facilitate their entry into the mathematical work of 3D metric geometry, as well as its study.
Based on previous research work in the modeling of civil structures [14,15,16], we could say that the skills associated with building geometric models are more linked to synthetic geometry than to analytic geometry. This construction of geometric models, such as that of Figure 1, are carried out with computer programs that we could identify with tools such as a generalized ruler and compass.
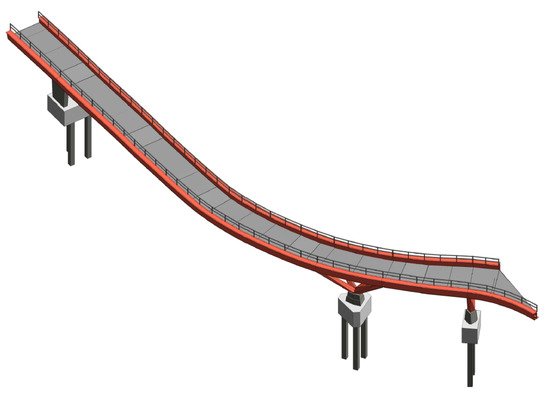
Figure 1.
A 3D geometric model of a steel footbridge at Huelva Port (Spain).
These computer programs have in their code algorithms, formulations, or techniques of analytical geometry. The geometric models in construction, to build works or to analyze them mechanically, are an example where the generalized synthetic geometry and analytical geometry are necessary. Moreover, in the building design, synthetic geometry techniques or strategies are also necessary to solve problems of 3D metric geometry.
In addition to the use of geometric models by structural engineers, in order to characterize the model with mechanical properties and thus be able to analyze it from the resistant point of view [14,15,16], there are other uses of these geometric models derived from the implementation of the BIM methodology in civil works and in building.
BIM is a collaborative work methodology that documents the entire life cycle of the building and infrastructure, making use of computer tools in order to generate a single repository with all the useful information for all the agents that participate in it and throughout its life cycle [17]. See Figure 2.

Figure 2.
A BIM model of a building (source: https://bim-level2.org/en/, accessed on 29 July 2019).
The use of this BIM methodology is becoming globally widespread due to the advantages it entails, including the modernization of the construction industry; suppression of quantities errors; coordination between the actors involved; and creation of a digital model, not only geometric, that serves as a single repository of information during the life cycle of the building or infrastructure.
Working on the skills used to build geometric models can help high school students enter the study of the mathematical work of 3D metric geometry.
Obviously, this last statement is a guess. This first research work gives rise to the implementation of the didactic proposal in the classroom in another subsequent work, and the results of evaluation and even university entrance exams are compared to measure the possible improvement that the proposal supposes for the students.
The rest of the paper has been structured as follows: Section 2 presents the methodology, Section 3 describes the background and theoretical framework, Section 4 presents the design of the study and research activity for 3D metric geometry, and Section 5 discusses the analysis of the results of the work. Finally, in Section 6, conclusions and future works are presented.
2. Methods
The methodology followed in the study carried out can be described by structuring it as follows (Figure 3):
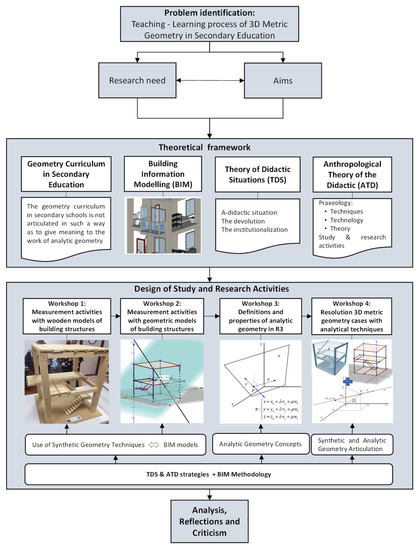
Figure 3.
Methodology workflow.
- The identification of a problem or issue that requires study or may be improved in the field of secondary education in mathematics didactics.
- The justification of the need for the research to be carried out.
- The objectives of the proposal.
- A description of the theoretical framework of the problem.
- The development of research for the design of the didactic proposal.
- An analysis of the work carried out, reflection, and criticism.
3. Background and Theoretical Framework
3.1. Summary of Geometry Curriculum at Compulsory Secondary and Higher Secondary Education Levels in the Region of Murcia (Spain)
It is intended here to analyze the contents of the geometry curriculum at the level of compulsory secondary education (CSE) and in the second year of A-levels in the Region of Murcia, the object of this study. These contents are included in Decrees 220/2015 and 221/2015 of the Region of Murcia Government (Spain).
From reading the mentioned Decrees, the following can be observed:
- Yes, there are contents dedicated to measuring areas, distances, and volumes in CSE and A-level.
- Not only 2D figures are studied in CSE; already in the second and third year of CSE, polyhedrons and revolution bodies appear as included content along with their areas, their volumes, and their symmetries.
- In the fourth year of CSE, there is already an initiation to analytic geometry in the plane: coordinates, vectors, equations of the line, parallelism, and perpendicularity.
- Only in the third year of CSE is there talk about the geometry of the plane and geometric place that are more purely synthetic contents. In the standards of these contents, there is talk of solving simple geometric problems using the midpoint of a segment and the mediatrix of an angle (Decree 220/2015, p. 30996). Therefore, in CSE there is a lack of use of deductive techniques of the Elements of Euclid to solve problems of the construction of figures.
- In the first year of A-level, metric geometry is studied in the plane: vectors, scalar product of two vectors, equation of the line, relative positions of lines.
- In the second year of A-level, metric geometry in space is studied, including: vectors in R3; scalar, vector, and mixed products; and equations of the line and plane and their relative position, along with problems of distances, areas, and volumes using algebra.
As some authors affirm, the geometry curriculum in secondary schools is not articulated in such a way as to give meaning to the appearance of analytic geometry [3]. This statement can also be verified from the analysis of textbooks as in Ref. [12]. They do not look back on the curriculum to relate one geometry to another.
On the other hand:
From a teaching point of view, and once the contents of compulsory education have been selected, there is a tendency to consider the «problem of the curriculum» only as a matter of sequencing and temporalization of contents, which leads to the problem of teaching methodology... The problem that should be posed is that of the reconstruction of the mathematical works selected in the curriculum as works that must be studied not only taught.[11], (p. 122)
This paper aims to reconstruct 3D metric geometry.
3.2. The Theory of Didactic Situations (TDS)
As Panizza explains, “Guy Brousseau’s Theory of Situations seeks the conditions for an artificial genesis of mathematical knowledge, under the hypothesis that they are not constructed spontaneously” [18] (p. 60).
In this same reference [18] (p. 60), we find that “The Theory of Situations is based on a constructivist conception—in the Piagetian sense—of learning”. Brousseau (1986), quoted by Panizza [18] (p. 60), says:
The student learns by adapting to an environment that is a factor of contradictions, difficulties, and imbalances, a bit like human society does. This knowledge, the result of the student’s adaptation, is manifested by new answers that are proof of learning.
From this theory, we can here highlight some key basic concepts that will be reflected in the didactic proposal to be designed. These concepts are:
- Didactic situation. According to Panizza [18] “... it is a situation intentionally constructed in order to make students acquire a certain knowledge”. In the situation, a group of students, a certain medium, and an educational system represented by the teacher must coexist.
- A-didactic situation. Brousseau (1986), cited by Panizza, defines it as follows:“any situation which, on the one hand, cannot be adequately mastered without the implementation of the knowledge that is intended and which, on the other hand, sanctions the decisions made by the student (good or bad) without the intervention of the teacher with regard to the knowledge that is put into play”.[18] (p. 61)
- The devolution. Again, Brousseau (1986), quoted by Panizza:“Devolution is the act by which the teacher makes the student accept responsibility for a learning situation (a-didactic) or a problem and the student accepts himself the consequences of this transfer”.[18] (p. 63)
- Institutionalization. According to Panizza, quoting Brousseau (1994):“The ‘official’ consideration of the teaching object by the student, and of the student’s learning by the teacher, is a very important social phenomenon and an essential phase of the didactic process: this double recognition constitutes the object of institutionalization”.[18] (p. 67)
3.3. The Anthropological Theory of the Didactic
To provide a small review on the Anthropological Theory of the Didactic of Chevallard (1999), we quote Corica and Marin [19]:
The fundamental theoretical construction of the Anthropological Theory of the Didactic (ATD), is the notion of praxeology or Mathematical Organization (MO). These emerge as an answer to a question or set of problematic questions that are called generative questions. Praxeologies consist of two levels:
In the same way, to introduce the concept of Study and Research Activities of the ATD, we also cite the same publication [19] (p. 93):
Following the recent research lines proposed by the ATD, the need arises to introduce functional study processes into teaching systems, where knowledge does not constitute monuments that the teacher teaches to students, but material and conceptual tools, useful for studying and solving problematic situations. The Study and Research Activities (SRA) emerge as a didactic model to address the problem. In this way, it is about overcoming the classic binary structure of the teaching of mathematics, which is characterized by the presentation of technological—theoretical elements and then tasks as a means for the application of the former.
In the didactic proposal object of the present study, the didactic device of the SRA is used to raise problematic questions “sufficiently rich, alive and fruitful that provoke in students the need to continue learning, and that facilitates opening a process of research, which allows to explore, conjecture and validate” (Ib., p. 94).
It is also intended that students’ responses involve the use of appropriate techniques and a discussion should occur about their justification.
3.4. Geometric Models in Architecture and Civil Engineering, the BIM Methodology
People have used geometric models in construction since ancient times. The need to transmit the graphic information of a design to the builders so that they can execute the work existed even before construction had the rank of science.
In ancient times (Greece and Rome), they designed following the rules of proportionality. If something has been built, it can be built again as long as the new work is proportional in its dimensions to the previous one. With the development of the strength of materials, it has been proven that the above statement is not true. However, what is certain is the need to graphically represent what is going to be built. This representation of the geometry of a work was drawn freehand, as Galileo did to represent a cantilevered wooden beam (ABCDE) in his book Dialogues concerning Two New Sciences (Figure 4) [20].
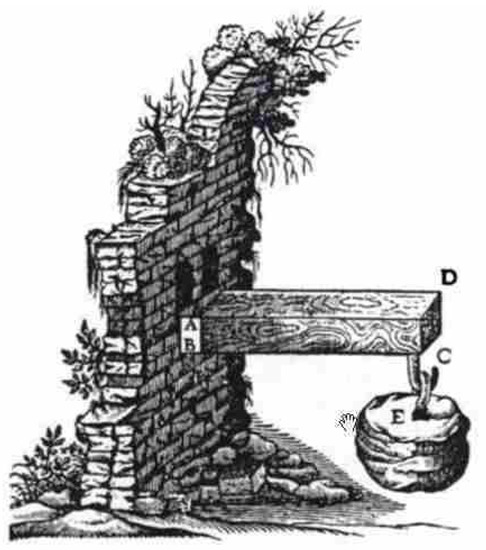
Figure 4.
Galileo’s beam (Source: https://oll.libertyfund.org/title/galilei-dialogues-concerning-two-new-sciences, accessed on 20 March 2022).
This process was later completed with a ruler, compass, and “rotring”. From the end of the 1980s, with computer-aided design (CAD), the ruler and compass were replaced by software commands that allowed the same operations to be performed with the advantage that editing the drawings was possible.
On the other hand, the geometric models of a work to be built have also been used to analyze the resistance of it.
Currently, 3D geometric and mechanical models are built for the analysis of the structure of the works (Figure 5).

Figure 5.
Bridge finite element models (Source: http://www.civil.bim.upct.es/cursos/m5-puentes-bim/, accessed on 29 July 2019).
With the implementation of the BIM methodology, already mandatory in Great Britain, Scandinavia, the USA, and Australia among others, 3D digital models are widely used and not only for structural analysis.
To explain what the BIM methodology is, we will cite a report by AENOR [21]:
BIM is a collaborative work methodology for the management of a project by means of a 3D digital model. It includes methodologies, processes, software and digital formats for the management of projects and construction works. It focuses on buildings, but also applies to civil works.(p. 4)
It could be defined as a digital representation of the physical and functional characteristics of a building, allowing information to be exchanged to make decisions throughout its life cycle (project, construction, use and deconstruction). It can be used to store data, perform calculations or manage the building. [...] BIM uses a common exportable language, which allows information to be shared between different agents and to carry out a real collaborative work.(p. 4)
More than 50% of international clients of construction companies demand or have an interest in the use of BIM, especially in Asia. It is estimated that BIM could: adjust project quantities by 37%; reduce building construction costs by 20%.(p. 4)
Figure 6 shows some of the uses of BIM during the life cycle of a building or infrastructure. The digital model or 3D digital model will be used for the design of the work, for structural analysis, to obtain graphic documentation (plans), to manufacture certain elements such as metal beams, to perform simulations of construction phases, to measure and budget the work, and to store useful information in the service phase for maintenance, etc.

Figure 6.
BIM in the life cycle of a construction. Uses (Source: https://www.expanda.es/blog/el-ciclo-de-vida-en-las-infraestructuras/, accessed on 29 July 2019).
In December 2018, in Spain, an inter-ministerial commission was created to ensure that public works are tendered with this methodology in the medium term. Therefore, from the data provided, it can be said that the transition from CAD to BIM is not a fad but a reality.
Three-dimensional geometric models are useful. Soon, their widespread use in architecture and construction engineering will be mandatory.
4. Design of 3D Metric Geometry Study and Research Activities
4.1. Overview of the Proposed Geometry Workshops
The workshops of geometry that are proposed in this work consist of carrying out a series of activities distributed in sessions in a conventional classroom or computer room.
Three-dimensional metric geometry in the second year of A-level of the sciences (last year of secondary education before university) can be taught in 24 sessions. This is the timing used by some secondary schools for this topic in Spain. In this A-level year, students have 4 h (sessions) of mathematics per week. Therefore, the time spent on the geometry block mentioned during the academic course is 6 weeks. Discounting 1 week for evaluation activities and another for review in the traditional style, the duration of the workshops can be set at 4 weeks. In these 4 weeks, there will be four workshops of activities. These are:
- Workshop 1. Measurement activities using wooden models of building structures.
- Workshop 2. Measurement activities using geometric models of building structures in GeoGebra.
- Workshop 3. Scalar, vector, and mixed product definitions of R3 vectors and their properties. Axioms of definition of planes and lines. Equations of lines and planes.
- Workshop 4. Resolution of cases with analytical techniques. Interpretation and justification of techniques. Application of techniques in construction engineering.
The maximum number of students in the classroom to carry out the workshops in an appropriate way is 25. In each workshop, the teacher will explain the tasks to be carried out by the students, pose some questions to answer, and resolve any doubts of the students.
4.2. Workshop 1 Measurement Activities Using Wooden Models of Building Structures
At the beginning of the first workshop, students receive a theoretical explanation about the BIM methodology and about the use of geometric concepts in this methodology.
The first workshop lasts four sessions. Students are given the problematic task of measuring distances, angles, areas, and volumes within a construction; more specifically, of a building of which we have the wooden model of its structure.
The resources available in this workshop are four wooden models, such as the one shown in Figure 7, a tape measure, ruler, compass, cardboard, pencils, and paper.

Figure 7.
Wooden model of the structure of a reinforced concrete (RC) building.
Organization of the workshop: students form groups of four or five per model. The models are assembled by the students looking at the photo (Figure 7). Once assembled, they will be able to use the mentioned resources to solve the following tasks:
- Task 1. Find out the distance from point A to point B (Figure 8).
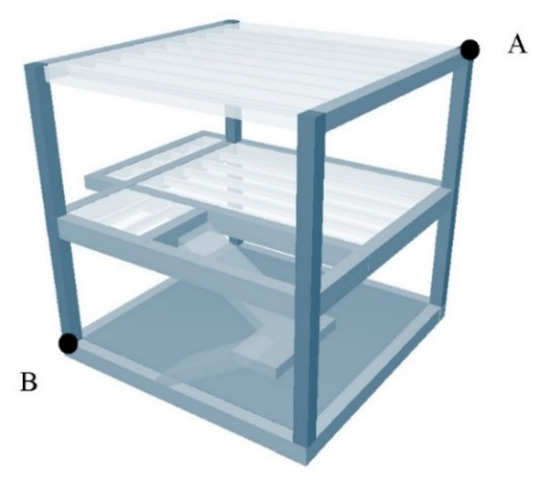 Figure 8. Model sketch I.
Figure 8. Model sketch I. - Task 2. Find out the value of the r angle that forms the first inclined plane of the stairs with the horizontal (Figure 9).
 Figure 9. Model sketch II.
Figure 9. Model sketch II. - Task 3. Find out the area of the roof and the slab on the first floor.
- Task 4. Find out the volume of the building (without considering balconies).
- Task 5. Obtain the distance between the line r and the point A (Figure 9).
 Figure 10. Model sketch III.
Figure 10. Model sketch III.- Task 7. Obtain the distance between point B and the plane of the second flight of stairs (Figure 11).
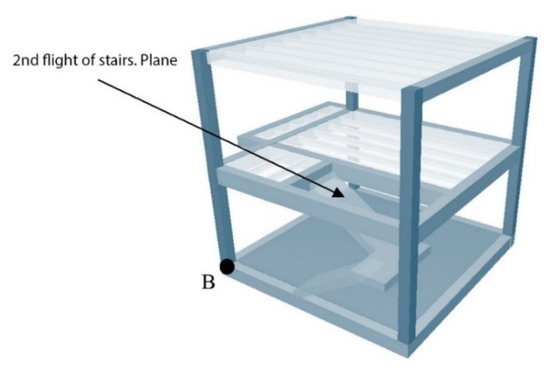 Figure 11. Model sketch IV.
Figure 11. Model sketch IV. - Task 8. Obtain the coordinates, choosing a reference system, of all the points of intersection between beams and between beams and pillars.
Once the tasks are solved, the different groups will share the results and discuss their validity.
They are also proposed to answer the following questions:
- Question 1. What techniques have you used? Have all students solved tasks in the same way?
- Question 2. What kind of problems can be solved with the techniques used?
- Question 3. What strategies have been followed to find out the distance between a point and a plane, and for the distance between two lines?
- Question 4. If the points, lines, and planes mentioned in the tasks were defined by coordinates of points, without having the references of the models, how would you proceed to find out the distances, angles, areas, and volumes object of the previous tasks?
4.3. Workshop 2 Measurement Activities Using Geometric Models of Building Structures in GeoGebra
The second workshop is a repetition of the first, but changing the wooden models for a digital model built with GeoGebra. This digital model or geometric model is built by the students in the first part of this second workshop by means of entering points by coordinates and drawing segments and polygons (Figure 12).
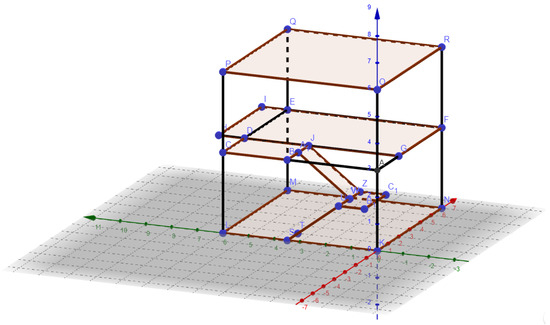
Figure 12.
Digital model or geometric model of the structure of a reinforced concrete building.
The resources available in this second workshop are the computers in the computer room with an internet connection. The software GeoGebra works online.
The problematic question, the tasks, and the final questions to be answered by the students after their study are the same as those collected in Workshop 1. The duration of this workshop is also four sessions (of one hour each).
In order to be able to use the GeoGebra computer tool to measure angles, distances, areas, and volumes, students are provided with an excerpt from the GeoGebra help with the following commands, among others:
- To draw one line perpendicular to another.
- To draw a line perpendicular to a plane.
- To measure distances between two points.
- To draw planes defined by three points or by a point and a line.
- To draw the point of intersection between line and plane.
- To measure angles that form two lines.
In this way, they will be able to build figures such as Figure 13 that solve Task 7.
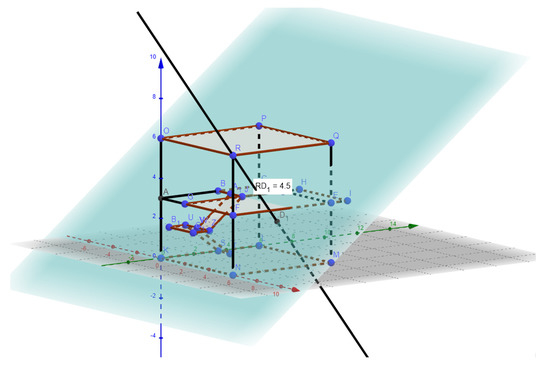
Figure 13.
Construction to solve Task 7 in Workshop 2. (Shared in url: https://www.geogebra.org/classic/bsg4x65f, accessed on 29 July 2019).
In Workshop 2, students work individually. Each student has access to a computer. Here, we can add some more question for students to compare the techniques and strategies used with those of Workshop 1. Can GeoGebra tools be considered as a generalized rule and compass? How have these new tools been built? What scientific basis supports them?
4.4. Workshop 3 Notion of Scalar, Vector, and Mixed Product of R3 Vectors and their Properties, Axioms of Planes and Lines Definition, Equations of Lines and Planes
Workshop 3 can be developed in a conventional classroom. The necessary resources are those that are already conventional in secondary education classrooms: digital whiteboard, projector, etc. This workshop also lasts four sessions. In general, the workshop consists of the teacher defining a series of concepts and the students “studying” the properties of those concepts.
For the development of this workshop, we will assume that students already know the Pythagorean Theorem, elementary trigonometry, the vector representation by coordinates in R2 and R3, the representation of a vector determined by two points, linearly dependent vectors, determinants, and the range of a matrix.
In this workshop, we also work in groups of four or five students. The workshop activities are the following:
- Activity 1. The teacher defines on the blackboard the notion of the scalar product of two vectors in R3. This notion, extracted from Lorente (n.d.) [22], is collected below:
Definition 1.

Definition of scalar product: The scalar product of two free vectors andis a real number (scalar) defined as:
whereandare the modules of the vectors ().is the cosine of the angle that the vectorsform. See Figure 14 (Volume III, p. 63).

Figure 14.
Angle between two vectors.
- Activity 2. Students are asked questions about the possible properties of the scalar product of two vectors: Is it commutative? Is it distributive with the sum? What is the scalar product of a vector by itself? When is the scalar product null? What is the geometric interpretation of the scalar product?To carry out this activity and answer the questions raised, students will have to use algebraic operations that they already know.
- Activity 3. The teacher asks the students about the validity of the following analytic expression of the scalar product of two vectors:To answer, the teacher proposes to operate as follows. Equation (3):
- Activity 4. The teacher defines the vectorial product concept for two vectors in R3.
Definition 2.
The vector product of two free vectorsandis another vector that we will designate asand that is defined by means of the following properties:
direction → the one perpendicular to and
sense → the sense of advance to the right of a corkscrew turning from to . Ref. [22], (volume II, p. 65).
- Activity 5. Students are asked questions about the possible properties of the vector product of two vectors: Is it commutative? If not, how is it? Is it distributive with the sum? When is it zero? What geometric interpretation can be given to the vector product of two vectors in R3?
- Activity 6. Students are asked to demonstrate, if they can, the following analytical expression:
- Activity 7. The teacher defines the notion of mixed product of three vectors in R3.
Definition 3.
The mixed product of three vectors, , , , which is designated as, is obtained from the scalar product of the first vector by the vector resulting from multiplying the other two vectors. (I.b, volume III, p. 65).
- Activity 8. Students are asked questions about the possible properties of the mixed product of three vectors: Is it distributive with the sum? What happens if we swap two vectors into the mixed product? What can be the geometric interpretation of the mixed product?
- Activity 9. Students are asked to apply the analytical expression of the vector product and that of the scalar product to obtain an analytic expression of the mixed product.
- Activity 10. Students are asked about the technique they have used to perform the above activities. Is another technique possible? In addition, the results of the activities are shared and the students are left to validate them according to their criteria.
- Activity 11. Institutionalization. It is intended, at least, to reach the following conclusions among all:
- −
- Analytical expression of the mixed product (I.b, volume III, p. 68):
- −
- Geometric interpretation of the scalar product of two vectors in R3 (Figure 15) (I.b, volume III, p. 64):where:
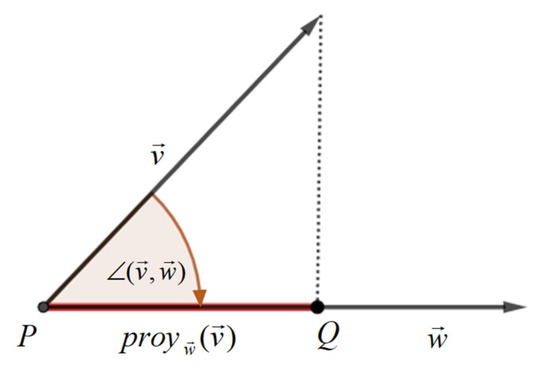 Figure 15. Geometric interpretation of the scalar product of two vectors.is the value of the projection of onis the value of the projection of on
Figure 15. Geometric interpretation of the scalar product of two vectors.is the value of the projection of onis the value of the projection of on - −
- Geometric interpretation of the vector product of two vectors in R3 (Figure 16):
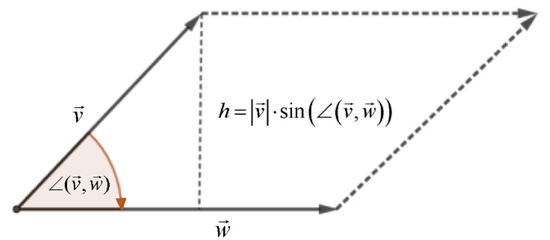 Figure 16. Geometric interpretation of the vector product of two vectors.
Figure 16. Geometric interpretation of the vector product of two vectors. - −
- Geometric interpretation of the mixed product of three vectors in R3 (Figure 17) (I.b, volume III, p. 67):
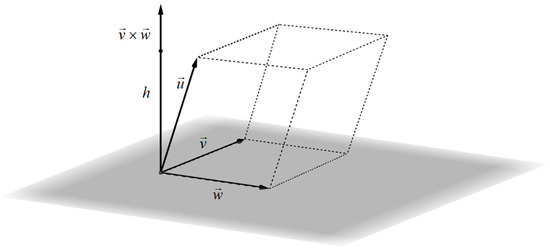 Figure 17. Geometric interpretation of the mixed product of three vectors.
Figure 17. Geometric interpretation of the mixed product of three vectors.
- Activity 12. Students are asked about the different ways of defining a line and a plane in space, as well as the relationship between the different ways of defining a plane or a line.
- Activity 13. The teacher shows on the blackboard the different forms of the equations of the line and of the plane in R3.
Definition 4.
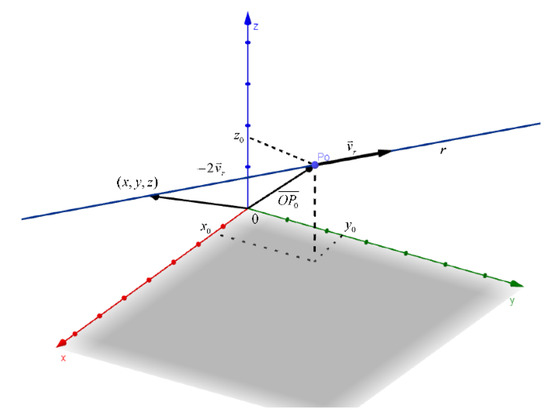
Equation of line in vector form (I.b, volume III, p. 32):
with free parameter.
In the above expression,are the coordinates of a point P0, andare the components of a vector. See Figure 18.

Figure 18.
Geometric interpretation of the line equation in vector form .
Definition 5.
Equation of the line in parametric form (I.b, Volume III, p. 32):
Definition 6.
Equation of the line in continuous form (I.b, Volume III, p. 33):
Definition 7.
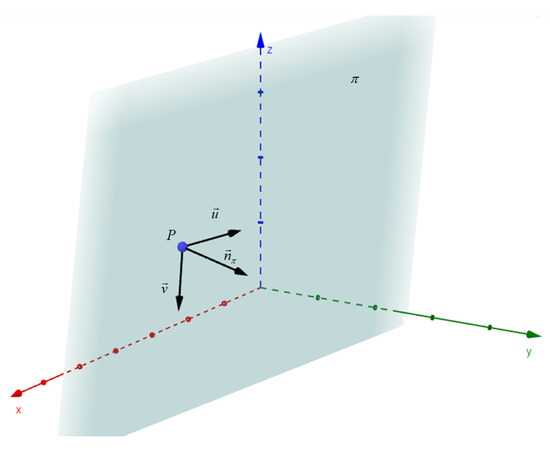
Equation of the plane in vector form (See Figure 19).The vector equation of a plane that passes through a pointand has two vectors parallel to the planeandnot proportional is (I.b, volume III, p. 39):

Figure 19.
Vectors of the π plane.
Definition 8.
Equation of the plane in parametric form (I.b, volume III, p. 39):
Definition 9.
General equation of the plane:
It is obtained from the development of the following determinant:
- Activity 14. Students are asked to tell how they can be passed from one form of equation to another and to show that the vector (A,B,C) is perpendicular to the plane .
Workshop 3 ends with this activity.
4.5. Workshop 4 Solving of Cases with Analytical Techniques, Interpretation and Justification of Techniques, Applications of Techniques in Construction Engineering
Once some analytical tools have been “built” in Workshop 3, it is time to begin solving cases within the problem raised (measuring distances, angles, areas and volumes in space) using analytical techniques.
Workshop 4 is also distributed into four sessions. The first of them is carried out in a computer room and the rest in a conventional classroom. The means are those described in Workshop 2 and 3. Again, the students “study” in groups of four or five. The activities are listed below:
- Activity 1. The students are asked to solve the questions of the first seven tasks already carried out in Workshop 1, but now using analytical techniques. To do this, students must reformulate the statement of these tasks to express it in terms of coordinates of points and equations of lines and planes. In this activity, they will be able to consult the geometric model of Figure 11 built in GeoGebra.
- Activity 2. It is now intended that students analyze some types of problems where geometric elements (points, segments, lines, and planes) are not particular elements, but represent any element. For example, students may be asked to analyze the calculation of the distance between two lines in space, or the angle between two planes, and the strategies to follow. This is so that they come to consider the problem of the relative positions between the elements and approach their analysis with algebraic techniques.
- Activity 3. Students are asked to discuss the justification of the techniques used in the four workshops held. What sense do they give to the analytic geometry they have studied?
- Activity 4. The teacher shows students one of the applications of analytic geometry: the construction of geometric models in architecture and civil engineering and BIM methodology—basically, what is described in Section 3.4 of this article.
5. Analysis of Proposed Study and Research Activities
To assess the work carried out to design activities of study and research of the metric geometry of second year A-level courses, the response given by these activities to the problems raised in the introduction and to those mentioned with the purpose of discussing TDS and ATD in Section 3 will be analyzed.
Problem 1. Disconnection between the scarce synthetic geometry of curriculum of secondary education and the analytical geometry that is taught in A-level courses.
This problem has been tangentially treated, i.e., not directly, since the chosen theme is geometry in space where the ruler and compass do not fit. Ancholea [3] makes a proposal to articulate synthetic geometry (with ruler and compass) with analytic geometry in the plane at first year A-level courses. In this case, there are problems solvable by synthetic and analytical techniques and problems whose “synthetic strategies” are useful for analytical resolution.
On the other hand, the techniques used to solve the tasks in Workshop 1 and 2 (with real or digital models) do seem to be valid to form strategies necessary for the resolution of the tasks of Workshop 4 with analytical techniques. If we consider GeoGebra commands (drawing a line in space, a point, a plane, finding intersections, etc.) as generalized rule and compass-type tools, we are somehow articulating synthetic and analytic geometry in space. Seen in another way, with the techniques used in Workshop 1 and 2 we move from specific data and objects and follow a series of steps, admitted and considered true, until we find the solution; this way of proceeding is synthesis. Therefore, the proposed geometry workshop articulates synthetic geometry with analytic geometry.
Problem 2. High school students fail to enter many of the mathematical works of the curriculum.
To enter these works, the students should not forget the questions which these mathematical works answer, should combine deductive reasoning with conjectural thinking, should identify and respect techniques, and should produce appropriate technology.
With the proposed activities, it is intended that students can put into practice deductive reasoning and conjectural thinking, use different techniques, and justify them.
Problems 3 and 4. The study of mathematics in the second year A-level courses is becoming the training to prepare for the university entrance exam. Recipes or algorithms are given for the resolution of exercises, with the danger of metacognitive slippage. Students learn the fully determined technique rather than learning the properties that allow for solving real problems.
In the proposed geometry workshop, lists of solved exercises are not given to students in order to solve other proposed ones by identifying them with the first ones. This would not allow entry into the mathematical work.
In addition, students must obtain the properties from the definitions and analytical steps. Therefore, they are to discover (“build”) the properties before solving issues where their application is required (Workshop 3 and 4).
TDS. A-didactic situations. It cannot be mastered without the implementation of the knowledge that is intended. On the other hand, it sanctions the decisions of the student.
Question 4 of Workshop 1 aims to create an a-didactic situation. This question reads:
If the points, lines, and planes mentioned in the tasks were defined by coordinates of points, without having the references of the models, how would you proceed to find out the distances, angles, areas, and volumes object of the previous tasks?
This question arises so that students would see the need for a new mathematical work, rather than to build it themselves at that time.
Activity 2 of Workshop 4 is also formulated to create an a-didactic situation. This activity asks to analyze the calculation of the distance between any two lines in space or the angle between any two planes, indicating the strategies to follow, and asks to discuss the different cases.
In this activity, the cases will be generated by the different relative positions of the lines between themselves and the planes between themselves. It is intended, among others, that the study of parallelism and perpendicularity or coincidence of lines with each other, and planes with each other, is carried out in an analytical way.
TDS. The devolution. Several of the activities in Workshop 3, for example, those that ask to study the properties of vector products, signify an act of devolution of the responsibility of learning to the student.
TDS. Institutionalization. Activity 11 of Workshop 3 corresponds to the institutionalization of properties of vector products in R3.
ATD. Study and Research Activities as a means to overcome the classic binary structure of the teaching of mathematics that is characterized by the presentation of technological–theoretical elements and then tasks as a means for the application of these elements.
In the set of activities proposed in this paper, it is intended that the techniques are discussed and that the properties are deduced. In this way, we try to avoid monumentalism based on functional study processes.
BIM. Current and future use of analytic geometry. To conclude this analysis of the didactic proposal carried out, we want to refer to the direct presentation to students of one of the uses of analytical geometry: geometric models in construction.
Although students make sense of metric geometry in space as a means of solving problems that cannot be solved without analytical techniques, it may also be interesting to show them the uses and power of this mathematical work in engineering and architecture.
6. Conclusions
The following conclusions can be drawn from the work developed:
- An innovative didactic proposal has been designed for metric geometry in the space of second year A-level courses, with a geometry workshop format, so that students can enter this mathematical work and reconstruct it within the framework of the Theory of Didactic Situations and the Anthropological Theory of the Didactic.
- The innovation of the proposal is not only provided by the change in teacher and student roles in the proposed workshop regarding traditional teaching but also due to the means used: wooden models of building structures and digital models.
- The proposed geometry workshops aim to serve as a previous step to reach the necessary level of abstraction to be able to carry out the analysis of problems such as calculating the distance between any two lines in space and the possible relative positions between them.
- The contextualization or setting of the geometry workshop in the world of the construction of structures can be a way to show—at least that is what is intended—the use of analytical geometry in the world of engineering and architecture, so that the student can give more meaning to this mathematical work.
- After the analysis carried out on the didactic proposal designed, it can be said that the proposed workshop answers, with a certain level of satisfaction, the following problems: the non-articulation of synthetic and analytical geometry; secondary school students fail to enter many of the mathematical works in the curriculum; teaching mathematics has become the training of students for university entrance exams.
- Only in the third year of CSE can we find content about geometry of the plane and geometric place in the curriculum; these are synthetic geometric contents. Therefore, in CSE there is a lack of use of deductive techniques of the Elements of Euclid to solve problems of the construction of figures. The CSE curriculum should incorporate more content about the construction of figures to develop students’ deductive reasoning.
- The proposal and analysis carried out are intended to be the first part of a larger study. The second part consists of putting into practice the didactic proposal. In this way, it will be possible to measure the improvement provided to the students of second year A-level courses in their evaluation results.
We conclude with a final thought: There are those who say that if the computer does everything for you, then you do not learn. In our opinion, students must study analytic geometry to be able to develop software for computers to solve problems on a real scale, not just academic; a scale where computers are needed. There will always be “students” (researchers or professionals) to use the software and to follow suitable criteria (related to the mathematical work) in solving problems at a real scale.
Author Contributions
Conceptualization, M.S.G.-C. and J.M.O.-N.; methodology, M.S.G.-C.; software, E.J.R.-J.; formal analysis, J.M.O.-N.; investigation, J.M.O.-N.; resources, E.J.R.-J.; writing—original draft preparation, J.M.O.-N.; writing—review and editing, M.S.G.-C.; project administration, J.M.O.-N. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by ERASMUS+ program of the European Commission, grant number 2020-1-ES01-KA203-083262: “Building BIM digital competences for Tertiary VET in the designing and management of construction projects” and “The APC was funded by the author”.
Acknowledgments
The authors want to thank Rubén Rocamora, who graduated from the Civil and Mining Engineering School of Technical University of Cartagena, for his work in the design and construction of wooden models of building structures for the workshops designed.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Brousseau, G. Introduction to the Study of the Theory of Didactic Situations; Libros del Zorzal: Buenos Aires, Argentina, 2007. (In Spanish) [Google Scholar]
- Balacheff, N.; Cooper, M.; Sutherland, R.; Warfield, V. Theory of Didactical Situations in Mathematics. Mathematics Education Library; Springer: Berlin/Heidelberg, Germany, 2002; Volume 19. [Google Scholar]
- Ancholea, B. The Functions of Symbolic Calculators in the Articulation between Synthetic Geometry and Analytic Geometry in Secondary. In An Overview of the TAD. III TAD International Conference; Bosch, M., Gascón, J., Ruiz Olarría, A., Artaud, M., Bronner, A., Chevallard, Y., Cirade, G., Ladage, C., Larguier, M., Eds.; CRM Documents Bellaterra: Barcelona, Spain, 2021; Volume 10, pp. 533–551. (In Spanish) [Google Scholar]
- Bosch, M.; Gascón, J. The integration of the moment of the technique in the process of studying fields of mathematical problems. Enseñanza Cienc. 1994, 12, 314–332. (In Spanish) [Google Scholar]
- Bosch, M.; Chevallard, Y.; García, F.J.; Monaghan, J. Working with the Anthropological Theory of the Didactic in Mathematics Education: A Comprehensive Casebook; Taylor & Francis: Milton Park, UK, 2019. [Google Scholar]
- Tezer, M.; Cumhur, M. Anthropological Theory of Didactics and the Probability of the Constructivist Approach Being a Solution to the Common Mistakes Made in Mathematics Lessons. Int. J. Educ. Sci. 2016, 15, 148–156. [Google Scholar] [CrossRef]
- Barquero, B.; Bosch, M.; Gascón, J. The unit of analysis in the formulation of research problems: The case of mathematical modelling at university level. Res. Math. Educ. 2019, 21, 314–330. [Google Scholar] [CrossRef]
- González-Martin, A.S.; Bloch, I.; Durand-Guerrier, V.; Maschietto, M. Didactic Situations and Didactical Engineering in university mathematics: Cases from the study of Calculus and proof. Res. Math. Educ. 2014, 16, 117–134. [Google Scholar] [CrossRef] [Green Version]
- Farias, L.M.S.; Júnior, J.V.N.; Souza, A. From Drawing to Figure and Theories of Didactic Situations and Instrumentation. Int. J. Sci. Res. 2019, 8, 1038–1048. Available online: https://www.ijsr.net/archive/v8i4/ART20194825.pdf (accessed on 20 March 2022).
- Gascón, J. Synthetic Geometry in ESO and Analytical in Baccalaureate. Two Completely Separate Worlds? SUMA: Madrid, Spain, 2002; pp. 13–25. (In Spanish) [Google Scholar]
- Chevallard, Y.; Bosch, M.; Gascón, J. Study Mathematics. The Missing Link between Teaching and Learning; Universidad de Barcelona: Barcelona, Spain, 1997. (In Spanish) [Google Scholar]
- González, L.; Valdés, Ä. Mathematics II. 2nd year Baccalaureate. Chapter 6: Metric Geometry in Space; Libros Marea Verde, 2015. Available online: www.apuntesmareaverde.org.es (accessed on 20 March 2022). (In Spanish).
- Musat, I. University Entrance Exam Problems. Mathematics II. Region of Madrid. Madrid. 2019. Available online: www.musat.net (accessed on 20 March 2022). (In Spanish).
- Olmos, J.M.; Astiz, M.A. Analysis of the lateral dynamic response of high pier viaducts under high-speed train travel. Eng. Struct. 2013, 56, 1384–1401. [Google Scholar] [CrossRef]
- Olmos, J.; Astiz, M. Improvement of the lateral dynamic response of a high pier viaduct under turbulent wind during the high-speed train travel. Eng. Struct. 2018, 165, 368–385. [Google Scholar] [CrossRef]
- Olmos, J.M.; Astiz, M. Non-linear vehicle-bridge-wind interaction model for running safety assessment of high-speed trains over a high-pier viaduct. J. Sound Vib. 2018, 419, 63–89. [Google Scholar] [CrossRef]
- Gosalves, J.; Murad, M.; Celdrán, A.; Fuentes, B.; Hayas, R.; López, J.; Zuñeda, P.P. BIM in 8 Points. BIM Commission; Ministerio de Fomento: Madrid, Spain, 2016. (In Spanish) [Google Scholar]
- Panizza, M. Teaching Mathematics at the Initial Level and the First Cycle of the EGB: Analysis and Proposals; Paidos Iberica: Barcelona, Spain, 2004. (In Spanish) [Google Scholar]
- Corica, A.R.; Marin, E.A. Study and research activity for teaching notions of geometry. Números. Rev. Didáct. Mat. 2014, 85, 91–114. (In Spanish) [Google Scholar]
- Galilei, G. Dialogues Concerning Two New Sciences; Macmillan: New York, NY, USA, 1638. [Google Scholar]
- AENOR. Standards in support of BIM. Standardization Reports. AENOR—Asociación Española de Normalización y Certificación. 2016. Available online: https://www.aenor.com/conocenos/sala-de-informacion-aenor/novedad?c=42364 (accessed on 20 March 2022). (In Spanish).
- Lorente, J.L. Mathematics II Notes to Prepare for the PAU Exam. Available online: http://joseluislorente.es/ (accessed on 20 March 2022). (In Spanish).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).