A Note on Pareto-Type Distributions Parameterized by Its Mean and Precision Parameters
Abstract
:1. Introduction
2. Pareto-Type Distributions with Alternative Parameterizations
2.1. Pareto Distribution
2.2. Power Function Distribution
2.3. Lomax Distribution
2.4. Generalized Pareto Distribution
2.5. Other Models Parameterized in Terms of the Mean and Precision Parameters
3. Modelling and Inference
- represents the mean of the response variable when all the covariates are equal to 0. Of course, this interpretation is valid as long as it makes sense.
- , represents the increment (in percentage terms) when the j-th covariates increased in 1 unit and the others are fixed.
A Simulation Study
4. Real-World Data Analysis
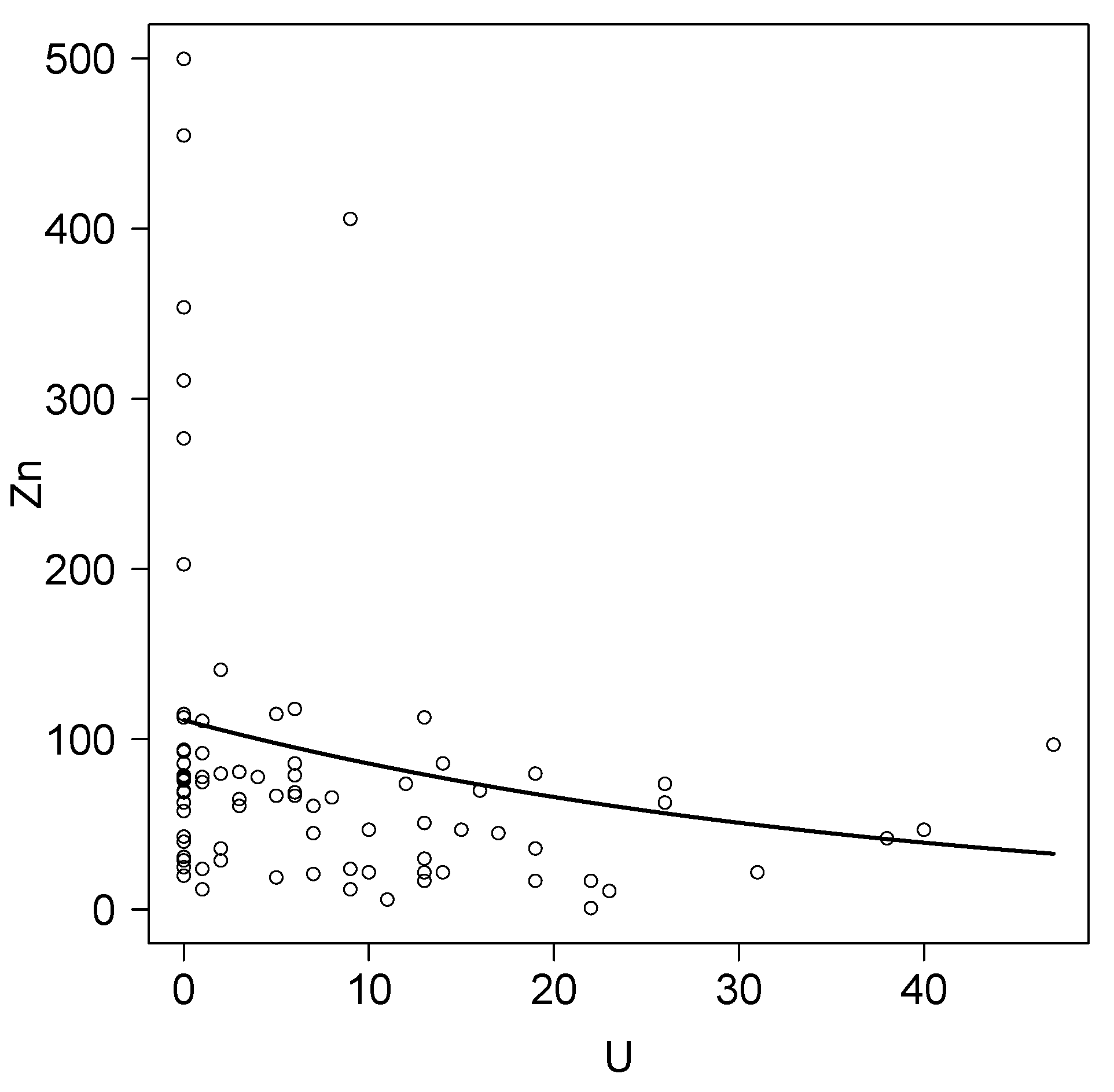
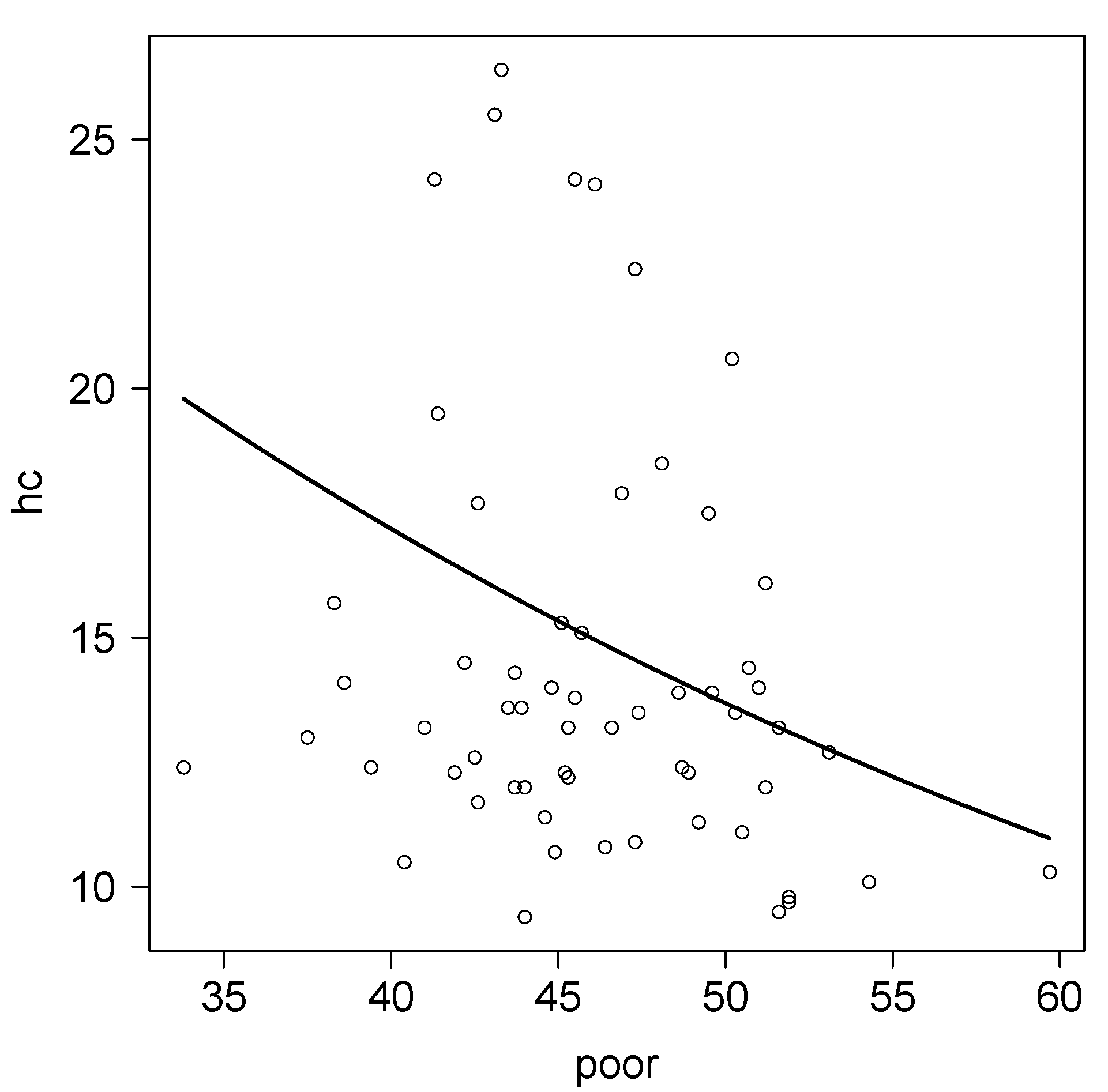
4.1. Lomax Regression Model
4.2. Pareto Regression Model
5. More Concluding Remarks and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pareto, V. Cours d’economie Politique; F. Rouge: Lausanne, Switzerland, 1987; Volume II. [Google Scholar]
- Wang, X.; Li, X. Generalized Confidence Intervals for Zero-Inflated Pareto Distribution. Mathematics 2021, 9, 3272. [Google Scholar] [CrossRef]
- Shrahili, M.; Al-Omari, A.I.; Alotaibi, N. Acceptance Sampling Plans from Life Tests Based on Percentiles of New Weibull–Pareto Distribution with Application to Breaking Stress of Carbon Fibers Data. Processes 2021, 9, 2041. [Google Scholar] [CrossRef]
- Sharpe, J.; Juárez, M.A. Estimation of the Pareto and related distributions—A reference-intrinsic approach. Commun. Stat.-Theory Methods 2021. [Google Scholar] [CrossRef]
- Arnold, B.C. Pareto Distribution; International Cooperative Publishing House: Burtonsville, MD, USA, 1983. [Google Scholar]
- Lomax, K.S. Business Failures: Another Example of the Analysis of Failure Data. J. Am. Assoc. 1954, 49, 847–852. [Google Scholar] [CrossRef]
- Pickands, J. Statistical inference using extreme order statistics. Ann. Stat. 1975, 3, 119–131. [Google Scholar]
- Bourguignon, M.; do Nascimento, F.F. Regression models for exceedance data: A new approach. Stat. Methods Appl. 2021, 30, 157–173. [Google Scholar] [CrossRef]
- Stasinopoulos, M.; Rigby, R. gamlss.dist: Distributions for Generalized Additive Models for Location Scale and Shape. 2021 R Package Version 5.3-2. Available online: https://CRAN.R-project.org/package=gamlss.dist (accessed on 25 December 2021).
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2021; Available online: https://www.R-project.org/ (accessed on 25 December 2021).
- Santos-Neto, M.; Cysneiros, F.J.A.; Leiva, V. and Barros, M. On a reparameterized Birnbaum–Saunders distribution and its moments, estimation and applications. REVSTAT–Stat. J. 2021, 12, 247–272. [Google Scholar]
- Gómez, Y.M.; Gallardo, D.I.; De Castro, M. A regression model for positive data based on the slashed half-normal distribution. REVSTAT–Stat. J. 2021, 19, 553–573. [Google Scholar]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Auto Contr. 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Dunn, P.K.; Smyth, G.K. Randomized quantile residuals. J. Comput. Graph. Stat. 1996, 5, 236–244. [Google Scholar]
| Scenario | Estimator | bias | se | cp | bias | se | cp | bias | se | cp |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | −0.0604 | 0.4442 | 0.909 | −0.0481 | 0.2941 | 0.941 | −0.0254 | 0.2046 | 0.947 | |
| −0.0326 | 0.6318 | 0.929 | −0.0125 | 0.4417 | 0.935 | −0.0052 | 0.3351 | 0.941 | ||
| 0.0669 | 0.6213 | 0.968 | 0.0407 | 0.5665 | 0.961 | 0.0316 | 0.4049 | 0.955 | ||
| 0.0934 | 0.5640 | 0.960 | 0.0689 | 0.4717 | 0.958 | 0.0283 | 0.3449 | 0.953 | ||
| 2 | −0.0992 | 0.4245 | 0.909 | −0.0616 | 0.2895 | 0.930 | −0.0427 | 0.1885 | 0.949 | |
| 0.0562 | 0.6192 | 0.920 | 0.0487 | 0.4412 | 0.932 | 0.0308 | 0.3064 | 0.946 | ||
| 0.0634 | 0.9408 | 0.938 | 0.0417 | 0.7089 | 0.941 | 0.0307 | 0.6292 | 0.945 | ||
| 0.0764 | 0.6649 | 0.936 | 0.0658 | 0.4683 | 0.943 | 0.0357 | 0.3787 | 0.946 | ||
| RGa | RLo | |||
|---|---|---|---|---|
| Estimate | se | Estimate | se | |
| 4.7518 | 0.1198 | 4.7114 | 0.1572 | |
| −0.0288 | 0.0100 | −0.0260 | 0.0108 | |
| −0.1212 | 0.0915 | 1.2420 | 0.9530 | |
| 0.0041 | 0.0079 | 0.0187 | 0.0732 | |
| AIC | 958.01 | 953.79 | ||
| BIC | 967.83 | 963.61 | ||
| RWe | RPa | |||
|---|---|---|---|---|
| Estimate | se | Estimate | se | |
| 3.7712 | 0.3870 | 3.7549 | 0.8921 | |
| −0.0239 | 0.0080 | −0.0228 | 0.0175 | |
| −0.9357 | 1.1873 | −8.5153 | 1.3215 | |
| 0.0487 | 0.0255 | 0.1982 | 0.0132 | |
| AIC | 345.11 | 326.47 | ||
| BIC | 353.48 | 334.84 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bourguignon, M.; Gallardo, D.I.; Gómez, H.J. A Note on Pareto-Type Distributions Parameterized by Its Mean and Precision Parameters. Mathematics 2022, 10, 528. https://doi.org/10.3390/math10030528
Bourguignon M, Gallardo DI, Gómez HJ. A Note on Pareto-Type Distributions Parameterized by Its Mean and Precision Parameters. Mathematics. 2022; 10(3):528. https://doi.org/10.3390/math10030528
Chicago/Turabian StyleBourguignon, Marcelo, Diego I. Gallardo, and Héctor J. Gómez. 2022. "A Note on Pareto-Type Distributions Parameterized by Its Mean and Precision Parameters" Mathematics 10, no. 3: 528. https://doi.org/10.3390/math10030528
APA StyleBourguignon, M., Gallardo, D. I., & Gómez, H. J. (2022). A Note on Pareto-Type Distributions Parameterized by Its Mean and Precision Parameters. Mathematics, 10(3), 528. https://doi.org/10.3390/math10030528








