A Methodology for Estimating Vehicle Route Choice from Sparse Flow Measurements in a Traffic Network
Abstract
:1. Introduction
- An a priori O-D matrix is assumed that may be an old O-D matrix or a matrix generated from surveys.
- The flows in the O-D matrix are mapped to the network using traffic assignment algorithms.
- Assigned flows are compared with measured flows.
- The a priori O-D matrix is adjusted to match the measured flows. For this, different solution approaches can be used.
- The adjusted O-D matrix is used again in step 1 until convergence of the assigned and measured flows and/or the a priori and estimated matrix.
2. Problem Statement
- 1.
- Method of computing how much each origin contributes to given bottleneck activation and resulting congestion;
- 2.
- Method of computing flows on links without direct flow measurements—all without simulation;
- 3.
- Method of determining the value of road sensor measurements (some may be redundant) and indicating places that need detection.
3. Computing Split Coefficients
3.1. Static Case
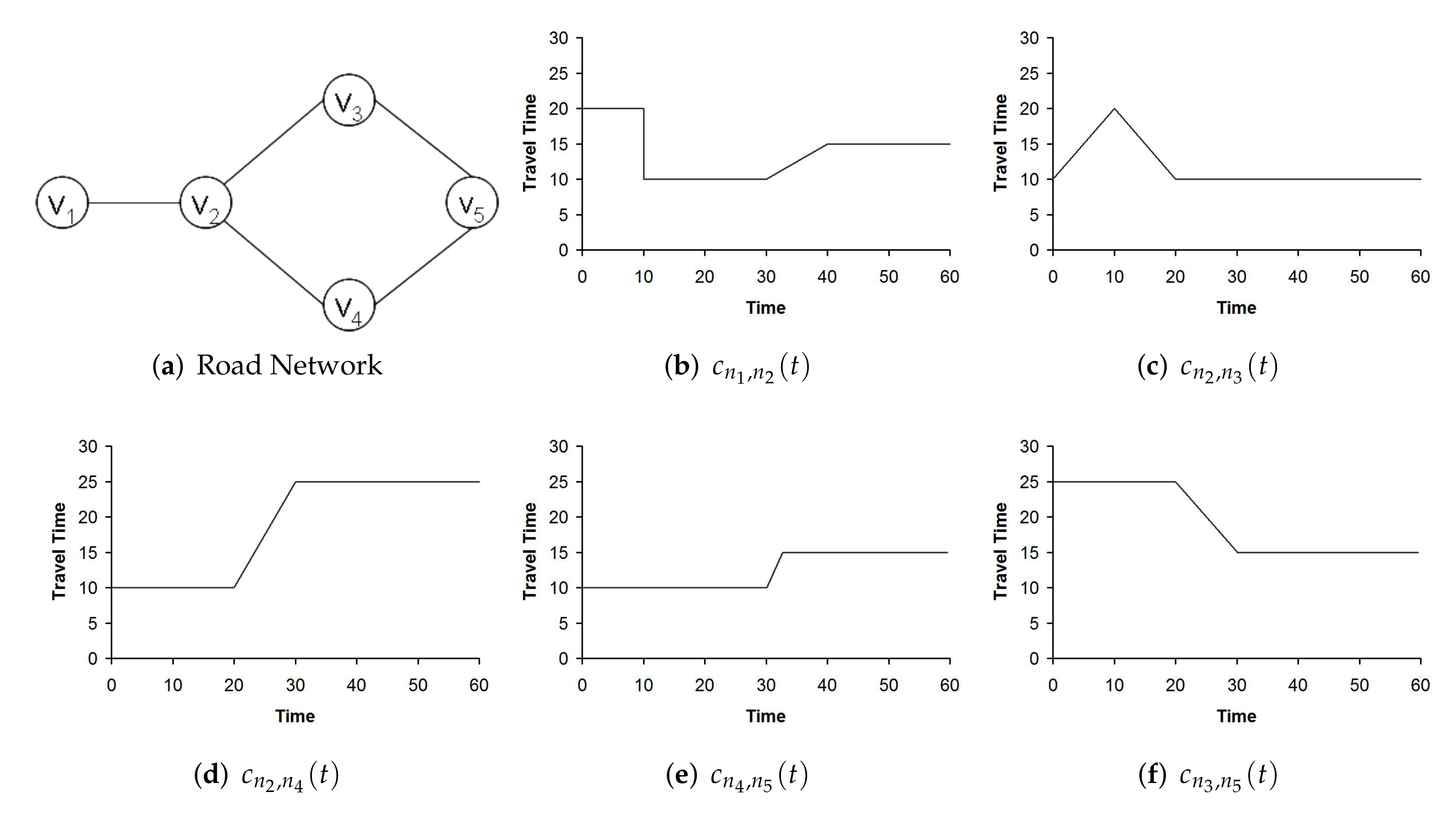
3.2. Accounting for Traffic Dynamics
4. Selecting Plausible Routes
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Van Zyulen, H.; Willumsen, L. The most likely trip matrix estimated from traffic counts. Transp. Res. Part B 1980, 14, 281–293. [Google Scholar] [CrossRef]
- Cascetta, E. Estimation of trip matrices from traffic counts and survey data: A generalized least squares estimator. Transp. Res. Part B 1984, 18, 289–299. [Google Scholar] [CrossRef]
- Bell, M. The real time estimation of origin-destination flows in the presence of platoon dispersion. Transp. Res. Part B 1991, 25, 115–125. [Google Scholar] [CrossRef]
- Krishnakumaria, P.; van Lint, H.; Djukic, T.; Cats, O. A data driven method for OD matrix estimation. Transp. Res. Part C 2020, 113, 38–56. [Google Scholar] [CrossRef] [Green Version]
- Willumsen, L. Estimation of an O-D Matrix from Traffic Counts—A Review; Working Paper 99; Institute of Transport Studies, University of Leeds: Leeds, UK, 1978. [Google Scholar]
- Evans, S. A relationship between the gravity model for trip distribution and the transportation problem in linear programming. Transp. Res. 1973, 7, 38–56. [Google Scholar] [CrossRef]
- Wardrop, J.G. Some Theoretical Aspects of Road Traffic Research. Proc. Inst. Civ. Eng. Part II 1952, 1, 325–378. [Google Scholar] [CrossRef]
- Chiu, Y.C.; Bottom, J.; Mahut, M.; Paz, A.; Balakrishna, R.; Waller, T.; Hicks, J. Dynamic Traffic Assignment. A Primer; Technical Report Circular E-153; Transportation Research Board: Washington, DC, USA, 2011. [Google Scholar]
- Kitamura, R.; Chen, C.; Pendyala, R.; Narayanan, R. Micro-simulation of daily activity-travel patterns for travel demand forecasting. Transportation 2000, 27, 25–51. [Google Scholar] [CrossRef]
- Bhat, C.; Zhao, H. The spatial analysis of activity stop generation. Transp. Res. Part B 2002, 36, 557–575. [Google Scholar] [CrossRef] [Green Version]
- Arrentze, T.; Timmermans, H. A need-based model of multi-day, multi-person activity generation. Transp. Res. Part B 2009, 43, 253–265. [Google Scholar] [CrossRef]
- Cantelmo, G.; Viti, F.; Cipriani, E.; Nigro, M. A Two-Steps Dynamic Demand Estimation Approach Sequentially Adjusting Generations and Distributions. In Proceedings of the Intelligent Transportation Systems Conference (ITSC), Gran Canaria, Spain, 15–18 September 2015; pp. 1477–1482. [Google Scholar]
- Scheffer, A.; Cantelmo, G.; Viti, F. Generating macroscopic, purpose-dependent trips through Monte Carlo sampling techniques. Transp. Res. Procedia 2017, 27, 585–592. [Google Scholar] [CrossRef]
- Cremer, M.; Keller, H. A new class of dynamic methods for the identification of origin-destination flows. Transp. Res. Part B 1987, 21, 117–132. [Google Scholar] [CrossRef]
- Yang, H.; Sasaki, T.; Iida, Y.; Asakura, Y. Estimation of origin-destination matrices from link traffic counts on congested networks. Transp. Res. Part B 1992, 26, 417–434. [Google Scholar] [CrossRef]
- Ashok, K.; Ben-Akiva, M. Alternative approaches for real-time estimation and prediction of time-dependent origin-destination flows. Transp. Sci. 2000, 32, 21–36. [Google Scholar] [CrossRef] [Green Version]
- Zhou, X.; Mahmassani, H. A structural state space model for real-time traffic origin-destination demand estimation and prediction in a day-to-day learning framework. Transp. Res. Part B 2007, 41, 823–840. [Google Scholar] [CrossRef]
- Castillo, E.; Rivas, A.; Jimenez, P.; Menendez, J. Observability in traffic networks. Plate scanning added by counting information. Transportation 2012, 39, 1301–1333. [Google Scholar] [CrossRef]
- Cascetta, E. Transportation Systems Engineering: Theory and Methods; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 47. [Google Scholar]
- Cantelmo, G.; Cipriani, E.; Gemma, A.; Nigro, M. An adaptive bi-level gradient procedure for the estimation of dynamic traffic demand. IEEE Trans. Intell. Transp. Syst. 2014, 15, 1348–1361. [Google Scholar] [CrossRef]
- Cipriani, E.; Nigro, M.; Fusco, G.; Colombaroni, C. Effectiveness of link and path information on simultaneous adjustment of dynamic O-D demand matrix. Eur. Transp. Res. Rev. 2014, 6, 139–148. [Google Scholar] [CrossRef] [Green Version]
- Antoniou, C.; Barcelo, J.; Breenc, M.; Bullejosb, M.; Casos, J.; Cipriani, E.; Ciuffo, B.; Djukic, T.; Hoogendoorn, S.; Marzano, V.; et al. Towards a generic benchmarking platform for origin–destination flows estimation/updating algorithms: Design, demonstration and validation. Transp. Res. Part C 2016, 66, 79–98. [Google Scholar] [CrossRef]
- Bera, S.; Krishna Rao, K.V. Estimation of Origin-Destination Matrix from Traffic Counts: The State of the Art. Eur. Transp. 2011, 49, 3–23. [Google Scholar]
- Meyer, M.; Miller, E. Urban Transportation Planning, 2nd ed.; McGraw-Hill: New York, NY, USA, 2000. [Google Scholar]
- Donoho, D.L. Compressed Sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Tikhonov, A.N. Solution of Incorrectly Formulated Problems and the Regularization Method. Dokl. Akad. Nauk SSSR 1963, 151, 501–504. [Google Scholar]
- Pilanci, M.; El Ghaoui, L.; Chandrasekaran, V. Recovery of Sparse Probability Measures via Convex Programming. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Lake Tahoe, NV, USA, 3–6 December 2012. [Google Scholar]
- Candes, E.J.; Wakin, M.B.; Boyd, S. Enhancing Sparsity by Reweighted l1 Minimization. J. Fourier Anal. Appl. 2008, 14, 877–905. [Google Scholar] [CrossRef]
- Lee, D. Numerically Efficient Methods for Solving Least Squares Problems; University of Chicago: Chicago, IL, USA, 2012. [Google Scholar]
- Wardrop, J.G.; Whitehead, J.I. Correspondence. Some Theoretical Aspects of Road Traffic Research. ICE Proc. Eng. Div. 1952, 1, 767–768. [Google Scholar] [CrossRef]
- Dreyfus, S.E. An Appraisal of Some Shortest-Path Algorithms. Oper. Res. 1969, 17, 395–412. [Google Scholar] [CrossRef]
- Halpern, J. Shortest Route with Time-dependent Length of Edges and Limited Delay Possibilities in Nodes. Oper. Res. 1977, 21, 117–124. [Google Scholar] [CrossRef]
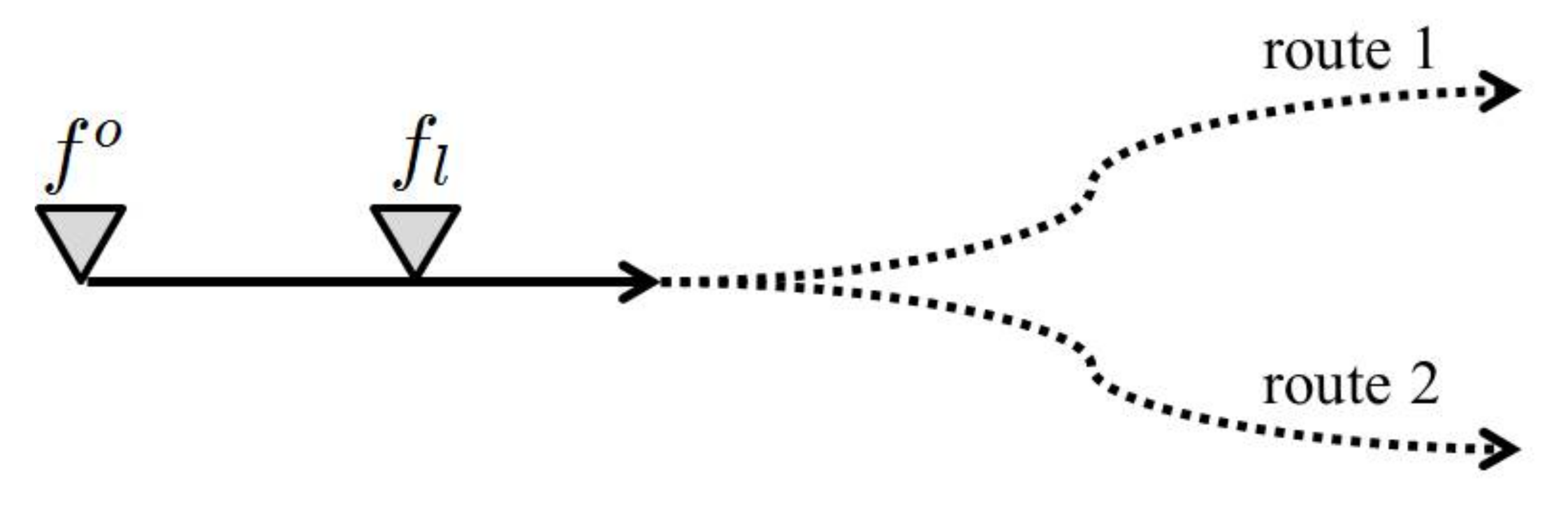

| Parameter | Description |
|---|---|
| Set of origins. Its size , the number of zones. | |
| Origin. | |
| Set of all routes. | |
| Subset of routes starting at origin . | |
| Route. | |
| Route starting at origin . | |
| Set of links that belong to one or more routes in . | |
| Subset of route links with flow measurements. | |
| () | Number of links in the set. |
| () | Link. |
| Link length. | |
| Subset of routes containing link . | |
| ( or ) | Number of routes in the set. |
| Route containing link . | |
| Flow (vehicle count) measured at origin . | |
| Flow (vehicle count) measured at link . | |
| Portion of flow directed to route . . | |
| Portion of flow , contributed by vehicles from origin o. . | |
| Speed measured or estimated at link . |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kurzhanskiy, A.A. A Methodology for Estimating Vehicle Route Choice from Sparse Flow Measurements in a Traffic Network. Mathematics 2022, 10, 527. https://doi.org/10.3390/math10030527
Kurzhanskiy AA. A Methodology for Estimating Vehicle Route Choice from Sparse Flow Measurements in a Traffic Network. Mathematics. 2022; 10(3):527. https://doi.org/10.3390/math10030527
Chicago/Turabian StyleKurzhanskiy, Alex A. 2022. "A Methodology for Estimating Vehicle Route Choice from Sparse Flow Measurements in a Traffic Network" Mathematics 10, no. 3: 527. https://doi.org/10.3390/math10030527
APA StyleKurzhanskiy, A. A. (2022). A Methodology for Estimating Vehicle Route Choice from Sparse Flow Measurements in a Traffic Network. Mathematics, 10(3), 527. https://doi.org/10.3390/math10030527






