Category of Intuitionistic Fuzzy Modules

Abstract

We study the relationship between the category of R-modules (${\mathbf{C}}_{\mathbf{R}-\mathbf{M}}$) and the category of intuitionistic fuzzy modules (${\mathbf{C}}_{\mathbf{R}-\mathbf{IFM}}$). We construct a category ${\mathbf{C}}_{\mathbf{Lat}(\mathbf{R}-\mathbf{IFM})}$ of complete lattices corresponding to every object in ${\mathbf{C}}_{\mathbf{R}-\mathbf{M}}$ and then show that, corresponding to each morphism in ${\mathbf{C}}_{\mathbf{R}-\mathbf{M}}$, there exists a contravariant functor from ${\mathbf{C}}_{\mathbf{R}-\mathbf{IFM}}$ to the category ${\mathbf{C}}_{\mathbf{Lat}}$ (=union of all ${\mathbf{C}}_{\mathbf{Lat}(\mathbf{R}-\mathbf{IFM})}$, corresponding to each object in ${\mathbf{C}}_{\mathbf{R}-\mathbf{M}}$) that preserve infima. Then, we show that the category ${\mathbf{C}}_{\mathbf{R}-\mathbf{IFM}}$ forms a top category over the category ${\mathbf{C}}_{\mathbf{R}-\mathbf{M}}$. Finally, we define and discuss the concept of kernel and cokernel in ${\mathbf{C}}_{\mathbf{R}-\mathbf{IFM}}$ and show that ${\mathbf{C}}_{\mathbf{R}-\mathbf{IFM}}$ is not an Abelian Category.

1. Introduction

The category theory is concerned with the mathematical entities and the relationships between them. Categories also emerge as unifying concepts in many fields of mathematics, particularly in all other areas of computer technology and mathematical physics. In the L.A. Zadeh [1] introductory paper, fundamental research is being carried out in the fuzzy sets context. Almost all of this mathematical development has been categorical. Several other researchers have developed and researched theories of fuzzy modules, fuzzy exact sequences of fuzzy complexes, and fuzzy homologies of fuzzy chain complexes [2,3,4,5,6].

K.T. Atanassov [7,8] suggested the interpretation of intuitionistic fuzzy sets that could be a generalized form of fuzzy sets. R. Biswas was the first to apply the criterion of intuitionistic fuzzy sets in algebra and led to the introduction of an intuitionistic fuzzy subgroup of a group in [9]. Later on, Hur and others in [10] and [11], brought the perception of the intuitionistic fuzzy subring and ideals. B. Davaaz and others in [12] delivered the perception of an intuitionistic fuzzy submodule of a module. Later, many mathematicians contributed to the study of intuitionistic fuzzy submodules, see [13,14,15,16,17,18,19]. The focus of this study is to carry the analysis of intuitionistic fuzzy modules over a commutative ring, to a categorical approach, to pave the way for future research.

Along with the commutative ring R with unity, we defined a category (${\mathbf{C}}_{\mathbf{R}-\mathbf{IFM}}$) of intuitionistic fuzzy modules where the classes of all intuitionistic fuzzy modules and intuitionistic fuzzy R-homomorphisms constitute objects and morphisms. The compositions of morphisms are the ordinary compositions of functions. Moreover, we reveal that $Hom(A,B)$ is an abelian group under the ordinary addition of R-homomorphisms, where A and B are intuitionistic fuzzy submodules. In the context of the additive composition, this structure appears to have a distributive influence on the left and at the right. This paper shows that ${\mathbf{C}}_{\mathbf{R}-\mathbf{IFM}}$ seems to be an additive category, even though it is not an abelian category (Section 4).

In this approach, we are implementing an important technological tool to “optimally intuitionistic fuzzify” the R-homomorphism families. This capability to intuitionistic fuzzify provides ${\mathbf{C}}_{\mathbf{R}-\mathbf{IFM}}$ with the top category structure over ${\mathbf{C}}_{\mathbf{R}-\mathbf{M}}$ (Section 3). We even characterize zero objects, kernels, cokernels in ${\mathbf{C}}_{\mathbf{R}-\mathbf{IFM}}$. Our objective is to study the intuitionistic fuzzy aspects of some algebraic structures, such as rings and modules. The study of fuzzy aspects of rings and modules is well developed, even then there are many scopes for further studies in intuitionistic fuzzification of such algebraic structures. The adopted approach is better than the previously developed fuzzy approach as it includes a non-membership function, which provides a more effective and efficient tool for dealing with uncertainties.

Finally, we have shown that the category of fuzzy modules ${\mathbf{C}}_{\mathbf{R}-\mathbf{FM}}$ is a subcategory of a category of intuitionistic fuzzy modules ${\mathbf{C}}_{\mathbf{R}-\mathbf{IFM}}$, and we established a contravariant functor from the category ${\mathbf{C}}_{\mathbf{R}-\mathbf{IFM}}$ to the category ${\mathbf{C}}_{\mathbf{Lat}}$ (= union of all ${\mathbf{C}}_{\mathbf{Lat}(\mathbf{R}-\mathbf{IFM})}$, corresponding to each object in ${\mathbf{C}}_{\mathbf{R}-\mathbf{M}}$). For basic definitions and results about category, we follow [20,21,22].

2. Materials and Methods

• Construct the category of intuitionistic fuzzy modules (${\mathbf{C}}_{\mathbf{R}-\mathbf{IFM}}$.
• Study the relationship between the category of R-modules (${\mathbf{C}}_{\mathbf{R}-\mathbf{M}}$) and the category of intuitionistic fuzzy modules (${\mathbf{C}}_{\mathbf{R}-\mathbf{IFM}}$).
• Analyze the concept of kernel and cokernel in ${\mathbf{C}}_{\mathbf{R}-\mathbf{IFM}}$.
• Investigate that ${\mathbf{C}}_{\mathbf{R}-\mathbf{IFM}}$ is not an abelian category.

3. Results

Throughout the paper, R is a commutative ring with unity 1 and $1\ne 0$. M is a unitary R-module, $\theta$ is a zero element of M, and I represents the unit interval $[0,1]$.

3.1. Preliminaries

Definition 1 

([20]). A category C is a quadruple $(Ob,Hom,id,o)$ consisting of:

• (C1) $Ob$, an object class;
• (C2) $Hom(X,Y)$ a set of morphisms is associated with each ordered object pair $(X,Y)$;
• (C3) a morphism $i{d}_X\in Hom(X,X)$, for each object X;
• (C4) a composition law holds i.e., if $f\in Hom(X,Y)$ and $g\in Hom(Y,Z)$, $gof\in Hom(X,Z)$; such that it satisfies the following axioms:
  • (M1) $ho\left(gof\right)=\left(hog\right)of$, $\forall f\in Hom(X,Y),g\in Hom(Y,Z)$ and $h\in Hom(Z,W)$;
  • (M2) $i{d}_{Y}of=foi{d}_X=f$, $\forall f\in Hom(X,Y)$;
  • (M3) a set of $Hom(X,Y)$ morphisms are pairwise disjoint.

Example 1. 

(1) 

$\mathit{Set}$, the category with sets as objects, functions as morphisms, and the usual compositions of functions, as compositions.

(2) 

$\mathit{Grp}$, the category with groups as objects, group homomorphisms as morphisms, and their compositions as compositions.

(3) 

$\mathit{Ab}$, the category with abelian groups as objects, group homomorphisms as morphisms, and their compositions as compositions.

Definition 2 

([21]). The opposite category $C^{op}$ of the specified category C is constructed when reversing the arrows, i.e., for each ordered object pair $(X,Y)$

$$Ho{m}_{C^{op}}(Y,X)=Ho{m}_C(X,Y)$$

Definition 3 

([21]). Category D is said to be a subcategory of the category C when $ob\left(D\right)\subseteq Ob\left(C\right)$, $Ho{m}_{\mathit{D}}(X,Y)\subseteq Ho{m}_{\mathit{C}}(X,Y)$ ordered object pair $\forall (X,Y)$ and composition of morphisms, and the identity of D should be the same as that of C.

Example 2. 

The category $\mathit{Grp}$ is a subcategory of $\mathit{Set}$.

Definition 4 

([21]). For the ordered object pair $(X,Y)$ of D, a full subcategory of a category C is a category D if $ob\left(D\right)\subseteq Ob\left(C\right)$ and $Ho{m}_D(X,Y)=Ho{m}_C(X,Y)$.

Example 3. 

The category $\mathit{Ab}$ is a full subcategory of $\mathit{Grp}$.

Definition 5 

([21]). A category C is called abelian if

 1.

C does have a zero object.

 2.

There is a product and a co-product for any pair of objects of C.

 3.

Each morphism in C does have a kernel and a cokernel.

 4.

Each monomorphism in C seems to be the kernel of its cokernel.

 5.

Any epimorphism in C seems to be the cokernel of its kernel.

Example 4. 

The category $\mathit{Ab}$ is an example of an abelian category.

Proposition 1 

([4]). The collection of all R-modules and R-homomorphisms is a category. This category is denoted by ${\mathit{C}}_{\mathit{R}-\mathit{M}}$.

Definition 6 

([21]). Let $C=\left(Ob\right(C),Hom(C),id,o)$ and $D=\left(Ob\right(D),Hom(D),id,o)$ be two categories and let $F_1:Ob\left(C\right)\to Ob\left(D\right)$ and $F_2:Hom\left(C\right)\to Hom\left(D\right)$ be maps. Then the quadruple $F=(C,D,F_1,F_2)$ is a functor provided:

(i) 

$X\in Ob\left(C\right)$ implies $F_1\left(X\right)\in Ob\left(D\right)$;

(ii) 

$f\in Hom(X,Y)$ implies $F_2\left(f\right)\in Hom(F_1\left(X\right),F_1\left(Y\right))$,$\forall X,Y\in Ob\left(C\right)$;

(iii) 

$F_2$ preserves composition, i.e., $F_2\left(gof\right)=F_2\left(g\right)o{F}_2\left(f\right)$,$\forall f\in Hom(X,Y)$ and $g\in Hom(Y,Z)$;

(iv) 

F preserves identities, i.e., $F_2\left(e_X\right)=e_{F_1\left(X\right)}$, $\forall X\in Ob\left(C\right)$.

Remark 1 

([21]).

(i) 

Instead of $F_1\left(X\right)$ we write $F\left(X\right)$.

(ii) 

In preference to $F_2\left(f\right)$ we write $F\left(f\right)$.

(iii) 

We call $F:C\to D$ a functor from C to D.

(iv) 

A functor defined above is called a covariant functor that preserves:

• The domains, the co-domains, and identities.
• The composition of arrows, it especially retains the path of the arrows.

(v) 

A contravariant functor F is similar to the covariant functor in addition to the other side of the arrow, $F\left(f\right):F\left(Y\right)\to F\left(X\right)$ and $F\left(gof\right)=F\left(f\right)oF\left(g\right),\forall f\in Hom(X,Y),g\in Hom(Y,Z)$.

Thus, a contravariant functor $F:C\to D$ is the same as a covariant functor $F:C^{op}\to D$.

Definition 7 

([22]). The category $C^S$ formed from a given category C is called a top category over C, if corresponding to every object A in C, the collection $s\left(A\right)$ of elements of C with the ordered relation defined on it, form a complete lattice, and the inverse image map $s\left(f\right),s\left(B\right)\to s\left(A\right)$, form a contravariant functor.

Definition 8 

([7,8,9]). An intuitionistic fuzzy set (IFS) A in X can be represented as an object of the form $A=\{<x,{\mu }_A\left(x\right),{\nu }_A\left(x\right)>:x\in X\}$, where the functions ${\mu }_A:X\to [0,1]$ and ${\nu }_A:X\to [0,1]$ denote the degree of membership (namely ${\mu }_A\left(x\right)$) and the degree of non-membership (namely ${\nu }_A\left(x\right)$) of each element $x\in X$ to A respectively and $0\le {\mu }_A\left(x\right)+{\nu }_A\left(x\right)\le 1$ for each $x\in X$.

Definition 9 

([12,13,15]). An IFS $A=({\mu }_A,{\nu }_A)$ of R-module M is called an intuitionistic fuzzy submodule (IFSM) if

(i) 

${\mu }_A\left(\theta \right)=1$, ${\nu }_A\left(\theta \right)=0$;

(ii) 

${\mu }_A(a+b)\ge {\mu }_A\left(a\right)\wedge {\mu }_A\left(b\right)$ and ${\nu }_A(a+b)\le {\nu }_A\left(a\right)\vee {\nu }_A\left(b\right)$, $\forall a,b\in M$;

(iii) 

${\mu }_A\left(ra\right)\ge {\mu }_A\left(a\right)$ and ${\nu }_A\left(ra\right)\le {\nu }_A\left(a\right)$, $\forall a\in M,r\in R$.

Example 5. 

Let $M={\mathbb{R}}^2$. Then M is an $\mathbb{R}$-module under usual componentwise addition and scalar multiplication composition. Then the intuitionistic fuzzy set $A=({\mu }_A,{\nu }_A)$ of M defined by

$${\mu }_A\left((x,y)\right)=\left\{\begin{array}{cc}1,\hfill & if (x,y)=(0,0)\hfill \\ 0.4,\hfill & if (x,y)\ne (0,0)\hfill \end{array}\right.;{\nu }_A\left((x,y)\right)=\left\{\begin{array}{cc}0,\hfill & if (x,y)=(0,0)\hfill \\ 0.1,\hfill & if (x,y)\ne (0,0).\hfill \end{array}\right.$$

is an intuitionistic fuzzy submodule of M.

Definition 10 

([13,19]). Let K as a submodule of an R-module M. The intuitionistic fuzzy characteristic function of K is defined by ${\chi }_K$, described by ${\chi }_K\left(a\right)=({\mu }_{{\chi }_K}\left(a\right),{\nu }_{{\chi }_K}\left(a\right))$, where

$${\mu }_{{\chi }_K}\left(a\right)=\left\{\begin{array}{cc}1,\hfill & if a\in K\hfill \\ 0,\hfill & if a\notin K\hfill \end{array}\right.;{\nu }_{{\chi }_K}\left(a\right)=\left\{\begin{array}{cc}0,\hfill & if a\in K\hfill \\ 1,\hfill & if a\notin K.\hfill \end{array}\right.$$

Clearly, ${\chi }_K$ is an IFSM of M. The IFSMs ${\chi }_{\left\{\theta \right\}},{\chi }_M$ are called trivial IFSMs of module M. Any IFSM of the module M apart from this is called proper IFSM.

Definition 11 

([17]). Let $A=({\mu }_A,{\nu }_A),B=({\mu }_B,{\nu }_B)$ are IFSM of R-modules M and N respectively. Then the map $f:A\to B$ is called an intuitionistic fuzzy R-homomorphism ( or IF R-hom ) from A to B if

(i) 

$f:M\to N$ is R-homomorphism and

(ii) 

${\mu }_B\left(f\left(a\right)\right)\ge {\mu }_A\left(a\right)$ and ${\nu }_B\left(f\left(a\right)\right)\le {\nu }_A\left(a\right),\forall a\in M$.

To avoid confusion between an R-homomorphism $f:M\to N$ and an intuitionistic fuzzy R-homomorphism $f:A\to B$. We denote the latter by $\overline{f}:A\to B$. So, given an IF R-homomorphism $\overline{f}:A\to B$, $f:M\to N$ is the underlying R-homomorphism of $\overline{f}$. The set of all IF R-homs from A to B is denoted by $Hom(A,B)$.

Example 6. 

Let $M=(\{0,1,2,3,4\},{+}_4)$ and $N=(\{0,1\},{+}_2)$ be two Z-modules. Define intuitionistic fuzzy sets $A=({\mu }_A,{\nu }_A)$ and $B=({\mu }_B,{\nu }_B)$ on M and N, respectively, as

$${\mu }_A\left(x\right)=\left\{\begin{array}{cc}0.8,\hfill & if x=0\hfill \\ 0.6,\hfill & if x=2\hfill \\ 0.4,\hfill & if x=1,3\hfill \end{array}\right.;{\nu }_A\left(x\right)=\left\{\begin{array}{cc}0,\hfill & if x=0\hfill \\ 0.3,\hfill & if x=2\hfill \\ 0.5,\hfill & if x=1,3\hfill \end{array}\right.$$

$${\mu }_B\left(y\right)=\left\{\begin{array}{cc}0.9,\hfill & if y=0\hfill \\ 0.3,\hfill & if y=1\hfill \end{array}\right.;{\nu }_B\left(y\right)=\left\{\begin{array}{cc}0,\hfill & if y=0\hfill \\ 0.5,\hfill & if y=1.\hfill \end{array}\right.$$

Then A and B are intuitionistic fuzzy submodules of M and N, respectively.

Define the mapping $f:M\to N$ by $f\left(a\right)=0,\forall a\in M$. Clearly, f is a R-homomorphism. Consider ${\mu }_B\left(f\left(0\right)\right)={\mu }_B\left(0\right)=0.9\ge 0.8={\mu }_A\left(0\right)$, ${\mu }_B\left(f\left(1\right)\right)={\mu }_B\left(0\right)=0.9\ge 0.4={\mu }_A\left(1\right)$, ${\mu }_B\left(f\left(2\right)\right)={\mu }_B\left(0\right)=0.9\ge 0.6={\mu }_A\left(2\right)$, ${\mu }_B\left(f\left(3\right)\right)={\mu }_B\left(0\right)=0.9\ge 0.4={\mu }_A\left(3\right)$. Also,${\nu }_B\left(f\left(0\right)\right)={\mu }_B\left(0\right)=0=0={\nu }_A\left(0\right)$, ${\nu }_B\left(f\left(1\right)\right)={\mu }_B\left(0\right)=0\le 0.5={\nu }_A\left(1\right)$, ${\nu }_B\left(f\left(2\right)\right)={\mu }_B\left(0\right)=0\le 0.3={\nu }_A\left(2\right)$, ${\nu }_B\left(f\left(3\right)\right)={\mu }_B\left(0\right)=0\le 0.5={\nu }_A\left(3\right)$. Thus, ${\mu }_B\left(f\left(a\right)\right)\ge {\mu }_A\left(a\right)$ and ${\nu }_B\left(f\left(a\right)\right)\le {\nu }_A\left(a\right),\forall a\in M$.

Hence, $\overline{f}:A\to B$ is an IF R-homomorphism.

Proposition 2. 

$Hom(A,B)$ form an additive abelian group. Moreover, it is a unitary R-module when R is a commutative ring with unity.

Proof. 

Since ${\mu }_B\left(\overline{0}\left(x\right)\right)={\mu }_B\left(0\right)=1\ge {\mu }_A\left(x\right)$ and ${\nu }_B\left(\overline{0}\left(x\right)\right)={\nu }_B\left(0\right)=0\le {\nu }_A\left(x\right)$ implies that there exists zero IF homomorphism $\overline{0}:A\to B$. Let $\overline{f},\overline{g}\in Hom(A,B)$ and $\forall x\in M$, we have ${\mu }_B\left((f+g)\left(x\right)\right)={\mu }_B(f\left(x\right)+g\left(x\right))\ge {\mu }_B\left(f\left(x\right)\right)\wedge {\mu }_B\left(g\left(x\right)\right)\ge {\mu }_A\left(x\right)\wedge {\mu }_A\left(x\right)={\mu }_A\left(x\right)$.

Similarly, we can show that ${\nu }_B\left((f+g)\left(x\right)\right)\le {\nu }_A\left(x\right)$. This shows that $\overline{f+g}\in Hom(A,B)$. Now, we can define $\overline{f}+\overline{g}=\overline{f+g}\in Hom(A,B)$. The addition obviously satisfies the commutative law and associative law. Also, define −$\overline{f}=\overline{-f}$ for every $\overline{f}\in Hom(A,B)$.

We have confidence in the definition, because: ${\mu }_B\left((-f)\left(x\right)\right)={\mu }_B(-\left(f\left(x\right)\right))={\mu }_B\left(f\left(x\right)\right)\ge {\mu }_A\left(x\right)$ and ${\nu }_B\left((-f)\left(x\right)\right)={\nu }_B(-\left(f\left(x\right)\right))={\nu }_B\left(f\left(x\right)\right)\le {\nu }_A\left(x\right),\forall x\in M$. This shows that $\overline{-f}\in Hom(A,B),\forall f\in Hom(A,B)$.

Precisely, $\overline{f}+\overline{0}=\overline{0}+\overline{f}$ and $\overline{f}+\overline{-f}=\overline{-f}+\overline{f}=\overline{0}$. This shows that $-\overline{f}$ works as the additive inverse of $\overline{f}$ and $\overline{0}$ is the zero element (or additive identity) in $Hom(A,B)$. Hence, $Hom(A,B)$ is an additive abelian group.

Furthermore, we define the R-scalar multiplication on $Hom(A,B)$ as follows:

For any $r\in R$ and $\overline{f}\in Hom(A,B)$ define $\left(r\overline{f}\right)\left(x\right)=r\overline{f}\left(x\right),\forall x\in M$.

As the map $x\rightarrowtail f\left(rx\right)$ is the ordinary R-homomorphism of M into N and

${\mu }_B\left(\left(r\overline{f}\right)\left(x\right)\right)={\mu }_B\left(r\overline{f}\left(x\right)\right)={\mu }_B\left(\overline{f}\left(rx\right)\right)\ge {\mu }_A\left(rx\right)\ge {\mu }_A\left(x\right)$ and ${\nu }_B\left(\left(r\overline{f}\right)\left(x\right)\right)={\nu }_B\left(r\overline{f}\left(x\right)\right)={\nu }_B\left(\overline{f}\left(rx\right)\right)\le {\nu }_A\left(rx\right)\le {\nu }_A\left(x\right)$. It follows that $r\overline{f}\in Hom(A,B)$. As R is a commutative ring. It is clear that $\left(r(\overline{f}+\overline{g})\right)\left(x\right)=\left(r\left(\overline{f+g}\right)\right)\left(x\right)=\overline{f+g}\left(rx\right)=(\overline{f}+\overline{g})\left(rx\right)=\overline{f}\left(rx\right)+\overline{g}\left(rx\right)=\left(r\overline{f}\right)\left(x\right)+\left(r\overline{g}\right)\left(x\right)=(r\overline{f}+r\overline{g})\left(x\right)$ implies that $r(\overline{f}+\overline{g})=r\overline{f}+r\overline{g}$. Moreover, for $r_1,r_2\in R$, we have $\left((r_1+r_2)\overline{f}\right)\left(x\right)=\overline{f}\left((r_1+r_2)x\right)=\overline{f}(r_{1}x+r_{2}x)=\overline{f}\left(r_{1}x\right)+\overline{f}\left(r_{2}x\right)=\left(r_1\overline{f}\right)\left(x\right)+\left(r_2\overline{f}\right)\left(x\right)=(r_1\overline{f}+r_2\overline{f})\left(x\right)$ implies that $(r_1+r_2)\overline{f}=r_1\overline{f}+r_2\overline{f}$. Also, $\left(\left(r_1{r}_2\right)\overline{f}\right)\left(x\right)=\overline{f}\left(\left(r_1{r}_2\right)x\right)=\overline{f}\left(r_1\left(r_{2}x\right)\right)=\left(r_2\overline{f}\right)\left(r_{1}x\right)=\left(r_1\left(r_2\overline{f}\right)\right)\left(x\right)\Rightarrow \left(r_1{r}_2\right)\overline{f}=r_1\left(r_2\overline{f}\right)$. Further, $(1.\overline{f})\left(x\right)=\overline{f}(1.x)=\overline{f}\left(x\right)$ implies that $1.\overline{f}=\overline{f}$.

Hence, $Hom(A,B)$ is a unitary R-module. □

If $f\in Hom(M,N)$ and $\overline{f}\in Hom(A,B)$, define

$$Ker\overline{f}=\{a\in M:{\mu }_B\left(f\left(a\right)\right)=1;{\nu }_B\left(f\left(a\right)\right)=0\}$$

and

$$Im\overline{f}=\{\overline{f}\left(a\right):a\in M\}$$

As $Kerf$ is the pre-image of $\left\{\theta \right\}$ under f, we have $Kerf\subseteq Ker\overline{f}$. Especially, if $B={\chi }_N$, then we have $Ker\overline{f}=A$, for all $\overline{f}\in Hom(A,B)$.

Proposition 3. 

Let A and B are IFSM of R-modules M and N, respectively, and $\overline{f}:A\to B$ is IF R-hom, then:

 (i)

$Ker\overline{f}$ is a submodule of M;

 (ii)

The restriction of A to $Ker\overline{f}$ i.e., ${A|}_{Ker\overline{f}}$ is an IFSM of A.

Proof. 

(i)

Since $\overline{f}:A\to B$ is IF R-hom.

Let $\theta$ be zero element of M, then $\theta \in Ker\overline{f}$. Let $a\in Ker\overline{f}$ and $r\in R$, then ${\mu }_A\left(\overline{f}\left(ra\right)\right)={\mu }_A\left(r\overline{f}\left(a\right)\right)\ge {\mu }_A\left(\overline{f}\left(a\right)\right)=1$ and ${\nu }_A\left(\overline{f}\left(ra\right)\right)={\nu }_A\left(r\overline{f}\left(a\right)\right)\le {\nu }_A\left(\overline{f}\left(a\right)\right)=0$ implies that $ra\in Ker\overline{f}$. In particular $-a\in Ker\overline{f}$. Further, if $a,b\in Ker\overline{f}$, Conveniently, we can predict $a+b\in Ker\overline{f}$. Thus, $Ker\overline{f}$ is a submodule of M.

(ii)

Let ${C=A|}_{Ker\overline{f}}$. Then $C=({\mu }_C,{\nu }_C)$, where ${\mu }_C\left(a\right)={\mu }_A\left(a\right)$ and ${\nu }_C\left(a\right)={\nu }_A\left(a\right),\forall a\in Ker\overline{f}$. Now it is simple to prove that C is an IFSM of M and $C\subseteq A$.

□

3.2. Categories of Intuitionistic Fuzzy Modules

In this section, we analyze the IF-modules category and the existence of the covariant functor between the modules category and IF-modules category.

Theorem 1. 

Let $A=({\mu }_A,{\nu }_A)$ and $B=({\mu }_B,{\nu }_B)$ are two IF modules of R-modules M and N respectively. Then the function $\beta :Hom(A,B)\to I\times I$ on R-module $Hom(A,B)$ defined by

$$\beta \left(\overline{f}\right)=({\mu }_{\beta \left(\overline{f}\right)},{\nu }_{\beta \left(\overline{f}\right)})$$

where ${\mu }_{\beta \left(\overline{f}\right)}=\wedge \{{\mu }_B\left(\overline{f}\left(a\right)\right):a\in M\}$ and ${\nu }_{\beta \left(\overline{f}\right)}=\vee \{{\nu }_B\left(\overline{f}\left(a\right)\right):a\in M\}$ is an intuitionistic fuzzy submodule of $Hom(A,B)$.

Proof. 

As shown in Proposition 2, $Hom(A,B)$ is an R-module, where the scalar multiplication on $Hom(A,B)$ is defined as $(r.\overline{f})\left(a\right)=r\overline{f}\left(a\right),\forall a\in M$.

Next, we show that the function $\beta :Hom(A,B)\to I\times I$ on R-module $Hom(A,B)$ defined by

$$\beta \left(\overline{f}\right)=({\mu }_{\beta \left(\overline{f}\right)},{\nu }_{\beta \left(\overline{f}\right)})$$

where ${\mu }_{\beta \left(\overline{f}\right)}=\wedge \{{\mu }_B\left(\overline{f}\left(a\right)\right):a\in M\}$ and ${\nu }_{\beta \left(\overline{f}\right)}=\vee \{{\nu }_B\left(\overline{f}\left(a\right)\right):a\in M\}$ is IFSM of $Hom(A,B)$.

Let $\overline{f}\in Hom(A,B)$ and $r\in R$, Consider

$$\begin{array}{ccc}\hfill {\mu }_{\beta (r.\overline{f})}& =& \wedge \{{\mu }_B\left((r.\overline{f})\left(a\right)\right):a\in M\}\hfill \\ & =& \wedge \{{\mu }_B((r.\overline{f}\left(a\right)):a\in M\}\hfill \\ & \ge & \wedge \{{\mu }_B\left(\overline{f}\left(a\right)\right):a\in M\}\hfill \\ & =& {\mu }_{\beta \left(\overline{f}\right)}.\hfill \end{array}$$

Thus ${\mu }_{\beta (r.\overline{f})}\ge {\mu }_{\beta \left(\overline{f}\right)}$. Likewise, we are able to exhibit that ${\nu }_{\beta (r.\overline{f})}\le {\nu }_{\beta \left(\overline{f}\right)}$.

Further, let $\overline{f},\overline{g}\in Hom(A,B)$ and $a\in M$. Consider

$$\begin{array}{ccc}\hfill {\mu }_{\beta (\overline{f}+\overline{g})}& =& \wedge \{{\mu }_B\left((\overline{f}+\overline{g})\left(a\right)\right):a\in M\}\hfill \\ & =& \wedge \{{\mu }_B(\overline{f}\left(a\right)+\overline{g}\left(a\right)):a\in M\}\hfill \\ & \ge & \wedge \{\left\{{\mu }_B(\overline{f}\left(a\right)\wedge \overline{g}\left(a\right))\right\}:a\in M\}\hfill \\ & =& \{\wedge \{{\mu }_B\left(\overline{f}\left(a\right)\right):a\in M\}\}\wedge \{\wedge \{{\mu }_B\left(\overline{g}\left(a\right)\right):a\in M\}\}\hfill \\ & =& {\mu }_{\beta \left(\overline{f}\right)}\wedge {\mu }_{\beta \left(\overline{g}\right)}.\hfill \end{array}$$

Thus, ${\mu }_{\beta (\overline{f}+\overline{g})}\ge {\mu }_{\beta \left(\overline{f}\right)}\wedge {\mu }_{\beta \left(\overline{g}\right)}$. Likewise, we are able to exhibit that ${\nu }_{\beta (\overline{f}+\overline{g})}\le {\nu }_{\beta \left(\overline{f}\right)}\vee {\nu }_{\beta \left(\overline{g}\right)}$.

Also, ${\mu }_{\beta \left(\overline{0}\right)}=\wedge \{{\mu }_B\left(\overline{0}\left(a\right)\right):a\in M\}=\wedge \{{\mu }_B\left(0\right):a\in M\}=1$.

Likewise, we can demonstrate that ${\nu }_{\beta \left(\overline{0}\right)}=0$. Hence $\beta$ is IFSM of R-module $Hom(A,B)$. □

Definition 12. 

The category ${\mathit{C}}_{\mathit{R}-\mathit{M}}=(Ob\left({\mathit{C}}_{\mathit{R}-\mathit{M}}\right),\mathit{H}\mathit{o}\mathit{m}\left({\mathit{C}}_{\mathit{R}-\mathit{M}}\right),o)$ has R-modules as objects and R-homomorphisms as morphisms, with composition of morphisms defined as the composition of mappings.

An IF-module category ${\mathit{C}}_{\mathit{R}-\mathit{IFM}}$ over the base category ${\mathit{C}}_{\mathit{R}-\mathit{M}}$ is completely described by two mappings:

$$\alpha :Ob\left({\mathit{C}}_{\mathit{R}-\mathit{M}}\right)\to I\times I;$$

$$\beta :Hom\left({\mathit{C}}_{\mathit{R}-\mathit{M}}\right)\to I\times I$$

IF-module category ${\mathit{C}}_{\mathit{R}-\mathit{IFM}}$ consists of

• (C1) Ob(${\mathit{C}}_{\mathit{R}-\mathit{IFM}}$) the set of objects as IFSMs on Ob(${\mathit{C}}_{\mathit{R}-\mathit{M}}$), i.e., the objects of the form $\alpha :Ob\left({\mathit{C}}_{\mathit{R}-\mathit{M}}\right)\to I\times I$;
• (C2) $\mathit{H}\mathit{o}\mathit{m}\left({\mathit{C}}_{\mathit{R}-\mathit{IFM}}\right)$ the set of IF R-homomorphisms corresponding to underlying R-homomorphisms from $\mathit{H}\mathit{o}\mathit{m}\left({\mathit{C}}_{\mathit{R}-\mathit{M}}\right)$, i.e., IF R-homomorphisms of the form $\beta :Hom\left({\mathit{C}}_{\mathit{R}-\mathit{M}}\right)\to I\times I$, such that for $f\in {\mathit{H}\mathit{o}\mathit{m}}_{{\mathit{C}}_{\mathit{R}-\mathit{M}}}(M,N)$,

  $$\beta \left(\overline{f}\right)=({\mu }_{\beta \left(\overline{f}\right)},{\nu }_{\beta \left(\overline{f}\right)})$$

  as defined in Theorem 1, a composition law associating to each pair of morphisms $f\in Hom(M,N)$ and $g\in Hom(N,P)$, a morphism $gof\in Hom(P,Q)$, such that the following axioms hold:
  • (M1) Associativity: $ho\left(gof\right)=\left(hog\right)of$, for all $f\in Hom(M,N)$, $g\in Hom(N,P)$ and $h\in Hom(P,Q)$;
  • (M2) preservation of morphisms: $\beta (g\circ f)=\beta \left(g\right)o\beta \left(f\right)$;
  • (M3) existence of identity: $\forall M\in Ob\left({\mathit{C}}_{\mathit{R}-\mathit{M}}\right)$ there is an identity $i_M\in {\mathit{H}\mathit{o}\mathit{m}}_{{\mathit{C}}_{\mathit{R}-\mathit{M}}}(M,M)$ such that $\beta \left(i_M\right)=\alpha \left(M\right)$.

Thus, A category of IF R-modules can be constructed as

$${\mathit{C}}_{\mathit{R}-\mathit{IFM}}=(Ob\left({\mathit{C}}_{\mathit{R}-\mathit{IFM}}\right),Hom\left({\mathit{C}}_{\mathit{R}-\mathit{IFM}}\right),o)$$

Proposition 4. 

${\mathit{C}}_{\mathit{R}-\mathit{M}}$ is a subcategory of ${\mathit{C}}_{\mathit{R}-\mathit{IFM}}$.

Proof. 

It follows from Definition 3, Proposition 1 and Theorem 1. □

Proposition 5. 

There exist a covariant functor from ${\mathit{C}}_{\mathit{R}-\mathit{M}}$ to ${\mathit{C}}_{\mathit{R}-\mathit{IFM}}$.

Proof. 

Define $\beta =({\mu }_{\beta },{\nu }_{\beta }):{\mathbf{C}}_{\mathbf{R}-\mathbf{M}}\to {\mathbf{C}}_{\mathbf{R}-\mathbf{IFM}}$ by $\beta \left(M\right)=({\mu }_{\beta }\left(M\right),{\nu }_{\beta }\left(M\right))$, where ${\mu }_{\beta }\left(a\right)+{\nu }_{\beta }\left(a\right)\le 1,\forall a\in M$.

Let $f\in {\mathit{H}\mathit{o}\mathit{m}}_{{\mathbf{C}}_{\mathbf{R}-\mathbf{M}}}(M,N)$. Thus $\beta \left(f\right)\in Hom\left({\mathbf{C}}_{\mathbf{R}-\mathbf{IFM}}\right)$, where $\beta \left(f\right):\beta \left(M\right)\to \beta \left(N\right)$ described by

$$\beta \left(f\right)({\mu }_{\beta },{\nu }_{\beta })=({\mu }_{\beta }\circ f^{-1},{\nu }_{\beta }\circ f^{-1}); \mathrm{where}$$

(i)

${\mu }_{\beta }(a+b)\ge {\mu }_{\beta }\left(a\right)\wedge {\mu }_{\beta }\left(b\right)$

(ii)

${\nu }_{\beta }(a+b)\le {\nu }_{\beta }\left(a\right)\vee {\nu }_{\beta }\left(b\right)$

(iii)

${\mu }_{\beta }(-a)={\mu }_{\beta }\left(a\right)$

(iv)

${\nu }_{\beta }(-a)={\nu }_{\beta }\left(a\right)$

(v)

${\mu }_{\beta }\left(ra\right)={\mu }_{\beta }\left(a\right)$

(vi)

${\nu }_{\beta }\left(ra\right)={\nu }_{\beta }\left(a\right)$

(vii)

${\mu }_{\beta }\left(0\right)=1$

(viii)

${\nu }_{\beta }\left(0\right)=0,\forall a,b\in M,r\in R$.

We want to prove that $\beta$ preserves object, composition, domain, and codomain identity.

Let $({\mu }_{\beta },{\nu }_{\beta })$, $({\mu }_{{\beta }_1},{\nu }_{{\beta }_1})\in Ob\left({\mathbf{C}}_{\mathbf{R}-\mathbf{IFM}}\right)$ such that $({\mu }_{\beta }\circ f^{-1},{\nu }_{\beta }\circ f^{-1})=({\mu }_{{\beta }_1}\circ f^{-1},{\nu }_{{\beta }_1}\circ f^{-1})$

⇒

${\mu }_{\beta }\circ f^{-1}={\mu }_{{\beta }_1}\circ f^{-1}$ and ${\nu }_{\beta }\circ f^{-1}={\nu }_{{\beta }_1}\circ f^{-1}$

⇒

${\mu }_{\beta }={\mu }_{{\beta }_1}$ and ${\nu }_{\beta }={\nu }_{{\beta }_1}\Rightarrow ({\mu }_{\beta },{\nu }_{\beta })=({\mu }_{{\beta }_1},{\nu }_{{\beta }_1})$

⇒

$\beta$ is well defined.

Let $f\in {\mathbf{Hom}}_{{\mathbf{C}}_{\mathbf{R}-\mathbf{M}}}(M,N),g\in {\mathbf{Hom}}_{{\mathbf{C}}_{\mathbf{R}-\mathbf{M}}}(N,P)$ then $gof\in {\mathbf{Hom}}_{{\mathbf{C}}_{\mathbf{R}-\mathbf{M}}}(M,P)$.

Then, $\beta \left(f\right)\in {\mathbf{Hom}}_{{\mathbf{C}}_{\mathbf{R}-\mathbf{IFM}}}(\beta \left(M\right),\beta \left(N\right))$, $\beta \left(g\right)\in {\mathbf{Hom}}_{{\mathbf{C}}_{\mathbf{R}-\mathbf{IFM}}}(\beta \left(N\right),\beta \left(P\right))$ and $\beta \left(gof\right)\in {\mathbf{Hom}}_{{\mathbf{C}}_{\mathbf{R}-\mathbf{IFM}}}(\beta \left(M\right),\beta \left(P\right))$. For any $({\mu }_{\beta },{\nu }_{\beta })\in \beta \left(M\right)$, we have

$$\begin{array}{ccc}\hfill \beta (g\circ f)({\mu }_{\beta },{\nu }_{\beta })& =& ({\mu }_{\beta }\circ {(g\circ f)}^{-1},{\nu }_{\beta }\circ {(g\circ f)}^{-1})\hfill \\ & =& ({\mu }_{\beta }\circ (f^{-1}\circ g^{-1}),{\nu }_{\beta }\circ (f^{-1}\circ g^{-1}))\hfill \\ & =& (({\mu }_{\beta }\circ f^{-1})\circ g^{-1},({\nu }_{\beta }\circ f^{-1})\circ g^{-1})\hfill \\ & =& \beta \left(g\right)({\mu }_{\beta }\circ f^{-1},{\nu }_{\beta }\circ f^{-1})\hfill \\ & =& \beta \left(g\right)\beta \left(f\right)({\mu }_{\beta },{\nu }_{\beta }).\hfill \end{array}$$

Therefore, $\beta (g\circ f)=\beta \left(g\right)\beta \left(f\right)$.

Moreover, $\beta \left(i_M\right)({\mu }_{\beta },{\nu }_{\beta })=({\mu }_{\beta }\circ i_M^{-1},{\nu }_{\beta }\circ i_M^{-1})=({\mu }_{\beta },{\nu }_{\beta })$ implies that $\beta \left(i_M\right)$ is the identity element in $\mathbf{H}\mathbf{o}\mathbf{m}\left({\mathbf{C}}_{\mathbf{R}-\mathbf{IFM}}\right)$. Hence, $\beta :{\mathbf{C}}_{\mathbf{R}-\mathbf{M}}\to {\mathbf{C}}_{\mathbf{R}-\mathbf{IFM}}$ is a covariant functor. □

3.3. Optimal Intuitionistic Fuzzification

In this section, we show that the category ${\mathbf{C}}_{\mathbf{R}-\mathbf{IFM}}$ forms a top category over the category ${\mathbf{C}}_{\mathbf{R}-\mathbf{M}}$. To prove this, we first construct a category ${\mathbf{C}}_{\mathbf{Lat}(\mathbf{R}-\mathbf{IFM})}$ of complete lattices corresponding to every object in ${\mathbf{C}}_{\mathbf{R}-\mathbf{M}}$ and then show that corresponding to each morphism in ${\mathbf{C}}_{\mathbf{R}-\mathbf{M}}$, there exists a contravariant functor from ${\mathbf{C}}_{\mathbf{R}-\mathbf{IFM}}$ to the category ${\mathbf{C}}_{\mathbf{Lat}}$ (=union of all ${\mathbf{C}}_{\mathbf{Lat}(\mathbf{R}-\mathbf{IFM})}$, corresponding to each object in ${\mathbf{C}}_{\mathbf{R}-\mathbf{M}}$) that preserve infima. Finally, we define the notion of kernel and cokernel for the category ${\mathbf{C}}_{\mathbf{R}-\mathbf{IFM}}$ and show that ${\mathbf{C}}_{\mathbf{R}-\mathbf{IFM}}$ is not an abelian category.

Let $A=({\mu }_A,{\nu }_A)$ and $B=({\mu }_B,{\nu }_B)$ are IFSM of R-modules M and N, respectively, and $f:M\to N$ is R-homomorphism. With the help of A and f, we can provide an IF module structure on N by

$${\mu }_{f\left(A\right)}\left(b\right)=sup\{{\mu }_A\left(a\right):f\left(a\right)=b\}\mathrm{and}{\nu }_{f\left(A\right)}\left(b\right)=inf\{\nu \left(a\right):f\left(a\right)=b\}.$$

It is clear that $f\left(A\right)=({\mu }_{f\left(A\right)},{\nu }_{f\left(A\right)})$ is an IFSM of and $\overline{f}:A\to f\left(A\right)$ is an IF R-hom.

With the help of B and f, we can provide an IF module structure on M by

$${\mu }_{f^{-1}\left(B\right)}\left(a\right)={\mu }_B\left(f\left(a\right)\right)\mathrm{and}{\nu }_{f^{-1}\left(B\right)}\left(a\right)={\nu }_B\left(f\left(a\right)\right).$$

Hence, $f^{-1}\left(B\right)=({\mu }_{f^{-1}\left(B\right)},{\nu }_{f^{-1}\left(B\right)})$ is an IFSM of M and $\overline{f}:f^{-1}\left(B\right)\to B$ is an IF R-hom.

Lemma 1. 

Let M and N are R-modules and $f:M\to N$ be R-homomorphism.

(i) 

If $A=({\mu }_A,{\nu }_A)$ is an IFSM of M, then there is an IFSM $f\left(A\right)=({\mu }_{f\left(A\right)},{\nu }_{f\left(A\right)})$ of N such that for any IFSM $({\mu }_B,{\nu }_B)$ of N, $\overline{f}:A\to B$ is an IF R-hom if and only if $f\left(A\right)\subseteq B$.

(ii) 

If $B=({\mu }_B,{\nu }_B)$ is an IFSM of N, then there is an IFSM $f^{-1}\left(B\right)=({\mu }_{f^{-1}\left(B\right)},{\nu }_{f^{-1}\left(B\right)})$ of M such that for any IFSM A of M, $\overline{f}:A\to B$ is an IF R-hom if and only if $A\subseteq f^{-1}\left(B\right)$.

Proof. 

(i) Now, $\overline{f}:A\to B$ is an IF R-hom if and only if ${\mu }_B\left(f\left(a\right)\right)\ge {\mu }_A\left(a\right)$ and ${\nu }_B\left(f\left(a\right)\right)\le {\nu }_A\left(a\right),\forall a\in M$. Let $b\in N$ be any element, then ${\mu }_{f\left(A\right)}\left(b\right)=\vee \{{\mu }_A\left(a\right):f\left(a\right)=b\}\le {\mu }_A\left(a\right)\le {\mu }_B\left(f\left(a\right)\right)$.

Likewise, we are able to exhibit that ${\nu }_{f\left(A\right)}\left(b\right)\ge {\nu }_B\left(f\left(a\right)\right)$ i.e., $f\left(A\right)\subseteq B$.

(ii) Now, $\overline{f}:A\to B$ is an IF R-hom if and only if ${\mu }_B\left(f\left(a\right)\right)\ge {\mu }_A\left(a\right)$ and ${\nu }_B\left(f\left(a\right)\right)\le {\nu }_A\left(a\right),\forall a\in M$. Now, ${\mu }_{f^{-1}\left(B\right)}\left(a\right)={\mu }_B\left(f\left(a\right)\right)\ge {\mu }_A\left(a\right)$ and ${\nu }_{f^{-1}\left(B\right)}\left(a\right)={\nu }_B\left(f\left(a\right)\right)\le {\nu }_A\left(a\right)$ implies that $A\subseteq f^{-1}\left(B\right)$. □

Observe that If $f\in Hom(M,N)$, now for each IFSM A [B] on M [N] one will have $f\left(A\right)$ [$f^{-1}\left(B\right)$] IFSMs, we conclude that f is trivially intuitionistic fuzzified relative to A [B]. In particular, we will say that for each IFSM A [B] of M [N], we have obtained IF R-hom $\overline{f}:A\to {\chi }_N$ [$\overline{f}:{\chi }_M\to B$].

Lemma 2. 

The set $s\left(M\right)=\left\{\right(\mu ,\nu ):M\to I\times I:(\mu ,\nu \left)\mathit{is}\mathit{IF}\mathit{module}\mathit{of}R-\mathit{module}M\right\}$ form a complete lattice associated with the order relation $({\mu }_1,{\nu }_1)\le ({\mu }_2,{\nu }_2)$ if ${\mu }_1\left(a\right)\le {\mu }_2\left(a\right)$ and ${\nu }_1\left(a\right)\ge {\nu }_2\left(a\right)$, $\forall a\in M$.

Proof. 

Let $\{({\mu }_i,{\nu }_i):i\in J\}$ be a collection of elements of $s\left(M\right)$. Then infimum and supremum on $s\left(M\right)$ are explicitly specified as:

$${\wedge }_{i\in J}({\mu }_i,{\nu }_i)\left(a\right)=(In{f}_{i\in J}\left\{{\mu }_i\left(a\right)\right\},Su{p}_{i\in J}\left\{{\nu }_i\left(a\right)\right\})$$

and

$${\vee }_{i\in J}({\mu }_i,{\nu }_i)\left(a\right)=(In{f}_{i\in J}\{\mu \left(a\right):({\mu }_i,{\nu }_i)\in s\left(M\right)\mathrm{and}{\mu }_i\le \mu ,\forall i\in J\},Su{p}_{i\in J}\{\nu \left(a\right):({\mu }_i,{\nu }_i)\in s\left(M\right)\mathrm{and}{\nu }_i\ge \nu ,\forall i\in J\}).$$

Then $s\left(M\right)$ form a complete lattice. □

Remark 2. 

(i) 

The least element of $s\left(M\right)$ is $\overline{0}$ and the greatest element of $s\left(M\right)$ is $\overline{1}$.

(ii) 

$s\left(M\right)$ under the order relation defined above form a category where

$Ob\left(s\right(M\left)\right)$ = all IF-modules of M and $Hom\left(s\right(M\left)\right)$ = order relation defined above.

(iii) 

Supremum can also be defined as ${\vee }_{i\in J}({\mu }_i,{\nu }_i)\left(a\right)=(Su{p}_{i\in J}\left\{{\mu }_i\left(a\right)\right\},In{f}_{i\in J}\left\{{\nu }_i\left(a\right)\right\})$, which only holds for IF sets but does not hold for IF modules including when J is finite.

For e.g., let $M=Z$-module Z and IFSMs $({\mu }_1,{\nu }_1)$ and $({\mu }_2,{\nu }_2)$ of M described as:

$$({\mu }_1,{\nu }_1)\left(t\right)=\left\{\begin{array}{cc}(1,0),\hfill & if t\mathit{is}\mathit{even}\hfill \\ (0,1),\hfill & if t\mathit{is}\mathit{odd}\hfill \end{array}\right.;({\mu }_2,{\nu }_2)\left(t\right)=\left\{\begin{array}{cc}(1,0),\hfill & if 3|t\hfill \\ (0,1),\hfill & if 3\nmid t.\hfill \end{array}\right.$$

Take $({\mu }_1,{\nu }_1)\vee ({\mu }_2,{\nu }_2)=({\mu }_3,{\nu }_3)$, where ${\mu }_3\left(t\right)=max\{{\mu }_1\left(t\right),{\mu }_2\left(t\right)\}$ and ${\nu }_3\left(t\right)=min\{{\nu }_1\left(t\right),{\nu }_2\left(t\right)\}$. Here we can check that $({\mu }_3,{\nu }_3))$ is not an IFSM of M, for $0={\mu }_3\left(1\right)={\mu }_3(3-2)\ngeqq {\mu }_3\left(3\right)\wedge {\mu }_3\left(2\right)=1$ and $1={\nu }_3\left(1\right)={\nu }_3(3-2)\nleqq {\nu }_3\left(3\right)\vee {\nu }_3\left(2\right)=0$.

Lemma 3. 

The set $t\left(M\right)=\left\{\right(\mu ,\nu ):M\to I\times I:(\mu ,\nu \left)\mathit{is}\mathit{IF}\mathit{module}\mathit{of}\mathit{R}-\mathit{module}M\right\}$ form a complete lattice associated with the order relation $({\mu }_1,{\nu }_1)\le ({\mu }_2,{\nu }_2)$ if ${\mu }_1\left(a\right)\ge {\mu }_2\left(a\right)$ and ${\nu }_1\left(a\right)\le {\nu }_2\left(a\right)$$\forall a\in M$.

Proof. 

Let $\{({\mu }_i,{\nu }_i):i\in J\}$ be a collection of elements of $t\left(M\right)$. Then infimum and supremum on $t\left(M\right)$ are explicitly specified as:

$${\wedge }_{i\in J}({\mu }_i,{\nu }_i)\left(a\right)=(Su{p}_{i\in J}\left\{{\mu }_i\left(a\right)\right\},In{f}_{i\in J}\left\{{\nu }_i\left(a\right)\right\})$$

and

$${\vee }_{i\in J}({\mu }_i,{\nu }_i)\left(a\right)=(In{f}_{i\in J}\{\mu \left(a\right):({\mu }_i,{\nu }_i)\in t\left(M\right)\mathrm{and}{\mu }_i\le \mu ,\forall i\in J\},Su{p}_{i\in J}\{\nu \left(a\right):({\mu }_i,{\nu }_i)\in t\left(M\right)\mathrm{and}{\nu }_i\ge \nu ,\forall i\in J\}).$$

Then $t\left(M\right)$ form a complete lattice. □

Remark 3. 

$t\left(M\right)$ under the order relation defined above form a category where $Ob\left(t\right(M\left)\right)$ = all IF-modules of M and $Hom\left(t\right(M\left)\right)$ = order relation as defined above.

Theorem 2. 

${\mathit{C}}_{\mathit{R}-\mathit{IFM}}$ is a top category over ${\mathit{C}}_{\mathit{R}-\mathit{M}}$.

Proof. 

This becomes sufficient to prove that, with every $M\in Ob\left({\mathbf{C}}_{\mathbf{R}-\mathbf{M}}\right)$, the corresponding complete lattice $s\left(M\right)$ specified in Lemma 2. For each $f\in {\mathbf{Hom}}_{{\mathbf{C}}_{\mathbf{R}-\mathbf{M}}}(M,N)$, $s\left(f\right):s\left(N\right)\to s\left(M\right)$ defined as $s\left(f\right)({\mu }_B,{\nu }_B)=({\mu }_{f^{-1}\left(B\right)},{\nu }_{f^{-1}\left(B\right)}),\forall ({\mu }_B,{\nu }_B)\in s\left(N\right)$ determine a contravariant functor $s:{\mathbf{C}}_{\mathbf{R}-\mathbf{IFM}}\to {\mathbf{C}}_{\mathbf{Lat}}$. Thus, we are trying to prove that

(i) 

for all $f\in {\mathbf{Hom}}_{{\mathbf{C}}_{\mathbf{R}-\mathbf{M}}}(M,N)$, $s\left(f\right)$ preserve infima,

(ii) 

for each $f,g\in {\mathbf{Hom}}_{{\mathbf{C}}_{\mathbf{R}-\mathbf{M}}}(M,N)$, $s(g\circ f)=s\left(f\right)\circ s\left(g\right)$ and

(iii) 

for each identity R-homomorphism $i_M:M\to M$, we have the identity function $s\left(i_M\right):s\left(M\right)\to s\left(M\right)$.

Consider $\{({\mu }_{B_i},{\nu }_{B_i}):i\in J\}\subset s\left(N\right)$ is a non-empty subfamily of $s\left(N\right)$, and let $a\in M$. Then,

$$\begin{array}{ccc}\hfill s\left(f\right)[\wedge ({\mu }_{B_i},{\nu }_{B_i})]\left(a\right)& =& (Inf\left\{{\mu }_{f^{-1}\left(B_i\right)}\right\},Sup\left\{{\nu }_{f^{-1}\left(B_i\right)}\right\})\left(a\right)\hfill \\ & =& (Inf\left\{{\mu }_{f^{-1}\left(B_i\right)}\left(a\right)\right\},Sup\left\{{\nu }_{f^{-1}\left(B_i\right)}\left(a\right)\right\})\hfill \\ & =& (Inf\left\{{\mu }_{B_i}\left(f\left(a\right)\right)\right\},Sup\left\{{\nu }_{B_i}\left(f\left(a\right)\right)\right\})\hfill \\ & =& (Inf\left\{{\mu }_{B_i}\right\},Sup\left\{{\nu }_{B_i}\right\})\left(f\left(a\right)\right)\hfill \\ & =& \wedge ({\mu }_{B_i},{\nu }_{B_i})\left(f\left(a\right)\right)\hfill \\ & =& \wedge ({\mu }_{B_i}\left(f\left(a\right)\right),{\nu }_{B_i}\left(f\left(a\right)\right))\hfill \\ & =& \wedge ({\mu }_{f^{-1}\left(B_i\right)}\left(a\right),{\nu }_{f^{-1}\left(B_i\right)}\left(a\right))\hfill \\ & =& \wedge ({\mu }_{f^{-1}\left(B_i\right)},{\nu }_{f^{-1}\left(B_i\right)})\left(a\right)\hfill \\ & =& \wedge \left[s\left(f\right)({\mu }_{B_i},{\nu }_{B_i})\right]\left(a\right).\hfill \end{array}$$

Thus, $s\left(f\right)$ preserves infima.

Let $f:M\to N,g:N\to T$ is homomorphism, and let $({\mu }_C,{\nu }_C)\in s\left(T\right)$ and $a\in M$, then

$$\begin{array}{ccc}\hfill s\left(gof\right)({\mu }_C,{\nu }_C)\left(a\right)& =& ({\mu }_{{\left(gof\right)}^{-1}\left(C\right)},{\nu }_{{\left(gof\right)}^{-1}\left(C\right)})\left(a\right)\hfill \\ & =& ({\mu }_{\left(f^{-1}o{g}^{-1}\right)\left(C\right)}\left(a\right),{\nu }_{\left(f^{-1}o{g}^{-1}\right)\left(C\right)}\left(a\right))\hfill \\ & =& ({\mu }_{\left(f^{-1}\left(g^{-1}\left(C\right)\right)\right)}\left(a\right),{\nu }_{\left(f^{-1}\left(g^{-1}\left(C\right)\right)\right)}\left(a\right))\hfill \\ & =& s\left(f\right)({\mu }_{g^{-1}\left(C\right)}\left(a\right),{\nu }_{g^{-1}\left(C\right)}\left(a\right))\hfill \\ & =& s\left(f\right)\left(s\left(g\right)({\mu }_C\left(a\right),{\nu }_C\left(a\right))\right)\hfill \\ & =& s\left(f\right)s\left(g\right)({\mu }_C,{\nu }_C)\left(a\right).\hfill \end{array}$$

Thus, $s\left(gof\right)=s\left(f\right)s\left(g\right)$.

Further, $i_M:M\to M$ is the identity R-homomorphism, such that $i_M\left(a\right)=a,\forall a\in M$. Then $s\left(i_M\right)$ be the identity element in $\mathbf{H}\mathbf{o}\mathbf{m}\left({\mathbf{C}}_{\mathbf{R}-\mathbf{IFM}}\right)$, for if $({\mu }_A,{\nu }_A)\in s\left(M\right)$ be any element, then $s\left(i_M\right)({\mu }_A,{\nu }_A)\left(a\right)=({\mu }_{i_M^{-1}\left(A\right)}\left(a\right),{\nu }_{i_M^{-1}\left(A\right)}\left(a\right))=({\mu }_{i_M\left(A\right)}\left(a\right),{\nu }_{i_M\left(A\right)}\left(a\right))=({\mu }_A\left(a\right),{\nu }_A\left(a\right))=({\mu }_A,{\nu }_A)\left(a\right)$. Hence proved. □

Remark 4. 

There exists a covariant functor $t:{\mathit{C}}_{\mathit{R}-\mathit{IFM}}\to {\mathit{C}}_{\mathit{Lat}}$ so $t\left(f\right):t\left(M\right)\to t\left(N\right)$ preserves suprema and is determined by $t\left(f\right)({\mu }_A,{\nu }_A)=({\mu }_{f\left(A\right)},{\nu }_{f\left(A\right)}),\forall ({\mu }_A,{\nu }_A)\in t\left(M\right)$ so that $t(g\circ f)=t\left(g\right)\circ t\left(f\right),\forall f:M\to N,g:N\to T$.

Proof. 

It is very simple to find that $t\left(f\right)$ preserves suprema and $t\left(i_M\right)$ is the identity element in $\mathbf{Hom}\left({\mathbf{C}}_{\mathbf{R}-\mathbf{IFM}}\right)$. Furthermore, we have

$$\begin{array}{ccc}\hfill t\left(gof\right)({\mu }_A,{\nu }_A)\left(a\right)& =& ({\mu }_{\left(gof\right)\left(A\right)}\left(a\right),{\nu }_{\left(gof\right)\left(A\right)}\left(a\right))\hfill \\ & =& ({\mu }_{g\left(f\right(A\left)\right)}\left(a\right),{\nu }_{g\left(f\right(A\left)\right)}\left(a\right))\hfill \\ & =& t\left(g\right)({\mu }_{f\left(A\right)}\left(a\right),{\mu }_{f\left(A\right)}\left(a\right))\hfill \\ & =& t\left(g\right)\left(t\left(f\right)({\mu }_A\left(a\right),{\nu }_A\left(a\right))\right)\hfill \\ & =& t\left(g\right)t\left(f\right)({\mu }_A\left(a\right),{\nu }_A\left(a\right))\hfill \\ & =& t\left(g\right)t\left(f\right)({\mu }_A,{\nu }_A)\left(a\right)\hfill \end{array}$$

Thus $t\left(gof\right)=t\left(g\right)t\left(f\right)$. Hence, the result is proved. □

Lemma 4. 

(i) Let $\{M_i:i\in J\}$, N are R-modules and $\mathfrak{A}=\{f_i:M_i\to N:i\in J\}$ be a collection of R-homomorphisms. If $\{A_i:i\in J\}$ is a collection of IFSMs of $M_i$, then there exists a smallest IFSM $B=({\mu }_B,{\nu }_B)$ of N so that ${\overline{f}}_i:A_i\to B$ is an IF R-hom, $\forall i\in J$, where $({\mu }_B,{\nu }_B)={(\mu ,\nu )}^{\mathfrak{A}}=({\mu }^{\mathfrak{A}},{\nu }^{\mathfrak{A}})$, here ${\mu }_B={\mu }^{\mathfrak{A}}=\vee \{{\mu }_{f_i\left(A_i\right)}:i\in J\}$ and ${\nu }_B={\nu }^{\mathfrak{A}}=\wedge \{{\nu }_{f_i\left(A_i\right)}:i\in J\}$.

(ii) Let M and $\{N_i:i\in J\}$ are R-modules and $\mathfrak{B}=\{g_i:M\to N_i:i\in J\}$ be a collection of R-homomorphisms. If $\{B_i:i\in J\}$ are IFSMs of $N_i$, then there exists a largest IFSM $A=({\mu }_A,{\nu }_A)$ of M so that ${\overline{g}}_i:A\to B_i$ is an IF R-hom, $\forall i\in J$, where $({\mu }_A,{\nu }_A)={(\mu ,\nu )}_{\mathfrak{B}}=({\mu }_{\mathfrak{B}},{\nu }_{\mathfrak{B}})$, here ${\mu }_A={\mu }_{\mathfrak{B}}=\wedge \{{\mu }_{g_i^{-1}\left(B_i\right)}:i\in J\}$ and ${\nu }_A={\nu }_{\mathfrak{B}}=\vee \{{\nu }_{g_i^{-1}\left(B_i\right)}:i\in J\}$.

Proof. 

(i) Using Lemma 1(i), for each $i\in J$, $A_i$ is IFSM of $M_i$, there exists IFSM $f_i\left(A_i\right)$ on N so that for every IFSM $B=({\mu }_B,{\nu }_B)$ of N, ${\overline{f}}_i:A_i\to B$ is an IF R-hom if and only if $f_i\left(A_i\right)\subseteq B$, i.e., ${\mu }_B\ge {\mu }_{f_i\left(A_i\right)}$ and ${\nu }_B\le {\nu }_{f_i\left(A_i\right)}$.

Let ${\mu }^{\mathfrak{A}}=\vee \{{\mu }_{f_i\left(A_i\right)}:i\in J\}$ and ${\nu }^{\mathfrak{A}}=\wedge \{{\nu }_{f_i\left(A_i\right)}:i\in J\}$. Subsequently, the consequence follows.

(ii) Using Lemma 1(ii), for each $i\in J$, $B_i$ is IFSM of N, then there exists an IFSM $g_i^{-1}\left(B_i\right)$ of M, such that for any IFSM $A=({\mu }_A,{\nu }_A)$ of M, $\overline{g_i}:A\to B_i$ is an IF R-hom if and only if $A\subseteq g_i^{-1}\left(B_i\right)$, i.e., ${\mu }_A\le {\mu }_{g_i^{-1}\left(B_i\right)}$ and ${\nu }_A\ge {\nu }_{g_i^{-1}\left(B_i\right)}$.

Let ${\mu }_{\mathfrak{B}}=\wedge \{({\mu }_{g_i^{-1}\left(B_i\right)}:i\in J\}$ and ${\nu }_{\mathfrak{B}}=\vee \{({\nu }_{g_i^{-1}\left(B_i\right)}:i\in J\}$. Subsequently, the consequence follows. □

Lemma 5. 

(i) Let $\{A_i:i\in J\}$ are IFSMs of $M_i,i\in J$ and $\mathfrak{A}=\{f_i:M_i\to N:i\in J\}$ be a family of R-homomorphisms and R-homomorphism $g:N\to T$ then

$${(\mu ,\nu )}^{{\mathfrak{A}}_{\mathfrak{1}}}=t\left(g\right){(\mu ,\nu )}^{\mathfrak{A}}\mathit{where}{\mathfrak{A}}_{\mathfrak{1}}=\{go{f}_i:M_i\to T:i\in J\}.$$

(ii) Let $\{B_i:i\in J\}$ are IFSMs of $N_i,\forall i\in J$ and $\mathfrak{B}=\{g_i:M\to N_i:i\in J\}$ be a family of R-homomorphisms and $h:L\to M$ a homomorphism then

$${(\mu ,\nu )}_{{\mathfrak{B}}_{\mathfrak{1}}}=s\left(h\right){(\mu ,\nu )}_{\mathfrak{B}}\mathit{where}{\mathfrak{B}}_{\mathfrak{1}}=\{g_{i}oh:L\to N_i:i\in J\}.$$

Proof. 

(i)

Let ${\mathfrak{A}}_{\mathfrak{1}}=\{g_i=go{f}_i:N_i\to T:i\in J\}$ be the collection of R-homomorphisms. Then, by Lemma 4(i), there exists IFSM $C=({\mu }_C,{\nu }_C)$ of T such that $g_i:A_i\to C$ is IF R-hom, $\forall i\in J$, where $({\mu }_C,{\nu }_C)={(\mu ,\nu )}^{{\mathfrak{A}}_{\mathfrak{1}}}=({\mu }^{{\mathfrak{A}}_{\mathfrak{1}}},{\nu }^{{\mathfrak{A}}_{\mathfrak{1}}})$, here ${\mu }^{{\mathfrak{A}}_{\mathfrak{1}}}=\vee \{{\mu }_{g_i\left(A_i\right)}:i\in J\}$ and ${\nu }^{{\mathfrak{A}}_{\mathfrak{1}}}=\wedge \{{\nu }_{g_i\left(A_i\right)}:i\in J\}$. Consider

$$\begin{array}{ccc}\hfill {(\mu ,\nu )}^{{\mathfrak{A}}_{\mathfrak{1}}}& =& \vee \{({\mu }_{g_i\left(A_i\right)},{\nu }_{g_i\left(A_i\right)}):i\in J\}\hfill \\ & =& \vee \{({\mu }_{\left(go{f}_i\right)\left(A_i\right)},{\nu }_{\left(go{f}_i\right)\left(A_i\right)}):i\in J\}\hfill \\ & =& \vee \{({\mu }_{\left(g\left(f_i\left(A_i\right)\right)\right)},{\nu }_{\left(g\left(f_i\left(A_i\right)\right)\right)}):i\in J\}\hfill \\ & =& \vee \{t\left(g\right)({\mu }_{f_i\left(A_i\right)},{\nu }_{f_i\left(A_i\right)}):i\in J\}\hfill \\ & =& t\left(g\right)\vee \{({\mu }_{f_i\left(A_i\right)},{\nu }_{f_i\left(A_i\right)}):i\in J\}\hfill \\ & =& t\left(g\right){(\mu ,\nu )}^{\mathfrak{A}}.\hfill \end{array}$$

(ii)

Let ${\mathfrak{B}}_{\mathfrak{1}}=\{h_i=g_{i}oh:L\to N_i:i\in J\}$ be the collection of R-homomorphisms. Then by Lemma 4 (ii), there exists IFSM $A=({\mu }_A,{\nu }_A)$ of L such that $h_i:A\to C_i$ is IF R-hom, $\forall i\in J$, where $({\mu }_A,{\nu }_A)={(\mu ,\nu )}_{{\mathfrak{B}}_{\mathfrak{1}}}=({\mu }_{{\mathfrak{B}}_{\mathfrak{1}}},{\nu }_{{\mathfrak{B}}_{\mathfrak{1}}})$, here ${\mu }_{{\mathfrak{B}}_{\mathfrak{1}}}=\wedge \{{\mu }_{h_i^{-1}\left(C_i\right)}:i\in J\}$ and ${\nu }_{{\mathfrak{B}}_{\mathfrak{1}}}=\vee \{{\nu }_{h_i^{-1}\left(C_i\right)}:i\in J\}$. Now, we have

$$\begin{array}{ccc}\hfill {(\mu ,\nu )}_{{\mathfrak{B}}_{\mathfrak{1}}}& =& \wedge \{({\mu }_{h_i^{-1}\left(C_i\right)},{\nu }_{h_i^{-1}\left(C_i\right)}):i\in J\}\hfill \\ & =& \wedge \{({\mu }_{{\left(g_{i}oh\right)}^{-1}\left(C_i\right)},{\nu }_{{\left(g_{i}oh\right)}^{-1}\left(C_i\right)}):i\in J\}\hfill \\ & =& \wedge \{({\mu }_{\left(h^{-1}o{g}_i^{-1}\right)\left(C_i\right)},{\nu }_{\left(h^{-1}o{g}_i^{-1}\right)\left(C_i\right)}):i\in J\}\hfill \\ & =& \wedge \{({\mu }_{h^{-1}\left(g_i^{-1}\left(C_i\right)\right)},{\nu }_{h^{-1}\left(g_i^{-1}\left(C_i\right)\right)}):i\in J\}\hfill \\ & =& \wedge \{s\left(h\right)({\mu }_{g_i^{-1}\left(C_i\right)},{\nu }_{g_i^{-1}\left(C_i\right)}):i\in J\}\hfill \\ & =& s\left(h\right)\wedge \{({\mu }_{g_i^{-1}\left(C_i\right)},{\nu }_{g_i^{-1}\left(C_i\right)}):i\in J\}\hfill \\ & =& s\left(h\right){(\mu ,\nu )}_{\mathfrak{B}}.\hfill \end{array}$$

Thus, ${(\mu ,\nu )}_{{\mathfrak{B}}_{\mathfrak{1}}}=s\left(h\right){(\mu ,\nu )}_{\mathfrak{B}}$. □

Remark 5. 

From Lemma 4 and Lemma 5, we are able to optimally intuitionistically fuzzify $f_i$ [$g_i$], in respect to the family of IFSMs $\{A_i:i\in J\}$ [$\{B_i:i\in J\}$].

Theorem 3. 

The category of IF modules ${\mathit{C}}_{\mathit{R}-\mathit{IFM}}$ has kernels and cokernels.

Proof. 

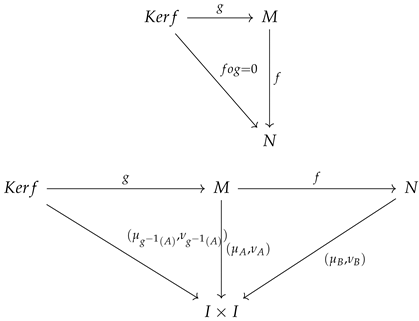
Let $A=({\mu }_A,{\nu }_A)$ and $B=({\mu }_B,{\nu }_B)$ be IFSM of R-modules M and N, respectively. Let $\overline{f}:A\to B$ be an IF R-hom corresponding to the R-homomorphism $f:M\to N$.

For Ker f, there exists an inclusion map $g:kerf\to M$ in order for the subsequent diagram commutes

For Ker $\overline{f}$, there exists an inclusion map $\overline{g}:g^{-1}\left(A\right)\to A$ such that the following diagram commutes

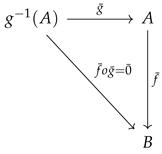Therefore, the kernel of $\overline{f}$ is defined as $g^{-1}\left(A\right)$ with the inclusion map $\overline{g}:g^{-1}\left(A\right)\to A$.

Thus, the kernel of $\overline{f}$ is given as $((kerf,g^{-1}\left(A\right)),\overline{g})$, where the inclusion map is $g:kerf\to M$.

Similarly, the cokernel of $\overline{f}$ is defined as $((N/Imf,\pi \left(B\right)),\overline{\pi })$, where the projection map $\pi :N\to N/Imf$ and $\overline{\pi }:B\to B_{N/Imf}$. □

Remark 6. 

Although the category of IF modules ${\mathit{C}}_{\mathit{R}-\mathit{IFM}}$ has kernels and cokernels even then it is not an abelian category.

By definition of the abelian category, every monomorphism should be normal, i.e, every monomorphism is a kernel of some morphism. An IF R-hom $\overline{h}:C\to A$ of IFSM C of M on being normal (i.e., being a kernel) C should be identical to $g^{-1}\left(A\right)$. Consequently, for $M\ne \left\{\theta \right\}$, the IF R-hom $\overline{1}:{\chi }_{\left\{\theta \right\}}\to {\chi }_M$ is a sub-object of ${\chi }_M$, which is not a kernel. Thus, ${\mathit{C}}_{\mathit{R}-\mathit{IFM}}$ is not an abelian category.

4. Discussion

In this paper, we studied the category of intuitionistic fuzzy modules ${\mathbf{C}}_{\mathbf{R}-\mathbf{IFM}}$ over the category of fuzzy modules ${\mathbf{C}}_{\mathbf{R}-\mathbf{M}}$ by constructing a contravariant functor from the category ${\mathbf{C}}_{\mathbf{R}-\mathbf{IFM}}$ to the category ${\mathbf{C}}_{\mathbf{Lat}}$ (=union of all ${\mathbf{C}}_{\mathbf{Lat}(\mathbf{R}-\mathbf{IFM})}$, corresponding to each object in ${\mathbf{C}}_{\mathbf{R}-\mathbf{M}}$). We showed that ${\mathbf{C}}_{\mathbf{R}-\mathbf{M}}$ is a subcategory of ${\mathbf{C}}_{\mathbf{R}-\mathbf{IFM}}$. Further, we showed that ${\mathbf{C}}_{\mathbf{R}-\mathbf{IFM}}$ is a top category that is not an abelian category.